Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Mar 20;121(13):2572–2579. doi: 10.1021/acs.jpca.7b00197

Excited-State Decay Paths in Tetraphenylethene Derivatives

Yuan-Jun Gao †, Xue-Ping Chang †, Xiang-Yang Liu †, Quan-Song Li §, Ganglong Cui †,*, Walter Thiel ‡,*
PMCID: PMC5385518  PMID: 28318255

Abstract

graphic file with name jp-2017-001973_0004.jpg

The photophysical properties of tetraphenylethene (TPE) compounds may differ widely depending on the substitution pattern, for example, with regard to the fluorescence quantum yield ϕf and the propensity to exhibit aggregation-induced emission (AIE). We report combined electronic structure calculations and nonadiabatic dynamics simulations to study the excited-state decay mechanisms of two TPE derivatives with four methyl substituents, either in the meta position (TPE-4mM, ϕf = 0.1%) or in the ortho position (TPE-4oM, ϕf = 64.3%). In both cases, two excited-state decay pathways may be relevant, namely, photoisomerization around the central ethylenic double bond and photocyclization involving two adjacent phenyl rings. In TPE-4mM, the barrierless S1 cyclization is favored; it is responsible for the ultralow fluorescence quantum yield observed experimentally. In TPE-4oM, both the S1 photocyclization and photoisomerization paths are blocked by non-negligible barriers, and fluorescence is thus feasible. Nonadiabatic dynamics simulations with more than 1000 surface hopping trajectories show ultrafast cyclization upon photoexcitation of TPE-4mM, whereas TPE-4oM remains unreactive during the 1 ps simulations. We discuss the chances for spectroscopic detection of the postulated cyclic photoproduct of TPE-4mM and the relevance of our findings for the AIE process.

Introduction

Aggregation-induced emission (AIE) is an important photophysical phenomenon associated with chromophore aggregation, first discovered in 2001 for 1-methyl-1,2,3,4,5-pentaphenylsilole.1 In this process, nonemitting luminogens are induced to emit by aggregate formation. These so-called AIEgens have found numerous technological applications, for example, in optoelectronic materials, organic light-emitting diodes, photodynamic therapy, chemical sensors, and biomedical probes, and many groups have engaged in the design and study of novel types of AIEgens.2−4

Understanding the mechanism underlying the AIE phenomena is essential to guide the development of novel AIEgens with improved performance and enhanced applicability. In experimental work, several photophysical mechanisms have been proposed to rationalize the AIE processes observed in different AIEgens, including E/Z photoisomerization, restriction of intramolecular rotation (RIR), restriction of intramolecular vibration (RIV), and, more generally, restriction of intramolecular motion (RIM).3−5

Tetraphenylethene (TPE) and its derivatives are prototypical AIEgens.6−12 TPE has a central ethylenic double bond and may thus be expected to undergo fast excited-state decay via E/Z photoisomerization, in analogy to other alkenes. However, it is not entirely clear whether and precisely how this photoisomerization is related to AIE. The origin of the AIE effect in TPE compounds has been studied by several groups through comparative experiments on a number of specifically designed TPE derivatives.4,13−17 This has led to the notion that isolated TPE molecules in solution dissipate the absorbed photon energy very quickly through rotations of their phenyl rings (friction with the surrounding solvent), leading to radiationless relaxation to the ground state; upon aggregate formation, these rotations become restricted, the nonradiative energy transfer is suppressed, and emission of light is induced (AIE through RIR).4 This commonly accepted view is appealing and well supported experimentally, but it does not offer a detailed atomistic model of the actual internal conversion process.

A recent theoretical study has explored the excited-state dynamics of isolated TPE through trajectory surface hopping (TSH) simulations using linear response time-dependent density functional theory (TD-DFT) within the Tamm–Dancoff approximation (TDA) at the PBE0/def2-SVP level.18 During the 1.5 ps simulation, only 3 out of 60 computed trajectories decayed to the ground state via the ethylenic twist pathway (E/Z photoisomerization), while 45 relaxed via photocyclization to ground-state 9,10-diphenyl-4a,4b-dihydrophenanthrene and 12 remained in the excited state.18

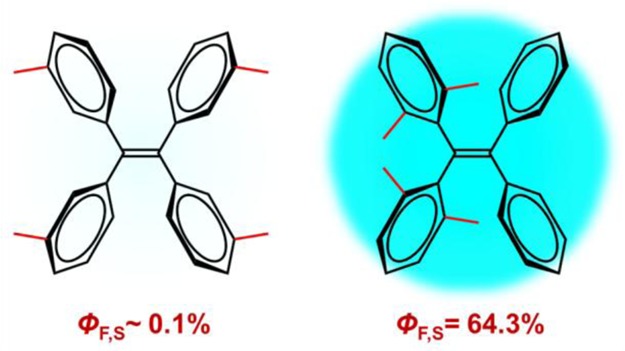
Here we focus on two particular TPE compounds, namely, the tetramethyl derivatives TPE-4mM and TPE-4oM (see Figure 1). TPE-4mM is a typical AIEgen because it has a very low fluorescence quantum yield of 0.1% in THF solution19 and becomes emissive upon aggregation.4 By contrast, TPE-4oM already fluoresces strongly in THF solution, with a quantum yield of 64% (i.e., an enhancement by a factor of more than 600 compared with TPE-4mM), so that any further increase by aggregation can only be moderate.14 In the RIR model, this is explained by steric hindrance; the ortho-methyl groups in TPE-4oM effectively suppress the rotation of the phenyl rings and hence also the proposed radiationless decay pathway, so that TPE-4oM is able to fluoresce.14 It is noteworthy that E/Z isomerization was not detected in TPE-4oM14 and was experimentally found to play only a minor role in TPE adducts.15

Figure 1.

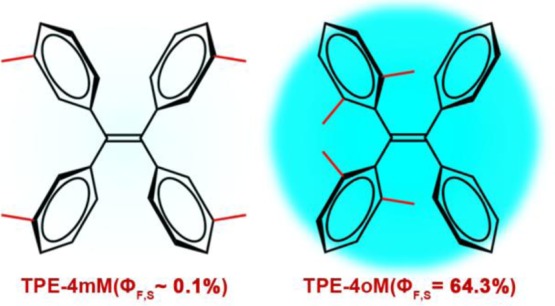
Figure 1

Open in a new tab

Two TPE compounds, that is, tetra(meta-methyl)-tetraphenylethylene (referred to as TPE-4mM) and tetra(ortho-methyl)-tetraphenylethylene (TPE-4oM), studied in this work. Also shown are their fluorescence quantum yields measured in THF solution.

Motivated by these intriguing experimental findings and the need for a detailed mechanistic understanding of the underlying photoinduced processes, we have combined static electronic structure calculations (TD-DFT, CASSCF, and MS-CASPT2) and OM2/MRCI nonadiabatic dynamics simulations to explore the relevant potential energy surfaces of TPE-4mM and TPE-4oM and to study the dynamics of the radiationless internal conversion processes. In particular, we examined the decay paths available to the initially populated excited state and the physical origin of the huge fluorescence enhancement in TPE-4oM relative to TPE-4mM. All present calculations were performed for isolated gas-phase molecules to identify the intrinsic mechanisms, which is a necessary first step toward understanding their behavior in more complex environments.4

Computational Details

Ab Initio Calculations

Ground-state (S0) conformers were first optimized using density functional theory (DFT) at the B3LYP and ωB97XD levels.20−25 The state-averaged complete active space self-consistent field (CASSCF) method (equal state weights, two roots) was employed to optimize minima in the S0 and S1 states. In all CASSCF geometry optimizations of minima and conical intersections, the active space comprised 10 electrons in 8 orbitals, which always included the π, π* orbitals of the central C=C double bond and phenyl substituents.

More accurate potential energy profiles were obtained from complete active space second-order perturbation calculations (CASPT2).26,27 These single-point CASPT2 energy evaluations were carried out by state-averaging over five roots with equal weights, using an ionization potential-electron affinity (IPEA) parameter of 0.2528 and an imaginary level shift of 0.2 au to avoid intruder-state issues.29 The Cholesky decomposition technique with unbiased auxiliary basis sets was used to accurately approximate the two-electron integrals.30

Vertical excitation energies were computed using the CASPT2 method and TD-DFT at the TD-B3LYP, TD-CAM-B3LYP, and TD-ωB97XD31,32 levels. The 6-31G* basis set33,34 was used for all CASPT2 and CASSCF minimum-structure optimizations, while the 3-21G basis set35,36 was employed for all CASSCF conical intersection optimizations. The following codes were applied: GAUSSIAN0937 for all DFT and TD-DFT calculations; MOLCAS8.038 for all SA-CASSCF optimizations (S0 and S1 minima, S1S0 conical intersections) and for all CASPT2 computations (at OM2/MRCI and CASSCF optimized structures)

Semiempirical Calculations

All semiempirical calculations were performed using the OM2/MRCI method (orthogonalization model 2, multireference configuration interaction) as implemented in the MNDO99 code.39−43 During geometry optimizations and dynamics simulations, all required energies, gradients, and nonadiabatic coupling elements were computed analytically. Minimum-energy conical intersections were optimized using the Lagrange–Newton approach.44,45

In the OM2/MRCI calculations, the restricted open-shell Hartree–Fock formalism was applied in the self-consistent field (SCF) treatment (i.e., the orbitals were optimized for the leading configuration of the S1 state with two singly occupied orbitals). The active space in the OM2/MRCI calculations included 12 electrons in 12 orbitals. In terms of the SCF configuration, it comprised the five highest doubly occupied orbitals, the two singly occupied orbitals, and the five lowest unoccupied orbitals. For the MRCI treatment, three configuration state functions were chosen as references, namely, the SCF configuration and the two closed-shell configurations derived therefrom (i.e., all singlet configurations that can be generated from the HOMO and the LUMO of the closed-shell ground state). The MRCI wave function was built by allowing all single and double excitations from these three references.

Nonadiabatic Dynamics Simulations

The nonadiabatic dynamics were studied by performing 1 ps OM2/MRCI TSH simulations. The initial structures and velocities were obtained by Wigner sampling.46 The number of trajectories starting from a given initial structure was chosen on the basis of the computed S0–S1 transition probabilities. A total of 600 surface-hopping trajectories were run for TPE-4mM and TPE-4oM, respectively, with all relevant energies, gradients, and nonadiabatic coupling vectors being computed on-the-fly as needed. For points with an S1–S0 energy gap of less than 10 kcal/mol, the fewest-switches criterion was applied to decide whether to hop. The time step was chosen to be 0.1 fs for nuclear motion and 0.0005 fs for electronic propagation. The unitary propagator evaluated at a midpoint was used to propagate the electronic motion. The translational and rotational motions were removed in each step. The empirical decoherence correction (0.1 au) proposed by Granucci et al.47 was employed. The final evaluations were done for the 558 and 568 trajectories of TPE-4mM and TPE-4oM that finished successfully and satisfied our energy continuity criterion (no changes greater than 30 kcal/mol between any two consecutive MD steps). Further technical details are given in our previous publications.48−57

Results

Vertical Excitation Energies

We first consider vertical transitions in TPE-4oM and TPE-4mM to identify the electronic state that is populated upon irradiation. Table S1 collects the computed S0 → S1 vertical excitation energies at the S0 minima of TPE-4mM and TPE-4oM obtained from different electronic structure methods. All of them predict that the S1 state is spectroscopically bright and has a large oscillator strength, for example, 0.74 for TPE-4mM and 0.46 for TPE-4oM at CASPT2, so that it can easily be populated. The CASPT2, TD-ωB97XD, and OM2/MRCI methods give very similar S0 → S1 vertical excitation energies: 101.7, 98.9, and 101.6 kcal/mol (4.41, 4.29, and 4.41 eV) for TPE-4oM and 96.9, 99.2, and 101.1 kcal/mol (4.20, 4.30, and 4.38 eV) for TPE-4mM, respectively. This good agreement is a prerequisite for using OM2/MRCI in excited-state dynamics simulations of TPE-4mM and TPE-4oM. In all three methods, the S1 state is dominated by a single HOMO–LUMO excitation; as expected, the HOMO and LUMO are of bonding and antibonding character around the central C=C double bond, respectively, with appreciable delocalization into the phenyl rings (see Table S1)

S1/S0 Conical Intersections

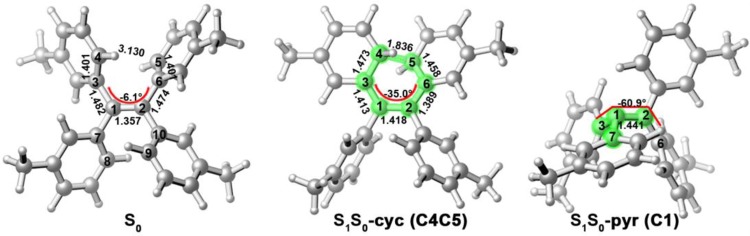
At the OM2/MRCI and CASSCF levels, we find two pairs of minimum-energy S1/S0 conical intersection structures for both TPE-4mM and TPE-4oM, respectively. The two methods give similar optimized structures and energies (see Figure S3 and Table S2). The first pair of S1/S0 conical intersections mediates the photoisomerization around the central C1=C2 double bond; they are labeled as S1S0-pyr (C1) and S1S0-pyr (C2); see Figures 2 and S2. In these structures, the central double bond is twisted significantly, and the local environment around either C1 or C2 is strongly pyramidized due to sudden polarization effects.58 Similar S1/S0 conical intersections have previously been found in the stilbene, diphenyldibenzofulvene, and TPE AIEgens.59−62

Figure 2.

Figure 2

Open in a new tab

S0 minimum (left), minimum-energy S1/S0 conical intersections for cyclization (middle), and photoisomerization (right) of TPE-4mM. Also shown are some key bond lengths (in Å) and the C3C1C2C6 dihedral angle (in degree). See the Supporting Information for related conical intersections of TPE-4mM and for the corresponding structures of TPE-4oM.

The second pair of S1/S0 conical intersections mediates excited-state cyclization processes, with formation of either a new C4–C5 or C8–C9 bond. These two conical intersection structures are labeled as S1S0-cyc (C4C5) and S1S0-cyc (C8C9),; see Figures 2 and S2. In the case of S1S0-cyc (C4C5) (see Figure 2), the C4–C5 distance of the forming bond is already significantly shorter compared with the S0 minimum, and in addition, there is a notable decrease (increase) in the C1–C3 and C2–C6 (C3–C4 and C5–C6) bond lengths, as expected for an electrocyclic ring closure to a cyclic diene species.

Energetically, the four conical intersections are close to one another in both TPE-4mM and TPE-4oM (see Table S2). For example, at the OM2/MRCI level, the relative energies for S1S0-cyc (C4C5) and S1S0-pyr (C1) are computed to be 79.4 and 80.7 kcal/mol for TPE-4mM, and they are 88.0 and 88.6 kcal/mol for TPE-4oM, respectively, with similar values for S1S0-cyc (C4C5) and S1S0-pyr (C1). These conical intersections are energetically accessible, in principle, because the vertical S0 → S1 excitation energies of TPE-4oM and TPE-4mM at the Franck–Condon point are considerably higher (ca. 101 kcal/mol at the OM2/MRCI level; see Table S1). Does this mean that they play equally important roles in the S1 excited-state decay dynamics?

LIIC Paths

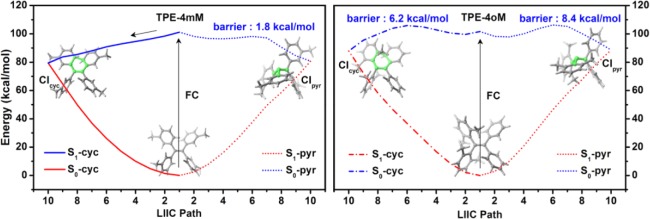
To answer the question, we first examine the pathways to these S1/S0 conical intersections. Thus, we present linearly interpolated internal coordinate (LIIC) paths connecting the Franck–Condon points and the two pairs of S1/S0 conical intersections. Figure 3 shows the OM2/MRCI-computed LIIC paths for TPE-4mM and TPE-4oM (see Figure S6 for corresponding paths from single-point CASPT2 calculations). In the case of TPE-4mM, the S1 path toward S1S0-cyc (C4C5) is barrierless at both the OM2/MRCI and CASPT2 levels so that cyclization should be facile; by contrast, the S1 path toward S1S0-pyr (C1) encounters small barriers of 1.8 (OM2/MRCI) and 8.4 (CASPT2) kcal/mol. Qualitatively similar energy profiles are obtained for the S1 paths of TPE- 4 mM toward S1S0-cyc (C4C5) and S1S0-pyr (C1) (see Figures 3 and S6). These findings are in line with the known experimental facts for TPE-4mM. First, the observed ultralow fluorescence quantum yield of ∼0.1%19 is caused by the access to the barrierless S1 cyclization path, which quickly dissipates excess photon energy so that fluorescence emission is very weak. Second, the experimental evidence that photoisomerization plays no role or only a minor role in photoexcited TPE compounds14,15 is consistent with the presence of a barrier on the computed S1 photoisomerization decay path.

Figure 3.

Figure 3

Open in a new tab

OM2/MRCI-computed LIIC paths connecting the Franck–Condon points and the S1/S0 conical intersections related to the cyclization and photoisomerization of TPE-4mM (left) and TPE-4oM (right). See the Supporting Information for the corresponding CASPT2 energy profiles.

In the case of TPE-4oM, the energy profiles for the S1 cyclization and photoisomerization decay paths have non-negligible barriers, about 3–8 kcal/mol at the OM2/MRCI level (Figures 3 and S6) and even higher at the CASPT2 level (Figure S6). Therefore, these S1 nonradiative decay channels are much less accessible in TPE-4oM compared with those in TPE-4mM, which rationalizes the experimental observation of a much higher fluorescence quantum yield (64.3%) of TPE-4oM in THF solution.14

Excited-State Dynamics

To gain more direct insight into the excited-state dynamics, we carried out 1200 trajectory-based surface-hopping (TSH) dynamics runs at the OM2/MRCI level (1 ps each), for both TPE-4mM and TPE-4oM.

For TPE-4mM, 492 of 558 successful trajectories hop to the S0 state within the 1 ps simulation time. All of these hops take place near the two S1S0-cyc (C4C5) and S1S0-cyc (C8C9) conical intersections, in almost equal number (249 vs 243, Table 1). It should be emphasized that we do not see any excited-state hops within the 1 ps simulation time via the other two conical intersection regions, that is, S1S0-pyr (C1) and S1S0-pyr (C2). This dynamical behavior is fully consistent with the results from the static electronic structure calculations: the S1 cyclization decay path is barrierless, while the S1 photoisomerization has a barrier of 1.8 kcal/mol at the OM2/MRCI level. The simulations are also consistent with the experimental observation that almost no E/Z isomerization can be detected for other TPE variants.13,17

Table 1. Numbers of Started and Successful Trajectories in the OM2/MRCI Dynamics Simulations and the Number of Hops Overall and via Individual Conical Intersections.

  TPE-4 mM TPE-4oM
started trajectories 600 600
successful trajectories 558 568
hops 492 0
S1S0-cyc (C4C5) 249 0
S1S0-cyc (C8C9) 243 0
S1S0-pyr (C1) 0 0
S1S0-pyr (C2) 0 0
Open in a new tab

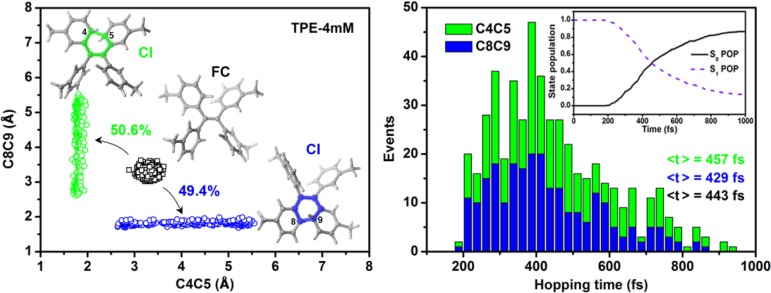
The left panel of Figure 4 shows the distribution of two key geometrical parameters, that is, the C4–C5 and C8–C9 distances, at all S1 → S0 hopping points of TPE-4mM. It was found that 50.6% of the hops to the S0 state occur in the neighborhood of the S1S0-cyc (C4C5) conical intersection, and the remaining 49.4% occur in the vicinity of the S1S0-cyc (C8C9) intersection. The S1 → S0 hopping-time distribution of TPE-4mM is shown in the right panel of Figure 4. During the first 200 fs, there are no S1 → S0 hops. This time period corresponds to the initial S1 relaxation from the Franck–Condon region via the S1 minima to the S1S0-cyc conical intersections. After 200 fs, the trajectories start to hop to the S0 state when they get close to the S1/S0-cyc conical intersections. We see an extended hopping-time distribution, which implies that some trajectories do not hop to the S0 state during their first approach to the S1/S0-cyc conical intersections, but only at a later encounter.

Figure 4.

Figure 4

Open in a new tab

(Left) Distribution of the C4–C5 and C8–C9 distances at all S1 → S0 hopping points of TPE-4mM. (Right) Distribution of the S1 → S0 hopping times via the two S1/S0 conical intersection regions related to the cyclization (blue and green bars). Average hopping times ⟨t⟩ are given for the two channels (blue and green) and for all hopping events (black). Also shown in the right panel are the time-dependent state populations of the S1 (dashed line) and S0 (solid line) electronic states. See the text for discussion.

The inset in the right panel of Figure 4 depicts the time-dependent populations of the S0 and S1 states of TPE-4mM during the OM2/MRCI dynamics simulations. As expected from the distribution of the hopping times, the S1 and S0 populations do not change at the beginning. After 200 fs, they start to change gradually until the end of the simulation, when there are ∼10% of the trajectories surviving in the S1 state while 90% have reached the S0 state. A fit of the time-dependent S1 population in terms of unimolecular rate theory48 yields an estimate of 566 fs for the S1 excited-state lifetime.

Two Typical Trajectories

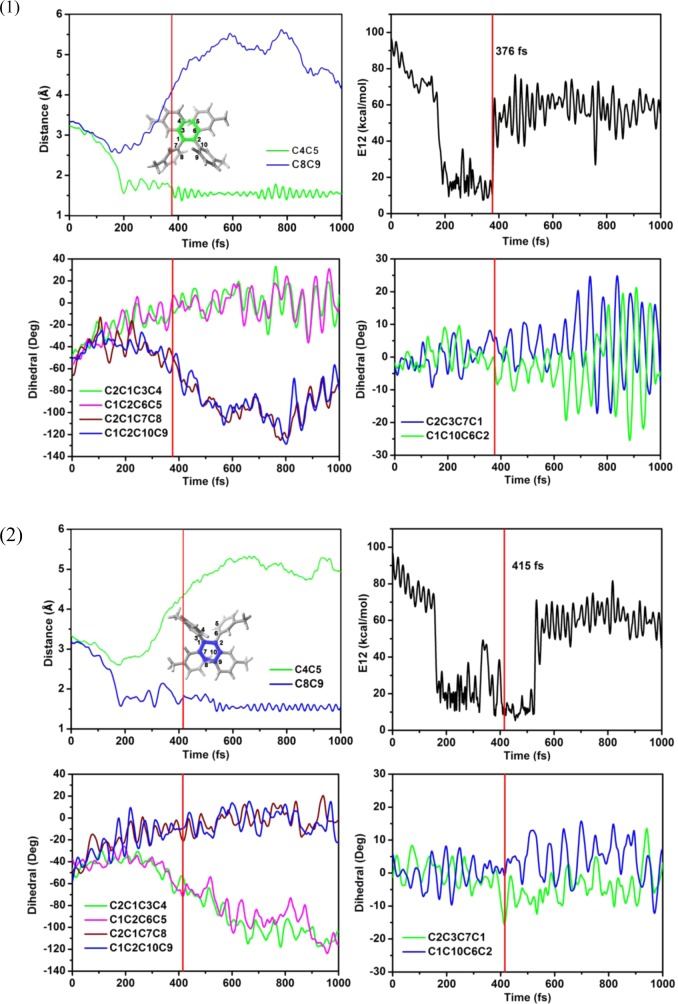
In this section, we discuss two typical cyclization trajectories in some detail. Figure 5 shows the time-dependent evolution of two key distances and six key dihedral angles in a typical trajectory for cyclization of TPE-4mM. It starts from a conformation with an initial C4–C5 distance of about 3.130 Å. Upon cyclization, this distance immediately decreases to about 1.8 Å within ∼200 fs, in conjunction with an almost synchronous decrease of the dihedral angles characterizing the phenyl rotations: C1–C2–C6–C5 from −55 to −20° and C2–C1–C3–C4 from −48 to −15°. By contrast, the C2–C3–C7–C1 and C1–C10–C6–C2 dihedral angles merely fluctuate slightly. In this run, the system does not decay to the S0 state when it first approaches the S1/S0 conical intersection region after 200 fs; instead, it oscillates for more than 150 fs (ca. 2 vibrational periods) and then hops to the ground state at 376 fs. Thereafter, the molecule evolves toward the cyclic conformation, accompanied by a decrease of the C2–C3–C7–C1 and C1–C10–C6–C2 dihedral angles until the end of the nonadiabatic dynamics simulations. Panel (2) shows a second typical cyclization trajectory, in which cyclization occurs at the other side of TPE-4mM (formation of the C8–C9 bond). The hopping time and the key geometric parameters show analogous behavior as that in the first trajectory. For comparison, corresponding time-dependent data are presented for a typical trajectory of TPE-4oM in the Supporting Information (Figure S7).

Figure 5.

Figure 5

Open in a new tab

Time-dependent physical variables obtained from typical OM2/MRCI trajectories of TPE-4mM (1 and 2): two key bond lengths (top left); S1–S0 energy gap (top right); six key dihedral angles (bottom)

Discussion

We first note that, contrary to the situation in TPE-4mM, none of the 568 successful trajectories of TPE-4oM reach the S0 state, showing that the S1S0-cyc and S1S0-pyr conical intersections are not accessible within the 1 ps simulation time. This is consistent with the existence of non-negligible barriers on the S1 excited-state cyclization and photoisomerization pathways at the OM2/MRCI and CASPT2 levels (see above). The propensity to remain in the S1 state during the simulations is in qualitative agreement with the experimental observation of a large fluorescence quantum yield in TPE-4oM.14 The surprisingly different fluorescence quantum yields of TPE-4mM (0.1%) and TPE-4oM (64.3%) are thus linked to the different topology of the S1 surfaces and hence to intrinsic properties of these TPE derivatives. For the same reasons, TPE-4oM does not behave as an AIEgen (in contrast to TPE-4mM).

Our simulations suggest that the ultrafast excited-state decay of TPE-4mM does not proceed by photoisomerization around the central ethylenic double bond but instead by barrierless S1 relaxation processes toward two S1S0-cyc conical intersections, which lead to intramolecular ring closure after internal conversion to the S0 ground state. This is consistent with the results from a recent TSH dynamics study of the parent TPE molecule at the TDA-TDDFT level, in which the vast majority of the trajectories led to photocyclization.18

Such photocyclization processes have generally not been considered in experimental studies of TPE-based AIEgens, which mostly advocate an explanation of AIE in terms of restricted intramolecular rotation of the phenyl rings.3−5 On the other hand, photocyclization pathways have been shown to exist in the closely related cis-stilbene molecule both experimentally63 and theoretically,64 and a corresponding cyclic intermediate has been identified in a photooxidation reaction of TPE.65 Moreover, photocyclization processes have been characterized in detail in related systems such as ortho-terphenyl and its derivatives, in which E/Z photoisomerization is blocked structurally.66−68 All of this evidence supports the notion that photocyclization may indeed be a viable relaxation mechanism in TPE-4mM and more generally in TPE-based AIEgens.

The formed cyclic ground-state isomers of TPE-4mM are thermodynamically unfavorable (see Table S3), lying about 30 (39) kcal/mol above the S0 minimum of TPE-4mM at the OM2/MRCI (B3LYP) level. Their computed vertical excitation energies are in the range of the visible spectrum (see Table S4) and are much lower than those computed for TPE-4mM (in the UV region; see Table S1). Therefore, the postulated cyclic S0 product of the excited-state decay of TPE-4mM should be detectable by electronic spectroscopy provided that it lives long enough. B3LYP calculations give a substantial barrier of ∼38 kcal/mol for the thermal ground-state ring opening to the S0 minimum of TPE-4mM (see Table S5), and there is also no sign of ring opening in 200 ps ground-state Born–Oppenheimer molecular dynamics simulations at the OM2 level. However, according to the recent TDA-TDDFT work on the parent TPE molecule, the cyclic S0 form is photochemically unstable; upon photoexcitation, it will undergo the reverse ring-opening reaction back to TPE in an ultrafast photoinduced process.18 Its spectroscopic detection is thus expected to be very challenging experimentally.

Conclusions

Finally, we emphasize again that all present calculations were performed on isolated TPE-4mM and TPE-4oM molecules to gain insight into their intrinsic properties and mechanisms. This has already allowed us to explain their different fluorescence behavior and to understand why TPE-4oM is not an AIEgen. Overlays of the optimized geometries of the S0 minimum of TPE-4mM and the relevant S1S0-cyc conical intersections reveal significant differences (see Figure S10), and hence, it seems not unlikely that aggregation of TPE-4mM may block access to these conical intersections and hence to the ground state, thus leading to the experimentally observed AIE behavior of TPE-4mM. Multiscale simulations of aggregates will be required to provide further computational support for this hypothesis.

To summarize, the present study shows that the intrinsic excited-state decay paths of TPE compounds are intimately related to their fluorescence properties and their performance as AIEgens. We hope that the theoretical insights gained will contribute to a better understanding and eventually to an improved design of AIEgens.

Acknowledgments

This work has been supported by Grants NSFC 21522302, 21520102005, and 21421003 (G.C.) and by an ERC Advanced Grant (OMSQC, W.T.).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpca.7b00197.

  • Active spaces in CASSCF, CASPT2, and OM2/MRCI computations; numerical results for relative energies and for key geometrical variables; additional LIIC paths; typical trajectory of TPE-4oM; and Cartesian coordinates of all structures (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp7b00197_si_001.pdf (6MB, pdf)

References

  1. Luo J.; Xie Z.; Lam J. W. Y.; Cheng L.; Chen H.; Qiu C.; Kwok H. S.; Zhan X.; Liu Y.; Zhu D.; Tang B. Z. Aggregation-Induced Emission of 1-Methyl-1,2,3,4,5- Pentaphenylsilole. Chem. Commun. 2001, 1740–1741. 10.1039/b105159h. [DOI] [PubMed] [Google Scholar]
  2. Hong Y. N.; Lam J. W. Y.; Tang B. Z. Aggregation-Induced Emission. Chem. Soc. Rev. 2011, 40, 5361–5388. 10.1039/c1cs15113d. [DOI] [PubMed] [Google Scholar]
  3. Mei J.; Hong Y.; Lam J. W.; Qin A.; Tang Y.; Tang B. Z. Aggregation-Induced Emission: The Whole Is More Brilliant Than the Parts. Adv. Mater. 2014, 26, 5429–5479. 10.1002/adma.201401356. [DOI] [PubMed] [Google Scholar]
  4. Mei J.; Leung N. L. C.; Kwok R. T. K.; Lam J. W. Y.; Tang B. Z. Aggregation-Induced Emission: Together We Shine, United We Soar!. Chem. Rev. 2015, 115, 11718–11940. 10.1021/acs.chemrev.5b00263. [DOI] [PubMed] [Google Scholar]
  5. Kwok R. T. K.; Leung C. W. T.; Lam J. W. Y.; Tang B. Z. Biosensing by Luminogens with Aggregation-Induced Emission Characteristics. Chem. Soc. Rev. 2015, 44, 4228–4238. 10.1039/C4CS00325J. [DOI] [PubMed] [Google Scholar]
  6. Tong H.; Hong Y.; Dong Y.; Häußler M.; Lam J. W. Y.; Li Z.; Guo Z.; Guo Z.; Tang B. Z. Fluorescent ″Light-Up″ Bioprobes Based on Tetraphenylethylene Derivatives with Aggregation-Induced Emission Characteristics. Chem. Commun. 2006, 3705–3707. 10.1039/B608425G. [DOI] [PubMed] [Google Scholar]
  7. Chen Q.; Bian N.; Cao C.; Qiu X. L.; Qi A. D.; Han B. H. Glucosamine Hydrochloride Functionalized Tetraphenylethylene: A Novel Fluorescent Probe for Alkaline Phosphatase Based on the Aggregation-Induced Emission. Chem. Commun. 2010, 46, 4067–4069. 10.1039/c002894k. [DOI] [PubMed] [Google Scholar]
  8. Wang M.; Zhang G.; Zhang D.; Zhu D.; Tang B. Z. Fluorescent Bio/Chemosensors Based on Silole and Tetraphenylethene Luminogens with Aggregation-Induced Emission Feature. J. Mater. Chem. 2010, 20, 1858–1867. 10.1039/b921610c. [DOI] [Google Scholar]
  9. Hu R.; Maldonado J. L.; Rodriguez M.; Deng C.; Jim C. K. W.; Lam J. W. Y.; Yuen M. M. F.; Ramos-Ortiz G.; Tang B. Z. Luminogenic Materials Constructed from Tetraphenylethene Building Blocks: Synthesis, Aggregation-Induced Emission, Two-Photon Absorption, Light Refraction, and Explosive Detection. J. Mater. Chem. 2012, 22, 232–240. 10.1039/C1JM13556B. [DOI] [Google Scholar]
  10. Huang J.; Yang X.; Wang J.; Zhong C.; Wang L.; Qin J.; Li Z. New Tetraphenylethene-Based Efficient Blue Luminophors: Aggregation Induced Emission and Partially Controllable Emitting Color. J. Mater. Chem. 2012, 22, 2478–2484. 10.1039/C1JM14054J. [DOI] [Google Scholar]
  11. Shi H.; Kwok R. T. K.; Liu J.; Xing B.; Tang B. Z.; Liu B. Real-Time Monitoring of Cell Apoptosis and Drug Screening Using Fluorescent Light-Up Probe with Aggregation-Induced Emission Characteristics. J. Am. Chem. Soc. 2012, 134, 17972–17981. 10.1021/ja3064588. [DOI] [PubMed] [Google Scholar]
  12. Xu B.; Xie M.; He J.; Xu B.; Chi Z.; Tian W.; Jiang L.; Zhao F.; Liu S.; Zhang Y.; Xu Z.; Xu J. An Aggregation-Induced Emission Luminophore with Multi-Stimuli Single- and Two-Photon Fluorescence Switching and Large Two-Photon Absorption Cross Section. Chem. Commun. 2013, 49, 273–275. 10.1039/C2CC36806D. [DOI] [PubMed] [Google Scholar]
  13. Wang J.; Mei J.; Hu R.; Sun J. Z.; Qin A.; Tang B. Z. Click Synthesis, Aggregation-Induced Emission, E/Z Isomerization, Self-Organization, and Multiple Chromisms of Pure Stereoisomers of a Tetraphenylethene-Cored Luminogen. J. Am. Chem. Soc. 2012, 134, 9956–9966. 10.1021/ja208883h. [DOI] [PubMed] [Google Scholar]
  14. Zhang G. F.; Chen Z. Q.; Aldred M. P.; Hu Z.; Chen T.; Huang Z.; Meng X.; Zhu M. Q. Direct Validation of the Restriction of Intramolecular Rotation Hypothesis Via the Synthesis of Novel Ortho-Methyl Substituted Tetraphenylethenes and Their Application in Cell Imaging. Chem. Commun. 2014, 50, 12058–12060. 10.1039/C4CC04241G. [DOI] [PubMed] [Google Scholar]
  15. Yang Z.; Qin W.; Leung N. L. C.; Arseneault M.; Lam J. W. Y.; Liang G.; Sung H. H. Y.; Williams I. D.; Tang B. Z. A Mechanistic Study of AIE Processes of TPE Luminogens: Intramolecular Rotation vs. Configurational Isomerization. J. Mater. Chem. C 2016, 4, 99–107. 10.1039/C5TC02924D. [DOI] [Google Scholar]
  16. Wu W.; Feng G.; Xu S.; Liu B. A Photostable Far-Red/Near-Infrared Conjugated Polymer Photosensitizer with Aggregation-Induced Emission for Image-Guided Cancer Cell Ablation. Macromolecules 2016, 49, 5017–5025. 10.1021/acs.macromol.6b00958. [DOI] [Google Scholar]
  17. Wang Y. J.; Shi Y.; Wang Z.; Zhu Z.; Zhao X.; Nie H.; Qian J.; Qin A.; Sun J. Z.; Tang B. Z. A Red to Near-IR Fluorogen: Aggregation-Induced Emission, Large Stokes Shift, High Solid Efficiency and Application in Cell-Imaging. Chem. - Eur. J. 2016, 22, 9784–9791. 10.1002/chem.201600125. [DOI] [PubMed] [Google Scholar]
  18. Prlj A.; Dos̆lić N.; Corminboeuf C. How does Tetraphenylethylene Relax from its Excited States?. Phys. Chem. Chem. Phys. 2016, 18, 11606–11609. 10.1039/C5CP04546K. [DOI] [PubMed] [Google Scholar]
  19. Shultz D. A.; Fox M. A. The Effect of Phenyl Ring Torsional Rigidity on the Photophysical Behavior of Tetraphenylethylenes. J. Am. Chem. Soc. 1989, 111, 6311–6320. 10.1021/ja00198a049. [DOI] [Google Scholar]
  20. Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
  21. Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  22. Lee C. T.; Yang W. T.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  23. Becke A. D. A New Mixing of Hartree–Fock and Local Density-Functional. Theories. J. Chem. Phys. 1993, 98, 1372–1377. 10.1063/1.464304. [DOI] [Google Scholar]
  24. Chai J.-D.; Head-Gordon M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
  25. Chai J.-D.; Head-Gordon M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. J. Chem. Phys. 2008, 128, 084106. 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
  26. Andersson K.; Malmqvist P.-Å.; Roos B. O.; Sadlej A. J.; Wolinski K. Second-Order Perturbation Theory with a CASSCF Reference Function. J. Phys. Chem. 1990, 94, 5483–5488. 10.1021/j100377a012. [DOI] [Google Scholar]
  27. Andersson K.; Malmqvist P.-Å.; Roos B. O. Second-Order Perturbation Theory with a Complete Active Space Self-Consistent Field Reference Function. J. Chem. Phys. 1992, 96, 1218–1226. 10.1063/1.462209. [DOI] [Google Scholar]
  28. Ghigo G.; Roos B. O.; Malmqvist P.-Å. A Modified Definition of the Zeroth-Order Hamiltonian in Multiconfigurational Perturbation Theory (CASPT2). Chem. Phys. Lett. 2004, 396, 142–149. 10.1016/j.cplett.2004.08.032. [DOI] [Google Scholar]
  29. Forsberg N.; Malmqvist P.-Å. Multiconfiguration Perturbation Theory with Imaginary Level Shift. Chem. Phys. Lett. 1997, 274, 196–204. 10.1016/S0009-2614(97)00669-6. [DOI] [Google Scholar]
  30. Aquilante F.; Lindh R.; Bondo Pedersen T. Unbiased Auxiliary Basis Sets for Accurate Two-Electron Integral Approximations. J. Chem. Phys. 2007, 127, 114107. 10.1063/1.2777146. [DOI] [PubMed] [Google Scholar]
  31. Marques M. A. L.; Ullrich C. A.; Nogueira F.; Rubio A.; Burke K.; Gross E. K. U.. Time-Dependent Density Functional Theory; Springer, 2006. [Google Scholar]
  32. Yanai T.; Tew D. P.; Handy N. C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  33. Ditchfield R.; Hehre W. J.; Pople J. A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. 10.1063/1.1674902. [DOI] [Google Scholar]
  34. Hariharan P. C.; Pople J. A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theor. Chem. Acc. 1973, 28, 213–222. 10.1007/BF00533485. [DOI] [Google Scholar]
  35. Binkley J. S.; Pople J. A.; Hehre W. J. Self-Consistent Molecular Orbital Methods. 21. Small Split-Valence Basis Sets for First-Row Elements. J. Am. Chem. Soc. 1980, 102, 939–947. 10.1021/ja00523a008. [DOI] [Google Scholar]
  36. Gordon M. S.; Binkley J. S.; Pople J. A.; Pietro W. J.; Hehre W. J. Self-Consistent Molecular-Orbital Methods. 22. Small Split-Valence Basis Sets for Second-Row Elements. J. Am. Chem. Soc. 1982, 104, 2797–2803. 10.1021/ja00374a017. [DOI] [Google Scholar]
  37. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheesem J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09, revision A.02; Gaussian, Inc.: Wallingford, CT, 2009.
  38. Aquilante F.; De Vico L.; Ferré N.; Ghigo G.; Malmqvist P.-Å.; Neogrády P.; Pedersen T. B.; Pitoňák M.; Reiher M.; Roos B. O.; et al. MOLCAS 7: The Next Generation. J. Comput. Chem. 2010, 31, 224–247. 10.1002/jcc.21318. [DOI] [PubMed] [Google Scholar]
  39. Weber W. Ph.D. Thesis, University of Zürich, 1996. [Google Scholar]
  40. Weber W.; Thiel W. Orthogonalization Corrections for Semiempirical Methods. Theor. Chem. Acc. 2000, 103, 495–506. 10.1007/s002149900083. [DOI] [Google Scholar]
  41. Dral P. O.; Wu X.; Spörkel L.; Koslowski A.; Weber W.; Steiger R.; Scholten M.; Thiel W. Semiempirical Quantum-Chemical Orthogonalization-Corrected Methods: Theory, Implementation, and Parameters. J. Chem. Theory Comput. 2016, 12, 1082–1096. 10.1021/acs.jctc.5b01046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Koslowski A.; Beck M. E.; Thiel W. Implementation of a General Multireference Configuration Interaction Procedure with Analytic Gradients in a Semiempirical Context Using the Graphical Unitary Group Approach. J. Comput. Chem. 2003, 24, 714–726. 10.1002/jcc.10210. [DOI] [PubMed] [Google Scholar]
  43. Thiel W.MNDO99 program, version 6.1; Max-Planck-Institut für Kohlenforschung: Mülheim, Germany, 2007.
  44. Yarkony D. R. Nuclear Dynamics near Conical Intersections in the Adiabatic Representation: I. the Effects of Local Topography on Interstate Transitions. J. Chem. Phys. 2001, 114, 2601–2613. 10.1063/1.1329644. [DOI] [Google Scholar]
  45. Keal T. W.; Koslowski A.; Thiel W. Comparison of Algorithms for Conical Intersection Optimisation Using Semiempirical Methods. Theor. Chem. Acc. 2007, 118, 837–844. 10.1007/s00214-007-0331-5. [DOI] [Google Scholar]
  46. Wigner E. On the Quantum Correction for Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. 10.1103/PhysRev.40.749. [DOI] [Google Scholar]
  47. Granucci G.; Persico M.; Zoccante A. Including Quantum Decoherence in Surface Hopping. J. Chem. Phys. 2010, 133, 134111. 10.1063/1.3489004. [DOI] [PubMed] [Google Scholar]
  48. Cui G. L.; Lan Z.; Thiel W. Intramolecular Hydrogen Bonding Plays a Crucial Role in the Photophysics and Photochemistry of the GFP Chromophore. J. Am. Chem. Soc. 2012, 134, 1662–1672. 10.1021/ja208496s. [DOI] [PubMed] [Google Scholar]
  49. Kazaryan A.; Lan Z.; Schäfer L. V.; Thiel W.; Filatov M. Surface Hopping Excited-State Dynamics Study of the Photoisomerization of a Light-Driven Fluorene Molecular Rotary Motor. J. Chem. Theory Comput. 2011, 7, 2189–2199. 10.1021/ct200199w. [DOI] [PubMed] [Google Scholar]
  50. Weingart O.; Lan Z.; Koslowski A.; Thiel W. Chiral Pathways and Periodic Decay in cis-Azobenzene Photodynamics. J. Phys. Chem. Lett. 2011, 2, 1506–1509. 10.1021/jz200474g. [DOI] [Google Scholar]
  51. Cui G. L.; Thiel W. Photoinduced Ultrafast Wolff Rearrangement: A Non-Adiabatic Dynamics Perspective. Angew. Chem., Int. Ed. 2013, 52, 433–436. 10.1002/anie.201207628. [DOI] [PubMed] [Google Scholar]
  52. Lu Y.; Lan Z.; Thiel W. Hydrogen Bonding Regulates the Monomeric Nonradiative Decay of Adenine in DNA Strands. Angew. Chem., Int. Ed. 2011, 50, 6864–6867. 10.1002/anie.201008146. [DOI] [PubMed] [Google Scholar]
  53. Spörkel L.; Thiel W. Adaptive Time Steps in Trajectory Surface Hopping Simulations. J. Chem. Phys. 2016, 144, 194108. 10.1063/1.4948956. [DOI] [PubMed] [Google Scholar]
  54. Dral P. O.; Wu X.; Spörkel L.; Koslowski A.; Thiel W. Semiempirical Quantum-Chemical Orthogonalization-Corrected Methods: Benchmarks for Ground-State Properties. J. Chem. Theory Comput. 2016, 12, 1097–1120. 10.1021/acs.jctc.5b01047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Liu X.-Y.; Chang X.-P.; Xia S.-H.; Cui G. L.; Thiel W. Excited-State Proton-Transfer-Induced Trapping Enhances the Fluorescence Emission of a Locked GFP Chromophore. J. Chem. Theory Comput. 2016, 12, 753–764. 10.1021/acs.jctc.5b00894. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Xia S.-H.; Cui G. L.; Fang W.-H.; Thiel W. How Photoisomerization Drives Peptide Folding and Unfolding: Insights from QM/MM and MM Dynamics Simulations. Angew. Chem., Int. Ed. 2016, 55, 2067–2072. 10.1002/anie.201509622. [DOI] [PubMed] [Google Scholar]
  57. Wang Y.-T.; Liu X.-Y.; Cui G. L.; Fang W.-H.; Thiel W. Photoisomerization of Arylazopyrazole Photoswitches: Stereospecific Excited-State Relaxation. Angew. Chem., Int. Ed. 2016, 55, 14009–14013. 10.1002/anie.201607373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Viel A.; Krawczyk R. P.; Manthe U.; Domcke W. The Sudden-Polarization Effect and its Role in the Ultrafast Photochemistry of Ethene. Angew. Chem., Int. Ed. 2003, 42, 3434–3436. 10.1002/anie.200351193. [DOI] [PubMed] [Google Scholar]
  59. Quenneville J.; Martínez T. J. Ab Initio Study of Cis-Trans Photoisomerization in Stilbene and Ethylene. J. Phys. Chem. A 2003, 107, 829–837. 10.1021/jp021210w. [DOI] [Google Scholar]
  60. Zhao G. J.; Han K. L.; Lei Y. B.; Dou Y. S. Ultrafast Excited-State Dynamics of Tetraphenylethylene Studied by Semiclassical Simulation. J. Chem. Phys. 2007, 127, 094307. 10.1063/1.2768347. [DOI] [PubMed] [Google Scholar]
  61. Gao X.; Peng Q.; Niu Y.; Wang D.; Shuai Z. Theoretical Insight into the Aggregation Induced Emission Phenomena of Diphenyldibenzofulvene: A Nonadiabatic Molecular Dynamics Study. Phys. Chem. Chem. Phys. 2012, 14, 14207–14216. 10.1039/c2cp40347a. [DOI] [PubMed] [Google Scholar]
  62. Li Q.; Blancafort L. A Conical Intersection Model to Explain Aggregation Induced Emission in Diphenyl Dibenzofulvene. Chem. Commun. 2013, 49, 5966–5968. 10.1039/c3cc41730a. [DOI] [PubMed] [Google Scholar]
  63. Rodier J. M.; Myers A. B. cis-Stilbene Photochemistry: Solvent Dependence of the Initial Dynamics and Quantum Yields. J. Am. Chem. Soc. 1993, 115, 10791–10795. 10.1021/ja00076a041. [DOI] [Google Scholar]
  64. Harabuchi Y.; Keipert K.; Zahariev F.; Taketsugu T.; Gordon M. S. Dynamics Simulations with Spin-Flip Time-Dependent Density Functional Theory: Photoisomerization and Photocyclization Mechanisms of cis-Stilbene in ππ* states. J. Phys. Chem. A 2014, 118, 11987–11998. 10.1021/jp5072428. [DOI] [PubMed] [Google Scholar]
  65. Aldred M. P.; Li C.; Zhu M.-Q. Optical Properties and Photo-Oxidation of Tetraphenylethene-Based Fluorophores. Chem. - Eur. J. 2012, 18, 16037–16045. 10.1002/chem.201202715. [DOI] [PubMed] [Google Scholar]
  66. Smith M. C.; Snyder J. A.; Streifel B. C.; Bragg A. E. Ultrafast Excited-State Dynamics of ortho-Terphenyl and 1,2-Diphenylcyclohexene: The Role of ″Ethylenic Twisting″ in the Nonadiabatic Photocyclization of Stilbene Analogs. J. Phys. Chem. Lett. 2013, 4, 1895–1900. 10.1021/jz400674n. [DOI] [PubMed] [Google Scholar]
  67. Molloy M. S.; Snyder J. A.; Bragg A. E. Structural and Solvent Control of Photochemical Nonadiabatic Bond Formation: Photocyclization of o-Terphenyl in Solution. J. Phys. Chem. A 2014, 118, 3913–3925. 10.1021/jp501988g. [DOI] [PubMed] [Google Scholar]
  68. Snyder J. A.; Bragg A. E. Structural Control of Nonadiabatic Bond Formation: The Photochemical Formation and Stability of 4a,4b-Dihydrotriphenylenes. J. Phys. Chem. A 2015, 119, 3972–3985. 10.1021/acs.jpca.5b01749. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp7b00197_si_001.pdf (6MB, pdf)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES