Patient-specific modeling of left ventricular electromechanics as a driver for haemodynamic analysis

Abstract

Aims

Models of blood flow in the left ventricle (LV) and aorta are an important tool for analysing the interplay between LV deformation and flow patterns. Typically, image-based kinematic models describing endocardial motion are used as an input to blood flow simulations. While such models are suitable for analysing the hemodynamic status quo, they are limited in predicting the response to interventions that alter afterload conditions. Mechano-fluidic models using biophysically detailed electromechanical (EM) models have the potential to overcome this limitation, but are more costly to build and compute. We report our recent advancements in developing an automated workflow for the creation of such CFD ready kinematic models to serve as drivers of blood flow simulations.

Methods and results

EM models of the LV and aortic root were created for four pediatric patients treated for either aortic coarctation or aortic valve disease. Using MRI, ECG and invasive pressure recordings, anatomy as well as electrophysiological, mechanical and circulatory model components were personalized.

Results

The implemented modeling pipeline was highly automated and allowed model construction and execution of simulations of a patient’s heartbeat within 1 day. All models reproduced clinical data with acceptable accuracy.

Conclusion

Using the developed modeling workflow, the use of EM LV models as driver of fluid flow simulations is becoming feasible. While EM models are costly to construct, they constitute an important and nontrivial step towards fully coupled electro-mechano-fluidic (EMF) models and show promise as a tool for predicting the response to interventions which affect afterload conditions.

What’s new?

• Biophysically detailed and anatomically accurate electromechanical (EM) insilico models of the left ventricle and aortic root were fitted to clinical data of four patients undergoing treatment for either aortic coarctation or aortic valve disease.

• The implemented model building and parameter calibration pipeline was highly automated and allowed model construction and execution of simulations of a patient’s heartbeat within 1 day.

• The calibrated models replicated clinically recorded electrocardiograms, pressure–volume loops and circumferential strains with acceptable accuracy. Thus, LV deformation predicted by the model can serve as CFD-ready kinematic input to fluid flow simulations for the analysis of hemodynamic flow patterns.

• In contrast to currently prevailing image-based kinematic models EM models mechanistically describe cardiac motion based on first principles and thus offer the potential to predict changes in flow patterns in response to interventions which alter afterload conditions.

Introduction

The heart is an electrically controlled mechanical pump, which drives blood from its cavities into the vascular system through mechanical deformation of its walls. The three major fields of physics governing a heartbeat—electrophysiology (EP), tissue mechanics and fluid flow—are bidirectionally coupled as follows. EP drives mechanical deformation through a process referred to as excitation–contraction coupling,¹ whereas deformation in turn influences the electrophysiological state of the heart through mechano-electric feedback mechanisms.^2,3 Depending on mechanical boundary conditions⁴ and external loads imposed, the active forces generated by the myocardium drive mechanical contraction and relaxation of the walls, forcing blood in, through and out of the heart’s chambers. In turn, the dynamic motion of blood flow and, more importantly, the physical state of the valves and the attached circulatory system strongly influence force development and deformation.

The multiple physical fields involved in shaping a heartbeat and their bidirectional coupling pose a significant challenge to the development of a comprehensive understanding of cardiac function. Biophysically detailed EMF computer models show promise as a framework that can facilitate quantitative investigations of underlying mechanisms at a high spatio-temporal resolution. Such models offer a powerful research tool that can efficiently probe cardiac physiology, provide a context for the interpretation of measured data and help to identify the key mechanisms regulating cardiac health. However, complete strongly coupled EMF models are rare due to their inherent complexity in terms of model formulation, numerical methods, software implementation and computational cost. By far the vast majority of computer modeling work has applied single-physics models; in some cases two different fields of physics have been coupled, either EP to mechanics^4–7 or mechanics to fluid flow.^8–10 Even less literature is found on EMF models that integrate all three fields of physics.^11,12 All studies, without exceptions, have resorted to simplifications such as assuming coupling to be governed by a unidirectional chain of causalities that ignores important regulatory mechanisms.

One important aspect of cardiac function is cardiovascular hemodynamics, especially in clinical diagnosis. While various invasive and noninvasive approaches are routinely used to assess a patient’s hemodynamic state, even the most advanced 4D tomographic imaging modalities provide information afflicted with uncertainties with limited spatio-temporal resolution and contrast.¹³ Hemodynamic models of blood flow in the LV and aorta are gaining significance as a tool to fill this gap, especially as they enable more detailed quantitative analyses of the interaction between LV deformation and hemodynamics.^14,15 In such fluid-structure interaction (FSI) problems, the use of image-driven modeling approaches prevails, where patient-specific kinematic models of endocardial motion are constructed by direct segmentation of time-dependent 4D medical imaging data. The resulting surface motion is then imposed as boundary conditions on a hemodynamic model. While such models show promise as a tool for analysing the current hemodynamic state of a patient, their predictive capabilities are limited in interventional scenarios such as aortic valve replacement, where afterload conditions of the LV post-treatment are known to be altered. An alternative to image-driven kinematic models is the use of biophysically detailed EM models of the LV. Once such EM models are properly parameterized, they can provide the spatio-temporal dynamics of the LV endocardium in the same way as kinematic models. However, since they comprehensively represent the entire physics of a heartbeat based on first principles, they may be able to make useful predictions on post-treatment cardiac function. Constructing such models is significantly more laborious, but they show high promise as a tool for predicting the response to any interventions which affect the conditions of afterload.^16–18

To unleash the full potential of computational models in clinical applications, such as the optimization of mechanical heart valves, the bidirectional coupling of EM models and cardiovascular hemodynamics is warranted. Such coupled EMF models are more versatile and potentially offer higher predictive power, but the additional complexity limits their wider adoption.

Based on our work on anatomically accurate EM models of the heart,^19,20 we report our recent advancements on developing an efficient high throughput modeling pipeline for EM models of the LV and aortic root, which are coupled with a lumped model of the circulatory system to be suitable for driving simulations of cardiac and vascular hemodynamics. Such EM-based simulations constitute an important and nontrivial step towards fully coupled EMF models, which, in principal, may provide useful predictions on a patient’s response to interventions affecting afterload. In our study, EP as well as active and passive mechanical properties of the LV are fit to reproduce clinically recorded EP and hemodynamic data of individual patients. Tagged MRI data are used for validating strain predictions of the model.

Methods

Patient data

Data of three patients with clinical indication for catheterization due to aorta coarctation (CoA) and one patient with aortic valve disease (AVD) and clinical indication for aortic valve treatment, all preceding a cardiac magnetic resonance study were used (see Table 1). CoA treatment indicators were an echocardiographic measured peak systole pressure gradient across the stenotic region >20 mmHg and/or arterial hypertension. AVD treatment indicators included valve area and/or systolic pressure drop across the valve. The study was approved by the institutional Research Ethics Committee following the ethical guidelines of the 1975 Declaration of Helsinki. Written informed consent was obtained from the participants’ guardians.

Table 1.

Patient characteristics from MRI, ECG and invasive catheter pressure recordings including end-diastolic volume (EDV), end-systolic volume (ESV), ejection fraction (EF), heart rate (HR), QRS duration and the maximum rate of rise of pressure ${(\mathrm{d}P/\mathrm{d}t)}_{\text{max}}$

	Sex	Age (years)	Disease	EDV (mL)	ESV (mL)	EF (%)	HR (1/min)	QRS (ms)	${(\mathrm{d}P/\mathrm{d}t)}_{\text{max}}$ (mmHg/ms)
Case 1	F	9	CoA	67 .9	22 .1	67 .5	64 .1	90	1 .97
Case 2	M	15	AVD	199 .6	50 .0	74 .9	80 .7	171	–
Case 3	M	10	CoA	81 .9	21 .8	73 .4	92 .6	104	2 .66
Case 4	M	15	CoA	111 .2	29 .8	73 .2	89 .3	88	2 .20

Note that AVD patients were not catheterized and as such no pressure recordings are available .

Building anatomical left ventricle and aortic root models

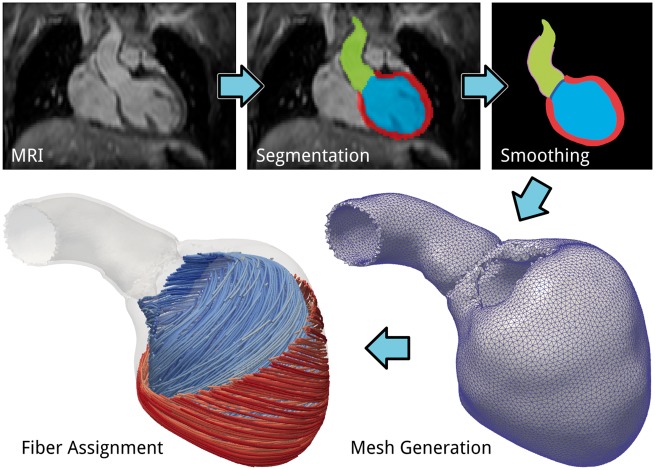
Finite element meshes of the cardiac anatomy are generated from 3D whole heart MRI acquired at end diastole (ED) with 1.458 mm × 1.548 mm × 2 mm resolution. Data were acquired at the German Heart Center Berlin (DHZB). Multi-label segmentation of the LV myocardium and cavity, left atrium (LA) and aortic cavities is done at the DHZB using the ZIB Amira software (https://amira.zib.de/). This segmentation is smoothed and upsampled to a 0.1-mm isotropic resolution using a variational smoothing method.²⁰ The wall of the aorta is automatically generated by dilation of the aortic cavity with a thickness of 1.2 mm, and the aorta is manually clipped just before the branch of the brachiocephalic artery. The purpose of this clipped aorta is to provide physiological boundary conditions for the mechanical problem which still allow a horizontal movement of the left ventricular base as it is observed invivo. The resulting high resolution multi-label segmentation is meshed using CGAL (http://www.cgal.org/) with a target size of 1.25 mm in the LV myocardium and 1 mm in the aorta wall. The various stages of the anatomical modeling workflow are illustrated in Figure 1.

Figure 1.

Illustration of the various stages of the anatomical model building workflow.

Electrophysiology model

To provide appropriate electromechanical delays for the EM model, a simplified EP model of the LV is used to generate activation sequences which serve as a trigger for the active stress component of the mechanics model. Activation sequences are indirectly parameterized using the QRS complex of a given patient’s ECG as guidance. Ventricular EP was represented by the tenTusscher–Noble–Noble–Panfilov model of the human ventricular myocyte.²¹ Activation sequences and electrical source distribution in the LV were computed on the mesh representing the LV in its end-diastolic configuration using a coupled reaction-Eikonal model, which, in contrast to commonly used reaction-diffusion models, enables the use of coarser and thus computationally less expensive mesh resolutions. ECGs were computed with a 1-ms time resolution as difference signals between unipolar extracellular electrograms, which were recovered at the approximate electrode positions at the torso surface using an integral solution of the electrocardiographic forward problem.²²

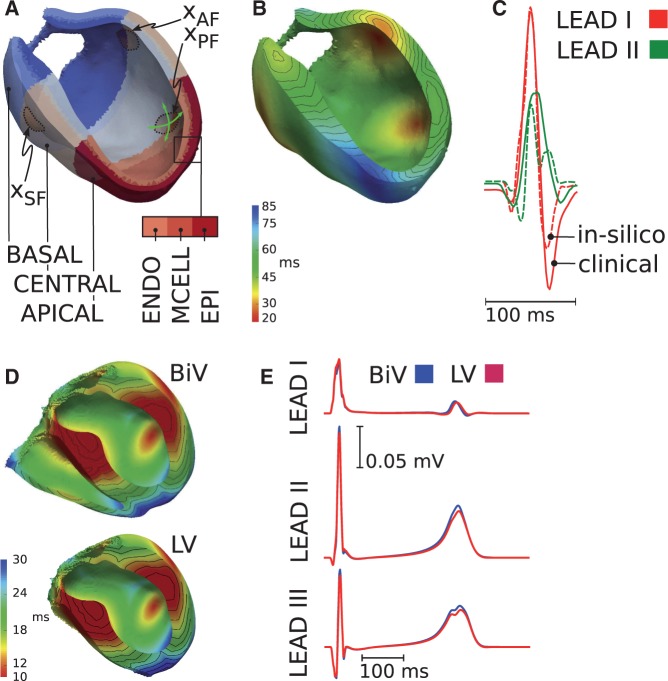
The ventricular activation sequence, which manifests in the ECG as the QRS complex, was determined by the location and timing of the sites of earliest activation at the endocardium, the conduction velocity within the His–Purkinje system (HPS), the fiber and sheet architecture of the myocardium and the associated orthotropic conduction velocities. In our LV model, sites of earliest endocardial activation were chosen to represent the approximate locations of the septal, anterior and posterior fascicles (Figure 2). In absence of an explicit representation of the HPS a longitudinal conduction velocity of 3.2 m/s was prescribed to an endocardial layer of 20% of the LV wall width to account for the fast HPS-mediated spread of depolarization waves over the endocardium. Conduction velocities transverse to the fiber orientation and along the sheet normal direction within the endocardial layer were taken as 2/3 and 1/3 of the longitudinal velocity, respectively. In the remainder of the myocardium, a longitudinal conduction velocity v_f was chosen and orthotropic velocity ratios $v_{\mathrm{f}}:v_{\mathrm{s}}:v_{\mathrm{n}}$ were kept fixed at 3:2:1.

Figure 2.

LV model: (A) chosen sites of earliest activation at anatomical locations of the septal ($x_{\text{SF}}$), anterior ($x_{\text{AF}}$) and posterior ($x_{\text{PF}}$) fascicles. (B) Simulated activation sequence. (C) Comparison of computed (dashed line) and measured (solid line) ECGs. BiV model: (D) simulated activation sequence for the BiV (top) and reduced LV (bottom) model. (E) Influence of the RV on the ECG. Computed ECGs are shown for the BiV (blue) and the LV (red) models.

Electrocardiogram fitting

Using a priori knowledge, the anatomical locations of the fascicles as well as the corresponding earliest activation times and the longitudinal conduction velocity v_f were iteratively adjusted to gradually improve the match in terms of QRS morphology, QRS duration, ΔQRS, and the orientation of the peak dipole vector in the frontal plane, α²³ between clinically recorded Einthoven I and II leads and the corresponding model prediction. Once the QRS complex tuning process was completed, repolarization parameters were adjusted to obtain concordant T-waves in both leads. Transmural heterogeneities were incorporated into the models by varying the distribution of endocardial, mid-wall and epicardial cells across the ventricular wall. Apico-basal heterogeneities were included by adjusting the maximum conductivity of the slow delayed rectifier current.²⁴ Lastly, conductivities in the endocardial, mid-wall and epicardial layers were rescaled to tune the T-wave amplitude.

Clinically recorded ECGs are the result of the combined electrical activity of both LV and RV, but ECG fitting is performed with a LV model in absence of the RV. We therefore tested that not including the RV in the model does not introduce any bias to the fitting of the ECG. For this reason a biventricular (BiV) model was constructed and the same fitting procedure was applied. As with the LV model, sites of earliest endocardial activation were chosen to represent the approximate locations of two distinct septal and lateral fascicles in the RV. ECGs were then computed with both the full BiV model and with the RV removed.

Modeling mechanical deformation

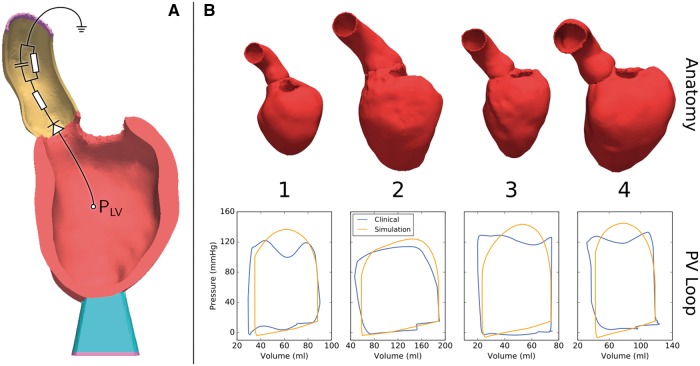
Mechanical deformation was simulated using the equilibrium equations of finite elasticity. The same discrete LV anatomy model with the same fiber architecture was used for both the solid mechanics and the EP problem. The LV myocardium was characterized as a hyperelastic, nearly incompressible, transversally orthotropic material with a nonlinear stress–strain relationship,²⁵ where the orthotropic material axes were aligned with the local fiber, sheet and sheet normal directions. Total stress was additively composed from passive and active stresses. A simplified phenomenological contractile model was used to represent active stress generation where model parameters correspond to rate of activation, active stress transient duration, peak stress and rate of relaxation.²⁶ This simplified model allows efficient fitting to patient data as the parameters for peak stress and time constant of contraction are related to the two clinical key parameters of interest, peak pressure and maximum rate of pressure increase, in an intuitive manner. Active stress generation was triggered with a prescribed electromechanical delay when the upstroke of the action potential crossed the −40 mV threshold. Mechanical boundary conditions were applied to remove rigid body motion by fixing the terminal rim of the clipped aorta (Figure 3A). The apex of the LV was stabilized by resting the LV on an elastic cushion which was rigidly anchored at its base. A lumped three-element Windkessel model was used to provide the pressure-flow relationship during ejection.²⁷ Details of the numerical approach were described previously.¹⁹

Figure 3.

(A) Representative anatomical model showing the mechanical boundary conditions. The end of the aortic root (yellow) and the end of a soft material block attached to the apex of the LV (blue) are fixed in space (purple). Outflow from the ventricle is regulated by a three-element Windkessel model (shown as a representative circuit). (B) Personalized anatomical models and pressure–volume (PV) loops for four patients.

Fitting of mechanics and haemodynamics model

Using the ED geometry, default material parameters and the recorded ED pressure an initial guess of the stress-free reference configuration was computed by unloading the model using a backward displacement method.²⁸ Since the clinically recorded data of the ED pressure–volume relation (EDPVR) are often limited, the unloading procedure was repeated with trial material parameters to fit the EDPVR and stress-free residual volume to the empiric Klotz relation.²⁹ During the isovolumetric contraction (IVC) phase the LV volume was held constant.⁶ Rate of contraction and peak stress of the active stress model were adjusted to fit the maximum rate of rise of pressure, ${(\mathrm{d}P/\mathrm{d}t)}_{\text{max}}$, during the IVC phase. When the LV pressure exceeded the aortic pressure, ejection was initiated by connecting the LV model with the lumped Windkessel model. Pressure and volume traces recorded from a given patient during ejection were used as input to fit the parameters of the Windkessel model, which represent flow resistance of the aorta as well as resistance and compliance of the systemic circulation.³⁰

Model validation

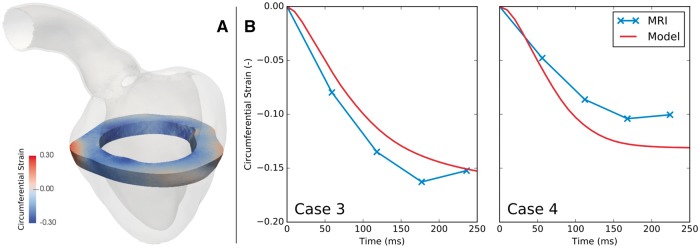
Models were qualitatively validated by comparing ECG, pressure and volume traces predicted by the model with clinically recorded data. As these data were used for fitting the model, they can only be used for assessing the quality of the fit, but not for an independent validation of model predictions. Tagged MRI data were therefore used to validate the strains predicted by the LV model. Two approaches were implemented. Firstly, circumferential strain was evaluated in the model and averaged over the same short axis slice used to acquire the 2D tagged MRI sequence in that patient (Figure 4A). This averaged strain was plotted over time and compared against the circumferential strain determined from analysis of the tagged MRI in a clinical tool, which evaluated circumferential strain using the Sine Wave Modeling approach described by Arts et al.³¹ Secondly, true fiber strains were computed at various depths along a line running transmurally across the LV mid lateral free wall (Figure 5). While true fiber strains are the quantity of primal interest, they cannot be measured accurately invivo with standard 2D tagged MRI techniques, but only in experimental studies.³²

Figure 4.

Validation of model predicted strain against MRI. (A) A slice of the model equivalent to the plane acquired in tagged MRI was extracted, and circumferential strain in this slice was evaluated from the model predicted deformations. (B) Model predicted circumferential strain was averaged over the slice and plotted over systole (red). These strains were compared with strains evaluated from tagged MRI (blue). This validation was performed for cases 3 and 4 only, as no tagged MRI was acquired in cases 1 and 2.

Figure 5.

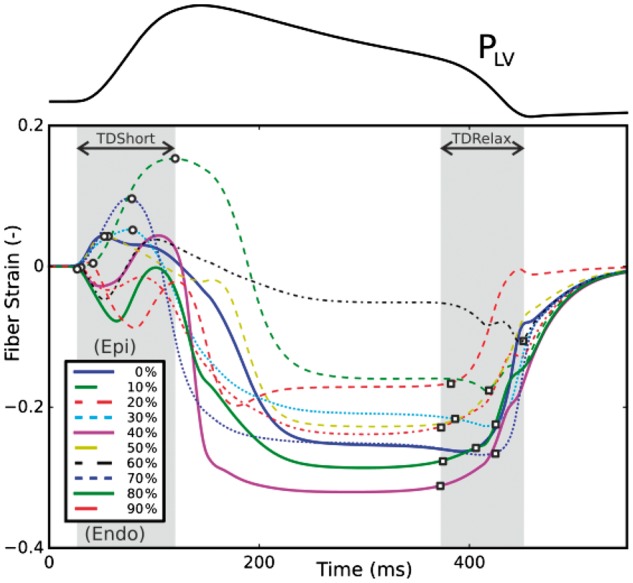
Transmural variability of fiber strain at varying depths from the epi- (0%) to endocardium (100%) along a transmural section of the mid lateral LV wall.

Results

Patient-specific anatomical left ventricle and aorta models

A set of four patient-specific anatomical models of LV and aortic root were generated using a recently developed automated model generation pipeline²⁰ (Figure 1). Apart from correcting the provided clinical segmentation, which required manual intervention, the entire model generation pipeline is fully automated. The individual stages of segmentation smoothing (<10 min), mesh generation, extraction of boundary conditions and fiber assignment (<10 min), facilitate the generation of a complete anatomical LV model in ∼20 min.

Electrophysiology model

First, a human biventricular model was constructed to quantify the influence of the RV on the ECG. Activation sequences and ECG traces were computed first for the biventricular configuration (BiV, Figure 2D top) and then for a reduced model with the RV removed (LV, Figure 2D bottom). The contribution of the RV to both QRS and T-wave is shown in Figure 2E. In both cases, activation was initiated at the septal fascicles and was completed after 37.2 ms. ECG morphologies were very similar in all three leads, but with slightly reduced QRS and T-wave amplitudes in leads I and II when the RV was not present. These rather marginal differences suggest that clinical ECGs are suitable for parameterizing EP in models without an RV.

Using patient-specific anatomical models of the LV, differences between model predicted and clinically recorded ECGs were minimized by adjusting the locations of the septal, anterior and posterior fascicles as well as the time of activation of the anterior and posterior fascicles relative to the septal fascicle. Fitting errors for ΔQRS and peak dipole orientation α were −13.5 ms/18.2 ms/–11.0 ms/–11.0 ms and 4.4°/0.4°/5.2°/−8.1°, respectively for the four cases studied. The fitted activation sequence and ECGs are shown for case 1 in Figure 2B and C.

Validation of coupled electromechanical model

Simulations of cardiac electromechanics were performed on four patient-specific anatomical models of the LV and aortic root (Figure 3B). Mechanical boundary conditions shown in Figure 3A were applied by fixing the model at the termination of the aortic root, and at the bottom of an elastic cushion attached to the apex of the LV. All models were unloaded first to arrive at their stress-free reference volume. The active contraction model was fitted to the maximum rate of LV cavity pressure development ${(\mathrm{d}P/\mathrm{d}t)}_{\text{max}}$. During the ejection phase, outflow of blood into the aorta was regulated by a fitted three-element Windkessel model of afterload. The coupled EM model approximated measured pressure and volume transients within the limits of uncertainty of the clinical data (Figure 3B), with the error in stroke volume ranging from 8.55% to 12.12% and the error in peak pressure ranging from 7.16% to 13.19%.

Measured strains based on tagged MRI and data reported in the literature³² were used for an independent validation of model predictions of LV deformation. As shown in Figure 4B for cases 3 and 4 (tagged MRI was not available in cases 1 and 2), there was overall agreement between circumferential strain calculated directly from the model and that estimated from MRI. Strains are plotted relative to the time of first shortening to ensure proper synchronization between data. There is some discrepancy between the model and MRI-derived strains in these two cases, however bearing in mind the limited effective resolution of the magnetization grid in tagged MRI, these discrepancies are within an acceptable margin for error. Nevertheless, our future planned inclusion of a realistic pericardial boundary condition will likely improve the realism of the deformations and strains predicted by our model.

Fiber strains in the mid lateral LV free wall at varying depth from the epicardium (0%) towards the endocardium (100%) were computed for each case. Transmural variability in fiber strains is shown in Figure 5 for case 3. Overall trends were in line with experimental findings. The onset of myofiber shortening occurred earlier in the endocardium than in the epicardium due to a short period of prestretch preceding myofiber shortening. A significant transmural gradient in fiber strain as well as in onset of shortening and relaxation was observed, with dispersions in the onset of shortening and relaxation of 69.5 ±30.8°ms and 97.8 ± 21.4°ms respectively.

Discussion

The presented methodology allows the efficient generation and execution of patient-specific EM models of LV and aortic root that are suitable for driving simulations of cardiac and vascular hemodynamics when coupled with a blood flow model. The feasibility of generating patient-specific EM models efficiently was demonstrated by modeling a set of four cases selected from a clinical trial of AVD and CoA patients. After appropriate parameterization, simulated LV beats faithfully reproduced invasively recorded hemodynamic data as well as QRS duration and morphology of Einthoven lead I and II ECG recordings, indicating that the insilico LV model is representative of the electromechanical behavior of the modeled patient heart. Such EM models can be either bidirectionally linked with a blood flow model using a body-conformal coupling^8,10,33,34 or a static body nonconformal coupling FSI approach such as the immersed boundary method^35,36 or fictitious domain methods,^37,38 or they can be used in a one-way coupling approach where the EM model is coupled to a blood flow model, but the feedback of hemodynamics back to the EM model is ignored.³⁹ Both uni- and bidirectionally coupled FSI models enable the approximation of sparse and noisy clinical flow data at an enhanced spatio-temporal resolutions, thus allowing the computation of derived quantities such as pressure gradients^40,41 or wall shear stresses,^42,43 which can normally be obtained only through invasive procedures such as catheterization.⁴⁴ While unidirectional FSI models are suitable for applications focused on analysing the hemodynamic status quo, bidirectional models may go beyond pure analysis and serve in a wider range of application scenarios by making predictions on LV performance in response to interventions that alter afterload conditions.

While no coupling with a fluid flow model was performed in this study as our main focus was on automating the workflow for building patient specific EM models to drive a fluid flow model, this constitutes an important and nontrivial step towards more holistic fully coupled EMF models that represent all the involved physical fields and their bidirectional mechanistic links based on first principles. An important building block is the anatomical modeling approach, which is based on a fully automatic, image-based unstructured meshing technique⁴⁵ that enables the generation of larger cohorts of models in high throughput modeling studies where geometric fidelity of a model is only limited by the quality of the segmentation process.²⁰

Model fitting and validation

Model fitting efforts were mainly focused on reproducing clinically recorded ECG data during the activation phase (Figure 2C), and on pressure and LV volume traces during the isovolumetric contraction and ejection phases, as these phases govern cardiac motion that is driving flow in the LV outflow tract across the aortic valve into the aorta. The ECG fitting procedure resulted in an acceptable fit of the ECG in terms of QRS morphology and duration. The computational costs of the ECG fitting procedure were minor. The EP simulation of an entire cardiac cycle including the prediction of the ECG lasted <15 s and, typically, less than 100 runs were required to achieve a satisfactory fit, amounting to an overall expenditure of time of <25 min. Nonetheless, in view of clinical applicability more automated data-driven fitting techniques will be indispensable to enable parameterization compatible within clinical time scales²³ and without the need for expert knowledge on the ECG genesis to steer the fitting procedure.⁴⁶

Fitting of the mechanical model components was computationally a more demanding endeavor. The major costs incurred for fitting passive mechanical tissue properties to the Klotz relationship (≈ 0.5°days) and the fitting of the active stress model (≈ 1°day). Fitting of the circulatory Windkessel parameter and the synchronization of volume with pressure traces was comparably cheap and could be typically achieved in <20 min. Executing the simulation of one heartbeat with the final fitted model lasted ∼4 h. Cost of fitting and execution time showed some variability between cases. The pediatric cases studied proved to be particularly costly to model due to the very high ejection fractions of pediatric patients, which imposed severe constraints on keeping the numerical solution process stable. With the developed modeling workflow the total cost of building a CFD-ready kinematic model based on biophysical EM models is in the range of 1–2 days, which is comparable in effort to 20–50 work hours for creating a CFD-ready image-based kinematic model.¹⁴

The accuracy of the fitted model must be assessed relative to the uncertainty of the data used for fitting. Clinical measurements of LV pressure and volume are in general afflicted with significant uncertainties. As evident in Figure 3, pressures in cases 1, 3 and 4 are apparently affected during ejection by the frequency response of the pressure transducer. Further, pressure and volume recordings were not performed simultaneously, and were recorded at different heart rates. These recordings must be synchronized, introducing additional uncertainties. Moreover, the pediatric cases studied featured very high ejection fractions which tended to be underestimated by the model. Such high ejection fractions are associated with significant deformation of the LV which complicates the task of finding a numerically stable setup to produce a large enough stroke volume.

As an independent validation of model prediction fiber strains were computed along a transmural line across the LV mid lateral free wall and compared against experimental data gathered from canine ventricles.³² While we observed similar trends in terms of onset of shortening in the transmural direction, there was a noticeable variation between the four cases and differences to experimental studies, for instance, the earliest onset of shortening was not always at the subendocardial layer and the onset was not progressively delayed towards the epicardium in all cases.

A direct comparison between simulated tagged MRI data based on and the circumferential and radial strain data derived from clinical MRI data is still ongoing. Due to longitudinal displacement of the LV during contraction and relaxation clinically measured strains based on tagged MRI yield ‘apparent’ strains, which deviate from real strains due to averaging effects over the LV volume moving in and out of the image plane. Our approach of accounting for these effects in a virtual tagged MRI experiment an analysing the generated 2D tags with the same clinically used software accounts for these discrepancies and thus facilitates a direct comparison on a like-to-like basis between clinical and simulated data. This aspect of the validation work is still ongoing and is not conclusive yet since strains computed by the clinical tag analysis software require further verification.

Unidirectional vs. bidirectional coupling

Unidirectionally coupled FSI models use kinematic models to describe the deformation of the LV endocardium, which serve as input to drive a blood flow model. Kinematic models can be constructed either by deriving endocardial deformations from segmented 4D image datasets⁴⁷ or by using biophysically based EM models as shown in this article, where the motion of the LV endocardium is extracted from a deforming 3D finite element model.³⁹ For applications such as the analysis of blood flow patterns in a given patient both approaches are suitable, but image-based kinematic models prevail as the construction of EM models is in general more involved. EM models require more clinical data as constraints, some of which such as LV pressure cannot be acquired noninvasively with imaging technologies. In contrast, deriving CFD-ready kinematic models from segmentation and reconstruction of patient specific cardiac motion seems less labor intense, although the model generation cannot yet be fully automated and various issues related to the spatio-temporal resolution of the image and ensuring a consistent topology of endocardial surfaces over time also impose a significant manual work burden.¹⁴ However, an important limitation of image-based kinematic modeling is the spatio-temporal resolution of current tomographic imaging modalities which requires interpolation for constructing the kinematic model. For instance, due to the limited temporal resolution—in the range of 50–200 ms—the accurate tracking of faster cardiac motion is effectively impeded. Moreover, the image-based assessment of local cardiac motion and deformation may also be inaccurate as the underlying frame-to-frame registration procedure relies on high-resolution volumetric images of small-scale anatomical features such as the endocardial trabeculae.⁴⁸ Such features act as material points that can be used in a registration procedure to track regional wall deformations throughout the cardiac cycle.⁴⁹

A key advantage of EM models is their ability to study the impact of any alteration in the EM physics on hemodynamics in both healthy and pathological scenarios.³⁹ As opposed to image-based kinematic models, EM models can be perturbed by modifying the EP activation sequence, tension development or preload and afterload conditions to provide the kinematics of an altered heartbeat, thus allowing to investigate also its impact on blood flow. Depending on the particular question under study therefore, the additional investment into a more elaborate model construction may be well justified.

However, to fully exploit the potential of EM models requires a bidirectional linked FSI model. Disorders such as AVD and CoA are characterized by pressure and/or volume overload affecting the linked system of the LV, aortic valve and aorta. Such overload conditions induce a complex cascade of myocardial and vascular wall remodeling which, if left untreated, can progress to heart failure. Therapies for correcting these conditions such as aortic valve repair or stenting affect not only intracardiac and vascular hemodynamics, but are known to have a significant impact upon LV performance itself due to altered afterload conditions. Here the use of EM models coupled with FSI-based models of cardiac and vascular hemodynamics may prove beneficial as they comprehensively represent the entire physics of a heartbeat based on first principles, and thus may be able to make useful predictions on post-treatment cardiac function. Therefore we anticipate EM models to play an increasingly important role in future clinical applications which go beyond analysing the status quo of a patient’s hemodynamics.

Limitations

The LV EM models used in this study provide a simplified representation of the patient’s heart. Many physiological aspects of cardiac EM function are not explicitly represented or simplified. The chosen mechanical boundary conditions are not representative of an invivo situation where the heart is enclosed by the pericardium.⁴ For the sake of faster fitting length dependence in the active stress model was ignored. Model parameters cannot be uniquely identified, even with the extensive datasets available. This is also true for the ECG-driven fitting of the electrical activation sequence. In principle, entirely different activation sequence may lead to an equally close or even better fit.

For the sake of validating the EM model a set of patients treated for coarctations was used as invasive catheterization is performed in these cases on a routinely basis. Typically with AVD patients as in case 2 this is not the case, that is, no pressure catheterization of the LV was performed and as such pressure traces are not available. In this case a characteristic LV pressure transient, scaled to match peak LV systolic pressure estimated from cuff pressure and the duration of ejection seen in the cine MRI derived volume transient, was used for parameterization of the model. Of particular relevance for the intended application of EM models as driver of fluid flow model is the careful validation of endocardial motion against cine MRI data. Such a comparison has not been performed yet as accurate segmentations have been performed only for the end-diastolic state.

Conclusions

Using efficient model generation and parameterization pipelines²⁰ along with computationally efficient numerics¹⁹ the use of EM models for driving simulations of cardiac and vascular hemodynamics is becoming a feasible option.³⁹ Despite the efficiency of the developed workflow, the costs involved in building and executing EM models remains significant, on the order of 1–2 days, but this is comparable to the cost of building CFD-ready image-based kinematic models.¹⁴ A potential main advantage of using EM models as drivers of fluid flow simulations is their capability of predicting the response to interventions which affect the conditions of afterload. Overall, the developed methodology constitutes an important and nontrivial step towards more holistic fully coupled EMF models that represent all the involved physical fields and their bidirectional mechanistic links based on first principles.