A QUANTITATIVE REVIEW OF OVERJUSTIFICATION EFFECTS IN PERSONS WITH INTELLECTUAL AND DEVELOPMENTAL DISABILITIES

Abstract

The overjustification hypothesis suggests that extrinsic rewards undermine intrinsic motivation. Extrinsic rewards are common in strengthening behavior in persons with intellectual and developmental disabilities; we examined overjustification effects in this context. A literature search yielded 65 data sets permitting comparison of responding during an initial no-reinforcement phase to a subsequent no-reinforcement phase, separated by a reinforcement phase. We used effect sizes to compare response levels in these two no-reinforcement phases. Overall, the mean effect size did not differ from zero; levels in the second no-reinforcement phase were equally likely to be higher or lower than in the first. However, in contrast to the overjustification hypothesis, levels were higher in the second no-reinforcement phase when comparing the single no-reinforcement sessions immediately before and after reinforcement. Outcomes consistent with the overjustification hypothesis were somewhat more likely when the target behavior occurred at relatively higher levels prior to reinforcement.

The merits of reinforcement procedures in educational settings have been debated for decades, and a common criticism of these procedures centers on what is often termed the overjustification hypothesis (Bem, 1972). The overjustification hypothesis predicts that rewards delivered by an external agent to engage in an activity reduce subsequent, internal, motivation to engage in that activity after explicit extrinsic rewards have been discontinued. By definition, an overjustification effect is manifest if levels of behavior following discontinuation of reward are lower than levels of behavior prior to reward.

Investigators have typically examined overjustification effects using between-group comparisons. These studies have frequently involved delayed consequences whose effectiveness as reinforcers had not been established. In one of the first studies on the topic, Deci (1971) rewarded college students’ performance on a number of tasks with either money or verbal rewards. The delivery of money appeared to negatively affect performance after discontinuation of monetary rewards, whereas participants provided with verbal rewards showed an increase in performance after discontinuation of verbal rewards relative to baseline responding. Greene and Lepper (1974) investigated the effects of expected and unexpected rewards on activity interest, defined as time spent engaging in an activity. They assigned typically developing school-aged children to an unexpected-reward group, an expected-reward group, or a no-reward group. For both reward groups, the external reward was a “good-player award” consisting of the child’s name and the school’s name engraved on a gold star. Task engagement was significantly lower after rewards relative to before rewards, but only when the reward was expected.

Subsequent studies have investigated the overjustification effect in educational settings using methods similar to Deci (1971) and Greene and Lepper (1974), but varied task and reward types, as well as the contingency between behavior and reward. Numerous reviews and meta-analyses have since focused on determining if and when the overjustification effect occurs and what variables predict the absence, presence, and degree of such an effect. For example, Cameron and Pierce (1994) separately reviewed studies that used group designs to determine reward effects on behavior and studies that used single-case research methodology to assess direct-acting effects of reinforcers on behavior. Studies using single-case designs were included only when a reinforcement effect was demonstrated by an increase in behavior during the reinforcement phase. Their meta-analysis revealed no consistent detrimental effect of either reinforcement or rewards on motivation. Results from group designs indicated that verbal rewards did not produce a decrease in time spent on task or enjoyment, gauged via questionnaires on self-reported interest in the activity. Tangible rewards produced no effect on performance when they were delivered unexpectedly as opposed to when they were announced in advance. However, expected rewards were not detrimental when they were delivered contingent on task performance. Results from the single-case design studies indicated that reinforcement led to an increase in time spent on the task in the second no-reinforcement phase relative to the first.

Few studies have examined overjustification effects using single-case research methodology to compare baseline levels of responding on educational tasks to levels after discontinuation of reinforcement. Bright and Penrod (2009) did not observe overjustification effects when academic task engagement of typically developing children was followed with either verbal praise or stimuli established as either reinforcing or nonreinforcing via reinforcer assessment. Other single-case analyses of the overjustification effect have produced similar results, suggesting that when contingent reinforcement is delivered, an overjustification effect is unlikely (e.g., Feingold & Mahoney, 1975; Vasta & Stirpe, 1979).

To date, no research synthesis of the overjustification effect has specifically focused on individuals with intellectual and developmental disabilities, yet a specific focus on this population seems warranted. Procedures based on applied behavior analysis are widely implemented with this population, as evidenced by reviews suggesting strong support for these interventions (e.g., Virués-Ortega, 2010), as well as backing by scientific, professional, and government organizations such as the American Academy of Child and Adolescent Psychology (Volkmar et al., 2014), Centers for Disease Control (Centers for Disease Control and Prevention, 2015), and U.S. Surgeon General (U.S. Department of Health and Human Services, 1999). As programmed reinforcement contingencies are a behavior-analytic technique commonly implemented with this population (Vollmer & Hackenberg, 2001), a focused examination seems highly relevant. The purpose of the current study was therefore to determine the likelihood of outcomes consistent with the overjustification hypothesis when reinforcement contingencies are withdrawn for persons with intellectual and developmental disabilities. This analysis was conducted by extracting data on response levels from published cases containing such an arrangement. Secondary analyses were conducted to (a) determine the likelihood of such an effect when data samples included only the periods immediately before and immediately after the reinforcement contingency, and (b) determine whether certain response or contingency variations consistently predicted decreases in response levels after the withdrawal of reinforcement.

METHOD

We conducted an electronic search of six journals that routinely publish preference and reinforcer assessment studies with persons with intellectual and developmental disabilities. Reinforcer assessments seemed ideal for this analysis because they permit a direct comparison of response levels before and after the introduction of a reinforcement contingency. The journals included Behavioral Interventions, Behavior Modification, the Journal of Applied Behavior Analysis, the Journal of Developmental and Physical Disabilities, Research in Autism Spectrum Disorders, and Research in Developmental Disabilities. We used the search function on each journal’s website using the key words “reinforcer assessment” anywhere in the article, from 1994 through 2014. The search identified 265 candidate studies, which we reviewed for inclusion using the criteria described below.

Inclusion Criteria

We included individual data sets in the analysis if they had the following characteristics: (a) reinforcer assessment data with a schedule of positive reinforcement for a previously mastered task (i.e., data sets in the context of acquisition were excluded, as the participant may have lacked the skills to complete the task prior to reinforcement); (b) a minimum of one ABA design (A = no-reinforcement, B = reinforcement) with a clear reinforcement effect (i.e., the authors of the study concluded that levels of behavior during the B phase were clearly and consistently above the A phases) and at least three data points in all phases; (c) mean levels of responding in the initial no-reinforcement phase that exceeded zero (i.e., data sets with no responding during the initial no-reinforcement phase were excluded because one cannot observe a postreinforcement decrease below zero); and (d) responding that was measured in terms of response rate (or frequency), percentage of intervals (or sessions), or percentage of trials in which behavior occurred. Moreover, all participants had to have been diagnosed with an intellectual or developmental disability. Using these criteria, we identified 65 qualifying data sets from 27 studies. Table 1 lists each participant from each study, along with task type, reinforcement schedule, and reinforcer type for each data set included in the analysis.

Table 1.

Study of Origin, Participant Name, Task, Reinforcement Schedule, and Reinforcer Type for Each Data Set Included in the Analysis

Study	Participant	Task	Schedule	Reinforcer
Clay et al., 2013	Alex	Put block in bowl	FR1	Social
	Kyle	Put block in bowl	FR1	Social
	Sofia	Put block in bowl	FR1	Social
DeLeon et al., 2014	Jillian	Sort office supplies	FR1	Leisure
DeLeon & Iwata, 1996	Jack	Press microswitch	FR1	Edible
	Rupert	Stamp paper	FR1	Edible
DeLeon et al., 1999	Charlene	Brush hair	FR1	Leisure
	Robbie	Match coins	FR1	Leisure
DeLeon et al., 1997	Alex	Fold towels	FR1	Leisure
	Sheila	Dry hands	FR1	Leisure
Frank-Crawford et al., 2012	Glenn	Place paper in bin	FR1	Edible
Graff & Ciccone, 2002	Andy	Press button	VR5/10	Edible
	George	Press button	VR5/10	Edible
	James	Press button	VR5/10	Edible
Graff & Gibson, 2003	Christopher	Press button	VR10	Edible
	Connor	Press button	VR10	Edible
	James	Press button	VR10	Edible
Graff et al., 2006	Charlie	Sort silverware	FR1	Edible
	James	Stamp paper	FR1	Edible
Graff & Larsen, 2011	Chris	Sort silverware	FR3	Edible
	Jess	Sort silverware	FR3	Edible
	Matt	Sort silverware	FR12	Edible
	Veronica	Sort silverware	FR5	Edible
Groskreutz & Graff, 2009	Derrick (1)	File paper	FI30s	Edible
	Luis (1)	File paper	FI30s	Edible
	Andrew (2)	Sort silverware	FI30s	Edible
	Derrick (2)	Fill dispenser	FI30s	Edible
	Stewart (2)	Sort silverware	FI30s	Edible
Hanley et al., 2003	Rob	Stamp/stuff paper	FR1	Leisure
Higbee et al., 2000	Brenda	Press microswitch	FR5	Edible/Leisure
	Casey	Press microswitch	FR15	Edible
	Daryl	Press microswitch	FR2	Leisure
	Marcy	Press microswitch	FR3	Edible/Leisure
	Marvin	Press microswitch	FR6	Edible
Higbee et al., 2002	Corey	Sort socks	Varied	Edible
	Kyle	Sort socks	Varied	Edible
	Steven	Sort socks	Varied	Edible
Logan et al., 2001	Jason	Press microswitch	FR1	Leisure
	Michael	Press microswitch	FR1	Leisure
	Robert	Press microswitch	FR1	Edible
Najdowski et al., 2005	Ethan	Transfer beans	FR1	Edible
	Sam	Put block in bucket	FR1	Edible
Nuernberger et al., 2012	Cade	Sort silverware	FR4	Social
	Natasha	Sort items	FR4	Social
	Nigel	Sort blocks	FR3	Social
Penrod et al., 2008	Cedar	Deposit bean	PR	Edible
	Sam	Track/touch card	PR	Edible
Piazza et al., 1997	Ty	Touch card	FR1	Leisure
Piazza et al., 1998	Jerry	Press switch	FR1	Social
	Tom	Press switch	FR1	Social
Roane et al., 2005	Floyd	Sort envelopes	PR	Leisure
	Melvin	Add single digits	PR	Leisure
Taravella et al., 2000	Brad	Put block in bucket	FR1	Leisure
	Mark	Stand In-square	FR1	Leisure
Tarbox et al., 2007	Sam	Press microswitch	FR1	Leisure
	Seth	String beads	FR1	Leisure
Tessing et al., 2006	Justin	Add single digits	FR2	Leisure
	Kyle	Add single digits	FR2	Leisure
Thompson & Iwata, 2000	Biz	Open container	FR1	Edible
	Deb	Open container	FR1	Edible
	Samantha	Open container	FR1	Edible
Wilder et al., 2008	Alex	Sort cards	FR2	Leisure
	Bill	Sort cards	FR2	Leisure
	Don	Sort cards	FR2	Leisure
Zarcone et al., 1996	Ray (2)	Stack cups	FR1	Leisure

Interobserver agreement (IOA)

From the 265 possible studies discovered in the initial search, a second reviewer (i.e., master’s or doctoral-level behavior analyst) coded 89 articles (33.6%) to determine if each data set met the inclusion criteria. The percentage of data sets in each article with agreement averaged 99% (range, 66.7% to 100.0%). Across articles, there was a total of four disagreements relating to participant diagnosis, appropriate ABA design, or presence of a reinforcement effect. For each disagreement, the two raters discussed the discrepancy and reached a consensus.

Data Analysis

Currently, there is no consensus on how to accurately derive quantitative estimates of treatment effects for studies using single-case research methodology (Shadish, Hedges, Horner, & Odom, 2015). What Works Clearinghouse has recommended the use of multiple computational procedures to assess the magnitude of treatment effects with the suggestion that stronger conclusions may be drawn when similar findings are observed across indices (Kratochwill et al., 2010). The present study computed treatment effects through use of both parametric and nonparametric metrics (Hedge’s g and Tau-U, respectively, described below).

Data extraction

GetData Graph Digitizer 2.22 was used to extract data points for each qualifying data set. GetData Graph Digitizer is a software program used for determining precise values of each data point in a digitized graph or plot. Using scanned JPEG format electronic images, X–Y data points were obtained from each qualifying data set by forming a digitized plot that overlapped the data display and assigning a range of values for the X and Y axes. From there, the program allows the researcher to identify the values of each data point given in scientific notation. We then calculated effect sizes (described below) with the known Y values to compare response levels before and after the reinforcement phase.

Effect size calculations and meta-analysis

Hedges’ g. We used Hedges’ g as the parametric measure of effect size. Typically, Cohen’s d (Cohen, 1988) is used in meta-analyses to reflect the difference between the means of two groups divided by the pooled within-group standard deviation (e.g., Deci, Koestner, & Ryan, 1999). Hedges’ g is based on Cohen’s d, but corrects for bias in small sample sizes (Cumming, 2012; Lakens, 2013). In the current analysis, we compared the mean levels of responding in the first and second no-reinforcement phases. We included only the first two no-reinforcement phases in each data set to account for possible reinforcement history effects across further phases and excluded one data set because we were unable to identify which of multiple reinforcer assessments came first, as they were depicted on separate graphs. We calculated the means and standard deviations using the data point values given by GetData Graph Digitizer, and used these to calculate g values. The formula used to calculate effect sizes was:

$$g=\frac{(M_1-M_2)}{(S{D}_1+S{D}_2)/2}\times (1-(3/(4\ast n-9)))$$

This formula was calculated with respect to the first and second no-reinforcement phases, where M₁ and M₂ are the respective means, SD₁ and SD₂ are the respective standard deviations, and n is the total number of data points being compared (i.e., n₁ + n₂). A positive g value reflects a mean decrease in responding in the second no-reinforcement phase relative to the first, an outcome consistent with the overjustification hypothesis. A negative g value, by contrast, reflects a mean increase in responding in the second no-reinforcement phase relative to the first, an outcome inconsistent with the overjustification hypothesis.

We also reanalyzed these outcomes using only the last three data points of each phase following recommendations from Marquis et al. (2000). Reinforcer assessments are typically arranged as within-series repeated measures, and those repeated measures are often associated with within-phase changes in response levels (i.e., transition states). For example, immediately after the discontinuation of reinforcement contingencies, response levels may still be influenced by the recent local history of reinforcement, and it may take several sessions for levels to stabilize as a result of the newly introduced contingency. One might therefore argue that response levels at stability are a more accurate reflection of intrinsic interest than the entire phase that includes behavior in transition. To minimize the potential influence of transition states, the reanalyses considered only the last three sessions of the first and second no-reinforcement phases.

Most studies that have examined the detrimental effects of extrinsic reinforcement on intrinsic motivation used between-subject experimental designs. In many of these studies, means of reward and no-reward groups were examined only once prior to introducing the independent variable (reward vs. no reward) and only once following the independent variable manipulation. To make the current results comparable to investigations conducted in this manner, we additionally examined data from the last session of the first no-reinforcement phase and the first session of the second no-reinforcement phase. Because effect size calculations are not possible for single data points, the data were statistically compared using a paired-sample t-test.

Tau-U analysis

The percent of nonoverlapping data (PND) has been commonly used to assess treatment effects in single-case research (Maggin, O’Keefe, & Johnson, 2011). However, PND does not describe the magnitude of treatment effects between phases and is influenced by trend and outliers (Wolery, Busick, Reichow, & Barton, 2010). Therefore, we used Tau-U, a distribution-free nonparametric data overlap metric that can control for baseline trend, as the overlap method (see Parker, Vannest, Davis, & Sauber, 2011, for computation). An additional benefit of using Tau-U is that the variance of Tau can be calculated and used to aggregate the effect sizes in a traditional meta-analytic model (Borenstein, Hedges, Higgins, & Rothstein, 2009). We calculated Tau-U using all data and Tau-U using only the last three data points for comparison with the g results via an online calculator developed by Vannest, Parker, and Gonen (2011) at singlecaseresearch.org.

Meta-analysis

We estimated a random-effects meta-analysis model using the Tau-U for all data, Tau-U for the last three data points, and variance of Tau values in the Metafor package (Viechtbauer, 2010) in R (R Core Team, 2013). We used a random-effects model because our goal was to generalize the findings beyond the studies in the current analysis (Scammacca, Roberts, Vaughn, & Stuebing, 2015) and to accurately model significant heterogeneity. A positive effect size would indicate that the levels of responding in the first no-reinforcement phase were higher than the second, which would be consistent with the overjustification hypothesis. However, a negative effect size would indicate that the levels of responding in the second no-reinforcement phase were higher than the first, suggesting that the overjustification effect was not observed.

Secondary analyses

We conducted secondary analyses to identify the conditions under which the delivery of known reinforcers was more likely to produce levels of behavior below initial baseline levels after reinforcement had been discontinued. Three of these analyses consisted of examining effect sizes as a function of reinforcer type (edible, leisure, social), schedule of reinforcement, and task type (a functional task that promoted skill development—e.g., sorting silverware, brushing hair—vs. nonfunctional task—e.g., button pressing). None of these analyses produced significant differences (data available upon request).

A fourth analysis examined the strength of the relation between effect sizes and levels of responding before reinforcement was introduced. Cameron, Banko, and Pierce (2001) conducted a meta-analysis that suggested an outcome consistent with the overjustification hypothesis was more likely when the task was of “high initial interest” before rewards were arranged. However, interest levels generally were classified according to subjective self-reports, via questionnaire. The purpose of our analysis was to determine if effects consistent with the overjustification hypothesis are more likely when the behavior occurs at a relatively high rate during the initial baseline, which may be a more objective approximation of high “initial interest.”

Absolute levels of responding are difficult to compare across individuals because of inherent differences in dependent variables (e.g., rate, frequency, percent intervals, etc.), tasks, participant abilities, and other variables. We therefore normalized initial levels of responding by transforming them into a proportion relative to the levels observed during the reinforcement periods (i.e., mean response levels of first no-reinforcement phase divided by mean response levels during the reinforcement phase). As such, higher proportions indicated that reinforcement increased responding by a lower percentage; lower proportions indicated that reinforcement increased responding by a higher percentage. A higher proportion is thus perhaps analogous to higher intrinsic interest (i.e., responding was already occurring at relatively higher levels prior to the introduction of reinforcement).

We examined the relation between this proportion and effect sizes for a subset of the total data sets—those for which the reinforcement phase consisted of only one schedule and one stimulus. We excluded data sets for which the reinforcement phase consisted of a concurrent schedule, a multielement design comparing multiple reinforcers, or if the schedule values varied within the reinforcement phase (e.g., FR 1 for the first three sessions, VR 3 for the next few sessions, etc.), as these factors may have diminished absolute levels of responding under the reinforcement contingency. After these exclusions, 25 of the 65 data sets remained for analysis. We then calculated a Pearson product-moment correlation coefficient to examine the relation between those proportions and effect sizes. The analysis was then repeated with only the last three data points of the no-reinforcement and reinforcement phases. If higher proportions can be interpreted as higher intrinsic interest, and the detrimental effects of extrinsic reinforcement are more common for behavior of higher intrinsic interest, then one would expect a positive relation between proportions and effect sizes.

Data Extraction Accuracy and Interobserver Agreement

Data extraction accuracy

We evaluated the accuracy of the GetData Graph Digitizer 2.22 program in extracting numerical values by comparing the program’s output to known values of hypothetical data sets we constructed. We created three separate graphs in Excel™, containing 30 data points each (10 in Phase A, 10 in Phase B, and 10 in return to Phase A) ranging from 0.0 to 2.6 responses per min in graph one, 12.8 to 80.0 responses per min in graph two, and 92.0 to 189.3 responses per min in graph three. We converted the graphs to JPEG files, and entered them into the program using the same procedures described for graphs extracted from published papers. For each data point, we divided the actual value by the observed value from the program, and multiplied by 100. The percentage accuracy for each data point in all phases averaged 100.0%, 100.0%, and 99.0% accuracy for the first, second, and third graph, respectively.

IOA

From the data sets included in the analysis, a trained graduate student independently analyzed 33 (50.8%) via the computer program GetData Graph Digitizer 2.22. The second observer extracted the value of each of the last 3 data points in the first and second no-reinforcement phases. We used percentage agreement to calculate interrater reliability among scores, dividing the smaller value by the larger value and multiplying by 100. Mean percentage agreement was 87.3% (range of data points, 0.0% to 100.0%; range of data sets, 54.4% to 99.7%). The occasional low measure of IOA typically occurred for data points near zero, due to the precision of the program at extremely low values. Specifically, for each data set, each observer used the software to manually plot the axes and select the data points to capture. Depending on the number of pixels in the data set and the meticulousness of the observer, the same data point could be plotted at .00 and .01. This is a minuscule absolute difference, in terms of the overall effect size for the data set, but would result in 0% agreement for that data point. This occurred for 12 data points, or 6.1% of the total sample.

RESULTS

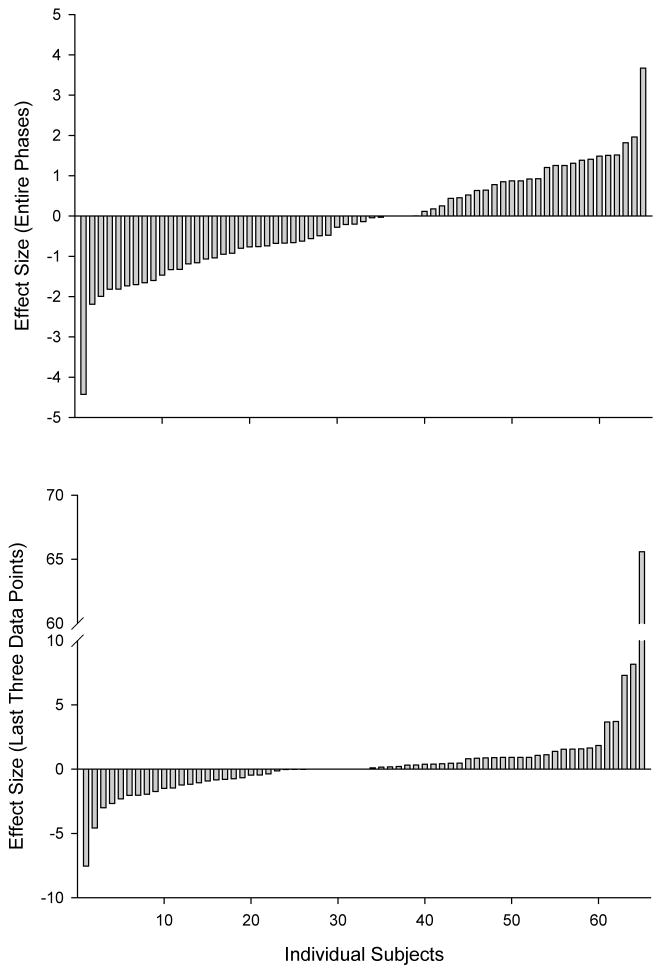
Figure 1 depicts the distribution of individual Hedges g effect sizes. The top panel represents all of the data from the first and second no-reinforcement phases. The values ranged from −4.43 to 3.67 with a mean effect size of −0.14 (median = −0.14, mode = 0.00). This distribution is slightly skewed below zero, a result inconsistent with the overjustification hypothesis. A single-sample t-test was conducted to test the hypothesis that the mean effect size differed from zero. The results of this analysis yielded a nonsignificant result (t = .90, p = .186), suggesting that the mean was not different from zero. That is, on average, effect sizes were just as likely to be positive as they were to be negative.

Figure 1.

Distribution of Hedges g effect sizes for each individual included in the analysis. Effect sizes in the top panel were calculated using the entire phase, effect sizes in the bottom panel were calculated using only the last three sessions of each phase.

The bottom panel of Figure 1 represents the data from only the last three sessions of the first and second no-reinforcement phases. The range of effect sizes was greater (−7.54 to 65.59), but the results were similar to the previous analysis with a mean effect size of 1.11 (median = 0.00, mode = 0.00). Although this distribution is skewed above zero, which would be consistent with the overjustification hypothesis, results of the single-sample t-test yielded a nonsignificant result (t = 1.06, p = .146). Furthermore, when this analysis was conducted again after excluding the one highly divergent outlier, the mean effect size was .10 (t = 1.02, p = .155), again suggesting that the mean was not different from zero. For this analysis, there were three datasets with no variation in responding in either no-reinforcement phase, precluding formal calculation of an effect size. However, for all three, the mean and standard deviation of the first no-reinforcement phase was identical to the second no-reinforcement phase, so we identified the effect size as 0.00. There were no such cases in the analysis that included data from the entire phase.

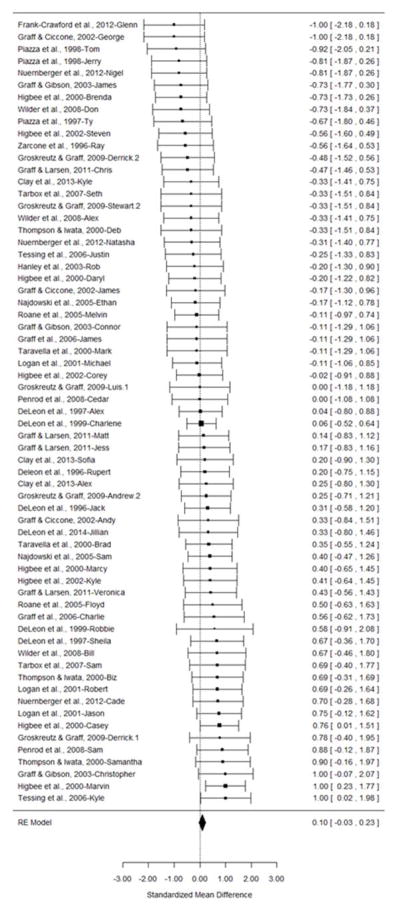
Figure 2 depicts the distribution of individual Tau-U effect sizes using the entire phase and the estimate of the mean effect size. The dark boxes in the forest plot denote the effect size for the individual data sets and the bars represent standard error. The dark diamond at the bottom represents the average weighted Tau-U effect size. The mean effect size across all 65 data sets was 0.099 (p =.14, 95% CI = −0.03, 0.23), which indicates results that are inconsistent with the overjustification hypothesis. Furthermore, when the individual effect sizes were calculated using only the last three data points in each phase, the mean effect was −0.032 (p = .69, 95% CI= −0.19, 0.12). Overall, the results from both meta-analysis models reveal no statistically significant differences between the first and second no-reinforcement phases.

Figure 2.

The forest plot distribution of individual effect sizes calculated using Tau-U and the estimate of the mean effect size. Effects sizes are calculated using the entire phase. Each row represents the data from a participant within a given study. For some participants, multiple data sets were available and a number was assigned to these participants to denote which data set was evaluated.

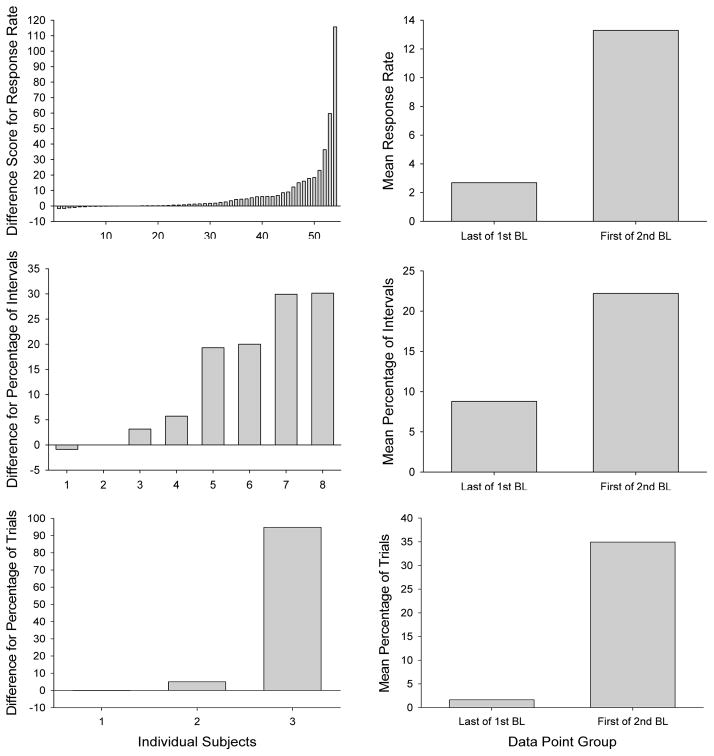
The three left panels of Figure 3 depict the distribution of difference scores for response rates (n = 54), percentage of intervals (n = 8), and percentage of trials (n = 3) when the last data point in the first no-reinforcement phase was subtracted from the first data point in the second no-reinforcement phase. The graphs show that difference scores, for each type of measurement, were strongly skewed above zero suggesting that values tended to be higher in the first session of the second no-reinforcement phase than in the last session of the first no-reinforcement phase, an outcome not consistent with the overjustification hypothesis.

Figure 3.

Distribution of difference scores (first point of second baseline – last point of first baseline) in the left panels and mean responding for the last point of the first no-reinforcement phase and first point of the second no-reinforcement phase in the right panels, across data sets depicting response rates (top panels), percentage of intervals (middle panels), and percentage of trials (bottom panels).

The three panels on the right side of Figure 3 depict the mean responding for the last point of the first no-reinforcement phase and first point of the second no-reinforcement phase. The upper right panel depicts mean response rates, which were significantly lower (p =.002) for the last point of the first no-reinforcement phase (M = 2.68) than the first point of the second no-reinforcement phase (M =13.29). The middle right panel depicts mean percentage of intervals, which were significantly lower (p = .011) for the last point of the first no-reinforcement phase (M = 8.79%) than the first point of the second no-reinforcement phase (M = 22.21%). The bottom right panel depicts mean percentage of trials, which were lower for the last point of the first no-reinforcement phase (M = 1.66%) than the first point of the second no-reinforcement phase (M = 34.9%), but the small sample size precluded a meaningful statistical analysis.

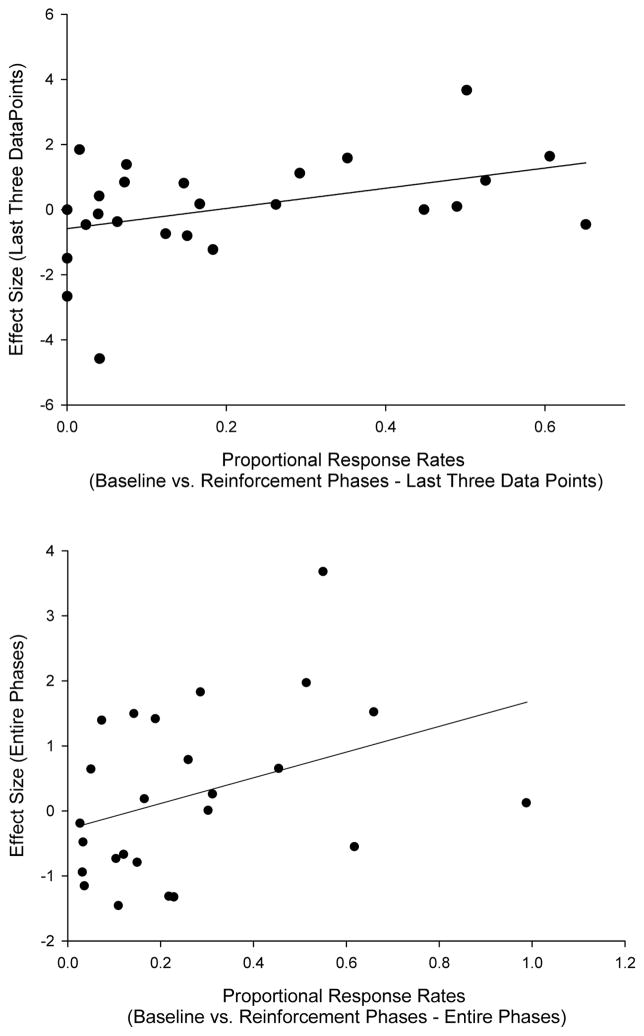
Figure 4 depicts scatterplots relating proportional response levels to effect size. The top panel represents all of the data from those phases. A Pearson product-moment correlation yielded a coefficient of .37 that approached significance (p = .065), with response levels accounting for 14.0% of the variance. The proportions in the bottom panel of Figure 4 represent data from only the last three sessions of the first no-reinforcement phase and the reinforcement phase. This relation yielded a significant r value of .41 (p =.041), with response levels accounting for 16.8% of the variance. These relations support the notion that effects consistent with the overjustification hypothesis are more likely to be observed for behavior that occurs at higher levels in the absence of extrinsic reinforcers (i.e., may be of higher “intrinsic interest”).

Figure 4.

Scatterplots depicting the relation between effect size and proportional response rates in baseline relative to response rates during reinforcement periods when the entire phases were used (top panel) and when only the last three data points of each phase were used (bottom panel). A line of best fit has been fitted to the data in each case.

DISCUSSION

Overall, the results suggest little evidence for a reliable overjustification effect on the behavior of individuals with intellectual and developmental disabilities when using a known reinforcer to increase levels of operant behavior. Both effect size metrics were just as likely to be negative (an outcome inconsistent with the overjustification hypothesis) as they were to be positive.

Analysis of local effects suggested that levels of responding tended to be higher immediately following the discontinuation of reinforcement than they were immediately prior to reinforcement (i.e., first data point of the second no-reinforcement phase was higher than the last data point of the first no-reinforcement phase) regardless of the measure. This outcome is contrary to the predictions of overjustification theory and results of many overjustification studies arranged in group designs. The results are more consistent with extinction effects, which are associated with a gradual reduction to the low levels observed prior to reinforcement.

We conducted subanalyses in an attempt to shed light on the circumstances under which overjustification effects may or may not be expected, including type of task, type of reinforcer, schedule of reinforcement, and level of responding in the absence of extrinsic reinforcers. The last was the only significant relation, suggesting that effect sizes tended to be somewhat higher when baseline levels of responding were proportionately higher in relation to reinforcement levels. These effects seem consistent with prior research on overjustification, which suggests that effects are more likely when tasks are inherently “interesting.” From a behavior-analytic perspective, this finding indicates an overjustification effect may be more likely for responses maintained in the absence of socially-mediated reinforcement. This observation seems particularly important in the context of work with persons with intellectual disabilities because behavior analysts generally only arrange reinforcement contingencies for responses that do not already occur at acceptable levels without programmed reinforcers.

Some limitations of this study should be noted. First, for this analysis, we used data from reinforcer assessments to directly compare responding before and after a reinforcement contingency. However, a limitation of evaluating reinforcer assessment data in the context of overjustification is that arbitrary responses may result in low levels of responding during the initial no-reinforcement phase. Observation of an overjustification effect necessarily requires initial prereinforcement responding to observe a decrement during postreinforcement responding. Thus, we only included datasets for which mean levels of responding in the initial no-reinforcement phase exceeded zero. Yet, our sample did include some datasets with zero responding during some sessions or a mean near zero, which may have affected the outcome. When analyzing the last three sessions of the first no-reinforcement phase, the percentage of sessions with zero responding averaged 20% across all data sets (range, 0% to 100%). Of the 65 data sets, 20 (31%) had at least one session with zero responding. Of those 20 data sets, the percentage of sessions with zero responding averaged 65% (range, 33% to 100%). When analyzing the entire first no-reinforcement phase, the percentage of sessions with zero responding averaged 19% across all data sets (range, 0% to 80%). Of the 65 data sets, 24 (37%) had at least one session with zero responding. Of those 24 data sets, the percentage of sessions with zero responding averaged 51% (range, 17% to 80%).

Second, our supplementary analyses using the last three data points of each phase were an attempt to capture levels of responding at steady state. This seemed a more representative and conservative approach. Sidman (1960) discussed that a steady state of responding should result in small amounts of variability within a phase, thus concluding that the effect of the independent variable had taken place. By evaluating effect sizes with the last three sessions of each phase, we presumed that any effect the independent variable would have on responding had occurred by that point. Still, an argument could be made that the last three data points in a phase do not always reflect a steady state, as single-case logic permits ending a phase on a clear trend as long as that trend is in a direction opposite from the anticipated effect of the independent variable.

Third, we used the between-group Hedges’ g for single-case design, thus treating data points as though they were independent. This approach was recommended by Busk and Serlin (1992), but has been questioned as computationally inaccurate as it does not account for serial dependence or trend, and is not directly comparable to the between-group standardized mean difference (Beretevas & Chung, 2008). In other words, Cohen’s (1988) rules of thumb for interpreting the magnitude of effect sizes do not apply when the metric is used for single-case design research. Therefore, we supplemented and supported the findings using Tau-U, a metric designed for single-case design.

There are a number of variables we did not examine, but could shed more light on the determinants of overjustification effects in future research. For example, many overjustification studies included a single reward period, whereas reinforcer assessments typically involve multiple exposures to the reinforcement contingencies. It remains possible that the duration of exposure to a reinforcement contingency might influence the likelihood of observing detrimental effects on responding. It might also be useful to examine the nature of that contingency. Eisenberger and Cameron (1996) noted differences between performance-dependent, completion-dependent, and response-independent arrangements for the delivery of rewards. Distinctions like these could perhaps be extracted more carefully from the literature on reinforcement procedures targeting persons with intellectual disabilities. Similarly, repeated exposure to the task itself could influence observed effects on responding. Peters and Vollmer (2014) demonstrated that extended exposure to preferred activities resulted in effects that were analogous to overjustification effects. A comparable decrease in engagement was observed across activities that had and had not been exposed to a reinforcement contingency.

Although we were unable to pinpoint circumstances in which the type of task produced an overjustification effect, it may be beneficial if future research could empirically evaluate overjustification effects with differences in the reinforcing effectiveness of the tasks. We defined “intrinsic interest” by the levels of responding during a no-reinforcement baseline relative to reinforcement. However, levels of nonreinforced responding are, at best, analogous to the construct “intrinsic interest” as there are several other variables that could influence response levels in the absence of programmed reinforcement (e.g., prior history of reinforcement). Also, as this measure is a ratio of responding during reinforcement, this precludes identification of intrinsic interest independent of reinforcement and should be considered a limitation. Future attempts to examine the influence of this variable might more directly gauge inherent interest in an activity, perhaps via a duration-based preference assessment (DeLeon, Iwata, Conners, & Wallace, 1999; Worsdell, Iwata, & Wallace, 2002).

Finally, it should be noted that the presence of an effect consistent with the overjustification hypothesis would not necessarily diminish the utility of arranging programmed reinforcement contingencies for persons with intellectual disabilities. In applied settings, reinforcement contingencies are arranged to establish or increase adaptive behaviors that do not already occur at sufficient levels. Perhaps some of these arrangements decrease intrinsic interest in the activity and the individual would not engage in those activities in the absence of reinforcement. On the other hand, programmed reinforcement contingencies are designed to establish repertories that can potentially place the individual in contact with more frequent reinforcement in the natural environment. For example, children are taught simple identity matching skills using contrived contingencies, not because identity matching should be something of inherent interest, but because the skills established serve as precursors for future instances of adaptive functioning. Whether the delivery of reinforcers enhances or detracts from a person’s intrinsic motivation at the local level is perhaps not as important as whether that reinforcement contingency facilitates the possibility of a more rewarding life.