Abstract
The classical definition of mesophyll conductance (g m) represents an apparent parameter (g m,app) as it places (photo)respired CO2 at the same compartment where the carboxylation by Rubisco takes place. Recently, Tholen and co-workers developed a framework, in which g m better describes a physical diffusional parameter (g m,dif). They partitioned mesophyll resistance (r m,dif = 1/g m,dif) into two components, cell wall and plasmalemma resistance (r wp) and chloroplast resistance (r ch), and showed that g m,app is sensitive to the ratio of photorespiratory (F) and respiratory (R d) CO2 release to net CO2 uptake (A): g m,app = g m,dif/[1 + ω(F + R d)/A], where ω is the fraction of r ch in r m,dif. We herein extend the framework further by considering various scenarios for the intracellular arrangement of chloroplasts and mitochondria. We show that the formula of Tholen et al. implies either that mitochondria, where (photo)respired CO2 is released, locate between the plasmalemma and the chloroplast continuum or that CO2 in the cytosol is completely mixed. However, the model of Tholen et al. is still valid if ω is replaced by ω(1−σ), where σ is the fraction of (photo)respired CO2 that experiences r ch (in addition to r wp and stomatal resistance) if this CO2 is to escape from being refixed. Therefore, responses of g m,app to (F + R d)/A lie somewhere between no sensitivity in the classical method (σ =1) and high sensitivity in the model of Tholen et al. (σ =0).
Keywords: CO2 transfer, Internal conductance, Mesophyll resistance
Introduction
The biochemical C3 photosynthesis model of Farquhar, von Caemmerer and Berry (1980), the FvCB model hereafter, has been widely used to interpret leaf physiology from gas exchange measurements. The model calculates the net rate of leaf photosynthesis (A) as the minimum of the Rubisco carboxylation activity-limited rate (A c) and the electron (e −) transport-limited rate (A j) of photosynthesis (see Appendix A). The partial pressure of CO2 at the carboxylation sites of Rubisco in the chloroplast stroma (C c) is a required input variable to calculate both A c and A j in the model. The drawdown of C c, relative to the CO2 level in the ambient air (C a), depends not only on stomatal conductance for CO2 transfer (g sc), but also on the mesophyll conductance for CO2 transfer between substomatal cavities and the site of CO2 carboxylation (g m). According to Fick’s diffusion law, g m can be expressed as follows (von Caemmerer and Evans 1991; von Caemmerer et al. 1994):
| 1 |
where C i is the partial pressure of CO2 at the intercellular air spaces.
This simple gas diffusion equation has been combined with the FvCB model to estimate g m (Pons et al. 2009), based on combined data of A–C i curves and chlorophyll fluorescence measurements on photosystem II e − transport efficiency (Harley et al. 1992; Yin and Struik 2009) or on combined gas exchange and carbon isotope discrimination measurements (Evans et al. 1986). When the g m estimation is based on combined gas exchange and chlorophyll fluorescence measurements (e.g. the ‘variable J method’, Harley et al. 1992), the A j part of the FvCB model is used, in which the linear e − transport rate (J) is estimated from chlorophyll fluorescence signals. Using this method, it has been reported that g m can decrease with increasing C i or with decreasing incoming irradiance I inc (Flexas et al. 2007; Vrábl et al. 2009; Yin et al. 2009). Similar patterns of variable g m have been reported with the isotope discrimination method (Vrábl et al. 2009), although with less consistency (Tazoe et al. 2009).
Equation (1) is based on net photosynthesis and assumes that respiratory and photorespiratory CO2 release occurs in the same compartment as CO2 fixation by Rubisco. However, CO2 fixation occurs in the chloroplast stroma, whereas (photo)respiratory CO2 is released in the mitochondria. The first step of photorespiration, the O2 fixation, takes place in the chloroplast to form phosphoglycolate. Phosphoglycolate is converted to glycolate and glyoxylate, and then to glycine in the peroxisome; glycine moves to the mitochondria and is decarboxylated there into CO2, NH3 and serine (Kebeish et al. 2007). The CO2 released in mitochondria, from either respiration or photorespiration, can be partially refixed by Rubisco in the chloroplast stroma, whereas the remaining portion escapes to the atmosphere (Busch et al. 2013). To quantify mesophyll resistance r m (the reciprocal of g m), there is a need to specify resistance components within the cell imposed by walls, plasmalemma, cytosol, chloroplast envelope and stroma (Evans et al. 2009; Terashima et al. 2011). Unlike the CO2 that comes from the substomatal cavities, the CO2 from the mitochondria does not need to cross the cell wall and plasmalemma, and thus experiences a different resistance. Considering this difference, Tholen et al. (2012) developed a theoretical framework to analyse g m as described below.
The total mesophyll diffusional resistance (r m,dif) can be described as the sum of a series of physical resistances comprising of intercellular air space, cell wall, plasmalemma, cytosol, chloroplast envelope and chloroplast stroma components (Evans et al. 2009): r m,dif = r ias + r wall + r plasmalemma + r cytosol + r envelope + r stroma. The resistance imposed by the gas phase component and the cytosol is generally small (Tholen et al. 2012), and may therefore be ignored. Tholen et al. (2012) combined r wall and r plasmalemma into the resistance at the cell wall–plasma membrane interface (r wp), and r envelope and r stroma into the total chloroplast resistance (r ch), so that r m,dif = r wp + r ch. Based on Fick’s diffusion law and considering two different resistance components encountered by CO2 from substomatal cavities and CO2 from the mitochondria, Tholen et al. (2012) derived the following relationship (their Eq. 6):
| 2 |
where F is the photorespiratory CO2 release and R d is the CO2 release in the light other than by photorespiration, both in the mitochondria. The model Eq. (2) is still a simplification of true resistance pathways, because (i) diffusion is a continuous process and there are many parallel pathways (Tholen et al. 2012) and (ii) the model ignores that some respiratory flux originates in the chloroplast (Tcherkez et al. 2012) and that there may be small activity of phosphoenolpyruvate carboxylase in cytosol (Douthe et al. 2012; Tholen et al. 2012).
Here we let r ch = ωr m,dif; then r wp = (1–ω)r m,dif, where ω is the relative contribution of r ch to the total mesophyll resistance r m,dif (= r wp+r ch). Equation (2) then becomes
| 3 |
Solving (C i−C c) from Eq. (3) and substituting it into Eq. (1) give
| 4 |
Equation (4) is equivalent to Eq. (9) of Tholen et al. (2012), in which g wp and g ch (i.e. the inverse of r wp and r ch, respectively) are used. We prefer Eq. (4) because it allows (i) to analyse how g m varies for a given total mesophyll resistance and (ii) to provide an analogue to an extended model that will be developed later.
Both Eq. (4) and Tholen et al.’s Eq. (9) tell that g m, as defined by Eq. (1), is influenced by the ratio of (photo)respiratory CO2 from the mitochondria to net CO2 uptake (F + R d)/A, thereby resulting in an apparent sensitivity of g m to CO2 and O2 levels (Tholen et al. 2012). This sensitivity does not imply a change in the intrinsic diffusion properties of the mesophyll; so, g m as defined by Eqs. (1) and (4) is apparent, and we denote it as g m,app hereafter. The sensitivity depends on ω: the higher is ω the more sensitive is g m,app to (F + R d)/A. If ω = 0, then g m,app is no longer sensitive to (F + R d)/A, Eq. (3) becomes Eq. (1) and g m,app becomes g m,dif—the intrinsic mesophyll diffusion conductance (= 1/r m,dif). In such a case, carboxylation and (photo)respiratory CO2 release occur in the same organelle compartment or if occurring in separate compartments, the chloroplast exerts a negligible resistance to CO2 transfer.
Equations (1) and (2) have been considered as two basic scenarios for CO2 diffusion path in C3 leaves (von Caemmerer 2013), both representing a simplified view on CO2 diffusion in the framework of whole leaf resistance models. Detailed views on the mechanistic basis of CO2 diffusion in relation to intracellular organelle positions could best be investigated using reaction–diffusion models (e.g. Tholen and Zhu 2011). However, uncertainties in the value of many required input diffusion coefficients and the complexity in nature are the major limitations of using these reaction–diffusion models (see Berghuijs et al. 2016 for discussions on simple resistance vs. reaction–diffusion models). We herein discuss an extended, yet simple, resistance model by considering various scenarios with regard to intracellular arrangement of organelles: (1) the relative positions of mitochondria and chloroplasts and (2) gaps between individual chloroplasts. We also discuss implications of these scenarios in estimating the fraction of (photo)respired CO2 being refixed.
A generalised model
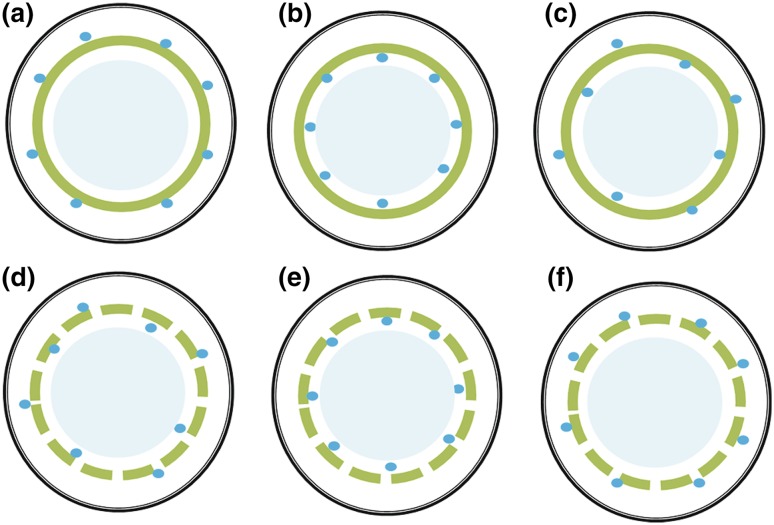
To develop a generalised model, we consider two possibilities of chloroplast distribution (either continuous or discontinuous) and three possibilities of mitochondria location (outer, inner or both outer and inner layers of cytosol). This gives six cases with regard to the arrangement of organelles within mesophyll cells (Fig. 1). In each scenario, mitochondria are intimately associated with chloroplasts, as commonly observed for real leaves (Sage and Sage 2009; Hatakeyama and Ueno 2016). Within our simple generalised model, we stay with the same notation of r wp and r ch, the two-resistance components as the essence of the model of Tholen et al. (2012). However, as we discuss later on, instead of assuming that r cytosol is negligible, we followed the approach of Berghuijs et al. (2015) that lumps part of r cytosol into r wp and the remaining part of r cytosol into r ch. Given the position of mitochondria shown in Fig. 1, nearly all cytosolic resistance, i.e. along the diffusion path length from plasmalemma to chloroplast outer membrane, can be lumped into r wp, whereas only a small remaining portion of r cytosol is lumped into r ch.
Fig. 1.
Schematic illustration of six scenarios for the arrangement of organelles in the mesophyll cell. In each panel, the outer double-lined black circle indicates the combined cell wall and plasmalemma, the green circle indicates chloroplast continuum (panels a–c) or the green circle segments indicate chloroplasts (panels d–f), the filled small blue symbols indicate mitochondria and the inner light blue circle represents vacuole
Case I
In this case, the coverage of chloroplasts is continuous and all mitochondria locate in the outer layer of cytosol (Fig. 1a). For this case, the net CO2 influx (A) from the intercellular air spaces is driven by the gradient between C i and C m(outer) (where C m(outer) is the CO2 partial pressure at the outer layer of the mesophyll cytosol facing chloroplast envelope), whereas the gradient between C m(outer) and C c drives the carboxylation flux (V c). Therefore, equations for the CO2 gradient between the compartments and involved resistance components are as follows: C c = C m(outer)−V c r ch and C m(outer) = C i−Ar wp. In the FvCB model, A is formulated as A = V c−F−R d. Combining these three equations actually gives rise to Eq. (2), from which Eq. (4) for the sensitivity of g m,app to (F + R d)/A was derived. Therefore, formulae for this Case I are in line with the framework as described by Tholen et al. (2012).
Tholen et al. (2012) also showed, based on their model framework, that the fraction of (photo)respired CO2 that is refixed by Rubisco can be quantified using the resistance components. We use x(F + R d) to denote the partial pressure of (photo)respired CO2 in mesophyll cytosol, where x is a conversion factor from flux to partial pressure for (photo)respired CO2 and has a unit of bar (mol m− 2 s− 1)−1. CO2 molecules from (photo)respiration can diffuse towards Rubisco but will experience r ch and a resistance derived from the carboxylation itself (r cx); so the refixation rate (R refix) is x(F + R d)/(r ch+r cx). A portion of the (photo)respired CO2 molecules can also escape from refixation and move out of the stomata to the atmosphere, experiencing r wp and the stomatal resistance for CO2 transfer r sc (including a small boundary layer resistance); so the rate of this leak or escape (R escape) is x(F + R d)/(r wp+r sc). The fraction of (photo)respired CO2 that is refixed by Rubisco (f refix) can be calculated by
| 5 |
This compares with Eq. (14) of Tholen et al. (2012) and shows that the refixation fraction can be calculated simply as the ratio of the resistance components that the escaped (photo)respired CO2 molecules have experienced to the total resistance along the full diffusion pathway.
Case II
The coverage of chloroplasts is continuous and all mitochondria locate in the inner layer of cytosol, closely behind chloroplasts (Fig. 1b). In this case, since there are no mitochondria between the plasmalemma and chloroplasts, in essence, r ch and r wp can be combined and the flux involved is the same for the CO2 gradient between C i and C m(outer) and between C m(outer) and C c, i.e. A (=V c–F–R d). This corresponds to the classical model, Eq. (1), that has commonly been used for estimating g m (von Caemmerer and Evans 1991; von Caemmerer et al. 1994).
In this case, all (photo)respired CO2 molecules have to experience r ch, in addition to r wp and r sc, if they are to escape from being refixed. As mitochondria locate closely behind chloroplasts and mitochondria and chloroplasts are treated essentially as one compartment in the classical model, (photo)respired CO2 molecules that diffuse towards Rubisco can be considered to experience r cx only; so R refix is x(F + R d)/r cx. The remaining (photo)respired CO2 that escape from refixation experience r ch, r wp and r sc; so, R escape is x(F + R d)/(r ch + r wp+ r sc). Then, f refix can be calculated by
| 6 |
Obviously, this predicts a higher refixation fraction than Eq. (5) does.
Case III
The coverage of chloroplasts is continuous and mitochondria locate in both inner and outer layers of cytosol (Fig. 1c). Let λ be the fraction of mitochondria that locate closely behind chloroplasts in the inner cytosol. Then (1−λ) is the fraction of mitochondria that locate in the outer cytosol. The flux associated with the gradient between C m(outer) and C c is the carboxylation flux (V c) minus the efflux of (photo)respired CO2 from the inner layer λ (F + R d), while the flux associated with the gradient between C i and C m(outer) is still A. Therefore, equations for the CO2 gradients between the compartments and involved resistance components are as follows:
| 7 |
| 8 |
Equation (7) without R d would be comparable to the third equation in Fig. 4 of von Caemmerer (2013) for modelling the photorespiratory bypass engineered by Kebeish et al. (2007). Combining Eqs. (7) and (8) with V c = A + F + R d gives rise to an equation in analogy to Eq. (2):
| 9 |
The same logic as for Eqs. (3) and (4) gives
| 10 |
Equation (10) suggests that the apparent g m as defined by Eq. (1) is still sensitive to (F + R d)/A, although the sensitivity factor changes from ω for Case I to ω(1−λ) now for Case III.
For this case, either refixed or escaped (photo)respired CO2 molecules have two parts, one part from the inner and the other from outer cytosol, and they experience different resistant components. Assuming for the purpose of simplicity that mitochondria are distributed in such a way that any variation in x between inner and outer cytosol is negligible, the refixed (photo)respired CO2 molecules R refix can easily be expressed as λx(F + R d)/r cx + (1−λ)x(F + R d)/(r ch + r cx), whereas the escaped (photo)respired CO2 R escape can be expressed as λx(F + R d)/(r ch + r wp + r sc) + (1−λ)x(F + R d)/(r wp+r sc). Then, f refix can be calculated by
| 11 |
This expression for f refix looks rather unwieldy but it covers Eqs. (5) and (6) for the previous two cases when λ is 0 and 1, respectively.
Case IV
This is the most general case, in which the coverage of chloroplasts is discontinuous and mitochondria locate in both inner and outer layers of cytosol (Fig. 1d). If chloroplast coverage is discontinuous, it is possible that some mitochondria lie exactly in the chloroplast gaps. This situation can be simplified by assigning part of (photo)respired CO2 in the gaps to the inner and the other part to the outer cytosol; so, λ is still defined as for Case III as the fraction of mitochondria that locate in the inner cytosol. However, another factor needs to be introduced to account for the direct effect of the chloroplast gaps as these gaps allow the diffusion of (photo)respired CO2 from the inner to the outer cytosol and vice versa. In our context here, we only need to define k as the factor allowing for a decrease (0 ≤ k < 1) or an increase (k > 1) in the fraction of inner (photo)respired CO2, caused by the chloroplast gaps. Then, Eq. (7) can be simply adjusted for Case IV:
| 12 |
while Eq. (8) remains unchanged. Then, equations for case IV, equivalent to Eqs. (9–11) for case III, can be easily defined by replacing the places of λ with kλ. This also means that the fraction of outer (photo)respired CO2 now becomes (1−kλ).
In fact, the lumped kλ can be re-defined as a single factor σ, which refers to the fraction of (photo)respired CO2 molecules that have to experience r ch, in addition to r wp and r sc, if they are to escape from being refixed. Then, a more general form of Eq. (3) or Eq. (9) becomes
| 13 |
and a more general form of Eqs. (10) and (11) becomes
| 14 |
| 15 |
As σ has a value between 0 and 1, it follows that the factor k varies between 0 and 1/λ. This suggests that the lower the λ is, the more likely it is that k > 1. However, the exact value of k and how k modifies λ (e.g. via the path between the chloroplasts vs through the chloroplast) are hard to quantify from the simple resistance model. As large gaps between chloroplasts decrease S c/S m, the ratio of chloroplast surface area to mesophyll surface area exposed to the intercellular air spaces (Sage and Sage 2009; Tholen et al. 2012; Tomas et al. 2013), the value of k must be associated with S c/S m. However, k may also depend on factors such as the CO2 influx from the intercellular air spaces. These dependences of k on λ, S c/S m, and other factors could best be analysed using reaction–diffusion models like the one by Tholen and Zhu (2011).
Two more special cases
Now we consider two more special cases. The first instance is the case in which the coverage of chloroplasts is discontinuous and all mitochondria locate in the inner layer of cytosol (Fig. 1e), and the second is that the coverage of chloroplasts is discontinuous and all mitochondria locate in the outer layer of cytosol (Fig. 1f). The diffused amount of (photo)respired CO2 from the inner to the outer cytosol (for the first instance) or from the outer to the inner cytosol (for the second instance) could be analysed by the use of a reaction–diffusion model. Again if σ also refers to the fraction of (photo)respired CO2 molecules that have to experience r ch, in addition to r wp and r sc, if they are to escape from being refixed, Eqs. (13–15) also apply to these two special cases.
Results and discussion
Dependence of A and gm,app on ω and σ values
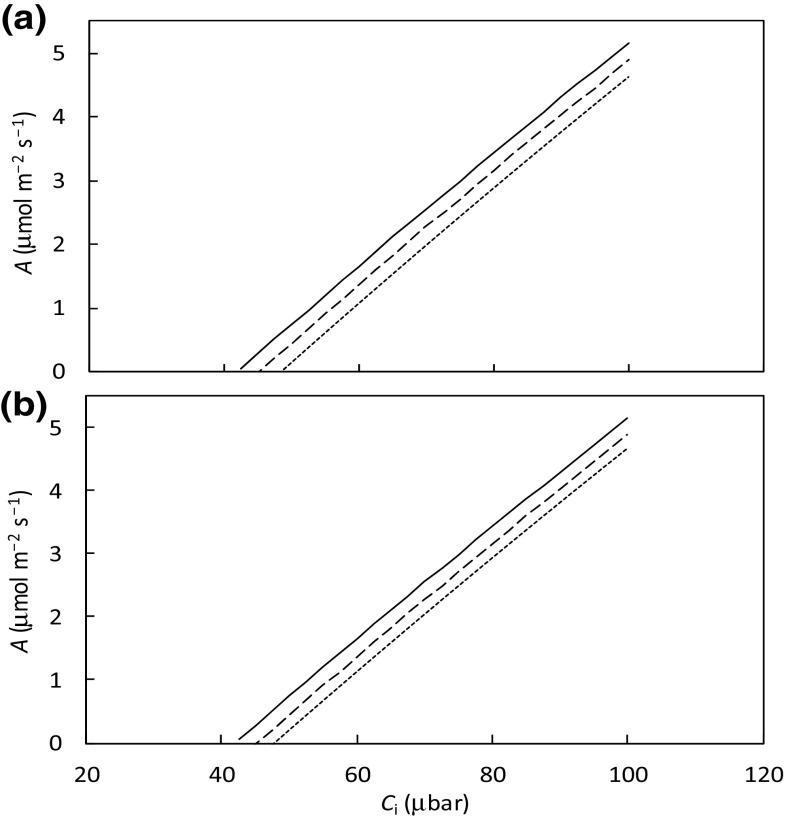
Equations for all illustrations in this section are all given in Appendix A. Figure 2 shows the initial section of simulated A–C i curves for various combinations of ω and σ values, indicating that a change in σ (i.e. the arrangement of chloroplasts and mitochondria in mesophyll cells) had a same magnitude of the effect as a change in ω (i.e. the physical resistance of chloroplast components relative to the total mesophyll resistance). Increasing σ (Fig. 2a) or decreasing ω (Fig. 2b) increased A for a given g m,dif. This is largely caused by varying amounts of refixation of (photo)respired CO2, which become increasingly important with decreasing C i. For example, the estimated f refix (Eq. 15) was 0.385, 0.333 and 0.285 for the three cases corresponding to solid, long-dashed and short-dashed lines of Fig. 2a, respectively (where r sc was set to have the same value as 1/g m,dif, and r cx was calculated as (C c + x 2)/x 1, also see Eq. B2 in Tholen et al. 2012). f refix can also be calculated for the three cases of Fig. 2b. Such differences in f refix can produce a significant difference in A (when C i is low) and in CO2 compensation point (Fig. 2). Differences in was already shown by von Caemmerer (2013) between two special cases, i.e. Case I (Fig. 1a) versus Case II (Fig. 1b). With increasing C i, refixation becomes less important, and differences in A are increasingly negligible (results not shown).
Fig. 2.
Simulated net CO2 assimilation rate (A) as a function of low C i, under ambient O2 condition: a for three values of σ (solid line for σ = 1, long-dashed line for σ = 0.5 and short-dashed line for σ = 0) if parameter ω stays constant at 0.5, and b for three values of ω (solid line for ω = 0, long-dashed line for ω = 0.5 and short-dashed line for ω = 0.9) if parameter σ stays constant at 0.5. Other parameter values used for this simulation: g m,dif = 0.4 mol m− 2 s− 1 bar − 1; V cmax = 80 μmol m− 2 s− 1; K mC = 291 μbar; K mO = 194 mbar; R d = 1 μmol m− 2 s− 1 and Rubisco specificity S c/o = 3.1 mbar μbar− 1 (the equivalent * = 34 μbar for the ambient O2 condition). Simulation used Eqn (18) in Appendix A
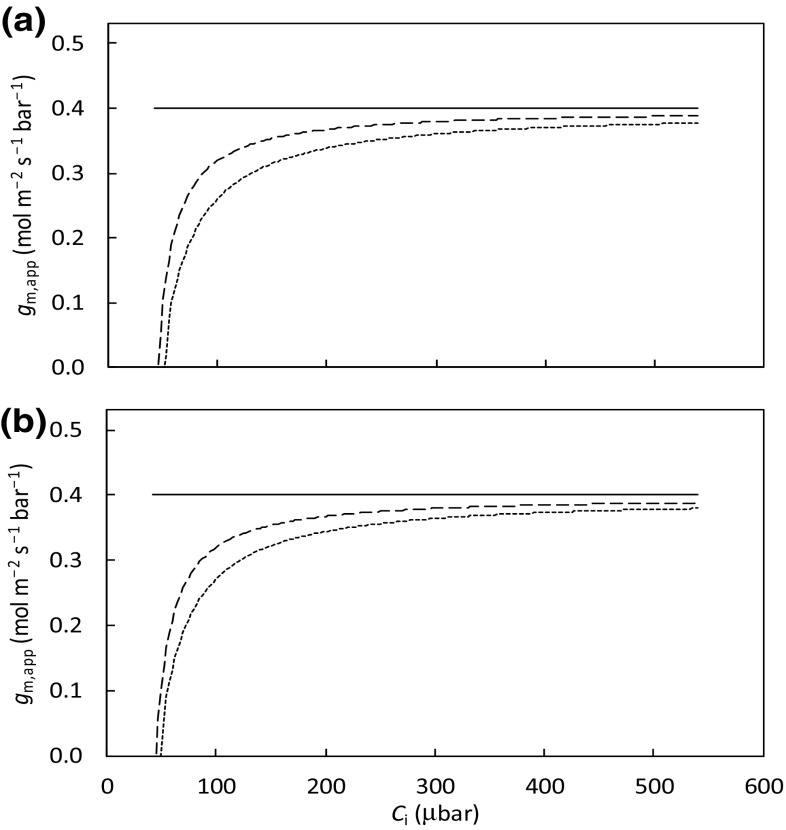
g m,app, calculated from Eq. (14), decreased with decreasing C i, although g m,dif was fixed as constant (Fig. 3). This variation did not occur only if σ = 1 (the horizontal line in Fig. 3a) or ω = 0 (the horizontal line in Fig. 3b), suggesting the classical g m model can arise either from σ = 1 (all mitochondria stay closely behind chloroplasts as if carboxylation and (photo)respiratory CO2 release occur in one compartment) or from ω = 0 (the chloroplast component in total mesophyll resistance is negligible). The short-dashed line in Fig. 3a represents the case when σ = 0, corresponding to the original model of Tholen et al. (2012) that applies to the case where all mitochondria locate in the outer cytosol. A change in organelle arrangement within a mesophyll cell resulted in a change in sensitivity of g m,app to C i as shown by the long-dashed line in Fig. 3a, which lies between the horizontal line and the short-dashed line.
Fig. 3.
Simulated apparent mesophyll conductance (g m,app) as a function of C i, under ambient O2 condition: a for three values of σ (solid line for σ = 1, long-dashed line for σ = 0.5 and short dash line for σ = 0) if parameter ω stays constant at 0.5 and b for three values of ω (solid line for ω = 0, long-dashed line for ω = 0.5 and short-dashed line for ω = 0.9) if parameter σ stays constant at 0.5. The value of J used for simulation was 125 μmol m− 2 s− 1. Other parameter values as in Fig. 2. Simulation used the method as described in Appendix A
The model of Tholen et al. (2012) as special case of the generalised model
It is evident from our analysis above that the original model of Tholen et al. (2012) applies to a special case of our generalised model, where (photo)respired CO2 is entirely released in the outer cytosol between the plasmalemma and the chloroplast layer. However, this case can hardly be observed in real leaves, where mitochondria occur mostly in the cell interior, closely behind chloroplasts (Sage and Sage 2009; Hatakeyama and Ueno 2016).
In our model, as stated earlier for the purpose of retaining model simplicity, a large part of r cytosol is lumped into r wp, and the remaining part is lumped into r ch. For their model, Tholen et al. (2012) assumed that cytosolic resistance is negligible. Although this assumption was made, as described by Tholen et al. (2012), only for the purpose of simplicity, it has implications. If r cytosol is so small that it can be neglected, then CO2 diffusion is so fast that the CO2 concentration anywhere in the cytosol should be the same independent of where the mitochondria are located, provided the cytosol is continuous (for example, allowed by an S c/S m lower than 1). Then the position of the mitochondria does not have any effect on f refix. Practically, the four cases for scenarios (a), (d), (e) and (f) in Fig. 1 would all be equivalent to the original Tholen et al. model (σ = 0). This is because λ = 0 in the case of Fig. 1a, or k = 0 in cases of Fig. 1d,e, or both λ and k = 0 in the case of Fig. 1 f. In this context, the original model of Tholen et al. (2012) would become an alternative special case of our model, that is, assuming that CO2 in the cytosol is completely mixed. If r cytosol is indeed negligible, then cases in Fig. 1d,e,f are no longer needed for developing the generalised model.
Can parameters ω and σ in the generalised model be measured?
In real cells, r cytosol may be very high (Peguero-Pina et al. 2012; Berghuijs et al. 2015) and therefore cannot be neglected. Then, r cytosol should appear in the model, making it dependent on the detailed morphology of the cell and location of mitochondria and chloroplasts, and this would require the use of a reaction–diffusion model. Within the resistance model framework, Tholen et al. (2012, in their Appendix C) and Tomas et al. (2013) analysed the possible effects of r cytosol in relation to S c/S m on g m. In our generalised model, any significant r cytosol value would mainly be lumped into parameter ω, while parameter σ encompasses any combination of chloroplast–mitochondria arrangement and S c/S m. This means that parameters ω and σ in our model can be experimentally measured, at least approximately.
Individual physical resistance components r wall, r plasmalemma, r cytosol, r envelope and r stroma have been calculated from microscopic measurements on leaf anatomy (Peguero-Pina et al. 2012; Tosens et al. 2012a, b; Tomas et al. 2013; Berghuijs et al. 2015), despite the uncertainties in the value of gas diffusion coefficients used for the calculation. These measurements can provide basic data to derive ω. For example, Berghuijs et al. (2015) showed that for tomato leaves, ω was about 0.65. Parameter σ depends on both S c/S m and the relative position of mitochondria to chloroplasts. In most annuals especially when leaves are young, S c/S m is high (close to 1; Sage and Sage 2009; Terashima et al. 2011; Berghuijs et al. 2015), σ should be predominantly determined by the relative position of mitochondria (i.e. σ ≈ λ, the proportion of mitochondria lying in the inner cytosol). Hatakeyama and Ueno (2016) showed that for 10 C3 grasses most mitochondria are located on the vacuole side of chloroplast in mesophyll cells and their data suggested that λ varies from 0.61 to 0.92 among these species, with an average of 0.8. Assuming these values are representative for young leaves of annual C3 species, then the collective value of ω(1−σ) in our model is about 0.13, a value closer to what the classical model represents (0) than the model of Tholen et al. (2012) does.
However, in woody species (e.g. Tosens et al. 2012a) or in old leaves of annual species (Busch et al. 2013), S c/S m can be as low as 0.4. Because the chloroplast coverage is low, especially when combined with a low r cytosol (Tosens et al. 2012b), ω(1−σ) must be close to what the model of Tholen et al. (2012) represents. However, parameter σ is hard to determine directly for this case as its component k may be interdependent on its other component λ. In such a case, σ may only be a “fudge factor” that lumps λ and S c/S m in a complicated manner, which may be elucidated by using reaction–diffusion models. Alternatively, the collective value of ω(1−σ) could be estimated (together with g m,dif) by fitting Eq. (18) in AppendixA to gas exchange data at various O2 levels, and then σ could be calculated if anatomical measurements reliably estimate ω; but this approach needs to be tested.
Can two-resistance models exclusively explain observed variable gm,app?
Compared with the classical model that uses a single resistance parameter, both Tholen et al. (2012) model and our generalised model partition mesophyll resistance into two components. In Fig. 3, we have shown the dependence in the sensitivity of g m,app on both ω and σ values. Our illustration for the general case (Fig. 3) still agrees qualitatively with Tholen et al. (2012), who, based on their two-resistance model, clearly showed the sensitivity of g m,app to the ratio of (F + R d) to A. They suggested that this sensitivity could explain the commonly observed decrease of g m,app with decreasing C i with a low C i range (e.g. Flexas et al. 2007; Yin et al. 2009). Since the (F + R d)/A ratio also varies with irradiance and temperature, one might wonder if their model explains any variation of g m,app with these factors. However, their framework, as stated by Tholen et al. (2012), cannot explain the commonly observed responses of g m,app to a change in C i within the higher C i range (e.g. Flexas et al. 2007) or in I inc (e.g. Yin et al. 2009; Douthe et al. 2012) or in temperature (e.g. Bernacchi et al. 2002; Yamori et al. 2006; Evans and von Caemmerer 2013; von Caemmerer and Evans 2015). In fact, Gu and Sun (2014) showed that even the response of g m,app to a change in C i (including the low C i range) could be simply due to possible errors in measuring A, J and C i, or to possible errors in estimating R d and S c/o, or could be due to the use of the NADPH-limited form of the FvCB model by the variable J method when the true form is the ATP-limited equation.
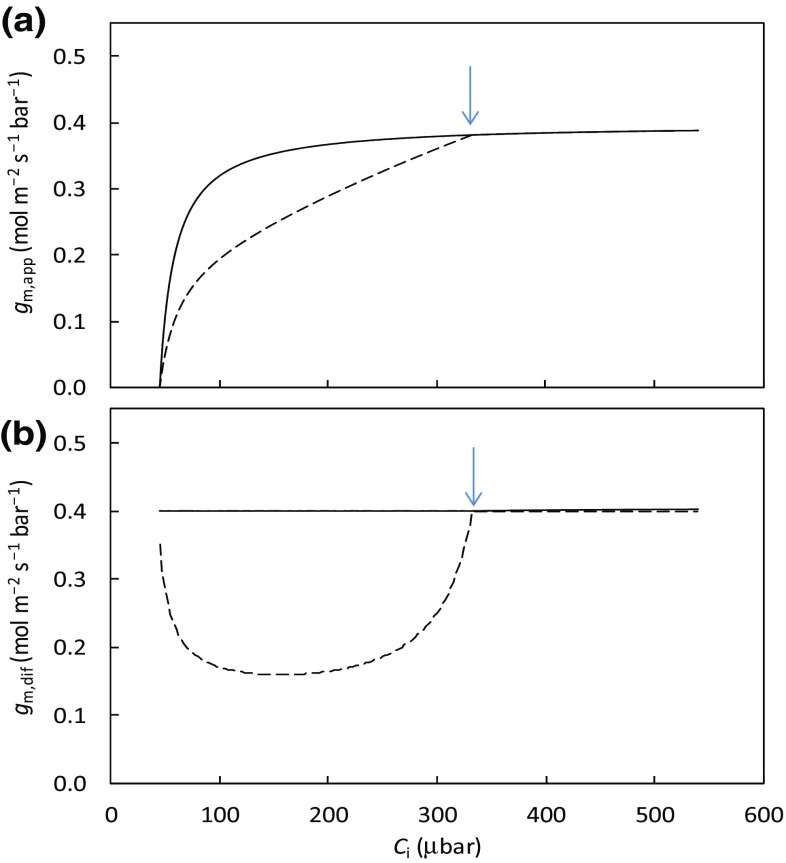
In the absence of any measurement errors, can the sensitivity of g m,app to the (F + R d)/A ratio be considered as the only explanation of g m,app sensitivity to C i within the low C i range? Here we want to (re-)state that the decline of g m,app with decreasing C i below a certain level, as assessed by the variable J method of Harley et al. (1992), can also be accounted for by the fact that the method is based only on the A j equation of the FvCB model (Yin et al. 2009). When C i is decreasing towards the CO2 compensation point, A is increasingly limited by A c rather than by A j. Under such conditions, part of the e − fluxes may become alternative e − transport not used in support of CO2 fixation and photorespiration. So, use of the variable J method, which is based on Eq. (1) and the A j equation of the FvCB model, may lead to underestimation of g m,app. This is shown in Fig. 4a, in which for a given fixed g m,dif (0.4 mol m− 2 s− 1 bar − 1), g m,app decreased with decreasing C i as expected from Eq. (14); but g m,app decreased more sharply if A j part of the model was applied to the low C i range which was actually A c-limited. One would expect that g m,dif calculated back from using the simulated A should be equal to the pre-fixed g m,dif (0.4 mol m− 2 s− 1 bar − 1). However, the calculated g m,dif if using only the A j part of the model as in the variable J method gave artifactually lower g m,dif values for the A c-limited part (Fig. 4b). In this calculation shown in Fig. 4, J was assumed to be a constant across C i levels, whereas actual fluorescence measured J may decline slightly with lowering C i in the low C i range (e.g. Cheng et al. 2001), probably reflecting a feedback effect of Rubisco limitation on electron transport. However, the feedback is not so complete that the variable J method, if applied to the low C i range, always tends to underestimate the actual mesophyll conductance. For these reasons, Yin and Struik (2009) stated that the proposal of the variable J method to be applied to the lower range of A–C i curve where J is variable (Harley et al. 1992) is inappropriate. A good correlation between values of g m estimated from the variable J method and the online isotopic method but not when C i is <200 µmol mol− 1 (Vrábl et al. 2009) further supports our statement.
Fig. 4.
Simulated apparent mesophyll conductance g m,app (a) or intrinsic diffusional mesophyll conductance g m,dif (b) as a function of C i under ambient O2 condition, with σ = 0.5 and ω = 0.5. g m,app and g m,dif were calculated using C c derived either from the full FvCB model (solid lines) or from the A j part of the model as in the variable J method (dashed lines). The arrow indicates the transition point from being A c-limited to being A j-limited. Input parameter values used for simulation are given in Figs. 2 and 3. Simulation used the method as described in Appendix A
Conclusions
The model of Tholen et al. (2012) considers the partitioning of intrinsic diffusion resistance but with little explicit consideration of intracellular organelle arrangements, especially not intracellular position of mitochondria and chloroplasts. We introduced the parameter σ for defining the fraction of (photo)respired CO2 molecules that have to experience all r ch, in addition to r wp and r sc, if these CO2 molecules are to escape from being refixed. σ has a value between 0 and 1, depending on the arrangement of organelles within mesophyll cells, i.e. (1) the relative position of chloroplasts and mitochondria and (2) the size of the gaps between chloroplasts. This provides a simple generalised form of the Tholen et al. model in a way that the latter model, Eq. (4), is still valid for all organelle arrangement scenarios if ω is replaced by ω(1−σ). The two parameters of our generalised model can be amenable to experimental estimation for young leaves of annual species where chloroplast coverage continues along the mesophyll cell periphery (S c/S m = 1). The model of Tholen et al. (2012) is the special case of our model when σ = 0, which arises either from λ = 0 (no mitochondria in the inner cytosol) combined with S c/S m = 1 or from a negligible r cytosol combined with S c/S m < 1. Our model shows that the sensitivity of g m,app to (F + R d)/A lies somewhere in between the classical method (ω = 0 or σ = 1, non-sensitive) and the Tholen et al. model (σ = 0, highly sensitive). Therefore, Tholen et al. (2012) may have overstated that the sensitivity of g m,app on (F + R d)/A in their model explains the commonly reported decline of g m,app with decreasing C i in the low C i range. In fact, the decline, if not due to measurement or parameter–estimation errors, could also be attributed, at least partly, to the variable J method that is wrongly applied to low C i range where CO2 assimilation is actually limited by Rubisco activity.
Acknowledgements
This research is financed in part by the BioSolar Cells open innovation consortium, supported by the Dutch Ministry of Economic Affairs, Agriculture and Innovation. We thank the reviewers and the coordinating editor (Dr. A.B. Cousins) for their very useful comments on the previous versions of the manuscript.
Appendix A
Equations used for simulation in this paper
The FvCB model calculates carboxylation rate (V c) as C c x 1/(C c + x 2), and photorespiratory CO2 release F as ( */C c)V c ; so, F can be expressed as follows:
| 16 |
where * is the CO2 compensation point in the absence of R d ( * depends on O2 partial pressure O and Rubisco specificity S c/o as 0.5O/S c/o), x 1 = J/4 and x 2 = 2 * for the A j-limited conditions and x 1 = V cmax (maximum carboxylation activity of Rubisco) and x 2 = K mC(1 + O/K mO) for the A c-limited conditions (K mC and K mO are Michaelis–Menten constants of Rubisco for CO2 and O2, respectively).
Also C c can be solved from the FvCB model as
| 17 |
Combining Eqs. (16–17) with Eq. (13) and solving the combined equations for A, step by step, result in a quadratic solution:
| 18 |
where
Equation (18) was used to generate A–C i response curves as shown in Fig. 2 for a given set of input parameter values.
When A is solved, C c can be solved from Eq. (18), and the solved C c was used as input to Eq. (1) to calculate g m,app. Alternatively, g m,app can be calculated directly from Eq. (14) with F calculated from eqn (16). This gave g m,app as shown in Figs. 3 and 4a.
When A, C c and F are all known, one can calculate back for g m,dif:
| 19 |
When C c and F are both based on the A j-limited part of the FvCB model, then eqn (19) gives an equation that calculates g m,diff, like the variable J method of Harley et al. (1992) for calculating g m,app. This was used to generate Fig. 4b.
References
- Berghuijs HNC, Yin X, Ho QT, van der Putten PEL, Verboven P, Retta MA, Nicolaï BM, Struik PC. Modeling the relationship between CO2 assimilation and leaf anatomical properties in tomato leaves. Plant Sci. 2015;238:297–311. doi: 10.1016/j.plantsci.2015.06.022. [DOI] [PubMed] [Google Scholar]
- Berghuijs HNC, Yin X, Ho QT, Driever SM, Retta MA, Nicolaï BM, Struik PC. Mesophyll conductance and reaction-diffusion models for CO2 transport in C3 leaves; needs, opportunities and challenges. Plant Sci. 2016;252:62–75. doi: 10.1016/j.plantsci.2016.05.016. [DOI] [PubMed] [Google Scholar]
- Bernacchi CJ, Portis AR, Nakano H, von Caemmerer S, Long SP. Temperature response of mesophyll conductance. Implication for the determination of Rubisco enzyme kinetics and for limitations to photosynthesis in vivo. Plant Physiol. 2002;130:1992–1998. doi: 10.1104/pp.008250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busch FA, Sage TL, Cousins AB, Sage RF. C3 plants enhance rates of photosynthesis by reassimilating photorespired and respired CO2. Plant Cell Environ. 2013;36:200–212. doi: 10.1111/j.1365-3040.2012.02567.x. [DOI] [PubMed] [Google Scholar]
- Cheng L, Fuchigami LH, Breen PJ. The relationship between photosystem II efficiency and quantum yield for CO2 assimilation is not affected by nitrogen content in apple leaves. J Exp Bot. 2001;52:1865–1872. doi: 10.1093/jexbot/52.362.1865. [DOI] [PubMed] [Google Scholar]
- Douthe C, Dreyer E, Brendel O, Warren CR. Is mesophyll conductance to CO2 in leaves of three Eucalyptus species sensitive to short-term changes of irradiance under ambient as well as low O2? Funct Plant Biol. 2012;39:435–448. doi: 10.1071/FP11190. [DOI] [PubMed] [Google Scholar]
- Evans JR, von Caemmerer S. Temperature response of carbon isotope discrimination and mesophyll conductance in tobacco. Plant Cell Environ. 2013;36:745–756. doi: 10.1111/j.1365-3040.2012.02591.x. [DOI] [PubMed] [Google Scholar]
- Evans JR, Sharkey TD, Berry JA, Farquhar GD. Carbon isotope discrimination measured concurrently with gas exchange to investigate CO2 diffusion in leaves of higher plants. Aust J Plant Physiol. 1986;13:281–292. doi: 10.1071/PP9860281. [DOI] [Google Scholar]
- Evans JR, Kaldenhoff R, Genty B, Terashima I. Resistances along the CO2 diffusion pathway inside leaves. J Exp Bot. 2009;60:2235–2248. doi: 10.1093/jxb/erp117. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, von Caemmerer S, Berry JA. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta. 1980;149:78–90. doi: 10.1007/BF00386231. [DOI] [PubMed] [Google Scholar]
- Flexas J, Diaz-Espejo A, Galmes J, Kaldenhoff R, Medrano H, Ribas-Carbό M. Rapid variation of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant Cell Environ. 2007;30:1284–1298. doi: 10.1111/j.1365-3040.2007.01700.x. [DOI] [PubMed] [Google Scholar]
- Gu L, Sun Y. Artefactual responses of mesophyll conductance to CO2 and irradiance estimated with the variable J and online isotope discrimination methods. Plant Cell Environ. 2014;37:1231–1249. doi: 10.1111/pce.12232. [DOI] [PubMed] [Google Scholar]
- Harley PC, Loreto F, Di Marco G, Sharkey TD. Theoretical considerations when estimating the mesophyll conductance to CO2 flux by analysis of the response of photosynthesis to CO2. Plant Physiol. 1992;98:1429–1436. doi: 10.1104/pp.98.4.1429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatakeyama Y, Ueno O. Intracellular position of mitochondria and chloroplasts in bundle sheath and mesophyll cells of C3 grasses in relation to photorespiratory CO2 loss. Plant Prod Sci. 2016;19:540–551. doi: 10.1080/1343943X.2016.1212667. [DOI] [Google Scholar]
- Kebeish R, Niessen M, Thirshnaveni K, Bari R, Hirsch H-J, Rosenkranz R, Stäbler N, Schönfeld B, Kreuzaler F, Peterhänsel C. Chloroplastic photorespiratory bypass increases photosynthesis and biomass production in Arabidopsis thaliana. Nature Biotechnol. 2007;25:593–599. doi: 10.1038/nbt1299. [DOI] [PubMed] [Google Scholar]
- Peguero-Pina JJ, Flexas J, Galmes J, Niinemets Ü, Sancho-Knapik D, Barredo G, Villarroya D, Gil-Pelegrin E. Leaf anatomical properties in relation to differences in mesophyll conductance to CO2 and photosynthesis in two related Mediterranean Abies species. Plant Cell Environ. 2012;35:2121–2129. doi: 10.1111/j.1365-3040.2012.02540.x. [DOI] [PubMed] [Google Scholar]
- Pons TL, Flexas J, von Caemmerer S, Evans JR, Genty B, Ribas-Carbo M, Brugnoli E. Estimating mesophyll conductance to CO2: methodology, potential errors, and recommendations. J Exp Bot. 2009;60:2217–2234. doi: 10.1093/jxb/erp081. [DOI] [PubMed] [Google Scholar]
- Sage TL, Sage RF. The functional anatomy of rice leaves: implications for refixation of photorespiratory CO2 and effects to engineer C4 photosynthesis into rice. Plant Cell Physiol. 2009;50:756–772. doi: 10.1093/pcp/pcp033. [DOI] [PubMed] [Google Scholar]
- Tazoe Y, von Caemmerer S, Badger MR, Evans JR. Light and CO2 do not affect the mesophyll conductance to CO2 diffusion in wheat leaves. J Exp Bot. 2009;60:2291–2301. doi: 10.1093/jxb/erp035. [DOI] [PubMed] [Google Scholar]
- Tcherkez G, Boex-Fontvieille E, Mahe A, Hodges M. Respiratory carbon fluxes in leaves. Curr Opin Plant Biol. 2012;15:308–314. doi: 10.1016/j.pbi.2011.12.003. [DOI] [PubMed] [Google Scholar]
- Terashima I, Hanba YT, Tholen D, Niinemets Ü. Leaf functional anatomy in relation to photosynthesis. Plant Physiol. 2011;155:108–116. doi: 10.1104/pp.110.165472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tholen D, Zhu X-G. The mechanistic basis of internal conductance: a theoretical analysis of mesophyll cell photosynthesis and CO2 diffusion. Plant Physiol. 2011;156:90–105. doi: 10.1104/pp.111.172346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tholen D, Ethier G, Genty B, Pepin S, Zhu X-G. Variable mesophyll conductance revisited: theoretical background and experimental implications. Plant Cell Environ. 2012;35:2087–2103. doi: 10.1111/j.1365-3040.2012.02538.x. [DOI] [PubMed] [Google Scholar]
- Tomas M, Flexas J, Copolovici L, Galmes J, Hallik L, Medrano H, Ribas-Carbo M, Tosens T, Vislap V, Niinemets Ü. Importance of leaf anatomy in determining mesophyll diffusion conductance to CO2 across species: quantitative limitations and scaling up by models. J Exp Bot. 2013;64:2269–2281. doi: 10.1093/jxb/ert086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosens T, Niinemets Ü, Vislap V, Eichelmann H, Castro Diez P. Developmental changes in mesophyll diffusion conductance and photosynthetic capacity under different light and water availabilities in Populus tremula: how structure constrains function. Plant Cell Environ. 2012;35:839–856. doi: 10.1111/j.1365-3040.2011.02457.x. [DOI] [PubMed] [Google Scholar]
- Tosens T, Niinemets Ü, Westoby M, Wright IJ. Anatomical basis of variation in mesophyll resistance in eastern Australian sclerophylls: news of a long and winding path. J Exp Bot. 2012;63:5105–5119. doi: 10.1093/jxb/ers171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Caemmerer S. Steady-state models of photosynthesis. Plant Cell Environ. 2013;36:1617–1630. doi: 10.1111/pce.12098. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Evans JR. Determination of the average partial pressure of CO2 in chloroplasts from leaves of several C3 plants. Aust J Plant Physiol. 1991;18:287–305. doi: 10.1071/PP9910287. [DOI] [Google Scholar]
- von Caemmerer S, Evans JR. Temperature responses of mesophyll conductance differ greatly between species. Plant Cell Environ. 2015;38:629–637. doi: 10.1111/pce.12449. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Evans JR, Hudson GS, Andrews TJ. The kinetics of ribulose-1,5-bisphosphate carboxylase/oxygenase in vivo inferred from measurements of photosynthesis in leaves of transgenic tobacco. Planta. 1994;195:88–97. doi: 10.1007/BF00206296. [DOI] [Google Scholar]
- Vrábl D, Vašková M, Hronková M, Flexas J, Šantrůček J. Mesophyll conductance to CO2 transport estimated by two independent methods: effect of variable CO2 concentration and abscisic acid. J Exp Bot. 2009;60:2315–2323. doi: 10.1093/jxb/erp115. [DOI] [PubMed] [Google Scholar]
- Yamori W, Noguchi K, Hanba YT, Terashima I. Effects of internal conductance on the temperature dependence of the photosynthetic rate in spinach leaves from contrasting growth temperatures. Plant Cell Physiol. 2006;47:1069–1080. doi: 10.1093/pcp/pcj077. [DOI] [PubMed] [Google Scholar]
- Yin X, Struik PC (2009) Theoretical reconsiderations when estimating the mesophyll conductance to CO2 diffusion in leaves of C3 plants by analysis of combined gas exchange and chlorophyll fluorescence measurements. Plant Cell Environ 32:1513–1524 with corrigendum in 33:1595 [DOI] [PubMed]
- Yin X, Struik PC, Romero P, Harbinson J, Evers JB, van der Putten PEL, Vos J. Using combined measurements of gas exchange and chlorophyll fluorescence to estimate parameters of a biochemical C3 photosynthesis model: a critical appraisal and a new integrated approach applied to leaves in a wheat (Triticum aestivum) canopy. Plant Cell Environ. 2009;32:448–464. doi: 10.1111/j.1365-3040.2009.01934.x. [DOI] [PubMed] [Google Scholar]