Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jun 11;5:11304. doi: 10.1038/srep11304

Optimizing cell viability in droplet-based cell deposition

Jan Hendriks 1,*, Claas Willem Visser 2,a,*, Sieger Henke 1, Jeroen Leijten 1, Daniël BF Saris 3,4, Chao Sun 2, Detlef Lohse 2, Marcel Karperien 1,b
PMCID: PMC5387118  PMID: 26065378

Abstract

Biofabrication commonly involves the use of liquid droplets to transport cells to the printed structure. However, the viability of the cells after impact is poorly controlled and understood, hampering applications including cell spraying, inkjet bioprinting, and laser-assisted cell transfer. Here, we present an analytical model describing the cell viability after impact as a function of the cell-surrounding droplet characteristics. The model connects (1) the cell survival as a function of cell membrane elongation, (2) the membrane elongation as a function of the cell-containing droplet size and velocity, and (3) the substrate properties. The model is validated by cell viability measurements in cell spraying, which is a method for biofabrication and used for the treatment of burn wounds. The results allow for rational optimization of any droplet-based cell deposition technology, and we include practical suggestions to improve the cell viability in cell spraying.

Droplet-based cell deposition is receiving increasing attention as a tool to construct or fill a variety of biological tissues. Striking examples are the cell spray treatment of burns1,2 or ulcers3, which provide faster and improved healing and are currently introduced in clinical practice. With one successful application in place, we seek to expand to other clinical areas including laparoscopic, endoscopic, and arthroscopic procedures4. This opens the possibility for minimally invasive cell therapy for tissue regeneration. A second example is the fabrication of functional tissue replacements in a laboratory, to enable curing non-functional tissues5,6,7. In current biofabrication technologies including ink-jet bioprinting8,9,10, laser-induced forward transfer11, valve-based bioprinting12,13, and cell spraying2,14,15,16,17, the cell transport from the initial cell suspension, called “bio-ink”, to the manufactured tissue is achieved by liquid droplet ejection and deposition. Although these technologies allow for high-viability cell deposition, limited throughput, limited precision, and poorly optimized cell-containing bio-inks are major obstacles in the controlled deposition of cells, such as required for the fabrication of functional tissues5,7.

To solve these issues and thereby optimize droplet-based cell deposition, knowledge of the cell viability as a function of the cell-containing droplet size and impact velocity is crucial. Ideally, single, highly reproducible impacts of droplets containing a single cell would be monitored for a large range of the impact parameters (droplet size, velocity, and material properties). Drop-on-demand systems provide such highly reproducible droplets, but usually the impact parameter space is relatively narrow for the cell-containing liquids used18,19,20,21,22,23. Therefore, to study post-impact cell viability, we use cell spray deposition, which allows for a much larger range of impact parameters. The substantial influence of the spray parameters on post-impact cell viability2,15,16,17,24 suggests that cell viability can be controlled, providing a model system to assess cell survival after impact. Additionally, the shear stress exerted on the cell within the spray nozzle is much lower than the shear stress during impact, which allows for assessment of the impact process alone (for other technologies this is not the case, as explained in supplementary section I).

The current work aims to understand the influence of the droplet impact on cell viability, which is applicable both to drop-on-demand and spray deposition technologies. We introduce a model describing the cell viability as a function of the cell-containing droplet size, the viscosity, and the impact velocity. The model is validated by cell spray experiments, following a two-step approach. First, the droplet size and impact velocity are measured and used to obtain model predictions as described. Subsequently, the cell viability after spraying is measured as a function of the air pressure, the liquid viscosity, the nozzle-substrate distance, and the substrate stiffness. The model is shown to accurately describe the viability measurements as a function of the input parameters. These results provide a powerful tool to rationally evaluate and improve clinical spray treatments and tissue engineering applications.

Results

Cell viability model

In cell spraying, cell damage is primarily expected during impact of the cell-containing droplets (see supplementary section I). In particular, impact generally results in cell deformation and elongation of the cell membrane25, as illustrated in Fig. 1(c,d). For an increase of the cell membrane area up to ~5%, the membrane is stretched, but remains intact. However, for larger extensions, rupture can be observed26. As rupture generally results in cell death, the probability of survival η is modeled as a function of the relative cell membrane area γ (compared to the undisturbed case) according to ref. 27:

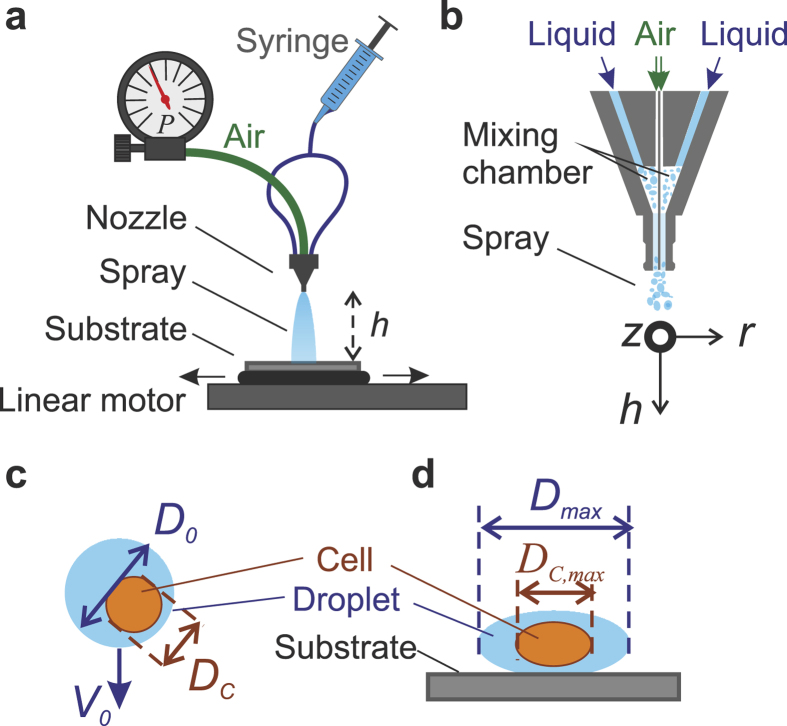
Figure 1. Overview of the experimental method and parameter definition.

Figure 1

Open in a new tab

A two-phase spray nozzle is used to generate the spray, and placed at a distance h from the surface. The cell-containing liquid (with viscosity μ) is delivered to the nozzle using a syringe pump (not shown). Air at controlled pressure P is applied to the nozzle gas inlet. The impact substrate is moved under the spray (indicated by horizontal arrows) using a linear motor, ensuring clean and homogeneous impact. Generally, a clean glass substrate is used, but gelatin-water mixtures (with gelatin weight fractions Cg) are used to assess the influence of the surface stiffness. (b) Cross-section of the nozzle, illustrating the air and liquid flows, and the coordinate system used. Figures (c) and (d) illustrate key variables describing the cell-containing droplets in air (c) and during impact (d).

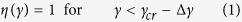graphic file with name srep11304-m1.jpg
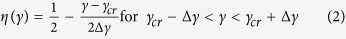graphic file with name srep11304-m2.jpg
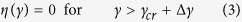graphic file with name srep11304-m3.jpg

with γcr = 1.5 the critical membrane expansion as quantitatively provided in ref. 27, and 2Δγ = 1 the range of surface expansion in which the cells partly survive. Key model conditions include an elastic cell response to stresses (which is fulfilled for shear rates 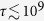Inline graphics−126; for the estimate of the shear stress see supplementary section I) and negligible lipid membrane replenishment during deformation (fulfilled for 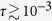Inline graphic s−128), which are met in the current work.

To obtain the relative cell membrane area γ, first a “clean” cell impact on a hard substrate is considered. The cell is described as a spherical liquid droplet with diameter Dc, velocity Vc, viscosity μc = 12 mPa s, density ρc = 1015 kg/m3 and surface tension σc = 0.072 N/m2 (key parameters are visualized in Fig. 1(c,d)). The maximal spreading diameter reached during impact Dc,max,0 is then calculated as a function of the cell Weber number, which describes the ratio between kinetic energy and surface energy29,30,31:

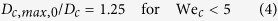graphic file with name srep11304-m6.jpg
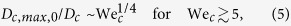graphic file with name srep11304-m7.jpg

with cell Weber number 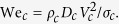Inline graphic These equations are valid for Newtonian liquids and for 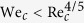Inline graphic29 (which is fulfilled for our experiments), in which the cell Reynolds number Rec = ρcVcDc/μc represents the ratio between inertia and viscosity. The cell shape is defined by assuming cell deformation into an oblate spheroid and volume conservation. At the instant of reaching its maximal extension, its height equals 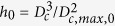Inline graphic. This provides the deformation M0 for an impacting cell, which is defined according to ref. 25:

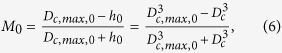graphic file with name srep11304-m11.jpg

i.e. M0 = 0 for a sphere, and M0 = 1 for a plane.

The potentially large influence of the surrounding droplet on the cell’s deformation was modeled numerically by Tasoglu et al.25. Re-interpreting their results provides a quantitative expression capturing the cell deformation M as a function of M0, the surrounding droplet’s diameter D0, and its viscosity μ0 (for details see supplementary section III, for viscosity-dominated deformation of compound drops see ref. 32):

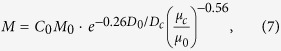graphic file with name srep11304-m12.jpg

with C0 a fitting parameter (which is set to C0 = 5, as discussed in supplementary section III). Subsequently, M is translated into the maximal spreading diameter of the (oblate-spheroid) cell as 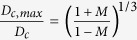Inline graphic, which is used below to calculate the cell surface area. Since this occasionally results in a cell diameter exceeding the droplet’s diameter, we additionally implement the condition Dc,max = min(Dc,max,0, Dmax). The surface area A of an oblate spheroid (the assumed shape of a single trypsinized cell) can be calculated as:

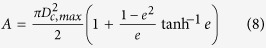graphic file with 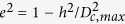name srep11304-m14.jpg

with Inline graphic. The relative surface area is given by 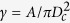Inline graphic, which completes the system.

Finally, the model is extended to account for the stiffness of the impact substrate. We assume impact on a liquid pool (with material properties equal to the droplet) as a soft surface limit. A droplet with diameter D0 and velocity V0 impacting on such a pool is (in first approximation) described by the impact of a droplet with diameter 2D0 and velocity 0.5V0 on a hard substrate33. As soft-surface droplet impact is not adequately understood even for basic model systems34, we propose an effective droplet diameter and velocity as:

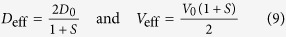graphic file with name srep11304-m17.jpg

with S an arbitrary stiffness parameter ranging from S = 0 for liquid surfaces to S = 1 for hard surfaces. A gelatin-water mixture is used to generate a substrate stiffness range corresponding to a large variety of natural tissues35,36. In the high-shear regime associated to fast micro-droplet impact the viscoelastic properties of these substrates cannot be measured by any standard viscometer. Therefore, the gelatin mass fraction Cg is used to define the stiffness: S = C1Cg, with C1 a fitting constant. Using C1 = 5 provides reasonable agreement between the model and our soft-surface impact measurements. For Cg > 1/C1 we define S = 1, which implies an effectively stiff surface for Cg > 0.2.

Figure 2 shows example model results. The viability probability of individual cells is shown as a function of the impact velocity, for different sizes of the surrounding droplet (Fig. 2(a)), and different relative viscosities (Fig. 2(b)). At low velocities, the cell viability is only weakly dependent on the impact parameters since a small and constant cell deformation is assumed for low Weber numbers (We < 5). For increasing velocities (corresponding to We > 5) a decrease in cell viability is observed. In this regime, the size of the surrounding droplet and its viscosity strongly affect cell viability. Larger surrounding droplets provide stronger cushioning and thereby increase the viability (Fig. 2(a)). Increasing the droplet viscosity negatively influences the cell viability, since for μc = μ0 the droplet will flow around the (relatively stiff) cell, whereas for μc < μ0 the cell flows to dampen the (relatively stiff) droplet’s impact, resulting in significant cell deformation and decreased viability. Finally, softer substrates provide increased cushioning as shown by the color gradient in Fig. 2(a). Here, the surface deforms such that the deformation of the droplet is reduced. Consequently, cell deformation is suppressed and a higher viability is expected. In conclusion, optimal cell viability is expected for slow, large, and low-viscosity cell-containing droplets impacting onto a soft surface.

Figure 2. Model predictions of the post-impact cell survival probability η as a function of the impact velocity V0, for a single-cell containing droplet.

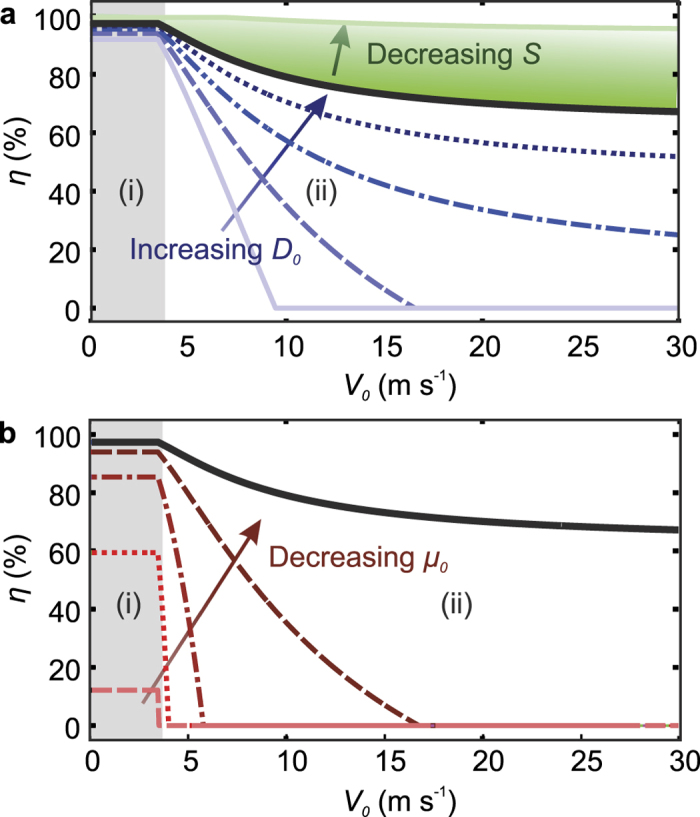
Figure 2

Open in a new tab

Figure (a) shows the influence of the droplet diameter D0 (indicated by lines representing 1 ≤ D0/Dc ≤ 3 in steps of 0.5) and the surface stiffness (indicated by the color gradient representing S = 1 (stiff substrate) to S = 0 (liquid pool)). Figure (b) shows the influence of the droplet viscosity (lines plotter for μ0 = 1, 2, 4, 8, 12  mPa s). The solid black lines indicate the viability values obtained for the reference parameters: D0/Dc = 3, μc/μ0 = 10, and S = 1. Region (i) (shaded) indicates the low-Weber number regime (We < 5). Here the cell deformation is small and independent of the impact velocity. In region (ii), decreasing viability is obtained for increasing velocities, due to increasing cell deformation.

Spray characterization

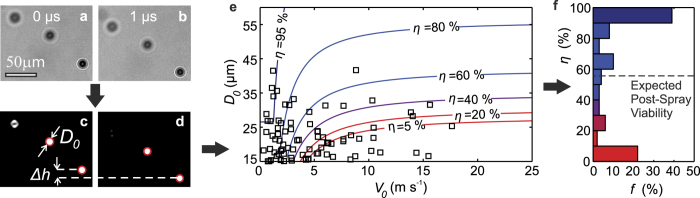
To obtain cell viability predictions from the model, the droplet size- and velocity are required. We obtain these parameters according to Fig. 3. First, the droplets are visualized as shown in Fig. 3(a,b). Automated image analysis then provides the droplet diameter D0 and velocity V0 = Δh/Δt, as illustrated in Fig. 3(c,d). For any spray experiment, a wide range of droplet sizes and velocities is observed. A representative sample of droplet sizes and velocities is indicated by the black markers in Fig. 3(e), which also contains indicative cell viability contours (similar graphs for different spraying parameters are included in supplementary section II). To obtain the cell viability, for each drop the cell survival probability was calculated as a function of the size, speed, viscosity, and surface stiffness. This provides a distribution of cell viability probabilities as shown in Fig. 3(f) (corresponding to the drop size and speed distributions), of which the average provides a single predicted cell viability value which is compared to experimental viability data in the following section.

Figure 3. Characterization of the spray.

Figure 3

Open in a new tab

An example image pair is shown before ((a) and (b)) and after image processing ((c) and (d)). As indicated by the circles in (c) and (d), two droplets are automatically detected using home-written image analysis software, which provides their diameter D0 and translation Δh. Figure (e) shows the droplet size- and velocity for P = 0.4 .105 Pa, μ = 1 mPa s, h = 3 cm. The markers (◻) show 100 statistically representative droplets constituting the spray. The contours represent predicted cell viability values (η). Figure (f) shows the relative incidence f of each cell survival probability η, which is binned for the sake of clarity. Averaging these probability values results in the expected post-spray cell viability (dashed line). The expected cell viability strongly depends on the spray parameters setting, as plotted in Fig. 5 (red diamond).

Cell viability measurements and model validation

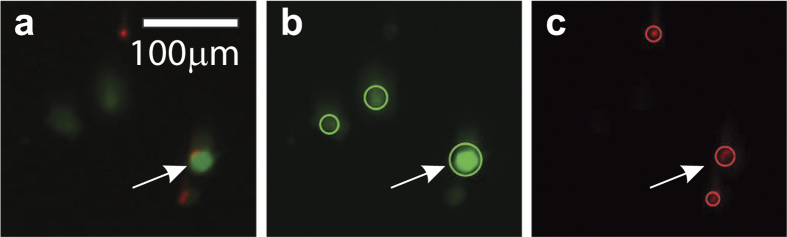
To measure the post-impact cell viability, spray experiments are performed using the setup displayed in Fig. 1. After spraying, the cells are collected and stained in a live-dead assay of which an example is shown in Fig. 4. Using automated image analysis, the cell viability is determined for each measurement. Figure 5 shows the measured cell viability as a function of the pressure, the nozzle-substrate distance, the viscosity, and the surface stiffness. The cell viability is also measured as a function of the time after spraying (see supplementary section V), demonstrating the long-term viability of the surviving cells.

Figure 4. Example live-dead assay.

Figure 4

Open in a new tab

Figure (a) shows the original image; figure (b) shows the calcein staining (in green), and figure (c) shows the EthD staining (in red). The circles in figures (b) and (c) indicate the automatically detected cells for each staining. The arrows show a cell in which both stainings are retrieved. These cells are considered damaged but viable, and therefore counted as live.

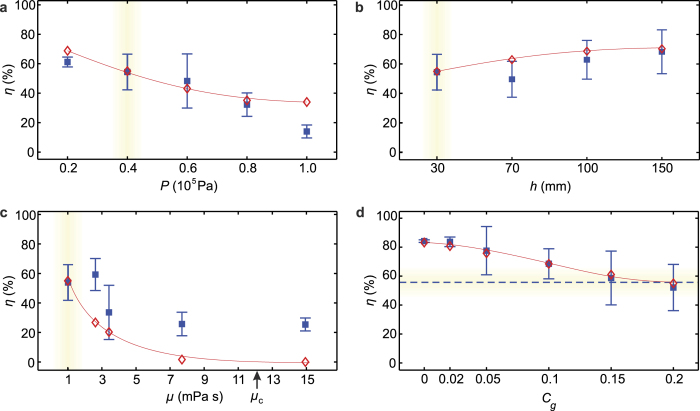
Figure 5. Cell viability η as a function of the spray control parameters.

Figure 5

Open in a new tab

Figures (a–d) indicate the viability as a function of the pressure P, the nozzle-substrate distance h, the liquid viscosity μ, and the substrate gelatin percentage, respectively. Measured values are indicated as blue squares Inline graphic with the error bar representing the standard deviation; red diamonds Inline graphic indicate model predictions. The lines are a guide to the eye for the model predictions (which cannot be displayed as smooth curves as they depend on the spray distributions, as explained in supplementary section II). The reference settings are P = 0.4 .105 Pa, μ = 1 mPa s, h = 3 cm, and a glass impact substrate, as indicated by the yellow shade in each plot.

The model is compared to cell viability measurements in Fig. 5. Good agreement is observed for the pressure, the nozzle-substrate distance, and the surface stiffness. In particular, except for the lower and upper pressure data points, the measured data is quantitatively described by the model, which is remarkable in view of the single fitting parameter used. Our model over-estimates the influence of increased viscosity, but still captures the trend. The origin of the lower cell viability for increasing pressure (4(a)) is that the spray consists of smaller drops impacting at increasing velocities, as shown in Fig. 6. Both factors result in stronger cell deformation and therefore cell death. Increasing the nozzle-substrate distance improves the cell viability, as shown in Fig. 5(b). Figure 6 shows that this trend is primarily caused by the decreasing droplet velocity far from the nozzle, which results in less deformation of the cell and increased viability. Higher viscosities result in a lower cell viability, as shown in Fig. 5(c). For high viscosity, the deformation of the cell-containing droplet primarily occurs within the cell. Consequently, the cell membrane is significantly stretched, and the viability decreases. Finally, decreasing the surface stiffness improves the viability (Fig. 5(d)), since the deforming surface “cushions” the impacting cell-containing droplet.

Figure 6.

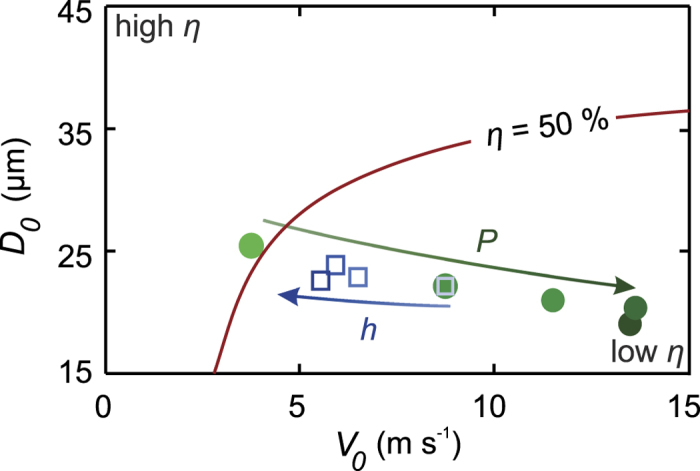
Figure 6

Open in a new tab

Viability as a function of the droplet size and speed. The line represents the 50% viability contour; additional contours are plotted in Fig. 3(e). The dots indicate the mean diameter versus the mean velocity as a function of the spray pressure (the arrow indicates increasing pressure for P = [0.2, 0.4, 0.6, 0.8, 1].105 Pa). The open squares indicate the distance from the nozzle for h = [30, 50, 100, 150] mm. For increasing pressure, the droplet size decreases and the impact velocity increases, resulting in a lower viability. For a larger distance from the nozzle, the impact speed decreases, resulting in improved viability. The influence of the viscosity and the surface stiffness is displayed in Fig. 2), since these variables do not affect the droplet size and speed.

Discussion

The model assumptions affect its applicability, and therefore deserve further discussion. First, the assumption that the cells are centered in the droplet will be approximately true for drop sizes just exceeding the cell size, but for larger droplets the cells may be located at the edge of the spreading film where the shear stresses are much higher than in the center31. Therefore, for larger drops such as generated for low pressures (see supplementary Figure 4(a)), the cell viability may be suppressed. This mechanism possibly explains the lower viability for P = 0.2 .105 Pa observed in Fig. 5(a). Second, following ref. 25, we assume that the cell viscosity is independent of the shear stress. As experiments reveal shear-thinning behavior of cells37,38, implementing shear thinning could further improve the model. Third, the influence of the droplet volume on the number of cells per drop is not yet taken into account. Finally, the influence of viscosity on cell deformation might be different from equation (7), since equation (7) is derived from numerical results for much larger cell-containing droplets (ref. 25, also see supplementary section III) whereas most of our droplets have a size just exceeding the cell size (supplementary Figure 3). Avoiding these assumptions by extending the model may result in even better agreement. Still, the agreement between our model and measurements is remarkable and provides evidence for correctly capturing the underlying physics.

Droplet impact-induced cell damage has far-reaching consequences for users as well as developers of cell spraying and other bioprinting technologies. In clinical practice, the need for adequate cell-spraying protocols39 is even more pressing than expected. In particular, manual operation of spray devices is common practice, but associated with variations in nozzle-substrate distance, the air pressure, and the viscosity. These variables should be carefully controlled to ensure high cell viabilities. The actual values may still depend on the nozzle design and the cell type, but increasing the spray distance and using low-viscosity spray suspensions, while avoiding hard impact surfaces, will generally improve cell survival.

However, harmful spraying conditions cannot always be avoided due to treatment-specific clinical requirements or constraints in biofabrication. For example, in arthroscopic procedures, the nozzle-surface distance is limited to at most 1 cm4. In view of our results, it is unclear whether the treatment success shown for burn treatments, where this distance usually exceeds 10 cm, can be reproduced in arthroscopic application (see Fig. 5(b)). Also, in many treatments, the impact surface is a tissue defect and therefore cannot be freely chosen or altered. Our hardest gelatin-containing surfaces result in similarly low viability as hard glass surfaces. These 20% gelatin surfaces are similar in stiffness to muscle tissue35, which is one of the softer human tissues36. Thus, clinically relevant surfaces are relatively stiff, possibly affecting cell survival. To solve this problem, the spray parameters require optimization. Similarly, the deposition of viscous, cell-containing hydrogels is usually required to preserve the desired 3D tissue architecture in biofabrication12. However, such liquids are likely to negatively affect the cell viability (see Fig. 5(c)). Decreasing the spray pressure2,15,16,17, using softer impact surfaces24, or increasing the nozzle-substrate distance can counteract the negative influence of the increased viscosity (see Fig. 5), but, unfortunately, these parameters are sometimes also constrained.

The greatest potential to improve cell viability in cell spraying therefore seems to be optimization of spray nozzle designs. Particularly, design optimization resulting in increased and monodisperse droplet sizes and reduced impact velocities would allow for successful cell deposition in an extended viscosity range. In this study we have used the Duploject system, which is approved for clinical application of fibrin glue by spraying and also used for cell spraying4. The spray produced by this nozzle is characterized by highly polydisperse droplet diameters and velocities. High-velocity impacts occur even for the most gentle spraying parameters, limiting the measured highest post-spray cell viabilities to 90%. Nozzle designs producing more monodisperse droplets may prevent these lethal events, even for high-throughput spraying of viscous liquids. Our experimental setup can be used to rationally optimize such future spray nozzles, which may substantially enhance the application window of cell-spraying.

Finally, other droplet-based cell deposition technologies may benefit from our approach. In ink-jet bioprinting, highly monodisperse cell-containing droplets40,41,42,43 are deposited. Here, typically, low-viscosity droplets of 40 m (exceeding the cell size by a factor of 3) impact at velocities below 10 ms−1. Good viability is generally measured in this range23, in agreement with our model (Fig. 2). However, reduced cell viability is observed for neural cells44. Our study suggests that especially decreasing the liquid viscosity or reducing the droplet ejection velocity could improve the cell viability of such more fragile cell types. These measures reduce the expected cell damage both in the nozzle and during impact, which are both likely causes of cell damage in ink-jet printing (see supplementary section 1). Using soft impact substrates or larger nozzle-substrate distances will still reduce impact-related damage, but nozzle-induced cell damage or poration10 cannot be suppressed in this manner.

Cell viability trends observed in laser-assisted bioprinting (LAB) are also described by our model. Here, a pulsed laser is focused onto a cell-containing liquid film, resulting in the deformation of this film and break-up into cell-containing droplets45,46. By placing a receiver substrate in the line-of-flight of the cell-containing droplet, deposition is achieved. Increased impact velocities result in decreased cell viability47,48, and soft impact surfaces improve cell survival49, analogous to our model results shown in Fig. 2. Surprisingly, improved cell viability was reported for increased viscosity48, but this was explained by the reduced impact velocity due to the increased viscosity. Studying the cell viability as a function of the liquid viscosity at a controlled impact velocity would therefore be highly interesting. Such experiments may also advance the understanding of cell membrane deformation due to pulsed shear stresses50, as occurring in cell-containing droplet impact.

In conclusion, we present and validate an analytical model describing the cell viability as a function of the droplet impact parameters. The model describes cell-viability trends in cell spraying, inkjet bioprinting, and laser-assisted cell transfer, confirming the general importance of droplet impact for cell survival in bioprinting. Since future biofabrication applications may involve high-throughput deposition of different, possibly more fragile, cell types contained by high-viscosity bio-inks, we expect that preventing cell damage will become even more important. In particular, post-spray cell survival will be cell-type dependent. In addition, different bio-inks may require distinct deposition parameters in combination with dedicated nozzle designs allowing monodisperse droplet ejection while maintaining low shear rates inside the nozzle. Our study provides a framework to optimize cell survival in such future applications, contributing to reliable biofabrication of complex 3D-tissue constructs of a clinically relevant size.

Methods

Cell culture

Neonatal rat dermal fibroblasts (ITK Diagnostics) were cultured in Minimum Essential Medium α (α-MEM) (Gibco) supplemented with 10% Fetal Bovine Serum (FBS) (Lonza), 1% L-Glutamine (Gibco) and 1% Pen/Strep (Gibco) at 37 °C and 5% CO2.

Cell suspension

Cells were harvested at 80% confluence by trypsinization and suspended at 1.5 × 106 cells per ml in culture medium excluding FBS for impact experiments. Optionally dextran (Sigma, 15–25 kDa) was added to the cell suspensions to increase the viscosity. The influence of the dextran concentration on the liquid viscosity was measured using a viscometer (Rheolab QC, Anton Paar). As shown in supplementary Figure 10, the measured viscosity is in agreement with literature values.

Cell viability measurements

Cell spray experiments were performed with the set-up shown in Fig. 1. Using a syringe pump, the cell suspension was pushed through a spray nozzle (Duploject spray system (Baxter AG). Photographs of this system, which is also known as bio-airbrush, are provided in supplementary Figure 9) at a controlled liquid flow rate of 2.4 ml per min. The impact surface consisted of a standard clean microscope slide covered with a PDMS mask to ensure a defined and reproducible impact area. These slides were optionally coated with a layer of gelatin (Type A, Sigma, d = 0.5 mm), in order to adjust the surface stiffness. A crucial aspect of the experiment is that impact occurs on a dry surface, i.e. that the cell spray does not impact onto previously sprayed droplets. To ensure this, the impact surface was reproducibly moved using a programmable linear motor. The substrate velocity was set such that 12 ± 0.5 mg of the sprayed liquid was collected for each experiment (the velocity was decreased for increasing nozzle-substrate distances since the spray density decreases for increasing distance from the nozzle). This weight corresponds to a liquid film of 18 μm (which is equivalent to ~1 cell thickness) and resulted in covering roughly half of the surface area with sprayed droplets, such that most droplets land on the dry surface. Within 10 s after each spray experiment, the surface was rinsed with FBS-free culture medium to collect the cells. The cells rinsed from three different samples (sprayed using equal parameter settings) were collected into a 12 ml centrifuge tube (Greiner). The contents of each tube were subsequently processed in a live-dead assay. For each parameter setting, three independent spray cycles were performed (i.e. 9 impact surfaces were collected in three different tubes). This approach provided three data points for each parameter setting, which were used to display the error bar in Fig. 5.

Live-dead assay

The collected cells were incubated in phosphate buffered saline (PBS), supplemented with 1 nM calcein AM and 6 nM ethidium homodimer, at 37 °C and 5% CO2 for 30 minutes. Each stained cell suspension sample was transferred to a well in a 24 wells-plate and 8 random spots per well were imaged (EVOS Fl microscope), within 2 hours after each spray experiment. Live (green) and dead (red) cells were automatically counted using a home-written Matlab script (Fig. 5 shows an example), resulting in an average of 450 ± 332 (s.d.) detected cells per sample (with a minimum of 12 cells). Cells stained both live and dead were considered damaged, but viable, so counted as alive. For each sample, viability was calculated accordingly. All measurements were subsequently corrected by setting the control viability (non-impact, measured at the same time) to 100%.

Spray characterization

As cell survival critically depends on the characteristics of the cell-containing droplets, the spray characteristics were determined in detail. The setup used is shown in supplementary Fig. 2. All spray-generating components were equal to the components used for assessment of the cell viability (Fig. 1). A dual-pulse ND:Yag laser with a pulse duration of 6 ns was used for brightfield illumination. To prevent fringes, the coherent laser light was diffused using a fluorescent plate placed in front of the laser. The non-coherent pulses were captured by a dual-shutter camera (Sensicam, PCO). The time delay between the illumination pulses was set to 1 μs, which is sufficiently long to measure the translation Δh of the droplets while preventing confusion between different droplets. All timings were controlled using a BNC 575 pulse-delay generator (not shown). A 10× long-distance objective was used, resulting in a field of view of 0.67 × 0.89 mm2. As the focal plane thickness of this objective is δF ≈ 0.1 ± 0.03 mm, a volume of 0.67 × 0.89 × 0.1 mm3 was visualized. As the spray is much larger than this volume, measurements were taken at different z- and h-positions to fully characterize the spray, as illustrated by the small rectangles in supplementary Figure 1(b) (the r-position is maintained at the nozzle axis).

For each measurement, 400 image pairs were obtained. Example images are shown in Fig. 3(a,b), where the downward translation of the droplets is clearly visible. Motion blur was prevented by the short illumination pulses of 6 ns. The droplets were automatically detected using a home-written Matlab script. Droplets appearing sufficiently sharp were automatically selected, as illustrated by the red circles in Fig. 3(c,d). Here, the top-left droplet was too blurred for detection and discarded. Although the droplets in Fig. 3 are similar in size, the image processing software allowed for successful detection of droplets in the range of 1 ≤ D0 ≤ 100 μm.

Soft substrate preparation

Glass microscope slides were optionally coated with a layer of gelatin (Type A, Sigma) of thickness 0.5 mm, and kept in air at room temperature for 30 min prior to the experiment. The surface stiffness was adjusted by adding gelatin mass fractions of Cg = [2, 5, 10, 20]% to PBS. PBS without gelatin was used in the soft-surface limit.

Additional Information

How to cite this article: Hendriks, J. et al. Optimizing cell viability in droplet-based cell deposition. Sci. Rep. 5, 11304; doi: 10.1038/srep11304 (2015).

Supplementary Material

Supplementary Information
srep11304-s1.pdf (2.9MB, pdf)

Acknowledgments

The financial support by the Foundation for Fundamental Research of Matter (FOM) is gratefully acknowledged by CWV, DL, and CS. MK and JH are supported by the Dutch Arthritis Association.

Footnotes

The authors declare no competing financial interests.

Author Contributions M.K., D.L., C.W.V. and J.H. designed the research; J.H. and S.H. provided the cell samples; J.H. and C.W.V. performed the measurements; C.W.V. and J.H. designed the model; J.H., C.W.V., C.S. and D.L. contributed analytic tools; J.H., C.S., M.K. and C.W.V. analyzed the data; D.S. and J.L. provided valuable input in data interpretation; C.S., D.L. and M.K. supervised the work; C.W.V., J.H. and M.K. wrote the first draft of the article; all authors discussed the work.

References

  1. Navarro F. A. et al. Sprayed keratinocyte suspensions accelerate epidermal coverage in a porcine microwound model. J. Burn. Care Rehabil. 21, 513–8 (2000). [DOI] [PubMed] [Google Scholar]
  2. Harkin D. G., Dawson R. A. & Upton Z. Optimized delivery of skin keratinocytes by aerosolization and suspension in fibrin tissue adhesive. Wound Repair Regen. 14, 354–63 (2006). [DOI] [PubMed] [Google Scholar]
  3. Kirsner R. S. et al. Spray-applied cell therapy with human allogeneic fibroblasts and keratinocytes for the treatment of chronic venous leg ulcers: a phase 2, multicentre, double-blind, randomised, placebo-controlled trial. Lancet 380, 977–85 (2012). [DOI] [PubMed] [Google Scholar]
  4. De Windt T. S. et al. Arthroscopic airbrush assisted cell implantation for cartilage repair in the knee: a controlled laboratory and human cadaveric study. Osteoarthr. Cartilage 1–8 (2014). [DOI] [PubMed] [Google Scholar]
  5. Murphy S. V. & Atala A. 3D bioprinting of tissues and organs. Nat. Biotechnol. 32, 773–785 (2014). [DOI] [PubMed] [Google Scholar]
  6. Mota C., Puppi D., Chiellini F. & Chiellini E. Additive manufacturing techniques for the production of tissue engineering constructs. J. Tissue Eng. Regen. Med. (2012). [DOI] [PubMed] [Google Scholar]
  7. Malda J. et al. 25th anniversary article: Engineering hydrogels for biofabrication. Adv. Mat. 25, 5011–28 (2013). [DOI] [PubMed] [Google Scholar]
  8. Wilson W. C. & Boland T. Cell and organ printing 1: protein and cell printers. Anat Rec. Part A 272, 491–6 (2003). [DOI] [PubMed] [Google Scholar]
  9. Derby B. Bioprinting: inkjet printing proteins and hybrid cell-containing materials and structures. J. Mat. Chem. 18, 5717–21 (2008). [Google Scholar]
  10. Binder K. W., Allen A. J., Yoo J. J. & Atala A. Drop-on-demand ink-jet bioprinting: a primer. Gene Ther. Reg. 06, 33–49 (2011). [Google Scholar]
  11. Guillemot F. et al. High-throughput laser printing of cells and biomaterials for tissue engineering. Acta Biomater. 6, 2494–500 (2010). [DOI] [PubMed] [Google Scholar]
  12. Moon S. et al. Layer by layer three-dimensional tissue epitaxy by cell-laden hydrogel droplets. Tissue Eng. Pt. C-Meth. 16, 157–66 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Faulkner-Jones A. et al. Development of a valve-based cell printer for the formation of human embryonic stem cell spheroid aggregates. Biofabrication 5, 015013 (2013). [DOI] [PubMed] [Google Scholar]
  14. Grossin L. et al. Step-by-Step Build-Up of Biologically Active Cell-Containing Stratified Films Aimed at Tissue Engineering. Adv. Mat. 21, 650–655 (2009). [Google Scholar]
  15. Tritz J. et al. Designing a three-dimensional alginate hydrogel by spraying method for cartilage tissue engineering. Soft Matter 6, 5165 (2010). [Google Scholar]
  16. Fredriksson C., Kratz G. & Huss F. Transplantation of cultured human keratinocytes in single cell suspension: a comparative in vitro study of different application techniques. Burns 34, 212–9 (2008). [DOI] [PubMed] [Google Scholar]
  17. Nahmias Y., Arneja A., Tower T. T., Renn M. J. & Odde D. J. Cell patterning on biological gels via cell spraying through a mask. Tissue Eng. 11, 701–8 (2005). [DOI] [PubMed] [Google Scholar]
  18. Di Risio S. & Yan N. Piezoelectric Ink-Jet Printing of Horseradish Peroxidase: Effect of Ink Viscosity Modifiers on Activity. Macromol. Rapid Commun. 28, 1934–1940 (2007). [Google Scholar]
  19. Nishiyama Y. et al. Development of a three-dimensional bioprinter: construction of cell supporting structures using hydrogel and state-of-the-art inkjet technology. J. Biomech. Eng. 131, 035001 (2009). [DOI] [PubMed] [Google Scholar]
  20. Ferris C. J., Gilmore K. G., Wallace G. G. & In het Panhuis, Biofabrication: an overview of the approaches used for printing of living cells. Appl. Microbiol. and Biot. 97, 4243–58 (2013). [DOI] [PubMed] [Google Scholar]
  21. Yamaguchi S., Ueno A., Akiyama Y. & Morishima K. Cell patterning through inkjet printing of one cell per droplet. Biofabrication 4, 045005 (2012). [DOI] [PubMed] [Google Scholar]
  22. Saunders R. E., Gough J. E. & Derby B. Delivery of human fibroblast cells by piezoelectric drop-on-demand inkjet printing. Biomaterials 29, 193–203 (2008). [DOI] [PubMed] [Google Scholar]
  23. Li E. Q., Tan E. K. & Thoroddsen S. T. Piezoelectric Drop-on-Demand Inkjet Printing of Rat Fibroblast Cells: Survivability Study and Pattern Printing. ArXiv (2013).1310.0656. [Google Scholar]
  24. Tirella A. & Ahluwalia A. The impact of fabrication parameters and substrate stiffness in direct writing of living constructs. Biotechnol. Prog. 28, 1315–20 (2012). [DOI] [PubMed] [Google Scholar]
  25. Tasoglu S., Kaynak G., Szeri A. J., Demirci U. & Muradoglu M. Impact of a compound droplet on a flat surface: A model for single cell epitaxy. Phys. Fluids 22, 1–15 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Barbee K. A. Mechanical cell injury. Ann. N. Y. Acad. Sci. 1066, 67–84 (2005). [DOI] [PubMed] [Google Scholar]
  27. Takamatsu H. & Rubinsky B. Viability of deformed cells. Cryobiology 39, 243–51 (1999). [DOI] [PubMed] [Google Scholar]
  28. Groulx N., Boudreault F., Orlov S. N. & Grygorczyk R. Membrane reserves and hypotonic cell swelling. J. Membr. Biol. 214, 43–56 (2006). [DOI] [PubMed] [Google Scholar]
  29. Clanet C., Béguin C., Richard D. & Quéré D. Maximal deformation of an impacting drop. J. Fluid Mech. 517, 199–208 (2004). [Google Scholar]
  30. Visser C. W., Tagawa Y., Sun C. & Lohse D. Microdroplet impact at very high velocity. Soft Matter 8, 10732 (2012). 1206.1574. [Google Scholar]
  31. Visser C. W. et al. Dynamics of high-speed micro-drop impact: Numerical simulations and experiments at frame-to-frame times below 100ns. Soft Matter 11, 1708–22 (2015). [DOI] [PubMed] [Google Scholar]
  32. Chen Y., Liu X., Zhang C. & Zhao Y. Enhancing and suppressing effects of an inner droplet on deformation of a double emulsion droplet under shear. Lab Chip 15, 1255–61 (2015). [DOI] [PubMed] [Google Scholar]
  33. Tran T., de Maleprade H., Sun C. & Lohse D. Air entrainment during impact of droplets on liquid surfaces. J. of Fluid Mech. 726, R3 (2013). [Google Scholar]
  34. Mangili S., Antonini C., Marengo M. & Amirfazli A. Understanding the drop impact phenomenon on soft PDMS substrates. Soft Matter 8, 10045 (2012). [Google Scholar]
  35. Jussila J. Preparing ballistic gelatine-review and proposal for a standard method. Forensic Sci. Int. 141, 91–8 (2004). [DOI] [PubMed] [Google Scholar]
  36. Meyers M. A., Chen P.-Y., Lin A. Y.-M. & Seki Y. Biological materials: Structure and mechanical properties. Prog. in Mater. Sci. 53, 1–206 (2008). [DOI] [PubMed] [Google Scholar]
  37. Lim C. T., Zhou E. H. & Quek S. T. Mechanical models for living cells-a review. J. Biomech. 39, 195–216 (2006). [DOI] [PubMed] [Google Scholar]
  38. Tsai M. A., Frank R. S. & Waugh R. E. Passive mechanical behavior of human neutrophils: power-law fluid. Biophys. J 65, 2078–88 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Allouni A., Papini R. & Lewis D. Spray-on-skin cells in burns: a common practice with no agreed protocol. Burns 39, 1391–4 (2013). [DOI] [PubMed] [Google Scholar]
  40. Boland T., Xu T., Damon B. & Cui X. Application of inkjet printing to tissue engineering. Biotechnol. J 1, 910–7 (2006). [DOI] [PubMed] [Google Scholar]
  41. Derby B. Printing and prototyping of tissues and scaffolds. Science 338, 921–6 (2012). [DOI] [PubMed] [Google Scholar]
  42. Khatiwala C., Law R., Shepherd B., Dorfman S. & Csete M. 3D Cell Bioprinting for Regenerative Medicine Research and Therapies. Gene Ther. Reg. 07, 1230004 (2012). [Google Scholar]
  43. Melchels F. P. et al. Additive manufacturing of tissues and organs. Prog. Polym. Sci. 37, 1079–1104 (2012). [Google Scholar]
  44. Xu T. et al. Viability and electrophysiology of neural cell structures generated by the inkjet printing method. Biomaterials 27, 3580–8 (2006). [DOI] [PubMed] [Google Scholar]
  45. Gruene M. et al. Laser Printing of Stem Cells for Biofabrication of Scaffold-Free Autologous Grafts. Tissue Eng. Pt. C-Methods 17, 79–87 (2011). [DOI] [PubMed] [Google Scholar]
  46. Guillotin B. & Guillemot F. Cell patterning technologies for organotypic tissue fabrication. Trends Biotechnol. 29, 183–90 (2011). [DOI] [PubMed] [Google Scholar]
  47. Lin Y., Huang G., Huang Y., Tzeng T.-R. J. & Chrisey D. Effect of laser fluence in laser-assisted direct writing of human colon cancer cell. Rapid Prototyping J 16, 202–208 (2010). [Google Scholar]
  48. Catros S., Guillotin B., Bačáková M., Fricain J.-C. & Guillemot F. Effect of laser energy, substrate film thickness and bioink viscosity on viability of endothelial cells printed by Laser-Assisted Bioprinting. Appl. Surf. Sci. 257, 5142–5147 (2011). [Google Scholar]
  49. Ringeisen B. R. et al. Laser printing of pluripotent embryonal carcinoma cells. Tissue Eng. 10, 483–91 (2004). [DOI] [PubMed] [Google Scholar]
  50. Li F., Chan C. U. & Ohl C. D. Yield strength of human erythrocyte membranes to impulsive stretching. Biophys. J 105, 872–9 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep11304-s1.pdf (2.9MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES