Two Types of Discontinuous Percolation Transitions in Cluster Merging Processes

Abstract

Percolation is a paradigmatic model in disordered systems and has been applied to various natural phenomena. The percolation transition is known as one of the most robust continuous transitions. However, recent extensive studies have revealed that a few models exhibit a discontinuous percolation transition (DPT) in cluster merging processes. Unlike the case of continuous transitions, understanding the nature of discontinuous phase transitions requires a detailed study of the system at hand, which has not been undertaken yet for DPTs. Here we examine the cluster size distribution immediately before an abrupt increase in the order parameter of DPT models and find that DPTs induced by cluster merging kinetics can be classified into two types. Moreover, the type of DPT can be determined by the key characteristic of whether the cluster kinetic rule is homogeneous with respect to the cluster sizes. We also establish the necessary conditions for each type of DPT, which can be used effectively when the discontinuity of the order parameter is ambiguous, as in the explosive percolation model.

The percolation transition (PT)¹, the emergence of a macroscopic-scale cluster at a finite threshold, has played a central role as a model for metal—insulator and sol—gel² transitions in physical systems as well as the spread of disease epidemics³ and opinion formation in complex systems. The ordinary percolation model and many models based on it exhibit continuous transitions as a function of increasing occupation probability. Recently, however, a great interest in discontinuous percolation transitions (DPTs) has been sparked by the explosive percolation model⁴ and the cascading failure model in interdependent networks⁵,⁶ because of their potential applications to real-world phenomena such as large-scale blackouts in power grid systems and pandemics⁷. The explosive percolation model was an attempt to generate a DPT in cluster merging (CM) processes⁴,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴, in which clusters are formed as links are added between two unconnected nodes following a given rule. However, recent extensive research¹⁵,¹⁶,¹⁷,¹⁸ shows that the explosive percolation transition in a random graph is continuous in the thermodynamic limit. This result has reinforced the robustness of continuous PTs in CM processes. Along with extensive studies on explosive percolation, a few models exhibiting DPTs in CM processes have been introduced. However, the patterns of DTP that they exhibit are not of the same type, which suggests that further studies are necessary for understanding the mechanism underlying such patterns. In this paper, we classify the patterns into two types and clarify the underlying mechanisms for each type of DPT.

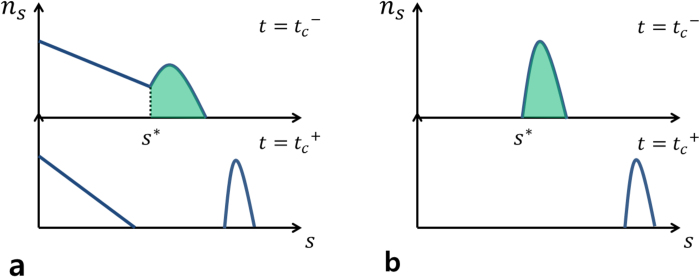
We consider a CM dynamics with N nodes of size one at the beginning. At each time step, an edge is added between two nodes selected according to a given dynamic rule. Then, CM kinetics occurs when the two nodes were selected from different clusters. The number of edges added to the system at a certain time step divided by the system size N is defined as the time t, which serves as a control parameter in PTs. As time passes, the fraction of nodes belonging to the largest cluster in the system, denoted as G(t), increases from zero. In the thermodynamic limit N → ∞, G(t), called the order parameter, exhibits a phase transition from zero to O(1) at a critical point t_c. Two types of DPTs are possible, as depicted in Fig. 1. For type-I DPTs, the order parameter G(t) increases dramatically with infinite slope all the way to unity at t_c = 1, whereas for type-II DPTs, it also increases similarly but up to a finite value 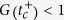at a critical point t_c < 1, after which it gradually increases to unity.

Figure 1. Schematic diagram of two types of DPTs in CM processes.

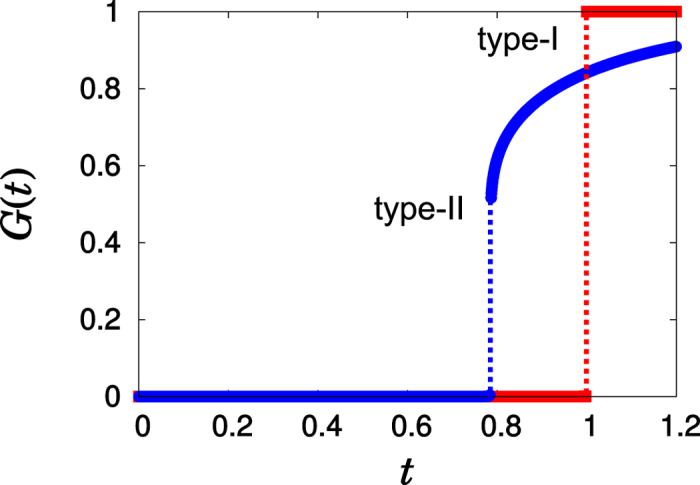
ΔG = 1 at t_c = 1 for type-I, and ΔG < 1 at t_c < 1 for type-II.

The pattern of type-I DPTs in CM processes can be found in various models such as a random aggregation model following the Smoluchowski coagulation equation with reaction kernel K_ij ~ (ij)^ω with 0 ≤ ω < 0.5¹⁹, the Gaussian model²⁰, the avoiding-a-spanning cluster²¹,²², and so on²³. The type-II DPT in CM processes can be found in a limited number of mathematical models²⁴,²⁵,²⁶. It would be more interesting to investigate the origin of type-II DPTs because this type of DPT can occur in other models, for example, the k-core percolation model²⁷,²⁸,²⁹,³⁰, discontinuous synchronization model³¹,³², jamming transition model³³, and generalized epidemic process model³⁴.

Results

Necessary conditions for two types of discontinuous percolation transitions

Here, we show that the two types of DPTs have different origins. To uncover those origins, we examine the cluster size distributions immediately before and after the percolation threshold, denoted as and , respectively, and defined later in the Methods. To induce a type-II DPT, it is necessary that the clusters at are heterogeneous in size, ranging from small cluster sizes to large ones. Among those clusters, primarily large clusters merge to create a macroscopic-scale giant cluster during a short time interval 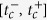. Beyond 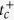, most of the merging is caused by remnant small clusters, the number of which is still O(N), which mainly join the giant cluster. On the other hand, for a type-I DPT, at 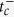, the remaining clusters are mainly homogeneous with mesoscopic-scale size, and they merge during the interval 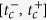to create a macroscopic-scale giant cluster. A schematic comparison of these kinetics between DPTs of types II and I is shown in Fig. 2.

Figure 2. Schematic illustrations of the cluster size distributions for two types of DPTs.

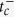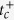Schematic illustrations of the cluster size distribution at and for (a) type-II and (b) type-I are depicted. The number of clusters at 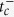in [1,s^*] is O(N) for (a) and o(N) for (b).

To quantify the origin, we propose the necessary conditions for each type of DPT as follows. Here n_s(t) denotes the number of s-size clusters divided by N, which changes with time.

1. Necessary condition for type-II DPT: At 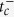, at least one characteristic cluster size s^* > 1 has to exist, which fulfills the following conditions in the thermodynamic limit: I-i) 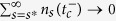, I-ii) 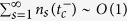, and I-iii) 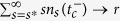(0 < r < 1).

2. Necessary condition for type-I DPT: At 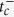, at least one characteristic cluster size s^* > 0 has to exist, which fulfills the following conditions in the thermodynamic limit: I-i) 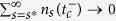, and II-ii) .

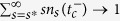The derivations of the two necessary conditions are presented in the Methods.

Two-species cluster aggregation model

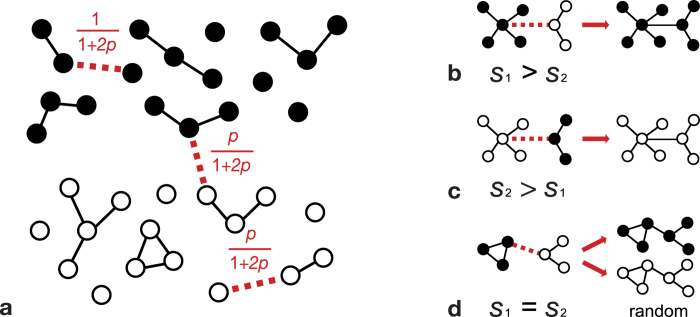
We introduce a cluster aggregation model that exhibits both type-I and -II DPTs as the model parameter changes. The dynamic rule is depicted schematically in Fig. 3. For this model, which is referred to as the two-species cluster aggregation (TCA) model, we start with N isolated nodes, half of which are colored black and the other half of which are white. The color may represent opinion, for example, the left- and right-wing positions on a political issue. According to the dynamic rule below, all nodes in the same cluster have the same color: either black or white. At each time step, we first select one case among the three possible combinations, (black, black), (black, white), or (white, white), with probabilities 1/(1 + 2p), p/(1 + 2p), and p/(1 + 2p), respectively, where p is a model parameter in the range 0 < p ≤ 1. Second, two clusters are selected following the colors selected but independently of the cluster sizes. Finally, two nodes—one from each cluster—are selected randomly and connected, which causes the two clusters to merge. If the two selected clusters are the same, then two distinct nodes from that cluster are connected.

Figure 3. Schematic illustrations of the dynamic rule of the TCA model.

(a) There are three types of CM processes, each of which depends on the species of merging clusters. The probabilities for each case are given in the figure.

The colors of all the nodes in the resulting merged cluster are updated according to the following rule: if the colors of the two clusters are the same, there is no change. However, if the colors are different, then the colors of all the nodes in the smaller cluster are changed to that of the larger cluster. This change may represent opinion formation following the so-called majority rule. If the clusters have the same size but different colors, then either color is picked with equal probability. We numerically show that if 0 < p < 1, the PT is discontinuous and occurs at a finite threshold, t_c < 1, and if p = 1, t_c = 1 [Fig. 4(a)]. We note that if 0 < p < 1, the symmetry between different species in the dynamic rule is broken; if p = 1, the symmetry is preserved.

Figure 4. Numerical tests of necessary conditions for type-II DPT in TCA model.

(a) G(t) vs. t in the TCA model for various values of p for a system size of N = 10⁵. From left to right, p = 0,0.2,0.4,0.6,0.8, and 1.0. (b) The cluster size distributions of black clusters n_0s(•) and white clusters n_1s(•) at 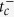(upper panel) and 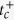(lower panel) for N = 2¹² × 10⁴. (c)  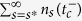(◻) and 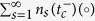vs. N. (d)  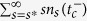(◻) and 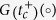vs. N. The two data sets converge to the value y₀ ≈ 0.63. Inset:  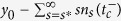(◻) and 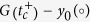vs. N, respectively. The slopes of the guidelines for (◻) in (c) and the inset of (d) are equal to −0.52. The data sets for (b), (c), and (d) are obtained for p = 0.5.

The dynamic rule, particularly in the process of updating the color of nodes, can be modified in several ways. Nevertheless, the overall behavior of the DPT does not change significantly. To facilitate an analytic solution, we modify the dynamic rule as follows: When the colors of the two selected clusters are different, we take black regardless of the cluster size, i.e., without following the majority rule. This modification enables us to set up a coupled Smoluchowski coagulation equation and, consequently, to analytically understand the evolution of a large cluster. When 0 < p < 0.5, the PT is discontinuous at a finite threshold t_c < 1 and ΔG < 1 (type-II DPT). When p ≥ 0.5, the PT is also discontinuous, but at t_c = 1 and ΔG = 1 (type-I DPT). A detailed derivation is presented in the Methods.

Numerical tests and symmetry-preserving (-breaking) dynamics

Here we test the necessary conditions for the TCA model and clarify the origin of the type-II DPT. For this purpose, we plot the cluster size distribution for the TCA model at 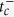and 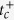in Fig. 4(b). At 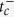, the size distributions of the white and black clusters decay exponentially in the asymptotic region. However, the size distribution of the black clusters is extended to a larger region owing to the symmetry-breaking properties of the dynamic rule. The nodes belonging to the extended (shaded) region correspond to the powder keg referred to in previous studies¹¹,¹²,¹⁶. The combined cluster size distribution exhibits crossover behavior from the region primarily composed of white clusters to that primarily composed of black clusters across a characteristic size, which we denote as s^*. This segregation is induced by the symmetry-breaking dynamic rule: Merging occurs with a higher probability between black clusters than between other types of clusters. Thus, black clusters grow more rapidly and belong to the region s > s^*. The cluster size distribution at 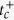, when the dramatically increasing order parameter G(t) changes to a gradually increasing G(t), is shown in the lower panel of Fig. 4(b). The difference between the two figures shows that during the interval 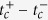, almost all the black clusters aggregate to form a large cluster, and a small number of white clusters merge with large black clusters as black clusters. This microscopic understanding of the mechanism of a type-II DPT is schematically illustrated in Fig. 5. This origin can also be observed in other models such as the so-called Bohman—Frieze—Wormald (BFW) model²⁴ and a half-restricted process model²⁵, which are shown in the supplementary information. On the basis of these numerical results for the merging processes, we made the assumption stated previously when the necessary conditions were set up.

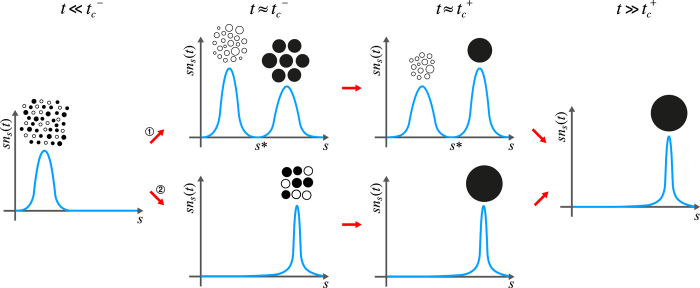
Figure 5. Schematic illustration of symmetry-preserving (-breaking) dynamics.

Schematic illustration of the formation of type-I and -II DPTs in CM processes through ① upper pathway and ② lower pathway, respectively.

We numerically confirm the necessary conditions that the number of clusters of size s > s^* at 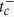is sub-extensive [condition I-i)]. The total number of clusters over the entire range of s is, however, extensive to N [condition I-ii)] [Fig. 4(c)], which is needed for a gradual increase of the order parameter beyond 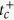. Next, we measure the number of nodes belonging to clusters of sizes s > s^*, finding that the order parameter converges to a finite value r ≈ 0.63 < 1 as the system size is increased. The nodes belonging to this region become the elements of a macroscopic-scale giant cluster, as can be seen for large N cases [condition I-iii)] [Fig. 4(d)]. Numerical testing of the necessary conditions is performed for other models such as the BFW model²⁴, the half-restricted process model²⁵, and the ordinary percolation model in a hierarchical network with long-range connection²⁶. The details are presented in the supplementary information.

Discussion

We investigated the origins of the two types of DPTs in CM processes and derived the necessary conditions for them. Our derivation is similar to the picture proposed by Friedman and Landsberg¹¹, in which the occurrence of an abrupt PT is determined by the number of the clusters in the powder keg region with s > s^*. They set the characteristic size as s^* ~ N^1−β with β < 1. Then, Δt < N^β−1, which is reduced to zero in the limit N → ∞. This criterion is the same as condition I-i) we obtained here. On the other hand, the authors of¹¹ did not classify the necessary conditions for a type-I or -II DPT separately. In a similar way, Hooyberghs and Schaeybroeck¹² proposed another criterion for a DPT, which is again limited to our necessary condition for a type-I DPT.

We have also introduced an analytically solvable model in which two species of clusters evolve through CM processes under the symmetry-breaking rule and showed that this symmetry breaking dynamics generates a type-II DPT. This phenomena can also be found in a model for synchronization transition³¹,³². The detail is presented in SI.

We remark that the origin of the type-II DPT in CM processes differs from that of DPTs driven by the cascading failure dynamics in interdependent networks⁵ or in the k-core percolation model²⁹. The cluster size distribution at 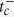for the latter case does not resemble that in the former case. Thus, the necessary conditions we studied cannot be applied to the latter case. In addition, when a type-II DPT is induced by the hierarchical structure as in²⁶, even though our necessary conditions were found to be valid, it is not clear yet whether the DPT originates from the symmetry-breaking kinetics.

Methods

Numerical testing

It is necessary to use the appropriate times 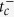and 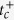. In Fig. 6, we illustrate how to take 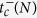and 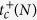in numerical tests of the necessary conditions. We used more than O(10¹¹/N) configurations for all numerical analyses.

Figure 6.

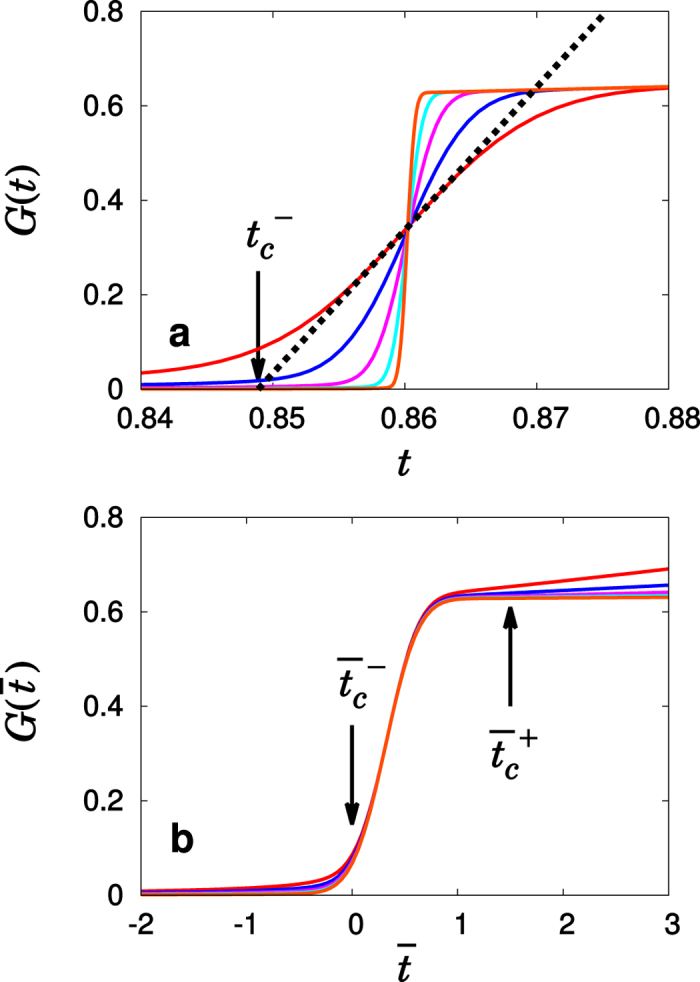
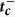and 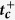used for numerical tests.G(t) vs. t for the TCA model with p = 0.5 for different system sizes, N/10⁴ = 1,4,16,64, and 256. (a) We draw a tangent at the time at which the slope dG(t)/dt becomes maximum, which is almost independent of N and denoted as t_c. The t intercept of the tangent of the curve G(t) is denoted as 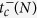. As the system size N is increased, the slope dG(t)/dt|_max increases. (b) We plot 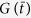of different system sizes vs. a rescaled time as 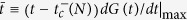. Then, the intercept of the tangent of the curve 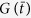is denoted as 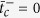, which is independent of N. Next, we take 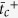as a crossover point from which 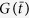begins to grow gradually. Then, .

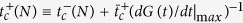Derivation of the necessary conditions

To derive the necessary conditions, we suppose the extreme case, in which CM dynamics occurs only between clusters of size s > s^* during a short time interval within 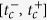. In this case, when intercluster links are added, the order parameter can increase the most rapidly. The number of links to connect all those clusters divided by N is 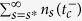, which is equivalent to .

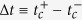First, we consider a type-II DPT. To verify condition I-i), we use the fact that if 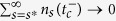in the limit N → ∞, then Δt → 0. During this interval, because the order parameter increases as much as O(1), the PT is discontinuous. Thus, condition I-i) provides a necessary condition for a discontinuous PT. To verify condition I-ii), we consider the inequality 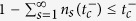, which comes from the fact that the number of links added up to 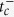is larger than (or equal to) the number of CM events. The equality holds when the model disallows the attachment of intracluster links. In general, when 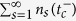goes to zero, 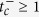in the thermodynamic limit. Condition I-ii), 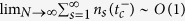, provides a necessary condition for the transition point to be 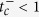. Next, let us define 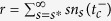, which corresponds to the size of the powder keg in¹¹. Then, 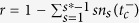. This quantity satisfies the following inequality: 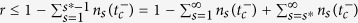. When conditions I-i) and I-ii) hold, r ≤ 1 − O(1). Thus, r < 1. Condition I-iii) is needed to exclude the case r = 0 for a continuous transition. Thus, conditions I-i), I-ii), and I-iii) are all needed for a type-II DPT.

We now consider a type-I DPT. Condition I-i) suggests that Δt → 0 in the thermodynamic limit. Condition II-ii) suggests that 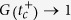. Then, using the inequality 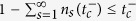, one can obtain 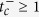in the thermodynamic limit. Thus, the percolation threshold is positioned at t_c ≥ 1. We remark that this necessary condition for a type-I DPT in CM processes is equivalent to .

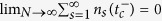Analytic calculation of the solvable two-species cluster aggregation model

Let n_0s(t) and n_1s(t) be the numbers of s-size black and white clusters per node, respectively, at time step t. The rate equations of the two quantities are written as

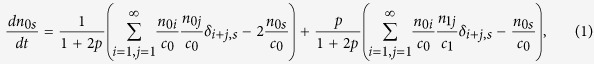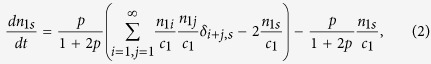where 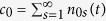and 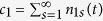are the number of finite black and white clusters per node at time t in the system, respectively. Next, we define the generating functions 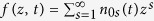and 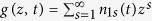, where the summation runs over finite clusters. As a result, the rate equations (1) and (2) are changed to

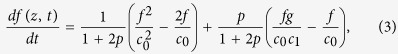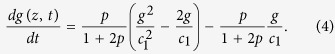Using c₀(t) = f(1,t) and c₁(t) = g(1,t), we obtain c₀(t) = 1/2 − t/(1 + 2p) and c₁(t) = 1/2 − 2pt/(1 + 2p). When 0 < p < 0.5, the percolation threshold can be obtained by setting c₀(t_c) = 0 but c₁(t_c) > 0, because c₀(t) decreases more rapidly than c₁(t). Thus, t_c = 1/2 + p, and a large black cluster emerges at t_c. The size of the jump in the order parameter at t_c can be obtained using the formula ΔG = 1 − f′(1,t_c) − g′(1,t_c), which reduces to ΔG = 1 − g′(1,t_c), because f′(1,t_c) = 0. Thus, the jump in the order parameter is determined to be 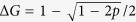. The PT is discontinuous at a finite threshold t_c < 1 and ΔG < 1 (type-II DPT).

When p ≥ 0.5, because c₁(t) decreases more rapidly than c₀(t), the percolation threshold can be obtained using c₁(t_c) = 0 and c₀(t_c) > 0. Thus, 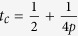. The size of the jump in the order parameter can be obtained using the formula ΔG = 1 − f′(1,t_c). However, f′(1,t_c) = 1 and f′(1,t) = 1 even for t < 1. Thus, ΔG = 0 for t < 1. When t > 1, f′(1,t) = 0. Thus, the order parameter behaves as ΔG = 1 for t > 1, and the threshold t_c = 1 (type-I DPT). These analytic results are checked numerically in the supplementary information.

Additional Information

How to cite this article: Cho, Y. S. and Kahng, B. Two Types of Discontinuous Percolation Transitions in Cluster Merging Processes. Sci. Rep. 5, 11905; doi: 10.1038/srep11905 (2015).