Maximizing Information Yield From Pheromone-Baited Monitoring Traps: Estimating Plume Reach, Trapping Radius, and Absolute Density of Cydia pomonella (Lepidoptera: Tortricidae) in Michigan Apple

Abstract

Novel methods of data analysis were used to interpret codling moth (Cydia pomonella) catch data from central-trap, multiple-release experiments using a standard codlemone-baited monitoring trap in commercial apple orchards not under mating disruption. The main objectives were to determine consistency and reliability for measures of: 1) the trapping radius, composed of the trap’s behaviorally effective plume reach and the maximum dispersive distance of a responder population; and 2) the proportion of the population present in the trapping area that is caught. Two moth release designs were used: 1) moth releases at regular intervals in the four cardinal directions, and 2) evenly distributed moth releases across entire approximately 18-ha orchard blocks using both high and low codling moth populations. For both release designs, at high populations, the mean proportion catch was 0.01, and for the even release of low populations, that value was approximately 0.02. Mean maximum dispersive distance for released codling moth males was approximately 260 m. Behaviorally effective plume reach for the standard codling moth trap was < 5 m, and total trapping area for a single trap was approximately 21 ha. These estimates were consistent across three growing seasons and are supported by extraordinarily high replication for this type of field experiment. Knowing the trapping area and mean proportion caught, catch number per single monitoring trap can be translated into absolute pest density using the equation: males per trapping area = catch per trapping area/proportion caught. Thus, catches of 1, 3, 10, and 30 codling moth males per trap translate to approximately 5, 14, 48, and 143 males/ha, respectively, and reflect equal densities of females, because the codling moth sex ratio is 1:1. Combined with life-table data on codling moth fecundity and mortality, along with data on crop yield per trapping area, this fundamental knowledge of how to interpret catch numbers will enable pest managers to make considerably more precise projections of damage and therefore more precise and reliable decisions on whether insecticide applications are justified. The principles and methods established here for estimating absolute codling moth density may be broadly applicable to pests generally and thereby could set a new standard for integrated pest management decisions based on trapping.

Insect monitoring traps baited with species-specific sex pheromones are ideal tools for determining if particular pests are present in a crop and when they are active (Witzgall et al. 2010), thereby allowing control measures to be optimally timed (Judd and Gardiner 1997). Such traps and lures are relatively inexpensive and provide critical information quickly. Thus, it is not surprising that the number of lure-baited traps deployed annually around the globe to monitor insect pests can now be estimated by extrapolation from the data of Witzgall et al. (2010) at well over 15 million. Such traps have become a cornerstone of integrated pest management (IPM).

Nevertheless, lure-baited monitoring traps have fallen short of original hopes (Cardé 1976) that they might be used to quickly and inexpensively estimate the absolute density of pests, which is the key variable for setting economic injury levels (Stern et al. 1959). In the absence of vetted procedures for translating capture numbers into absolute pest density estimates, pest managers resort to experience-based relative thresholds or indices for action (Riedl and Croft 1974, Schouest and Miller 1994, Reddy and Manjunatha 2000, Cuthbertson and Murchie 2005) that are usually based on years of correlating given catches with unacceptable levels of damage in particular locales. Currently, Michigan growers are advised to apply an insecticide when a single codling moth (Cydia pomonella) trap baited with codlemone captures a cumulative of six or more first-generation males or three or more second-generation males in an apple crop not under mating disruption (Gut and Wise 2016). The seasonal threshold across all three codling moth adult generations is approximately 12 per trap per season. Adoption of such indices for action has greatly improved pest management practices over regular calendar spraying. However, relative thresholds often lack sufficient precision and scientific grounding to allow growers to confidently withhold sprays so as to raise profits (Pimentel 1993) while reducing environmental damage (Miranowski 1980) as well as delaying insecticide resistance (Varela et al. 1993, Bouvier et al. 2001). Lack of understanding of the operative mechanisms governing pest–trap interactions has been a barrier to progressing beyond indices of pest abundance to the higher standard of using economic injury levels based on absolute pest abundance, as IPM theory professes (Stern et al. 1959).

Knowledge Required to Translate Catch Numbers Into Absolute Pest Density

Accurate estimation of absolute pest density from a catch number recorded in a pheromone-baited trap requires knowledge of: 1) the pest’s distribution in space and time; 2) the pest’s movement patterns before and after encountering pheromone; 3) the farthest distance from which the trap can be reached, both unassisted and assisted by pheromone; and 4) the average probability of capture (T_fer) for all individuals in the trapping area of known size (Miller et al. 2015). As suggested by Riedl and Croft (1974), reliably linking catch number with absolute pest density across a growing season may be difficult or perhaps impossible if the pest’s distribution were never reproducible and its movement patterns and activity levels over a lifetime varied substantially through time and with particular geography. On the other hand, estimating absolute pest density by trapping becomes feasible if insects foraging for pheromone move randomly, i.e., execute “random walks” (Berg 1993, Miller et al. 2015) that ironically cause the overall population to exhibit highly reproducible properties like those well-quantified in physics and chemistry, e.g., diffusion, temperature, molecular flux, and heat transfer. Any population of molecules or other random walkers (fliers; Berg 1993), including those simulated by a computer (Weston 1986, Byers 1993, Miller et al. 2015), released from one point into a thin layer of static medium will, on average, disperse equally in all directions so as to impart spatial regularity by forming a disk populated throughout but with lowest mean density at its leading edge. Moreover, random walkers unevenly released as hot-spots quickly populate their arena fully randomly. Likewise, the trapping area for a trap collecting randomly distributed random walkers will itself be a regular disk (Miller et al. 2015) whose radius is composed of the behavioral reach of the attractive plume from the trap plus the maximum dispersive distance for the local pest population (Hartstack et al. 1971, Wall and Perry 1987, Miller et al. 2015). Thus, the feasibility for translating capture numbers into absolute pest density depends upon whether the pest behaves as a random walker so as to impart regularity to its distribution, movement pattern, dispersive distance, and mean probability of capture.

Evidence for Random Walks by Flying Insects Not in Contact With Pheromone

The flight patterns of male insects responding to pheromone plumes have been very well-characterized (Kennedy et al. 1974, Baker et al. 1984, Cardé 1984, Cardé and Willis 2008), often in wind tunnels (Miller and Roelofs 1978) and sometimes in the field (Baker and Roelofs 1981, Elkinton et al. 1984, Baker and Haynes 1996). Males so stimulated execute positive optomotor anemotaxis. This entails using visual cues from perceived ground flow over the visual system to steer upwind when flying in and along the edges of the pheromone plume while regularly zig-zagging to maintain plume contact. Doing so enables the responder to efficiently arrive at the pheromone source, be it a female or a trap baited with pheromone.

On the other hand, flight patterns before pheromone contact have been rarely studied and are subject to considerable speculation. As summarized by Cardé et al. (2012 and references therein), the dominant expectation has been that insects foraging for pheromone plumes, but not yet encountering one, will raise their probability of contacting a presumed large plume by moving in straight lines and using some non-random search strategy like flying up- or cross-wind. Arguments have been offered for the superiority of certain of these wind-directed tactics over others (Janzen 1984, Dusenbery 1990). However, despite their appeal to humans, very little evidence is available that insects actually use wind- or geography-directed tactics when foraging for plumes. In fact, the extraordinary study by Cardé et al. (2012), using videography to directly measure the headings of bog moths, Virbia lamae, foraging for but not yet contacting pheromone plumes, elegantly demonstrated that no heading with respect to wind direction or geographic feature was favored over any other. The flight headings of foraging bog moth males were random and consistent with random walking while using a modest path meander.

A related prediction that should hold for a population of insects foraging for pheromone plumes using random walks is that, when released from one point and not limited by crop edges, they should disperse to occupy a radially symmetric disk. The regularity of such dispersal can be measured by superimposing a dense grid of traps over the mover population after allowing it time to disperse from a single point. Indeed, symmetric dispersion from a single release point has been reported for codling moth (Worthley 1932), pine saw fly (Neodiprion sertifer) (Wedding et al. 1995, Östrand and Anderbrant 2003), oriental fruit moth (Grapholita molesta) (Ellis and Hull 2013), and painted apple moth (Teia anartoides) (Guichard et al. 2010). We are aware of no insect studies yielding notably skewed dispersive disks that would falsify the random walk model of search for pheromone plumes. Such results and a large body of evidence that local dispersion of small animals not yet guided by cues from resources frequently occurs by diffusion (Kareiva and Shigesada 1983, Rudd and Gandour 1985, Fagan 1997, Okubo and Levin 2001, Benhamou 2007, Patterson et al. 2008, Nathan and Giuggioli 2013) justify renewed attempts, like that of Miller et al. (2015), to derive estimates of absolute pest density from capture numbers in attractive traps based on a foundation of random walks.

Examples of Past Attempts to Estimate Absolute Pest Density From Capture Number in Attractive Traps

The first such attempt of which we are aware (Hartstack et al. 1971) occurred before pheromone-baited traps were available and it used captures of marked moths released at defined distances from a single UV light-trap, an experimental approach pioneered by Wolf et al. (1971). Coming from an engineering background and familiar with molecular processes, Hartstack et al. (1971) were willing to assume that, over their lifetimes and despite the difference in size, dispersing insects would not behave differently in principle from molecular dispersal. Further assumptions were: 1) marked and released moths behaved no differently from wild moths; 2) moths dispersed randomly; 3) irrespective of exact initial origin, pests per area would quickly become homogeneous and be directly proportional to area alone; and 4) trapping area would be a regular disk whose radius was maximum dispersive distance for the local pest population plus attraction distance of the lamp. Hartstack et al. (1971), as clarified by Turchin and Odendaal (1996), reasoned that the number of insects present in a narrow annulus (ring) of trapping area centered on the trap would equal annulus area × insects per area. Moreover, the probability of capture of insects from a given annulus could be and was measured experimentally after releasing known numbers of pest from defined distances. Maximum trapping radius was taken as the farthest distance yielding a capture. Then, the number of insects caught would be given by the sum (for all annuli of the trapping area) of probability of capture for each annulus multiplied by its area. Finally, the absolute density of insects in some new trapping area with size equal to that found during calibration can be calculated by dividing the catch number per single trap by the weighted average probability of capture for all annuli (T_fer in the current vocabulary; Hartstack et al. 1971, Turchin and Odendaal 1996, Miller et al. 2015), or more directly by integrating using calculus. Although their methods varied slightly from the above, Hartstack et al. (1971) reported that, for the highly mobile tobacco hornworm, Heliothis virescens, the trapping radius for their single light trap was > 3,000 m, yielding a huge trapping area of approximately 2,800 ha. A capture of 100 moths per single light trap equated to 110 moths per ha. Östrand and Anderbrant (2003) extended this approach when estimating absolute density of pine sawfly, Neodiprion sertifer, in Sweden using traps baited with female sex pheromone. The trapping radius for their single trap was approximately 1,000 m; therefore, the trapping area was approximately 314 ha. Capture of 112 males over one adult generation translated into only 23 males per ha per generation.

Additional researchers (Byers et al. 1989, Mason et al. 1990, Dodds and Ross 2002, Sufyan et al. 2011, Byers 2012) have used similar approaches to propose that absolute pest density could be quantified for various types of insect pests using capture number. But, curiously, no examples can yet be identified where such procedures are actually implemented in pest management for any crop. Reasons for this gap should be explored and remedied. Explanations for the failure to adopt practices that could elevate pest management decisions from an art, best done by a select few experts with vast experience with the given cropping system, into a science open to all might include: lack of confidence in the assumptions upon which the translations from capture number to absolute density have been based, lack of confidence that the calibrations will hold for other times and places where crop and environmental conditions differ, and lack of awareness of this timely opportunity. The science of pest management stands in need of a well-replicated proof-of-concept study that examines the feasibility and reproducibility of using capture numbers in traps for absolute pest density determinations over several growing seasons and at multiple locations.

Study Objectives and Rationale for Using Codling Moth for Proof-of-Concept

The current study aims to provide proof-of-concept for procedures to translate capture number in monitoring traps into absolute pest density based on field experiments using the single-trap, multiple-release design (Wolf et al. 1971, Turchin and Odendaal 1996) measuring probability of male codling moth catch from specified distances of release (specific T_fer designated spT_fer; Miller et al. 2015). Here we put into practice the techniques for interpreting catch and measuring maximum dispersive distance and pheromone plume reach recently proposed and detailed by Miller et al. (2015). Moreover, these experiments were conducted at both high and low codling moth densities, so as to represent conditions encountered by growers spraying often or little. The techniques and principles being validated here should be broadly applicable to diverse pests that forage using random walks.

Codling moth is a global pest of pome fruits having high economic importance whose management is based on relative capture numbers in pheromone traps (Witzgall et al. 2008). Pheromone chemistry for codling moth has been thoroughly studied and optimized (Witzgall et al. 2008) along with trap design. The biology of codling moth has been well-documented (Geier 1963 and references therein). Estimates for maximum dispersive distance of male codling moth range from 150 m (Worthley 1932) to 8 km along a river valley in a male-only environment to as low as 55 m in a short-term, mixed-sex experiment (Howell and Clift 1974) and as much as 10 km on flight mills (Schumacher et al. 1997). As summarized by Mani and Wildbotz (1977), however, the maximum dispersive distance achieved by approximately 95% of laboratory-reared and wild-collected populations is thought to be under 400 m. Very important for the feasibility of the current study, large numbers of reproductively sterilized codling moth, shown to disperse similarly to wild moths (Mani and Wildbotz 1977), could be purchased for well-replicated field studies.

Simulation Results Guiding the Current Codling Moth Study

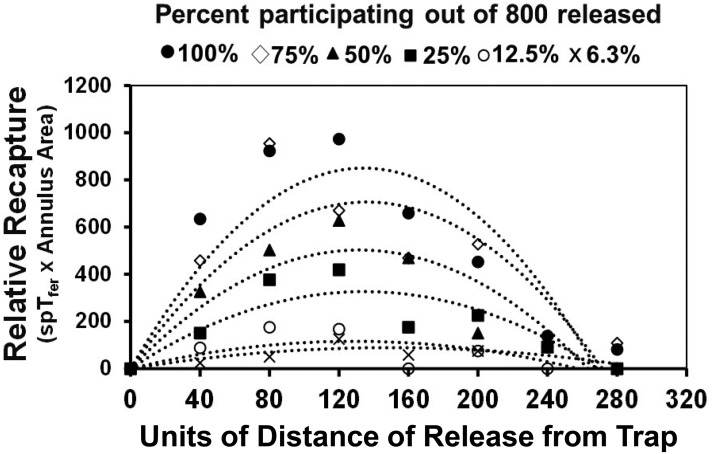
Before commencing with multiple years of large-scale field experiments in commercial apple orchards under grower rather than experimenter management, we needed to know whether measures of trapping radius would vary markedly if some cooperating growers elected to apply insecticides over some of the plots in which we released Sterile Insect Release (SIR) moths, thereby altering intended codling moth density. Once we obtained preliminary data for behavioral reach of the pheromone plume and maximum dispersive distance for a given population of codling moth released into Michigan apple orchards, a preview (Fig. 1) of likely catch patterns of simulated random walkers under differing survival regimes was generated using Weston MultiMover computer software (Miller et al. 2015) operating across varying run times. The results of Fig. 1 typify outcomes of various iterations of simulation experiments testing the hypothesis that trapping radius is not highly sensitive to varying number of participants in experimental runs. Here the number of simulated insects released at each distance was 800 (similar to the number used below in Experiment 1 of our codling moth study), and 3,000 steps were taken with a meander of circular standard deviation of 30^° (Miller et al. 2015). To scale the simulations to field experiments, each step and each computer unit can be considered as one meter. These conditions approximated the realized maximum dispersion distance for codling moth measured preliminarily. The distance of release from the trap appears on the x-axis of Fig. 1, while the y-axis is a measure of proportion of simulated individuals caught relative to the increasing area of the respective release annulus (ring of area). As seen in Fig. 1, the heights of capture profiles diminish as participant numbers decrease and proportion caught from any given distance (spT_fer) continues to be calculated on the basis of 800 insects released. The data of Fig. 1 demonstrate that measures of maximum dispersion for random-walking pests will not be greatly impacted by such mortality, even if its severity is unknown. Note that no profile reached the x-intercept before a release distance of 280 distance units (nearly 80% of the maximum measurable under the highest level of participants). This knowledge provides a needed a priori theoretical and experimental defense for the approach taken in the following field experiments where the actual number of surviving codling moth could not always be ascertained.

Fig. 1.

Computer simulation results showing change in pattern of capture profiles to be expected if not all of the codling moths released into the forthcoming experiments lived. Individuals not participating simulate those killed by an insecticide. SpT_fer indicates proportion of insects captured after release at a particular distance, for the purpose of this demonstration always calculated on the basis of 800 movers released. Annulus area indicates a ring out of the full trapping area (composite of all annuli) sampled by a single trap. In all cases, the CSD for headings for new steps was 30° and the total number of steps was 3,000. The trend lines were fit using a second-order polynomial.

Materials and Methods

Source and Handling of Codling Moths

Mixed-sex codling moths, internally marked with Calco red vegetable dye, were purchased from the mass-rearing SIR facility in Osoyoos, British Columbia. Newly eclosed moths were sterilized at the rearing facility with 33 krad of gamma radiation from a Cobalt 60 source. A prescribed number of 9-cm-diameter petri dishes filled with sterilized codling moths was shipped overnight to Michigan State University in coolers maintained at approximately 5°C with cold-packs; they always arrived at approximately 10:30 h, allowing moths to be released the same day. Owing to the very high numbers of moths used (from 2,100 to 20,000 per run), the need for rapid releases did not permit separation by sex; therefore, all releases were males plus females. Arriving moths were immediately dispensed into 540-ml polypropylene cups (Fabri-Kal Corp., Kalamazoo, MI) in batches of approximately 100 and dusted with approximately 10 mg of fluorescent powder (DayGlo Color, Cleveland, OH). Periodically, one cup was selected at random and all moths were counted and sexed to confirm release numbers and sex ratio, which was confirmed to fall within the range of 47-54% males across all experiments. Moths for each release distance were uniquely colored. Capped cups containing moths and dye were repacked into coolers (Igloo Products Corp, Katy, Texas) at approximately 5°C for the 1-h transport to the orchard blocks. Moths were released the day of receipt at approximately 13:00 h. Chilled moths were allowed to acclimate to outdoor ambient temperature before being lightly swirled to promote uniform coloration and then hand-thrown into the air at each pre-flagged release point. Ejected moths flew in all directions and alighted in the foliage of adjacent trees within a few seconds.

Estimate of Proportion of Purchased Codling Moths Capable of Participating

At semi-regular intervals during these experiments, the entire population from randomly selected and newly arrived petri dishes (approximately 400 males and 400 females) was released into 3 by 3 by 2-m tents (Instant Up Canopy Quest model: CEH00296 American Sports Licensing, Wilmington, DE 19805) with insect netting sidewalls enclosing two 2-m-high apple trees and four pheromone-baited delta traps (detailed below) suspended near the tops of the trees. Traps were checked and liners changed daily so as to ascertain the proportion of released males available for capture and over what period catch persisted. Recapture of powdered versus un-powdered codling moth males was compared in tents on four occasions.

Orchards

Experiments were conducted in various commercial apple orchards (details in Table 1) in and around Sparta, Michigan, during the growing seasons of 2013-2015. These orchards were not and had not been under mating disruption during the preceding 3 yr. Experiments were timed to avoid releases of moths during weeks when insecticide applications were planned; nevertheless, it was possible and likely that residual effects of previous sprays occurred in some blocks.

Table 1.

Orchard planting details, varieties of apples, and GPS coordinates

Orchard #	Tree spacing	Row spacing	Tree height	Planting style	Apple varieties1	GPS coordinates	Sprays occurred
1	5.5 m	7.6 m	4.5 m	Large trees	I, R	43° 02′04.36″ N 85° 42′06.72″ W	No
2	5.5 m	7.6 m	3.5 m	Trellis trees	F, G, D, J	43° 10′03.24″ N 85° 46′55.36″ W	Yes
3	1.5 m	4.8 m	3 m	Trellis trees	G, D, J, M	43° 07′35.22″ N 85° 21′37.24″ W	Yes
4	2.5 m	5.0 m	3.5 m	Trellis trees	F, G, H, S	43° 09′11.50″ N 85° 46′57.04″ W	Yes
5	2.5 m	5.0 m	3.5 m	Trellis trees	F, G, H, S	43° 09’08.89″ N 85° 47′49.65″ W	Yes

¹Fuji – F, Gala – G, Golden delicious –D, Honey Crisp – H, Ida Red – I, Jonagold – J, McIntosh – M, Rome – R, Sweet Tango – S.

Experiment 1 – Cardinal-Direction Releases

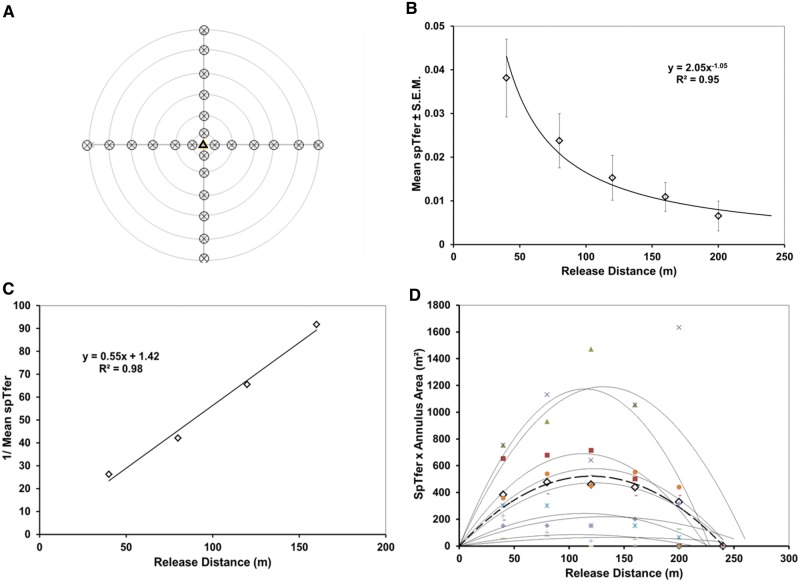
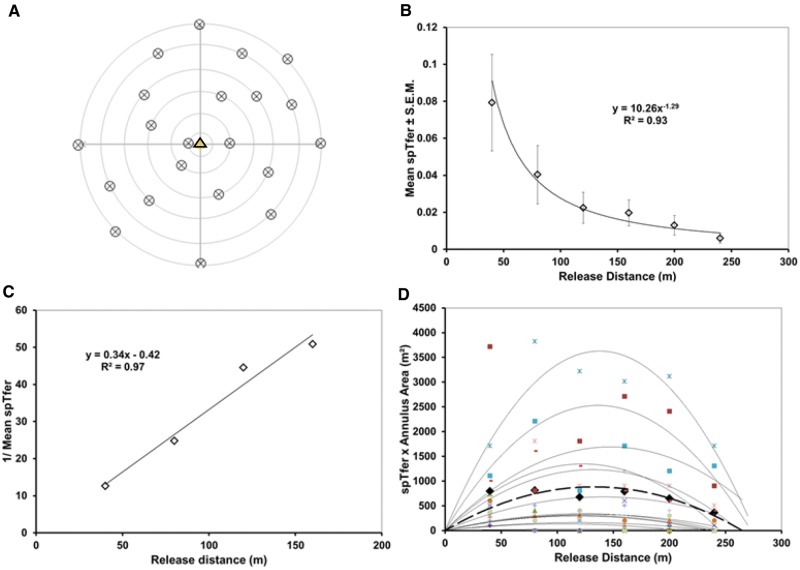
This experiment was conducted from June through August of 2013 in three 18-ha orchard blocks of mixed cultivars (Orchards: 1, 2, and 3 of Table 1). Release points were flagged in the four cardinal directions from the central trap (Fig. 2A) at distances of 40, 80, 120, 160, 200, and 240 m. In five of the replicates, approximately 800 males (and approximately 800 females) were released per distance. One replicate was conducted with approximately 1,000 males (and females). Three additional replicates were conducted with populations of approximately 1,600 males (and equal numbers of females) per distance. A single delta trap (Pherocon VI; Trécé Inc., Adair, OK) containing a CML2 gray septum lure (Trécé, Inc) loaded only with codlemone ((E,E)-8,10-dodecadien-1-ol; Roelofs et al. 1971) was placed in the top third of the canopy of a tree near the center of each block. The septum was held aloft of the sticky trap-liner by a pin through the trap roof. Traps were checked daily; sticky liners containing ensnared moths were replaced and examined in the laboratory under a combination of UV illumination (22W fluorescent Circline BL #2851L, BioQuip products, Rancho Dominguez, CA; 15 W fluorescent tube BL #2806, BioQuip products, Rancho Dominguez, CA; and 32 UV LED retrofit bulb, Battery Junction, Old Saybrook, CT, in an ML300L 3-cell D flashlight, Mag Instruments, Ontario, CA) to determine coloration of powder on moths. Moths were always inspected for sex and internal red dye to distinguish them from the sparse wild population.

Fig. 2.

Experiment 1, central-trap, cardinal-direction release. A. Pattern of release across the 18 ha. One trap was deployed at the center of this array. B. Proportion caught by release distance (probability of catch from a specified release distance, spT_fer); mean of nine replicates. C. Inverse of proportion caught by distance (MAG plot transformation). D. SpT_fer × annulus area over release distance (Miller plot transformation) of each replicate and their mean (bold dashed line).

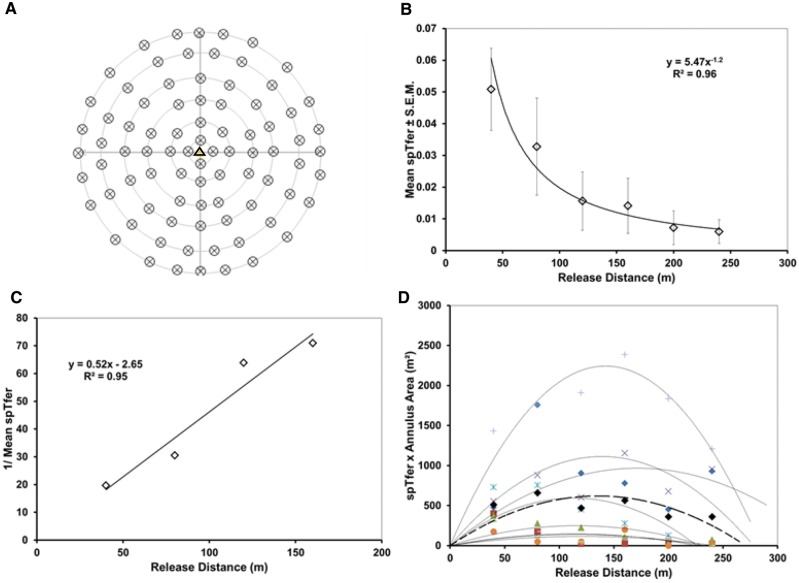
Experiment 2 – Even Release With High Populations

This experiment was conducted from June through August of 2015. Here moths were released in approximately 30 min with the aid of an ATV (four-wheeled motorcycle) at 84 release points (Fig. 3A) throughout Orchards 1, 4, and 5 of Table 1 concurrently, so that approximately 400 male moths/ha were evenly distributed across the 18 ha for a total of approximately 8,400 males in each of the nine replicates. Moths within each annulus were uniquely powdered. Radii of annuli were 40, 80, 120, 160, 200, and 240 m.

Fig. 3.

Experiment 2, even-release throughout 18 ha. A. Pattern of release. One trap was deployed at the center of this array. B. Specific trap findability over distance; mean of nine replicates. C. MAG plot transformation. D. Miller plot of each replicate and their mean (bold dashed line).

Experiment 2.5 – Even Releases With Very High Populations

In July and August of 2014, 20,000 moths were released evenly throughout 16 ha of Orchard 1 (Table 1) at 100 flagged locations (Fig. 4A), creating a population of approximately 1,250 male moths/ha. Distances of 40, 80, 120, 160, and 200 m were uniquely marked with Dayglow powder as described earlier. Releases were completed in approximately 30 min using an ATV. Three replicates were conducted through time.

Fig. 4.

Experiment 2.5, even-release with very high populations. A. Pattern of moth release. One trap was deployed at the center of this array. B. Mean specific trap findability (of the three replicates) over distance. C. MAG plot transformation of spT_fer data. D. Miller plot of each replicate along with their mean (bold dashed line).

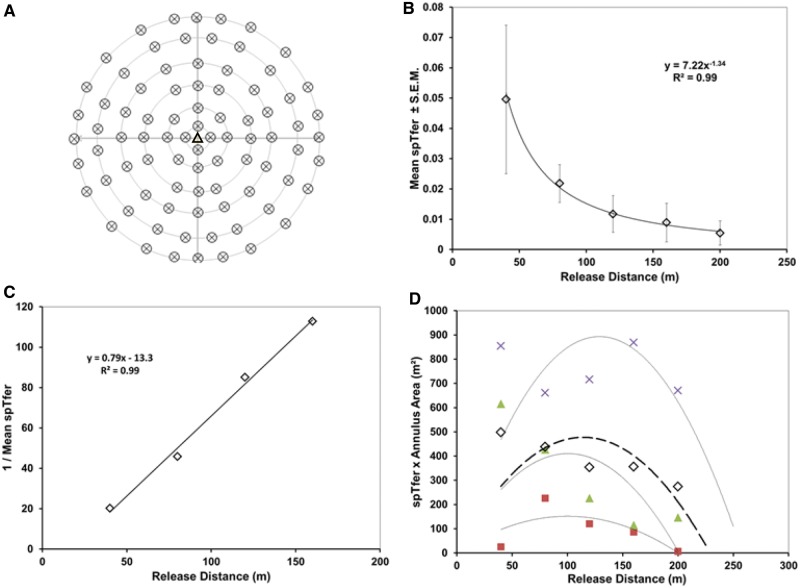
Experiment 3 – Even Release With Low Populations

This experiment followed the protocol for Experiment 2. However, a low-population, even-release condition was achieved by releasing the same number of moths per release point, as in Experiment 2, but with only one-quarter of the release points (Fig. 5A) across the 18-ha experimental plots resulting in 100 moths per ha for a total of 2,100 male moths in each of the 15 replicates.

Fig. 5.

Experiment 3, low-population over 18 ha. A. Pattern of moth release. One trap was deployed at the center of this array. B. Mean spT_fer versus distance for 15 low-population runs. C. The MAG plot transformation of mean spT_fer data. D. Miller plot transformation for each of the 15 replicates and their mean (bold dashed line).

Data Analysis

Data were graphed according to the conventions of Miller et al. (2015) to yield: 1) an untransformed plot of proportion of released moths captured versus distance of release, 2) 1/proportion of released moths captured versus distance of release (MAG plot), and 3) annulus area × proportion of released moths captured versus distance of release (Miller plot).

Areas of annuli were calculated by annulus area = π ${(R}_2^2-R_1^2)$, where R₁ is the inner radius and R₂ is the outer radius of each annulus centered on the trap. When release distances are regularly spaced, the inner and outer radii of each annulus will be the release radius minus ½ the distance between release points and the release radius plus ½ the distance between release points, respectively. The untransformed plot provides confirmation that release distances were appropriately selected and suggests that the moths moved randomly when it produces a smooth concave line with an asymptotic approach to zero catch. The untransformed plot is also the only appropriate place to report the variance measured around mean captures that, upon transformations, become distorted and not useful. For random walkers, MAG plots will be initially linear (Miller et al. 2015), yielding a slope that can be used to deduce plume reach from the standard curve of Miller et al. (2015; Fig. 4.12). Slopes of MAG plots and therefore determinations of plume reach are insensitive to the actual number of participants. Miller plot data were fitted with a second-order polynomial forced through the origin; the right-most x-intercept then gives approximately 95% of the maximum dispersive distance. Height of the Miller plot at points along the x-axis reveals the relative contribution of those distances to overall catch. Releases at further distances would theoretically appear as an asymptotic tail that would represent the last 5% of possible catch (unpublished computer simulation data by J. Schenker). Catch from this outer edge becomes highly improbable in field experiments; thus, a procedure to estimate maximum dispersion for 95% of the population, as used here, is more useful to applied researchers.

For even-release experiments, where all annuli were populated with the same codling moth density, T_fer (the proportion of insects caught out of all insects in the full trapping area) was calculated by dividing mean catch per single trap by total number of male codling moth released per trapping area of the experiment. Calculation of T_fer for cardinal direction experiments, where number released did not increase with distance, was performed by dividing mean annulus area × spT_fer (proportion caught at a defined distance) by mean annulus area (see Table 5.1 example of Miller et al. 2015).

Results

Estimate of Proportion of Purchased Codling Moths Capable of Participating

Based on captures of codling moth males released into insecticide-free apple trees under field tents, we estimate that 60-90% of purchased SIR males were flight-worthy and responsive to pheromone and thus able to participate in these experiments. Subsequent to release, the data below will show that the proportion of participants in some orchards was further reduced, apparently by the insecticides they had received. In all cases, catch was highest 1-3 d after release and tailed off to zero by one week. Powder-marked moths performed identically to unmarked moths in small-cage tests.

Experiment 1 – Cardinal-Direction Releases

Of the 4,000 to 9,600 male moths released, less than 3% were recovered on average. The mean spT_fer for the closest release at 40 m was 0.038 ± 0.01 (mean ± SEM, n = 9). As is typical for random walkers (Miller et al. 2015), catch decreased smoothly with a regular increment of distance from the central trap to a mean spT_fer of 0.006 at the furthest distance of 200 m (Fig. 2B) and approached the x-axis asymptotically. The MAG plot (Fig. 2C) produced a straight line over the closest four data points with a slope of 0.55. Using a MAG plot standard curve (Fig. 4.12 of Miller et al. 2015), plume reach was estimated at <5 m. The Miller plot of these data (Fig. 2D) bears a striking resemblance to the random-walker simulation data of Fig. 1. Its projected x-intercept indicated the 95% maximum trapping radius was approximately 240 m. Thus, trapping radius, comprised by plume reach plus maximum dispersive distance, was overwhelmingly dominated by the latter. A trapping radius of 240 m equates to a trapping area of 18 ha. Mean T_fer was 0.01 ± 0.003 (± SEM, n = 9; range 0.001 to 0.025).

Experiment 2 – Even Releases With High Populations

As expected, results of Experiment 2 were strikingly similar to those of Experiment 1. For even releases at 8,000 moths per 18 ha, the average T_fer was 0.01 ± 0.005 (range 0.002 to 0.05). The untransformed data from even release under high populations (Fig. 3B) show that the mean spT_fer for the closest distance of 40 m was 0.05 ± 0.02 (mean ± SEM, n = 12). Catch decreased with distance from the central trap to a mean spT_fer of 0.006 at the furthest distance of 240 m (Fig. 3B). The MAG plot (Fig. 3C) initially produced a straight line with a slope of 0.52. Again, this slope equates to a plume reach of <5 m. The Miller plot (Fig. 3D) supports a maximum dispersive distance for 95% of the population at approximately 275 m, resulting in a trapping area of approximately 24 ha.

Experiment 2.5 – Even Releases With Very High Populations

Results for Experiment 2.5 were very similar to those of Experiments 1 and 2. With released populations of 20,000 males in 16 ha, T_fer averaged 0.02 ± 0.01 (±SEM). The highest T_fer measured was 0.05 and the lowest was 0.003. The expected concave line with asymptotic approach to the x-axis can be seen in Fig. 4B. The initial slope of the MAG plot line (Fig. 4C) estimates plume reach at <5 m. Transformation of these data to the Miller plot (Fig. 4D) estimated the dispersive distance of 95% of the population at approximately 230 m for a trapping area of approximately 17 ha.

Experiment 3 – Even Release With Low Populations

When populations were released at only approximately 2,000 per 18 ha, the mean proportion caught was approximately 0.02 ± 0.007 (± SEM; range 0.001 to 0.08). Plotting the data as spT_fer over release distance produced a concave line with an asymptotic approach to the x-axis (Fig. 5B). The mean spT_fer for the closest release distance of 40 m was 0.08 (± 0.02, n = 15). Catch decreased with distance from the central trap to a mean spT_fer of 0.01 (± 0.006, n = 15) at the furthest distance of 240 m. Transformation of the data to the MAG plot produced an initial straight line (Fig. 5C) whose slope was 0.33, which equates to a plume reach of <5 m. Transformation of the data to the Miller plot (Fig. 5D) revealed a mean maximum dispersive distance for 95% of the population at approximately 270 m, resulting in an estimated trapping area of 23 ha.

Discussion

Estimate of Proportion of Purchased Codling Moths Capable of Participating

Releasing known populations of codling moth within small field cages permitted males to fly and respond to standard monitoring traps, confirming that an overwhelming majority (approximately 80%) of these SIR moths were behaviorally competent to participate in these experiments. Similar levels of competency were recorded in the very large-cage experiments of Miller et al. (2010). High competency is independently corroborated by the good match between the maximum y-values (approximately 1,000) for the Miller plots of Fig. 1 and the three highest lines in Fig. 2D, which represent orchards receiving no insecticide and moth populations matching mover numbers of Fig. 1. Although probably not surprising, given the attention this codling moth rearing facility pays to quality control, very high robustness of these codling moth males is remarkable when considering the shipping and handling they experienced before release.

Consistency and Pattern of Trapping Outcomes Indicate Codling Moth Is a Random Walker

A remarkable outcome of the present research is the consistency recorded for plume reach (<5 m), trapping radius, and trapping area (240–275 m and 18-24 ha, respectively), as well as T_fer (0.01–0.025), despite using cardinal-direction releases and even releases as well as varying codling moth densities across three growing seasons at eight different experimental sites in Western Michigan using laboratory-reared codling moth produced across three different years, airmailed cross-country, powdered with fluorescent dye, and then immediately released into apple orchards to find sources of pheromone plumes across their <7 d life spans. Rather than showing that trapping results are too variable to provide a foundation for estimates of pest population density, current results strongly support the hypothesis that trap–codling moth interactions consistently and reliably express themselves despite variation in environmental factors like wind direction and local geography. The capture patterns emerging from these field data closely match those from a wide range of manipulative experiments using computer-simulated random walkers (Miller et al. 2015). These matches include: smoothly concave untransformed profiles of distance of release versus spT_fer that asymptotically approach a catch of zero; initial linearity of plots of release distance versus 1/spT_fer (MAG plots); and rapidly rising, peaking, then tailing plots for distance of release versus annulus area × spT_fer (Miller plots) that gradually rather than abruptly reach zero catch. These multiple lines of unique evidence compel us to conclude that codling moth is a biological random walker. As specified by Miller et al. (2015), this means that headings for new displacement steps are apparently randomly picked from a normal distribution of possible headings centered on straight ahead and with a circular standard deviation of approximately 6-30°. When each individual codling moth male follows this simple rule of stochastic behavior, a population of such movers will exhibit spatially consistent properties that can reveal absolute pest density via capture number. Furthermore, we conclude that the principles governing movement by small mobile animals like insects can be very similar to those governing molecular displacement. Therefore, the vast knowledge base from studies of atomic and molecular populations can and should be put to use on the problem of estimating pest density via trapping.

Approximations of Male Codling Moth Flight Paths When Foraging for Pheromone Plume

Given the excellent match between the outcomes of the computer simulations that produced Fig. 1 and the codling moth field results, representative flight paths for codling moth males could be produced using the Weston MultiMover software of Miller et al. (2015). Panels A-F of Fig. 6 show simulated flight paths of six individual simulated codling moth males as they would appear after 3,000 steps (3 km) to a viewer looking down upon a 9-ha rectangular orchard when a single male was released near its center. By overlaying such tracks on a Google Earth image of our orchard having180 trees per ha, it was possible to count that about 280 tree canopies would be visited in the lifetime of an average male codling moth. As seen in Fig. 6, foraging with a meander of circular standard deviation of 30^° balances intensive local search with intermittent forward excursions. However, the probability is very low that successive forward excursions will have a common heading; thus, a typical simulated codling moth track folds back upon itself to produce a radius of net dispersion of little more than 100 m. But entirely owing to chance alone, the forward excursions of a simulated individual occasionally follow a common heading to produce a track with unusually long net displacement like that of Fig. 6 Panel G. Over 1,000 simulation records were examined to find this one atypical example of net displacement of 350 m.

Fig. 6.

Panels A–G illustrate the tracks of individual computer-simulated random walkers using movement patterns like those deduced from field data for codling moth. The normal distribution from which new steps were randomly selected had a circular standard deviation of 30^° and the total number of steps was 3,000. Individual codling moth males are predicted to generate similar search patterns when each gray box is taken as a section of apple orchard of about 10 ha with the release point near its center.

Only after techniques are found to continuously track tiny animals like codling moth across great distances in the field will it become possible to directly test whether actual codling moth tracks match the deduced approximations of Fig. 6. Nevertheless, we are confident of this bold prediction because it is congruent with the findings of other researchers using entirely different approaches. For example, Schumacher et al. (1997) used flight mills to document that flight output by both codling moth males and females is a consistent 8-10 km of total displacement over a lifetime. However, because insects on a flight mill only fly forward against the wind reducing their groundspeed but do not carry their own weight, we suggest that values for flight propensity on flight mills need to be cut at least in half for estimates of total displacement for free flight. Thus, our estimate of 3 km for total lifetime displacement by released codling moth becomes a reasonable match to the Schumacher et al. (1997) data.

Behaviorally Active Plume Reach of the Codling Moth Trap in Apple Is Small

Plumes evoking male moth attraction as long as 60, 50, and 30 m have been revealed in the field by direct behavioral observations of, e.g., responding gypsy moths (Lymantria dispar) (Elkinton et al. 1984), European pine sawflies (Neodiprion sertifer) (Östrand and Anderbrant 2003), and oriental fruit moths (Grapholita molesta) (Baker and Roelofs 1981), respectively. By that standard, our estimate of approximately  < 5 m plume reach for the codling moth monitoring trap in apple is tiny. Nevertheless, we are confident in the accuracy of the current measures of codling moth plume reach based on the MAG plot slope method (Miller et al. 2015) because: 1) it has a strong basis in mathematical theory and simulation-modeling, 2) the method returned (Miller et al. 2015) an estimate of 30-50 m for European pine sawfly data that had been previously measured by direct observation (Östrand and Anderbrant 2003) to be approximately 50 m, and 3) Grieshop et al. (2010) previously found that plume reach from the identical codling moth monitoring trap was likely < 10 m because traps never ensnared marked and released codling moth males quickly unless releases were directly down-wind and very close to the trap.

As documented by Lewis and Macaulay (1976) for pea moth (Cydia nigricana), we postulate that the dense and complex architecture within an apple orchard, as opposed to above it, caused atmospheric turbulence that dispersed the codling moth pheromone plume more quickly in our study than would happen in a simpler environment. The above and other reports of large plumes come mainly from experiments conducted in open understories of forests or in open fields of low-growing vegetation. In addition, codlemone (12-carbon primary alcohol) is one of the smallest of lepidopteran pheromones and thus adsorbs less strongly (Gut et al. 2004) onto the antennae. Furthermore, the antennae of codling moth males are not notably specialized for collecting pheromone from air as are the antennae of male gypsy moths and pine sawflies. Thus, the active space for codling moth sexual communication might be already small irrespective of crop architecture.

Measurements of attractive plume reach for monitoring traps have been rare and difficult. Diverse methodologies have been attempted (Murlis et al. 1992, Murlis et al. 2000), including direct observations of responding insects, release–recapture, field electroantennograms, and gas-liquid chromatography analysis of air samples. Even when achieved, a given estimate for plume reach by these methods may apply only to a subset of all possible environmental conditions encountered by a trap operating in the field over several days. By contrast, the MAG plot slope method has the advantages of being less labor-intensive and of always time-averaging. Thus, the novel approach of estimating plume reach via geometry solves a difficult and long-standing problem in chemical ecology and could make plume-reach determinations routine.

Knowing plume reach will be helpful in assessing the sampling power of a trapping system and judging its potential for direct pest control by, e.g., mass-trapping. Traps emitting long plumes are better sampling devices than those emitting short plumes, like that found here for codling moth. A long plume can increase trapping radius appreciably and it will actively collect many more pests than will a short plume when shifting wind directions cause such respective plumes to sweep across the crop. The computer simulations of Miller et al. (2015) suggest that effective mass-trapping requires spacing no more than 1.5 times the plume reach. Thus, the number of traps required for control by mass-trapping is entirely dependent upon plume reach, which should be ascertained before mass-trapping or attract-and-kill tactics are attempted. Codling moth does not appear to be a good candidate for mass-trapping using a device like the current standard monitoring trap.

Radius and Trapping Area of the Codling Moth Trap in Apple Are Large

The plume reach for the codling moth trap was just a few meters, while the 95% trapping radius (TR₉₅) was approximately 260 m. Therefore, the maximum dispersive distance for 95% of members of a local codling moth population was nearly 260 m. The radii of trapping annuli contributing the most to overall catch are revealed by the x-values associated with the maximum y-values of a Miller plot. For codling moth, the annulus contributing the most to catch (see Panel D of Figures 2 through 5) had a radius of approximately 125 m. It follows that travel of codling moth males from their points of origin to the plume contributes far more (approximately 98% of the total) to the average overall journey into a trap than does travel of males in the plume. Nevertheless, guidance of the final leg by pheromone is critical to trapping success, because it is rare that any catch is registered when no pheromone is emitted from a codling moth trap.

The above information and the simple calculation of trapping area of approximately 21 ha given a trapping radius of approximately 260 m enables informed suggestions for optimal deployment of codling moth monitoring traps in orchards not under mating disruption. Despite a surprisingly tiny plume reach, the trapping area for codling moth is considerably larger than once presumed. Suggestions can be found (Gut and Wise 2016) that optimal monitoring requires one codling moth trap for every ha of orchard; one trap per 2-4 ha is acceptable in large, uniform blocks. However, such a trap density is excessive in light of the current data. Deployment of multiple traps per 21-ha orchard is likely to provide a more reliable (less noisy) measure of pest abundance, and this approach to enhancing precision will be explored in a subsequent report on line-trapping. But placing multiple traps with small plumes close to one another will have little influence on the distance from which codling moth is being sampled. Counter-intuitively, the codling moth males found in a trap are more likely to have originated >100 m away from the trap than near the trap. Although the probability of capturing a given individual is highest when the trap is nearby, the nearby area and therefore the total number of randomly distributed pests associated with a nearby annulus is considerably less than that for a distant annulus (Miller et al. 2015). It therefore would be unsafe to restrict insecticide applications targeting codling moth to apple blocks only immediately adjacent to a trap registering a catch.

Converting Codling Moth Catch Number to Absolute Density

Once trapping area and T_fer are known and shown to be reproducible, as in the current study, absolute pest density in a new location and given in units of pests per trapping area is obtained simply by dividing capture number by T_fer (Miller et al. 2015). In the current case, T_fer measured in commercially managed Michigan apple was approximately 0.02. Therefore, a codling moth male catch of 1, 3, 10, and 30 equates to 50, 150, 500, and 1,500 males per 21 ha, or 2.4, 7, 24, and 71 males per ha, respectively. Given that the sex ratio of codling moth is 1:1, this estimate holds for females. The curtain can now be lifted on how many codling moth are present in a typical commercial apple orchard in Michigan, where capture numbers are maintained at or under 5 males per trap per control period. The answer has surprised growers and pest managers alike; catch of 5 males per trap equates to only 250 females per 21 ha, or 12 females per ha (5 per ac). Thus, when spraying at this threshold and spending $120 per ha for the insecticide, cost per killed female codling moth is a seemingly high $10 per female or $0.5 per hatchling larva.

The above information enables codling moth catch in a standard monitoring trap to be translated into estimates of damage in a Michigan apple crop not under mating disruption (Table 2). Catch of male codling moth per trap per 21-ha trapping area is converted to males per trapping area by dividing catch by a T_fer of 0.02. As the sex ratio of codling moth is 1:1, absolute density of female codling moth equals that of male codling moth. The mean number of eggs produced and laid by codling moth females varies slightly with temperature (Agndam et al. 2009) but can be safely estimated at 50 (Geier 1963 and references therein). However, only about 33% of eggs laid in the field produce larvae that successfully attack apples (Geier 1963). Thereafter, success in pupating and eclosing as an adult is 90 and 85%, respectively (Geier 1963). Injury frequency expected from each codling moth female can then be estimated at 17 apples (50 × 0.33) under a regime of no insecticide. The number of infested apples per 21-ha trapping area (Column 4 of Table 2) can then be estimated by multiplying females per trapping area by 17 events per female per trapping area. According to Michigan Agricultural Statistics, apple fruit load currently averages approximately 360,000 apples per ha, which translates into 7.56 million apples per 21-ha trapping area. As shown in Column 5 of Table 2, the estimated % infestation estimated for each catch of Column 1 can be computed by dividing infested apples per trapping area (Column 4) by 7.56 million and then multiplying the quotient by 100. The threshold for rejection of apples from the Michigan fresh market followed by diversion to apple juice is 0.5% infestation. It becomes apparent by inspection of Table 2 that the catch threshold indicative of severe economic loss is approached at 30 male codling moth per trap per growing season, and it is crossed at a catch of 45. The current action threshold of a cumulative catch of approximately 12 codling moths per season, arrived at by trial and error, is thus shown to be reasonable, albeit strongly tipped toward safety. The current research suggests that this capture threshold might be raised so as to elevate grower profits by reducing pest control costs.

Table 2.

Demonstration of how codling moth male capture in a single pheromone-baited monitoring trap deployed in a Michigan apple orchard not under mating disruption can be translated into an estimate of percent apple infestation

Male codling moth caught per trap	Male codling moth per 21 haa	Female codling moth per 21 hab	Infested apples per 21 hac	% Infestationd
1	50	50	850	0.011
3	150	150	2,550	0.033
10	500	500	8,500	0.11
30	1,500	1,500	25,500	0.33
100	5,000	5,000	85,000	1.10

^a Male codling moth per trapping area of 21 ha equals catch divided by a T_fer of 0.02.

^b Codling moth sex ratio is 1:1.

^c Each codling moth female results in an estimated 17 infested apples.

^d The average number of apples per 21 ha of Michigan orchard is approximately 7.56 million. % Infestation equals (infested apples per 21 ha divided by 7.56 million) × 100.

Caution in setting the actual economic threshold for codling moth is justified, however, because of this pest’s capacity for rapid population growth. Moreover, there is considerable inherent variability in catch in any single monitoring trap. A grower cannot risk the crop without confidence in the accuracy of the recorded moth catch. Trapping is a stochastic process shaped by random interactions of moving insects with a trap. Under a constant pest density that yields a particular mean catch, there is a high likelihood that a number well above or below the mean will be recorded if only a single monitoring trap is deployed. Adding more traps per area sampled will decidedly increase the accuracy of catch interpretations, but it must be done as cheaply as possible. A report on the idea of line-trapping will follow shortly that should help fill this catch reliability gap.

Should Females Be Present or Absent During Experiments and Calibrations?

Calling by females during the flight window of male moths would represent a competing point source and could theoretically affect instantaneous catch in the monitoring trap and the measures of the trapping performance reported here. However, including females more closely approximates conditions that growers and pest managers actually experience with a sex ratio of 1:1. Excluding females from experiments might produce larger estimates of the maximum dispersive distance of the males, but these would be artificial because a few calling codling moth females are always present under field conditions. However, we have seen very high consistency of these measures using mixed-sex populations ranging from approximately 130/ha to 1,250/ha in unbounded orchards, suggesting that there is little female effect on eventual outcomes. One reason for modest female impact could be that the period of male sexual activity brackets that for females so as to provide males ample opportunity to interact with traps when females are not emitting pheromone. Another would be that most mated females drop out of the competition, eventually leaving only the trap. Finally, Miller et al. (2015) have shown that the distances over which attractive point sources compete appreciably are much more limited than previously guessed because actual competition requires certainty that a male would actually visit both alternatives. Therefore, the presence or absence of females is predicted to have a minor influence on trapping interpretations.

Recommendations for Applying This Approach to Other Pests

The principles and methods used here to estimate absolute density via trapping should be broadly applicable to any pest or beneficial animal that forages locally by random walks. Measures of plume reach and trapping radius are critical for understanding pest detectability and should be a research priority for any invasive species. An optional listing or recommended steps in applying the current approach to estimating absolute animal density from monitoring trap capture data is provided in Supplemental Materials [online only].