Abstract
The aquatic bacterium Caulobacter crescentus attaches to solid surfaces through an adhesive holdfast located at the tip of its polar stalk, a thin cylindrical extension of the cell membrane. In this paper, the elastic properties of the C. crescentus stalk and holdfast assembly were studied by using video light microscopy. In particular, the contribution of oligomers of N-acetylglucosamine (GlcNAc) to the elasticity of holdfast was examined by lysozyme digestion. C. crescentus cells attached to a surface undergo Brownian motion while confined effectively in a harmonic potential. Mathematical analysis of such motion enabled us to determine the force constant of the stalk-holdfast assembly, which quantifies its elastic properties. The measured force constant exhibits no dependence on stalk length, consistent with the theoretical estimate showing that the stalk can be treated as a rigid rod with respect to fluctuations of the attached cells. Therefore, the force constant of the stalk-holdfast assembly can be attributed to the elasticity of the holdfast. Motions of cells in a rosette were found to be correlated, consistent with the elastic characteristics of the holdfast. Atomic force microscopy analysis indicates that the height of a dried (in air) holdfast is approximately one-third of that of a wet (in water) holdfast, consistent with the gel-like nature of the holdfast. Lysozyme, which cleaves oligomers of GlcNAc, reduced the force constant to less than 10% of its original value, consistent with the polysaccharide gel-like nature of the holdfast. These results also indicate that GlcNAc polymers play an important role in the strength of the holdfast.
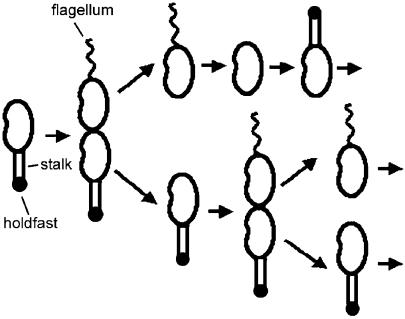
Caulobacter crescentus is a gram-negative bacterium ubiquitous in fresh water, soil, and seawater (1, 2, 14, 23-25). These environments are often very dilute in nutrients, such as the essential nutrient inorganic phosphate. C. crescentus exhibits a dimorphic life cycle (Fig. 1) that probably provides an advantage in such competitive environments. The hallmark of the dimorphic life cycle is the ordered synthesis of polar structures visible by microscopy, which allows developmental stages to be easily defined. Approximately one-third of the C. crescentus life cycle is spent in an obligatory free-swimming dispersal mode known as the swarmer phase. The most notable structure that defines the swarmer cell phase is the single polar flagellum. Flagellar motility allows the swarmer cell to explore new microenvironments where nutrients may be more plentiful. While in the swarmer phase, C. crescentus cannot initiate DNA replication or cell division. After the obligatory swarmer phase, the cell differentiates into a stalked cell by initiating DNA replication, releasing the flagellum, and synthesizing a stalk, a thin cylindrical extension of the cell membrane (24). Synthesis of the adhesive holdfast occurs early during swarmer cell differentiation (11) at the same pole as the stalk, resulting in its positioning at the tip of the stalk. The stalked cell elongates, initiates cell division, and synthesizes a flagellum at the pole opposite the stalked pole, generating an asymmetric cell that divides to produce a new swarmer cell and a stalked cell. Upon division, the stalked cell can immediately begin a new round of DNA replication and cell division.
FIG. 1.
Schematic illustration of C. crescentus cell cycle (see text for description).
The adhesive holdfast serves to anchor cells to abiotic and biotic surfaces. It has been hypothesized that the ability to remain attached to a surface results in better access to limited nutrients, especially under flow (21). The strength of adhesion depends on the following factors: the contact between the holdfast and the surface, the contact between the holdfast and the stalk, and the mechanical properties of the holdfast itself. A well-known theory for the adhesion of bacterial cells to a solid surface is that the cell is bridged by extracellular polysaccharides (18, 29). Direct measurement of nonspecific adhesive force between a single polysaccharide xanthan molecule and the tip of an atomic force microscope (AFM) showed that this force is up to 2 nN (8, 16), large enough to immobilize a bacterial cell. The holdfast may have a gel-like structure, such as that of the extracellular matrix of a biofilm (3, 5, 32). Beyond that, however, little is known about the mechanical properties of the holdfast.
The C. crescentus holdfast is composed of extracellular polysaccharides and additional components, such as proteins and uronic acids (21, 35). Previous experiments have shown that oligomers of N-acetylglucosamine (GlcNAc) are an important component in the holdfast of some strains. In those experiments, digestion of oligomers of GlcNAc by lysozyme or chitinase disrupted rosettes of C. crescentus, groups of cells attached to each other by their holdfast (21). Genetic screens have identified genes required for holdfast synthesis (hfsABD) (31) and genes required for the attachment of the holdfast to the tip of the stalk (hfaABD) (13, 31). Two of the hfs genes, hfsA and hfsD, encode homologs of proteins involved in polysaccharide export in other gram-negative bacteria, suggesting that they are required to export holdfast polysaccharide (31). Mutations in the hfaABD genes result in inefficient attachment of the holdfast to the tip of the stalk (4, 13). The holdfasts of hfa mutants are shed into the surrounding medium and are found attached to surfaces.
The stalk of a C. crescentus cell has a diameter of approximately 100 nm and a length of up to several micrometers (12, 23). The holdfast has a size comparable to the diameter of the stalk. The simple shape and the small size of the holdfast allow for treatment of its mechanical properties as a whole entity. In this paper, we set out to measure the elasticity of the stalk-holdfast assembly by video optical microscopy and the morphology of the holdfast by atomic force microscopy.
Polysaccharides, such as N-acetylglucosamine (GlcNAc), are a major component of extracellular adhesive matrices, such as those found in biofilms (15, 21). In this study, the role of oligomers of GlcNAc in the elasticity of the holdfast was examined by a lysozyme assay. The results of this study may be relevant to a variety of similar systems. For example, our results are likely applicable to polar polysaccharide adhesins, such as the holdfasts of Asticcacaulis biprosthecum and Asticcacaulis excentricus (26), and to the polar polysaccharide adhesins of Hyphomonas strain MHS-3 (28) and Bradyrhizobium japonicum (17).
MATERIALS AND METHODS
Strains.
All C. crescentus strains were cultured in peptone-yeast extract (PYE) medium (24) at 30°C. Antibiotics were used to supplement the medium, as necessary, at the following concentrations: 5 μg of kanamycin/ml and 20 μg of nalidixic acid/ml for plates and 2.5 μg of kanamycin/ml for liquid medium. The C. crescentus strains used in this study were CB15 (wild type), YB2780 (CB15 hfaB::miniTn5lacZ), which has a holdfast shedding phenotype (31), and YB2833 (CB15 ΔhfsA), which does not synthesize a holdfast (31).
Light microscopy.
Two types of sample preparations of CB15 wild-type cells were made for optical microscopy. The first type was made by simply placing a drop of cell culture between a coverslip and a glass slide, which was sealed with vacuum grease. The holdfast can attach the cell to the surface of the coverslip or glass slide. For the second type of preparation, a thin glass fiber of several micrometers in diameter was placed between the coverslip and the glass slide. In this case, the cells occasionally attached to the glass fiber as well. All samples were incubated for 3 h at 30°C before observation.
A Nikon Eclipse E800 microscope was used for imaging in the phase-contrast mode and with an oil immersion ×100 objective lens (Plan Apo). Video segments containing 1,000 frames were taken at 10 or 20 frames per second with version 6 of the MetaMorph software package (Universal Imaging, Downingtown, Pa.).
Lysozyme assay.
Thirty milliliters of fresh PYE growth medium, a 3-ml overnight culture of CB15 wild type, and up to six coverslips were added to a 9-cm culture plate. The plate was incubated at room temperature for 1 h with gentle shaking, and some cells attached to the coverslips. The coverslips were then rinsed in water and transferred to another plate with 30 ml of fresh PYE. The cells were allowed to grow for another 6 h. During this period, the PYE growth medium was changed every 2 h to control the density of cells attached to the surface.
Two hundred microliters of lysozyme (concentration, 10 mg/ml; L-6876; Sigma) in 10 mM Tris-HCl, pH 8.0, was applied to a glass slide with a depression in the central location (Fisher Scientific). The depression slide was then covered by a coverslip with attached cells. The edges of the assembly were sealed with vacuum grease. Video segments of motions of cells were recorded at a rate of 10 frames per second, starting at different time points after the cells were exposed to the lysozyme solution. A control experiment was performed by following the same procedure with the same buffer but without lysozyme.
Measurements of center positions.
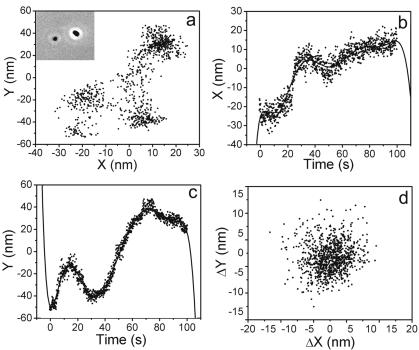
Positions of an object's center were obtained by using the Integral Morphology function in MetaMorph. The threshold function was first applied to the image, and then the center of the object was measured automatically. A 1.8-μm-diameter latex bead fixed on a substrate was used as a test object to determine the spatial resolution of this method. A 1,000-frame video was taken, and positions of the bead were recorded (Fig. 2A). Projections of the bead's center on the x and y axes are shown in Fig. 2B and C as functions of time. The measured uncertainty in the center position was caused by two factors: one is the intensity variations among the frames, which affect the shape and position of the imaged bead after thresholding, hence the center position; another factor is stage drift. Due to the large mass of the stage, the drift of its position as a function of time is expected to be a smooth function, which can be removed by either one of two standard methods. (i) Fourier transform can be applied to the position-versus-time data. The stage drift can then be removed by filtering out low-frequency signals. The validity of the Fourier analysis relies on the assumption that the stage drift is a periodic function. We tried this method with a Fast Fourier Transform filter built with Origin, a commercial software package. The results were not very reliable, as they depended on the choice of cutoff frequency, which is not well defined. (ii) The second method is fitting the data to a smooth polynomial function and then subtracting the fit function from the data. The differences between the experimental data and the fit are caused by other sources of error of the center position determination. In this method, the order of the polynomial fit function is not well defined. In practice, any high-order polynomial can be used. We compared the seventh-, eighth-, and ninth-order polynomial functions for fitting the data and found little difference in the outcome of the analysis. After the initial tests, all data throughout this work were treated by using the ninth-order polynomial fits. Figure 2D shows the distribution of error values. The standard deviation of the bead's position along the x or y axis is found to be approximately 4 nm when the bead is actually stuck to a slide and thus fixed to the microscope stage. The fluctuation of the cell body was 1 order of magnitude higher than the stuck beads and thus was reliably measured.
FIG. 2.
Measurement of center positions of an immobilized latex bead from a video containing 1,000 frames. (A) Center position of the smaller latex bead on the left in the inset. The inset shows a phase contrast image of two beads stuck to the microscope slide. (B and C) Positions for the smaller bead as functions of time along the x axis and y axis, respectively. Solid lines are fits to ninth-order polynomials. (D) Distribution of center positions after the subtraction treatment described in the text.
Calculation of force constant.
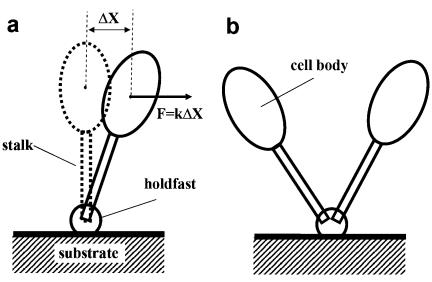
When a stalked cell is stuck to a surface, the holdfast and stalk assembly work together to constrain the cell body at an equilibrium position. When a force perpendicular to the stalk is applied to the cell body, as shown in Fig. 3A, the cell body will displace from the equilibrium position by ΔX. Assuming an elastic nature of the holdfast and stalk assembly, the force will be proportional to the displacement in the linear regime, that is, F = kΔX, where k is defined as the force constant. The random collision of molecules in the surrounding fluid with the cell body gives rise to a force that displaces the cell body randomly. This phenomenon is called Brownian motion. The stalk and holdfast assembly actually provide a restoring force that tends to return the cell body to the equilibrium position after displacement due to Brownian motion. In physics terminology, the stalk and holdfast assembly provide a potential kΔX2/2 to constrain the cell body. The potential of such a mathematical form is called a harmonic potential. The probability P of the cell body with displacement ΔX in Brownian motion is described by the Boltzmann distribution, 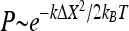 , where kB is the Boltzmann constant, and T is the absolute temperature (10). The displacement ΔX and the probability P are both measured based on the recorded video. By fitting the probability to the Boltzmann distribution, the force constant k can be calculated. Alternatively, the force constant k can be determined by another simple calculation, k = kBT/<ΔX2>, where <ΔX2> is the value of ΔX2 averaged over 1,000 equal time intervals.
, where kB is the Boltzmann constant, and T is the absolute temperature (10). The displacement ΔX and the probability P are both measured based on the recorded video. By fitting the probability to the Boltzmann distribution, the force constant k can be calculated. Alternatively, the force constant k can be determined by another simple calculation, k = kBT/<ΔX2>, where <ΔX2> is the value of ΔX2 averaged over 1,000 equal time intervals.
FIG. 3.
(A) Schematic illustration of a stalked cell attached to a surface via a holdfast. Thermal fluctuation causes a displacement ΔX of the cell body from the equilibrium position (dashed), which results in a restoring force perpendicular to the stalk, F = kΔX, where k is the force constant of the stalk and holdfast assembly. (B) Schematic drawings of a C. crescentus rosette of two cells attached to a solid surface via the holdfast.
AFM.
CB15 cells were imaged by AFM in air. A drop of cell culture was spread on a Plus slide (Fisher Scientific) and then blow-dried. The sample was further dried for 20 min in low-humidity air to remove the residual water within the cells.
The AFM samples of the holdfasts from YB2780 were prepared as previously described (22). Briefly, an overnight culture of YB2780 was grown for 16 h in PYE at 30°C. The overnight culture was diluted in PYE to an optical density at 600 nm of 0.15 and then grown at 30°C until an optical density at 600 nm of 0.5 to 0.8 was reached. Two hundred microliters of such a culture was placed on a Fisherbrand Plus slide and allowed to grow at 30°C for 5 h in a humidity box. The glass slide was then washed with water to remove loosely attached cells from the surface. The sample was first imaged in water. It was then completely blow-dried and imaged in air. Samples for holdfast-deficient mutant YB2833 were prepared by following the same procedure.
All images were obtained by using a Nanoscope IIIa Dimension 3100 atomic force microscope (Digital Instruments, Santa Barbara, Calif.) with either the tapping mode in water or the contact mode in air.
RESULTS
Force constant of the stalk and holdfast assembly.
In order to gain insight into the mechanical properties of the C. crescentus holdfast, we performed an analysis of the Brownian motion of cells attached to glass through their holdfast. An example of analysis for a cell is given in Fig. 4. The cell in the inset of Fig. 4A is attached to a glass fiber through a stalk and a holdfast. Without thermal agitation, the cell body would remain motionless at a position constrained by the holdfast and the stalk. Brownian motion causes a frequent deviation from the equilibrium position, giving rise to a deformation on the stalk and holdfast assembly. This deformation leads to an immediate restoring force, which tends to return the cell body to its equilibrium position. Assuming an elastic nature of the holdfast and stalk assembly, the restoring force will be proportional to the displacement in the linear regime (see the Calculation of force constant section above).
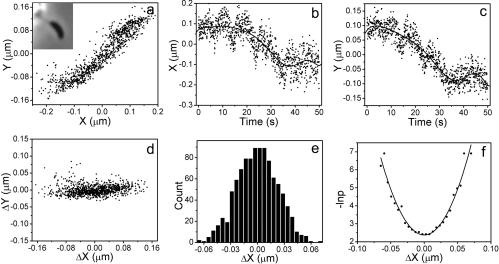
FIG. 4.
Data treatment of cell displacement. (A) Trajectory of a cell shown in the inset that is attached to a glass fiber through its stalk and holdfast. (B and C) Projections of center positions along x and y axes as functions of time. Solid lines are curves of ninth-order polynomial fits. (D) The displacement of the cell center positions perpendicular to the stalk (ΔX) and along the stalk (ΔY) after removing the stage drift. (E) Distribution of displacements perpendicular to the stalk axis. Only displacements in the range of −0.07 to 0.07 μm were counted. (F) Probability plotted as −ln P against displacement perpendicular to the stalk axis. The solid line is a fit applying the equation −ln P = (kΔX2/2 + E0)/kBT.
The cell center position was measured by using the same method as that described in Materials and Methods for latex beads. The cell's trajectory is shown in Fig. 4A. The X and Y projections of the measured center positions of the cell as functions of time are shown in Fig. 4B and C. The projections were then corrected by a ninth-order polynomial fit to remove contribution from the stage drift (see Materials and Methods). The trajectory of the cell due to Brownian motion was thus obtained. We then separated the displacement perpendicular to and along the stalk, noted as ΔX and ΔY in Fig. 4D, by rotating the trajectory.
The body of a cell attached to a glass fiber through the stalk and holdfast assembly constantly deviates from the focal plane of the microscope while the cell is under observation due to the Brownian motion perpendicular to the focal plane. This deviation results in an additional error that is significant in the direction along the stalk axis. Perhaps due to this source of error, the standard deviation of the cell center position along the stalk axis was measured to be 23 nm (see Fig. 4D), which is much larger than that of a fixed latex bead. However, since the effect of defocusing does not contribute to the error in the direction of motion perpendicular to the stalk axis, the total error for the position perpendicular to the stalk is expected to remain comparable to that determined for the fixed bead.
The displacement perpendicular to the stalk is a measure of Brownian motion of the cell body. A total of 1,000 positions were counted. The distribution of this displacement is shown in Fig. 4E and the minus logarithm of probability, −ln P, as a function of ΔX is shown in Fig. 4F. We fit the plot in Fig. 4F using −ln P = A + kΔX2/2kBT, where A is a constant determined by fitting. This fitting formula is a modification of the Boltzmann equation discussed in Materials and Methods. The curve shown in Fig. 4F fits the experimental data very well, indicating that the assumption of an elastic nature of the stalk and holdfast assembly is reasonable. The force constant obtained by the fitting is 8.3 × 10−6 N/m. This force constant is contributed to by the stalk and holdfast assembly.
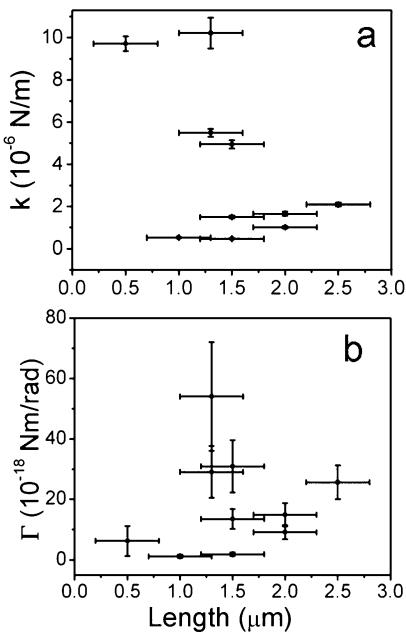
The force constants of 10 cells were measured and plotted against stalk length (Fig. 5A). Some fluctuations are so small that the fluctuation is buried in the error of the method used to determine the center position; therefore, we only measured the force constant of cells with larger fluctuations. The data show that the measured force constant varies over an order of magnitude and that the values do not depend on the stalk length.
FIG. 5.
Stalk length dependence of force constant and torsional constant. (A) Force constants of stalk and holdfast assembly of 10 CB15 wild-type cells attached to a glass fiber. (B) Torsional constants of the holdfasts of these 10 cells.
The displacement of the cell body is a combined outcome of the bending of the stalk and the elastic deformation of the holdfast. The bending of the stalk increases with increased stalk length, consistent with the common intuition that a longer stick can be bent more easily than a shorter one. Alternatively, if the stiffness of the stalk is great compared to that of the holdfast, then the displacement of the cell body is primarily attributed to the elastic deformation of the holdfast. Since the measurement results do not show a dependence of the force constant on stalk length, we conclude that the measured force constant is that due to the elastic deformability of the holdfast.
One caveat of our analysis of the dependence of the force constant on stalk length is that the measurement of the stalk length introduces a large error due to the difficulty in discerning the two ends of the stalk. One end of the stalk is connected to the cell body and the other is fixed to a glass fiber. Both ends are difficult to resolve by light microscopy. Therefore, the force constants were calculated based on the position of the cell center and not the position of the junction between the stalk and the cell body or stalk base. However, even after the force constants were recalculated for the stalk base, they still showed no dependence on the stalk length (data not shown), confirming that the measured force constant ought to be attributed to the elastic deformation of the holdfast.
Size distribution of holdfasts.
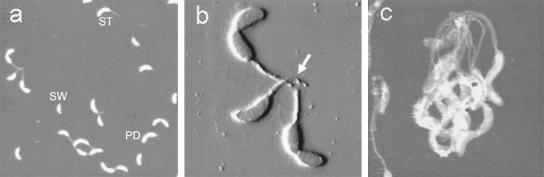
As shown in the previous section, the variation in the fluctuation of the cell bodies is not caused by the difference in stalk length. One possibility is that this variation reflects differences in size and/or mechanical strength of individual holdfasts. We used AFM to image C. crescentus cells and holdfasts in order to analyze the size variation of holdfasts. C. crescentus cells can exist as individual cells or as rosettes, groups of cells attached to each other through their stalks and by sharing their holdfasts. Figure 6 shows three AFM images of C. crescentus CB15 cells dried on a glass slide and imaged in air. The three main cell types of C. crescentus, namely, swarmer, stalked, and predivisional cells, can easily be distinguished in the AFM images. All stalks have a diameter of approximately 100 nm, but their length varies. Stalk length depends upon the age of the cells and can grow to more than 30 μm (7, 27). Figure 6B is an enlargement of three cells forming a rosette (seen on the left side of Fig. 6A). The holdfast of this rosette is indicated by an arrow. C. crescentus cells can also form rosettes composed of many cells, as shown in Fig. 6C.
FIG. 6.
AFM images showing the morphology of wild-type C. crescentus cells. (A) An AFM height image showing the predominant shapes of three types of dried CB15 cells (30- by 30-μm scan area): swarmer (SW), stalked (ST), and predivisional (PD) cells. (B) An enlarged deflection image of a rosette of three cells from panel A (8 by 8 μm). The area containing the holdfast of this rosette is indicated by an arrow. (C) An AFM height image of a rosette of many cells (8 by 8 μm).
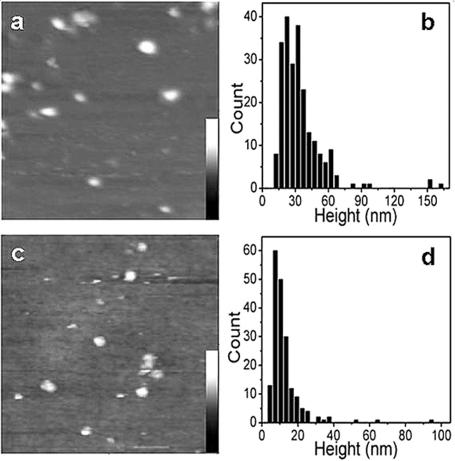
In order to facilitate our analysis of holdfast size by AFM, we used the holdfast-shedding mutant YB2780, which can detach from a holdfast that is bound to a surface. Previous qualitative analysis of shed holdfasts labeled with a fluorescent lectin indicated that their size variation was similar to the size variation of holdfasts in wild-type cells (4). Figure 7A is an AFM image of shed holdfasts on a glass slide surface imaged in water. We measured the heights of a total of 233 holdfasts and determined their distribution (Fig. 7B). The height of the holdfasts varies from 10 to 100 nm, with a few exceptional cases in which the holdfasts are higher than 150 nm. Most of the holdfasts are around 30 nm high, with an average height of 34.3 nm. The observed variation in the size of holdfasts may account for the range of force constants determined based on the fluctuation of cell bodies, although we were not able to perform these two sets of measurements with the same sets of cells.
FIG. 7.
AFM images and analysis of shed holdfasts. (A) AFM image of holdfasts of YB2780 mutant cells shed on a glass slide surface in water (1 by 1 μm). The height scale bar is from 0 to 180 nm. (B) Height distribution of wet holdfasts in water, as measured by AFM. (C) AFM image of dried holdfasts of YB2780 cells shed on glass slide surface in air (1 by 1 μm). The height scale bar is from 0 to 40 nm. (D) Height distribution of dried holdfasts in air, as measured by AFM.
The elastic behavior of holdfasts depends on an intact network of GlcNAc.
The fact that the C. crescentus holdfast is composed, in part, of polysaccharides suggests that it may have gel-like properties. If this were the case, the height of holdfasts would decrease as they were dried. We used AFM to compare the heights of wet and dry holdfasts. The shed holdfast sample analyzed in the previous section was dried and imaged with AFM in air (Fig. 7C). The height distribution of the dry holdfasts is shown in Fig. 7D. Indeed, the height of air-dried holdfasts was much smaller than that of holdfasts measured in water; it averaged 12.5 nm, which is approximately one-third of that of wet holdfasts. No particles were observed in the samples of the holdfast-deficient mutant, YB2833, confirming that the particles in Fig. 7A and C were holdfasts. These results support the notion that the holdfast behaves as a polysaccharide gel.
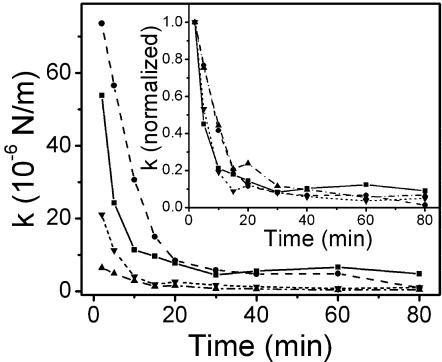
Since the holdfast is a polysaccharide gel as suggested above, cleavage of the GlcNAc polysaccharide of the holdfast is expected to affect its elastic properties. To show the contribution of oligomers of GlcNAc to the elasticity of holdfast, cells attached to a coverslip surface were exposed to a 10-mg/ml solution of lysozyme. Lysozyme cleaves oligomers of GlcNAc and therefore is expected to reduce the force constant of the holdfast. Fluctuations of the cell bodies were recorded, and the force constant of each cell was determined by using k = kBT/<(ΔX)2>. As described in Materials and Methods, this method is equivalent to the method using the Boltzmann distribution for particles under Brownian motion in a harmonic potential. Figure 8 shows the force constants of four cells as a function of time after the cells were exposed to lysozyme. The force constants of these cells vary over a large range before exposure to lysozyme. The attachments of some cells are so stiff that the fluctuation of cell body is close to the resolution limit of our method. However, no matter how stiff the attachment was initially, the force constants of all cells decreased dramatically within the first 20 min and then approached lower values of less than 1/10 of those measured at 2 min after exposure to the lysozyme, as shown in the inset in Fig. 8. In contrast, no observable change in elasticity was found in the control experiment when there was no lysozyme in the buffer (data not shown). Interestingly, all of the cells treated with lysozyme remained attached to the surface even after 24 h. These results indicate that oligomers of GlcNAc play a crucial role in holdfast elasticity. The fact that lysozyme was unable to break the holdfast completely suggests that additional adhesive components besides GlcNAc exist and are involved in surface attachment by the holdfast.
FIG. 8.
Force constants of the holdfast-stalk complex of four cells as functions of time after the cells were exposed to a 10 mg/ml solution of lysozyme at room temperature. The inset shows the force constants for each cell normalized by the values at 2 min after exposure to lysozyme, showing that the force constants decrease to less than about 10% of those measured at 2 min.
Correlations between the Brownian motions of cells in a rosette.
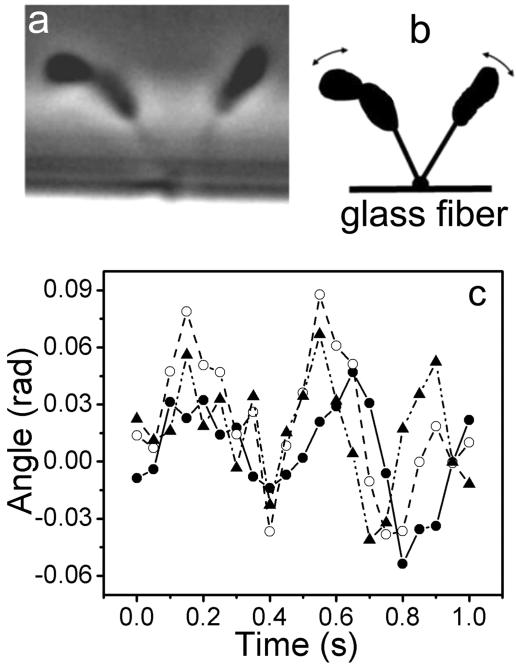
In order to obtain more information on the elastic properties of holdfasts, Brownian motions of cells in rosettes were recorded. Figure 9A shows a rosette of two cells attached to a glass fiber, which is schematically illustrated in Fig. 9B. The displacement of each cell was measured as described above. The calculated force constant was 0.43 × 10−6 N/m for the cell on the left and 1.3 × 10−6 N/m for the cell on the right. To obtain the rotation angle of each cell, the displacement perpendicular to the stalk of the cell was divided by the distance from the holdfast to the cell center. The rotation angles of each cell and the differences between those of the two cells were plotted against time. A segment of the data is shown in Fig. 9C. There is an obvious correlation between motions of the two cells, indicating a mechanical coupling between the two cells through the shared holdfast. The motion of one cell is possibly transferred to the other through the holdfast. The root mean square rotation angle is 0.024 for the right cell and 0.059 for the left cell. The root mean square of the difference between rotation angles of the two cells is 0.05, indicating that although the motions of the two cells are correlated there is a significant extent of independence in the Brownian motion of each cell. If the two cells had been completely correlated, they would have the same root mean square rotation angle.
FIG. 9.
Correlation of Brownian motions between two cells in a rosette. (A) Phase contrast image of two cells forming a rosette attached to a glass fiber. (B) Schematic illustration of the two-cell rosette shown in Fig. 9A. The observed trajectories of Brownian motions are indicated by the arrows. (C) Rotation angles of the left cell (open circles) and the right cell (filled circles) and the differences between those of the two cells (filled triangles) are shown as a function of time.
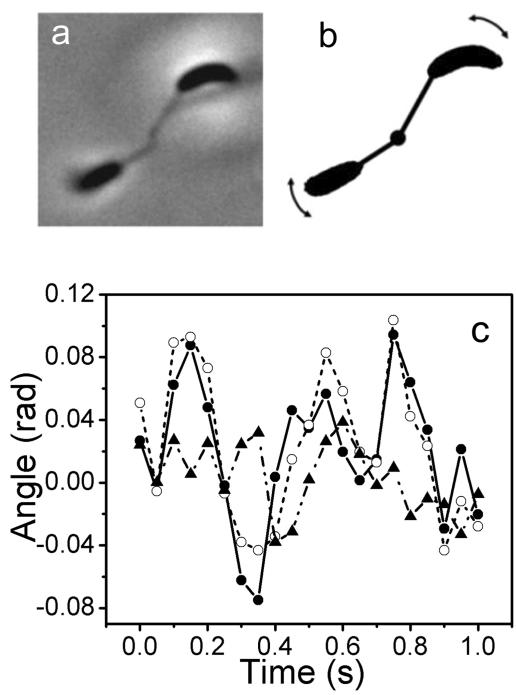
Figure 10A is a rosette of two cells attached to the surface of a coverslip by their holdfast. The calculated force constant is 4.2 × 10−7 N/m for the left cell and 1.8 × 10−7 N/m for the right cell. The rotation angles of each cell and the differences between those of the two cells were plotted against time (Fig. 10C). The root mean square rotation angle is 0.046 for the right cell, 0.072 for the left cell, and 0.026 for the difference between the two cells. The root mean square rotation angle of the difference is significantly smaller than that of individual cells, indicative of a high degree of correlation between the motions of the two cells.
FIG. 10.
Correlation of Brownian motions of two cells in a rosette attached to the surface of a coverslip. (A) Phase contrast image of two cells forming a rosette. (B) Schematic illustration of the two-cell rosette as shown in Fig. 10A. The observed trajectories of Brownian motions are indicated by the arrows. (C) Rotation angles of the left cell (open circles) and the right cell (filled circles) and the differences between those of the two cells (filled triangles) are shown as a function of time.
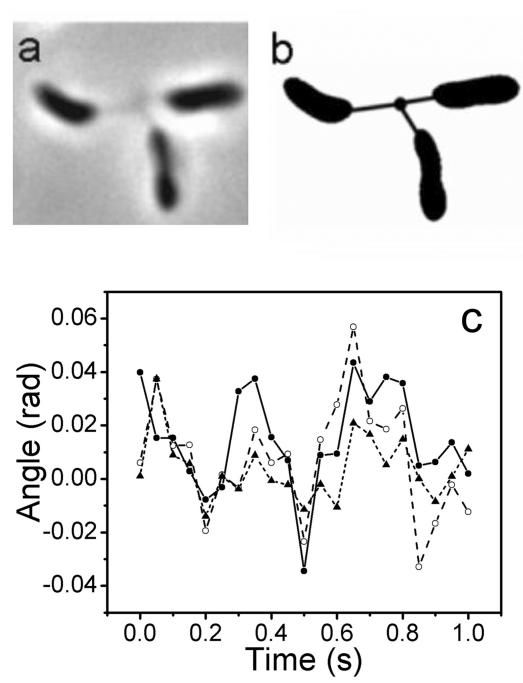
Correlations in Brownian motions were also observed for rosettes having more than two cells. For example, a rosette of three cells attached to the surface of a coverslip is shown in Fig. 11A and is schematically illustrated in Fig. 11B. The measured force constant is 1.6 × 10−6 N/m for the left cell, 1.1 × 10−6 N/m for the lower cell, and 4.7 × 10−6 N/m for the right cell. The rotation angles are shown in Fig. 11C. The motions of the three cells were also correlated. The root mean square rotation angle is different for each cell. It is 0.012 for the right cell, 0.019 for the left cell, and 0.021 for the lower cell. These results are similar to those for the rosettes of two cells.
FIG. 11.
Correlations of Brownian motions of three cells in a rosette attached to the surface of a coverslip (A) Phase contrast image of three cells forming a rosette. (B) Schematic illustration of the three-cell rosette shown in Fig. 11A. (C) Rotation angles of the left cell (filled circles), the lower cell (open circles), and the right cell (triangles) are plotted against time.
These observations show that the motions of cells in a rosette are correlated. Such a correlation is not due to hydrodynamic coupling, which has been shown to give rise to an opposite behavior, namely, an anticorrelation (19). It has been shown for a similar system that when two microsized beads are confined in a harmonic potential within a few microns from each other in a viscous fluid, the hydrodynamic coupling causes them to move in opposite directions. Instead, the results of our measurements demonstrate an elastic link between the cells, since each pair of cells tends to move in the same direction most of the time. Since the holdfast was shown to be an elastic matrix for single cells, the sharing of an integral holdfast is the simplest explanation of the observed correlative motions. However, these results also do not exclude the possibility that small elastic fibers are formed as connectors between the stalks in a rosette. A more quantitative analysis of data acquired with much higher frequencies is required to distinguish between the two possibilities.
DISCUSSION
For a stalked cell attached to a surface as shown in Fig. 3A, the following deformations are possible when the cell displaces from its equilibrium position by Brownian motion: (i) bending of the stalk, (ii) deformation of the holdfast between the stalk and the substrate, and (iii) deformation at the junction between the stalk and the cell body. The attachment between the stalk and the cell body is strong and stiff, since the stalk is an extension of the cell wall (24). The first two contributions to deformation are discussed below.
Force constant of the stalk.
As a simple estimate, the stalk is considered to be a hollow tube. The outer diameter of the tube, dout, is about 100 nm. Assuming that the thickness of the wall of the tube equals that of the cell wall, which is approximately 20 nm, the inner diameter of the stalk, dinner, is about 60 nm. The bending force constant of a tube of length L can be calculated by using the following expression (9): ktube = {πE(dout4 − dinner)}/12L3, where E is the Young's modulus of the cell wall, describing its stiffness. Young's moduli of the cell walls of a few strains of bacteria have been measured to be higher than 3 × 107 Pa (20, 30, 33, 34, 36). If the C. crescentus cell wall has a comparable Young's modulus, then stalks that are 0.5 to 2.5 μm long are estimated to have force constants of about 7 × 10−6 to 9 × 10−4 N/m, which are much larger than most measured force constants of C. crescentus cells in their attachment to substrates through the stalk and holdfast assembly (see Fig. 5A).
Based on the ktube equation, the bending force constant of the stalk depends on stalk length as L−3. However, the measured force constant of the cells shows no dependence on stalk length (Fig. 5A). This finding implies that the displacement of a cell attached to a surface through a stalk and a holdfast does not arise from the bending of the stalk. Hence, we conclude that the stalk behaves much like a rigid rod, with negligible bending under thermal fluctuations, and that the fluctuations of cell body are due to deformation of the holdfast. Accordingly, the variation in the force constants reflects a variation in the elastic properties of individual holdfasts. Since we have shown that holdfasts have gel-like properties and vary in size, the simplest explanation for the variation in the force constants of holdfasts is that this variation is correlated to the size of the holdfasts.
Elasticity of the holdfast.
It is hard to distinguish between contributions to the force constant by the deformation of the holdfast material, the deformation of the contact between the holdfast and the stalk end, and the deformation of the contact between the substrate and the holdfast. Since the holdfast is involved in all three cases, one can simply treat it as a whole and calculate an apparent torsional constant. Such a constant is calculated for the 10 measured cells (shown in Fig. 5B) corresponding to those cells whose overall force constants are shown in Fig. 5A, based on the assumption that the stalk is a rigid rod compared to the holdfast. The large error in the torsional constant is partially due to the error in determining the distance from the holdfast to the cell center. The values are highly scattered, varying from 1.2 × 10−18 to 54 × 10−18 Nm/rad. Such a broad range may be due to the differences in the holdfast size as explained above. The torsional constant is expected to be sensitive to the shape and size of the holdfast, based on the general property of elastic materials. The broad range of the torsional constants may also be due to structural heterogeneity within the holdfasts, their contact to the stalk end, or their adhesion strength to the solid surface. Since the holdfast behaves like a gel composed largely of polysaccharides, a variation in gel density could also cause a difference in the torsional constant. A parameter more descriptive of the elastic property of the holdfast would be its elastic modulus, a material property that would not depend on the size or shape of the holdfast. Unfortunately, such a parameter could not be determined in our fluctuation imaging experiments since the dimensions of the holdfasts are too small to be precisely measured by phase contrast microscopy.
Little is known about the structure of the holdfast and the contacts of the holdfast to the stalk and the solid surface. The heights of wet and dried holdfast materials measured by AFM (Fig. 7) show that the macromolecular component of a wet holdfast, a majority of which may be polysaccharides, is quite high. Polysaccharides are adhesive materials that have strong nonspecific interaction with a solid substrate as well as strong adhesive force between molecules within the material (6, 32). The dense polysaccharide structure is expected to form a dense gel, which explains the elasticity of the holdfast. When bonds within polysaccharides are broken (for example, when the oligomers of GlcNAc are cleaved by lysozyme), the gel becomes weaker and the elasticity of the holdfast decreases. This result suggests that the GlcNAc polysaccharide plays an important role in the strength of the holdfast.
More information on the interaction between the stalks and the holdfast in a rosette was obtained from the correlation analysis of the cells (Fig. 9, 10, and 11). A model for a two-cell rosette is shown in Fig. 3B. From the high correlation of motions between cells in a rosette, the elastic nature of the holdfast can be inferred. However, fluctuations of the relative angle between the two stalks suggest that they each have an independent component of motion as well. A direct interpretation of the fluctuations is the deformation of the contact between the holdfast and the stalk end. The observed torsional constant for each cell can be considered an in-series assembly of the torsional constant of the stalk and that of the attachment to the solid surface (similar to springs attached to each other end to end). Thus, the detected torsional constants for the left and right cells are, respectively, Γleft = ΓLΓhf/(ΓL + Γhf) and Γright = ΓRΓhf/(ΓR + Γhf), where ΓL and ΓR are the torsional constants of the contact between the holdfast and the left cell stalk and that between the holdfast and the right cell stalk. Γhf is the torsional constant of the holdfast material attached to a solid surface, including the contribution from the contact between the holdfast and the substrate surface, which is assumed to be equal for the left and the right cells. If the strength of the contact between the holdfast and each stalk is much stronger than the elasticity of the holdfast itself—that is, if Γhf ≪ ΓL and Γhf ≪ ΓR—then there will be a higher correlation between motions of the two cells (Γleft ≅ Γright ≅ Γhf). An example of this case is the rosette in Fig. 10, for which the torsional constants of the left cell and the right cell are (2.0 ± 0.6) × 10−18 Nm/rad and (2.1 ± 0.4) × 10−18 Nm/rad, respectively. If contacts between the stalks and the holdfast are weaker than the elasticity of the holdfast, the torsional constant of the two cells may be very different and the correlation between their motions should be lower. Figure 9 is a case of weak stalk-holdfast contact. The torsional constants of the left and right cells are (3.0 ± 0.7) × 10−18 and (17.2 ± 2.9) × 10−18 Nm/rad, respectively. The existence of some rosettes with high correlation and some with low correlation reflects the diversity in the range of interaction strength, which also suggests that there may be some elastic fibers connecting some but not all stalks in a rosette.
In conclusion, a combined approach of optical microscopy and AFM has been employed in this study, which elucidates some important functional properties of the adherent cells of C. crescentus. The stalk of a C. crescentus can be approximated as a rigid rod. The holdfast, through which the stalk attaches to a solid substrate, can be modeled as an elastic leaf spring. Motions of cells in a rosette are correlated, consistent with the elasticity of the holdfast. Lysozyme cleaves oligomers of GlcNAc in a holdfast, reducing the force constant to less than 10% of its original value. Thus, oligomers of GlcNAc play a crucial role in the holdfast elasticity, although the polysaccharides are not completely responsible for holding the holdfast together. The fact that the holdfast is a localized structure whose sole function is likely to be in adhesion makes it easier to design experiments to investigate the mechanisms of bacterial attachment to surfaces unambiguously. Understanding the elastic properties of the holdfast may be a useful step towards understanding the same properties of extracellular matrices.
Acknowledgments
This work was supported by the National Institutes of Health grant GM61336 to J. Reilly and Y.V.B. and the National Science Foundation awards DMR 9988389 and DMR 0320676 to J.X.T. We also appreciate additional support by Indiana University and Brown University.
REFERENCES
- 1.Ausmees, N., and C. Jacobs-Wagner. 2003. Spatial and temporal control of differentiation and cell cycle progression in Caulobacter crescentus. Annu. Rev. Microbiol. 57:225-247. [DOI] [PubMed] [Google Scholar]
- 2.Brun, Y. V., and R. Janakiraman. 2000. Dimorphic life cycles of Caulobacter and stalked bacteria, p. 297-317. In Y. V. Brun and L. Shimkets (ed.), Prokaryotic development. ASM Press, Washington, D.C.
- 3.Christensen, B. E. 1989. The role of extracellular polysaccharides in biofilms. J. Biotechnol. 10:181-202. [Google Scholar]
- 4.Cole, J., G. G. Hardy, D. Bodenmiller, E. Toh, A. J. Hinz, and Y. V. Brun. 2003. The HfaB and HfaD adhesion proteins of Caulobacter crescentus are localized in the stalk. Mol. Microbiol. 49:1671-1683. [DOI] [PubMed] [Google Scholar]
- 5.Donlan, R. M. 2002. Biofilms: microbial life on surfaces. Emerg. Infect. Dis. 8:881-889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Frank, B. P., and G. Belfort. 1997. Intermolecular forces between extracellular polysaccharides measured using the atomic force microscopy. Langmuir 13:6234-6240. [Google Scholar]
- 7.Gonin, M., E. M. Quardokus, D. O'Donnol, J. Maddock, and Y. V. Brun. 2000. Regulation of stalk elongation by phosphate in Caulobacter crescentus. J. Bacteriol. 182:337-347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Grandbois, M., M. Beyer, M. Rief, H. Clausen-Schaumann, and H. E. Gaub. 1999. How strong is a covalent bond? Science 283:1727-1730. [DOI] [PubMed] [Google Scholar]
- 9.Howard, J. 2001. Mechanics of motor proteins and the cytoskeleton. Sinauer Associates, Inc., Sunderland, Mass.
- 10.Huang, K. 1987. Statistical mechanics, 2nd ed. Wiley, New York, N.Y.
- 11.Janakiraman, R. S., and Y. V. Brun. 1999. Cell cycle control of a holdfast attachment gene in Caulobacter crescentus. J. Bacteriol. 181:1118-1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jones, H. C., and J. M. Schmidt. 1973. Ultrastructural study of crossbands occurring in the stalks of Caulobacter crescentus. J. Bacteriol. 116:466-470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kurtz, H. D., Jr., and J. Smit. 1992. Analysis of a Caulobacter crescentus gene cluster involved in attachment of the holdfast to the cell. J. Bacteriol. 174:687-694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kurtz, H. D., Jr., and J. Smith [sic]. 1994. The Caulobacter crescentus holdfast: identification of holdfast attachment complex genes. FEMS Microbiol. Lett. 116:175-182. (Erratum, 119:395.) [DOI] [PubMed] [Google Scholar]
- 15.Leriche, V., P. Sibille, and B. Carpentier. 2000. Use of an enzyme-linked lectinsorbent assay to monitor the shift in polysaccharide composition in bacterial biofilms. Appl. Environ. Microbiol. 66:1851-1856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li, H., M. Rief, F. Osterhelt, and H. E. Gaub. 1998. Single-molecule force spectroscopy on xanthan by AFM. Adv. Mater. 3:316-319. [Google Scholar]
- 17.Maddock, J., M. Alley, and L. Shapiro. 1994. Polarized cells, polar actions. J. Bacteriol. 175:7125-7129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Marshall, K. C. 1985. Mechanisms of bacterial adhesion at solid-water interface, p. 133-161. In D. C. Savage and M. M. Fletcher (ed.), Bacterial adhesion: mechanism and physiological significance. Plenum Press, New York, N.Y.
- 19.Meiners, J.-C., and S. R. Quake. 1999. Direct measurement of hydrodynamic cross correlations between two particles in an external potential. Phys. Rev. Lett. 82:2211-2214. [Google Scholar]
- 20.Mendelson, N. H., J. E. Sarlls, C. W. Wolgemuth, and R. E. Goldstein. 2000. Chiral self-propulsion of growing bacterial macrofibers on a solid surface. Phys. Rev. Lett. 84:1627-1630. [DOI] [PubMed] [Google Scholar]
- 21.Merker, R. I., and J. Smit. 1988. Characterization of the adhesive holdfast of marine and freshwater caulobacters. Appl. Environ. Microbiol. 54:2078-2085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ong, C. J., M. L. Y. Wong, and J. Smit. 1990. Attachment of the adhesive holdfast organelle to the cellular stalk of Caulobacter crescentus. J. Bacteriol. 172:1448-1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Poindexter, J. L. S., and G. Cohen-Bazire. 1964. The fine structure of stalked bacteria belonging to the family Caulobacteraceae. J. Cell Biol. 23:587-607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Poindexter, J. S. 1964. Biological properties and classification of the Caulobacter crescentus group. Bacteriol. Rev. 28:231-295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Poindexter, J. S. 1981. The Caulobacters: ubiquitous unusual bacteria. Microbiol. Rev. 45:123-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Poindexter, J. S. 1992. Dimorphic prosthecate bacteria: the genera Caulobacter, Asticcacaulis, Hyphomicrobium, Pedomicrobium, Hyphomonas, and Thiodendron, p. 2176-2196. In A. Balows, H. G. Trüper, M. Dworkin, W. Harder, and K.-H. Schleifer (ed.), The prokaryotes. Springer-Verlag, New York, N.Y.
- 27.Poindexter, J. S., and J. T. Staley. 1996. Caulobacter and Asticcacaulis stalk bands as Indicators of stalk age. J. Bacteriol. 178:3939-3948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Quintero, E. J., K. Busch, and R. M. Weiner. 1998. Spatial and temporal deposition of adhesive extracellular polysaccharide capsule and fimbriae by Hyphomonas strain MHS-3. Appl. Environ. Microbiol. 64:1246-1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Robb, I. D. 1984. Stereo-biochemistry and function of polymers, p. 39-49. In K. C. Marshall (ed.), Microbial adhesion and aggregation. Springer-Verlag, Berlin, Germany.
- 30.Smith, A. E., Z. Zhang, C. R. Thomas, K. E. Moxham, and A. P. J. Middelberg. 2000. The mechanical properties of Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 97:9871-9874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Smith, C. S., A. Hinz, D. Bodenmiller, D. E. Larson, and Y. V. Brun. 2003. Identification of genes required for synthesis of the adhesive holdfast in Caulobacter crescentus. J. Bacteriol. 185:1342-1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sutherland, L. W. 2001. Biofilm exopolysaccharides: a strong and sticky framework. Microbiology 147:3-9. [DOI] [PubMed] [Google Scholar]
- 33.Thwaites, J. J., and N. H. Mendelson. 1989. Mechanical properties of peptidoglycan as determined from bacterial thread. Int. J. Biol. Macromol. 11:201-206. [DOI] [PubMed] [Google Scholar]
- 34.Thwaites, J. J., and U. C. Surana. 1991. Mechanical properties of Bacillus subtilis cell walls: effect of removing residual culture medium. J. Bacteriol. 173:197-203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Umbreit, T. H., and J. L. Pate. 1978. Characterization of the holdfast region of wild-type cells and holdfast mutants of Asticcacaulis biprosthecum. Arch. Microbiol. 118:157-168. [Google Scholar]
- 36.Yao, X., M. Jericho, D. Pink, and T. Beveridge. 1999. Thickness and elasticity of gram-negative murein sacculi measured by atomic force microscopy. J. Bacteriol. 181:6865-6875. [DOI] [PMC free article] [PubMed] [Google Scholar]