Modelling lagged associations in environmental time series data: a simulation study

Abstract

This study assesses two alternative approaches for investigating linear and non-linear lagged associations in environmental time series data, comparing through simulations simple methods based on moving average summaries with more flexible distributed lag linear and non-linear models. Results indicate that the latter provide estimates with no or low bias and close-to-nominal confidence intervals, even for long-lagged associations and in the presence of strong seasonal trends. Moving average models represent a viable alternative only in the presence of relatively short lag periods, and when the lag interval is correctly specified. In contrast, the use of moving averages to roughly approximate long and complex lag patterns, or the specification of an interval different than the actual lag period, can result in substantial biases. More flexible approaches based on distributed lag linear or non-linear models provide noteworthy advantages, in particular when complex lagged associations are assumed.

Introduction

Relationships between environmental factors and various health outcomes are sometimes characterized by lag patterns,^1–4 and epidemiologists have proposed a number of modelling approaches to account for this additional complexity in defining exposure–response associations.^5–8 In particular, these methods are required in the presence of long lag periods, which have been previously reported in associations with cold temperatures,^3,9,10 and, to a lesser extent, air pollutants.^11–14 However, there is little evidence on the comparative performance of alternative models, or on their sensitivity to assumptions about the shape of the lag structure or the length of the lag interval. In addition, recent published articles, specifically evaluating the health burden of cold temperature, have contended that part of the estimated associations can be due to the confounding effect of season, if long lags are assumed.^15,16 On the other hand, no empirical or well-grounded theoretical evidence is provided in support of these statements.

Clearly, the problem of modelling such phenomena has important implications in environmental epidemiology, and more generally in biomedical research. This contribution aims to address the issue through a simulation study on the comparative performance of two alternative methods for investigating lagged associations.

Modelling lagged associations

In environmental time series studies, the outcome, commonly daily mortality or morbidity counts, is usually compared with levels of environmental exposures in a Poisson regression allowing for overdispersion.¹⁷ This model represents the counts of outcome events y_t at day t as:

$$\text{log}\left[\text{E}\left({\text{y}}_{\text{t}}\right)\right]=\alpha +s\left(x_t,\dots ,x_{t-\ell },\dots x_{t-L}\right)+g(t)+{\displaystyle \sum _{p=1}^P{v}_p\left(z_{pt}\right)}$$ (1)

The function g(t), usually a spline whose flexibility is defined by the number of degrees of freedom per year, controls for seasonal and long-term trends. Additional potential confounders z_p showing day-to-day variability are controlled for through functions v_p. The function s describes the association with the exposure of interest x measured over the lag interval ℓ = 0, … , L, with L as maximum lag.

Two main methods have been proposed to define s(x_t,…, x_t−L).

Moving average models

A simple approach relies on averaging the exposure over the lag interval. For linear exposure-response relationships, the parameterization reduces to the moving average of lagged exposures. Adopting some liberty in the algebraic notation, here and in equations below, with the exclusion of the model coefficients, the moving average can be computed as:

$$s\left(x_t,\dots x_{t-L}\right)={\displaystyle \sum _{\ell =0}^L\frac{x_{\ell }}{L}}$$ (2)

However, the definition is not straightforward when non-linear dependencies are assumed, and modelled through an exposure-response function f(x). In this case, the moving average can be defined in two alternative forms:

$$s\left(x_t,\dots x_{t-L}\right)=f\left({\displaystyle \sum _{\ell =0}^L\frac{x_{\ell }}{L}}\right)$$ (3.1)

$$s\left(x_t,\dots x_{t-L}\right)={\displaystyle \sum _{\ell =0}^L\frac{f(x_{\ell })}{L}}$$ (3.2)

The form in Eq. (3.1) applies the function f to the moving average of x, while the form in Eq (3.2) is the moving average of the values transformed by f. The latter is defined over the whole range of the observed data. The former, although being defined in a narrower range of x, as the extreme values are averaged out, is simpler to compute and frequently applied in environmental studies.^9,15,18,19

Distributed lag linear and non-linear models

In an alternative and more advanced approach, the lag structure can be explicitly modelled through a lag-response function w(ℓ) expressed in the lag dimension ℓ, with the function s defined as:

$$s\left(x_t,\dots x_{t-L}\right)={\displaystyle \sum _{\ell =0}^L{x}_{t-\ell }w(\ell )}$$ (4)

This parameterization, applicable to describe linear lagged associations, is known as a distributed lag model (DLM), and simplifies to the moving average in Eq. 2 when w(ℓ) is a constant function. In its original development for econometric time series,²⁰ and the following application in environmental epidemiology,⁵ a polynomial function was used to specify w(ℓ). A simpler alternative is represented by an unconstrained distributed lag model, where lag-specific effects are modelled by indicators for each lag. Further developments of the framework are detailed in recent publications. Specifically, these illustrate the use of alternative functions for modelling the lag response,^21,22 the extension to non-linear exposure-response relationship,^21,22 and the generalization beyond time series data.²³ In particular, the non-linear extension to distributed lag non-linear models (DLNMs) is obtained by expressing the association through the combination of the exposure-response and lag-response functions. This combination produces a bi-dimensional exposure-lag-response function f ∙ w(x,ℓ). In this case s, termed cross-basis function, is represented as:

$$s\left(x_t,\dots x_{t-L}\right)={\displaystyle \sum _{\ell =0}^{L}f\cdot w\left(x_{t-\ell },\ell \right)}$$ (5)

Distributed lag non-linear models simplifies to the linear counterpart in Eq. 4 when f(x) is assumed linear, and to the second moving average form defined in Eq. (3.2) when the lag-response function w(ℓ) is a constant term. In this contribution, I will refer generally to distributed lag models, pointing out if linear or non-linear when required. These models have been recently applied to study health effects of environmental factors.^{12–14,24,25}

Simulation settings

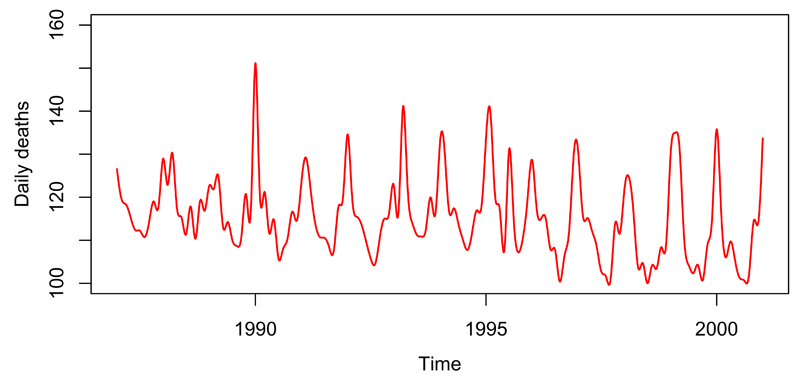
These alternative methods were comparatively assessed by simulating associations between air pollution and temperature with all-cause mortality, using real daily time series data from Chicago in the period 1987-2000.²⁶ The data represent aggregated series and are publicly available, and therefore no ethical review was required. The simulated exposures were derived as the ozone series, standardized over the range 0 to 50 part per billion (ppb), and the temperature series, standardized over the range -20°C to 35°C. The baseline mortality was obtained as the predicted curve from the regression model fitting a natural cubic spline of time with 10 df/year to the real mortality series, thus simulating the complex seasonal trend represented in Figure 1.

Figure 1.

Baseline mortality trend as death counts showing the complex seasonal and long-term patterns simulated using real daily time series from London in the period 1993-2006.

The excess risk associated with the exposures was defined by scenarios of linear ozone-mortality and non-linear temperature-mortality dependencies, assuming either short or long-lagged associations. Specifically, the following scenarios were generated:

1. Linear short-lag scenario (Scenario 1): ozone is associated linearly with mortality over a short lag period, limited to 0-3 days.

2. Linear long-lag scenario (Scenario 2): ozone is associated linearly with mortality at longer lags, with the excess risk smoothly decreasing over the following 20 days.

3. Non-linear short-lag scenario (Scenario 3): both hot and cold temperatures are associated non-linearly with mortality over a short lag period, limited to 0-3 days.

4. Non-linear long-lag scenario (Scenario 4): temperature shows a non-linear relationship, with hot temperatures associated only with short lags as in Scenario 3, and cold temperatures associated at longer lags, extended for up to 20 days with a peak at lag 4.

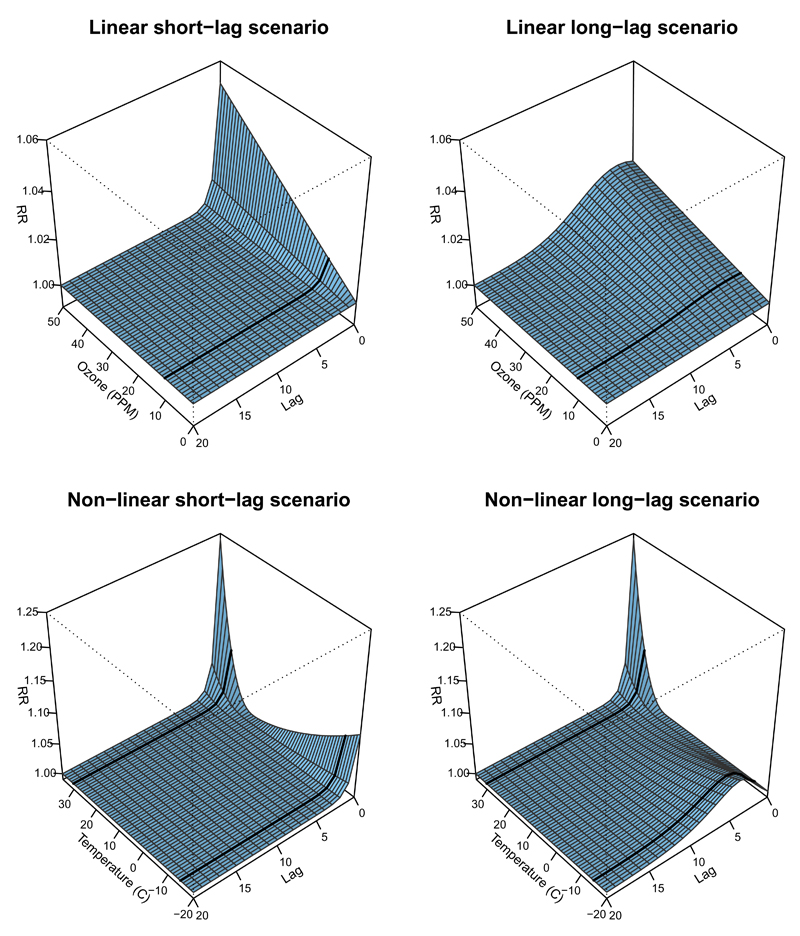
The four simulated exposure–lag–response surfaces, compatible with estimates previously reported in the literature,^{12,14,24,25,27} are illustrated in Figure 2. The mortality series in each replicate was simulated assuming a Poisson distribution with expectation equal to the baseline counts multiplied by the excess due to the risk of the exposure cumulated over the lag period. Technical details are provided in eAppendix 1 (Supplemental Digital Content).

Figure 2.

Simulated exposure-lag-response surfaces as relative risk (RR) in four scenarios describing the linear association between ozone and mortality and the non-linear association between temperature and mortality, each characterized by short and long-lag patterns. The bold lines represent lag-response relationships at 10 ppb of ozone and at -15°C and 30°C of temperature.

Performance and inferential properties of the two approaches were compared by fitting regressions with the same splines of time used when simulating the data, and the following models for the associations with the exposures:

• Three moving average models, computed using the forms in Eq. 2 (in Scenarios 1 and 2) and in Eq. (3.2) (in Scenarios 3 and 4), with lag periods of 0-3, 0-7, and 0-20, respectively.

• A distributed lag linear (in Scenarios 1 and 2) and non-linear (in Scenarios 3 and 4) model with the lag-response function w(ℓ) specified by a natural cubic spline with 3 knots equally spaced in the log scale, plus intercept, over lag 0-20.

The non-linear exposure-response function f(x) for both the moving average models and the distributed lag non-linear model in Scenarios 3 and 4 was specified by a quadratic B-spline with 3 knots at the 10^th, 75^th and 90^th percentiles of temperature distribution. These choices follow models applied in previous work.²⁴

A set of sensitivity analyses was carried out to test the impact of alternative specifications of the function w(ℓ) in distributed lag models (with details provided below), and differences between moving average models adopting the two forms of moving average in Eq. (3). In addition, the impact of overdispersion was assessed by simulating data from a negative binomial distribution with overdispersion parameter 𝜙 = 1.3.

The simulation results are based on 5000 replicates, and are summarized in terms of bias (difference between the true simulated log-relative risk [log-RR] and average of its estimates across the replicates), coverage (percentage of times the confidence interval of the estimates includes the true log-RR) and root mean square error (RMSE, average across replicates of the squared difference between the true simulated and estimated log-RR). The latter can be interpreted as the sum of the bias and the imprecision of the estimator. These statistics are reported as the average across the curve representing the exposure–response association cumulated over the lag period. An algebraic definition is provided in eAppendix 2 (Supplemental Digital Content).

The R scripts illustrating a simple example of simulation of the data and fit of the models, and then fully reproducing the results, are available at www.ag-myresearch.com.

Results

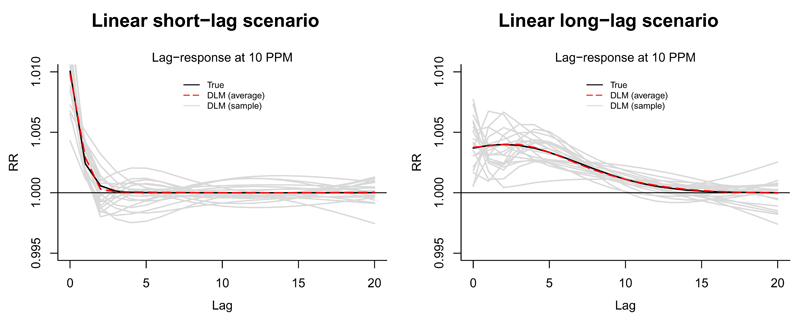
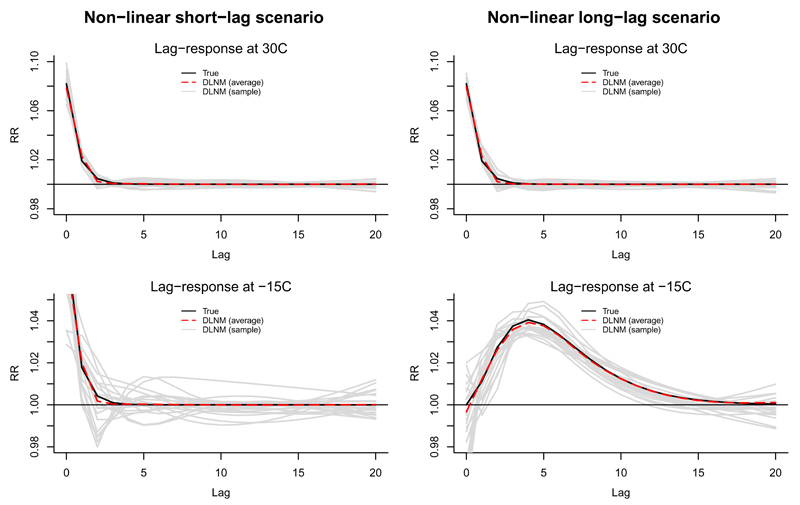
Figure 3 and Figure 4 demonstrate the good performance of the distributed lag models in recovering the lag-response curves corresponding to 10 ppb of ozone and -15°C and 30°C of temperature, respectively, simulated in the four scenarios and also represented as bold black lines in Figure 2. These findings are confirmed by Figure 5, which reports the average estimates of the overall cumulative exposure–response relationships. The graphs suggest that distributed lag models provide nearly unbiased estimates of the associations.

Figure 3.

Lag-response relationships as relative risk (RR)at 10 ppb of ozone in the linear short-lag (left column) and linear long-lag (right column) scenarios, estimated by the distributed lag model (DLM). The curves represent the real simulated relationship (continuous black lines), the average of the estimated relationship across 5000 replicates (dashed red lines), and a sample of the estimated relationship in 20 replicates (continuous grey lines), respectively.

Figure 4.

Lag-response relationships as relative risk (RR)at 30°C (top row) and -15°C (bottom row) in the non-linear short-lag (left column) and non-linear long-lag (right column) scenarios, estimated by the distributed lag non-linear model (DLNM). The curves represent the real simulated relationship (continuous black lines), the average of the estimated relationship across 5000 replicates (dashed red lines), and a sample of the estimated relationship in 20 replicates (continuous grey lines), respectively.

Figure 5.

Overall cumulative exposure-response relationships as relative risk (RR)estimated by the distributed lag (DL) models and two moving average models with lag 0-3 and 0-20 (MA0-3 and MA0-20). The graphs represent the linear association with ozone (top panels) and the non-linear association with temperature (bottom panels) in the short-lag (left panels) and long-lag (right panels) scenarios. The slopes represent the real simulated relationship (continuous black lines) and the average of the estimated relationship across 5000 replicates (dashed lines, with different colours and patterns depending on the model).

The panels of Figure 5 report also comparable estimates for moving average models with lag periods 0-3 and 0-20. The results suggest that the lag 0-3 model shows little bias in compatible short-lag scenarios (left panels), but, as expected, it considerably under estimates the excess risk when long lagged associations occur, namely with ozone in the top-right panel and with cold temperature in the bottom-right panel of Figure 5. The reverse occurs to the lag 0-20 model, with the left panels of Figures 5 indicating a strong downward bias in moving average models when the lag interval is extended further than the simulated lag period. Interestingly, in the non-linear long-lag scenario, moving average models show biases even when the lag period is correctly specified. The moving average model with lag 0-7 shows an intermediate behaviour, as illustrated in eFigure 1. Results in eFigure 2 indicate that the two forms of moving average defined in Eq. (2.1)-(2.2) provide almost identical estimates, although the latter is defined over the whole exposure range. The bias generated by the strong assumptions of moving average models about the shape of the exposure–lag–response risk surface, compared to the flexibility of distributed lag models, are illustrated in eFigure 3.

Table 1 complements the illustration of the findings, comparing the inferential performance of the four models. Distributed lag models show the lowest bias and nominal coverage in both scenarios. In terms of root mean square error, the higher precision favours the moving average model with lag 0-3 in the short-lag scenario, but this is counterbalanced in the long-lag scenario by the bias previously discussed. The extension of the lag interval of the moving average to 0-20 shows no improvement, as this model provides less precise estimates without eliminating the bias. All moving average models are also affected to some extent by under coverage, which is very pronounced in scenarios with non-linear relationships.

Table 1.

Bias, coverage of 95% confidence intervals and root mean square error (RMSE), reported for the distributed lag linear (DLM) and non-linear (DLNM) model and for moving average (MA) models with different lag intervals (0-3, 0-7, and 0-20), in four alternative simulated scenarios. An algebraic definition of bias, coverage and RMSE is provided in eAppendix 2 (Supplemental Digital Content).

Model	Linear short-lag scenario			Linear long-lag scenario
	Bias (x100)	coverage	RMSE (x100)	Bias (x100)	coverage	RMSE (x100)
DLM	0.03	0.95	2.81	0.05	0.95	2.77
MA0-3	0.22	0.94	0.99	4.92	0.00	5.00
MA0-7	0.49	0.94	1.44	1.87	0.70	2.28
MA0-20	1.16	0.94	3.02	0.10	0.95	2.75
	Non-linear short-lag scenario			Non-linear long-lag scenario
	Bias (x100)	coverage	RMSE (x100)	Bias (x100)	coverage	RMSE (x100)
DLNM	0.43	0.94	3.42	0.62	0.94	3.38
MA0-3	0.76	0.89	1.47	7.33	0.27	7.54
MA0-7	1.68	0.84	2.38	3.34	0.50	3.73
MA0-20	3.06	0.84	4.55	1.95	0.89	3.89

Results of the sensitivity analysis are summarized in Table 2, and can be compared with the main results reported in Table 1. The simplification of the function w(ℓ) of distributed lag models in short-lag scenarios, either by using an unconstrained parameterization over lag 0-3 or by reducing the number of knots to 2 over the lag period 0-7, substantially increase the precision of the estimates, with root mean square error comparable with the moving average lag 0-3 models (Analyses 1-4). The different specification of w(ℓ) in long-lag scenarios, using two or four knots, does not seem to affect the estimates (Analyses 5-6). The presence of overdispersion, if modelled through a quasi-Poisson family, slightly decrease precision but does not introduce biases in distributed lag models (Analysis 7). Results of the sensitivity analyses are reported graphically in eFigure 4.

Table 2.

Bias, coverage of 95% confidence intervals and root mean square error (RMSE), reported for distributed lag linear (DLM) and non-linear (DLNM) models, in sensitivity analyses using different model specifications in various scenarios. Modelling choices are those defined in the main simulation analysis, with reported changes.

	Scenario	Model	Bias (x100)	coverage	RMSE (x100)
Analysis 1	Linear short-lag	Unconstrained DLM, lag 0-3	0.01	0.95	0.98
Analysis 2	Linear short-lag	DLM, w(ℓ) with 2 knots over lag 0-7	0.00	0.95	1.37
Analysis 3	Non-linear short-lag	Unconstrained DLNM, lag 0-3	0.41	0.92	1.34
Analysis 4	Non-linear short-lag	DLNM, w(ℓ) with 2 knots over lag 0-7	0.42	0.94	1.76
Analysis 5	Non-linear long-lag	DLNM, w(ℓ) with 2 knots	0.99	0.94	3.44
Analysis 6	Non-linear long-lag	DLNM, w(ℓ) with 4 knots	0.59	0.94	3.38
Analysis 7	Non-linear long-lag, with overdispersiona	DLNM with quasi-Poisson family	0.62	0.94	3.85

^aSimulated using a negative binomial distribution with overdispersion parameter 𝜙 = 1.3

Discussion

This simulation study compares alternative approaches to model epidemiologic associations characterized by lag patterns. Results indicate that standard methods based on moving average models can introduce important biases, in particular in the presence of extended lag periods. In contrast, more flexible methods based on distributed lag models appropriately account for lagged dependencies, with no or minimal bias in point estimates and confidence intervals.

The framework of distributed lag models has the advantage of offering a direct representation of the lag structure, through lag-response relationships estimated by the data. This extra dimension provides additional information on the phenomenon under study. Results in Figures 3–5 and Table 1 demonstrate that these models can correctly retrieve the underlying association, summarized as overall cumulative (net) risk or as lag-specific contributions, even when the lag interval is extended well beyond the true lag period. Simpler methods based on moving average models represent a viable alternative only in the presence of relatively short lag periods and when the lag interval is correctly specified. Conversely, the application of moving average models to roughly approximate long and complex lag patterns, or the extension of the moving average beyond the actual lag interval, can result in substantial biases, in particular when modelling non-linear relationships.

The inflexible specification of the lag structure is the main reason why moving average models are outperformed by distributed lag models. As mentioned above, the former can be interpreted as special cases of the latter in which the lag-response function w(ℓ) is defined as a constant. This definition implies the strong assumption that all the exposures experienced within the lag interval equally contribute to the overall cumulative excess risk, as demonstrated in eFigure 3 (Supplemental Digital Content). In contrast, flexible specifications within the distributed lag modelling framework allow more realistic lag structures, when for instance more recent exposures are associated with higher lag-specific excess risks if compared to more lagged exposures.

In the simple scenario describing a situation in which the lag interval is short and correctly specified, moving average models benefit from a higher precision in the estimates, which can avoid artifactual interpretation of the results. However, it should be noted that alternative and more efficient specifications of the lag-response function w(ℓ), obtained for instance by reducing the lag interval and/or by selecting simpler functions, are available within the distributed lag modelling framework. These alternative choices for the lag-response function, illustrated in the sensitivity analysis, improve the performance of the distributed models in simpler scenarios by increasing the precision, without introducing biases in point estimates and confidence intervals. It should be acknowledged, however, that the flexibility of the distributed framework presents the additional complexity of selecting bi-dimensional exposure–lag–response functions, if compared to unidimensional moving average models. The choice can be based on evidence from previous studies, as in the examples above, or on existing selection methods (such as the Akaike information criterion) proposed in methodologic publications.^22,23 Furthermore, model selection in distributed lag models is an issue of current research, and future developments are likely to provide improved selection criteria.

An important result of this simulation study is the provision of empirical evidence that the flexible modelling of the lag dimension is not affected by the presence of complex seasonal trends. These findings contradict claims, recently suggested in the literature,^15,16 that increased mortality risks attributed to lagged associations with cold temperature are partly due to confounding effects by season. This simulation study demonstrates that complex exposure–lag–response associations can be effectively disentangled from strong seasonal trends.

In conclusion, this study provides some guidance on the use of alternative methods to model lagged associations, identifying limitations of standard approaches and advantages of recent and more flexible methods.

Supplementary Material

Supplemental Digital Content. Additional information on the simulation of the four exposure-lag-response risk surfaces (eAppendix 1) and on the definition of bias, coverage and root mean square error (RMSE) (eAppendix 2), and additional graphs. pdf