Pharmacodynamic Modeling of Ciprofloxacin Resistance in Staphylococcus aureus

Jeffrey J Campion; Patrick J McNamara; Martin E Evans

doi:10.1128/AAC.49.1.209-219.2005

. 2005 Jan;49(1):209–219. doi: 10.1128/AAC.49.1.209-219.2005

Pharmacodynamic Modeling of Ciprofloxacin Resistance in Staphylococcus aureus

Jeffrey J Campion ¹, Patrick J McNamara ², Martin E Evans ^1,^*

PMCID: PMC538881 PMID: 15616298

Abstract

Three pharmacodynamic models of increasing complexity, designed for two subpopulations of bacteria with different susceptibilities, were developed to describe and predict the evolution of resistance to ciprofloxacin in Staphylococcus aureus by using pharmacokinetic, viable count, subpopulation, and resistance mechanism data obtained from in vitro system experiments. A two-population model with unique growth and killing rate constants for the ciprofloxacin-susceptible and -resistant subpopulations best described the initial killing and subsequent regrowth patterns observed. The model correctly described the enrichment of subpopulations with low-level resistance in the parent cultures but did not identify a relationship between the time ciprofloxacin concentrations were in the mutant selection window (the interval between the MIC and the mutant prevention concentration) and the enrichment of these subpopulations. The model confirmed the importance of resistant variants to the emergence of resistance by successfully predicting that resistant subpopulations would not emerge when a low-density culture, with a low probability of mutants, was exposed to a clinical dosing regimen or when a high-density culture, with a higher probability of mutants, was exposed to a transient high initial concentration designed to rapidly eradicate low-level resistant grlA mutants. The model, however, did not predict or explain the origin of variants with higher levels of resistance that appeared and became the predominant subpopulation during some experiments or the persistence of susceptible bacteria in other experiments where resistance did not emerge. Continued evaluation of the present two-population pharmacodynamic model and development of alternative models is warranted.

Mathematical models that are carefully constructed by using data from in vitro and in vivo studies may provide insights into the population dynamics underlying the emergence of antimicrobial resistance. If such models accurately predict the outcome of antimicrobial therapy, they could facilitate the design of dosing regimens to prevent resistance by allowing rapid analysis of multiple dosing strategies.

A number of pharmacodynamic models have been proposed to explain the population dynamics leading to antimicrobial resistance and to predict dosing regimens that may prevent the emergence of resistance. Some were derived from those modeling the effects of chemotherapeutic agents on eukaryotic cells (19). Zhi and coworkers proposed a model that successfully predicted the effects of single and multiple doses of piperacillin on Pseudomonas aeruginosa infections in neutropenic mice (36). Others expanded this one-population model by adding mathematical terms to account for the emergence of resistance (22, 25), the maximum number of bacteria that can grow in a given environment (18, 25, 35), or the appearance of resistant mutants from susceptible bacteria by a stochastic process (23). Recently, an indirect physiological model has been proposed where the antimicrobial is assumed to stimulate the natural cell death rate (24).

In previous work, we evaluated the emergence of resistance when ciprofloxacin-susceptible Staphylococcus aureus strains were exposed to simulated ciprofloxacin regimens in an in vitro hollow-fiber system. The rate of initial killing approached a maximum, and the rate of regrowth decreased with increasing average steady-state concentration (C_{avg ss}). Regimens providing C_{avg ss} intermediate between the MIC and mutant prevention concentration (MPC) resulted in the strongest selection of low-level resistant variants in the inoculum and the subsequent appearance of high-level resistant variants, whereas regimens providing C_{avg ss} slightly above the MIC or close to the MPC exerted a weaker selective pressure. A regimen providing ciprofloxacin concentrations above the MPC for the whole dosing interval eradicated low-level resistant variants in the inoculum and prevented the emergence of bacteria with high-level resistance. These data suggested that dosing should target low-level resistant variants in the inoculum to prevent the emergence of bacteria with high-level resistance (8).

To fully characterize the relationship between pharmacokinetics and the emergence of resistance, a wide range of concentration-time profiles would need to be simulated in the in vitro system. We postulated that the utility of in vitro system studies may be enhanced if they were paired with a pharmacodynamic model. Such a model could then be used to predict the fate of susceptible and resistant bacterial subpopulations as a function of antimicrobial concentration. Promising strategies identified from model simulations could be tested in the in vitro system.

In this paper, three different pharmacodynamic models of increasing complexity were developed and evaluated by using pharmacokinetic, viable count, subpopulation, and resistance mechanism data from the in vitro system experiments described in a companion paper (8) and herein. The simplest model had equivalent growth and killing rate constants for the susceptible majority and resistant minority subpopulations. This model has been previously proposed by several investigators (25, 35, 36). The second model had unique growth and killing rate constants for each subpopulation, consistent with the concept that resistance imposes a biological cost in fitness (1). The third model had unique growth and killing rate constants for susceptible and resistant subpopulations, like the second model, but also allowed for the appearance of resistant bacteria from the susceptible subpopulation at a fixed rate. This model allowed for possible adaptation during ciprofloxacin exposure (30). We show that the two-population pharmacodynamic model with unique growth and killing rate constants for susceptible and resistant bacterial subpopulations best described and predicted the emergence of ciprofloxacin resistance in S. aureus populations exposed to different pharmacokinetic profiles.

MATERIALS AND METHODS

Data for pharmacodynamic modeling.

Models were developed by using data obtained from in vitro hollow-fiber system experiments with two ciprofloxacin-susceptible (MIC, 0.5 μg/ml) methicillin-resistant S. aureus strains (S. aureus MRSA 8043 and MRSA 8282) (8). Additional in vitro system experiments were performed to characterize the growth and killing by ciprofloxacin of the most resistant grlA mutants (MRSA 8043C0-1 [S80Y; MIC, 4 μg/ml] and MRSA 8282C0-1 [A116P; MIC, 2 μg/ml]) detected in the parent cultures. The S80Y and A116P grlA mutants were also chosen because they were the most prevalent genotypes found among the low-level resistant variants in the starting cultures and because macrodilution time-kill studies (see Appendix) suggested that more-resistant bacteria, such as the grlA/gyrA double mutants (MIC, 4 to 16 μg/ml) that appeared at the end of in vitro system experiments, would have been selected by all, rather than just some, of the simulated ciprofloxacin dosage regimens had they been present in the starting cultures.

Killing was assessed by exposing the grlA mutants to a simulated dosage regimen of 6,250 mg every 12 h for 24 h. This regimen was designed to achieve concentrations that produced near-maximal killing rates of each mutant in macrodilution time-kill studies (see Fig. A1). Determination of viable counts and avoidance of antibiotic carryover was accomplished by using techniques described previously (8).

Resistance rates.

Resistance rates (μ) for MRSA 8043 and MRSA 8282 at ciprofloxacin concentrations of 1 and 2 μg/ml were determined by fluctuation analysis. For each strain, 20 culture tubes containing ∼10² cells in Trypticase soy broth (Difco Laboratories, Detroit, Mich.) were incubated at 37°C for 24 h. Aliquots were then spread onto Mueller-Hinton agar (Difco) containing ciprofloxacin, the bacteria were incubated for 48 h, and the colonies were enumerated. Resistance rates (μ) were estimated by using the Ma-Sandri-Sarkar maximum-likelihood method (31).

Pharmacodynamic modeling.

Three different models of increasing complexity were developed to describe changes in the ciprofloxacin-susceptible majority (S) and ciprofloxacin-resistant minority (R) subpopulations over time during in vitro system experiments. Each model incorporated a logistic growth expression to characterize the competition between the S and R subpopulations for growth in the in vitro system (21). The killing of bacteria by ciprofloxacin in each model was assumed to occur according to a maximum effect (E_max) pharmacodynamic relationship, where the killing rate is a saturating function of antimicrobial concentration (14).

The simplest model was one with equivalent growth rate and ciprofloxacin killing rate constants for S and R (model 1). Changes in S and R over time were described by the following differential equations:

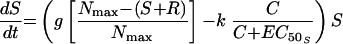(1)

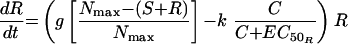(2)

where S and R are the sizes of susceptible and resistant subpopulations at time t, g is the net growth rate constant (g = b − x, where b is the rate of cell division and x is the death rate due to all causes other than the antimicrobial), N_max is the carrying capacity of the in vitro system, k is the rate constant for maximal bacterial killing, EC₅₀ is the ciprofloxacin concentration at which 50% of the maximal killing occurs, and C is the ciprofloxacin concentration at time t.

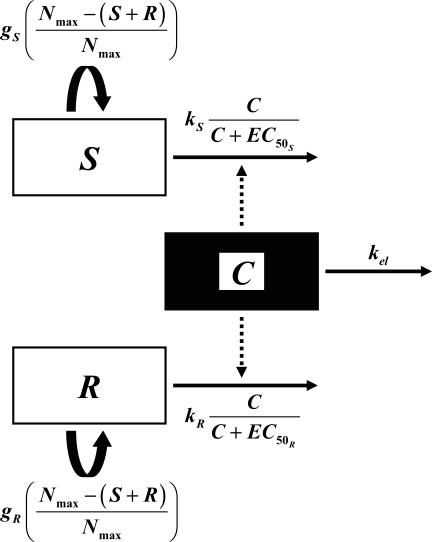
The second model had unique, rather than equal, growth rate and killing rate constants for S and R (model 2) (Fig. 1). Changes in S and R over time were described by the following equations:

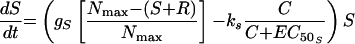(3)

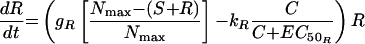(4)

The most complex model featured unique growth rate and killing rate constants for S and R as in model 2 but, in addition, allowed for the appearance of R from S at a rate μ (model 3). Changes in S and R over time were described by the following equations:

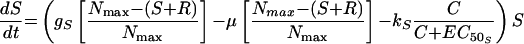(5)

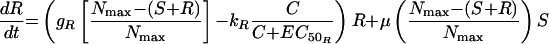(6)

The pharmacodynamic models made several simplifying assumptions. First, the growth of S and R was influenced by the total numbers of S and R in relation to N_max. Second, there was no postantibiotic effect. Third, antimicrobial concentrations were uniform throughout the peripheral compartment (i.e., there was no spatial heterogeneity in C), and finally, the rate of conversion of S←R was negligible compared to S→R.

FIG. 1. — Schematic of the two-population pharmacodynamic model with unique growth (g) and ciprofloxacin killing rate (k) constants for susceptible (S) and resistant (R) subpopulations (model 2). The legend for remaining symbols is given in Materials and Methods.

The size of the susceptible subpopulation at time zero (S₀) in all models was fixed as the actual viable count observed at the start of each in vitro system experiment. The size of the resistant subpopulation at 0 h (R₀) was included as a parameter in all models because of the difficulty in precisely quantifying the small numbers of resistant bacteria in the starting cultures by traditional microbiological techniques.

For pharmacodynamic modeling, initial estimates of g, k, EC₅₀, and N_max for the S. aureus strains were obtained by graphical analysis of in vitro system data (available from the corresponding author upon request). Estimates of R₀ were obtained from the observed frequencies of variants resistant to 1 μg of ciprofloxacin/ml in the starting cultures (8). For model 3, the initial estimates of μ used for pharmacodynamic modeling were the resistance rates for MRSA 8043 and MRSA 8282 obtained at ciprofloxacin concentrations of 1 μg/ml.

Predicted ciprofloxacin concentrations (C) from a one-compartment pharmacokinetic model were linked to the pharmacodynamic models because of the rapid equilibration of ciprofloxacin concentrations between the central and peripheral (bacterial) compartments of the hollow-fiber in vitro system (8). Predicted central compartment pharmacokinetic profiles for each ciprofloxacin dosage regimen were simulated by using mean pharmacokinetic parameter estimates obtained from nonlinear regression analysis of concentration-time profiles from all in vitro system experiments. Pharmacodynamic model parameters were fitted to measured viable counts as a function of time by using a nonlinear regression program (WinNonlin, version 4.0; Pharsight Corp., Mountain View, Calif.). Subroutines were written in which pharmacodynamic model equations were expressed as simultaneous differential equations. The differential equations were solved by integration by using the Nelder-Mead algorithm (27). The viable count data were transformed to their log₁₀ values before the fitting procedure. Each of the three candidate two-population models was simultaneously fit to viable count-time data for each parent strain and the corresponding grlA mutant. For MRSA 8043 and MRSA 8043C0-1, viable count-time data from all 16 experiments (replicate growth controls and ciprofloxacin simulations for five dosage regimens with MRSA 8043 plus the replicate growth controls and ciprofloxacin 6,250 mg every 12 h simulations with MRSA 8043C0-1) were used during the fitting process. However, for MRSA 8282 and MRSA 8282C0-1, the models were fit to viable count-time data from 15 experiments, with data from one of the ciprofloxacin 750 mg every 12 h simulations with MRSA 8282 excluded. The viable count time data from this experiment, in which no bacterial regrowth occurred, were excluded for several reasons. First, the correlation between viable counts in the replicate experiments with this simulated regimen was much lower (r = 0.588) than in all other dosage regimen simulations with either MRSA 8282 or MRSA 8043 (r ≥ 0.914). Second, the excluded data were from the only dosage regimen experiment in which low-level variants resistant to ciprofloxacin concentrations of ≥1 μg/ml were not detected in the starting population. The goodness of the model fits was evaluated by determining correlation coefficients (r), performing residual analysis, and evaluating the precision of parameter estimates (11). The runs test was used to determine whether model-fitted curves deviated systematically from observed viable count data. The pharmacodynamic model of best fit among the candidate models was discerned by the second-order Akaike Information Criterion (AIC_c) (7).

Stochastic simulations.

Simulations were also performed to predict the appearance of resistant variants from the susceptible subpopulations of MRSA 8043 and MRSA 8282 during each in vitro system experiment. Resistant bacteria were assumed to arise at a rate μ from the susceptible subpopulation. The expected number of resistant variants (R) that appeared from the susceptible subpopulation was given by the following equation:

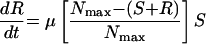(7)

where S is the size of the susceptible subpopulation at time t according to equation 5. Parameter estimates from the model of best fit and μ from the fluctuation analyses (see resistance rates above) were used in equations 5 and 7. Mathematical simulations were performed with a numerical integration program (Stella, version 8.0; High Performance Systems, Inc., Hanover, N.H.) to determine the expected number of variants resistant to ciprofloxacin at 1 and 2 μg/ml in MRSA 8043 and MRSA 8282 populations at the start of each in vitro system experiment. During ciprofloxacin exposure, the appearance of R from S over 96 h or until S subpopulations became extinct (i.e., the population fell below 1 CFU), whichever occurred first, was also estimated.

The appearance of resistant variants was assumed to follow a Poisson distribution, so the probability of appearance of at least one resistant variant [P (R ≥ 1)] from the susceptible subpopulation was given by the following equation:

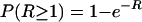(8)

Pharmacodynamic model predictive performance.

Predictions of the pharmacodynamic model of best fit were tested in the in vitro system in duplicate. The methods for pharmacokinetic, pharmacodynamic, resistant subpopulation, and nucleotide sequence analysis were the same as those reported previously (8).

RESULTS

In vitro system experiments.

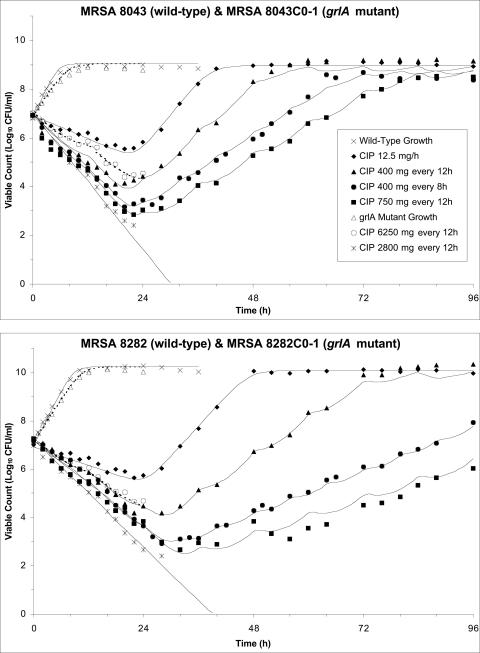
The net growth rate of MRSA 8043C0-1 and MRSA 8282C0-1 was less than that of the corresponding parent strains (Fig. 2). The net killing rate of the grlA mutants was less than that of the parent strains even though the ciprofloxacin exposure was higher (area under the concentration-time curve from 0 to 24 h [AUC_0-24]/MIC of the 6,250 mg every 12 h regimen ranged from 139 to 277 h; AUC_0-24/MIC of the 750 and 2,800 mg every 12 h regimens ranged from 73.2 to 113 h) (8).

Resistance rates.

Resistance rate (μ) estimates (mutations/cell/generation) at ciprofloxacin concentrations of 1 and 2 μg/ml were 9.1 × 10⁻⁹ and 1.3 × 10⁻¹⁰ for MRSA 8043 and 5.3 × 10⁻⁹ and 5.2 × 10⁻¹¹ for MRSA 8282, respectively.

Pharmacodynamic modeling.

All three candidate models described the patterns of bacterial killing and growth observed during in vitro system experiments. The correlation (r) between model-predicted and observed viable counts ranged from 0.976 to 0.997 for MRSA 8043/8043C0-1 and from 0.933 to 0.999 for MRSA 8282/8282C0-1 in all three models. Observed viable counts were randomly scattered about the fitted curves of each model with two exceptions (the replicate experiments with 400 mg of ciprofloxacin every 12 h with MRSA 8043 and 400 mg of ciprofloxacin every 8 h with MRSA 8282). In these instances, there was a systematic deviation (P < 0.05, runs test) in observed viable counts above or below the fitted killing and regrowth curves with each model. This deviation may have been due to differences in the initial size of the susceptible and resistant subpopulations in replicate experiments. Comparison of the three models by using AIC_c showed that model 2 was best (Table 1).

TABLE 1.

Selection statistics for pharmacodynamic models (7)^a

Strain	Model no.	K	log(L)	AIC_c	Δ_i	W_i
MRSA 8043	1	6	−561.04	1,134.34	18.89	0.00
	2	8	−549.51	1,115.45	0.00	0.81
	3	9	−549.88	1,118.30	2.84	0.19
MRSA 8282	1	6	−582.20	1,176.67	20.16	0.00
	2	8	−570.02	1,156.51	0.00	0.84
	3	9	−570.63	1,159.85	3.34	0.16

Open in a new tab

K, number of estimated parameters in the model; log(L), maximized log-likelihood function; AIC_c = second-order Akaike selection criterion; Δ_i = simple AIC_c differences; W_i = Akaike weights for models in the set.

Model 1 had significant bias (P < 0.05, runs test) in model-predicted versus observed viable counts, with the model underpredicting the growth rate of MRSA 8043 and MRSA 8282 and overpredicting the killing rate of MRSA 8043C0-1 and MRSA 8282C0-1 by ciprofloxacin during the 6,250 mg every 12 h experiments. Model 2 had the least bias and most precise parameter estimates among the evaluated models (Table 2). For both strains, the coefficient of variation (CV) of all parameter estimates, except R₀, was ≤11.2%. Estimates of R₀ were less precise (CV of 28.0% for MRSA 8043/8043C0-1 and 35.5% for MRSA 8282/8282C0-1). There was a strong positive correlation between g_S and k_S for both MRSA 8043 (r = 0.989) and MRSA 8282 (r = 0.994). The high interdependence of g_S and k_S estimates from the initial killing phase was anticipated, since the model was fit to viable count data that reflected the net result of growth and killing. All other model parameters, including g_R and k_R, were less strongly correlated (r = −0.836 to 0.675). The univariate 95% confidence intervals for g, k, and EC₅₀ estimates for S and R did not coincide. However, the planar 95% confidence intervals of g and k, but not of EC₅₀, for S and R, which take into account the correlation among parameters, overlapped slightly. Model 2 correctly characterized the trends in bacterial killing and growth observed during in vitro system experiments (Fig. 2). Model 3 resulted in some parameter estimates that were as precise as those of model 2 (CV of ≤10.7% for g_S, k_S, EC₅₀_S, g_R, k_R, EC_50R, and N_max), but other estimates that were less precise (CV of up to 43,910% for R₀ and μ).

TABLE 2.

Parameter estimates for the two-population pharmacodynamic model (model 2)^a

Strain	g_S (h⁻¹)	g_R (h⁻¹)	k_S (h⁻¹)	k_R (h⁻¹)	EC_50S (μg/ml)	EC_50R (μg/ml)	R₀ (CFU/ml)	N_max (CFU/ml)
MRSA 8043	0.99 (0.09)	0.66 (0.02)	1.56 (0.09)	1.17 (0.02)	0.21 (0.02)	5.19 (0.27)	1.06 (0.30)	1.10 × 10⁹ (0.08 × 10⁹)
MRSA 8282	0.93 (0.07)	0.70 (0.02)	1.39 (0.07)	1.10 (0.02)	0.18 (0.02)	2.72 (0.15)	1.24 (0.44)	1.70 × 10¹⁰ (0.20 × 10¹⁰)

Open in a new tab

Results are means with standard errors in parentheses.

Pharmacodynamic model predictions.

Predictions of the model of best fit (model 2) for the growth of parent strains and their corresponding grlA mutants were in concordance with viable counts observed during growth control experiments (Fig. 2). The model predicted that, in the absence of ciprofloxacin, S would grow exponentially until the carrying capacity of the in vitro system was reached. As this occurred, the competing R subpopulation of each strain would also plateau but at values that were ∼7 to 8 log₁₀ lower than the carrying capacity. In contrast, the model predicted that R grown in the absence of S would reach the carrying capacity of the in vitro system.

The model suggested that S would be eradicated (i.e., decline to <1 CFU) during all ciprofloxacin regimen simulations, with the time required for extinction decreasing as the intensity of ciprofloxacin exposure increased. The model indicated that 51 h (MRSA 8043) to 63 h (MRSA 8282) would be required to extinguish S exposed to the low ciprofloxacin concentration produced by the continuous infusion simulation (0.63 μg/ml) but only 36 h (MRSA 8043) to 46 h (MRSA 8282) would be necessary to eradicate S exposed to higher concentrations attained with 2,800 mg every 12 h (C_{avg ss}, 12.1 μg/ml).

The model also correctly predicted that there would be a net growth of R with all ciprofloxacin regimens except 2,800 mg every 12 h and that the net growth of R would decrease at increasing ciprofloxacin exposures, as evidenced by flattening of the regrowth curves from 24 to 96 h.

The model predicted that enrichment of R relative to S would occur at 24 h with all in vitro system experiments except the 2,800 mg every 12 h dosage regimen. It suggested that R would constitute 63.9 to 87.6% of the total MRSA 8043 population at 24 h with regimens providing C_{avg ss} of 0.63 to 3.30 μg/ml but only 1.9 to 42.3% of the total MRSA 8282 population for the same ciprofloxacin exposures. For all dosage regimen simulations except 2,800 mg every 12 h with both strains, the model predicted that R subpopulations would constitute the entire population at 96 h.

The model did not identify a relationship between the time (T_MSW) ciprofloxacin concentrations were in the mutant selection window (MSW, the interval between the MIC and the MPC) and the enrichment of R. Constant and fluctuating pharmacokinetic profiles that failed to eradicate R and that produced concentrations entirely outside (T_MSW = 0%) or within (0% < T_MSW ≤ 100%) the window for variable periods of time were predicted to result in selection of R.

Predictions from stochastic simulations.

The stochastic equations predicted that the probability of variants resistant to 1 μg of ciprofloxacin/ml in the starting populations would range from 78.0 to 92.6% for MRSA 8043 and from 78.1 to 96.7% for MRSA 8282. The probability of variants resistant to 2 μg of ciprofloxacin/ml would range from 2.0 to 6.0% for MRSA 8043 and from 2.6 to 9.0% for MRSA 8282. These predictions are consistent with results from the 24 in vitro system experiments where resistant variants were recovered on agar containing 1 μg of ciprofloxacin/ml in 91.7% of experiments and on agar containing 2 μg of ciprofloxacin/ml in 12.5% of experiments (8).

Pharmacodynamic model predictive performance.

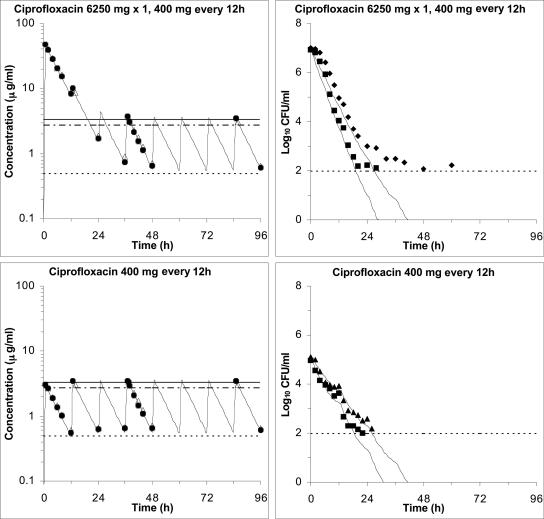
We postulated that eradication of resistant variants of MRSA 8043 and MRSA 8282 likely to be present in starting cultures of ∼10⁷ CFU/ml (see stochastic predictions above) may prevent the subsequent emergence of bacteria with higher levels of resistance. Pharmacodynamic parameter estimates (Table 2) from model 2 were used to design an experimental regimen that would eradicate low-level resistant variants in the starting populations. This regimen was tested in the in vitro system and consisted of a single high ciprofloxacin dose (6,250 mg) to eradicate R followed, 12 h later, by a standard dose at conventional intervals (400 mg every 12 h) to eliminate the remaining S bacteria (Fig. 3, top left panel). The regimen produced first dose C_max/MIC ratios for MRSA 8043 and MRSA 8282 of 86.3 and 82.7 and AUC_0-24/MIC ratios of 659 and 652 h, respectively. The corresponding first dose C_max/MPC ratios for MRSA 8043 and MRSA 8282 were 13.0 and 14.7, and the AUC_0-24/MPC ratios were 99.3 and 116 h, respectively. Ciprofloxacin concentrations were above the MPC 99.7% of the time (T_MSW ≤ 0.3%) during the first 24 h of the experiments. The C_max/MIC (MPC) and AUC₂₄/MIC (MPC) indices decreased and the T_MSW increased as concentrations obtained with the initial high dose declined. The subsequent simulated dose of 400 mg given every 12 h provided steady-state C_max/MIC and AUC₂₄/MIC ratios of 7.16 and 6.80 and 86.8 and 88.4 h for MRSA 8043 and MRSA 8282, respectively. The T_MSW was 95.3 and 87.2% for MRSA 8043 and MRSA 8282, respectively, during the last 60 h of the experiments.

FIG. 3. — Validation of pharmacodynamic model predictions in the in vitro system. Ciprofloxacin concentrations (left panels) and MRSA 8043 and MRSA 8282 viable count profiles (right panels) for an experimental ciprofloxacin dosage regimen (single 6,250-mg dose followed by 400 mg every 12 h) designed to prevent the emergence of resistant subpopulations likely to be present in a culture of 10⁷ CFU/ml (top) and for a conventional ciprofloxacin dosage regimen of 400 mg every 12 h with a culture of 10⁵ CFU/ml not likely to contain resistant subpopulations (bottom). The concentration-time panels show measured central (closed symbols) and peripheral (open symbols) compartment concentrations, predicted central compartment pharmacokinetic profiles (lines) from the one-compartment pharmacokinetic model, and MICs (dotted line) and MPCs for MRSA 8043 (solid line) and MRSA 8282 (dash-dotted line). The viable count-time panels show pharmacodynamic model-predicted (curves) and observed (symbols) viable counts for MRSA 8043 (squares) and MRSA 8282 (diamonds). The reliable limit of detection in the experiments was 100 CFU/ml.

The detection of resistant variants in the starting cultures of these experiments was in agreement with the stochastic predictions (above). For example, grlA mutants (S80Y) were recovered from the inocula (geometric mean, 8.3 × 10⁶ CFU/ml) on agar containing 1 to 2 μg of ciprofloxacin/ml in both replicate experiments with MRSA 8043. Variants were recovered from the starting populations (geometric mean, 1.1 × 10⁷ CFU/ml) on agar containing 0.5 to 1 μg of ciprofloxacin/ml in both replicate experiments with MRSA 8282, although grlA mutants (S80Y) were detected in only one of the experiments. When the cultures were exposed to the experimental ciprofloxacin regimen, viable counts declined to the reliable lower limit of detection (10² CFU/ml) and persisted below that level for the remainder of the experiments (Fig. 3, top right panel). No subpopulations with increased MICs or MBCs or mutations in the quinolone resistance-determining regions (QRDRs) of grlA/B or gyrA/B were found in the persisting bacteria at 96 h. Overall, the observed decrease in viable counts for both strains was consistent with predictions of the pharmacodynamic model. However, the model tended to slightly overpredict the decrease in viable counts during the initial 12 h and then again as the counts neared the limit of detection.

Our stochastic simulations predicted that the probability of MRSA 8043 and MRSA 8282 variants resistant to ciprofloxacin concentrations of 1 and 2 μg/ml in the starting populations would be ≤1.0 and <0.1%, respectively, when the density of the cultures was ∼10⁵ CFU/ml. The model also predicted that the probability that variants resistant to 1 and 2 μg of ciprofloxacin/ml would arise from the susceptible population during ciprofloxacin exposure would be ≤5.8 and <0.1%, respectively. Under lower inoculum conditions, the two-population pharmacodynamic model effectively collapses to a one-population model containing only susceptible bacteria.

These predictions were tested when MRSA 8043 and MRSA 8282 cultures containing ∼10⁵ CFU/ml were exposed to a simulated clinical ciprofloxacin dosage regimen of 400 mg every 12 h (Fig. 3, bottom left panel). The pharmacokinetic-pharmacodynamic indices attained during these experiments were similar to the values observed in previously reported experiments with larger inocula (∼10⁷ CFU/ml) that resulted in the emergence of resistance (8). No variants resistant to ciprofloxacin concentrations of ≥0.5 μg/ml or with mutations in the QRDRs of grlA/B and gyrA/B were detected in the starting cultures (geometric mean, 9.9 × 10⁴ CFU/ml for MRSA 8043 and 1.2 × 10⁵ CFU/ml for MRSA 8282) during replicate experiments. When the cultures were exposed to the 400 mg every 12 h regimen in the in vitro system, viable counts declined at a rate similar to that observed in earlier experiments with larger populations (8). In contrast to these experiments, however, bacterial counts continued to decrease and fell below the reliable limit of detection (Fig. 3, bottom right panel), consistent with predictions of the pharmacodynamic model. Organisms persisted below the limit of detection for the remaining time in all experiments, but no subpopulations with increased ciprofloxacin MICs or MBCs or mutations in the QRDRs of grlA/B or gyrA/B were detected in replicate experiments with either strain.

DISCUSSION

We hypothesized that a two-population pharmacodynamic model could be used to predict the emergence of ciprofloxacin resistance in S. aureus populations. Three candidate models were constructed by using elements of earlier models (18, 19, 22, 23, 25, 35, 36) and pharmacokinetic, viable count, subpopulation, and resistance mechanism data from our in vitro system experiments (8). All three candidate models described the patterns of bacterial killing and growth observed during the in vitro system experiments. The simplest model (model 1), with equivalent growth and ciprofloxacin killing rate constants, had the most biased parameter estimates. It underpredicted the growth rate of the susceptible subpopulations and overpredicted the ciprofloxacin killing rate of the resistant subpopulations. The most complex model (model 3), which included a parameter (μ) for conversion of susceptible to resistant bacteria, resulted in the least-precise parameter estimates. There was insufficient information in the viable count data alone for this model to precisely estimate certain parameters (R₀ and μ).

The model of intermediate complexity (model 2), with unique growth and killing rate constants for susceptible and resistant subpopulations, resulted in parameter estimates with the least bias and greatest precision. All model parameter estimates seemed realistic. For instance, the estimated net growth rate constants (including lower and upper univariate 95% confidence intervals) for R were lower than those for S. The corresponding net doubling times of the MRSA 8043 and MRSA 8282 grlA mutants calculated by using the growth rate estimates were 63 and 69 min, and those of the wild-type parent strains were 42 and 45 min, respectively, which are consistent with those reported for other S. aureus strains (9, 13, 16, 34). The model-estimated killing rate (k) constants (including lower and upper univariate 95% confidence intervals) for R were also lower than those for S, and the estimated EC₅₀ (including lower and upper planar 95% confidence intervals) of the resistant grlA mutants were higher than the EC₅₀s of the susceptible parent stains. The differences in killing rate constants and EC₅₀ for S and R subpopulations are consistent with previous observations that the rate of killing of S. aureus grlA mutants is less than that of wild-type bacteria at comparable ciprofloxacin exposures (16, 28). The wide difference in the confidence interval estimates for EC₅₀ compared to k suggests that the disparity in the rate of killing between the two subpopulations is mainly due to differences in this parameter and, to a lesser extent, differences in k. Finally, although estimates of R₀ were less precise than other parameter estimates, the estimates seemed to be reasonable. The resistance frequencies in the starting cultures of our in vitro system experiments ranged from <3.0 ×10⁻⁷ to 3.0 × 10⁻⁶ and <1.1 ×10⁻⁷ to 4.2 × 10⁻⁷ when the bacteria were subcultured on agar containing ciprofloxacin concentrations of 1 and 2 μg/ml, respectively (8). Since the starting populations of these experiments were ∼10⁷ CFU/ml, the resistance frequencies we observed were consistent with the R₀ values of ∼1 CFU/ml estimated by the model. The R₀ value is also consistent with measured resistance frequencies for first-step S. aureus mutants reported by others (12, 15).

The model correctly characterized the growth of wild-type MRSA 8043 and MRSA 8282 strains and the appearance of resistant subpopulations during growth control experiments in the in vitro system. The model predicted that this emerging R subpopulation would represent a progressively declining proportion of the total over time because of the differential growth rate between resistant and susceptible bacteria. This was in agreement with our observations in the in vitro system where the number of resistant variants recovered on agar containing 0.5, 1, and 2 μg of ciprofloxacin/ml increased, although their frequency relative to the total population decreased (8). The model also correctly described the growth of the grlA mutants, MRSA 8043C0-1 and MRSA 8282C0-1, in the in vitro system.

The model-predicted enrichment of resistant subpopulations in the presence of ciprofloxacin was consistent with the results of our in vitro system experiments (8). Increased numbers of low-level resistant variants, recovered on agar containing 0.5 to 2 μg of ciprofloxacin/ml, were observed at 24 h in all dosage simulations in which resistance emerged. In concordance with model predictions, the enrichment of low-level resistant subpopulations of MRSA 8043 at 24 h was greater than that of MRSA 8282. In our in vitro system experiments, the observed number of variants resistant to ciprofloxacin concentrations of at least 0.5 μg/ml comprised 33 to 100% of the MRSA 8043 population but only 6 to 27% of the MRSA 8282 population at 24 h (8). As predicted by the model, the number of low-level resistant variants of both strains increased progressively over the next 72 h so that by 96 h these resistant variants comprised the entire population. The model correctly predicted that resistant subpopulations would not emerge when MRSA 8043 and MRSA 8282 cultures were exposed to a simulated regimen of 2,800 mg every 12 h.

We validated pharmacodynamic model predictions by using the in vitro system. No resistance emerged when we exposed MRSA 8043 and MRSA 8282 populations (∼10⁷ CFU/ml) containing small numbers (<100 CFU/ml) of grlA mutants to a single large simulated ciprofloxacin dose (6,250 mg) followed by a clinical dosage regimen (400 mg every 12 h). Although observed viable counts were higher during the experiment than predicted by the pharmacodynamic model, it is unclear whether this deviation represented variability in the concentration-effect asymptote or a paradoxical effect. The latter is a decrease in bactericidal effect at high ciprofloxacin concentrations, possibly due to partial inhibition of RNA synthesis (33). Although several researchers have confirmed that high fluoroquinolone peak/MIC ratios produced with multiple dosing regimens eradicate bacteria and suppress the emergence of resistance (6, 10, 29), to our knowledge, we are the first to demonstrate the effectiveness of an approach using a single high dose followed by standard dosing. Our in vitro system experiments suggested that pharmacodynamic parameters (C_max/MIC and AUC/MIC ratios) associated with the first dose or during the first 24 h may be more predictive than steady-state parameters in preventing the selection of grlA mutants in S. aureus populations.

We are aware that application of a dosing strategy with a high dose may not be possible in the clinical setting because of concentration-related toxicity. However, this approach may be feasible as newer fluoroquinolones, possessing increased potency against wild-type S. aureus strains and grlA mutants, are developed (5, 17, 32).

The importance of subpopulations with low-level resistance to the emergence of resistance was also shown by our in vitro system experiments with bacterial cultures of lower density (∼10⁵ CFU/ml). The stochastic simulations predicted that variants with low-level resistance were unlikely to be present in the smaller populations, and hence, resistance would not emerge during exposure to clinically relevant ciprofloxacin concentrations. Our data clearly show that resistant subpopulations did not emerge with a simulated clinical dosage regimen that had previously failed with larger populations containing resistant variants. When low-level resistant variants are not present, the two-population pharmacodynamic model effectively collapses to a one-population model. Ciprofloxacin concentrations obtained with standard clinical dosage regimens may be sufficient to kill the susceptible population in these situations.

The utility of the pharmacodynamic model depends in part on the precision of parameter estimates. Most model parameters, except the initial size of the resistant subpopulation (R₀), were estimated with good precision (CV < 11.2%). In contrast, R₀ estimates had CV ranging from 28 to 36%. R₀ was included as a model parameter due to the inherent difficulties in detecting small subpopulations of resistant variants in bacterial cultures by using traditional microbiologic methods. To eliminate R₀ as a model parameter, new laboratory techniques to precisely measure small populations of bacteria (<10 CFU/ml) are needed. One such approach may be the use of molecular beacons in real-time PCR (P. Chung, M. E. Evans, J. A. Moscow, and P. J. McNamara, Abstr. Am. Assoc. Pharm. Sci., abstr. W5253, 2002). Until such methods are available, a possible alternative is to use artificial cultures of genetically related S. aureus strains with known resistance mechanisms. The mixed-culture approach may minimize the error associated with estimating R₀ and permit better control of the genetic composition of the population.

The usefulness of the proposed pharmacodynamic model also depends on the generality of the parameter estimates. The parameter estimates developed with the model with grlA mutants may not be applicable to bacteria with different resistance mechanisms (e.g., efflux or small colony variants). It is interesting, however, that the model correctly characterized the emergence of subpopulations with low-level resistance in those experiments where grlA mutants were not detected in the starting cultures. This suggests that knowing the susceptibility phenotypes of the resistant subpopulations may be sufficient for designing regimens to prevent the emergence of resistance. Studies with additional S. aureus strains and resistant variants with different mechanisms of resistance are necessary to test this hypothesis and determine realistic model parameter ranges for susceptible and resistant subpopulations with different genotypes and phenotypes.

We and others have speculated that grlA mutants with low-level resistance constitute an important subpopulation from which variants with higher levels of resistance evolve (3, 4, 8). Resistance in some of our in vitro system experiments appeared to occur stepwise from low-level resistant variants through sequential mutations in topoisomerase genes. Although the model described the apparent selection of grlA mutants, it did not explain the origin of variants recovered on agar containing up to 16 μg of ciprofloxacin/ml or the appearance of grlA/gyrA double mutants at the end of some experiments.

Alternative models may also mimic the observed total viable count data and be more consistent with the appearance of highly resistant variants at the end of our in vitro experiments. Such models may contain three (or more) subpopulations with different susceptibility phenotypes (susceptible and low- and high-level resistant subpopulations) or genotypes (wild-type, grlA mutant, and grlA/gyrA double mutant subpopulations). In these models, bacterial subpopulations with higher levels of ciprofloxacin resistance would arise from subpopulations with low-level resistance during antimicrobial exposure (phenotypic model) or by sequential mutations in topoisomerase genes (genotypic model). Another alternative model may be one in which bacteria continually adapt to the presence of ciprofloxacin through changes in phenotype (e.g., progressively up-regulate efflux). However, our experience with model 3 suggests that successful development of these more complex alternatives is probably not feasible because of difficulties in obtaining precise estimates from viable count data when additional parameters are incorporated into the model. Although more complex models may better characterize the evolution of higher levels of fluoroquinolone resistance in S. aureus, the critical factor in preventing the emergence of these highly resistant variants may be eradication of subpopulations with low-level resistance. The present model predicts many of the conditions necessary to successfully eliminate these low-level variants without the need to invoke more complex models.

The present model also does not explain the persistence of susceptible bacteria, in numbers below the reliable limit of detection, in those in vitro system experiments where resistance did not emerge. These bacteria may have been specialized survivor cells that comprised a small proportion (<10⁻⁵) of the starting populations and were refractory to the lethal effect of ciprofloxacin (20). We did not attempt to build persistence into the models, as others have proposed (2). The inclusion of this additional parameter in the model may have made it more difficult to estimate other parameters with good precision.

The two-population pharmacodynamic model we developed described the conditions under which selection of resistant variants occurred and correctly predicted ciprofloxacin dosage regimens that suppressed the emergence of resistant variants in two S. aureus strains. Although our model was constructed by using data from only two strains and one antimicrobial in an in vitro system, we believe our findings have general applicability. The predictive performance of the model attests to the potential power of this approach in designing dosage regimens to suppress the emergence of resistance. Additional in vitro model experiments are necessary to further refine and validate the model reported in this study. In addition, the utility of alternative models should be explored. When the model is optimized and paired with experiments in the in vitro system, it may be possible to more precisely define the relationship between antimicrobial concentrations and the emergence of fluoroquinolone resistance in S. aureus. Appropriately developed models may also facilitate and expedite evaluation of dosage regimens to prevent the emergence of resistance. We encourage the continued development and testing of pharmacodynamic models of bacterial resistance.

Acknowledgments

This work was supported in part by Public Health Service grant GM-066072 (to M.E.E.) from the National Institute of General Medical Sciences and by a grant from the Society of Infectious Diseases Pharmacists. J.J.C. was supported by the American Foundation for Pharmaceutical Education and the University of Kentucky Research Challenge Trust.

APPENDIX

Macrodilution time-kill studies.

Time-kill experiments, which allowed rapid assessment (compared to in vitro system experiments) of the growth and killing of bacterial subpopulations at multiple ciprofloxacin concentrations, were performed to determine which resistant subpopulation (R) to incorporate into the pharmacodynamic models. Two R subtypes of each strain with different degrees of ciprofloxacin resistance were tested based on resistant variants that were recovered in earlier in vitro system experiments (8). The first R subtype, the grlA mutants MRSA 8043C0-1 (S80Y) and MRSA 8282C0-1 (A116P), demonstrated low-level ciprofloxacin resistance. These grlA mutants were the most-resistant variants (MIC, 2 to 4 μg/ml) recovered from the bacterial populations present at the beginning of the in vitro system experiments. The second R subtype, the grlA/gyrA double mutants MRSA 8043C96-1 (S80Y/S84L) and MRSA 8282C96-1 (A116P/S84L), exhibited high-level ciprofloxacin resistance. These grlA/gyrA mutants were the most-resistant variants (MIC, 16 μg/ml) detected in bacterial populations after 96 h of exposure to a simulated dosage regimen of 400 mg every 8 h in the in vitro system.

The macrodilution time-kill experiments were performed in triplicate according to approved guidelines (26) by using an inoculum of approximately 10⁷ CFU/ml. Bacterial killing over 24 h was evaluated at ciprofloxacin concentrations ranging from one to eight times the MIC. Determination of viable counts and avoidance of antibiotic carryover was accomplished by using techniques described previously (8). Linear regression was used to estimate initial (0 to 4 h) growth and apparent ciprofloxacin-mediated bacterial killing rates. The viable count data were transformed to their natural logarithm values before performing linear regression. The actual rate of bacterial killing at each ciprofloxacin concentration was calculated by subtracting the apparent killing rate from the growth rate.

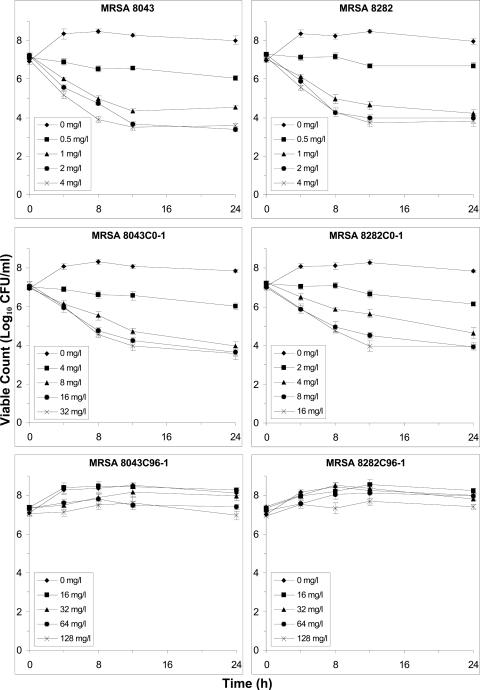
Growth rates of the grlA and grlA/gyrA mutant derivatives were significantly lower than those of the wild-type parent strains (Fig. A1). For grlA mutants MRSA 8043C0-1 and MRSA 8282C0-1, net growth rates (mean ± standard deviation) were 0.51 ± 0.05 h⁻¹ and 0.47 ± 0.04 h⁻¹ compared to 0.83 ± 0.04 h⁻¹ (P = 0.024, analysis of variance and Fisher's least significant difference test) and 0.78 ± 0.03 h⁻¹ (P = 0.035) for MRSA 8043 and MRSA 8282, respectively. The growth rates of grlA/gyrA mutants MRSA 8043C96-1 and MRSA 8282C96-1 were 0.58 ± 0.06 h⁻¹ and 0.56 ± 0.05 h⁻¹, significantly lower than those of the parent strains (P = 0.046 for MRSA 8043 and P = 0.048 for MRSA 8282) but not significantly different from those of the grlA mutants.

The initial rate of killing of the wild-type parent strains and the grlA mutants from 0 to 4 h increased at higher ciprofloxacin concentrations (Fig. A1). The rate of killing was near maximal values at four to eight times the MIC. The decline in viable counts for grlA mutants was slower than that for their respective parent strains at comparable ciprofloxacin exposures relative to the MIC. The grlA mutants were killed at significantly slower rates than their respective parent strains. The killing rates at eight times the MIC were 1.29 ± 0.14 h⁻¹ and 1.23 ± 0.17 h⁻¹ for MRSA 8043C0-1 and MRSA 8282C0-1 compared to 1.86 ± 0.12 h⁻¹ and 1.71 ± 0.14 h⁻¹ for MRSA 8043 (P = 0.039) and MRSA 8282 (P = 0.047). In contrast, there was no net killing of the highly ciprofloxacin-resistant grlA/gyrA double mutant derivatives with ciprofloxacin concentrations of up to eight times the MIC. The highest ciprofloxacin concentration tested in the time-kill studies with the grlA/gyrA double mutants (128 μg/ml) exceeded the average steady-state concentration simulated during all of the earlier in vitro system experiments (0.63 to 12.1 μg/ml) (8). The time-kill experiments suggest that if grlA/gyrA double mutants were present in the starting cultures during in vitro system experiments, they would have been selected with all rather than just some of the simulated ciprofloxacin dosage regimens (400 mg every 8 and 12 h). These data led us to conclude that the grlA mutant derivatives of the parent strains instead of grlA/gyrA double mutants should be incorporated into the candidate pharmacodynamic models as the R subpopulation.

REFERENCES

1.Andersson, D. I., and B. R. Levin. 1999. The biological costs of antibiotic resistance. Curr. Opin. Microbiol. 2:489-493. [DOI] [PubMed] [Google Scholar]
2.Austin, D. J., N. J. White, and R. M. Anderson. 1998. The dynamics of drug action on the within-host population growth of infectious agents: melding pharmacodynamics and pathogen population dynamics. J. Theor. Biol. 194:313-339. [DOI] [PubMed] [Google Scholar]
3.Baquero, F., M. C. Negri, M. I. Morosini, and J. Blazquez. 1998. Antibiotic-selective environments. Clin. Infect. Dis. 27(Suppl. 1):S5-S11. [DOI] [PubMed] [Google Scholar]
4.Baquero, F., M. C. Negri, M. I. Morosini, and J. Blazquez. 1997. The antibiotic selective process: concentration-specific amplification of low-level resistant populations, p. 93-111. In S. B. Levy (ed.), Antibiotic resistance: origins, evolution, selection, and spread. Wiley, Chichester, United Kingdom. [DOI] [PubMed]
5.Bauernfeind, A. 1997. Comparison of the antibacterial activities of the quinolones Bay 12-8039, gatifloxacin (AM 1155), trovafloxacin, clinafloxacin, levofloxacin and ciprofloxacin. J. Antimicrob. Chemother. 40:639-651. [DOI] [PubMed] [Google Scholar]
6.Blaser, J., B. B. Stone, M. C. Groner, and S. H. Zinner. 1987. Comparative study with enoxacin and netilmicin in a pharmacodynamic model to determine importance of ratio of antibiotic peak concentration to MIC for bactericidal activity and emergence of resistance. Antimicrob. Agents Chemother. 31:1054-1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Burnham, K. P., and D. R. Anderson. 2002. Model selection and multimodel inference: a practical information-theoretic approach, 2nd ed. Springer, New York, N.Y.
8.Campion, J. J., P. J. McNamara, and M. E. Evans. 2004. Evolution of ciprofloxacin-resistant Staphylococcus aureus in in vitro pharmacokinetic environments. Antimicrob. Agents Chemother. 48:4733-4744. [DOI] [PMC free article] [PubMed]
9.Dalhoff, A. 1985. Differences between bacteria grown in vitro and in vivo. J. Antimicrob. Chemother. 15(Suppl. A):175-195. [DOI] [PubMed] [Google Scholar]
10.Drusano, G. L., D. E. Johnson, and M. Rosen. 1993. Pharmacodynamics of a fluoroquinolone antimicrobial agent in a neutropenic rat model of Pseudomonas sepsis. Antimicrob. Agents Chemother. 37:483-490. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Gabrielsson, J., and D. Weiner. 2000. Pharmacokinetic/ pharmacodynamic data analysis: concepts and applications, 3rd ed. Apotekarsocieteten, Stockholm, Sweden.
12.Gilbert, D. N., S. J. Kohlhepp, K. A. Slama, G. Gurnkemeier, G. Lewis, R. J. Dworkin, S. E. Slaughter, and J. E. Legett. 2001. Phenotypic resistance of Staphylococcus aureus, selected Enterobacteriaceae, and Pseudomonas aeruginosa after single and multiple in vitro exposures to ciprofloxacin, levofloxacin, and trovafloxacin. Antimicrob. Agents Chemother. 45:883-892. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Gladstone, G. P., and E. J. G. Glencross. 1960. Growth and toxin production of staphylococci in cellophane sacs in vivo. Br. J. Exp. Pathol. 41:313-333. [PMC free article] [PubMed] [Google Scholar]
14.Holford, N. H. G., and L. B. Sheiner. 1981. Understanding the dose-effect relationship: clinical application of pharmacokinetic-pharmacodynamic models. Clin. Pharmacokinet. 6:429-453. [DOI] [PubMed] [Google Scholar]
15.Hori, S., Y. Ohshita, Y. Utsui, and K. Hiramatsu. 1993. Sequential acquisition of norfloxacin and ofloxacin resistance by methicillin-resistant and -susceptible Staphylococcus aureus. Antimicrob. Agents Chemother. 37:2278-2284. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Hyatt, J. M., D. E. Nix, and J. J. Schentag. 1994. Pharmacokinetic and pharmacodynamic activities of ciprofloxacin against strains of Streptococcus pneumoniae, Staphylococcus aureus, and Pseudomonas aeruginosa for which MICs are similar. Antimicrob. Agents Chemother. 38:2730-2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Ince, D., X. Zhang, and D. C. Hooper. 2003. Activity of and resistance to moxifloxacin in Staphylococcus aureus. Antimicrob. Agents Chemother. 47:1410-1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Jumbe, N., A. Louie, R. Leary, W. Liu, M. R. Deziel, V. H. Tam, R. Bachhawat, C. Freeman, J. Kahn, K. Bush, M. N. Dudley, M. H. Miller, and G. L. Drusano. 2003. Application of a mathematical model to prevent in vivo amplification of antibiotic-resistant bacterial populations during therapy. J. Clin. Investig. 112:275-285. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Jusko, W. J. 1973. A pharmacodynamic model for cell-cycle-specific chemotherapeutic agents. J. Pharmacokinet. Biopharm. 1:175-200. [Google Scholar]
20.Keren, I., N. Kaldalu, A. Spoering, Y. Wang, and K. Lewis. 2004. Persister cells and tolerance to antimicrobials. FEMS Microbiol. Lett. 230:13-18. [DOI] [PubMed] [Google Scholar]
21.Kingsland, S. E. 1985. Modeling nature: episodes in the history of population ecology. University of Chicago Press, Chicago, Ill.
22.Li, R. C., D. E. Nix, and J. J. Schentag. 1994. Pharmacodynamic modeling of bacterial kinetics: β-lactam antibiotics against Escherichia coli. J. Pharm. Sci. 83:970-975. [DOI] [PubMed] [Google Scholar]
23.Lipsitch, M., and B. R. Levin. 1997. The population dynamics of antimicrobial chemotherapy. Antimicrob. Agents Chemother. 41:363-373. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Meagher, A. K., A. Forrest, A. Dalhoff, H. Stass, and J. J. Schentag. 2004. Novel pharmacokinetic-pharmacodynamic model for prediction of outcomes with an extended-release formulation of ciprofloxacin. Antimicrob. Agents Chemother. 48:2061-2068. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Mouton, J. W., A. A. T. M. M. Vinks, and N. C. Punt. 1997. Pharmacokinetic-pharmacodynamic modeling of activity of ceftazidime during continuous and intermittent infusion. Antimicrob. Agents Chemother. 41:733-738. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.National Committee for Clinical Laboratory Standards. 1999. Methods for determining bactericidal activity of antimicrobial agents; approved guidelines, M26-A, vol. 19. National Committee for Clinical Laboratory Standards, Wayne, Pa.
27.Nelder, J. A., and R. Mead. 1965. A simplex method for function minimization. Comput. J. 7:308-313. [Google Scholar]
28.Ng, E. Y., M. Trucksis, and D. C. Hooper. 1996. Quinolone resistance mutations in topoisomerase IV: relationship to the flqA locus and genetic evidence that topoisomerase IV is the primary target and DNA gyrase is the secondary target of fluoroquinolones in Staphylococcus aureus. Antimicrob. Agents Chemother. 40:1881-1888. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Preston, S. L., G. L. Drusano, A. L. Berman, C. L. Fowler, A. T. Chow, B. Dornseif, V. Reichl, J. Natarajan, and M. Corrado. 1998. Pharmacodynamics of levofloxacin. A new paradigm for early clinical trials. JAMA 279:125-1129. [DOI] [PubMed] [Google Scholar]
30.Riesenfeld, C., M. Everett, L. J. V. Piddock, and B. G. Hall. 1997. Adaptive mutations produce resistance to ciprofloxacin. Antimicrob. Agents Chemother. 41:2059-2060. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Rosche, W. A., and P. L. Foster. 2000. Determining mutation rates in bacterial populations. Methods 20:4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Schmitz, F. J., C. vonEiff, M. Gondolf, A. C. Fluit, J. Verhoef, G. Peters, U. Hadding, H.-P. Heinz, and M. E. Jones. 1999. Staphylococcus aureus small colony variants: rate of selection and MIC values compared to wild-type strains, using ciprofloxacin, ofloxacin, levofloxacin, sparfloxacin, and moxifloxacin. Clin. Microbiol. Infect. 5:376-378. [DOI] [PubMed] [Google Scholar]
33.Smith, J. T. 1986. The mode of action of 4-quinolones and possible mechanisms of resistance. J. Antimicrob. Chemother. 18(Suppl. D):21-29. [DOI] [PubMed] [Google Scholar]
34.Watson, D. L., and J. A. Prideaux. 1979. Comparisons of Staphylococcus aureus grown in vitro and in vivo. Microbiol. Immunol. 23:543-547. [DOI] [PubMed] [Google Scholar]
35.Yano, Y., T. Oguma, H. Nagata, and S. Sasaki. 1998. Application of logistic growth model to pharmacodynamic analysis of in vitro bactericidal kinetics. J. Pharm. Sci. 87:1177-1183. [DOI] [PubMed] [Google Scholar]
36.Zhi, J., C. H. Nightingale, and R. Quintiliani. 1988. Microbial pharmacodynamics of piperacillin in neutropenic mice of systemic infection due to Pseudomonas aeruginosa. J. Pharmacokinet. Biopharm. 16:355-375. [DOI] [PubMed] [Google Scholar]

[r1] 1.Andersson, D. I., and B. R. Levin. 1999. The biological costs of antibiotic resistance. Curr. Opin. Microbiol. 2:489-493. [DOI] [PubMed] [Google Scholar]

[r2] 2.Austin, D. J., N. J. White, and R. M. Anderson. 1998. The dynamics of drug action on the within-host population growth of infectious agents: melding pharmacodynamics and pathogen population dynamics. J. Theor. Biol. 194:313-339. [DOI] [PubMed] [Google Scholar]

[r3] 3.Baquero, F., M. C. Negri, M. I. Morosini, and J. Blazquez. 1998. Antibiotic-selective environments. Clin. Infect. Dis. 27(Suppl. 1):S5-S11. [DOI] [PubMed] [Google Scholar]

[r4] 4.Baquero, F., M. C. Negri, M. I. Morosini, and J. Blazquez. 1997. The antibiotic selective process: concentration-specific amplification of low-level resistant populations, p. 93-111. In S. B. Levy (ed.), Antibiotic resistance: origins, evolution, selection, and spread. Wiley, Chichester, United Kingdom. [DOI] [PubMed]

[r5] 5.Bauernfeind, A. 1997. Comparison of the antibacterial activities of the quinolones Bay 12-8039, gatifloxacin (AM 1155), trovafloxacin, clinafloxacin, levofloxacin and ciprofloxacin. J. Antimicrob. Chemother. 40:639-651. [DOI] [PubMed] [Google Scholar]

[r6] 6.Blaser, J., B. B. Stone, M. C. Groner, and S. H. Zinner. 1987. Comparative study with enoxacin and netilmicin in a pharmacodynamic model to determine importance of ratio of antibiotic peak concentration to MIC for bactericidal activity and emergence of resistance. Antimicrob. Agents Chemother. 31:1054-1060. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r7] 7.Burnham, K. P., and D. R. Anderson. 2002. Model selection and multimodel inference: a practical information-theoretic approach, 2nd ed. Springer, New York, N.Y.

[r8] 8.Campion, J. J., P. J. McNamara, and M. E. Evans. 2004. Evolution of ciprofloxacin-resistant Staphylococcus aureus in in vitro pharmacokinetic environments. Antimicrob. Agents Chemother. 48:4733-4744. [DOI] [PMC free article] [PubMed]

[r9] 9.Dalhoff, A. 1985. Differences between bacteria grown in vitro and in vivo. J. Antimicrob. Chemother. 15(Suppl. A):175-195. [DOI] [PubMed] [Google Scholar]

[r10] 10.Drusano, G. L., D. E. Johnson, and M. Rosen. 1993. Pharmacodynamics of a fluoroquinolone antimicrobial agent in a neutropenic rat model of Pseudomonas sepsis. Antimicrob. Agents Chemother. 37:483-490. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r11] 11.Gabrielsson, J., and D. Weiner. 2000. Pharmacokinetic/ pharmacodynamic data analysis: concepts and applications, 3rd ed. Apotekarsocieteten, Stockholm, Sweden.

[r12] 12.Gilbert, D. N., S. J. Kohlhepp, K. A. Slama, G. Gurnkemeier, G. Lewis, R. J. Dworkin, S. E. Slaughter, and J. E. Legett. 2001. Phenotypic resistance of Staphylococcus aureus, selected Enterobacteriaceae, and Pseudomonas aeruginosa after single and multiple in vitro exposures to ciprofloxacin, levofloxacin, and trovafloxacin. Antimicrob. Agents Chemother. 45:883-892. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r13] 13.Gladstone, G. P., and E. J. G. Glencross. 1960. Growth and toxin production of staphylococci in cellophane sacs in vivo. Br. J. Exp. Pathol. 41:313-333. [PMC free article] [PubMed] [Google Scholar]

[r14] 14.Holford, N. H. G., and L. B. Sheiner. 1981. Understanding the dose-effect relationship: clinical application of pharmacokinetic-pharmacodynamic models. Clin. Pharmacokinet. 6:429-453. [DOI] [PubMed] [Google Scholar]

[r15] 15.Hori, S., Y. Ohshita, Y. Utsui, and K. Hiramatsu. 1993. Sequential acquisition of norfloxacin and ofloxacin resistance by methicillin-resistant and -susceptible Staphylococcus aureus. Antimicrob. Agents Chemother. 37:2278-2284. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r16] 16.Hyatt, J. M., D. E. Nix, and J. J. Schentag. 1994. Pharmacokinetic and pharmacodynamic activities of ciprofloxacin against strains of Streptococcus pneumoniae, Staphylococcus aureus, and Pseudomonas aeruginosa for which MICs are similar. Antimicrob. Agents Chemother. 38:2730-2737. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r17] 17.Ince, D., X. Zhang, and D. C. Hooper. 2003. Activity of and resistance to moxifloxacin in Staphylococcus aureus. Antimicrob. Agents Chemother. 47:1410-1415. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r18] 18.Jumbe, N., A. Louie, R. Leary, W. Liu, M. R. Deziel, V. H. Tam, R. Bachhawat, C. Freeman, J. Kahn, K. Bush, M. N. Dudley, M. H. Miller, and G. L. Drusano. 2003. Application of a mathematical model to prevent in vivo amplification of antibiotic-resistant bacterial populations during therapy. J. Clin. Investig. 112:275-285. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r19] 19.Jusko, W. J. 1973. A pharmacodynamic model for cell-cycle-specific chemotherapeutic agents. J. Pharmacokinet. Biopharm. 1:175-200. [Google Scholar]

[r20] 20.Keren, I., N. Kaldalu, A. Spoering, Y. Wang, and K. Lewis. 2004. Persister cells and tolerance to antimicrobials. FEMS Microbiol. Lett. 230:13-18. [DOI] [PubMed] [Google Scholar]

[r21] 21.Kingsland, S. E. 1985. Modeling nature: episodes in the history of population ecology. University of Chicago Press, Chicago, Ill.

[r22] 22.Li, R. C., D. E. Nix, and J. J. Schentag. 1994. Pharmacodynamic modeling of bacterial kinetics: β-lactam antibiotics against Escherichia coli. J. Pharm. Sci. 83:970-975. [DOI] [PubMed] [Google Scholar]

[r23] 23.Lipsitch, M., and B. R. Levin. 1997. The population dynamics of antimicrobial chemotherapy. Antimicrob. Agents Chemother. 41:363-373. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r24] 24.Meagher, A. K., A. Forrest, A. Dalhoff, H. Stass, and J. J. Schentag. 2004. Novel pharmacokinetic-pharmacodynamic model for prediction of outcomes with an extended-release formulation of ciprofloxacin. Antimicrob. Agents Chemother. 48:2061-2068. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r25] 25.Mouton, J. W., A. A. T. M. M. Vinks, and N. C. Punt. 1997. Pharmacokinetic-pharmacodynamic modeling of activity of ceftazidime during continuous and intermittent infusion. Antimicrob. Agents Chemother. 41:733-738. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r26] 26.National Committee for Clinical Laboratory Standards. 1999. Methods for determining bactericidal activity of antimicrobial agents; approved guidelines, M26-A, vol. 19. National Committee for Clinical Laboratory Standards, Wayne, Pa.

[r27] 27.Nelder, J. A., and R. Mead. 1965. A simplex method for function minimization. Comput. J. 7:308-313. [Google Scholar]

[r28] 28.Ng, E. Y., M. Trucksis, and D. C. Hooper. 1996. Quinolone resistance mutations in topoisomerase IV: relationship to the flqA locus and genetic evidence that topoisomerase IV is the primary target and DNA gyrase is the secondary target of fluoroquinolones in Staphylococcus aureus. Antimicrob. Agents Chemother. 40:1881-1888. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r29] 29.Preston, S. L., G. L. Drusano, A. L. Berman, C. L. Fowler, A. T. Chow, B. Dornseif, V. Reichl, J. Natarajan, and M. Corrado. 1998. Pharmacodynamics of levofloxacin. A new paradigm for early clinical trials. JAMA 279:125-1129. [DOI] [PubMed] [Google Scholar]

[r30] 30.Riesenfeld, C., M. Everett, L. J. V. Piddock, and B. G. Hall. 1997. Adaptive mutations produce resistance to ciprofloxacin. Antimicrob. Agents Chemother. 41:2059-2060. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r31] 31.Rosche, W. A., and P. L. Foster. 2000. Determining mutation rates in bacterial populations. Methods 20:4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]

[r32] 32.Schmitz, F. J., C. vonEiff, M. Gondolf, A. C. Fluit, J. Verhoef, G. Peters, U. Hadding, H.-P. Heinz, and M. E. Jones. 1999. Staphylococcus aureus small colony variants: rate of selection and MIC values compared to wild-type strains, using ciprofloxacin, ofloxacin, levofloxacin, sparfloxacin, and moxifloxacin. Clin. Microbiol. Infect. 5:376-378. [DOI] [PubMed] [Google Scholar]

[r33] 33.Smith, J. T. 1986. The mode of action of 4-quinolones and possible mechanisms of resistance. J. Antimicrob. Chemother. 18(Suppl. D):21-29. [DOI] [PubMed] [Google Scholar]

[r34] 34.Watson, D. L., and J. A. Prideaux. 1979. Comparisons of Staphylococcus aureus grown in vitro and in vivo. Microbiol. Immunol. 23:543-547. [DOI] [PubMed] [Google Scholar]

[r35] 35.Yano, Y., T. Oguma, H. Nagata, and S. Sasaki. 1998. Application of logistic growth model to pharmacodynamic analysis of in vitro bactericidal kinetics. J. Pharm. Sci. 87:1177-1183. [DOI] [PubMed] [Google Scholar]

[r36] 36.Zhi, J., C. H. Nightingale, and R. Quintiliani. 1988. Microbial pharmacodynamics of piperacillin in neutropenic mice of systemic infection due to Pseudomonas aeruginosa. J. Pharmacokinet. Biopharm. 16:355-375. [DOI] [PubMed] [Google Scholar]

PERMALINK

Pharmacodynamic Modeling of Ciprofloxacin Resistance in Staphylococcus aureus

Jeffrey J Campion

Patrick J McNamara

Martin E Evans

Abstract