The Dynamic Surface Tension of Water

Abstract

The surface tension of water is an important parameter for many biological or industrial processes, and roughly a factor of 3 higher than that of nonpolar liquids such as oils, which is usually attributed to hydrogen bonding and dipolar interactions. Here we show by studying the formation of water drops that the surface tension of a freshly created water surface is even higher (∼90 mN m^–1) than under equilibrium conditions (∼72 mN m^–1) with a relaxation process occurring on a long time scale (∼1 ms). Dynamic adsorption effects of protons or hydroxides may be at the origin of this dynamic surface tension. However, changing the pH does not significantly change the dynamic surface tension. It also seems unlikely that hydrogen bonding or dipole orientation effects play any role at the relatively long time scale probed in the experiments.

The surface tension of any liquid is positive, which can be understood from the fact that on average a molecule on the surface has fewer neighbors and hence fewer attractive van der Waals interactions than a molecule in the bulk. It therefore costs energy to create new surfaces and indeed, reasonable estimates of the surface tensions of apolar liquids can be obtained in this way.¹ For water, however, an analogous approach leads to a calculated surface tension that is roughly a factor of three smaller than the experimental one.¹ One usually attributes the high surface tension to missing hydrogen bonds at the surface, but it has turned out to be very difficult to calculate or simulate their contribution to the surface tension in both theory and simulations.² One test of the hydrogen bond argument would be to make use of the fact that the relaxation (reorientation) time of hydrogen bonds in the bulk is on the order of a few ps.³ Hence, if the reorientation time scale at the interface is similar, one would expect any relaxation of the surface tension to take place on this timescale. Here we study the surface relaxation of water and find that water exhibits a dynamic surface tension with a relaxation time that is on the order of 1 ms or larger, indicating that an essential ingredient is missing for understanding the value of the water surface tension.

We study the formation and breakup of droplets of water emanating from an orifice (Figure 1). Drop formation has received much attention recently and it was shown that the breakup mechanism is universal for different liquids, meaning that the form of the breakup and its time dependence are uniquely determined by the forces acting on the liquid neck that separates the main drop from the orifice.^4,5 For low-viscosity liquids such as water, only surface tension forces drive the breakup of the liquid neck while inertial forces slow it down. This leads to a dynamics characteristic of a singularity at finite time, in which the neck diameter goes to zero as

1

where D_min is the width of the fluid neck at its minimum (Figure 1), A is a numerical prefactor, σ is the surface tension, ρ is the density, and t₀ is the breakup time. The (t₀ – t) term, in the following referred to as τ, is characteristic of the finite time singularity that occurs at t₀, in which the deformation rate of the surface diverges. Consequently, if one knows the prefactor A, one can infer the surface tension from the drop formation dynamics in a situation where the breakup process creates freshly formed air–water interface at a diverging rate. The latter is easy to see from volume conservation; taking the liquid neck as a cylinder of height h, its constant volume is ∼ D_min²h so that h ∼ (t₀ – t)^−4/3 and consequently the area D_minh ∼ (t₀ – t)^−2/3 diverges at t₀.

Figure 1.

Pinch-off images at subsequent stages of the droplet pinch-off process. The minimum neck diameter is obtained from ultrarapid camera movies (54.000 fps) and subsequent image analysis. Time to pinch-off is 5 ms, 1 ms, 0 ms, −0.5 ms, and −1 ms (left to right). The experiments were performed with two different capillary sizes (240 μm and 2 mm); the drop size in the image is 2.25 mm.

Determination of the Universal Prefactor. Despite the fact that the prefactor A should be universal and therefore independent of any initial conditions or the nature of the inviscid fluid itself, there is considerable uncertainty in the literature⁴⁻¹¹ as to what the value of A in eq 1 should be. Most published experimental results were obtained from ultrarapid imaging and suggest prefactors of 0.9–1.1,¹⁰ 1.1¹¹ or 1.14–1.36.¹² An alternative approach based on measuring the electrical conductance of the filament yielded a prefactor as low as 0.2.⁸ A similar disagreement appears in the associated numerical simulations, where values between 1.26,¹¹ 1.4,¹⁰ and 1.46¹³ can be deduced from the presented drop breakup dynamics curves. In certain simulations, the presented asymptotics even seem to display a time dependence that is wholly inconsistent with there being a universal asymptotic dynamics.¹⁰ In addition, none of the existing experimental and numerical accounts explicitly gives a value for the prefactor. These remarkable discrepancies warrant an in-depth investigation of this fundamental hydrodynamics problem. This is beyond the scope of the present paper and will be addressed at in a separate study. In the present work we will first provide an unambiguous determination of the prefactor using different simple liquids and subsequently use the derived value for A as a reference for the determination of the water surface tension of a pristine water–air interface.

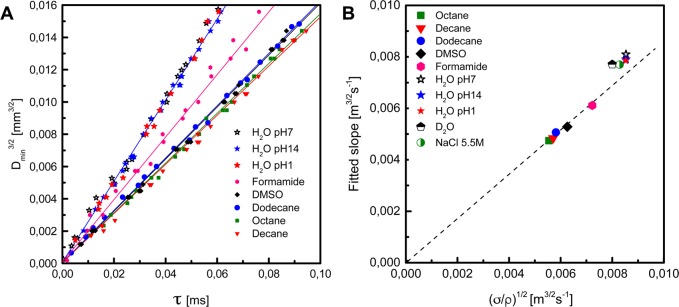
We follow the thinning dynamics using an ultra high-speed camera attached to a microscope to have both maximal temporal and spatial resolution. For liquids with different ratios σ/ρ, we arrive at good agreement with eq 1 (Figure 2A) with a value of the prefactor A of 0.9 ± 0.01 (Figure 2B). For water, however, the identical experiment is not on the same line, and shows a systematic deviation. Previous experiments on water, helium, and mercury breakup do not agree on the prefactor.⁷⁻¹⁰ The data of Chen et al., although noisier, appear to agree with our data at least close to the breakup point, but deviate for longer times and the helium and mercury experiments give very different prefactors. From numerics,^10,13 the prefactor was determined to be A ∼ 1.4, which disagrees with most of the experiments. We therefore use the precise and universal prefactor obtained in our experiments on a series of other liquids of known surface tension. The surface tensions were verified independently on the liquids used in the snap-off experiments. Using this prefactor does not lead to the expected value of the surface tension of ∼72 mN m^–1, but rather to a surprisingly high value of ∼90 mN m^–1. This strongly suggests that the surface tension of a newly formed water surface on a time scale <1 ms is different from the equilibrium surface tension, implying that some surface relaxation must take place.

Figure 2.

Determination of the prefactor in eq 1. (A) Linear fits of ultrarapid camera imaging data to the capillary-inertial law for inviscid fluids (D_min = Aτ^2/3). By plotting the data in this way, a stringent test is obtained for the applicability of the scaling; the slope C of the fitted lines can then be used to determine the prefactor A. (B) By plotting the slopes obtained from panel a versus (σ/ρ)^1/2, we derive a prefactor A = 0.9 ± 0.01 (slope C = A^3/2(σ/ρ)^1/2). Water, D₂O, and sodium chloride solution show a significant deviation from the theoretical prediction and are thus not taken into consideration for the calculation of the universal prefactor. The presented data were obtained using a capillary of 240 μm diameter.

This gives a bound on the characteristic time for the surface tension crossover (∼ ms) that is very different from that of the relaxation of the bulk hydrogen bonds (∼ ps). One possible mechanism that has been proposed and was suggested to lead to a similar time scale^1,14 is the establishment of an equilibrium distribution of OH^– and H⁺ ions close to the interface. The (uncontested) positive sign of the surface potential of water implies that its surface charge correspondingly carries a net negative sign in equilibrium and at neutral pH.¹⁵⁻¹⁷ The usual interpretation of this is that, on average, the OH^– are closer to the surface than the H⁺ ions, which implies the establishment of an OH^– “adsorption” equilibrium at the surface.¹⁴ However, at very low pH, the surface charge becomes positive due to the excess of H⁺ present.^17,18 In principle, this could both account for the higher value of the dynamic surface tension at short times and the existence of the characteristic time: if the OH^– ions are depleted at early times, this would increase the surface tension, and the characteristic time is the time for establishing the adsorption equilibrium. In our case, the diffusion coefficient of OH^– ions is ∼10^–9 m²/s,¹⁹ so that establishing the diffusion equilibrium over the typical diameter of the fluid neck of 1 μm takes ∼1 ms. In some molecular dynamics simulations,²⁰ spectroscopic investigations,²¹ and studies on acid adsorption,²²⁻²⁴ it is suggested that H⁺ adsorption may also occur at the water–air interface indicating that the underlying mechanism could be even more complex. We therefore now investigate the effect of pH.

Effect of pH. Such a dynamic surface tension is well-known for surface-active agents, and, indeed, the same experiment as done here in the presence of surfactants shows that close to drop breakup, the surface tension is significantly higher than the equilibrium one, just as is observed here.^25,26 If there is no adsorption barrier, the characteristic time follows from the adsorption dynamics as τ ∼ Γ²/Dc², where Γ is the equilibrium adsorption, c the bulk concentration, and D the diffusion coefficient of the surface-active species. Characteristic times are also found to be on the order of ∼1 ms in surfactant adsorption experiments.²⁷ This suggests for our experiments that changing the bulk concentration c should have a strong influence on the relaxation time. In our experiment, we can easily change the bulk concentration of protons or hydronium ions by several orders of magnitude by adjusting the pH with either acid (HCl) or base (NaOH). However, the data show that neither of these additions changes the short-time value of the dynamic surface tension (Figure 2A). From the simple argument given above, one would have anticipated to retrieve the equilibrium surface tension upon addition of an excess of OH^– ions (data at pH = 14, Figure 2). A relaxation time independent of the bulk concentration can be obtained if there is an adsorption barrier at the surface that is the rate-limiting step for the arrival of molecules from the bulk onto the surface. This is, for instance, frequently encountered for charged surfactants,²⁸ where the charged surfactants at the surface constitute an electrostatic barrier for the adsorption of further charged molecules. In our case though, if the barrier is electrostatic, one would again expect a large decrease of the characteristic time upon changing the pH, since the characteristic time in this case is τ ∼ κ²/D,²⁸ with κ the Debye length that varies with the amount of electrolyte added. Thus, the data would only be consistent with the existence of an adsorption energy barrier that comes from a different origin. However, what the physical mechanism would be is unclear.

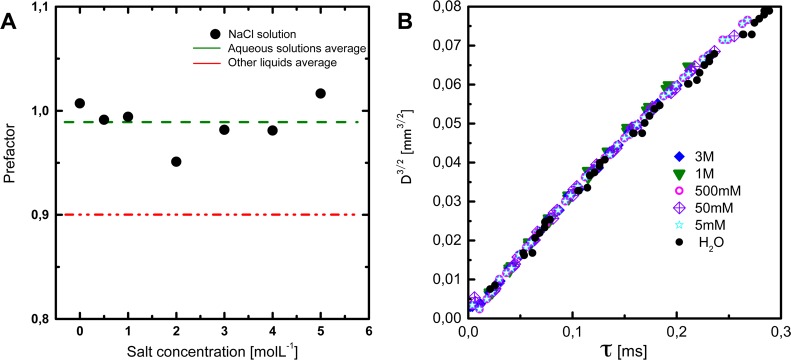
Effect of Salt Concentration. A related check of the ionic redistribution explanation is to see whether there is a characteristic time for the depletion of certain species from the interface. The obvious approach for studying dynamic depletion effects is to study salt solutions. Salts are strongly depleted from the aqueous interface, which in equilibrium increases the surface tension close to the values that are found here for the dynamic tension. In addition, large amounts of salt strongly screen any electrostatic interaction between the surface and the bulk and should therefore prevent adsorption of any charged moieties. Surprisingly, we could not detect any effect of the salt concentration on the surface relaxation behavior on short time scales (Figure 3B). The various salt solutions (Figure 3A) again behave very similarly to water with a similarly high prefactor compared to the simple liquids.

Figure 3.

Effect of salt. (A) Apparent prefactors obtained from pinch-off experiments. The derived prefactor appears to be independent of the salt concentration. (B) Pinch-off dynamics of aqueous solutions at early times. Water and brine display an almost identical surface relaxation mechanism with surface tension values of 90 mN m^–1 for the pristine interface. The data overlap since the increase in surface tension induced by the addition of salt is similar to the increase in density.

Discussion. Our ultrarapid camera experiments on droplet formation and breakup of different pure liquids therefore provide strong evidence for the existence of a high dynamic surface tension for water and various aqueous solutions on an approximately millisecond time scale. In the past, higher than equilibrium surface tension values for water have been reported on short time scales. However, they have all remained highly controversial due to methodological and analytical shortcomings. As early as 1926, Schmidt and Steyer reported elevated values of 80–100 mN m^–1 for the surface tension of freshly formed water/air interfaces, that would relax to the equilibrium value within roughly 1 ms.²⁹ Critics nevertheless stated that a viscosity effect in the constricted quartz capillary rather than the actual dynamic surface tension is measured by the falling meniscus method they employed.³⁰ A few years later, an improved technique, the “bell method”, yielded similar results, which, nevertheless, remained equally dubious due to the ambiguity related to the exact determination of the surface age.^14,31 Finally, Kochura and Rusanov measured both the surface tension and the surface potential of water with the oscillating and the smooth jet method, respectively.¹⁴ These two independent techniques likewise suggested a dynamic water surface tension with initial values considerably above the equilibrium value and a similar relaxation time of ca. 0.5 ms. However, again, the suitability of the oscillating jet method for determining the surface tension of pristine surfaces on a submillisecond time scale has remained controversial: the associated hydrodynamics are incompletely understood which, in turn, entails considerable uncertainties in the complex analysis procedure.³² In contrast to the above-mentioned methodologies, our method of studying droplet breakup dispenses with the experimental shortcomings and analytical ambiguity. The experimental procedure is very robust, and the associated pinch-off dynamics is very well understood for inviscid fluids.

Taken together, we were able to unambiguously relate the drop breakup dynamics to the surface tension of a wide variety of pure liquids with the exception of pure, heavy, and salty water. For aqueous systems, a considerable and systematic deviation was found. The origin of the slow surface relaxation process, which a dynamic surface tension implies, remains, however, incompletely understood. Various theories have been proposed in the past to account for this phenomenon. A much-discussed idea^18,33−35 is that ion adsorption processes in the first fraction of a millisecond after surface creation are directly responsible for the observed high surface tension. We have shown here that, for pure water, this indeed gives the correct order of magnitude. Yet our detailed measurements also show that the high surface tension is observed irrespective of salt and OH^–/H⁺ concentration levels. This is only possible if bulk diffusion or an electrostatic energy barrier at the surface are not the rate-limiting steps for OH^– adsorption. An alternative and rather straightforward argument goes that the observed surface tension relaxation is merely due to traces of contaminant surfactants that are, in practice, very hard to avoid. However, it has been shown in both theory³⁶ and experiments^25,26 that, in drop breakup experiments, the diverging rate of surface formation makes the adsorption or even presence of surfactants irrelevant, at least close to breakup. Further, these contaminants can only reduce the surface tension. In addition, the characteristic time for adsorption of surfactants at low concentrations lies in the range of several milliseconds and should be even higher for very small contaminant concentrations,³⁷ which again shows that impurities should be irrelevant on our submillisecond time scale.

Another possible explanation, perhaps related to the collective nature of the dipole fluctuations, would be a slow reorientation dynamics near the surface. In bulk, dielectric relaxation is known to occur on a much, much faster time scale (∼ ps)³. Although it has been argued that close to surfaces the relaxation might be one or 2 orders of magnitude slower,^38,39 this is still a very a long way from the observed characteristic relaxation time of ∼1 ms, even if one takes into account the possibility of a higher order water structure close to the surface.¹⁴ On the other hand, it also seems unlikely that the observed deviations for water and the various aqueous solutions are due to hydrodynamic effects. For instance, flows have been shown to dampen out the capillary wave fluctuations of the surface and hence to increase the tension.⁴⁰ However, if such an effect is present here, it would happen at nanometer length and picosecond or nanosecond time scales, and would hence not be observable in our experiment.⁴⁰ More importantly, it would also occur for the other liquids tested here, which have similar viscosities, surface tensions, and densities.

In conclusion, we are at present unable to offer a complete explanation for our results. In spite of this, the implications are rather large: the observed high dynamic tension should, for instance, be relevant for spray formation, jet destabilization, drop impact, and drop formation as there are very short time scale surface dynamics in all of these processes.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b00267.

• Details of employed experimental materials and methods (PDF)

Author Contributions

D.B. and H.K. conceived the idea and the experiments. I.M.H., A.D., and H.K. performed the experiments. I.M.H., A.D., J.K.B., H.K., and D.B. interpreted the experimental results. I.M.H. and D.B. wrote the article with input from A.D., J.K.B., and H.K.

The authors declare no competing financial interest.