Signal enhancement and Patterson-search phasing for high-spatial-resolution coherent X-ray diffraction imaging of biological objects

Abstract

In this decade coherent X-ray diffraction imaging has been demonstrated to reveal internal structures of whole biological cells and organelles. However, the spatial resolution is limited to several tens of nanometers due to the poor scattering power of biological samples. The challenge is to recover correct phase information from experimental diffraction patterns that have a low signal-to-noise ratio and unmeasurable lowest-resolution data. Here, we propose a method to extend spatial resolution by enhancing diffraction signals and by robust phasing. The weak diffraction signals from biological objects are enhanced by interference with strong waves from dispersed colloidal gold particles. The positions of the gold particles determined by Patterson analysis serve as the initial phase, and this dramatically improves reliability and convergence of image reconstruction by iterative phase retrieval. A set of calculations based on current experiments demonstrates that resolution is improved by a factor of two or more.

Biological cells comprise spatially hierarchical and highly functionalized components from organelles measured in micrometers to macromolecules of nanometer sizes. An understanding of their physicochemical function requires visualization of internal structures of whole cells and/or organelles as close to the native state as possible.

Coherent X-ray diffraction imaging (CXDI)¹ is a promising technique to study such non-crystalline objects. The high penetrating power of X-rays allows visualization of internal structures of thick objects in micrometer to sub-micrometer dimensions at nanometer resolution. Thus, CXDI fills a gap among other techniques, since it could resolve finer structures of samples that are too thick for electron microscopy beyond the resolution limit of optical microscopy. In CXDI experiments, spatially coherent X-rays irradiate a sample object, and the Fraunhofer diffraction pattern of the object on the Ewald sphere² is recorded on an area detector (Fig. 1a). When the diffraction pattern is sampled at a spacing finer than the Nyquist interval on the detector (oversampling; OS)³, iterative phase retrieval (PR) algorithms⁴ can recover phase information of the object directly from the diffraction pattern. Thereby, we can obtain a projection map of sample objects within a given spatial resolution, where the curvature of the Ewald sphere can be regarded as a flat plane perpendicular to the incident X-ray beam (projection approximation²).

Figure 1. Setup for XFEL-CXDI of biological samples and the model used in this study.

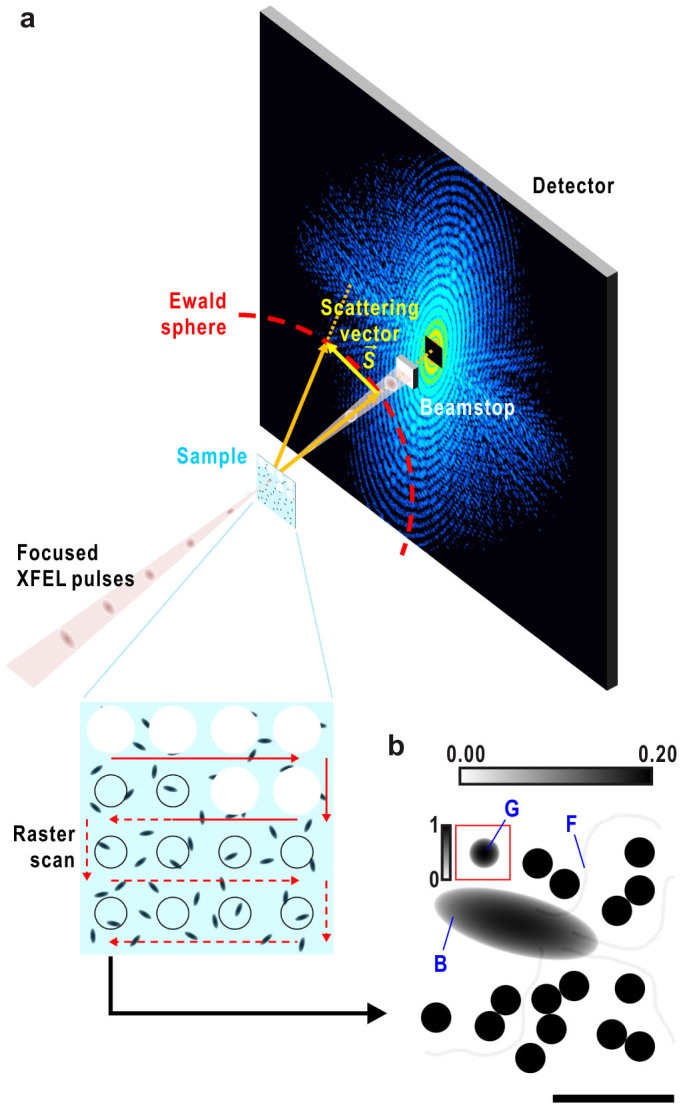
(a) Schematic illustration of cryo-CXDI based on our recent experiments at SACLA¹¹. Frozen-hydrated sample particles are densely dispersed on thin support film¹¹,³². The sample stage is raster scanned to deliver fresh samples for exposure of every focused X-ray pulse. The samples explode just after irradiation of XFEL. Diffraction patterns on the Ewald sphere are recorded on a detector located downstream of the sample, but the central part of the patterns is blocked by a beamstop. (b) Projected electron densities of a model sample. The model is composed of a bacterial cell (B), four flagella (F) and 16 CG particles of 250 nm (G). Gradient scale bar at the top refers to the display contrast relative to the maximum value of the cell and CG particles. One CG particle inside a red square is shown at a lower contrast with the gradient scale bar on the left. Bar indicates ~1 μm.

Biological samples are extremely sensitive to radiation even at cryogenic temperatures⁵, yet need to be imaged with significant doses of X-rays due to their small scattering cross-section. X-ray free-electron laser (XFEL) sources launched recently⁶,⁷ have the potential to solve this contrary problem, since the femto-second pulse duration and the high photon flux density of XFELs allow diffraction data collection before sample destruction⁸. Thus far, XFEL-CXDI has visualized a large virus⁹ and a macromolecular assembly¹⁰, an organelle¹¹ and a bacterium¹² at resolutions of 30–60 nm. However, the small scattering cross-section of biological samples remains a big obstacle to extending the resolution of electron density maps with the currently available photon flux density of XFELs.

Another serious problem in CXDI is the quality and incompleteness of experimental diffraction data. Iterative PR calculations starting from a diffraction pattern with poor signal-to-noise ratios and unobserved data (particularly in the lowest-resolution area where there is a beamstop; Fig. 1a) often diverge yielding an incorrect solution¹³ (Supplementary Fig. 1). Reliable initial phase is extremely helpful in overcoming these problems and can lead to the correct structure.

Here, we propose an approach to enhance signals from biological objects and to obtain a reliable initial phase. We use colloidal gold (CG) particles and image the particles and biological objects together (Fig. 1b). Interference between the strong diffraction waves from the CG particles and weak waves from the biological object can enhance the signals from the biological object to a detectable level¹⁴,¹⁵,¹⁶,¹⁷. The positions of the gold particles determined by Patterson analysis serve as the initial phase¹⁸,¹⁹. CG is relatively nonreactive and this approach is compatible with imaging biological objects under physiological conditions.

We first demonstrate the feasibility of the method based on calculations derived from CXDI experiments at the Japanese XFEL facility, SACLA¹¹. Then, we discuss the potential and limitations of the method in practical applications.

Results

Strategy

When biological objects and CG particles are simultaneously irradiated by a square-shaped (a × a) X-ray beam with wavelength λ and uniform flux density of I₀, the Fraunhofer diffraction intensity 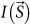at scattering vector 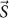is given as¹⁶,

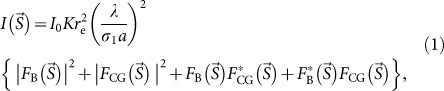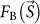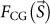where and are structure factors of a biological object and CG particles, respectively, K is the detector efficiency for the X-rays, σ₁ is the OS ratio of the diffraction pattern in one direction³, and r_e is the classical electron radius ( = 2.82 × 10⁻¹⁵ m). The average electron density of CG (4,664 electrons/nm³) is approximately ten times higher than that of biological objects (433 electrons/nm³)²⁰. Thus, the diffraction signals from biological objects are significantly enhanced through the third and fourth interference terms between the structure factors of the biological samples and the CG particles.

The high electron density of the CG particles yields strong peaks in a Patterson map, which is calculated by a Fourier transform of the diffraction pattern. Every peak in the Patterson map represents the relative position (cross-vector) between two gold particles. By solving the Patterson map, we can obtain the positions of the gold particles, and the solution can serve as the initial phase for PR calculations from diffraction data. Thus, the CG particles function in a similar way to heavy atoms in heavy-atom derivatives for initial phasing in X-ray crystallography¹⁸,¹⁹, but the CG particles are more powerful, as the scattering from CG is much stronger.

Extending diffraction signals from weak scatterers to a higher-resolution range

In order to reconstruct biological objects with a wide range of density contrast, we prepared a model of a bacterial cell with flagella²¹ comprising a large spindle-shaped object (1,400 × 500 nm) and four thin filaments (30 nm diameter) (Fig. 1b and Table 1). Under the experimental conditions of CXDI at SACLA¹¹ (Supplementary Table 1), a diffraction pattern with photon counting noises (Poisson noises), after removing central data (25 × 25 pixels; ≤S_low = 1.7 μm⁻¹) blocked by the beamstop (Fig. 1a), was calculated from the model, and gave signals up to a resolution of ~25 nm (S = ~40 μm⁻¹). 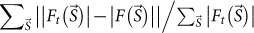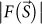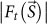The noise level defined as is 13.9% (Table 1), where and are structure amplitudes with and without Poisson noises, respectively²².

Table 1. Parameters of test models and data statistics of image reconstruction by the proposed method.

Parameters of test models
Bacterium
Bacterial cell size (nm)	1400 × 500
Flagellar diameter (nm)	30
Colloidal gold
Diameter (nm)	-	250	250	250	250	150	100
Number of particles	0	16	8	4	2	37	125
Scattering contribution* (%)	-	77	62	44	27	61	59
Projected density contrast of gold to the bacterial cell	-	5	5	5	5	3	2
Noise level in structure amplitude†(%)	13.9	4.6	5.9	7.2	8.1	5.4	4.8

*Contribution from colloidal gold to the total scattering cross-section.

†Defined as where and are structure amplitudes with and without Poisson noises²².

‡Absolute differences between the positions of gold particle in the model and those determined by step1.

§See Eq. 5 in Methods (refs. ^18–19).

||See Eq. 7 in Methods (ref. ³).

¶See section “Averaging of reconstructed maps” in Methods.

**FRC = 0.5 (ref. ²⁶).

††Defined as, where is observed intensity.

We then added 16 spheres representing CG particles with a diameter of 250 nm (Fig. 1b). The projected electron density of a single CG particle is five times higher than that of the cell model (Table 1). A diffraction pattern calculated from this cell-CG model (Fig. 1b) also shows a concentric ring pattern (Fig. 2b), but now dominated by the contribution from the CG particles¹⁴,¹⁵,¹⁷. Each ring is composed of small speckles with an oversampling ratio σ₂ of ~12, where 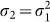. Diffracted photons from this model attain a resolution of more than ~14 nm (S = ~70 μm⁻¹), which is ~1.8 times higher than that from the cell alone. The noise level becomes to be 4.6% (Table 1) and the signal-to-noise ratio of the highest diffraction intensity defined as 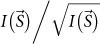is ~3 at S = ~70 μm⁻¹. This value satisfies the Rose criterion ( 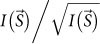≥ 2.5; ref. 23), which is a generally accepted requirement for a statistically reliable measurement of a signal. Throughout this paper, we refer to the diffraction patterns in Figs. 2a and b as observed data, and those from biological objects imaged with CG particles as signal-enhanced diffraction patterns.

Figure 2. Calculated diffraction patterns of test models.

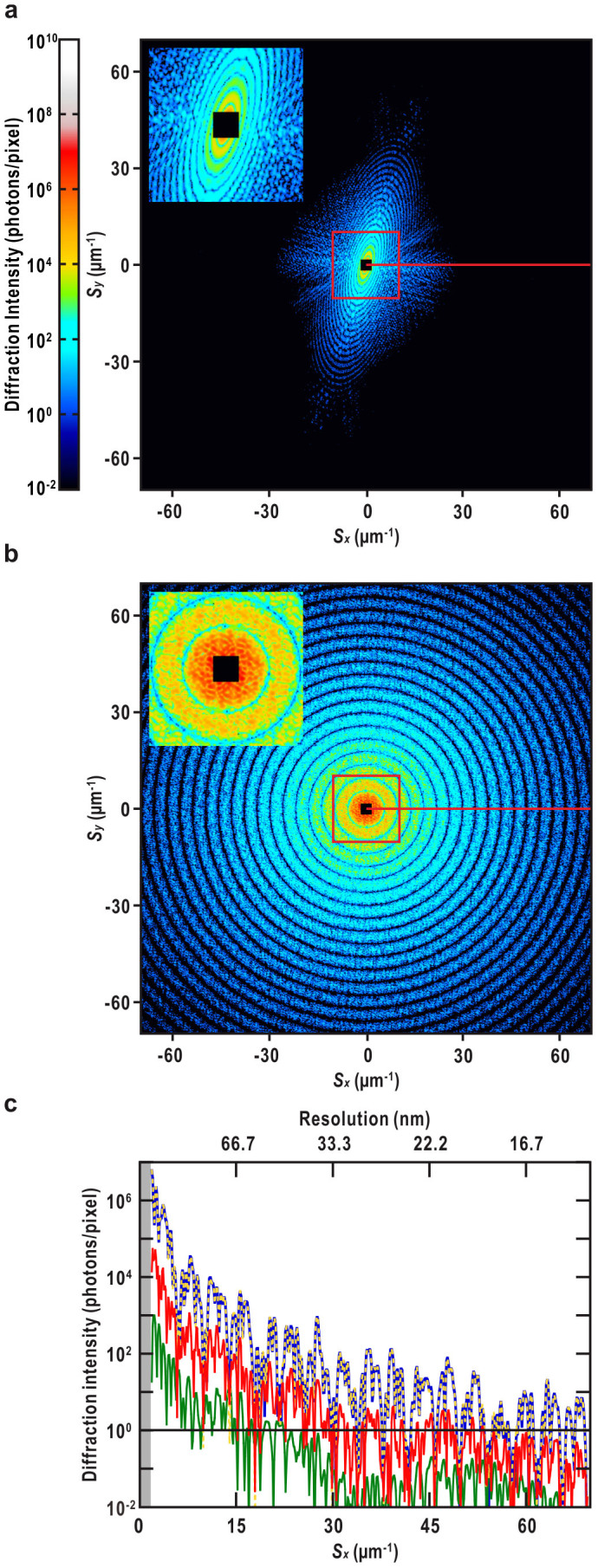
(a) Diffraction pattern calculated from the model shown in Fig. 1b without CG particles. Poisson noises were added. (b) The same as in (a) but with the CG particles (Fig. 1b). Each diffraction pattern is composed of 1024 × 1024 pixels and the highest resolution along the S_x and S_y axes is 14.3 nm (S = 69.8 μm⁻¹). Insets on the upper left show enlarged views of areas surrounded by red squares. The centermost part, where data cannot be collected due to the beamstop, is indicated by a black-filled square (25 × 25 pixels: S_low = 1.7 μm⁻¹). Gradient bar for display scale of intensity is shown on the left in (a). (c) Intensity profiles along red horizontal lines in (a) and (b) calculated from the individual components in Eq. 1, without Poisson noises added. The curves are displayed as: all the objects, blue solid line; the bacterial cell (the first term in Eq. 1), green solid line; the CG particles (the second term), yellow dotted line; and the absolute of the interference term (the third and fourth terms), red solid line. The missing region at center is in gray.

Interference terms (Eq. 1) in the cell-CG model in the calculated spatial-frequency range (excluding the valleys in the concentric ring patterns (Fig 2b)) can enhance the diffraction intensity by one order of magnitude compared with that of the cell-alone model (Fig. 2c).

Initial phasing by Patterson search

We failed in obtaining interpretable projection maps of the cell-CG model from the diffraction pattern in Fig. 2b using a conventional algorithm composing the hybrid-input-output⁴ (HIO) PR and shrink-wrap²⁴ (SW) shape estimation (Supplementary Fig. 1b). Evidently the conventional algorithm alone is unsuitable for retrieving density maps of such complex objects consisting as they do of weak scatterers and many stronger ones. Diffraction patterns from these samples probably yield unstable supports during iterative PR calculation.

Instead, we first carried out a Patterson analysis to determine the positions of the CG particles (step 1 in Fig. 3). The much higher electron density of CG yields strong peaks at cross-vector positions of CG particles. However, broadening of the peaks resulting from the large size of the gold particle often hampers peak separation and solving the Patterson map (Fig. 4a). Hence, we sharpened the Patterson map with normalized structure amplitudes¹⁸ (Fig. 4b), and then applied the Patterson superposition algorithm¹⁸,¹⁹ (Eq. 5 in Methods), which is commonly used to solve the Patterson map in X-ray crystallography for initial phasing from heavy-atom derivatives. The algorithm found 16 distinct peaks, corresponding to the correct positions of the 16 CG particles (Fig. 4c), with positional errors of less than one pixel (Table 1).

Figure 3. Flow-chart of the method proposed for image reconstruction from the signal-enhanced diffraction pattern.

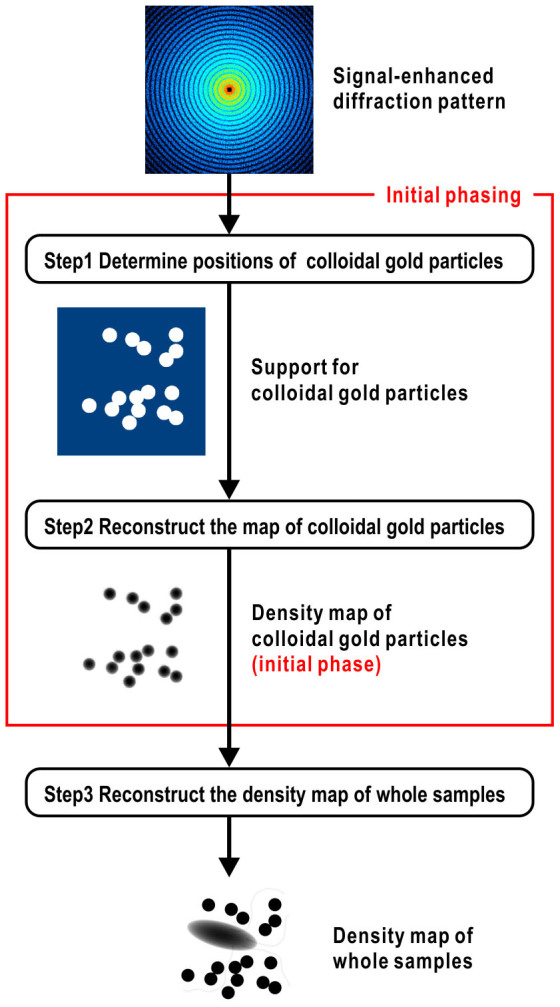
Figure 4. Determination of the positions of the CG particles by Patterson analysis.

(a) Original Patterson map calculated from the signal-enhanced diffraction pattern shown in Fig. 2b. (b) Sharpened Patterson map calculated from the square of the normalized structure amplitude obtained from the same pattern. Insets show zoom-up views of areas enclosed by yellow boxes. (c) A superposition minimum function (SMF; Eq. 5 in Methods) map showing the positions of the CG particles, obtained from the Patterson map in (b) by the Patterson superposition algorithm. Gradient bars for display scale are shown on the left for the maps in (a) and (b), respectively. Display scale of the map in (c) also refers to the gradient bar in (b). Bars represent ~360 nm (50 pixels).

Refinement of initial phase

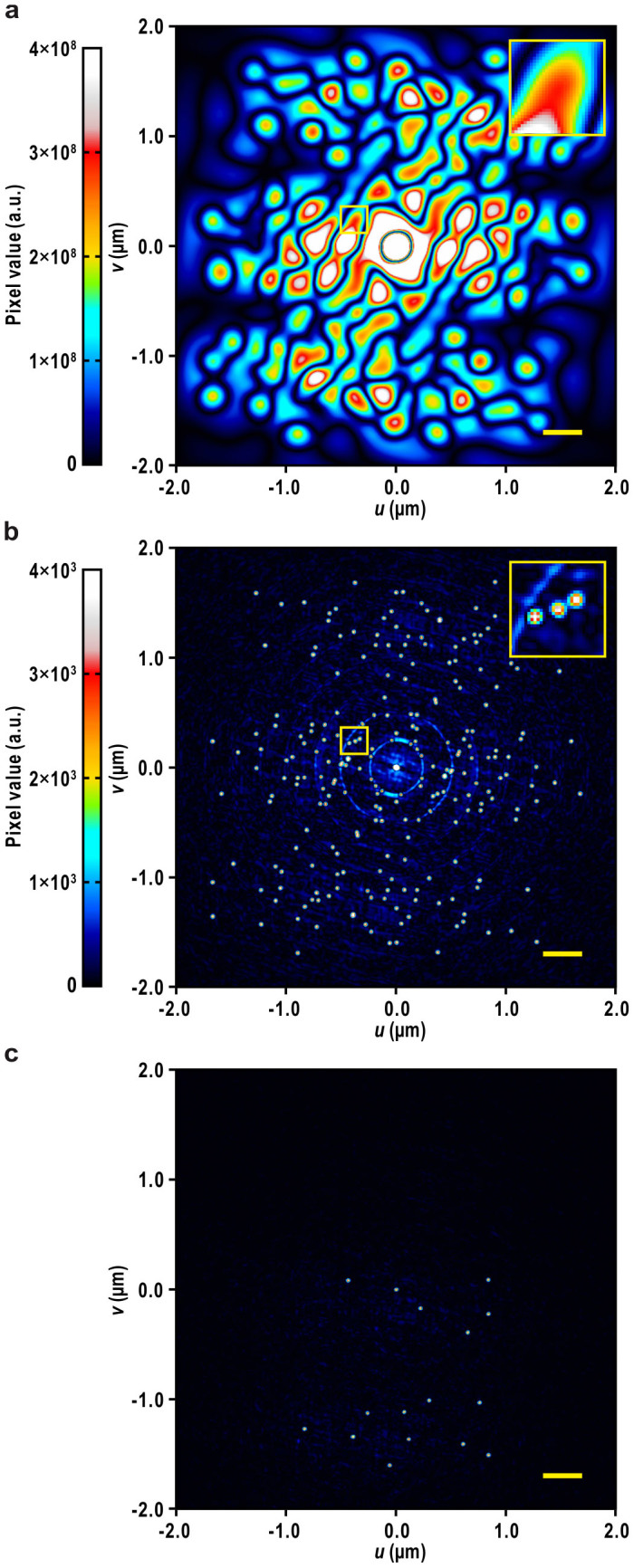
Next, we assigned a loose support on each CG particle, and retrieved the electron density maps of the CG particles by the HIO-PR algorithm (step 2 in Fig. 3). The PR calculation started from random densities to minimize model bias, and the support was kept unchanged during iteration of HIO. The diffraction signals from the CGs were much larger than those from the biological samples (Fig. 2c), which resulted in a reliable map for all 16 CG particles (similar shapes and projected densities to the model at the correct positions (Fig. 5a)). This step can be regarded as a refinement of the initial phase information. We carried out 100 independent HIO-PR calculations starting from different initial random densities, and all the resulting density maps had the same features within the support. There was strong cross correlation between pairs of individual reconstructions (>98.7% see Table 1).

Figure 5. Initial phasing and reconstruction of the density map of all the sample objects.

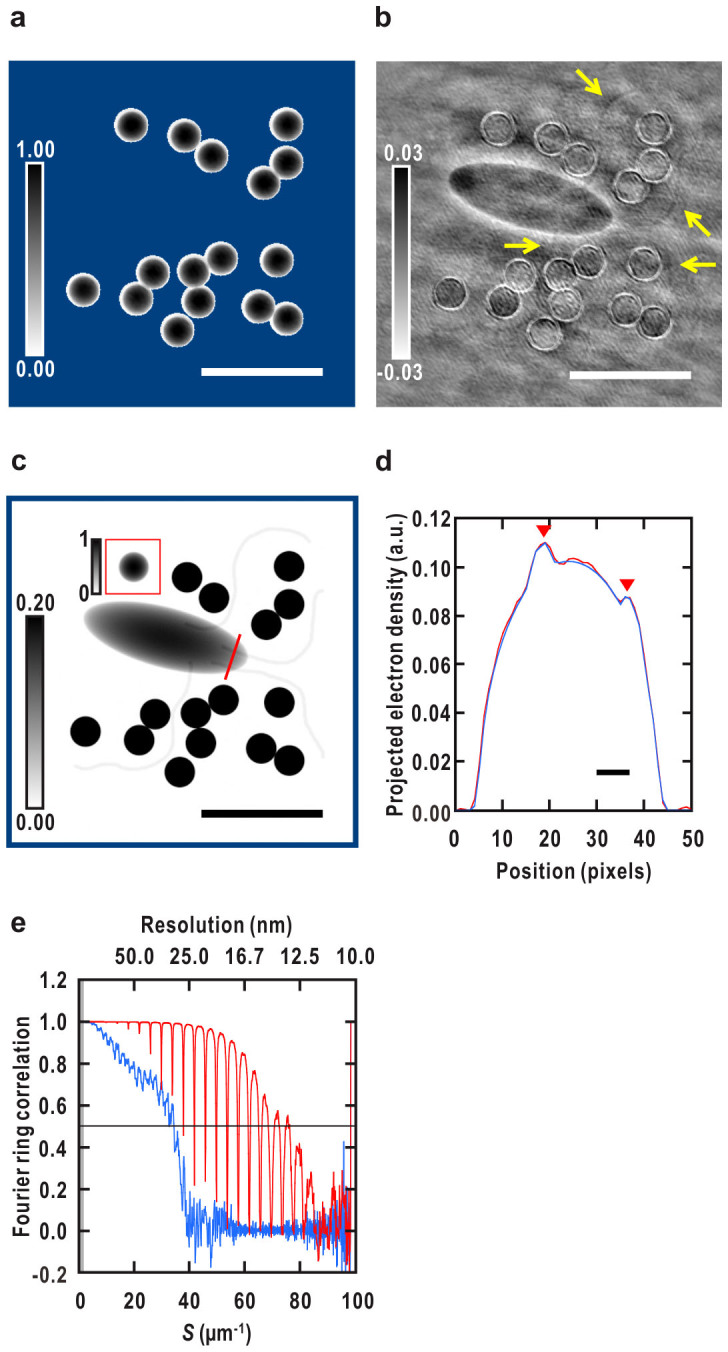
(a) A typical reconstructed map of the CG particles shown in Fig. 1b. Outside the fixed support area is in blue. (b) A difference Fourier map between the observed amplitude (the square root of Fig. 2b) of the cell-CG model and that of a density map of the CG particles with the phase from the map of the CG particles in (a). Calculated as Eq. 9 (Methods). Arrows indicate densities of the flagella (c.f. Fig. 1b). (c) Reconstructed density map of all the objects shown in Fig. 1b. Average of 100 independent reconstructions. A blue square surrounding the entire map corresponds to the inside of the initial support. Bars represent ~1 μm (140 pixels) in (a)–(c). (d) Density profiles of the reconstruction in red and the test model in blue along a red line in (c). Densities of two filaments inside the cell are indicated by down-pointing triangles. Bar represents ~50 nm (7 pixels). (e) FRC analysis of the density map of all the objects. A FRC curve between the test model (Fig. 1b) and the averaged map of all the objects in (c) is shown in red and a FRC curve between the cell model and an averaged map of the bacterium alone reconstructed from the diffraction pattern without CG (Supplementary Fig. 1a) is shown in blue. The horizontal black line indicates a resolution criterion for the reconstruction (FRC = 0.5). The missing region at center is in gray in (e).

We calculated difference Fourier maps²⁵ (Eq. 9 in Methods) between the observed amplitude (the square root of Fig. 2b) of the cell-CG model and that of a density map of CG particles with a refined phase set of CG particles. The difference map clearly resolves densities corresponding to the bacterial cell and the flagella (Fig. 5b), demonstrating that the refined phase set in step 2 can yield structural information of not only CG particles but also of the biological objects.

Reconstruction of the density map of biological objects

We used each map of CG particles as an initial model to reconstruct the entire map of the cell-CG model by HIO-SW PR calculation (step 3 in Fig. 3). The initial support was a large square shape covering the entire area and was periodically updated using the SW algorithm. Retrieved phase sets were further refined by the oversampling smoothness PR algorithm²².

The average reconstruction clearly reveals electron densities corresponding to the cell and the four flagella, even though the projected electron density of a single flagellum is only 1.1% of those of the CG (Fig. 5c). A line profile of the averaged map (Fig. 5d) reproduces well the density distributions of the original model without spreads around neighboring pixels, indicating a point resolution comparable to the pixel size (~7 nm).

The spatial resolution of the map is estimated to be ~13 nm by Fourier ring correlation (FRC) between the reconstructed map and the original model²⁶ (see Eq. 10 in Methods), whereas the resolution of the cell-alone model (Fig. 2a) is limited to ~29 nm (Fig. 5e and Table 1). Thus, imaging biological targets with CG extends spatial resolution more than two-fold. The signal-to-noise ratios of the highest intensities at the achieved resolutions are 3.7 and 2.4 for the models with and without the CG particles, respectively (Table 1).

Number and size of colloidal gold particles

To examine how number and size of CG particles influence image reconstruction, we analyzed test models as summarized in Table 1. First, we examined the same cell model but with 2, 4 and 8 CG particles of 250 nm. Density maps of the CG models tended to be more unstable with fewer CG particles, as monitored by the error metric γ (Eq. 7 in Methods; ref. 3). However, good score density maps did allow entire map reconstruction in all cases (2, 4 and 8 CG particles). Thus, the protocol has the desired outcome for samples with CG of at least 25% total scattering cross-section (Table 1).

Then, we prepared two cell models with 37 CG particles of 150 nm and 125 CG particles of 100 nm. The scattering cross-section of CG for both the models is ~60%, which corresponds to a model comprising the cell and eight CG particles of 250 nm (Table 1). For the cell model with the 150 nm particles, a Patterson search identified not only 37 sharp peaks correctly, but also false peaks. The false peaks probably arose because correlation values between some CG particles and the bacterium happened to be at non-negligible levels, as the projected electron density of a single 150 nm particle is nearly half that of a 250 nm particle. Nevertheless, even with such faulty supports, projection maps of the CG particles and biological objects were successfully reconstructed (Supplementary Fig. 2). In contrast, the number and density of the 100 nm particles prevented correct positioning even in a sharpened Patterson map.

Discussion

In this study, we have developed a method for high-resolution CXDI of biological non-crystalline objects using CG particles, whereby diffraction signals from biological objects are enhanced and determination of the initial phase for image reconstruction is facilitated. The method retrieves phases up to resolutions where the signal-to-noise ratios of the highest intensities are ~3 (Table 1), and improves resolution of single-shot XFEL-CXDI more than two-fold under our recent experimental setup¹¹ (Figs. 2b and 5c–e). Due to the high phasing power of strong scatterers¹⁷, the method can robustly reconstruct projection maps of cellular objects with a low projected density, such as flagella protruded from a cell body. Periodic updates of the supports by the SW algorithm perform well in our scheme (Fig. 5c), overcoming the usual drawback of the SW algorithm in often removing low-contrast objects around major masses.

Although the FRC plot (red curve in Fig. 5e) indicates that the resolution of the entire map is ~13 nm, the quality of the retrieved phase becomes relatively lower at a periodicity corresponding to valleys when the same structure factors of the CG particles are used (Fig. 2b). However, this effect would be less severe in real situations as the shapes of individual CG particles are not very uniform (Supplementary Fig. 3). Also, a mixture of CG particles of various sizes could help.

To retrieve phase information from experimental diffraction patterns, it is critical to start from a reliable initial phase. From the position of the gold particles determined by Patterson search (step 1), an iterative PR allows reconstruction of projection maps of CG particles (step 2), and is less dependent on the shape and size of each CG particle and the density distribution inside the particle. Thus, this process refines the initial phase set, and the refined phase information, indeed, has the power to resolve biological objects including low-density structures (Fig. 5b). Phase improvement methods such as solvent flattening and density modification developed for X-ray crystallography²⁵ may further improve the phase set. A combination of different phase sources including anomalous scattering is also feasible, which could provide more objective phase information as in the case of X-ray crystallography²⁵. These features indicate that the method is robust, versatile and has the possibility of further refinements.

Although the present results derived from XFEL-CXDI experiments reached a resolution limited by the scope of the projection approximation, X-rays with shorter wavelength could extend this (see Eq. 4 in Methods)². In CXDI using synchrotron radiation (SR-CXDI)¹¹,²⁷,²⁸,²⁹, radiation damage of samples is a major limiting factor in attaining a higher resolution⁵. Our method may improve this situation, since the enhancement of diffraction signals allows imaging with lower X-ray doses. This could be particularly useful for collecting many tilt series of the same sample in tomography. When diffraction signals can be enhanced to a resolution beyond the projection approximation, reconstruction of a higher-resolution map, beyond the limit of the Ewald sphere from a number of diffraction datasets collected at different tilt angles³⁰, becomes possible. Here, CG particles could also work as fiducial markers for more precise alignment as in electron tomography³¹.

The proposed method works better with strong signals from CG, but the number of CG particles should be reduced to less than several tens in order to solve the Patterson maps correctly (Table 1). Hence, we recommend adding several tens of CG particles of ≥150 nm around biological targets. Preparation of such samples in a frozen-hydrated state is possible using a freezing machine with a humidity-controller and/or an adhesion-promoting membrane for sample support¹¹,³². Supplementary Fig. 3 shows examples of suitable samples prepared under controlled humidity. Micro-patterning devices could also be used to place CG particles around biological targets³³. Our method is compatible with droplets of samples ejected from a liquid jet injector³⁴ if CG is added to the sample solution. Experiments of signal-enhanced CXDI based on the calculations reported here are presently underway in our team.

Methods

Preparation of test models

The size of test images is 600 × 600 pixels with a pixel size of 3.6 nm. The whole area corresponds to ~2.2 × 2.2 μm², which is roughly equal to that of the focused X-ray beam under our coherent X-ray diffraction imaging (CXDI) experiments at SACLA¹¹. A bacterial cell was expressed as an ellipsoid with a semi-major axis length (a) of 700 nm and a semi minor axis length (b) of 250 nm, and its projected electron density ρ_B (x, y) was calculated as,

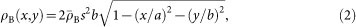where 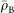is the average electron density of the bacterial cell, and s a pixel size. We assumed that 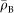was equal to the average electron density of protein and calculated to 433 electrons/nm³ from the average composition of protein (H_48.6C_32.9N_8.9O_8.9S_0.3) and its density of 1.35 g/cm³ (ref. ²⁰). This assumption should hold, since cells are densely packed with macromolecules, mostly protein and nucleic acids³⁵. Flagella filaments were drawn as curved lines with a thickness of 30 nm (ref. ²¹), and the projected electron density was calculated by multiplying the thickness and the average electron density.

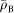A colloidal gold (CG) particle was approximated as a sphere with a radius d, and its projected electron density ρ_CG (x, y) was calculated as,

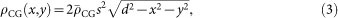where 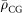, the average electron density of a CG particle, was calculated to be 4,664 electrons/nm³ from its density of 19.31 g/cm³. CG particles were placed randomly around the bacterial cell model as in Fig. 1b.

In this model, most buffer solution surrounding the bacterium was assumed to be removed. This is necessarily requisite to obtain diffraction patterns with the good contrast, and we can routinely prepare these samples under humidity control (Supplementary Fig. 3).

Calculation of diffraction patterns

The Fraunhofer diffraction patterns of the test models were calculated using Eq. 1 with the experimental parameters¹¹,³⁶ (Supplementary Table 1). Due to the statistical nature of photons, the diffraction intensity observed on a pixel fluctuates around the actual value according to Poisson statistics. We adopted this noise model and added Poisson noise to the calculated diffraction patterns. Other noises such as dark current and readout noises of the detector are very small³⁷ and were not considered.

Correct representation of the projected electron density of the object can be obtained from a diffraction pattern on a plane perpendicular to the incident X-ray beam, but the diffraction pattern lying on the Ewald sphere is only measured on the detector (Fig. 1). The separation S_sep between the plane and the Ewald sphere surface at a given spatial frequency S is expressed as,

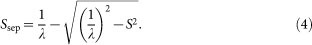The Ewald sphere is regarded as a flat plane (projection approximation), when S_sep is less than at least 1/2D, where D is the thickness of the object along the direction of incident X-ray²,¹⁶. In this study, we used a safer condition, namely that S_sep is less than 1/(4D) (ref. ²), where the highest resolution along the S_x- and S_y-axes was set to 14.3 nm (S = 69.8 μm⁻¹).

Image reconstruction by the Patterson search and phase retrieval

The algorithm for PR from the observed diffraction patterns is composed of three steps as follows (Fig. 3).

Step 1: Determination of the positions of CG particles

The observed amplitude was first normalized with the square root of circular-averaged observed intensities and a Patterson map was calculated by the Fourier transform of the square of the normalized amplitude¹⁸. If this sharpened Patterson map was too noisy for peak search, the Patterson map was smoothed by convoluting a Gaussian function with a full width at half maximum (FWHM) of four pixels.

Then, we applied the Patterson superposition algorithm¹⁸,¹⁹ to the sharpened Patterson map 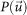. In this algorithm, a superposition minimum function (SMF),

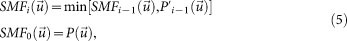is calculated recursively. Here, 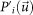is a shifted version of the original sharpened Patterson map 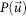onto the position of a peak arbitrarily chosen from i-th SMF and 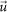is a positional vector in the sharpened Patterson map. In an ideal case, the second SMF gives the positions of all the CG particles. We repeated the calculation of the SMF map until the number of peaks was unchanged, and the third SMF usually gave the correct solution. Positional errors of CG particles determined from peak positions in the SMF maps are summarized in Table 1.

Step2: Reconstruction of the projection map of CG particles

We assigned a loose circular support with a diameter of 1.1-times larger than the CG particles onto each position of CG derived from the SMF maps. Then, density maps within the supports were reconstructed by the Hybrid-Input-Output (HIO) algorithm⁴ implemented in the ZOCHO¹⁶,³⁸ program of the SITENNO program suite³⁹. Each reconstruction was started from random densities and 10,000 iterations of the HIO calculation were performed with fixed supports.

As a reciprocal-space constraint, calculated structure amplitudes were replaced with the observed amplitudes except for the central missing data. We applied a real space constraint with a feedback parameter β of 0.90 as,

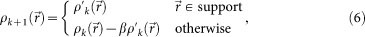where 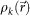and 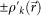are projected electron densities at k-th cycle before and after the reciprocal space constraint is applied. We also adopted a constraint that all densities were real numbers, which promoted faster convergence of the iterative HIO calculation. The stability of the solutions for each HIO cycle was monitored with an error metric γ (ref. ³) as,

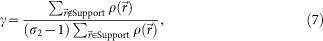where σ₂ is the oversampling ratio³ in two dimensions. γ represents the ratio of total electron densities inside and outside of the support.

Step 3: Reconstruction of the density map of biological objects

The projected electron density map of all the objects was reconstructed using the ZOCHO program. A reconstructed density map of the CG particles obtained in step 2 and a square loose support covering whole objects (1.3-times larger than the whole view) were used as an initial model. Table 1 summarizes γ values of the density map of the CG particles up to step 3. The phase retrieval (PR) calculation consisted of 10,000 cycles of HIO and shrink-wrap²⁴ (SW) after every 100 HIO iterations, and following 1,000 HIO for the optimal convergence of the reconstructions. For improvement of the support by SW, we defined inside support as the area having electron density higher than ~4.5% of the projected density of the flagella model. Then, the reconstructions were refined by 5,000 cycles of oversampling smoothness²² (OSS) PR-calculation. The edges of the supports used in the SW and the OSS were weighted down by Gaussian. The FWHMs of the Gaussian functions were reduced from 4.1 to 1.3 pixels by a step of 2% for the SW in real space and from 1024 to 1 pixel by a step of 0.14% for the OSS in Fourier space. For comparison, we carried out conventional reconstructions by the HIO and SW algorithms starting from random densities (Supplementary Fig. 1).

Averaging of reconstructed maps

To minimize errors of the PR calculation, we calculated 100 independent reconstructions for each test model, and aligned them to each other by maximizing the correlation coefficient defined as,

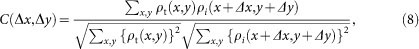where ρ_i (x, y) and ρ_t (x, y) represent densities of i-th reconstructions and that used for a template, respectively.

For the initial template, we used a reconstruction with the largest sum of cross-correlation values between this reconstruction and the others. Reconstructions with low cross-correlation values were excluded from the average (Table 1). Then, individual density maps were aligned again to this average, and were averaged as the final projected electron density map (Fig. 5c and Supplementary Figs 1a and 2b).

Difference Fourier analysis

The phasing power of refined phase sets obtained in step 2 was examined by the difference Fourier map²⁵, calculated as,

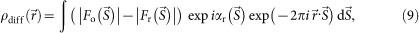where 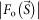is an observed structure amplitude, an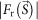d and 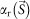are amplitude and phase of a density map of CG particles, respectively. The central unobserved 25 × 25 pixels were filled with zero. When objects not included in the initial phase set are small, a difference Fourier map ideally gives densities of these objects with about a half weight of the original densities²⁵.

Fourier ring correlation

The resolution of the average of the reconstructed maps was estimated by the Fourier ring correlation (FRC)²⁶ as,

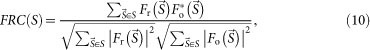where 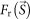and 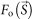are structure factors of the averaged map and the original map, respectively. The resolution was taken to be the spatial frequency at which the FSC drops below 0.5 (ref. ²⁶).

Supplementary Material

Supplementary Information

Supplementary Information