Decoupling local mechanics from large-scale structure in modular metamaterials

Significance

The forward-design approach to mechanical metamaterials determines a structure’s properties after it is designed. In contrast, the inverse-design approach specifies parameter domains then optimizes a cost function to achieve a desired property. The former approach guarantees a structure will exist but lacks the ability to prescribe function. The latter approach has prescribed function, but existence is not guaranteed. Here, we trivialize these design challenges for metamaterials by decoupling local mechanical properties from the bulk structure, allowing both to be specified independently. This work introduces a design strategy that substantially advances the capacity to engineer mechanical metamaterials by specifically using modular units with more free design parameters than constraints. The fundamental strategy is explicitly demonstrated with an origami- and kirigami-inspired structure.

Abstract

A defining feature of mechanical metamaterials is that their properties are determined by the organization of internal structure instead of the raw fabrication materials. This shift of attention to engineering internal degrees of freedom has coaxed relatively simple materials into exhibiting a wide range of remarkable mechanical properties. For practical applications to be realized, however, this nascent understanding of metamaterial design must be translated into a capacity for engineering large-scale structures with prescribed mechanical functionality. Thus, the challenge is to systematically map desired functionality of large-scale structures backward into a design scheme while using finite parameter domains. Such “inverse design” is often complicated by the deep coupling between large-scale structure and local mechanical function, which limits the available design space. Here, we introduce a design strategy for constructing 1D, 2D, and 3D mechanical metamaterials inspired by modular origami and kirigami. Our approach is to assemble a number of modules into a voxelized large-scale structure, where the module’s design has a greater number of mechanical design parameters than the number of constraints imposed by bulk assembly. This inequality allows each voxel in the bulk structure to be uniquely assigned mechanical properties independent from its ability to connect and deform with its neighbors. In studying specific examples of large-scale metamaterial structures we show that a decoupling of global structure from local mechanical function allows for a variety of mechanically and topologically complex designs.

Recent experiments with mechanical metamaterials (1–3) have demonstrated constitutive relations including pentamode behavior (4), negative effective bulk modulus (5), and negative Poisson ratio (6). As a design motif, origami, the art of paper folding, offers interesting possibilities to realize these properties in a wide range of contexts. Because origami is grounded in a centuries-old art form, this approach to creating complex 3D structures benefits from a large body of established techniques. Indeed, from simple flat sheets, studies have documented structures with negative Poisson ratio (7–10), reprogrammable stiffness (11), multistability (12–14), curved metasurfaces (15–17), topologically protected modes (18), tunable low-energy deformations (19), and multiple degrees of freedom (DOF) (20). These examples generally involve relatively simple repeated folding patterns where creasing DOF compete with local and global geometric constraints. As such, collective interactions lead to the observed macroscopic constitutive relations. However, to apply origami design motifs to next-generation devices we must address the challenge of creating folding diagrams for an arbitrarily prescribed large-scale structure, independently from the structure’s desired metamaterial properties.

In most quantitative studies of tessellated origami metamaterials the folding pattern is deeply coupled to the structure’s mechanics. Consequently, the design space for large-scale bulk structure is tightly constrained by the selection of metamaterial properties. Here, we overcome this difficulty with inspiration from two distinct branches of origami. One of these branches specifically explores structures constructed with two or more pieces of folded paper. These modular origami structures can incorporate hundreds of folded sheets connected together by inserting flaps from one module, which are created during the folding process, into pockets of adjacent modules. The bulk structure is then held together through a tensegrity-like pattern of stresses and friction (21). Our second source of inspiration is the branch of origami that intersects with paper cutting known as kirigami. In this art form, elaborate structures are designed by combining folding and cutting. Mechanically speaking, the removal of material by cutting provides opportunities to introduce additional design parameters and DOF. Combining modular origami with kirigami leads to a metamaterial design strategy that takes mechanically distinct kirigami modules and treats them as voxels in a larger structure. When the kirigami module has more design parameters $N_p$ than constraints imposed by bulk assembly of multiple units $N_c$, each voxel can have its mechanical properties independently prescribed from their adjacent neighbors. In essence, this approach where $N_p-N_c>0$ solves the inverse-design problem (22) and enables a decoupling of large-scale structure from local mechanical function.

Results and Discussion

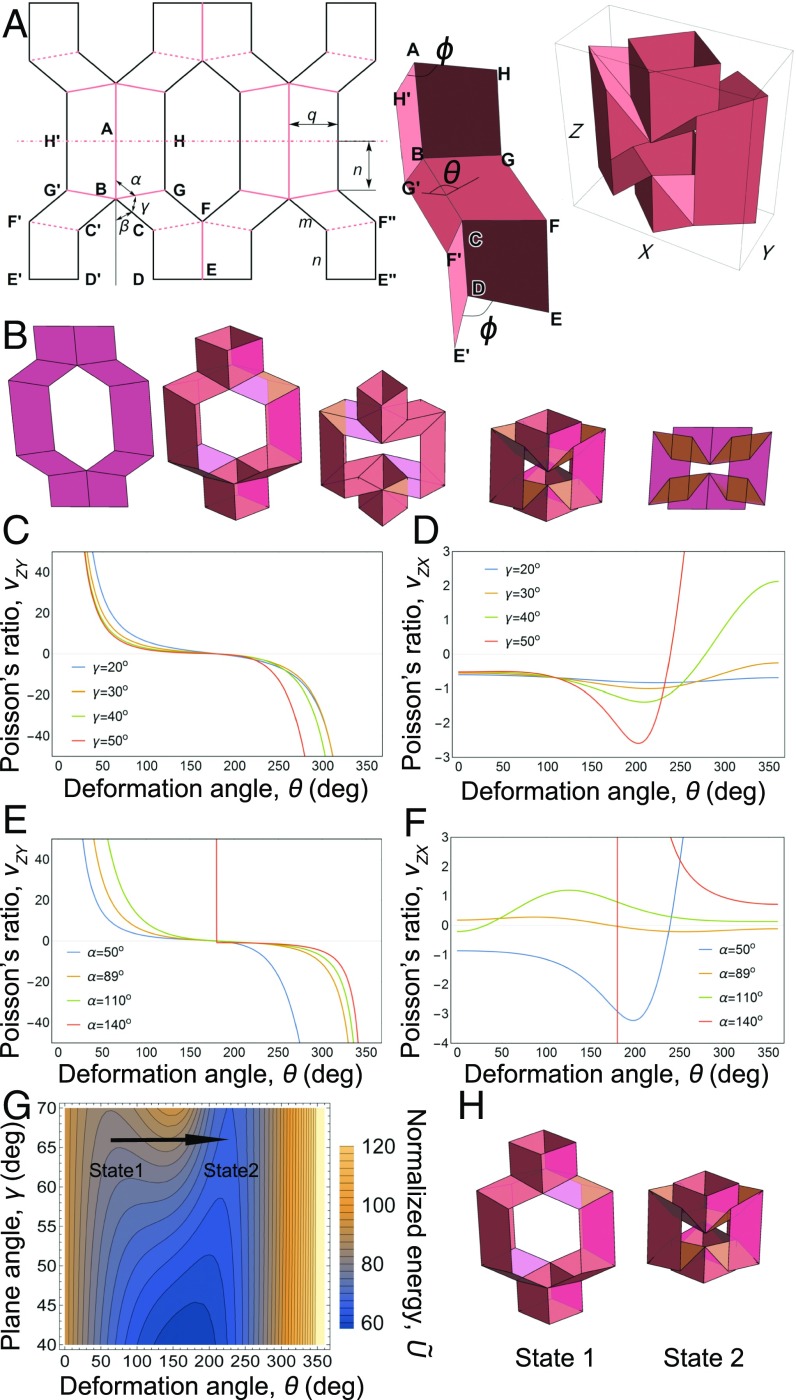
It is possible to conceive innumerable structures for metamaterial assembly that illustrate the general $N_p-N_c>0$ design strategy. To focus our efforts on a specific example, we designed a kirigami-inspired lantern-like pattern formed by cutting a thin sheet (Fig. 1A, black outline), folding along the prescribed lines to form hinge-like creases (Fig. 1A, pink dashed and solid lines), and bonding adjacent edges to form crease-like hinges (Fig. 1A, e.g., $BCD$ bonds $BC\prime D\prime$; 3D rendering shows the module’s assembled form, SI Appendix, Fig. S1). The cutting and folding geometry is determined by angles $\alpha ,\gamma$, and lengths $m,n,$ and $q$ so that $N_p=5$. Each assembled module has only a single kinematic DOF represented here by the dihedral angle $\theta$ measured between planes $BCFG$ and $BCF\prime G\prime$. Although this choice for the DOF is not unique, $\theta$ conveniently varies from $0°$ to $360°$ when the module is designed with parameters that avoid self-intersection during folding (Fig. 1B and Materials and Methods).

Fig. 1.

Geometry-driven metamaterial properties of a kirigami lantern-like module. (A) The design pattern of one module (Left) involves cutting a thin sheet along the thick black lines, then folding along the mountain (dashed) and valley (solid) creases. Edges $BCD$ and $BC\prime D\prime$ are bonded to create crease-like hinges in each of the four symmetric quadrants. Similarly, $F\prime E\prime$ is bonded to $F^{″}{E}^{″}$, along with the symmetric edges in the module’s upper half. The plane angle parameters $\alpha$ and $\gamma$ and lengths $m$, $n$, $q$ determine the 3D structure shown in the $1/4$ (Middle) and full (Right) unit module. The dihedral angle $\theta$ is chosen to quantify the module’s configuration. Parameters $\varphi$ and $\beta$ are useful for the mathematical description of the geometry (Materials and Methods). (B) The module takes various forms determined by the configuration angle $\theta =0°,90°,180°,270°,$ and $360°$. Poisson ratios (C) ${\nu }_{ZY}$ and (D) ${\nu }_{ZX}$ as functions of folding configuration for $\alpha =60°$ and $\gamma =20°,30°,40°,$ and $50°$. Poisson ratios (E) ${\nu }_{ZY}$ and (F) ${\nu }_{ZX}$ as functions of folding configuration for $\gamma =40°$ and $\alpha =50°,89°,110°$, and $140°$. Calculations in C–F use $m/q=n/q=1.5$. (G) The normalized elastic energy $\stackrel{\sim }{U}$ as a function of $\gamma$ and $\theta$ for parameter values $\alpha =100°,m/q=n/q=1$, $k_2/k_1=1.5$, and ${\theta }_0=10°$. Arrow indicates the module undergoes a bistable transition between two energetic minima during folding. (H) The module’s configuration for the two mechanically stable states in G. Reading left to right in B and H corresponds to compression along $\widehat{z}$, whereas right to left corresponds to tension along $\widehat{z}$.

When constructed from rigid sheets that neither bend nor stretch the kirigami module’s kinematics are fully determined by geometry. As $\theta$ varies the structure simultaneously undergoes longitudinal and transverse deformations in its dimensions $X(\theta ),Y(\theta )$, and $Z(\theta )$ (Fig. 1 A and B). From these quantities we can calculate the Poisson ratios ${\nu }_{ZX}$ and ${\nu }_{ZY}$, which are essentially the ratios of strain (Materials and Methods). In addition to taking values well beyond the 0 to 0.5 range found in most common materials, we found wide regions of parameter space for $\alpha$ and $\gamma$ as well as wide regions in configuration space $\theta$ that supports two simultaneously negative Poisson ratios (Fig. 1 C–F and SI Appendix, Figs. S2 and S3). Combining the kinematic equations with a linear elastic energy expression reveals further useful properties for bulk metamaterial design (Materials and Methods). Specifically, we find the kirigami module can exhibit monostability or bistability depending on the parameter values for $\alpha$ and $\gamma$ (Fig. 1 G and H and SI Appendix, Fig. S4), which were experimentally confirmed in hand-folded models (SI Appendix, Figs. S4–S6). Having shown the basic lantern-like kirigami module has a wide range of mechanical features, we shift to the more acute challenge of designing large-scale metamaterials with prescribed mechanical properties.

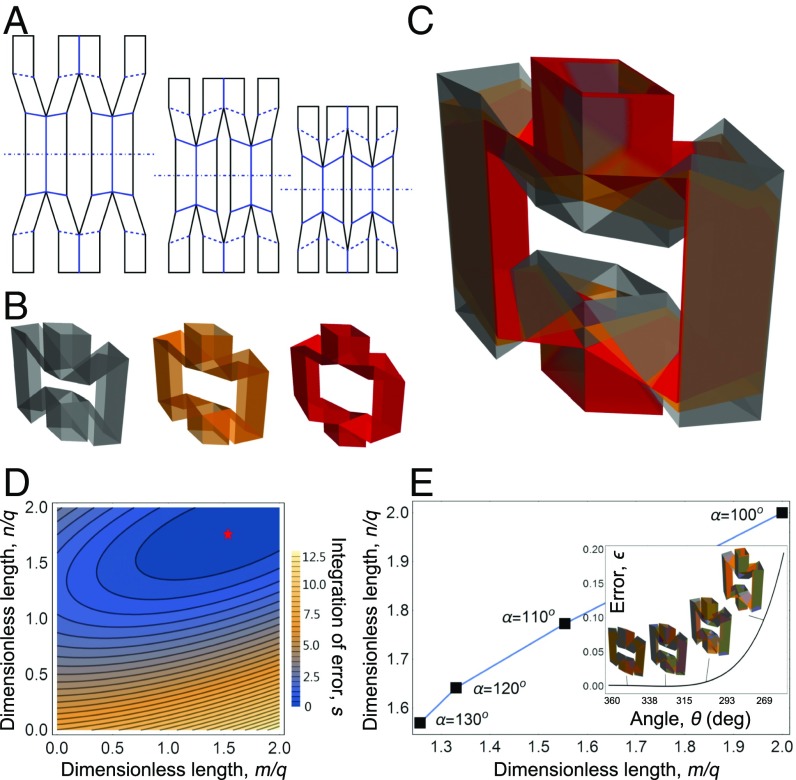
Insights from modular origami art suggest large-scale metamaterials can be assembled by voxelizing the desired large-scale shape into cuboids and assembling the voxelized geometry from a collection of kirigami-inspired modules. As mechanical building blocks, we require each module to be geometrically compatible with its neighbors within design tolerances. In the general case, this condition means voxels are able to freely deform without (i) colliding into their neighbors, (ii) separating from their neighbors, or (iii) experiencing geometric frustration. In the specific example of the lantern-like kirigami module studied here, these conditions impose $N_c=4$ constraints for all $\theta$ in the prescribed folding domain $[{\theta }_a,{\theta }_b]$: The dimensions $X(\theta ),Y(\theta )$, $Z(\theta )$, and the angle $\mathrm{\angle }EDE\prime$ must match for all voxels. The first three constraints ensure voxels do not intersect during folding, and the fourth constraint ensures structures can be rigidly connected along the $\widehat{z}$-axis. Because the basic module has five independent design parameters, these four constraints imposed by bulk assembly leave $N_p-N_c=5-4=1$ free parameter to choose mechanical properties of each voxel. As an example, we picked a set of parameters for a target module (Fig. 2 A–C, gray module) and constructed two additional geometrically compatible modules with independently prescribed $\alpha$ (Fig. 2 A–C, orange and red modules). The remaining parameter values for these additional modules were found by calculating an error function $ϵ(\theta )$ between the target and candidate geometries (Materials and Methods) and searching for optimal parameter values that minimize the integrated error $s={\int }_{{\theta }_a}^{{\theta }_b}ϵd\theta$ over the design interval, which in this case was chosen to be $[300°,360°]$. A subspace projection of the parameter landscape helps visualize the optimization and shows a local minimum representing optimal values for the dimensionless lengths $m/q$ and $n/q$ (Fig. 2D, red star). Varying $\alpha$ to other prescribed values shifts this local minimum within the subspace, leading to different values for the optimized parameters (Fig. 2E, points). Generally, we found our method reliably produced geometric compatibility satisfying tight error tolerances within the prescribed folding domain (Fig. 2E, Inset, $ϵ$ for $300\le \theta \le 360°$) but that these same designs become incompatible outside the prescribed bounds (Fig. 2E, Inset, $ϵ$ for $\theta <300°$). With this approach for designing geometrically compatible and mechanically distinct building blocks we now focus on voxelizing and assembling 1D, 2D, and 3D large-scale metamaterials.

Fig. 2.

Geometric compatibility of modular kirigami voxels. (A) Design patterns and (B) structure for three geometrically compatible voxels where the first structure (gray: $\alpha =100°,\gamma =62.4°$ and $m/q=n/q=2$) is the target, and the second (orange: $\alpha =110°,\gamma =57.7°,m/q=1.55$, and $n/q=1.77$) and third (red: $\alpha =120°,\gamma =51.2°,m/q=1.33$, and $n/q=1.64$) are determined by parameter optimization over a prescribed folding domain. (C) Overlapping the three voxels shows how different design patterns can simultaneously satisfy the $N_c=4$ conditions for geometric compatibility in $X$, $Y$, $Z$, and $\mathrm{\angle }EDE\prime$ (e.g., $X_{\text{gray}}=X_{\text{orange}}=X_{\text{red}}$ and $Y_{\text{gray}}=Y_{\text{orange}}=Y_{\text{red}}$, etc.). This mutual consistency allows geometrically compatible voxels to be interchangeable within a large-scale structure assembled from a mechanically heterogeneous collection of modules. (D) Identifying geometric compatibility requires minimizing the integrated error $s$ over the design parameters. This projection of parameter space shows the local minimum of $s$ (red star) as a function of dimensionless lengths $n/q$ and $m/q$. (E) Varying folding angle $\alpha$ changes the optimal values of $n/q$ and $m/q$ that minimize error between the target structure and the structure being optimized for geometric compatibility. (Inset) The error function from which we calculate and minimize the integrated error $s$.

A simple metamaterial for experimentally validating geometric and mechanical predictions is a 1D chain of voxels aligned on the $\widehat{z}$-axis (SI Appendix, Figs. S5 and S6). We fabricated these structures with one, two, and three voxels from thin sheets and measured their force–displacement relation. These data compared favorably with the simple energetic model predictions (Materials and Methods), and we generally found the results to be reproducible up to material-specific plastic deformations arising from multiple cycles of testing. A notable exception between the model and data was observed when one voxel with large $m$, which was predicted to undergo a bistable transition, instead underwent two bistable transitions (SI Appendix, Figs. S5 and S6). In these data, we found the lower portion of the voxel hopped between bistable states as the strain increased, while the upper portion hopped between bistable states as further strain was applied. Because the energetic model is symmetric with respect to inversion along $\widehat{z}$, the transitions of a voxel’s upper and lower sections between states 1 and 2 are predicted to occur simultaneously (Fig. 1 G and H). Real materials and practical fabrication methods, however, introduce heterogeneities that break this symmetry. As a whole, these experiments generally show mechanical properties in voxelized 1D metamaterials can be predicted, prescribed, and designed, but nevertheless, experimental validation is still important.

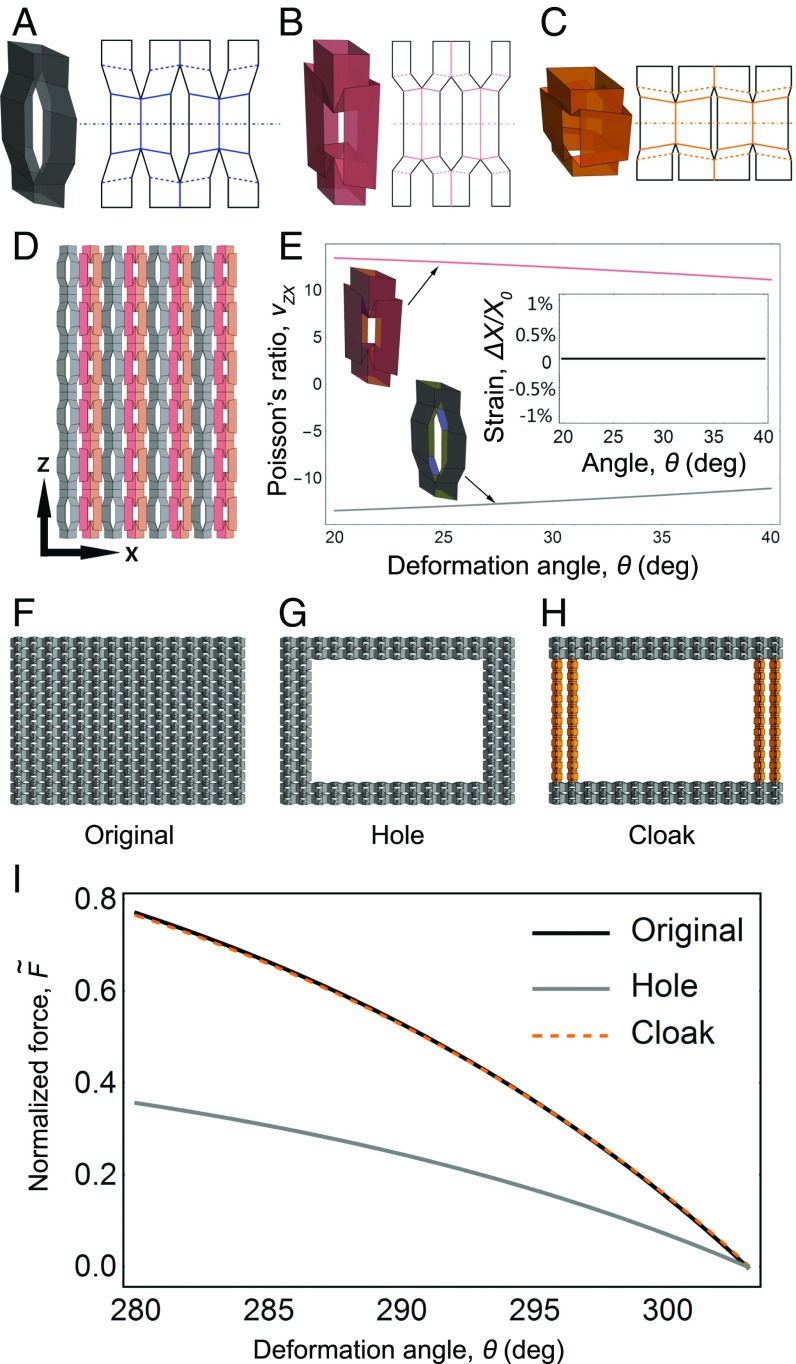
Next, we use the $N_p-N_c>0$ design strategy to construct 2D bulk metamaterials, which by scaling up in dimension allows for greater mechanical and topological complexity. The two examples we study mask bulk deformations of a large-scale structure using a target module with prescribed properties (Fig. 3A) and geometrically compatible modules optimized to (i) neutralize bulk strain in the $\widehat{x}$ direction (Fig. 3B) and (ii) “cloak” a structural hole (Fig. 3C). In our first example, the 2D structure is voxelized into a series of 1D stripes alternating target and geometrically compatible modules (Fig. 3D). When compressed along the $\widehat{z}$-axis, the target module’s $\theta$-dependent Poisson ratio ${\nu }_{ZX}$ is compensated for by the compatible module, whose Poisson ratio is optimized to be equal and opposite (Fig. 3E, pink and gray lines). The collective effect is to allow for deformations along the $\widehat{z}$-axis while neutralizing bulk strain along the $\widehat{x}$-axis (Fig. 3E, Inset). Interestingly, the zero bulk Poisson ratio engineered into this structure is what makes cork useful as a bottle stopper; cork stoppers provide a tight transverse seal while still allowing for longitudinal motion in or out of the bottle’s opening (23). In our second example, a homogeneous 2D structure composed from the target module (Fig. 3F) is structurally weakened with a hole (Fig. 3G) and then reinforced with geometrically compatible modules (Fig. 3H). In terms of the bulk properties, the original and reinforced structures have Young’s moduli of 8.1 kPa, whereas the weakened structure has a Young’s modulus $\approx 53\%$ lower at 3.8 kPa. In this example, we optimized the free parameter of the reinforcing module to restore the initially prescribed bulk force–displacement relation to its original form (Fig. 3I and Materials and Methods). When probed with external loads, this new heterogeneous structure can function as a mechanical cloak by obscuring any contents placed in the hole.

Fig. 3.

Assembly of kirigami modules into voxelized 2D mechanical metamaterials. Starting with the (A) target voxel (gray; $\alpha =100°,\gamma =62.4°$ and $m/q=n/q=1$), we generate a (B) geometrically compatible strain-neutralizing voxel (pink; $\alpha =80°,\gamma =62.4°,m/q=1$, and $n/q=1.77$) and a (C) geometrically compatible mechanically reinforcing voxel (orange; $\alpha =96.9°,\gamma =63.3°,m/q=0.24$, and $n/q=0.71$). (D) Forming a striped pattern of the target (gray) and strain-neutralizing (pink) voxels leads to a structure where the (E) $\theta$-dependent Poisson ratio of the two voxel types cancels out to create a large-scale metamaterial with zero strain along the $\widehat{x}$-axis during compression. (F) Forming a homogeneous 2D bulk metamaterial from target voxels leads to a structure with prescribed mechanical properties. (G) By removing target voxels, we create a cavity that introduces topological complexity, but the structure as a whole deviates from the prescribed mechanical properties. (H) By replacing a subset of target voxels (gray) with reinforcing voxels (orange) that were optimized to match the mechanical response over the prescribed folding domain, we are able to restore the original structure’s target properties. (I) Calculations for the normalized force response $\stackrel{\sim }{F}(\theta )$ demonstrates the ability to have independent structural and mechanical properties. Deviations between the original and hole-cloaking structure are constrained by the optimization error tolerance.

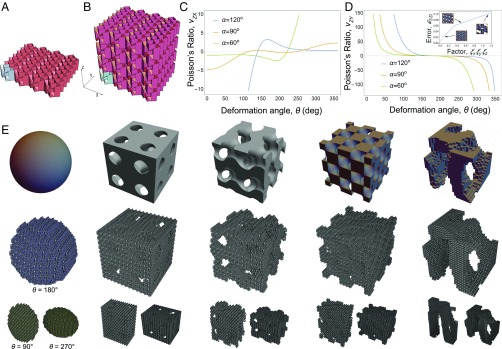
Topological complexity can be greatly increased in large-scale 3D metamaterials. To construct such structures, we voxelize the $\widehat{x}\widehat{y}$-plane (Fig. 4A) and stack along the $\widehat{z}$-axis to create a cuboidal structure with all modules in the same orientation (Fig. 4B). As with the 1D and 2D structures, this 3D voxelization of space is independent from the prescribed mechanical properties of the modules as long as geometric compatibility and $N_p-N_c>0$ are satisfied. For a demonstrative example of what can be achieved with the same $4\times 7\times 4$ cuboidal volume (Fig. 4B), we chose three sets of parameters and calculated the respective Poisson ratios (Fig. 4 C and D). These data illustrate how the same large-scale structure can have distinct mechanical properties. For practical purposes, it is important to note the accuracy between a target 3D structure and a structure fabricated from finite-size voxels will be tunable. These differences, quantified by an error metric such as ${ϵ}_{3D}$ (Methods and Materials), can be reduced by scaling down the voxel size relative to the target structure (Fig. 4D, Inset), which produces a practical trade-off between structural accuracy and the total number of voxels needed for an application. To fully demonstrate the potential of the $N_p-N_c>0$ design strategy, we chose five large-scale 3D target structures including a sphere, three triply periodic minimal surfaces, and a micro-CT volumetric scan of mouse femur bone (Fig. 4E, first row). We voxelized these structures, arbitrarily prescribed one set of mechanical properties on all modules involved, and calculated the various configurations as a function of $\theta$ (Fig. 4E, second and third rows). Although all of these 3D structures have identical kinematics, we see the decoupling of large-scale structure from local mechanical properties trivializes the design challenge of simultaneously achieving prescribed mechanical and topological complexity.

Fig. 4.

Assembly of kirigami modules into voxelized 3D mechanical metamaterials. (A) Tessellating voxels in the $\widehat{x}\widehat{y}$-plane leads to metamaterials that are (B) stackable along the $\widehat{z}$-axis. These structures have mechanical properties independent of their ability to tessellate 3D space. Plots of the Poisson ratios (C) ${\nu }_{ZX}$ and (D) ${\nu }_{ZY}$ as a function of deformation angle $\theta$ show a wide range of allowable behaviors for the same $4\times 7\times 4$ cuboid bulk structure in B, but with variable parameters for $\alpha$ and $\gamma$. For the plots shown here, we chose $\gamma =\text{arcsin}[(9/10)\sin (\alpha )]$ to obtain a wide variety of behavior in ${\nu }_{ZX}$. D, Inset shows the error ${ϵ}_{3D}$ between target 3D structure and voxelized 3D structure as a function of the product of scaling factors ${\xi }_x,{\xi }_y$, and ${\xi }_z$ (Materials and Methods). Larger values of $\xi$ lead to larger voxels with a coarser approximation of the target structure, whereas lower values of $\xi$ have smaller voxels and a more fine approximation. (E) The top row shows five target 3D structures representing a sphere, three triply-periodic minimal surfaces, and a digitized micro-CT scan of a mouse femur bone. The second and third rows are renderings of the different voxelized 3D metamaterials with folding configurations given by $\theta =90°,180°$, and $270°.$ Increasing $\theta$ corresponds to compression along $\widehat{z}$, whereas decreasing $\theta$ corresponds to tension along $\widehat{z}$. Although all structures have identical compressive properties ($\alpha =60°,\gamma =51°$, and $m/q=n/q=1$), the scaling factor triplets $⟨{\xi }_x,{\xi }_y,{\xi }_z⟩$ are $⟨0.37,0.21,0.26⟩$ for the sphere and triply-periodic minimal surfaces, whereas the micro-CT scan has $⟨{\xi }_x,{\xi }_y,{\xi }_z⟩=⟨8,9,5⟩\times {10}^{-3}$. These large-scale metamaterials highlight the complex topology that can be achieved independent from the prescribed mechanical properties using the $N_p-N_c>0$ design strategy.

Conclusion

The design principle for decoupling local mechanics and bulk structure in 1D, 2D, and 3D metamaterials introduced here broadly applies to all classes of metamaterials. Nevertheless, by working with a specific example of the lantern-like kirigami module we found a number of insights useful for any practical realization of the $N_p-N_c>0$ design strategy. For example, if the fabrication material is brittle, it may be advantageous to design structures using a homogeneous set of modules. By ensuring all voxels in the metamaterial are identical the compressive behavior is always geometrically compatible and the risk of failure reduced. However, if the fabrication material is pliable, then heterogeneous structures can activate additional bending or stretching DOF, offering greater design flexibility with less restrictive design tolerances. Another consideration is what manufacturing approaches are practical for the structures introduced here. Hand-crafted devices have an obviously limited throughput, but technologies such as 3D-printed self-folding polymers seem viable in light of recent demonstrations (24). At much smaller scales, DNA self-assembly has been used to create folding structures where oligo hybridization is a means to form both thin sheets and hinge-like crease patterns (25, 26). Thus, at the nanoscale, there are opportunities to mass-produce self-assembled biocompatible mechanical metamaterials with these uniquely addressable building blocks (27).

Throughput aside, the strategy of decoupling large-scale structure from mechanical function by modular design reduces cooperative and collective effects, greatly simplifying the inverse-design problem. By taking a tolerance-defined approach with finite parameter domains, we are able to generate geometric diagrams for bulk metamaterial structures using the lantern-like module (Materials and Methods and SI Appendix, Fig. S7). These designs can be optimized to minimize failure, cost, or complexity while still faithfully reproducing the desired function in specific applications. As such, the future for this design strategy where the number of parameters for each module is greater than the number of constraints imposed by bulk assembly seems well-suited for a variety of applications in next-generation smart materials, tissue engineering scaffolds, or even deployable architectural elements (SI Appendix, Fig. S8).

Materials and Methods

Geometry and Mechanics of Kirigami Lantern-Like Module.

Given a cutting and folding pattern (Fig. 1A), where by definition $\beta =\pi -\alpha -\gamma >0$, the kirigami module fits into a cuboidal volume of size $X(\theta )\times Y(\theta )\times Z(\theta )$, where $X=2\left[q\cdot \cos (\varphi /2)+m\cdot \sin (\psi )\right],Y=2q\cdot \sin (\varphi /2)$ and $Z=2[2n-m\cdot \cos (\psi )+q\cdot \cot (\alpha )].$ Here, we express all angles in radians and have used $\varphi =2\hspace{0.17em}\text{arcsin}[\sin (\theta /2)\cdot \sin (\gamma )/\sin (\alpha )]$, which can be interpreted as the angle $\mathrm{\angle }EDE\prime$, and $\psi$, which can be interpreted as the angle $\mathrm{\angle }BCD$. To express $\psi$ in terms of the geometry’s defining parameters, we assume $\alpha >\gamma$ to arrive at the piecewise expression $\psi ={\psi }_1+{\psi }_2$ for $\pi /2\ge \alpha >\gamma$ and $\psi =\pi -{\psi }_1+{\psi }_2$ for $\alpha >\pi /2>\gamma$, where ${\psi }_1=\text{arcsin}[\sin (\alpha )\cos (\varphi /2){(\cos {(\alpha )}^2+{\left(\sin (\alpha )\cos (\varphi /2)\right)}^2)}^{-1/2}]$ and ${\psi }_2=\text{arcsin}[\sin (\gamma )\cos (\theta /2){(\cos {(\gamma )}^2+{\left(\sin (\gamma )\cos (\theta /2)\right)}^2)}^{-1/2}]$. Analogous expressions can be written for $\alpha <\gamma$.

To prevent self-intersection, the kirigami module must obey $n-m\cdot \cos (\alpha -\gamma )>0$ and $n-m\cdot \cos (\alpha -\gamma )+q\cdot \cot (\alpha )>0$. The first condition can be interpreted as avoiding collisions between the points $F$ and $F\prime$ with their symmetric points on the upper half of the module, and the second condition avoids collisions between $C$ and $C\prime$ with their symmetric points on the upper half of the module (Fig. 1 A and B). For parameters $\alpha ,\gamma ,m,n$, and $q$, which violate these inequalities, the geometrically permitted values of $\theta$ that avoid self-intersection are bounded by a hypersurface in the five-dimensional parameter space that can be directly calculated from the structure’s kinematics.

From the definitions of $X(\theta )$, $Y(\theta )$, and $Z(\theta )$ we calculated the Poisson ratios ${\nu }_{ZY}=-(Z/Y)(dY/dZ)$ and ${\nu }_{ZX}=-(Z/X)(dX/dZ)$. In these calculations, increasing $\theta$ corresponds to macroscopic deformations under compression along $\widehat{z}$, whereas decreasing $\theta$ corresponds to macroscopic deformations under tension along $\widehat{z}$. Mechanical properties of the kirigami module were calculated by modeling creases as torsional springs with spring constant $k_1$ that rest at a preferred angle ${\theta }_0$. Joined edges, such as $BCD$ and $BC\prime D\prime$, are similarly treated as torsional springs with the same rest angle but with a different spring constant $k_2$. Using a common rest angle for creases and crease-like joined edges while assigning two different spring constants reflects the details of how experimental samples were fabricated (SI Appendix). These choices can be easily modified according to the context of how modules are assembled. For the case considered here, the energy function takes the form $U=\frac{1}{2}[4k_1\cdot \overline{AB}\cdot {(\varphi -{\theta }_0)}^2+2k_1\cdot \overline{EF}\cdot {(\pi -\varphi -{\theta }_0)}^2+16k_1\cdot \overline{BG}\cdot {({\theta }_{ABGH,CBGF}-{\theta }_0)}^2+2k_2\cdot \overline{E\prime F\prime }\cdot {(\pi -\varphi -{\theta }_0)}^2+4k_2\cdot \overline{CD}\cdot {(\varphi -{\theta }_0)}^2+4k_2\cdot \overline{BC}\cdot {(\theta -{\theta }_0)}^2].$ Here, we use overlines to denote length between two points. Specifically, $\overline{AB}=\overline{EF}=\overline{E\prime F\prime }=n+q\cdot \cot (\alpha )$, $\overline{BG}=q/\sin (\alpha )$, $\overline{CD}=n$, and $\overline{BC}=m$. Dividing $U$ by $q{k}_1$ leads to the normalized energy $\stackrel{\sim }{U}=U/q{k}_1$ (Fig. 1G), which we find exhibits parameter domains with monostability and bistability (SI Appendix, Fig. S4). Note that this stability landscape is not driven by the competition between creasing and bending DOF, as has been shown with other origami structures (11), nor is it driven by a topological discontinuity in configuration space. Instead, the stability landscape found here arises strictly from geometry, which forces some creases to move away from their rest angle (e.g., $\overline{BG},\overline{BC}$, and $\overline{CF}$) while allowing others to return to their rest angle (e.g., $\overline{AB},\overline{CD}$, and $\overline{EF}$). In this idealized model, the transition between bistable states is a symmetric process where the top and bottom portions of the kirigmi module simultaneously hop between stable configurations. In real materials, small heterogeneities can lead to sequential hopping (SI Appendix, Figs. S5 and S6). As a consequence, a 1D structure with $N$ voxels is capable of supporting up to $4^N$ distinct stable configurations (SI Appendix, Fig. S4).

Optimizing Voxels for Geometric Compatibility.

As described in the text, geometrically compatible metamaterials are constructed in a two-step process. Step one is to analyze the number of available design parameters $N_p$ and pick a set of values that produces the desired properties. For the specific example of the lantern-like module, these chosen parameters are denoted ${\alpha }_0,{\gamma }_0,m_0,n_0,$ and $q_0$. Step two is to assemble the bulk metamaterial either from (i) identical voxels, which are by definition geometrically compatible for all folding configurations, or from (ii) dissimilar voxels, which are designed to be geometrically compatible by optimizing parameters to satisfy the design tolerances over the folding interval $[{\theta }_a,{\theta }_b]$.

For geometric compatibility, there are $N_c$ constraints imposed on each voxel in the bulk structure. In the specific example discussed in the text of the lantern-like module, $N_c=4$. The constraint on $\mathrm{\angle }EDE\prime$, which is the angle $\varphi (\theta \mathit{\text{;}}\alpha ,\gamma )$ (Fig. 1A), ensures voxels have matching $\varphi (\theta )$ over $[{\theta }_a,{\theta }_b]$ and $\sin (\gamma )\propto \sin (\alpha )$. In light of these observations, the constraint that $Y(\theta )$ also match between voxels implies $q\equiv q_0$ for every voxel. Our error function used to match a candidate voxel to a target voxel is then simply defined as $ϵ(\theta )={[\frac{X(\theta \mathit{\text{;}}\alpha ,\gamma ,m,n,\varphi )-X(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0,{\varphi }_0)}{q_0}]}^2+{[\frac{Z(\theta \mathit{\text{;}}\alpha ,\gamma ,m,n,\varphi )-Z(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0,{\varphi }_0)}{q_0}]}^2$, where $\varphi$ is a function of $\theta$ parametrized by $\alpha$ and $\gamma$. The parameters $\alpha ,\gamma ,m,$ and $n$, along with the already set value of $q=q_0$, define the geometry of the voxel being optimized for compatibility. To find the optimal set of parameters, we calculate the integrated error $s={\int }_{{\theta }_a}^{{\theta }_b}ϵ(\theta )d\theta$ and seek a set of parameters that satisfy $[ϵ({\theta }_a),ϵ({\theta }_b)]<\delta$, where $\delta$ is our design tolerance. Typically, the solution that minimizes $s$ satisfies this condition, but pathological situations can be constructed where near-minimum values of $s$ can satisfy the overall design tolerances with more desirable results.

When constructing the large-scale 2D metamaterial with zero Poisson ratio (Fig. 3 D and E) our error function used for calculating geometrically compatible design patterns was adapted to penalize nonzero ${\nu }_{ZX}$. Specifically, we used ${ϵ}_{2D}(\theta )={[\frac{Z_O(2\pi -\theta \mathit{\text{;}}\alpha ,\gamma ,m,n,\varphi )-Z_T(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0,{\varphi }_0)}{q_0}]}^2+{[\frac{\partial \left[X_O(2\pi -\theta \mathit{\text{;}}\alpha ,\gamma ,m,n,\varphi )+X_T(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0,{\varphi }_0)\right]/\partial \theta }{\partial Z_T(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0,{\varphi }_0)/\partial \theta }]}^2$. The first term penalizes differences between the target module’s height $Z_T$ and the optimized module’s height $Z_O$. The second term penalizes Poisson effects, which are calculated using the sum of target and optimized module widths. To more easily find a set of parameters that satisfy the zero bulk Poisson ratio along the $\widehat{x}$-direction, we set the optimized functions to depend on $2\pi -\theta$ whereas the target function depends on $\theta$. This ensures solutions are symmetric about $\theta =\pi$ and is similar in principle to an expression of the form $\sin (\theta )+\sin (2\pi -\theta )=0$. In calculating the bulk strain (Fig. 3E, Inset) we defined $X_0=X(\theta =0)$ and $\mathrm{\Delta }X=X(\theta )-X_0$.

For the mechanical cloak (Fig. 3 F–I) we performed a similar optimization with structures that consist of a $15\times 15$ lattice. The original structure contains 225 voxels (Fig. 3F), the structure with the hole contains 104 voxels (Fig. 3G), and the cloaking structure contains 60 gray voxels and 44 orange voxels (Fig. 3H). Force-extension relations were calculated with $F_{\text{original}}(\theta )=\frac{\partial \left[225\cdot U(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0)\right]/\partial \theta }{\partial \left[15\cdot Z(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0)\right]/\partial \theta },F_{\text{hole}}(\theta )=\frac{\partial \left[104\cdot U(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0)\right]/\partial \theta }{\partial \left[15\cdot Z(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0)\right]/\partial \theta }$, $F_{\text{cloak}}(\theta \mathit{\text{;}}\alpha ,\gamma ,m,n)=\frac{\partial \left[60\cdot U(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0)+44\cdot U(\theta \mathit{\text{;}}\alpha ,\gamma ,m,n)\right]/\partial \theta }{\partial \left[4\cdot Z(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0)+11\cdot Z(\theta \mathit{\text{;}}\alpha ,\gamma ,m,n)\right]/\partial \theta }$, where $U$ and $Z$ denote the energy and height of a voxel, ${\alpha }_0,{\gamma }_0,m_0,n_0,$ and $q_0$ are the geometric parameters of the gray target voxel. Parameters for the orange reinforcing voxels were obtained by minimizing the integrated error $s$ over the design interval with the error function ${ϵ}_{\text{cloak}}(\theta )={[\frac{F_{\text{cloak}}(\theta \mathit{\text{;}}\alpha ,\gamma ,m,n)-F_{\text{original}}(\theta )}{F_{\text{original}}(\theta =\pi )}]}^2+{[\frac{Z(\theta \mathit{\text{;}}\alpha ,\gamma ,m,n)-Z(\theta \mathit{\text{;}}{\alpha }_0,{\gamma }_0,m_0,n_0)}{q_0}]}^2$, where we set $\sin (\gamma )\propto \sin (\alpha )$ to ensure the constraints imposed on $\varphi (\theta \mathit{\text{;}}\alpha ,\gamma )$ were obeyed throughout the structure’s heterogeneous columns. Thus, we obtain values for $\alpha ,\gamma ,m,$ and $n$ for the orange voxels that allow us to reconstitute the mechanical properties of the original structure. For the force-extension calculations, we chose ${\theta }_0=10°$, $k_1=0.02$ N/mm, $k_2=0$, and $q=1$ cm, then calculated $\stackrel{\sim }{F}(\theta )=d\stackrel{\sim }{U}/d(Z/q)$. These values were chosen to approximate our experimental materials (SI Appendix). We note that for this structure the error function being optimized only generates geometric compatibility along $Z$ and allows for gaps along $X$. For this particular application, the extra constraint on $X$ is unnecessary.

To quantify differences between large-scale target 3D metamaterial structures, and approximate voxelized structures, we define ${ϵ}_{3D}=1-V_{\text{voxel}}/V_{\text{target}}$. Here, $V_{\text{target}}$ is the volume of the desired 3D shape and $V_{\text{voxel}}=N\cdot ({\xi }_{x}X)\cdot ({\xi }_{y}Y)\cdot ({\xi }_{z}Z)$ is the volume of the structure assembled from metamaterial voxels. In this expression, $N$ is the total number of voxels, $X,Y,Z$ are dimensions of a single module, and the scaling factors ${\xi }_x,{\xi }_y,{\xi }_z$ control how small the voxels are in the structure. That is, ${\xi }_{x}X=X_{\text{voxel}}$, ${\xi }_{y}Y=Y_{\text{voxel}}$, and ${\xi }_{z}Z=Z_{\text{voxel}}$. As such, smaller values for ${\xi }_x,{\xi }_y,$ and ${\xi }_z$ lead to a greater number $N$ of smaller voxels, which, in turn, better approximates the target structure. In the limit where the ${\xi }_x,{\xi }_y,{\xi }_z\to 0$, we have $N\to \mathrm{\infty }$ in such a way that $V_{\text{voxel}}\to V_{\text{target}}$ and ${ϵ}_{3D}$ vanishes.

Design Patterns.

Design patterns for 1D and 2D metamaterials are typically straightforward to generate from a voxelized structure. For example, folding diagrams for the 1D and both 2D metamaterials are essentially the structure split into a “front” and “back” connected along one edge (SI Appendix, Fig. S7). Folding patterns for 3D metamaterials, however, can be substantially more difficult to generate. Fortunately, methods for continuously transforming 3D objects is an active field of research in computational geometry, and the existing body of work offers potential solutions (28, 29). Alternatively, multisheet assembly methods are also possible and have been described in detail elsewhere (30, 31).