Conformational dynamics and role of the acidic pocket in ASIC pH-dependent gating

Significance

Many physiological processes are regulated by pH. The acid-sensing ion channels (ASICs) are neuronal pH sensors involved in learning, fear behavior, neurodegeneration after ischemic stroke, and pain sensation. The mechanism by which acidic pH activates ASICs is still poorly understood. We show here that the “acidic pocket,” the binding site of several toxins, is not essential for channel function but has, rather, a modulatory role. Furthermore, we describe the structural rearrangements occurring in this domain during ASIC activity, and highlight the importance of the “palm” domain in channel opening and current decay. In this study, we provide insights on the molecular mechanisms controlling ASIC activity together with a rational basis for the development of ASIC-targeting drugs.

Abstract

Acid-sensing ion channels (ASICs) are proton-activated Na⁺ channels expressed in the nervous system, where they are involved in learning, fear behaviors, neurodegeneration, and pain sensation. In this work, we study the role in pH sensing of two regions of the ectodomain enriched in acidic residues: the acidic pocket, which faces the outside of the protein and is the binding site of several animal toxins, and the palm, a central channel domain. Using voltage clamp fluorometry, we find that the acidic pocket undergoes conformational changes during both activation and desensitization. Concurrently, we find that, although proton sensing in the acidic pocket is not required for channel function, it does contribute to both activation and desensitization. Furthermore, protonation-mimicking mutations of acidic residues in the palm induce a dramatic acceleration of desensitization followed by the appearance of a sustained current. In summary, this work describes the roles of potential pH sensors in two extracellular domains, and it proposes a model of acidification-induced conformational changes occurring in the acidic pocket of ASIC1a.

Acid-sensing ion channels (ASICs) are Na⁺-permeable channels (1) that participate in neuronal signaling under conditions involving pH changes, such as neuronal activity, ischemia, and inflammation. ASICs are involved in fear behaviors, learning, neurodegeneration after ischemic stroke, and pain sensation (2, 3). Functional ASICs are composed of three identical or homologous subunits (4, 5).

These channels respond to extracellular acidification with a transient current, because, after opening, they rapidly enter a nonconducting, so-called “desensitized” functional state. Crystal structures of chicken ASIC1 (∼90% sequence homology to human ASIC1a) reveal presumably desensitized (5, 6) and toxin-opened conformations (7–9). Single ASIC subunits have a shape similar to that of a hand holding a small ball (5), and thus their domains have been named accordingly (Fig. 1A). The palm domain forms the internal scaffold of the channel along the central vertical axis. The thumb and the finger point toward the exterior of the channel and enclose, together with the β-ball, the “acidic pocket” (AcP), a region containing many acidic residues (Fig. 1A) (5).

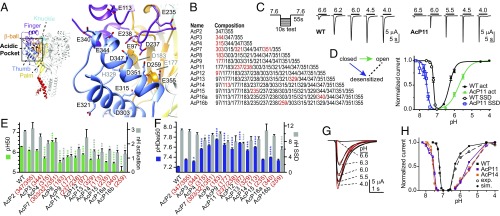
Fig. 1.

Combined mutation of AcP residues preserves almost normal ASIC1a function. (A) Structural image, showing a human ASIC1a model based on the chicken ASIC1 structure (8). (Left) Trimer structure. Individual domains of one subunit are colored and labeled. (Right) Close-up view of the AcP formed by the thumb, the finger, and the β-ball. The residues that were mutated are indicated. (B) Mutant composition. Each number in the right column represents a neutralization mutation, Glu to Gln, Asp to Asn, and His to Asn. The new mutations from one construct to another are marked in red. (C) Representative current traces of WT and the mutant AcP11. The pH protocol is schematically indicated on the left. (D) The pH dependence of activation and SSD of WT and AcP11 (n = 4–6). Normalized current amplitudes are plotted as a function of stimulation pH for activation (filled symbols) and as a function of the conditioning pH for SSD (open symbols). The solid lines represent fits to the Hill equation (SI Materials and Methods). The kinetic scheme of ASIC functional states is shown, emphasizing, with a green arrow, the activation, and, with a blue arrow, the SSD transition. (E) The pH dependence of activation, plotting pH of half-maximal activation (pH50) values as green bars (left axis) and the Hill coefficient (nH) in gray (right axis). The conditioning pH in these experiments was 7.6 to 8.0, depending on the mutant, to ensure stable recordings without occurrence of SSD. For each mutant, the numbers in red indicate the residues mutated in addition to the mutations already present in the preceding mutant; n = 4–125. (F) The pH dependence of SSD, showing pH of half-maximal SSD, pHDes50 values as blue bars, and nH values of SSD in gray; n = 5–56. (G) Experimental current traces (black) of an activation curve of ASIC1a WT and corresponding traces generated by the 32-state model (red; SI Materials and Methods). (H) Activation and SSD curves of WT, AcP11, and AcP14 generated experimentally (filled symbols) or by the 32-state model (open symbols). (*P < 0.05; **P < 0.01; ***P < 0.001; ****P < 0.0001; different from WT.)

Due to the presence of many acidic residues, the AcP was initially proposed as a pH sensor of ASICs (5). Although mutation of AcP Glu and Asp residues shifts the pH dependence of ASIC activation to more acidic values (5, 10–12), H⁺-sensing residues have also been identified outside the AcP (10, 12, 13), indicating that the AcP is not the only extracellular pH-sensing domain. Its importance is, however, underlined by the fact that it constitutes the binding site of several ASIC-specific toxins (7, 14).

In the present study, we asked whether acid sensing in the AcP and the palm is required for ASIC activation and whether the timing of conformational changes in the AcP is compatible with a role in activation. We show that combined, conservative mutation of potential pH-sensing residues in the AcP changes the pH dependences, but still allows ASIC opening and desensitization. Analogous mutations in the palm accelerated desensitization and led to the appearance of a secondary, sustained current. Voltage clamp fluorometry (VCF) analysis indicates the occurrence of rapid and slow conformational changes in the AcP, compatible with a role in both activation and desensitization, and allows us to propose a model of conformational changes in this domain.

Results

Acidic Residues in the Acidic Pocket Are Not Required for ASIC Activation.

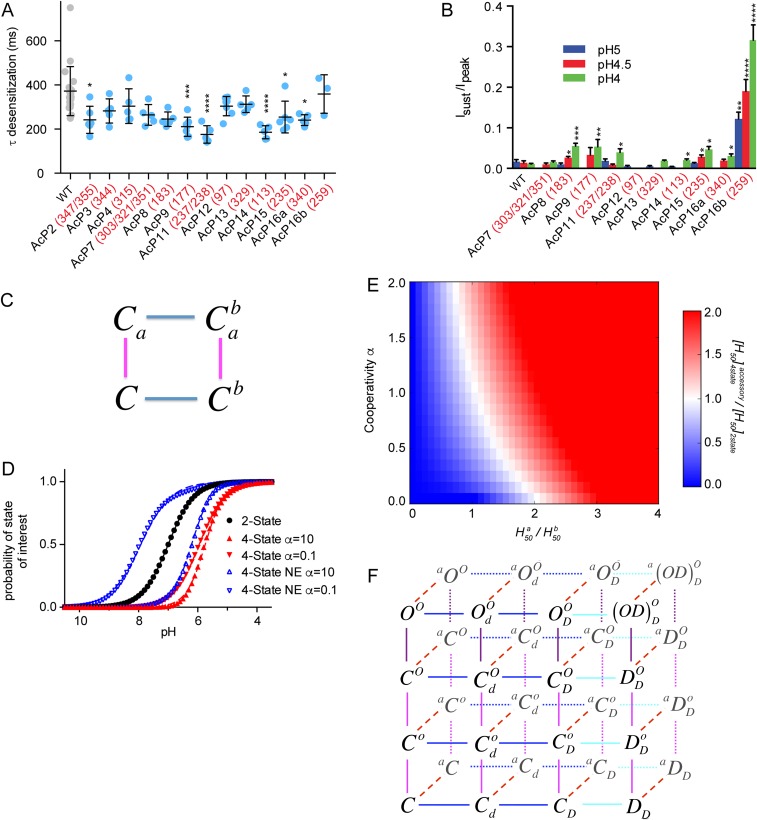
To determine the importance of pH sensing in the AcP for ASIC1a function, we combined neutralization mutations of all Asp, Glu, and His residues of the AcP to Asn or Gln (Fig. 1 A and B). When all of the protonable residues of the AcP were mutated, these channels, expressed in Xenopus oocytes, still produced transient currents upon extracellular acidification. Some mutants displayed up to twofold accelerated kinetics of current decay (Fig. S1A), in accordance with previous studies that described altered current kinetics of AcP mutants (15, 16). Some mutants showed a sustained current, which was, however, small in all mutants except AcP16b (Fig. S1B), indicating that desensitization is, in most mutants, complete at the end of an acidification.

Fig. S1.

ASIC modeling and properties of AcP mutants. (A) Desensitization kinetics of AcP mutants. The current decay phase of ASIC currents was fitted to a single exponential; n = 3–19. The red numbers in the labels indicate the residues mutated in addition to the mutations already present in the preceding mutant (with a lower number of mutations; generally on the left). (B) Sustained current/peak current amplitude (I_sust/I_peak) ratio of AcP mutants determined at pH 5, 4.5, and 4, as indicated; n = 3–18. (C and D) Illustration of the effect of a neutralization mutation on the pH50 and Hill coefficient in (C) a four-state model with two protonation sites. The neutralization mutation is modeled as one of the sites being always protonated and corresponds to a two-state kinetic model. Results for the two-state models (corresponding to the mutant) were obtained from Eq. S9 and are shown as black circles, to which a Hill function was fitted (black line) yielding a pH50 = 7.0 and Hill coefficient n = 1. WT channels correspond to a four-state model (Eqs. S2–S5) with one of the protonation transitions (transition from C_a to ${\text{C}}_{\text{a}}^{\text{b}}$) having the exact same parameters as in the two-state model (black circles). If both protonations are essential for the observed transition, the state of interest is $C_a^b$; therefore we plot $P\left(C_a^b\right)$ obtained from Eq. S5. In this case, WT channels (red triangles) have lower pH50 and higher (or equal) Hill coefficient than the mutant (black circles), both for positive (red upward triangles) and negative (red downward triangles) cooperativity between the two protonation sites. As before, pH50 and Hill coefficients were obtained from the fit of a Hill function (red lines). Finally, if protonation a is accessory to the transition of interest (NE, not essential), the states of interest correspond to $C_a^b$ and $C^b$; therefore we plot $P\left(C^b\right)+P\left(C_a^b\right)$ (blue triangles) obtained from Eqs. S4 and S5. In this case, the WT channel can have a pH50 that is either larger (downward blue triangles) or smaller (upward blue triangles) than the mutant channel. Note that, as shown analytically in Eq. S13, the Hill coefficient of the WT channel is smaller (respectively larger) than that of the mutant for negative (respectively positive) cooperativity. (E) ${\left[H_{50}\right]}_{4state}^{accessory}/{\left[H_{50}\right]}_{2state}$ (i.e., the ratio of the [H₅₀] of the four-state model where protonation of site a is accessory vs. the [H₅₀] of the mutant in which site a has been mutated to a residue mimicking protonation) is shown as a function of $\left[H_{50}^a\right]/[H_{50}^b]$ and α (Eq. S12). Red regions indicate ${\left[H_{50}\right]}_{4state}^{accessory}>{\left[H_{50}\right]}_{2state}$ (pH₅₀ is increased by the mutation) and blue indicates ${\left[H_{50}\right]}_{4state}^{accessory}<{\left[H_{50}\right]}_{2state}$ (pH₅₀ is decreased by the mutation). (F) Model used for fitting experimental traces of WT, AcP11, and AcP14 activation and SSD, as described in SI Materials and Methods. The model is composed of 32 states corresponding to three sets of protonation sites (o = activation, d = desensitization, and a = AcP) and four conformations [C = closed, O = open, D = closed-desensitized, and (OD) = open-desensitized].

The pH of half-maximal activation (pH50) was generally shifted by ∼0.5 pH units to more acidic values compared with WT (green symbols and bars in Fig. 1 D and E). The Hill coefficient, a measure of the steepness of the pH-current relationship and of the cooperativity of the process, decreased from ∼3 in WT to ∼1.5 in most channels containing more than seven AcP mutations (gray bars in Fig. 1E). The pH dependence of steady-state desensitization (SSD), the direct transition from the closed to the desensitized state (blue arrow in the scheme of Fig. 1D), was determined by exposing oocytes to a series of conditioning test pH solutions for 55 s, each followed by a short application of an acidic pH solution. The pH dependence of SSD was shifted to more alkaline values by the combination of AcP mutations (blue symbols and bars in Fig. 1 D and F), although the values are less alkaline for constructs containing >14 neutralization mutations.

As shown above, neutralization mutations of protonable residues in the AcP induced the following functional changes: (i) They shift the pH50 of activation to more acidic values; (ii) they shift the pH50 of SSD to more alkaline values; and (iii) they decrease the Hill coefficient of activation, but not of SSD. Neutralization mutations of Asp and Glu, mimicking protonated acidic residues, correspond to gain of function mutations, which are expected to lead to an alkaline shift in pH dependence as observed for neutralization mutations of key proton-sensing residues in the K⁺ channel KcsA (17). Although our mutagenesis approach does not indicate whether a mutated residue is a pH sensor or has other roles in conformational transitions, it is very likely that at least some of these residues are pH sensors. Because the observed effects of AcP mutations appear to be complex, we use kinetic models to illustrate how these mutations may affect pH dependence. Consider a four-state model as depicted in Fig. S1C, corresponding to a system with two protonation sites, either of which can be protonated or not. A neutralization mutation will correspond to having one of the sites always protonated, reducing the problem to a two-state model. We show that, if protonation of both sites is required for the transition to the state of interest (e.g., the open state), then a neutralization mutation will always lead to an increase in pH50 accompanied by a decrease of the Hill coefficient (SI Materials and Methods and Fig. S1D). However, if protonation of only one of the sites is required, then mutation of the other one can lead to both an increase or a decrease in pH50 and an increase or a decrease in the Hill coefficient (Fig. S1 D and E and SI Materials and Methods). The observed effects of AcP mutations therefore suggest a nonessential role of this domain in activation. To test this hypothesis, we built a kinetic model of ASIC comprising three sets of protonation sites: (i) sites in the AcP, (ii) other sites responsible for desensitization, and (iii) sites leading to activation (Fig. S1F and SI Materials and Methods). The model was fitted to traces of complete activation and SSD curves of ASIC1a WT and the mutants AcP11 and AcP14. The model reproduced the experimental data reasonably well if protonation of the AcP was considered accessory for activation, regardless of whether the same protonation events in the AcP were modeled as required or were accessory for desensitization (Fig. 1 G and H and Fig. S1F), but not if they were considered essential for activation. The parameters of the fitted models indicated that protonation of the AcP shows a negative cooperativity with protonation of activation sites, and a positive cooperativity with protonation of desensitization sites. The modeling suggests, therefore, that protonation-mimicking mutations of the AcP induced an acidic shift in activation pH dependence due to the negative cooperativity between these two types of protonation.

Combined Mutations of Potential pH Sensors in the Palm Accelerate Desensitization and Give Rise to a Nondesensitizing Current.

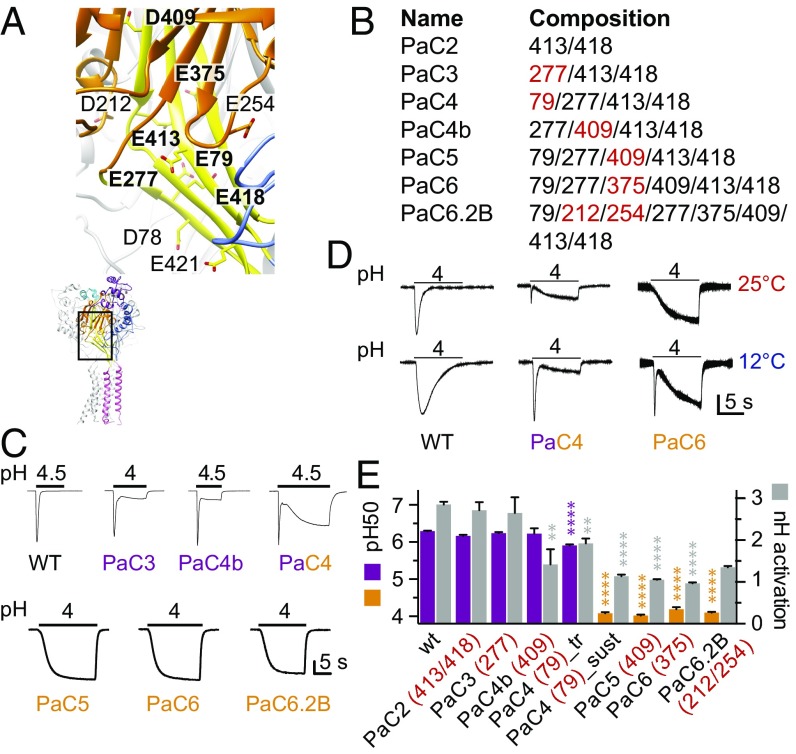
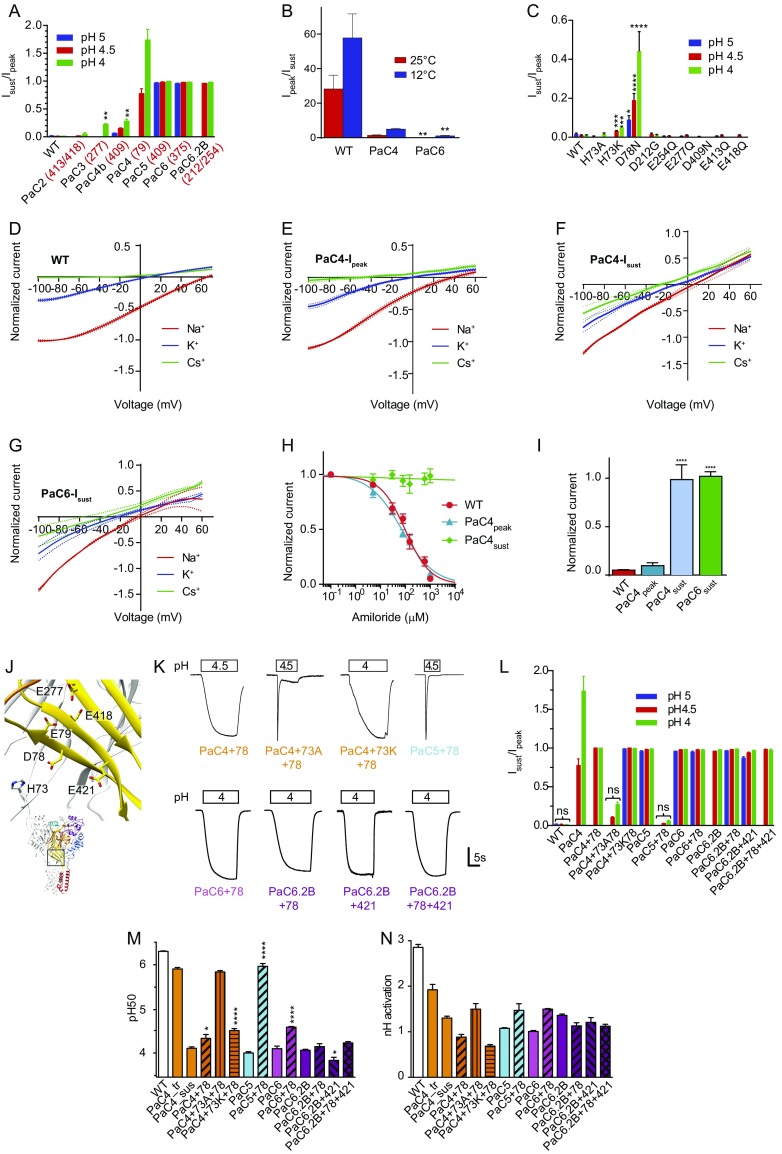
To assess the role of pH sensing in the palm, we combined mutations of the six acidic residues of the lower and middle palm (palm core, “PaC,” bold in Fig. 2A), and subsequently, in addition, the two nearby β-ball residues D212 and E254 (Fig. 2 A and B). The most striking feature of these combined mutants is the appearance of a sustained current component and, with increasing number of mutations, a complete disappearance of the transient current (Fig. 2C and Fig. S2A). The disappearance of the peak current could be due to either loss of channel activation or very fast desensitization; to distinguish between these two possibilities, we measured the mutant channels at a lower temperature, which is known to strongly slow down desensitization but not activation (18). We uncovered a peak current in PaC6, and observed a strong increase of the PaC4 peak current amplitude relative to that of the sustained current (Fig. 2D and Fig. S2B). This demonstrates that the combined mutations such as PaC6 accelerate desensitization to an extent that the transient current disappears.

Fig. 2.

Combined mutations of palm residues accelerate desensitization and induce a sustained current. (A) Structural image of the palm (yellow) and β-ball (orange) domains of one ASIC1a subunit, showing the acidic residues investigated here, with residues of the “palm core” (see Results) highlighted in bold. (B) Mutant composition. The new mutations from one construct to another (compared with the construct with lower number of mutations) are marked in red. B, β-ball; PaC, palm core. (C) Representative current traces of different palm mutants. The vertical bar corresponds to (in microamperes) 6 (WT), 3 (PaC3), 4 (Pa4b), 1 (PaC4), 1.25 (PaC5), 0.5 (PaC6), and 0.24 (PaC6.2B). (D) Representative current recordings of WT, PaC4, and PaC6 at the indicated temperatures. The vertical bar corresponds to (in microamperes) 4.6 (WT), 3.2 (PaC4), and 1 (PaC6). In C and D, the conditioning pH was 7.4. (E) The pH dependence of activation, pH50 values (colored bars), and nH of activation (gray bars); n = 5–128. The pH50 values of transient currents are shown in purple, and those of sustained currents are shown in orange. (*P < 0.05; **P < 0.01; ***P < 0.001; ****P < 0.0001; different from WT.)

Fig. S2.

Properties of palm mutants. (A) I_sust/I_peak ratio of combined palm mutants; n = 3–18. (B) The I_peak/I_sust ratio is plotted for WT, PaC4, and PaC6 at the indicated temperatures. Data were recorded at pH 4 from a conditioning pH of 7.4 (n = 7–10). (C) I_sust/I_peak ratio of single palm mutants; n = 4–28. Mutations to Cys of E79 and E421 have been shown to induce an I_sust/I_peak ratio of 5 ± 1% and 1 ± 1%, respectively (21). For bar graphs of I_sust/I_peak, note that, for some mutants, the I_sust/I_peak ratio was not measured at all three pH values. (D−G) Current−voltage relationship of (D) ASIC1a WT-I_peak, (E) PaC4-I_peak, (F) PaC4-I_sust, and (G) PaC6-I_sust in the presence of either Na⁺ (red), K⁺ (blue), or Cs⁺ (green) in the extracellular solution. The holding potential was −60 mV, and 90-ms voltage ramps from −100 mV to +80 mV were applied. The pH 5-induced ramp current was calculated as the difference between the ramp current obtained during the acidification (during the peak or the sustained phase) and the ramp current measured during the conditioning period at pH 7.4. For each cell, the pH 5-induced currents with extracellular Na⁺-, K⁺-, and Cs⁺-containing solution were normalized to the amplitude measured with Na⁺ at −80 mV. Dotted lines represent SEM of independent experiments (n = 3–11). (H) The pH 5.5-induced current as a function of amiloride concentration, normalized to the control condition. IC₅₀ values obtained from the fits were 125 ± 43 μM (WT-I_peak) and 65 ± 13 μM (PaC4-I_peak); n = 6. (I) Effect of 1 mM amiloride on WT and mutant currents as indicated. The I_amiloride/I_control ratio obtained at pH 5.5 is shown; n = 6–8. (J) Structural image showing residues pointing to the wrist that were mutated. Note that D78 is oriented toward H73 of a neighboring subunit. (K) Representative current traces of palm mutants in which residues H73, D78, and/or E421 were mutated in the background of various PaC mutants. H73 was mutated to Ala or Lys, because mutation to Asn resulted in very small currents. The vertical bar corresponds to the following current amplitude, in microamperes: 0.6 (PaC4+78), 0.5 (PaC4+73A+78), 0.45 (PaC4+73K+78), 5 (PaC5+78), 2 (PaC6+78), 0.6 (PaC6.2B+78), 0.2 (PaC6.2B+421), and 1 (PaC6.2B+78+421). The color of the label refers, as the color of bars in L−N, to the PaC mutant on which the mutant is based. (L) I_sust/I_peak of the indicated mutants; n = 6–28. (M and N) The pH50 and nH of activation of palm−wrist mutants; n = 6–129. The color indicates the palm mutant on which the mutant is based; the pattern refers to the added mutations. Statistically significant differences from WT or the corresponding palm mutant on which palm−wrist mutants are based (M and N; i.e., PaC4+78 is compared with PaC4_tr, etc.) are indicated as *P < 0.05, **P < 0.01, ***P < 0.001, and ****P < 0.0001. For A, C, and L, all values close to 1 and higher were different from the WT I_sust/I_peak; for other values as indicated with the asterisks.

The slowly developing sustained current is only induced by cumulative palm mutations, as no single neutralization mutation of acidic residues of the palm, except for D78, induced any sustained currents (Fig. S2C). This sustained current is distinct from the transient current with regard to several properties. (i) In contrast to the WT peak current, the sustained current has almost completely lost its cation selectivity (Fig. S2 D–G; P_Na/P_K ratio of 9.8 ± 0.4, 5.2 ± 0.4, 2.5 ± 0.3 and 2.7 ± 0.9 for WT, PaC4 peak, PaC4, and PaC6 sustained current, respectively; n = 3–11, P < 0.01); (ii) it is not inhibited by the pore blocker amiloride (Fig. S2 H and I); and (iii) its pH dependence of activation is shifted by two pH units to more acidic values (Fig. 2E).

Additional mutation of the two acidic palm residues pointing toward the wrist, D78 and E421, or the wrist residue H73 (Fig. S2J) in PaC mutants did not further change the current properties in most cases (Fig. S2 K–N). In two of these mutants, a transient current was reconstituted. The pH dependence of the tested palm mutants correlated with the type of current—transient vs. sustained—and not with the number of mutations (Fig. 2E and Fig. S3M). This correlation, together with the different current properties, further confirms that these nondesensitizing currents are profoundly different types of openings, and may be related to sustained ASIC currents induced by some chemical compounds and lipids (19, 20).

Fig. S3.

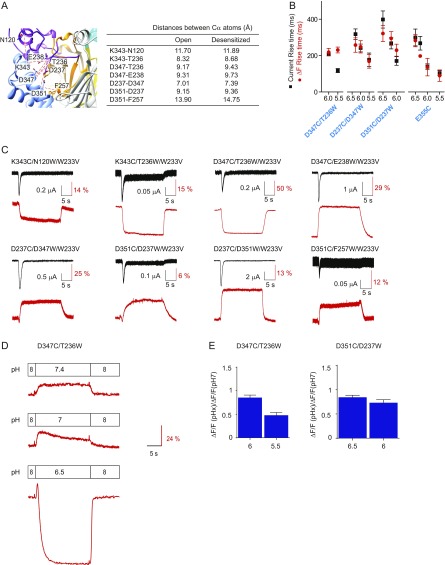
VCF experiments of the AcP. (A) (Left) Close-up view of the AcP showing the residues of pairs that gave rise to fluorescence signals. (Right) Distances (in angstroms) between the Cα atoms of the corresponding residues, measured in homology models of the open [4NTW (8)] and desensitized [4NYK (6)] structures. (B) Current and ΔF kinetics at various stimulation pH conditions. Comparison of current activation and ΔF kinetics (of the first ΔF component) of selected mutants measured at different pH; n = 3–12. ΔF and current signals were correlated (Table S2) in all conditions except pH5.5 for D347C/T236W^first and pH6.3 for E355C^first. (C) Representative current (black) and fluorescence (red) traces of triple mutants in response to extracellular acidification to pH 6. They represent the double mutants used in the VCF part of the study, in which in addition the mutation W233V was introduced to verify that this nearby Trp residue had not influenced the ΔF signals. The conditioning pH for these experiments was 7.4. The traces are representative of 4 to 9 oocytes. Note that all these mutants gave consistent ΔF and current signals, except for D351C/F257W/W233V, which produced small signals that were not present in all oocytes tested. (D and E) Possible errors in the measurement of the kinetics of ΔF signals containing two components, and correction of the rise time values. (D) Representative ΔF traces of the D347C/T236W mutant obtained under different pH changes, to illustrate the overlap of the negative ΔF component over the positive component at more acidic pH conditions. (E) ΔF amplitude ratio of the first ΔF component at the indicated pH and its amplitude at pH 7 (where the signal was maximal); n = 6–21. These ratios were used to correct the rise time values as indicated in SI Materials and Methods.

Conformational Changes in the Acidic Pocket.

By which mechanisms do the palm and the AcP influence ASIC function? The comparison of toxin-opened and desensitized ASIC structures showed evidence for a centripetal movement of the three lower palm domains during desensitization (7). Accessibility studies combined with molecular dynamics simulations suggested that this conformational change in the palm is transduced into closure of the pore (21).

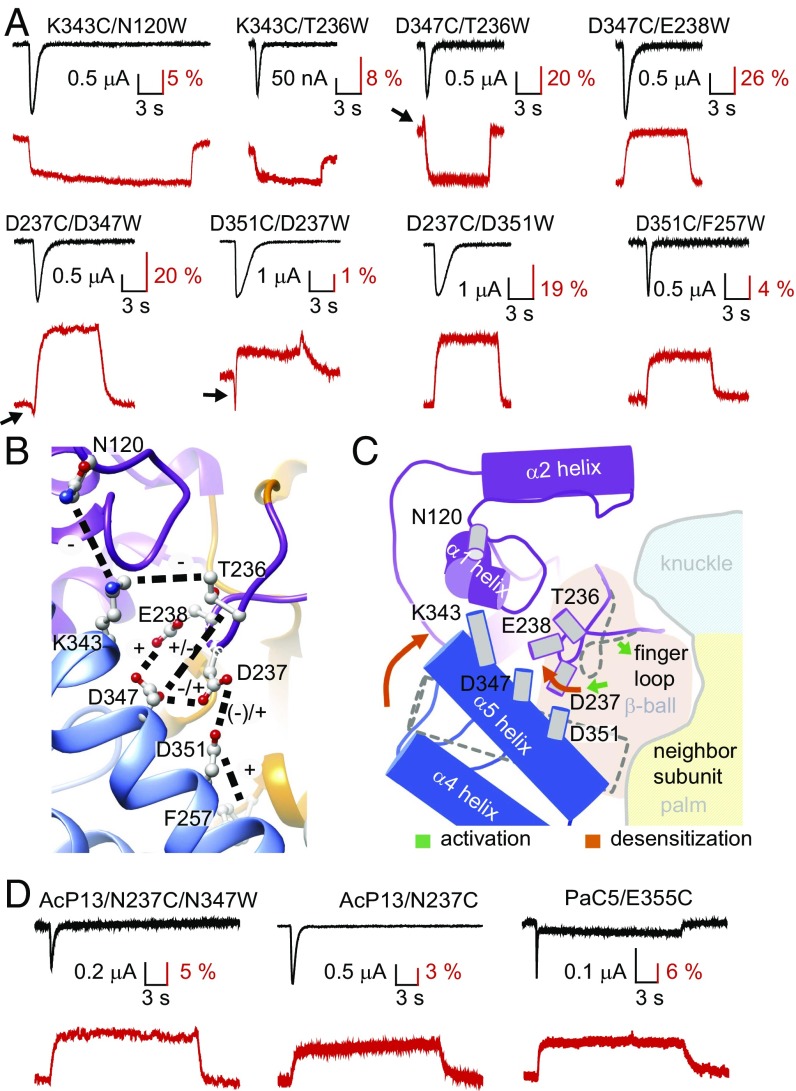
To obtain information on possible conformational changes in the AcP during gating, we applied VCF, which employs simultaneous measurement of ionic currents and of the fluorescence intensity of fluorophores placed at specific sites of the channel (Fig. 3A). Attachment of the fluorophores AlexaFluor488 (Fig. 3B) or CF488A to engineered Cys residues at different positions of the AcP did not, in most mutants, lead to measurable fluorescence changes (ΔF) during channel activity (Table S1). Changes in fluorescence intensity of fluorophores are due to alterations in the environment and/or quenching by nearby amino acid residues. Trp is known as a strong fluorescence quencher (22). To allow the measurement of ΔF signals in this domain, we have paired engineered Cys residues as fluorophore docking positions with engineered Trp residues as quenchers across the AcP (Fig. 3A and Fig. S3A).

Fig. 3.

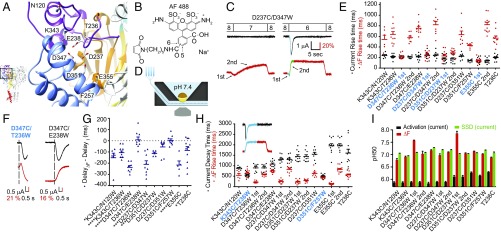
Fluorescence changes in the AcP associated with channel opening and desensitization. (A) Close-up view of the AcP, showing the residues that were mutated to Cys (to dock fluorophores) and/or to the quenching residue Trp. (B) Structure of the fluorophore AlexaFluor488. (C) Representative current and ΔF traces at pH 7 and 6 of the mutant D237C/D347W, highlighting, in green and blue, the parts of the pH 6 traces used for kinetic analysis. Note that the ΔF trace has two components, as highlighted with the arrows. (D) Schematic view of the oocyte recording chamber used for measurements of current and ΔF kinetics (SI Materials and Methods). (E) Scatter graph comparing the rise time of the channel opening (black) and the ΔF onset (red) in response to acidification from the conditioning pH 7.4 to the stimulation pH 6 in paired experiments; n = 6–12. For mutants containing two ΔF components, the two are distinguished as first and second. Correlation between the ΔF and current signal is indicated by labeling in bold turquoise (see criteria in Table S2). (F) Representative current and ΔF traces showing (Left) a mutant in which the start of the ΔF signal precedes that of the current (D347C/T236W) and (Right) one in which the two signals start at the same time (D347C/E238W). The vertical dashed line indicates the beginning of the ΔF. (G) Scatter dot plot of the difference in the ΔF and current delay of appearance (delay_ΔF − delay_I) measured at pH 6; n = 5–11. (H) Scatter graph comparing the current decay time (black) and the fluorescence rise time (red) in response to acidification from pH 7.4 to pH 6 in paired experiments; n = 6–12. Bold turquoise labels indicate correlation between ΔF onset and current decay kinetics (Table S2). (Inset) In blue, the parts of current and ΔF traces whose kinetics were compared. (I) The pH of half-maximal amplitude (pH50) for current (black columns) and fluorescence activation (red), and the pH of current SSD (green); n = 4–16.

Table S1.

ΔF/F amplitude of mutants

Mutant	Ratio ΔF/F amplitude, %	n
D237CC	−6.83 ± 2.13	8
D351CC	0.4 ± 0.92	5
K343C	1.20 ± 0.43	4
K343CC	0.3 ± 0.05	3
D347C	1.08 ± 0.31	8
T236C	37.89 ± 6.78	8
E355C	7.27 ± 1.25	3
K343C/N120WC	−8.07 ± 1.22	6
K343C/T236W	−8.48 ± 2.74	3
D347C/T236W	−7.80 ± 2.43	4
D347C/E238W	39.94 ± 19.88	3
D237C/D347WC*	22.56 ± 12.17	6
D351C/D237WC	6.51 ± 1.28	6
D351C/F257WC	9.36 ± 1.15	5
D237C/D351WC	16.63 ± 4.87	7
AcP13/N237C	7.91 ± 0.68	4
AcP13/N237C/N347W	8.13 ± 1.27	13
PaC5/E355C	8.58 ± 1.41	11

The absolute ΔF/F values, obtained at pH 6, are indicated. Mutant channels were labeled with AlexaFluor488, except where indicated with a superscript “C,” in which case channels were labeled with CF488A.

^*The pH is 6.2 instead of 6 in four of six experiments.

Cys/Trp double mutants of the AcP produced transient acid-induced currents, and various types of ΔF signals. The ΔF of several Cys/Trp mutants contained two components, an initial rapid negative or positive ΔF that was followed by a slower ΔF of the opposite polarity, as illustrated by current and ΔF traces of the mutant D237C/D347W (Fig. 3C, lower traces). To associate ΔF signals with functional transitions, we compared the kinetics of the ΔF and the current signals, measured as rise time (the time to pass from 10 to 90% of the full amplitude). We measured the pH 6-induced ΔF and currents from approximately the same oocyte surface by using a recording chamber in which the solution flows under the oocyte (Fig. 3D and SI Materials and Methods). The onset kinetics of the fast ΔF component of the mutants D347C/T236W, D237C/D347W, D351C/D237W, and E355C match the kinetics of current appearance (Fig. 3E and Fig. S3B; Table S2 for a correlation analysis). These ΔF signals started 100 ms to 250 ms before the current (Fig. 3 F and G), strongly suggesting that the monitored movements in these mutants are correlated with channel opening. The second ΔF components and the ΔF signals of all other mutants were slower than current appearance (Fig. 3E), and the difference in delay was smaller or absent. The ΔF onset was, in most mutants, faster than the current decay (Fig. 3H), and only two mutants, K343C/T236W and D351C/F257W, showed ΔF onset kinetics correlated with current desensitization. The transitions occurring after channel opening may thus be associated with desensitization or with its preparation.

Table S2.

Steepness factor of linear regression of kinetics

Mutant	pH	Steepness Factor
A. Rise timeΔF vs. rise timecurrent at pH6
K343C/N120W		2.30 ± 0.27
K343C/T236W		2.91 ± 0.27
D347C/T236W first		1.05 ± 0.08
D347C/T236W second		2.73 ± 0.17
D347C/E238W		3.45 ± 0.18
D237C/D347W first		1.03 ± 0.08
D237C/D347W second		3.15 ± 0.39
D351C/D237W first		1.28 ± 0.15
D351C/D237W second		1.43 ± 0.23
D351C/F257W		3.00 ± 0.16
D237C/D351W		2.72 ± 0.34
E355C first		0.90 ± 0.11
E355C second		5.11 ± 0.67
T236C		2.73 ± 0.25
B. Rise timeΔF vs. rise timecurrent at indicated pH value
D347C/T236W first	5.5	1.85 ± 0.20
D351C/D237W first	6.5	0.79 ± 0.09
	6.2	1.10 ± 0.09
D237C/D347W first	6.3	0.82 ± 0.09
	5.5	0.79 ± 0.20
E355C first	6.5	0.82 ± 0.14
	6.3	0.71 ± 0.10
	5.5	0.77 ± 0.10
C. Rise timeΔF vs. decay timecurrent at pH6
K343C/N120W		0.60 ± 0.09
K343C/T236W		1.13 ± 0.09
D347C/T236W first		0.23 ± 0.02
D347C/T236W second		0.62 ± 0.05
D347C/E238W		0.67 ± 0.05
D237C/D347W first		0.18 ± 0.02
D237C/D347W second		0.61 ± 0.06
D351C/D237W first		0.15 ± 0.02
D351C/D237W second		0.19 ± 0.02
D351C/F257W		0.81 ± 0.07
D237C/D351W		0.40 ± 0.04
E355C first		0.06 ± 0.00
E355C second		0.41 ± 0.02
T236C		0.32 ± 0.03

For mutant categories A and B, for each mutant and pH condition, ΔF rise time values were plotted for individual experiments as a function of the current rise time. For mutant category C, for each mutant and pH condition, ΔF rise time values were plotted for individual experiments as a function of the current decay time. The „steepness factor“ for the mutants in this table corresponds to the steepness of linear regressions to these data points; the indicated error is the error of the linear regression; n is as indicated in the legends of Fig. 3 and Fig. S3B. ΔF and current kinetics were considered as correlated for a given mutant and pH condition if the steepness of the linear regression was not more than a factor of 0.75 different from 1, and thus between 0.75 and 1.33 (highlighted in bold).

The pH dependence of the ΔF signals was, in most mutants, close to that of SSD, and was more alkaline than the pH dependence of current activation (Fig. 3I); hence these conformational changes could be part of channel desensitization. The ΔF signals sharing the kinetics of current appearance also showed such a shifted pH dependence, indicating that they occur at more alkaline pH than channel opening. This observation does not rule out their possible implication in channel opening, but it indicates that there must be other conformational changes required for activation, which have a lower pH50 than those occurring in the AcP and would therefore govern the pH50 of activation. This shift in pH dependence is reminiscent of the leftward shift in voltage dependence of ΔF versus currents in voltage-gated K⁺ channels (23, 24).

Hypothesized Movements Based on VCF Observations.

The proximity of a quenching group decreases the total fluorescence (F) of a fluorophore, but may generate an activity-induced ΔF if there is a change in distance between the fluorophore and the quenching group. The specific ΔF signals of the single Cys mutants used in the Cys/Trp pairs were of very small amplitude compared with the ΔF signal of related Cys/Trp pairs (Table S1), indicating that the ΔF observed in double mutants is due to the additional presence of the engineered Trp. Control experiments showed that the only endogenous Trp residue in the proximity of the palm, W233, did not affect these signals (compare Fig. S3C and Fig. 4A). A positive ΔF indicates, therefore, an increase in distance between the Trp residue and the Cys-attached fluorophore, whereas a negative ΔF indicates a decrease in this distance. These ΔF signals do not exactly reflect the distance changes between the Cys and Trp of a given pair, because the fluorophore has itself a diameter of 7 Å to 10 Å and is attached to the Cys residue by a linker (Fig. 3B), with an estimated distance between the docking site and the center of the fluorophore of 5 Å to 15 Å (from molecular dynamics trajectories, Corry research group, karri.anu.edu.au/handy/). This limitation has to be considered as a factor of imprecision in the following interpretation of the VCF data.

Fig. 4.

Predicted conformational changes in the AcP. (A) Representative, paired current (black) and fluorescence (red) traces of double mutants in response to extracellular acidification to pH 6. Black arrows point to fast ΔF components. (B) View of the AcP with the mutated residues, indicating, by dashed black lines, the different Cys/Trp pairs. For each double mutant, the nature of the ΔF signal is indicated by “+” or “−“ signs (“+” denotes increase in ΔF); for mutants with composite ΔF signal, the left sign represents the first component. (C) Scheme indicating the deduced conformational changes in the AcP during opening and steps preceding and correlated with desensitization, as discussed in the Results. The gray cylinders represent residues mutated for the VCF experiments. The dotted outlines of the finger loop and α5 thumb helix represent their hypothesized position in the closed state. Hypothesized conformational changes are illustrated by arrows, the green arrows standing for conformational changes occurring during activation, and the orange arrows standing for subsequent steps occurring before and during desensitization. (D) Representative current and ΔF traces of the mutants AcP13/N237C/N347C, AcP13/N237C, and PaC5/E355C. Note that not only the N237C/N347W pair, but also the single mutation N237C, induced measurable ΔF signals, indicating that, in the changed environment of the AcP13 mutant, the N237C ΔF did not depend on the presence of a nearby Trp residue and does not reflect a change in distance between the fluorophore and the Trp residue. The PaC5/E355C mutant showed, in approximately half of the experiments, a rapid transient and a sustained component and, in the other half, only a sustained current.

The nature of the ΔF signals of different Cys/Trp double mutants (Fig. 4A) is summarized in the ASIC structure (Fig. 4B) with dotted lines between the paired residues and with “+” indicating an increase, and “-” a decrease, in ΔF. The early, rapid ΔF signals suggest, therefore, a short-lived approach of D237 toward D347 and D351, and an increase of the T236−D347 distance, which occurs during or slightly before activation. The VCF analysis suggests that these movements are then followed by a decrease of the N120–K343 and T236–D347 distances, and by an increase of the D237–D347, D237–D351, and E238–D347 distances, and, with the time course of desensitization, an increase of the F257–D351 and a decrease of the K343−T236 distances.

We estimate that the higher amplitude of the slower ΔF components is due to a larger conformational change, because, in the ΔF signals composed of a rapid and a slow component, the ΔF of both components depends on the quenching by the engineered Trp, and rapid and slow signals were compared within the same Cys/Trp pair. Most likely, the conformational changes generating these ΔF signals are part of a continuous movement of the involved AcP domains. The initial, fast ΔF signals that are correlated with channel activation may represent a tilting of the finger loop that would bring D237 and E238, located at the lower end of the loop, closer to the α5 helix, and T236, which is higher up, farther away from the α5 helix (green arrows in Fig. 4C). The distance changes involving residues T236, D237, and E238 occurring after activation are best explained by a movement of this finger loop toward the outside of the protein (right orange arrow in Fig. 4C). This movement may involve a partial rotation of the loop, thereby bringing T236 closer to K343 and D347, as well as moving D237 and E238 away from D347 and D351. The α5 helix likely undergoes a movement relative to the other domains that brings its outer end (K343) closer to the finger and its inner part (D351) farther away from the β-ball.

ΔF Signals in Mutants Containing Protonation-Impaired Domains.

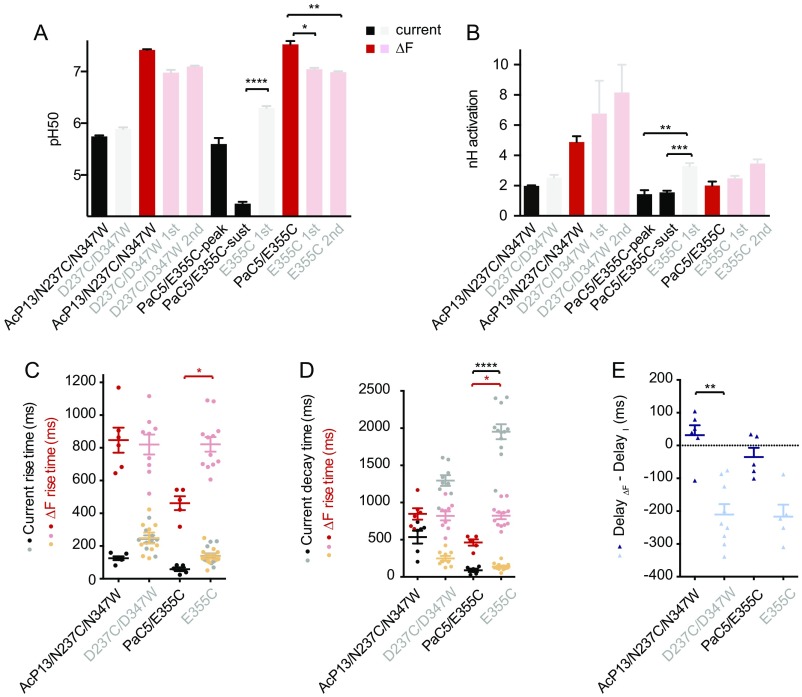
To determine whether conformational changes depend on protonation events in the AcP and the palm, we introduced a fluorophore/quencher pair in the AcP mutant AcP13, and the E355C mutation in the palm mutant PaC5, thus two mutants in which a large number of acidic residues have been neutralized. In both, AcP13/N237C/N347W and PaC5/E355C, the slow, but not the fast, ΔF component was present (Fig. 4D and Fig. S4). The absence of a fast ΔF component in these mutants may be due to a requirement of protonation of AcP or palm residues for the rapid ΔF signal. We cannot, however, exclude the possibility that this absence is due to a changed environment, especially for AcP13/N237C/N347W. The fact that the slower ΔF signal is still present in the combined mutants indicates that neither protonation of AcP nor palm residues is required for the slower conformational changes occurring in the AcP. E355C showed, as expected, faster current decay kinetics in the PaC5 background, and this acceleration was also reflected in the ΔF onset kinetics (P < 0.0001 and <0.05, respectively; Fig. S4D).

Fig. S4.

Combined neutralization and VCF mutations. The figure shows pH and kinetic parameters of the combined mutants AcP13/N237C/N347W and PaC5/E355C (red and black symbols and bars) and compares them to these mutants in the WT background, D237C/D347W and E355C (gray and faintly colored symbols and bars). (A and B) The pH50 and nH of current activation (black and gray) and ΔF (red tones) of the Cys and Cys/Trp mutants combined with the mutant AcP13 or PaC5, compared with values obtained with the Cys and Cys/Trp mutants alone (n= 4–7). (C) Current and ΔF rise time. (D) Current decay time and ΔF rise time. Orange symbols in C and D represent the first ΔF component. (E) Delay_ΔF − Delay_I of the same mutants (n = 5–12). *P < 0.05; **,P < 0.01; ***P < 0.001, and ****P < 0.0001 for the comparison between AcP13/N237C/N347W and D237C/D347W, and between PaC5/E355C and E355C; for mutants with two ΔF components, only the kinetics of the second ΔF components were compared.

Discussion

We show, in this study, that the presence of protonable residues in the AcP and the palm is not essential for ASIC activation but plays other roles: In the AcP, acidic residues allow the fine-tuning of ASIC pH dependence, whereas, in the palm, they control the desensitization kinetics and prevent the appearance of a sustained current. Our VCF analysis provides evidence of conformational changes in the AcP correlated to activation and desensitization, and proposes a likely sequence of conformational changes in the AcP upon extracellular acidification.

The observed acceleration of the desensitization kinetics in palm mutants was much stronger than kinetic changes of palm mutants investigated in previous studies (10, 21) and led to the disappearance of the transient current at room temperature. The fact that acceleration was induced by mutations that mimic protonated side chains suggests that protonation events in the palm lead to desensitization.

The AcP is the binding site of the two gating modifier toxins PcTx1 and Mambalgin (7, 9, 25–27). Nonconservative mutations in the AcP of ASICs have induced strong changes in the pH dependence (11, 28), whereas conservative mutations of Asp and Glu residues induced modest (5, 12) or no changes in activation pH dependence (10). The acidic residues E344, D347, D351, and E355 of the thumb α5 helix that are at the center of the interaction with the finger loop are better conserved between ASIC1a and ASIC2 (three of four) than between ASIC1a and ASIC3 (one of four), whose pH dependence is close to that of ASIC1a. These differences appear not to affect the conformational changes in the AcP, because at least the slow ΔF signals were still present after neutralization of many AcP residues (Fig. 4D). For ASIC2, it was shown that regions outside the AcP, mostly the first ∼90 residues after the TM1, are critical for channel function (29, 30). These observations are consistent with an important regulatory, but not essential, role of the AcP in ASIC activation. The AcP also controls the kinetics and pH dependence of desensitization (15, 16, 27), a role that is underlined here by the slow ΔF signals, which may reflect conformational changes leading to desensitization. In ENaC, the AcP may also have a regulatory role, because it was shown to contain a binding site for Na⁺ involved in channel inhibition (31).

Experimental evidence for conformational changes in the AcP was recently provided by luminescence resonance energy transfer (LRET) measurements showing that the distance between residues of the thumb and the finger is decreased in the desensitized compared with the closed state (28). We describe here the time course of this closing movement and suggest that it concerns, rather, the external end of the AcP, which opens on its inner side. Such a movement of the inner part of the AcP is supported by the recent observation that formation of a disulfide bond between the thumb residue E355C and R175C of the palm locks the channel in the closed state (32). The slower conformational changes in the AcP do not depend on protonation events in the AcP or the palm, indicating that these conformational changes in the AcP are induced by protonation events occurring outside the AcP or the palm. Protonation of AcP residues, or binding of ligands to the AcP, may influence the kinetics and possibly the amplitude of these conformational changes and thereby modulate ASIC function.

Our observation of large ΔF signals occurring between opening and desensitization, suggesting conformational changes in the AcP, contradicts the findings with crystal structures of ASIC1, which show an almost identical conformation of the AcP in toxin-opened and desensitized channels (7). It is possible that the toxin-opened ASIC conformation studied in crystal structures is different from the H⁺-opened conformation. Evidence for important conformational changes during ASIC desensitization comes from the observation that ASIC currents show a strong temperature dependence of desensitization. In contrast, the temperature dependence of activation is much weaker (18). These observations are consistent with the small-amplitude ΔF signals correlated to activation and the large-amplitude ΔF signals correlated to later events. The above-mentioned LRET experiments (28) and a recent Cys accessibility study (15) also suggest conformational changes in the AcP upon acidification. To affect channel activity, conformational changes in the AcP need to change the conformation of the ASIC pore. The downward movement of the internal end of the α5 helix during desensitization would likely be transmitted to the pore via the β-turn structure that is part of a palm−thumb loop and interacts with the external end of the transmembrane domain, or via the palm.

Materials and Methods

WT and mutant human ASIC1a were expressed in Xenopus laevis oocytes. All experiments with Xenopus were carried out in accordance with the Swiss federal law on animal welfare, following protocols that had been approved by the committee on animal experimentation of the Canton de Vaud. ASIC currents were measured by two-electrode voltage clamp, and VCF experiments were carried out as described previously (ref. 33; Table S3), with the exception that a different measuring chamber, allowing measurement of current and fluorescence from approximately the same oocyte surface, was used for the kinetics experiments. Kinetic models were fitted directly to the measured currents using the Data2Dynamics software (34). Data are presented as mean ± SEM. Individual experimental data points are provided in Supporting Information. Detailed material and methods are provided in SI Materials and Methods.

Table S3.

Test for possible intrinsic pH dependence of fluorophores

Mutant	Ratio ΔF/Fdesensitized-to-open/ΔF/Fclosed-to-open protocol, %
T236C	−0.8 ± 3.1
E355C	9.8 ± 2.8
K343C/ N120WC	28.4 ± 1.9
K343C/ T236W	26.9 ± 7.5
D347C/ T236W	17.86 ± 1.9
D347C/ E238W	16.9 ± 4.6
D351C/ D237WC	−11.9 ± 10.0
D351C/ F257WC	31.5 ± 9.4
D237C/D347WC*	26.0 ± 5.0
D237C/D351WC	0.2 ± 3.9

To test for a possible intrinsic pH dependence of the fluorophore in the experiment, labeled channels were desensitized by exposing them for 30 s to pH 6.8, before switching to the stimulation pH 6. In this protocol, pH 6 did not induce currents. If a ΔF signal is measured in this protocol, either it reflects an electrically silent transition or it is due to the intrinsic pH dependence of the fluorophore at its location in the protein. Shown here is the ratio of the ΔF/F of the desensitized-to-open protocol (i.e., pH 6.8 to pH 6) to the ΔF/F of the closed-to-open protocol (i.e., pH 7.4 to pH 6) as a percentage; n = 3–8. A low ratio indicates that there is no intrinsic pH dependence of the fluorophore, and a higher ratio indicates the presence of either electrically silent transitions or of an intrinsic pH dependence of the fluorophore in the experimental conditions. This ratio was measured with the fluorophore AlexaFluor488 or, where indicated with a superscript “C,” with CF488A.

^*For the mutant D237C/D347W, the indicated values are from two experiments at pH 6. At pH 6.2, the ratio was 17.3 ± 9.2 (n = 4). The ratio was not measured for the combined VCF/PaC or APc mutants, because they still showed currents after exposure to conditioning pH ≤ 6.8.

SI Materials and Methods

Molecular Biology.

The human ASIC1a sequence was subcloned in a pSP65-derived expression vector containing 3′ and 5′ nontranslated sequences of Xenopus laevis β-globin. Site-directed mutagenesis was done by using the Quikchange approach. All mutations were confirmed by sequencing (Synergen Biotech). Combined mutations were neutralization mutations, i.e., Asp to Asn, Glu to Gln, and His to Asn, except for D212, which was mutated to Gly. Mutation of D212 to Asn abolished channel function (no pH 5-induced membrane current in two series of experiments). Because all other ASIC subunits contain a Gly residue at the homologous position, D212 was mutated to Gly to disrupt a possible protonation of this side chain. The mutant channel D212G was functional. In vitro transcription was carried out with the mMessage mMachine SP6 kit (Ambion/Life Technologies).

Oocyte Handling and Injection.

All experiments with Xenopus were carried out in accordance with the Swiss federal law on animal welfare, following protocols that had been approved by the committee on animal experimentation of the Canton de Vaud. Oocytes were isolated and cultured as described previously (12). Briefly, healthy stage V and VI oocytes of female Xenopus laevis frogs were treated with collagenase for isolation and defolliculation. They were subsequently injected with 50 nL to 100 nL of cRNA (0.02 μg/μL to 0.5 μg/μL). Oocytes were kept in modified Barth’s saline (MBS) containing (in millimolars) 85 NaCl, 1 KCl, 2.4 NaHCO₃, 0.33 Ca(NO₃)₂, 0.82 MgSO₄, 0.41 CaCl₂, 10 Hepes, and 4.08 NaOH. For some experiments, oocytes were kept in an MBS containing 10 mM NaCl, with 75 mM NaCl replaced by N-methyl-d-glutamine. Oocytes that were later used for VCF were incubated after the injection for 1 h in MBS containing 10 mM 3-maleimidopropionic acid (Bachem) to modify free Cys residues of endogenous oocyte proteins at the cell surface. Measurements were done 24 h to 56 h after injection.

Solutions and Reagents.

The standard recording solution was composed of (in millimolars) 110 NaCl, 2 CaCl₂, and 10 Hepes for pH values ≥ 6.8. Solutions with a pH < 6.8 contained Mes instead of Hepes. The pH was adjusted using NaOH. In some experiments, NaCl was replaced by N-methyl-glucosamine (120 mM) that is not conducted by ASICs. For measurement of the current−voltage relationship, the recording solution contained (in millimolars) 110 NaCl, 2 MgCl₂, and 10 Hepes (or 10 Mes for pH ≤ 6.7). To investigate the permeability to K⁺ and Cs⁺ ions, NaCl was substituted by the same concentration of KCl or CsCl. The pH was adjusted using NaOH, KOH, and CsOH, for solutions containing Na⁺, K⁺, and Cs⁺, respectively. For experiments performed at different temperatures, the extracellular solution contained Mops (which is less temperature-dependent) as pH buffer instead of Hepes or Mes; 10 mM stock solutions of AlexaFluor488 C-5 Maleimide (AlexaFluor488, Life Technologies) and CF488A (Biotium) were prepared in DMSO and stored in aliquots at −20 °C.

Electrophysiology.

All experiments of the VCF part were carried out with oocytes that had been previously exposed to CF488 maleimide or AlexaFluor488 maleimide. Currents were recorded by two-electrode voltage clamp at −60 mV (−40 mV for VCF experiments) with a Dagan TEV-200 amplifier at a sampling rate of 1 ms and low-pass filtering at 2 kHz. Oocytes were impaled with two glass electrodes filled with 1 M KCl, with a resistance of <0.8 MΩ. The perfusion speed was set to 5 mL/min to 15 mL/min, and switching between different solutions was controlled by electrovalves. To generate activation and SSD curves, the recording chamber was perfused with conditioning pH solution, and, every minute, ASICs were activated with stimulation solution for 5 s to 10 s. For measurements of current−voltage relationship, the holding potential was −60 mV and 90-ms voltage ramps from −100 mV to +80 mV were applied every 200 ms. The conditioning pH was 7.4, and the stimulation pH was 5. For experiments performed at different temperatures, the temperature of the perfusion solution was monitored in the perfusion chamber with a temperature-sensitive probe (Th-10Km; Cell MicroControls) and changed by the perfusion solutions between 12 °C and 25 °C.

VCF.

A total number of 30 engineered Cys−Trp pairs in the AcP were generated and tested by VCF. They had been chosen based on the following criteria: (i) The distance between their Cα atoms was ≤ 15 Å; (ii) one of the residues was on the thumb helix, the other on the other side of the AcP; (iii) the side chains of these residues were oriented toward each other; and (iv) the residue to be mutated to Cys appeared accessible from the solution as judged from the crystal structure. Only the eight pairs whose ΔF signal was specific according to the criteria shown in Table S3, and of which the corresponding Cys mutant alone did not induce a measurable ΔF, were included in the study. VCF experiments were mostly performed as described previously (33). Labeling was carried out in the dark with 5 μM CF488A maleimide or AlexaFluor488 C-5 maleimide at 19 °C for 15 min. The light source was an Intensilight lamp (C-HGFI; Nikon). The emitted signal was detected by a 40× Nikon objective and quantified by a photodiode (S1336-18BQ; Hamamatsu Photonics). The ΔF was normalized to the total fluorescence intensity F, as determined with a scalable offset device. A low-pass eight-pole Bessel filter was used to amplify and filter the signal at 50 Hz. On most mutants, we tested the two fluorophores CF488A and AlexaFluor488. We used the one with the higher signal amplitude and better apparent specificity for the experiments. As a measure of specificity, we determined the ΔF induced by acidification to pH 6 from the conditioning pH 7.4 and also from the conditioning pH of 6.8, at which the tested ASICs were desensitized and did not open. We considered the ΔF induced by the pH change from 6.8 to 6 as a potential pH effect on the fluorophore itself and determined the ratio ΔF (pH6.8→6)/ΔF(pH7.4→6) as a measure of the potentially nonspecific fraction of the signal. All mutants showed some ΔF in the pH 6.8-to-6 transition, which was, however, generally <30% of the ΔF amplitude measured in response to the pH drop from 7.4 to 6 (Table S3). For most measurements, oocytes were placed in an RC-25 recording chamber (Warner Instruments), as described previously (33). For kinetic measurements, we used a specially designed chamber to measure and compare the ΔF and current kinetics from similar oocyte surfaces (Fig. 3D). This chamber contained an upper compartment that was connected, by a hole of 0.85 mm diameter, to a lower channel. The oocyte was placed in the upper compartment in the hole, bathed in recording solution at the conditioning pH, e.g. pH 7.4, and impaled with the electrodes. The bottom side of the oocyte was exposed to the lower channel, allowing the solution to flow under the oocyte, as described previously (35). The chamber was made based on a prototype kindly provided by G. Akk, Washington University in St. Louis, St. Louis.

Data Analysis.

Current recordings were controlled and recorded using Chartmaster and analyzed with Chartmaster or Fitmaster (HEKA Electronics). Normalized activation curves were fitted to the Hill equation [(I = I_max/(1 + (10^−pH50/10^−pH)^nH], where I_max is the maximal current, pH₅₀ is the value at which the current amplitude is half-maximal, and nH is the Hill coefficient (GraphPad Prism). SSD curves were fitted to an analogous equation. The kinetics of ΔF and current signals were determined as rise times, the time to get from 10 to 90% of the maximal amplitude. The permeability ratio of two ions A and B was calculated from reversal potential (E_rev) values determined from voltage ramps obtained when the ASIC current was induced by acidification in an extracellular solution containing either the cation A or B, from the relationship ΔE_rev = E_rev,B – E_rev,A = (RT/zF)ln(P_B[B]_o/P_A[A]_o), where R is the Gas constant (8.3145 J mol⁻¹ K⁻¹), T is the absolute temperature (in K), z is the valence of the ions, F is the Faraday's constant (96485 C mol⁻¹), P_{B(or A)} is the permeability of B (or A), and [B]_o and [A]_o are the extracellular concentrations of ions B and A (36). Structural images were made with Chimera (37) from a human ASIC1a homology model, based on the crystal structure of chicken ASIC1, which shares 90% sequence homology with human ASIC1a [PDB number 4NTW (8)].

Analysis of Two-Component ΔF Signals.

For mutants with two ΔF components, it might be possible that, under certain pH conditions, the second component may decrease the apparent amplitude of the first component, which would lead to an underestimation of the rise time of the first component. This possible error was estimated and corrected as indicated in Fig. S3 D and E. In the mutants with a composite ΔF signal, the pH dependence of the first component was generally shifted to alkaline values with regard to the pH dependence of the second ΔF component and reached maximal amplitudes at pH 7. This difference in pH dependence allowed observation of the first signal alone at alkaline pH values; in these mutants, saturation of the amplitude of the first ΔF component occurred at pH values at which the amplitude of the second ΔF component was still small (Fig. S3D). If, at an acidic pH at which the second ΔF component had a high amplitude, the amplitude of the first component decreased (as illustrated in Fig. S3D), this probably indicated that the accelerated second component had cut a part of the first ΔF component. We observed, indeed, a decrease of the amplitude of the first ΔF component in the mutants D347C/T236W and D351C/D237W. Such a decrease of the amplitude of the first ΔF component at more acidic pH was not observed with the mutant D237C/D347W (higher ΔF amplitude at pH 6.2 than at pH 7), and it was previously shown that this is not the case for the E355C mutant (33). In principle, if this decrease in the two double mutants reflects the partial suppression of the first ΔF component by the second one, it leads to an underestimation of rise time. We have therefore corrected the individual rise time values of the first ΔF component of these mutants measured at pH x by dividing the measured rise time by the ratio ΔF/F at pH x/ΔF/F at pH7 (Fig. S3E). An alternative would have been a double exponential fit for the two components. Due to the short duration of the first component, such fits were, however, not reliable.

Data Presentation and Statistics.

Statistical comparison of two mean values was done with the t test. For statistical analysis of more than two mean values, we determined first the distribution of the experimental population, and used, for Gaussian distributions, ANOVA followed by Tukey’s multiple comparisons test (Graphpad Prism 6). For non-Gaussian distributions, nonparametric tests (Kruskal-Wallis, followed by Dunn’s multiple comparisons test) were used. The data are presented as mean ± SEM. Individual data points and numbers of experiments are provided in Dataset S1. The numbers correspond to the number of individual oocytes, from which measures were taken.

SI Kinetic Models

By using a four-state kinetic model, we first show how mutations that mimic a protonated pH sensor affect the midpoint and the steepness of the pH-dependent state when the protonation step affected by the mutation is either (i) essential or (ii) accessory for reaching the state of interest (e.g., the open state).

A second, more complex model is then used to fit the experimental data to better understand the mechanism underlying the observed functional effects of AcP mutations.

Analytic Solutions for Four-State and Two-State Kinetic Models.

We consider a four-state kinetic model (Fig. S1C) representing a channel with two protonation sites (indicated by subscript a and superscript b), both of which can be protonated or not (states $C$, $C_a$, $C^b$, and $C_a^b$). We use this simple four-state model to obtain analytic expressions for the pH50 and Hill coefficient of a transition of interest (e.g., to state $C_a^b$) and show how these are affected by mutation at one of the two sites in two situations: (i) both protonations are essential for the transition of interest (we observe $C_a^b$); (ii) only protonation of b is required for the transition of interest (we observe $C^b+C_a^b$).

Let $K_{A\to B}$ be the transition rate from state A to state B; then our model is given by

$$K_{C\to C_a}=k_a{\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a};\hspace{0.17em}{K}_{C_a\to C}=k_a$$

$$K_{C\to C^b}=k_b{\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b};\hspace{0.17em}{K}_{C^b\to C}=k_b$$

$$K_{C_a\to C_a^b}=\alpha k_b{\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b};\hspace{0.17em}{K}_{C_a^b\to C_a}=k_b$$

$$K_{C^b\to C_a^b}=\alpha k_a{\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a};\hspace{0.17em}{K}_{C_a^b\to C^b}=k_a.$$

[H] is the proton activity [$\text{pH}=-lo{g}_{10}\left(\left[H\right]\right)$], $\left[H_{50}^a\right]$ is the proton activity at which proton sensor a is protonated in half of the channels, and similarly for $\left[H_{50}^b\right]$. Here $n_a$ and $n_b$ correspond to the number of protons in sensors a and b, and $\alpha$ is the cooperativity between sensors a and b ($\alpha >1$ corresponds to a positive cooperativity; i.e., protonation of a makes protonation of b easier, while $\alpha <1$ corresponds to negative cooperativity). Finally $k_a$ (respectively $k_b$) is the protonation rate for sensors a (respectively b) at $\left[H\right]=\left[H_{50}^a\right]$ (respectively $\left[H\right]=\left[H_{50}^b\right]$). These parameters do not influence the equilibrium state but only the rate at which the system reaches equilibrium at a given pH. Note that only the forward transitions (protonation) are pH-dependent, just as ligand binding depends on the concentration of ligands whereas unbinding does not.

At equilibrium, we have

$$\{\begin{array}{l}P\left(C_a\right)={\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a}P\left(C\right)\\ P\left(C^b\right)={\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}P\left(C\right)\\ P\left(C_a^b\right)=\alpha {\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}P\left(C_a\right)\\ P\left(C_a^b\right)=\alpha {\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a}P\left(C^b\right)\\ 1=P\left(C\right)+P\left(C_a\right)+P\left(C^b\right)+P\left(C_a^b\right)\end{array},$$ [S1]

with P(C_x) denoting probability of the channel being in state C_x. From this system of equations (Eq. S1), we can easily obtain the equilibrium probabilities

$$P\left(C\right)=\frac{1}{F\left(\left[H\right]\right)}$$ [S2]

$$P\left(C_a\right)=\frac{{\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a}}{F\left(\left[H\right]\right)}$$ [S3]

$$P\left(C^b\right)=\frac{{\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}}{F\left(\left[H\right]\right)}$$ [S4]

$$P\left(C_a^b\right)=\frac{\alpha {\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a}{\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}}{F\left(\left[H\right]\right)}$$ [S5]

with

$$F\left(\left[H\right]\right)=1+{\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a}+{\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}+\alpha {\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a}{\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}.$$ [S6]

For the remainder of this section, we will assume that both transitions correspond to single protonation sites ($n_a=1$ and $n_b=1$). Let us first consider the case where both protonations are needed for the transition of interest, so we define ${\left[H_{50}\right]}_{4state}$ as the proton concentration at which half the channels have both sites protonated, $P(C_a^b,{\left[H_{50}\right]}_{4state})=1/2$. It follows from Eq. S5 that

$${\left[H_{50}\right]}_{4state}=\frac{\left[H_{50}^a\right]+\left[H_{50}^b\right]+\sqrt{{(\left[H_{50}^a\right]+\left[H_{50}^b\right])}^2+4\alpha \left[H_{50}^a\right]\left[H_{50}^b\right]}}{2\alpha }>\frac{\left[H_{50}^a\right]+\left[H_{50}^b\right]}{\alpha }.$$ [S7]

The Hill coefficient for this transition ($C\to C_a^b$) is given by

$$\begin{array}{l}{n}_{4state}={\frac{d}{dlog\left(\left[H\right]\right)}log\left(\frac{P\left(C_a^b\right)}{1-P\left(C_a^b\right)}\right)|}_{\left[H\right]=\left[H_{50}\right]}\\ =\left[H\right]{\frac{d}{d\left[H\right]}log\left(\frac{\alpha \left[H\right]\left[H\right]}{\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left(\left[H_{50}^a\right]+\left[H_{50}^b\right]\right)}\right)|}_{\left[H\right]=\left[H_{50}\right]}\\ =\frac{\left[H\right]}{\alpha \left[H\right]\left[H\right]}{\left(2\alpha \left[H\right]-\frac{\alpha \left[H\right]\left[H\right]\left(\left[H_{50}^a\right]+\left[H_{50}^b\right]\right)}{\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left(\left[H_{50}^a\right]+\left[H_{50}^b\right]\right)}\right)|}_{\left[H\right]=\left[H_{50}\right]}\\ =2-{\frac{\left[H\right]\left(\left[H_{50}^a\right]+\left[H_{50}^b\right]\right)}{\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left(\left[H_{50}^a\right]+\left[H_{50}^b\right]\right)}|}_{\left[H\right]=\left[H_{50}\right]}\\ =1+{\frac{\left[H_{50}^a\right]\left[H_{50}^b\right]}{\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left(\left[H_{50}^a\right]+\left[H_{50}^b\right]\right)}|}_{\left[H\right]=\left[H_{50}\right]}>1.\end{array}$$ [S8]

Let us now consider how the pH50 and n would be affected by a neutralization mutation of one of the two protonation sites. For this, we consider that a neutralization mutation corresponds to one of the sites being always protonated (in this example, the site “a”), so that we are left with a two-state model (states $C_a$ and $C_a^b$) for which it is easy to show that

$$P_{2state}\left(C_a^b\right)=\frac{\alpha {\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}}{1+\alpha {\left(\frac{\left[H\right]}{\left[H_{50}^b\right]}\right)}^{n_b}}$$ [S9]

$${\left[H_{50}\right]}_{2state}=\frac{\left[H_{50}^b\right]}{\alpha }$$ [S10]

$$n_{2state}=1.$$ [S11]

From the comparison of Eq. S7 with Eq. S10 and Eq. S8 with Eq. S11, it is clear that

$$\begin{array}{l}{\left[H_{50}\right]}_{4state}>{\left[H_{50}\right]}_{2state}\Rightarrow pH{50}_{4state}<pH{50}_{2state}\\ n_{4state}>n_{2state},\end{array}$$

so that, in this model (two protonation sites, both needed for the transition of interest), a protonation-mimicking mutation will always increase the pH50 while decreasing the Hill coefficient. This is exemplified in Fig. S1D showing simulated data with such a four-state model (red triangles and lines) and the impact of a neutralization mutation (black circles and line).

If, instead, we consider the first protonation (“a”) as accessory to the transition of interest brought about by the second protonation (i.e., that in this case, both $C^b$ and $C_a^b$ are “states of interest”), we get, for the four-state model,

$$P(C_a^b,{\left[H_{50}\right]}_{4state}^{accessory})+P(C^b,{\left[H_{50}\right]}_{4state}^{accessory})=1/2$$

$${\left[H_{50}\right]}_{4state}^{accessory}=\frac{\left[H_{50}^a\right]-\left[H_{50}^b\right]+\sqrt{{(\left[H_{50}^a\right]-\left[H_{50}^b\right])}^2+4\alpha \left[H_{50}^a\right]\left[H_{50}^b\right]}}{2\alpha }.$$

Let us now show that ${\left[H_{50}\right]}_{4state}^{accessory}$ can be both smaller and larger than ${\left[H_{50}\right]}_{2state}$, which is equivalent to the ratio ${\left[H_{50}\right]}_{4state}^{accessory}/{\left[H_{50}\right]}_{2state}$ being either smaller or larger than 1.

$$\frac{{\left[H_{50}\right]}_{4state}}{{\left[H_{50}\right]}_{2state}}=\frac{\alpha {\left[H_{50}\right]}_{4state}}{\left[H_{50}^b\right]}=\frac{1}{2}\left[\left(\frac{\left[H_{50}^a\right]}{\left[H_{50}^b\right]}-1\right)+\sqrt{{\left(\frac{\left[H_{50}^a\right]}{\left[H_{50}^b\right]}-1\right)}^2+4\alpha \frac{\left[H_{50}^a\right]}{\left[H_{50}^b\right]}}\right].$$ [S12]

Eq. S12 is plotted in Fig. S1E as a function of $\left[H_{50}^a\right]/\left[H_{50}^b\right]$ and $\alpha$, clearly showing that ${\left[H_{50}\right]}_{4state}^{accessory}$ can be larger (red region in Fig. S1E) or smaller (blue region in Fig. S1E) than ${\left[H_{50}\right]}_{2state}$. This proves that a protonation-mimicking mutation of a site that is accessory to the transition of interest can either decrease or increase the pH50.

Similarly, we now calculate the Hill coefficient in the case of protonation a being accessory to the observed transition (transition to $C^b+C_a^b$). In this case, the Hill coefficient is defined as

$$\begin{array}{l}{n}_{4state}^{accessory}={\frac{d}{dlog\left(\left[H\right]\right)}log\left(\frac{P_{C_a^b}+P_{C^b}}{1-P_{C_a^b}-P_{C^b}}\right)|}_{\left[H\right]=\left[H_{50}\right]}\\ =\left[H\right]{\frac{d}{d\left[H\right]}log\left(\frac{\alpha \left[H\right]\left[H\right]+\left[H_{50}^b\right]\left[H\right]}{\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left[H_{50}^a\right]}\right)|}_{\left[H\right]=\left[H_{50}\right]}\\ =\frac{\left[H\right]}{\alpha \left[H\right]\left[H\right]+\left[H_{50}^b\right]\left[H\right]}{\left(2\alpha \left[H\right]+\left[H_{50}^b\right]-\frac{\left(\alpha \left[H\right]\left[H\right]+\left[H_{50}^b\right]\left[H\right]\right)\left[H_{50}^a\right]}{\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left[H_{50}^a\right]}\right)|}_{\left[H\right]=\left[H_{50}\right]}\\ =1+\frac{\alpha \left[H\right]\left[H\right]}{\alpha \left[H\right]\left[H\right]+\left[H_{50}^b\right]\left[H\right]}-{\frac{\left[H\right]\left[H_{50}^a\right]}{\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left[H_{50}^a\right]}|}_{\left[H\right]=\left[H_{50}\right]}\\ =1+{\frac{\alpha \left[H\right]\left[H\right]\left(\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left[H_{50}^a\right]\right)-\left[H\right]\left[H_{50}^a\right]\left(\alpha \left[H\right]\left[H\right]+\left[H_{50}^b\right]\left[H\right]\right)}{\left(\alpha \left[H\right]\left[H\right]+\left[H_{50}^b\right]\left[H\right]\right)\left(\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left[H_{50}^a\right]\right)}|}_{\left[H\right]=\left[H_{50}\right]}\end{array}$$

$$=1+{\frac{\left[H_{50}^a\right]\left[H_{50}^b\right]\left[H\right]\left[H\right]\left(\alpha -1\right)}{\left(\alpha \left[H\right]\left[H\right]+\left[H_{50}^b\right]\left[H\right]\right)\left(\left[H_{50}^a\right]\left[H_{50}^b\right]+\left[H\right]\left[H_{50}^a\right]\right)}|}_{\left[H\right]=\left[H_{50}\right]}.$$ [S13]

Note that the second term in Eq. S13 will be positive for $\alpha >1$ and negative for $\alpha <1$($\alpha$ is always positive, so the denominator is always positive). So it is clear that a mutation mimicking the protonation of an accessory site will lead to a decrease in Hill coefficient for positive cooperativity (if $\alpha >1$, then $n_{4state}^{accessory}>1=n_{2state}$), and an increase in Hill coefficient in case of negative cooperativity (if $\alpha <1$ then $n_{4state}^{accessory}<1=n_{2state}$). These results are exemplified in Fig. S1D showing the equilibrium probabilities for such a four-state model (blue triangles and lines) and the impact of a neutralization mutation on its pH50 and Hill coefficient (black circles and line), thus illustrating that the pH50 shift of such a mutation can be alkaline or acidic.

Kinetic Model for Fitting Experimental ASIC1a Data.

The kinetic model of ASIC1a, illustrated in Fig. S1F, is composed of 32 states corresponding to three sets of protonation sites (o = activation, d = desensitization, and a = AcP) and four conformations [C = closed, O = open, D = closed-desensitized, and (OD) = open-desensitized]. For computational reasons (see below), the protonation of closed channels toward opening and desensitization is represented by two steps each (C→C^o→C^O, C→C^d→C^D), which does not mean that exactly two protonation steps are involved. Opening and desensitization involve a final pH-independent transition (C^O→O^O, C^D→D^D). Evidence for such a ligand-independent transition before opening comes from several studies with ligand-gated ion channels (38, 39). Each of these 16 states can exist with the proton sensor in the AcP protonated or not (e.g., C and ^aC), yielding a total of 32 states.

Protonation transitions are described by their pH50 (or the equivalent proton concentration [H₅₀]) at which the protonation and deprotonation rates are equal, the Hill coefficient n, and their transition rate at pH = pH50, k. For example, protonation of the AcP

$$K_{C\to {}^{a}C}=k_a{\left(\frac{\left[H\right]}{\left[H_{50}^a\right]}\right)}^{n_a}=k_a{10}^{-n_a(\text{pH}-{\text{pH}}_{50}^a)},$$ [S14]

whereas the reverse transition is given by

$$K_{{}^{a}C\to C}=k_a.$$

Similar expressions were also used for the protonations of activation and desensitization sites, except that these transitions were split into two identical transitions (C→C^o→C^O, C→C^d→C^D); this was done because these transitions have large Hill coefficients (we found values of ∼11 for desensitization and 3 for activation), which led to difficulties in the simulation. Splitting these transitions decreases the corresponding Hill coefficient by a factor of 2, which allowed for easier integration of the equations.

$$K_{C\to C_d}=k_d{10}^{-n_d(\text{pH}-{\text{pH}}_{50}^d)};\hspace{0.17em}{K}_{C_d\to C}=k_d$$ [S15]

$$K_{C_d\to C_D}=k_d{10}^{-n_d(\text{pH}-{\text{pH}}_{50}^d)};\hspace{0.17em}{K}_{C_D\to C_d}=k_d$$

$$K_{C\to C^o}=k_o{10}^{-n_o(\text{pH}-{\text{pH}}_{50}^o)};\hspace{0.17em}{K}_{C^o\to C}=k_o$$ [S16]

$$K_{C^o\to C^O}=k_o{10}^{-n_o(\text{pH}-{\text{pH}}_{50}^o)};\hspace{0.17em}{K}_{C^O\to C^o}=k_o.$$

The rates of the pH-independent transitions to the open and desensitized states are

$$K_{C^O\to O^O}=f_O;\hspace{0.17em}{K}_{O^O\to C^O}=b_O$$ [S17]

$$K_{C_D\to D_D}=f_D;\hspace{0.17em}{K}_{D_D\to C_D}=b_D.$$ [S18]

We included cooperativity between protonation of the AcP and the other protonations, as well as with channel opening and desensitization.

$$K_{{}^{a}C\to {}^{a}C_d}={\alpha }_D{K}_{C\to C_d}$$ [S19]

$$K_{{}^{a}C\to {}^{a}C^o}={\alpha }_O{K}_{C\to C^o}$$ [S20]

$$K_{{}^{a}C_D\to {}^{a}D_D}={\beta }_D{K}_{C_D\to D_D}$$ [S21]

$$K_{{}^a{C}^O\to {}^{a}O^O}={\beta }_O{K}_{C^O\to O^O}.$$ [S22]

The four cooperativity parameters (${\alpha }_D$,${\alpha }_O$,${\beta }_D$, and ${\beta }_O$) are always positive, with values below 1 indicating negative cooperativity (e.g., if ${\alpha }_D<1$, protonation of AcP will make the protonation of the desensitization sites harder), and values above 1 corresponding to positive cooperativity (e.g., if ${\alpha }_D>1$, protonation of AcP will make the protonation of the desensitization sites easier). To respect microscopic reversibility, Eqs. S19–S22 also lead to cooperativity between the other transitions and protonation of the AcP,

$$K_{C_d\to {}^{a}C_d}={\alpha }_D{K}_{C\to {}^{a}C};\hspace{0.17em}{K}_{C_D\to {}^{a}C_D}={\alpha }_D{\alpha }_D{K}_{C\to {}^{a}C}$$

$$K_{C_o\to {}^{a}C_o}={\alpha }_O{K}_{C\to {}^{a}C};\hspace{0.17em}{K}_{C_O\to {}^{a}C_O}={\alpha }_O{\alpha }_O{K}_{C\to {}^{a}C}$$

$$K_{C_d^o\to {}^{a}C_d^o}={\alpha }_D{\alpha }^O{K}_{C\to {}^{a}C};\hspace{0.17em}{K}_{C_D^o\to {}^{a}C_D^o}={\alpha }_D{\alpha }_D{\alpha }^O{K}_{C\to {}^{a}C}$$

$$K_{C_d^O\to {}^{a}C_d^O}={\alpha }_D{\alpha }^O{\alpha }^O{K}_{C\to {}^{a}C};\hspace{0.17em}{K}_{C_D^O\to {}^{a}C_D^O}={\alpha }_D{\alpha }_D{\alpha }^O{\alpha }^O{K}_{C\to {}^{a}C}$$

$$K_{D_D\to {}^{a}D_D}={\alpha }_D{\alpha }_D{\beta }_D{K}_{C\to {}^{a}C};\hspace{0.17em}{K}_{D_D^o\to {}^{a}D_D^o}={\alpha }_O{\alpha }_D{\alpha }_D{\beta }_D{K}_{C\to {}^{a}C};\hspace{0.17em}{K}_{D_D^O\to {}^{a}D_D^O}={\alpha }_O{\alpha }_O{\alpha }_D{\alpha }_D{\beta }_D{K}_{C\to {}^{a}C}$$

$$K_{O^O\to {}^{a}O^O}={\alpha }_O{\alpha }_O{\beta }^O{K}_{C\to {}^{a}C}\hspace{0.17em};\hspace{0.17em}{K}_{O_d^O\to {}^{a}O_d^O}={\alpha }_D{\alpha }_O{\alpha }_O{\beta }^O{K}_{C\to {}^{a}C};\hspace{0.17em}{K}_{O_D^O\to {}^{a}O_D^O}={\alpha }_D{\alpha }_D{\alpha }_O{\alpha }_O{\beta }^O{K}_{C\to {}^{a}C}$$

$$K_{(O{D)}_D^O\to {}^a\left(\mathit{OD}\right)_D^O}={\alpha }_O{\alpha }_O{\alpha }_D{\alpha }_D{\beta }_D{\beta }^O{K}_{C\to {}^{a}C}.$$

The remaining rates are all equivalent to one of the rates defined above. For the reverse reactions, all rates for reactions shown with the same color in Fig. S1F are identical,

$$K_{{}^{a}C_d\to C_d}=K_{{}^{a}C_D\to C_D}=K_{{}^{a}C^o\to C^o}=K_{{}^{a}C^O\to C^O}=K_{{}^{a}C_d^o\to C_d^o}=K_{{}^{a}C_D^o\to C_D^o}=K_{{}^{a}C_d^O\to C_d^O}=K_{{}^{a}C_D^O\to C_D^O}=K_{{}^{a}C\to C}$$

$$K_{{}^{a}O^O\to O^O}=K_{{}^{a}O_d^O\to O_d^O}=K_{{}^{a}O_D^O\to O_D^O}=K_{{}^{a}C\to C}$$

$$K_{{}^{a}D_D\to D_D}=K_{{}^{a}D_D^o\to D_D^o}=K_{{}^{a}D_D^O\to D_D^O}=K_{{}^a\left(\mathit{OD}\right)_D^O\to {\left(\mathit{OD}\right)}_D^O}=K_{{}^{a}C\to C}$$

$$K_{C_d^o\to C^o}=K_{C_d^O\to C^O}=K_{O_d^O\to O^O}=K_{{}^{a}C_d^o\to {}^{a}C^o}=K_{{}^{a}C_d^O\to {}^{a}C^O}=K_{{}^{a}O_d^O\to {}^{a}O^O}=K_{{}^{a}C_d\to {}^{a}C}=K_{C_d\to C}$$

$$K_{C_D^o\to C_d^o}=K_{C_D^O\to C_d^O}=K_{O_D^O\to O_d^O}=K_{{}^{a}C_D^o\to {}^{a}C_d^o}=K_{{}^{a}C_D^O\to {}^{a}C_d^O}=K_{{}^{a}O_D^O\to {}^{a}O_d^O}=K_{{}^{a}C_D\to {}^{a}C_d}=K_{C_D\to C_d}$$

$$K_{{}^{a}D_D\to {}^{a}C_D}=K_{D_D^o\to C_D^o}=K_{D_D^O\to C_D^O}=K_{{}^{a}D_D^o\to {}^{a}C_D^o}=K_{{}^{a}D_D^O\to {}^{a}C_D^O}=K_{{\left(\mathit{OD}\right)}_D^O\to O_D^O}=K_{{}^a\left(\mathit{OD}\right)_D^O\to {}^{a}O_D^O}=K_{D_D\to C_D}$$

$$K_{C_d^o\to C_d}=K_{C_D^o\to C_D}=K_{D_D^o\to D_D}=K_{{}^{a}C^o\to {}^{a}C}=K_{{}^{a}C_d^o\to {}^{a}C_d}=K_{{}^{a}C_D^o\to {}^{a}C_D}=K_{{}^{a}D_D^o\to {}^{a}D_D}=K_{C^o\to C}$$

$$K_{C_d^O\to C_d^o}=K_{C_D^O\to C_D^o}=K_{D_D^O\to D_D^o}=K_{{}^{a}C^O\to {}^{a}C^o}=K_{{}^{a}C_d^O\to {}^{a}C_d^o}=K_{{}^{a}C_D^O\to {}^{a}C_D^o}=K_{{}^{a}D_D^O\to {}^{a}D_D^o}=K_{C^O\to C^o}$$

$$K_{O_d^O\to C_d^O}=K_{O_D^O\to C_D^O}=K_{(O{D)}_D^O\to D_D^O}=K_{{}^{a}O^O\to {}^{a}C^O}=K_{{}^{a}O_d^O\to {}^{a}C_d^O}=K_{{}^{a}O_D^O\to {}^{a}C_D^O}=K_{{}^a\left(\mathit{OD}\right)_D^O\to {}^{a}D_D^O}=K_{O^O\to C^O}.$$

For the forward rates, this is not the case because of cooperativity, and we have

$$K_{C^o\to C_d^o}=K_{C^O\to C_d^O}=K_{O^O\to O_d^O}=K_{C_d\to C_D}=K_{C_d^o\to C_D^o}=K_{C_d^O\to C_D^O}=K_{O_d^O\to O_D^O}=K_{C\to C_d}$$

$$K_{{}^{a}C^o\to {}^{a}C_d^o}=K_{{}^{a}C^O\to {}^{a}C_d^O}=K_{{}^{a}O^O\to {}^{a}O_d^O}=K_{{}^{a}C_d\to {}^{a}C_D}=K_{{}^{a}C_d^o\to {}^{a}C_D^o}=K_{{}^{a}C_d^O\to {}^{a}C_D^O}=K_{{}^{a}O_d^O\to {}^{a}O_D^O}=K_{{}^{a}C\to {}^{a}C_d}$$

$$K_{C_D^o\to D_D^o}=K_{C_D^O\to D_D^O}=K_{O_D^O\to (O{D)}_D^O}=K_{C_D\to D_D}$$

$$K_{{}^{a}C_D^o\to {}^{a}D_D^o}=K_{{}^{a}C_D^O\to {}^{a}D_D^O}=K_{{}^{a}O_D^O\to {}^a\left(\mathit{OD}\right)_D^O}=K_{{}^{a}C_D\to {}^{a}D_D}$$

$$K_{C_d\to C_d^o}=K_{C_D\to C_D^o}=K_{D_D\to D_D^o}=K_{C_d^o\to C_d^O}=K_{C_D^o\to C_D^O}=K_{D_D^o\to D_D^O}=K_{C^o\to C^O}=K_{C\to C^o}$$

$$K_{{}^{a}C_d\to {}^{a}C_d^o}=K_{{}^{a}C_D\to {}^{a}C_D^o}=K_{{}^{a}D_D\to {}^{a}D_D^o}=K_{{}^{a}C^o\to {}^{a}C^O}=K_{{}^{a}C_d^o\to {}^{a}C_d^O}=K_{{}^{a}C_D^o\to {}^{a}C_D^O}=K_{{}^{a}D_D^o\to {}^{a}D_D^O}=K_{{}^{a}C\to {}^{a}C^o}$$

$$K_{C_d^O\to O_d^O}=K_{C_D^O\to O_D^O}=K_{D_D^O\to {\left(\mathit{OD}\right)}_D^O}=K_{C^O\to O^O}$$

$$K_{{}^{a}C_d^O\to {}^{a}O_d^O}=K_{{}^{a}C_D^O\to {}^{a}O_D^O}=K_{{}^{a}D_D^O\to {}^a\left(\mathit{OD}\right)_D^O}=K_{{}^{a}C^O\to {}^{a}O^O}.$$

The current is defined from the fraction of channels in an open state and the conductance of the channels as

$$I=G\times (O^O+O_d^O+O_D^O+{}^{a}O^O+{}^{a}O_d^O+{}^{a}O_D^O).$$

Voltage and ion concentrations were the same for all experiments and were therefore not explicitly modeled (absorbed in the conductance $G$).

Fit of the Kinetic Models to the Experimental Data.

The 32-state kinetic model of ASIC comprised 17 free parameters: 3 for protonation of the AcP ($p{H}_{50}^a$, $n_a$, and $k_a$; Eq. S14), 3 for the protonation of the activation sites ($p{H}_{50}^o$, $n_o$, and $k_o$; Eq. S16), and 3 for the protonation of the desensitization sites ($p{H}_{50}^d$, $n_d$, and $k_d$; Eq. S15), 1 for each of channel opening, closing, desensitization, and recovery ($f_O$, $b_O$, $f_D$, and $b_D$; Eqs. S17 and S18), and 4 cooperativity coefficients (${\alpha }_O$, ${\alpha }_D$, ${\beta }_O$, and ${\beta }_D$; Eqs. S19–S22).

Each mutant was described by three parameters, each changing one of the parameters describing the protonation of the AcP,

$${\text{pH}}_{50}^a\Rightarrow {\text{pH}}_{50}^a+\mathrm{\Delta }{\text{pH}}_{50}^a\hspace{1em}\text{with}\hspace{1em}\mathrm{\Delta }{\text{pH}}_{50}^a>0$$

$$n_d\Rightarrow \epsilon \times n_d\hspace{1em}\text{with}\hspace{1em}0<\epsilon <1$$

$$k_d\Rightarrow \gamma \times k_d.$$

As we fitted the model to data for the WT channel and two mutants, this added six parameters. Finally, the data used came from six different cells (one for activation and one for desensitization for the WT and both mutant channels), which added six parameters describing the overall conductance of ASICs for each cell. This gave a total of 29 free parameters.

The model was fit to measured currents from the activation (step from conditioning pH to different acidic pH; Fig. 1C) and desensitization protocols (step from different conditioning pH to an acidic pH; blue arrow in Fig. 1D). Specifically, we used currents from seven activation and six desensitization steps for the WT, five activation and eight desensitization steps for the AcP11 mutant, and seven activation and six desensitization steps for the AcP14 mutant. The model was fitted to all of the traces simultaneously, using the Data2Dynamics software (34) with a deterministic optimization procedure repeated more than 50 times from different starting parameters obtained from a Latin hypercube sampling (40).

Kinetic Model with Protonation of AcP Essential for Activation or Desensitization.

The above model was modified to describe a situation where protonation of the AcP is an essential component of either activation or desensitization, i.e., the channel can only activate or desensitize if the AcP is protonated. In the former case, this was simply represented by removing the open states without the AcP protonated ($O^O$, $O_d^O$, $O_D^O$, and $O{D}_D^O$) whereas, for the latter (AcP essential for desensitization), we removed the desensitized states without AcP protonated ($D_D$, $D_D^o$, $D_D^O$, and $O{D}_D^O$).