Ion and inhibitor binding of the double-ring ion selectivity filter of the mitochondrial calcium uniporter

Significance

Mitochondrial calcium homeostasis is vital to cellular activities such as aerobic ATP production and cell death. Calcium uptake by mitochondria is achieved using an intricately regulated calcium channel, known as mitochondrial calcium uniporter (MCU). MCU demonstrates high calcium selectivity and conductance but little is known about its ion selectivity filter. We used paramagnetic NMR to show that the double carboxylate rings formed by the “DXXE” signature sequence of MCU is the ion selectivity filter and that the two ion binding sites can afford high ion affinity via positive cooperativity. We also showed that the channel inhibitor Ru360 directly blocks at the selectivity filter. Our approach demonstrates the promising application of NMR in investigating ion channels interacting with ions and blockers.

Abstract

The calcium (Ca²⁺) uniporter of mitochondria is a holocomplex consisting of the Ca²⁺-conducting channel, known as mitochondrial calcium uniporter (MCU), and several accessory and regulatory components. A previous electrophysiology study found that the uniporter has high Ca²⁺ selectivity and conductance and this depends critically on the conserved amino acid sequence motif, DXXE (Asp-X-X-Glu) of MCU. A recent NMR structure of the MCU channel from Caenorhabditis elegans revealed that the DXXE forms two parallel carboxylate rings at the channel entrance that seem to serve as the ion selectivity filter, although direct ion interaction of this structural motif has not been addressed. Here, we use a paramagnetic probe, manganese (Mn²⁺), to investigate ion and inhibitor binding of this putative selectivity filter. Our paramagnetic NMR data show that mutants with a single carboxylate ring, NXXE (Asn-X-X-Glu) and DXXQ (Asp-X-X-Gln), each can bind Mn²⁺ specifically, whereas in the WT the two rings bind Mn²⁺ cooperatively, resulting in ∼1,000-fold higher apparent affinity. Ca²⁺ can specifically displace the bound Mn²⁺ at the DXXE site in the channel. Furthermore, titrating the sample with the known channel inhibitor ruthenium 360 (Ru360) can displace Mn²⁺ binding from the solvent-accessible Asp site but not the inner Glu site. The NMR titration data, together with structural analysis of the DXXE motif and molecular dynamics simulation, indicate that the double carboxylate rings at the apex of the MCU pore constitute the ion selectivity filter and that Ru360 directly blocks ion entry into the filter by binding to the outer carboxylate ring.

Calcium (Ca²⁺) uptake by mitochondria is a long-known physiological phenomenon that is important for regulating various cellular activities such as aerobic metabolism and cell death (1–3). This uptake of Ca²⁺ is achieved by a Ca²⁺ uniporter whose activity can be blocked by ruthenium red (RuR) or ruthenium 360 (Ru360) (4). It was later shown by patch-clamping the inner mitochondrial membrane that this uniporter achieves remarkably high Ca²⁺ conductance and selectivity (5). Only about 5 y ago was the molecular identity of the channel component of the uniporter identified using integrative genomics approaches (6, 7). This channel is commonly referred to as the mitochondrial calcium uniporter (MCU). In metazoans, however, the uniporter is much more complex than just the pore-forming subunit; it is a holocomplex (also called a uniplex) containing other regulatory components. Among them, the single-pass transmembrane (TM) protein EMRE (Essential MCU REgulator) is absolutely required for the MCU to conduct ions (8). Two soluble components in the intermembrane space, MICU1 and MICU2, are Ca²⁺-sensing proteins that gate the activity of MCU based on outside Ca²⁺ concentrations through EMRE (9–12). The current consensus is that the minimum requirements for uniporter-mediated Ca²⁺ flux in metazoans are MCU and EMRE, whereas in lower organisms such as Dictyostelium that lack EMRE, MCU is able to operate (13).

In an earlier study, we determined the pore architecture of the MCU channel using structural data obtained from solution NMR and negative-stain EM experiments (14). That structural study was performed on a Caenorhabditis elegans MCU construct with the N-terminal domain (NTD; residues 1–165) deleted, denoted as cMCU-ΔNTD. This protein construct has been shown to function as the full-length MCU in the mitochondrial Ca²⁺ uptake assay (14). The MCU is a homopentamer with the second TM helix forming a hydrophilic pore across the presumed lipid bilayer. The TM pentamer is further stabilized by a C-terminal domain that forms a coiled-coil pentamer outside the membrane. Perhaps the most interesting structural element is two parallel carboxylate rings formed by the Asp240-X-X-Glu243 (DXXE) motif at the entrance of the pore, on the intermembrane space side of the channel. For convenience, the conserved Asp240 and Glu243 are denoted here as D and E, respectively. The D ring is solvent-exposed and the E ring is located deeper inside the pore. Although NMR restraints were insufficient to provide the precise conformation of the carboxylate rings, the approximate dimensions of the D and E rings, as estimated based on the backbone Cβ positions, are 7 and 11 Å, respectively, which are consistent with specific cation binding (15–17). Moreover, functional mutagenesis showed that mutating either D or E causes MCU to lose channel activity nearly completely (6), providing further support for DXXE’s role in recruiting and selecting ions.

In general, the selectivity filter is an important determinant of ion selectivity and conductivity of a channel (18, 19). The uniporter demonstrates very high Ca²⁺ conductance (i.e., a maximum reported flux of 5 × 10⁶ Ca²⁺ s⁻¹ at 105 mM Ca²⁺ and −160 mV voltage) (5). The uniporter is also strongly selective, with ∼10³- to 10⁶-fold higher selectivity for Ca²⁺ over Na⁺ (5). Both conductance and selectivity of the uniporter are high compared with, for example, the Ca²⁺ release-activated Ca²⁺ channel Orai and the CorA Mg²⁺ channel. In the case of Orai, there is only one ring of six glutamate side chains at the pore entrance (17). The CorA Mg²⁺ channel shows a pentameric selectivity ring but formed with Asn (15, 16). Moreover, Ru360 is a potent blocker of MCU conductance and has been suggested to bind to the apex of the channel according to mutagenesis studies (6, 20). It is not known whether Ru360 blocks Orai or CorA. Although previous functional studies established channel properties of MCU and the putative mechanism of Ru360 inhibition (5, 6, 14), structural information on ion and inhibitor binding is still missing.

In this study, to gain insights into understanding how MCU manages to achieve both high Ca²⁺ conductance and selectivity we focused on addressing whether the DXXE motif is capable of binding divalent cations, which is obviously a requirement of being the selectivity filter, and, if so, how it interacts with the ion in the double-ring configuration. While researchers await a high-resolution structure of the MCU bound to Ca²⁺, we sought to capitalize on the NMR system developed for the cMCU-ΔNTD to address the above question. Because Ca²⁺ is not suitable for directly probing ion binding by NMR, we used paramagnetic manganese (Mn²⁺), which is also a permeable divalent cation of MCU (5), to map residue-specific ion binding. We found that Mn²⁺ interacts with the DXXE motif in a highly specific manner and that the bound Mn²⁺ can be displaced with Ca²⁺. By combining mutagenesis and paramagnetic NMR measurements we also found that the D and E carboxylate rings can bind Mn²⁺ in a cooperative manner and that Ru360 can only interact with the solvent-accessible D ring. Our results show that the double-ring structural element formed by DXXE is the ion selectivity filter of MCU and that Ru360 inhibits MCU activity by directly blocking this filter.

Results

Mn²⁺ Binds Specifically to the DXXE Motif, Which Can Be Displaced by Ca²⁺.

Equilibrium ion binding properties of channels have been extremely difficult to measure using common biophysical methods such as isothermal titration calorimetry unless it is done with extreme care and precision, as has been demonstrated by a previous study that measured K⁺ binding constants of the K⁺ channel (21). A favorable feature of NMR is the ability to provide residue-specific binding information. Calcium ion is NMR-invisible and its binding to protein can only be indirectly inferred by chemical shift changes. Fortunately, previous channel recording studies reported four different MCU-permeable divalent cations (Ca²⁺, Sr²⁺, Mn²⁺, and Ba²⁺) (5), among which Mn²⁺ is a commonly used paramagnetic probe in NMR studies of Ca²⁺ and Mg²⁺ binding proteins (22–24). In the case of MCU, Mn²⁺ is a relevant ion for investigating Ca²⁺ binding because (i) Mn²⁺ can be conducted by MCU, (ii) the Ca²⁺ current can be reduced by low concentrations of Mn²⁺ (5), indicating that Mn²⁺ competes with Ca²⁺ for binding at the ion selectivity site, and (iii) Mn²⁺ and Ca²⁺ are both divalent cations that have similar coordination numbers (25). We thus used Mn²⁺ as a paramagnetic probe and used an NMR titration experiment to map the binding site(s) of the divalent cation in MCU.

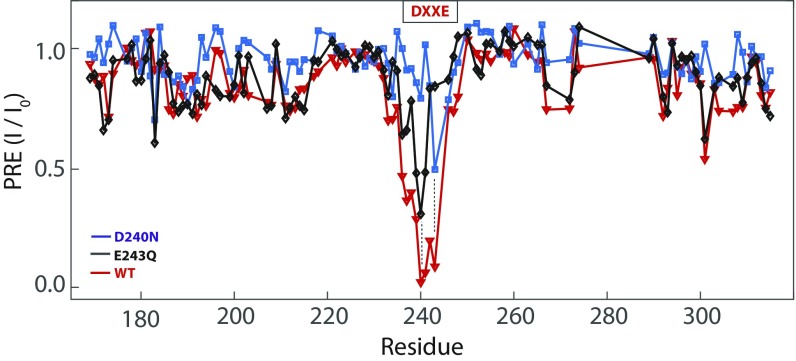
The NMR experiments were performed using uniformly [¹⁵N, ¹³C, ²H]-labeled cMCU-∆NTD, which was expressed in Escherichia coli and purified by nickel–nitrilotriacetic acid affinity, ion exchange, and size-exclusion chromatography using a previously established protocol (14) (Materials and Methods and Fig. S1). We titrated a 20 µM (pentamer) cMCU-∆NTD sample with Mn²⁺ at concentrations ranging from 0–40 µM (Materials and Methods). At each Mn²⁺ concentration, residue-specific NMR signal reduction due to paramagnetic relaxation enhancement (PRE) caused by the Mn²⁺ was measured using the 2D ¹H-¹⁵N transverse relaxation optimized spectroscopy (TROSY)–heteronuclear single-quantum correlation (HSQC) and the 3D HNCO that correlates the chemical shifts of backbone ¹H, ¹⁵N, and ¹³C nuclides. During the Mn²⁺ titration, the DXXE motif showed the most rapid peak intensity reduction, with almost complete disappearance of the peaks of D and E at 20 µM Mn²⁺ (Fig. 1A). The 3D HNCO allowed examination of all assigned residues of cMCU-∆NTD (Fig. 1B) by resolving the peak overlaps in the 2D spectrum. The residue-specific PRE is defined here as the ratio between the peak heights in the presence (I) and absence (I₀) of Mn²⁺. Our data show that the severely affected region with I/I₀ ≤ 0.2 is exclusively the DXXE motif (Fig. 1 C and D). The residues with less significant PRE (0.2 < I/I₀ ≤ 0.5) are mostly in the short loop between the DXXE and the first TM helix (Fig. 1D). To further resolve the paramagnetic effects on D and E, we plotted I/I₀ as a function of [Mn²⁺], which shows that the PRE on D is stronger than on E (Fig. 1 E and F). The above results provide direct evidence of specific binding of a divalent cation to the DXXE structural element.

Fig. S1.

NMR sample preparation of cMCU-ΔNTD. (A) Size-exclusion elution profile of cMCU-ΔNTD from the Superdex 200 10/300 GL column in 20 mM MES (pH 6.4), 75 mM NaCl, 0.48 mM Foscholine-14, and 0.3 mM NaN₃. (B) SDS/PAGE analysis of the elution peak in A showing sample purity >95%. The lane numbers correspond to the elution fraction numbers in A. (C) The 2D ¹H-¹⁵N TROSY-HSQC spectrum of (¹⁵N, ¹³C, ²H)-labeled cMCU-ΔNTD from A, recorded at 750 MHz ¹H frequency and 306 K.

Fig. 1.

Specific PRE of the WT DXXE motif induced by Mn²⁺. (A) Superimposition of 2D ¹H-¹⁵N TROSY-HSQC spectra of 20 µM (pentamer) U-[¹⁵N, ¹³C, ²H] cMCU-∆NTD without (red) and with (cyan) 40 µM Mn²⁺ shows that PRE effects of Mn²⁺ are localized in the DXXE motif. (B) Comparison of 3D TROSY-HNCO spectra of 20 µM (pentamer) U-[¹⁵N, ¹³C, ²H] cMCU-∆NTD before (Top) and after (Bottom) addition of 40 µM Mn²⁺, showing the specific PREs of the DXXE motif in more resolved spectra. (C) Mapping the strong PREs (I/I₀ ≤0.5) in A onto the cMCU-∆NTD structure (red: I/I₀ ≤ 0.2; cyan: 0.2 < I/I₀ ≤ 0.5). (D) Backbone amide PRE is plotted against residue number for the TM domain. The residues with overlap or without assignment are labeled with an asterisk. (E) The D240 and E243 peak intensities decrease with Mn²⁺ titration. The data were obtained from 2D ¹H-¹⁵N TROSY-HSQC spectra with Mn²⁺ titrated into 20 µM (pentamer) cMCU-∆NTD. (F) Plots of I/I₀ vs. [Mn²⁺] for D240 (black) and E243 (red) of the WT cMCU-∆NTD and recovery of I/I₀ upon addition of 10, 20, and 30 mM Ca²⁺.

Upon saturating the DXXE with Mn²⁺ we examined whether Ca²⁺ can displace the bound Mn²⁺, leading to the recovery of D and E NMR signals. The sample was then titrated with 10, 20, and 30 mM Ca²⁺. At each Ca²⁺ concentration, 2D ¹H-¹⁵N TROSY-HSQC and 3D TROSY-HNCO spectra were recorded. At 10 mM Ca²⁺, we can see obvious peak recovery for D240 and E243 (Fig. S2). The peak intensities for D240 and E243 recovered to ∼20% at 30 mM Ca²⁺ concentration (Fig. 1F), above which the NMR sample became unstable. The inefficient displacement of Mn²⁺ by Ca²⁺ indicates that Ca²⁺ binding is much weaker than Mn²⁺.

Fig. S2.

Comparison of 3D TROSY-HNCO spectra of 20 µM (pentamer) U-[¹⁵N, ¹³C, ²H] cMCU-∆NTD without Mn²⁺ or Ca²⁺ (Top), with 20 µM Mn²⁺ (Middle) addition, and with 20 µM Mn²⁺ and 30 mM Ca²⁺ (Bottom), showing specific PREs of the DXXE motif due to Mn²⁺ and specific displacement of Mn²⁺ by Ca²⁺.

The Two Carboxylate Rings Can Bind Mn²⁺ Separately and Cooperatively.

We next investigated whether each of the D and E carboxylate rings can specifically bind divalent cations. It is not possible to address this question by functional mutagenesis because mutating either D or E would almost completely abrogate channel activity (6, 7) and thus prohibit functional readout. We thus performed similar Mn²⁺ titration on the single carboxylate ring mutants including the D240N (or NXXE) and the E243Q (or DXXQ) mutants. These mutants were expressed and purified as was done for cMCU-∆NTD. Size-exclusion profiles show that the mutants have the same oligomeric state as cMCU-∆NTD (Fig. S3A). Moreover, the NMR spectra of the mutated and original cMCU-∆NTDs are essentially the same except for perturbation of a few residues adjacent to the site of mutation, indicating that the mutations did not alter the channel conformation (Fig. S3B). We then performed Mn²⁺ titration on the mutants using titration protocols similar to that used for the cMCU-∆NTD in Fig. 1.

Fig. S3.

NMR sample preparation of the single-ring cMCU-ΔNTD mutants DXXQ and NXXE. (A) Overlay of size-exclusion elution profiles of cMCU-ΔNTD variants DXXE, DXXQ, and NXXE from the Superdex 200 10/300 GL column in 20 mM MES (pH 6.4), 75 mM NaCl, 0.48 mM Foscholine-14, and 0.3 mM NaN₃. (B) Superposition of 2D ¹H-¹⁵N TROSY-HSQC spectrum of DXXE (red) with that of DXXQ (cyan) on the left and NXXE (cyan) on the right, showing that the mutations did not cause significant changes in the protein structure.

The results show that the D peak of the DXXQ mutant and the E peak of the NXXE mutant are both sensitive to Mn²⁺ titration, although the rate of intensity reduction with respect to [Mn²⁺] is significantly lower than the corresponding rates of the WT DXXE (Fig. 2 A and B). The results indicate that the single carboxylate rings are capable of binding Mn²⁺. We also found that the Q of the DXXQ mutant experienced much less paramagnetic effect compared with D (Fig. 2C), and the same is true for the N of the NXXE mutant (Fig. 2D), indicating that Mn²⁺ binding by D or E in the single-ring mutants is specific. At 40 μM Mn²⁺, which caused saturation of PRE of D and E in DXXE, the D and E of the single-ring mutants showed 70% and 50% signal reduction, respectively (Fig. 2E). The complete PRE maps of the mutants are shown in Fig. S4. Overall, the results in Fig. 2 suggest that the single carboxylate ring is significantly weaker in recruiting Mn²⁺ than the double-ring WT.

Fig. 2.

PRE of the mutant DXXQ and NXXE motifs induced by Mn²⁺. (A) PRE (I/I₀) vs. [Mn²⁺] plots for D240 in the WT DXXE (black) and the DXXQ mutant (blue). The channel concentration is 20 µM. (B) PRE vs. [Mn²⁺] plots for E243 in the WT DXXE (red) and the NXXE mutant (green). The channel concentration is 20 µM. (C) PRE vs. [Mn²⁺] plots for D240 (blue) and Q243 (gray) in the DXXQ mutant. (D) PRE vs. [Mn²⁺] plots for E243 (green) and N240 (gray) in the NXXE mutant. (E) At 40 μM Mn²⁺, which caused PRE saturation of D and E in the WT DXXE, the D and E of the single-ring mutants showed 70% and 50% signal reduction, respectively. (F) Comparison between the PRE-derived [Mn²⁺]_bound/[channel] and simulated binding curves for the one-site (Eq. 1) and two-site (Eq. 2) systems (Materials and Methods). For the one-site mutants, [Mn²⁺]_Bound/[channel] (calculated as 1− I/I₀) and simulated curves are shown for DXXQ (yellow) and NXXE (red). For the two-site WT, the [Mn²⁺]_Bound/[channel] points were calculated using Eq. 3 (shown in purple). The two-site binding curves with n = 1 (no cooperativity), n = 100, and n = 1,000 are shown in black, blue, and purple, respectively.

Fig. S4.

The complete PRE (I/I₀) vs. residue number plots for three cMCU-∆NTD variants: DXXE (red), DXXQ (black), and NXXE (blue). The two dashed lines mark residue positions 240 and 243.

To interpret the Mn²⁺ titration data more quantitatively, we estimated the apparent dissociation constant (K_d) using the PRE readouts. Because the channel concentration is not much lower than that of the ion, the simplified condition [Mn²⁺]_total ≈ [Mn²⁺]_free no longer holds. Hence, we simulated binding curves at a fixed channel concentration (20 μM) and a range of K_d values using the full analytical solution describing the fraction of ion-bound sites and estimated K_d by comparing the experimental data with the simulated curves. For the single-ring mutants, the analytical solution used was that for one binding site (Eq. 1 and Fig. S5). In terms of the observed PRE, the fraction of ion-bound sites is given by 1− I/I₀. By identifying the simulated curve that agrees best with the experimental (1− I/I₀) vs. [Mn²⁺] data, the apparent K_d could be estimated. Using such analysis, we found that the apparent K_d values for the single-ring mutants are ∼30 μM for the E ring and ∼10 μM for the D ring (Fig. 2F).

Fig. S5.

Comparison of (1 – PRE) of D (yellow) or E (red) of the single-ring mutants with simulated binding curves for the one-site model. For the PRE data, 20 µM mutant channels were titrated with 0, 4, 6, 10, 15, 20, 25, 30, and 40 µM Mn²⁺ under our NMR titration condition. The binding curve was plotted using Eq. 1 for a fixed channel concentration (20 µM) at K_d values of 1, 10, 30, 100, and 300 μM.

For the WT DXXE, the equilibrium binding equation used was that for two nonidentical binding sites (Eq. 2 and Fig. S5). By using the intrinsic K_d of the D and E sites obtained from the mutants, the two-site binding curves without and with cooperativity were simulated (Fig. 2F). Direct conversion of PRE data to [Mn²⁺]_Bound/[channel] in the two-site case is, however, not straightforward due to cross-site PRE. For example, the sum of 1− I/I₀ for D and E at 20 μM Mn²⁺ and 20 μM channel, which should be ≤1 (or one Mn²⁺ per channel), is around 1.6 (Fig. S6). The extra PRE is due to a cross-site effect because one ion can shuttle rapidly back and forth between the two sites to induce PRE at both sites. In addition, the cross-site PRE includes long-range PRE between the two sites. Therefore, [Mn²⁺]_Bound/[channel] was calculated from the PRE data after subtracting the cross-site PRE as in Eq. 3 (Materials and Methods). Comparing experimentally derived [Mn²⁺]_Bound/[channel] with the simulated curves showed that having two nearby but independent sites (cooperativity factor n = 1) cannot account for the increased sensitivity to Mn²⁺ relative to the one-site mutant (Fig. 2F). Cooperativity must be introduced to obtain close agreement with the experimental data, and a qualitative comparison suggests a cooperativity factor (n) around 1,000.

Fig. S6.

Sum of (1 – PRE) for the D site and (1 – PRE) for the E site at various Mn²⁺ concentrations for the WT DXXE. This is the raw PRE data before correction to subtract the cross-site PRE.

Ru360 Binds to the D but Not the E Site.

Ru360, a linear dimer containing two octahedral ruthenium centers (Fig. 3A), is a potent inhibitor of mitochondrial Ca²⁺ uniporter (20). Earlier functional mutagenesis studies of the human MCU (HsMCU) showed that mutating S259 (S238 in cMCU) to Ala did not significantly affect MCU-mediated Ca²⁺ uptake but conferred resistance to Ru360 block (6). The NMR structure of the cMCU-∆NTD shows that this serine (S238) is located at the apex of the pore adjacent to D240 (Fig. 3B), suggesting the possibility of Ru360’s directly binding to the DXXE selectivity filter. Ru360 is not strongly paramagnetic and thus could not be used to directly induce PRE to map its binding site. It is nevertheless possible to test Ru360 binding to the D and E carboxylate rings by measuring Ru360 displacement of the bound Mn²⁺.

Fig. 3.

The Ru360/Mn²⁺ replacement titration for the single-ring mutants. (A) The crystal structure of Ru360 showing a linear dimer containing two octahedral rutheniums linked by an oxygen bridge with the ends of the molecule capped with formates. (B) The cMCU-∆NTD NMR structure showing that S238 is located at the apex of the pore adjacent to D240. (C) D240 peak intensity recovery by Ru360 titration at 0, 0.1, 0.5, and 1 mM. The mutant channel concentration used for Mn²⁺ and Ru360 titration is 20 µM. (D) The D240 recovery curve is shown as normalized peak intensity vs. [Ru360], in which the normalized peak intensity is defined as I (peak height at a given concentration of Ru360)/I₀ (peak height without Mn²⁺ or Ru360). (E) The E243 peak recovery by Ru360 titration at 0, 0.1, 0.5, and 1 mM. (F) The E243 recovery curve as in C but shows no peak recovery.

We first tested whether Ru360 competes with Mn²⁺ in binding to the D ring. The DXXQ mutant was first titrated with Mn²⁺ up to a concentration of 20 μM, at which the peak intensity decreased by ∼60% (Fig. 3 C and D). Then the sample was titrated with 0–1 mM Ru360. Increasing Ru360 concentration led to rapid recovery of the D peak intensity with an apparent K_d of ∼100 μM (Fig. 3 C and D). We then tested Ru360 binding to the E site by performing the same titration experiment using the NXXE mutant. In this case, titrating Mn²⁺ up to 20 μM led to ∼30% peak intensity reduction (Fig. 3 E and F). However, subsequent Ru360 titration did not recover the peak intensity (Fig. 3 E and F). These results indicate that Ru360 binds to the D ring but not to the E ring.

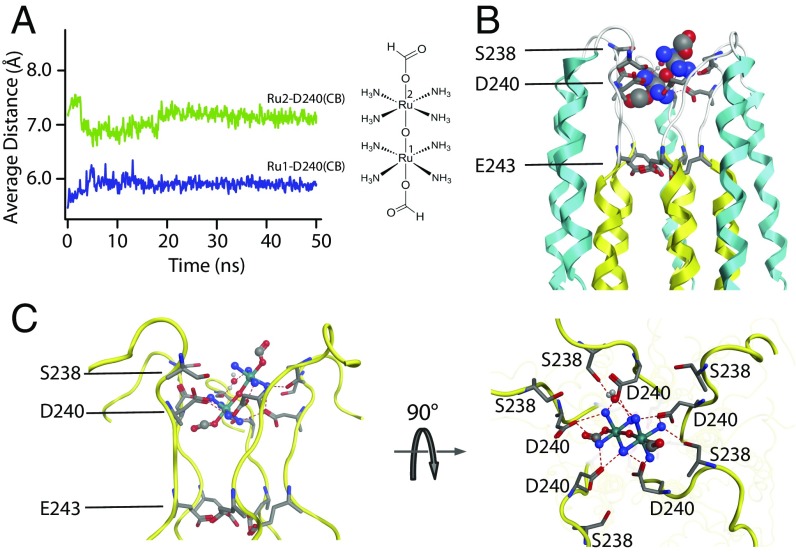
It is still possible, however, that Ru360 binds to a site near the D ring and causes the D ring to lose Mn²⁺ affinity via allosteric mechanism. We thus carried out further molecular dynamics (MD) simulation to examine whether direct Ru360 binding to the D ring is energetically favorable. The MD simulation system consists of the cMCU-∆NTD structure and Ru360 embedded in 1-palmitoyl-2-oleoyl-sn-glycero-3-phospcholine (POPC) lipid bilayer (Materials and Methods). Ru360 was vertically placed along the fivefold axis near the channel apex at the beginning of the simulation. After ∼25 ns of simulation, the system reached equilibrium and Ru360 indeed bound stably at the channel entrance, showing ∼45° tilt angle relative to the channel axis and extensive contacts with the D ring (Fig. 4 A and B). The amine groups of Ru360 interact strongly with side-chain carboxylate and backbone oxygen atoms of D by forming hydrogen-bonding meshwork (Fig. 4C). In addition, the amino groups of Ru360 showed interaction with S238 (Fig. 4C). The simulation did not suggest any Ru360 interactions with E243.

Fig. 4.

MD simulation of Ru360 binding to the MCU pore. (A) The distances between the ruthenium centers of Ru360 and the β carbons of D240 (averaged over the five protomers) vs. simulation time. (B) The average Ru360 position relative to the cMCU-∆NTD NMR structure showing the overall location of the inhibitor. (C) Zoomed side and top views of Ru360 interacting with D240 of the DXXE selectivity filter, showing possible hydrogen bonds between MCU and Ru360 (dashed lines).

Discussion

We have shown highly specific binding of Mn²⁺ to the pentameric carboxylate rings formed by the DXXE motif of MCU. We have also shown that each of the rings formed by D and E alone is capable of binding Mn²⁺, although at much weaker apparent affinity. The observed interactions between Mn²⁺ and the carboxylate rings are also selective because there are many accessible clusters of acidic residues in the protein but only those of the DXXE motif showed strong PRE at low Mn²⁺ concentration (DXXE resonances essentially disappeared at 1:1 channel:ion ratio). Moreover, because the bound Mn²⁺ can be specifically displaced by Ca²⁺, the reported Mn²⁺ binding to the DXXE carboxylate rings should hold for Ca²⁺, except the binding affinity and cooperativity are likely different according to the different conductance (5).

Based on previous functional mutagenesis of DXXE and the direct proof of DXXE’s binding to a divalent cation reported in this study we can now more confidently assign the DXXE motif as the MCU ion selectivity filter and elucidate its structure in the context of ion selectivity and conductance. On a first look at the DXXE structure, the solvent-accessible D ring resembles strongly to the pentameric N ring of the CorA Mg²⁺ channel and the hexameric E ring of the Orai Ca²⁺ channel. Orai is considered as highly selective for Ca²⁺ (half-maximal block of monovalent current at ∼10 µM Ca²⁺) but having rather modest conductivity (up to 10⁴ ions per second) (26–29). The pore structure of Orai suggests that the selectivity filter is a single ring of glutamates, which is compatible with a single high-affinity Ca²⁺ binding site with a fast on-rate and a slow off-rate (17). For the CorA channel, the pentameric N ring is directly involved in coordinating Mg²⁺, although in the absence of Mg²⁺ the channel is nonselective and permeable to cations (30).

The NMR structural and titration data show that both D and E rings can bind Mn²⁺ separately and they are aligned in parallel uniaxial configuration. The multiple ion binding sites along the pore axis is reminiscent of the selectivity filter of the tetrameric K⁺ channels, and thus comparison with the high-resolution structure of KcsA ought to be informative for understanding the high ion selectivity and conductance. The KcsA channel has 10,000-fold higher selectivity for K⁺ over Na⁺ and a conductance of 10⁸ K⁺ ions per s (close to the diffusion limit) (19); it is a textbook example of an ion channel having both high selectivity and high conductivity (31). The selectivity filter of KcsA is formed by four equivalent signature sequences (TVGYG) in extended conformation. The backbone carbonyl oxygen atoms of VGYG are aligned toward the center of the filter pore, forming four parallel squares (labeled S1–S4 from the extracelleular side) capable of coordinating K⁺ or water molecules (19).

In one of the proposed ion coordination models for KcsA, two K⁺ ions can be coordinated either at the S1 and S3 sites or at the S2 and S4 sites, with water molecules bound to the alternate sites between the two K⁺ ions (Fig. 5A) (32, 33). In the high-resolution crystal structures, the distance between the two K⁺ ions is ∼7.5 Å (19, 32). Based on the structural finding, it has been suggested that a single K⁺ ion could be held very tightly (21), but that the presence of two K⁺ ions in close proximity results in mutual repulsion, which enables fast ion conduction by exploiting electrostatic repulsive forces (19). A similar mechanism could explain the fast Ca²⁺ conduction by the MCU because the average distance between the D and E rings in the NMR structure ensemble is 8.0 Å with ∼1.5 Å uncertainty (Fig. 5B), consistent with the separation between the K⁺ binding sites S1 and S3 or S2 and S4 in KcsA. We thus propose that each of the two pentameric rings formed by DXXE serves as an ion-binding center, and that two bound Ca²⁺ are separated by ∼8 Å in the selectivity pore and are likely bridged by an intervening water molecule as in the KcsA.

Fig. 5.

Proposed model for Ca²⁺ binding to the MCU selectivity filter. (A) Coordination of K⁺ ions either at the S1 and S3 sites or at the S2 and S4 sites, with water molecules (red sphere) bound to the alternate sites between the two K⁺ ions (green sphere). The distance between the two K⁺ ions is 7.5 Å [atomic coordinates from Protein Data Bank (PDB) ID code 1BL8]. (B) The NMR structure ensemble of the DXXE motif showing the average distance between the D and E rings is 8.0 ± 1.5 Å (atomic coordinates from PDB ID code 5ID3). The green spheres represent hypothetical ions bound at the two ring positions. (C) The proposed Ca²⁺ pentagonal bipyramid coordination as five oxygen atoms of D or E ring coordinate ion in a plane while water molecules on the two sides of the plane interact with the ion along the pore axis.

The pentagonal bipyramid coordination arrangement could also explain high selectivity and would agree well with the coordination number of seven for Ca²⁺, because five oxygen atoms of the D or E ring coordinate ions in a plane while water molecules on the two sides of the plane interact with the ion along the pore axis (Fig. 5C). The pentagonal bipyramid conformation is common for Ca²⁺-binding proteins (Fig. S7), for example, the canonical EF-hand motif, the HRV (rhinovirus) protein (34, 35), and the Ca²⁺ ATPase (36). Ion selectivity is the result of highly specific ion binding to the permeation pathway (18), and we propose that the double carboxylate rings of MCU generate strong ion affinity through positive cooperativity. Although the NMR titration method is only suitable for measuring micromolar K_d values, comparing the Mn²⁺ titrating data with simulations suggests that the upper limit of apparent K_d is ∼10 nM, which is three orders of magnitude larger than the 10 and 30 μM K_d values for the individual D and E rings, respectively. Indeed, such cooperativity is expected in the pentagonal bipyramid coordination model, in which the two ions are bridged by interactions with the same water molecule. The strong Mn²⁺ binding is also consistent with the very slow Mn²⁺ flux reported by previous patch-clamp experiments (5).

Fig. S7.

Diagrammatic representation of the calcium coordination on the fivefold axis for the pentameric rhinovirus protein (35). The two representations are from different serotypes of human rhinovirus (HRV): (Left) HRV14 and (Right) HRV3.

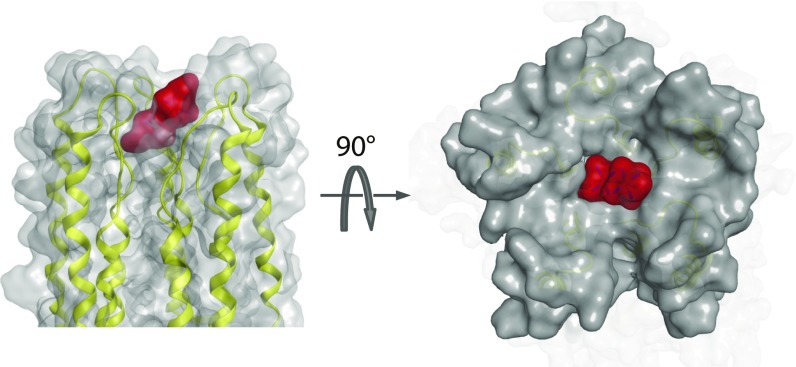
The binding of Ru360 to the apex of the MCU pore has already been suggested based on the mutagenesis of S259 in human (6) and S238 in C. elegans (14). In the cMCU structure, S238 is adjacent to the D ring, and its hydroxyl group possibly interacts with the amine groups of Ru360 (Fig. 4A). Our Ru360 titration data of the single-ring mutants show that Ru360 displaces Mn²⁺ at the D ring but not at the E ring, suggesting that Ru360 interacts with the negatively charged D ring. Therefore, Ru360–MCU complex should be mediated by electrostatic and hydrogen-bonding interactions between the Ru360 amine groups and the electronegative carboxylate groups of D240 and the hydroxyl group of S238, as suggested by the MD simulation (Fig. 4C). In addition to the polar contacts, size and shape complementarily also seemed important because the diameter of the Ru360 allows a snug fit of the compound to the hollow at the channel apex (Fig. S8).

Fig. S8.

Shape and surface complementarity between MCU and Ru360. The surfaces of the pore region of MCU and Ru360 are shown in gray and red, respectively. The Ru360–MCU complex model was generated by MD simulation in Fig. 4.

In summary, we provide direct evidence of specific binding of a divalent cation to the conserved DXXE motif of MCU and show that ion binding to the aspartate and glutamate rings is cooperative. The NMR titration data together strongly indicate that the DXXE motif forms the Ca²⁺ selectivity filter of MCU, similar to the K⁺ selectivity filter of the KcsA channel. It was not clear whether the Ser-to-Ala mutations near the pore entrance (S259A in human and S238A in C. elegans) confer resistance to Ru360 blocking via allosteric mechanism or direct abrogation of Ru360 binding at the pore entrance. Our Ru360/Mn²⁺ displacement data show that Ru360 directly binds to the solvent-accessible aspartate ring formed by the DXXE motif. Therefore, Ru360 inhibits the channel by directly blocking the entrance to the selectivity pore. The NMR titrations were all performed in the absence of the channel activator EMRE, and thus the channel under study is presumably in a state that can bind but not conduct divalent cations. A recent study suggests that EMRE may directly interact with the TM domain of MCU (37). Hence, the effect of EMRE on ion binding to the selectivity filter, if any, remains to be investigated.

Materials and Methods

Protein Expression and Purification.

E. coli-codon optimized DNA encoding residues 167–316 of the C. elegans MCU (cMCU-ΔNTD) with C-terminal 6-His tag was expressed and purified as described previously (14). The final NMR sample for 2D ¹H-¹⁵N TROSY-HSQC spectra contains 20µM cMCU-∆NTD (pentamer) in 20 mM MES, pH 6.4, 75 mM NaCl, ∼1 mM foscholine-14, 0.3 mM NaN₃, and 5% (vol/vol) D₂O. The mutants D240N and E243Q samples were prepared with the same way as for the original cMCU-∆NTD.

NMR Titration Experiments.

All NMR titration experiments were performed on a 750-MHz Bruker spectrometer equipped with cryogenic probe at 306 K. Uniformly (¹⁵N, ¹³C, 85% ²H)-labeled cMCU-ΔNTD and its mutants at 20 µM concentration (pentamer) were used for titration. MnCl₂ stock solution was added to 300 µL protein sample to reach final concentrations of 4, 6, 10, 15, 20, 25, 30, and 40 µM. For Ru360 titration, 0.1, 0.5, and 1 mM Ru360 was added in the same manner. At each ligand concentration point, 2D ¹H-¹⁵N TROSY-HSQC and 3D TROSY-HNCO spectra were recorded. The spectra were processed using NMRPipe and analyzed using Sparky.

MD Simulations.

MD simulations were performed using the Desmond 4.5 package. The OPLS-AA 2005 force field in a neutral POPC bilayer with appropriate number of counter ions was used to balance the net charge of the system solvated in 0.15 M NaCl. The cMCU-ΔNTD channel structure, Ru360, and POPC bilayer were embedded in a periodic orthorhombic box (∼14 × 14 × 14 ų) containing the explicit simple point charge (SPC) water molecules, which ensured that the surfaces of the MCU and Ru360 were covered by bilayer and/or water molecules. MD simulations were carried out for 50 ns with the periodic boundary conditions in the NPT ensemble [in which the amount of substance (N), pressure (P) and temperature (T) were conserved].

One-Site and Two-Site Binding Models.

The general solution of one-site binding used for simulating binding curves in Fig. 2F is

$$\frac{S_B}{P_T}=\frac{\left(P_T+S_T+K_{\text{d}}\right)\pm \sqrt{{(P_T+S_T+K_{\text{d}})}^2-4P_T{S}_T}}{2P_T},$$ [1]

where P_T and S_T are the total channel and Mn²⁺ concentrations, respectively, and S_B is the concentration of bound Mn²⁺.

The general solution of two-site binding with cooperativity included is

$$n{K}_1{K}_2{S}_B^3+\left(-K_1-K_2-2n{K}_1{K}_2{S}_T^2-2n{K}_1{K}_2{P}_T^2\right)S_B^2+\left[1+\left(K_1+K_2\right)S_T+n{K}_1{K}_2{S}_T^2+\left(K_1+K_2\right)P_T+4n{K}_1{K}_2{S}_T{P}_T\right]S_B+\left[-\left(K_1+K_2\right)S_T-2n{K}_1{K}_2{S}_T^2\right]P_T=0,$$ [2]

where P_T, S_T, and S_B are defined as above, K₁ and K₂ are binding constants for the E and D binding sites, respectively, and n is the cooperativity factor. Derivations are given in SI Materials and Methods.

Converting PRE Data to Population of Bound Mn²⁺.

For the two-site case, the number of bound Mn²⁺ per channel, [Mn²⁺]_Bound/[channel], is the sum of (1 – PRE) for the D site and (1 – PRE) for the E site subtracting the contribution from cross-site PRE. The cross-site PRE is introduced when a bound Mn²⁺ (at one site in a channel) can hop to an unbound site within the same channel, and this is given by the product of the number of bound Mn²⁺ per channel and the probability of having an unbound site in the channel (2[channel] − [Mn²⁺])/(2[channel]). In addition, the cross-site PRE includes long-range PRE between the two sites, and this can be estimated similarly as in the case of ion hopping except it is much weaker because the intersite PRE distances are substantially longer than the intrasite PRE distances. Combining the above yields

$$\frac{{\left[{\text{Mn}}^{2+}\right]}_{\text{Bound}}}{\left[\text{channel}\right]}=\left(2-{\text{PRE}}_{\text{D}}-{\text{PRE}}_{\text{E}}\right)-\left(1+X\right)\frac{{\left[{\text{Mn}}^{2+}\right]}_{Bound}}{\left[\text{channel}\right]}\left(\frac{2\left[\text{channel}\right]-\left[{\text{Mn}}^{2+}\right]}{2\left[\text{channel}\right]}\right),0\le \left[{\text{Mn}}^{2+}\right]\le 2\left[\text{channel}\right],$$ [3]

where PRE_D and PRE_E are the I/I₀ measured for the D and E resonance, respectively, at each of the titration points and X is the ratio of the intersite PRE to the intrasite PRE, observed for the DXXQ and NXXE mutants in Fig. 2 C and D at each of the Mn²⁺ concentrations.

SI Materials and Methods

Full Analytical Solution for Calculating One-Site Binding.

• K_d: dissociation constant for D240 (K₂) or E243 (K₁)

• P_T : total mutant channel concentration

• P : concentration of unbound mutant channel

• S_T: total Mn²⁺ concentration

• S_B: concentration of bound Mn²⁺ or Mn²⁺-channel complex

• S: concentration of free Mn²⁺

$$K_{\mathrm{d}}=\frac{PS}{S_B}$$

$$K_{\mathrm{d}}=\frac{(P_T-S_B)(\left[S_T\right]-S_B)}{S_B}$$

$${\left[S_B\right]}^2-(K_{\mathrm{d}}+P_T+\left[S_T\right])S_B+P_T\left[S_T\right]=0$$

$$\frac{S_B}{P_T}=\frac{\left(P_T+\left[S_T\right]+K_{\mathrm{d}}\right)\pm \sqrt{{(P_T+\left[S_T\right]+K_{\mathrm{d}})}^2-4P_T\left[S_T\right]}}{2P_T}$$

Full Analytical Solution for Calculating Two-Site Binding.

• P₀: unbound channel concentration

• P₁: concentration of channel with E site bound

• P₁′: concentration of channel with D site bound

• P₂: concentration of channel with both sites bound

• P_T : total channel concentration

• S_T: total Mn²⁺ concentration

• S_B: concentration of bound Mn²⁺

• S: concentration of free Mn²⁺

$$K_1=\frac{P_1}{P_{0}S}\hspace{0.17em};\hspace{0.17em}{K}_2=\frac{P_1^{\prime }}{P_{0}S}\hspace{0.17em};\hspace{0.17em}{K}_3=\frac{P_2}{P_{1}S}\hspace{0.17em};\hspace{0.17em}{K}_4=\frac{P_2}{P_1^{\prime }S}$$

$$K_1{K}_3=K_2{K}_4$$

$$\frac{S_B}{P_T}=\frac{P_1+P_1^{\prime }+2P_2}{P_T}=\frac{P_{0}S(K_1+K_2)+2P_0{S}^2{K}_1{K}_3}{P_0+S{P}_0(K_1+K_2)+P_0{S}^2{K}_1{K}_3}=\frac{S{K}_1+S{K}_2+2S^2{K}_1{K}_3}{1+S{K}_1+S{K}_2+S^2{K}_1{K}_3}$$

$$\frac{S_B}{P_T}=\frac{(S_T-S_B)K_1+(S_T-S_B)K_2+2{(S_T-S_B)}^2{K}_1{K}_3}{1+(S_T-S_B)K_1+(S_T-S_B)K_2+{(S_T-S_B)}^2{K}_1{K}_3}$$

Set $K_3=n{K}_2,\hspace{0.17em}n\hspace{0.17em}\text{is cooperativity factor}$

For independent binding: n = 1

For positive cooperative binding: n > 1

For negative cooperative binding: n < 1

$$\frac{S_B}{P_T}=\frac{(S_T-S_B)K_1+(S_T-S_B)K_2+2n{(S_T-S_B)}^2{K}_1{K}_2}{1+(S_T-S_B)K_1+(S_T-S_B)K_2+n{(S_T-S_B)}^2{K}_1{K}_2}$$

$$\frac{S_B}{P_T}=\frac{S_T(K_1+K_2)-S_B(K_1+K_2)+2n{K}_1{K}_2{S}_T^2+2n{K}_1{K}_2{S}_B^2-4n{K}_1{K}_2{S}_T{S}_B\hspace{0.17em}}{1+S_T(K_1+K_2)-S_B(K_1+K_2)+n{K}_1{K}_2{S}_T^2+n{K}_1{K}_2{S}_B^2-2n{K}_1{K}_2{S}_T{S}_B}$$

$$n{K}_1{K}_2{S}_B^3+(-K_1-K_2-2n{K}_1{K}_2{S}_T^2-2n{K}_1{K}_2{P}_T^2)S_B^2+[1+(K_1+K_2)S_T+n{K}_1{K}_2{S}_T^2+(K_1+K_2)P_T+4n{K}_1{K}_2{S}_T{P}_T]S_B+[-(K_1+K_2)S_T-2n{K}_1{K}_2{S}_T^2]P_T=0$$

The solution for S_B was obtained by solving the above cubic equation.

MD Simulations.

The Desmond 4.5 package was used for MD simulations and OPLS-AA 2005 force field in a neutral POPC bilayer with appropriate number of counter ions was used to balance the net charge of the system solvated in 0.15 M NaCl. The cMCU-ΔNTD pentamer structure (PDB ID code 5ID3) was placed in the lipid bilayer using the Desmond system building such that the TM domain spans the lipid bilayer. Ru360 was vertically placed along the fivefold axis near the D240 carboxylate ring at the beginning of the simulation.

The cMCU-ΔNTD structure, Ru360, and POPC bilayer were embedded in a periodic orthorhombic box (∼14 × 14 × 14 ų) containing the explicit SPC water molecules. MD simulations were carried out with periodic boundary conditions in NPT ensemble in which the amount of substance (N), pressure (P), and temperature (T) are conserved. Nosé–Hoover temperature coupling (38) and the Martina–Tobias–Klein method (39) with isotropic scaling (40) were used to control the simulation temperature (310 K) and atmospheric pressure (1 atm). The particle-mesh Ewald method (41, 42) was used to calculate long-range electrostatic interactions with grid spacing of 0.8 Å. A RESPA integrator (43) was used for which the electrostatic and van der Waals interactions were cut off at 9 Å.

Before the long production MD simulations, the system was equilibrated using the default membrane relax protocol provided in Desmond, which consists of a series of restrained minimizations and MD simulations that are designed to slowly relax the system without deviating too much from the initial protein coordinates. After removing all geometric restraints (bonds, angles, planarity, chirality, dihedral, etc.) used in the 2-ns system minimization and relaxation, the system was subject to 50-ns NPT production simulation without any restriction. The configurations and energies were recorded at 2-ps intervals.