Significance
Complete activation of the phototransduction G-protein cascade of dark-adapted rod photoreceptors causes outer segments to undergo 10% elongation and large local increases in backscattering, as measured in vivo with noninvasive, high-resolution optical coherence tomography. Maximal elongation is caused by a potentially harmful 20% increase in internal osmotic pressure generated by excess osmolytes arising from phototransduction. The light-stimulated elongation and backscattering responses can be explained by an osmo-elastic model of cytoplasmic swelling, combined with changes in refractive index consequent to the swelling and translocation of the G-protein subunits into the cytosol. Disease conditions that affect the structural integrity of rods may cause them to be especially vulnerable to osmotic stress caused by bright light.
Keywords: osmotic stress, phototransduction, optical coherence tomography, intrinsic optical signals, photoreceptor waveguiding
Abstract
The light responses of rod and cone photoreceptors have been studied electrophysiologically for decades, largely with ex vivo approaches that disrupt the photoreceptors’ subretinal microenvironment. Here we report the use of optical coherence tomography (OCT) to measure light-driven signals of rod photoreceptors in vivo. Visible light stimulation over a 200-fold intensity range caused correlated rod outer segment (OS) elongation and increased light scattering in wild-type mice, but not in mice lacking the rod G-protein alpha subunit, transducin (Gαt), revealing these responses to be triggered by phototransduction. For stimuli that photoactivated one rhodopsin per Gαt the rod OS swelling response reached a saturated elongation of 10.0 ± 2.1%, at a maximum rate of 0.11% s−1. Analyzing swelling as osmotically driven water influx, we find the H2O membrane permeability of the rod OS to be (2.6 ± 0.4) × 10−5 cm⋅s−1, comparable to that of other cells lacking aquaporin expression. Application of Van’t Hoff’s law reveals that complete activation of phototransduction generates a potentially harmful 20% increase in OS osmotic pressure. The increased backscattering from the base of the OS is explained by a model combining cytoplasmic swelling, translocation of dissociated G-protein subunits from the disc membranes into the cytoplasm, and a relatively higher H2O permeability of nascent discs in the basal rod OS. Translocation of phototransduction components out of the OS may protect rods from osmotic stress, which could be especially harmful in disease conditions that affect rod OS structural integrity.
Optical coherence tomography (OCT) is a noninvasive, label-free light-scattering method with broad applicability in biomedicine (1, 2). OCT has been universally adopted in clinical ophthalmology to map human retinal layer structure (2) and is widely used for angiography of the eye (3) and heart (4, 5) and for in vivo biopsy of skin and other tissues (6, 7). Ocular OCT has also been used in vivo to measure “intrinsic optical signals” from the photoreceptor layer of the retina (8, 9), including from individual human cone photoreceptors (10–14). In no case, however, has the molecular mechanism underlying an intrinsic optical signal been unequivocally identified. The value of OCT in both clinical and basic science would clearly be enhanced were it possible to identify the molecular events underlying light-activated, photoreceptor-specific OCT signals.
The rod-dominant photoreceptor layer of the mouse retina is an ideal preparation for application of OCT to the investigation of macromolecular signaling mechanisms. Mouse rod outer segments (OS) are in effect genetically manipulable, femtoliter test tubes whose protein constituents (15, 16), as well as their biochemical reactions (17–19) and light-stimulated translocations (20–22), are well known and have been measured primarily with ex vivo methods. Advances in imaging technology have now made it possible to achieve subcellular-resolution imaging of the mouse retina in vivo (23–26). We recently developed a multimodal ocular imaging system for mice that combines confocal laser scanning ophthalmoscopy (SLO) and OCT (27) and used this system to quantify photoactivation (bleaching) of rhodopsin in vivo (28). Using nonstimulating near-infrared OCT we observed a photoreceptor layer-specific, bleaching-induced increase in light scattering. Here we show that this increased backscattering arises from rods, that it requires the rod G-protein alpha-subunit transducin (Gαt), and that it is triggered by an osmotically induced increase in the cytoplasmic volume of the rod OS. We use these results to measure the hydraulic conductivity of the rod plasma membrane, to quantify osmolyte production by G-protein activation, to estimate a spring constant for previously reported molecular links between the rod disc membranes, and to quantitatively explain the backscattering from rods in terms of refractive index changes arising from OS swelling and light-stimulated translocation of G protein from the disc membranes.
Results
Photoactivation of Rhodopsin Increases Near-Infrared Backscattering from Rods and Causes Lengthening of Their OS.
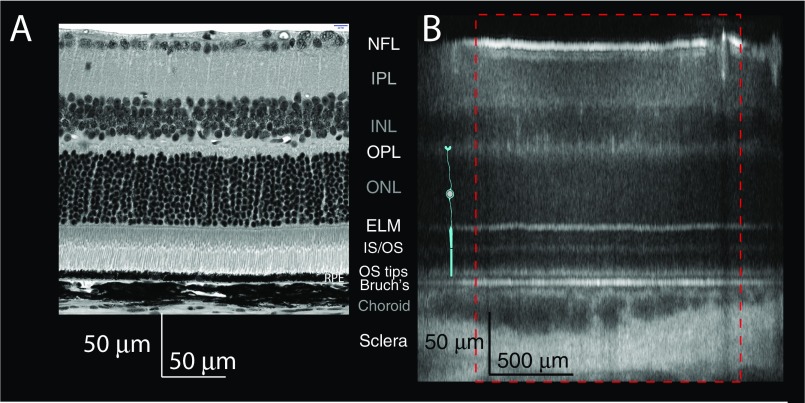
A brief 488-nm light exposure that photoactivated 10% of the rhodopsin in rod photoreceptors (Fig. 1A) produced dramatic changes in light backscattered from the posterior eye, as measured with near-infrared OCT (Fig. 1 B and C). Comparison of an OCT B-scan image taken in the dark-adapted state with one taken 2 min after the light exposure (Fig. 1 B and C) revealed large changes in backscattering in multiple retinal layers, and Movie S1 of the B scans shows these effects to reach broad maxima around 2 min and subside toward baseline thereafter. To quantify these changes, we derived axial intensity profiles from the 5-min series of OCT scans (Fig. 1D). Inspection of the profile plots revealed a number of distinct phenomena that were reliably repeated in multiple experiments, including altered backscattering from (i) the external limiting membrane (ELM), (ii) the inner/outer segment (IS/OS) junction, (iii) the OS tip, (iv) Bruch’s membrane (BrM) and (v) the sclera, and (vi) an increase in distance between the IS/OS junction and BrM and between the ELM and BrM.
Fig. 1.
Light stimulation triggers lengthening of rod OS and increased backscattering from the OS base and tips. (A) Light exposure and OCT scanning protocol. A blue-green rectangle representing the visual field to which 488 nm light was delivered with an SLO is superimposed upon an en face projection of an OCT scan of the retina of an albino (BALB/c) mouse; the single SLO scan took 0.92 s and isomerized 10% of the rhodopsin. OCT B scans at the positions of the four red dashed lines were taken every 0.92 s for 5 min. (B and C) OCT B scans taken before (B) and 2 min after (C) the 488-nm light exposure (the complete time series of B scans is provided in Movie S1). Retinal layer abbreviations are as follows: BrM, Bruch’s membrane; ELM, external limiting membrane; INL, inner nuclear; IPL, inner plexiform; IS/OS, inner/outer segment junctions; NFL, neurofiber layer; ONL, outer nuclear; OPL, outer plexiform. The layer identifications are confirmed with histology in Fig. S1. (D) Axial backscattering profiles generated by averaging all of the OCT A scans (axial linescans) in the region identified by the red dashed rectangles in B and C. The profiles represent data collected in the dark before stimulation (black trace) and 25 s (blue), 52 s (green), 80 s (yellow), and 121 s (red) after delivery of the stimulus. A schematic rod (cyan) drawn to scale in B–D serves to localize key OCT features relative to rod anatomy. D, Inset (gray rectangle) shows an expanded view of the portion of the profiles circumscribed by the dashed rectangle. All A scans were aligned to the strong BrM reflectance before averaging. (E) The amplitude of the OCT backscattering from the base of the OS (IS/OS) and from the OS tip plotted as functions of time. The large colored symbols plot results extracted from the correspondingly colored traces in D, whereas the smaller solid black symbols were extracted from the other scans taken over the 5-min epoch. (F) The magnitude of the shift of the axial position of the center of the OCT bands arising from backscattering by the ELM and IS/OS plotted as a function of time. The dashed lines plot the initial slope and saturated level, respectively, whereas the red curve is generated with an osmo-elastic model described in the text. (G) The position shift of the IS/OS band plotted as a function of the amplitude of the OCT backscattering from the IS/OS and OS tips. (H and I) Magnitude of OCT backscattering signals from BrM, the sclera, and the ELM as a function of time. (J) BrM and ELM OCT signals plotted as covariates of IS/OS. [Here and throughout the paper, OCT signals are presented on a common scale: Thus “OCT signal” signifies S2OCT × 10−8, where SOCT is the amplitude of the FD-OCT signal (Materials and Methods).] S2OCT(z) is used because it is linearly proportional to the intensity of the light backscattered from depth z (Materials and Methods, Eqs. 5–7). For clarity, the lateral (x)- and axial (y)-scale factors for the OCT B scans in Fig. 1 B and C are not equal (cf. Fig. S1). The data were obtained from a BALB/c (albino) mouse.
To further analyze these phenomena we plotted their magnitudes as functions of time (Fig. 1 E, F, H, and I) and as covariates (Fig. 1 G and J). The time courses of the increases in backscattering from the IS/OS and OS tips were similar to each other (Fig. 1 D, Inset, and E) and similar to the time course of the anterior (leftward) shift of the IS/OS junction (Fig. 1F), suggesting that these physically distinct photoreceptor-layer effects were driven by a common mechanism. The leftward shift in the IS/OS peak has a distinctive linear rising phase, however, whereas the backscattering signals from the IS/OS and OS tips have a delayed, sigmoidal rise. Covariate analysis of these three photoreceptor-layer–specific signals confirmed their positive correlation, but underscored differences in their kinetics (Fig. 1G). Notably, whereas the ELM backscatter peak shifted toward the vitreous in lockstep with that of the IS/OS junction (Fig. 1F), the amplitude of the ELM backscatter changed very little (Fig. 1I). This suggests that elongation of the OS induces the IS to be displaced in tandem, while also revealing that backscattering from the ELM and IS/OS is caused by distinct mechanisms. [The OS tips appear to undergo a 0.3-μm displacement toward the vitreous. This is likely an artifact of the increased scattering by the tips (Effect of Limited OCT Axial Resolution on the Backscatter Profile of the Distal Rod OS and Fig. S2).] In contrast to the backscattering from the IS/OS and OS tips, those from BrM and the sclera had biphasic kinetics, initially decreasing after the stimulus presentation and then returning toward baseline (Fig. 1H). Plotting these latter signals as a function of the IS/OS backscatter signal (Fig. 1J) further highlighted the distinctive character of the scattering from the layers posterior to the photoreceptors and retinal pigment epithelium (RPE). Overall, these data and analyses reveal the various light-stimulated effects to be layer specific and distinctive in kinetics and clearly not a generic tissue response. The use of an albino BALB/c mouse, which lacks melanin pigmentation in the RPE and choroid, allowed the OCT beam to penetrate all of the way to the sclera, but closely similar results were obtained with pigmented (C57BL/6J) mice (Fig. 2 and Table 1).
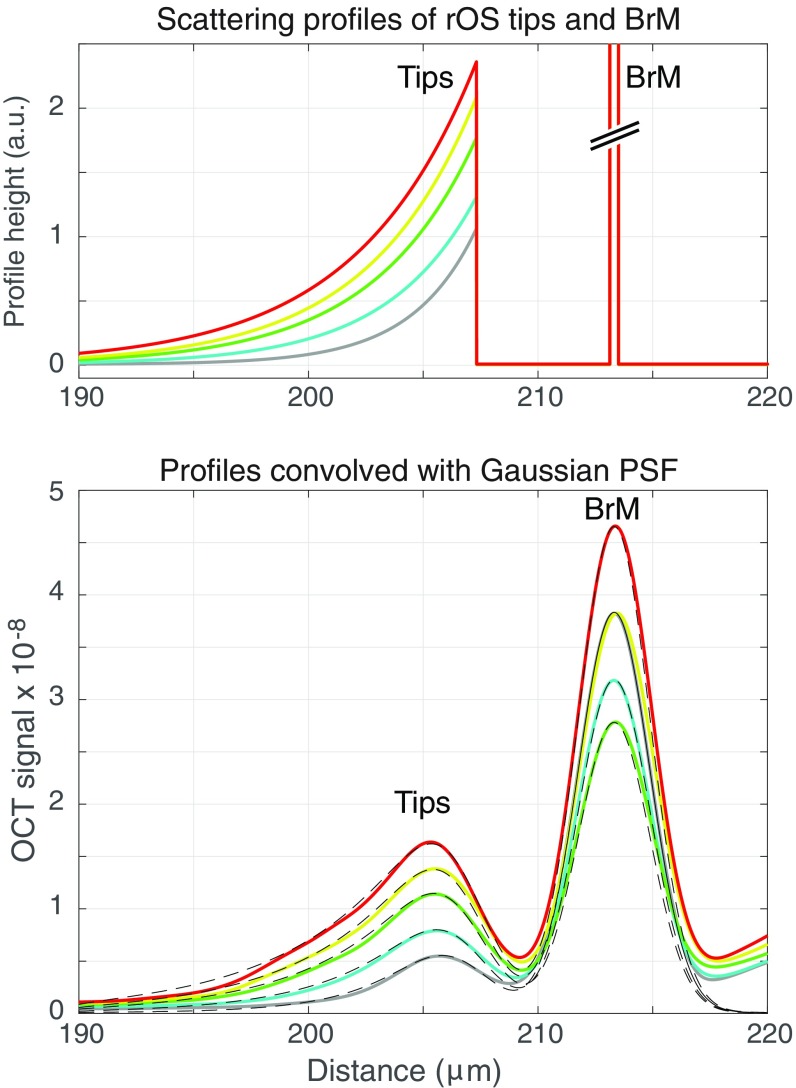
Fig. S2.
Effect of limited OCT axial resolution and increased backscattering on the apparent position of the distal tips of the rod OS in the profile plots of Fig. 1D, Inset. (Upper) Hypothetical scattering profiles of the rod OS tips and BrM. The rod OS profiles are represented by exponential functions with maxima at the tips and decay toward the middle of the OS; the space constants vary from 2.8 μm (gray curve) to 5.2 μm (red curve). The width of the BrM profiles was fixed at 0.35 μm based on mouse retinal EM data (101); the BrM amplitudes ranged from 80 to 133 and cannot readily be displayed on a common ordinate scale. (Lower ) The colored traces are replotted from Fig. 1D, Inset. The dashed black lines plot the corresponding backscattering profiles from the Upper panel convolved with a Gaussian having a FWHM of 1.83 μm, the equivalent axial psf of the OCT system. The predicted profiles closely match the BrM and tips peaks, including the shifts of the latter toward the vitreous.
Fig. 2.
OS elongation and increased backscattering are triggered by rhodopsin activation of the Gαt. A–C, Left present OCT profiles obtained in experiments identical to that in Fig. 1, but with mice of different genotypes: A and B are from mice null for Gαt (Gnat1−/−), but having relatively low (A) and relatively high (B) melanin expression; the dark-adapted OCT profiles of the low-melanin mouse in the posterior eye more closely resemble that of the albino mouse in Fig. 1, enabling both the IS/OS boundary and OS tips boundary to be seen. In pigmented mice (B and C) melanin backscattering from the RPE and choroid obscure the OS tips and BrM. However, in the pigmented mice the choriocapillaris “dip” (CC) in the profiles provided a sharply defined locus for alignment of the scans. Note that the profile data in Insets (gray boxes) are presented with identical x and y scaling. A–C, Center and Right present the amplitude of the backscatter from the IS/OS (Center) and the position shift of the IS/OS boundary (Right), respectively, extracted from the full set of profiles. The colored symbols correspond to the OCT profile scans at the time points indicated in Fig. 1 legend, whereas the solid black symbols were extracted from profiles not shown. The relatively high variability of the position shift data of the Gnat1−/− is due to the relatively small amplitude of the IS/OS backscatter amplitude.
Table 1.
Features of rod osmotic swelling and backscatter increases measured with OCT
| Rod OS | Water influx into rod OS | Backscatter from IS/OS | |||||||
| Strain, N | Length, μm | Increase, μm | Max. rate, μm3⋅s−1 | Total, μm3 | LP, cm3⋅s−1⋅dyn−1 | Pf, cm⋅s−1 | Dark, S2OCT × 10−8 | Light, S2OCT × 10−8 | Ratio |
| BALB/c, 11 | 19.3 ± 0.1 | 2.1 ± 0.1 | 0.033 ± 0.006 | 3.2 ± 0.2 | 1.7 ± 0.1 × 10−14 | 2.3 × 10−5 | 0.12 ± 0.01 | 0.55 ± 0.05 | 4.9 ± 0.5 |
| C57Bl6/J, 7 | 21.1 ± 0.6 | 1.9 ± 0.2 | 0.032 ± 0.011 | 2.8 ± 0.2 | 2.0 ± 0.2 × 10−14 | 2.8 × 10−5 | 0.06 ± 0.01 | 0.22 ± 0.05 | 3.5 ± 0.4 |
| Gnat1−/−, 10 | 21.7 ± 1.3 | 0.007 ± 0.12 | — | — | — | — | 0.10 ± 0.02 | 0.08 ± 0.01 | 0.9 ± 0.1 |
The first row identifies features of mouse rod OS measured with OCT, the second row identifies measured parameters associated with the feature, and the third row gives the physical units of the latter (where appropriate). Numerical entries are mean ± SEM of data from the experimental paradigm illustrated in Fig. 1 (10% bleaching exposure). Length measurements assumed an average refractive index of 1.410 for the rod OS. Water influx parameters were estimated from fitting the osmo-elastic model (Eq. 1) to rod OS elongation data (e.g., Fig. 1F, red trace), assuming the dark-adapted cytoplasmic volume is 56% of the rod OS envelope volume (Fig. 4 and Osmo-Elastic Model of Light-Induced Rod OS Swelling). For the rod OS diameter of 1.4 μm (61), the cytoplasmic volume of a 20-μm long, dark-adapted mouse rod OS is 17.2 μm3. S2OCT specifies the backscatter power in instrumental units of the OCT. Hydraulic conductivity (LP) and water permeability (Pf) were computed for each experiment with Eq. 2, as described in the text.
Activation of the Rod G-Protein Transducin Is Necessary for the Elongation and Backscattering Changes of the Rod OS Layer.
We tested the hypothesis that the increased backscattering and OS elongation are caused by activation of rod phototransduction by repeating the experiment of Fig. 1 in mice lacking Gαt (Gnat1−/−). Although having normal ultrastructure and a full complement of rhodopsin, rod OS of Gnat1−/− mice do not transduce light into electrical signals (29). None of the light-stimulated changes observed in wild-type mice—with the exception of that from BrM—were observed in Gnat1−/− mice with either weak (Fig. 2A) or normal pigmentation (Fig. 2B). Pigmented C57BL/6J control mice exhibited changes very similar to those of albino mice (Fig. 2C), showing that whereas melanin screens backscatter from the rod tips and from BrM and deeper layers, its presence does not affect the OCT signals originating in layers anterior to the RPE (Table 1). These results establish that activation of Gαt by photoisomerized rhodopsin is necessary for production of the photoreceptor-layer–specific backscattering increases and for the concomitant increase in OS length.
Rhodopsin Bleaching Dependence, Kinetics, and Reversibility of the Backscattering Signals.
To obtain further insight into the phototransduction-induced increases in rod OS backscattering and length, we measured the time courses of these effects in response to light varied in intensity over a 200-fold range (Fig. 3). Both effects were graded in amplitude and duration with stimulus strength (Fig. 3 A–D). Amplitude vs. intensity plots showed them to have similar dependence on the fraction of rhodopsin isomerized per rod (Fig. 3 E and F). The light sensitivity of these effects is far lower, however, than that of the rod electrical response. The mouse rod cGMP-activated current, when measured in vivo under identical conditions, is half-saturated by a flash producing ∼100 photoactivated rhodopsins (R*) (30). In contrast, the OS elongation measured in our experiments was half-saturated by a stimulus that bleached ∼2% of the rhodopsin and produces ∼106 R* (Fig. 3E). These data strongly reject the hypothesis that the elongation is triggered by the closure of the cGMP-gated (CNG) channels or attendant water transport via AQP4 channels in Müller cells, which swell in response to K+ uptake (31). First, the rod OS swelling and backscattering increases are more than four orders of magnitude less sensitive to light than the closure of the CNG channels that underlies the rod’s electrical response (Fig. 3 E and F). Second, the intense stimuli used here completely close the CNG channels in less than 1 s, and the consequent light-dependent K+o increase and uptake by Müller cells would be expected to have comparable light sensitivity and kinetics. In contrast, at its maximal rate elongation takes more than 100 s to reach its saturated amplitude (Fig. 1 E and F and Fig. 3 A–D). Third, the elongation is confined to the OS layer, defined by the backscattering from the OS tips and IS/OS junction (Fig. 1 and Fig. S1), layers of the retina in which Müller cells project only minimal apical processes. Fourth, recent work using a somewhat different stimulation paradigm has confirmed histologically that the mouse rod OS layer elongates under light conditions that give rise to elongation visualized with OCT (32).
Fig. 3.
Rhodopsin bleach dependence and kinetics of rod elongation and backscattering increases. Results were obtained with the experimental paradigm of Fig. 1, using both albino (BALB/c) mice (A and B) and pigmented (C57Bl6/J) mice (C and D) with light exposures that bleached between 0.04% and 95% of the rhodopsin (symbol key in A). E and F plot the dependence of the amplitudes of the elongation (E) and IS/OS backscatter increases as a function of the bleach level. The smooth curve in E is an exponential function that reaches 1-e−1 of the saturated level at a 2.6% level of bleaching; the smooth curves in F are quadratic functions that serve to highlight the declining rate of backscatter increase with increasing bleach level. In A–D the symbols plot mean values, and the colored backgrounds plot the SEMs of the traces. Each trace is the average of at least 6 experiments from both eyes of at least three mice. For the lower bleach levels up to 44 individual experiments were averaged. (OCT data collection was truncated short of 300 s in the experiments with the three lowest bleach levels.) The fraction bleached can be converted into photoisomerizations per rod (R*) by multiplying by 7 × 107, the average number of rhodopsin molecules per mouse rod (81).
Fig. S1.
Comparison of plastic section from the central retina (∼0.5 mm from optic nerve) of a C57BL6/J mouse (A) with the OCT B-scan results of Fig. 1B (B). The plastic section was scanned with a Nikon A1 confocal microscope with a 40× objective in transmitted light mode. The histological data were displayed so that the ELM and BrM in the two panels are aligned, but the scale bars in the two panels were obtained from the respective instrument calibrations. (Labels of the more highly reflecting layers are shown in white font, whereas the weakly reflecting layers are labeled in gray.) As in main text Figs. 1 and 4, a schematic rod (cyan) is overlaid on the OCT B scan. Note that whereas the histological section has equal horizontal and vertical scales, the scales for OCT B scans are not equal, and the histology is of a pigmented C57BL/6 mouse, whereas the OCT B scan is from an albino BALB/c mouse. Bruch's, Bruch's membrane; ELM, external limiting membrane; INL, inner nuclear; IPL, inner plexiform; IS/OS, inner/outer segment junctions; NFL, neurofiber layer; ONL, outer nuclear; OPL, outer plexiform.
The Molecular Mechanism of the Rod OS Elongation and Backscattering.
We sought to explain the OS swelling and backscattering increases in terms of events associated with rhodopsin activation of Gαt (Fig. 4). As the increases in scattering imply a substantial redistribution of the molecular mass in the rod OS that underlies its unusually high refractive index of 1.41 (33) and previous in vitro investigations found light-scattering changes dependent on Gαt (34, 35), we focused on the role of Gαt. Because the G-protein heterotrimer Gαtβ1γ1 is present in the dark-adapted rod OS at 1:8 relative to rhodopsin (36, 37) and has more than twice rhodopsin’s mass per molecule, it comprises ∼20% of the total mass of transduction-associated proteins in the dark-adapted rod OS. In the dark-adapted state, inactive Gαtβ1γ1 is anchored to OS disc membranes by N-terminal myristoylation of Gαt and C-terminal farnesylation of Gγ1 (38). Activation of Gαt by light exposures that isomerize large fractions of rhodopsin causes the Gαt and Gβ1γ1 subunits to dissociate not only from one another, but also from the disc membrane, as established by translocation of Gαt and Gβ1γ1 to the IS in vivo in prolonged bright light (39). Because rod OSs behave as osmometers, swelling or shrinking when exposed to altered osmotic strength media (40, 41), we hypothesized that transduction reactions associated with complete activation of Gαt induce osmotic swelling and that the swelling, combined with mass redistribution of Gαt and Gβ1γ1 from the disc membranes into cytosol, might in turn underlie the scattering increases at the IS/OS and OS tips. We tested this hypothesis by developing a model that incorporates relevant facts about the mouse rod OS and comparing predictions of the model with our data.
Fig. 4.
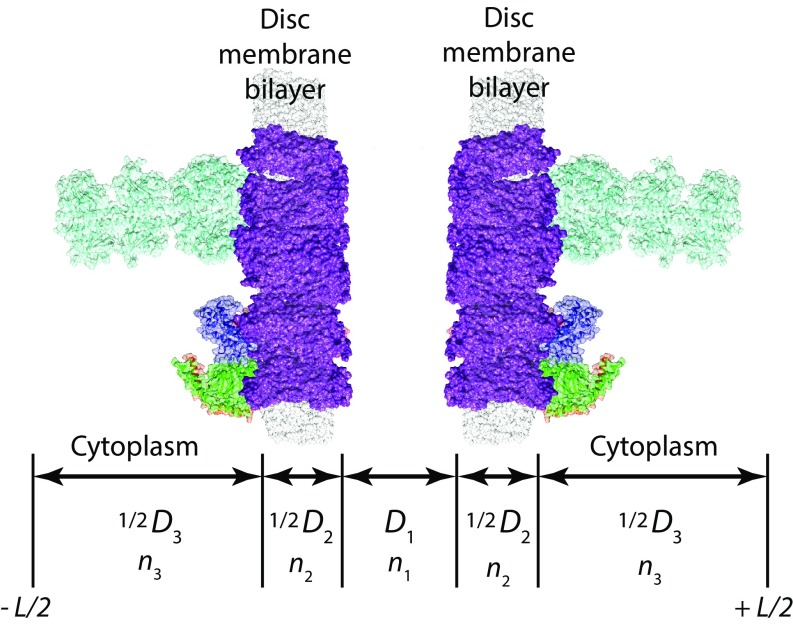
Cellular and molecular elements underlying rod osmotic swelling. (A) Rod schematic (cyan) overlaid on a micrograph of a plastic section of a mouse retina. (B) Electron micrograph of the base of a mouse rod OS from the classic study of Carter-Dawson and LaVail, reprinted with permission from ref. 61. (C) Structural model of 20-nm × 20-nm patches of two pairs of adjacent disc bilayers in a dark-adapted rod OS, identified in B. Illustrated are rhodopsins (purple, eight per patch, corresponding to 25,000 μm−2), two heterotrimers (Gαt, blue; Gβ1 green; Gγ1, red), and one phosphodiesterase (cyan). The disc-to-disc spacing was set to 32 nm (Materials and Methods). (D) Molecular-scale consequences of osmotic swelling: The interdiscal cytoplasmic space is stretched by ∼20%, and the G-protein heterotrimers are dissociated into Gαt and Gβ1γ1 components and solubilized. ELM, external limiting membrane; ONL, outer nuclear; OPL, outer plexiform.
Maximal Activation of Phototransduction Increases Rod OS Osmolarity by at Least 65 mOsM.
In constructing a model for phototransduction-induced osmotic swelling of the rod OS, we first considered the consequences of water influx. As moderate osmotic perturbation alters only rod OS length and not width (40, 41), length increases can be readily converted into volume changes and influx rates. The swelling response showed a light dependence consistent with maximal activation of Gαt, reaching a saturated amplitude in response to light that isomerizes ∼1 R* per Gαt (Figs. 1F and 3 A and C). Because the disc membranes occupy ∼50% of the OS volume (Fig. 4 B and C), the saturated 10% elongation corresponds to an ∼20% increase in cytoplasmic volume (Fig. 4D). Assuming the saturated swelling is a purely osmotic equilibrium, Van’t Hoff’s law dictates that the fractional volume increase is proportional to the incremental osmotic pressure; i.e.,
| [1] |
where Πrest is the resting (dark-adapted) osmotic pressure, and is the incremental osmotic pressure generated by ΔnS mol of novel osmolyte released into the cytoplasmic volume Vcyto,rest. Because Πrest/RT = 325 mOsM is normal rodent plasma osmolarity (42), the 20% cytoplasmic volume increase implies the surprising result that maximal activation of phototransduction increases the rod OS cytoplasmic osmolarity by = 65 mOsM. This value must be considered a lower limit, however, because the rod OS may possess an elastic mechanism to resist swelling, as we shortly examine.
The Hydraulic Conductivity of the Rod OS Membrane Is Consistent with That of a Membrane Lacking Aquaporin Channels.
Our results also determine an upper limit for the water permeability of the rod OS plasma membrane. Water inflow () should obey an osmo-elastic relation (43–45)
| [2] |
where Lp is hydraulic conductivity, SROS is the surface area of the rod OS, and P is the pressure from an elastic restoring force (cf. Eq. S1). Eq. 2 can be reformulated as a rate equation for the incremental cytoplasmic volume ΔVcyto, whose solution predicts the time course of the light-stimulated rod OS (represented by ROS) volume increase (Fig. 1F, red curve; Fig. 3 A and C, gray curves; and Osmo-Elastic Model of Light-Induced Rod OS Swelling and Fig. S3). The initial slope (Fig. 1F, dashed line) multiplied by the rod OS cross-section (1.54 μm2) yields the maximal water influx, whose average value is 0.03 μm3⋅s−1 (Table 1). Applying Eq. 2 with SROS = 110 μm2 and P = 0, we thus find LP = 1.6 × 10−2 μm3⋅s−1⋅dyn−1, corresponding to a water permeability coefficient Pf = (RT/VW) × LP = 2.3 × 10−5 cm⋅s−1 (VW = 18.2 cm3⋅mol−1). This estimate of Pf is notably lower than that measured by Preston et al. (46) for oocytes at 25 °C not expressing aquaporin channels (2.6 × 10−3 cm⋅s−1), but closer to that (2.0 × 10−4 cm⋅s−1) measured by Prescott and Zeuthen (47) in the same preparation.
Fig. S3.
Predicted dependence of the swelling of the rod OS disc stack on Hooke’s law constant kH of the interlinked stack. (Left) Steady-state rod OS fractional volume increase as a function of light-stimulated osmolarity increase, ΔΠ0/RT (steady-state solution to Eq. S6) for different values of kH (Eq. S4). The leftmost (solid black) curve represents kH = 0, i.e., purely osmotic equilibrium. The black solid circles are the values that apply to the results of Fig. 1, for which cytoplasmic swelling was 20.5%. (Right) kH plotted as a function of osmolarity increase, corresponding to the black solid circles in the Left. Nonzero kH values imply an osmolarity increase (abscissa) greater than the purely osmotic equilibrium (blue solid circle). (Calculations are for the experiment in Fig. 1.) In estimating a value for a molecular spring constant between discs, we assumed an osmotic increment of 75 mOsM (red arrow), 10 mOsM above the minimum level (65 mOsM) dictated by the conclusion that the saturated elongation (Figs. 1 and 3) corresponds to an osmotic equilibrium.
Estimating the Spring Constant of an Elementary Rod OS Elastic Element.
Freeze-fracture and cryoelectron tomographic investigations have revealed macromolecular structures that appear to link adjacent disc membranes (48, 49). Because most proteins can act as elastic elements (50), it is reasonable to hypothesize that such disc-to-disc “linkers” serve as springs that resist swelling, affording some protection of the rod OS from stimulus-induced osmotic overload. As rod OSs primarily swell axially in response to osmotic challenge (40, 41), if the OS has an elastic response, the steady-state elongation should obey Hookes’ law
| [3] |
where is the increment in osmolarity, /RT = 65 mOsM is the minimum increment compatible with the data, AROS is the rod OS cross-section, kH is the spring constant, and is the steady-state length increase. For example, for = 75 mOsM, kH = 12 dyn⋅cm−1 (12 pN⋅nm−1). Because molecular springs between individual pairs of discs will act in parallel to oppose osmotic swelling, while the discs are in series, the overall spring constant of the rod OS is related to the molecular spring constant kmolecular by
| [4] |
Here ρ is the spatial density of the spring-like molecules, AROS is the surface area of a disc, and Ndisc is the total number of discs. Nickell et al. (49) report a disc “spacer” density ρ = 492 μm−2, and so given 625 discs in the 20-μm–length rod OS of this study, the elementary elastic unit is estimated to have a spring constant of kmolecular = 15 pN⋅nm−1. This is well within the range of the spring constants for proteins from single-molecule methods in the nondenaturing range of stretch (50, 51). More generally, our experiments provide a means of testing hypotheses about the identity of any component of the rod OS that could act as a molecular spring. An interesting candidate is the cGMP phosphodiesterase, which may span the interdiscal space (Fig. 4 C and D) and is present at 1:310 relative to rhodopsin (52), so that it has a surface density on pairs of discs of 250 μm−2, intriguingly close to that of the as-yet unidentified “spacers” (49).
An elastic response by the rod OS disc stack is not the only mechanism by which the rod could protect itself from phototransduction-induced osmotic stress. Another mechanism is the active or passive (diffusional) redistribution of excess osmolytes between segments. Diffusional redistribution driven by concentration gradients will very likely occur and, if so, would contribute to underestimation of the osmotic stimulus. One well-studied light-stimulated redistribution from the OS to the IS is that of Gαt and Gβ1γ1 (20, 39, 53). In this case, however, the total quantity of osmolyte (∼1.5 mM) and the maximum rate of redistribution (∼0.002 s−1) (39) appear too small to materially affect the rod OS elongation measured here. Nonetheless, the initial step in this redistribution—dissociation of Gαt and Gβ1γ1 from the disk membranes—may contribute to increased backscattering, as now discussed.
The Increased Backscattering from the Base and Tips of Rods Arises from Light-Induced G-Osmotic Swelling and G-Protein Translocation.
It has long been known that light-stimulated translocation of Gαt and Gβ1γ1 into the aqueous phase can produce scattering changes in vitro in suspensions of disc membranes or permeabilized rod OSs (17, 35, 54), and so we investigated whether similar translocation from the disk membrane into swollen cytosol could give rise to increased scattering at the rod OS base and tips. Backscattering occurs at retinal layer boundaries where forward-propagating light encounters a change in refractive index. The average refractive indexes of the IS and OS of rods have been measured to be = 1.40 and = 1.41 (33). These exceptionally high refractive indexes, which arise from dense concentration of proteins and lipids, enable photoreceptors to act as dielectric wave guides, trapping and condensing light in the IS and guiding it into the OS (28, 55–57).
We considered two hypotheses as explanations of the increased rod OS backscattering: (i) Solubilization of Gαt and Gβ1γ1 combined with osmotic swelling causes the refractive index of the rod OS to change uniformly relative to those of the IS and of the extracellular space and RPE cells surrounding the OS tip (8) and (ii) solubilization of Gαt and Gβ1γ1 combined with osmotic swelling causes the index of refraction at the base and tip of the OS to decrease relative to that of the remainder of the OS. Hypothesis i was rejected, as follows. In the dark-adapted rod the exceptionally high refractive indexes of the IS and OS (33) certainly exceed those of the extracellular matrix and RPE near the OS tips. Calculations based on well-known dielectric mixing models (58–60) predict that 10% elongation of the rod OS will cause the average refractive index of the OS to decrease (Model of the Light-Induced Backscatter Increase from the OS and Fig. S4). As a consequence, the refractive index differentials between the IS and the OS, and between the OS tip and the adjacent media, are both predicted by hypothesis i to decrease, leading to decreased rather than to increased backscattering as is observed.
Fig. S4.
CK (59) three-layer model of the rod OS. The unit cell comprises one disc flanked by half of the cytoplasmic gap on either side (compare with Fig. 4 in the main text). Adapted with permission from ref. 59.
The alternative hypothesis (ii) rests on the fact that a number of basal discs (and possibly distal discs) of the rod OS are not closed and internalized in the OS, but rather like classic cone discs are contiguous with the plasma membrane (61, 62) (Fig. 5). As a consequence osmotically driven water influx through noninternalized basal discs will be substantially increased relative to that of the rest of the rod OS. We combined this insight with a three-layer model of the refractive index of the OS (59) and a model of the rod OS base (Fig. 5 A and B) and found that the resultant model (Estimation of the Absolute Retinal Reflectivity Measured by the OCT System, Fig. S5, and Tables S1 and S2) could predict the time course of increased backscattering (Fig. 5F). Although the model is not unique and will certainly undergo further tests and refinement, it nonetheless serves as a proof of principle, namely that a combination of osmotic and electromagnetic theory can provide a simultaneous account of the correlated but physically distinct rod OS swelling and backscattering increases.
Fig. 5.
Modeling of the light-induced backscattering increase from the base of the rod OS. (A) Electron micrograph of the base of a mouse rod OS from the recent study of Ding et al. (62). Reprinted with permission from Vadim Arshavsky (Duke University, Durham, NC). The “rod OS base” as defined for the backscattering model (red dashed region) is a cylindrical portion of the rod comprising three elements: the IS component (colored yellow); the OS component, comprising eight basal discs in various stages of assembly (pale purple); and the intervening extracellular space (cyan). In this instance, Ding et al. showed that eight basal disc membranes remain fused with the plasma membrane and would thus contribute to an elevated water permeability of the rod OS base. (B) Depiction of a 3D model of the rod OS component of the base (i.e., portion of based disc composed of nascent discs). A dielectric mixing model was developed that combines the predicted time-varying refractive index of the basal discs dictated by osmotically induced swelling, and Gαt and Gβ1γ1 dissociation and solubilization, with portions of the rod OS base that are IS (yellow) or extracellular (cyan). (Model of the Light-Induced Backscatter Increase from the OS). (C) Fractional increases in the length of the main (“middle”) portion of the rod OS and the basal discs predicted by the model. (D) Changes in the refractive indexes of the basal and middle portions of the rod OS predicted by the model along with the unchanging refractive index of the rod IS. (E) Rod OS swelling data from Fig. 1F (solid black circles), with prediction of the osmo-elastic model (red curve). (F) “IS/OS” (rod OS base) backscatter data (solid black circles) adjusted from the measured value of S2OCT converted to equivalent Fresnel reflectivity compared with the model prediction (red curve) (Estimation of the Absolute Retinal Reflectivity Measured by the OCT System).
Fig. S5.
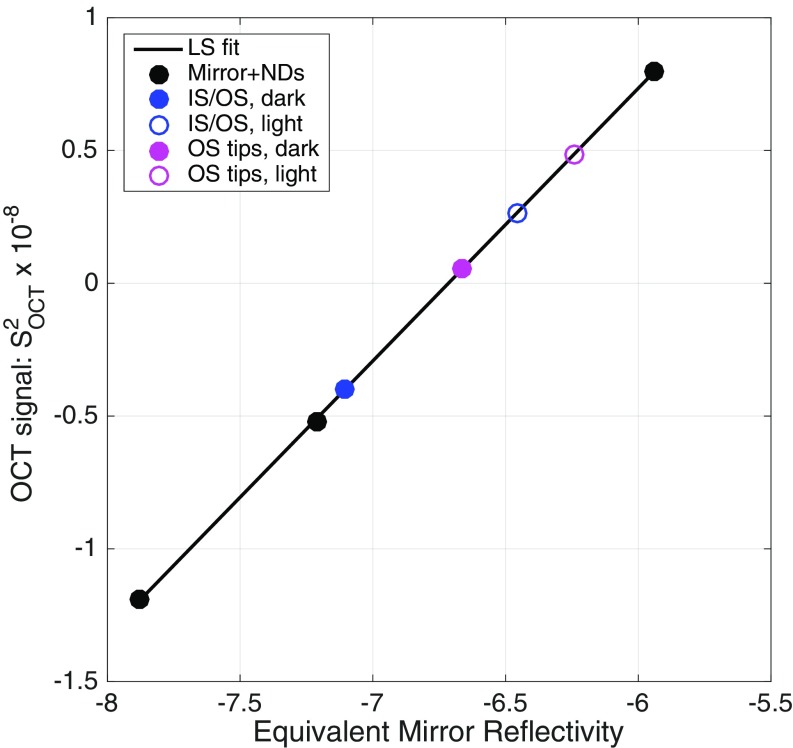
Initial estimates of the apparent reflectivity of photoreceptor layers. ND filters were selected so that the OCT signals obtained with them (●) spanned the range of the signals obtained in the experiments with mice (Table 1); the equivalent reflectivity is the two-pass density. The least-squares (LS) fitted line has a slope in this log-log plot of 1.027. The experimental data (Table 1) were placed at the corresponding ordinate values, in the standard absolute magnitude used throughout this paper (Materials and Methods). Assuming the slope unity in log-log coordinates, we obtain the relation S2OCT = 7.9 × 1014 × RM,eq, where RM,eq is the equivalent reflectivity of the ND-filter attenuated mirror.
Table S1.
Rod OS layer thicknesses and refractive indices
| Layer name | Parameter | Distance, nm | Fraction | Parameter | Refractive index | Notes |
| Dark-adapted rod OS | ||||||
| Intradiscal space | D1 | 5.0 | 0.156 | n1 | 1.380 | |
| 2 disc bilayers | D2 | 9.6 | 0.300 | n2 | 1.510 | * |
| Cytoplasm | D3 | 17.4 | 0.544 | n3 | 1.360 | †,‡ |
| Total | Dcell | 32.0 | 1.000 | nOS | 1.410 | |
| Maximally light adapted (complete activation) | ||||||
| Intradiscal space | D1 | 5.0 | 0.142 | n1 | 1.380 | |
| 2 disc bilayers | D2 | 8.8 | 0.250 | n2 | 1.510 | § |
| Cytoplasm | D3 | 21.4 | 0.608 | n3 | 1.367 | ¶ |
| Total | Dcell | 35.2 | 1.000 | nOS | 1.406 | * |
G protein in the dark-adapted state was treated as contributing a thin component to the overall bilayer thickness, equivalent to the total volume of the G protein per disc face divided by the total disc face surface area.
Adult rat blood serum was reported to be 1.351 (102).
The value 1.36 was used by Corless and Kaplan (59).
The thickness of the bilayers was decreased by the equivalent thickness contributed by Gt.
The increase in the cytoplasmic gap is 23%, for an overall length increase in Dcell of 10%. The latter corresponds to the measured fractional length increase of the rod OS (main text, Table 1).
Table S2.
Attenuation factors arising from rod waveguide properties, alignment, and other morphological features of the rod
| Factor | Fold attenuation | Description | Comments and source |
| i | 1.3 | Fraction of 860-nm power in the core of the mouse rod waveguide | (12, 15) |
| ii | ∼2 | Variation across the OCT B-scan field | Beam axis vs. photoreceptor waveguide axis |
| iii | ∼2 | Variation across experiments in optimal alignment of mouse | System optical axis vs. mouse eye optical axis |
| iv | 5–6 | Apodization by optical system pupil | Assuming rod N.A. = 0.25 |
| v | 2–5 | Ultrastructure of the IS/OS (OS base): inhomogeneity and surface tilt | Fig. 5; Δz ≤ 0.4 μm vs. λ = 0.86 nm |
| vi | ∼2 | Axial distribution of the IS/OS (Fig. S1) vs. the axial psf | |
| All | ∼100−300 | Total attenuation |
Discussion
Our results establish that mouse rod OSs elongate and undergo increased backscattering from their base and tip when stimulated with light that strongly activates rod phototransduction (Figs. 1–3).
Rod OS Elongation Is Caused by G-Protein–Induced Osmotic Swelling.
Previous investigations have reported light-induced changes in the length of photoreceptor OSs measured in vivo (32), including recently from human cone OSs (10). Three lines of evidence presented in this work support the hypothesis that the elongation reported here results from osmotically induced swelling triggered by excess osmolytes generated by phototransduction reactions at or downstream of Gαt activation. First, the swelling response is absent in mice lacking Gαt expression (Gnat1−/−; Fig. 2). Second, the magnitude of the swelling response is saturated by stimuli that produce ∼1R* per Gαt and so clearly maximally activates phototransduction (Fig. 3). These two lines of evidence reject the hypothesis that activation of rhodopsin per se or production of retinoid byproducts drives the swelling, as Gnat1−/− mice have normal OSs and rhodopsin (29), and a 100% bleaching stimulus causes no more swelling than a 10% bleach in normal mice (Fig. 3A). Third, the elongation data yield an estimate of the rod OS H2O permeability that is reasonable for a membrane lacking aquaporin (46). The estimate of the minimal osmotic increment (20%; 65 mOsM) underlying the maximal swelling is unexpectedly large and must be even larger if swelling is resisted by spring-like links between the disc membranes (49) or osmolyte diffusion between ISs and OSs.
Phototransduction-Generated Osmotic Stress and Mechanisms of Protection.
Our work shows that the exposure of the dark-adapted eye to light that isomerizes only 10% of the rhodopsin produces an ineluctable osmotic stress in rods, the most numerous cell in the retina. Red blood cells (RBCs) have mechanisms that allow them to cope with osmotic stress such as encountered in their passage through the kidney. Nonetheless, standard osmotic fragility assays show that ∼50% of normal RBCs rupture in a 45% hypo-osmotic medium, whereas abnormal RBCs are disrupted by substantially lower osmolarity decreases (e.g., refs. 63 and 64). Translocation of dissociated Gαt and Gβ1γ1 off the disc membrane and to the IS (20, 39) will reduce potentially dangerous osmotic stress caused from stimuli that bleach large fractions of rhodopsin. The retinas of individuals with hereditary or other disease conditions that impair the structural integrity of rods, however, may have elevated light-damage susceptibility arising from an inability to cope normally with transduction-induced osmotic stress.
Explaining Transduction-Induced Backscattering from the Base of the OS.
Previous studies have reported light-stimulated increases in backscattering from the photoreceptor layer of the retina in vivo (8, 9, 12, 14). OCT enables the retinal layer of these light-stimulated “intrinsic optical signals” to be precisely determined, and we have focused on those arising from the OS layer (Figs. 1–3). We hypothesize that these intrinsic signals arise from changes in the local refractive index in the rod OS caused by osmotically induced cytoplasmic swelling and translocation of Gαt and Gβ1γ1 into the cytosol (Fig. 4). A key finding of our study is that OS elongation and increased backscattering at the IS/OS boundary—despite arising from physically distinct processes—are interlinked by their kinetics and light dependence, i.e., the degree of stimulation of the phototransduction cascade (Figs. 1–3). Moreover, our analysis has shown that the magnitude and kinetics of these distinct but concurrent processes can be explained by a framework incorporating an osmo-elastic rod OS response and a physical model of the backscattering process (Fig. 5 and Model of the Light-Induced Backscatter Increase from the OS).
Activation and Deactivation of Phototransduction After Strong Bleaching of Rhodopsin.
Because a single fully active rhodopsin (R*) is capable of activating hundreds of G proteins per second (34, 65), it may seem surprising that a 10% bleaching exposure, which produces R* equimolar to Gαtβ1γ1, is required for maximal rod OS elongation (Fig. 3). Distinguishing between rate and amplitude saturation in the context of the osmo-elastic model of elongation helps resolve this puzzle. Rate saturation—the maximal rate of OS length increase—in the model is reached when complete activation of phototransduction produces the maximum possible osmotic stimulus. In contrast, amplitude saturation in reached only when the very slow water entry brings the OS into osmotic equilibrium. Because the rate of elongation reaches its maximal value after exposure to stimuli that bleach 0.38% or less rhodopsin (Fig. 3 A and C), our analysis implies that at least 26 Gαts are activated per R* at the lowest bleach levels used in our experiments.
Dark adaptation after strong bleaching of rhodopsin has been traditionally investigated in vivo with psychophysical and electrophysiological methods (reviewed in ref. 66). These methods can be used only at times when phototransduction activity has decayed to the extent that at least some CNG channels are open and capable of being closed in response to subsequently delivered light stimuli used to measure sensitivity. The OCT methodology used here is not limited to conditions when CNG channels are open and affords the possibility of investigating deactivation of phototransduction in vivo in heretofore unexplored conditions. Indeed, the OCT elongation and backscattering signals clearly exhibit substantial “turnoff” over 5 min after exposures that bleach up to 10% of the rhodopsin (Fig. 3 A–D), suggesting that G-protein deactivation and reassociation with the disc membranes is occurring. This deactivation in turn implies that R* activity is decreasing over this time window, for otherwise repeated activation of G protein would presumably keep the G protein dissociated. It is unlikely that rhodopsin regeneration contributes to the inferred decline in R* activity, because the maximal rates of regeneration in BALB/c and C56Bl6/J mice differ by threefold [2.2% min−1 and 0.7% min−1, respectively (67)], whereas the recoveries of the OCT signals in the two strains are closely comparable (Fig. 3 A–D), and moreover even at the faster rate only 11% of the initially bleached rhodopsin would be regenerated. An alternative explanation is that activated rhodopsin molecules, which at such high bleach levels likely overwhelm deactivation by rhodopsin kinase and arrestin, are undergoing spontaneous decay. Notably, spontaneous decay of metarhodopsin II in mouse rods has a time constant of ∼40 s (68–70), comparable to the time course of the decline of OCT signals observed here.
Limitations of the Experimental Protocol.
Our results are necessarily limited by the sampling rate (1.1 Hz) of our OCT B-scan sampling protocol and by issues such as the physical stability of the mouse eye and the long-term clarity of its ocular media. The relatively low sampling rate may miss important intrinsic optical signals that occur on faster timescales, especially immediately after light stimulation. Improvements in methodology including the use of adaptive optics should allow characterization with nonstimulating OCT of mouse retinal intrinsic optical signals that occur on both shorter and longer timescales than used here.
Intrinsic Optical Signals from Human Cones and Rods.
As noted in the Introduction, intrinsic optical signals from individual human cone photoreceptors have been measured by a number of groups (10–14). The advanced state of adaptive-optics OCT methodology for the human eye enables such cone-specific intrinsic optical signals to be characterized with great precision and sensitivity, and rapid advances in measurement and clinical applicability of human photoreceptor optophysiology can certainly be expected (71). It remains to be seen whether elongation and backscattering increases in human cones and rods can be understood with the principles applied here to mouse rods. The fact that human cones can escape from electrical saturation in the presence of steady lights that bleach upward of 90% of their visual pigment (72), whereas rods are driven into electrical saturation by far less intense light, reveals that cones possess adaptational mechanisms that efficiently reduce the gain of phototransduction at high bleach levels and presumably also reduce the production and the effect of excess osmolytes. Moreover, cone OSs whose disc membranes are contiguous with the plasma membrane also have much greater surface/volume ratios than rods and likely also use ionic transport mechanisms to counter the osmotic stress of excess osmolytes produced by phototransduction.
Materials and Methods
Animals.
All mouse husbandry and handling were in accord with protocols approved by the University of California Animal Care and Use Committee, which strictly adheres to all NIH guidelines and satisfies the Association for Research in Vision and Ophthalmology guidelines for animal use. Young adult pigmented C57BL/6J and albino BALB/c mice were obtained from Jackson Laboratories at age 2 mo and maintained on a 12:12, ∼100-lux light cycle. The Gnat1−/− line was maintained in the laboratory and genotyped with standard protocols as previously described (29). Although lacking Gαt expression, rods of Gnat1−/− mice have a full complement of rhodopsin, which bleaches normally (29). Mice used for experiments were 3–6 mo of age. Anesthesia and imaging protocols are provided in ref. 28. Pupils were fully dilated to a diameter >2 mm with tropicamide and phenylephrine before experiments, as previously described (28), obviating vignetting of the ∼0.5-mm OCT and SLO beams as they entered the eye. In addition, the conjugate aperture for the fiber-optic launch of the OCT sample arm light collector was much smaller than the dilated pupil, further ensuring that the OCT system’s backscatter intensities were precisely calibrated.
Optical System and OCT Calibration.
The combined SLO/Fourier-domain (FD)-OCT imaging system and calibration of the OCT depth scale, retinal scan area, and rhodopsin bleaching are described in detail in ref. 28. The superluminescent diode that served as the OCT light source has a 132-nm band (FWHM) centered on 860 nm and delivered 600 μW at the mouse pupil plane. Although OCT data are usually presented in a logarithmic (decibel) scale, we instead used a linear scale to more readily analyze the backscatter signals and compare them with predictions of reflectivity changes. We now provide a brief explanation of the FD-OCT signal intensity scaling. Thorough analysis of the signals in FD-OCT has been presented (e.g., refs. 73 and 74). Adopting the notation of Fercher et al. (ref. 73, equation 4.19), the Fourier transform of the signal spectrogram satisfies
| [5] |
where is the free-space wavenumber, is the spectral density (proportional to intensity) as a function of K, z is the conjugate space coordinate of the sample, is the autocorrelation function, and “∝” signifies proportionality. For a delta-like reflectivity of magnitude R at sample position zR, the backscattering potential is given by and (neglecting small terms) the autocorrelation is
| [6] |
(ref. 73, equation 4.20). Thus, for a signal proportional to the local axial reflectivity R(z) we used
| [7] |
where SOCT corresponds to the “raw” 16-bit FD-OCT signal. To estimate the proportionality factor in Eq. 7, we performed an absolute calibration of the apparent sample reflectivity, using a mirror attenuated by neutral density filters as a delta-like reflectivity (Estimation of the Absolute Retinal Reflectivity Measured by the OCT System and Fig. S5).
Data Collection, Processing, and Analysis.
The protocol used in the present experiments for OCT data collection and photobleaching is described in the context of Fig. 1. Each 0.92-s cycle of OCT scanning collected 4 closely spaced B scans comprising 512 A scans in the center of a 51° field of view (FOV). The 4 B scans were aligned with Matlab cross-correlation (“xcorr”), and A scans from the central 35° FOV segmented and aligned axially with the BrM peak (Balb/c) or with the choriocapillaris “dip” (C57Bl6/J). Average A-scan profiles (e.g., Fig. 1D) were obtained by averaging the aligned A scans from five successive cycles (4.6 s).
A-scan profiles were analyzed for their OCT signals at specific times and axial locations (with respect to BrM or RPE reference). Averaging across experiments was performed only on these extracted signals, and points were plotted as mean ± SEM (Fig. 3). Theoretical curves were fitted to data by least-squares methods with custom Matlab software, as described below and in Model of the Light-Induced Backscatter Increase from the OS.
Structural Model of the Rod OS.
CHARMM-GUI (75, 76) was used to assemble an all-atoms model of 20-nm × 20-nm patches of disc membrane around 10 randomly spaced and randomly oriented rhodopsins [Protein Data Bank (PDB) ID 2I36] with transmembrane orientation based on prediction from the Orientations of Proteins in Membranes database (77). Lipids (PC, PE, PS, and cholesterol) were distributed in the inner and outer membrane leaflets according to results from bovine rod OS (78, 79). The spacings between the bilayer pair comprising an individual disc and between the pair of discs in the model were set for the dark-adapted state as described in Model of the Light-Induced Backscatter Increase from the OS and Fig. S4. Gαtβ1γ1 in its inactive heterotrimeric state (1GOT) docked to rhodopsin (3SN6) and dissociated subunits Gαt (1TND) and Gβ1γ (1TBG) and PDE6 (3IBJ) were added as required. The volumes of heterotrimeric Gαtβ1γ1 and its subunits were computed with Chimera (80).
Theoretical Models of Rod OS Osmotically Induced Swelling and Backscattering Increases.
A model of bleaching-induced rod OS osmotic swelling was developed based on well-established physical and physiological principles (Osmo-Elastic Model of Light-Induced Rod OS Swelling) and tested by fitting the model to data to extract key features and parameters such as hydraulic conductivity. A model of the backscattering increases at the base of the rod OS was created by analysis of the refractive index distribution of the OS and of how this is affected by light-induced cytoplasmic swelling and the dissociation of Gαt and Gtβγ from the disc membranes (Model of the Light-Induced Backscatter Increase from the OS). The backscattering model includes the osmo-elastic model and the simultaneous acquired swelling and backscattering data were fitted simultaneously (Osmo-Elastic Model of Light-Induced Rod OS Swelling and Model of the Light-Induced Backscatter Increase from the OS).
Histological Identification of the OCT Backscattering Layers
To confirm the retinal layer and layer boundary assignments of the mouse OCT results, we compared OCT B-scan data with retinal plastic sections (Fig. S1). One of the distinctive features revealed in the histological section is that in contrast to the relatively thin boundaries of the ELM and BrMs, the IS/OS boundaries of different rods are not coplanar, but vary in their depth location. Measurements from images such as Fig. S1A revealed the range of the IS/OS boundary position to be ∼5 μm. This variation contributes to axial broadening of the IS/OS band in the OCT images and was taken into consideration in the development of the model of backscattering from the IS/OS and base of the rod OS (Model of the Light-Induced Backscatter Increase from the OS).
Effect of Limited OCT Axial Resolution on the Backscatter Profile of the Distal Rod OS
A small (0.29 μm) shift in the position of the backscattering peak attributed to the rod OS tips relative to the BrM peak can been seen in Fig. 1D, Inset. We think that this shift is a consequence of the finite axial resolution of the OCT system, rather than being caused by a physical displacement of the rod OS tips relative to BrM. To test this hypothesis we made a model of the backscattering profiles of the distal portion of the retina up to and including BrM in which the relative positions of the rod OS tips and BrM were invariant, whereas the scattering amplitudes varied (Fig. S2). The model demonstrates that the shift can arise from the limited axial resolution, which in effect convolves backscatter over a distance corresponding to the coherence length, and we accept this as the most parsimonious account.
Osmo-Elastic Model of Light-Induced Rod OS Swelling
Swelling of the Main Portion of the Rod OS.
Water influx into the rod OS is assumed to obey an osmo-elastic rate equation (43–45):
| [S1] |
Here (unit: cm3⋅s−1) represents the influx; LP (cm3⋅s−1⋅dyn−1) is the hydraulic conductivity; SM (cm2) is the membrane surface area; is the incremental intracellular osmotic pressure (dyn⋅cm−2), with the intracellular osmotic pressure and normal mouse plasma osmotic pressure; and P(t) (dyn⋅cm−2) is a restoring pressure arising from a reactive force that resists water-induced swelling. Both the left-hand side and the right-hand side of Eq. S1 can be recast in terms of the change in the cytoplasmic volume of the rod OS, as follows.
First, treating the incremental mole quantity ΔmS of solute/osmolyte produced by rapid, total activation of phototransduction in the rod OS as effectively instantaneous relative to the time course of swelling (Fig. 1), the internal osmotic pressure is given by
| [S2] |
where Π0 = (m0/V0)RT, ΔΠ = (ΔmS/V0)RT, and V0 is the dark-adapted cytoplasmic volume of the rod OS. Thus,
| [S3] |
Second, the restoring force was assumed to obey Hooke’s law, so that the reactive force generated in response to an OS elongation ΔL(t) is given by
| [S4] |
where AROS is the cross-sectional area of the rod OS, and kH is the spring constant of the entire OS. As rod OSs swell primarily by elongation in response to osmotic challenge (40, 41), P(t) in Eq. S4 can be rewritten in terms of the volume change:
| [S5] |
Finally, substituting from Eqs. S3 and S5, Eq. S1 was reformulated as a rate equation for the fractional increase in cytoplasmic volume,
| [S6] |
is a constant, and second-order terms in y(t) have been neglected. Eq. S6 is formally related to the rate equation governing Michaelis–Menten enzyme kinetics and admits an analytical solution in terms of the Lambert-W function (82, 83). The solution predicts that the increase in OS volume will not follow exponential kinetics, but rather have a linear, rate-limited initial segment, as observed (Figs. 1F and 5E). The steady-state solution (t → ∞) to Eq. S6 yields a family of linear functions that depend on the value of the Hooke’s law constant kH (Fig. S3). The solution to Eq. S6 used to predict the rod OS elongation in Figs. 1F and 5E assumed a 75-mOsM step increase in osmolytes (), corresponding to a spring constant for the whole disc stack of kH = 13.5 dyn⋅cm−1 (13.5 pN⋅nm−1) (red arrow in Fig. S3). The other parameters of Eq. S6 were obtained from the geometry of the mouse rod OS, except for the hydraulic conductivity, which was obtained from the fit (but can also be obtained directly from the initial slope and asymptotic level).
Swelling of the Basal Portion of the Rod OS.
To understand why backscattering increases occur at the base of the rod OS, we considered the distinctive features of the base that arise from its being the site of continual disc synthesis (Figs. 4B and 5A) (62, 84). In published images a number of nascent discs ranging from 5 to 12 are seen to be contiguous with the plasma membrane of the rod OS. It follows that the plasma membrane area in the region of such nascent discs is ∼15-fold greater per unit length than in the adjacent, mature rod OS, with further consequences. First, on the assumption that the basal disc membrane has the same hydraulic conductivity as the rest of the OS plasma membrane, the “patent” nascent discs will cause the base to have an up to 15-fold higher water permeability per unit length than the rest of the rod OS. Thus, the same initial osmotic stimulus per unit cytoplasmic volume will cause water to flow into the base at an initially higher rate. Second, because the rod OS is a single fluid-containing compartment, stress from increased cytoplasmic volume must be everywhere the same, but the strain in the base is likely greater, owing to the greater membrane surface and likely weaker disc–disc links. It can be shown that in such a linked-rod OS with two segments having different spring constants the fractional length increases of the segments will obey the relation
| [S7] |
where kBase is the spring constant per unit length for the base (proportional to the disc–disc spring constant, if the links serve as springs) and kROS is the spring constant per unit length for the rest of the rod OS. Thus, Eq. S7 predicts that with a weaker spring constant the basal region will undergo more rapid inflation and have a proportionately greater cytoplasmic volume increase. The more rapid cytoplasmic swelling of the rod OS base will create a diffusional gradient that tends to drive additional osmolytes into the base. Because the osmolytes are most likely nucleotides, which have an effective axial diffusion coefficient in the mouse rod OS of Deff ∼ 40 μm2⋅s−1 (85, 86), the 20-μm rod OS will equilibrate within a few seconds to such perturbations, and on the timescale of the swelling the spatial gradient of osmolytes will remain small (Figs. 1F and 3 A and C). We thus modeled the swelling of the base with the same osmo-elastic formulation as used for the OS as a whole (Eq. S6), but allowed the base to have a weaker spring constant. We also allowed the water influx term (LP SM,base/VBase) (Eq. S6) to be somewhat higher. Thus, for Fig. 5C kBase/kROS = 0.35 and the influx rate was 44% higher.
Model of the Light-Induced Backscatter Increase from the OS
To explain the bleaching-induced rod OS backscattering increases (Fig. 5), we developed a biophysical model based on these principles: (i) Mouse rods are cylindrical dielectric waveguides, capturing light in their IS and condensing it as it propagates to the OS (55–57, 87, 88; compare also ref. 28); (ii) backscattering from photoreceptors occurs at internal refractive index transitions; (iii) the effective refractive index of structures such as the disc stack with spacing (∼30 nm) substantially shorter than the wavelength of light can be calculated with “dielectric mixing” equations (58–60); and (iv) rod OS elongation occurs through an osmo-elastic increase of the interdiscal cytoplasmic space (Osmo-Elastic Model of Light-Induced Rod OS Swelling).
Waveguiding by Mouse Rods.
The waveguide parameter
| [S8] |
governs many aspects of the waveguide behavior, including the number of modes that can propagate and the fraction of light guided in the fiber core (56, 57). Here λ is the free-space wavelength, ρ the fiber radius, and ncore and nclad the refractive indexes of the core and cladding, respectively. We estimate that V = 2.04 for both the IS and OS of the mouse rod, given λ = 860 nm for the OCT, using for the IS ncore,RIS = 1.404, nclad,RIS = 1.37 and for the OS ncore,ROS = 1.410, nclad,ROS = 1.34 (see below). This value of V not only reveals that mouse rods are unimodal waveguides for the OCT wavelengths, but also predicts that the fraction of the total OCT beam power guided in the fiber core is ∼75% (56). Notably, the refractive index of the OS is predicted to decline from its dark-adapted value (1.410), dictated by osmotic swelling and dissociation of Gt from the disk membranes, as next described.
The Refractive Indexes of the Mouse Rod ISs and OSs.
The average refractive index of the rodent OS was reported to be 1.410 and that of the IS to be 1.404 based on Sidman’s classic investigation, and RIS is rod IS (33). To calculate how changes when the rod OS swells, we used the dielectric layer model of Corless and Kaplan (59). The Corless and Kaplan (“CK”) model has a unit cell (Fig. S4) with three layers and corresponding thicknesses and refractive indexes, namely (i) the intradiscal space, (ii) the disc bilayer, and (iii) the cytoplasm, and computes the resultant “average” refractive index of the rod OS with a well-established dielectric “mixing formula” (58, 60). Thus, given the set of distances and refractive indexes {[Di, ni], i = 1–3} (Fig. S4), the average rod OS refractive index is given by
| [S9] |
where are the distances normalized by the total unit cell distance, and the dielectric constants of the individual layers are The distances and refractive indexes used in the modeling are provided in Table S1, and their selection is described below.
We used molecular modeling of a bilayer with embedded rhodopsin molecules (Materials and Methods and Fig. 4) to determine the thickness of the bilayers (4.8 nm), because empirical measurements derived from EM necessarily blur and thereby overestimate the membrane thickness. Clearly, the membrane thickness is no greater than rhodopsin’s hydrophobic core (∼5.2 nm), as rhodopsin has substantial extramembrane mass in both cytoplasmic and intradiscal compartments (89–92). The intradiscal space was set to 5.0 nm based on the intradiscal (“extracellular”) extent of rhodopsin. The unit cell thickness was set to Dcell = 32 nm for the dark-adapted case for consistency with published data (table 1 of ref. 49), including X-ray diffraction data of living rod OS (93, 94). It bears emphasis, however, that because (as shown by our results) the rod OS reacts in vivo within seconds to osmotic imbalance, the vagaries of tissue fixation likely contribute to variability and perhaps systematic error in published estimates of the unit OS cell dimensions. The refractive index of the rod OS bilayer membrane was set to 1.51 based on analyses of the dielectric constant of bilayers (95, 96) and the CK model of rod OS birefringence. The two remaining refractive index values were chosen to be consistent with published data, but were fine-tuned to yield (for the dark-adapted rod OS) = 1.410 with Eq. S9.
Changes in Refractive Index of the OS During Osmotic Swelling.
The backscattering model incorporated the osmo-elastic model of swelling (Osmo-Elastic Model of Light-Induced Rod OS Swelling), which assumes that photobleaching of 10% of the rhodopsin alters the rod OS in three ways. First, within a few seconds the fully activated phototransduction cascade generates a step increase of osmolytes. Second, Gt rapidly separates into two moieties, Gtα and Gtβγ, which then dissociate from the disc membrane into the cytoplasm (Fig. 4C). Third, water influx causes the cytoplasmic volume to increase according to the osmo-elastic model. Both swelling and translocation of the G-protein subunits off the disc membranes into the cytoplasm contribute to the rod OS refractive index change. Swelling affects the refractive index by gradually increasing the thickness (D3) of the cytoplasmic component of the unit cell (Eq. S9 and Table S1). The effect of the mass transport of Gtα and Gtβγ from the membrane to the cytoplasm was treated as follows. First, a thin layer (corresponding to the equivalent volume of all of the G protein distributed over two membrane surfaces) was subtracted from each cytoplasmic disc face, and the total volume of the cytoplasm was equivalently augmented. The change in the refractive index with swelling and Gtα and Gtβγ solubilization was calculated in two ways: (i) with the Maxwell–Garnett mixing theory for dielectric spheres embedded in a host dielectric medium (58) and (ii) with the empirical differential refractometry approach of Barer and Joseph (97) as updated by Zhao et al. (98), which quantifies the effect of solubilized protein on a solution’s refractive index. The two approaches gave very similar dependencies of the cytoplasmic refractive index as a function of the increase in the cytoplasmic gap (D3) and so were averaged. Standard curves of the cytoplasmic refractive index n3 vs. unit cell fractional length increase were generated (Fig. 5C), and the overall change in the rod OS refractive index was then calculated with Eq. S9 (Fig. 5D, black trace).
Model of the Backscatter from the Basal Discs.
We focused on modeling the IS/OS backscattering signal because a great deal was known and has recently been learned about the ultrastructure of this portion of the rod (61, 62) (Fig. 5). Specifically, it is now incontrovertibly clear that nascent rod OS basal discs are formed by evagination of the plasma membrane and that up to 12 such discs remain contiguous with the plasma membrane before becoming separated and internalized within the rod OS as more discs are synthesized (62) (Fig. 5A). As described above, we hypothesized that these distinctive features of the basal discs increase the water permeability of the rod OS base by increasing the plasma membrane surface area and that the spring constant of the basal discs is weaker relative to that of the middle portion of the rod OS. These two features cause the basal rod OS to swell to a relatively greater extent than the rest of the OS. To calculate the change in refractive index we treated the rod OS base as a cylinder comprising three components (Fig. 5A): (i) 8 nascent discs (spaced in the dark-adapted state in the same manner as the discs in the middle portion of the OS), (ii) the tip of the IS, and (iii) a small extracellular volume intercalated between the IS and the OS. We made a three-dimensional model of the basal disc stack (Fig. 5B) consistent with published EM results (61, 62) and calculated the overall refractive index of the rod OS base by a volumetric weighting analogous to Eq. S9. The swelling of the basal discs was assumed to follow the osmo-elastic model, but with increased water permeability and a reduced spring constant. In the model prediction of Fig. 5, for example, the spring constant of the basal discs was 35% that of the rest of the rod OS, and the water permeability (per unit length of the base OS) was increased by 30%. The corresponding predicted changes in refractive indexes of the rod OS base and the rest of the OS are illustrated in Fig. 5D (the IS refractive index was held fixed at 1.404).
Backscattering at the IS/OS junction of each rod was assumed to come from two reflecting interfaces spaced ∼250 nm apart (Fig. 5A, red dashed box): (i) the interface of the rod OS base with the rest of the IS and (ii) the interface of the rod OS base with the middle portion of the rod OS. The interfaces were treated as Fresnel reflectors with surfaces perpendicular to the rod waveguide. Thus, writing and for the time-dependent refractive indexes of the middle portion of the rod OS and of the rod OS base, we calculated the time-dependent reflection coefficients (e.g., Fig. 5D)
| [S10] |
The axial resolution of the OCT system (∼2 μm) does not allow two reflectors spaced so closely to be resolved, and the OCT signal from a single rod with two such reflecting surfaces can be highly sensitive to the distance between them, as it would potentially involve constructive or destructive interference. However, in our experiments the spatial point-spread function (psf) of the OCT subtends approximately seven rods (90th percentile of spatially integrated power), so that the recorded signal from the IS/OS is created by a weighted combination of ∼14 interfering back-reflected beams. Statistical modeling of the OCT signal (99) suggests that the resultant speckle field for the IS/OS junction will have a value S2OCT(zBase) proportional to the sum of the reflected light from all of the reflecting surfaces subtended by the psf. This conclusion is strengthened by the fact that the axial location of IS/OS boundaries of different rods subtended by the psf varies over a 5-μm range (Fig. S1). Thus, in this backscatter model, we assumed the OCT signal to be proportional to the sum of the light reflected by the two Fresnel surfaces of an individual model rod OS base, i.e., proportional to
| [S11] |
(The model can be naturally extended to single photoreceptors, but the interference of the light reflected from the two surfaces must then be taken into account.)
The overall osmo-elastic and backscattering model predicts the kinetics of the simultaneously measured rod OS swelling and IS/OS backscattering, including the relative increase of the latter signal (Fig. 5 E and F), even though these two phenomena arise from different physical mechanisms. However, the absolute power of the IS/OS backscatter signal predicted by Eq. S11 was initially found to be approximately two orders of magnitude greater than the measured value, when the latter was calibrated by direct comparison with a model eye. We realized, however, that there were substantial losses in light capture of the back-reflected beam, as well as losses arising from alignment of the rod OS axis with respect to the OCT beam across the field of view and alignment from experiment to experiment, and so we incorporated these losses into the modeling, as described in the next section.
Estimation of the Absolute Retinal Reflectivity Measured by the OCT System
We initially estimated the absolute reflectivity corresponding to the OCT signals obtained from the photoreceptor layer (Table 1 and Fig. 5) as follows. We performed an experiment in which we substituted for the mouse a model eye composed of a lens with a mirror in its back focal plane. The effective reflectivity of the mirror was varied by inserting calibrated neutral density (ND) filters in the sample arm, and the OCT signal [SOCT(zM)]2 corresponding to the mirror location zM was extracted in the same way as signals from the mouse eye and plotted as a function of reflectivity (Fig. S5). The OCT signals for the IS/OS and OS tips from Table 1 were plotted on the same graph at the appropriate ordinate values. The projections of these values onto the abscissa provide estimates of the absolute reflectivity of these boundaries. However, they underestimate the retinal reflectivity, as they do not take into consideration a number of factors that attenuate the OCT signals coming from the mouse, but not those from the mirror in the experiment of Fig. S5. The core issue is that described above in the beginning of Model of the Light-Induced Backscatter Increase from the OS, namely that the photoreceptors are dielectric waveguides. For the central wavelength (860 nm) of our OCT mouse rods have a waveguide parameter number V ∼ 2.0 (Eq. S8) and thus act as weakly guiding single-mode fibers (56), with a close match of V for IS and OS despite the change in core diameter. The backscatter model assumes that the back reflection at the IS/OS boundary follows free-space Fresnel theory. Detection of light backscattered from the IS/OS junction is consequently subject to the optical Stiles–Crawford effect, which is more sensitive to the alignment of the imaging beam with respect to the photoreceptor optical axis than the psychophysical SCE (100). We identified several factors connected with the optical SCE and an additional factor associated with IS/OS ultrastructure that reduce S2OCT(zIS/OS), the measured OCT signal from the IS/OS junction relative that predicted by the model. Overall, our analysis indicates that the reflection at the IS/OS junction is likely 100−300 times stronger than the value estimated from the calibrations obtained in the experiment with the model eye of Fig. S5. Thus, for example, if the experimentally measured value of S2OCT(zIS/OS) corresponds to a reflection coefficient of 10−7 compared with reflections from a mirror attenuated by neutral density filters (Fig. S5), the actual reflection coefficient of the IS/OS junction would be 2.5 × 10−6–7.5 × 10−6. The various factors (i–vi) are provided in Table S2 along with rough estimates of their magnitude, with brief descriptions, as follows:
-
i)
Due to weak coupling of the optical mode at 860 nm for rods, waveguide theory predicts that only 0.75 of the power of the guided mode propagates in the waveguide core of the rod IS. We note, however, that the rod ISs occupy nearly the entire retinal cross-section (28), and the core and cladding are not clearly delineated as in isolated fibers.
-
ii)
In our experiments, we acquire OCT B scans over a relatively large FOV (Fig. 1). Analysis shows a systematic variation in S2OCT(zIS/OS) in the FOV, with the highest signal strength in the center. We attribute this variation to a variation between the waveguide optical axis and the OCT beam axis. We estimate that spatial averaging of the A scans across the field (Fig. 1A, dashed region) results in an approximately twofold reduction in S2OCT(zIS/OS) relative to the maximal signal in the field center.
-
iii)
We also observed variation in S2OCT(zIS/OS) measured from different mice and sometimes from the same mouse between different imaging sessions. Our measured values vary by a factor of 4, and we believe that this variation arises from variation in alignment of the optical axis relative to the waveguide axis of the photoreceptors. We estimate that this effect reduces the average value of S2OCT(zIS/OS) by a factor of ∼2.
-
iv)
Another effect connected to the optical SCE is created by a mismatch between the optical system’s detection pupil (detection numerical aperture) and the rod photoreceptor acceptance angle (N.A.). Thus, light backscattered from the IS/OS junction is distributed over the N.A. of the rod waveguide, but only a fraction of this light is captured by the imaging system, whose detection pupil is 0.46 mm at the mouse pupil. Assuming the N.A. of the mouse rod is ∼0.25, this apodization reduces S2OCT(zIS/OS) by a factor of about 6.
-
v)
Another effect that likely reduces S2OCT(zIS/OS) is attributed to ultrastructural inhomogeneity (or gradual instead of step changes in refractive index) and surface tilt of the IS/OS and OS base (Fig. 5B). Our model treats the OS base as a cylinder of uniform refractive index, computed first with the CK formula (Eq. S9) applied to the nascent rod discs and then with a volumetric averaging over the refractive indexes of the IS and extracellular space in the base. The disc fraction of the base can be considered a refractive surface tilted with respect to the waveguide optical axis (Fig. 5B), with the result that backscatter will be overestimated in a model that treats the OS base as having a uniform refractive index.
-
vi)
Finally, the ∼5-μm axial variation in the position of the IS/OS junction (Fig. S1) will cause a reduction in S2OCT(zIS/OS) because the theoretical axial resolution of the OCT is ∼2 μm, and only backscatter within this depth range will be averaged in an individual OCT A-scan pixel.
The net result of these considerations is that S2OCT(zIS/OS) is substantially reduced, and the reflectivity of the OS base is expected to be 100- to 300-fold higher than what is measured. We incorporated these ideas into the modeling by implementing in the search routine that fitted the backscatter model a loss factor that could range between 100 and 300. Thus, the predicted time course of rod OS base reflectivity RBase,eff(t) (Eq. S11) was fitted to S2OCT(zIS/OS) by least squares by minimizing the sum squared error
where m = 7.9 × 1014 is the “mirror equivalent” scaling factor (Fig. S5), and θ represents the other parameters of the model, which include the number of basal discs (8), the fraction of extracellular volume in the base (0.07) (Fig. 5A), the index of refraction of the extracellular space (1.36), the index of refraction of the IS (1.404), the ratio kROS/kBase (3.28), and the relative rate of water flow into the base (1.22). To obtain the fit of Fig. 5F the loss factor had the value 155. Equally good fits to simultaneously acquired elongation and backscattering data from 11 wild-type mice were obtained with similar parameter values.
Supplementary Material
Acknowledgments
We thank Prof. Roy Curry [University of California, Davis (UC Davis)] and Prof. Nader Engheta (University of Pennsylvania) for helpful comments on the osmo-elastic and backscattering modeling, respectively; Gabriel Peinado for help with characterization of the Gnat1−/− mice; and Dr. Sarah Karlen for assistance with mouse anesthesia and colony management. This research was supported by National Institutes of Health Grant EY02660 (to E.N.P.), a National Science Foundation Industry–University Cooperative Research Centers Program, Center for Biophotonic Sensors and Systems grant (to R.J.Z.), Grant EY012576 (National Eye Institute UC Davis core grant), and a UC Davis Research Investments in Science and Engineering (RISE) grant.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1620572114/-/DCSupplemental.
References
- 1.Drexler WF, Fujimoto JG, editors. Optical Coherence Tomography. Springer; New York: 2015. [Google Scholar]
- 2.Fujimoto J, Huang D. Foreword: 25 years of optical coherence tomography. Invest Ophthalmol Vis Sci. 2016;57(9):OCTi–OCTii. doi: 10.1167/iovs.16-20269. [DOI] [PubMed] [Google Scholar]
- 3.Gao SS, et al. Optical coherence tomography angiography. Invest Ophthalmol Vis Sci. 2016;57(9):OCT27–OCT36. doi: 10.1167/iovs.15-19043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jang IK, et al. In vivo characterization of coronary atherosclerotic plaque by use of optical coherence tomography. Circulation. 2005;111(12):1551–1555. doi: 10.1161/01.CIR.0000159354.43778.69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gonzalo N, et al. Second-generation optical coherence tomography in clinical practice. High-speed data acquisition is highly reproducible in patients undergoing percutaneous coronary intervention. Rev Esp Cardiol. 2010;63(8):893–903. doi: 10.1016/s1885-5857(10)70183-3. [DOI] [PubMed] [Google Scholar]
- 6.Li X, et al. High-resolution optical coherence tomographic imaging of osteoarthritic cartilage during open knee surgery. Arthritis Res Ther. 2005;7(2):R318–R323. doi: 10.1186/ar1491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fujimoto JG, Pitris C, Boppart SA, Brezinski ME. Optical coherence tomography: An emerging technology for biomedical imaging and optical biopsy. Neoplasia. 2000;2(1-2):9–25. doi: 10.1038/sj.neo.7900071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Srinivasan VJ, Wojtkowski M, Fujimoto JG, Duker JS. In vivo measurement of retinal physiology with high-speed ultrahigh-resolution optical coherence tomography. Opt Lett. 2006;31(15):2308–2310. doi: 10.1364/ol.31.002308. [DOI] [PubMed] [Google Scholar]
- 9.Yao X, Wang B. Intrinsic optical signal imaging of retinal physiology: A review. J Biomed Opt. 2015;20(9):090901. doi: 10.1117/1.JBO.20.9.090901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hillmann D, et al. In vivo optical imaging of physiological responses to photostimulation in human photoreceptors. Proc Natl Acad Sci USA. 2016;113(46):13138–13143. doi: 10.1073/pnas.1606428113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jonnal RS, et al. In vivo functional imaging of human cone photoreceptors. Opt Express. 2007;15(24):16141–16160. [PMC free article] [PubMed] [Google Scholar]
- 12.Grieve K, Roorda A. Intrinsic signals from human cone photoreceptors. Invest Ophthalmol Vis Sci. 2008;49(2):713–719. doi: 10.1167/iovs.07-0837. [DOI] [PubMed] [Google Scholar]
- 13.Kocaoglu OPL, et al. Photoreceptor disc shedding in the living human eye. Biomed Opt Express. 2016;7(11):4554–4568. doi: 10.1364/BOE.7.004554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schmoll T, Kolbitsch C, Leitgeb RA. In vivo functional retinal optical coherence tomography. J Biomed Opt. 2010;15(4):041513. doi: 10.1117/1.3463008. [DOI] [PubMed] [Google Scholar]
- 15.Liu Q, et al. The proteome of the mouse photoreceptor sensory cilium complex. Mol Cell Proteomics. 2007;6(8):1299–1317. doi: 10.1074/mcp.M700054-MCP200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Skiba NP, et al. Proteomic identification of unique photoreceptor disc components reveals the presence of PRCD, a protein linked to retinal degeneration. J Proteome Res. 2013;12(6):3010–3018. doi: 10.1021/pr4003678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Arshavsky VY, Lamb TD, Pugh EN., Jr G proteins and phototransduction. Annu Rev Physiol. 2002;64:153–187. doi: 10.1146/annurev.physiol.64.082701.102229. [DOI] [PubMed] [Google Scholar]
- 18.Arshavsky VY, Burns ME. Photoreceptor signaling: Supporting vision across a wide range of light intensities. J Biol Chem. 2012;287(3):1620–1626. doi: 10.1074/jbc.R111.305243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Arshavsky VY, Wensel TG. Timing is everything: GTPase regulation in phototransduction. Invest Ophthalmol Vis Sci. 2013;54(12):7725–7733. doi: 10.1167/iovs.13-13281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Calvert PD, Strissel KJ, Schiesser WE, Pugh EN, Jr, Arshavsky VY. Light-driven translocation of signaling proteins in vertebrate photoreceptors. Trends Cell Biol. 2006;16(11):560–568. doi: 10.1016/j.tcb.2006.09.001. [DOI] [PubMed] [Google Scholar]
- 21.Kerov V, et al. Transducin activation state controls its light-dependent translocation in rod photoreceptors. J Biol Chem. 2005;280(49):41069–41076. doi: 10.1074/jbc.M508849200. [DOI] [PubMed] [Google Scholar]
- 22.Majumder A, et al. Transducin translocation contributes to rod survival and enhances synaptic transmission from rods to rod bipolar cells. Proc Natl Acad Sci USA. 2013;110(30):12468–12473. doi: 10.1073/pnas.1222666110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Geng Y, et al. Adaptive optics retinal imaging in the living mouse eye. Biomed Opt Express. 2012;3(4):715–734. doi: 10.1364/BOE.3.000715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jian Y, Zawadzki RJ, Sarunic MV. Adaptive optics optical coherence tomography for in vivo mouse retinal imaging. J Biomed Opt. 2013;18(5):56007. doi: 10.1117/1.JBO.18.5.056007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zawadzki RJ, et al. Adaptive-optics SLO imaging combined with widefield OCT and SLO enables precise 3D localization of fluorescent cells in the mouse retina. Biomed Opt Express. 2015;6(6):2191–2210. doi: 10.1364/BOE.6.002191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang P, Goswami M, Zam A, Pugh EN, Zawadzki RJ. Effect of scanning beam size on the lateral resolution of mouse retinal imaging with SLO. Opt Lett. 2015;40(24):5830–5833. doi: 10.1364/OL.40.005830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang P, et al. In vivo wide-field multispectral scanning laser ophthalmoscopy-optical coherence tomography mouse retinal imager: Longitudinal imaging of ganglion cells, microglia, and Müller glia, and mapping of the mouse retinal and choroidal vasculature. J Biomed Opt. 2015;20(12):126005. doi: 10.1117/1.JBO.20.12.126005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhang P, Goswami M, Zawadzki RJ, Pugh EN., Jr The photosensitivity of rhodopsin bleaching and light-induced increases of fundus reflectance in mice measured in vivo with scanning laser ophthalmoscopy. Invest Ophthalmol Vis Sci. 2016;57(8):3650–3664. doi: 10.1167/iovs.16-19393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Calvert PD, et al. Phototransduction in transgenic mice after targeted deletion of the rod transducin alpha-subunit. Proc Natl Acad Sci USA. 2000;97(25):13913–13918. doi: 10.1073/pnas.250478897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Peinado GA, Fortenbach C, Naarendorp F, Pugh EN, Burns ME. Rapid responses of mammalian rods in vivo are rate-limited by RGS9. J Gen Physiol. 2017 doi: 10.1085/jgp.201611692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Verkman AS, Ruiz-Ederra J, Levin MH. Functions of aquaporins in the eye. Prog Retin Eye Res. 2008;27(4):420–433. doi: 10.1016/j.preteyeres.2008.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li Y, Fariss RN, Qian JW, Cohen ED, Qian H. Light-induced thickening of photoreceptor outer segment layer detected by ultra-high resolution OCT imaging. Invest Ophthalmol Vis Sci. 2016;57(9):OCT105–OCT111. doi: 10.1167/iovs.15-18539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sidman RL. The structure and concentration of solids in photoreceptor cells studied by refractometry and interference microscopy. J Biophys Biochem Cytol. 1957;3(1):15–30. doi: 10.1083/jcb.3.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Heck M, Hofmann KP. Maximal rate and nucleotide dependence of rhodopsin-catalyzed transducin activation: Initial rate analysis based on a double displacement mechanism. J Biol Chem. 2001;276(13):10000–10009. doi: 10.1074/jbc.M009475200. [DOI] [PubMed] [Google Scholar]
- 35.Kühn H, Bennett N, Michel-Villaz M, Chabre M. Interactions between photoexcited rhodopsin and GTP-binding protein: Kinetic and stoichiometric analyses from light-scattering changes. Proc Natl Acad Sci USA. 1981;78(11):6873–6877. doi: 10.1073/pnas.78.11.6873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lobanova ES, et al. Transducin gamma-subunit sets expression levels of alpha- and beta-subunits and is crucial for rod viability. J Neurosci. 2008;28(13):3510–3520. doi: 10.1523/JNEUROSCI.0338-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lobanova ES, et al. Transducin translocation in rods is triggered by saturation of the GTPase-activating complex. J Neurosci. 2007;27(5):1151–1160. doi: 10.1523/JNEUROSCI.5010-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kosloff M, Alexov E, Arshavsky VY, Honig B. Electrostatic and lipid anchor contributions to the interaction of transducin with membranes: Mechanistic implications for activation and translocation. J Biol Chem. 2008;283(45):31197–31207. doi: 10.1074/jbc.M803799200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sokolov M, et al. Massive light-driven translocation of transducin between the two major compartments of rod cells: A novel mechanism of light adaptation. Neuron. 2002;34(1):95–106. doi: 10.1016/s0896-6273(02)00636-0. [DOI] [PubMed] [Google Scholar]
- 40.Korenbrot JI, Brown DT, Cone RA. Membrane characteristics and osmotic behavior of isolated rod outer segments. J Cell Biol. 1973;56(2):389–398. doi: 10.1083/jcb.56.2.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Korenbrot JI, Cone RA. Dark ionic flux and the effects of light in isolated rod outer segments. J Gen Physiol. 1972;60(1):20–45. doi: 10.1085/jgp.60.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Russel ES, Bernstein SE (2007) Blood and blood formation. Biology of the Laboratory Mouse, eds Green EL, Jackson Lab Staff (Dover, Mineola, NY), 2nd Ed, Chap 17.
- 43.Renken EM, Curry FE. Transport of water and solutes across capillary endothelium. In: Giebisch G, Tosteson DC, Ussing HH, editors. Membrane Transport in Biology. Springer; Berlin: 1978. pp. 1–45. [Google Scholar]
- 44.Kedem O, Katchalsky A. Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim Biophys Acta. 1958;27(2):229–246. doi: 10.1016/0006-3002(58)90330-5. [DOI] [PubMed] [Google Scholar]
- 45.Kleinhans FW. Membrane permeability modeling: Kedem-Katchalsky vs a two-parameter formalism. Cryobiology. 1998;37(4):271–289. doi: 10.1006/cryo.1998.2135. [DOI] [PubMed] [Google Scholar]
- 46.Preston GM, Carroll TP, Guggino WB, Agre P. Appearance of water channels in Xenopus oocytes expressing red cell CHIP28 protein. Science. 1992;256(5055):385–387. doi: 10.1126/science.256.5055.385. [DOI] [PubMed] [Google Scholar]
- 47.Prescott DM, Zeuthen E. Comparison of water diffusion and water filtration across cell surfaces. Acta Physiol Scand. 1953;28(1):77–94. doi: 10.1111/j.1748-1716.1953.tb00960.x. [DOI] [PubMed] [Google Scholar]
- 48.Roof DJ, Heuser JE. Surfaces of rod photoreceptor disk membranes: Integral membrane components. J Cell Biol. 1982;95(2 Pt 1):487–500. doi: 10.1083/jcb.95.2.487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nickell S, Park PS, Baumeister W, Palczewski K. Three-dimensional architecture of murine rod outer segments determined by cryoelectron tomography. J Cell Biol. 2007;177(5):917–925. doi: 10.1083/jcb.200612010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sułkowska JI, Cieplak M. Stretching to understand proteins - a survey of the protein data bank. Biophys J. 2008;94(1):6–13. doi: 10.1529/biophysj.107.105973. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 51.Carvalho FA, Martins IC, Santos NC. Atomic force microscopy and force spectroscopy on the assessment of protein folding and functionality. Arch Biochem Biophys. 2013;531(1-2):116–127. doi: 10.1016/j.abb.2012.11.007. [DOI] [PubMed] [Google Scholar]
- 52.Zhang X, Wensel TG, Kraft TW. GTPase regulators and photoresponses in cones of the eastern chipmunk. J Neurosci. 2003;23(4):1287–1297. doi: 10.1523/JNEUROSCI.23-04-01287.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kerov V, Artemyev NO. Diffusion and light-dependent compartmentalization of transducin. Mol Cell Neurosci. 2011;46(1):340–346. doi: 10.1016/j.mcn.2010.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Vuong TM, Chabre M, Stryer L. Millisecond activation of transducin in the cyclic nucleotide cascade of vision. Nature. 1984;311(5987):659–661. doi: 10.1038/311659a0. [DOI] [PubMed] [Google Scholar]
- 55.Snyder AW, Pask C. Letter: Waveguide modes and light absorption in photoreceptors. Vision Res. 1973;13(12):2605–2608. doi: 10.1016/0042-6989(73)90261-7. [DOI] [PubMed] [Google Scholar]
- 56.Snyder AW, Love JD . Optical Waveguide Theory. Chapman & Hall; London: 1983. [Google Scholar]
- 57.Snyder AW, Menzel R. Photoreceptor Optics. Springer; New York: 1975. [Google Scholar]
- 58.Sihvola A. Electromagnetic Mixing Formulas and Applications. Institution of Electrical Engineers; London: 1999. [Google Scholar]
- 59.Corless JM, Kaplan MW. Structural interpretation of the birefringence gradient in retinal rod outer segments. Biophys J. 1979;26(3):543–556. doi: 10.1016/S0006-3495(79)85270-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Thornburg W. The form birefringence of lamellar systems containing three or more components. J Biophys Biochem Cytol. 1957;3(3):413–419. doi: 10.1083/jcb.3.3.413. [DOI] [PubMed] [Google Scholar]
- 61.Carter-Dawson LD, LaVail MM. Rods and cones in the mouse retina. I. Structural analysis using light and electron microscopy. J Comp Neurol. 1979;188(2):245–262. doi: 10.1002/cne.901880204. [DOI] [PubMed] [Google Scholar]
- 62.Ding JD, Salinas RY, Arshavsky VY. Discs of mammalian rod photoreceptors form through the membrane evagination mechanism. J Cell Biol. 2015;211(3):495–502. doi: 10.1083/jcb.201508093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kalfa TA, Connor JA, Begtrup AH. EPB42-related hereditary spherocytosis. GeneReviews. 1993 Available at https://www.ncbi.nlm.nih.gov/books/NBK190102/. Accessed March 9, 2017.
- 64.Stewart AK, et al. Loss-of-function and gain-of-function phenotypes of stomatocytosis mutant RhAG F65S. Am J Physiol Cell Physiol. 2011;301(6):C1325–C1343. doi: 10.1152/ajpcell.00054.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Leskov IB, et al. The gain of rod phototransduction: Reconciliation of biochemical and electrophysiological measurements. Neuron. 2000;27(3):525–537. doi: 10.1016/s0896-6273(00)00063-5. [DOI] [PubMed] [Google Scholar]
- 66.Lamb TD, Pugh EN., Jr Dark adaptation and the retinoid cycle of vision. Prog Retin Eye Res. 2004;23(3):307–380. doi: 10.1016/j.preteyeres.2004.03.001. [DOI] [PubMed] [Google Scholar]
- 67.Lyubarsky AL, et al. Mole quantity of RPE65 and its productivity in the generation of 11-cis-retinal from retinyl esters in the living mouse eye. Biochemistry. 2005;44(29):9880–9888. doi: 10.1021/bi0505363. [DOI] [PubMed] [Google Scholar]
- 68.Xu J, et al. Prolonged photoresponses in transgenic mouse rods lacking arrestin. Nature. 1997;389(6650):505–509. doi: 10.1038/39068. [DOI] [PubMed] [Google Scholar]
- 69.Burns ME, et al. Deactivation of phosphorylated and nonphosphorylated rhodopsin by arrestin splice variants. J Neurosci. 2006;26(3):1036–1044. doi: 10.1523/JNEUROSCI.3301-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Imai H, et al. Molecular properties of rhodopsin and rod function. J Biol Chem. 2007;282(9):6677–6684. doi: 10.1074/jbc.M610086200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Jonnal RS, et al. A review of adaptive optics optical coherence tomography: Technical advances, scientific applications, and the future. Invest Ophthalmol Vis Sci. 2016;57(9):OCT51–OCT68. doi: 10.1167/iovs.16-19103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Shevell SK. Saturation in human cones. Vision Res. 1977;17(3):427–434. doi: 10.1016/0042-6989(77)90035-9. [DOI] [PubMed] [Google Scholar]
- 73.Fercher AF, Drexler W, Hitzenberger CK, Lasser T. Optical coherence tomography - principles and applications. Rep Prog Phys. 2003;66(2):239–303. [Google Scholar]
- 74.Wojtkowski M. High-speed optical coherence tomography: Basics and applications. Appl Opt. 2010;49(16):D30–D61. doi: 10.1364/AO.49.000D30. [DOI] [PubMed] [Google Scholar]
- 75.Jo S, Kim T, Im W. Automated builder and database of protein/membrane complexes for molecular dynamics simulations. PLoS One. 2007;2(9):e880. doi: 10.1371/journal.pone.0000880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Jo S, Lim JB, Klauda JB, Im W. CHARMM-GUI Membrane Builder for mixed bilayers and its application to yeast membranes. Biophys J. 2009;97(1):50–58. doi: 10.1016/j.bpj.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lomize MA, Lomize AL, Pogozheva ID, Mosberg HI. OPM: Orientations of proteins in membranes database. Bioinformatics. 2006;22(5):623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- 78.Miljanich GP, Sklar LA, White DL, Dratz EA. Disaturated and dipolyunsaturated phospholipids in the bovine retinal rod outer segment disk membrane. Biochim Biophys Acta. 1979;552(2):294–306. doi: 10.1016/0005-2736(79)90284-0. [DOI] [PubMed] [Google Scholar]
- 79.Wu G, Hubbell WL. Phospholipid asymmetry and transmembrane diffusion in photoreceptor disc membranes. Biochemistry. 1993;32(3):879–888. doi: 10.1021/bi00054a020. [DOI] [PubMed] [Google Scholar]
- 80.Pettersen EF, et al. UCSF Chimera--a visualization system for exploratory research and analysis. J Comput Chem. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 81.Lyubarsky AL, Daniele LL, Pugh EN., Jr From candelas to photoisomerizations in the mouse eye by rhodopsin bleaching in situ and the light-rearing dependence of the major components of the mouse ERG. Vision Res. 2004;44(28):3235–3251. doi: 10.1016/j.visres.2004.09.019. [DOI] [PubMed] [Google Scholar]
- 82.Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE. On the Lambert W function. Adv Comput Math. 1996;5(4):329–359. [Google Scholar]
- 83.Mahroo OA, Lamb TD. Recovery of the human photopic electroretinogram after bleaching exposures: Estimation of pigment regeneration kinetics. J Physiol. 2004;554(Pt 2):417–437. doi: 10.1113/jphysiol.2003.051250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Burgoyne T, et al. Rod disc renewal occurs by evagination of the ciliary plasma membrane that makes cadherin-based contacts with the inner segment. Proc Natl Acad Sci USA. 2015;112(52):15922–15927. doi: 10.1073/pnas.1509285113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Gross OP, Pugh EN, Jr, Burns ME. Spatiotemporal cGMP dynamics in living mouse rods. Biophys J. 2012;102(8):1775–1784. doi: 10.1016/j.bpj.2012.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Holcman D, Korenbrot JI. Longitudinal diffusion in retinal rod and cone outer segment cytoplasm: The consequence of cell structure. Biophys J. 2004;86(4):2566–2582. doi: 10.1016/S0006-3495(04)74312-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Snyder AW, Pask C. The Stiles-Crawford effect--explanation and consequences. Vision Res. 1973;13(6):1115–1137. doi: 10.1016/0042-6989(73)90148-x. [DOI] [PubMed] [Google Scholar]
- 88.Pask CS, Snyder AW. Angular sensitivity of lens-photoreceptor systems. In: Snyder AW, Menzel R, editors. Photoreceptor Optics. Springer; New York: 1975. pp. 159–174. [Google Scholar]
- 89.Okada T, et al. X-Ray diffraction analysis of three-dimensional crystals of bovine rhodopsin obtained from mixed micelles. J Struct Biol. 2000;130(1):73–80. doi: 10.1006/jsbi.1999.4209. [DOI] [PubMed] [Google Scholar]
- 90.Palczewski K, et al. Crystal structure of rhodopsin: A G protein-coupled receptor. Science. 2000;289(5480):739–745. doi: 10.1126/science.289.5480.739. [DOI] [PubMed] [Google Scholar]
- 91.Teller DC, Okada T, Behnke CA, Palczewski K, Stenkamp RE. Advances in determination of a high-resolution three-dimensional structure of rhodopsin, a model of G-protein-coupled receptors (GPCRs) Biochemistry. 2001;40(26):7761–7772. doi: 10.1021/bi0155091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Scheerer P, et al. Structural and kinetic modeling of an activating helix switch in the rhodopsin-transducin interface. Proc Natl Acad Sci USA. 2009;106(26):10660–10665. doi: 10.1073/pnas.0900072106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Pascolini D, Blasie JK, Gruner SM. A 12 A resolution X-ray diffraction study of the profile structure of isolated bovine retinal rod outer segment disk membranes. Biochim Biophys Acta. 1984;777(1):9–20. doi: 10.1016/0005-2736(84)90491-7. [DOI] [PubMed] [Google Scholar]
- 94.Schwartz S, Cain JE, Dratz EA, Blasie JK. An analysis of lamellar x-ray diffraction from disordered membrane multilayers with application to data from retinal rod outer segments. Biophys J. 1975;15(12):1201–1233. doi: 10.1016/S0006-3495(75)85895-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Huang W, Levitt DG. Theoretical calculation of the dielectric constant of a bilayer membrane. Biophys J. 1977;17(2):111–128. doi: 10.1016/S0006-3495(77)85630-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Stern HAF, Feller SE. Calculation of the dielectric permittivity profile for a non-uniform system: Application to a lipid bilayer. J Chem Phys. 2003;118(7):13. [Google Scholar]
- 97.Barer R, Joseph S. Refractometry of living cells. 1. Basic principles. Q J Microsc Sci. 1954;95(4):399–423. [Google Scholar]
- 98.Zhao H, Brown PH, Schuck P. On the distribution of protein refractive index increments. Biophys J. 2011;100(9):2309–2317. doi: 10.1016/j.bpj.2011.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Pircher M, Gotzinger E, Leitgeb R, Fercher AF, Hitzenberger CK. Speckle reduction in optical coherence tomography by frequency compounding. J Biomed Opt. 2003;8(3):565–569. doi: 10.1117/1.1578087. [DOI] [PubMed] [Google Scholar]
- 100.Gao W, Cense B, Zhang Y, Jonnal RS, Miller DT. Measuring retinal contributions to the optical Stiles-Crawford effect with optical coherence tomography. Opt Express. 2008;16(9):6486–6501. doi: 10.1364/OE.16.006486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Dithmar S, Curcio CA, Le NA, Brown S, Grossniklaus HE. Ultrastructural changes in Bruch’s membrane of apolipoprotein E-deficientmice. Invest Ophthalmol Vis Sci. 2000;41(8):2035–2042. [PubMed] [Google Scholar]
- 102.Hatai S. The refractive index of the blood serum of the albino rat at different ages. J Biol Chem. 1918;35:527–552. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.