DNA nanostructures constructed with multi-stranded motifs

Abstract

Earlier studies in DNA self-assembly have foretold the feasibility of building addressable nanostructures with multi-stranded motifs, which is fully validated in this study. In realizing this feasibility in DNA nanotechnology, a diversified set of motifs of modified domain lengths is extended from a classic type. The length of sticky ends can be adjusted to form different dihedral angles between the matching motifs, which corresponds to different connecting patterns. Moreover, the length of rigidity core can also be tuned to result in different dihedral angles between the component helices of a certain motif therefore different numbers of component helices. The extended set of motifs is used for self-assembly of complex one dimensional, two dimensional and three dimensional structures.

INTRODUCTION

Since the emergence of DNA nanotechnology, many generations of rationally designed DNA motifs have showcased the self-assembly capability of synthetic DNA molecules (1–11). The self-assembly of DNA nanostructures under such a paradigm is analogous to building versatile models using LEGO bricks. With a few species of component strands, the overall complexity of most of the structures in early studies of the field remained relatively low (12,13). As a latecomer however, DNA origami method, in which a long single-stranded ‘scaffold’ is used to recruit hundreds short ‘staple’ strands of unique sequences to form a desired shape, has become the state of the art to construct increasingly more complex nanostructures (14–21). Although it was long believed that the LEGO approach, which was introduced in the field of DNA nanotechnology much earlier than DNA origami, could be applied to form complex structures, the fully addressable mega-Dalton structures only got realized by single-stranded tiles and bricks rather recently (22–25). Afterward, the LEGO approach was extended to one of the classic multi-stranded motif types, double crossover (DX) motif, to form discrete DNA nanostructures as complex as the counterparts from DNA origami approach (26).

Here we further validate the feasibility of using multi-stranded motifs to construct addressable structures, especially three dimensional (3D) structures. The motifs in this study are diversified from a classic type of motif introduced by Mao and co-workers.(27). In the basic configuration, two component strands form a rigidity core of two duplexes in between crossovers with four sticky ends (Figure 1A). The two C-shaped component strands for a certain motif are intertwined in this configuration, so we call it as double-C-shaped motif. The length of sticky ends can be tuned to form different dihedral angles between matching motifs. Sticky ends of 10 nucleotides (nt), 16 and 8 nt correlate to dihedral angles of ∼180°, ∼0° and ∼90° respectively and corresponding two dimensional (2D), one dimensional (1D) and 3D structures were successfully constructed accordingly. We then further modified the length of rigidity core from 16 (one and a half turns) to 13 or 12 nt. The modifications resulted in different dihedral angles between the component helices of a certain motif (∼90° for a 13-nt rigidity core and ∼120° for a 12-nt rigidity core) and hence different numbers of component helices (four helices for a 13-nt rigidity core and six helices for a 12-nt rigidity core). We call them quadruple-C- and hextuple-C-shaped motifs respectively. These 3-D motifs point to a new strategy of making 3-D structures directly from 3-D building blocks.

Figure 1.

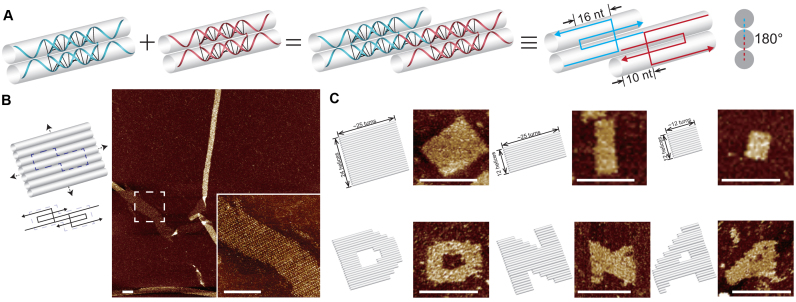
Double-C-shaped motifs with 10-nt sticky ends and the resulted nanostructures. (A) Schematics of matching motifs. Panels from left to right: individual motifs; two matching motifs; two matching motifs in simplified strand diagram; cross section view. (B) Infinite structure. Left: structure diagram with dashed box highlighting a repeating unit; right: atomic force microscopy (AFM) image (insect shows a magnified view). (C) Finite structures. Top, from left to right: 24H × 25T, 12H × 25T and 12H × 12T rectangles; bottom, from left to right: three patterns, ‘D’, ‘N’ and ‘A’ based on the 24H × 25T rectangle. Structure diagrams (left) and the corresponding AFM images (right) are shown as pairs. Scale bars: 100 nm.

MATERIALS AND METHODS

We use the Uniquimer software to design the full layout of a certain structure (28). Note that graphic user interface is not available for the design of 3D structures so the full complementary mapping information was obtained manually. DNA sequences of the structures were then generated by Uniquimer to comply with the programmed intra- and inter-motif base pairings and the minimal sequence symmetry. Minimal sequence symmetry might reduce the spurious pairing thus increase the yields of structure self-assembly, so such a criterion was adopted though random sequences with the appropriate pairing information could also lead to the formation of desired structures (22,23,25). For the finite 1D structures, the unpaired domains of the terminal motifs are replaced by poly(T) domains. Likewise, for the finite 2D or 3D structures, the unpaired domains of boundary (2D) or surface (3D) motifs are replaced by poly(T) domains. Such a design was known to reduce undesired pairing or blunt end stacking (22,25).

Component strands were ordered from Bioneer Corp. (http://www.bioneer.com) and unpurified strands were mixed at a nominal concentration without careful adjustment of stoichiometry. Different component strand concentrations, Mg²⁺ concentrations and annealing ramps were tested to determine the optimal self-assembly conditions. Optimal conditions were chosen as the following: 1 μM per strand for infinite structures or 200 nM per strand for finite structures (except for infinite structure with double-C-shaped motifs of 16-nt sticky ends, which was prepared at 2 μM per strand); 20 mM Mg²⁺; a 72 h slow cooling from 90 to 25°C for infinite structures or a 17 h slow cooling from 90 to 25°C for finite structures.

After annealing, the samples of infinite structures were subjected to atomic force microscopy (AFM) or transmission electron microscopy (TEM) directly and the samples of finite structures were subjected to agarose gel electrophoresis-based purification before AFM or TEM imaging. Almost all the finite structures we tried out resulted in a discrete band after agarose gel electrophoresis (with SYBR safe staining), which indicated successful structural formation. AFM or TEM imaging confirmed that infinite and finite structures self-assembled as designed. In total, we successfully designed and constructed twelve finite structures and six infinite structures with multi-stranded motifs of different configurations respectively. Gel yields of finite structures ranged from 9 to 38% (Supplementary Figures S5, 9, 10 and 14) and measured dimensions under AFM and TEM were in nice agreement with the designs. Supplementary Table S1 summarizes the experimental results of multiple structures.

RESULTS

Our first design inherits the original configuration of double-C-shaped motif. Each motif is composed of two component strands with four consecutive domains, which are 10, 16, 16 and 10 nt respectively. The 16-nt domains are paired with the counterparts of the other component strand to form a rigidity core of two bundled duplexes with four 10-nt domains serving as sticky ends to pair with four neighboring motifs respectively (Figure 1A). In such a design, the two motifs of the matching pair are roughly arranged coplanar with each other, with the bottom helix of one motif to be joined by a top helix of the other one. Similar connecting pattern applies to all four motifs surrounding one. In other words, two matching motifs along DNA helix axes are arranged with a dihedral angle of ∼180° (Figure 1A, right). We designed infinite 2D structures with two or four species of motifs (Figure 1B; Supplementary Figures S1 and 2). Because of the intrinsic curvature and flexibility, the resulted structures rolled up in a tube shape. We then designed a finite structure with the same domain length arrangement (rigidity core: 16 nt; sticky ends: 10 nt), a rectangle of 24 parallel helices with each measuring about ∼25 helical turns (24H × 25T; Figure 1C and Supplementary Figure S3). Such a 24H × 25T rectangle consists 120 species of motifs (260 strands of distinct sequences). Two smaller finite rectangles (12H × 25T and 12H × 12T) were cropped out from the 24H × 25T rectangle (Figure 1C and Supplementary Figure S3). Moreover, the 24H × 25T rectangle served as modular canvas for design and construction of three different patterns, ‘D’, ‘N’ and ‘A’ (Figure 1C and Supplementary Figure S4).

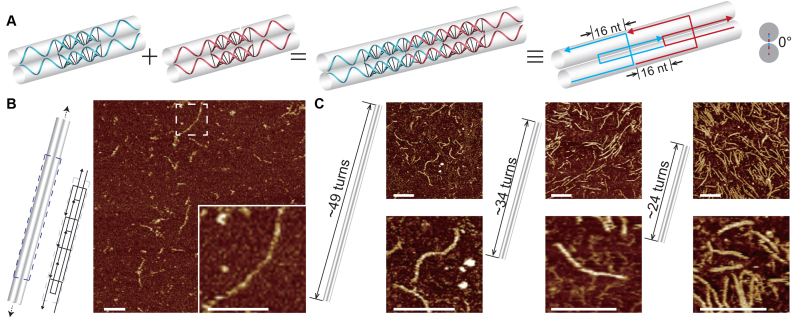
With the length of 16-nt domains in between crossover points unchanged, we then designed two more connecting patterns between matching motifs with sticky ends of different lengths. Sticky ends of 16 nt were designed in one new connecting pattern. Because the distance between neighboring crossovers measures full turns (32 nt), the motifs are connected coaxial in tandem to form a 1D double-duplex track. In other words, neighboring motifs along DNA helix are arranged with a dihedral angle of ∼0° (Figure 2A). For such a connecting pattern, we designed infinite 1D track self-assembled with four species of motifs (Figure 2B and Supplementary Figure S7). We also designed three finite 1D structures consisting of 14 species of motifs (30 strands of distinct sequences), 10 species of motifs (22 strands of distinct sequences) and 7 species of motifs (16 strands of distinct sequences) respectively (Figure 2C and Supplementary Figure S8).

Figure 2.

Double-C-shaped motifs with 16-nt sticky ends and the resulted nanostructures. (A) Schematics of matching motifs. Panels from left to right: individual motifs; two matching motifs; two matching motifs in simplified strand diagram; cross section view. (B) Infinite structure. Left: structure diagram with dashed box highlighting a repeating unit; right: AFM image (insect shows a magnified view). (C) Finite structures. From left to right: 2H × 49T, 2H × 34T and 2H × 24T tracks. Structure diagrams (left) and the corresponding AFM images (right) are shown as pairs. Scale bars: 100 nm.

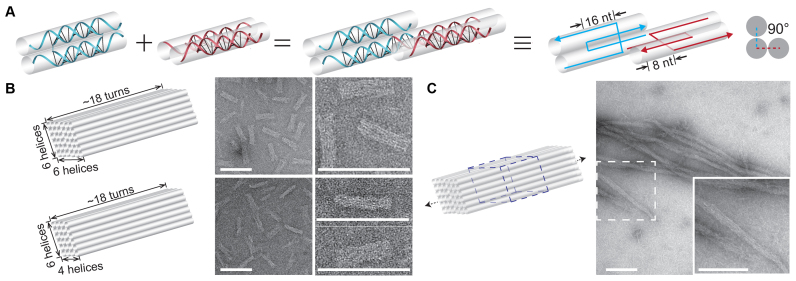
In the other new connecting pattern, the sticky ends were set to be 8 nt. Two matching motifs pair up to form a dihedral angle of 90° via association of the 8-nt sticky ends (Figure 3A). A motif must adopt one of two classes of orientations, horizontal or vertical and the two classes are arranged alternatingly along the helix axes. Under such a scheme, we designed a finite 3D cuboid of 6 helices by 6 helices bundled and each helix measures ∼18 helical turns (6H × 6H × 18T; Figure 3B and Supplementary Figure S11). It consists of 168 species of motifs (324 strands of distinct sequences). A smaller 4H × 6H × 18T cuboid (Figure 3B and Supplementary Figure S12) was trimmed from the 6H × 6H × 18T one and it consists of 108 species of motifs (216 strands of distinct sequences). We also modified half of the 6H × 6H × 18T cuboid (84 species of motifs or 168 strands) as a repeating unit to grow a 1D crystal with a 6H × 6H cross-section (Figure 3C and Supplementary Figure S13).

Figure 3.

Double-C-shaped motifs with 8-nt sticky ends and the resulted nanostructures. (A) Schematics of matching motifs. Panels from left to right: individual motifs; two matching motifs; two matching motifs in simplified strand diagram; cross section view. (B) Finite structures. Top: 6H × 6H × 18T cuboid; bottom: 4H × 6H × 18T cuboid. Structure diagrams (left) and the corresponding transmission electron microscopy (TEM) images (right) are shown as pairs. (C) Infinite structure. Left: structure diagram with dashed box highlighting a repeating unit; right: TEM image (insect shows a magnified view). Scale bars: 100 nm.

To further expand the design space, we modified the length of rigidity core between crossovers to change the dihedral angle between the neighboring component helices within the motif. The original 16-nt rigidity core can be translated ∼180° dihedral angle between the two component helices. When the length of rigidity core is modified to 13 nt, the dihedral angle of between adjacent helices becomes ∼90°. As a consequence, the quadruple-C-shaped motif is designed to have four helices instead of two (Figure 4A). Likewise, a 12-nt rigidity core corresponds to ∼120° dihedral angle and six component helices for the hextuple-C-shaped motif (Figure 4B). Infinite 4-helix or 6-helix rod was designed to self-assemble with motifs (single species of motif) lining up repetitively in tandem (Figure 4C and E; Supplementary Figures S15 and 18). Similarly, two finite 4-helix rods (4H × 32T and 4H × 20T) consisting of 16 species of motifs (64 strands) and 10 species of motifs (40 strands) respectively, and two finite 6-helix rods (6H × 30T and 6H × 16T) with 15 species of motifs (90 strands) and 8 species of motifs (48 strands) respectively, were constructed (Figure 4D and F; Supplementary Figures S16, 17, 19 and 20).

Figure 4.

Quadruple-C-shaped/hextuple-C-shaped motifs and the resulted nanostructures. Schematics of matching motifs in (A) quadruple-C-shaped and (B) hextuple-C-shaped. Panels from left to right: individual motifs; two matching motifs; two matching motifs in simplified strand diagram; cross section view. Infinite structures from (C) quadruple-C-shaped and (E) hextuple-C-shaped motifs. Left: structure diagram with dashed box highlighting a repeating unit; right: TEM image (insect shows a magnified view). Finite structures from (D) quadruple-C-shaped (4H × 32T on top and 4H × 20T at bottom) and (F) hextuple-C-shaped motifs (6H × 30T on top and 6H × 16T at bottom). Structure diagrams (left) and the corresponding TEM images (right) are shown as pairs. Scale bars: 100 nm.

DISCUSSION

Sticky end designs of 5 and 16 nt share the same connecting pattern since two lengths result in similar dihedral angle between matching motifs. We have also tried motifs with 5-nt sticky ends, but such a weak inter-motif association was not sufficient to hold the entire structure together (Supplementary Figure S6), especially for finite one (results not shown).

We noticed that the 24H × 25T rectangle structure was prone to breaking after purification process or sample deposition on surface. Similar fragility was also observed for other addressable structures from LEGO approach (22,26). It could be mitigated by structural enforcement treatments such as enzymatic and chemical ligation (26,29).

This is the first study to systematically build 1D, 2D and 3D structures using multi-stranded motifs and it is also the first time for 3D structures to be constructed with multi-stranded motifs. The results in this study further validate the long held belief in the field that LEGO approach with classic multi-stranded motifs are capable of self-assembly into complex 1D, 2D and 3D structures. The similar design principles from single-stranded tiles/bricks and multi-stranded motifs can be applied to the motifs in this study perfectly to form complex structures (22,25,30–34). It is also worth noting that the yield of the 6H × 6H × 18T cuboid is higher than similar structures with DNA bricks (25). This study shows that the hierarchical assembly from multi-stranded motifs can simplify the thermodynamic landscape for the self-assembly process because of the significantly fewer species of building blocks. The multi-stranded motifs themselves have geometrically adjusted to the best fit during the motif forming process, therefore, the overall structures (especially the 3D structures) from multi-stranded motifs, would have fewer kinetic traps than those from single-stranded tiles/bricks.

LEGO approach has already been successfully implemented in single-stranded tiles/bricks and some multi-stranded motifs (e.g. DX motifs). Other motifs from the rich collection of structural DNA nanotechnology will be the natural extension of such an approach in future prospects. Moreover, the self-assembly principles distilled from DNA nanotechnology can also be applied to other microscopic objects and even macroscopic objects when they are engineered to mimic the programmable and collective binding of DNA molecules.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Natural Science Foundation of China [31570860] (to B.W.); Thousand Talents Program Young Investigator Award; Tsinghua University-Peking University Joint Center for Life Sciences startup fund (to B.W.); University Grants Council of the Hong Kong Government Earmarked Grant [16302415] (to Y.M. and B.W.); Tongji University China 985 Grant (to Y.M.). Funding for open access charge: National Natural Science Foundation of China [31570860].

Conflict of interest statement. A provisional patent based on the current work is pending.