A prior-based integrative framework for functional transcriptional regulatory network inference

Abstract

Transcriptional regulatory networks specify regulatory proteins controlling the context-specific expression levels of genes. Inference of genome-wide regulatory networks is central to understanding gene regulation, but remains an open challenge. Expression-based network inference is among the most popular methods to infer regulatory networks, however, networks inferred from such methods have low overlap with experimentally derived (e.g. ChIP-chip and transcription factor (TF) knockouts) networks. Currently we have a limited understanding of this discrepancy. To address this gap, we first develop a regulatory network inference algorithm, based on probabilistic graphical models, to integrate expression with auxiliary datasets supporting a regulatory edge. Second, we comprehensively analyze our and other state-of-the-art methods on different expression perturbation datasets. Networks inferred by integrating sequence-specific motifs with expression have substantially greater agreement with experimentally derived networks, while remaining more predictive of expression than motif-based networks. Our analysis suggests natural genetic variation as the most informative perturbation for network inference, and, identifies core TFs whose targets are predictable from expression. Multiple reasons make the identification of targets of other TFs difficult, including network architecture and insufficient variation of TF mRNA level. Finally, we demonstrate the utility of our inference algorithm to infer stress-specific regulatory networks and for regulator prioritization.

INTRODUCTION

Transcriptional regulatory networks specify the molecular regulators (such as transcription factor (TF) proteins and signaling proteins) of target gene expression, and are important for specifying gene expression patterns in diverse dynamic processes such as development, stress response and disease. Regulatory networks have two components: structure and parameters (1). The structure specifies which regulators regulate which genes, and the network parameters specify how combinations of TFs and signaling proteins functionally regulate the expression of a gene. In recent years, there has been significant progress in revealing the structure of regulatory networks (2–4); however, our understanding of network parameters and how genome-wide regulatory networks drive overall system behavior is limited even in well-studied systems such as yeast.

Regulatory network reconstruction using either experimental or computational methods has been challenging for a number of reasons. First, any single experimental technology is not sufficient to reveal the circuitry. For example, while ChIP-chip and ChIP-seq assays are used to reveal the structure of the network, many events might be associated with non-functional binding and discriminating functional and non-functional binding is in itself non-trivial (5). In contrast, regulatory connections inferred by genetically perturbing a TF are not able to discriminate between direct and indirect effects. Second, regulatory networks tend to be context-specific; that is, the set of regulatory connections that are active may vary significantly between conditions (6). Experimentally generating such datasets for all conditions and time points is not feasible, and therefore a limited number of TFs known to be associated with specific conditions have been examined (e.g. MSN2/4 in various stresses (1,7), HOG1, SKO1 for osmotic stress (1)). Computational network inference methods that use genome-wide expression profiling for a set of conditions have served as scalable approaches that are complementary to experimentally defining networks because expression datasets are commonly available across multiple species and contexts. Furthermore, expression-based network reconstruction methods can be used to predict expression levels of genes in new conditions or in response to a perturbation. However, when applied to infer eukaryotic regulatory network structure, the success of different methods has been modest (8), although the reasons for this low performance are not completely clear. In particular, poor performance of these methods could be because of a number of reasons, such as, the inability of expression alone to discriminate between causal and correlational edges, lack of variation in the expression level of regulators, post-transcriptional and translational control of gene expression.

To address these challenges, we make two contributions. First, we developed a regulatory network inference algorithm to integrate diverse regulatory genomics datasets in order to reconstruct a transcriptional regulatory network. Our approach is based on a probabilistic graphical model (PGM)-based representation of regulatory networks (9) and extends our previously published algorithm (Roy et al. (10)). Our work is motivated by the success of prior-based methods for network inference (11–14), however unlike these existing approaches our approach to integrating diverse datasets uses structure priors (15–17), which to our knowledge have not been applied to genome-scale networks with thousands of genes. Our approach can be used to integrate different numbers of prior data sources and at its minimum requires expression and sequence motifs, which are easily available for most species and conditions. Second, we performed an extensive comparison of networks inferred using different classes of methods on different types of large scale perturbation studies to identify important determinants of predictive performance. We use several metrics to evaluate the quality of the inferred networks based on the structure of the network, the ability of the network to predict expression, as well as, the ability to recover evolutionarily conserved co-expression patterns.

We apply our method and metrics to study transcriptional regulatory networks as well as to gain insight into the context-specific regulation for the yeast Saccharomyces cerevisiae. Yeast serves as a good model system for our study because a significant portion of its regulatory network has been interrogated using different complementary experimental methods including ChIP-chip (18,19), TF knockout (20,21) and protein binding arrays (22). In addition, yeast has large collections of gene expression profiles measured under different types of genetic and environmental perturbations including single gene knockouts, natural genetic variation and environmental stresses. We compare different classes of network reconstruction methods on different types of large scale expression datasets. These methods range from those that assume linear or non-linear relationships among regulators and target expression profiles, as well as those that have used priors to improve network inference but using approaches different from ours. We find that adding sequence motifs as priors greatly improves the quality of the structure of inferred regulatory networks and the network can predict the effect of knocking out a TF. An important outcome of our analysis is insight into the type of perturbation that is most useful for inferring these networks; we suggest that natural genetic variation is the most useful type of perturbation in yeast and likely in human. We find that all methods are able to recover some TF target relationships, however, there are some TFs that are inherently unpredictable by any method. Finally, we use our method to create an expansive regulatory network [for yeast] that integrates motif, ChIP and knockouts and to infer stress-specific regulatory networks. We use the network's ability to predict expression to prioritize regulators in a condition-specific manner and identify known regulators as well as novel regulators, including RNA binding proteins, that have not been implicated in these stresses.

MATERIALS AND METHODS

Probabilistic graphical model-based integrative approach to regulatory network inference

A regulatory network is defined as a network that describes regulatory relationships between TFs and target genes, and a regulatory edge indicates that the expression levels of a target gene changes as a function of activity of its regulator (1). To represent such networks we use PGMs, which are powerful models for representing and modeling the structure and function of regulatory networks (9,23). In a PGM, there are two main components: a graph structure , and a set of parameters Θ. The graph structure describes the statistical dependencies among the nodes, each node representing a regulator or a target gene. The parameters describe how the regulator set of a gene specifies the target gene expression level. PGMs are a very general class of mathematical models; the specific model we use is called a dependency network (24). In such networks, a regulatory network is constructed by solving a set of per-gene regression problems, where the expression of a gene is predicted as a function of its upstream regulators. Our integrative network reconstruction method, MERLIN+Prior, is based on a Bayesian framework of learning PGMs and extends our previous purely expression-based network inference method, MERLIN (10), to integrate additional non-expression datasets. We first briefly describe the MERLIN approach and describe our extensions to integrate additional datasets as model priors.

The MERLIN+Prior network inference algorithm

The overall intuition of our approach is that there can be a large number of regulators that can potentially explain the expression of a gene. However, one can use additional non-expression datasets to provide support for a regulatory interaction. By incorporating these additional datasets, we aim to identify a regulatory interaction between a regulator and a target gene that might not be evident based on expression alone. The MERLIN algorithm is based on a Bayesian framework of learning a PGM representing the regulatory network and uses a graph prior distribution to encourage learning a modular regulatory network. In this framework, we need to find the graph structure, and parameters Θ that can best explain the given dataset 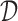, , 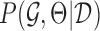which by Bayes rule is proportional to the data likelihood 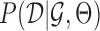, prior distribution of the parameters, 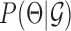and a prior distribution over the graph :

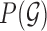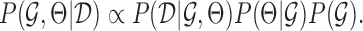In MERLIN, we defined a prior distribution over a graph as, 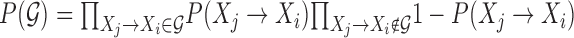, where P(X_j → X_i) is the probability of an edge being present in the prior graph.

To integrate different types of datasets we extend the MERLIN edge prior as follows:

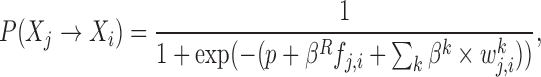where p denotes the sparsity parameter, β^R indicates the modularity parameter and f_{j, i} specifies the tendency of a regulator X_j to regulate other genes in X_i's modul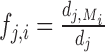e, where 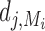is the number of targets of X_j in X_i's module and d_j is total number of targets of X_j. β^k control the importance of the k^th prior network, and 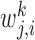quantifies our confidence in the edge X_j → X_i in the k^th prior network. Increasing β^k and 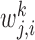increase the prior probability to add the edge X_j → X_i to the network. The different types of regulatory evidences that can be integrated in our approach include sequence-specific motif instances within the promoter of a target gene, presence of a TF binding on the target gene, as well as measured effect on expression of genes after TF knockout or knockdown (Figure 1). The version of the above prior that uses the module prior is called MERLIN+Prior. In addition we also tested another version of this approach that does not use the module prior (β^R = 0) called the PGG+Prior.

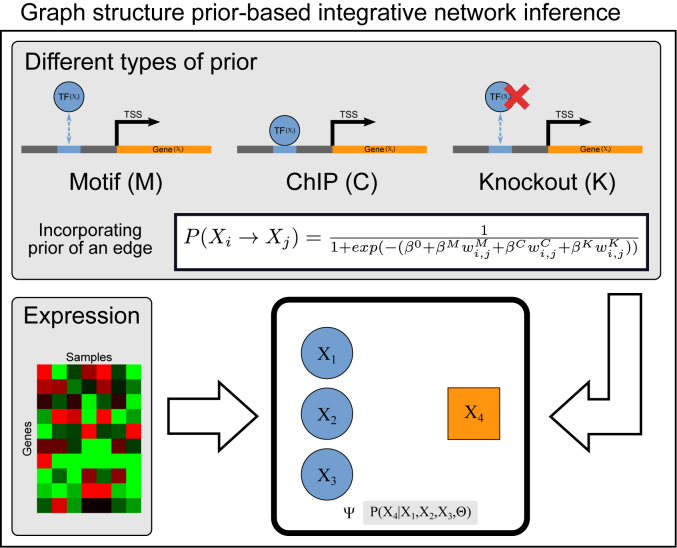
Figure 1.

Overview of our approach to integrate diverse regulatory genomic datasets as structure priors. X_i and X_j denote a regulator (such as a transcription factor) and a target gene respectively. For each candidate edge X_i → X_j, different sources of prior networks can be used. The figure shows three different types of prior networks: ChIP, Motif and Knockout. Each prior network can be weighted, for example 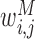denotes the weight of the regulatory edge in the motif network. Different prior networks are combined to specify the prior probability of an edge using a single logistic function with prior parameters β⁰, β^M, β^K, β^C. β⁰ controls for network sparsity, while the other parameters specify importance of the prior networks. The regulatory network is itself represented as a dependency network learned by estimating a set of conditional probability distributions. In the example, the conditional distribution of the target gene X₄ is specified by three regulators, X₁, X₂, X₃. Ψ denotes a particular form of conditional probability distributions that is parameterized by Θ.

The MERLIN+Prior network inference algorithm is similar to the MERLIN algorithm and iterates between two steps: (i) update the graph structure given the current module assignment, (ii) update the module assignments given the current graph structure (10). In the first step, the algorithm performs a greedy score-based search to add the edge that improves the overall score of the network. In the second step, the algorithm uses the regulatory program inferred in previous step and similarity in expression profiles to update the module assignments. The score of an edge is defined by the increase in the pseudo likelihood of the model on adding the edge together with the change in the model prior (including the current module assignments and additional priors to support the edge). This requires us to define the distribution over the parameters, 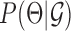and the data likelihood, 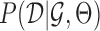. To maximize 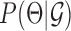we set Θ to its maximum likelihood setting. The data likelihood, 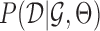is

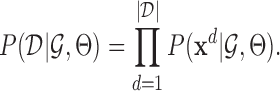Here, 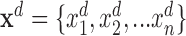is the joint assignment of expression values of all the n genes in d^th sample in the dataset, 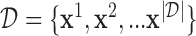. In a dependency network, which is the type of PGM we use, the likelihood of the joint assignment 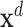over random variables is approximated by the pseudo likelihood (24), which decomposes as a product over individual conditional probability distributions for each random variable X_i, given its parents :

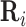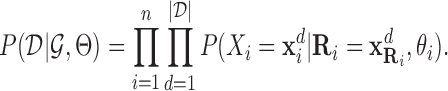The term 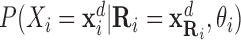is estimated as a multivariate conditional Gaussian distribution. The algorithm starts with a given initial module assignment (as input) and iterates between these two steps until convergence (the delta likelihood of the model becomes lower than a threshold) or after a fixed number of iterations. Further details of how the modules are defined based on co-expression and co-regulation and how it is iteratively updated are described in (10).

Selecting the prior parameters for MERLIN and PGG

To set the prior parameter when using one prior network (Motif), we tested different values of the prior parameter β^Motif ∈ {0.5, 1, 2, 3, 4, 5} for PGG+Prior and selected the parameter that produced highest AUPR (β^Motif = 5). Similarly we tested values of β^Motif ∈ {3, 4, 5, 6, 7} for MERLIN+Prior and found (β^Motif = 5) to give the best AUPR. Other MERLIN-specific parameters including sparsity, modularity and clustering cut-off parameters were set to default configurations of −5, 4 and 0.6, respectively, which were selected by applying MERLIN (without prior) to a simulated network in a cross validation framework, as previously described in (10). A similar strategy was used for other methods with multiple input configurations as described in the method descriptions below.

When using multiple prior networks (ChIP, Motif and Knockout), we trained a binary classifier, to estimate the relative importance of different prior networks. The classifier was trained to predict if a TF-target pair interacts or not, and the feature vector of the pair consisted of confidence of the edge in each of the prior networks (and 0 if the edge was not observed in that prior network). We defined the positive set as the intersection of edges in the MacIsaac network and edges in which the target's expression was significantly altered after TF knockout from Kemmeren et al. (25). This positive set constitutes 1,026 edges (∼27%) of the MacIsaac gold-standard. We defined a negative set based on the complement of the positive set with the same size of random edges. We enforced an additional constraint that if there are kⁱ edges in the positive set that are in the i^th prior network, we should have the same number of edges from the i^th prior network in the negative set. This was important because if the number of elements without a feature (with value of 0) was higher in negative set, the classifier would only need to distinguish between 0 and non zero to separate elements in positive and negative set and we will observe an erroneous high accuracy. By having the same ratio of missing features in the positive and negative sets, we ensured that the classifier will not be biased toward presence or absence of a feature. We used lassoglm function in Matlab and trained a classifier (in a 10-fold cross validation scheme) to predict the label of an edge based on its weight in the given prior networks. We used the regression coefficients of this model to set the relative importance of different prior networks (β^Motif = 2, β^ChIP = 5, β^Knockout = 3.5). We compared this setting with an alternative setting where all the prior networks had the same importance (β^Motif = β^ChIP = β^Knockout = 5) and observed that even though both configurations perform better than the model inferred using only Motif prior network, the model with different importance values for different prior networks perform better. Because we used part of the MacIsaac network for learning the hyper parameters, there is danger of overestimating the performance on the MacIsaac gold standard. However, we find that the majority of true positive edges are from the portion of gold standard that was not included in this training set (Supplementary Data) suggesting that the prior parameter training is not resulting in over fitting.

Prior networks

Our MERLIN+Prior approach is flexible and can incorporate different types of prior networks. Here we considered three types of prior networks, Motif, ChIP and Knockout. For the motif prior network, we used position-specific matrices from Gordân et al. (22) and position-specific matrices from YeTFaSCo (26). We scanned yeast promoters defined by 1000 bp upstream of the first ATG of a gene using the TestMotif program (27). For the ChIP-chip prior network, we used two ChIP-chip networks (18,28). We also had a prior network based on genetic knockouts in YPD (20,29). In each case we created the edge weights using a percentile rank (when ranking edges based on their P-value). In the case of motif and ChIP-chip, where we had two prior networks each, we took the union of the two networks and summed the edge weights for common edges. We expect the gold standard and prior edges to overlap, however, the prior edge weights give a noisy observation of the gold standard edge. The details of these networks and their overlap with the gold standard networks are described in Table 1.

Table 1. Statistics of different prior networks used.

Network	#edges	#regulators	#targets	#overlap with MacIsaac (%)	#overlap with YEASTRACT type ≥ 2 (%)	#overlap with YEASTRACT count ≥ 3 (%)	#overlap with Hu (%)
Motif	187 079	197	5506	1856 (49%)	1844 (44%)	1837 (48%)	1457 (14%)
ChIP	229 936	318	5557	2281 (60%)	1758 (42%)	2112 (55%)	1237 (12%)
Knockout	96 809	262	5543	564 (15%)	833 (20%)	800 (21%)	8756 (85%)

The first three columns show the number of edges, number of regulators and the number of target genes. The last three columns show the number of edges from the prior networks overlapping with each of the gold standard networks. In parentheses are shown the percentage of the gold standard edges that number corresponds to.

Description of existing network inference methods compared

We used four freely available expression-based network inference methods to compare to our method: (i) GENIE3, (ii) LARS-EN, (iii) Inferelator, (iv) TIGRESS.

GENIE3

GENIE3 is a dependency network learning algorithm which uses tree-based ensembles and was one of the best performers in the DREAM network inference challenge (8). We downloaded MATLAB implementation of GENIE3 (30) from the software's webpage (http://homepages.inf.ed.ac.uk/vhuynht/software.html). GENIE3 has two main parameters: the number of trees, and the number of features to be used at each split. For each of these settings we tested multiple configurations: number of trees, nb_trees ∈ {100, 500, 1000,1500, 2000, 10 000} and number of features examined at each tree split, K ∈ {sqrt,all}, where sqrt will use the square root of the number of regulators, while all will use all the regulators. We selected the one that produced highest AUPR on MacIsaac network (nb_trees = 10 000 and K = sqrt). We extracted the top 1 million edges, and used the reported edge confidences to create precision-recall curves.

LARS-EN

LARS-EN is based on elastic net regression that combines both L1 and L2 regularization for variable selection method and was shown to perform better than LASSO in many cases while producing a sparse model (31). We used MATLAB implementation of LARS-EN from Imm3897 package downloaded from http://www2.imm.dtu.dk/pubdb/views/publication_details.php?id=3897 in a stability selection procedure (see section ‘Stability selection scheme for learning networks’). In each run of the LARS-EN, for each target gene, we used the expression profile of that gene as response and the expression profile of all candidate regulators as regression variables. If a target gene was one of the candidate regulators, we removed that gene from the regression variable matrix. We tested L2 regularization parameter, lambda2, ∈ {1E-6, 1E-5, 1E-4, 1E-3, 1E-2, 1E-1}, while allowing cross-validation to select the L1 penalty. We used the LARS-EN inbuilt cross validation routine with K=5 fold cross validation, for each value of lambda2 tested. Changing L2 did not significantly change the performance of the inferred networks (AUPR was the same up to 4^th decimal digit, we used lambda2 = 1E-6).

Inferelator

Inferelator is a network inference method that uses ordinary differential equations (ODEs) to model the dynamic nature of the regulatory networks and was recently extended to incorporate biological prior knowledge (11,32). We used the unweighted version of the motif network as the prior network for Inferelator. The latest implementation of the Inferelator package was provided by the Bonneau lab (23 October 2014). The Inferelator package has two methods for incorporating priors: modified elastic net (MEN) and bayesian best subset regression (BBSR). We tested both MEN and BBSR methods with the recommended prior weight settings (both high and low) and used MEN with prior weight = 0.01 (high setting) as this gave the best AUPR. We set the degradation rate (tau) to 20.1 based on literature (33).

TIGRESS

TIGRESS (34) is a network inference method that uses least angle regression (LARS) in a stability selection framework, and was ranked among the best performers in the DREAM5 network inference challenge (8). We downloaded the MATLAB implementation of the algorithm from http://cbio.ensmp.fr/∼ahaury/svn/dream5/html/index.html. TIGRESS parameter settings are R: number of resamplings that should be used to run stability selection (default = 1000); α: controls the randomization level and is a scalar 0 < α ≤ 1, where if α=1, no randomization is used (default = 0.2); L: number of LARS steps that should be considered (default = 5). We tested multiple different parameter settings: R = {200, 500, 1000}, L = {3, 5, 10, 15, 20, 25, 30} and α = {0.1, 0.2, 0.3, 0.5} and selected the one that produced highest AUPR on the MacIsaac network (number of resamplings, R = 1000, α = 0.3 and L = 30).

Stability selection scheme for learning networks

We ran MERLIN and PGG (with and without prior), and LARS-EN algorithms within a stability selection framework (35,36) to estimate edge confidence. Stability selection is a subsampling approach to estimate confidence in the model structure in model selection problems including the structure learning and clustering. The Inferelator and GENIE3 approaches have their own built-in subsampling frameworks that output an edge confidence. Existing work in expression-based network inference (34), and also our own experiments (Supplementary Data), have shown that stability selection can greatly improve the quality of the inferred network. In our stability selection scheme, for each dataset we produced 100 random subsets with the same number of genes and randomly selected a subset of columns equal to half the size of the original dataset. We learned the model on each subset and merged the resulting networks. In the merged network, the weight of each edge corresponds to the frequency of observing that edge in the 100 learned models. Running these methods on different subsamples, datasets, and with different parameter settings is time intensive; to exploit the parallel nature of this approach, we used the resources of the UW-Madison Center For High Throughput Computing (CHTC, http://chtc.cs.wisc.edu).

Description of expression datasets

Yeast expression datasets

We used different yeast expression datasets for different computational experiments (Table 2). Briefly, there were four computational tasks we addressed in this paper: (i) regulatory network inference, (ii) validation of inferred networks based on predictive power, (iii) validation of inferred networks based on conserved co-expression, (iv) inference of condition-specific networks. For inference of the regulatory networks using our existing inference algorithms, we prepared three different types of expression datasets (Table 2): (i) natural variation (Nat Var), (ii) knock-out experiments (Knockout), (iii) response to stress (StressResp). For natural variation dataset, we used combination of expression datasets from Brem et al. (37), Smith et al. (38) and Zhu et al. (39). For the Knockout dataset, we combined the expression datasets from Chua et al. (21) and Hu et al. (20). For Stress response dataset, we used expression data from Gasch et al. (40). When combining multiple datasets for one type of perturbation (natural variation or knockout) we only used the genes that were present in the intersection of those datasets after preprocessing. For preprocessing, in each dataset, for each column we subtracted the mean and divided by the standard deviation. If more than 20% of the measurements of a column were missing, we removed that column. For each gene, if more than 50% of its measurements were missing, we removed that row from the dataset, otherwise we filled the missing values of a gene with the average expression value of that gene. If a gene was repeated multiple times, we collapsed the repeated rows by taking their average. Biological replicates of samples were collapsed by taking their average.

Table 2. Number of genes, regulators and samples in each expression dataset.

Dataset	#genes	#Regulators	#experiments	Used in
Natural variation (Nat. Var)	5661	537	377	Inference (Figure 2)
Knockout	5978	536	539	Inference (Figure 2)
Stress response (StressResp)	6138	536	173	Inference (Figure 2)
Hold out data	5478	533	2605	Validation (predictable targets, Figure 2)
Heat stress	6137	536	24	Condition specific inference (Figure 7)
Osmotic stress	4711	465	23	Condition specific inference (Figure 7)
Evol. cons. (S. cerevisiae)	5304	529	30	Validation (evolutionary conservation, Figure S6)

Rows correspond to different datasets and columns show different statistics.

For assessing the predictive power of different inferred networks (inferred using any of the three above datasets), we used the expression dataset from Kemmeren et al. (25). This dataset served as a ‘hold-out’ set as it was not used for learning any of the networks. For the experiments on evolutionary conserved edges, we used expression datasets of short time series under salt and heat shock in six different species of yeast (Candida albicans, Candida glabrata, Kluyveromyces lactis, Saccharomyces castellii, Schizosaccharomyces pombe and Saccharomyces cerevisiae) from Wapinski et al. (41), Roy et al. (42) and Thompson et al. (43). Finally, for learning condition-specific regulatory experiments, in addition to datasets from Gasch et al. (40) we used additional expression datasets of yeast under osmotic stress from Ni et al. (44), Wapinski et al. (41), Lee et al. (45) and Chasman et al. (46).

Human expression datasets

We used multiple gene expression datasets from human lymphoblastoid cell lines (LCL) to represent two types of perturbation: stress response and natural variation (Supplementary Data). Although there is regulator perturbation data for multiple TFs from Cusanovich et al. (47), we used this to derive our gold standard regulatory network (see below) and therefore could not use it for network inference. LCLs, including the GM12878 cell line, are among the most well-studied cell lines and have similar types of perturbation datasets as in yeast. For natural variation type of data, we used the expression dataset from Geuvadis (48) (EBI ArrayExpress accession E-GEUV-3) and Niu et al. (49) (Gene expression Omnibus (GEO) accession GSE23120). For stress response, we searched in GEO for studies using LCLs and downloaded several datasets. These include a dataset from Benton et al. (50) (GSE20320), Junaid et al. (51) (GSE29141), Forrester et al. (52) (GSE41840), Luca et al. (53) (GSE44248), Su et al. (54) (GSE51709), Glover et al. (55) (GSE71521) and two other datasets (GSE22639, GSE51454). Each sample was first normalized by subtracting the mean (RNA-seq datasets were first log transformed) followed by collapsing any replicates. We combined all stress response datasets into one dataset (201 samples in total, after collapsing replicates), and quantile normalized the data (quantilenorm function in MATLAB). We selected 4084 genes that were observed in all the datasets.

Evaluation of different network inference methods

We used multiple strategies to evaluate the structure and the function of networks inferred from different types of methods and datasets.

Gold standard regulatory networks

For yeast we had three gold standard standards, one from MacIsaac et al. (56), and two from YEASTRACT (57). The MacIsaac network is the most well-known gold standard for yeast and was used for a large comparative study for many purely expression-based network inference algorithms (8). The YEASTRACT is a curated database of experimentally validated (and potential) regulatory interactions between TFs and target genes from different types of experiment (e.g. direct like ChIP-chip or indirect like TF overexpression or knockout). One of the YEASTRACT networks, referred here as type ≥2, included edges found in two or more different types of experimental assays. The second YEASTRACT network, referred here as count ≥3, included edges that were detected in three or more experiments (regardless of the assay type). The statistics of these networks are given in Table 3. For our experiments of different types of priors and gold standards, we used a fourth gold standard from Hu et al. (20), which was derived from knockouts of TFs. For human, our gold standard network was a functional regulatory network consisting of the intersection of functional edges and binding edges defined by Cusanovich et al (47). After intersecting the TFs and target genes with those that had expression, our gold standard had 6,389 edges connecting 17 TFs and 2755 target genes.

Table 3. Statistics of different gold standard networks used, the number of edges, the number of regulators and the number of target genes.

Network	#edges	#regulators	#targets
MacIsaac	3802	114	1883
YEASTRACT (type ≥ 2)	4219	119	2167
YEASTRACT (count ≥ 3)	3818	119	2067
Hu	10 101	264	2334

Area Under the Precision-Recall (AUPR) and Receiver operating characteristic (AUROC) curves

The AUPR and AUROC are established metrics to assess the similarity of the inferred network to a known gold standard. To compute the precision-recall curve we sorted the edges by decreasing confidence. For precision, we computed the percentage of the top k of N edges that were in the gold standard network, where N is the maximum number of edges in the inferred network. Similarly, for recall, we computed the percentage of the edges in the gold standard network that are in the top k edges of the inferred network. To produce the precision and recall and receiver operating characteristic curves and calculate the area under the curves, we used the AUCCalculator Java package (58). AUPRs and AUROCs were computed for all three yeast gold standard networks using networks inferred by applying the different network reconstruction methods on three expression datasets (Nat. Var, StressResp, Knockout, Table 2).

Assessing the effect of the prior networks on the inferred networks

To assess the impact of the prior network on the inferred networks including overestimation of performance, we performed two different analyses: first, we split the edges of the gold standard networks that were in the prior network and those that were not (See Table 1 for the number of edges in gold standards and prior networks). Next we computed the AUPR on these two parts of the gold standard using networks inferred on the Nat Var dataset using both methods that used prior or did not use prior (Supplementary Data). This analysis shows that on part of the gold standard that does not have prior support, the prior-based methods perform only slightly worse than methods that do not use prior support. Second, we examined different types of prior and gold standard networks. This is important because, in practice, we expect that the prior is a weighted network that has some overlap in edges with the gold standard, otherwise, the prior would not be helpful. However, depending upon the source of the network, we might observe better or worse performance on a given gold standard network. We used ChIP, motif and knockout networks separately as a prior for the MERLIN-P algorithm, and compared these inferred networks to the MacIsaac gold standard (56) and a knockout-based gold standard from Hu et al. (20). We note that the Motif and ChIP priors are independent of the knockout gold standard, and the knockout prior is independent of the MacIsaac gold standard (Supplementary Data). This analysis showed that the prior-based framework remains beneficial compared to non-prior based network inference methods even when the prior and gold standard are obtained from different experimental approaches.

Identifying predictable transcription factors

We defined predictable TFs based on the MacIsaac gold standard regulatory network. For each TF in the MacIsaac network, we computed the significance in overlap of the targets of this TF with the predicted targets of this TF in a purely expression or expression+prior based network. A TF was considered predictable if the overlap was significant based on a corrected hypergeometric test P-value < 0.05 with the Benjamini-Hochberg correction for multiple hypothesis testing.

Calculating the predictive power of networks

For a given inferred network we obtain the regulators for each target gene in the top 30K edges of the network. We construct a linear model for each target gene where the expression of the target gene is a linear function of the expression of its regulators. We estimate parameters of this model on the dataset that was used to infer the network, and then test the model on an unseen dataset (in this case expression dataset from Kemmeren et al. (25)). As a measure of predictive power, we calculate the Pearson correlation between the predicted expression profile and actual expression profile of the target gene. To assess the significance of the observed correlation values, we produce 100 random networks. In generating a random network, we satisfy two conditions: (i) the in-degree of the target gene in the random and actual network should be the same, and (ii) the regulator set of target gene in the random and actual network should not have any overlap. For each target gene we compute the correlation of predicted and observed expression profiles in all the random networks. We calculate the significance of predicting the target gene's expression level by counting the number of times the correlation in a random network was higher than the correlation in the actual network. Finally, for a given network, we calculate the percentage of target genes that was significantly predicted better than random (≤0.05).

Fraction of functional edges

We obtained the knockout dataset from Kemmeren et al. (25), which used LIMMA (59) to estimate the differentially expressed genes under the deletion of another gene. For a given network, we calculated the fraction of functional edges as the percentage of the top 30K edges that were associated with a significant change (p-value ≤ 0.05) in expression of the target gene in the deletion strain of the regulator gene.

Evolutionary conservation of edges

We further evaluated the yeast inferred networks based on evolutionary conservation of correlation values. Edges in an inferred network, defined by the top 30K edges, were considered to have evolutionarily conserved signatures if the orthologous TF-target edge in another species were more co-expressed than orthologous non TF-target pairs (not in the top 30K edges), based on a KS-test (P-value < 0.05). We obtained the expression dataset from six different yeast species (C. albicans, C. glabrata, K. lactis, S. castellii, S. pombe and S. cerevisiae) measured under various stress conditions (41–43). We first compared the distributions in S. cerevisiae, the species for which we specifically inferred networks. Next for each of the five remaining species, we mapped the edges from the inferred network to the second species using one-to-one orthology from Wapinski et al. (60). Briefly, for a given edge, we mapped the TF and target gene from S. cerevisiae to the corresponding orthologous gene in the second species (only if this mapping was 1-to-1). This resulted in 3880–22 728 edges, with S. pombe having the fewest edges and S. castellii having the largest number of edges. We created the foreground distribution using the correlation between the regulator and target gene in the mappable edges and the background as all possible pairs of regulators and targets spanning these edges but excluding the TF-target inferred pairs.

Inference of condition-specific regulatory networks and regulator prioritization

As a second application of our prior-based integrative network learning approach, we inferred condition-specific regulatory networks. To infer the condition-specific networks for heat and osmotic stress datasets, we created 20 subsamples with 14 measurements for each dataset. We ran MERLIN+Prior on each subsample separately using as prior the top 30K edges of our expansive regulatory network (that is the network inferred on Nat.Var. dataset when using ChIP, Motif and Knockout as prior networks). We set β = 5 for prior importance parameter. We generated a consensus network for each of these stress conditions. The heat shock or osmotic stress response (OSR)-specific network was defined by the set of edges in 3 or more of the 20 sub samples.

Given a learned network on training expression dataset, we rank regulators based on the overall importance of the regulator to accurately predict the expression levels of genes in a given condition. The importance of a regulator is defined by the sum of the importance of all of its outgoing edges, and is therefore a function of its degree as well as the predictive model learned in the training set. For each gene, j, let 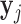be the n × 1 vector of expression values in n different time points or samples associated with a specific condition. We assume the expression of a gene is a linear combination of the expression of its regulators. Let 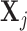denote n × k expression matrix, each column representing the expression levels of one of j's k regulators, and 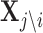represent the expression matrix without the i^th regulator. Let {β₀, β₁, ...β_k} denote the regression coefficients calculated in the training set (Nat.Var for these experiments). The importance of the edge between regulator i and target gene j, is defined by the change in the mean squared error between two linear models:

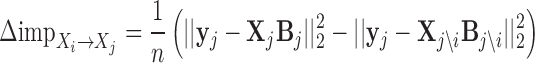A positive value of importance means that removing the edge increases the error of the model, and higher the difference the more important is an edge. If the regulator i's target set is 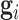, then the importance of i is .

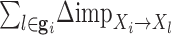RESULTS

Addition of prior greatly improves the inferred network structure; however, methods are comparable for predicting expression

We compared five purely expression-based network inference methods and three prior-based methods that included priors across different types of datasets. The non-prior expression-based network inference methods include GENIE3 (30), LARSEN (31), TIGRESS (34), MERLIN (10) and PGG (Per Gene Greedy network inference which does not incorporate modules, ‘Materials and Methods’ section). Our prior-based methods included PGG+Prior, MERLIN+Prior and Inferelator (11). The difference between PGG+Prior and MERLIN+Prior is that MERLIN+Prior includes a module prior while PGG+Prior does not. In these experiments, we only used the motif prior network for all three prior-based methods because this is the most readily available non-expression dataset for an organism.

We used five evaluation metrics to evaluate the quality of the inferred networks: (i) area under the precision-recall curve (AUPR), (ii) number of predictable TFs, (iii) fraction of target genes for which their expression can be accurately predicted in a test condition, (iv) fraction of functional edges between a TF and target gene inferred from significant change in expression of the target gene if the TF is knocked out, (v) evolutionary conservation of TF-target co-expression. The AUPR measure and the number of predictable TFs evaluated the connectivity structure of the network, whereas the remaining three assessed the parameters or functional aspect of the network. We computed these metrics on networks inferred on three different types of datasets (Table 2): natural genetic variation (Nat Var, (37–39)), large scale regulator knockout followed by genome-wide expression profiling (Knockout, (20,21)) and a large compendia of stress response expression profiles (StressResp, (40)).

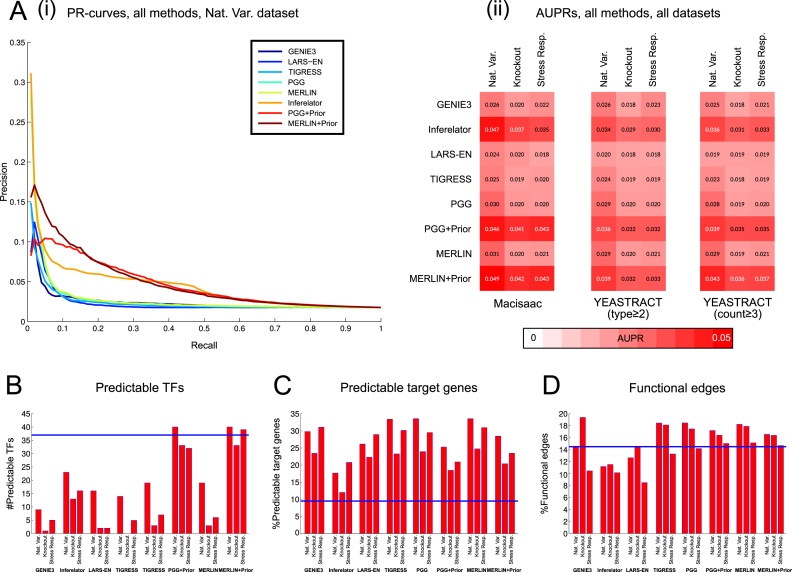
To compute the AUPRs, we used three networks as gold standards. One gold standard was from MacIsaac et al. (56), which was used also by the DREAM network inference challenge that compared a large number of expression-based network inference methods (8). The other two gold standards were from YEASTRACT (57) and included: (i) edges that were found in two or more different types of experimental assays (e.g. ChIP-chip and TF knockout, ‘type ≥2’), (ii) edges that were detected in three or more experiments regardless of the assay type (‘count ≥ 3’). Figure 2A(i) shows the PR curves of networks inferred using the natural variation data. We find that methods that incorporate priors (MERLIN+Prior, PGG+Prior and Inferelator), achieve higher AUPRs compared to methods that do not. Among the different prior-based methods, MERLIN+Prior (which combines sequence-specific motifs and network modularity) is the best performing approach. This high performance for the prior-based methods was observed for other datasets and different gold standard networks (columns in Figure 2A(ii)). Supplementary Data reports the precision of inferred network from different methods on different datasets at several recall points (also available in Supplementary Data). As expected, for prior-based methods, we observed higher precision at the same recall point, compared to purely expression based methods. Although the AUPR is a more precise measure for network reconstruction because of the large number of non-interactions, area under receiver operating characteristic (AUROC) is also often reported for computationally inferred networks (8). We computed AUROC using each of the gold standards and observed significant improvement in methods that incorporate prior (Supplementary Data). The performance of the methods using priors depends both on the gold standard, and, extent of overlap between the prior network and the gold standard. We therefore computed AUPRs for the part of the gold standard with prior and without prior. We find the prior-based integrative framework to perform slightly worse on parts of the network without prior (Supplementary Data). Further, when the prior and gold standard are obtained from different types of experiments, the gold standard can be more accurately predicted with our framework compared to without using prior (Supplementary Data, see Supplementary Data for more details.)

Figure 2.

Evaluation of different prior and non-prior based network inference methods. (A(i)) Precision-Recall curves comparing the networks inferred by applying eight different methods, GENIE3, LARS-EN, TIGRESS, PGG, MERLIN, Inferelator, PGG+Prior and MERLIN+Prior, to the natural variation (Nat. Var) dataset. Methods with prior (Inferelator, MERLIN+Prior, PGG+Prior) used the motif network as prior. Precision and recall values are computed using the MacIsaac ChIP-chip network as the gold standard. (A(ii)) Area under the Precision Recall curve (AUPR) values of these eight methods using three different expression datasets (Nat. Var, Knockout, StressResp) computed on three different gold-standard networks. These gold standard networks include the MacIsaac network from (A(i)) and two variants of the YEASTRACT network. (B) Number of predictable regulators defined by the TFs whose target sets can be inferred well by the inferred networks. The number of predictable regulators are estimated using the eight network inference methods on the three expression datasets. (C) Percentage of predictable target genes defined by the fraction of target genes whose expression can be predicted better than 95% of random networks. (D) Percentage of functional edges (with significant knockout effect) in the inferred networks from the different methods on three expression datasets. Blue line shows the performance of the top 30K edges from the motif network. Analysis in B–D was done using the top 30K edges in each inferred network.

While AUPR is an edge-based measure that assesses how well candidate regulatory edges are ranked by a method, examining other components of the network can provide a more fine-grained assessment of a method. To this end we identified ‘predictable TFs,’ defined as TFs with significant overlap between their targets in the gold standard and the inferred networks. We selected top 30K edges from each inferred network to assess statistical significance based on the hypergeometric test with Benjamini-Hochberg correction for multiple hypothesis testing (‘Materials and Methods’ section). A method with more predictable TFs is considered superior to a method with fewer predictable TFs. As a baseline we used the motif network which we provided as a prior to the methods. We found that motifs alone can recover targets of several TFs, but this is lower than both our methods with prior. Our prior-based methods, PGG+Prior and MERLIN+Prior recovered 40 predictable regulators, while the non-prior based methods recovered targets of 10–20 regulators in Nat.Var, Figure 2B), suggesting that the prior-based methods were more successful in predicting the network structure. Among the non-prior based methods, MERLIN and PGG had the largest number of predictable TFs (Figure 2B). Overall, our comparison based on both AUPR and the number of predictable TFs, which assess the structure of the inferred networks, showed that methods that used motifs as a prior were significantly better than methods without prior. To assess the robustness of this metric to the size of the network, we selected different network sizes and repeated our analysis. We observed similar trends across different network sizes, which suggest this analysis is robust to the number of selected edges (Supplementary Data, Supplementary Data).

Having determined that the ability of a method to infer network structure is significantly improved by integrating motifs, we next evaluated the functional aspect of the inferred networks by examining the ability of the network to predict expression. We did this in two ways. First, we trained a linear model using the network structure inferred by a method using a particular expression dataset and tested it on an unseen holdout dataset (Figure 2C, predictable targets). Second, we asked whether the targets of TFs predicted by the network inference methods exhibited significant change in expression when the TF is perturbed (Figure 2D, functional edges). For both these questions we used a recently generated knockout dataset from Kemmeren et al. (25) that profiled the mRNA expression levels response to 1484 individual gene knockouts as part of a large genetic knockout study in S. cerevisiae. This data was not used for training and served as an independent validation dataset. As for the predictable TF metric, we found consistent results with this metric on networks with different numbers of edges (Supplementary Data, Supplementary Data).

To define the fraction of predictable targets in an inferred network, we used the linear model trained on the original dataset (dataset used to infer the network) and predicted the expression of all the target genes (as a function of expression of their regulators) in the new holdout dataset (‘Materials and Methods’ section). All methods infer networks that are significantly more predictive of expression compared to the purely motif-based network, underscoring the importance of expression-based datasets for inferring network structure and parameters (Figure 2C, blue line). The purely expression-based methods (GENIE3, LARS-EN, TIGRESS, PGG and MERLIN) are able to perform very well as far as this metric is concerned (Figure 2C). In fact, prior-based methods suffer in predictive power compared to the non-prior counterparts (e.g. PGG versus PGG+Prior, and MERLIN versus MERLIN+Prior). This result shows the importance of assessing inferred network models using both structure and parameters: while purely expression-based methods are not able to recover as many ChIP-chip edges as the expression+prior-based methods, their ability to predict expression in new conditions is as good or better than methods that are able to more accurately recover the structure of the network.

To assess the extent to which the inferred networks are functional, we measured the agreement between genes that are differentially expressed in a TF knockout from Kemmeren et al. (25) and the predicted targets of the same TF in the inferred network (Figure 2D, ‘Materials and Methods’ section). For each edge in the inferred network that was examined in the knockout dataset, we asked whether the perturbation of the regulator in that edge significantly affected the expression of its target (P-value ≤ 0.05). We called these edges ‘functional’ and calculated the percentage of functional edges in the inferred network. Consistent with our observation of predictive power of target gene expression, we find that both our prior and non-prior-based methods are able to perform at par, producing similar fractions of functional edges. Among the methods that used a prior, MERLIN+Prior and PGG+Prior performed better (15–17%) compared to Inferelator (10–12%) on different datasets.

Finally, we used evolutionary conservation to assess the functional aspect of the inferred network structures (‘Materials and Methods’ section). To this end, we obtained the expression dataset from six different yeast species (C. albicans, C. glabrata, K. lactis, S. castellii, S. pombe and S. cerevisiae) measured under various stress conditions (41–43). Using MERLIN+Prior, we find that the edges inferred in the network are significantly more correlated than edges in background across all species (Supplementary Data). Repeating this experiment using the networks inferred using other methods (on Nat.Var. dataset, Figure S6G–L), we observed that MERLIN+Prior remained the method with the most significant difference among other prior-based methods. The correlation of edges inferred by purely expression-based methods (MERLIN, PGG, TIGRESS and GENIE3) tend to have more significant KS-test P-value, which is likely because the selected TFs of a target gene are more predictive and correlated with the expression of the target gene if expression alone is used as a criteria for network inference. In summary, our prior-based network inference approach is able to infer network structures with the highest structure accuracy compared to existing approaches and are as predictive of gene expression as all methods compared. This suggests that integrating expression with sequence-specific motifs can infer regulatory networks with both physical and functional edges.

Genetic variation is the most informative type of dataset for inferring regulatory networks in yeast

Although the integration of different types of expression and non-expression datasets can improve the quality of inferred networks, the type of experimental perturbations can influence the quality of the inferred network structure. Such perturbations include single gene knockouts, natural variation and environmental perturbations. Hence, we used our comparative analysis of performance of different methods on different datasets described before to examine the impact of the type of perturbation on the quality of inferred networks. We find that the networks inferred using natural variation data have the highest AUPRs for all methods (Figure 2A(ii)) and the highest number of predictable regulators (Figure 2B). This difference is more significant for the methods that did not use prior, which is expected because the prior establishes a constraint on the inferred networks. When examining the predictive power of networks inferred from the different types of datasets assessed using the number of expression-predictable target genes (Figure 2C), we find that Nat.Var. is the best for the TIGRESS, PGG and MERLIN methods (both with and without prior versions), tied with the StressResp data for LARS-EN and better than the Knockout data for GENIE3 and Inferelator. Finally, based on the number of functional edges we find a slight advantage for the networks inferred on Knockout dataset, even though this dataset was produced from different studies (20,21) and independent from the Kemmeren et al. dataset (25) used to extract the functional edges. Importantly, the fraction of functional edges inferred using the Nat.Var. dataset is never the worst for any of the methods compared. These results suggest that among the different types of large-scale perturbations compared in this study, natural genetic variation data is the most informative type of perturbation for inferring network structure as well as for learning parameters.

To assess the generality of this observation, we examined various human expression datasets as well (Supplementary Data, Supplementary Data). We focused on data from LCLs because a large amount of ChIP-seq data exists for the Gm12878 LCL from the ENCODE project (61) and is the cell line of choice in human genetic variation studies (48,49) as well as different stress-like perturbations (See ‘Materials and Methods’ section for details). Compared to stress, we find that datasets that measure the impact of genetic variation had higher AUPRs, especially in the no-prior case (Supplementary Data), had higher fraction of functional edges (Supplementary Data) and had greater fraction of predictable targets (Supplementary Data). As we incorporate prior, the difference between the different types of perturbations is reduced and we observe an increase in the number of predictable TFs for stress response at higher prior settings (Supplementary Data). Our initial results in human offer promising evidence that genetic variation is a better type of perturbation for lymphoblastoid network inference.

Comparison of inferred networks from different methods identifies inherently predictable and unpredictable TFs

We next examined the extent to which the methods agreed on the inferred networks across datasets and the predictable TFs originally introduced in Figure 2B. As expected, prior-based methods were less sensitive to the choice of the dataset and agreed more with each other, than purely expression-based methods (Supplementary Data, Supplementary Data). The specific TFs that are predictable by the different methods are shown in Figure 3. Even though the number of predictable regulators from different methods vary, there are some overlaps between these lists. Because of the similarity among the PGG and MERLIN methods and their prior versions, we compared which TFs were predictable by either PGG/MERLIN and either LARSEN, TIGRESS, GENIE3 or Inferelator. In all, there are 57 predictable TFs among the list of TFs in the MacIsaac gold standard network. Among the 57 predictable regulators we find TFs that are predictable by different categories of methods. Seven TFs (GCR1, HAP1, HAP4, INO2, MET32, STE12 and ZAP1) were predictable by all categories of methods (GENIE3, TIGRESS, LARS-EN and PGG or MERLIN). Thirty of the 57 TFs are predictable by at least one of the expression-based methods on one of the datasets, and there are 23 TFs that are predictable by at least two (for example GCN4 and CIN5 are predictable by LARS-EN and PGG or MERLIN). On the other hand, there are 26 TFs (for example GAL4 and REB1) that are predictable only by prior-based methods (Inferelator, PGG+Prior or MELRIN+Prior) and half of these TFs (14) were predictable by Inferelator and PGG or MERLIN+Prior. Taken together, these results show that despite the variability and dependence on the different datasets, methods for inferring networks are mutually consistent with each other with considerable overlap among the specific set of TFs that are predictable. Such common predictions are indicative of network components that are robustly identifiable by different methods and can be used to study what aspects of a network can be identified based on expression-based network inference methods. Several additional TFs were predictable uniquely by MERLIN+Prior or PGG+Prior (SKO1, SWI5, YAP6, etc.). The complete set of predictable TFs provides an upper bound on what can be predicted based on expression-based network inference methods.

Figure 3.

Significance of overlap of target sets of regulators in an inferred network compared to the MacIsaac gold standard network. The value shows the fold enrichment of true (as determined by MacIsaac) targets of a TF in the predicted target set of a TF. The gray color means that the target set of that regulator did not have a significant overlap with its target set in the MacIsaac gold standard.

Using a prior network improves our ability to construct functional regulatory networks, however, there are still numerous TFs whose targets in the MacIsaac gold standard network are not predictable using expression. We call such TFs as ‘unpredictable TFs’. There can be multiple reasons for the inability to recover the targets of such TFs: (i) the TF does not vary in the expression dataset and therefore is a poor predictor of a target gene's expression, (ii) the TF's mRNA level is not predictive of its target gene's expression levels because of more complex regulatory programs of such TFs (e.g. post-transcriptional or post-translational regulation), (iii) certain topological properties of the gold-standard network might make a TF more or less predictable.

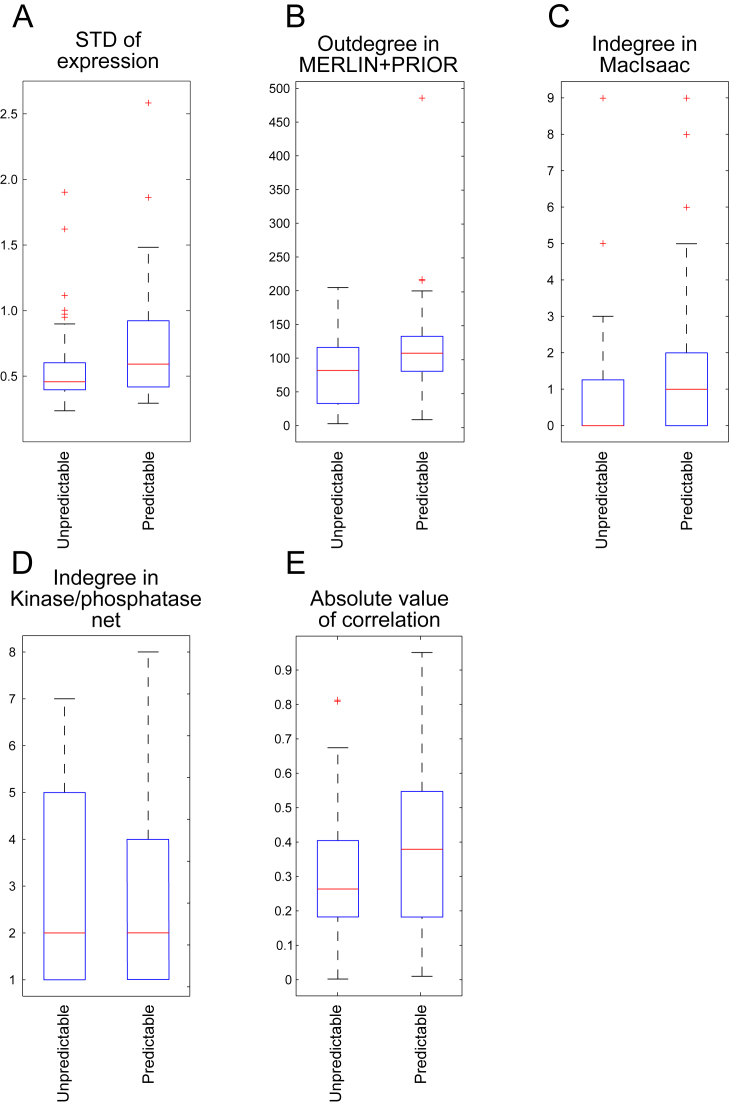
To assess whether unpredictable TFs arise because of their lack of variation at the mRNA level, we examined the out-degree (number of predicted targets) of these TFs as well as the variance in expression of TFs in the Nat.Var dataset. Our rationale for using the out-degree is that if the TFs do not vary at the mRNA level, they are likely not good predictors of expression of any target gene (Figure 4A and B). The predictable TFs have higher out-degree (KS test P-value < 0.00024) and greater variation (KS test P-value < 0.0123) suggesting that the predictable TFs have a tendency to be good predictors of expression. However, given that there were several unpredictable TFs with high out-degree, this alone is unlikely to explain the predictable and unpredictable TFs.

Figure 4.

Analysis of predictable and non-predictable TFs. (A) Variation in expression in predictable versus unpredictable TFs using the Nat. Var. dataset. (B) Out-degree of predictable and unpredictable TFs in MERLIN+PRIOR inferred networks. (C) In-degree of predictable and unpredictable TFs in MacIsaac network. (D) Indegree of predictable and unpredictable TFs in Kinase/phosphatase network. (E) The absolute value of correlations of the NCA inferred activity and actual expression of predictable and unpredictable TFs.

We next asked if the unpredictable TFs were more or less transcriptionally regulated based on the rationale that more complex transcriptional regulation would make it more difficult to infer their regulatory state from mRNA alone. To this end we compared the in-degrees (the number of regulators of a TF) of the predictable and unpredictable TFs in the MacIsaac network (Figure 4C). The greater the in-degree of a gene, the more complex is the regulatory program of a gene. We observed that the difference in in-degree of predictable and unpredictable TFs is not significant in the MacIsaac network (KS test P-value < 0.4399) suggesting that the complexity of the transcriptional program of the regulators does not explain the unpredictable TFs. Similarly we asked whether unpredictable TFs are more heavily targeted by post-translational modifications by examining their in-degree in kinase/phosphatase-substrate networks (62,63) (‘Materials and Methods’ section). However, here too we did not see a significant difference in the in-degree of predictable and unpredictable TFs (KS test P-value < 0.4625, Figure 4D). Thus, we did not find support for the unpredictable TFs to have a significantly more complex transcriptional or post-translational regulatory input program; however, we are limited by the lack of context specificity of these existing interactions.

To examine whether the reasons for failing to capture the targets of the unpredictable TFs is due to the discrepancy between a TF's mRNA level and its activity on a target gene, we used network component analysis (NCA) (64). NCA is an approach to infer the ‘hidden’ activity levels of TFs for a given network structure and the expression levels of genes. Briefly, for a given network structure, NCA assumes that the expression profiles of target genes of a regulator is a linear combination of an unobserved regulator signal. It then infers these signals and the weights of the linear combination. These inferred signals can be interpreted as ‘hidden activity’ of the TFs. We applied NCA to infer the activity levels of TFs using the MacIsaac network structure and Nat.Var. expression dataset. If the inferred TF activity is more correlated to TF mRNA levels of predictable TFs compared to unpredictable TFs, one can conclude that using TF mRNA levels as proxies for its activity is responsible for the difficulty in predicting targets of unpredictable TFs. However, comparison of the NCA inferred levels to actual mRNA levels of the TFs shows that the absolute value of correlation of unpredictable TFs is only moderately lower than the predictable TFs (KS test P-value < 0.0464, median for unpredictable TFs (0.2636) is lower than that for predictable TFs (0.3794), Figure 4E). Thus, the discrepancy between the mRNA levels and the actual TF's activity level plays a minor role in unpredictable TFs.

Finally, we asked if the architectural properties of the subnetworks associated with unpredictable TFs versus predictable TFs are different. Network motifs (65) are repeating subnetworks and form core building blocks of a larger network. It was recently shown that regulators in positions of three node motifs are under evolutionary constraint and tend to be conserved between species (66). We used FANMOD tools (67) to find network motifs in the MacIsaac network restricting to the subnetwork with interactions only between the 86 TFs (the rest of the 28 TFs were not connected to the TF–TF subnetwork). This network had 23 feed forward loops, which included 11 TFs that were in the ‘driver’ position, that is, they have no incoming regulators. Among these 11, 10 were predictable TFs (hypergeometric P-value < 1E-3). Furthermore, out of 12 TFs in first passenger position, 10 are predictable TFs (hypergeometric P-value < 1E-2) but out of 11 TFs in second passenger position, only 4 were predictable (hypergeometric P-value < 0.86). This suggests that predictable TFs tend to be upstream in a regulatory cascade. It is therefore likely that architectural properties associated with the network are associated with the ease with which we can predict a regulator's targets.

Taken together these results suggest that with the exception of the network motif position, no single factor is solely responsible for the difficulty in predicting the targets of the unpredictable TFs, however, several of the properties tested here each contribute, albeit in small ways, to the difficulty of identifying targets of unpredictable TFs.

Unpredictable TFs are associated with surrogate TFs that share similar functional pathways

So far we characterized the differences between the predictable and unpredictable TFs; next, we asked if there are specific regulators in the inferred networks that are predicted to regulate the targets of the unpredictable TFs, and if these regulators are functionally related to the unpredictable TFs. We examined target sets of each TF in the MacIsaac network and asked what MERLIN+Prior TFs were significantly associated with them (significant overlap of the MERLIN+Prior TF's targets with the targets of the TF in the MacIsaac network based on hypergeometric test P-value < 0.05). Of the 91 MacIsaac TFs that had at least 5 target genes in the MacIsaac network, we found 78 TFs that were associated with one or more MERLIN+Prior TFs. We call these MERLIN+Prior TFs as the ‘surrogate TFs’ of the MacIsaac TF. A subset of these 78 TFs were the predictable TFs (Table S4). Interestingly, in many cases, one or more of the MERLIN+Prior TFs was also more correlated to the NCA-inferred activity of the MacIsaac TF than the expression level of the MacIsaac TF itself (Table S4, MERLIN TFs in top20 column), indicating that the MERLIN+Prior TFs better explain the expression levels of the targets of the MacIsaac TF than the MacIsaac TF.

MERLIN TFs that serve as surrogates for a MacIsaac TF's target set might be involved in the same pathway as the MacIsaac TFs. To test whether the surrogate TFs predicted by MERLIN+Prior were in the same functional pathway as the MacIsaac TF, we counted the number of genetic and physical interactions (from BioGRID database (62)) between a MacIsaac TF and its corresponding enriched regulator from MERLIN+Prior. Considering all MacIsaac TFs and associated MERLIN TFs as two separate sets, we found significantly higher number of genetic and physical interactions spanning these two TF sets compared to what is expected by random (genetic interactions z-score 5.351, physical interactions z-score 4.740, P-value ≤ 1E-5). These results suggest that expression-based inference methods can infer either the target set of a TF accurately, or infer a regulator that is functionally associated with the TF of interest.

Inferring condition-specific networks and prioritizing regulators

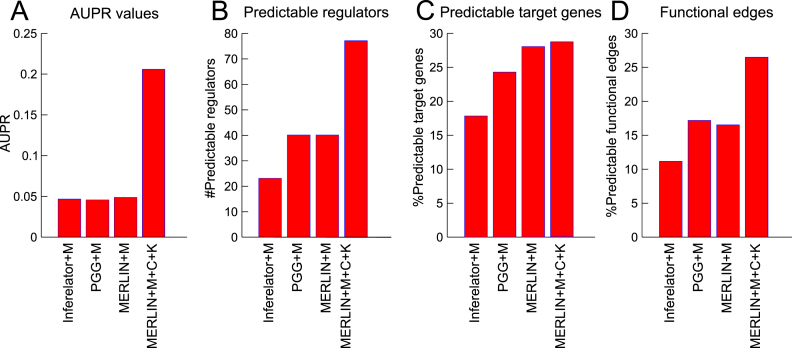
The previous sections have shown that both expression and non-expression datasets are important for inferring regulatory networks. Furthermore, our MERLIN+Prior approach is able to reconstruct regulatory networks that have high quality structure (as measured by AUPR and the number of predictable TFs) and is functionally accurate (as measured by the percentage of predictable target genes, the percentage of edges that can predict the impact of TF knockouts and evolutionary conservation of TF-target correlation). However, thus far, we used only sequence-specific motifs to have as unbiased a comparison to our gold standards that were derived from ChIP-chip and/or TF knockouts. We next sought to create a larger, expansive regulatory network for yeast that combined ChIP-chip, sequence-specific motifs and TF knockout data as three different prior networks within the MERLIN+Prior framework using Nat.Var. as the training dataset (‘Materials and Methods’ section). This network has a significantly improved agreement with the gold standard network structure as measured by AUPRs, number of predictable TFs (Figure 5A and B), ability to predict expression of target genes (Figure 5C) and the ability to recover functional edges (Figure 5D). While the improvement in structure (AUPR and predictable TFs) is expected because the MacIsaac network was largely derived from ChIP-chip experiments (18), the improvement in the functional part of the network (predictive power and functional edge recovery) were notable because only a small fraction of the predictable targets (16%) and functional edges (7%) came from the positive training set used to set the prior parameters (‘Materials and Methods’ section). We used this regulatory network to address two target applications relevant to condition-specific regulatory networks: (i) prioritize regulators associated with a specific stress, (ii) infer condition-specific regulatory networks.

Figure 5.

Performance of MERLIN+Prior using the three prior networks, ChIP (C), Motif (M) and Knockout (K) compared to other prior-based methods that use only the motif prior network. The MERLIN+Prior network that uses all three types of priors is called MERLIN+M+C+K. (A) AUPR, (B) Number of predictable regulators, (C) Percentage of predictable targets, (D) Percentage of functional edges (edges that are associated with significant effect on the expression of the target gene after knockout of the regulator associated with the edge).

Predicting important regulators for different stresses

An important application of a genome-scale regulatory network is to identify important regulators of a process (e.g. response to a particular stress) that can then be tested experimentally. We therefore prioritized regulators based on their ability to predict the expression level of target genes in a new condition. We considered the compendia of stress response experiments from Gasch et al. (40) each experiment comprising 5–24 time points. To rank the regulators in a given stress condition, we calculated a measure of importance for the regulators in a given stress condition using the top 30K edges of the expansive regulatory network (‘Materials and Methods’ section). Briefly, we first learned linear regression functions for each target gene using the regulators in the top 30K edges and the Nat.Var. dataset. Next, using these regression functions, we predicted the expression levels of target gene from the expression level of its regulators in the new conditions. We computed the change in prediction error when the regulator is removed from the network. The importance of a regulator was the sum of the change in prediction error across all predicted target genes of this regulator. The larger the total prediction error on regulator removal, the more important the regulator. We then ranked all the regulators in the inferred network based on this measure of importance.

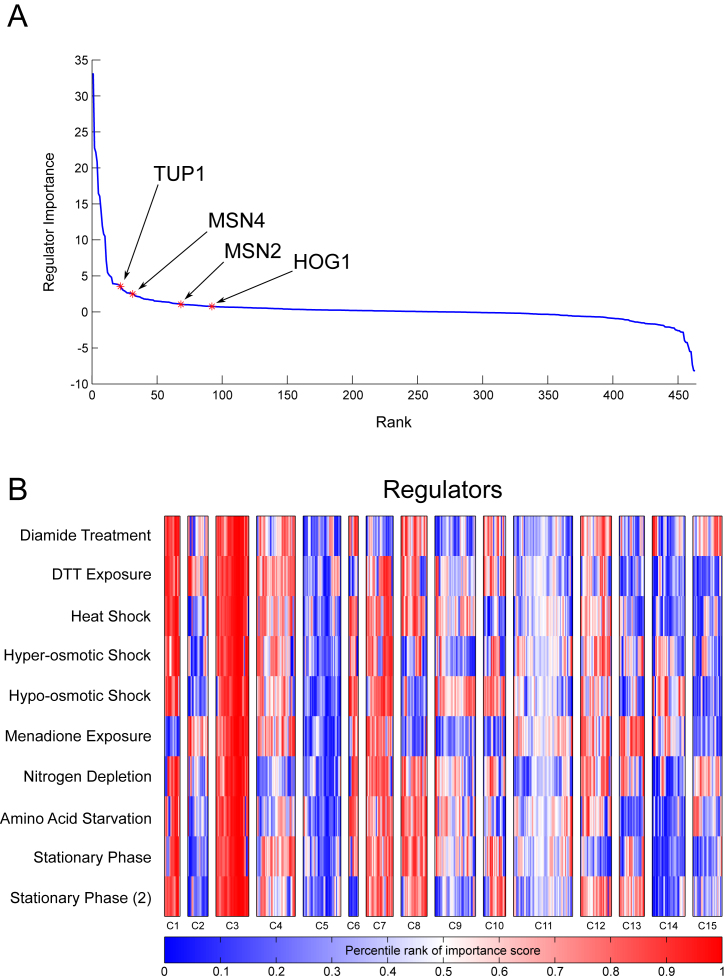
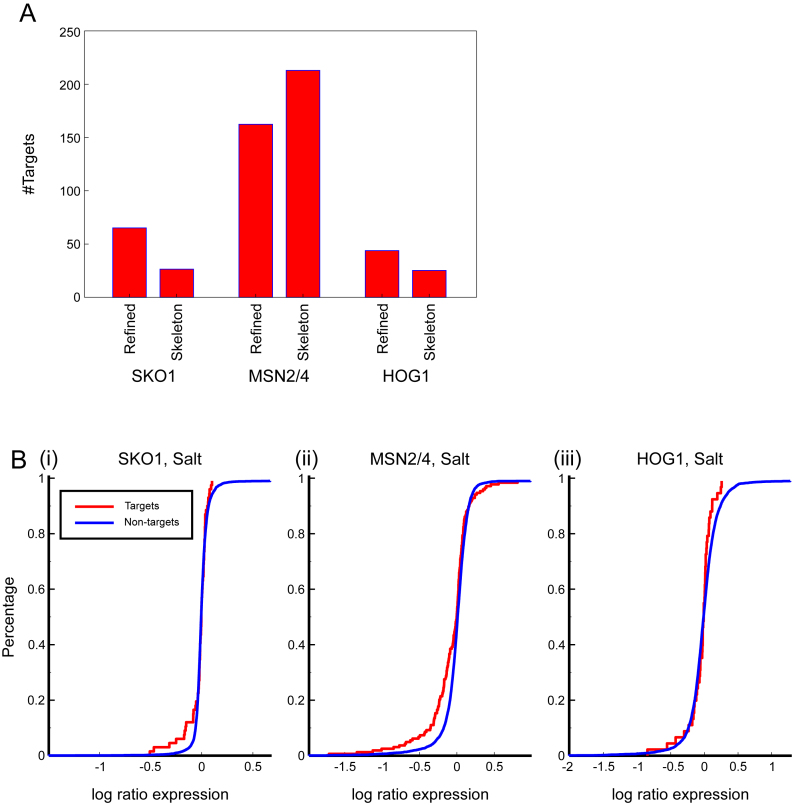
We applied our ranking strategy to predict important regulators for the available stress conditions: osmotic stress, heat shock, amino acid starvation, stationary phase and oxidative stress. Several of the highly ranked regulators are known to be involved in response to stress. For example, MSN2/4, key regulators of stress response (68), HOG1, a member of MAPK family (which are involved in signal transduction pathways in OSR (69)) and TUP1 (involved in response to osmotic stress (70)) (Figure 6A), were all ranked highly in osmotic stress. Similarly, GCN4, MET28 and MET32, which are involved in amino acid starvation and sulfur metabolism, are ranked in the top 30 regulators for amino acid starvation. Several regulators were ranked highly in multiple conditions suggesting that the same regulator might be important for multiple stresses. To identify regulators with different condition-specific patterns we clustered the regulators based on their ranking in different conditions (Figure 6B). We observed many interesting patterns in the resulting clusters that are indicative of the specificity of regulators in different subsets of conditions. For example, cluster C3 contained regulators that were ranked high in all of the conditions and included regulators like USV1 and GRE3. Both these regulators are known to be involved in multiple stresses (USV1: in growth on non-fermentable carbon sources, as well as osmotic stress; GRE3 associated with osmotic, oxidative, heat shock stresses). We also observe clusters that contain regulators that were ranked high only in some conditions. For example, cluster C2 is associated with regulators ranked highly in Diamide, DTT treatment and Menadione, cluster C15 was associated with Diamide Treatment and Nitrogen depletion, and C14 was associated with Hyper and Hypo-osmotic stress and Menadione. The full list of regulators ranked per condition is available as a Supplementary Data and can be used to guide validation studies using genetic perturbation studies.

Figure 6.

(A) The ranking of regulators in the Hyper-osmotic stress condition according to regulator importance score. Known important regulators are shown. (B) Clustering of TF importance scores for 10 different stress conditions. Columns show the conditions and rows show the regulators. The difference between Stationary Phase and Stationary Phase (2) is that one is a longer version of the other time course.

Inferring condition-specific network topology

Our prior-based approach is general and can be used to refine a given input network with condition-specific data to obtain a condition-specific network. As a proof of principle of our approach to predict condition-specific network topology from a small number condition-specific experimental samples we used OSR and heat shock response (HSR). For osmotic stress we combined datasets from Gasch et al. (40) with time courses from two additional sources (41,42) to produce a total of 23 samples. For heat shock, we used the samples from Gasch et al. (40) only, which had 24 samples per gene. We used our expansive regulatory network as a ‘skeleton’ network and then refined it using a condition-specific network for OSR and for heat shock using the MERLIN+Prior framework.

Our OSR-specific regulatory network connected 465 regulators to 4698 target genes. We evaluated the OSR-specific network for its ability to recapitulate known important regulators of osmotic stress, namely HOG1, SKO1 as well general regulators of stress response, MSN2/4. We found an increase in the number of predicted targets of both HOG1 and SKO1 in the OSR-specific network compared to the skeleton network, but a decrease of targets of MSN2/4 (Figure 7A). This is likely because MSN2/4 is associated with general stress response rather than a specific process.

Figure 7.

Validation of osmotic stress condition-specific network. (A) Number of predicted targets of SKO1, MSN2/4 and HOG1 in the inferred networks. ‘Skeleton’ refers to the expansive network inferred on the Nat. Var. dataset by integrating three different prior networks. ‘Refined’ refers to the condition-specific network produced by refining the ‘Skeleton’ network using condition-specific expression data. (B) Comparison of log ratio of a regulator knockout to wild-type expression level of targets and non-target genes of a particular regulator. Genome-wide expression levels of the wild-type and knockout strains are measured in salt stress. Each plot shows the empirical CDF of expression of predicted targets and non-targets using the refined regulatory network.

To validate the predicted targets of important OSR-specific regulators, we obtained the expression levels of HOG1, SKO1 and MSN2/4 knockout strains under salt from Capaldi et al. (1). We compared the log ratio of expression levels in the knockout strain versus the wild type of the predicted targets and non targets in the salt stress. We found that the targets of MSN2/4 and SKO1 are significantly down-regulated compared to non-targets (t-test P-value < 1E-2) in the knockout versus wild type. We see a similar shift in expression for HOG1 however the p-value is not significant (t-test P-value < 0.17) (Figure 7B). Taken together these results enabled us to gain confidence in the ability of our prior-based framework to infer context specific regulatory networks.

Given that both SKO1 and HOG1 gained additional regulatory edges compared to the condition unspecific prior skeleton network, we asked if we could identify additional regulators based on the change in connectivity between the skeleton and the OSR-specific network. We ranked regulators based on the difference in their target set size in the prior and OSR-specific network. Among the top ranking genes were several genes that so far have not been associated with OSR. In particular, one such regulator is GTS1. Mutations in GTS1 are known to have phenotypes in cell size, sporulation and life span. Among other top regulators were two RNA binding proteins namely JSN1 and PUF2 (Tables S6 and S7). RNA binding proteins play important roles in the post-transcriptional processing and have been shown to specifically affect the rate of mRNA turnover and dynamics from P-bodies in osmotic stress (71). We observed similar properties with the HSR-specific regulatory network as well, which connected 536 regulators and 6115 target genes. Interestingly, here we found RNA binding proteins as well, but that were ordered differently from those in osmotic stress. In particular, among the top ranking regulators is GIS2, that also binds to mRNA and localizes to RNA processing bodies. GIS2 is known to interact with HSP60 (62) as well as other heat shock protein families such as SSA1 and SSA2 (62), implicating a novel role of GIS2 in heat shock stress response.

In summary, our general prior-based framework can be used to infer condition-specific regulatory networks and to predict condition-specific regulators. Our predicted networks recapitulate the targets of known important regulators of the specific stress response and identify several novel regulators.

DISCUSSION

Computational inference of genome-scale regulatory networks is a long standing challenge in systems biology especially in eukaryotic systems. Expression-based network inference methods are among the most popular computational network reconstruction methods because genome-wide expression datasets are widely available in different conditions and contexts (3,72), and because they enable the construction of predictive regulatory network models that can predict the expression level of target genes in new conditions or in response to perturbations (73,74). However, expression alone may not be sufficient to infer regulatory networks in eukaryotic systems (8). Here we developed a general approach to integrate different types of regulatory network evidences to infer a network and performed a comprehensive characterization of the potential factors that influence network inference from gene expression data. Our work allowed us to gain several important insights into the ability of expression-based network inference methods to recover network topologies.

Type of perturbation

Guidance into the utility of different types of datasets that are available for network inference is greatly needed. While it is clear that large compendia of perturbed expression profiles are important for network inference, it is not clear what types of experimental perturbations are the most important. An important insight that we gained from our analysis was the utility of natural genetic variation in informing the network structure. Irrespective of the method used, the natural genetic variation data was able to infer the networks that were most accurate, both with respect to structure as well as with respect to network parameters. We tested the utility of natural genetic variation and stress perturbations for inferring a regulatory network in human LCL and found natural genetic variation to be more useful for this network as well. However, the datasets in human are relatively small in size compared to the size of the network inferred and we could not examine knockout based datasets. Furthermore, the relative impact of the prior is much less for human compared to yeast. In particular, the prior provides evidence for only 79 out of 539 candidate regulators, whereas the yeast prior network included 197 out of the 537 candidate regulators. Future work, which includes more controlled stress related perturbations as well as regulator perturbation experiments would be needed to provide further support of this observation in humans and other multi-cellular organisms.

Parameter prior versus structure prior based methods

Among the earliest prior-based methods for regulatory network inference are those based on defining a prior on the graph structure (15–17). For example, Werhli et al. (15) defined an energy function to measure the similarity of a candidate graph to an input prior graph, while Mukherjee et al. (17) and Hill et al. (75) make use of concordance functions that measure the similarity of a candidate graph with a prior graph. However, these approaches have relied on the Markov Chain Monte Carlo, which are computationally expensive. While Hill et al. describe a more efficient Empirical Bayes approach it has been applied to proteomic data of tens of genes. On the other hand, parameter prior based approaches (11,12,14,76) use priors to control the extent of network sparsity. Briefly, these approaches are based on a dependency network learning paradigm, where network inference is addressed by solving a set of regression tasks. These methods assume an L1 (lasso, sparsity imposing) or L1/L2 (sparsity with correlated regulators, (11)) regularization and shrink regression weights of most regulators to 0. The prior-based versions of these methods use additional prior data to decrease the penalty for edges with prior support. This decrease in penalty can be set using a hyper-parameter (11,76) or can be further modeled as a regulatory potential parameterized by regulatory features capturing properties of the regulator and target gene (14). Such approaches are computationally more tractable than the structure-prior based approaches and more suitable for inferring a genome-scale network. Our approach was to impose a structure prior within a dependency network learning framework to enable efficient network learning. Instead of having a fully Bayesian solution on the posterior graph structure, we used stability selection, an ensemble learning approach that has been shown to improve purely expression-based network inference (34). This provided a way to approximate the posterior distribution over network edges on a genome-wide scale and provided significantly improved performance compared to a parameter prior-based approach.

Supervised versus unsupervised network inference

While the approach taken in this work is to integrate expression with structure priors within an unsupervised network learning framework, a complementary approach is to integrate these data within a supervised network inference (77–80). Under the supervised learning paradigm, the ‘global’ approach trains a single classifier to discriminate between interactions and non-interactions, while the ‘local’ approach trains a per-regulator classifier to learn discriminative expression signatures of targets and non-targets (80). Training examples in both local and global approaches are derived from an established ground truth, however, the local approach was shown to be more powerful than the global approach (80). In contrast, in an unsupervised learning framework, we do not assume the presence of any known examples, which makes this framework more broadly applicable but also makes the learning problem and validation much harder. The two frameworks also differ in the prediction of a new regulatory edge. In a classification/supervised setting, the probability of presence of new edges is computed independently and is dependent upon the edges present in the training set. In the unsupervised setting, the prior probability of an edge is assumed to be independently computed based on non-expression (e.g. sequence motif, ChIP binding) features. However, the inclusion of new edges are not independent of each other but rather the result of the tradeoff between their prior probability based ranking and their ability to explain expression of a target gene. A third important difference is from the perspective of a target gene. In the local model setting, a target gene can have a regulator only if there is an existing classifier that is trained on this regulator. In contrast, in the unsupervised setting there is no such constraint. For a target gene with no prior information, our approach would behave similar to an approach using only expression (Supplementary Data). Despite differences in these two learning paradigms, we note that both approaches are dependent upon the quality of the structural priors. When the structural priors are of high quality both approaches would be benefitted and the discriminative nature of supervised learning could enable it to gain more performance improvement than an unsupervised learning framework (81). However, when the priors are of low quality both learning paradigms will likely suffer in performance. In an unsupervised setting, because the structural priors are used only as guides in the edge selection process in the final inferred network, such an approach is robust in performance in the presence of a large number of edges with unknown status and/or noisy priors (Supplementary Data, (11)). An important direction of future work is to systematically compare the sensitivity of local supervised methods and unsupervised methods with prior in the presence of noisy priors.

Importance of estimating and evaluating both network structure and parameters

Expression-based network inference has been an active area of research and a large number of methods have been developed (2–4,8). However, success has generally been measured based on the ability of a method to recover the structure, but not how well the network is able to make a prediction in a new condition. We find that methods including ours that use priors are able to recover the structure of the network much better. However, when comparing methods based on their ability to predict expression in new conditions, non-prior methods often outperformed prior-based methods. This is not surprising because the score improvement on adding a particular edge in a prior-based framework is the sum of the improvement in the expression likelihood, and the prior probability of adding an edge. With a structure prior, the algorithm may select an edge that does not improve the expression part of the score as much as in the case without priors, but has a lower penalty (higher prior probability of being present). Furthermore, if an edge contributes to improved better predictive power in the training set, we expect it to generalize to better prediction in the test set. However, expression alone makes it difficult to discriminate between a highly correlated TF/regulator-gene pair versus a true causal relationship between a TF/regulator and a target gene. Thus to gain mechanistic insight, in addition to having good predictive power, methods that integrate expression with other types of regulatory evidences are more relevant than purely expression-based network inference methods.

Another important question that arises in the evaluation of structure with prior-based approaches is the extent to which the prior network influences the edges in the inferred network and whether this overestimates the performance of prior-based network inference methods. Overestimation can occur if the prior is a binary network and the gold standard shares edges with the prior. In our experiments, the prior is weighted and the shared edges with the gold standard are expected to see the benefit of the prior. We find that on parts of the network where there is prior support, the performance is indeed significantly improved, but for other parts (with no prior support) there is a minor decrease in performance. This decrease in performance can be explained by presence of false edges (with respect to the gold standard) in the prior network. When multiple regulators can explain the expression of a target gene equally well, the prior network can help us to select the right regulator for that target gene. However, if the right regulator is not present in the prior network, incorporating a noisy prior can select the wrong regulators. These results show the importance of the quality of prior network in the accuracy of inferred networks: a noisy prior network (that includes many false edges and does not include the true edges) can greatly hamper the performance of the prior-based methods. Another potential case of overestimation is when prior and the gold standard are from the same type of experimental assay, the inferred network is likely to appear more correct compared to the case when the prior and gold standards come from a different assay. Therefore, when assessing the performance of the method, different types of priors and gold standard networks should be considered. Our results show that even when the prior and gold standard networks are produced from different types of experimental data, prior-based methods can improve the accuracy of the inferred networks over purely expression-based networks (Supplementary Data).

Inherently predictable and unpredictable TFs

Despite a large number of methods, the success of methods has been modest for simple eukaryotes like yeast (8). By performing a systematic comparison of different types of methods (with and without prior; linear and non-linear dependencies), we were able to identify success and failure cases of network inference. In particular there are some TFs whose targets can be sufficiently well-predicted based on expression, whereas several TFs remain unpredictable. Network architecture, variation in a TF's mRNA level, as well as the using a TF's mRNA level as a proxy for its activity, might play an important role in determining the predictability of the targets of such TFs. Reassuringly, for several of these unpredictable TFs, we found surrogate regulators that were predicted to regulate a significant fraction of its targets and were likely to be in a genetic or physical interaction with the unpredictable TF. Thus the expression-based TFs were in the same genetic interaction pathways and therefore relevant to the ChIP-chip based TF. We expect that integration of additional datasets that inform us of additional levels of regulation (e.g. post-translation modifications of TFs) will help improve the target identification of unpredictable TFs.

Identification of condition-specific networks and regulator prioritization

Regulatory networks are fundamentally context-specific. A simple approach to infer context-specific networks is to ‘remove’ TF-target edges where both or either the TF or target gene is not expressed in the condition of interest (82,83). However, the skeleton network might be incomplete and miss edges that are unique to a new condition. While this issue could be addressed by inferring networks ‘de novo’ in the new condition, doing so is problematic because there are typically not enough samples from the condition of interest to learn a network. Instead, we propose a prior-based approach where we first reconstruct the skeleton regulatory network inferred using multiple sources of data (not available for one condition) and then refine the network structure using condition-specific expression data. We predicted a global OSR-specific and global HSR-specific regulatory network and found our network to better recapitulate the effects of important regulator knockouts than the non-specific skeleton network. We also developed network regulator prioritization schemes based on the network topology that is sensitive to the condition of interest, thus predicting regulators that are important for that condition. By applying our approach to different types of stress conditions we revealed commonalities among the stress response regulators as well as regulators that were unique to a few conditions.

In summary, expression-based network inference is an important tool in systems biology research. In this work we have addressed several critical questions that provide insight into the approach, dataset and the limits of expression-based network inference. As more organisms are sequenced, we believe that our insights will inform the experimental design both for capturing the initial network structure as well as for guiding experiments to refine the network.

IMPLEMENTATION AND AVAILABILITY

The MERLIN+Prior code, example datasets, our inferred networks and documentation are available at https://bitbucket.org/roygroup/merlin-p.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

NSF CAREER Award [NSF DBI: 1350677]; Sloan Foundation Research Fellowship [FG-BR2014-010]. Funding for open access charge: NSF CAREER Award [NSF DBI: 1350677]; Sloan Foundation Research Fellowship [FG-BR2014-010].

Conflict of interest statement. None declared.