The Closed State of the Thin Filament Is Not Occupied in Fully Activated Skeletal Muscle

Abstract

Muscle contraction is powered by actin-myosin interaction controlled by Ca²⁺ via the regulatory proteins troponin (Tn) and tropomyosin (Tpm), which are associated with actin filaments. Tpm forms coiled-coil dimers, which assemble into a helical strand that runs along the whole ∼1 μm length of a thin filament. In the absence of Ca²⁺, Tn that is tightly bound to Tpm binds actin and holds the Tpm strand in the blocked, or B, state, where Tpm shields actin from the binding of myosin heads. Ca²⁺ binding to Tn releases the Tpm from actin so that it moves azimuthally around the filament axis to a closed, or C, state, where actin is partially available for weak binding of myosin heads. Upon transition of the weak actin-myosin bond into a strong, stereo-specific complex, the myosin heads push Tpm strand to the open, or O, state allowing myosin binding sites on several neighboring actin monomers to become open for myosin binding. We used low-angle x-ray diffraction at the European Synchrotron Radiation Facility to check whether the O- to C-state transition in fully activated fibers of fast skeletal muscle of the rabbit occurs during transition from isometric contraction to shortening under low load. No decrease in the intensity of the second actin layer line at reciprocal radii in the range of 0.15–0.275 nm⁻¹ was observed during shortening suggesting that an azimuthal Tpm movement from the O- to C-state does not occur, although during shortening muscle stiffness is reduced compared to the isometric state, and the intensities of other actin layer lines demonstrate a ∼2-fold decrease in the fraction of myosin heads strongly bound to actin. The data show that a small fraction of actin-bound myosin heads is sufficient for supporting the O-state and, therefore the C-state is not occupied in fully activated skeletal muscle that produces mechanical work at low load.

Introduction

Muscle contraction is powered by an interaction of myosin heads with actin monomers, which form the backbone of thin filaments. The fuel for work production by the actin-myosin motor is provided by ATP hydrolysis. Contraction and relaxation of skeletal and cardiac muscles are regulated by Ca²⁺ ions via regulatory proteins, troponin (Tn) and tropomyosin (Tpm), associated with the actin filaments to form Ca²⁺-regulated thin filaments. Tpm is a coiled-coil dimer that lies on the surface of the actin filament in a long helical groove with a pitch of ca. 36 nm. Tpm dimers bind each other in a head-to-tail manner to form two continuous strands running along the whole length of an actin filament. Tn consists of three subunits: Tn-C, Tn-I and Tn-T. The steric blocking model proposed more than 40 years ago (1, 2, 3, 4) suggests that in the absence of Ca²⁺, Tpm obstructs myosin-binding sites on actin and thus keeps muscle in the relaxed state. Ca²⁺ binding to Tn-C releases Tn-I from actin and allows Tpm to move azimuthally around the thin filament axis and enables myosin binding to actin. Later (5) a more detailed three-state model based on biochemical studies was suggested. This model was later supported by electron microscopy, EM (6). According to this model that was later combined with a crystallography-based model of Ca²⁺-regulation of Tn (7), in the absence of Ca²⁺, a mobile inhibitory segment of Tn-I binds actin and keeps the Tn-Tpm strand in a position where it obstructs the myosin binding sites on actin (blocked, or B-state) thus making them inaccessible to myosin. In the B-state muscle is relaxed. Ca²⁺ binding to Tn-C opens a hydrophobic pocket between the long α-helix and the Ca²⁺-binding domain of Tn-C. The switch segment of Tn-I located in the vicinity of the inhibitory segment binds the pocket, releases the Tn-Tpm complex from actin and causes Tpm movement around the filament axis by ∼25°, partially releasing the Tpm obstruction of the myosin binding sites on actin. In this closed, or C-state, myosin heads attach to actin monomers on the filament to form weakly bound complexes. The subsequent transition of the actin-myosin complex to a strongly, stereo-specifically bound form causes further Tpm movement by ∼10° to the open, or O-state, of the regulatory system.

In vitro biochemical and EM studies used a saturating concentration of myosin heads to induce the transition between the C- and O-states (5, 6). An estimate of the size of the effective regulatory unit in vitro has shown that a single myosin head strongly bound to actin in the regulated thin filament containing Tpm and Tn effectively switches 10–12 neighbor actin monomers to the O-state (8). This means that the regulatory unit spreads to 55–66 nm.

However, the question remains whether the C- to O-state transition takes place upon a change in the fraction of myosin heads bound to actin in muscle fibers able to contract in a Ca²⁺ dependent manner. We used low angle x-ray diffraction to monitor changes in the Tpm azimuthal position. This approach was used 40 years ago for monitoring the B- to C-state transition during the onset of contraction of skeletal frog muscle by Kress et al. (9) who measured the time course of the changes in the intensity of the second actin layer line, A2, with a meridional spacing of ∼(18 nm)⁻¹ at a radial spacing of ∼(24 nm)⁻¹. They found that the B- to C-state transition precedes not only tension rise but also changes in the equatorial x-ray reflections which reflect the mass transfer from thick (myosin) to thin (actin) filaments. The authors observed a monotonic change in the intensity of x-ray reflections so could not detect any multi-step process, although it is likely that in the experiments (9) two consecutive transitions took place, firstly from the B- to C-state and then from C- to the O-state.

Here we report the results of measurement of changes in the 2D diffraction patterns in fully activated rabbit muscle fibers. The membranes of the fibers were permeabilized to allow complete control of the myofibrillar space. The change in activated state was caused by a transition from isometric contraction to steady shortening under a load in the range of 28–38% of the isometric level, at a constant temperature in the range 26–32°. Such a transition is accompanied by a substantial reduction in muscle stiffness (10, 11) suggesting that the fraction of the myosin heads strongly bound to actin also decreases substantially during shortening. Tpm movement was monitored by measuring the intensity of the A2 actin layer at reciprocal radii range of 0.15–0.275 nm⁻¹ in the low angle x-ray diffraction pattern. Simulation performed using high resolution structural models of the actin-Tpm complexes shows that in this radial range the A2 intensity depends on the azimuthal Tpm movement independently on the fraction of myosin heads bound to actin (12). The x-ray diffraction results show no evidence of a C- to O- transition during the change in state from isometric to shortening.

Materials and Methods

Muscle fiber samples and apparatus

Experiments were performed with thin bundles of three fiber segments from m. psoas of the rabbit, which were dissected, prepared and stored as described previously (13). The instruments and processes were described previously, including the Joule temperature-jump (T-jump) set-up, the change and measurement of muscle length and force, the remote control system and the composition of experimental solutions (14).

X-ray diffraction experiments

The experiments were carried out at beam line ID02 (ESRF, Grenoble, France) at constant wavelength of ∼0.1 nm at x-ray flux of 3.7–3.8 × 10¹³ photons/s. The x-ray beam was focused on the FReLoN CCD detector. Two series of experiments with identical protocol, but different detector-to-sample distances and detector resolution were performed. In the first series of six experiments, the detector operating at 1024 × 256 pixel resolution was placed 2.25 m from the sample; the beam size at the vertically-mounted fiber was 200 × 300 μm (vertically × horizontally, FWHM). In the second set of six experiments a broader range of reciprocal spaces up to 0.31 nm⁻¹ was examined: the detector operated at 480 × 480 pixel resolution and was placed 1.5 m from the sample; the beam size on the sample was 200 × 400 μm (vertically × horizontally, FWHM).

Experimental protocol

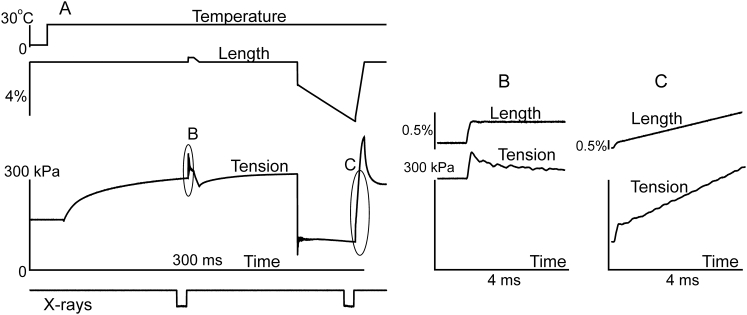
A bundle of three muscle fibers was activated by transfer from the relaxing to the activating solution containing 30 μM Ca²⁺ at 0–2°C at sarcomere length of 2.4–2.45 μm. After several seconds the bundle was transferred to an empty trough where its temperature increased to 4–5°C. The bundle was then subjected to a T-jump of 22–27°C amplitude that increased its temperature to 26–32°C. When steady-state isometric tension has developed, the bundle was exposed to the x-rays for 10–15 ms and the diffraction pattern was recorded at the detector. Then, a small length step shortening was applied to the bundle followed by a ramp shortening at a velocity of 1.2–1.5 muscle length per second so that tension decreased and reached a near steady-state level of 0.28–0.38 of the isometric value. At the end of shortening with a total amplitude of 4–5.5% of the initial bundle length, another x-ray diffraction pattern was recorded. Exposure time was equal for the two frames. In some experiments small step stretches of ∼0.3% of fiber length accomplished in 0.16 ms were applied just after each x-ray frame to measure instantaneous muscle stiffness (Fig. 1). The mechanical responses to a T-jump, step stretches and shortening in a representative experiment, and the signal of the electrically-operated x-ray shutter opening detected by a pin diode are shown in Fig. 1. After the protocol, the bundle was returned to a trough containing relaxing solution. The time during which the bundle remained in air was kept less than 3.5 s. The protocol was repeated several times in each of six fiber bundles, in each of two series of experiments until isometric tension at the higher temperature decreased to 85% of its initial level or the bundle broke. Isometric force at 26–32°C was 217 ± 17 kN/m² (mean ± SE, n = 12, full range 150–305 kN/m²).

Figure 1.

(A, top to bottom) A typical time course of temperature, length change, tension and x-ray shutter opening signal during a run of the experimental protocol in a bundle of three muscle fibers (from top to bottom, (A)). Step stretches were applied to the bundle immediately after each x-ray frame to measure instantaneous stiffness. (B and C) Expanded views of the parts of the record indicated by ellipses (B) and (C), respectively, in (A).

Data analysis

To correct for an increase in the bundle volume exposed to the x-rays during shortening, the second pattern was divided by a factor corresponding to the average extent of shortening of the bundle in the middle of the second frame (Fig. 1). The factor was 1.04–1.06 depending on the amount of shortening at the middle of the second x-ray exposure. The diffraction patterns collected in all runs of an identical protocol before and during shortening were added together. The background x-ray signal was subtracted and the patterns were mirrored as described previously (14). The meridional and off-meridional x-ray intensities were obtained using radial integration and background subtraction (14). The regions of radial integration were as follows: 0–0.02 nm⁻¹ (meridian), 0.02–0.036 nm⁻¹ (1,0 row line), 0.036–0.063 nm⁻¹ (1,1 row line), 0.063–0.15 nm⁻¹, and 0.15–0.275 nm⁻¹ (high angle). It was shown that the peak of the first myosin layer line, M1, is located within the 1,0 row line, while that of first actin layer line, A1, is located within the 1,1 row line (14, 15).

Modeling

A direct modeling approach used for simulation of the diffraction patterns from the regulated thin filaments in the actin-myosin lattice in the overlap zone of sarcomeres was described previously (12, 16). The calculations in the current work were based on an atomic model of the actin-Tpm-myosin complex derived from cryo-EM data (17). Only actin, Tpm and myosin heads with stereo-specifically attached motor domains were considered (20 and 40% of the total number of the heads in the overlap zone). The “neck” regions of the attached myosin heads were bent toward their origins at the backbone of myosin filaments (18). The calculations also considered that thin filaments in the non-overlap zone of the sarcomeres remain in the C-state independently of the fraction of myosin heads strongly bound to actin in the overlap zone. The transitions from the O- to C- and further to B-states were assumed to be accompanied by 10° and further 25° movement of Tpm with respect to the axis of the thin filament without rotation around the Tpm coiled-coil axis (12).

Results

Changes in instantaneous muscle stiffness upon transition from isometric contraction to shortening

To measure changes in instantaneous muscle stiffness caused by a transition from isometric contraction to steady shortening under low load, step stretches by ∼0.3% of muscle length completed in 0.16 ms were applied to the bundles just after the end of the first and the second x-ray exposure during the protocol (Fig. 1). Upon shortening stiffness decreased from 32.6 to 17.9 MPa (Fig. 1), i.e., to 55% of its isometric value. On average, the load during shortening was 28–38% of isometric. The average stiffness during shortening was 63 ± 6% (mean ± SD, n = 5) of that in isometric conditions.

Changes in the x-ray actin layer lines caused by muscle shortening

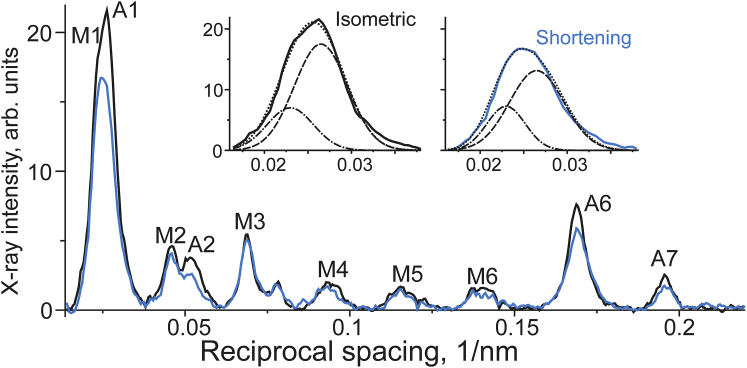
The intensities of the off-meridional x-ray reflections integrated at the reciprocal radii of 0.02–0.15 nm⁻¹ during isometric contraction and at the end of steady shortening collected in a set of experiments with a longer camera length and higher detector resolution are shown in Fig. 2.

Figure 2.

Off-meridional x-ray intensity plotted against meridional reciprocal spacing was collected from 43 runs of the experimental protocol in six bundles of muscle fibers during isometric contraction and steady shortening (solid lines, see color code). The intensity was integrated along equatorial direction at reciprocal radii from 0.005 to 0.15 nm⁻¹. Some myosin (M) and actin (A) layer lines are labeled. Inset: intensity profiles in the region of the M1 and A1 layer lines, and their breakdown into their Gaussian components, namely, the M1 (dash-dot lines) and A1 (dashed lines) layer lines during isometric contraction and shortening (see color code). To see this figure in color, go online.

The transition from isometric contraction to steady shortening under low load caused a decrease in the intensity of the actin but not of the myosin layer line (Fig. 1). As the most informative (14, 16) first actin layer line, A1, was not separated from the neighbor myosin M1 layer line, we estimated the amount of the decrease in the A1 intensity, I_A1, using Gaussian decomposition (19). Namely, we fitted the profile of the combined M1/A1 actin layer line into two Gaussian profiles which correspond to the M1 and A1 components. The results of such analysis are shown in the insets in Fig. 2. Upon shortening, the A1 component decreased to 75% of its isometric level while the M1 component did not change intensity. The A6 and A7 intensities, I_A6 and I_A7, also decreased to 82 and 71% of their isometric levels, respectively, when isometrically contracting muscle bundles were allowed to shorten under a load of about a third of isometric tension (Figs. 2 and 3).

Figure 3.

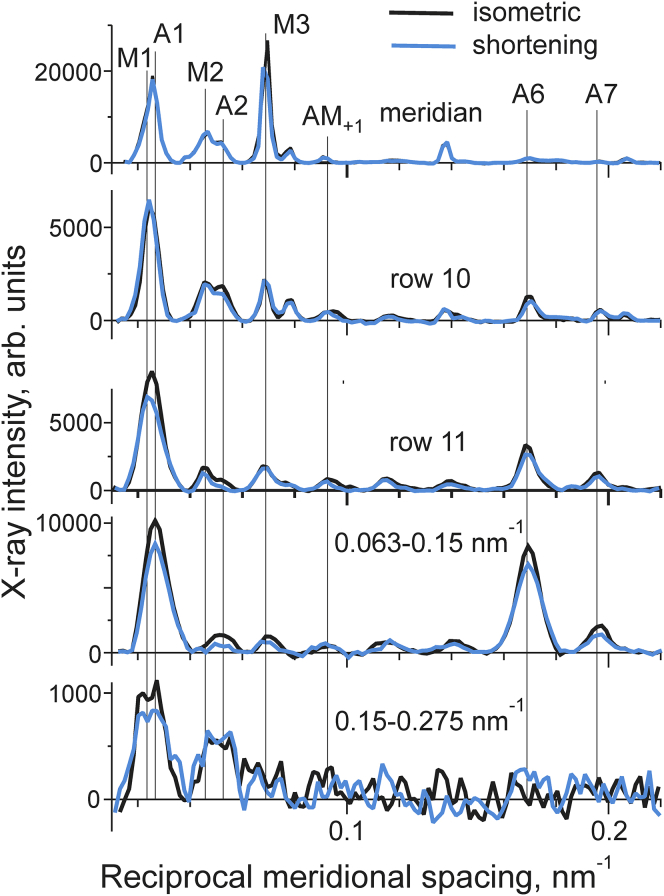
The x-ray intensity profiles during isometric contraction and at the end of shortening (color code is shown at the top) were plotted against reciprocal meridional spacing. The intensities were obtained by integration along the equator at reciprocal radial ranges shown above each panel (see also Materials and Methods section). The positions of the actin (A1, A2, A6, and A7), myosin (M1, M2, and M3) and actin-myosin (AM₊₁) layer lines are labeled. To see this figure in color, go online.

Changes in the high angle part of the actin layer lines caused by shortening

X-ray intensities obtained in another set of experiments with a shorter camera allowed us to estimate changes in the actin layer lines A1 and A2 in the radial region up to 0.3 nm⁻¹. The results of those experiments are presented in Fig. 3.

The only pronounced change in the meridian is a decrease in the intensity of the myosin meridional reflection M3 upon transition from isometric contraction to a steady shortening. This shortening-induced decrease in the M3 intensity was discovered by Huxley et al. (20) in whole frog muscle. The off-meridional intensities of the actin layer lines A1, A2, A6, and A7 and the beating actin-myosin layer line AM₊₁ at ∼(10.3 nm)⁻¹ at reciprocal radii up to 0.15 nm⁻¹ decreased upon shortening. As myosin heads strongly bound to actin contribute to the intensities of the actin layer lines in this range of reciprocal radii (12, 16), the data suggest that during shortening the fraction of such myosin heads becomes lower than that during isometric contraction.

In contrast, at reciprocal radii more than 0.15 nm⁻¹ the intensity of the A2 layer line did not change upon the transition from isometric to the shortening state. The amplitude of the peak on the outer part of the A1 layer line decreased slightly while its width somewhat increased (Fig. 3), so that the total A1 intensity did not change significantly.

Modeling of the x-ray diffraction pattern

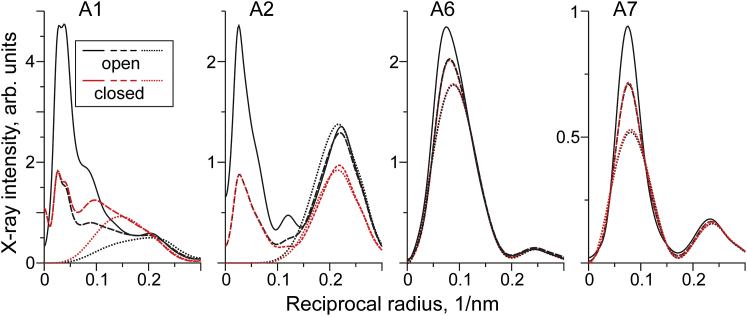
To find the regions in the x-ray diffraction pattern where changes in the intensity unambiguously report the Tpm movement independently from the fraction of myosin heads bound to actin, we performed direct modeling of the diffraction patterns at different positions of the tropomyosin strand on the thin filaments and with different fractions of myosin heads bound to actin. For this, the structural model (17) and a direct modeling approach (12, 16) were used. Calculations were performed for 0, 20 and 40% of myosin heads stereo-specifically bound to actin in the overlap zone of sarcomeres. Thin filaments in the non-overlap zone were always assumed to be in the closed state. The results of these calculations are shown in Fig. 4.

Figure 4.

The intensities of A1, A2, A6, and A7 actin layer lines calculated at different positions of the tropomyosin strand in the overlap zone of thin filament and with different fractions of myosin heads bound to actin. Solid, dashed, and dotted lines correspond to 40%, 20%, and 0% of myosin heads strongly bound to actin in the “open” (O-state) and “closed” (C-state) positions of Tpm, the color code is shown on the left. The O-state is the original structural model (17) while the C-state was obtained by azimuthal movement of the Tpm strand around the thin filament axis by 10°. To see this figure in color, go online.

As expected, the contribution of the actin-bound myosin heads to the A1 and A2 actin layer lines is limited to the range of 0–0.15 nm⁻¹. Outside this range, the A1 and A2 intensities depend only on the position of the Tpm strand on the thin filament and can be used for monitoring the transitions between different states of the regulatory proteins. On the other hand, the intensities of the A6 and A7 actin layer lines do not depend on the Tpm position.

X-ray diffraction measurement of Tpm movement

A number of models have been suggested to interpret the observed changes in the intensities of the actin layer lines in terms of Tpm movement on the surface of the actin filament (21, 22, 23). As these models are based on low resolution structures, they do not provide a quantitative description of the x-ray intensities observed in muscle diffraction experiments. Even the ratio of the intensities of bright A6 and A7 actin layer lines with spacings of ∼(5.9 nm)⁻¹ and ∼(5.1 nm)⁻¹ were not reproduced correctly in models for a spatial resolution worse than 2–2.5 nm (23).

In contrast to those early models, our model, to our knowledge, is the first one based on high resolution EM structures (17, 24). It provides a quantitative fit to the A2, A6, and A7 actin layer lines (12). The transition from the B-state in relaxed muscle fibers to the O-state in rigor is well described by the model including significant changes in the A2 intensity at reciprocal radii >0.15 nm⁻¹ (Fig. S1). The results of the modeling presented in Fig. S1 and in (12) suggest that the A2 intensity at reciprocal radial range of 0.15–0.3 nm⁻¹ gives a reliable index of Tpm movement, unaffected by contamination from other reflections and contribution from myosin heads. Calculations show that the transition from the O- to C-state should result in 26–33% reduction in the A2 intensity at reciprocal radii of 0.15–0.275 nm⁻¹ when the presence of the non-overlap zone in sarcomeres was taken into account.

Discussion

Reduction in the fraction of actin bound myosin heads upon shortening

Our stiffness measurements (Fig. 1) show that during shortening instantaneous muscle stiffness decreased to ∼63% of its isometric level. A substantial fraction of compliance of contracting muscle is caused by compliance of the actin and myosin filaments (25). For permeabilized fibers from rabbit muscle, the filament compliance was estimated to be 19 nm/MPa per half sarcomere, i.e., about half of the compliance of isometrically contracting muscle is caused by filament compliance (26). Taking into account that filament compliance is in series with that of the crossbridges, the increase in the compliance by a factor of 1/0.63 = 1.58 upon muscle shortening corresponds to an increase in the crossbridge compliance by at least a factor of two: 1.58 − 0.5 = 1.08 vs. 1.0 − 0.5 = 0.5. We therefore conclude that the fraction of actin-bound myosin heads which contribute to muscle stiffness was reduced by at least a factor of two after transition from isometric contraction to steady shortening under load of about a third of its isometric level.

A decrease in the A1, A2, A6 and A7 intensities also suggests that shortening induced a substantial decrease in the fraction of myosin heads stereo-specifically bound to actin. This decrease estimated from the decrease in I_A1 using the approach developed previously (14) also suggests a ∼2-fold decrease in this fraction. Changes in the intensities of the A6 and A7 layer lines upon a transition from isometric contraction to a steady shortening at a load of about a third of isometric tension found here (Figs. 2 and 3) were similar to those observed in whole frog muscle (27, 28). Such changes are predicted by a model in which the fraction of strongly bound myosin heads decreases from 40 to 20% (Fig. 4). As the fraction of strongly bound myosin heads during isometric contraction at a near-physiological temperature is ∼40% (14), we estimate that during shortening in our experiments this fraction decreased to ∼20% of all myosin heads in the overlap zone being strongly bound during muscle shortening at a velocity of 1.2–1.5 muscle lengths/s at 26–32°C.

How many strongly bound myosin heads are needed to keep Tpm in the O-state

The absence of a decrease in the A2 intensity at reciprocal radii above 0.15 nm⁻¹ suggests that a ∼2-fold reduction in the fraction of the actin-bound myosin heads does not induce the O- to C-state transition in the Tpm position on thin filament. This means that even a small fraction of myosin heads strongly bound to actin during muscle shortening is sufficient for keeping Tpm in the O-state. Taking this fraction to be 20% of the total number of 300 myosin heads per half of a thick filament, we obtain 300 × 0.2 = 60 strongly bound heads at full overlap. As the number of actin filaments is twice that of myosin filaments and there are two Tpm strands running along each thin filament, in average we have 15 myosin heads strongly bound to actin monomers in each actin filament region controlled by a Tpm strand. Taking the length of the overlap zone of thin and thick filaments to be ∼750 nm at full filament overlap in the sarcomeres, one obtains the average distance between myosin heads strongly bound to actin along a Tpm strand to be 50 nm. The theory of Smith et al. (29, 30) suggests that the persistence length of the Tpm strand that is considered as an elastic beam held in the vicinity of its position in the C-state by electrostatic forces between Tpm and the actin surface is ∼20 nm. Thus, on average, a single myosin head strongly bound to actin is able to maintain the O-state of the Tpm segment over a distance of ∼40 nm (2 × 20 nm). Later, a more precise theory was suggested (31) that accounts for the intrinsic helical shape of the Tpm strand. It turned out that the helical shape of the beam produces effective tension in the Tpm strand making it similar to a stretched string. This tension increases the effective length of a Tpm segment that is involved in the azimuthal shift of the protein filament when a myosin head binds strongly to actin. Estimates show that the “helicity induced tensile force” increases the effective length of the Tpm strand involved into the C- to O-state transition induced by binding of a single myosin head by a factor of ∼2 (Fig. S1 from (31). Therefore, the length of the Tpm segment involved into azimuthal movement upon binding of a head to actin is twice that estimated previously, and is ∼80 nm. A similar length of at least 60.5 nm = 11 × 5.5 nm was recently measured for an effective regulatory unit of a single regulated thin filament by direct visualization of binding of myosin molecules in vitro (32) and estimated in the in vitro experiments more than 20 years ago (8). This explains why at the average distance between myosin heads strongly bound to actin along the Tpm strand of ∼50 nm the strand remains in the O-state. It is worth mentioning that our data provide the lower limit for the size of the regulatory unit that is switched on to the O-state upon binding of a single myosin head to actin. We cannot exclude that fewer actin-bound myosin heads are able to keep the filament in the O-state. We also cannot exclude the possibility that further reduction in the fraction of strongly bound myosin heads, for example during shortening at maximal velocity, would cause the O- to C-state transition which is not seen during shortening under a load about one-third of the isometric load. Our experiments have been performed at full Ca²⁺ saturation of the regulatory system and they do not provide any information concerning the possible coexistence of the B- C- and O-states at partial activation of the thin filaments.

Conclusion

Our data suggest that the C-state is not observed in skeletal muscle fully activated with Ca²⁺. Even a small fraction of myosin heads which remain bound to actin during muscle shortening at low load is sufficient to maintain the regulatory system in the open state.

Author Contributions

S.Y.B. and N.A.K. contributed equally to this work. S.Y.B., N.A.K., M.A.F., and A.K.T. designed research; all authors performed research; N.A.K. and A.K.T. analyzed data; S.Y.B., N.A.K., M.A.F., and A.K.T. wrote the article.

Editor: James Sellers.