Line Tension Controls Liquid-Disordered + Liquid-Ordered Domain Size Transition in Lipid Bilayers

Abstract

To better understand animal cell plasma membranes, we studied simplified models, namely four-component lipid bilayer mixtures. Here we describe the domain size transition in the region of coexisting liquid-disordered (Ld) + liquid-ordered (Lo) phases. This transition occurs abruptly in composition space with domains increasing in size by two orders of magnitude, from tens of nanometers to microns. We measured the line tension between coexisting Ld and Lo domains close to the domain size transition for a variety of lipid mixtures, finding that in every case the transition occurs at a line tension of ∼0.3 pN. A computational model incorporating line tension and dipole repulsion indicated that even small changes in line tension can result in domains growing in size by several orders of magnitude, consistent with experimental observations. We find that other properties of the coexisting Ld and Lo phases do not change significantly in the vicinity of the abrupt domain size transition.

Introduction

Phase separation in the plasma membrane (PM) would have important implications for the life of a cell. PM properties could then change sharply over a small range of temperature or composition. Any factor that changes the energy per unit length of the interface (i.e., the line tension) could drive changes in interface length and thus domain size. However, the characterization of phase separation in cells has remained elusive due in part to the complexity of the PM: the lipid and protein components are numerous and diverse (1, 2, 3, 4), the two bilayer leaflets have very different compositions, and leaflet coupling is poorly understood (5).

The complexity of the PM makes chemically well-defined model membranes a valuable tool for studying principles governing phase coexistence. Phase diagrams are useful for describing the phase regions and the compositional ranges relevant to the PM. As shown in Fig. 1, coexistence of liquid-ordered (Lo) and liquid-disordered (Ld) phases occurs in mixtures of high melting temperature (high-T_m) lipids, low melting temperature (low-T_m) lipids, and cholesterol (chol) (6, 7, 8, 9). Domain size in the Ld + Lo region can be tuned by composition alone in mixtures of this type (10). At one extreme, domain growth is limited to the nanometer size scale, as found for 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC)/1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC)/chol (11, 12). At the other extreme, domain growth is limited only by vesicle size; in these mixtures, domains in giant unilamellar vesicles (GUVs) are many microns in diameter, as with DSPC/1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC)/chol (7). For convenience, we refer to these extreme cases as “nanodomains” and “macrodomains”, respectively.

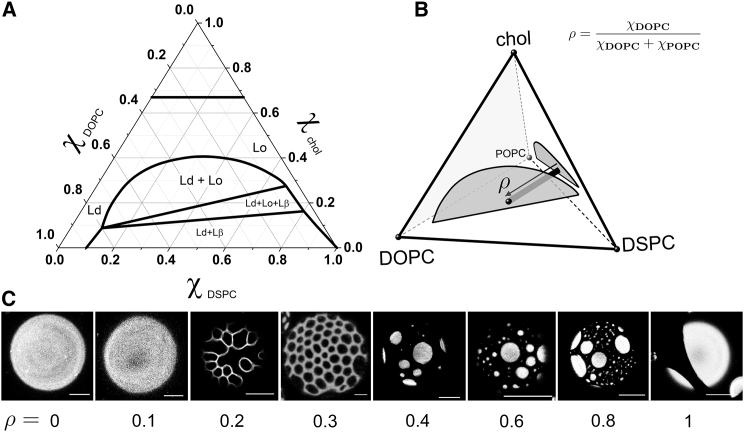
Figure 1.

Phase diagrams and phase morphologies in four-component mixtures. (A) Ternary phase diagram of DSPC/DOPC/Chol at 23°C (9). (B) Partial quaternary (tetrahedral) phase diagram of DSPC/DOPC/POPC/chol showing the Ld + Lo regions (shaded) of DSPC/DOPC/chol (near face) and DSPC/POPC/chol (far-right face) (9). Sample series referred to in the main text as ρ-trajectories connect a composition on the DSPC/POPC/chol face (ρ = 0, nanodomains) to a composition on the DSPC/DOPC/chol face (ρ = 1, macrodomains), where ρ represents the ratio of DOPC to total low-T_m lipid (i.e., DOPC + POPC). (C) Phase morphologies observed in GUVs along a ρ-trajectory in DSPC/(DOPC+POPC)/chol = 0.39/0.39/0.22: uniform (ρ < 0.2); modulated (0.2 ≤ ρ < 0.4); macroscopic round domains (ρ ≥ 0.4). Images were collected with a confocal microscope using 0.02 mol % C12:0 DiI. Scale bars, 10 μm.

Studies of the four-component mixture DSPC/DOPC/POPC/chol revealed that Ld + Lo domains remain nanoscopic at low DOPC fraction until an abrupt 100-fold size change occurs at higher DOPC fraction (10, 13). As we show here both experimentally and by modeling, increasing line tension drives this nano-to-macro transition. In the course of this size transition, macroscopic patterning of phases or “modulated phase morphology” occurs (10, 13). These patterns result from curvature energies that compete with line tension on a round vesicle to break up domains (14, 15, 16). The transition from nanometer-scale to micron-scale domains is apparent by imaging giant vesicles: GUVs appear uniform, then patterned, and then with large rounded domains as the compositional range is traversed (10, 13).

The abrupt domain size change that occurs with changing mixture composition is the main subject of this work. We show in six different mixtures how line tension increases abruptly when visible domains first appear. In contrast, we find that other properties of Ld and Lo phases do not change sharply even when the domain size does. We propose a model for this abrupt transition in which domain size is determined by a competition between line tension and dipole repulsion. Our results have implications for both how cells could potentially change domain size and what interactions could be responsible for the small size of domains in the PM.

Materials and Methods

Materials

Phospholipids were purchased from Avanti Polar Lipids (Alabaster, AL). Purity of phospholipids was found to be better than 99.5% using thin layer chromatography. Briefly, ∼20 μg of lipid was spotted on washed and activated Adsorbosil thin-layer chromatography plates (Alltech, Deerfield, IL) and developed in the solvent system chloroform/methanol/water = 65/25/4. Phospholipid concentrations were determined by inorganic phosphate assay (17), with an error < 1% from 10 replicates. Chol was from Nu-Chek Prep (Elysian, MN), and its stock solutions were made at defined concentrations using standard gravimetric procedures. The fluorescent dyes 1,1′-didodecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate (C12:0 DiI) and 2-(4,4-difluoro-5,7-dimethyl-4-bora-3a,4a-diaza-s-indacene-3-pentanoyl)-1-hexadecanoyl-sn-glycero-3-phosphocholine (BODIPY-PC) were from Invitrogen (Carlsbad, CA). Concentrations were determined by absorption spectroscopy using extinction coefficients of 143,000 M⁻¹ cm⁻¹ and 91,800 M⁻¹ cm⁻¹, respectively. Spin-labeled lipid 1-palmitoyl-2-(16-doxyl stearoyl) phosphatidylcholine (16PC) was a gift from Boris Dzikovski of the National Biomedical Center for Advanced ESR Technology at Cornell University. F^4,5GWALP23 synthesized according to Gleason et al. (18) was a gift from Roger Koeppe and Denise Greathouse. The peptide was dissolved in 2,2,2-trifluorethanol purchased from Sigma-Aldrich (St. Louis, MO), with the peptide concentration measured by tryptophan absorbance at 280 nm of a 1:500 dilution in methanol, using an extinction coefficient of 5500 M⁻¹ cm⁻¹. The buffer used in fluorescence experiments contained 5 mM PIPES (Sigma-Aldrich), 200 mM KCl (Sigma-Aldrich), and 1 mM EDTA (Sigma-Aldrich), at pH 7.0. Sucrose was from Fisher Scientific (Fair Lawn, NJ), and glucose from Teknova (Hollister, CA).

Composition conventions used

Lipid composition and the phase boundaries of each mixture are the key variables in this work, as shown in Fig. 1. We studied lipid mixtures of the type high-T_m lipid/low-T_m phosphatidylcholines (PCs)/chol: n-palmitoyl-D-erythro-sphingosylphosphorylcholine (pSM)/DOPC/POPC/chol; egg sphingomyelin (eSM)/DOPC/1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine (SOPC)/chol; eSM/DOPC/POPC/chol; DSPC/1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC)/1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC)/chol; DSPC/DPhPC/POPC/chol; DSPC/DOPC/POPC/chol; brain sphingomyelin (bSM)/DOPC/POPC/chol; bSM/DOPC/1-palmitoyl-2-linoleoyl-sn-glycero-3-phosphocholine (16:0,18:2PC)/chol; bSM/DOPC/SOPC/chol; and bSM/1-stearoyl-2-docosahexaenoyl-sn-glycero-3-phosphocholine (SDPC)/POPC/chol.

For molecular dynamics (MD) simulations, we used the mixture 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC)/1,2-dilinoleoyl-sn-glycero-3-phosphocholine (DUPC)/1-palmitoyl-2-linoleoyl-sn-glycero-3-phosphocholine (PUPC)/chol.

For all mixtures we define a key compositional parameter, the replacement ratio ρ (10, 13, 16), as the replacement of low-T_m nanodomain-forming PC for low-T_m macrodomain-forming PC. For example, when POPC is replaced by DOPC, ρ = [DOPC]/[DOPC + POPC] (Fig. 1 B), and when SOPC is replaced by DOPC, ρ = [DOPC]/[DOPC + SOPC]. For experiments at a single ρ-value, we describe the lipid composition with the mole fraction of each mixture component, e.g., DSPC/DOPC/POPC/chol = 0.39/0.35/0.04/0.22 for ρ = 0.1, and for experiments along ρ, composition is noted as DSPC/DOPC + POPC/chol = 0.39/0.39/0.22.

GUV preparation and phase morphology determination

GUVs were made by electroformation (19) with modifications. Briefly, each sample contained ∼300 nmol of a lipid mixture in 200 μL chloroform. A lipid film was created by evenly spreading the chloroform solution on indium tin oxide-coated microscope slides (Delta Technologies, Stillwater, MN) prewarmed on a hotplate with surface temperature measured at ∼50°C. After residual solvent was removed under vacuum for 2 h at ∼50 mTorr, indium tin oxide slides were sealed with Buna-N O-rings to create a chamber, which was then filled with 100 mM sucrose solution. Films were held above the transition temperature for 2 h in an AC field of 5 Hz, ± 1 Vpp, using a Wavetek Meterman FG2C Function Generator (Meterman, Everett, WA), followed by cooling to 23°C using a Digi-Sense Temperature Controller R/S (Cole Palmer, Vernon Hills, IL). Cooling rates for line tension measurements were varied to control domain size as described in the Supporting Material, and line tension was found to be independent of cooling rate (Fig. S4). GUVs were harvested into 100 mM glucose solution then allowed to settle for 1 h to remove debris before microscopy observations at 23°C. A wide-field microscope, Eclipse Ti (Nikon Instruments, Melville, NY) equipped with a 60×/1.2 NA water immersion objective, was used for all image-based experiments except partition coefficient determination, where an Eclipse C2+ Confocal Microscope (Nikon Instruments) was used. To keep the harvested GUVs intact, an osmolality difference between the sucrose and glucose solutions of <5 mOsmol/kg H₂O was ensured with the use of an osmometer (model No. 5004; Precision Systems, Natick, MA).

GUVs were visualized at 23°C using a wide-field fluorescence microscope. Sample chambers for observation consisted of a No. 1.5 coverslip and traditional microscope slide separated with a silicone spacer (Sigma-Aldrich) of 0.25 mm thickness. Fields of view were selected with bright field illumination before fluorescent images were acquired from emission of C12:0-DiI, which partitions into the Ld phase (20). For phase morphology determination we used this probe at 0.02 mol % of total lipid in the sample to limit light-induced artifacts (21). Images were acquired using a Zyla 5.5 sCMOS camera (Andor Technology, Belfast, UK). For each field of GUVs appearing to be free of defects (e.g., multiple layers or tethers), a series of approximately five 200-ms exposures was taken to capture the surface of GUVs opposite the coverslip. At various values of ρ for the four-component mixtures in this study, the numbers of GUVs with uniform, modulated, and macroscopic patterns were counted. GUVs appearing uniform but with compositions found by spectroscopic methods to have coexisting Lo and Ld phases (8, 9, 22) were counted as nanoscopic, as in Fig. 1 C (ρ = 0 and 0.1). GUVs at intermediate ρ-values exhibiting thin stripes or nonrounded small domains were considered to be modulated, as in Fig. 1 C (ρ = 0.2 and 0.3). Macroscopic GUVs were counted as those with large, rounded domains.

Line tension measurements

Line tension was measured using the flicker spectroscopy method of Esposito et al. (23). Briefly, the fluctuation spectrum of a phase domain boundary on a GUV is decomposed into Fourier modes that are related to line tension by

$$\langle {\left|{\mathit{u}}_{\mathit{n}}\right|}^2\rangle =\frac{2k_{\text{B}}T}{\sigma \pi R_0\left(n^2\mathrm{-}1\right)},$$ (1)

where n is the mode number, u_n is the mode amplitude, σ is the line tension, R₀ is the radius of a circle yielding the domain area, k_B is the Boltzmann constant, and T is the absolute temperature. For all measurements discussed below, the line tension value was the same whether the fluctuating domain was Ld or Lo and was independent of GUV size or domain size, as shown in more detail in Fig. S5. Additional details of the microscope setup, cooling methods, analysis methodology, and line tension controls are in the Supporting Material.

Bending energy measurements

Bending moduli were measured by fluctuation analysis of GUVs. Fluctuations at the GUV equator were observed by phase contrast microscopy (Fig. S8 A). Fluctuation spectra obtained from GUV contours were used to calculate the bending modulus through the relationship

$$\langle {\left|u\left(q\right)\right|}^2\rangle \mathrm{=}\frac{{\mathit{k}}_{\text{B}}\mathit{T}}{\mathit{\kappa }{\mathit{q}}^4+\mathit{\sigma }{\mathit{q}}^2},$$ (2)

where u(q) is the displacement normal to the membrane, q = (qx, qy) is the wave vector corresponding to the displacement, k_B is the Boltzmann constant, T is the absolute temperature, κ is the bending modulus, and σ is membrane tension. Tension was determined as in Pécréaux et al. (24), and the bending modulus calculated as in Gracià et al. (25). Additional information on measurement methods is provided in the Supporting Material.

The bending moduli of the coexisting phases were determined by measuring single-phase GUVs at the Ld and Lo tieline endpoint compositions at various values of ρ for DSPC/DOPC/POPC/chol. Tieline endpoint compositions near the lower boundary of the Ld + Lo region were taken from Konyakhina et al. (9) and are provided in Table S1.

Partition coefficient (K_p) measurements

Determination of 16PC K_p from electron spin resonance spectra

One hundred eleven samples were prepared along a ρ-trajectory of DSPC/DOPC + POPC/chol = 0.39/0.39/0.22 from ρ = 0 to 1, with all samples having coexisting Ld + Lo phases. Lipid stock solutions were combined with 0.3 mol % of the spin-labeled lipid 16PC. Chloroform was then removed under nitrogen flow, followed by high vacuum for 8 h. Lipid mixtures were hydrated with 18 MΩ-cm water (EMD Millipore, Billerica, MA) at 47°C for 1 h, vortexing every 15 min. Samples were centrifuged at 14,000 × g for 30 min to form lipid pellets, and the supernatant removed. Pellets were transferred into electron spin resonance (ESR) capillary sample tubes and centrifuged again with a hematocrit centrifuge at 3300 × g for 30 min before the tubes were sealed. Samples were held at room temperature for a minimum of 5 h after centrifugation before recording spectra on an ELEXSYS E500 CW ESR Spectrometer (Bruker, Billerica, MA) operated at X-band frequency (9.4 GHz) with 0.5 Gauss modulation. Reported spectra are the average of 16 scans obtained at 20–24°C.

ESR spectra were modeled as a linear combination of Ld- and Lo-phase spectra with relative amounts corresponding to the relative fraction of 16PC in either phase (26, 27, 28). We analyzed the composite Ld + Lo spectrum for each ρ-value using the corresponding tieline endpoint Ld and Lo spectra, assuming the tieline endpoint Ld and Lo spectra changed linearly with ρ. In fact, the Ld and Lo spectra changed little over the entire range of ρ from 0 to 1. Fitting was performed by least squares minimization of the entire spectrum. Details of the fitting procedure are found in the Supporting Material. Using the fitted fractions of 16PC in the two phases, K_p values were determined by comparing the fraction of 16PC in either phase to the phase mole fraction obtained from the Lever-Arm Rule on the corresponding tielines (8). We use the convention that K_p > 1 corresponds to preference for Ld phase. For ρ = 0, 0.3, and 1, the tieline endpoint Ld and Lo ESR spectra were simulated (see Fig. S13) with nonlinear least squares analysis of slow-motional ESR spectra (26, 27, 28).

Determination of BODIPY-PC K_p from fluorescence measurements

BODIPY-PC K_p was measured in bSM/DOPC/POPC/chol spectrophotometrically in a cuvette, and in GUVs with a confocal fluorescence microscope, in both cases using a dye/lipid ratio of 1:2500. For single-dye fluorescence experiments, typically 61 samples were prepared along a tieline. Phospholipid, chol, and dye were added in a glass tube using a repeating dispenser and a glass syringe. Aqueous buffer was added to each sample, and chloroform removed by rapid solvent exchange, as previously described in Buboltz and Feigenson (29), except that the equilibration started at 55°C, with cooling at 2°C/h to 23°C. Steady-state fluorescence was measured at ambient temperature (23°C) with excitation/emission wavelengths at 500/520 nm, slits 5/5 nm, and 10 s integration time using a model No. F-7000 FL Spectrofluorimeter (Hitachi High Technologies America, Schaumburg, IL). K_p values were determined as above (8). For microscopy experiments, GUVs of bSM/DOPC + POPC/Chol = 0.40/0.40/0.20 were formed by electroformation. Images were obtained at 23°C with a 60× water immersion objective. Additional details of K_p determination, including line scan protocols and self-quenching corrections, are described in the Supporting Material.

Model for calculating equilibrium domain size

Our approach to modeling domain size is to identify an interaction that could compete with line tension but not scale linearly with line tension. Dipole repulsion within the bilayer could be such an interaction, as described by Amazon and Feigenson (30). An initial question is whether dipoles in one leaflet would have their fields largely cancelled by the opposing dipoles in the other leaflet. This does occur for the terminal methyl dipoles that give rise to long-range repulsion in lipid monolayers (31), but the dipoles of interest in this study are located farther apart in the interfacial region.

To explore the implications of dipole repulsion for domain size, we modeled the total energy of a phase-separated bilayer as a sum of a phase boundary energy from line tension E_perim that scales with domain perimeter and an electrostatic potential energy E_elec arising from permanent lipid dipoles, with $E_{\text{total}}=E_{\text{perim}}+E_{\text{elec}}$. For N_D domains of total area α, $E_{\text{perim}}=2\pi R_D{N}_D\sigma$, where σ is the line tension and $R_D=\sqrt{\alpha /\left(\pi N_D\right)}$ is the domain radius. For lipids distributed identically in the two bilayer leaflets and dipoles aligned with the bilayer normal, the total electrostatic potential energy of the bilayer is a sum of intra- and interleaflet contributions, i.e., $E_{\text{elec}}=2V_{\text{intra}}+V_{\text{inter}}$, and

$$V_{\text{intra}}=N_D\frac{1}{2}\frac{N_L^2}{4\pi \epsilon {\epsilon }_0}{\int }_a^{2R_D}\frac{{\left(\Delta \varphi \epsilon {\epsilon }_0{A}_L\right)}^2}{r^3}P\left(r,R_D\right)dr,$$ (3)

$$V_{\text{inter}}=N_D\frac{N_L^2}{4\pi \epsilon {\epsilon }_0}{\int }_0^{2R_D}\left[\frac{3{\left(h\Delta \varphi \epsilon {\epsilon }_0{A}_L\right)}^2}{{\left(h^2+r^2\right)}^{5/2}}-\frac{{\left(\Delta \varphi \epsilon {\epsilon }_0{A}_L\right)}^2}{{\left(h^2+r^2\right)}^{3/2}}\right]P\left(r,R_D\right)dr,$$ (4)

where N_L is the total number of lipid dipoles per leaflet in the domain, A_L is the average lipid molecular area, h is the separation distance between opposing dipole layers, ε₀ is the permittivity of free space, ε is the dielectric constant (here, the dielectric constant of the bilayer region near the dipoles), $a=2\sqrt{A_L/\pi }$ (the lower limit of the V_intra integral) is the distance of closest approach between two dipoles, and Δϕ is the electrostatic potential difference between the domain and surrounding phase. The distribution of dipole separation distances P(r,R_D) within the domain is given by the pair-distance distribution function for a disk (for details see the Supporting Material section Dipole-Dipole Repulsion Model),

$$P\left(r,R_D\right)=\frac{r}{\pi R_D^3}\left\{4R_D{\tan }^{-1}\left[\frac{R_D}{r}\sqrt{4-{\left(r/R_D\right)}^2}\right]-r\sqrt{4-{\left(r/R_D\right)}^2}\right\}.$$ (5)

This model does not explicitly treat the influence of the water and ionic strength. Instead, we made use of the finding by Zhou and Schulten (32) that the contribution of the lipid headgroups and the oriented water nearly cancel, so that the measured membrane dipole potential is determined by the lipid ester moieties. Additional details and a full derivation are found in the Supporting Material.

Nanodomain size measurements

Large unilamellar vesicle (LUV) samples for domain size measurements were prepared as follows. Lipid mixtures were prepared by transferring volumes of lipids and chol stocks in chloroform to a glass vial with a glass syringe (Hamilton USA, Reno, NV). Organic solvent was removed with a nitrogen stream and gentle heating, followed by vacuum drying for > 12 h. Dry lipid films were hydrated with a 34.5% (v/v) D₂O/H₂O mixture preheated to 50°C and vortexed to generate multilamellar vesicles (MLVs). The MLV suspension was incubated at 50°C for 1 h, followed by five freeze/thaw cycles between −80 and 50°C. LUVs were prepared using a Mini Extruder (Avanti Polar Lipids) assembled with a single polycarbonate filter (30-, 50-, 100-, or 200-nm diameter pore size) and heated to 50°C. Final sample concentrations were 10–20 mg/mL, which allowed for sufficient water between vesicles to eliminate the interparticle structure factor (33).

Small-angle neutron scattering (SANS) experiments were conducted at Oak Ridge National Laboratory (ORNL), using both the CG-3 BioSANS instrument of the High Flux Isotope Reactor and the BL-6 extended Q-range small-angle neutron scattering (EQ-SANS) instrument of the Spallation Neutron Source. LUV suspensions were loaded into 1 mm path-length quartz banjo cells (Hellma USA, Plainview, NY) and mounted in a temperature-controlled cell holder with ∼1°C accuracy. BioSANS data were collected at a 14.5 m sample-to-detector distance using 6 Å wavelength neutrons (full width half-maximum 15%), resulting in a total scattering vector of 0.005 < q < 0.06 Å⁻¹. EQ-SANS data were taken at a 4.0 m sample-to-detector distance with a 6.0–9.5 Å wavelength band for a total scattering vector of 0.01 < q < 0.1 Å⁻¹. Scattered neutrons were collected with a two-dimensional (2D) (1 × 1 m) ³He position-sensitive detector (ORDELA, Oak Ridge, TN) with 192 × 192 pixels (BioSANS) or 256 × 192 pixels (EQ-SANS). The 2D data were reduced using the software Mantid (34). During reduction, data were corrected for detector pixel sensitivity, dark current, and sample transmission, and the background scattering from water was subtracted. The one-dimensional scattering intensity $I\left(q\right)$ [$q=4\pi \text{sin}\left(\theta \right)/\lambda$, where λ is the neutron wavelength and 2θ is the scattering angle relative to the incident beam] was obtained by radial averaging of the corrected 2D data.

Nanodomain sizes were determined by analysis of I(q) data using a coarse-grained Monte Carlo method described in Heberle et al. (11) and Pan et al. (35). Additional details are found in the Supporting Material.

MD simulations

Coarse-grained MD simulations were performed to characterize the size, shape, and dynamics of nanodomains. Simulations of phase-separated DPPC/DUPC/PUPC/chol systems with 20,000 total lipids were examined at ρ-values 0.5, 0.65, and 0.8. The simulations contained approximately four times as many lipids as previously studied for an identical composition (36), enabling consideration of the effect of system size on measured nanodomain properties. Bilayers were constructed using the CHARMM-GUI tool and then tiled to quadruple the system size (37, 38, 39, 40). The Martini force field (version 2.1) was implemented in GROMACS 4.6.6 (41, 42, 43, 44) using an NPT ensemble with a 30 fs time step under periodic boundary conditions in a box ∼74 × 74 × 12 nm. A temperature of 295 K and pressure of 1 atm were maintained by a V-rescale thermostat (time constant 1 ps) and semiisotropic Parrinello-Rahman barostat (time constant 12 ps), respectively. Temperature bath coupling was separate for lipids and solvent. The GPU-compatible Verlet cutoff scheme was used with electrostatic and van der Waals potentials shifted to reach zero at 1.1 nm. Center-of-mass motion was removed each 10 time steps. All simulations were conducted on Titan at the Oak Ridge Leadership Computing Facility.

Analysis was performed using a custom Python script incorporating the MDTraj library (45). A Voronoi tessellation of lipids in a single leaflet determined each molecule’s nearest neighbors as those with which it shared a Voronoi ridge. Phase determination for each lipid was based on the lipid and its nearest neighbors, with enrichment in DPPC and chol serving as a marker of the Lo phase, and depletion of these lipids a marker of the Ld phase. For details, see the Supporting Material.

Results

The mixtures examined here are described by phase diagrams of the type shown in Fig. 1 A for a three-component lipid mixture of DSPC/DOPC/chol (9). More generally, this phase behavior occurs for mixtures of the type (high-T_m PC or sphingomyelin)/(low-T_m PC)/chol, as found by several researchers (46, 47). Important for our studies is that a mixture is separated into immiscible liquid domains. To study this behavior, we employ vesicles of different size and lamellarity (LUVs, GUVs, and MLVs) as dictated by the constraints of different experimental techniques. Whereas vesicle size constrains the maximum possible domain size, curvature has no measurable effect on the structure of PC bilayers for vesicle diameters larger than 50 nm (33, 48) as used in this study. Furthermore, although the presence of multiple lamellae increases the cooperativity of phase transitions in single component bilayers, the same transitions are nevertheless seen in LUVs, GUVs, and MLVs (49). These findings suggest that vesicle size and curvature do not significantly affect phase behavior.

Phase boundaries, as shown in Fig. 1 A, have been determined as described in the literature (7, 8, 9, 22), mainly using steady-state fluorescence spectroscopy, fluorescence microscopy, ESR, and differential scanning calorimetry. Other researchers have found similar boundaries by use of nuclear magnetic resonance and x-ray diffraction (46, 50, 51). The mixture DSPC/POPC/chol is described by a similar phase diagram to that in Fig. 1 A (9), except that the coexistence of Ld + Lo domains was detected by Förster resonance energy transfer, ESR, and SANS, but not visualized with optical microscopy, suggesting domains of a size below the optical resolution limit (11, 12). In the four-component lipid mixture DSPC/DOPC/POPC/chol, this transition can be explored with the replacement of POPC by DOPC, where ρ = [DOPC]/[DOPC + POPC], as in Fig. 1 B. As described below, we measured how physical properties, including domain size, line tension, bending rigidity, order and rotational diffusion of a probe, and probe partitioning, change along this ρ-trajectory.

Domain size exhibits an abrupt transition with composition that is correlated with line tension

We recorded the visual appearance of domains examined in GUVs with fluorescence microscopy. Fig. 1 C shows images of GUVs composed of DSPC/DOPC/POPC/chol having compositions along a ρ-trajectory and is a representative example for all mixtures studied. For ρ = 0 and 0.1, GUVs appeared uniform, but Förster resonance energy transfer, ESR, and SANS studies revealed nanodomains with sizes below optical resolution (8, 9, 22). At higher ρ-values from 0.4 to 1, GUVs exhibited large, round domains with micron-sized diameters. In the course of the transition between GUVs with uniform appearance and GUVs with large and round domains, we observed a composition range where GUVs showed modulated phase patterns; we previously termed this region the “ρ-window” (9, 10, 13, 16). Fig. 1 C reveals modulated phases for DSPC/DOPC/POPC/chol at ρ = 0.2 and 0.3. These modulated phase patterns mark the first appearance of visible domains, and thus a pronounced change in domain size from tens of nanometers to microns.

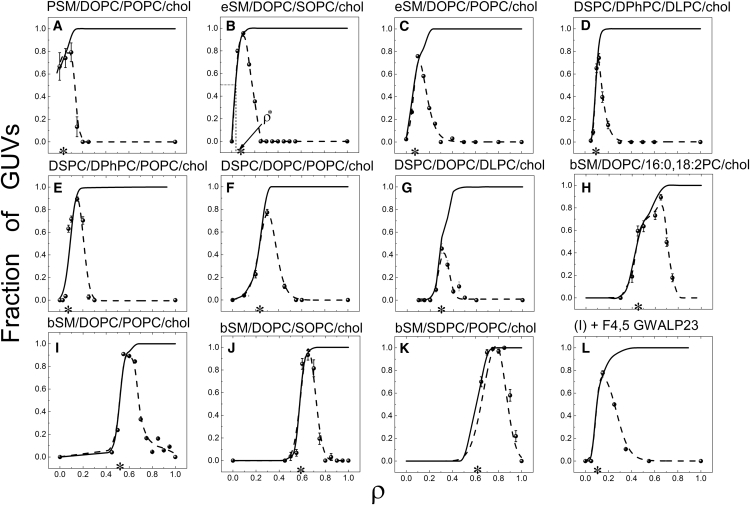
Similar abrupt domain size transitions were observed for 12 other mixtures, although at different ρ-values for each mixture, as shown in Fig. 2. The fraction of GUVs exhibiting either modulated phases or round macroscopic domains is indicated by a solid line in Fig. 2; we emphasize this sum because it better represents the domain size transition from nanodomains (uniform GUVs) to visible domains. For convenience in the following discussion, we define ρ^∗ as the composition at which half of GUVs have visible domains. Below, we show that ρ^∗ is correlated with line tension. As shown in Fig. 2, the size transition marked by ρ^∗ depended upon both the high-T_m and the low-T_m lipids. For example, in mixtures of DOPC/POPC/chol with the high-T_m lipids pSM, eSM, DSPC, or bSM, ρ^∗ appeared at 0, 0.07, 0.24, and 0.52, respectively (Fig. 2, A, C, F, and I). The nature of the low-T_m nanodomain-forming PC also affected ρ^∗: For mixtures of bSM/DOPC/chol with the components 16:0,18:2-PC, POPC (16:0–18:1PC), or SOPC (18:0–18:1), ρ^∗ appeared at 0.45, 0.52, and 0.58, respectively (Fig. 2, H, I, and J). Thus, increased unsaturation and shorter acyl chains of the low-T_m nanodomain-forming lipid shifted ρ^∗ to lower values in these mixtures, consistent with a previous report that a thinner Ld phase results in a greater hydrophobic mismatch and possibly a higher line tension (11) inducing the formation of visible domains at lower ρ. Also consistent with thickness mismatch-driven line tension is the observation that low-T_m macrodomain-forming PCs with different hydrophobic thickness resulted in different ρ^∗ values: in mixtures with DSPC/DLPC/chol (Fig. 2, D and G) and DSPC/POPC/chol (Fig. 2, E and F), a smaller amount of DPhPC (hydrophobic thickness 27.2 Å at 30°C (48)) compared to DOPC (hydrophobic thickness 29.1 Å at 30°C (52)) was needed to form macroscopic domains. Finally, contrary to theoretical predictions that hybrid and nonhybrid lipids should behave differently (53), DLPC and POPC resulted in a nearly identical ρ-window (13, 54) in mixtures with DSPC/DOPC/chol (Fig. 2, F and G).

Figure 2.

(A–L) Morphology of coexisting Ld + Lo domains changes with ρ. In GUVs prepared from four-component lipid mixtures, phase domain morphology changes from uniform (i.e., no visible domains), to modulated patterns, to macroscopic round domains as ρ is varied from 0 to 1. The fraction of GUVs showing modulated domain morphology is plotted as a function of ρ for different four-component lipid mixtures (dashed lines). (Solid line) Fraction of GUVs showing modulated phases + the fraction of GUVs showing macroscopic domains. (Asterisk) Midpoint of the domain size transition, denoted as ρ^∗. Data for (F), (G), and (K) originally appeared in Heberle et al. (54), Goh et al. (13), and Konyakhina and Feigenson (55), respectively. Lipid compositions of GUVs are described in Table S1.

We also examined mixtures with compositions that are closer to that of the PM. In bSM/SDPC/POPC/chol (55), we found a high ρ^∗ value of 0.61 (Fig. 2 K), an indication of enhanced stability of nanoscopic domains. In contrast, a mixture containing an α-helical transmembrane peptide appears to have a markedly increased line tension. Fig. 2, I and L, shows the ρ-trajectory for bSM/DOPC/POPC/chol in the absence and presence of 4 mol % of F^4,5GWALP23, respectively, revealing a decrease in ρ^∗ from 0.52 to 0.1 induced by the peptide.

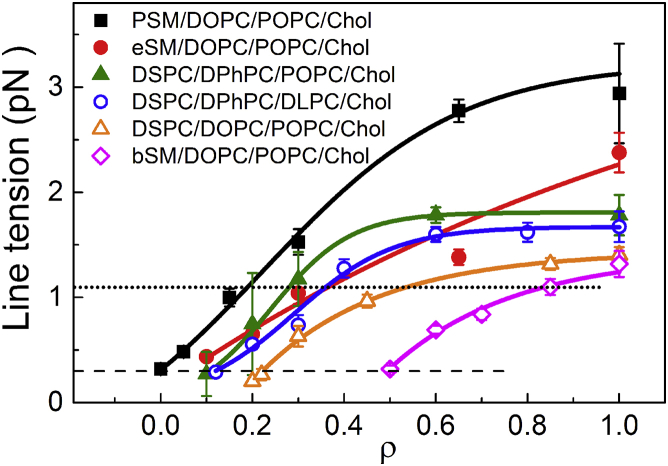
We used GUV flicker spectroscopy to measure line tension for six mixtures, shown in Fig. 3. Comparing these data to the ρ-windows in Fig. 2, several trends are apparent: 1) for each of the mixtures, the ρ-value where micron-scale domains first appeared corresponds to a line tension of ∼0.3 pN; 2) large, round domains always correspond to line tensions >∼1.1 pN; 3) line tension values for high-T_m sphingomyelins followed the trend pSM > eSM > bSM in mixtures with DOPC/POPC/chol, consistent with a progressively higher ρ-window for SM in this series, with ρ^∗ = 0.1, 0.15, and 0.55, respectively (Fig. 2, A, C, and I); 4) with the high-T_m lipid DSPC, similar line tensions and ρ^∗ values were found in mixtures with DPhPC/DLPC/chol and with DPhPC/POPC/chol, whereas lower line tension and a higher ρ^∗ were found with DOPC/POPC/chol. We conclude that changes in ρ^∗ for these lipid mixtures reflect changes in the Ld/Lo line tension.

Figure 3.

Line tension increases in a ρ-trajectory. Line tension for six four-component lipid mixtures measured with GUV flicker spectroscopy. In all mixtures, visible domains first appear at ∼0.3 pN (dashed line), while domains become fully rounded at ∼1.1 pN (dotted line). Line tension was measured by fluctuation analysis of either an Lo or Ld domain using wide-field fluorescence microscopy at 23°C with fluorescent dye C12:0-DiI at 0.2 mol %. Error bars correspond to SE.

Physical and chemical properties of Ld and Lo phases do not change at the abrupt domain size transition

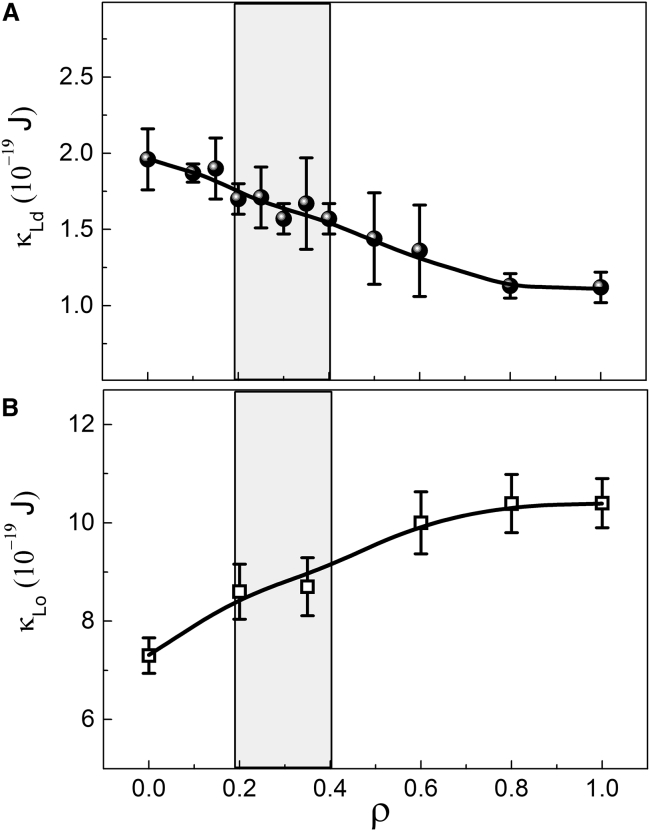
We measured a phase property of the bilayer, the bending modulus κ, for single-phase GUVs. These measurements were performed separately for Ld and Lo compositions from the nanoscopic to the macroscopic regime (ρ = 0–1), including the region where an abrupt domain size transition occurs. Fig. 4 shows the bending moduli of the Ld and Lo phases, κ_Ld and κ_Lo, for DSPC/DOPC/POPC/chol. As ρ was varied from 0 to 1, κ_Ld decreased from 1.9 to 1.1 × 10⁻¹⁹ J, while κ_Lo increased from 7.3 to 10.4 × 10⁻¹⁹ J. For both the Ld and Lo phases, variation in bending moduli over the entire ρ trajectory was less than twofold, and only 5–10% within the region of abrupt domain size change indicated by the shaded regions (corresponding to the ρ-window of Fig. 2 F).

Figure 4.

Lo and Ld bending moduli do not show abrupt transitions in a ρ-trajectory. The bending modulus of (A) Ld phase (κ_Ld) and (B) Lo phase (κ_Lo) measured at different ρ-values in DSPC/DOPC/POPC/chol. As POPC is replaced by DOPC (i.e., increasing ρ), κ_Ld gradually decreases, while κ_Lo gradually increases. Within the ρ-window where domain size exhibits an abrupt increase (shaded region), changes in bending rigidity of either phase are <10%. Error bars correspond to SE (n > 5).

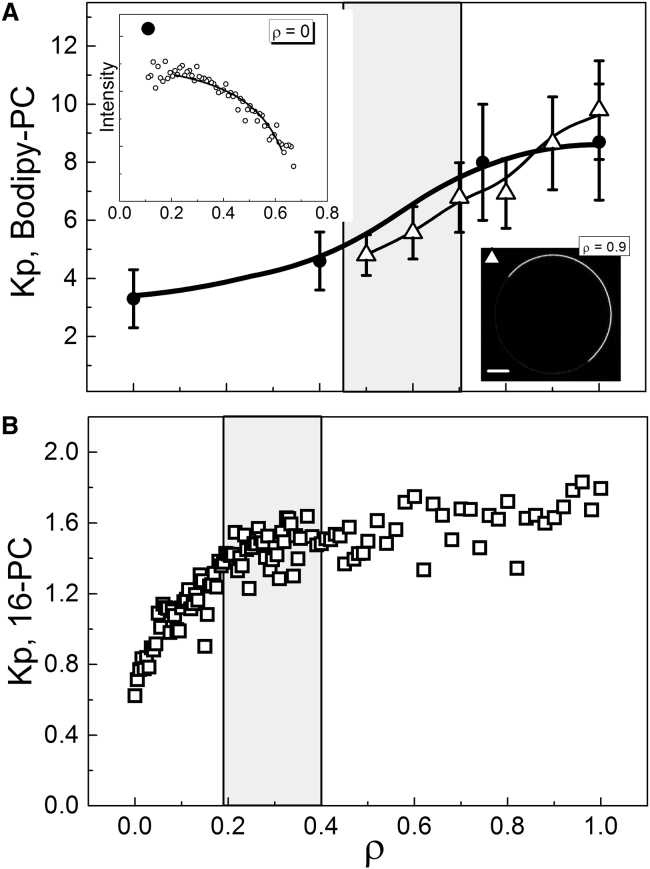
We also measured the partition coefficient K_p between Ld + Lo domains of a fluorescent probe, BODIPY-PC, and an ESR probe, 16PC, in the composition range ρ = 0–1. Here, K_p = [probe]^Ld/[probe]^Lo and K_p > 1 indicates preference for Ld phase. Fig. 5 A shows the K_p of BODIPY-PC in bSM/DOPC/POPC/chol obtained either from fluorescence microscopy measurements of GUVs (open triangles) or from fluorescence spectroscopic measurements (solid circles), revealing good agreement between these methods. The K_p of BODIPY-PC increases from 3 to 9 over the composition range ρ = 0–1, and by ∼30% in the vicinity of the abrupt domain size transition indicated by the shaded region (corresponding to the ρ-window of Fig. 2 I). For the ESR probe 16PC, K_p values in DSPC/DOPC/POPC/chol increase from 0.7 to 1.8 over the composition range ρ = 0–1 (Fig. 5 B). There are no abrupt changes in K_p, and in particular <10% change in the shaded region corresponding to the ρ-window of Fig. 2 F, where domain size changes hundreds of fold. Moreover, the order parameter S₀ and rotational diffusion coefficient R_⊥ of 16PC in the Ld and Lo phases hardly changed: Table 1 shows nearly constant values of S₀ and R_⊥ for ρ = 0, 0.3, and 1, representative of nanoscopic, transition, and macroscopic compositions. We conclude that physical and chemical properties of Ld and Lo phases do not undergo abrupt changes despite the abrupt change in domain size that occurs along a ρ-trajectory.

Figure 5.

Probe partition coefficients do not show abrupt transitions along a ρ-trajectory. Partition coefficient K_p between Ld and Lo phases for: (A) the fluorescence probe BODIPY-PC in bSM/DOPC/POPC/chol, and (B) the spin-label probe 16PC in DSPC/DOPC/POPC/chol. Within the ρ-window where domain size exhibits an abrupt increase (shaded regions), changes in K_p are gradual. Also shown in (A) are: (upper-left inset) the fluorescence intensity (symbols) and fit to a partitioning model (solid line) of Bodipy-PC along a thermodynamic tieline at ρ = 0, and (lower-right inset) fluorescence micrograph revealing the partitioning of Bodipy-PC in a GUV at ρ = 0.9 (scale bars, 5 μm, temperature 23°C). For details, see the Supporting Material.

Table 1.

ESR Reveals Small Changes of Ld and Lo Phases along the Domain Size Transition

ρ	Ld Phase		Lo Phase
	S0	R⊥ (log10 s−1)	S0	R⊥ (log10 s−1)
0	0.13	8.4	0.36	8.6
0.3	0.12	8.5	0.36	8.6
1.0	0.11	8.5	0.34	8.5

Order parameter, S₀, and rotational diffusion coefficient, R_⊥, of the spin probe 16PC in Ld and Lo phases for different ρ-values that represent nanoscopic, transition, and macroscopic lipid compositions.

Competing interactions could drive the domain size transition

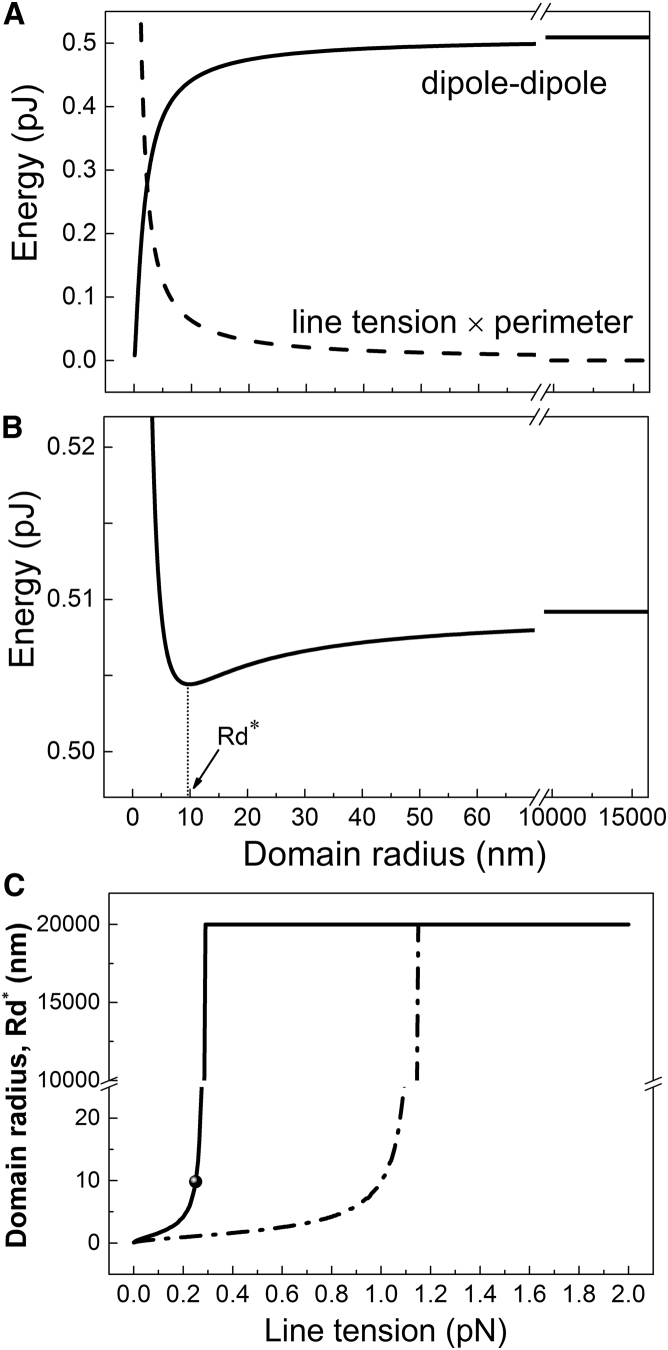
With no evidence of an abrupt transition in several properties characteristic of Ld and Lo phases, we next explored what kind of interaction could lead to an abrupt transition in domain size. We modeled the dependence of domain size on line tension together with dipole-dipole repulsion that could originate, for example, in the permanent dipoles of the carbonyl-glycerol backbone (Fig. S14). Fig. 6 A shows the energies of the individual competing interactions (i.e., boundary energy arising from line tension and electrostatic energy arising from dipole-dipole repulsion) as a function of domain radius, calculated for a line tension of 0.25 pN. Fig. 6 B reveals that the total energy is minimized at a particular domain size, which we define as the equilibrium domain radius R_d^∗. Fig. 6 C shows R_d^∗ as a function of line tension. At very low line tensions, electrostatic repulsion dominates and numerous small domains are favored. At high line tensions, the boundary energy dominates and a single, large domain is favored. These two competing interactions are balanced at intermediate line tensions, resulting in stable domains with nanoscopic sizes. The precise location of the transition is influenced by the choice of model parameters: for example, increasing the Ld/Lo electrostatic potential difference Δϕ from 0.1 V (solid line) to 0.2 V (dot-dashed line) increases domain repulsion, thereby stabilizing nanodomains to higher line tension values.

Figure 6.

A model of competing interactions describes the domain size transition. (A) Energetic contributions from domain interface (line tension × perimeter) and dipole-dipole repulsion as a function of domain radius, calculated for a line tension value of 0.25 pN. (B) The sum of interfacial and electrostatic energy in (A) exhibits a minimum value at domain radius R_d^∗. (C) R_d^∗ plotted versus line tension reveals an abrupt domain size transition for model parameters ε = 8, h = 3.0 nm, A_L = 60 Å², and Δϕ = 0.1 V (solid line) or 0.2 V (dot-dashed line). A description of model parameters is found in the Supporting Material.

We further examined several model parameters to find the line tension value where the domain size transition occurs (Figs. S15 B and S16). The critical line tension value λ^∗ at which domain size abruptly increases depends strongly on the dipole potential difference: we found that varying Δϕ over the range 0.05–0.5 V resulted in λ^∗ values increasing from 0.08 to 8 pN. Large changes were also observed upon varying the dielectric constant ε over the range 2–20, which resulted in λ^∗ increasing from 0.05 to 0.8 pN. In contrast, varying the separation distance of the dipole layers h, or the area per dipole A_L, had negligible influence on the critical line tension value. Although the precise line tension value at the domain size transition depends on the choice of model parameters, the finding of an abrupt transition is robust. It occurs for a wide range of parameter values, as well as in related models where the domain potential is treated as arising from discrete dipoles, or from pairs of discrete charges, or where the electrostatics of both the domain and the surrounding in a spherical phase-separated vesicle are treated separately. These results are presented in the Supporting Material.

Nanoscopic domains are not significantly influenced by vesicle size, but have a complex shape

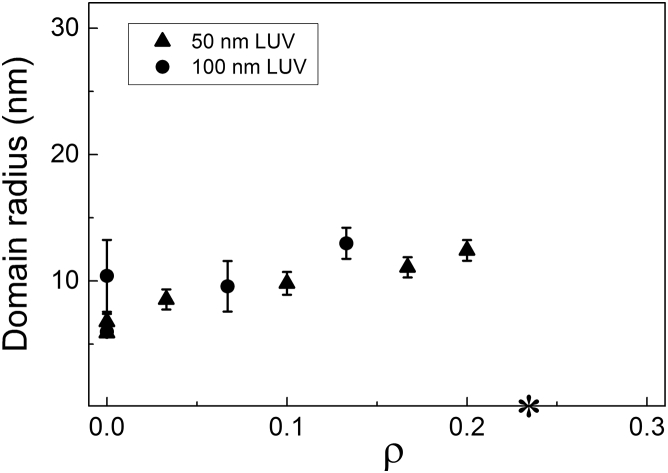
In the nanoscopic regime, GUVs appear uniform (e.g., Fig. 1 C, ρ = 0 and 0.1), thus different experimental methods are required to study the coexistence of Ld + Lo domains. We used SANS to measure domain size in 50- and 100-nm diameter LUVs composed of DSPC/DOPC/POPC/chol, finding only a small influence of vesicle size on nanodomain size as a function of ρ (Fig. 7). Additional details about the minimal dependence of nanodomain size on LUV size are found in the Supporting Material.

Figure 7.

SANS reveals domain size in the nanoscopic regime along ρ. Domain radius obtained from Monte Carlo modeling of SANS data for LUVs composed of DSPC/DOPC/POPC/chol. Within the nanoscopic regime at ρ < 0.2, domain radius increases gradually from 6 to 12 nm for LUVs of either 50 nm diameter (triangles) or 100 nm diameter (circles). The asterisk marks ρ^∗, where 50% of the GUVs were observed with modulated phases or with macrodomains.

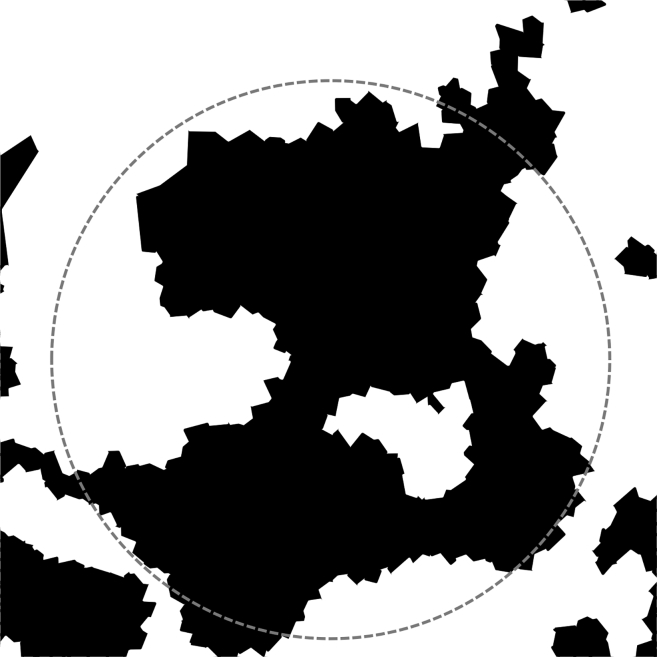
Our SANS model assumes round nanodomains to facilitate analysis. However, coarse-grained MD simulations revealed a more complex domain morphology. Fig. 8 shows a characteristic simulation snapshot of a nanodomain for ρ = 0.65 after 3.6 μs of simulation, together with a circular outline diameter of ∼25 nm as a reference. These simulations show that nanodomains are in general not circular. Rather, they display complex and dynamic morphology, even in an equilibrated system long after separation into coexisting Ld + Lo domains.

Figure 8.

Simulated nanodomains have a complex morphology. A top-down view of a nanodomain in a coarse-grained MD simulation of DPPC/DUPC/PUPC/chol at ρ = 0.65 reveals a complex, noncircular domain shape. Voronoi cells of lipids in the Lo phase are shown in black, while those in the Ld phase are shown in white. The snapshot was obtained after 3.6 μs of simulation at a temperature of 22°C. A dashed gray circle of 25 nm diameter is shown as a reference.

Discussion

As we show in this work, the energy per unit length of the interface (i.e., the line tension) in a phase-separated bilayer can be dramatically influenced by lipid composition, thereby driving changes in interface length and thus domain size. Cells could control the size of coexisting domains in the PM and thereby modulate signaling simply by changing the high-T_m or the low-T_m lipids, or any other factors that change line tension. We used four-component mixtures to control the transition of coexisting Ld + Lo domains from nanoscopic to macroscopic sizes (10). The high-T_m lipids we examined were pSM, bSM, eSM, and DSPC, chosen for biological prevalence or because of extensive prior characterization. The low-T_m lipids were POPC, DOPC, DLPC, SDPC, and DPhPC, chosen either for biological prevalence or because these lipids create macroscopic Ld + Lo domains.

The domain size transition is correlated with line tension

As ρ is increased, Ld and Lo domains in each of the mixtures in Fig. 2 undergo a change in size of two orders of magnitude at ρ^∗, from tens of nanometers in diameter to the visible micron scale. This size increase occurs over a change of only ∼2–5% in the total lipid composition, which corresponds to ∼20% variation in ρ. This width of the ρ-window also has a component from the compositional variation of individual GUVs that has been estimated to be ±5 mol % (56), so the true size change could be even more abrupt.

For the mixtures shown in Fig. 3, the line tension value where macroscopic domains first appear is in every case ∼0.3 pN. It is possible that an interaction that competes with line tension, e.g., dipole-dipole repulsion, is overwhelmed by a line tension of 0.3 pN. The domain size just below this ρ-value might provide information on the dipole magnitude and dielectric constant in that region of the bilayer. Another possibility is that below 0.3 pN, thermal fluctuations break up domains.

Comparing Figs. 2 and 3, ρ^∗ occurs at a line tension of ∼1.1 pN for each mixture. We previously modeled the domain size transition as arising from a competition between line tension and curvature (16) and found that this model could reproduce experimental observations including modulated phase patterns (10, 13). Bending energy opposes line tension by penalizing large domains of the stiffer Lo phase on curved surfaces, and macroscopic patterns occur when the two interactions are more balanced. Modulated morphology might give way to rounded macroscopic domains at roughly the same value of line tension perhaps because the rigidity difference between Ld and Lo is similar for the mixtures studied here.

Another simple relationship emerges from a comparison of Figs. 2 and 3, namely that smaller values of ρ^∗ in every case correspond to higher values of the line tension. A higher ρ^∗ can therefore be a useful surrogate for lower line tension: compared to the conditions needed to determine line tension, a 10-fold lower dye concentration and ∼10-fold lower cumulative light exposure are needed to determine ρ^∗, resulting in a much lower probability of photochemical artifacts (21). Using ρ^∗ data we can therefore more readily investigate mixtures containing unstable polyunsaturated lipids. For example, photochemical instability of the 22:6 acyl chain of SDPC precludes measuring line tension, yet phase boundaries (55) as well as ρ^∗ could be determined for the mixture, bSM/SDPC/POPC/chol (Fig. 2 K). The strikingly high value of ρ^∗ = 0.61 indicates quite low line tension until the mixture has a high fraction of SDPC. In a sense, line tension is just barely enough for bSM/SDPC/chol phase domains to be macroscopic. Another interesting case is bSM/DOPC/POPC/chol with a significant fraction of transmembrane helical peptide as a component. Upon adding the α-helical peptide GWALP23 to the otherwise lipid-only mixtures, ρ^∗ drops from ρ = 0.52 to 0.1 for bSM/DOPC/POPC/chol (Fig. 2, I and L), and from ρ = 0.58 to 0.3 for bSM/DOPC/SOPC/chol (S.P.W., unpublished data). These observations reveal that this peptide significantly increases the line tension. In a previous MD simulation we found that GWALP23 is depleted from the Ld/Lo interface, consistent with the peptide increasing line tension (57).

Properties of Ld and Lo domains do not change abruptly despite the abrupt domain size transition

We studied different properties of Ld and Lo phases along the domain size transition from nanoscopic to macroscopic phase separation. Well-resolved phase diagrams were required for this work. A previously determined four-component phase diagram enabled finding phase boundaries for each ρ-value in the representative mixture DSPC/DOPC/POPC/chol (9). Although our compositional trajectories were always within the Ld + Lo coexistence region, the tieline endpoints change with ρ. Accurate phase boundaries are needed to apply the Lever-Arm Rule to study Lo and Ld properties such as bending modulus, order parameter, rotational diffusion, and probe partition between these phases. Defining ρ^∗ for each mixture enabled our finding that the abrupt increase in domain size is not accompanied by abrupt changes in any measured Ld and Lo phase properties. A potentially important corollary is that because no abrupt changes with domain size are observed in the particular properties we chose to measure here, we suggest that measurement of these properties in the macroscopic regime is likely to reflect the properties of the nanoscopic domains. In general, it is more convenient to measure macroscopic domain properties, which we here establish as providing useful information about nanoscopic domain properties.

We measured the bending modulus for both Ld and Lo phases over the entire range of ρ-values. In the compositional range where domain size changes dramatically (the shaded regions in Fig. 4), the bending moduli change by just a few percent. The Ld bending modulus decreases with increasing ρ (i.e., increasing DOPC; Fig. 4 A), consistent with observations that single-component membranes of low-T_m lipids with one saturated chain, like POPC, are rigidified by cholesterol while DOPC membranes are not (24, 25, 58, 59). The DSPC/DOPC/POPC/chol phase diagram (9) indicates that the Ld composition does not depend on ρ, having a similar concentration of DSPC, low-T_m lipid, and chol at all ρ-values. In contrast, the Lo composition contains proportionally more DSPC and chol, and less low-T_m lipid, as ρ increases. Consequently, the Lo phase bending modulus increases with increasing ρ (Fig. 4 B).

Another phase-dependent property characteristic of coexisting Ld + Lo domains is the partition coefficient K_p for a molecule that can equilibrate between the two environments. We measured K_p for the mixtures DSPC/DOPC/POPC/chol (Fig. 5 B) and bSM/DOPC/POPC/chol (Fig. 5 A). For both a paramagnetic ESR probe (16PC) and a fluorescent probe (BODIPY-PC), we observed compositional dependence as ρ was varied from 0 to 1, with K_p increasing by approximately threefold over the entire range of ρ, but without abrupt changes at the composition ρ^∗ where domain size changes abruptly in both lipid mixtures. Another finding emerges from the single dye fluorescence experiments performed in the nanoscopic regime: simple, hyperbolic partitioning curves are observed in both the nanodomain region (Fig. 5 A, left inset) and the macrodomain region (raw data not shown). We conclude that Ld and Lo phase fractions in the nanoscopic regime follow the Lever-Arm Rule just like macroscopic phase separation.

Using ESR, we also examined the order parameter and rotational diffusion rate of 16PC in Ld and Lo phases of DSPC/DOPC/POPC/chol. Changes in these parameters were surprisingly small (Table 1), consistent with only gradual variation in phase properties.

Competition between line tension and dipole repulsion drives the domain size transition

What is responsible for the abrupt increase in domain size observed for 12 different mixtures? A simple model of line tension competing with dipole repulsion reproduces the abrupt domain size transition observed in experiments (Fig. 6). The model relies on the dipoles in each leaflet being far enough apart as not to cancel, having a significant component oriented along the bilayer normal, and being located in a low enough dielectric that the field persists for several lipid neighbors. We do not know the dielectric constant in part because we do not know the actual dipole location. We also do not know the difference in dipole density between Lo and Ld domains, because that would require measurements of the Lo phase that are not yet reliable. Still, reasonable ranges of these parameters all show an abrupt domain size transition (Figs. S15 and S16).

We do not know which dipoles might be involved in limiting domain size. We chose to model repulsion that would be consistent with carbonyl groups, in part because experiments with ether-linked chains show a decrease in bilayer potential (60), although such experiments do not rule out the very real possibility that ester- versus ether-induced conformational changes could influence a measured dipole potential. Also, the carbonyl-carbonyl distances across the bilayer are relatively well defined and thus suitable to model. An oriented bound water molecule could be a source of dipole-dipole repulsion, if located in a low dielectric region such that the electric field would persist over several lipid neighbors. In these symmetric bilayers, dipoles of the terminal methyls could not be the source of the repulsion as they are in lipid monolayers, because the apposing leaflet methyl dipoles would be so close and of the same type of phase (and thus the same motional and orientational state) as to cancel. However, we do not rule out that in asymmetric bilayers the terminal methyls could contribute to dipole-dipole repulsion. Additionally, the methyl dipoles might contribute significant electrostatic repulsion for nanodomains that are not in register across the leaflets (61). In brief, we have not proven that our treatment of dipole-dipole repulsion correctly describes the interaction that occurs on the tens of nanometer scale to compete with line tension. We have only shown that with reasonable values of key parameters, the difference of dipole potential between Ld and Lo domains and the dielectric constant near those dipoles, the observed behavior is reproduced in our model: domain size abruptly changes by two orders of magnitude with a small change in line tension.

It could be that for line tension <∼0.3 pN the amplitudes of thermal fluctuations are sufficient for preventing the coalescence of domains. This could occur, for example, if the fluctuations approached the size of the domains themselves. For example, at ρ = 0, domain diameter measured by SANS is ∼15 nm (Fig. 7). Fluctuations of this magnitude would occur with a line tension of ∼0.1 pN (23). However, this consideration does not address the dramatic size change observed experimentally. In this regard, MD simulations have shown that registration of domains together with domain size both dramatically increase at a domain size of ∼15 nm (36). These findings point to enhanced coupling of the two leaflets and domain stability both being enabled at a particular domain size. Because these are observations from MD simulations, which would include implicitly any dipole-dipole effects, we are not able to separate these effects in the simulations.

Hybrid and nonhybrid lipids have similar line activity

We have previously concluded that emphasis on a special behavior of hybrid lipids in forming nanodomains is misleading (54). For five of the six mixtures shown in Fig. 3, we used POPC as the nanodomain-forming low-T_m lipid. Starting at ρ = 1 where line tension is greatest, the ρ-trajectory could be described as substituting a fraction of POPC into the high line tension mixture. In four of the mixtures, POPC hardly lowers line tension until it becomes nearly 40 mol % of the low-melting lipid. When the nanodomain-forming low-T_m lipid is DLPC instead of POPC, the same result is observed. These experiments suggest that hybrid lipid POPC behaves similarly to the nonhybrid lipid DLPC to decrease line tension. Both POPC and DLPC might be described as weakly line active.

Nanodomains have a complex morphology

The large MD simulations performed in this study better reveal nanodomain size and morphology. Compared to previous studies (36), our large box size of 74 × 74 nm allowed for multiple independent Lo nanodomains to exist in the Ld surround in a leaflet of coexisting Ld + Lo phases. We find nanodomain size to be consistent with SANS measurements, on the order of 25 nm. In a 3.6 μs simulation at ρ = 0.65 (see the Supporting Material for a movie and simulation snapshots at other ρ-values), after the first microsecond of equilibration, nanodomains are easily recognized, but their morphology is highly dynamic throughout the simulation, and it is never circular.

Conclusions

We investigated the nature of the abrupt domain size transition observed in four-component lipid mixtures mimicking the PM composition. We find that various Ld and Lo phase properties measured as functions of ρ can be explained by treating Ld + Lo nanodomains as coexisting phase domains, and that the domain size transition does not appear to be a phase transition. However, the more important point is the phenomenon itself, namely that coexisting nanoscopic domains containing hundreds to thousands of lipids coalesce over a narrow composition range into domains hundreds of times larger. We find that line tension is the key parameter that controls this size transition, and line tension depends strongly on the nature of both the high-T_m and low-T_m lipids. In summary:

• 1)The size of coexisting Ld + Lo domains changes abruptly in composition space.
• 2)Line tension has the decisive role in controlling the abrupt size transition.
• 3)Ld or Lo phase parameters show only gradual changes even as domain size changes abruptly.
• 4)Phase behaviors measured for Ld + Lo macrodomains are a good surrogate for behaviors of nanodomains.
• 5)Hybrid lipids 18:0,22:6-PC, 16:0,18:1-PC, 16:0,18:2-PC, or 18:0,18:1-PC reduce line tension only weakly.
• 6)Visible Ld + Lo phase domains first appear at line tension ∼0.3 pN in six different lipid mixtures.
• 7)Dipole repulsion within the bilayer might stabilize nanodomains.
• 8)MD simulations of a large patch of lipids show that a nanodomain is not round, but has complex and fluctuating morphology.

Author Contributions

R.D.U. and T.A.E. designed and performed the research, analyzed the data, cowrote the article, and contributed equally to the work; S.P.W., M.D.W., W.-C.T., M.B.K., and S.W. designed and performed the research and analyzed the data; T.L.T. and J.K. designed experiments; D.G.A. and F.A.H. designed and performed the research, analyzed the data, and cowrote the article; and G.W.F. designed the research, analyzed the data, and cowrote the article.

Editor: David Cafiso.

Supporting Material

Movie S1. Molecular Dynamics Movie Demonstrating the Dynamic Shape and Evolution of Nanodomains

Movie shows the progression of a single four-component system as it develops during phase separation and then continues its rearranging. The time progression reveals the complex, noncircular morphology of a domain and its fluctuating nature. Lipids are colored by type (DUPC in blue, PUPC in cyan, DPPC in red, and cholesterol in yellow). Phases are not marked, but the formation of patches rich in DPPC and cholesterol (red and yellow) clearly shows the formation of Lo domains.