Abstract
Proper organelle size is critical for many cell functions. However, how cells sense and control their organelle size remains elusive. Here, we develop a general model to study the size control of mitotic spindles by considering both extrinsic and intrinsic factors, such as the limited number of building blocks of the spindle, the interaction between the spindle and cell boundary, the DNA content, the forces generated by various molecular motors, and the dynamics of microtubules. We show that multiple pairs of chromatids, two centrosomes, and microtubules can self-assemble to form a mitotic spindle robustly. We also show that the boundary-sensing and volume-sensing mechanisms coexist in small cells, but both break down in large cells. Strikingly, we find that the upper limit of spindle length naturally arises from the geometric asymmetry of the spindle structure. Thus, our findings reveal, to our knowledge, a novel intrinsic mechanism that limits the organelle size.
Introduction
Improper organelle size can lead to cell dysfunction (1). For example, as the main organelle accomplishing chromosome segregation, spindle size is critical for cell division process. The defects in mitotic spindle size can reduce the fidelity of the chromosome separation (2). Spindle size was traditionally expected to scale up with cell size because bigger organelles may be required to fulfill their biological functions in bigger cells (3, 4, 5, 6). However, experiments showed that the diameter of dividing cells changes two orders of magnitude from 1200 to 12 μm when the Xenopus laevis egg develops from a fertilized egg into a tadpole (7). During this process, spindle length is proportional to cell size only in small cells, but it reaches an upper limit (∼60 μm) in large cells (7). The spindle size can be regulated by many intrinsic factors, such as the growth dynamics of microtubules (MTs) (8, 9, 10), the length distribution of MTs (11, 12), signaling gradients (13, 14), and the mass conservation of the building blocks of spindles (15, 16, 17). However, how mitotic spindle size is detected and controlled by the cell across multiple length scales and why there exists a size limit of mitotic spindles is still elusive.
In the prevailing models about the spindle size, only the polar MTs and kinetochore MTs were considered (9, 18). These models did not contain the effects of cell size, and thus cannot be used to study how the cell size regulates the spindle size. In the models for positioning (19, 20, 21) and orientation (22, 23) of spindles, the interactions between MTs and cell cortex were mainly considered, which is probably one of the ways in which the cell boundary influences the spindle. But these models did not consider the spindle structure and spindle size, and only treated the spindle as a point or a rigid body with fixed size and shape. In addition, it has been shown that the cell volume can influence the number of building blocks of spindles, and thus it can influence the spindle size (15, 16, 17). Therefore, to study how the cell size regulates the spindle size, we need a more general model that considers not only the spindle structure, but also the effects of cell boundary and cell volume.
In this article, we develop such a general model to answer these questions. We show mitotic spindles can be robustly self-assembled from chromosomes, centrosomes, and MTs. Strikingly, we find that although many factors can regulate spindle size, geometric asymmetry directly leads to the existence of the upper limit of the mitotic spindle size. Our results also verify the experimental observations and reveal the mechanism about whether cell volume or cell shape determines the spindle length.
Materials and Methods
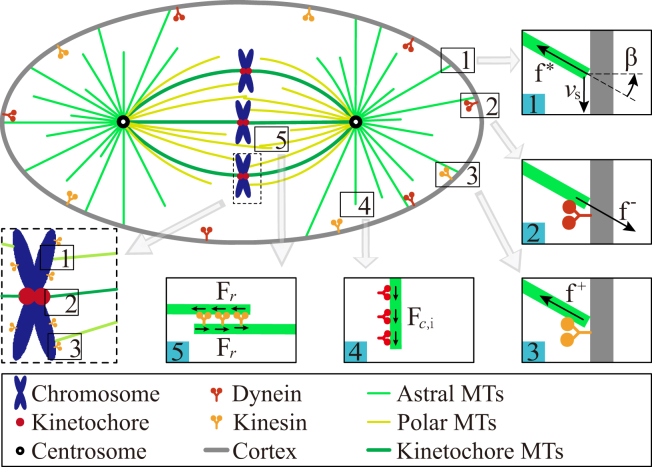
The self-assembly of mitotic spindles is investigated in a computational model. As shown in Fig. 1, the mitotic spindle has two centrosomes and several pairs of chromatids. Each pair of chromatids has two attachment sites, named kinetochores. MTs nucleated from centrosomes switch between growing and shrinking states randomly (dynamic instability) to search for kinetochores (24). After MTs catch both kinetochores, tension between duplicated chromatids is built up and the whole structure is stabilized. So, chromosomes can be aligned near the spindle equator. In the meanwhile, the whole spindle can be positioned to the cell center and oriented to the long axis of the cell when other specified mechanisms are absent (22, 25, 26, 27). During this self-assembly process, various mechanical forces are crucial for the positioning, orientation, and size control of mitotic spindles. Descriptions of force-generation mechanisms and kinetics of MTs, molecular motors, centrosomes, and chromosomes are given in the following.
Figure 1.
Schematic of the five force-generation mechanisms in mitotic spindles, including the pushing force generated by MT polymerization (inset 1), the pulling force general by cortical dynein (inset 2), the pushing force generated by cortical kinesin (inset 3), the pulling force generated by cytoplasmic dynein (inset 4), and the pushing force generated by kinesin on the antiparallel MTs. The chromosome provides similar forces to the cortex in insets 1–3 (dotted box). To see this figure in color, go online.
Nucleation and dynamic instability of microtubules
The MTs are nucleated either from the centrosome radially (Fig. 1) or from the existing MTs as branches, and their minus ends are anchored in the centrosome or the original MT (20, 28, 29, 30). For the nucleation from centrosomes, we assume a nucleating rate k0. Considering the facts that the forces on the branching MTs are all transmitted to the centrosome to drive its motion, we assume all MTs are nucleated from the centrosome as proposed in previous works (20, 21, 31). In these previous models, the directions of MTs were usually distributed uniformly, because only the astral MTs were considered. However, there is a much higher density of MTs on the toward-chromosome side, which is mainly because much MTs can be nucleated in the region from the centrosome to the chromosomes (30). To describe a more realistic spindle, we firstly assume MTs are nucleated randomly and uniformly in all directions at a nucleating rate of k0. And then we superpose a nucleating rate (kn = k0/2) in the region from the centrosome to the chromosomes. Considering the ratio of spindle width to spindle length is almost constant (32), we define the region as a cone whose axis is the spindle axis (pole-to-pole axis) and the apex angle is 60°.
Besides, MTs display the dynamic instability, i.e., they randomly switch between growing state and shrinking state. In this work, we define the rescue rate (from shrinking to growing) and catastrophe rate (from growing to shrinking) of MTs are k1 and k2, respectively. Both of them are assumed to be constant in the cytoplasm. The MTs elongate at a speed of v1 in the growing state, and shorten at a speed of v2 in the shrinking state. As a result, the length of freely growing MT varies wavily over time.
Pushing force induced by microtubule polymerization
Due to the confinement of cell boundary, MTs cannot grow infinitely. Once a growing MT contacts the cell cortex, it will generate a pushing force on the cell cortex due to its growth (5, 33, 34). If the pushing force exceeds a critical value, the MT will be buckled (35, 36). The critical force is given by Euler buckling formula fc = π2κ/l2 (19, 21, 37, 38), where κ and l denote the bending rigidity and the length of the MT, respectively. Because the pushing force increases slowly with the growth of MT after it exceeds the buckling force, we assume the pushing force is a constant and equals the Euler buckling force once the MT is buckled (19, 21, 37, 38). When MTs are very short, the Euler buckling force fc will exceed the stall force of MTs fstall. In this case, the pushing force is limited by the polymerization of MTs. Therefore, the pushing force induced by MT polymerization is given as (38)
| (1) |
The pushing force given in Eq. 1 is naturally length-dependent so that the buckled MTs can behave as not only the force generator but also the position sensor inside the cell. Equation 1 can also be easily modified to consider the effects of the lateral confinement by the surrounding elastic cytoskeleton (38).
In addition, experiment has shown that the blocked MTs can slip along the cell cortex (37) (Fig. 1, inset 1). The slipping of MTs can change their orientation and length. The velocity of the tip is given by (21)
| (2) |
Here ξ is the friction coefficient associated with the slipping; and β is the angle between the MT and the normal to the cell cortex (Fig. 1, inset 1). Apparently, the slipping behavior can influence the distribution of MTs.
It should be noted that if MTs attach the chromosome arms, they can also apply pushing forces on the chromosome and slip along the chromosome arms (Fig. 1). We assume that the pushing force and slipping velocity on the chromosome arms follow the same rules defined in Eqs. 1 and 2.
Forces and dynamics of molecular motors
Molecular motors widely distribute in cells. Driven by the energy of the hydrolysis of ATP, they can bind to and walk along MTs (33). If molecular motors bind to MTs and cell cortex simultaneously, they can generate forces on the MTs. The direction of the force is opposite to the walking direction. For example, dynein can walk to the minus end of MTs and generates a pulling force, while kinesin can walk to the plus end and generates a pushing force (33). In this work, we consider both kinesin and dynein, and we use the superscripts + and − to indicate them, respectively. The force generated by the motor is velocity-dependent as (39, 40)
| (3) |
where parameters and are the stall force and the unloaded velocity of kinesin (+) or dynein (−), respectively; the parameter f± is the force on the motor; and v± is the walking velocity of the motor. Conversely, the velocity of the molecular motor can also be determined by the force as
| (4) |
We use and to represent the binding rates of individual kinesin and dynein, which are usually expected to be proportional to the densities of unbound motors. We assume that the density of unbound motors is uniform so that and are both constant. The binding motors may detach from MTs stochastically. We define the unbinding rates of kinesin and dynein as and , which both increase exponentially with the loads as (33, 41)
| (5) |
where f± is the force on the motor; is a characteristic force representing the sensitivity of the unbinding rate to the load; and is the unloaded unbinding rates of kinesin and dynein.
Motors have various states, such as binding to cortex or chromosome, free in the cytoplasm, transporting cargos or cross linking MTs. In the following sections, we will discuss how the motors in different states generate forces and how they affect the size control of the spindle.
Cortical motors
Some molecular motors are anchored on the cortex. The motor can bind to and apply forces on the MTs that are slipping on the cell cortex (Fig. 1, insets 2 and 3). If we neglect the poleward flux of MTs, the relative velocity between MT and the motor equals the velocity component of centrosome in the MT direction (38). Thus, the force generated by a cortical motor (f+ or f−) can be obtained from Eq. 3. If we assume each cortical motor binding to the same MT has the same velocity, the total force on the MT is , where N+ and N− are the numbers of kinesins and dyneins on the MT. Here the positive value of Fi means pushing force while the negative value means pulling force. Usually, the number of dyneins on the cortex is much larger than that of kinesins so that Fi is a pulling force (Fi < 0). However, if Fi is a pushing force and the MT is buckled due to this pushing force, the force equals the buckling force as shown in Eq. 1. Therefore, the force induced by the cortical motors on the MT is given as
| (6) |
where ; and is the force on the motor when the MT is buckled. In this case, the velocity of each motor is still equal so that the force can be obtained from Eqs. 3 and 6 as
| (7) |
| (8) |
where , ; and the velocities of motors on buckled MTs are
| (9) |
| (10) |
Cytoplasmic motors
In very large cells, MTs at metaphase are too short to contact the cell cortex. In this case, it has been proposed that motors anchored in the cytoplasm can generate length-dependent pulling forces based on the observation that the centrosome moved to the opposite direction after the MTs on one side were depolymerized by UV irradiation (42). The cytoplasmic dyneins bind to the MT and walk to the minus end of the MT to generate pulling forces (Fig. 1, inset 4). The pulling force is length-dependent because the number of dyneins bound to the MT is proportional to the MT length. Therefore, the pulling force induced by the cytoplasmic motors on a MT is given as
| (11) |
where η is the pulling force per unit MT length; and li is the total length of the MT. The velocity of cytoplasmic dyneins carrying a cargo and walking along the MT almost equals the unloaded velocity (43, 44), which indicates the pulling force generated by a single motor is very small (see Eq. 3).
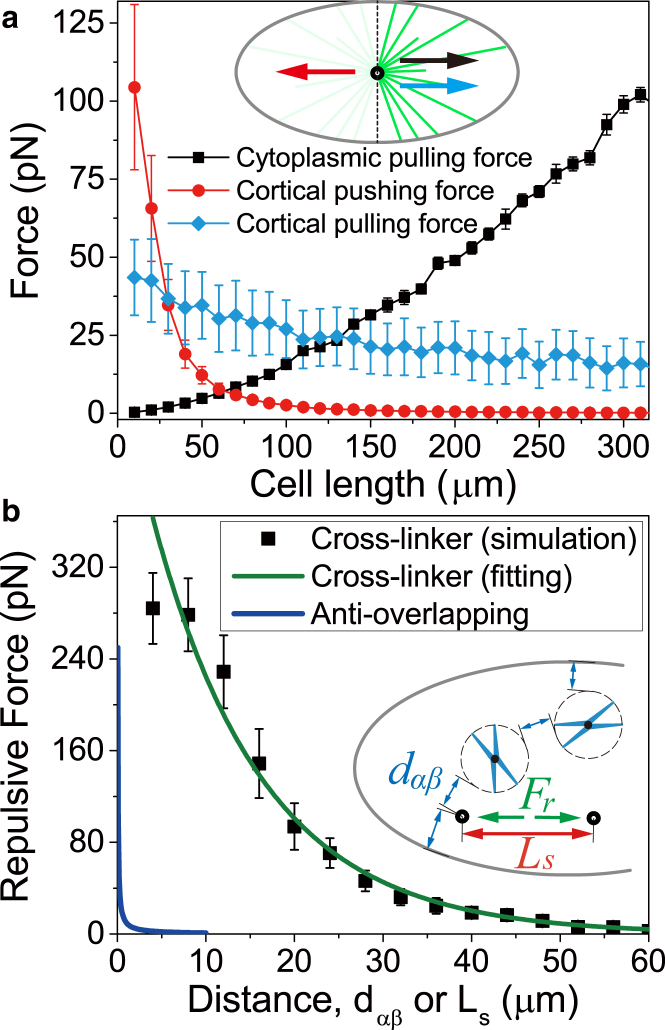
It is noted that pushing forces generated by MT polymerization or cortical motors (Eqs. 1 and 6) and the pulling forces generated by cytoplasmic motors (Eq. 11) are all length-dependent. The MTs can be longer in a larger cell, so that the cell size can regulate these forces in a certain way. To clearly see the features of the forces generated by the cortex and cytoplasm, we tentatively fix a single pole centrally in the cell and calculate the force on the pole generated by each mechanism (Fig. 2 a). It is shown that the cortical pulling force decreases with the cell size slightly, because the cortical pulling force is length-independent but fewer MTs can reach the cortex due to the dynamic instability. The cortical pushing force decreases with cell size sharply, because the force is inversely proportional to the square of MT length (Eq. 1), while the cytoplasmic pulling force increases with cell size, because the force is proportional to MT length (Eq. 11). We find that in small cells, the cortical force dominates the spindle pole; while in large cells, the cytoplasmic force dominates the spindle pole (Fig. 2 a).
Figure 2.
The features of the forces by the force-generation mechanisms considered in the model. (a) A quantitative comparison between the cytoplasmic force and cortical force generated by the MTs on the right side of the cell when the single centrosome is fixed in the cell center (inset). Here, the cortical pushing force contains the MT polymerization and molecular motors. (b) The antioverlapping force and the repulsive force by cross-linkers Fr are plotted as the functions of the distances that are defined in the inset. The repulsive force by cross linkers is obtained by simulations without chromosomes (see Fig. S1) and is fitted exponentially (green curve). To see this figure in color, go online.
Chromosome motors
Besides the cortex and cytoplasm, dyneins and kinesins are also distributed on the chromosome arms and they can also bind to MTs (41). The resultant force on the chromosome arms is a pushing force, named the “polar ejection force” (5, 33, 41). Therefore, without loss of generality, we neglect the pulling force applied by dyneins on the chromosome arms and assume only the kinesins on the chromosome arms apply forces. The binding rate of kinesins is defined as . When they bind to MTs, these kinesins can apply a pushing force like cortical kinesins (Eq. 3). The force on the MT also follows Eq. 6 with . Moreover, once a polymerizing MT encounters a chromosome, it will also apply a pushing force on the chromosome. If the pushing force due to kinesins or the MT polymerization exceeds the Euler buckling force, the MT will also buckle. Therefore, the polar ejection forces proposed in previous models (33, 41) can be attributed to both the pushing of kinesin motors and the pushing of polymerizing MT plus ends (5, 38).
We define the central region of the chromosome as the kinetochore (Figs. 1 and S1 in the Supporting Material). The MTs that encounter the kinetochores can attach to the kinetochores and generate pulling forces due to the depolymerization of MTs (45). Conversely, the binding MTs can also detach from the kinetochores. Because the dynamics of this process is similar to the binding and unbinding of dyneins (33, 45, 46), we simply assume MTs can attach to the kinetochore at a rate , and unbind from the kinetochore at a rate as Eq. 5. The pulling force generated by the depolymerization of MTs also follows Eq. 6 with .
Cross-linking motors
Some cytoplasmic motors can bind to a pair of antiparallel polar MTs to serve as cross linkers (Fig. 1, inset 5) (5). These motors can also walk actively and apply forces on the antiparallel polar MTs. Experiments have found that Kip1 and Cin8 can generate pushing forces (9, 47, 48), and play an important role in maintaining the spindle length. Thus, it should be added to the model. We have assumed a portion of MTs are nucleated (kn) directed to the region that defines the spindle. The cross linkers are also assumed active in this region. If two MTs that come from different poles are close enough, the molecular motors can bind to both of them and apply forces on the two MTs (see Fig. S1). We define a threshold distance dl. When the minimal distance of two MTs is <dl = 0.5 μm, they can be bound by a cross linker at a rate of (both kinesin and dynein are considered). And the cross linkers can unbind at a rate of , which is also load-dependent as Eq. 5. Besides, the cross linkers can generate pulling forces or pushing forces like cortical motors (Eqs. 3 and 6).
Antioverlapping force
The centrosomes and chromosomes are all confined in the cell and they cannot overlap with each other. Furthermore, neither of them can penetrate the cell cortex. To avoid the overlap or penetration, we define the repulsive force between any two objects (centrosomes, chromosomes, or the cell cortex) as
| (12) |
where C = 10 pN × μm is a constant used in the simulation; and is the least distance between the two objects (Fig. 2 b). Here we define the circumcircle of the chromosome as its boundary. Index α and β represent two of the centrosomes or chromosomes and the cell cortex. The antioverlapping force values are plotted and compared in Fig. 2 b.
Centrosome and chromosome dynamics
All MTs can transfer their axial forces to the centrosome, and MTs attaching chromosomes can apply forces on the chromosomes. Combining the forces in Eqs. 1, 6, 11, and 12, the force balance equation of centrosome is given by
| (13) |
where O is the subset of MTs nucleated from this centrosome and associated with cell cortex, chromosomes, or antiparallel MTs; P is the subset of MTs nucleated from this centrosome; is the unit vector in the direction of the ith MT; the parameters ξp and are the viscous drag coefficient and velocity of the centrosome, respectively; the index α represents the centrosome considered in Eq. 13; and Q includes the other centrosome, chromosomes, and the cell cortex. It should be noted that we have neglected the inertial forces due to the low Reynolds number of this system.
Similarly, the force balance equations of chromosomes are given as
| (14) |
| (15) |
Here H is the subset of MTs associated with the chromosome; the parameters ξc and ζc are the translational and rotational viscous drag coefficients of the chromosome, respectively; is the centroid velocity of the chromosome; is a vector pointing from the chromosome center to the location where the force is applied; αc is the orientation angle of the chromosome; index α represents the chromosome considered in Eq. 14; and W includes the other chromosomes, the two centrosomes, and the cell cortex.
The two centrosomes can be treated as particles due to their small size, but the shape of the chromosome is complex. In this work, based on experimental observations (49, 50, 51), we simply assume each pair of chromatids is an x-shaped rigid body with a thickness of 0.8 μm (see Fig. S1), and we use the Eulerian angles to describe their rotating in the 3D space.
Mass conservation of tubulins
It has been proposed that the depletion of tubulin or other building blocks of the spindle can lead to a volume-dependent spindle scaling (8, 15). In our model, we can also study how the mass conservation of the building blocks of the spindle contributes to the size control and the upper limit of the spindle size. The building blocks of the spindle, including the tubulin and MT-associated protein, all can influence the spindle mass. Because tubulin is the main component of spindles, here we only consider the mass conservation of tubulin and assume other components are sufficient, as has been assumed in previous works (8, 15). If the synthesis and degradation of tubulin is balanced, the total mass of tubulin is conserved in a cell, i.e., the sum of the tubulin dimers in the spindle MTs and the soluble tubulin dimers in the cytoplasm keeps constant as
| (16) |
Here C0 and C are the number of tubulin dimers per unit volume of the cytoplasm before and after spindle assembly, respectively; V is the cell volume; LMT is the total length of spindle MTs; and d0 is the length of tubulin dimer, and each tubulin dimer increases the MT length by d0/13 for a MT with 13 protofilaments.
In the cytoplasm, tubulin has a diffusion coefficient of 4 ∼ 10 μm2/s (52), which means the tubulin has an average displacement ∼5 μm/s, while the MT polymerization rate is ∼0.1 μm/s, which is an order-of-magnitude lower than diffusion. Therefore, the MT self-assembly is not a diffusion-limited process, and we can assume the concentration of tubulin is always uniform. Obviously, the soluble tubulin concentration decreases with the spindle assembly, and it will influence the polymerization velocity of MTs (53). The polymerization velocity can be given as (54)
| (17) |
Here the parameters kon and koff are the association and dissociation rates of the tubulin dimer, respectively; and the parameter f∗ is the force on the growing end of the MT. Particularly, for free MT the force is zero and we can write the growth velocity as
| (18) |
where Ccr is the critical concentration (54); and kc = d0kon. Therefore, the growth velocity is proportional to the soluble tubulin concentration. Combining Eqs. 16 and 18, the growth velocity of free MTs is
| (19) |
Here, both LMT and v1 are the functions of time as the spindle assembles.
The value of koff/kon is very low for growing MTs (53). Therefore, without loss of generality, in our simulation we assume koff = 0, i.e., Ccr = 0. It is worth noting that Eq. 17 can also be used to describe the shrink velocity of shortening MTs. In this case, the ratio koff/kon is much bigger than 1 so that the velocity in Eq. 17 is negative and nearly independent of the force (53). When the mass conservation is considered, the polymerization velocity decreases to a stable value during the self-assembly of spindles (see Fig. S2). However, if the mass conservation of tubulin is not considered, the polymerization velocity is assumed as always constant. Moreover, although recent experiment showed that the tubulin concentration can also influence the nucleation rate of MTs (53), to simplify the problem and focus on the upper limit of the spindle, we assume the nucleation rate is constant. In a word, we can control the mass conservation of tubulin by the polymerization velocity of MTs as in Eq. 19, which can capture the key feature of the experiment (15). More detail can be found in the Supporting Material.
Three- and two-dimensional simulations
A three-dimensional (3D) simulation can be carried out based on the above description. However, such a complex system leads to the very low computational efficiency, which hinders the deep exploration of spindle size regulation and the discerning of the source of upper limit among so many influencing factors. Therefore, instead of 3D simulation, we use two-dimensional (2D) simulation to investigate the regulation of spindle size. Although the degrees of freedom are greatly reduced, an inevitable problem in 2D is that MTs cannot bypass the chromosomes so that some antiparallel MTs cannot be considered in the model. To solve this problem, we adopt a superposition method, i.e., we first figure out the interaction of antiparallel MTs separately, and then add it to the system with chromosomes.
Specifically, we remove the chromosomes and just consider the interaction of antiparallel MTs. We assume only the crossed MTs can be bound by kinesins, and applied forces. The binding rate, unbinding rate, and force are the same as the cortical motors (see Fig. S1). For each pole-to-pole distance, the repulsive force on spindle poles can be calculated. The repulsive force versus pole-pole distance is shown in Fig. 2 b. We find that the curve is nonlinear, and it can be fitted very well with an exponential function
| (20) |
where A and B are two constants; and Ls is the pole-to-pole distance, i.e., the spindle length (see Fig. S1). The direction of the repulsive force is along the spindle axis. In our simulation, we use A = 360 pN and B = 0.08 μm−1 based on the fitting result (Fig. 2 b). In theory, the overlapping length, the amount of accessible MTs, and the pushing force (critical buckling force) all decrease with the pole-to-pole distance nonlinearly, which results in the exponential decay of the repulsive force. If the pole-to-pole distance is large enough, the repulsive force will be negligible (Fig. 2 b).
Simulation method
Monte Carlo simulation was performed to investigate the self-assembly and size limit of mitotic spindles (see Fig. S3). The 3D cell is assumed as a spheroid with long axis of 30 μm and two short axes of 15 μm. The 2D cell is assumed to have an elliptical shape with long axis 30 μm and short axis 15 μm, unless otherwise stated. The parameters used in the simulation are summarized in Table S1, unless otherwise indicated. The dynamic process is simulated by using the software MATLAB (The MathWorks, Natick, MA). Initially, the two centrosomes and multiple chromosomes are randomly positioned inside the cell. The initial number of the MTs on each centrosome is 50 and these MTs are evenly distributed in all directions.
In each time step, new MTs are nucleated in random directions. For each MT, we record its length, direction, and state. Each MT has four states, including growing, shrinking, slipping, and binding (see Fig. S3). In the time step, we firstly determine if the MT switches its state. The random switching events include the catastrophe, rescue, binding, and unbinding, while the other change of states is deterministic based on the geometric conditions. Each random switching event has its rate, based on which we can calculate the probability of the event in a time step. A random number in (0, 1) is generated uniformly, and if it is less than the probability, the random switching will occur in the time step (33, 55, 56). Then we base on the MT state to change its length and orientation deterministically. The force generated by each MT can be calculated based on length, direction, and state. Therefore, the resultant force on each centrosome and chromosome can be calculated to obtain their instantaneous velocity and new position by using Eqs. 13–15. Given that the magnitude of each rate in Table S1 is ∼10−2/s, the time step is chosen as Δt = 1 s. The system is iteratively solved for up to 24,000 time steps, corresponding to 400 min in real time. For very large cells, more time steps might be needed due to the increasing time spent on the larger length scale. More details of the simulation are given in the Supporting Material.
Results
Self-assembly of mitotic spindles
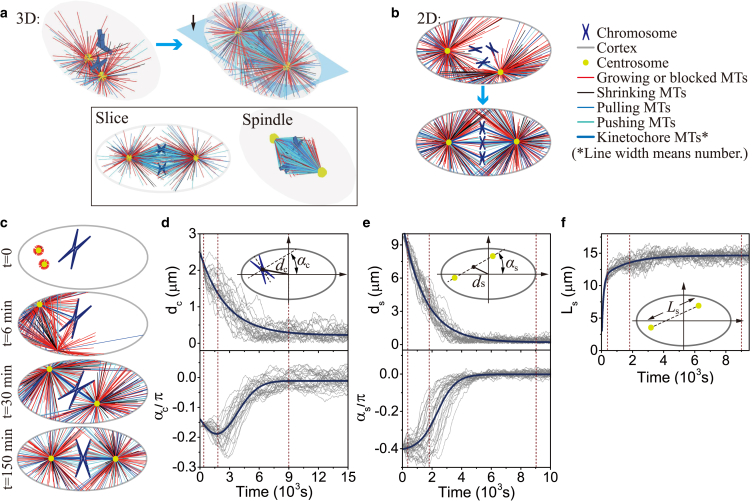
As an example, two centrosomes and three pairs of chromatids can self-assemble to form a spindle structure (Figs. 3 a and S4; Movie S1), which shows the robustness of the model. Similar results can also be obtained by 2D simulations (Figs. 3 b and S5; Movie S2). A movie with high time-resolution (Movie S3) clearly shows the slipping, buckling, and random switch between growing and shrinking states of MTs in 2D simulations. We notice that the spindles have similar positioning, orientation, and stable length in 2D and 3D simulations (Figs. S4 and S5), but the 2D simulation has lower complexity and computational cost. Therefore, we use 2D simulations to investigate the regulation and upper limit of the spindle size.
Figure 3.
Self-assembly of mitotic spindles. (a) (Top) Self-assembly of three pairs of chromatids and two centrosomes obtained by 3D simulations (see Fig. S4; Movie S1). (Bottom) The slice view (marked by the black arrow) of the spindle, and the spindle structure with hidden astral MTs. (b) Self-assembly of three pairs of chromatids and two centrosomes obtained by 2D simulations (see Fig. S5; Movie S2). Here, the antiparallel MTs are hidden, and we use the line width to represent the number of kinetochore MTs because they overlap each other. The number of overlapping kinetochore MTs is given in Fig. S7. (c) Self-assembly of one pair of chromatids and two centrosomes obtained by 2D simulations (see Movie S4). The time evolution of (d) chromosome position dc and orientation αc, (e) spindle position ds and orientation αs, and (f) spindle length Ls, is achieved by 20 times of simulations. The parameters used in the simulation are summarized in Table S1. To see this figure in color, go online.
We found if we replace N pairs of chromatids by one pair of chromatids and increase chromosome size by N times proportionally, spindle length is almost unchanged (see Figs. S5 and S6). Therefore, to improve computational efficiency without loss of generality, we use one pair of chromatids in the following simulations, although it seems unrealistic. The self-assembly of one pair of chromatids and two centrosomes is given in Fig. 3, c–f; Movie S4. Both the position dc and orientation αc of the chromosome decrease with time, and finally the chromosome is positioned to the spindle equator (Fig. 3 d). Simultaneously, the position ds and orientation αs of the spindle approach zero with time, and finally the whole spindle is positioned to the cell center and oriented along the long axis of the cell (Fig. 3 e). A stable spindle length (the pole-to-pole distance) can be obtained (Fig. 3 f), which allows us to investigate how cells sense and control spindle size. The different initial positions and orientations of chromosomes and centrosomes can only alter the self-assembly path, but do not change the stable spindle length (see Figs. S6 and S7).
Notice that MTs can be in bounded or unbounded growth regime depending on an average growth rate (57, 58), and the MT growth in egg extract is usually bounded (57). So here we only consider the bounded growth. The length distribution of MTs is exponential in bounded growth (57, 58), as shown in Fig. S8.
It should be noted that in the simulation, the centrosomes and chromosomes move with fluctuation, which is inevitable for stochastic simulation. The fluctuation will be decreased with increasing number of MTs. However, we found the computational efficiency is still very low when a large number of MTs is used, especially in large cells. This largely hinders the study of the upper limit of spindle size. Therefore, we need to simplify the model to some extent. Firstly, we noticed that the velocities of centrosomes and chromosomes are almost two orders-of-magnitude smaller than the unloaded velocity of the motor. This indicates that the force generated by the motor is approximately equal to the stall force, i.e., (see Eq. 3). We also found that most MTs only have one motor bound to them (see Fig. S9). Therefore, to increase efficiency, we assume each MT can only be captured by one motor. These simplifications only have little quantitative effect on the results (see the comparison in Fig. S9), but the computational efficiency is significantly increased. Therefore, we use this simplified model to investigate the upper limit of spindle size in the following simulations.
Factors that influence the spindle size
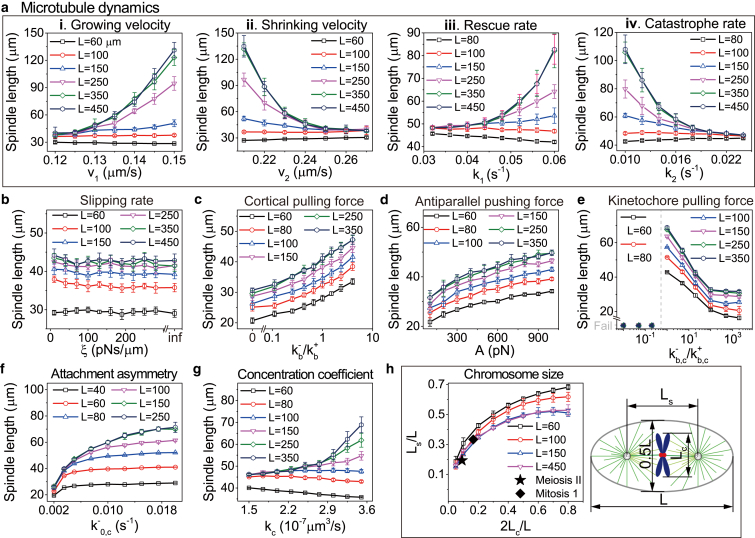
We found multiple factors can influence spindle length. For example, MT dynamics plays an important role in determining spindle length (Fig. 4 a). In large cells, spindle length increases with the growing velocity and rescue rate of MTs, while it decreases with shrinking velocity and catastrophe rate. This is consistent with the experimental (8, 10, 11) and computational (9) results. However, it must be noted that cell boundary was not considered in these in vitro experiments and simulations (8, 9, 10, 11). Therefore, these results are only applicable to large cells because cell boundary is less important for large cells. In small cells, we found the opposite trend, i.e., spindle length decreases with growing velocity and rescue rate, while it increases with shrinking velocity and catastrophe rate. This may be caused by the confinement of cell boundary in small cells, and it has not been reported and still needs further experimental verification. Other parameters of MT dynamics, such as the nucleation rate and katanin-mediated severing of MTs, may also alter spindle length (11, 12), which is not discussed here.
Figure 4.
The factors that influence spindle size. (a) Roles of the parameters of MT dynamics in governing spindle length, including: (i) growing velocity v1, (ii) shrinking velocity v2, (iii) rescue rate k1, and (iv) catastrophe rate k2. (b) Role of the slipping of MTs on cortex in governing the spindle length. Here, ξ is the friction coefficient associated with the slipping in Eq. 2. (c) Spindle length increases with the binding rate of the cortical dyneins , which is normalized by the binding rate of the cortical kinesins. (d) Spindle length increases with the pushing force on the antiparallel MTs. Because the antiparallel MTs are simulated separately in 2D simulations, we change the parameter A in Eq. 20, which corresponds to the parameters of the cross-linker dynamics. (e) Spindle size decreases with the pulling force generated by the MTs bound to the kinetochores. Here, we change both the binding rates of kinetochores and chromosome kinesins . The ranges of parameters are shown in Table S1. On the left of the dotted line, the stable spindle cannot be assembled. (f) The attachment asymmetry can regulate spindle length. is the unloaded unbinding rate of dyneins that connect MTs and chromosome. (g) The mass conservation of tubulin regulates spindle length. The label kc is the concentration coefficient defined in Eq. 18. (h) Spindle length increases with chromosome size (or equivalently chromosome number when chromosome size is fixed). The lengths of the meiosis II spindle and the mitosis stage 1 spindle were measured from the experimental results (7) and compared with our simulation. Both chromosome size Lc and spindle length Ls are normalized by cell length L. To see this figure in color, go online.
Because the cell boundary has significant influence on the spindle size, other cortex-associated factors, such as the molecular motors and slipping rate on the cortex, may also regulate the spindle size. As expected, the spindle size increases with the binding rate of cortical dyneins in both small and large cells (Fig. 4 c), which is because more cortical MTs apply pulling forces, and pull the spindle poles outward. This result is reasonable but has not been tested in experiments. Here, we only change the binding rate of cortical dyneins; other parameters of cortical motors, such as the binding rate of kinesin and the unbinding rates of the two types of motors, may also alter spindle length in a similar way, but is not shown here. However, we find that the slipping rate on cortex has little effect on the spindle size (Fig. 4 b). The reason may be that the slipping of MTs on cortex only changes the spatial distribution of MTs, but not the amount of pulling and pushing MTs.
Likewise, the forces inside the spindle, including the forces generated by kinetochores, chromosome arms, and the cross linkers, can also regulate the spindle size. For example, the spindle size increases with the repulsive force generated by the cross linkers between antiparallel MTs (Fig. 4 d), which is consistent with the experimental and computational results (18). Similarly, the spindle size decreases with the binding rate of kinetochores (Fig. 4 e), because the pulling forces increase and pull the spindle poles inward. This result is in agreement with the experimental observation that if the artificial kinetochores are added to the spindle, the spindle will shorten (47). We find that if the binding rate of kinetochores is too low, the spindle cannot be self-assembled to form a stable structure. In this case, the chromosomes also cannot be aligned on the equatorial plane. In the meanwhile, if the pulling force on kinetochores is too strong, the spindle poles will be pulled together. Considering the fact that the number of binding sites is limited on kinetochores, we assumed a kinetochore cannot bind >60 MTs, thus the spindle size cannot keep decreasing with the binding rate of kinetochores.
Attachment asymmetry can also regulate spindle length (38). If the binding or unbinding rates of kinetochores and kinesins on MT-chromosome attachments are different from dyneins and kinesins on MT-cortex attachments, the attachment asymmetry exists (38). This difference breaks the symmetry between chromosome MTs and astral MTs so that it can effectively regulate spindle length. Experiments found MT-kinetochore attachments can be stabilized by tension (46) or Aurora B (59). Therefore, the attachment asymmetry does exist in spindles. We found spindle length increases with the unloaded unbinding rate of dyneins that connect MTs and chromosomes (Fig. 4 f). The bigger leads to a decreasing number of MTs captured by kinetochores and a smaller pulling force between chromosome and centrosome, so the spindle length becomes bigger. There are also other ways to achieve the attachment asymmetry: for example, the bigger the unloaded unbinding rate of kinesins connecting MTs and chromosome , the smaller the spindle length becomes.
Mass conservation of the building blocks of the spindle is another important factor. It has been proposed that the depletion of tubulin can lead to a volume-dependent spindle scaling (8, 15). In our model, we can also study how the mass conservation of tubulin regulates spindle size. We found that the polymerization velocity of MTs is proportional to −1/V, where V is cell volume (Eq. 19). This indicates tubulin dimers are more likely to be depleted in small cells so that the polymerization velocity is smaller. In fact, experiments showed that if cell size is smaller than a critical value, mitotic spindles cannot be formed at all (15). In contrast, in very large cells (V→∞), tubulin is nearly unlimited so that the polymerization velocity approaches a constant (Eq. 19). When the mass conservation is considered, we found spindle length increases with the polymerization parameter kc defined in Eq. 18 in large cells, but decreases in small cells (Fig. 4 g). Similar to Fig. 4 a, cell boundary may provide extra influences in small cells.
Finally, for a given cell size, we found spindle length increases with chromosome size if we only consider one pair of chromosomes (or increases with chromosome number if the size of each chromosome is fixed) (Fig. 4 h). The result is in good agreement with the experimental data, which showed the meiosis II spindle containing only half the number of chromosomes as the mitosis stage 1 spindle has smaller spindle length (7).
It should be noted that in all panels of Fig. 4, the spindle size does not change with the cell size in the large cells, which indicates the upper limit of spindle size always exists. Therefore, the dynamics of MTs and molecular motors can only change the value of the upper limit, but not eliminate it. There should be other mechanisms that result in the existence of spindle size limit.
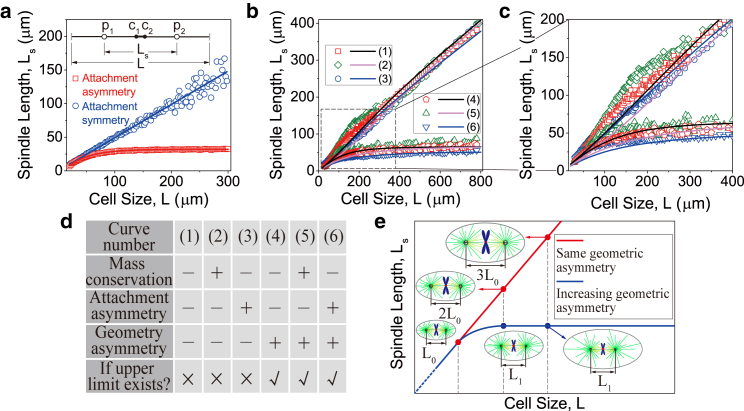
Geometric asymmetry induces upper limit of mitotic spindle size
It has been proposed that the mass conservation of tubulin can lead to a volume-dependent spindle scaling and an upper limit of spindle length also exists in vitro experiments (15, 16). This upper limit corresponds to the steady-state spindle length in unencapsulated extracts (15). However, tubulin or other building blocks are nearly unlimited in unencapsulated extracts (6). This indicates that the size limit of mitotic spindles might be determined by some intrinsic mechanism other than the mass conservation of spindle components.
To test this idea, we considered the mass conservation of tubulin carefully and applied a series of numerical experiments. Firstly, we considered a one-dimensional (1D) model (Fig. 5 a) similar to our previous work (38) except that the dynamic instability of MTs is considered explicitly here (for detail, see the Supporting Material). For each centrosome, if the obstacles (cell cortex or chromosomes) on its left side and right side are geometrically identical, we call it geometrically symmetric. Otherwise, it is geometrically asymmetric. If the binding or unbinding rates of kinetochores and kinesins on MT-chromosome attachments are different from dyneins and kinesins on MT-cortex attachments, we say the attachment is asymmetric (38). The geometry and attachment asymmetry break the symmetry between chromosome MTs and astral MTs so that they can effectively regulate spindle length. In the 1D model (Fig. 5 a), it is obviously geometrically symmetric, but the attachment asymmetry can still exist.
Figure 5.
Geometric asymmetry induces the upper limit of mitotic spindle size. (a) Simplified 1D model. The labels p1 and p2 are the positions of centrosomes; c1 and c2 are the positions of sister chromatids. Spindle length and cell length are Ls and L, respectively. (b–e) The 2D computational model. (b) Spindle length is plotted as the function of cell size, obtained by simulations. The solid lines are obtained by solving the minimal analytical model. (c) The detail of (b) in small cells. (d) The table summarizes the six simulations in (b) and (c). (e) Schematic of the mechanism of the geometric asymmetry. The degree of the geometric asymmetry changes (blue curve) or remains fixed (red curve). The slope of the straight line in (b) is determined by the ratio of Lc/L (an indicator of geometric asymmetry) as shown in Fig. 4h. To see this figure in color, go online.
We found there is no upper limit if the attachment asymmetry is eliminated in the 1D model (Fig. 5 a, blue curve). This is quite obvious if we treat the problem of the spindle length regulation as the problem of the positioning of the two centrosomes. Because spindle length is measured as the pole-to-pole distance, the positions of centrosomes determine spindle length. Obviously, if both attachment and geometry are symmetric, each centrosome will be positioned to the center of the half cell (Fig. 5 a). This is because the mass conservation of tubulin alone cannot break the left-right symmetry in the 1D cell. If we neglect the small distance between the two kinetochores, spindle length will approximately equal one-half of the cell length no matter how large the cell is. Therefore, the mass conservation of tubulin alone cannot result in the size limit of spindles in the 1D cell.
In the 2D model (Fig. 5, b–e), it is naturally geometrically asymmetric for each centrosome because the shapes of cell cortex and chromosomes are different. Therefore, we cannot eliminate the geometric asymmetry in this case. But we can do a thought experiment, i.e., we can keep the same degree of the geometric asymmetry by proportionally increasing chromosome size with cell size (Fig. 5 e). We studied six cases (Fig. 5, b–d). We found the mass conservation of tubulin (Cases 2 and 5) or the attachment asymmetry (Cases 3 and 6) alone cannot guarantee the existence of the upper limit. Without considering the mass conservation of tubulin (Cases 4 and 6) or the attachment asymmetry (Cases 4 and 5), the upper limit still exists. In contrast, the upper limit always exists whenever chromosome size is fixed, but the degree of geometric asymmetry increases with cell size (Cases 4–6). However, there is no upper limit whenever chromosome size is proportional to cell size, because the degree of geometric asymmetry is fixed (Cases 1–3).
Therefore, we conclude that the upper limit of spindle length in a 2D cell is induced by the inherent geometric asymmetry of the spindle structure. The upper limit naturally emerges when a chromosome’s size is fixed (or we have a fixed number of chromosomes), and this limit equals the steady-state spindle length in unencapsulated extracts (15) (cell volume V→∞). In very large cells, because the influence of cell cortex is nearly negligible, spindle size is cooperatively limited by the confinement of the chromosomes, the pushing force between antiparallel MTs generated by cross-linking motors, and the length-dependent pulling force by cytoplasmic dyneins.
Notice that the attachment asymmetry alone can result in the upper limit of spindle size in the 1D model (Fig. 5 a), which seems to contradict the results of the 2D model (Fig. 5, b–d). In fact, when chromosome size is proportionally increased with cell size, spindle size is mainly determined by chromosome size (Fig. 4 h). In this case, the influence of the attachment asymmetry is overridden by the influence of the proportionally increasing chromosome size in the 2D model.
Minimal analytical model for upper limit of mitotic spindle size
To provide a deeper insight about the mechanism of the spindle size limit, we also develop a minimal analytical model to capture the key features of the system. Because the spindle length is measured by the pole-to-pole distance in experiments and simulations, the problem of the spindle size regulation is reduced to solve the positions of spindle poles. The spindle poles interact with the cortex or chromosomes through the pushing forces and pulling forces of MTs. The resultant force is pushing force at short ranges and pulling force at long ranges, which is similar to the Lennard-Jones Potential. Therefore, we write the total energy of the system as
| (21) |
The first two terms of Eq. 21 are the interaction between the poles and the cortex; the parameters r1 and r2 are the distance from the pole to the cortex at the direction angle φ (Fig. S1); ε represents the depth of the potential well, which is proportional to the total amount of MTs or spindle mass; and σ determines the equilibrium position, which represents the ratio of pushing astral MTs to pulling astral MTs.
The last two terms of Eq. 21 are the interaction between the two spindle poles. It should be noted that the chromosome is not considered explicitly in this simplified model. The two spindle poles interact with each other through the chromosomes or antiparallel polar MTs indirectly.
The third term of Eq. 21 is the interaction between the two poles through chromosomes, where Lc is the chromosome size; Ls is the spindle length; L0 is constant; and σp represents the ratio of pushing chromosome MTs to pulling chromosome MTs. It should be noted that the chromosome arms only provide pushing forces. Therefore, both chromosome size Lc and spindle mass ε can change the ratio of pushing chromosome MTs and pulling chromosome MTs σp. Therefore, for simplicity, we assume σp = (ε/ε0)(Lc/L0)σc, where σc is the reference value for the ratio of pushing chromosome MTs and pulling chromosome MTs, and ε0 is a constant. When mass conservation is not considered, ε = ε0.
The fourth term of Eq. 21 is the interaction between the two poles through antiparallel polar MTs. As we derived in Eq. 20, the repulsive force between antiparallel MTs is , where A and B are two constants. Therefore, the interaction of antiparallel polar MTs U can be obtained by integration of the repulsive force Fr because Fr = −dU/dLs.
We can minimize the total energy to obtain the stable spindle length Ls. The results are shown as the solid lines in Fig. 5, b and c. The mass conservation, the attachment asymmetry, and the geometrical asymmetry can be manipulated by changing ε, σc, and Lc/L0, respectively (Table S2). It is noted that the interaction between spindle poles and the cortex varies with the cell size (the first two terms of Eq. 21). However, the interaction between two poles cannot keep changing with the cell size (the last two terms of Eq. 21). Therefore, the upper limit of spindle size still exists in the absence of mass conservation and attachment asymmetry. When we keep the same degree of the geometric asymmetry, i.e., keep the chromosome size Lc proportional to the cell size L, the interaction between two poles will keep changing with the cell size, and the upper limit disappears. These results agree with the numerical simulations very well (Fig. 5, b and c).
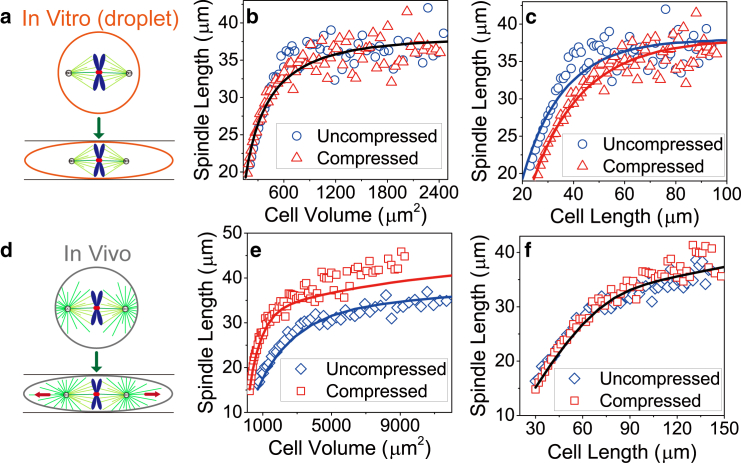
Boundary-sensing and volume-sensing mechanisms coexist in mall cells but fail in large cells
Interestingly, experiments found that Xenopus egg extract droplets possessing the same volume but different shapes have the same spindle length (15, 16). Therefore, in extract droplets, cell volume rather than cell shape determines spindle length (15, 16). However, in vivo experiments showed that the spindle elongates after the cell is compressed (60). If cell volume determines spindle length as proposed in the limit component model (15, 16), spindle length should decrease after the compression. The reason is that after compression, cell volume will decrease due to the efflux of water and ions induced by external forces (61) so that spindle length decreases accordingly. Apparently, this is inconsistent with the compression experiment (60). This indicates that different mechanisms of spindle length regulation may be employed or dominant in vivo and in vitro experiments (3, 5, 60). We noticed the major difference between these experiments is that astral MTs are lacking in the spindles assembled in extract droplets (15, 16). Thus, we wonder whether astral MTs lead to the different experimental results.
In Fig. 6, we increase cell size of the compressed and uncompressed cells with fixed aspect ratio and calculate spindle length. We found if astral MTs are removed artificially (Fig. 6 a), spindle length curves of the compressed and uncompressed cells collapse onto the same curve when plotted as the function of cell volume (cell area in the 2D model) (Fig. 6 b), but they separate when plotted as the function of cell length (Fig. 6 c). This is consistent with in vitro experiments (15, 16). Without astral MTs, spindles cannot sense the droplet boundary through the interaction between MTs and droplet boundary, but it can sense droplet volume though the depletion of tubulin. Therefore, the volume-sensing mechanism dominates in extract droplets.
Figure 6.
Volume-sensing mechanism versus boundary-sensing mechanism. (a–c) Spindle length scaling in uncompressed and compressed extract droplets (in vitro). Spindle length in extract droplets is plotted as the function of (b) cell volume and (c) cell length. Astral MTs are removed here because they are lacking in the spindles assembled in the extract droplets. (d–f) Spindle length scaling in uncompressed and compressed cells (in vivo). The solid lines are obtained by solving the minimal analytical model. To see this figure in color, go online.
In contrast, if astral MTs exist (Fig. 6 d), we get the opposite conclusion, i.e., the two curves collapse onto the same curve when plotted as the function of cell length (Fig. 6 f). This indicates that when astral MTs exist, the boundary-sensing mechanism dominates even if the mass conservation of tubulin is considered. This is consistent with the experiment (60). Movie S5 shows the dynamic evolution of spindle length after the cell is compressed, which agrees with the experiment (60) qualitatively. Many components of our model, such as the velocity-dependent forces by motors (Eq. 3), the force-dependent unbinding rates of motors (Eq. 5), and the length-dependent MT buckling and cytoplasmic pulling force (Eqs. 1 and 11), are controlled mechanically. Therefore, length, velocity, and force can be sensed accordingly, and the whole spindle can sense cell shape and size, and adjust its own size accordingly.
Therefore, in small cells, spindles can sense cell size and control their own size due either to the confinement of cell boundary (boundary-sensing mechanism) or to the limit component of building blocks (volume-sensing mechanism). However, the boundary-sensing mechanism overrides the volume-sensing mechanism when astral MTs exist. The latter mechanism is significant only when astral MTs vanish. Both mechanisms fail to regulate spindle size in very large cells because MTs can barely reach the cell boundary (see Fig. S8) and the number of building blocks is nearly unlimited in very large cells (6) (see Fig. S2). Therefore, in very large cells, the spindle loses the ability to sense cell size, and the spindle size is determined by the inherent geometric asymmetry of the spindle structure, as we proposed above.
Discussion
In this work, we developed a mechanical model to investigate the control mechanism of spindle size and why there is an upper limit of spindle size. Our model reproduced the scaling law that the spindle size increases with cell size and approaches an upper limit, which is in agreement with the in vivo and in vitro experiments (7, 16). Like previous models for spindle size (8, 9, 18), we perturbed various parameters of MT dynamics and molecular motors to investigate their influence on the spindle size. But the upper limit of the spindle size always exists, which indicates there are other inherent mechanisms that lead to the spindle size limit. An experiment can be used to test whether the perturbation of MTs or motors can recover the scaling with cell size when spindle size has reached its upper limit. A possible explanation of the upper limit is the limited component model (15). However, we still observed the size limit of spindles when the component is supplied unlimitedly. Another explanation of the upper limit is the attachment symmetry, i.e., the MT-kinetochore attachments are more stable than the MT-cortex attachments (38). But we still observed the size limit of spindle when the stability of the two attachments are the same. An experiment can be designed to test whether the upper limit will disappear when the MT-kinetochore attachments are perturbed to reduce their stability.
Strikingly, we found the existence of the upper limit of spindle size is only induced by the inherent geometric asymmetry. In other words, the chromosome always has a limited size (i.e., limited content in experiments), which is independent of the increase of cell size. In very large cells, because few MTs can reach the cell boundary, the spindle size is only determined by the chromosome size. Therefore, the spindle has a size limit no matter whether the cell boundary exists. Only if the chromosome size increases with the cell size proportionally will the upper limit disappear, because the degree of geometric asymmetry is kept. This is consistent with the previous experiment that the geometrical condition can influence the spindle width (32). Such a thought experiment cannot be achieved in practice because the chromosome content is always limited in cells. But it is possible to explore whether the inherent length of spindles can increase with the chromosome size.
Besides the spindle size limit, the regulation of the spindle size was also studied and plentiful results were obtained. We got some outputs that are in agreement with experimental results. For example, the spindle can elongate when increasing the growing velocity (or MT length) (8), increasing the spindle components (15), increasing the kinetochore pulling force (47), compressing the cell (60), or decreasing the pushing force on antiparallel MTs (18). These results indicate our model can successfully capture many key phenomena and features of spindle size. In the meanwhile, we also have some results that have not been tested in experiments. For instance, we found that in small cells the spindle size decreases linearly with the growing velocity of MTs under the influence of cell boundary, which is different from the results of in vitro experiments done without considering the cell boundary (8). We also found that the spindle size is independent of the slipping rate of MTs on the cortex, but can increase with the enhancing of cortical pulling force. And these results can be tested experimentally in the future.
Compared with the previous model, our model has a major advantage in that more complete mechanisms are considered. Therefore, we not only reproduced the control mechanisms of spindle size that have been found in experiments, but also provided some interesting predictions that can be tested in the future. Here, we considered not only the mass conservation of tubulins affected by the cell volume, but also the interaction between the spindle and the cell boundary—so our model can capture the spindle size scaling, and reveal why spindle size limit exists. The previous models for positioning or orientation of spindles usually described the spindle by a point or a rigid body with fixed size and shape (20, 21, 22, 23); in contrast, we added the spindle structure in the model explicitly, which allows us to investigate the potential impact of spindle size on positioning and orientation, and chromosome segregation in the future. Finally, unlike the previous analytical model (21, 22), our computational model is dynamic, so that it can be used to investigate what can influence the efficiency of cellular activity in future work. Our model may also be applicable to the spindlelike structures (62, 63).
We have shown that there is only a quantitative difference between 2D and 3D simulations (see Figs. S4 and S5). Therefore, to improve computational efficiency, we used a 2D computational model. One limitation of the 2D model is that it is more difficult for MTs to bypass chromosomes. We introduced a superposition method to solve this problem, i.e., we first figured out the interaction of antiparallel MTs separately, and then added it to the system with chromosomes. But in 3D cells, MTs can easily bypass chromosomes because their volume is small. To simplify the problem, here we neglected the branching MTs as proposed in previous works (9, 20, 21, 31), because they have the same polarity as mother MTs and the forces on the branching MTs are all transmitted to centrosomes to drive their motion (30). We further neglected the severing of MTs. It has been shown that the severing of MTs can decrease the MT length, and thus, can also influence the spindle size (9). But, obviously, they cannot lead to the existence of the upper limit of spindle. Also, due to the spindle size being defined by the distance between two poles, we described the mechanical deformation of MTs implicitly. We only recorded their states and calculated the forces that they apply on the chromosomes, centrosomes, or cortex as done by many previous models (20, 21). Therefore, MTs were all represented by straight lines in the movies. We can treat MTs as elastic rods and compute their deformations (9, 64), but the complexity is largely increased. Although we made these assumptions and simplifications, our model can capture the key features of spindle size and it can be used to study other related problems.
Author Contributions
H.J. initiated and supervised the project; H.J. developed the theory; J.L. performed the simulation; and H.J. and J.L. analyzed the data and wrote the article.
Acknowledgments
We thank Timothy J. Mitchison for valuable comments on the article.
This work was supported by the National Natural Sciences Foundation of China (under grants No. 11622222, 11472271, and 11342010), the Thousand Young Talents Program of China, and the Fundamental Research Funds for the Central Universities (under grant No. WK2480000001).
Editor: Andrew Spakowitz.
Footnotes
Supporting Materials and Methods, nine figures, two tables, and five movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30244-8.
Supporting Citations
References (65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75) appear in the Supporting Material.
Supporting Material
The movements of chromosomes are shown synchronously.
References
- 1.Chan Y.-H.M., Marshall W.F. How cells know the size of their organelles. Science. 2012;337:1186–1189. doi: 10.1126/science.1223539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Goshima G., Saitoh S., Yanagida M. Proper metaphase spindle length is determined by centromere proteins Mis12 and Mis6 required for faithful chromosome segregation. Genes Dev. 1999;13:1664–1677. doi: 10.1101/gad.13.13.1664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Goshima G., Scholey J.M. Control of mitotic spindle length. Annu. Rev. Cell Dev. Biol. 2010;26:21–57. doi: 10.1146/annurev-cellbio-100109-104006. [DOI] [PubMed] [Google Scholar]
- 4.Levy D.L., Heald R. Mechanisms of intracellular scaling. Annu. Rev. Cell Dev. Biol. 2012;28:113–135. doi: 10.1146/annurev-cellbio-092910-154158. [DOI] [PubMed] [Google Scholar]
- 5.Dumont S., Mitchison T.J. Force and length in the mitotic spindle. Curr. Biol. 2009;19:R749–R761. doi: 10.1016/j.cub.2009.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mitchison T.J., Ishihara K., Wühr M. Size scaling of microtubule assemblies in early Xenopus embryos. Cold Spring Harb. Perspect. Biol. 2015;7:a019182. doi: 10.1101/cshperspect.a019182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wühr M., Chen Y., Mitchison T.J. Evidence for an upper limit to mitotic spindle length. Curr. Biol. 2008;18:1256–1261. doi: 10.1016/j.cub.2008.07.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Reber S.B., Baumgart J., Jülicher F. XMAP215 activity sets spindle length by controlling the total mass of spindle microtubules. Nat. Cell Biol. 2013;15:1116–1122. doi: 10.1038/ncb2834. [DOI] [PubMed] [Google Scholar]
- 9.Loughlin R., Heald R., Nédélec F. A computational model predicts Xenopus meiotic spindle organization. J. Cell Biol. 2010;191:1239–1249. doi: 10.1083/jcb.201006076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mitchison T.J., Maddox P., Kapoor T.M. Roles of polymerization dynamics, opposed motors, and a tensile element in governing the length of Xenopus extract meiotic spindles. Mol. Biol. Cell. 2005;16:3064–3076. doi: 10.1091/mbc.E05-02-0174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Loughlin R., Wilbur J.D., Heald R. Katanin contributes to interspecies spindle length scaling in Xenopus. Cell. 2011;147:1397–1407. doi: 10.1016/j.cell.2011.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Srayko M., O’Toole E.T., Müller-Reichert T. Katanin disrupts the microtubule lattice and increases polymer number in C. elegans meiosis. Curr. Biol. 2006;16:1944–1949. doi: 10.1016/j.cub.2006.08.029. [DOI] [PubMed] [Google Scholar]
- 13.Caudron M., Bunt G., Karsenti E. Spatial coordination of spindle assembly by chromosome-mediated signaling gradients. Science. 2005;309:1373–1376. doi: 10.1126/science.1115964. [DOI] [PubMed] [Google Scholar]
- 14.Greenan G., Brangwynne C.P., Hyman A.A. Centrosome size sets mitotic spindle length in Caenorhabditis elegans embryos. Curr. Biol. 2010;20:353–358. doi: 10.1016/j.cub.2009.12.050. [DOI] [PubMed] [Google Scholar]
- 15.Good M.C., Vahey M.D., Heald R. Cytoplasmic volume modulates spindle size during embryogenesis. Science. 2013;342:856–860. doi: 10.1126/science.1243147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hazel J., Krutkramelis K., Gatlin J.C. Changes in cytoplasmic volume are sufficient to drive spindle scaling. Science. 2013;342:853–856. doi: 10.1126/science.1243110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Weber S.C., Brangwynne C.P. Inverse size scaling of the nucleolus by a concentration-dependent phase transition. Curr. Biol. 2015;25:641–646. doi: 10.1016/j.cub.2015.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Goshima G., Wollman R., Vale R.D. Length control of the metaphase spindle. Curr. Biol. 2005;15:1979–1988. doi: 10.1016/j.cub.2005.09.054. [DOI] [PubMed] [Google Scholar]
- 19.Howard J. Elastic and damping forces generated by confined arrays of dynamic microtubules. Phys. Biol. 2006;3:54–66. doi: 10.1088/1478-3975/3/1/006. [DOI] [PubMed] [Google Scholar]
- 20.Zhu J., Burakov A., Mogilner A. Finding the cell center by a balance of dynein and myosin pulling and microtubule pushing: a computational study. Mol. Biol. Cell. 2010;21:4418–4427. doi: 10.1091/mbc.E10-07-0627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pavin N., Laan L., Jülicher F. Positioning of microtubule organizing centers by cortical pushing and pulling forces. New J. Phys. 2012;14:105025. [Google Scholar]
- 22.Minc N., Burgess D., Chang F. Influence of cell geometry on division-plane positioning. Cell. 2011;144:414–426. doi: 10.1016/j.cell.2011.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Théry M., Jiménez-Dalmaroni A., Jülicher F. Experimental and theoretical study of mitotic spindle orientation. Nature. 2007;447:493–496. doi: 10.1038/nature05786. [DOI] [PubMed] [Google Scholar]
- 24.Mogilner A., Craig E. Towards a quantitative understanding of mitotic spindle assembly and mechanics. J. Cell Sci. 2010;123:3435–3445. doi: 10.1242/jcs.062208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Théry M., Bornens M. Cell shape and cell division. Curr. Opin. Cell Biol. 2006;18:648–657. doi: 10.1016/j.ceb.2006.10.001. [DOI] [PubMed] [Google Scholar]
- 26.Xiong F., Ma W., Megason S.G. Interplay of cell shape and division orientation promotes robust morphogenesis of developing epithelia. Cell. 2014;159:415–427. doi: 10.1016/j.cell.2014.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Strauss B., Adams R.J., Papalopulu N. A default mechanism of spindle orientation based on cell shape is sufficient to generate cell fate diversity in polarised Xenopus blastomeres. Development. 2006;133:3883–3893. doi: 10.1242/dev.02578. [DOI] [PubMed] [Google Scholar]
- 28.Ishihara K., Nguyen P.A., Mitchison T.J. Microtubule nucleation remote from centrosomes may explain how asters span large cells. Proc. Natl. Acad. Sci. USA. 2014;111:17715–17722. doi: 10.1073/pnas.1418796111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Brugués J., Nuzzo V., Needleman D.J. Nucleation and transport organize microtubules in metaphase spindles. Cell. 2012;149:554–564. doi: 10.1016/j.cell.2012.03.027. [DOI] [PubMed] [Google Scholar]
- 30.Petry S., Groen A.C., Vale R.D. Branching microtubule nucleation in Xenopus egg extracts mediated by augmin and TPX2. Cell. 2013;152:768–777. doi: 10.1016/j.cell.2012.12.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kozlowski C., Srayko M., Nédélec F. Cortical microtubule contacts position the spindle in C. elegans embryos. Cell. 2007;129:499–510. doi: 10.1016/j.cell.2007.03.027. [DOI] [PubMed] [Google Scholar]
- 32.Hara Y., Kimura A. An allometric relationship between mitotic spindle width, spindle length, and ploidy in Caenorhabditis elegans embryos. Mol. Biol. Cell. 2013;24:1411–1419. doi: 10.1091/mbc.E12-07-0528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Civelekoglu-Scholey G., Sharp D.J., Scholey J.M. Model of chromosome motility in Drosophila embryos: adaptation of a general mechanism for rapid mitosis. Biophys. J. 2006;90:3966–3982. doi: 10.1529/biophysj.105.078691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tolić-Nørrelykke I.M. Push-me-pull-you: how microtubules organize the cell interior. Eur. Biophys. J. 2008;37:1271–1278. doi: 10.1007/s00249-008-0321-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gittes F., Mickey B., Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Holy T.E., Dogterom M., Leibler S. Assembly and positioning of microtubule asters in microfabricated chambers. Proc. Natl. Acad. Sci. USA. 1997;94:6228–6231. doi: 10.1073/pnas.94.12.6228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Laan L., Pavin N., Dogterom M. Cortical dynein controls microtubule dynamics to generate pulling forces that position microtubule asters. Cell. 2012;148:502–514. doi: 10.1016/j.cell.2012.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jiang H. Cell size modulates oscillation, positioning and length of mitotic spindles. Sci. Rep. 2015;5:10504. doi: 10.1038/srep10504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.King S.J., Schroer T.A. Dynactin increases the processivity of the cytoplasmic dynein motor. Nat. Cell Biol. 2000;2:20–24. doi: 10.1038/71338. [DOI] [PubMed] [Google Scholar]
- 40.Svoboda K., Block S.M. Force and velocity measured for single kinesin molecules. Cell. 1994;77:773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
- 41.Campàs O., Sens P. Chromosome oscillations in mitosis. Phys. Rev. Lett. 2006;97:128102. doi: 10.1103/PhysRevLett.97.128102. [DOI] [PubMed] [Google Scholar]
- 42.Wühr M., Tan E.S., Mitchison T.J. A model for cleavage plane determination in early amphibian and fish embryos. Curr. Biol. 2010;20:2040–2045. doi: 10.1016/j.cub.2010.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nam W., Epureanu B.I. Highly loaded behavior of kinesins increases the robustness of transport under high resisting loads. PLOS Comput. Biol. 2015;11:e1003981. doi: 10.1371/journal.pcbi.1003981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gross S.P., Welte M.A., Wieschaus E.F. Dynein-mediated cargo transport in vivo. A switch controls travel distance. J. Cell Biol. 2000;148:945–956. doi: 10.1083/jcb.148.5.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Banigan E.J., Chiou K.K., Liu A.J. Minimal model for collective kinetochore-microtubule dynamics. Proc. Natl. Acad. Sci. USA. 2015;112:12699–12704. doi: 10.1073/pnas.1513512112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Akiyoshi B., Sarangapani K.K., Biggins S. Tension directly stabilizes reconstituted kinetochore-microtubule attachments. Nature. 2010;468:576–579. doi: 10.1038/nature09594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nannas N.J., O’Toole E.T., Murray A.W. Chromosomal attachments set length and microtubule number in the Saccharomyces cerevisiae mitotic spindle. Mol. Biol. Cell. 2014;25:4034–4048. doi: 10.1091/mbc.E14-01-0016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Syrovatkina V., Tran P.T. Loss of kinesin-14 results in aneuploidy via kinesin-5-dependent microtubule protrusions leading to chromosome cut. Nat. Commun. 2015;6:7322. doi: 10.1038/ncomms8322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Silkworth W.T., Nardi I.K., Cimini D. Timing of centrosome separation is important for accurate chromosome segregation. Mol. Biol. Cell. 2012;23:401–411. doi: 10.1091/mbc.E11-02-0095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kato Y.T.A. Chromosome morphology and the origin of maize and its races. Evol. Biol. 1984;17:219–253. [Google Scholar]
- 51.Skibbens R.V., Skeen V.P., Salmon E.D. Directional instability of kinetochore motility during chromosome congression and segregation in mitotic newt lung cells: a push-pull mechanism. J. Cell Biol. 1993;122:859–875. doi: 10.1083/jcb.122.4.859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Salmon E.D., Saxton W.M., McIntosh J.R. Diffusion coefficient of fluorescein-labeled tubulin in the cytoplasm of embryonic cells of a sea urchin: video image analysis of fluorescence redistribution after photobleaching. J. Cell Biol. 1984;99:2157–2164. doi: 10.1083/jcb.99.6.2157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wieczorek M., Bechstedt S., Brouhard G.J. Microtubule-associated proteins control the kinetics of microtubule nucleation. Nat. Cell Biol. 2015;17:907–916. doi: 10.1038/ncb3188. [DOI] [PubMed] [Google Scholar]
- 54.Dogterom M., Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. 1997;278:856–860. doi: 10.1126/science.278.5339.856. [DOI] [PubMed] [Google Scholar]
- 55.Wollman R., Cytrynbaum E.N., Mogilner A. Efficient chromosome capture requires a bias in the ‘search-and-capture’ process during mitotic-spindle assembly. Curr. Biol. 2005;15:828–832. doi: 10.1016/j.cub.2005.03.019. [DOI] [PubMed] [Google Scholar]
- 56.Paul R., Wollman R., Mogilner A. Computer simulations predict that chromosome movements and rotations accelerate mitotic spindle assembly without compromising accuracy. Proc. Natl. Acad. Sci. USA. 2009;106:15708–15713. doi: 10.1073/pnas.0908261106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Verde F., Dogterom M., Leibler S. Control of microtubule dynamics and length by cyclin A- and cyclin B-dependent kinases in Xenopus egg extracts. J. Cell Biol. 1992;118:1097–1108. doi: 10.1083/jcb.118.5.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Dogterom M., Leibler S. Physical aspects of the growth and regulation of microtubule structures. Phys. Rev. Lett. 1993;70:1347–1350. doi: 10.1103/PhysRevLett.70.1347. [DOI] [PubMed] [Google Scholar]
- 59.Liu D., Vader G., Lens S.M. Sensing chromosome bi-orientation by spatial separation of aurora B kinase from kinetochore substrates. Science. 2009;323:1350–1353. doi: 10.1126/science.1167000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Dumont S., Mitchison T.J. Compression regulates mitotic spindle length by a mechanochemical switch at the poles. Curr. Biol. 2009;19:1086–1095. doi: 10.1016/j.cub.2009.05.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Jiang H., Sun S.X. Cellular pressure and volume regulation and implications for cell mechanics. Biophys. J. 2013;105:609–619. doi: 10.1016/j.bpj.2013.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Petry S., Pugieux C., Vale R.D. Augmin promotes meiotic spindle formation and bipolarity in Xenopus egg extracts. Proc. Natl. Acad. Sci. USA. 2011;108:14473–14478. doi: 10.1073/pnas.1110412108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Dinarina A., Pugieux C., Nédélec F. Chromatin shapes the mitotic spindle. Cell. 2009;138:502–513. doi: 10.1016/j.cell.2009.05.027. [DOI] [PubMed] [Google Scholar]
- 64.Odell G.M., Foe V.E. An agent-based model contrasts opposite effects of dynamic and stable microtubules on cleavage furrow positioning. J. Cell Biol. 2008;183:471–483. doi: 10.1083/jcb.200807129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Drechsel D.N., Hyman A.A., Kirschner M.W. Modulation of the dynamic instability of tubulin assembly by the microtubule-associated protein tau. Mol. Biol. Cell. 1992;3:1141–1154. doi: 10.1091/mbc.3.10.1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Burakov A., Nadezhdina E., Rodionov V. Centrosome positioning in interphase cells. J. Cell Biol. 2003;162:963–969. doi: 10.1083/jcb.200305082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gombos L., Neuner A., Schiebel E. GTP regulates the microtubule nucleation activity of γ-tubulin. Nat. Cell Biol. 2013;15:1317–1327. doi: 10.1038/ncb2863. [DOI] [PubMed] [Google Scholar]
- 68.Inoué S., Salmon E.D. Force generation by microtubule assembly/disassembly in mitosis and related movements. Mol. Biol. Cell. 1995;6:1619–1640. doi: 10.1091/mbc.6.12.1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Goshima G., Nédélec F., Vale R.D. Mechanisms for focusing mitotic spindle poles by minus end-directed motor proteins. J. Cell Biol. 2005;171:229–240. doi: 10.1083/jcb.200505107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Joglekar A.P., Hunt A.J. A simple, mechanistic model for directional instability during mitotic chromosome movements. Biophys. J. 2002;83:42–58. doi: 10.1016/S0006-3495(02)75148-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Gao T., Blackwell R., Shelley M.J. Multiscale polar theory of microtubule and motor-protein assemblies. Phys. Rev. Lett. 2015;114:048101. doi: 10.1103/PhysRevLett.114.048101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Toba S., Watanabe T.M., Higuchi H. Overlapping hand-over-hand mechanism of single molecular motility of cytoplasmic dynein. Proc. Natl. Acad. Sci. USA. 2006;103:5741–5745. doi: 10.1073/pnas.0508511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Wang Z., Khan S., Sheetz M.P. Single cytoplasmic dynein molecule movements: characterization and comparison with kinesin. Biophys. J. 1995;69:2011–2023. doi: 10.1016/S0006-3495(95)80071-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Nédélec F. Computer simulations reveal motor properties generating stable antiparallel microtubule interactions. J. Cell Biol. 2002;158:1005–1015. doi: 10.1083/jcb.200202051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Janson M.E., Loughlin R., Tran P.T. Crosslinkers and motors organize dynamic microtubules to form stable bipolar arrays in fission yeast. Cell. 2007;128:357–368. doi: 10.1016/j.cell.2006.12.030. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The movements of chromosomes are shown synchronously.