Rats tactually explore their world by brushing and tapping their whiskers against objects. Each whisker's geometry will have a large influence on its mechanics and thus on the tactile signals the rat obtains. We performed a meta-analysis of seven studies to generate equations that describe systematic variations in whisker geometry across the rat's face. We also quantified the geometry of the whisker medulla. A database provides access to geometric parameters of over 500 rat whiskers.
Keywords: whisker, trigeminal, active sensing, touch, behavior
Abstract
Many rodents tactually sense the world through active motions of their vibrissae (whiskers), which are regularly arranged in rows and columns (arcs) on the face. The present study quantifies several geometric parameters of rat whiskers that determine the tactile information acquired. Findings include the following. 1) A meta-analysis of seven studies shows that whisker base diameter varies with arc length with a surprisingly strong dependence on the whisker's row position within the array. 2) The length of the whisker medulla varies linearly with whisker length, and the medulla's base diameter varies linearly with whisker base diameter. 3) Two parameters are required to characterize whisker “taper”: radius ratio (base radius divided by tip radius) and radius slope (the difference between base and tip radius, divided by arc length). A meta-analysis of five studies shows that radius ratio exhibits large variability due to variations in tip radius, while radius slope varies systematically across the array. 4) Within the resolution of the present study, radius slope does not differ between the proximal and distal segments of the whisker, where “proximal” is defined by the presence of the medulla. 5) Radius slope of the medulla is offset by a constant value from radius slope of the proximal portion of the whisker. We conclude with equations for all geometric parameters as functions of row and column position.
NEW & NOTEWORTHY Rats tactually explore their world by brushing and tapping their whiskers against objects. Each whisker's geometry will have a large influence on its mechanics and thus on the tactile signals the rat obtains. We performed a meta-analysis of seven studies to generate equations that describe systematic variations in whisker geometry across the rat's face. We also quantified the geometry of the whisker medulla. A database provides access to geometric parameters of over 500 rat whiskers.
rats use rhythmic motions of their whiskers to tactually explore the world around them (Richardson et al. 1909; Vincent 1912; Welker 1964). There are no sensors along the whisker length; instead, all tactile signals are transmitted to mechanoreceptors embedded in a richly innervated follicle at the whisker base (Ebara et al. 2002). Mechanoreceptors in the follicle transduce these tactile signals into electrical activity that is subsequently transmitted to the trigeminal ganglion (Gibson and Welker 1983; Jones et al. 2004; Leiser and Moxon 2007; Lichtenstein et al. 1990; Lottem and Azouz 2011; Szwed et al. 2003; Zucker and Welker 1969) and from there to the trigeminal nuclei, sensory thalamus, and ultimately somatosensory cortex (Bosman et al. 2011).
The geometry of the vibrissa plays an important role in the mechanical signals generated at the whisker base (Boubenec et al. 2012; Carl et al. 2012; Hartmann et al. 2003; Hires et al. 2013; Huet and Hartmann 2016; Huet et al. 2015; Kan et al. 2013; Neimark et al. 2003; Quist and Hartmann 2012; Yang and Hartmann 2016) and hence the neural responses generated by trigeminal ganglion neurons (Bush et al. 2016; Campagner et al. 2016). As yet, however, several of the geometric properties of the whiskers are poorly quantified, including their base diameter and “taper,” which has been defined in several different ways in previous studies. In addition, previous studies (Birdwell et al. 2007; Boubenec et al. 2012; Hartmann et al. 2003; Hires et al. 2013, 2016; Kan et al. 2013; Neimark et al. 2003; Quist et al. 2014) have modeled the whisker as a solid, conical, cantilever beam, but it is well known that the proximal portion of the whisker contains a low-density region called the medulla that can be approximated as hollow (Adineh et al. 2015; Carl et al. 2012; Chernova 2003; Chernova and Kulikov 2011; Hausman 1930; Voges et al. 2012).
In the present study, we aimed to quantify variations in whisker arc length, base diameter, taper, and medulla geometry across the array, and to develop equations that describe relationships between these parameters. These equations can be used to investigate some consequences of vibrissa geometry for whisking dynamics (Yang AE, Belli HM, and Hartmann MJ, unpublished observations).
METHODS
All procedures involving animals were approved in advance by the Animal Care and Use Committee of Northwestern University.
Data Collection
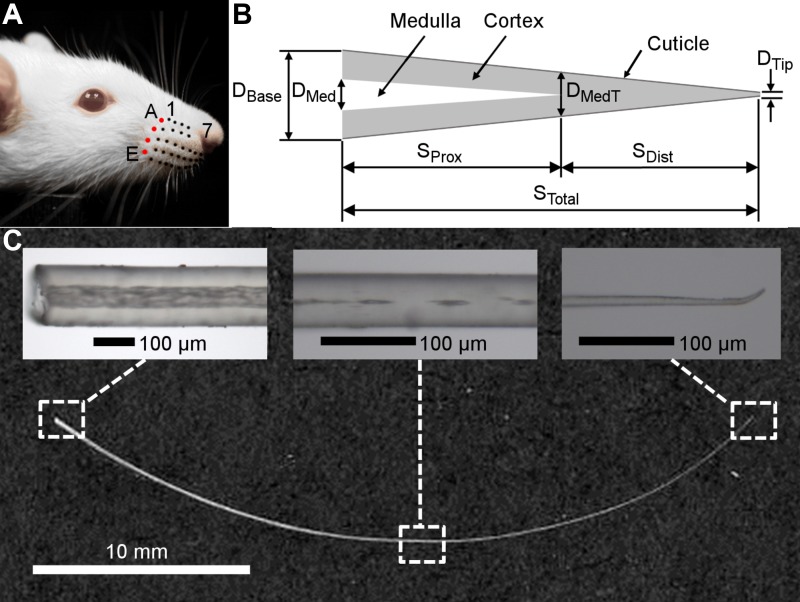
Two datasets were collected for the present work. In both datasets, the row and column position of each whisker was identified and recorded according to the convention depicted in Fig. 1A.
Fig. 1.
Geometric parameters of the whisker. A: each whisker is identified by its row and column position. In this photo, black and red dots have been drawn on the basepoint locations of the whiskers for visual clarity. From dorsal to ventral, the five rows are identified by the letters A–E, while the arcs (columns) are given the numbers 1–7 from caudal to rostral. The four whiskers of the caudal-most arc (colored red) are called the “Greek arc” or “Greek column” and are denoted from dorsal to ventral by the letters α, β, γ, and δ. B: schematic (not to scale) of the structural elements of the whisker. The whisker is modeled as a straight, tapered, conical frustum with base diameter (DBase) and tip diameter (DTip). The medulla is represented as a hollow cone that occupies the proximal region of the whisker. The diameter of the medulla at its base is denoted by DMed, and the diameter of the whisker at the point of medulla termination is labeled as DMedT. The total whisker arc length (STotal) is divided into a proximal portion occupied by the medulla (SProx) and a distal portion that does not include the medulla (SDist). The geometry of the cuticle was not quantified separately from the cortex in the present work. C: scanned image of the E2 whisker is shown along with three representative images to illustrate typical whisker geometry near the base, middle, and tip. The three images were not obtained from the E2 whisker; they were chosen to best illustrate the features described. The image near the base is from a C1 whisker (×10 magnification; left). The image at the location of medulla termination is from an E5 whisker (×20 magnification; middle). The image near the tip is from an E3 whisker (×20 magnification; right).
All whiskers were extracted within hours after euthanasia in unrelated experiments. Whiskers were not plucked from their follicles. Instead, each whisker was grasped near its base with fine surgical forceps and then cut at its base with surgical scissors. This procedure ensured that we did not mass the portion of the whisker internal to the follicle. Extreme care was taken to ensure consistency in the location at the base at which the whisker was cut.
Dataset 1: geometric parameters (excludes mass and medulla measurements).
Three hundred and forty-eight vibrissae were acquired from the left and right arrays of six female Long-Evans rats (Charles River, LE no. 006). Each rat was between 3 mo and 1.5 yr old and weighed between 226 and 300 g.
To obtain measurements of arc length, whiskers were scanned at a resolution of 2,400 dpi (10.6 μm/pixel) on a flatbed scanner (Epson Perfection 4180 Photo). These images were then either imported into the commercial software Reconstruct or into MATLAB to measure arc length. Measurement error was approximately two pixels on each end of the whisker, or ∼10.6 μm/pixel × 2 pixels/endpoint × 2 endpoints = ∼42.4 μm.
The diameter at the whisker base was measured using one of two upright transmitted light microscopes to capture digital images. The first microscope was a Phenix XSP-10 Series microscope with a ×40 objective and a high-resolution (3,088 × 2,056 pixels) digital camera (Canon Digital EOS Rebel) mounted on a ×10 eyepiece. These images were imported either into the software Reconstruct or into MATLAB where the whisker base diameter was measured. The second microscope was a Leica DM750 microscope with a ×10 objective and an Excelis HDS Accuscope HD Camera (1,920 × 1,080-pixel resolution) through a trinocular head. Rather than importing images into Reconstruct or into MATLAB, the base diameters were measured under the microscope using software associated with the camera (CaptaVision Imaging Software).
To determine measurement error, both the resolution and resolving power of visible light through the particular camera, microscope, and objective were calculated. The resolution of each imaging apparatus was calibrated by capturing an image of a laser-etched 100-μm grid with the appropriate objective and measuring this known length with the associated software. Resolving power was calculated based on the wavelength range of visible light and the numerical aperture of the objective. The resolving power of visible light through all scopes and objectives was found to be larger than the resolution of the camera, so measurement error was calculated based only on resolving power. In each case, measurement error was found to be approximately one pixel on each side of the base of the whisker, which corresponds to ∼1 μm for the first microscope and 2 μm for the second microscope.
Dataset 2: mass and medulla measurements in addition to geometric parameters.
A total of 70 vibrissae were collected from the left and right arrays of three Sprague-Dawley rats (Charles River, SD no. 400). Of these 70 whiskers, 37 were obtained from a female rat, 14 from the left array and 23 from the right array; 19 whiskers were obtained from the left array of a male rat; and 14 whiskers were obtained from the right array of a second male rat. The female rat was ∼13 mo old and weighed ∼350 g, and both male rats were ∼3 mo old and weighed ∼300 g.
Whole whiskers were massed using a Mettler-Toledo UMX2 microbalance (resolution 0.1 μg). The mass measurements were performed within 2–3 h after cutting to prevent dehydration.
After massing, whole whiskers were scanned at 1,200 dpi (∼21.2 μm/pixel) on the flatbed scanner (Epson Perfection 4180 Photo). These images were then imported into the commercial software Reconstruct to measure the total arc length of the vibrissa. Measurement error was approximately two pixels on each end of the whisker, or ∼21.2 μm/pixel × 2 pixels/endpoint × 2 endpoints = ∼85 μm.
Again, one of two upright transmitted light microscopes was used to capture digital images. The first was the same Phenix XSP-10 Series microscope described previously, with a ×4 or ×10 objective and a high-resolution (3,088 × 2,056 pixels) digital camera (Canon Digital EOS Rebel) mounted on a ×10 eyepiece. This microscope was primarily used to identify the location of medulla termination to bisect the whisker shaft at this point (Fig. 1B). For cases in which the medulla termination was ambiguous (e.g., discontinuous, as shown in Fig. 1C), a judgment call had to be made about the position of medulla termination. The point of medulla termination was selected by cutting at the location where the length of the discontinuous segments began to consistently decrease in relationship to the length of the spacing between these segments. For most whiskers, the difference between possible medulla termination sites was <1 mm. Both proximal and distal segments were then remassed within 24–48 h of their initial cutting from the rat and rescanned on the same scanner to estimate the arc length of each segment.
The second microscope was an Olympus BX60 with ×10, ×20, and ×40 objectives, and a MBF Bioscience Stereo Investigator DV-47 color camera. Images were imported into the software Reconstruct, where four measurements were obtained: the diameter of the whisker at its base (×10), the diameter of the whisker at the location of medulla termination (×20), the diameter of the whisker at its tip (×40), and the diameter of the medulla at the whisker base (×10).
Again, to determine measurement error, both the resolution and resolving power of visible light through the particular camera, microscope, and objective were calculated. The resolution and resolving power were calculated as described above. At all magnification levels, resolving power was found to be greater than the resolution of the microscope, so measurement error was calculated based only on resolving power. Estimated measurement error was, therefore, ∼1 μm/pixel × 1 pixel/endpoint × 2 endpoints = ∼2 μm at ×10 magnification, ∼0.7 μm/pixel × 1 pixel/endpoint × 2 endpoints = ∼1.4 μm at ×20 magnification, and ∼0.5 μm/pixel × 1 pixel/endpoint × 2 endpoints = ∼1 μm at ×40 magnification.
Using the methods described above, we measured and computed the parameters shown in Fig. 1B and Table 1.
Table 1.
Measured and calculated whisker variables
| Variable Name | Description |
|---|---|
| Measured variables | |
| DBase | Diameter of the whisker at its base |
| DTip | Diameter of the whisker at its tip |
| DMedT | Diameter of the whisker at the location where the medulla terminates |
| DMed | Diameter of the medulla at its base |
| DMed_Tip ≡ 0 | Diameter of the medulla at its tip is defined to be zero |
| STotal | Total arc length of the whisker |
| SProx | Arc length of the whisker proximal to medulla termination |
| SDist | Arc length of the whisker distal to medulla termination |
| MTotal | Total mass of the whisker |
| MProx | Mass of the whisker proximal to medulla termination |
| MDist | Mass of the whisker distal to medulla termination |
| Calculated variables | |
| RBase ≡ DBase/2 | Radius of the whisker at its base |
| RTip ≡ DTip/2 | Radius of the whisker at its tip |
| RMedT ≡ DMedT/2 | Radius of the whisker at the location where the medulla terminates |
| RMed ≡ DMed/2 | Radius of the medulla at its base |
Data Reduction
Dataset 2 included a total of 70 whiskers (used in Figs. 2, 3, and 4); however, no tip diameter measurements were collected for the 14 whiskers of the left array of the female Sprague-Dawley rat. In addition, four distal segments were lost during diameter measurements. Because distal whisker segments were often <10 μg in mass and <10 mm in length, it was easy to lose segments due to static electricity or air currents when transporting between experimental setups. Figure 6, therefore, uses a reduced dataset of 52 whiskers (70 − 18 = 52).
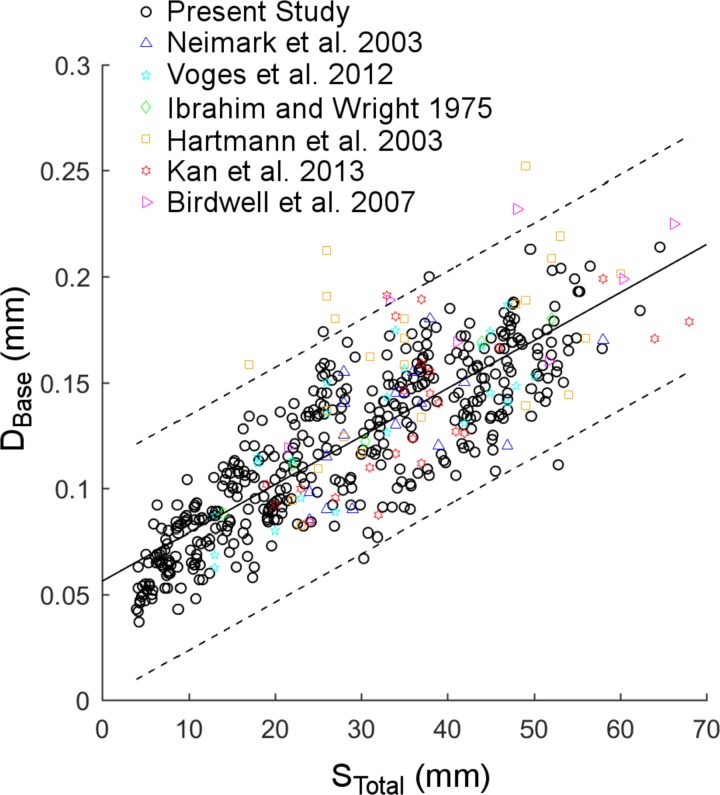
Fig. 2.
Diameter of the whisker base (DBase) as a function of arc length (STotal) for seven studies (519 whiskers total). The relationship between DBase and STotal obtained in the present study (418 whiskers) is not significantly different from the relationship for 101 whiskers obtained from six previous studies. Notice the large scatter about the trend line and the presence of four to five distinct diagonal “bands” within the data, sloping upwards from left to right.
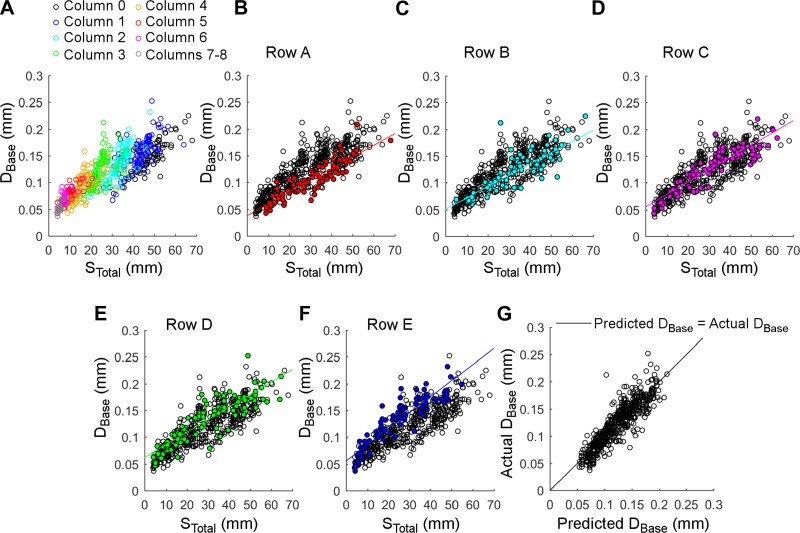
Fig. 3.
Relationship between base diameter (DBase) and whisker arc length (STotal) as a function of column and row position. A: when color coded by column position within the array, clear diagonal bands characterize the relationship between DBase and STotal. Best linear fits for each of the columns are indicated in Table 2. Column 0 indicates the Greek arc. B–F: clear groupings also emerge when the relationship between DBase and STotal is color coded by row position within the array. Although the slope is similar for all rows, the intercept varies considerably, as can be seen in the upwards vertical translation of the line of best fit from Row A to Row E, respectively (see Table 2). G: Eq. 2 predicts DBase with a high degree of accuracy as a function of STotal and row and column position.
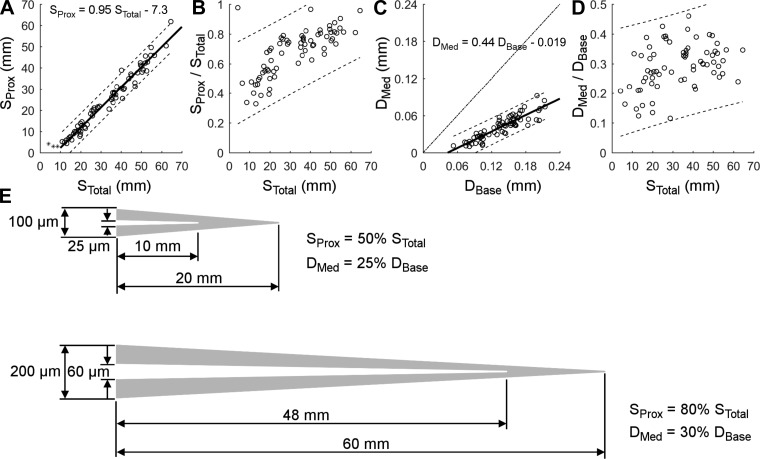
Fig. 4.
Length of the medulla (SProx) and base diameter of the medulla (DMed) as a function of whisker arc length (STotal) and base diameter (DBase), respectively. A–D: data from the 70 whiskers of dataset 2. A: the medulla arc length is linearly related to the total arc length. The linear fit excludes 3 whiskers with length less than 10 mm. B: the fraction of the total arc length occupied by the medulla increases for longer whiskers. C: the diameter of the medulla at the whisker base is linearly related to the base diameter. Dashed line is where the medulla diameter equals the base diameter. D: the medulla diameter occupies 11–46% of the base diameter. E: schematics provide visual intuition for the size and shape of the medulla compared with the shape of the whole whisker. Relative to shorter whiskers, longer vibrissae have a larger fraction of their length occupied by the medulla, but the ratio of medulla base diameter to whisker base diameter increases only slightly for larger whiskers.
Fig. 6.
Both subplots use reduced dataset 2, which consisted of 52 whiskers. A: within the resolution of the present study, radius slope is not significantly different between proximal and distal whisker segments. Out of 52 whiskers, 36.5% had a proximal radius slope greater than that in the distal region; the remaining 63.5% had a distal radius slope greater than the proximal slope. B: the medulla radius slope is smaller by a constant offset than the proximal radius slope of the whisker. The offset is 0.0012.
Datasets Used in Meta-analysis
Several previous studies have measured geometric parameters across the whisker array for both male and female rats of various strains (Sprague-Dawley, Wistar-Hannover, and Long-Evans). We combined data from the present study with that from six earlier studies to perform a meta-analysis of whisker diameter and arc length. Four of the previous studies measured diameters at the base and tip, as well as total whisker arc length (Hartmann et al. 2003; Ibrahim and Wright 1975; Neimark et al. 2003; Voges et al. 2012). Two of the previous studies only measured base diameter and arc length (Birdwell et al. 2007; Kan et al. 2013). All six studies identified the row and column position of the whiskers within the array. Birdwell et al. (2007) used 7 whiskers from female Sprague-Dawley rats (age not specified), and Kan et al. (2013) used 24 whiskers from one 3-mo-old female Sprague-Dawley rat. The number of whiskers from all other datasets is indicated in column 2 of Table 5 in the results.
Table 5.
Meta-analysis of radius ratio and radius slope across five studies
| Study | Age, Sex, Strain (Whiskers) | Origin of Data | Radius Ratio | Radius Slope |
|---|---|---|---|---|
| Ibrahim and Wright (1975) | 3- to 6-mo-old Male Wistar rat (5 whiskers) | “In rats α, β, γ and δ vibrissae are 3-5 μm at their tips and 160–180 μm at the widest part excluding the club.” (p. 52). Fig. 8A provides data about the arc length of whiskers α, β, γ, and δ. | Smallest possible ratio: 80/2.5 = 32; largest possible ratio: 90/1.5 = 60. | Arc length data (in mm) taken from Fig. 8A, ∼140 days: α = 44; β = 51, γ = 52, δ = 59. Min possible radius slope = (80 − 2.5)/59,000 = 1.31 × 10−3. Max possible radius slope = (90 − 1.5)/44,000 = 2.01 × 10−3. |
| Fig. 6 plots diameter as a function of arc length for the β, A1, A2, A3, and A4 rat vibrissae. The resolution of Fig. 6 is severely limited at the tip. The data were extracted from the figure and are provided in Table 3, Data from Ibrahim and Wright (1975), in the present paper. | Based on data from Table 3 in present work [from Fig. 6 of Ibrahim and Wright (1975)]. Mean ± SD: 27 ± 8. Median: 24. | Based on data from Table 3 in present work [from Fig. 6 of Ibrahim and Wright (1975)]. Mean ± SD: 2.16 × 10−3 ± 0.523 × 10−3. Median: 1.89 × 10−3. | ||
| Neimark et al. (2003) | Unknown age, sex, strain (18 whiskers) | Table 2 provides arc length, base diameter, and tip diameter for 18 whiskers. The whiskers include the Greek column and columns 1, 2, and 3 of rows A–E. | Based on Table 2 in Neimark et al. (2003). Mean ± SD: 29 ± 35. Median: 23. | Based on data from Table 2 in Neimark et al. (2003). Mean ± SD: 1.76 × 10−3 ± 0.457 × 10−3. Median: 1.75 × 10−3. |
| Hartmann et al. (2003) | Adult, female, Sprague-Dawley (24 whiskers) | Fig. 6c shows a log-log plot of diameter vs. arc length for 24 rat whiskers. These original data are provided in Table 3, Data from Hartmann et al. (2003), in the present paper, along with tip diameters. | Based on Table 3 in present work [from Fig. 6c in Hartmann et al. (2003)]. Mean ± SD: 36 ± 20. Median = 33. | Based on Table 4 in present work [from Fig. 6c in Hartmann et al. (2003)]. Mean ± SD: 2.26 × 10−3 ± 0.822 × 10−3. Median = 2.04 × 10−3. |
| Voges et al. (2012) | 14 mo, female, Wistar Hannover (23 whiskers) | Figs. 3 and 4 show data for arc length, base diameter, and tip diameter. The original data were obtained from the authors and provided in Table 3, Data from Voges et al. (2012), in the present paper. | Based on data from Table 4 in present work [from Figs. 3 and 4 of Voges et al. (2012)]. Mean ± SD: 62 ± 31. Median = 51. | Based on data from Table 4 in present work [from Figs. 3 and 4 of Voges et al. (2012)]. Mean ± SD: 2.17 × 10−3 ± 0.553 × 10−3. Median = 2.02 × 10−3. |
| Belli et al. (2016) (present study) | 3–13 mo, male and female, Sprague-Dawley (52 whiskers) | Data collected in present study and tabulated in Table 4. | Mean ± SD: 29 ± 11. Median = 28 | Mean ± SD: 2.48 × 10−3 ± 1.10 × 10−3. Median = 2.18 × 10−3. |
Columns are as follows: study information; age, sex, strain, and number of whiskers; origin of data; means, SD, and median for the five studies for radius ratio; and the means, SD, and median across each of the five studies for radius slope. The Radius Ratio and Radius Slope columns for Ibrahim and Wright (1975) show only extrema for radius ratio because of the large measurement uncertainties in the tip and base diameters. Another version of this table is available as Supplemental Table S2 and at https://github.com/SeNSE-lab/RatWhiskerGeometry.git formatted for readability and scientific clarity.
Statistical Analysis and Error Propagation
All statistical analyses were performed in MATLAB. As described above, we carefully accounted for measurement error of whisker parameters by comparing the resolution and resolving power of visible light through the particular camera, microscope, and objective when acquiring these geometric parameters. Rather than plot the individual measurement error in Figs. 2 and 4, 95% confidence bounds were plotted about each fit to account for both measurement error and the natural deviation in biological data. These confidence limits were generated using the MATLAB prediction interval function (“predint”) with simultaneous observation bounds. Because radius ratio and radius slope were calculated, not measured variables, error propagation (NIST/SEMATECH 2012) was used to compute the error bars for each whisker in Fig. 5.
Fig. 5.
Quantification of radius ratio (RatioR) and radius slope (SlopeR) as functions of whisker arc length. B–G use data from all 122 whiskers across the 5 studies of the meta-analysis, with error bars computed via propagation of error. A: two parameters are required to define the geometry of a whisker. The top schematic illustrates that two whiskers with the same SlopeR can have very different RatioR. The bottom schematic illustrates that two whiskers with different SlopeR can have the same RatioR. B: the RatioR (RBase/RTip) is extremely variable and does not exhibit a strong relationship with arc length (STotal). RatioR is extremely sensitive to changes in the radius of the whisker tip, which can vary considerably due to wear, damage, and barbering. Error bounds vary greatly. C: SlopeR [(RBase − RTip)/STotal] is larger for shorter whiskers than for longer whiskers. Error bounds are much smaller than those calculated for RatioR. D: SlopeR increases with column position from caudal to rostral. E: within each column, SlopeR tends to increase slightly from dorsal (row A) to ventral (row E). F: schematic of SlopeR as a function of both row and column position across the array shows a strong trend by column and weak trend by row. G: the best prediction for SlopeR (Eq. 7) is linear with row and quadratic with column. The diagonal line represents the relationship where actual SlopeR = predicted SlopeR.
RESULTS
All data used in the present study are provided in Supplemental Table S1, available in the data supplement online at the Journal of Neurophysiology Web site. This same file is also publicly available on GitHub (https://github.com/SeNSE-lab/RatWhiskerGeometry.git) with the goal of allowing other researchers to add additional datasets.
A Meta-analysis of Arc Length and Base Diameter as a Function of Arc Length
We surveyed the literature for data that described the diameter and arc length of rat vibrissae. We excluded studies that used mice (Hires et al. 2013, 2016; Pammer et al. 2013). Our survey yielded six studies, in addition to the present work, that provided measurements of both base diameter and arc length (Birdwell et al. 2007; Hartmann et al. 2003; Ibrahim and Wright 1975; Kan et al. 2013; Neimark et al. 2003; Voges et al. 2012). As described in methods, the present study contained two datasets (datasets 1 and 2), and the remaining six studies constituted datasets 3–8.
We began with the goal of finding an expression for total whisker arc length (STotal) as a function of the whisker's row and column position within the array. Using the MATLAB prediction interval function (“predint”) with simultaneous observation bounds, prediction bounds were determined on linear fits for STotal as a function of both row and column identity for each of the eight datasets. Considerable overlap was observed across all eight sets of bounds (see discussion for more details), indicating that across datasets there were no substantial differences in STotal as a function of row and column identity. Note that this analysis implicitly contains comparisons across rat sex and strain as well as across different laboratories; see column 2 of Table 5 for a list of the sex and strain used in each study.
Given the consistency of results across datasets, all data were grouped, and the best linear fit relationship between STotal and Row and column (Col) position across all 519 whiskers was found to be:
| 1 |
where STotal has units of millimeters, Row varies between 1 and 5 (representing the A through E rows), and Col varies between 0 and 8. The adjusted R2 is 0.85.
We next aimed to find the functional relationship between base diameter (DBase) and STotal. Two previous studies on whisker resonance approximated the relationship between base diameter and arc length as a power law (Hartmann et al. 2003; Neimark et al. 2003). Although this relationship served as a useful empirical approximation in the context of these resonance experiments, it is statistically inappropriate to assert a power-law relationship unless the data vary over several orders of magnitude (Clauset et al. 2009).
When the relationship between DBase and STotal for each of the eight datasets was plotted individually, the highest order fit for each of the eight individual data sets that avoided overfitting was found to be linear. For dataset 1 (348 whiskers), the best fit was DBase = 0.0022 STotal + 0.054, while for dataset 2 (70 whiskers), the best fit was DBase = 0.0021 STotal + 0.071. In these equations, DBase and STotal both have units of millimeters. The equation for dataset 2 is identical to that used in Yang and Hartmann (2016), except for rounding differences.
Again using the MATLAB prediction interval function with simultaneous observation bounds, prediction bounds were determined on the linear fits between DBase and STotal for each of the eight datasets. Considerable overlap was observed across all eight sets of bounds, so all data were grouped. When the eight datasets were combined, the quadratic model yielded a slightly better fit than the linear model on the basis of the Akaike Information Criterion (AIC). However, the linear regression models fit by individual datasets suggested that a quadratic model was overfitting the data. Thus, for the combined data, a linear model was selected as the best fit (root mean square error: 0.023; R2: 0.69). Results are shown in Fig. 2 for all 519 whiskers. The line of best fit shown in the figure is: DBase = 0.0023 STotal + 0.056, again with DBase and STotal both expressed in units of millimeters.
The linear model shown in Fig. 2 is dissatisfying for two closely related reasons. First, there is large variance about the fit for all seven studies. Second, visual inspection suggests that the trend consists of several diagonally slanted “bands” of data points, rather than a single trend. We tested the possibility that these diagonal bands were related to the row and column positions of the whiskers within the array.
The Relationship between Whisker Base Diameter and Arc Length Varies with Row and Column Position in the Array
Continuing to use all 519 whiskers from all 7 studies, we investigated the possibility that the large variance and diagonal bands observed in Fig. 2 were associated with the whiskers' positions within the array. Figure 3 shows these relationships, and the corresponding equations are provided in Table 2.
Table 2.
Equations for diameter at the whisker base as a function of whisker arc length when examined by row and column position
| Model | No. of Whiskers | Equation | Root MSE | R2 |
|---|---|---|---|---|
| Equations for DBase as a function of STotal when examined by column | ||||
| Column 0 (Greek) | 77 | DBase = 0.0025 STotal + 0.032 | 0.023 | 0.46 |
| Column 1 | 97 | DBase = 0.0034 STotal + 0.0082 | 0.022 | 0.49 |
| Column 2 | 90 | DBase = 0.0049 STotal − 0.026 | 0.018 | 0.63 |
| Column 3 | 97 | DBase = 0.0038 STotal + 0.028 | 0.024 | 0.37 |
| Column 4 | 80 | DBase = 0.0032 STotal + 0.041 | 0.020 | 0.39 |
| Column 5 | 36 | DBase = 0.0031 STotal + 0.048 | 0.011 | 0.49 |
| Column 6 | 24 | DBase = 0.0038 STotal + 0.043 | 0.010 | 0.52 |
| Columns 7 and 8 | 18 | DBase = 0.0088 STotal + 0.0066 | 0.006 | 0.59 |
| Equations for DBase as a function of STotal when examined by row | ||||
| Row A | 89 | DBase = 0.0022 STotal + 0.038 | 0.015 | 0.78 |
| Row B | 95 | DBase = 0.0021 STotal + 0.051 | 0.020 | 0.67 |
| Row C | 108 | DBase = 0.0023 STotal + 0.055 | 0.016 | 0.83 |
| Row D | 117 | DBase = 0.0023 STotal + 0.062 | 0.019 | 0.79 |
| Row E | 110 | DBase = 0.0030 STotal + 0.056 | 0.018 | 0.85 |
DBase, diameter at the whisker base; STotal, whisker arc length; Root MSE, root mean square error.
Because a whisker's column position within the array is strongly correlated with its arc length (Brecht et al. 1997; Towal et al. 2011), color coding the data by column position as in Fig. 3A clearly reveals clusters within the relationship between DBase and STotal. There are remarkably distinct gaps between some of the column clusters, particularly notable between columns 1 and 2 and between columns 2 and 3. More surprising, however, is that the relationship between base diameter and arc length also varies strongly with row (Fig. 3, B–F). For a given arc length, whiskers in more dorsal rows have smaller diameters than whiskers in more ventral rows. The equations of Table 2 show that the relationship between base diameter and arc length is best expressed on a per-row, rather than a per-column basis.
Because both row and column influence the relationship between DBase and STotal, we expanded the single linear regression for base diameter as a function of arc length to include predictors for column and row. Interaction terms between STotal and Row and between STotal and Col were not significant. With DBase and STotal expressed in millimeters, the best single-predictor model with significant coefficient estimates was found to be:
| 2 |
where Row ranges between 1 and 5, and Col varies between 0 (for the Greek arc) and 8. Figure 3G shows the actual DBase vs. predicted DBase, as calculated from Eq. 2. The prediction of Eq. 2 is strong, having a root mean square error of 0.018 and an adjusted R2 of 0.80.
Medulla Length Varies Linearly with Whisker Arc Length; Medulla Diameter Varies Linearly with Whisker Base Diameter
Although several studies have quantified whisker base diameter and arc length, few have quantified the hollow region known as the medulla. This structure will have important consequences for whisker dynamics because it will change the mass distribution of the whisker (Boubenec et al. 2012; Hartmann et al. 2003; Kan et al. 2013; Neimark et al. 2003; Quist et al. 2014).
Previous studies have found that the medulla occupies between 50% and 75% of the overall length of the whisker (Voges et al. 2012). The resolution of this result was limited, however, because it was based on dividing the whisker length into quartiles and determining within each quarter where the medulla terminated. Examining the location of medulla termination as a continuous variable (Fig. 4A) shows that medulla length is tightly linearly correlated with whisker arc length for vibrissae longer than ∼10 mm (R2 = 0.97). This relationship is provided in Eq. 3 and predicts negative (nonphysical) values of SProx (proximal portion occupied by the medulla), when STotal is less than 7.3 mm/0.95 = 7.7 mm.
| 3 |
If the intercept in Fig. 4A were zero, the medulla would occupy a constant fraction of the total whisker length. However, the intercept is not zero, so the fraction occupied by the medulla varies widely: it occupies anywhere between 33% and 98% of the total arc length (Fig. 4B). On average, longer whiskers have a larger fraction of their length occupied by the medulla than shorter whiskers.
A similar analysis is shown for the base diameter of the medulla (DMed) in Fig. 4, C and D. The base diameter of the medulla scales linearly with the base diameter of the whisker (Fig. 4C). This relationship is provided in Eq. 4 (R2 = 0.80). The ratio of medulla base diameter to whisker base diameter, however, is quite variable. The diameter of the medulla at the whisker base (DMed) varies between 11% and 46% of the diameter at the whisker base (DBase) (Fig. 4D).
| 4 |
Summarizing the results of Fig. 4, A–D, features of the medulla geometry (both length and diameter at the base) scale linearly with whisker geometry, but nonzero intercepts mean that variable fractions of the whisker are occupied by the medulla. An intuition for these relationships is provided in the schematic of Fig. 4E. The percentage of the total whisker length occupied by the medulla is much larger for longer whiskers than for shorter whiskers, whereas the percent of the total base diameter occupied by the medulla diameter is only slightly greater for larger whiskers than for shorter whiskers.
Defining the “Taper” of a Whisker: a Meta-analysis of Radius Slope and Radius Ratio
A variety of studies of mammalian vibrissae and hairs have used the word “taper” and similar phrases differently. Williams and Kramer (2010) define whisker taper as the ratio of base radius to tip radius. Quist et al. (2011) and Quist and Hartmann (2012) use the phrase “taper ratio” to mean the exact same quantity. The difference between the base and tip radii divided by the length of the whisker is defined as the “slope of radius” by Neimark et al. (2003). This same quantity is implicitly defined as taper by Hires et al. (2016) and is explicitly defined as taper by Sterbing-D'Angelo et al. (2016).
As can be seen in the schematics in Fig. 5A, two parameters are required to describe the taper of a whisker. The ratio of base radius (RBase) to tip radius (RTip) can vary dramatically, while the slope of the whisker remains constant. Conversely, the ratio of RBase to RTip can remain constant, while the slope varies. To avoid this semantic confusion, we avoid use of the word taper entirely and instead propose:
| 5a |
| 5b |
| 6a |
| 6b |
where DTip is tip diameter. Note that diameter ratio (RatioD) and radius ratio (RatioR) will always be exactly equal, but diameter slope (SlopeD) will always be larger than radius slope (SlopeR) by a factor of two.
In performing a meta-analysis of RatioR and SlopeR, we were able to use only those studies that included measurements of the whisker tip, as well as measurements of whisker base diameter and arc length. Of the six previous studies used in the meta-analysis of Figs. 2 and 3, four included values for tip diameter (Hartmann et al. 2003; Ibrahim and Wright 1975; Neimark et al. 2003; Voges et al. 2012). One of these four studies (Neimark et al. 2003) explicitly tabulates data for 18 whiskers, including arc length, base diameter and tip diameter, and radius slope. The data from Neimark et al. (2003) are not repeated in the present work, as they can be found in Table 2 of that study.
Data for the other three studies (Hartmann et al. 2003; Ibrahim and Wright 1975; Voges et al. 2012) are provided in Table 3 in the present work. To obtain the data in Table 3, we scanned in the figures from Ibrahim and Wright (1975) and extracted these points in MATLAB, yielding a total of five whiskers. We also obtained the original measures of base diameter, tip diameter, and arc length for the 24 whiskers used in Hartmann et al. (2003) and the 23 whiskers from Voges et al. (2012). Measurements from the 52 whiskers of the present study (reduced dataset 2; see methods, Data Reduction), are tabulated in Table 4.
Table 3.
Quantification of radius ratio and radius slope obtained from previous studies
| Origin of Data | Whisker | DBase, μm | DTip, μm | STotal, mm | RBase/RTip | (RBase − RTip)/STotal |
|---|---|---|---|---|---|---|
| Data from Ibrahim and Wright (1975) | ||||||
| We scanned Fig. 6 from Ibrahim and Wright (1975) | β | 180 | 5 | 52 | 36 | 1.68 × 10−3 |
| A1 | 169 | 5 | 44 | 34 | 1.86 × 10−3 | |
| A2 | 122 | 5 | 31 | 24 | 1.89 × 10−3 | |
| A3 | 111 | 5 | 22 | 22 | 2.41 × 10−3 | |
| A4 | 88 | 5 | 14 | 18 | 2.96 × 10−3 | |
| Data from Hartmann et al. (2003) | ||||||
| DBase and STotal are shown in Fig. 6c of Hartmann et al. (2003); DTip was obtained by reexamining the data used in Hartmann et al. (2003) | α | 209 | 4 | 52 | 52 | 1.97 × 10−3 |
| β | 144 | 2 | 54 | 72 | 1.31 × 10−3 | |
| γ | 202 | 8 | 60 | 25 | 1.62 × 10−3 | |
| δ | 171 | 5 | 56 | 34 | 1.48 × 10−3 | |
| A1 | 139 | 3 | 49 | 46 | 1.39 × 10−3 | |
| B1 | 189 | 5 | 49 | 38 | 1.88 × 10−3 | |
| C1 | 220 | 6 | 53 | 37 | 2.02 × 10−3 | |
| D1 | 252 | 4 | 49 | 63 | 2.53 × 10−3 | |
| E1 | 187 | 10 | 48 | 19 | 1.84 × 10−3 | |
| A2 | 133 | 14 | 37 | 10 | 1.61 × 10−3 | |
| B2 | 162 | 47 | 31 | 3 | 1.85 × 10−3 | |
| C2 | 117 | 5 | 30 | 23 | 1.87 × 10−3 | |
| D2 | 180 | 10 | 35 | 18 | 2.43 × 10−3 | |
| E2 | 171 | 11 | 35 | 16 | 2.29 × 10−3 | |
| A3 | 83 | 2 | 23 | 42 | 1.76 × 10−3 | |
| B3 | 212 | 3 | 26 | 71 | 4.02 × 10−3 | |
| C3 | 158 | 8 | 35 | 20 | 2.14 × 10−3 | |
| D3 | 180 | 6 | 27 | 30 | 3.22 × 10−3 | |
| E3 | 191 | 6 | 26 | 32 | 3.56 × 10−3 | |
| A4 | 94 | 4 | 22 | 24 | 2.05 × 10−3 | |
| B4 | 109 | 2 | 25 | 55 | 2.14 × 10−3 | |
| C4 | 137 | 4 | 26 | 34 | 2.56 × 10−3 | |
| D4 | 124 | 4 | 28 | 31 | 2.14 × 10−3 | |
| E4 | 158 | 2 | 17 | 79 | 4.59 × 10−3 | |
| Data from Voges et al. (2012) | ||||||
| Original data were obtained from the authors of Voges et al. (2012) | α | 140 | 2 | 47 | 70 | 1.47 × 10−3 |
| A1 | 131 | 3 | 42 | 44 | 1.52 × 10−3 | |
| A2 | 89 | 1 | 27 | 89 | 1.63 × 10−3 | |
| A3 | 80 | 2 | 20 | 40 | 1.95 × 10−3 | |
| A4 | 63 | 1 | 13 | 63 | 2.38 × 10−3 | |
| β | 153 | 3 | 50 | 51 | 1.50 × 10−3 | |
| B1 | 145 | 3 | 45 | 48 | 1.58 × 10−3 | |
| B2 | 126 | 2 | 33 | 63 | 1.88 × 10−3 | |
| B3 | 95 | 2 | 23 | 48 | 2.02 × 10−3 | |
| B4 | 69 | 3 | 13 | 23 | 2.54 × 10−3 | |
| C1 | 167 | 2 | 44 | 84 | 1.88 × 10−3 | |
| C2 | 143 | 2 | 33 | 72 | 2.14 × 10−3 | |
| C3 | 113 | 1 | 22 | 113 | 2.55 × 10−3 | |
| C4 | 87 | 2 | 13 | 44 | 3.27 × 10−3 | |
| δ | 148 | 1 | 48 | 148 | 1.53 × 10−3 | |
| D1 | 174 | 7 | 45 | 25 | 1.86 × 10−3 | |
| D2 | 156 | 2 | 35 | 78 | 2.20 × 10−3 | |
| D3 | 135 | 2 | 26 | 68 | 2.56 × 10−3 | |
| D4 | 112 | 1 | 18 | 112 | 3.08 × 10−3 | |
| E1 | 187 | 5 | 47 | 37 | 1.94 × 10−3 | |
| E2 | 175 | 6 | 34 | 29 | 2.49 × 10−3 | |
| E3 | 150 | 3 | 26 | 50 | 2.83 × 10−3 | |
| E4 | 115 | 3 | 18 | 38 | 3.11 × 10−3 | |
The tip diameter in Ibrahim and Wright (1975) was not visible at the resolution of the figure, so the mean tip diameter from the present study was used as an approximation for all five whiskers. The base and tip diameter data for Voges et al. (2012) were obtained from the authors as the averages of three measurements. These averages have been rounded to the nearest micrometer. All values of radius ratio are reported to the nearest integer. These values can be rounded to a single significant digit for consistency with the measurement precision of tip diameter.
Table 4.
Whisker parameters from the present study used in the calculation of radius slope and radius ratio (Reduced Dataset 2: 52 whiskers)
| Rat No. | Sex | Side | Whisker | DBase, μm | DMed, μm | DMedT, μm | DTip, μm | STotal, mm | SProx, mm | SDist, mm | RBase/RTip | (RBase − RTip)/STotal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | F | R | A1 | 139 | 49 | 45 | 5 | 37.5 | 25.8 | 11.7 | 28 | 1.79 × 10−3 |
| 1 | F | R | A2 | 104 | 12 | 45 | 12 | 28.7 | 21.0 | 7.7 | 9 | 1.60 × 10−3 |
| 1 | F | R | A3 | 85 | 14 | 51 | 3 | 19.9 | 8.5 | 11.4 | 28 | 2.06 × 10−3 |
| 1 | F | R | B1 | 160 | 54 | 43 | 6 | 46.9 | 32.9 | 14.0 | 27 | 1.64 × 10−3 |
| 1 | F | R | B2 | 73 | 17 | 48 | 5 | 19.6 | 7.7 | 11.9 | 15 | 1.73 × 10−3 |
| 1 | F | R | C1 | 163 | 44 | 39 | 4 | 50.4 | 38.0 | 12.4 | 41 | 1.58 × 10−3 |
| 1 | F | R | C2 | 166 | 56 | 43 | 4 | 35.2 | 25.0 | 10.2 | 42 | 2.30 × 10−3 |
| 1 | F | R | C3 | 125 | 33 | 50 | 5 | 23.2 | 13.2 | 10.0 | 25 | 2.59 × 10−3 |
| 1 | F | R | C4 | 100 | 24 | 64 | 3 | 15.6 | 6.0 | 9.6 | 33 | 3.11 × 10−3 |
| 1 | F | R | C6 | 53 | 11 | 49 | 5 | 4.2 | 4.1 | 0.1 | 11 | 5.71 × 10−3 |
| 1 | F | R | D1 | 205 | 71 | 38 | 5 | 56.5 | 45.9 | 10.6 | 41 | 1.77 × 10−3 |
| 1 | F | R | D2 | 178 | 74 | 45 | 7 | 37.4 | 27.3 | 10.1 | 25 | 2.29 × 10−3 |
| 1 | F | R | D4 | 107 | 35 | 58 | 14 | 14.4 | 7.1 | 7.3 | 8 | 3.23 × 10−3 |
| 1 | F | R | E1 | 213 | 84 | 38 | 8 | 49.6 | 42.4 | 7.2 | 27 | 2.07 × 10−3 |
| 1 | F | R | E3 | 174 | 68 | 37 | 9 | 25.6 | 19.8 | 5.8 | 19 | 3.22 × 10−3 |
| 1 | F | R | E4 | 134 | 52 | 52 | 5 | 17.0 | 9.9 | 7.1 | 27 | 3.79 × 10−3 |
| 1 | F | R | α | 145 | 43 | 43 | 6 | 47.0 | 31.2 | 15.8 | 24 | 1.48 × 10−3 |
| 1 | F | R | β | 161 | 45 | 43 | 6 | 40.3 | 38.9 | 1.4 | 27 | 1.92 × 10−3 |
| 1 | F | R | γ | 158 | 54 | 43 | 4 | 51.0 | 39.1 | 11.9 | 40 | 1.51 × 10−3 |
| 2 | M | R | A1 | 143 | 44 | 29 | 4 | 43.9 | 34.9 | 9.0 | 36 | 1.58 × 10−3 |
| 2 | M | R | A3 | 95 | 26 | 44 | 3 | 21.9 | 12.0 | 9.9 | 32 | 2.10 × 10−3 |
| 2 | M | R | A4 | 75 | 11 | 55 | 19 | 12.0 | 4.8 | 7.2 | 4 | 2.33 × 10−3 |
| 2 | M | R | B1 | 163 | 60 | 40 | 5 | 52.0 | 42.3 | 9.7 | 33 | 1.52 × 10−3 |
| 2 | M | R | B2 | 148 | 51 | 37 | 7 | 36.6 | 28.4 | 8.2 | 21 | 1.93 × 10−3 |
| 2 | M | R | B3 | 89 | 24 | 47 | 3 | 19.2 | 10.6 | 8.6 | 30 | 2.24 × 10−3 |
| 2 | M | R | B4 | 81 | 10 | 62 | 3 | 13.1 | 4.3 | 8.8 | 27 | 2.98 × 10−3 |
| 2 | M | R | C2 | 159 | 52 | 40 | 4 | 36.5 | 28.0 | 8.5 | 40 | 2.12 × 10−3 |
| 2 | M | R | C3 | 115 | 29 | 38 | 3 | 19.9 | 13.7 | 6.2 | 38 | 2.81 × 10−3 |
| 2 | M | R | C4 | 101 | 16 | 53 | 4 | 15.0 | 7.6 | 7.4 | 25 | 3.23 × 10−3 |
| 2 | M | R | D1 | 203 | 68 | 34 | 4 | 52.1 | 45.6 | 6.5 | 51 | 1.91 × 10−3 |
| 2 | M | R | D5 | 105 | 22 | 60 | 4 | 12.9 | 5.9 | 7.0 | 26 | 3.91 × 10−3 |
| 2 | M | R | E3 | 151 | 58 | 39 | 4 | 26.6 | 21.0 | 5.6 | 38 | 2.76 × 10−3 |
| 2 | M | R | E4 | 132 | 47 | 45 | 4 | 18.5 | 12.5 | 6.0 | 33 | 3.46 × 10−3 |
| 2 | M | R | E5 | 93 | 31 | 55 | 3 | 10.9 | 5.2 | 5.7 | 31 | 4.13 × 10−3 |
| 2 | M | R | α | 154 | 47 | 39 | 4 | 50.3 | 40.8 | 9.5 | 39 | 1.49 × 10−3 |
| 2 | M | R | β | 134 | 40 | 38 | 7 | 45.1 | 36.3 | 8.8 | 19 | 1.41 × 10−3 |
| 2 | M | R | γ | 134 | 44 | 41 | 4 | 49.7 | 41.3 | 8.4 | 34 | 1.31 × 10−3 |
| 2 | M | R | δ | 101 | 25 | 41 | 6 | 35.8 | 28.2 | 7.6 | 17 | 1.33 × 10−3 |
| 3 | M | L | A1 | 154 | 60 | 39 | 6 | 41.7 | 30.3 | 11.4 | 26 | 1.77 × 10−3 |
| 3 | M | L | A4 | 76 | 16 | 48 | 5 | 13.9 | 6.4 | 7.5 | 15 | 2.55 × 10−3 |
| 3 | M | L | B1 | 171 | 68 | 40 | 3 | 48.2 | 37.7 | 10.5 | 57 | 1.74 × 10−3 |
| 3 | M | L | B2 | 153 | 50 | 38 | 5 | 35.3 | 26.1 | 9.2 | 31 | 2.10 × 10−3 |
| 3 | M | L | B3 | 99 | 27 | 41 | 5 | 20.6 | 12.8 | 7.8 | 20 | 2.28 × 10−3 |
| 3 | M | L | C2 | 167 | 56 | 40 | 3 | 36.6 | 27.7 | 8.9 | 56 | 2.24 × 10−3 |
| 3 | M | L | C4 | 103 | 26 | 51 | 3 | 16.5 | 8.9 | 7.6 | 34 | 3.03 × 10−3 |
| 3 | M | L | D3 | 134 | 57 | 41 | 6 | 24.9 | 18.3 | 6.6 | 22 | 2.57 × 10−3 |
| 3 | M | L | D4 | 136 | 45 | 46 | 5 | 20.6 | 14.5 | 6.1 | 27 | 3.18 × 10−3 |
| 3 | M | L | D6 | 81 | 18 | 65 | 4 | 8.6 | 2.9 | 5.7 | 20 | 4.48 × 10−3 |
| 3 | M | L | E3 | 158 | 62 | 44 | 5 | 26.4 | 20.2 | 6.2 | 32 | 2.90 × 10−3 |
| 3 | M | L | E6 | 92 | 15 | 59 | 3 | 6.4 | 3.0 | 3.4 | 31 | 6.95 × 10−3 |
| 3 | M | L | α | 160 | 48 | 48 | 3 | 44.9 | 37.1 | 7.8 | 53 | 1.75 × 10−3 |
| 3 | M | L | β | 171 | 53 | 38 | 5 | 54.9 | 49.6 | 5.3 | 34 | 1.51 × 10−3 |
F, female; M, male; R, right; L, left. All values of radius ratio are reported to the nearest integer. These values can be rounded to a single significant digit for consistency with the measurement precision of tip diameter.
Tables 3 and 4, together with data from Neimark et al. (2003), thus provide measurements of arc length, base diameter, and tip diameter from a total of 122 (24 + 5 + 18 + 23 + 52) whiskers across 5 studies, corresponding to Hartmann et al. (2003), Ibrahim and Wright (1975), Neimark et al, (2003), Voges et al. (2012), and the present work. These studies were used to perform a meta-analysis of radius ratio and radius slope. Results are plotted in Fig. 5 and summarized in Table 5. To best understand the data, it is useful to iterate between the figure and the table.
Figure 5B plots the radius ratio for the raw data presented in Tables 3 and 4, as well as for Neimark et al. (2003). RatioR is extremely variable, ranging between 2 and 148. This variability is expected because the tip of the whisker is highly susceptible to damage due to wear and barbering. There is a small but significant trend for the radius ratio to increase with arc length. RatioR for each of the five studies is summarized in the fourth column of Table 5. The average RatioR across all 5 studies (122 whiskers) is 37 ± 25 (mean ± SD) with a median of 32. The mean and median values are more than twice the previous estimate of 15 obtained by Williams and Kramer (2010); this discrepancy is addressed further in discussion.
Radius slope is much more consistent across all five studies, as shown in Fig. 5C and summarized in the fifth column of Table 5. Figure 5C plots radius slope as a function of total whisker arc length for the raw data presented in Tables 3 and 4 and from Neimark et al. (2003). A strong relationship between radius slope and arc length is observed: shorter whiskers get thinner along their length faster than do longer whiskers. Values of SlopeR range between 0.00104 and 0.00695 (mean ± SD = 0.00226 ± 0.000893; median = 0.00204).
The functional relationship shown in Fig. 5C is obviously dominated by the factor of inverse arc length (1/STotal) included in the definition of SlopeR. To differentiate between the effects of whisker arc length and whisker position within the array, we constructed plots of SlopeR as a function of row and column position, as shown in Fig. 5, D–F. Radius slope clearly increases with column position, from caudal to rostral (Fig. 5D). In addition, when plotted as a function of row position, Fig. 5E further shows that SlopeR increases very slightly from dorsal to ventral: the E-row whiskers get thinner along their length just slightly faster than the A-row whiskers. Figure 5F shows the effects of row and column position on SlopeR presented in Fig. 5, D and E, on a color-coded schematic of the rat vibrissal array. We fit univariate models for SlopeR as a function of row and column. Criteria for selecting the highest order model while avoiding overfitting was on the basis of AIC and predicted vs. actual value plots. We then combined these univariate relationships into a multivariate model and found radius slope to be a function of both row and column with a clear dependence on column squared:
| 7 |
In Eq. 7, as in all previous equations, Row varies between 1 and 5. However, because the dataset has been reduced (from 519 to 122 whiskers), Col varies between 0 and 6. The quality of the fit of Eq. 7 to the experimental data is shown in Fig. 5G, and the adjusted R2 is 0.81.
It is important to note that, because RTip is so much smaller than RBase, it will typically contribute very little to the calculation of slope in Eqs. 5b and 6b. Across the five datasets that included tip diameter measurements (122 whiskers), we found that excluding RTip (i.e., setting RTip equal to zero in Eq. 6b) increased slope by a median value of only 3.3% and by less than 15% for all but nine whiskers. This result means that, to first order, the ratio of DBase to STotal is generally an excellent approximation for SlopeD, and the ratio of RBase to STotal is an excellent approximation for SlopeR.
In principle, then (after dividing by a factor of 2 and STotal), Eq. 2 could be used to approximate the SlopeR of the whisker instead of Eq. 7. We compared the quality of fit for SlopeR computed using Eq. 2 after dividing by 2STotal with that computed using Eq. 7. We calculated the difference between the actual value for SlopeR and each value for SlopeR predicted by Eqs. 2 and 7. We then found the mean of these differences. We found that, on average, Eq. 2 was ∼13% in error of the actual data, with a tendency to overpredict SlopeR. On average, Eq. 7 was ∼12% in error of the actual data, with a tendency to underpredict SlopeR.
Variations in Radius Slope between Proximal and Distal Regions of the Whisker
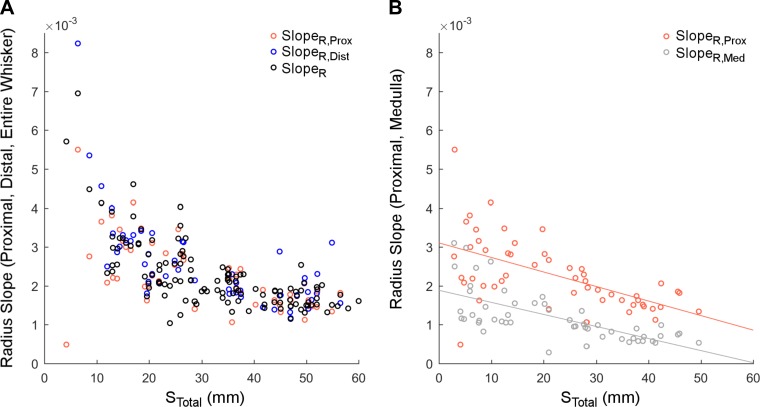
Given that the proximal region of the whisker contains the medulla, a natural thought was to look for differences in SlopeR between the proximal and distal regions of the whiskers. In analogy to the definition for SlopeR of Eq. 6b, we computed the proximal (SlopeR,Prox) and distal radius slope (SlopeR,Dist) as:
| 8a |
| 8b |
where RMedT is the radius of the whisker at the point of medulla termination, and SDist is the distal arc length of the whisker that does not include the medulla. Using the data from Table 4 that included measurements of the medulla (reduced dataset 2, 52 whiskers), we compared these estimates of SlopeR,Prox and SlopeR,Dist from Eqs. 8a and 8b with the radius slope calculated from Eq. 6b. As shown in Fig. 6A, and confirmed by a Bonferroni-corrected Wilcoxon signed-rank test between each paired set, no significant differences were observed between these three estimates.
However, when the ratio of proximal slope to distal slope was analyzed as a function of column, the majority of whiskers in columns 1 and 2 had proximal slopes greater than distal slopes (12 out of 18). In contrast, the majority of whiskers in columns 3–6 had proximal slopes smaller than distal slopes (19 out of 25). Surprisingly, the majority (8/9) of whiskers in the Greek column also had proximal slopes smaller than distal slopes. Across all whiskers, the ratio of proximal to distal slopes ranged between 0.002 and 1.5. Finding systematic differences between SlopeR,Prox and SlopeR,Dist is likely to require a higher resolution analysis in which radius is measured at many points along the whisker arc length (Hires et al. 2016; Ibrahim and Wright 1975; Williams and Kramer 2010).
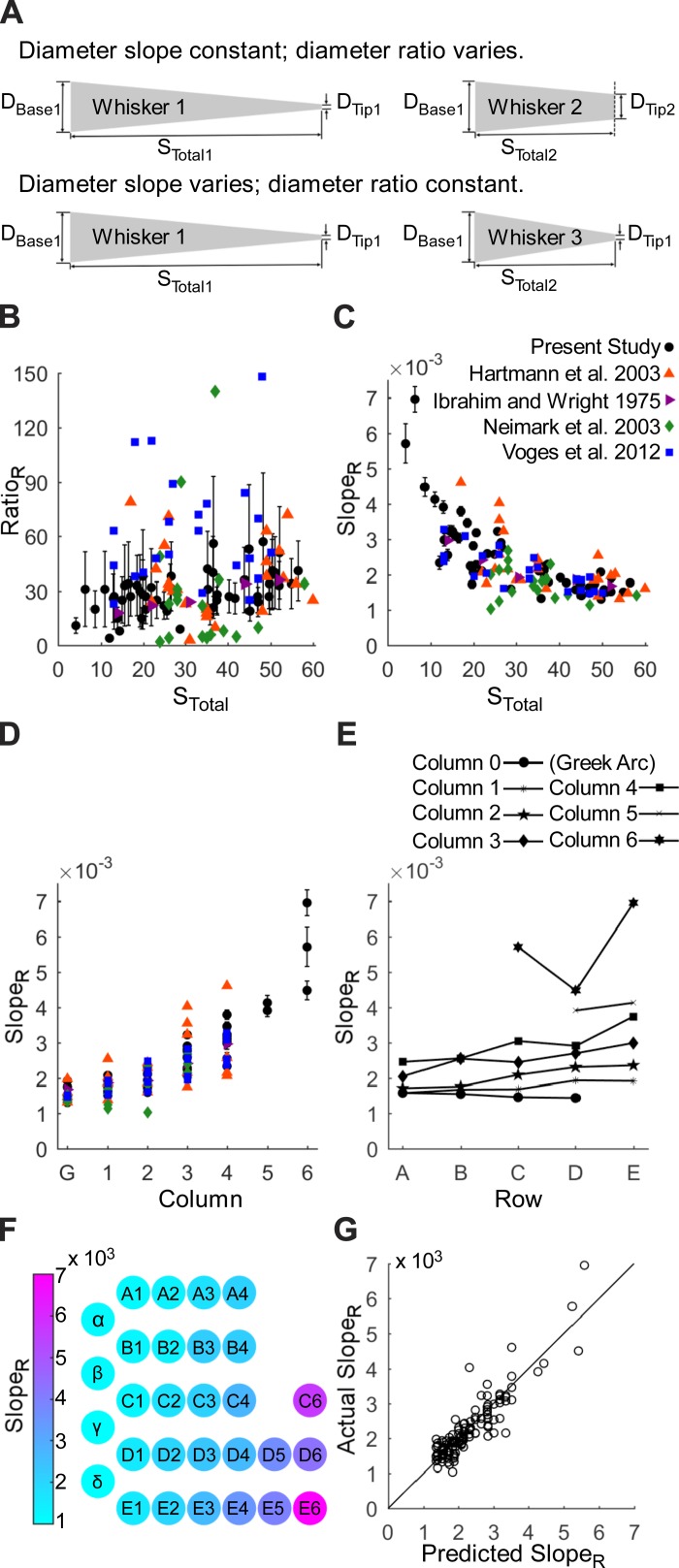
Finally, we compared the radius slope measured in the proximal portion of the whisker (Eq. 8a) with the radius slope of the medulla, defined as:
| 9 |
Figure 6B reveals a significant difference between the proximal radius slope of the whisker (SlopeR,Prox) and the radius slope of the medulla (SlopeR,Med) (two-sided Wilcoxon signed-rank text, P < 0.001). On average, the medulla radius slope is significantly less than that of the proximal radius slope. The best fit equations for the proximal radius slope and the medulla radius slope were, respectively, SlopeR,Prox = 0.0031 − 0.000037 SProx and SlopeR,Med = 0.0019 − 0.000031 SProx. We tested the hypothesis that the difference between these two slopes was equal to zero using a Z-score method (Paternoster et al. 1998). We found no significant difference between these two slopes (Z = 0.73, P < 0.47). This suggests that medulla radius slope is approximately a constant offset from proximal radius slope by the difference in intercepts of our two equations, i.e., 0.0031 − 0.0019 = 0.0012.
Summary: Equations for Whisker Geometry across the Vibrissal Array
The present work has developed equations that describe how the geometry of individual whiskers varies across the array. All equations assume that Row varies between 1 and 5. Eqs. 1 and 2 assume that Col varies between 0 and 8, while Eq. 7 assumes Col varies between 0 and 6, with 0 representing the Greek arc.
We assume that the three quantities easiest for experimentalists to measure are row, column, and arc length. In the case that only row and column position are known, total arc length can be estimated (in units of mm) based on Eq. 1:
| 1 |
Equations 2, 3, 4, and 7 developed in the present work can then be used in conjunction with STotal (either as measured experimentally or from Eq. 1) to calculate the whisker's base diameter, medulla length, medulla diameter, and radius slope.
To describe base diameter as a function of arc length (STotal), we recommend referencing the equations in Table 2 by individual row and column position. If a single equation is necessary, Fig. 3G shows that base diameter is well described as a function of arc length while adjusting for differences across row and column:
| 2 |
Figure 4A shows that medulla arc length is a function of total arc length for whiskers longer than 10 mm:
| 3 |
Figure 4C shows that the base diameter of the medulla is a function of the base diameter of the whisker:
| 4 |
Figure 5F shows that radius slope varies according to both row and column position:
| 7 |
Together, Eqs. 2, 3, 4, and 7 can then be used to estimate whisker geometry for use in simulations.
DISCUSSION
The present work has identified systematic trends in whisker geometry across the array, including trends in the geometry of the whisker medulla. A shorter whisker is not simply a scaled version of a larger whisker. These results mean that whiskers in different row and column positions will bend differently when they touch an object. In addition, whiskers in different row and column positions will have different density distributions along their lengths, which will alter their dynamics (Boubenec et al. 2012; Quist et al. 2014; Yan et al. 2013; Yang AE, Belli HM, and Hartmann MJ, unpublished observations).
Variations in Whisker Arc Length across the Array
As indicated in results, considerable overlap was observed in the prediction bounds for all eight datasets when total arc length was plotted as a function of row and column identity. Therefore, all data were grouped to obtain the best linear fit between total arc length and row and column position (Eq. 1). However, the bounds for the Kan et al. (2013) and Birdwell et al. (2007) datasets were wider than both the upper and lower limits of those from the present study. For completeness, we therefore also found the best linear equation for STotal as a function of row and column position after excluding these two datasets. The equation after excluding the two datasets was found to be STotal = 42 + 2.0 Row − 7.6 Col (Adj. R2 = 0.87). Whisker lengths computed using this equation differ from those computed using Eq. 1 by less than 0.8 mm, indicating that the datasets from Kan et al. (2013) and Birdwell et al. (2007) had little effect on the final relationship.
It is also informative to compare Eq. 1 with the equation for whisker arc length obtained by Towal et al. (2011). The equation for arc length as a function of row and column position given by Towal et al. (2011) is:
| 10 |
In Eq. 10, Row varies between 1 and 5 as in the present work, but all column variables are coded as {1, 2, 3, . . .} rather than the convention used here, in which Col varies between 0 and 7. The values for STotal obtained from Eqs. 1 and 10 differ by less than 3 mm for the largest whiskers, and by less than 1.5 mm for the smaller, more rostral whiskers.
The Relationship between the Diameter of the Whisker Base and Whisker Arc Length
When evaluated over whiskers of all lengths, the relationship between the diameter at the whisker base (DBase) and the total whisker arc length (STotal) may at first appear linear (Fig. 2). However, closer examination reveals that the relationship depends on both column and row position (Fig. 3). The dependence on column position is somewhat expected, because the arc length of the whisker is itself correlated with column position (Brecht et al. 1997; Ibrahim and Wright 1975; Towal et al. 2011). The equations in the top half of Table 2 indicate that, when separated by column, DBase and STotal are linearly related with an average correlation coefficient of ∼0.5.
Surprisingly, however, the relationship between DBase and STotal depends even more strongly on row position than it does on column position. Table 2 indicates that, when separated by row, DBase and STotal are strongly linearly related, with an average correlation coefficient close to 0.8. Thus the relationship between DBase and STotal is much more linear within a row than within a column. For a given length, whiskers in more ventral rows have larger DBase than whiskers in more dorsal rows. We suggest that whiskers in the ventral rows are thicker because they tend to be in more continuous contact with the ground (Arkley et al. 2014; Hobbs et al. 2016a, 2016b; Thé et al. 2013).
Parameters that Define the “Taper” of a Whisker
The word “taper” has been defined differently across studies. Some have used the radius ratio (or diameter ratio) to define taper (Huet and Hartmann 2016; Huet et al. 2015; Quist et al. 2014; Williams and Kramer 2010). Other studies have used the radius slope (or diameter slope) to define taper (Hires et al. 2013, 2016; Neimark et al. 2003).
The schematic of Fig. 5A illustrates why neither of these definitions alone is sufficient to characterize the geometry of the whisker: both are needed. The aspect ratio of the whisker is defined by three parameters (RBase, RTip, STotal). If any one of those three parameters is fixed, two equations are then required to define the whisker's geometry. These are Eqs. 5b and 6b in the present work, defining the radius ratio (RatioR) and radius slope (SlopeR).
RatioR is extremely sensitive to tiny variations in RTip: even a 2- to 3-μm change in RTip can change RatioR by a factor of 2. Accordingly, a comparative analysis across five studies from separate laboratories (Fig. 5B, Table 5) shows that the radius ratio varies greatly even for whiskers in the same row and column position. Across all five studies, the median RatioR was 32, but the range was extremely large. For example, the data of Neimark et al. (2003) include RatioR that range from 2 to 140, with an average of 29. If two outliers are removed, however, the average decreases to ∼15, consistent with the analysis of Williams and Kramer (2010). The whisker tip is often damaged due to wear, breakage, and barbering, and its exact size is unlikely to be of behavioral importance to the rat.
In contrast, SlopeR exhibits clear and systematic variations across the array. The slope of a whisker will have a strong influence on its quasi-static bending, as well as on its dynamic behavior (Hartmann 2015; Hartmann et al. 2003; Hires et al. 2013; Neimark et al. 2003; Ritt et al. 2008; Solomon and Hartmann 2008, 2010, 2011; Wolfe et al. 2008; Yu et al. 2016). SlopeR is not constant across the array: it is larger for shorter, more rostral whiskers than for longer, more caudal whiskers (Fig. 5D). There is also a slight increase in SlopeR from dorsal to ventral, except for the Greek column of whiskers (Fig. 5E). Shorter whiskers exhibit a steeper variation in cross-sectional diameter per unit length than longer whiskers. Thus, when the same point load is applied to a rostral and caudal whisker at the same radial distance of contact, the rostral whisker will exhibit larger variations in local curvature change along its length than will the caudal whisker (Solomon and Hartmann 2011; Yang and Hartmann 2016).
Medulla Geometry Varies between Rostral and Caudal Whiskers
To date, all studies of whisker dynamics have assumed that the whisker is a solid conical frustum (Boubenec et al. 2012; Hartmann et al. 2003; Lucianna et al. 2016; Neimark et al. 2003; Quist et al. 2014; Yan et al. 2013). The presence of the medulla, however, will change the mass distribution along the whisker length, which will have a significant effect on whisker dynamics.
The present work reveals close linear relationships between medulla geometry and whisker geometry. As shown in Fig. 4A, there is an exceptionally tight linear relationship between medulla arc length (SProx) and total whisker length (STotal), R2 = 0.97. A somewhat weaker linear relationship is found between medulla base diameter (DMed) and whisker base diameter, R2 = 0.80 (Fig. 4C). Because both of these equations have nonzero intercepts, the fraction of the whisker occupied by the medulla increases for longer whiskers (Fig. 4, B, D, and E). These density changes may influence the dynamics of the whisker (Yang AE, Belli HM, and Hartmann MJ, unpublished observations).
Conclusions and Future Directions
To develop models of whisker mechanics during natural exploratory behavior requires accurate quantification of geometry, both at the level of the entire whisker array (Knutsen et al. 2008; Towal et al. 2011), as well as at the level of individual vibrissae. The geometry of the individual whisker will have a large influence on the mechanical signals generated at the whisker base during both noncontact and contact whisking. The equations developed in the present work can be incorporated into mechanical models to quantify the signals at the base of each whisker during exploratory whisking behavior.
GRANTS
This work was supported by National Science Foundation (NSF) awards CAREER IOS-0846088 and EFRI-0938007, as well as National Institutes of Health (NIH) R01-NS-093585 to M. J. Z. Hartmann. H. M. Belli was supported in part by NIH F31-NS-090872-01A1. C. S. Bresee was supported in part by NSF IGERT: Integrative Research in Motor Control and Movement Grant DGE-0903637, and by NIH Grant T32 HD-057845.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
H.M.B. performed experiments; H.M.B., A.E.T.Y., and M.J.Z.H. analyzed data; H.M.B., A.E.T.Y., C.S.B., and M.J.Z.H. interpreted results of experiments; H.M.B., A.E.T.Y., and M.J.Z.H. prepared figures; H.M.B., A.E.T.Y., and M.J.Z.H. drafted manuscript; H.M.B., A.E.T.Y., C.S.B., and M.J.Z.H. edited and revised manuscript; H.M.B., A.E.T.Y., C.S.B., and M.J.Z.H. approved final version of manuscript; M.J.Z.H. conceived and designed research.
Supplementary Material
ACKNOWLEDGMENTS
We thank Dr. Brian Quist and Rafay Faruqi for beginning to carefully characterize whisker length and base diameter. We thank the laboratory of Prof. Catherine Woolley for use of the MBF Bioscience Olympus BX60 microscope and DV-47 color camera. We thank the authors of Voges et al. (2012) and Neimark et al. (2003) for generously sharing their original data.
REFERENCES
- Adineh VR, Liu B, Rajan R, Yan W, Fu J. Multidimensional characterisation of biomechanical structures by combining atomic force microscopy and focused ion beam: a study of the rat whisker. Acta Biomater 21: 132–141, 2015. [DOI] [PubMed] [Google Scholar]
- Arkley K, Grant RA, Mitchinson B, Prescott TJ. Strategy change in vibrissal active sensing during rat locomotion. Curr Biol 24: 1507–1512, 2014. [DOI] [PubMed] [Google Scholar]
- Birdwell JA, Solomon JH, Thajchayapong M, Taylor MA, Cheely M, Towal RB, Conradt J, Hartmann MJZ. Biomechanical models for radial distance determination by the rat vibrissal system. J Neurophysiol 98: 2439–2455, 2007. [DOI] [PubMed] [Google Scholar]
- Bosman L, Houweling A, Owens C, Tanke N, Shevchouk O, Rahmati N, Teunissen WHT, Ju C, Wei Gong W, Koekkoek SKE, De Zeeuw CI. Anatomical pathways involved in generating and sensing rhythmic whisker movements. Front Integr Neurosci 5: 53, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boubenec Y, Shulz DE, Debregeas G. Whisker encoding of mechanical events during active tactile exploration. Front Behav Neurosci 6: 74, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brecht M, Preilowski B, Merzenich MM. Functional architecture of the mystacial vibrissae. Behav Brain Res 84: 81–97, 1997. [DOI] [PubMed] [Google Scholar]
- Bush N, Schroeder C, Hobbs JA, Yang A, Huet L, Solla S, Hartmann M. Decoupling kinematics and mechanics reveals coding properties of trigeminal ganglion neurons in the rat vibrissal system. eLife 5: e13969, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campagner D, Evans MH, Bale MR, Erskine A, Petersen RS. Prediction of primary somatosensory neuron activity during active tactile exploration. eLife 5: e10696, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carl K, Hild W, Mampel J, Schilling C, Uhlig R, Witte H. Characterization of statical properties of rat's whisker system. IEEE Sens J 12: 340–349, 2012. [Google Scholar]
- Chernova OF. Architectonic and diagnostic significance of hair cortex and medulla. Biol Bull 30: 53–62, 2003. [PubMed] [Google Scholar]
- Chernova OF, Kulikov VF. Structural differences between the shafts of mammalian vibrissae and hairs and their causes. Dokl Biol Sci 438: 182–185, 2011. [DOI] [PubMed] [Google Scholar]
- Clauset A, Shalizi CR, Newman MEJ. Power-law distributions in empirical data. SIAM Rev Soc Ind Appl Math 51: 661–703, 2009. [Google Scholar]
- Ebara S, Kumamoto K, Matsuura T, Mazurkiewicz JE, Rice FL. Similarities and differences in the innervation of mystacial vibrissal follicle-sinus complexes in the rat and cat: A confocal microscopic study. J Comp Neurol 449: 103–119, 2002. [DOI] [PubMed] [Google Scholar]
- Gibson JM, Welker WI. Quantitative studies of stimulus coding in first-order vibrissa afferents of rats. 1. Receptive field properties and threshold distributions. Somatosens Res 1: 51–67, 1983. [DOI] [PubMed] [Google Scholar]
- Hartmann MJ, Johnson NJ, Towal RB, Assad C. Mechanical characteristics of rat vibrissae: resonant frequencies and damping in isolated whiskers and in the awake behaving animal. J Neurosci 23: 6510–6519, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann MJZ. Vibrissal mechanical properties. Scholarpedia J 10: 6636, 2015. [Google Scholar]
- Hausman LA. Recent studies of hair structure relationships. Sci Mon 30: 258–278, 1930. [Google Scholar]
- Hires SA, Pammer L, Svoboda K, Golomb D. Tapered whiskers are required for active tactile sensation. eLife 2: e01350, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hires SA, Schuyler A, Sy J, Huang V, Wyche I, Wang X, Golomb D. Beyond Cones: an improved model of whisker bending based on measured mechanics and tapering. J Neurophysiol 116: 812–824, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobbs JA, Towal RB, Hartmann MJZ. Evidence for functional groupings of vibrissae across the rodent mystacial pad. PLoS Comput Biol 12: e1004109, 2016a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobbs JA, Towal RB, Hartmann MJZ. Spatiotemporal patterns of contact across the rat vibrissal array during exploratory behavior. Front Behav Neurosci 9: 356, 2016b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huet L, Hartmann M. Simulations of a vibrissa slipping along a straight edge and an analysis of frictional effects during whisking. IEEE Trans Haptics 9: 158–169, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huet LA, Schroeder CL, Hartmann MJZ. Tactile signals transmitted by the vibrissa during active whisking behavior. J Neurophysiol 113: 3511–3518, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim L, Wright EA. Growth of rats and mice vibrissae under normal and some abnormal conditions. J Embryol Exp Morphol 33: 831–844, 1975. [PubMed] [Google Scholar]
- Jones LM, Depireux DA, Simons DJ, Keller A. Robust temporal coding in the trigeminal system. Science 304: 1986–1989, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kan QH, Rajan R, Fu J, Kang GZ, Yan WY. Elastic modulus of rat whiskers–a key biomaterial in the rat whisker sensory system. Mater Res Bull 48: 5026–5032, 2013. [Google Scholar]
- Knutsen PM, Biess A, Ahissar E. Vibrissal kinematics in 3D: tight coupling of azimuth, elevation, and torsion across different whisking modes. Neuron 59: 35–42, 2008. [DOI] [PubMed] [Google Scholar]
- Leiser SC, Moxon KA. Responses of trigeminal ganglion neurons during natural whisking behaviors in the awake rat. Neuron 53: 117–133, 2007. [DOI] [PubMed] [Google Scholar]
- Lichtenstein SH, Carvell GE, Simons DJ. Responses of rat trigeminal ganglion neurons to movements of vibrissae in different directions. Somatosens Mot Res 7: 47–65, 1990. [DOI] [PubMed] [Google Scholar]
- Lottem E, Azouz R. A unifying framework underlying mechanotransduction in the somatosensory system. J Neurosci 31: 8520–8532, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucianna FA, Albarracin AL, Vrech SM, Farfan FD, Felice CJ. The mathematical whisker: a review of numerical models of the rat's vibrissa biomechanics. J Biomech 49: 2007–2014, 2016. [DOI] [PubMed] [Google Scholar]
- Neimark MA, Andermann ML, Hopfield JJ, Moore CI. Vibrissa resonance as a transduction mechanism for tactile encoding. J Neurosci 23: 6499–6509, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Institutes of Standards and Techology/SEMATECH. E-Handbook of Statistical Methods (Online). Gaithersburg, MD: NIST, 2012. http://www.itl.nist.gov/div898/handbook/ [12 July 2016]. [Google Scholar]
- Pammer L, O'Connor DH, Hires SA, Clack NG, Huber D, Myers EW, Svoboda K. The mechanical variables underlying object localization along the axis of the whisker. J Neurosci 33: 6726–6741, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paternoster R, Brame R, Mazerolle P, Piquero A. Using the correct statistical test for the equality of regression coefficients. Criminology 36: 859–866, 1998. [Google Scholar]
- Quist BW, Hartmann MJZ. Mechanical signals at the base of a rat vibrissa: the effect of intrinsic vibrissa curvature and implications for tactile exploration. J Neurophysiol 107: 2298–2312, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quist BW, Seghete V, Huet LA, Murphey TD, Hartmann MJZ. Modeling forces and moments at the base of a rat vibrissa during noncontact whisking and whisking against an object. J Neurosci 34: 9828–9844, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson F, Peterson HA, Bingham WV, Shepherd WT. A study of sensory control in the rat. Psychol Monogr 12: 1–124, 1909. [Google Scholar]
- Ritt JT, Andermann ML, Moore CI. Embodied information processing: vibrissa mechanics and texture features shape micromotions in actively sensing rats. Neuron 57: 599–613, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomon JH, Hartmann MJZ. Artificial whiskers suitable for array implementation: accounting for lateral slip and surface friction. IEEE Trans Rob Autom 24: 1157–1167, 2008. [Google Scholar]
- Solomon JH, Hartmann MJZ. Extracting object contours with the sweep of a robotic whisker using torque information. Int J Rob Res 29: 1233–1245, 2010. [Google Scholar]
- Solomon JH, Hartmann MJZ. Radial distance determination in the rat vibrissal system and the effects of Weber's law. Philos Trans R Soc Lond B Biol Sci 366: 3049–3057, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sterbing-D'Angelo S, Liu H, Yu M, Moss CF. Morphology and deflection properties of bat wing sensory hairs: scanning electron microscopy, laser scanning vibrometry, and mechanics model. Bioinspir Biomim 11: 056008, 2016. [DOI] [PubMed] [Google Scholar]
- Szwed M, Bagdasarian K, Ahissar E. Encoding of vibrissal active touch. Neuron 40: 621–630, 2003. [DOI] [PubMed] [Google Scholar]
- Thé L, Wallace ML, Chen CH, Chorev E, Brecht M. Structure, function, and cortical representation of the rat submandibular whisker trident. J Neurosci 33: 4815–4824, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towal RB, Quist BW, Gopal V, Solomon JH, Hartmann MJZ. The morphology of the rat vibrissal array: a model for quantifying spatiotemporal patterns of whisker-object contact. PLoS Comput Biol 7: e1001120, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent SB. The function of the vibrissae in the behavior of the white rat (PhD dissertation). In: Animal Behavior Monographs. Chicago, IL: Univ. of Chicago, 1912, vol. 1, no. 5. [Google Scholar]
- Voges D, Carl K, Klauer GJ, Uhlig R, Schilling C, Behn C, Witte H. Structural characterization of the whisker system of the rat. IEEE Sens J 12: 332–339, 2012. [Google Scholar]
- Welker WI. Analysis of sniffing of the albino rat. Behaviour 22: 223–244, 1964. [Google Scholar]
- Williams CM, Kramer EM. The advantages of a tapered whisker. PLoS One 5: e8806, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe J, Hill DN, Pahlavan S, Drew PJ, Kleinfeld D, Feldman DE. Texture coding in the rat whisker system: slip-stick versus differential resonance. PLoS Biol 6: 1661–1677, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan W, Kan Q, Kergrene K, Kang G, Feng XQ, Rajan R. A truncated conical beam model for analysis of the vibration of rat whiskers. J Biomech 46: 1987–1995, 2013. [DOI] [PubMed] [Google Scholar]
- Yang AET, Hartmann MJZ. Whisking kinematics enables object localization in head-centered coordinates based on tactile information from a single vibrissa. Front Behav Neurosci 10: 145, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu YSW, Graff MM, Hartmann MJZ. Mechanical responses of rat vibrissae to airflow. J Exp Biol 219: 937–948, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker E, Welker WI. Coding of somatic sensory input by vibrissae neurons in rats trigmeinal ganglion. Brain Res 12: 138–156, 1969. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.