Layer-Specific Organization of Local Excitatory and Inhibitory Synaptic Connectivity in the Rat Presubiculum

Abstract

The presubiculum is part of the parahippocampal spatial navigation system and contains head direction and grid cells upstream of the medial entorhinal cortex. This position within the parahippocampal cortex renders the presubiculum uniquely suited for analyzing the circuit requirements underlying the emergence of spatially tuned neuronal activity. To identify the local circuit properties, we analyzed the topology of synaptic connections between pyramidal cells and interneurons in all layers of the presubiculum by testing 4250 potential synaptic connections using multiple whole-cell recordings of up to 8 cells simultaneously. Network topology showed layer-specific organization of microcircuits consistent with the prevailing distinction of superficial and deep layers. While connections among pyramidal cells were almost absent in superficial layers, deep layers exhibited an excitatory connectivity of 3.9%. In contrast, synaptic connectivity for inhibition was higher in superficial layers though markedly lower than in other cortical areas. Finally, synaptic amplitudes of both excitatory and inhibitory connections showed log-normal distributions suggesting a nonrandom functional connectivity. In summary, our study provides new insights into the microcircuit organization of the presubiculum by revealing area- and layer-specific connectivity rules and sets new constraints for future models of the parahippocampal navigation system.

Introduction

The Spatial Navigation System

The parahippocampal cortex is an essential part of the mammalian spatial navigation system and contains several specialized subregions. Among these is the presubiculum, a 6-layered cortex that receives input from different brain areas such as the retrosplenial cortex, the subiculum and the anterodorsal and laterodorsal thalamus (Van Groen and Wyss 1990; Wyss and Van Groen 1992). By transmitting vestibular and head directional information, these projections enable neurons in the presubiculum to tune their activity to the animal's head direction (Taube et al. 1990; Taube 2007; Peyrache et al. 2015; Tukker et al. 2015; Preston-Ferrer et al. 2016). In turn, the presubiculum itself provides strong projections to the medial entorhinal cortex (MEC) (Caballero-Bleda and Witter 1993; Honda and Ishizuka 2004; Canto et al. 2008, 2012; Kononenko and Witter 2012), which also contains head direction cells downstream of the presubiculum (Taube 1995; Sargolini et al. 2006). Grid cells, representing another type of spatial information, were first described in the MEC (Hafting et al. 2005), but have also been found in the pre- and parasubiculum (Boccara et al. 2010). In contrast to head direction representation, grid cell activity has so far only been described in the parahippocampal cortex. Lesion studies indicate that interconnectivity and interdependence of the spatially tuned regions, including the presubiculum, is complex and not fully understood (Liu et al. 2004; Cauter et al. 2008; Bonnevie et al. 2013; Winter et al. 2015). However, it can be concluded that navigational tuning of neuronal activity requires both external drive and an appropriate intrinsic network topology (Bonnevie et al. 2013; Rowland et al. 2016).

To elucidate the network properties underlying the emergence of grid cell activity, most studies have focused on the MEC (Burgalossi et al. 2011; Schmidt-Hieber and Häusser 2013; Rowland et al. 2016). Proposed models for grid cell generation include various continuous attractor network models and oscillatory interference models (Zhang 1996; Fuhs and Touretzky 2006; McNaughton et al. 2006; Burak and Fiete 2009; Bush and Burgess 2014; Solanka et al. 2015). While the relevant network principles are still under debate, either recurrent excitatory or recurrent inhibitory connections are generally assumed as the major mechanism (Couey et al. 2013; Pastoll et al. 2013; Buetfering et al. 2014; Fuchs et al. 2016). The plausibility of these models depends on the constraints imposed by the respective biological network topologies. As the most upstream subregion in the parahippocampal cortex, the presubiculum forms a suitable touchstone for models of these spatially modulated activities.

Intrinsic Anatomy of the Presubiculum

There is increasing knowledge about the diversity of cell types in the presubiculum (Abbasi and Kumar 2013; Simonnet et al. 2013; Nassar et al. 2015; Preston-Ferrer et al. 2016), but little is known about its network topology. In the presubiculum, layers I to III are usually referred to as superficial layers and layers V and VI as deep layers. Superficial and deep layers are separated by the plexiform layer IV or “lamina dissecans” (Van Groen and Wyss 1990; Canto et al. 2008; Simonnet et al. 2013). With respect to interlaminar synaptic communication, superficial layers in the presubiculum have been suggested to be mostly unidirectionally connected to deep layers (Honda et al. 2008). Furthermore, distinct response properties upon afferent stimulation suggested that connectivity within the presubicular deep layers is higher than within superficial layers although direct and more detailed evidence is lacking so far (Funahashi and Stewart 1997).

The intrinsic properties of excitatory and inhibitory cells in the presubiculum have been studied in rats and mice (Abbasi and Kumar 2013; Simonnet et al. 2013; Nassar et al. 2015; Preston-Ferrer et al. 2016). Classification of pyramidal cells based on intrinsic electrophysiological properties revealed a majority of regular spiking cells in both superficial and deep layers (Abbasi and Kumar 2013; Simonnet et al. 2013) and a smaller population of intrinsic bursting cells either restricted to layer IV (Simonnet et al. 2013) or distributed in the superficial layers (Abbasi and Kumar 2013). Recent in vivo studies have discovered further diversity of pyramidal cell in layers II and III with respect to their calbindin-expression, target-specific projections, theta rhythmicity and modulation by head direction (Preston-Ferrer et al. 2016). Furthermore, several types of presubicular interneurons have been reported in transgenic mice (Nassar et al. 2015). These comprise a variety of interneuron subtypes similar to other cortical areas (Markram et al. 2004), including fast-spiking (FS) parvalbumin (PV)-positive cells.

In the present study, we chose a systematic approach to analyze the synaptic network topology of the presubiculum by performing simultaneous multiple whole-cell recordings from pyramidal cells and interneurons in acute brain slices of a transgenic rat line selectively expressing Venus-yellow-fluorescent protein (Venus-YFP) under the promoter of the vesicular GABA transporter (VGAT) (Uematsu et al. 2008). To obtain a general overview of the connectivity across all layers, we initially classified recorded cells as being pyramidal cells or interneurons, thus keeping the number of synaptic types feasible for the analysis. This broad approach allowed us to identify distinct network topologies in the superficial and deep layers: superficial layers exhibited a feedback inhibitory network largely lacking recurrent excitation while deep layers contained excitatory connections among pyramidal cells, but showed a lower connectivity between pyramidal cells and interneurons. In a second step, we extended our analysis by differentiating between FS and nonfast spiking (NFS) interneurons.

Analysis of postsynaptic potential amplitudes of unitary synaptic connections revealed log-normal distributions in almost all synaptic subgroups, suggesting a general principle of nonrandom features in the organization of the presubicular microcircuits (Song et al. 2005; Buzsáki and Mizuseki 2014). In summary, our results reveal the specific network topology of the presubiculum and provide constrains for future models of grid cell generation and head direction tuning.

Materials and Methods

Slice Preparation

For whole-cell patch-clamp recordings, acute brain slices were prepared from postnatal 19- to 35-day-old (P19–P35) transgenic Wistar rats expressing Venus-YFP under the VGAT promoter (Uematsu et al. 2008). A total of 762 cells were recorded in 122 slices from 32 animals and thereby 4250 potential synaptic connections were tested. Animal handling and all procedures were carried out in accordance with guidelines of local authorities (Berlin, [T0215/11], [T0109/10]), the German Animal Welfare Act and the European Council Directive 86/609/EEC. Animals were decapitated after receiving isoflurane anesthesia and the head was immediately submerged in an ice-cold sucrose artificial cerebrospinal fluid (ACSF) slicing solution containing in mM: 80 NaCl, 2.5 KCl, 3 MgCl₂, 0.5 CaCl₂, 25 glucose, 85 sucrose, 1.25 NaH₂PO₄ and 25 NaHCO₃ (320–330 mOsm), enriched with carbogen (95% O₂, 5% CO₂).

Horizontal 300 µm thick slices 3 to 5.5 mm above the interaural plane were cut on a Leica VT1200 vibratome (Leica Biosystems) and subsequently stored in the sucrose ACSF solution heated to 30 °C for 30 min of recovery. Slices cut at between 3 and 4 mm were attributed to the ventral part, slices at between 4 and 5.5 mm were attributed to the dorsal part of the presubiculum. An interface storage chamber was constructed in a way that slices were kept just beneath the liquid surface to optimize their oxygen supply. After the recovery period, slices were either transferred to the recording chamber or stored in the oxygenated sucrose ACSF for up to 5 h at room temperature.

Whole-Cell Patch-Clamp Recordings

Recordings were performed in a submerged recording chamber perfused with ACSF solution (34 °C) containing in mM: 125 NaCl, 2.5 KCl, 1 MgCl₂, 2 CaCl₂, 25 glucose, 1.25 NaH₂PO₄, and 25 NaHCO₃ (310–320 mOsm), enriched with carbogen (95% O₂, 5% CO₂). Somatic whole-cell patch-clamp recordings were performed using pipettes pulled from borosilicate glass capillaries (2 mm outer/1 mm inner diameter; Hilgenberg) on a horizontal puller (P-97, Sutter Instrument Company). The pipettes were filled with intracellular solution containing in mM: 130 K-gluconate, 6 KCl, 2 MgCl₂, 0.2 EGTA, 5 Na₂-phosphocreatine, 2 Na₂ATP, 0.5 Na₂GTP, 10 HEPES buffer and 0.1% biocytin for morphological analysis (290–300 mOsm, pH adjusted to 7.2 with KOH). Filled pipettes had a resistance of 3–7 MΩ. We did not correct membrane potentials for liquid junction potential.

Cells were visualized using infrared differential interference contrast microscopy (Olympus BX-51WI) equipped with a digital camera (Olympus XM10). The border to the subiculum was characterized by the broadening of the pyramidal cell band and the border to the parasubiculum was located after the curve at the transition to the straight part of the pia (Fig. 1A). Interneurons were selected prior to patching by their VGAT-YFP fluorescence observed in epifluorescence illumination using a 490 nm LED light source (Thorlabs). We recorded from up to 8 cells simultaneously, selecting cells up to a depth of 80 µm beneath slice surface (mean ± standard deviation: 42 ± 12 µm) with intersomatic distances ranging between 25 and 150 µm (mean ± standard deviation: 78 ± 31 µm). The mean series resistance of the recordings was 40 MΩ and compensated using the automatic bridge balance of the amplifier. Recordings were performed using 4 two-channel Multiclamp 700B amplifiers (Molecular Devices) in current-clamp mode. Data were low-pass filtered at 6 kHz using the amplifiers built in Bessel filter and digitized with a Digidata 1550 (Molecular Devices) at a sampling rate of 20 kHz. The pClamp 10.4 software package (Molecular Devices) was used for data acquisition and analysis.

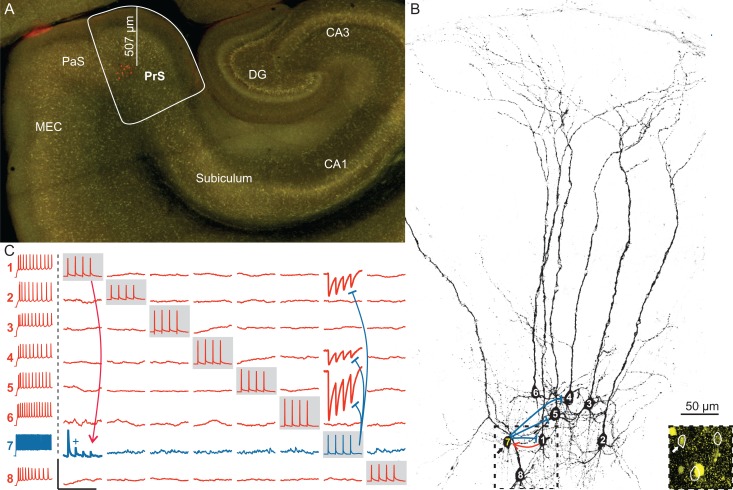
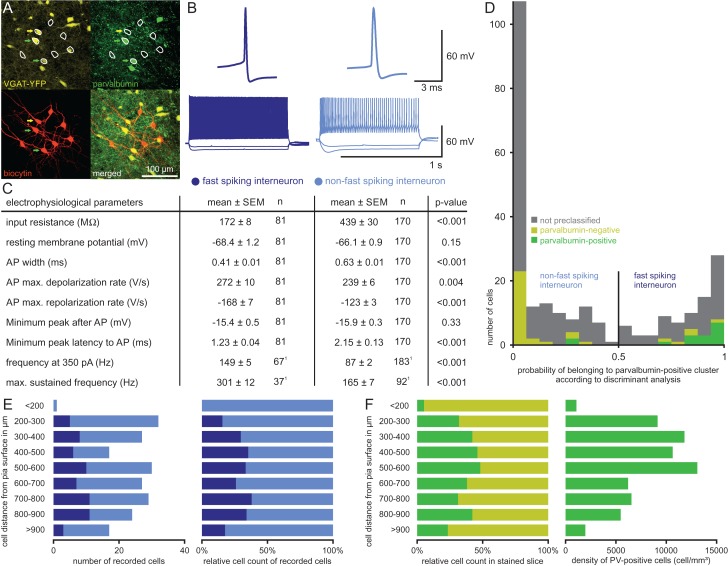
Figure 1.

Multiple simultaneous whole-cell recordings in the presubiculum. (A) Low-power VGAT-YFP-fluorescent image showing an overview of a horizontal hippocampal slice with the dentate gyrus (DG), the CA3, CA1 areas and the subiculum, as well as the parahippocampal region including the presubiculum (PrS), the parasubiculum (PaS), and the MEC. Eight cells in the PrS were recorded simultaneously and filled with biocytin (red). Their depth measured from the pial surface along the dendritic axis is shown by the distance bar (570 µm). (B) High-power projected image of a confocal stack of the biocytin-filled cells in panel (A). PCs are numbered in white, one IN in yellow (7). Inset: confocal image corresponding to the dashed box illustrating the YFP-positive cell body of the IN (arrow). (C) Averaged current-clamp traces of the 8 neurons shown in panels (A) and (B) revealed 4 synaptic connections out of the total 56 tested possible connections. The firing pattern of each cell is shown in the left column, PCs in red and the IN in blue. Traces recorded from one neuron are represented in one row, simultaneously recorded traces from all neurons are shown in a single column. While a single neuron was activated by eliciting a train of 4 APs (gray boxes), the postsynaptic responses were monitored in the other neurons. The excitatory connection onto the IN is indicated by a red line, inhibition of PCs by blue lines. Scale bars: horizontal 250 ms, vertical 100 mV for APs, 1 mV for postsynaptic traces (vertical scale bar for EPSP with + is 5 mV).

Intrinsic Electrophysiological Properties

Series and input resistance were measured in voltage-clamp mode using a 200 ms long 10 mV pulse and calculated from the peak amplitude at the start of the pulse and the steady state value at the end, respectively. The resting membrane potential (RMP) was determined as the mean of a 10 ms long baseline before the first step current injection after switching to current-clamp mode. Action potential (AP) threshold was taken as the inflection point on the initial rise of the AP. We searched for the first negative peak following the AP to detect fast afterhyperpolarization (AHP). The detection time window was set to 20 ms, meaning for cells without a fast AHP, such as most pyramidal cells, the time point of the negative peak was determined by the end of the detection time window. The amplitude of the AHP was measured relative to the AP threshold and the latency was taken from the AP peak. Firing pattern of the cells was characterized by a set of 1 s long current pulses starting at an amplitude of −100 pA increasing to 800 pA (in a subset up to 1500 pA) in increments of 50–300 pA. Firing frequencies were analyzed at 350 pA within a time window of 200–400 ms after pulse onset. In a subset of cells, the maximum sustained frequency was determined at the largest current pulse that showed a continuous AP train response without substantial broadening or attenuation of the APs.

Visualization of Recorded Neurons

After recording and filling the cells, slices were immersion-fixed in a solution containing 4% paraformaldehyde and 4% sucrose in 0.1 M phosphate buffer (PB) for a minimum of 12 h (overnight) at 4 °C. Slices were then rinsed extensively in 0.1 M PB and subsequently permeabilized in a solution containing 0.3–0.5% Triton X-100 in 0.1 M PB. Biocytin-filled cells were visualized using avidin-conjugated Alexa Fluor-647 (Invitrogen; dilution 1:1000) before being cover-slipped using an aqueous mounting medium. Imaging of the slices was performed on a confocal laser-scanning microscope (Olympus FluoView FV1000) using a 4× objective for overview, 20× objective (NA 0.8) for morphological assessment, and a 60× silicon oil immersion objective (NA 1.3) to determine colocalization of YFP and the biocytin signal in the individual cells. Excitation was elicited by the 514 nm line of an Argon laser for YFP and a 643 nm diode laser for the Alexa Fluor 647 in biocytin-labeled neurons. Selected cells were morphologically reconstructed using the Simple Neurite Tracer plug-in (Longair et al. 2011) in the Fiji distribution of ImageJ software (http://fiji.sc/) from confocal image stacks obtained with a 30× silicone-immersion objective (NA 1.05).

Immunocytochemistry

Immunocytochemical labeling for PV was performed as described previously (Booker et al. 2013, 2014). Briefly, following a 1 h incubation in 0.25 M PB saline (PBS) with 0.9% NaCl, 10% normal goat serum (NGS, Vector Laboratories) and 0.3% Triton X-100 at room temperature, the slices were transferred into a solution containing a mouse monoclonal primary antibody against PV (Swant, dilution at 1:10 000) in PBS, 5% NGS, 0.3% Triton X-100, and 0.05% NaN₃ for 48–72 h at 4 °C. Subsequently, the slices were repeatedly rinsed in PBS for 1 h and incubated overnight with the secondary antibodies (goat Alexa Fluor-405-conjugated antimouse; Invitrogen, dilution at 1:500) in PBS, 3% NGS at 4 °C. For slices containing biocytin-filled neurons, the secondary antibody solution also contained avidin-conjugated Alexa Fluor-647 (see above). After incubation the slices were rinsed extensively in 25 mM PBS, then in 0.1 M PB and embedded in anaqeuos fluorescent mounting medium under cover slips. Immunolabeling was assessed on the confocal laser-scanning microscope using either a 30× or a 60× silicon oil immersion objective (NA 1.05 or 1.3, respectively). In some slices, to illustrate layering, a Nissl-like fluorescent staining was performed (NeuroTrace Red, 530/615, Molecular Probes N21482, 1:100 dilution in PB, applied for 15 min). Excitation wavelengths used were 405 and 643 nm diode laser lines.

Volume density of YFP and PV interneurons and the proportions of PV cells were determined in a total of 8 immunolabled slices from 3 animals. Confocal image stacks were taken from the top 50 µm of the embedded slices at 0.5 µm steps between image planes along the z-axis. A 150–270 µm wide rectangular counting template spanning all layers was superimposed on the parasubicular side of the presubiculum, and the cells were counted in 100 µm depth divisions along the layers in these stacks using ImageJ software. Cell densities were calculated within these frames using the optical disector approach (West and Gundersen 1990). Shrinkage of the slices along the z-axis was not compensated.

Cell and Layer Classification

We recorded a total of 762 cells and used the transgenic VGAT-YFP rat model in all our experiments. YFP expression was used as a guidance to preselect interneurons. However, the identity of the recorded neuron was rigorously confirmed only in 223 of the 762 recorded cells (67 YFP-positive, 156 YFP-negative). Therefore, to guarantee a uniform systematic classification, we established a discriminant analysis using 8 electrophysiological parameters. The discriminant analysis used linear combination of multiple variables to generate a discriminant function which best separated the 223 cells in which the presence or absence of YFP-expression was confirmed. This discriminant function was then applied to the entire sample of 762 cells (McLachlan 2004).

The YFP-expression of the above-mentioned subset of 223 cells was used as the grouping variable and the following 8 electrophysiological properties as independent variables: input resistance, RMP, AP width, AP maximum depolarization rate, AP maximum repolarization rate, minimum peak after AP, latency of minimum peak after AP, and firing frequency at 350 pA stimulation. As the firing frequency at 350 pA for 63 cells and the input resistance of 9 cells were not determined, we replaced these values by the mean value of all cells. This approach allows a classification based on the other available parameters, while the replaced mean parameters have a negligible influence on the classification. It has been previously shown that this approach provides comparable results with other estimation techniques (Jackson 1968). The a priori probability was determined by the given group size. This classification function was then applied to all 762 cells, including cells with identified YFP-expression. The classification resulted in a group of 511 pyramidal cells and another group of 251 interneurons.

When evaluating the classification, we found that 5 cells classified as pyramidal cells elicited short latency IPSPs in the postsynaptic cells. Therefore, we reassigned them to the group of interneurons. One of these cells was YFP-positive further confirming the reclassification of these neurons. One cell initially classified as interneuron by the discriminant analysis exhibited a firing pattern with an initial burst followed by pyramidal cell shaped APs and was therefore reassigned to the pyramidal cell group. A binary classification approach certainly bears limitations especially for cells with intermediate firing properties. Therefore, to assess the quality of this statistical approach, we analyzed the probabilities of each cell belonging to one of the cluster calculated by the discriminant analysis in SPSS (Fig. 2C).

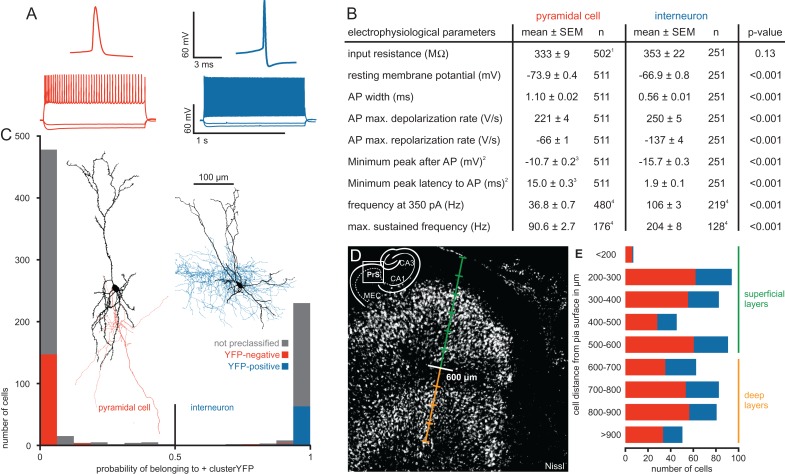
Figure 2.

Electrophysiological properties and morphology of pyramidal cells and interneurons in the presubiculum. (A) Representative AP traces and firing patterns of the 2 cell types. (B) Table of electrophysiological parameters for each cell type including P values from statistical comparison using Mann–Whitney U Test. ¹For 9 PCs, the input resistance was not determined. ²We used the minimum potential in a time window of 20 ms following the AP and its latency as a simplified measurement to detect a possible fast AHP. ³PCs mostly lacked a fast AHP, therefore their potentials and latencies were shifted to higher values confined by the 20 ms time window. ⁴Firing frequencies were determined in subsets of cells. (C) Histogram showing the probability of a cell belonging to the IN cluster calculated by the discriminant analysis. Red and blue bars represent cells with confirmed VGAT-YFP expression. Note the good separation of PCs and INs, the almost complete lack of VGAT-YFP expression in the PC cluster and its reliable expression in the IN cluster. Gray bars represent cells in which the YFP-expression was not rigorously determined. Cells with a probability higher than 0.5 were classified as INs, cells with a lower probability as PCs. Two representative samples of morphologically reconstructed cells are shown (PC with red axon, IN with blue axon). (D) An overview image of a Nissl-stained section of the presubiculum illustrates the separation between superficial layers (green) and deep layers (orange) at 600 µm, corresponding to the cell sparse layer IV. The scale bar indicates 100 µm steps. A schematic overview in the corner depicts the region relative to the hippocampus. (E) Number of recorded cells plotted against their depth measured from pia. IN in blue and PC in red. Lines indicate the distinction in superficial (green) and deep layers (orange).

A similar discrimination analysis method was used to classify the interneurons into an FS and an NFS group. A subset of 32 slices with a total of 196 cells were immunohistochemically examined for PV-expression. Out of these, 50 cells were YFP-positive (146 cells were YFP-negative putative PCs). Of the 50 YFP-positive interneurons, 16 were found to be PV-positive and 34 PV-negative. We then performed a discriminant analysis using the confirmed presence or absence of PV-expression of these 50 cells as the grouping variable and their electrophysiological properties as independent variables (AP width, maximum depolarization and repolarization rate, latency and peak of the AHP, firing frequency at 350 pA). The discriminant classification function was subsequently applied to all 251 interneurons, including the 50 stained interneurons.

The distance of the cells to the pial surface was measured along the axis of the apical dendrites visible in the infrared image of the acute slices and confirmed post hoc in the confocal image stacks of the visualized neurons. This axis could be reliably determined and often differed from the perpendicular axis to the curved pial surface (Supplementary Fig. 1). We divided the presubiculum in superficial and deep layers guided by the cell sparse lamina dissecans (layer IV), which was approximately at 600 µm from the pia along the aforementioned dendritic axis (Simonnet et al. 2013). Accordingly, cells within 600 µm from the pia were classified as belonging to the superficial layers while cells beyond 600 µm were attributed to the deep layers (Fig. 2D,E). Although no further detailed sublayer analysis was attempted, we estimate 0–200 µm to correspond to layer I, 200–300 µm to layer II, 300–600 µm to layer III. As for deeper layers, we assume layer V to be around 700–900 µm. Intersomatic distances were determined by calculating the Euclidian distance between the cells based on their 3D coordinates. Positions in the z-axis (depth of cell from slice surface) were determined using the z-coordinates of the microscope while focusing first on the slice surface and then on the soma of the cell.

Synaptic Connectivity

For connection screening, 4 APs were elicited in a single cell at 20 Hz by injecting 1–2 ms suprathreshold current pulses of 1–2.5 nA. Each recording sweep was 8 s long and the individual cells were stimulated sequentially in 1 s intervals; therefore, each cell was activated once in every 8 s (0.125 Hz) (Fig. 1C). Recording time was 30 min on average to allow sufficient time for the diffusion of biocytin and a complete filling of the cells. About 40–50 sweeps were averaged for the analysis of postsynaptic responses. Every postsynaptic trace was closely examined and an existing unitary synaptic connection was identified when postsynaptic potentials (EPSPs, IPSPs) were tightly correlated with the burst of presynaptic APs with a maximum latency of <3 ms to ensure the detection of monosynaptic connections. This allowed us to detect unitary postsynaptic potentials as small as 0.04 mV in average amplitude, though we cannot rule out having missed connections of even smaller amplitudes. Although our focus was to characterize chemical synapses, some interneuron pairs exhibited positive postsynaptic potentials with a simultaneous onset together with the presynaptic AP in both cells. We classified these reciprocal connections as electrical gap junctions. However, we did not perform hyperpolarizing step pulses or pharmacological isolation to reliably detect electrical couplings. Furthermore, interneurons were not selected to be closely located, therefore our observations likely underestimate gap junction coupling in this region.

Synaptic transmission was analyzed in averaged traces elicited by 20 Hz AP trains. We used the membrane potential immediately preceding the onset of the postsynaptic potential as the baseline to measure the peak amplitude of the responses. The paired pulse ratio (PPR) was calculated as the ratio of the second to the first postsynaptic peak amplitude. Synaptic latency was measured as the time from the presynaptic AP peak to the onset of the EPSP or IPSP. Hyperpolarizing connections were classified as inhibitory connections. At 5 connections made by neurons originally identified as pyramidal cells by the discriminant analysis we also observed hyperpolarizing synaptic events. Therefore, these neurons were reclassified as interneurons (see cell classification above). All other connections established by presynaptic neurons classified as pyramidal cells exhibited depolarizing potentials and were therefore unequivocally regarded as EPSPs. In the initial experiments, we recorded cells at their RMP (n = 368) and observed, in few cases, depolarizing potentials elicited by presynaptic interneurons in postsynaptic cells with resting potentials below −75 mV. This prompted us to control the membrane potential in all subsequent recordings (n = 394 cells) at −65 mV with automated slow bias current injection. Under this condition, we consistently detected hyperpolarizing IPSPs. Both hyper- and depolarizing IPSPs recorded from postsynaptic neurons at a membrane potential more negative than −65 mV (n = 282) were excluded from the postsynaptic amplitude analysis. This affected 59 (47 onto pyramidal cells and 12 onto interneurons) out of total 198 detected inhibitory connections. No pharmacological assessment of the neurotransmitters and the postsynaptic receptors involved was performed at any of the connections.

Statistical Analysis

We aggregated the table of connection probabilities with the table of cell properties through a relational database in Microsoft Access 2013 and exported the combined database into IBM SPSS Statistics 22 for further statistical analysis. Statistical comparison between experimentally determined frequency of found and tested connections was analyzed using the Fisher's exact test. Confidence intervals for the difference between the assumed binomial proportions were calculated using a simple asymptotic method without continuity correction (Newcombe 1998). For further analysis of connection probabilities, we used statistical tests applicable to the contingency table. The Cochran-Armitage test, also called chi-square linear-by-linear-association test for trends, was used to detect a statistical significant trend in a data series such as the distance-dependent decrease of the connection probability (Armitage 1955). To test the conditional independence of the layer-specific differences in connection probability while accounting for other potentially confounding variables such as intersomatic distance, age group, or dorsoventral axis, we used the Mantel–Haenszel test (Mantel 1963). In a contingency table with more than 2 groups, such as in our orientation analysis, a statistically significant chi-square test indicates an association between the variables. However, it does not reveal the contribution of each group to this result. By calculating the adjusted residual of each group, statistically significant deviations from the expected value of the null hypothesis can be detected (adjusted residual >1.96) (Agresti and Kateri 2011; Scharpe 2015). To test the probability of observed reciprocal pairs with the assumption of a random network, we performed the binomial test. If unidirectional connections were assumed to be established independently of other connections at the experimentally determined probability, then the random probability of a reciprocal connection was calculated by multiplying the probability of each of the 2 involved unidirectional connections. Since this corresponds to a binomial distribution, a binomial test was performed to determine whether the observed reciprocal rate is significantly higher than the expected random probability (Newman et al. 2001).

The distribution of synaptic properties was assessed using the Kolmogorov–Smirnov test which can statistically reject a normal distribution for P < 0.05. For P > 0.05, the null hypothesis of a normal distribution could not be discarded. When applied to a logarithmic scale, this test can be used for the detection of log-normal distributions. Synaptic property values are shown in median and interquartile range to better depict dispersion given the nonparametric distribution in many groups as revealed by the Kolmogorov–Smirnov test. Synaptic properties were compared using the nonparametric Mann–Whitney U test. The effect size r was calculated in rank-transformed values with the z-value of the Mann–Whitney U test (Rosenthal and Hedges 1994). Here, r = 0.1 depicts a small effect, r = 0.3 a medium effect, and r = 0.5 a large effect. To test for equivalence, we chose the confidence interval approach and refrained from calculating observed power due to its direct relationship to the observed P value (Hoenig and Heisey 2001). We calculated the median difference and its 95% confidence interval using the Hodges–Lehman estimator (SPSS function). If the confidence interval of the median difference between the 2 groups lies within a range considered inconsequential, it is statistically significant equivalent at the alpha level of 0.05 (Tryon 2001). However, if the comparison is neither statistically different nor equivalent, we have to state that it is statistically inconclusive given the available data. P values below 0.001 or above 0.05 are indicated as P < 0.001 or P > 0.05, respectively.

Results

Classification of Pyramidal Cells and Interneurons

To analyze the local network connectivity, we performed multiple whole-cell recordings of up to 8 cells simultaneously in acute brain slices of VGAT-YFP transgenic rats aged P19–P35. The presubiculum was located as a curved region between the subiculum and the parasubiculum in a horizontal slice (Fig. 1A, see Materials and Methods). We determined the depth of the cells based on their distance from the pia along the dendritic axis (Fig. 1B, Supplementary Fig. 1). We recorded cells in all layers of the presubiculum and examined their electrophysiological properties (Fig. 2A,B). Of the 762 cells recorded, we could unambiguously classify 223 cells as pyramidal cells (PCs, n = 156) or interneurons (IN, n = 67) by the clear presence or absence of YFP-expression. This allowed us to perform a discriminant analysis using the YFP-expression as a grouping variable and 8 electrophysiological properties as independent variables creating a group of 511 pyramidal cells and another group of 251 interneurons (see Materials and Methods). This discrimination based on the electrophysiological parameters yielded a very clear separation of the 2 groups with only few cells having a probability between 0.3 and 0.7 of belonging to the IN cluster (pIN). Since the probability of belonging to the PC cluster is 1 – pIN and the separation value is 0.5, these cells have a probability below 0.7 of belonging to their assigned cluster (IN 3/251, PC 10/511, Fig. 2C). This result is further supported by the classification of all 67 YFP-positive cells as interneurons and 153 YFP-negative cells as pyramidal cells while only 3 cells classified as interneurons appeared to be false-negative for YFP, corresponding to the 2–5% of false-negative cells observed in cortical areas of this transgenic rat line (Uematsu et al. 2008).

The electrophysiological parameters between pyramidal cells and interneurons differed significantly except for their input resistance (Fig. 2B, mean ± standard error of mean). Pyramidal cells had a lower RMP (PC −73.9 ± 0.4 mV vs. IN −66.9 ± 0.8 mV, P < 0.001), a broader AP half width (PC 1.10 ± 0.02 ms vs. IN 0.56 ± 0.01 ms, P < 0.001) and a lower AP de- and repolarization rate (maximal depolarization rate: PC 221 ± 4 V/s vs. IN 250 ± 5 V/s, P < 0.001; maximal repolarization rate: PC −66 ± 1 V/s vs. IN −137 ± 4 V/s, P < 0.001). Interneurons exhibited a fast and strong AHP (latency: 1.9 ± 0.1 ms; amplitude: −15.7 ± 0.3 mV), while pyramidal cells mostly lacked any short-latency, fast AHP resulting in a much larger latency of the negative peak after the APs (15.0 ± 0.3 ms, P < 0.001). Please note, however, that this value was limited by the 20 ms detection time window (see Materials and Methods). Hence, the average amplitude of −10.7 mV ± 0.2 measured at that negative peak does not represent a fast, but rather a medium AHP. Furthermore, interneurons exhibited a much higher firing frequency, both at 350 pA stimulation (PC 36.8 ± 0.7 Hz vs. IN 106 ± 3 Hz, P < 0.001) and at the maximum sustained stimulation (PC 90.5 ± 2.7 Hz vs. IN 204 ± 8 Hz, P < 0.001). We also observed 22 neurons with an initial burst of APs. We included these neurons into the pyramidal cell group. In fact, these cells exhibited electrophysiological properties similar to those of pyramidal cells, but had a more depolarized RMP (bursting PC −64.6 ± 1.9 mV vs. regular PC −73.3 ± 0.4 mV, P < 0.001) in good agreement with previous reports (Simonnet et al. 2013). In contrast to previous studies, however, we found these bursting neurons throughout all layers and not restricted to layer IV (Simonnet et al. 2013) or superficial layers (Abbasi and Kumar 2013).

Given reports of a functional separation of the presubiculum into superficial and deep layers, we also subdivided the presubiculum in superficial and deep layers using the cell sparse region at 600 µm as a boundary (Fig. 2D, see Materials and Methods), corresponding to the layer IV or “lamina dissecans” (Canto et al. 2008; Simonnet et al. 2013). We recorded from cells throughout all layers (Fig. 2E). Note that the ratio of pyramidal cells to interneurons is influenced by the intentional preselection of YFP-positive cells for recordings and therefore does not reflect the proportions of these cells within the neuronal population.

Layer-Specific Synaptic Excitatory and Inhibitory Connectivity in the Presubiculum

Simultaneous recordings from up to 8 cells allowed us to screen up to 56 possible synaptic connections at once. Using this approach, a total of 4250 possible connections were tested and subdivided into 4 different synaptic categories: pyramidal cell to pyramidal cell (PC–PC), pyramidal cell to interneuron (PC–IN), interneuron to pyramidal cell (IN–PC) and interneuron to interneuron (IN–IN). Synaptic connections were detected by eliciting a train of 4 APs at 20 Hz in each cell consecutively while monitoring postsynaptic responses in the other simultaneously recorded cells (Fig. 1C). For all tested connections, we averaged 40–50 sweeps and identified existing unitary synaptic connections when postsynaptic potentials showed a temporal correlation to the burst of presynaptic APs (see Materials and Methods for further criteria).

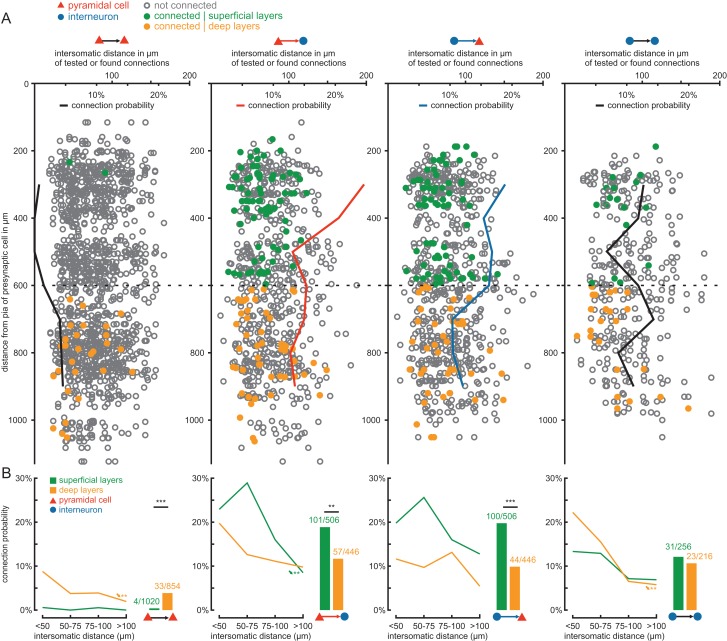
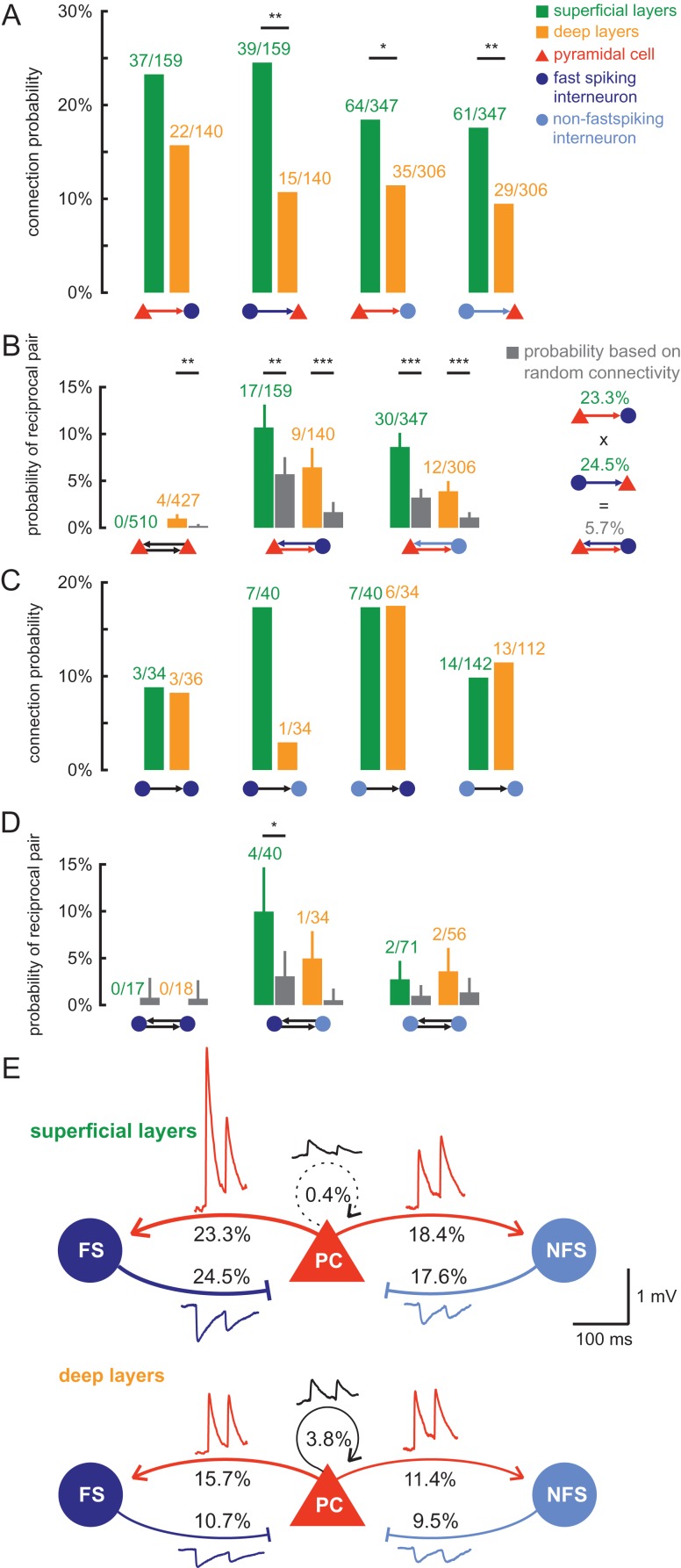
We first analyzed the probability of the 4 types of synaptic connections in all layers by calculating the ratio of identified connections to all tested ones and plotting these against the depth of the presynaptic soma measured from the pia (Fig. 3A, note that exact coordinates were determined for a subset of 3160 connections). We found that connections between pyramidal cells were almost absent in the superficial layers, but increased in probability toward the deeper layers. In contrast, connection probability between pyramidal cells and interneurons was higher in the superficial layers and lower in the deeper layers. These differences further support our functional separation of the presubiculum into a superficial and a deep layer with an apparent boundary at a depth of 600 µm (Fig. 2D). We pooled the connections according to this definition (Fig. 3B) and found that the PC–PC connectivity in the deep layers (3.9%, 33/854) was markedly higher than in the superficial layers (0.4%, 4/1020, P < 0.001). In contrast, PC–IN connection probability was higher in the superficial (20%, 101/506) than in the deep layers (12.8%, 57/446, P = 0.003) and significantly higher than PC–PC connection probability (superficial layer P < 0.001, deep layer P < 0.001). The same was observed for IN–PC connections (superficial 19.8%, 100/506 vs. deep 9.9%, 44/446, P < 0.001). The connectivity among interneurons was evenly distributed between superficial and deep layers (superficial 12.1%, 31/256 vs. deep 10.7%, 23/216, P > 0.05). We also found 4 pairs of interneurons which seemed to be electrically coupled (1 FS–FS pair in superficial layer, 3 NFS–NFS pairs in deep layers). However, given that our experimental approach was optimized for the efficient detection of chemical synapses, the proportion of coupled pairs observed in our study is likely to be an underestimate of the actual frequency of gap junctions in this region (see Materials and Methods).

Figure 3.

Layer-specific excitatory and inihibitory connectivity in presubicular circuits. (A) Of the total 4250 possible connections tested, exact positions of the pre- and postsynaptic cells were determined for 3160 tested connections. In the diagrams, each circle or dot represents a tested connection: a green dot indicates a detected synaptic connection in the superficial layers, an orange dot a connection in the deep layers, and the open gray circles depict tested connections without synaptic coupling. For each tested connection type, the depth of the presynaptic cell measured from the pial surface along the dendritic axis (vertical axis) was plotted against the intersomatic distance between the cells (values above horizontal axis). The black, red, and blue lines represent the connection probability of each synaptic type, calculated as the ratio of observed to tested connections (values below horizontal axis), plotted against the distance to pia (vertical axis) as a moving average of 2 values. The division between superficial and deep layers is shown as a dotted line at 600 µm. (B) The connection probability as a function of intersomatic distance in each layer is shown for the different synaptic groups. Asterisks with arrows depict statistically significant distance-dependent decrease of connection probability calculated using the Cochran-Armitage test, **P < 0.01. The adjacent bar graphs depict the pooled connection probability in the superficial (green bars) and deep layers (orange bars). Numbers indicate found and tested connections. Statistical comparisons between the layers were calculated using Fisher's exact test, **P < 0.01, ***P < 0.001.

We next analyzed the distance-dependence of the connections and calculated the intersomatic distance as the Euclidian distance using all 3 spatial axes. Z-distances contributed only marginally with a narrow distribution of z-positions around 42 ± 12 µm below surface (mean ± standard deviation). Among pyramidal neurons, the connection probability was highest for cells within 50 µm of intersomatic distance (superficial layer: 0.6%, 1/172; deep layers: 8.8%, 13/148). We found that the probability of connections tended to decrease toward greater intersomatic distances for all 4 connection types (Fig. 3B). To test whether these observations are of statistical significance, we used the Cochran–Armitage test (see Materials and Methods). The decrease in connection probability was statistically significant in deep layers for PC–PC (P = 0.008) and for IN–IN (P = 0.009) and in superficial layers for PC–IN connections (P = 0.002). When all layers were considered, there was a significant decrease with distance for all synaptic groups: PC–PC (P = 0.007), PC–IN (P < 0.001), IN–PC (P = 0.03), and IN–IN (P = 0.004). To rule out that the previously observed layer-specific difference in connection probability was due to the significant distance-dependence, we tested for conditional independence using the Mantel–Haenszel test. It showed that the observed layer-specific differences are still statistically significant despite the distance-dependence: PC–PC P < 0.001, PC–IN P = 0.02, and IN–PC P = 0.001.

To assess age-dependent influences on our findings, the dataset was separated into 2 age groups: P19–P23 and P24–P35. Although we observed an age-dependent decrease of connectivity in most groups, the observed layer-specific differences persist and are statistically significant in all but one group (Supplementary Fig. 2). The Mantel–Haenszel test confirmed that the layer-specific differences are still statistically significant despite differences in the age groups (PC–PC P < 0.001, PC–IN P = 0.004, IN–PC P < 0.001).

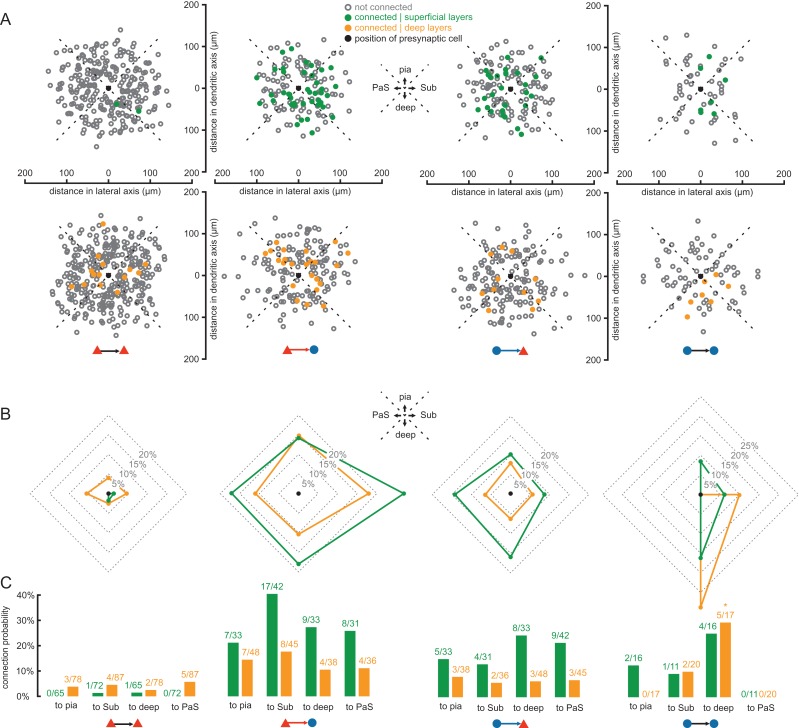
Finally, we analyzed potential preferences of connections to any specific orientation in the x–y plane of the slices in 1345 connections for which the vector linking the pre- to the postsynaptic neuron could be determined along the dendritic and transverse axes (Fig. 4). We divided the data in 4 different orientation groups and observed no significant preference in PC–PC, PC–IN, and IN–PC connections (Fig. 4B,C). The connectivity in deep IN–IN connections, however, appeared to have a significant preference of orientation (P = 0.008) with the connectivity to deeper layers exhibiting the highest deviation with an adjusted standardized residual of 3.2 (Fig. 4C). However, this finding was based on a low sample size of 5, whereby 3 of these IN–IN connections were detected in the same cell cluster (Supplementary Fig. 3). Therefore, further experiments are required to confirm this observation.

Figure 4.

Orientation preference of connectivity around presynaptic cell. (A) The position along the dendritic (vertical) and transverse (horizontal) axes of the postsynaptic cell relative to the presynaptic cell (black dot) is shown for a subset of 1345 tested connections in which the orientation of the dendritic axis could be adjusted to the vertical axis. Connections were separately pooled according to layers (upper row: superficial; lower row: deep) and connection types (columns). Colored dots indicate detected synaptic connections (green: superficial layers; orange: deep layers). Open gray circles represent tested but not connected pairs. The black dot marks the origin of the coordinates, representing the position of the presynaptic cell. Quadrants representing different directions were defined: pia surface, subiculum (Sub), deep layers, and parasubiculum (PaS). (B) Polar graphs indicate pooled connection probabilities for each of the 4 directions according to the defined quadrants (green line: superficial layers; orange line: deep layers). (C) Bar graphs of pooled connection probabilities for each direction, layer, and synaptic group. Numbers indicate found and tested connections. The asterisk represents a significant deviation from the expected value of the null hypothesis (adjusted residual > 1.96).

Properties of FS and NFS Interneurons

So far, we have considered all interneurons as belonging to a single group despite their well-known diversity (Markram et al. 2004; Nassar et al. 2015). Facing this enormous complexity, we focused on a simple classification by comparing FS interneurons to NFS interneurons (Fig. 5B). This approach was motivated by the assumed critical role of FS PV-positive interneurons in the modulation of grid and head direction cell activities (Couey et al. 2013; Buetfering et al. 2014; Tukker et al. 2015). To detect FS interneurons, we immunostained a subset of 50 interneurons for PV (Fig. 5A) and performed a discriminant analysis based on their electrophysiological properties, yielding a group of 81 FS interneurons and another group of 170 NFS interneurons (Fig. 5D, see Materials and Methods). While 14 of the 16 PV-positive cells were classified as FS interneurons, 29 of the 34 PV-negative cells were classified as NFS interneurons. The probability distribution showed a minimum around 0.5 and only 34 of the 251 cells (13 FS and 21 NFS) fell into the range between 0.3 and 0.7 which corresponds to a probability below 0.7 of belonging to the respective clusters (Fig. 5D). Thus, our classification was highly reliable for the majority of interneurons (>86%). Nevertheless, we cannot exclude that some interneurons with intermediate properties were misclassified (Nassar et al. 2015).

Figure 5.

Classification of FS versus NFS interneurons. (A) Confocal images of slice with 8 recorded cells (white circles). Upper left: YFP-expression in yellow was found in 3 cells (arrows). Upper right: PV-immunostaining in green revealed 2 immunopositive cells (green arrow: PV-positive; yellow arrow: PV-negative). Lower left: Biocytin staining in red shows further 5 PCs without YFP- or PV-expression. Lower right: Overlay of all 3 channels. (B) Example AP traces and firing patterns of each IN class. (C) Table of electrophysiological parameters for the 2 IN classes. Statistical comparison for each parameter was performed using Mann–Whitney U test. ¹Firing frequencies were determined for a subset of cells. (D) Histogram showing the probability of a cell belonging to the FS cluster calculated by the discriminant analysis. Colored bars represent 50 INs for which PV-expression was investigated (green bars: PV-positive; yellow bars: PV-negative), gray bars represent INs not stained for PV. Cells with a probability higher than 0.5 were classified as FS interneurons, cells with a lower probability as NFS interneurons. (E) Distribution of IN classes across the layers as classified based on electrophysiological properties. Left: Absolute numbers of INs classified as FS interneurons (dark blue bars) and NFS interneurons (light blue bars) plotted against their depth measured from the pia. Right: Proportion of the 2 classes of recorded INs plotted against their depth. (F) IN class distribution across the layers in immunohistochemically stained slices. Left: Proportion of PV-positive INs (green bars) and PV-negative INs (yellow bars) plotted against their depth. Right: Cell density of PV-positive INs plotted against their depth.

Both interneuron classes differ in their electrophysiological properties (mean ± standard error of mean) except for RMP and AHP amplitude (Fig. 5C). FS interneurons exhibited significantly lower input resistance (FS 172 ± 8 MΩ vs. NFS 439 ± 30 MΩ, P < 0.001), lower AP half width (FS 0.41 ± 0.01 ms vs. NSF 0.63 ± 0.01 ms, P < 0.001), higher AP de- and repolarization rates (maximal AP depolarization rate: FS 272 ± 10 V/s vs. NFS 239 ± 6 V/s, P = 0.004; maximal AP repolarization rates: FS −168 ± 7 V/s vs. NFS −123 ± 3 V/s, P < 0.001), shorter latency of fast AHP (FS 1.23 ± 0.04 ms vs. NFS 2.15 ± 0.13 ms, P < 0.001) and higher firing frequencies (at 350 pA: FS 149 ± 5 Hz vs. NFS 87 ± 2 Hz, P < 0.001; at maximum sustained stimulus: FS 301 ± 12 Hz vs. NFS 165 ± 7 Hz, P < 0.001).

In the recorded sample, the 2 classes of interneurons had comparable distributions in superficial layers (32.6% FS) and deep layers (31.9% FS) (Fig. 5E). Similarly, quantification of PV-positive interneurons among the YFP-expressing cells in immunolabeled slices resulted in a proportion of 35.2% in the superficial and 33.3% in the deep layers (Fig. 5F). Thus, the layer-specific ratio of FS interneurons within the total interneuron population determined by our discrimination analysis was comparable to, albeit slightly lower than the immunohistochemically determined proportion of PV-positive cells (Fig. 5F). Despite the comparable relative proportions of PV-positive cells, their density was over 2-fold higher in the superficial (11 119 ± 1029 mm^–3, excluding the cell-sparse layer I) than in the deep layers (4734 ± 637 mm^–3). Mophological reconstructions of upper-layer interneurons revealed multipolar somato-dendritic morphology with smooth dendrites spanning multiple neighboring layers and dense axonal arborization in layer II (Supplmentary Fig. 4A–D). Furthermore, axons of PV-positive interneurons formed basket-like structures around somata of putative pyramidal cells (Supplementary Fig. 4E,F), similar to those of basket cells in other corical areas (Markram et al. 2004).

Connectivity of FS and NFS Interneurons

After the interneuron discrimination, we analyzed their subtype-specific connectivity and found no significant subtype-specific differences in connection probability (Fig. 6A). FS interneurons in the superficial layer exhibited a slightly higher interconnectivity with pyramidal cells than NFS interneurons which was not statistically significant (PC–FS 23.3% vs. PC–NFS 18.4%, P > 0.05 and FS–PC 24.5% vs. NFS–PC 17.6%, P > 0.05). Instead, common layer-specific differences could be observed irrespective of interneuron classification: connection probabilities were higher in superficial than in deep layers, although this trend failed to be statistically significant for the PC–FS group (Fig. 6A). Thus, our analysis of FS and NFS interneurons indicates that interneuron diversity does not challenge our results and general approach to assess network topology in the presubiculum.

Figure 6.

Connectivity and reciprocity of interneuron subtypes. (A) Unidirectional connection probability for IN excitation and PC inhibition shown for different IN subtypes (dark blue: FS; light blue: NFS) and layers (green: superficial; orange: deep). Statistical comparisons between the layers were calculated using the Fisher's exact test, *P < 0.05, **P < 0.01, ***P < 0.001. (B) Observed probability of reciprocal pair in each layer (green and orange bars) compared with the expected reciprocal rate under the random assumption (gray bar). Error bars represent standard deviation assuming binomial distribution. Statistical difference was assessed using the binomial test, ***P < 0.001, **P < 0.01. Right: Example calculation for expected reciprocal rate under the assumption that unidirectional connections are independently established. (C) Unidirectional connection probability between INs for each subtype and layer. (D) Reciprocal rate between INs compared with the random probability as described in (C), *P < 0.05. (E) Schematic figure of the connection probabilities between the different cell types in the superficial and deep layers of the presubiculum. Transmission properties are represented by modified traces that depict the mean of the postsynaptic amplitude, PPR and half-width for each synaptic group.

Since attractor network models of grid and head direction activity require bidirectional recurrent connectivity (Couey et al. 2013; Pastoll et al. 2013; Solanka et al. 2015), we searched for reciprocally connected pairs and calculated their probability by considering the number of tested pairs. No reciprocal connections were found between pyramidal cells in the superficial layers, while the reciprocal rate was 0.9% in deep layers (Fig. 6B). This was higher than expected, if we presume that reciprocal pairs arise from random and independent unidirectional connections with an experimentally determined probability of 3.9% (3.9% × 3.9% = 0.15%). This assumed random connectivity corresponds to a binomial distribution. Therefore, we compared the experimentally determined reciprocal connectivity with the expected probability using a binomial test (see Materials and Methods). For deep PC–PC connections, the higher reciprocity was indeed statistically significant (P = 0.004). Reciprocal connections between PC–FS and PC–NFS pairs were also significantly overrepresented irrespective of the layer (Fig. 6B). Moreover, reciprocal pairs showed a tendency toward larger postsynaptic amplitudes than unidirectional connections, which was statistically significant in the deep layers (Supplement Fig. 5C). Finally, recurrent inhibitory connections are also involved between different pyramidal cells through an interneuron, such as a PC > IN > PC connection. We found 43 PC > FS > PC (30 in superficial and 13 in deep layers) and 101 PC > NFS > PC connections (70 in superficial and 31 in deep layers), which is more than the number of reciprocal pairs highlighting the importance of this connectivity pattern.

We further analyzed the connectivity among interneurons (Fig. 6C). Note that given our focus on excitatory connectivity, the number of simultaneously recorded interneurons was low. Therefore, the number of tested connections (n = 472) was substantially lower than in the other groups. This fact, combined with the diversity of interneurons, limited our analysis. The connection probability was comparable between layers for FS–FS (7.0% for superficial vs. 8.3% for deep layers, respectively), NFS–FS (17.5%, 17.6%), and NFS–NFS connections (9.9%, 11.6%), except for FS–NFS (superficial 17.5% vs. deep 3%, P > 0.05). No reciprocal pairs were found between FS interneurons (Fig. 6D). A total of 9 reciprocal interneuron pairs were found, but given the small sample size per groups, the number was only significantly higher than expected in superficial FS–NFS pairs (10% found vs. 3.1% expected, P = 0.03). To analyze whether both interneuron types can be targeted by 1 pyramidal cell, 135 pyramidal cells were identified which were simultaneously recorded with both FS and NFS interneurons. Of these pyramidal cells, 12 cells connected onto both interneuron classes.

Synaptic Properties of the Different Cell Types Along the Dorsoventral Axis

Since grid cell activity in the presubiculum was reported in the dorsal region (Boccara et al. 2010) and since the MEC has an inhibitory gradient along the dorsoventral axis (Beed et al. 2013), we asked whether the presubiculum also exhibits a dorsoventral divergence of network topology. Alternatively, the ventral and dorsal parts of the presubiculum may be considered as a single area in terms of cytoarchitecture and projection targets (Honda and Ishizuka 2004). To test these 2 alternative hypotheses, we divided our dataset into recordings obtained from the ventral and dorsal presubiculum (see Materials and Methods). Although variations of connection probabilities between ventral and dorsal recordings were present, the general principles of connectivity described above for the superficial and deep layers could be confirmed in both subregions of the presubiculum (Table 1).

Table 1.

Synaptic connectivity and strength

Subdivision			Connectivity			Peak amplitude (mV)
Synapse	Region	Layer	Found	Tested	Probability	Median [interquartile range]	n
PC–PC	Ventral	Superficial	2	746	0.3%a	0.33 [0.19;0.46]	2
		Deep	19	524	3.6%a	0.32 [0.14;0.47]	19
	Dorsal	Superficial	2	274	0.7%b	0.22 [0.13;0.31]o	2
		Deep	14	330	4.2%b	0.17 [0.1;0.25]p	14
PC–FS	Ventral	Superficial	23	124	18.5%g	2.31 [0.24;6.36]l	23
		Deep	10	60	16.7%	0.57 [0.21;2.22]	10
	Dorsal	Superficial	14	35	40.0%c,g	1.4 [0.58;3.31]j,m,o	14
		Deep	12	80	15.0%c	0.55 [0.22;0.705]j,p	12
PC–NFS	Ventral	Superficial	37	243	15.2%h	0.47 [0.22;1.78]k,l	37
		Deep	24	219	11.0%	0.43 [0.135;1.1]	24
	Dorsal	Superficial	27	104	26.0%d,h	0.18 [0.13;0.23]k,m	27
		Deep	11	87	12.6%d	0.36 [0.1;1.3]	11
FS–PC	Ventral	Superficial	32	124	25.8%	−0.33 [−0.77;−0.19]	18
		Deep	11	60	18.3%i	−0.13 [−0.17;−0.09]	2
	Dorsal	Superficial	7	35	20.0%e	−0.58 [−0.66;−0.52]n	7
		Deep	4	80	5.0%e,i	−0.42 [−0.51;−0.31]	4
NFS–PC	Ventral	Superficial	42	243	17.3%f	−0.2 [−0.68;−0.11]	23
		Deep	22	219	10.0%f	−0.28 [−0.38;−0.09]	15
	Dorsal	Superficial	19	104	18.3%	−0.19 [−0.33;−0.12]n	19
		Deep	7	87	8.0%	−0.18 [−0.28;−0.06]	7

The connection probability, calculated by the number of detected synaptic connections divided by the number of tested possible connections, is shown for different synaptic types, in the dorsal and ventral regions, and for the superficial and deep layers. Given the nonparametric distribution of the peak amplitudes of postsynaptic potentials, their central tendency and dispersion are depicted using the median and the interquartile range that is the interval from the 25th to the 75th percentile. Superscripts indicate P values below 0.05 of statistical comparisons between subgroups. Same superscripts indicate the 2 compared values. Due to correction for multiple comparisons using the Bonferroni method, the given P values are only statistically significant at α = 0.05 if they are below 0.013 for excitatory connections or below 0.017 for inhibitory connections. Statistical differences in connection probability were assessed using the Fisher's exact test. P values of layer comparison: a 0.011, b 0.009, c 0.007, d 0.028, e 0.033, and f 0.03. Region comparison: g 0.012, h 0.023, and i 0.014. Note that the excitatory connection probability onto PC is significantly lower than onto IN in all subgroups. Comparisons for postsynaptic amplitude were assessed using Mann–Whitney U test. P values for layer comparison: j 0.011. Region comparison: k < 0.001. Comparison between synaptic groups: l 0.031, m < 0.001, n 0.001, o 0.017, and p 0.011. See Supplementary Tables 1–5 for further statistics. Except for PC–PC connection probability, none of the other nonsignificant comparisons can be declared as statistically equivalent.

Connection probability and other synaptic properties were analyzed for layer-, region-, and cell type-specific differences (Table 1, Supplementary Tables 1–5). Due to significant deviation from normal distribution in many subgroups according to the Kolmogorov–Smirnov test, synaptic properties were compared using the Mann–Whitney U test. The difference in connectivity was assessed using the Fisher's exact test. We adjusted for multiple comparison using the Bonferroni correction method and included the effect size for each comparison. To assess whether a nonsignificant difference was due to equivalence or insufficient sample size, we calculated the 95% confidence interval for the difference (see Materials and Methods).

Despite variations of connection probabilities between the ventral and dorsal region (Table 1 and Supplementary Table 1), we could confirm that the overall layer-specific difference in connectivity is still statistically significant in all subgroups (Mantel–Haenszel test: PC–PC P < 0.001, PC–FS P = 0.048, PC–NFS P = 0.019, FS–PC P = 0.044, NFS–PC P = 0.004). PC–PC connectivity in both regions was sparse in the superficial layers and higher in the deep layers (ventral: superficial 0.3% vs. deep 3.6%, P < 0.001; dorsal: superficial 0.7% vs. deep 4.2%, P = 0.009). Excitation onto interneurons was more frequent in superficial than in deep layers for both regions, but statistically significant only for dorsal PC–FS connections (superficial 40% vs. deep 15%, P = 0.007). Inhibitory connectivity onto pyramidal cells appeared higher in superficial than in deep layers in both regions; however, those comparisons failed to be statistically significant. Significant region-specific differences were detected in superficial PC–FS connections (ventral 18.5% vs. dorsal 40%, P = 0.01) and deep FS–PC connections (ventral 18.3% vs. dorsal 5%, P = 0.01). Additionally, our confidence interval approach showed that the PC–PC connectivity between subregions is statistically equal (α = 0.05) within a difference of 1% (superficial) or 2.1% (deep). Excitatory connectivity onto interneurons was significantly higher than onto pyramidal cells in all subgroups.

Synaptic connectivities did not only differ in their probabilities, but also in the amplitude of their postsynaptic responses (Table 1 and Supplementary Table 2, values depicted as median [interquartile range]). Due to the numerous subgroups and comparisons in our cross-analysis, only statistically significant differences are reported here. As for target cell-specific differences, excitation onto interneurons in dorsal superficial layers is stronger onto FS than NFS interneurons (PC–FS 1.4 [0.58;3.1] mV vs. PC–NFS 0.18 [0.13;0.23] mV, P < 0.001). Likewise, pyramidal cell inhibition in dorsal superficial layers is also stronger by FS than NFS interneurons (FS–PC −0.58 [−0.66;−0.52] mV vs. NFS–PC −0.19 [−0.33;−0.12] mV, P = 0.001). Furthermore, excitation onto FS was stronger than onto PC in dorsal deep layers (PC–FS 0.55 [0.22;0.71] mV vs. PC–PC 0.32 [0.14;0.47] mV, P = 0.011). A layer-specific difference was detected in dorsal PC–FS connections (superficial 1.4 [0.58;3.1] mV vs. deep 0.55 [0.22;0.71] mV, P = 0.011). A region-specific difference could be found in superficial PC–NFS connections (ventral 0.47 [0.22;1.78] mV vs. dorsal 0.18 [0.13;0.23] mV, P < 0.001). In case of nonsignificant differences, the statistical equivalence could not be determined, thereby not allowing further statistical conclusions (see Materials and Methods for further explanation of the equivalence test).

We additionally analyzed synaptic transmission properties and found evidence for layer- and cell type-specific differences in PPR (Supplementary Table 3). Neither half duration of postsynaptic potentials nor their onset latency showed significant layer- or region-specific differences. However, we found cell type-specific latency differences in connections involving FS interneurons in different regions and layers (Supplementary Tables 4 and 5).

In summary, functional differences in excitatory and inhibitory synaptic transmission for different connection types, layers and regions were identified. We confirmed that the observed layer-specific connectivity existed regardless of interregional variability and found that the PC–PC connectivity was statistically equivalent between the ventral and dorsal subregions of the presubiculum.

Log-Normal Distribution of Synaptic Amplitudes Suggests Nonrandom Functional Connectivity

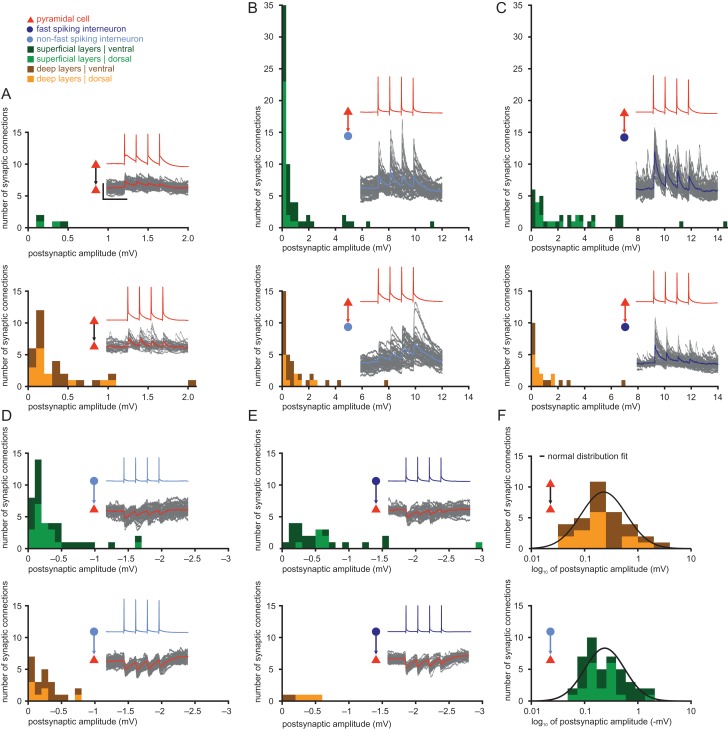
We also examined the mean amplitude distribution of postsynaptic potentials and observed a high variability in all synaptic types across all layers (Fig. 7). Pyramidal cells in the deep layers exhibited many weak and a few strong synapses at their excitatory input (Fig. 7A), in line with previously reported results (Song et al. 2005; Lefort et al. 2009; Ikegaya et al. 2013; Cossell et al. 2015). We found skewed distribution for synapses between pyramidal cells and interneurons as well, most prominently at PC–IN synapses with many weak (<0.6 mV) and a few very strong connections with amplitudes above 5 mV, in 3 cases even above 10 mV (Fig. 7B,C). The inhibitory postsynaptic amplitudes were similar, but with an overall less skewed distribution (Fig. 7D,E).

Figure 7.

Heavy-tailed distribution of synaptic amplitudes. The postsynaptic amplitude distributions are shown for different synaptic groups and both layers. Each histogram further distinguishes between ventral connections (dark green in superficial layers, brown in deep layers) and dorsal connections (light green in superficial layers, orange in deep layers). Example recording traces are shown for each group: the presynaptic APs are shown in the color of the presynaptic cell and the recorded postsynaptic traces are shown in gray, while the average trace is shown in the color of the postsynaptic cell. Scale bars: horizontal 100 ms, vertical 50 mV for APs, 1 mV for postsynaptic potentials. (A) PC–PC, bin size 0.1 mV. (B) PC–NFS, bin size 0.3 mV. (C) PC–FS, bin size 0.3 mV. (D) NFS–PC, bin size 0.1 mV. (E) FS–PC, bin size 0.1 mV. (F) Distributions of deep PC–PC and superficial NFS–PC amplitudes are shown on a logarithmic scale to illustrate log-normal features in excitatory and inhibitory connections. Black line represents the normal distribution fit for the sample.

Studies have suggested that the heavy-tail of PC–PC amplitudes can be best described by a log-normal distribution (Song et al. 2005; Ikegaya et al. 2013). Therefore, we tested the amplitude distribution of the different synapses subdivided for the 2 layers and the 2 interneuron classes and found that they are significantly nonnormally distributed (Kolmogorov–Smirnov test P < 0.001), except for groups with small sample size: superficial PC–PC (insufficient data), deep FS–PC (P > 0.05), and deep NFS–PC connections (P > 0.05). To investigate possible log-normal features of all connection types, we plotted the amplitudes on a logarithmic scale and tested again for normal distribution using the Kolmogorov–Smirnov test (see an example in Fig. 7F and pooled data in Supplementary Fig. 5A,B). After this conversion, synaptic amplitudes did not significantly differ from normal distribution in all synapses (P > 0.05), suggesting a log-normal distribution for these synapses, except for the superficial PC–NFS connections (P = 0.01). Considering that the PC–NFS synapse is the only one exhibiting significantly different synaptic amplitudes between the ventral and dorsal region, we repeated the Kolmogorov–Smirnov test on PC–NFS synaptic amplitudes subdivided by these 2 regions. The logarithmized synaptic amplitudes in these groups did not differ significantly from a normal distribution (P > 0.05), suggesting a log-normal amplitude distribution in these connections as well.

Thus, our data show that log-normally distributed synaptic amplitudes, a signature of nonrandom synaptic connectivity, are not only a hallmark of excitatory connections (Song et al. 2005; Ikegaya et al. 2013), but can be found in all synaptic connections in the presubiculum irrespective of cell type or layer.

Discussion

In this study, we assessed the network topology and the unitary synaptic properties between pyramidal cells and interneurons in the rat presubiculum. We found layer-specific differences in connectivity both for excitation and inhibition, further supporting the previously proposed functional division of the presubiculum into superficial and deep layers (Funahashi and Stewart 1997). We provide direct evidence for an almost complete lack of recurrent excitation between pyramidal cells in the superficial layers, while connectivity between deep pyramidal cells resembled other parahippocampal subregions (Dhillon and Jones 2000; Böhm et al. 2015). In contrast, interneuron excitation and pyramidal cell inhibition were more frequent in superficial than in deep layers. The overrepresentation of reciprocal connections together with the log-normal distribution of synaptic amplitudes suggest nonrandom features in the network topology of the presubiculum.

Layer-Specific Excitatory Network Topology

We investigated 1020 connections between superficial pyramidal cells in the presubiculum up to a depth of 600 µm from the pia and only found 4 connections with small amplitudes (0.13–0.46 mV), indicating an absence of substantial excitatory connectivity in these superficial layers of the presubiculum. This differs from the more complex excitatory network in the superficial layers of the MEC (Dhillon and Jones 2000; Couey et al. 2013; Pastoll et al. 2013; Fuchs et al. 2016): initial studies have suggested that connections among stellate cells are essentially absent (Couey et al. 2013; Pastoll et al. 2013), while a more recent study distinguished 4 types of excitatory cells in layer II of the MEC (Fuchs et al. 2016). Although Fuchs et al. confirmed the lack of connections between prototypical stellate cells, they revealed specific connectivity between the other excitatory cell types, such as intermediate pyramidal cells onto prototypical stellate cells (10%). Additionally, more abundant excitatory connections have been described in layer III (8.4%) of the entorhinal cortex (Dhillon and Jones 2000). In the presubiculum, the superficial layers represent a network topology without recurrent excitation, indicating that the local spatial tuning of pyramidal cells here must be generated through interaction with inhibitory cells in marked contrast to the MEC.

The connectivity between deep pyramidal cells in the presubiculum was substantially higher (3.8% overall and 8.2% for cells closer than 50 µm), similar to the probability of 11.5% observed in layer V of the MEC (Dhillon and Jones 2000) and 4–7% in the subiculum (Böhm et al. 2015). Hence, the deep layers of the presubiculum seem to exhibit a more complex network topology than the superficial layers and may have characteristics like the deep layers of the MEC.

We focused on the local synaptic connections within layers, while previous studies have already described layer-specific interlaminar connectivity in the presubiculum. Superficial layers provide very strong projections to deep layers while the projections from deep to superficial layers are only minor (Funahashi and Stewart 1997; Honda et al. 2008). The MEC, on the other hand, exhibits strong connections from deep to superficial layers (Köhler 1986; Beed et al. 2010). In addition, numerous studies have highlighted layer-specific efferent projections to the MEC. In particular, it has been shown that layer III of the presubiculum projects primarily to layer III of the MEC (Caballero-Bleda and Witter 1993; Honda and Ishizuka 2004; Preston-Ferrer et al. 2016). Thus, the activity patterns in the superficial layers of the presubiculum tuned by the specific local network topology are largely unidirectionally transmitted to their downstream targets.

Target Cell Specificity of Excitatory Connections

Throughout all layers, excitatory connectivity was higher onto interneurons than onto pyramidal cells and higher in superficial than deep layers (Fig. 6). We detected some pyramidal cells targeting different interneuron types at once while synaptic amplitudes and PPRs exhibited target cell-specific differences among interneuron types in superficial layers (Supplementary Tables 2 and 3). Similar cell type-specific short-term plasticity has been previously observed in other cortical regions and postulated as a central mechanism in the dynamics of information processing, such as frequency-dependent activation of various local inhibitory pathways (Markram et al. 1998; Watanabe et al. 2005).

In slice preparations, cutting of axons can lead to an underestimation of connection probabilities, especially for greater intersomatic distances as included in this study (up to 150 µm). The difference in connection probability onto pyramidal cells and interneurons made by the same excitatory axons, however, argues against the possibility that the extremely low connection probability between superficial pyramidal cells is a consequence of selective cutting of excitatory axons (Fig. 3 and Supplementary Fig. 1). Moreover, we have shown that the observed layer-specific differences persist, even if the distance-dependent decrease of connectivity is accounted for.

Layer-Specific Inhibitory Network Topology

In the presubiculum, the connection probability from interneurons onto pyramidal cells is higher in superficial (17–25%) than in deep layers (9–11%), while connectivity between interneurons is similar between the layers (10–12%). However, the overall connectivity is rather low compared with neighboring regions. In layer II of the MEC, inhibitory connectivity onto excitatory cells differs depending on interneuron subtypes, ranging from 5–25% for 5HT3A interneurons (Fuchs et al. 2016) to 40–60% for FS interneurons (Couey et al. 2013; Pastoll et al. 2013; Fuchs et al. 2016). Similar differences have been found in the subiculum (NFS–PC 29%, FS–PC 49%) (Böhm et al. 2015). The low inhibitory connectivity in the presubiculum persisted when only connections from FS interneurons were analyzed (10–25%) although axonal arborizations of reconstructed interneurons appear to be typical (Supplementary Fig. 4). Thus, our results indicate that presubicular interneurons do not provide a “blanket of inhibition” (Fino and Yuste 2011), possibly reflecting specific principles of network organization such as a preferential reciprocal connectivity between pyramidal cells and interneurons (Fig. 6C).

In addition, we rarely found evidence for disynaptic inhibition, despite strong excitatory input to FS interneurons (data not shown). This is in contrast to observations in the MEC stellate cell FS interneuron network (Couey et al. 2013). However, disynaptic inhibition likely occurs in the intact presubiculum due to feed-forward activation of neurons toward a balanced state in combination with local interneuron excitation (Van Vreeswijk and Sompolinsky 1996). The properties of the EPSPs onto FS interneurons still allow reliable and precisely timed AP generation in these cells (Geiger et al. 1997; Galarreta and Hestrin 2001).

Log-Normal Synaptic Weights

Previous studies of synaptic amplitudes between pyramidal cells have shown that their distribution is not normal but rather log-normal, exhibiting a heavy tail of large amplitudes (Song et al. 2005; Lefort et al. 2009; Ikegaya et al. 2013; Cossell et al. 2015). Various implications of log-normal synaptic weight distributions between pyramidal cells for network dynamics have been proposed, such as optimal noise level for efficient spike communication (Teramae et al. 2012) or faster response and higher stability of the network (Iyer et al. 2013).

In this study, we not only found log-normally distributed synaptic amplitudes for excitation between pyramidal cells, but also for interneuron excitation and pyramidal cell inhibition. These findings support the concept of log-normal processes being a general principle in the brain across different scales (Buzsáki and Mizuseki 2014).

Possible mechanisms underlying the emergence of few strong among many weak excitatory connections have been attributed to different types of neuronal plasticity (Zheng et al. 2013). We suggest that synaptic amplitudes between pyramidal cells and interneurons studied here are adjusted by specific activity-dependent plasticity mechanisms. This argument is further supported by our finding that amplitudes of reciprocal pairs, especially in the deep layers, are stronger than those of unidirectional connections (Supplementary Fig. 5C). Learning rules implementing activity-dependent plasticity have already been used to adjust synaptic weights for recurrent synapses between pyramidal cells and interneurons in a model for grid cell development (Widloski and Fiete 2014). Although it remains to be shown for the presubiculum, increasing evidence from other brain regions has demonstrated activity-dependent plasticity of PC–IN excitation (Alle et al. 2001; Lamsa et al. 2005) as well as IN–PC inhibition (Holmgren and Zilberter 2001; Lourenço et al. 2014).

The Feedback Inhibitory Microcircuit of the Superficial Layers Represents a New Model System to Elucidate Spatial Navigation Computation

Since communication between pyramidal cells in superficial layers of the presubiculum can only be achieved through interaction with interneurons, and since there is no layer-specific difference for grid cell activity in the presubiculum (Boccara et al. 2010), our findings indicate that grid cell activity can be established irrespective of the presence or absence of recurrent excitation. In this scenario, communication between pyramidal cells through interneurons becomes crucial for local computation. The overrepresented reciprocity and abundant PC > IN > PC connections found in our dataset support recent experimental and theoretical work pointing to recurrent inhibitory microcircuits as the major mechanism underlying grid cell activity (Couey et al. 2013; Pastoll et al. 2013; Solanka et al. 2015). Continuous attractor network models based on recurrent inhibition either assume an all-or-none inhibitory connectivity with an excitatory input (Couey et al. 2013) or incorporate interactions between excitatory and inhibitory neurons (Pastoll et al. 2013; Widloski and Fiete 2014; Solanka et al. 2015) although the latter is more applicable to experimentally determined synaptic connectivity such as revealed in our study (Shipston-Sharman et al. 2016).

Some models incorporating recurrent inhibition predict inhibitory cells to be spatially modulated (Pastoll et al. 2013). In accordance with this implication, FS interneurons of the presubiculum exhibit weak head direction tuning (Tukker et al. 2015) though grid firing activity of these presubicular interneurons has yet to be studied. In the MEC, grid-like firing fields of PV-positive interneurons have not been observed (Buetfering et al. 2014). However, extended models have suggested that interneurons in the presence of noise can have very low grid scores while still participating in grid cell generation (Solanka et al. 2015).

We believe that the superficial presubiculum provides an ideal experimental system to constrain future models and to develop a mechanistic understanding of grid cell generation. While the superficial presubiculum resembles the MEC by exhibiting distinct pyramidal cell populations differentiated by calbindin-expression and functional activity (Preston-Ferrer et al. 2016), it exhibits a simpler excitatory network topology. The MEC contains a more diverse population of excitatory cells differing in spatial activity, including the stellate cell and their corresponding subtypes (Sun et al. 2015; Fuchs et al. 2016). In addition, these excitatory neuronal types are interconnected in a cell type-specific manner (Fuchs et al. 2016) whereas the connectivity between pyramidal cells in the superficial presubiculum is essentially lacking.

Within the presubiculum, layer II has been proposed to be the principal source of grid activity (Preston-Ferrer et al. 2016) while grid fields in superficial layers of the MEC have been suggested to require organized feedforward projections (Tocker et al. 2015). Considering the unidirectional projections of the superficial presubiculum to the MEC (Kerr et al. 2007; Honda et al. 2008; Canto et al. 2012), it seems more likely that entorhinal grid activity is inherited from the presubiculum rather than vice versa.

Conclusion

We have shown that the presubiculum, as a region including head direction and grid cell activity, has distinct network structures in the superficial and deep layers. The relatively simple network topology in the superficial layers indicates that these spatially modulated activities can already be accomplished by a rather low intralaminar connectivity in combination with nonrandom features such as an overrepresentation of reciprocity and log-normal synaptic weight distributions. Due to the functional embedding of the superficial layers of the presubiculum, our results indicate that feedback inhibitory networks are sufficient for the local generation of grid activity, as suggested for the stellate cell-FS interneuron network in the MEC (Couey et al. 2013; Pastoll et al. 2013). In summary, we emphasize that the superficial presubiculum represents a suitable network to investigate the essential mechanisms required for grid cell generation and head direction cell tuning.

Supplementary Material

Supplementary data are available at Cerebral Cortex online.

Funding

Deutsche Forschungsgemeinschaft (Cluster of Excellence NeuroCure EXC 257, Research Unit Interneuron Synaptic Plasticity FOR 2143 and Research Training Groups GRK 1123 and GRK 1589).