Abstract
Social learning is fundamental to human interactions, yet its computational and physiological mechanisms are not well understood. One prominent open question concerns the role of neuromodulatory transmitters. We combined fMRI, computational modelling and genetics to address this question in two separate samples (N = 35, N = 47). Participants played a game requiring inference on an adviser’s intentions whose motivation to help or mislead changed over time. Our analyses suggest that hierarchically structured belief updates about current advice validity and the adviser’s trustworthiness, respectively, depend on different neuromodulatory systems. Low-level prediction errors (PEs) about advice accuracy not only activated regions known to support ‘theory of mind’, but also the dopaminergic midbrain. Furthermore, PE responses in ventral striatum were influenced by the Met/Val polymorphism of the Catechol-O-Methyltransferase (COMT) gene. By contrast, high-level PEs (‘expected uncertainty’) about the adviser’s fidelity activated the cholinergic septum. These findings, replicated in both samples, have important implications: They suggest that social learning rests on hierarchically related PEs encoded by midbrain and septum activity, respectively, in the same manner as other forms of learning under volatility. Furthermore, these hierarchical PEs may be broadcast by dopaminergic and cholinergic projections to induce plasticity specifically in cortical areas known to represent beliefs about others.
Keywords: hierarchical prediction errors, theory of mind, Bayesian inference, fMRI, dopamine, COMT
Introduction
As we navigate our complex social world, we interact with other agents whose motivations and intentions are not always easily discernible and may additionally fluctuate in time. Adapting our social behaviour flexibly requires ‘theory of mind’ (ToM), an ability to represent and infer on others’ mental states (Baron-Cohen et al., 1985; Frith and Frith, 2005). One influential idea concerning the implementation of ToM is that humans employ and continuously update models for simulating and predicting others’ behaviour (Yoshida et al., 2008; Behrens et al., 2009). While this idea has received empirical support (Behrens et al., 2008; Nicolle et al., 2012; Diaconescu et al., 2014), our understanding of how such models may be instantiated algorithmically and physiologically is far from complete.
In particular, major open questions concern the computational quantities involved in predicting others’ intentions and how they might be encoded by different neuromodulatory transmitter systems. Previous computational approaches to social learning have focused on prediction errors (PEs) in the context of reinforcement learning (Behrens et al., 2008; Jones et al., 2011; Lohrenz et al., 2013; Xiang et al., 2013; Christopoulos and King-Casas, 2015). These studies have shown that social PEs were not only represented in brain regions involved in reward learning—including the caudate (Klucharev et al., 2009; Biele et al., 2011) and orbitofrontal cortex (Campbell-Meiklejohn et al., 2010)—but also in regions associated with ToM processes, such as the superior temporal sulcus, temporal parietal junction (TPJ) and dorsomedial prefrontal cortex (PFC) (Behrens et al., 2009). Notably, these regions were particularly active in response to negative social PEs signalling social norm violations and misleading behaviour (Behrens et al., 2008). Social learning may thus partially draw on the same computational mechanisms as postulated for reward learning, i.e. PE-dependent value updates mediated by dopamine (DA). So far, however, there is limited experimental evidence beyond these computational neuroimaging studies that support a role of DA in social learning.
Other studies in animals and humans have implicated the cholinergic system in social cognition (Cara et al., 2007; de Chaumont et al., 2012), highlighting the role of the cholinergic basal forebrain (Ferreira et al., 2001, 2003) and one of its subregions, the septum (Biele et al., 2011), for social learning. This raises the possibility that DA and acetylcholine (ACh) may play distinct roles in social learning, for example, by encoding different types of prediction errors. A similar scenario was recently found for sensory associative learning where hierarchically related and precision-weighted PEs have been linked to dopaminergic and cholinergic signals (Iglesias et al., 2013). Whether a similar dichotomy exists for social learning has yet to be examined.
Here, we address this question using a Bayesian framework, the Hierarchical Gaussian Filter (HGF, Mathys et al., 2011, 2014), which was recently introduced to social learning paradigms (Diaconescu et al., 2014). This proposes that humans employ a hierarchical generative model to infer, from the observed behaviour of others, the mental states or beliefs, which cause these actions. While structurally similar to the model introduced by (Behrens et al., 2007), it is particularly suited for model-based fMRI analysis since it provides subject-specific estimates of PEs (and their precision-weighting) on each trial and each level of the model.
In this study, we investigated hierarchical precision-weighted PEs during social inference and their potential link to neuromodulatory systems by a combination of computational modelling, genetics and fMRI. We use a deception-free social learning task adapted from (Behrens et al., 2008) which requires inference on the changing intentions of an adviser (Diaconescu et al., 2014). Notably, using two samples of volunteers from separate studies (N = 35 and N = 47), we could verify the reproducibility of our results. In the following, we report those results which generalised across both studies.
Methods
Participants
Eighty-two healthy male adult volunteers between 19 and 30 years (mean age = 25 ± 3.4; all right-handed) participated in two separate studies. Both studies had approval by the Ethics Committee of the Canton of Zurich (KEK-ZH-Nr. 2010-0312/3 and KEK-ZH-Nr. 2012-0567). The second sample corresponded to the placebo group from a pharmacological study whose complete results will be reported elsewhere. Written informed consent was obtained from all participants.
Only men participated in the study to avoid potential influences of the menstrual cycle on neuromodulatory processes and synaptic plasticity (Fernandez et al., 2003; Dreher et al., 2007). All volunteers had normal or corrected-to-normal vision. Volunteers with a previous history of neurological or psychiatric diseases or drug abuse were excluded from participation. Furthermore, participants were excluded if they were taking medication or had consumed alcohol within 24 hours of participation in the study.
Selection of single nucleotide polymorphisms (SNPs)
Deoxyribonucleic acid (DNA) was collected from saliva samples using Isohelix swabs. SNP analyses were performed using the Fluidigm BioMark System (AROS, Aarhus, Denmark) and independently replicated using allelic discrimination assays (TaqMan SNP Genotyping Assays, Life Technologies). The genotyping PCR was carried out on a 7900HT Fast Real-Time PCR System (Applied Biosystems) and the resulting fluorescence data was analyzed with Sequence Detection Software (SDS) 2.3 (Applied Biosystems). The SNP selection was guided by the a priori hypothesis that social learning is modulated by tonic DA levels which may encode the precision of beliefs or predictions and serve to weight trial-wise prediction errors (Friston et al., 2012; Iglesias et al., 2013). We focused on two genes which play central roles for the synthesis and metabolism of DA, respectively: tyrosine hydroxylase (rs3842727), the rate-limiting enzyme for DA synthesis and Catechol-O-Methyltransferase or COMT (rs4680), a key enzyme for DA metabolism in prefrontal cortex, but also the ventral striatum (Matsumoto et al., 2003; Meyer-Lindenberg et al., 2005; Frank et al., 2007; Mier et al., 2010). The SNPs obtained were used in the random effects group analysis as covariates of interest.
Procedure
Stimuli
In a previous study (Diaconescu et al., 2014), we introduced an interactive economic game in which a pair of volunteers (randomly assigned to ‘player’ and ‘adviser’ roles) performed a probabilistic reinforcement learning task with monetary incentives (Figure 1). Players were informed about the odds of winning by a visual pie chart that indicated the winning probability of two available choice options. Advisers received additional information about the outcome, with a constant accuracy of 80%.
Fig. 1.
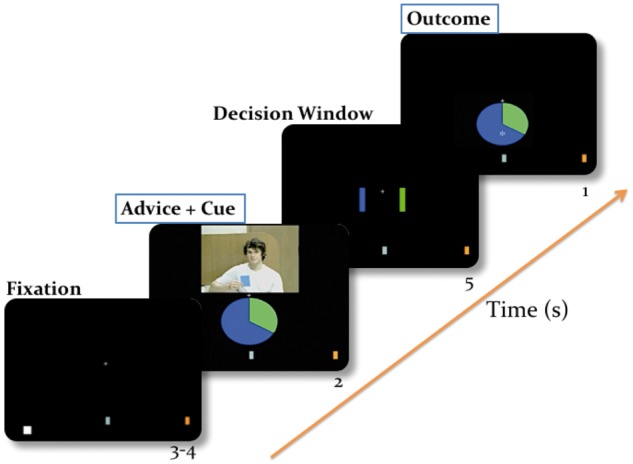
Binary lottery game: Eighty-two healthy male volunteers predicted one of 2 winning colors in a standard probabilistic reinforcement learning task and aimed to increase their score to maximize monetary reward. They were provided with information about the outcome probability (which changed in time) by a pie chart with a probability structure corresponding to a binary outcome. All the trials contained one of 6 visual cue types (75:25, 65:35, 55:45, 45:55, 35:65 and 25:75 blue: green pie charts) and the outcome (blue or green) was randomly drawn from the corresponding distributions. For every prediction they made, they also were given advice on which option to choose via pre-recorded videos. Critically, the pay-out for the adviser was structured such that his motivation to provide valid or misleading information varied across the game. The player therefore had to learn about the time-varying intentions of the adviser in order to decide whether to trust him or not.
The players’ goal was simple: they had to maximize their final payout by making correct predictions on as many trials as possible. By contrast, the advisers’ incentive structure to help or mislead the player was designed to include periods of both cooperation and competition. Specifically, the payment of the advisers depended on whether the players’ cumulative score would, at the end of the game, lie within predefined ‘silver’ or ‘gold’ ranges (see Supplementary Figure 1a and b). Depending on the player’s current performance, advisers would therefore variably offer helpful or misleading suggestions about the most likely outcome. The players did not know these details but were generally informed that the advisers had a distinct incentive structure, and to achieve their goals, their intention to provide helpful suggestions might change over the course of the task. Further details about this paradigm can be found in Diaconescu et al. (2014).
We received informed consent from all volunteers in this initial study to record and use the advice-giving videos in subsequent fMRI studies. Based on the predominant strategy employed by the advisers (Diaconescu et al., 2014), three of the recorded full-length videos were edited into 2-s video clips of advice giving. All the videos were selected from trials in which the advisers truly intended to provide helpful or misleading advice, which was determined by debriefing after the experiment. All video clips were matched in terms of their luminance, contrast and colour balance using the video software Adobe Photoshop Premiere CS6.
In this study, one of the three chosen advisers was randomly assigned to each participant. No differences in performance and degree of reliance on the advice were observed between the three adviser types.
Experimental design
To predict the outcome of the lottery, participants could rely on the visual pie chart, the social advice or integrate these social and non-social sources of information. While the predictive strength of the non-social cue was provided explicitly on every trial, participants were required to learn about volatility, i.e. the changing nature of the adviser’s intentions, in order to judge whether and how to exploit the advice.
In total, the task consisted of 189 trials, which contained 6 visual cue types (75:25, 65:35, 55:45, 45:55, 35:65 and 25:75% blue: % green pie charts). Participants indicated their predictions during a 6-s decision phase, which immediately followed the presentation of advice and visual cue. Participants received visual feedback after the decision phase. For every correct prediction, the participant’s score increased by one point; for every missed trial or incorrect prediction, the score decreased by one point. The participant’s final payment was proportional to his total score, plus a potential bonus (additive), if the cumulative score reached his silver or gold targets (see Figure 1). The assignment of the blue or green colours to the button presses (left or right) was counterbalanced across participants.
The task was programmed and presented using Cogent 2000 (Wellcome Laboratory of Neurology, University College London, London, UK) under Matlab (Mathworks). At the end of the study, all participants were debriefed about the task and were asked about the strategy they had employed during the game.
The same experimental paradigm was used in two separate fMRI studies with different groups of volunteers (N = 35 and N = 47, respectively). The second sample corresponded to a group of participants from a pharmacological study who received placebo. Otherwise, the experimental procedure differed only in terms of the stimulus input structure (see Supplementary Figure 1c for details). In the second fMRI study, we optimized the trial sequence by simulations seeking to maximize parameter identifiability.
Data acquisition
In the first fMRI study, images were acquired using a Philips Achieva 3T whole-body scanner with an 8-channel SENSE head coil (Philips Medical Systems, Best, The Netherlands) at the Laboratory for Social and Neural Systems Research, Dept. of Economics, University of Zurich.
We acquired gradient echo T2*-weighted echo-planar images (EPIs) with blood-oxygen-level dependent (BOLD) contrast (slices/volume = 37; repetition time = 2.5 s; voxel size = 2 × 2 × 3 mm3; interslice gap = 0.6 mm; field of view (FOV) = 192 ×192 × 180 mm; echo time (TE) = 36 ms; flip angle = 90°). Oblique-transverse slices with +15° right-left angulation were acquired. The experimental task was run in two sessions with 740 and 580 volumes in the first and the second session, respectively, together with five discarded volumes at the start of each scanning session to ensure T1 effects were at equilibrium. A high-resolution inversion-recovery T1-weighted 3D-TFE (turbo field echo) structural image was also acquired for each participant (301 slices; voxel size = 1.1 × 1.1 × 0.6 mm3; FOV = 250 mm; TE = 3.4 ms).
In the second fMRI study, images were recorded using a Philips Ingenia 3T whole-body scanner with a 32-channel SENSE head coil (Philips Medical Systems, Best, The Netherlands) at the Institute for Biomedical Engineering, University of Zurich and ETH Zurich. The sequence and acquisition parameters were identical to the previous study with the exception of 33 slices/volume acquired in the EPIs.
In both studies, stimuli were projected onto a display, which participants viewed through a mirror fitted on top of the head coil (NordicNeuroLab LCD MR-compatible 32-inch monitor). Participants’ heart rate and respiration was recorded during scanning with a 4-electrode electrocardiogram (ECG) and a breathing belt.
Data pre-processing and analysis
FMRI data were preprocessed and analyzed using the SPM12 software package version 6225 (Wellcome Trust Centre for Neuroimaging, London, UK; http://www.fil.ion.ucl.ac.uk/spm).
The functional images were realigned, unwarped and coregistered to the participant’s own structural scan. The structural image was processed using a unified segmentation procedure combining segmentation, bias correction and spatial normalization (Ashburner and Friston, 2005); the same normalization parameters were then used to normalize the EPI images. Finally, EPI images were smoothed with a Gaussian kernel of 6 mm full-width half-maximum.
Correction for physiological noise was performed with the PhysIO toolbox (Kasper et al., 2016) using Fourier expansions of different order for the estimated phases of cardiac pulsation (3rd order), respiration (4th order) and cardio-respiratory interactions (1st order). This toolbox is part of the open source software package TAPAS (http://www.translationalneuromodeling.org/tapas).
Computational modelling framework
In our previous behavioural study using the interactive version of the social learning task with real human advisers (Diaconescu et al., 2014), we conducted a systematic comparison of alternative models, which might explain the observed behaviour. Here, we repeat this analysis for the adapted version of the paradigm with videotaped advice, as described above.
The computational framework adopted in this study is guided by Bayesian theories of brain function, which suggest that the brain maintains and continuously updates a model of the environment and uses this model to infer the causes of its sensory inputs (Dayan et al., 1995; Friston, 2005, 2010; Rao and Ballard, 1999; Bastos et al., 2012). A basic feature of our modelling approach is the division into perceptual and response models (for details, see Daunizeau et al., 2010). In other words, participants are thought to update their beliefs about states of the external world based on the sensory inputs they receive (perceptual model) and use these beliefs to make decisions (response model).
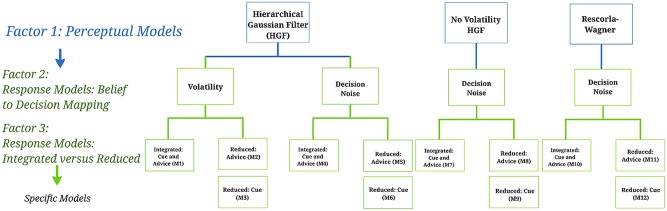
Our model space was structured hierarchically as is shown in Figure 2. With regard to the perceptual model, we operated under the general assumption that participants employ a generative model of their sensory inputs (Daunizeau et al., 2010; Mathys et al., 2011) in order to infer on the advice validity and the intentions of the adviser. Different hypotheses about the exact way in which participants learned from advice and integrated social and non-social sources of information were formalised in a series of models, as described in the next section. The main question was whether the participants’ model of the adviser’s intentions had a hierarchical structure and was capable of taking into account potential changes in the adviser's strategy into its predictions about advice reliability. We thus compared a hierarchical Bayesian model, the HGF (Mathys et al., 2011, 2014) () to a non-hierarchical Rescorla-Wagner (RW) reinforcement learning model (Rescorla and Wagner, 1972) () and a non-hierarchical version of the HGF () (Diaconescu et al., 2014).
Fig. 2.
Hierarchical structure of the model space: perceptual models, response models, specific models: The models considered in this study have a 3 x 2 x 2 factorial structure. The specific models at the bottom represent individual models of social learning in which both social and non-social sources of information are considered. The nodes at the highest level represent the perceptual model families (three-level HGF, reduced two-level HGF and RW). Two response models were formalized under the HGF model: decision noise in the mapping of beliefs to decisions either (1) depended dynamically on the estimated volatility of the adviser’s intentions (‘Volatility’ model) or (2) was a free parameter over trials (‘Decision noise’ model). At the second level, the response model parameters can be divided further according to the weighing of social and non-social information—these models assume that participants’ beliefs are based on (1) both cue and advice information and (2) advice, or (3) cue probabilities (pie chart) only. [reprinted from Diaconescu et al., 2014].
With regard to the response models, we examined whether participants based their decisions on (i) the integration of advice and cue probabilities (the ‘Integrated’ model family for models ), (ii) the advice accuracy only (‘Reduced: advice’ model family for models ) or (iii) the visually-cued probability only (‘Reduced: cue’ model family for models ). As in our previous study (Diaconescu et al., 2014), we also considered two different mechanisms of how beliefs were transformed into responses. First, participants’ decisions might be perturbed by (fixed) decision noise (‘Decision noise’ model family for models ). Alternatively, participants’ decision noise might vary trial-by-trial with the estimated volatility of the adviser’s intentions (‘Volatility’ model family for models ). In other words, the more volatile an adviser is perceived, the less a participant might rely on his current belief about advice validity for making a decision and hence the less deterministic his belief-to-response mapping.
Perceptual model: HGF
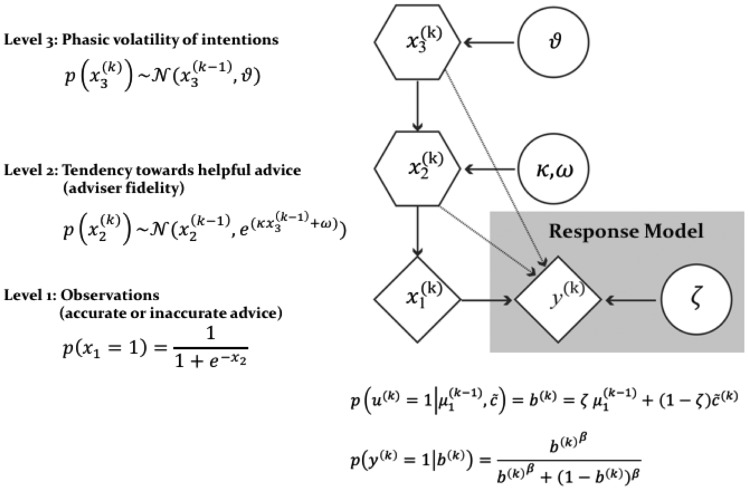
The HGF is a hierarchical model of perception and learning, which allows for inference on an agent’s belief and uncertainty about the state of the world from observed behaviour (see Mathys et al., 2011 for theoretical background and Diaconescu et al., 2014 for a recent application to social learning). Its generic nature has enabled a series of recent behavioural and neuroimaging studies on different forms of learning and decision-making (Iglesias et al., 2013; Diaconescu et al., 2014; Hauser et al., 2014; Schwartenbeck et al., 2014; Vossel et al., 2014a,b; Vossel et al., 2015). According to this model, an agent continuously revises a generative (predictive) model of its sensory inputs, which allows for inference on hidden environmental states that are hierarchically organized and cause the sensory inputs the agent experiences on each trial k. In the HGF, these states evolve in time as Gaussian random walks where, at any given level, the step size is controlled by the state of the next-higher level (Mathys et al., 2011, 2014).
In the specific case of our social learning paradigm, represents a categorical variable or the advice accuracy. Any single piece of advice is either accurate or inaccurate . All states higher than are continuous. State represents the adviser’s fidelity in logit space. The highest state represents the rate at which the advisers’ intentions change; this determines the log-volatility of adviser fidelity (log variance of the step size of ). The exact equations describing these relations and the overall generative model are summarised by Figure 3; a detailed description can be found in Diaconescu et al. (2014).
Fig. 3.
Graphical representation of the HGF and the response model. In this graphical notation, circles represent constants and diamonds represent quantities that change in time (i.e., that carry a time/trial index). Hexagons, like diamonds, represent quantities which change in time, but additionally depend on the previous state in time in a Markovian fashion. x1 represents the accuracy of the current piece of advice, x2 the adviser’s fidelity or tendency to give helpful advice and x3 the current volatility of the adviser’s intentions. Parameter κ determines how strongly x2 and x3 are coupled, ω determines the tonic volatility component and ϑ represents the volatility of x3. The response model has 2 layers: (1) the computation of the integrated belief or p(outcome|advice, cued probability), i.e., the probability of the outcome given both the non-social cue and the advice; (2) the chosen action, drawn from the integrated belief using a sigmoid decision rule. Parameter ζ determines the weight of the advice compared to the non-social cue. y represents the subject’s binary response (y = 1: deciding to accept the advice, y = 0: going against the advice).
Three subject-specific parameters determine how the above states evolve in time as a function of the inputs (including the visual pie chart, advice, trial outcome) and influence each other. Firstly, determines the coupling between the second and third level in the hierarchy, capturing the degree to which a subject utilises his estimate of the adviser’s changing intentions to infer on his current fidelity. Secondly, represents a constant (baseline) component of the log-volatility of . It captures the subject-specific magnitude of the belief update about the adviser’s fidelity that is independent of . Thirdly, (meta-volatility) determines the evolution of or how rapidly the volatility of the adviser’s intentions changes in time.
A key idea of the HGF framework is that agents ‘invert’ the generative model in Figure 3 (i.e., they update their beliefs about the hierarchically coupled states in the external word) by employing an efficient variational approximation to ideal Bayesian inference (see Mathys et al., 2011 for details). The update rules that emerge from this approximation have a simple and interpretable form with structural similarity to classical reinforcement learning models but with an adaptive learning rate determined by the next higher level in the hierarchy. Specifically, at each hierarchical level i, updates of beliefs (posterior means ) on each trial k are proportional to precision-weighted PEs, (Equation 1). In essence, the belief adjustment is the product of the PE from the level below , weighted by a precision ratio :
| (1) |
where
| (2) |
Here, and represent estimates of the precision of the prediction about input from the level below (i.e., precision of the data) and of the belief at the current level, respectively. What follows from this expression is that PEs are given a larger weight (and thus updates are more pronounced) when the precision of the data (input from the lower level) is high relative to the precision of the prior belief.
The low-level (advice validity) PE or , which updates estimates about the adviser fidelity or , represents a magnitude error:
| (3) |
with
| (4) |
| (5) |
By contrast, the high-level PE, which serves to update estimates about the volatility of the adviser’s intentions or , represents a probability PE (in logit space).
| (6) |
with
| (7) |
| (8) |
with the weighting factors defined as:
| (9) |
| (10) |
Equation 7 shows , the unweighted high-level PE. The denominator of this ratio contains the predicted uncertainty about the adviser fidelity based on the previous trial, whereas the numerator contains the observed uncertainty. Thus, whenever the observed uncertainty exceeds the predicted, the fraction is greater than one and the high-level PE becomes positive. Conversely, when the observed uncertainty is less than the predicted, the PE is negative.
In other words, represents a PE about the certainty of the estimate of adviser fidelity. This renders it conceptually similar (but not identical) to "expected uncertainty" (Yu and Dayan, 2005), which had been operationalised as the difference between an estimate of cue validity and certainty (compare the Supplementary Material in Iglesias et al., 2013).
Response models
The response model embodies a (probabilistic) mapping from the agent’s beliefs to decisions (Daunizeau et al., 2010). As participants had access to both social and non-social information, our first response model assumed that participants integrated the social and non-social sources of information in order to predict the accuracy of the advice. Specifically, using as the weight the player assigns to the social information, the integrated belief that the advice on trial k is accurate is:
| (11) |
Here, serves to balance , the participant’s current belief that the adviser will give valid advice, against , the probability (as signaled by the visual pie chart) of the recommended advice being correct. For example, let us consider the scenario when the adviser recommends the participant to pick ‘blue’. According to our formalism, if the inferred probability of advice accuracy is 80% ( = 0.80) and the pie chart indicates that blue is 25% likely (= 0.25), a participant who weights the two sources of information equally ( = 0.5) would predict that the probability that the outcome is blue is 55%. Two additional response models were created by reducing this model, either assuming that participants only relied on the advice during decision-making (i.e., setting ) or that they only took into account the cued probability (i.e., ).
The probability that the participant follows his integrated belief, and thus the advice (to a degree specified by ), was described by a sigmoid function; here, responses are coded as when going with the advice, as opposed to when going against it):
| (12) |
where represents the inverse of the decision temperature: as , the sigmoid function approaches a step function with a unit step at (i.e., no decision noise). As described above, we considered two alternatives regarding how this belief-to-response mapping might be structured: One option is the presence of constant decision noise; here, becomes a subject-specific free parameter. Alternatively, the decision temperature parameter might vary with the estimate of adviser volatility, . In other words, this model assumed that the more volatile an adviser was perceived, the less deterministic the player’s belief-to-response mapping.
Using the same set of priors for the model parameters as in our previous study (Supplementary Table 1), maximum-a-posteriori (MAP) estimates of model parameters were obtained using the HGF toolbox version 3.0. This MATLAB-based toolbox is freely available as part of the open source software package TAPAS at http://www.translationalneuromodeling.org/tapas.
Bayesian model selection and family inference
Using Bayesian model selection (BMS), we inferred on the model subjects most likely used to predict the outcome. For a single subject, this involves computing a free-energy approximation to the model evidence , the probability of the data y given a model m (Friston et al., 2007; Daunizeau et al., 2010a). We used random effects inference to compare candidate models at the group level. This relies on a hierarchical scheme, which accounts for the possibility that the behaviour of different participants is governed by different models (Stephan et al., 2009; Rigoux et al., 2014). This results in a posterior probability for each model, given the group data; alternatively, the relative goodness of models can be expressed in terms of so-called "exceedance probabilities". The exceedance probability of a model is the probability that this model has a higher posterior probability than any other model (in the set of models considered) (Stephan et al., 2009). One can also derive a ‘protected’ exceedance probability, which protects against the possibility that any difference between models might have arisen by chance (Rigoux et al., 2014).
Given the structure of our model space, we also used family-level inference (Penny et al., 2010) to determine (i) the most likely type of perceptual model, pooling across all response models and (ii) the most likely response model type, pooling across all perceptual models (see Diaconescu et al., 2014 for more details of this application in the context of social learning).
Model-based fMRI analysis
The fMRI data were modelled voxel-wise, including the subject-specific trajectories of computational quantities from the winning model in a general linear model (GLM). Computational variables of interest were used as parametric modulators of regressors encoding trial components, as described below. We did not orthogonalise the parametric modulators.
At the lowest level in hierarchy, we examined the precision-weighted PE about advice validity ( in Equation 3), which serves to update estimates of the adviser’s fidelity. We focused on the signed advice PE following the analysis approach by (Behrens et al., 2008), because we wanted to contrast trials, in which the adviser was more helpful than predicted (positive PEs) to those in which he was more misleading (negative PEs). While the former constitutes positive social feedback (as in Biele et al., 2011), the latter signals a potential shift in the adviser’s strategy or intentions and a possible need for behavioural adaptation by the subject.
At the highest level in the hierarchy, we examined the precision-weighted PE about adviser fidelity (i.e., advice-outcome contingency in logit space), in Equation 6. This PE represents a teaching signal for updating the estimate about the (log) volatility of the adviser’s intentions; again, we used the signed PE as a regressor. The corresponding parametric modulators in the GLM were modelled as events that were time-locked to the display of trial outcome.
To also address the question whether individuals who weighted the social advice more exhibited a stronger activation of ‘theory of mind’ regions in trials when they followed the advice compared to trials, in which they decided against the advice, we expanded the regression model at the single-subject level. Thus, we also modelled the decision phase (time-locked to the presentation of the advice) using the inferred adviser fidelity or (Equation 1) as a parametric modulator.
To summarize, the following regressors (plus their temporal and dispersion derivatives) were included in the model:
Cue & advice: phases when both the binary lottery and the social advice were presented onscreen;
Cue & advice x adviser fidelity: advice presentation phase, modulated by the predicted adviser fidelity on each trial;
Outcome: phases when the outcome of the trial was presented onscreen;
Outcome x low-level PE: monitor phase, modulated by the precision-weighted advice PE on each trial;
Outcome x high-level PE: monitor phase, modulated by the precision-weighted volatility PE on each trial.
Finally, 18 physiological noise regressors computed using the PhysIO toolbox (Kasper et al., 2016) and 6 motion parameter vectors from the realignment procedure were included as regressors of no interest to account for BOLD signal variance induced by physiological noise (cardiac pulsation and respiration) and head motion, respectively.
Random effects group analysis across all 82 participants was performed using the standard summary statistics approach in GLM analyses of fMRI data (Penny and Holmes, 2007). We used one-sample t tests to separately examine positive and negative BOLD responses for the learning trajectories of interest. To examine individual differences in the representation of hierarchical PEs as a function of tonic DA levels, we used the tyrosine hydroxylase and COMT polymorphism labels as covariate variables of interest.
For all analyses, we report any BOLD responses that survived whole-brain family-wise error (FWE) correction, either at the peak-level (P < 0.05) or at the cluster level, based on Gaussian random field (GRF) theory (P < 0.05) with P < 0.001 voxel-level cut-off (Friston, 2007). The coordinates of all brain regions were expressed in Montreal Neurological Institute (MNI) space; anatomical designations for local maxima were obtained by visual inspection and additionally verified using the MNI AAL atlas (Maldjian et al., 2003).
In addition to whole-brain analyses, we performed region-of-interest (ROI) analyses based on an anatomical mask of the dopaminergic midbrain, which included the substantia nigra (SN) and the ventral tegmental area (VTA). The mask was created using an anatomical atlas based on magnetization transfer weighted structural MR images (see Bunzeck and Düzel, 2006) (see Supplementary Figure 5a). Additionally, given that septal activity had previously been implicated in high-level precision-weighted PEs (Iglesias et al., 2013) and social learning (Biele et al., 2011), we created a mask comprising both the medial and lateral regions of the septum. A basal forebrain mask was created using the anatomical toolbox in SPM12 (http://www.fil.ion.ucl.ac.uk/spm) and defined using the maximum probability map from a probabilistic cytoarchitectonic atlas warped into MNI space (see Eickhoff et al., 2005; Zaborszky et al., 2008). This map included the different compartments of the basal forebrain with cholinergic neurons (septum, the diagonal band of Broca and subpallidal regions including the basal nucleus of Meynert; see Supplementary Figure 5b). FWE correction for multiple comparisons was performed for the entire ROI resulting from combining both anatomical masks from midbrain and septum.
Results
In the two studies, two separate groups of healthy volunteers (N = 82 in total) inferred on the trustworthiness of an adviser in order to accumulate points in a probabilistic task with monetary incentives. Because the adviser’s intentions varied as a function of his (hidden) strategy, optimal performance required learning about the advice validity as well as the adviser’s changing intentions.
Performance accuracy averaged at 68 ± 4% (mean ± standard deviation) in study 1 and 67 ± 2% in study 2, indicating that participants reached the silver target and received on average a CHF 10 bonus at the end of the studies. Furthermore, we found that the risk associated with the binary lottery influenced participants’ decisions: Participants relied significantly more on the advice for the 55:45 cue options compared to the 75:25 option (t(34) = 22.38, P < 0.05 in study 1, t(46) = 10.62, P < 0.05 in study 2). Notably, the impact of the cue probabilities on decisions was lower in study 2 compared to study 1, because participants relied more on the social advice in the second study. Since individual choices not only depended on cue probabilities, but also on the inferred adviser’s fidelity, we performed further model-based analysis of choice behaviour.
Model comparison and posterior parameter estimates
Our first step in the analysis comprised model comparison, using random effects Bayesian model selection (BMS) to evaluate the balance between fit and complexity of all models shown in Figure 2. When considering all models individually and separately for each study, the three-level HGF with the ‘Integrated’ response model ( outperformed the rest of the models in each participant (Tables 1a and 2a). When adopting a family-level perspective, the three-level HGF family (outperformed non-hierarchical models (), such as the reduced HGF (no volatility) and the RW models (Tables 1b and 2b). Concerning the response models, the family of response models assuming that participants integrate both social and non-social sources of information (i.e., ) best explained participants’ choices (Tables 1c and 2c). Notably, all of these model selection results replicated the findings from our previous study (Diaconescu et al., 2014), which used a different group of subjects and a fully interactive paradigm with real human advisers. Furthermore, all BMS results were reproduced across both fMRI studies (see Tables 1 and 2).
Table 1A.
Results of Bayesian model selection (fMRI Study 1): model protected exceedance probabilities (xp).
| HGF | No volatility HGF | RW | |
|---|---|---|---|
| Cue and Advice | 0.9226 | 0.012 | 0.0576 |
| Advice | 0.0052 | 0.0023 | 0.0003 |
| Cue | 0 | 0 | 0 |
Table 2A.
Results of Bayesian model selection (fMRI Study 2): Model protected exceedance probabilities (xp)
| HGF | No volatility HGF | RW | |
|---|---|---|---|
| Cue and advice | 0.9361 | 0.0001 | 0.0002 |
| Advice | 0.0609 | 0 | 0 |
| Cue | 0 | 0 | 0 |
Table 1B.
Family-level inference (fMRI Study 1: perceptual model set): posterior model probability or p(r|y) and model exceedance probabilities (xp)
| HGF with volatility | No volatility HGF | Rescorla-Wagner | |
|---|---|---|---|
| p(r|y) | 0.548 | 0.2331 | 0.2189 |
| xp | 0.9398 | 0.0364 | 0.0238 |
Table 2B.
Family-level inference (fMRI Study 2: perceptual model set): posterior model probability or p(r|y) and model exceedance probabilities (xp)
| HGF with Volatility | No Volatility HGF | Rescorla-Wagner | |
|---|---|---|---|
| p(r|y) | 0.8818 | 0.0299 | 0.0883 |
| xp | 1 | 0 | 0 |
Table 1C.
Family-level inference (fMRI Study 1: family model set): Posterior model probability or p(r|y) and model exceedance probabilities (xp)
| Integrated | Reduced: advice | Reduced: cue | |
|---|---|---|---|
| p(r|y) | 0.94 | 0.0533 | 0.0067 |
| xp | 1 | 0 | 0 |
Table 2C.
Family-level inference (fMRI Study 1: family model set): posterior model probability or p(r|y) and model exceedance probabilities (xp)
| Integrated | Reduced: advice | Reduced: cue | |
|---|---|---|---|
| p(r|y) | 0.8482 | 0.15 | 0.0018 |
| xp | 1 | 0 | 0 |
Additionally, we used multiple regression to evaluate how well our model explained participants’ performance (percentage of correct responses). As in our previous study (Diaconescu et al., 2014), we found that the MAP estimates extracted from the winning model (), i.e., , and , jointly predicted participants’ performance accuracy across both fMRI studies (R2 = 28.36%, F = 4.09, P < 0.018 in fMRI study 1 and R2 = 39%, F = 2.53, P < 0.02 in fMRI study 2; see Tables 1d and 2d for average MAP estimates). Post hoc tests suggested that the explanatory power could be chiefly attributed to the social weighting parameter , a result which held across both studies: (R2 = 17.67%, F = 7.08, P < 0.01 in fMRI study 1 and R2 = 15%, F = 7.72, P < 0.01 in fMRI study 2). The positive slope of the associated regression coefficient indicated that participants who weighted the advice more than the non-social cue during decision-making performed better on the task.
Table 1D.
Average MAP estimates of the learning and decision-making parameters of the winning model
| Model | Mean | SD |
|---|---|---|
| HGF () | ||
| κ | 0.41 | 0.09 |
| ω | −1.47 | 1.13 |
| ϑ | 0.38 | 0.11 |
| 0.40 | 0.10 |
Table 2D.
Average MAP estimates of the learning and decision-making parameters of the winning model
| Model | Mean | SD |
|---|---|---|
| HGF () | ||
| κ | 0.52 | 0.15 |
| ω | −2.80 | 2.44 |
| ϑ | 0.43 | 0.13 |
| 0.45 | 0.22 |
FMRI analysis of hierarchical PEs
Our fMRI analysis focused on the neural representation of precision-weighted PEs across the hierarchical levels of the HGF. For each computational quantity of interest, our model-based fMRI analysis proceeded in four steps: first, we performed whole-brain analyses separately in two independent samples of N = 35 and N = 47 volunteers; second, we focused on our anatomically defined regions of interest (ROIs) using a combined mask of dopaminergic and cholinergic nuclei (midbrain and basal forebrain; see Methods); third, we examined how PE representations varied as a function of COMT polymorphisms. Following the procedure of a recent study (Iglesias et al., 2013), we adopted a very conservative approach to assess the reproducibility of the PE effects across the two fMRI studies. That is, we used a voxel-wise ‘logical AND’ conjunction (Nichols et al., 2005) on the FWE-thresholded activation maps from both fMRI studies. In the following, we focus on those activations for which this procedure showed an overlap of significant activations in both fMRI studies.
Low-level precision-weighted prediction errors
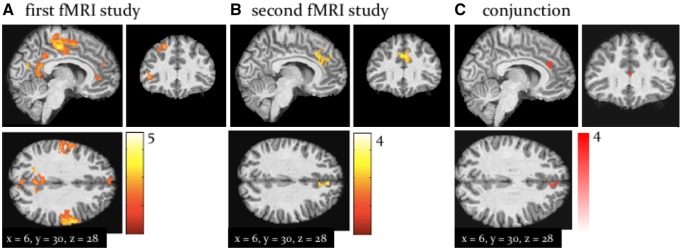
By fitting computational trajectories to participants’ fMRI data, we found that across both fMRI studies (the signed precision-weighted PE about advice validity) was represented in the left caudate, right anterior cingulate cortex (ACC), left middle cingulate cortex, the bilateral anterior insula and the right dorsomedial and dorsolateral PFC (whole-brain, peak-level FWE corrected P < 0.05; Figure 4; Table 3). Activity in these regions scaled with the magnitude of negative PEs; that is, these regions were more active on trials when the other agent was more misleading than predicted, signalling increased perspective-taking demands and the need to update one’s model of the other agent.
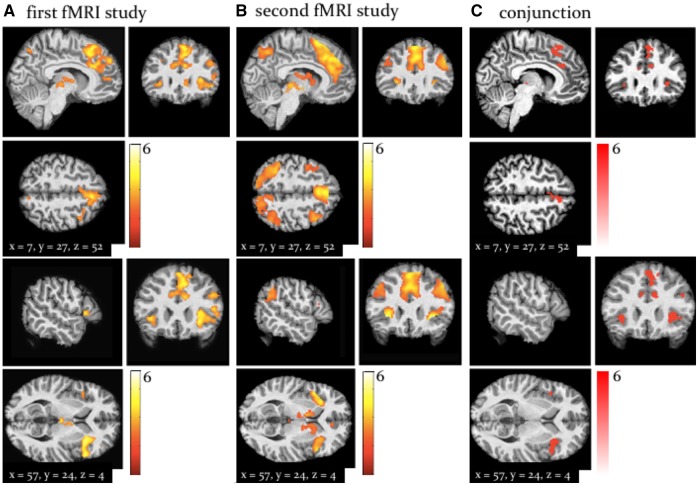
Fig. 4.
Whole-brain activation by Activations by signed precision-weighted prediction error about the adviser fidelity in the first fMRI study (A) and the second fMRI study (B). Both activation maps are shown at a threshold of P < 0.05, FWE corrected for multiple comparisons across the whole brain. To highlight replication across studies, panel C shows the results of a ‘logical AND’ conjunction, illustrating voxels that were significantly activated in both studies.
Table 3.
Low-level precision-weighted PEs about advice validity (and adviser fidelity)
| fMRI study 1: epsilon 2 | |||||
|---|---|---|---|---|---|
| Hemisphere | x | y | z | t score | |
| Ventral tegmental area/substantia nigra | R | 12 | −18 | −11 | 2.91 |
| Anterior cingulate cortex | R | 4 | 36 | 30 | 4.45 |
| Dorsomedial PFC | L | −8 | 26 | 54 | 3.48 |
| Insula | R | 34 | 18 | −2 | 6.65 |
| Insula | L | −30 | 27 | 0 | 3.78 |
| Superior frontal cortex | L | −21 | 38 | 33 | 4.53 |
| Dorsolateral PFC | L | −38 | 21 | 8 | 4.82 |
| Dorsolateral PFC | R | 44 | 15 | 7 | 6.1 |
| fMRI study 2: epsilon 2 | |||||
| Ventral tegmental area/substantia nigra | R | 4 | −16 | −10 | 5.84 |
| Ventral tegmental area/substantia nigra | L | −2 | −20 | −16 | 4.75 |
| TPJ | L | −34 | −46 | 42 | 8.93 |
| TPJ | R | 52 | −50 | 30 | 8.93 |
| Caudate | L | −8 | 2 | 10 | 5.86 |
| Anterior cingulate cortex | R | 2 | 22 | 28 | 5.45 |
| Middle temporal cortex | L | −44 | −32 | −8 | 4.42 |
| Superior temporal cortex | L | −40 | −40 | 2 | 3.34 |
| Insula | R | 32 | 20 | −4 | 10.31 |
| Insula | L | −32 | 18 | −4 | 8.94 |
| Dorsomedial PFC | L | 0 | 26 | 54 | 7.27 |
| Dorsomedial PFC | R | 4 | 26 | 60 | 7.88 |
| Dorsolateral PFC | R | 48 | 18 | 4 | 6.28 |
| Conjunction: epsilon 2 | |||||
| Ventral tegmental area/substantia nigra | R | 9 | −15 | −9 | 3.81 |
| Caudate | L | −8 | 4 | 9 | 2.74 |
| Anterior cingulate cortex | R | 8 | 32 | 27 | 4.24 |
| Insula | R | 36 | 20 | −2 | 6 |
| Insula | L | −38 | 18 | −5 | 4.77 |
| Middle frontal cortex | R | 33 | 12 | 49 | 3.2 |
| Dorsomedial PFC | R | 6 | 29 | 54 | 4.2 |
| Dorsolateral PFC | R | 42 | 16 | 7 | 4.46 |
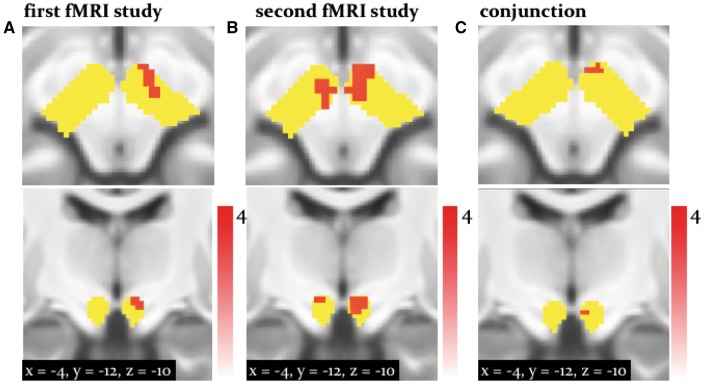
One particularly notable finding in this context was a significant activation of the midbrain (ventral tegmental area, VTA/substantia nigra, SN) by PEs signalling misleading advice (negative ). In the second study, this activation was even more pronounced and also survived whole-brain cluster-level correction (P < 0.05; Figure 5; Table 3).
Fig. 5.
Activation by (midbrain): Activation of the dopaminergic VTA/SN associated with the signed precision-weighted prediction error about the adviser fidelity. This activation is shown at P < 0.05 FWE corrected for the volume of our anatomical mask comprising both dopaminergic and cholinergic nuclei (yellow). (A) results from the first fMRI study. (B) Second fMRI study. (C) The results of a ‘logical AND’ conjunction, illustrating voxels that were significantly activated in both studies.
In the second study, we also observed activations by negative advice PEs in the bilateral TPJ and right middle and superior temporal cortices (peak-level corrected, P < 0.05; Figure 4; Table 3).
In both studies, the left precuneus signalled positive PEs in response to trials when the adviser was more helpful than predicted. In the first study, however, both the left anterior TPJ and the fusiform gyrus showed positive PE effects (whole-brain, cluster-level FWE corrected p < 0.05; Supplementary Figure 2; Supplementary Table 2).
High-level precision-weighted prediction errors
At the highest level in the hierarchy, we found that or the signed precision-weighted PE about the adviser’s strategy (which drives updates to beliefs about the volatility of the adviser’s intentions) correlated positively with activity in the right dorsal middle cingulate cortex peaking at [7, −12, 42] in the first study (Figure 6A). Furthermore, in the second study, the effect of high-level PE was localized to the right dorsal anterior cingulate cortex (ACC) with a group-level peak at [6, 30, 28] (whole-brain cluster-level FWE corrected p < 0.05; Figure 6B;Table 4).
Fig. 6.
Whole-brain activation by Activations by signed precision-weighted PE about the adviser’s strategy in the first (A) and the second fMRI study (B). Both activation maps are shown at a cluster-level threshold of P < 0.05 (k = 100), FWE corrected for multiple comparisons across the whole brain. To highlight replication across studies, (C) shows the results of a ‘logical AND’ conjunction, illustrating voxels that were activated in both studies at P < 0.001 uncorrected.
Table 4.
High-level precision-weighted PEs about adviser volatility
| Hemisphere | x | y | z | t score | |
|---|---|---|---|---|---|
| fMRI study 1: epsilon 3 | |||||
| Septum | L | −5 | 8 | −7 | 4.11 |
| Dorsal middle cingulate cortex | R | 7 | −12 | 42 | 4.78 |
| fMRI study 2: epsilon 3 | |||||
| Septum | L | −5 | 12 | −7 | 3.43 |
| Dorsal anterior cingulate cortex | R | 6 | 30 | 28 | 4.58 |
| Conjunction: epsilon 3 | |||||
| Septum | L | −5 | 12 | −7 | 2.9 |
| Dorsal anterior cingulate cortex | R | 6 | 30 | 28 | 2.39 |
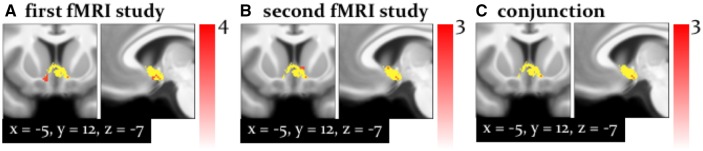
Additionally, in both studies, the right middle cingulate sulcus, parietal regions, such as the right paracentral lobule correlated negatively with this high-level PE (whole-brain, cluster-level FWE corrected P < 0.05; Supplementary Figure 3). Finally, and perhaps most remarkably, both studies showed a positive correlation of the high-level precision-weighted PE with activity in the left septum (P < 0.05 FWE corrected for the entire mask volume, Figure 7), a subregion of the cholinergic basal forebrain.
Fig. 7.
Activation by (septum): Activation of the cholinergic septum associated with the signed precision-weighted prediction error about the adviser’s strategy. This activation is shown at P < 0.05 FWE corrected for the volume of our anatomical mask comprising both dopaminergic and cholinergic nuclei (yellow). (A) Results from the first fMRI study. (B) Second fMRI study. (C) The results of a ‘logical AND’ conjunction, illustrating voxels that were significantly activated in both studies.
Genetic factors for individual variability in social learning
To elucidate the influence of DA on learning from advice, we examined how hierarchical PE representations varied as a function of SNPs of genes encoding TH and COMT, which play key roles for DA synthesis and metabolism, respectively. We did not observe any variation in low- and high-level PE representations as a function of TH polymorphisms, nor did polymorphisms of COMT seem to affect high-level PEs in our paradigm.
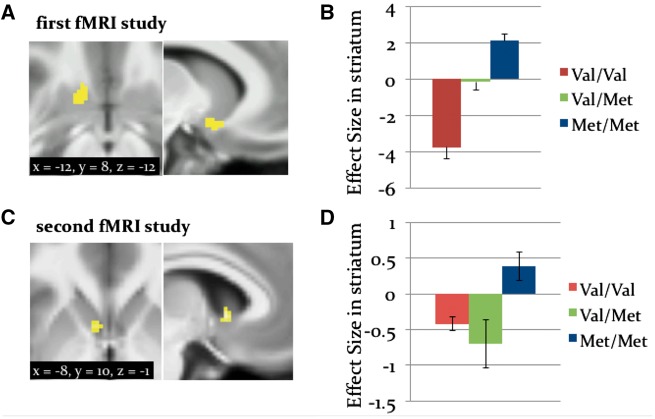
By contrast, we found an enhanced representation of (precision-weighted PE about advice validity) as a function of Val-to-Met COMT polymorphisms in the left ventral striatum in fMRI study 1 (Figure 8A) and in the left dorsal striatum in fMRI study 2 (Figure 8C). Specifically, Met/Met carriers, who have reduced efficacy of COMT and enhanced tonic DA levels, showed larger effects of in the striatum compared to Val/Val or Val/Met carriers. This effect was detected in the first fMRI study (whole-brain, peak-level FWE corrected P < 0.05; Figure 8B), and reproduced in the second fMRI study, albeit less robustly (whole-brain, cluster-level FWE corrected P < 0.05; Figure 8D). While COMT is usually considered in the context of prefrontal cortex function, it is worth pointing out that it is also involved in DA metabolism in the striatum (Matsumoto et al., 2003; Chen et al., 2004); see Discussion.
Fig. 8.
Whole-brain activation by : Variations as a function of COMT Larger effects of signed precision-weighted prediction error about the adviser fidelity were enhanced in Met/Met allele carriers compared to Val/Met and Val/Val in the ventral striatum with a center of gravity at [x = −12, y = 8, z = −12]. A & B: results from the first fMRI study. A distinct effect by was also detected in the striatum at [x = −8, y = 10, z = −1] in the second fMRI study in C and D.
Finally, in the first study, effects of COMT variability in low-level PE representation were also found in the left dorsolateral PFC (see Supplementary Figure 4), although this result was not reproduced in the second fMRI study. These differences may be due to the fact that there was a less balanced distribution for the COMT polymorphisms in the second fMRI study compared to the first. The distributions of the COMT polymorphisms were the following: fMRI study 1 with 8 Val/Val, 17 Val/Met and 10 Met/Met allele carriers and fMRI study 2 with 10 Val/Val, 27 Val/Met and 9 Met/Met allele carriers.
Discussion
Predicting the intentions of others is central to human interactions. However, the computational principles and neural mechanisms underlying this more sophisticated form of learning are not well understood. In this study, we combined hierarchical Bayesian models with an ecologically valid, deception-free paradigm, fMRI and genetics to address the question of the role of neuromodulatory systems in social learning. We found that hierarchically structured belief updates about the adviser’s fidelity and changing intentions best explained participants’ decisions to consider the advice. Furthermore, hierarchically coupled PEs mapped onto distinct neuromodulatory systems as previously shown for sensory learning under volatility (see Iglesias et al., 2013). Specifically, low-level PEs that updated predictions about the adviser’s fidelity activated the dopaminergic midbrain. The link of DA to low-level PEs in social learning was further supported by the finding of variability in PE magnitude in the striatum as a function of COMT, a single nucleotide polymorphism that modulates tonic DA levels by altering the metabolism of DA. The genotype favouring higher concentrations of DA lead to enhanced activity for signed advice PEs in the striatum, a regions with high COMT mRNA expression (Matsumoto et al., 2003; Chen et al., 2004).
On the other hand, high-level PEs used to update predictions about the (log) volatility of the adviser’s intentions were represented in the cholinergic basal forebrain. This result provides additional support for the proposal that ACh signals expected uncertainty (Yu and Dayan, 2005), which is related to the high-level PE in the sense that the latter also represents a difference between belief certainty (given the adviser’s estimated intentions) and a conditional probability, the adviser’s fidelity (see also the discussion in Iglesias et al., 2013).
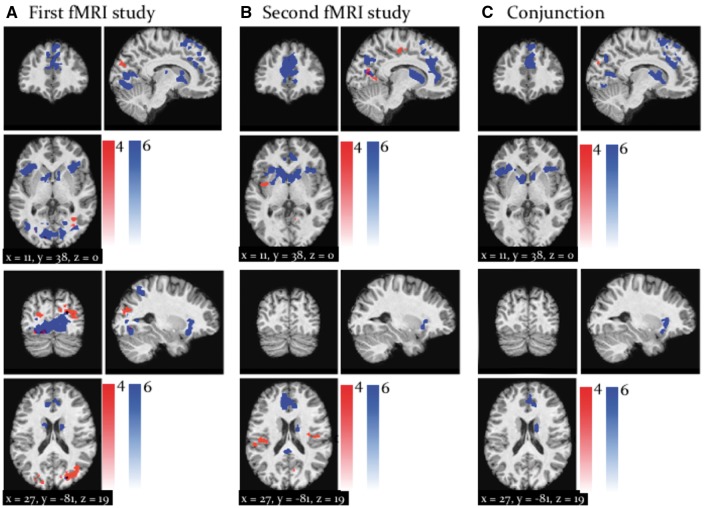
During the decision phase of the task, we found that on trials when the subject followed the advice, the bilateral fusiform gyrus and middle cingulate gyrus activated in response to increases in the predicted adviser's fidelity (Figure 9; regions in red). Conversely, when deciding to go against the advice, the predicted adviser fidelity activated regions associated with ‘theory of mind’ processes, such as the left anterior insula, right TPJ, bilateral paracingulate cortex and bilateral dorsomedial PFC, as well as the right caudate (Figure 9; regions in blue). Remarkably, in spite of the different input structure, these effects were also consistent across the two fMRI studies (see Figure 9C).
Fig. 9.
Whole-brain activation by : Activations by inferred adviser fidelity or when deciding to take the advice (red) and when deciding to go against the advice (blue) in the first (A) and the second fMRI study (B). Both activation maps are shown at a threshold of P < 0.05, FWE corrected for multiple comparisons across the whole brain. To highlight replication across studies, (C) shows the results of a ‘logical AND’ conjunction, illustrating voxels that were significantly activated in both studies.
General and domain-specific roles of prediction errors
To our knowledge, our results provide the first demonstration that distinct social PEs (with regard to current advice validity and the adviser’s general trustworthiness, respectively) activate different neuromodulatory nuclei, i.e., the dopaminergic midbrain and the cholinergic basal forebrain. When comparing our present findings to recent work based on the same computational framework but studying associative learning about purely sensory events under volatility (Iglesias et al., 2013), some remarkable similarities arise: Despite profound differences in the target of learning (simple auditory and visual stimuli in Iglesias et al. 2013, and abstract concepts such as advice validity and adviser trustworthiness in the current study), both studies found that key computational quantities—i.e., low- and high-level precision-weighted PEs—were encoded by activity in the dopaminergic midbrain and the cholinergic basal forebrain, respectively.
In contrast to the striking similarity of how PEs were encoded by activity in subcortical neuromodulatory nuclei, PE-induced cortical activations differed considerably and thus may reflect context-specific aspects of the respective learning process. For example, while the activations by low-level PEs (about visual stimulus outcome) reported by Iglesias et al. (2013) included visual and parietal regions, the present study found activation by low-level PEs (about advice validity) in regions commonly assumed to support ‘theory of mind’ processes. For example, the low-level precision-weighted PE signals in the current study were found in the paracingulate cortex, a region associated with mentalizing during interactive games (Gallagher et al., 2002; Kircher et al., 2009; Rilling and Sanfey, 2011). In terms of the posterior parietal activations, the present study found low-level precision-weighted PE effects in the TPJ, whereas in Iglesias et al. (2013), the effect of outcome PE was localized to the inferior parietal lobule. Furthermore, the peak of the anterior insula activation was also slightly more anterior than in Iglesias et al. and found in an insular region previously reported as linked to ‘theory of mind’ processes (Lamm and Singer, 2010; Schurz et al., 2014). These observations corroborate and extend previous considerations by Behrens et al. (2008) on the role of DA for social and reward learning, respectively.
Taken together, the results from Iglesias et al. (2013) and the current study suggest that hierarchical precision-weighted PEs represent generic computational quantities that may be used across a range of different learning processes and may be encoded by the same neuromodulatory transmitters, but are used in a context-specific fashion to trigger synaptic plasticity in distinct circuits involved in different forms of learning.
PE activations of areas implicated in social learning and inference
In this study, the activations by the two hierarchically related PEs from our computational model were found in cortical areas whose relevance for social learning and inference has been highlighted by numerous previous studies. Low-level precision-weighted PEs about advice validity were found to be encoded by activity in several dopaminoceptive cortical regions, such as the TPJ, the dorsomedial and dorsolateral PFC, ACC, SMA and insula. For example, the TPJ has been associated with socially-guided decisions (Carter et al., 2012) and mentalizing functions, such as thinking about others’ beliefs or desires (Saxe and Kanwisher, 2003; Saxe and Wexler, 2005; Young and Saxe, 2009), while activation of the dorsomedial PFC has been reported when participants simulated others’ intentions (Behrens et al., 2008; Frith and Frith, 2006, 2012) and decisions (Nicolle et al., 2012). Consistent with the PE-related activations we found, responses in these regions were previously reported to be reduced when new information about the other person was better predicted (Ma et al., 2012; Mende-Siedlecki et al., 2013; Garvert et al., 2015). Similarly, and again consistent with our findings, activity in the TPJ and dorsomedial PFC was previously found to scale with negative PEs, signalling a violation of social norms, which requires participants to take the perspective of their interacting partner (Behrens et al., 2008). Finally, the insula has been proposed to encode PEs in multiple domains, including social cognition (Singer et al., 2009).
Although several of the advice PE () activations reported in this paper have previously been associated with ‘theory of mind’ processes (Decety and Lamm, 2006; Lamm et al., 2009; Carrington and Bailey, 2009; Chang et al., 2011; Frith and Frith, 2012), these activations may not be specific to social learning tasks. For example, the insula, TPJ and dorsolateral PFC have also been shown to activate during probabilistic reinforcement learning tasks when the reward value of available response options changed (Cools et al., 2002; Remijnse et al., 2005; Mitchell et al., 2008). Furthermore, a network consisting of the bilateral dorsolateral frontal cortex, anterior insula and caudate—a subset of the regions showing effects—has been repeatedly identified in response to unexpected or cognitively demanding processes in a wide range of studies (O’Reilly et al., 2013; Boorman et al., 2016; Crittenden et al., 2016; Schwartenbeck et al., 2016).
Furthermore, it is important to note that distinct sections of the TPJ were differentially recruited in response to predictions and PEs. Effects of (inferred) adviser fidelity were localized to the right posterior TPJ with peak activation at [48, −58, 21] (Decety and Lamm, 2006; Mars et al., 2011). This region of the TPJ has previously shown to be recruited by mentalizing functions (Behrens et al., 2008; Hampton et al., 2008; Morishima et al., 2012; Boorman et al., 2013; Suzuki et al., 2015).
On the other hand, the low-level advice PE or was localised to the more anterior region of the TPJ, with an activation peak at [52, −50, 30]. This region was shown to be functionally coupled with an ‘attentional reorienting’ network, that included the anterior insula and ventrolateral PFC (Corbetta et al., 2008; Mars et al., 2012), suggesting that may possibly also contribute to shifts in attention, beyond its role in belief-updating processes in social learning.
In contrast, high-level PEs (for updating estimates of the (log-)volatility of the adviser’s intentions) showed context-specificity in our social learning paradigm, engaging regions with known ‘theory of mind’ functions (see Frith and Frith, 2005, 2006 for reviews). We found that these high-level PEs were not only reflected by activity in the cholinergic septum (Mesulam, 1995; Zaborszky et al., 1999), but were also represented in the dorsal middle cingulate cortex peaking at [7, −12, 42] in the first study and in the dorsal ACC with a group-level peak at [6, 30, 28] in the second study. The dorsal middle cingulate cortex has previously been linked to volatility (Behrens et al., 2007) and intentionality processing (see Apps et al., 2013 for a review), respectively.
Dopamine and acetylcholine in social learning
In humans, strong empirical evidence points to the involvement of DA in signaling reward PEs (Schultz, 1997; O’Doherty et al., 2003; Montague et al., 2004; D’Ardenne et al., 2008; Klein-Flügge et al., 2011; Schaaf et al., 2014) and novelty (Bunzeck and Düzel, 2006). While there are far fewer empirical studies on DA in a social context, several animal and human behavioural and neuroimaging studies suggest that DA may play a pivotal role for social learning and inference, too (e.g., Berton et al., 2006; Behrens et al., 2008, 2009; Klucharev et al., 2009; Campbell-Meiklejohn et al., 2012). The present study contributes a concrete facet of DA’s role for social learning, showing that a precision-weighted social PE activated both the dopaminergic midbrain and dopaminoceptive ‘theory of mind’ regions in cortex. Importantly, this precision-weighted low-level PE was neither related to reward nor novelty; instead, it determined belief updates about advice validity, signalling the need for perspective-taking in adapting to a potentially changing adviser.
The same PE showed an interesting dependency on genotype, specifically, on allelic variants of the COMT gene, which encodes an enzyme (of the same name) with an important role for DA metabolism. In general, the enzyme COMT modulates tonic DA levels in the striatum and the PFC (Mier et al., 2010) and, in turn, affects different types of learning (Frank et al., 2007). The Val allele is associated with greater enzymatic efficacy and lower DA levels than the methionine-encoding Met allele. In the present work, in contrast to Val/Val and Val/Met carriers, Met/Met individuals (with reduced COMT efficacy and hence higher DA levels) showed an enhanced effect of low-level PEs in the ventral striatum in both fMRI experiments. (The first experiment also found a COMT effect in left dorsolateral PFC, however, this result was not reproduced in the second experiment). While COMT is usually considered to be particularly important for prefrontal DA metabolism, it is worth pointing out in this context that the ventral striatum also expresses COMT mRNA (Matsumoto et al., 2003, Chen et al., 2004) and several previous human neuroimaging studies have indicated COMT-related effects on activity in the ventral striatum (e.g. Yacubian et al., 2007; Camara et al., 2010).
In contrast to DA, the role of ACh for social cognition has arguably received considerably less attention. Having said this, the cholinergic septum has previously been associated with social learning, for example, Biele and colleagues (2011) showed that the septum was particularly sensitive to positive outcomes following advice-taking. Furthermore, an interesting although presently speculative link may exist between our results and those by Biele et al. (2011) and the neuroanatomy of septal-hypothalamic interactions. That is, given the nature of the septum-activating high-level PE (which updates beliefs about trustworthiness) in our paradigm, it is interesting to note that reciprocal projections between septum and hypothalamus exist which are involved in regulating oxytocin release (DeFrance, 1976; Landgraf and Neumann, 2004). Oxytocin, in turn, has previously been shown to potentiate social exchange by increasing trust (Kosfeld et al., 2005), reducing social stress (Heinrichs et al., 2003) and increasing ‘theory of mind’ processes (Domes et al., 2007).
Strengths and limitations of this study
The most obvious limitation of our present study is that the use of fMRI does not permit concluding with certainty that our PE activations of midbrain and basal forebrain truly reflect the activity of dopaminergic and cholinergic neurons, respectively (see also the discussion in Iglesias et al., 2013). These regions also contain glutamatergic and GABAergic neurons and future pharmacological and other interventional studies will need to establish a firm link between our computational markers and neuromodulatory transmitters.
In addition, our study has one notable feature, which can be seen as a limitation or a strength. That is, our experimental design did not emphasize the recursive nature of social inference, which is an important component of theory of mind (see Devaine et al., 2014a, 2014b). This is because the advice in our paradigm was provided by video, based on real but pre-recorded adviser-player interactions (Diaconescu et al., 2014). This may limit social cognition during our paradigm to level 1 theory of mind inference (inferring the mental state of the adviser), since higher levels (‘I think what he thinks what I think…’) are not only not needed, but will be implausible to the player. From one perspective, this is a disadvantage because it restricts the conclusions drawn from this study to a particular level of social inference and does not cover the full spectrum of theory of mind. On the other hand, it can be seen as an advantage because it removes uncertainty about individual differences in the level of reasoning and allows for straightforward application of efficient models like the HGF, which do not capture the recursive nature of social interactions (compare the discussion in Diaconescu et al., 2014). Additionally, the task design ensures that participants engage in the same learning process, because the players’ strategy is not dependent on variations in the advisers’ deceptive skills. Finally, the recursive depth of social inference during interactive games such as investor-trustee is typically limited to level 1 or level 2 depth-of-reasoning, suggesting that participants simulate their partner’s intentions without simultaneously inferring their partner’s model of them (Yoshida et al., 2008; Xiang et al., 2012).
In this article, we report results that could be reproduced across two separate fMRI experiments in different groups of volunteers. These two fMRI experiments differed in three ways: first, the volatility of the input structure was different across the two studies (see Methods section); second, unlike the first study, in the second study, participants were administered placebo, thereby placing them in a potentially different experimental setting; third, the signal-to-noise ratio in subcortical medial regions relative to the rest of the cortex may have differed because an 8-channel compared to a 32-channel head coil were used in the first and the second fMRI study, respectively. In spite of these differences, the reproducibility of the findings is remarkable: The segregated effects of low- and high-level PEs in dopaminergic and cholinergic systems respectively were reproduced in both fMRI studies.
Across the two studies, we also found some differences in the representation of the high-level PE. In the first study, elicited increased activity in the left dorsal middle cingulate cortex (whole-brain, cluster-level FWE corrected P < 0.05; Figure 6a;Table 4) whereas in the second study, activated the right dorsal ACC (whole-brain, cluster-level FWE corrected P < 0.05; Figure 6b;Table 4). These differences might be due to the distinct input structure and increased volatility schedule utilized in the second study compared to the first (see Supplementary Figure 1c).
Conclusions and outlook
In conclusion, this study employed a multimodal framework that integrates computational modelling, fMRI and genetic analyses to identify key mechanisms of social inference that generalized across two separate fMRI experiments, despite differences in task structure and fMRI data acquisition methods.
Our study makes four important contributions to current conceptualizations of the neural mechanisms of social learning. First, and most generally, it extends empirical support for the relevance of precision-weighted PEs—as postulated by previous Bayesian theories of brain function (Friston, 2005)—to social cognition. Second, it emphasizes a specific role of DA in the encoding of low-level PEs about social value, such as advice validity. Third, it suggests a specific role for ACh in social cognition that concerns the encoding of more abstract, high-level PEs, such as adviser trustworthiness. Fourth, we find activations of dopaminergic and cholinergic nuclei by hierarchically related PEs that are remarkably analogous to previous results obtained with a purely sensory learning task (Iglesias et al., 2013). This suggests that precision-weighted PEs may constitute generic computational quantities, which are used in similar ways across learning domains. At the same time, the differences of the cortical activations reported in this study and by Iglesias et al. (2013) suggest that these PEs are utilized in a context and circuit-specific way, e.g. as plasticity-inducing ‘teaching signals’ that are broadcast via dopaminergic and cholinergic projections specifically to those cortical regions, which are involved in the respective learning context.
The examination of the computational quantities critical for social learning in healthy volunteers provides a model-based characterization that may serve as a benchmark for future studies on mechanisms of maladaptive ‘theory of mind’ functions. Aspects of this hierarchical learning and weighting of social and non-social sources of information during decision-making may be differentially impaired in psychiatric disorders such as schizophrenia, borderline personality disorder or autism spectrum disorder (Corcoran et al., 1995; King-Casas et al., 2008; Yoshida et al., 2010). For example, differential impairment in DA- vs ACh-dependent processes may contribute to explaining individual variability in symptoms as well as treatment responses (Stephan et al., 2006). Once the relevance of our putative DA/ACh markers for social inference has been causally established using pharmacological studies in healthy volunteers, we intend to extend this computational framework to studies of patients exhibiting salient deficiencies in social learning, including schizophrenia and autism.
Supplementary Material
Acknowledgements
We are grateful for support by the UZH Forschungskredit (AOD), the René and Susanne Braginsky Foundation (KES), the University of Zurich (KES) and the UZH Clinical Research Priority Program (CRPP) ‘Molecular Imaging’ (KES). CM is supported by a Joint Initiative involving Max Planck Society and University College London on Computational Psychiatry and Aging Research.
Supplementary data
Supplementary data are available at SCAN online.
Conflict of interest. None declared.
References
- Apps M.A.J., Lockwood P.L., Balsters J.H. (2013). The role of the midcingulate cortex in monitoring others’ decisions. Frontiers in Neuroscience 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Ardenne K., McClure S.M., Nystrom L.E., Cohen J.D. (2008). BOLD responses reflecting dopaminergic signals in the human ventral tegmental area. Science 319, 1264–7. [DOI] [PubMed] [Google Scholar]
- Baron-Cohen S., Leslie A.M., Frith U. (1985). Does the autistic child have a “theory of mind”?. Cognition 21, 37–46. [DOI] [PubMed] [Google Scholar]
- Bastos A.M., Usrey W.M., Adams R.A., Mangun G.R., Fries P., Friston K.J. (2012). Canonical microcircuits for predictive coding. Neuron 76, 695–711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens T.E.J., Woolrich M.W., Walton M.E., Rushworth M.F.S. (2007). Learning the value of information in an uncertain world. Nature Neuroscience 10, 1214–21. [DOI] [PubMed] [Google Scholar]
- Behrens T.E.J., Hunt L.T., Woolrich M.W., Rushworth M.F.S. (2008). Associative learning of social value. Nature 456, 245. U45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens T.E.J., Hunt L.T., Rushworth M.F.S. (2009). The computation of social behavior. Science 324, 1160–4. [DOI] [PubMed] [Google Scholar]
- Berton O., McClung C.A., DiLeone R.J., et al. (2006). Essential role of BDNF in the mesolimbic dopamine pathway in social defeat stress. Science 311, 864–8. [DOI] [PubMed] [Google Scholar]
- Biele G., Rieskamp J., Krugel L.K., Heekeren H.R. (2011). The neural basis of following advice. Plos Biol 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boorman E.D., O’Doherty J.P., Adolphs R., Rangel A. (2013). The behavioral and neural mechanisms underlying the tracking of expertise. Neuron 80, 1558–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boorman E.D., Rajendran V.G., O’Reilly J.X., Behrens T.E. (2016). Two anatomically and computationally distinct learning signals predict changes to stimulus-outcome associations in hippocampus. Neuron 89, 1343–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunzeck N., Düzel E. (2006). Absolute coding of stimulus novelty in the human substantia nigra/VTA. Neuron 51, 369–79. [DOI] [PubMed] [Google Scholar]
- Cara B.D., Panayi F., Gobert A., et al. (2007). Activation of dopamine D1 receptors enhances cholinergic transmission and social cognition: a parallel dialysis and behavioural study in rats. International Journal of Neuropsychopharmacology 10, 383–99. [DOI] [PubMed] [Google Scholar]
- Camara E., Krämer U.M., Cunillera T., et al. (2010). The effects of COMT (Val108/158Met) and DRD4 (SNP −521) dopamine genotypes on brain activations related to valence and magnitude of rewards. Cerebrla Cortex 20, 1985–96. [DOI] [PubMed] [Google Scholar]
- Campbell-Meiklejohn D.K., Bach D.R., Roepstorff A., Dolan R.J., Frith C.D. (2010). How the opinion of others affects our valuation of objects. Current Biology 20, 1165–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell-Meiklejohn D.K., Simonsen A., Jensen M., et al. (2012). Modulation of social influence by methylphenidate. Neuropsychopharmacology 37, 1517–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrington S.J., Bailey A.J. (2009). Are there theory of mind regions in the brain? A review of the neuroimaging literature. Human Brain Mappings 30, 2313–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter R.M., Bowling D.L., Reeck C., Huettel S.A. (2012). A distinct role of the temporal-parietal junction in predicting socially guided decisions. Science 337, 109–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang L.J., Smith A., Dufwenberg M., Sanfey A.G. (2011). Triangulating the neural, psychological, and economic bases of guilt aversion. Neuron 70, 560–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J., Lipska B.K., Halim N., et al. (2004). Functional analysis of genetic variation in catechol-O-methyltransferase (COMT): effects on mRNA, protein, and enzyme activity in postmortem human brain. American Journal of Human Genetics 75, 807–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christopoulos G.I., King-Casas B. (2015). With you or against you: social orientation dependent learning signals guide actions made for others. NeuroImage 104, 326–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cools R., Clark L., Owen A.M., Robbins T.W. (2002). Defining the neural mechanisms of probabilistic reversal learning using event-related functional magnetic resonance imaging. J. Neuroscience 22, 4563–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta M., Patel G., Shulman G.L. (2008). The reorienting system of the human brain: from environment to theory of mind. Neuron 58, 306–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corcoran R., Mercer G., Frith C.D. (1995). Schizophrenia, symptomatology and social inference: Investigating "theory of mind" in people with schizophrenia. Schizophrenia Research 17, 5–13. [DOI] [PubMed] [Google Scholar]
- Crittenden B.M., Mitchell D.J., Duncan J. (2016). Task encoding across the multiple demand cortex is consistent with a frontoparietal and cingulo-opercular dual networks distinction. Journal of Neuroscience 36, 6147–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J., Ouden H.E.M., den P.,M., Kiebel S.J., Stephan K.E., Friston K.J. (2010). Observing the observer (I): Meta-Bayesian models of learning and decision-making. PLoS One 5, [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Chaumont F., Coura R.D.S., Serreau P., et al. (2012). Computerized video analysis of social interactions in mice. Nature Methods 9, 410–7. [DOI] [PubMed] [Google Scholar]
- Dayan P., Hinton G.E., Neal R.M., Zemel R.S. (1995). The Helmholtz machine. Neural Computation 7, 889–904. [DOI] [PubMed] [Google Scholar]
- Decety J., Lamm C. (2006). Human empathy through the lens of social neuroscience. Scientific World Journal 6, 1146–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeFrance J.F. (1976). The Septal Nuclei ( Springer Science & Business Media; ). [Google Scholar]
- Devaine M., Hollard G., Daunizeau J. (2014a). The social Bayesian brain: does mentalizing make a difference when we learn?. PLoS Computational Biology 10, e1003992.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devaine M., Hollard G., Daunizeau J. (2014b). Theory of mind: did evolution fool us?. PLoS ONE 9, e87619.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaconescu A.O., Mathys C., Weber L.A.E., et al. (2014). Inferring on the intentions of others by hierarchical bayesian learning. PLoS Computational Biology 10, e1003810.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domes G., Heinrichs M., Michel A., Berger C., Herpertz S.C. (2007). Oxytocin improves "Mind-Reading" in humans. Biol Psychiatry 61, 731–3. [DOI] [PubMed] [Google Scholar]
- Ferreira G., Meurisse M., Gervais R., Ravel N., Lévy F. (2001). Extensive immunolesions of basal forebrain cholinergic system impair offspring recognition in sheep. Neuroscience 106, 103–16. [DOI] [PubMed] [Google Scholar]
- Ferreira G., Poindron P., Lévy F. (2003). Involvement of central muscarinic receptors in social and nonsocial learning in sheep. Pharmacology Biochemistry & Behavior 74, 969–75. [DOI] [PubMed] [Google Scholar]
- Frank M.J., Moustafa A.A., Haughey H.M., Curran T., Hutchison K.E. (2007). Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proceedings of the National Academy of Sciences 104, 16311–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K. (2005). A theory of cortical responses. Philosophical Transactions of the Royal Society B: Biological Sciences 360, 815–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K. (2007). Chapter 19 - topological inference In: Friston Karl, Ashburner John, Kiebel Stefan, Thomas Nichols J.A., Penny William -, Friston Karl, Penny William, Statistical Parametric Mapping, editors. London: Academic Press. [Google Scholar]
- Friston K. (2010). The free-energy principle: a unified brain theory?. Nature Reviews Neuroscience 11, 127–38. [DOI] [PubMed] [Google Scholar]
- Friston K.J., Shiner T., FitzGerald T., et al. (2012). Dopamine, affordance and active inference. PLOS Computational Biology, 8, e1002327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frith C., Frith U. (2005). Theory of mind. Current Biology 15, R644–5. [DOI] [PubMed] [Google Scholar]
- Frith C.D., Frith U. (2006). The neural basis of mentalizing. Neuron 50, 531–4. [DOI] [PubMed] [Google Scholar]
- Frith C.D., Frith U. (2012). Mechanisms of social cognition. Annual Review of Psychology 63, 287–313. [DOI] [PubMed] [Google Scholar]
- Gallagher H.L., Jack A.I., Roepstorff A., Frith C.D. (2002). Imaging the intentional stance in a competitive game. NeuroImage 16, 814–21. [DOI] [PubMed] [Google Scholar]
- Garvert M.M., Moutoussis M., Kurth-Nelson Z., Behrens T.E.J., Dolan R.J. (2015). Learning-induced plasticity in medial prefrontal cortex predicts preference malleability. Neuron 85, 418–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampton A.N., Bossaerts P., O’Doherty J.P. (2008). Neural correlates of mentalizing-related computations during strategic interactions in humans. Proceedings of the National Academy of Sciences 105, 6741–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauser T.U., Iannaccone R., Ball J., et al. (2014). Role of the medial prefrontal cortex in impaired decision making in juvenile attention-deficit/hyperactivity disorder. JAMA Psychiatry 71, 1165–73. [DOI] [PubMed] [Google Scholar]
- Heinrichs M., Baumgartner T., Kirschbaum C., Ehlert U. (2003). Social support and oxytocin interact to suppress cortisol and subjective responses to psychosocial stress. Biological Psychiatry 54, 1389–98. [DOI] [PubMed] [Google Scholar]
- Iglesias S., Mathys C., Brodersen K.H., et al. (2013). Hierarchical prediction errors in midbrain and basal forebrain during sensory learning. Neuron 80, 519–30. [DOI] [PubMed] [Google Scholar]
- Jones R.M., Somerville L.H., Li J., et al. (2011). Behavioral and neural properties of social reinforcement learning. Jounrnal of Neuroscience 31, 13039–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasper L., Bollmann S., Diaconescu A.O., et al. (2017). The physio toolbox for modeling physiological noise in fMRI Data. Journal of Neuroscience Methods, 276, 56–72. [DOI] [PubMed] [Google Scholar]
- King-Casas B., Sharp C., Lomax-Bream L., Lohrenz T., Fonagy P., Montague P.R. (2008). The rupture and repair of cooperation in borderline personality disorder. Science 321, 806–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kircher T., Blümel I., Marjoram D., et al. (2009). Online mentalising investigated with functional MRI. Neuroscience Letters 454, 176–81. [DOI] [PubMed] [Google Scholar]
- Klein-Flügge M.C., Hunt L.T., Bach D.R., Dolan R.J., Behrens T.E.J. (2011). Dissociable reward and timing signals in human midbrain and ventral striatum. Neuron 72, 654–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klucharev V., Hytonen K., Rijpkema M., Smidts A., Fernandez G. (2009). Reinforcement learning signal predicts social conformity. Neuron 61, 140–51. [DOI] [PubMed] [Google Scholar]
- Kosfeld M., Heinrichs M., Zak P.J., Fischbacher U., Fehr E. (2005). Oxytocin increases trust in humans. Nature 435, 673–6. [DOI] [PubMed] [Google Scholar]
- Lamm C., Singer T. (2010). The role of anterior insular cortex in social emotions. Brain Structure and Function 214, 579–91. [DOI] [PubMed] [Google Scholar]
- Lamm C., Meltzoff A.N., Decety J. (2009). How do we empathize with someone who is not like us? A functional magnetic resonance imaging study. Journal of Cognitive Neuroscience 22, 362–76. [DOI] [PubMed] [Google Scholar]
- Landgraf R., Neumann I.D. (2004). Vasopressin and oxytocin release within the brain: a dynamic concept of multiple and variable modes of neuropeptide communication. Frontiers in Neuroendocrinology 25, 150–76. [DOI] [PubMed] [Google Scholar]
- Lohrenz T., Bhatt M., Apple N., Montague P.R. (2013). Keeping up with the Joneses: interpersonal prediction errors and the correlation of behavior in a tandem sequential choice task. PLoS Computational Biology 9, e1003275.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma N., Vandekerckhove M., Baetens K., Overwalle F.V., Seurinck R., Fias W. (2012). Inconsistencies in spontaneous and intentional trait inferences. Social Cognitive and Affective Neurosci ence7, 937–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maldjian J.A., Laurienti P.J., Kraft R.A., Burdette J.H. (2003). An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. NeuroImage 19, 1233–9. [DOI] [PubMed] [Google Scholar]
- Mars R.B., Sallet J., Schuffelgen U., Jbabdi S., Toni I., Rushworth M.F.S. (2011). Connectivity-based subdivisions of the human right "Temporoparietal Junction Area": Evidence for different areas participating in different cortical networks. Cerebral Cortex 22, 1894–903. [DOI] [PubMed] [Google Scholar]
- Mathys C., Daunizeau J., Friston K.J., Stephan K.E. (2011). A Bayesian foundation for individual learning under uncertainty. Frontiers in Human Neuroscience 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathys C.D., Lomakina E.I., Daunizeau J., et al. (2014). Uncertainty in perception and the Hierarchical Gaussian Filter. Frontiers in Human Neuroscience 8, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto M., Weickert C.S., Akil M., et al. (2003). Catechol O-methyltransferase mRNA expression in human and rat brain: evidence for a role in cortical neuronal function. Neuroscience 116, 127–37. [DOI] [PubMed] [Google Scholar]
- Mende-Siedlecki P., Cai Y., Todorov A. (2013). The neural dynamics of updating person impressions. Social Cognitive and Affective Neuroscience 8, 623–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mesulam M.M. (1995). Cholinergic pathways and the ascending reticular activating system of the human Brain. Annals of New York Academy of Sciences 757, 169–79. [DOI] [PubMed] [Google Scholar]
- Mier D., Kirsch P., Meyer-Lindenberg A. (2010). Neural substrates of pleiotropic action of genetic variation in COMT: a meta-analysis. Molecular Psychiatry 15, 918–27. [DOI] [PubMed] [Google Scholar]
- Mitchell D.G.V., Rhodes R.A., Pine D.S., Blair R.J.R. (2008). The contribution of ventrolateral and dorsolateral prefrontal cortex to response reversal. Behavioral Brain Research 187, 80–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montague P.R., Hyman S.E., Cohen J.D. (2004). Computational roles for dopamine in behavioural control. Nature 431, 760–7. [DOI] [PubMed] [Google Scholar]
- Morishima Y., Schunk D., Bruhin A., Ruff C.C., Fehr E. (2012). Linking brain structure and activation in temporoparietal junction to explain the neurobiology of human altruism. Neuron 75, 73–9. [DOI] [PubMed] [Google Scholar]
- Nichols T., Brett M., Andersson J., Wager T., Poline J.B. (2005). Valid conjunction inference with the minimum statistic. NeuroImage 25, 653–60. [DOI] [PubMed] [Google Scholar]
- Nicolle A., Klein-Flügge M.C., Hunt L.T., Vlaev I., Dolan R.J., Behrens T.E.J. (2012). An agent independent axis for executed and modeled choice in medial prefrontal cortex. Neuron 75, 1114–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Doherty J.P., Dayan P., Friston K., Critchley H., Dolan R.J. (2003). Temporal difference models and reward-related learning in the human brain. Neuron 38, 329–37. [DOI] [PubMed] [Google Scholar]
- O’Reilly J.X., Jbabdi S., Rushworth M.F.S., Behrens T.E.J. (2013). Brain systems for probabilistic and dynamic prediction: computational specificity and integration. PLoS Biology 11, e1001662.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao R.P.N., Ballard D.H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature Neuroscience 2, 79–87. [DOI] [PubMed] [Google Scholar]
- Remijnse P., Nielen M., Uylings H., Veltman D. (2005). Neural correlates of a reversal learning task with an affectively neutral baseline: an event-related fMRI study. NeuroImage 26, 609–18. [DOI] [PubMed] [Google Scholar]
- Rescorla R.A., Wagner A.R. (1972). A Theory of Pavlovian Conditioning: Variations in the Effectiveness of Reinforcement. New York: Appleton-Century-Crofts. [Google Scholar]
- Rilling J.K., Sanfey A.G. (2011). The neuroscience of social decision-making. Annual Review of Psychology 62, 23–48. [DOI] [PubMed] [Google Scholar]
- Rigoux L., Stephan K.E., Friston K.J., Daunizeau J. (2014). Bayesian model selection for group studies — Revisited. NeuroImage 84, 971–85. [DOI] [PubMed] [Google Scholar]
- Saxe R., Kanwisher N. (2003). People thinking about thinking people: The role of the temporo-parietal junction in "theory of mind.". NeuroImage 19, 1835–42. [DOI] [PubMed] [Google Scholar]
- Saxe R., Wexler A. (2005). Making sense of another mind: the role of the right temporo-parietal junction. Neuropsychologia 43, 1391–9. [DOI] [PubMed] [Google Scholar]
- Schultz W. (1997). Dopamine neurons and their role in reward mechanisms. Current Opinion in Neurobiology 7, 191–7. [DOI] [PubMed] [Google Scholar]
- Schurz M., Radua J., Aichhorn M., Richlan F., Perner J. (2014). Fractionating theory of mind: a meta-analysis of functional brain imaging studies. Neuroscience Biobehavioral Review 42, 9–34. [DOI] [PubMed] [Google Scholar]
- Schwartenbeck P., FitzGerald T.H.B., Mathys C., Dolan R., Friston K. (2014). The dopaminergic midbrain encodes the expected certainty about desired outcomes. Cerebral Cortex. [DOI] [PMC free article] [PubMed]
- Schwartenbeck P., FitzGerald T.H.B., Dolan R. (2016). Neural signals encoding shifts in beliefs. NeuroImage 125, 578–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer T., Critchley H.D., Preuschoff K. (2009). A common role of insula in feelings, empathy and uncertainty. Trends in Cognitive Science 13, 334–40. [DOI] [PubMed] [Google Scholar]
- Schaaf M.E., van der S., van M.R., Geurts D.E.M., Schellekens A.F.A., et al. (2014). Establishing the dopamine dependency of human striatal signals during reward and punishment reversal learning. Cerebral Cortex 24, 633–42. [DOI] [PubMed] [Google Scholar]
- Stephan K.E., Baldeweg T., Friston K.J. (2006). Synaptic plasticity and dysconnection in schizophrenia. Biology Psychiatry 59, 929–39. [DOI] [PubMed] [Google Scholar]
- Stephan K.E., Penny W.D., Daunizeau J., Moran R.J., Friston K.J. (2009). Bayesian model selection for group studies. NeuroImage 46, 1004–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki S., Adachi R., Dunne S., Bossaerts P., O’Doherty J.P. (2015). Neural mechanisms underlying human consensus decision-making. Neuron 86, 591–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossel S., Mathys C., Daunizeau J., et al. (2014a). Spatial attention, precision, and bayesian inference: a study of saccadic response speed. Cerebral Cortex 24, 1436–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossel S., Bauer M., Mathys C., et al. (2014b). Cholinergic stimulation enhances bayesian belief updating in the deployment of spatial attention. Journal of Neuroscience 34, 15735–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossel S., Mathys C., Stephan K.E., Friston K.J. (2015). Cortical coupling reflects bayesian belief updating in the deployment of spatial attention. Journal of Neuroscience 35, 11532–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang T., Ray D., Lohrenz T., Dayan P., Montague P.R. (2012). Computational phenotyping of two-person interactions reveals differential neural response to depth-of-thought. PLoS Computational Biology 8, e1002841.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang T., Lohrenz T., Montague P.R. (2013). Computational substrates of norms and their violations during social exchange. Journal of Neuroscience 33, 1099–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yacubian J., Sommer T., Schroeder K., et al. (2007). Gene–gene interaction associated with neural reward sensitivity. Proceedings of the National Academy of Sciences 104, 8125–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida W., Dolan R.J., Friston K.J. (2008). Game theory of mind. PLOS Computational Biology 4, e1000254.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida W., Dziobek I., Kliemann D., Heekeren H.R., Friston K.J., Dolan R.J. (2010). Cooperation and heterogeneity of the autistic mind. Journal of Neuroscience 30, 8815–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young L., Saxe R. (2009). Innocent intentions: a correlation between forgiveness for accidental harm and neural activity. Neuropsychologia 47, 2065–72. [DOI] [PubMed] [Google Scholar]
- Yu A.J., Dayan P. (2005). Uncertainty, neuromodulation, and attention. Neuron 46, 681–92. [DOI] [PubMed] [Google Scholar]
- Zaborszky L., Pang K., Somogyi J., Nadasdy Z., Kallo I. (1999). The basal forebrain corticopetal system revisited. Annals of the New York Academy of Sciences 877, 339–67. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.