Abstract
Key points
We develop a new biophysically rooted, physiologically constrained conductance‐based synaptic model to mechanistically account for short‐term facilitation and depression, respectively through residual calcium and transmitter depletion kinetics.
We address the specific question of how presynaptic components (including voltage‐gated ion channels, pumps, buffers and release‐handling mechanisms) and interactions among them define synaptic filtering and short‐term plasticity profiles.
Employing global sensitivity analyses (GSAs), we show that near‐identical synaptic filters and short‐term plasticity profiles could emerge from disparate presynaptic parametric combinations with weak pairwise correlations.
Using virtual knockout models, a technique to address the question of channel‐specific contributions within the GSA framework, we unveil the differential and variable impact of each ion channel on synaptic physiology.
Our conclusions strengthen the argument that parametric and interactional complexity in biological systems should not be viewed from the limited curse‐of‐dimensionality standpoint, but from the evolutionarily advantageous perspective of providing functional robustness through degeneracy.
Abstract
Information processing in neurons is known to emerge as a gestalt of pre‐ and post‐synaptic filtering. However, the impact of presynaptic mechanisms on synaptic filters has not been quantitatively assessed. Here, we developed a biophysically rooted, conductance‐based model synapse that was endowed with six different voltage‐gated ion channels, calcium pumps, calcium buffer and neurotransmitter‐replenishment mechanisms in the presynaptic terminal. We tuned our model to match the short‐term plasticity profile and band‐pass structure of Schaffer collateral synapses, and performed sensitivity analyses to demonstrate that presynaptic voltage‐gated ion channels regulated synaptic filters through changes in excitability and associated calcium influx. These sensitivity analyses also revealed that calcium‐ and release‐control mechanisms were effective regulators of synaptic filters, but accomplished this without changes in terminal excitability or calcium influx. Next, to perform global sensitivity analysis, we generated 7000 randomized models spanning 15 presynaptic parameters, and computed eight different physiological measurements in each of these models. We validated these models by applying experimentally obtained bounds on their measurements, and found 104 (∼1.5%) models to match the validation criteria for all eight measurements. Analysing these valid models, we demonstrate that analogous synaptic filters emerge from disparate combinations of presynaptic parameters exhibiting weak pairwise correlations. Finally, using virtual knockout models, we establish the variable and differential impact of different presynaptic channels on synaptic filters, underlining the critical importance of interactions among different presynaptic components in defining synaptic physiology. Our results have significant implications for protein‐localization strategies required for physiological robustness and for degeneracy in long‐term synaptic plasticity profiles.
Keywords: computational model, degeneracy, global sensitivity analysis, paired‐pulse ratio, presynaptic ion channels, synaptic physiology
Key points
We develop a new biophysically rooted, physiologically constrained conductance‐based synaptic model to mechanistically account for short‐term facilitation and depression, respectively through residual calcium and transmitter depletion kinetics.
We address the specific question of how presynaptic components (including voltage‐gated ion channels, pumps, buffers and release‐handling mechanisms) and interactions among them define synaptic filtering and short‐term plasticity profiles.
Employing global sensitivity analyses (GSAs), we show that near‐identical synaptic filters and short‐term plasticity profiles could emerge from disparate presynaptic parametric combinations with weak pairwise correlations.
Using virtual knockout models, a technique to address the question of channel‐specific contributions within the GSA framework, we unveil the differential and variable impact of each ion channel on synaptic physiology.
Our conclusions strengthen the argument that parametric and interactional complexity in biological systems should not be viewed from the limited curse‐of‐dimensionality standpoint, but from the evolutionarily advantageous perspective of providing functional robustness through degeneracy.
Abbreviations
- AH
axon hillock
- AIS
axon initial segment
- AMPAR
AMPA receptor
- AP
action potential
- CaL
L‐type Ca2+ channel
- CaN
N‐type Ca2+ channel
- ER
endoplasmic reticulum
- GHK
Goldman–Hodgkin–Katz
- GSA
global sensitivity analysis
- GPCR
G‐protein coupled receptor
- HCN
hyperpolarization‐activated cyclic nucleotide‐gated channel
- InsP3
inositol triphosphate
- InsP3R
inositol triphosphate receptor
- KA
A‐type K+ channel
- KDR
delayed rectifier potassium channel
- MS
myelin sheath
- NoR
node of Ranvier
- PPR
paired pulse ratio
- SC
Schaffer collateral
- SERCA
sarcoplasmic endoplasmic reticulum calcium ATPase
- STA
spike‐triggered average
- STP
short‐term plasticity
- STPR
short‐term plasticity ratio
- TTA
transmission‐triggered average
- VGCC
voltage‐gated calcium channel
- VGIC
voltage‐gated ion channel
- VKM
virtual knockout model
Introduction
Neuronal information processing emerges as a gestalt of pre‐ and post‐synaptic filtering, with critical contributions from intricate interactions among constituent components. Although the importance of pre‐ and post‐synaptic filtering has been assessed, with clear analyses pointing to specific contributions of the two sides of the synapse to neuronal filters (Zucker, 1989, 1999; Johnston et al., 1996; Abbott et al. 1997; Tsodyks & Markram, 1997; Dittman et al. 2000; Magee, 2000; Fortune & Rose, 2001; Abbott & Regehr, 2004; Awatramani et al. 2005; Johnston & Narayanan, 2008; Sjostrom et al. 2008; Spruston, 2008; Fioravante & Regehr, 2011; Narayanan & Johnston, 2012; Regehr, 2012; Ratte et al. 2013; Das & Narayanan, 2014; Stuart & Spruston, 2015), a crucial difference in existing analyses pertains to the impact of voltage‐gated ion channels (VGICs) on pre‐ vs. post‐synaptic filtering. Although the role of post‐synaptically expressed VGICs in altering information filtering has received widespread attention (Johnston et al. 1996; Magee, 2000; Narayanan & Johnston, 2007, 2008; Johnston & Narayanan, 2008; Spruston, 2008; Ratte et al. 2013; Das & Narayanan, 2014, 2015; Rathour & Narayanan, 2014; Stuart & Spruston, 2015), the quantitative impact of pre‐synaptically expressed VGICs, especially of channels other than those that mediate spike generation and release‐mediating calcium influx, on synaptic filters has not been assessed thoroughly. This lacuna is especially striking because the expression of VGICs in presynaptic terminals and the role of these channels in regulating synaptic transmission and short‐term plasticity (STP) are well established across several synaptic subtypes (Roberts et al. 1990; Sheng et al. 1993; Veh et al. 1995; Cooper et al. 1998; Meir et al. 1999; Qian & Saggau, 1999; Geiger & Jonas, 2000; Southan et al. 2000; Cuttle et al. 2001; Dodson & Forsythe, 2004; Awatramani et al. 2005; Bender et al. 2007; Rancz et al. 2007; Huang et al. 2011; Novak et al. 2013; Kirizs et al. 2014).
Additionally, as neuronal physiology is driven by spatiotemporal interactions among several coexpressing ion channels, it is essential to assess the impact of interactions among channels in defining specific synaptic filters, which can take different profiles such as low‐, high‐ or band‐pass structures depending on the delicate balance between short‐term facilitation and depression (Tsodyks & Markram, 1997; Dittman et al. 2000; Fortune & Rose, 2001; Abbott & Regehr, 2004). In doing this, it is also important to ask if the emergence of a specific type of filter is critically reliant on rigid constraints on the expression profiles of channels and other presynaptically expressed mechanisms, or if such emergence exhibits degeneracy (Edelman & Gally, 2001; Stelling et al. 2004; Whitacre & Bender, 2010) where disparate structural components could come together to elicit analogous synaptic filters. Answers to these questions are critical in the light of analyses, which largely span post‐synaptic structures, that demonstrate the translation of such degeneracy to robustness of biological function (Tononi et al. 1999; Edelman & Gally, 2001; Stelling et al. 2004; Marder & Goaillard, 2006; Whitacre & Bender, 2010; Marder, 2011; O'Leary et al. 2014; Rathour & Narayanan, 2014; Anirudhan & Narayanan, 2015; Drion et al. 2015; Srikanth & Narayanan, 2015; Rathour et al. 2016). Importantly, precise maintenance of specific STP profiles and associated filter structures is extremely crucial from the perspective of their critical roles in encoding, estimation, processing and decoding of afferent temporal information (Abbott et al. 1997; Tsodyks & Markram, 1997; Markram et al. 1998; Buonomano, 2000; Dittman et al. 2000; Fortune & Rose, 2001; Chung et al. 2002; Fuhrmann et al. 2002; Cook et al. 2003; Abbott & Regehr, 2004; Carlson, 2009; Pfister et al. 2010; Barak & Tsodyks, 2014). From this functional perspective of maintaining robustness in STP profiles and filter structures, it essential to ask if such robustness is tightly regulated by specific mechanisms or could be achieved through disparate synaptic components.
To fill these lacunae and address questions on the role of presynaptic mechanisms and their interactions in regulating synaptic filtering and STP profiles, in this study we first developed a biophysically rooted, conductance‐based synaptic model to assess frequency‐dependent synaptic filtering in response to propagating trains of action potentials (APs) impinging the terminal at different input frequencies. After demonstrating the versatility of the model in matching different types of synaptic filters, we used the model to quantitatively assess the individual impact of altering different presynaptic components, including VGICs, and calcium‐ and release‐handling mechanisms. Next, in assessing the impact of interactions among these presynaptic mechanisms in arriving at specific filter structures, we used global sensitivity analysis (GSA) and demonstrated that near identical filters could be achieved with several non‐unique combinations of synaptic parameters showing weak pairwise correlations. Apart from pointing to degeneracy in the emergence of synaptic filtering and STP, our study shows that the delicate balance between short‐term facilitation and depression that is required to achieve such emergence could be obtained through a multitude of presynaptic mechanisms that are governed by non‐unique combinations of constituent parameters. Our conclusions have significant implications for protein localization strategies required for functional robustness in neuronal structures and for the emergence of specific long‐term synaptic plasticity profiles and associated degeneracy there. These observations further emphasize the need to prioritize the role of holistic interactions in the emergence of neuronal physiology. Importantly, these analyses contribute additional evidence that parametric and interactional complexity in biological systems should not be viewed from the limited curse‐of‐dimensionality standpoint, but from the evolutionarily advantageous perspective of providing functional robustness through degeneracy (Edelman & Gally, 2001; Stelling et al. 2004; Whitacre & Bender, 2010).
Methods
A simplified conductance‐based model, comprising (Fig. 1 A, B) a presynaptic neuronal soma projecting through a myelinated axon to a presynaptic terminal apposed to a postsynaptic spine compartment, was used to study presynaptically expressed forms of STP. The rationale behind the inclusion of a presynaptic soma and a minimal axonal arbour was to avoid artifacts that arose when APs were generated by direct current injection into a stand‐alone presynaptic terminal. In our configuration, the current was injected into the soma of the presynaptic neuron, which avoided current injection artifacts at the terminal's AP traces and effected a biophysically rooted model to assess the impact of VGICs in the terminal on propagating APs.
Figure 1. Model description and quantifications for synaptic filtering and short‐term plasticity.
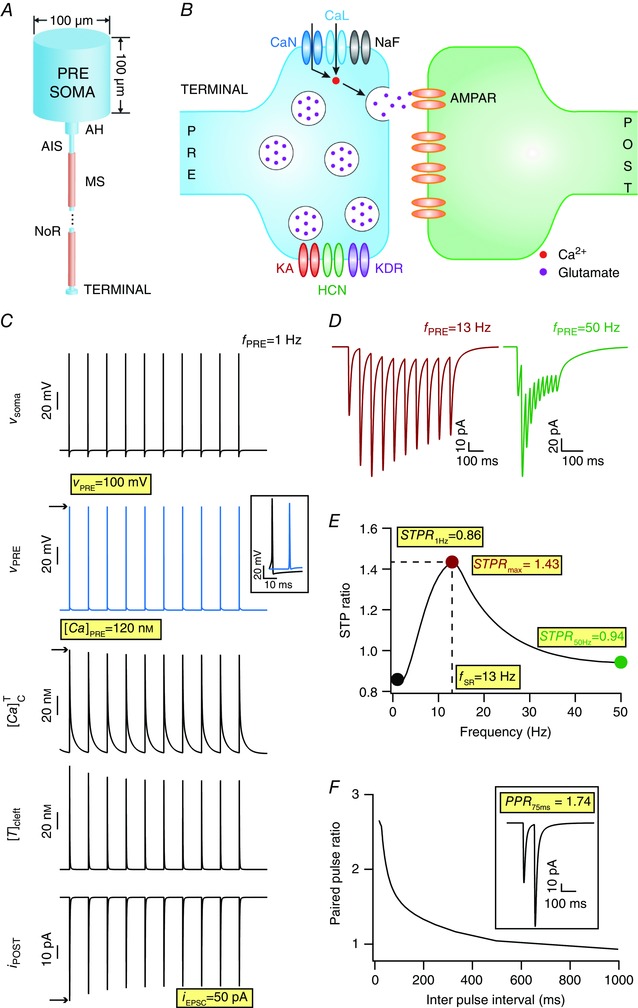
A, schematic of the presynaptic neuronal model, including the axonal segments enabling propagation of APs to the terminal. AIS, axonal initial segment; AH, axon hillock; MS, myelin sheath; NoR, nodes of Ranvier. B, schematic of a synapse showing the presynaptic terminal (PRE) and the postsynaptic spine (POST) with all the channels and receptors used in this study. Channels on the presynaptic terminal are: KA, A‐type K+; HCN, hyperpolarization‐activated cyclic‐nucleotide gated; KDR, delayed rectifier K+; NaF, fast Na+; CaN, N‐type Ca2+; CaL, L‐type Ca2+. Receptors on the postsynaptic side are: AMPAR, α‐amino‐3‐hydroxy‐5‐methyl‐4‐isoxazolepropionic acid receptors. C, (top‐to‐bottom) action potential generated at presynaptic soma (v soma), AP propagated to terminal (v PRE) (inset shows an AP propagation delay of 12 ms between the soma and the terminal), calcium spikes triggered at terminal by invasion of APs ([Ca]PRE), neurotransmitter released into the cleft due to calcium elevation at the terminal ([T]cleft), excitatory postsynaptic current (EPSC; i POST) consequent to postsynaptic receptor opening after neurotransmitter binding, with the somatic firing frequency (f PRE) set at 1 Hz. D, EPSC traces for f PRE set at 13 Hz (left) and 50 Hz (right). E, short‐term plasticity (STP) ratio (STPR) profile obtained for f PRE spanning 1–50 Hz in a model tuned to replicate the band‐pass structure of the CA3–CA1 Schaffer collateral synapses. The frequency at which STPR reaches its maximum value (STPR max) was defined as the synaptic resonant frequency (f SR). STPR values obtained with f PRE = 1 Hz (STPR 1Hz) and with 50 Hz (STPR 50Hz) were also used as quantifications of the STP profile. F, paired pulse ratio (PPR, ratio between the EPSC response amplitude to the second stimulus and that to the first stimulus) decreases as the inter‐pulse interval (IPI) increases. Inset shows example response at an IPI of 75 ms. Note that the eight measurements highlighted in yellow were used as quantifications of synaptic filtering and STP throughout this study. [Color figure can be viewed at wileyonlinelibrary.com]
Presynaptic neuronal model and AP propagation
The morphological configurations of the model's presynaptic components were set as follows. The soma was a cylindrical single compartment with both length and diameter set at 100 μm (length × diameter = 100 × 100 μm). The soma was connected to an axon hillock (AH; 15 × 3 μm), which in turn was connected to an axonal initial segment (AIS; 25 × 2 μm). The rest of the axon was modelled as a series of 50 pairs of myelinated axonal section (modelled as a passive compartment of 200 × 2 μm) and node of Ranvier (4 × 1 μm). This axon terminated at the presynaptic terminal, modelled as a cylinder of length 0.5 μm and diameter of 2 μm. All model components were segmented into smaller compartments as per the d λ rule (Carnevale & Hines, 2006) to ensure that each compartment was smaller than 0.1λ100, where λ100 was the space constant of the model component computed at 100 Hz.
The default passive electrical parameters for the model components were: specific membrane resistivity, R m = 40 kΩ.cm2; cytoplasmic axial resistivity, R a = 120 Ω.cm; specific membrane capacitance, C m = 1 μF.cm–2. All passive properties were uniform for all the sections except for segments that represented the myelinated part of the axon, where R m = 80 kΩ.cm2 and C m = 0.5 μF.cm–2 to account for myelination. All sections of this presynaptic neuron, except myelinated parts of the axon, were endowed with fast sodium (Na) and delayed rectifier potassium (KDR) channels to enable active AP propagation from the soma to the terminal. Apart from Na and KDR channels, L‐type calcium (CaL), N‐type calcium (CaN), hyperpolarization activated cyclic nucleotide gated (HCN) and the transient A‐type potassium (KA) channels were also inserted into the presynaptic terminal (Fig. 1 B). Kinetics and voltage‐dependent properties for all conductances were derived from experimental measurements in hippocampal CA3 pyramidal neurons (Migliore et al. 1995). For the base model, the Na and KDR conductances in the presynaptic compartments were tuned to obtain APs with a width of ∼2 ms that propagated to the terminal with minimal attenuation. The sodium conductance values at the AIS and at the nodes of Ranvier were set to be higher than at the soma, and it was confirmed that AP initiation occurred at the AIS. We incorporated CaN and CaL channel conductances into the presynaptic terminal to account for experimental observations that suggest a role for both these channels in neurotransmitter release at the Schaffer collateral synapses (Ahmed & Siegelbaum, 2009). Both these calcium currents (CaN and CaL) were modelled using the Goldman–Hodgkin–Katz (GHK) conventions (Goldman, 1943; Hodgkin & Katz, 1949) and included a gating variable to account for calcium‐dependent inactivation (Migliore et al. 1995; Budde et al. 2002).
APs were generated by somatically injecting a train of 10 current pulses of 2 nA amplitude and 2 ms duration at different frequencies ranging from 1 to 50 Hz. The APs passively propagated through myelinated sections, and were regenerated at the nodes of Ranvier, thereby maintaining the continuity and reliability of signal propagation to the terminal. This procedure was used to stimulate the presynaptic terminal at different firing frequencies (f PRE).
Calcium handling in the presynaptic terminal
Neurotransmitter release is tightly coupled to the cytosolic calcium concentration at the terminal (), as binding of vesicles to the plasma membrane for subsequent release depends on [Ca2+] in the terminal. We incorporated a detailed reaction‐diffusion model for calcium in the presynaptic terminal, with calcium ON and OFF mechanisms and radial diffusion adopted from Ashhad & Narayanan (2013). Specifically, the cytosolic calcium dynamics in the terminal was modelled by the partial differential equation (Sneyd et al. 1995; Fink et al. 2000; Ashhad & Narayanan, 2013):
| (1) |
where D Ca (220 μm2 s–1) represented the diffusion coefficient for Ca2+ (Allbritton et al. 1992; Klingauf & Neher, 1997), and α (0.9) defined the density of inositol triphosphate receptors (InsP3R) on the endoplasmic reticulum (ER). J InsP3R, J leak, J SERCA, J VGCC, R buf and J pump represented Ca2+ flux due to InsP3Rs, ER leak channels, sarcoplasmic endoplasmic reticulum Ca2+ ATPase (SERCA) pumps, voltage‐gated calcium channels (VGCCs), buffer and plasma membrane Ca2+ extrusion pumps, respectively, and are defined below. Radial diffusion of Ca2+ was implemented by radially compartmentalizing the terminal section into four concentric annuli. The was determined by the [Ca2+] in outer most annulus (Carnevale & Hines, 2006).
As there are several lines of evidence for the presence of presynaptic ER, and for its role in regulating terminal calcium (Llano et al. 2000; Brain et al. 2001; Emptage et al. 2001; Han et al. 2001; Verkhratsky, 2002; Zucker & Regehr, 2002; Bouchard et al. 2003; Bardo et al. 2006; Cabezas & Buno, 2006), release kinetics and STP across different synaptic structures, we explicitly incorporated ER release, pump and leak mechanisms into our model. InsP3R‐dependent release from ER was modelled as a function of cytosolic InsP3 concentrations as follows (Li & Rinzel, 1994; Fink et al. 2000; Ashhad & Narayanan, 2013):
| (2) |
where (3500 μm s–1) represents the maximal rate of release, K InsP3 (0.8 μm) is the dissociation constant for InsP3 binding to InsP3R, K act (0.3 μm) denotes the dissociation constant for Ca2+ binding to an activation site on the receptor and [Ca]ER represents the calcium concentration within ER (0.4 mm). h represents the probability of the inhibition site on InsP3R being unoccupied, which evolved with time as:
| (3) |
where k on (2.7 μm–1s–1) defines the on rate of Ca2+ binding to the inhibition site and K inh (0.2 μm) represents the dissociation constant of Ca2+ unbinding from the inhibition site. This mechanism was implemented to account for inhibition of Ca2+ release from InsP3Rs at high (Li & Rinzel, 1994; Ashhad & Narayanan, 2013).
The rate of Ca2+ influx into cytosol from ER leak channels was modelled as (Fink et al. 2000):
| (4) |
where L was chosen such that the net flux of Ca2+ at resting state (–65 mV) was around zero.
Ca2+ current through VGCCs (L‐ and N‐type) was converted to Ca2+ concentration as (Poirazi et al. 2003; Ashhad & Narayanan, 2013):
| (5) |
where I Ca denotes the net inward Ca2+ current, diam the diameter of the section and F Faraday's constant.
Ca2+ uptake by the SERCA pump was modelled as follows (Fink et al. 2000):
| (6) |
where V max (4 × 10–4 mm ms–1) was the maximal rate of the SERCA pump and K P (0.27 μm) is the dissociation constant of Ca2+ binding to the pump.
Ca2+ efflux through plasma membrane calcium extrusion pumps was modelled as follows (Fink et al. 2000; Ashhad & Narayanan, 2013):
| (7) |
where Ca th (200 nm) defines the threshold for beyond which the extrusion pumps were activated, and γ represents the density of the pump.
The rate of change in due to stationary buffers was implemented as (Fink et al. 2000; Ashhad & Narayanan, 2013):
| (8) |
| (9) |
and
| (10) |
where [B] and [CaB] represent the free and calcium‐bound buffer concentrations in the section. (=1000 mm –1 ms–1) and are the rate constants for calcium binding to and unbinding from buffer. This pseudo steady state approximation was based on the assumption that bound buffer concentration was in rapid equilibrium with surrounding Ca2+. The value of K D was set to 4 μm. The total buffer concentration (T buf = 0.52 μm) was defined as the sum of free and bound buffer concentrations.
Short‐term plasticity
The evolution of STP in the conductance‐based model synapse was modelled through a system of coupled differential equations. Whereas the residual calcium, and thereby synaptic facilitation (Zucker, 1989; Zucker & Regehr, 2002), would automatically be accounted for by the mechanistic models used for calcium handling, accounting for synaptic depression warranted an explicit model for terminal neurotransmitter concentration and transmitter replenishment (Sudhof, 2012, 2013, 2014).
The evolution of [T]T, the concentration of neurotransmitter in the presynaptic terminal, was modelled as (default parametric values are listed in Table 1):
| (11) |
where represents the steady‐state value of [T]T, τTT denotes the replenishment rate of the neurotransmitter in the presynaptic terminal and f T governs the intensity of neurotransmitter release into the cleft. The calcium concentration was raised to the power of three to account for the cooperativity among calcium ions binding to synaptotagmin, the calcium sensor, in effectuating the release process (Sudhof, 2012, 2013, 2014). A baseline cytosolic concentration 50 nm of was subtracted from (eqn 11).
Table 1.
Range of parameter values considered for global sensitivity analysis
| Parameter (unit) | Symbol | Default value | Distribution range | |
|---|---|---|---|---|
| Maximum sodium conductance (mS cm–2) |
|
53.866 | 40–60 | |
| Maximum potassium conductance (mS cm–2) |
|
16.384 | 12–18 | |
| Maximum L‐type calcium conductance (mS cm–2) |
|
0.938 | 0.5–0.8 | |
| Maximum N‐type calcium conductance (mS cm–2) |
|
0.8 | 0.92–1.2 | |
| Maximum HCN conductance (mS cm–2) |
|
0.188 | 0.1–20 | |
| Maximum A‐type potassium conductance (mS cm–2) |
|
15.907 | 10–1000 | |
| Calcium threshold for plasma membrane extrusion pumps (nm) |
|
200 | 170–250 | |
| Average rate of Ca2+ flux density in plasma membrane extrusion pumps (μm s–1) | γ | 19 × 1010 | 4 × 1010–1 × 1012 | |
| Average amplitude of SERCA pump uptake (μm ms–1) | V max | 0.4 | 0.35–0.58 | |
| Dissociation constant for stationary buffer (μm) | K D | 4 | 3.5–4.4 | |
| Total stationary buffer concentration (mm) | T bufs | 0.522645 | 0.5–0.7 | |
| Steady‐state neurotransmitter concentration in terminal (mm) |
|
0.0001 | 0.00005–0.0001 | |
| Replenishment rate of neurotransmitter at terminal (ms) | τTT | 125 | 50–250 | |
| Decay constant of neurotransmitter in the cleft (ms) | τTC | 0.0001 | 0.00002–0.0001 | |
| Per‐AP intensity of neurotransmitter release into the cleft (mm –1 mm –1 mm –1 ms–1) | f T | 11 × 109 | 4 × 109–2.75 × 1010 |
The evolution of [T]C, the concentration of neurotransmitter in the synaptic cleft, was modelled as:
| (12) |
where τTC denotes the reuptake rate of the neurotransmitter from the cleft. Note that the second term of this equation is the negative of the second term in eqn (11).
Postsynaptic structure and receptor models
The postsynaptic neuronal compartment was modelled as a cylinder of 2 μm diameter × 0.5 μm length. The postsynaptic structure was purely passive, as our goal here was to evaluate the role of presynaptic VGICs in regulating synaptic filtering and STP. Ionotropic receptors located on the postsynaptic structure, whose opening was regulated by presynaptically released transmitter concentration, resulted in an EPSC that was modelled as the AMPA receptor (AMPAR) current (Fig. 1 A). The kinetics of the AMPAR current was adopted from previous literature (Narayanan & Johnston, 2010; Ashhad & Narayanan, 2013; Honnuraiah & Narayanan, 2013), which was modelled as the sum of currents carried by sodium and potassium ions:
| (13) |
where the sodium and potassium currents followed the GHK conventions (Goldman, 1943; Hodgkin & Katz, 1949):
| (14) |
| (15) |
represents the maximum permeability of the AMPAR, whose default value was set at 0.1 μm s–1. The relative permeability ratios P Na and P K were equal and set to 1 (Dingledine et al. 1999). s(t) governed the kinetics of AMPAR current, and was gated by the cleft transmitter concentration as follows (Destexhe et al. 1998):
| (16) |
where αs and βs were forward and reverse rates for the opening of the AMPAR, and were computed as and , with τd (3 ms) and τr (0.6 ms) respectively defining the decay time constant and the rise time constant (Andrasfalvy & Magee, 2001). We normalized s(t) such that 0 ≤ s(t) ≤ 1.
Physiological measurements
We used eight different physiological measurements to quantify model performance, and to compare physiological equivalents (Fig. 1). To quantify STP profiles, trains of 10 pulses were injected into the presynaptic soma at different frequencies (f PRE), which ultimately elicited 10 EPSCs (measured under voltage‐clamp of the postsynaptic compartment at –70 mV), after AP propagated through the axon into the terminal eliciting calcium influx through the VGCCs on the terminal that resulted in neurotransmitter release into the cleft. The STP profile was constructed as a function of f PRE (Fig. 1 E), with an STP ratio (STPR) measured for each value of f PRE. STPR, for any given value of f PRE, was computed as the ratio between the average EPSC amplitude of the last three input pulses (pulses 8–10) and the amplitude of the first of the 10 EPSCs in the train (Dittman et al. 2000).
| (17) |
where A EPSC (i) represents the amplitude of the ith EPSC in the train of 10 EPSCs. Pair‐pulse ratio (PPR) was computed as the ratio between the second EPSC amplitude and the first EPSC amplitude, with the inter‐pulse interval set at 75 ms:
| (18) |
All eight measurements used here are highlighted in Fig. 1 C–F, with a description provided in the Results.
Global sensitivity analysis: generation of random models and their validation
We used a GSA technique (Foster et al. 1993; Goldman et al. 2001; Rathour & Narayanan, 2012 b, 2014; Anirudhan & Narayanan, 2015; Srikanth & Narayanan, 2015) to study how the variability within a set parameter distribution and interactions among them would affect the measurements that quantified STP profiles and synaptic filtering. To generate models for GSA, we first tuned a base model such that the parameters (Table 1) and the measurements were confined to corresponding physiological limits in experimental observations (Dittman et al. 2000) and elicited a band‐pass‐like STP profile (Fig. 1 E). In total, 7000 unique models were generated using a random sampling procedure on 15 different model parameters, each governed by a uniform distribution spanning the lower–upper bounds given in Table 1. Ranges of these model parameters were chosen by assessing their extreme values (through single‐ and cross‐sensitivity analyses) where there was incomplete propagation of APs into the terminal, or depolarization‐induced block in the terminal (both due to extreme values for the Na/K conductances in the presynaptic terminal), or hindrance to achieving the band‐pass structure of the synaptic filters (because of heavy or weak calcium decay or because of extreme conditions of transmitter pool depletion/replenishment). We computed all the eight measurements for each of these 7000 models, and investigated whether these measurements were within their respective valid ranges (Table 2). In total, 104 out of 7000 models (∼1.5%) had all eight measurements within their respective acceptable ranges (Table 2) obtained from corresponding experimental values (Dobrunz et al. 1997; Klingauf & Neher, 1997; Dittman et al. 2000; Magee & Cook, 2000; Andrasfalvy & Magee, 2001; Narayanan & Johnston, 2007), implying that they matched with experimental constraints with reference to all quantified measurements, and were declared as valid models for ensuing analyses.
Table 2.
Limits on measurements to select valid models for global sensitivity analysis
| Measurement | Symbol | Base model value | Valid range |
|---|---|---|---|
| Terminal action potential amplitude | v PRE | 100 mV | ≥90 mV |
| Terminal calcium transient amplitude | [Ca]PRE | 120 nm | 100–300 nm |
| First EPSC response | i EPSC | 50 pA | <100 pA |
| Maximum STP ratio | STPR max | 1.43 | 1.245–3 |
| Resonance frequency | f SR | 13 | 7–24 Hz |
| STP ratio at 1 Hz | STPR 1Hz | 0.86 | 0.85–1.13 |
| STP ratio at 50 Hz | STPR 50Hz | 0.94 | 0.9–1.145 |
| Paired pulse ratio for IPI of 75 ms | PPR 75ms | 1.74 | 0.75–4 |
Virtual knockout models
Within the GSA framework, virtual knockout models (VKMs) constitute a powerful technique to quantitatively assess the contribution of specific channels to chosen measurements (Rathour & Narayanan, 2014; Anirudhan & Narayanan, 2015). In assessing these contributions using VKMs, we knocked‐out a specific channel conductance individually from each of the 104 valid models, and computed each of the eight measurements after this knockout. We then computed the percentage change in each of these measurements from their respective valid base model values (when all the channels were intact) to quantify the acute impact of knocking out that channel on specific measurements. This procedure was repeated for all six channel conductances present in the presynaptic terminal (Na, KDR, CaL, CaN, HCN and KA) and the statistics of percentage changes in each measurement for each VKM were assessed.
We used these statistics to also compute the contribution strength of each channel to the eight different measurements (Rathour & Narayanan, 2014). Specifically, if Mp(Ci) were considered to represent the mean percentage change of measurement p (1 ≤ p ≤ 8) of VKMs derived by deleting channel Ci (1 ≤ i ≤ 6), then the contribution strength of a channel Cq for a given measurement p was computed as (Rathour & Narayanan, 2014):
where |.| represents the absolute value of the arguments and maxi |Mp (Ci)| denotes the maximum value of |Mp (Ci)| spanning all the VKMs. This procedure spanned all measurements and all channels. For visualization of these contribution strengths (Rathour & Narayanan, 2014), , we generated a matrix of circles with channels (q) and measurements (p) represented as rows and columns, respectively. We set the diameter of the circles forming element (q, p) of this matrix to be proportional to , such that the largest and smallest circles would respectively be for elements maxq |Mp (Cq)| and minq |Mp (Cq)| (see Fig. 8 F). Note that the linear extrapolation from to circle diameters was a measurement‐dependent process, and was performed independently for each measurement Mp.
Figure 8. Quantification of the differential contribution of each presynaptic voltage‐gated ion channel subtype to the emergence of short‐term plasticity profile and synaptic filtering.
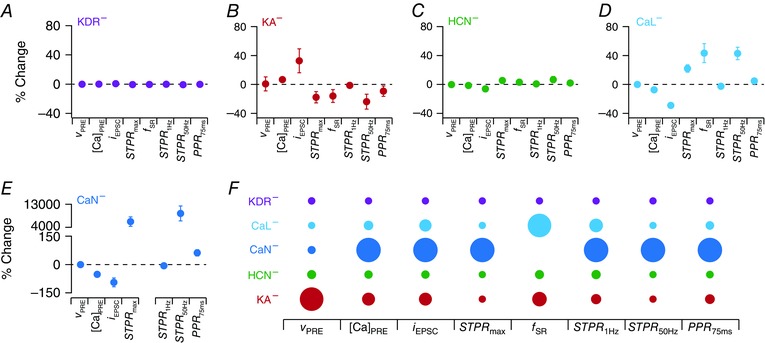
A–E, statistics of percentage changes computed in each of the different physiological measurements (represented as mean ± SD; see Fig. 7) when channels, KDR (A), KA (B), HCN (C), CaL (D) and CaN (E), were individually knocked‐out. F, diagrammatic representation of the contribution strength of individual channel conductances to different physiological measurements. Larger size of the circle implies greater contribution (on average) of the specific channel (different rows) to the corresponding physiological measurement (different columns). [Color figure can be viewed at wileyonlinelibrary.com]
Computational details
All the simulations were performed using the NEURON simulation package (Carnevale & Hines, 2006) at resting membrane potential of –65 mV and temperature of 34°C, with an integration time step of 25 μs. Analyses were performed with custom‐written software in MATLAB and Igor Pro (WaveMetrics, Inc., Lake Oswego, OR, USA).
Results
Our first goal was to develop a conductance‐based biophysically rooted model of a synapse to study the impact of VGICs expressed in the presynaptic terminal on STP profiles and associated synaptic filtering. In doing this, we constructed an active presynaptic neuronal model containing a soma connected to an axon that terminated on a terminal bouton and a passive postsynaptic structure that was equipped only with ionotropic receptors for the neurotransmitter released from the presynaptic terminal (Fig. 1 A, B). This configuration allowed us to assess the impact of propagating APs arriving at the terminal with different frequencies (f PRE), initiating a sequence of events that would culminate in neurotransmitter release. Specifically, these propagating APs activated several VGICs, including VGCCs, expressed in the presynaptic terminal and either mediated (by calcium channels) or modulated (by other channels) calcium influx into the terminal. Calcium dynamics in the presynaptic terminal was modelled in detail, specifically including biophysical models of the plasma membrane and ER calcium pumps, calcium buffers, calcium leak and release from the ER and diffusion (eqn 1).
In modelling STP, the residual calcium from previous APs would automatically be accounted for in our model, given the mechanistic nature of calcium decay. Cytosolic calcium in the presynaptic terminal was then translated to transmitter release through a dynamic formulation that was also governed by the transmitter concentration in the terminal and a parameter governing the intensity of transmitter release for each AP (eqn 11). These design configurations offered a critical advantage in that a separate parameter to govern facilitation was not necessary, and residual calcium and associated kinetics would mechanistically account for short‐term facilitation and its strength. Finally, we modelled terminal transmitter replenishment defined by a specified replenishment rate (eqn 11), which mechanistically governed short‐term depression (when replenishment rate was lower than the presynaptic firing rate). Together, in agreement with associated physiological observations (Zucker, 1989; Zucker & Regehr, 2002; Sudhof, 2012, 2013, 2014), the kinetics of residual calcium and replenishment rate regulated the balance between short‐term facilitation and depression and their dependence on input stimulus rate.
Transmitter released into the cleft at the end of the release process was subjected to a time‐dependent decay to account for diffusion and for reuptake mechanisms (eqn 12). Finally, on the postsynaptic side, a ligand‐gated receptor model was implemented such that its opening was gated by the concentration of transmitter in the cleft (eqn 13). Together, the model provides an ideal mechanistic setup to quantitatively understand the role of different VGICs and other presynaptic mechanisms on synaptic filtering.
Versatility of the model formulation in matching different types of synaptic filters
Using the model setup described above as the base, we stimulated the terminal with 10 pulses of different presynaptic firing frequencies (f PRE) to characterize synaptic physiological properties using eight different measurements (highlighted in Fig. 1): synaptic resonance frequency (f SR), the frequency at which maximum STPR (eqn 17) was observed; maximum STP ratio (STPR max), the STP ratio at resonance frequency; STP ratio for 1 Hz stimulus (STPR 1Hz); STP ratio for 50 Hz stimulus (STPR 50Hz); paired pulse ratio (PPR 75ms) for inter‐pulse interval of 75 ms; amplitude of the first (in a train of 10) AP at terminal (v PRE); amplitude of calcium elevation in the presynaptic terminal (represented by ) elicited in response to the first AP ([Ca]PRE) and the amplitude of first EPSC response (i EPSC). The base model was tuned to elicit a band‐pass synaptic filter (Fig. 1 C–F), which along with other measurements match those from Schaffer collateral synapses from CA3 to CA1 pyramidal neurons (Dobrunz et al. 1997; Klingauf & Neher, 1997; Dittman et al. 2000; Magee & Cook, 2000; Andrasfalvy & Magee, 2001; Narayanan & Johnston, 2007).
Next, to illustrate the versatility of the model in its ability to match high‐ and low‐pass synaptic filters (Dittman et al. 2000), we altered specific parameters in the base model and demonstrate the model's ability in achieving this (Fig. 2). The low‐pass filter characteristic was obtained by reducing the calcium influx into cytosol from ER stores, increasing the replenishment time of neurotransmitter (τTT) and the intensity of neurotransmitter release (f T). On the other hand, the high pass filter profile was attained by reducing the average rate of Ca2+ flux density at plasma membrane (γ), increasing the maximum neurotransmitter concentration () and reducing both τTT and f T. Note that these parametric changes constitute one possible way to achieve low‐ and high‐pass synaptic filters, but not the only possible route for achieving these filter structures (see below). Together, these results demonstrate the model's capabilities in matching different types of synaptic filters and STP profiles in a model that was endowed with specific equivalents of constitutive components in a synapse.
Figure 2. Illustration of the ability of the modelling framework to replicate a wide range of synaptic plasticity profiles.
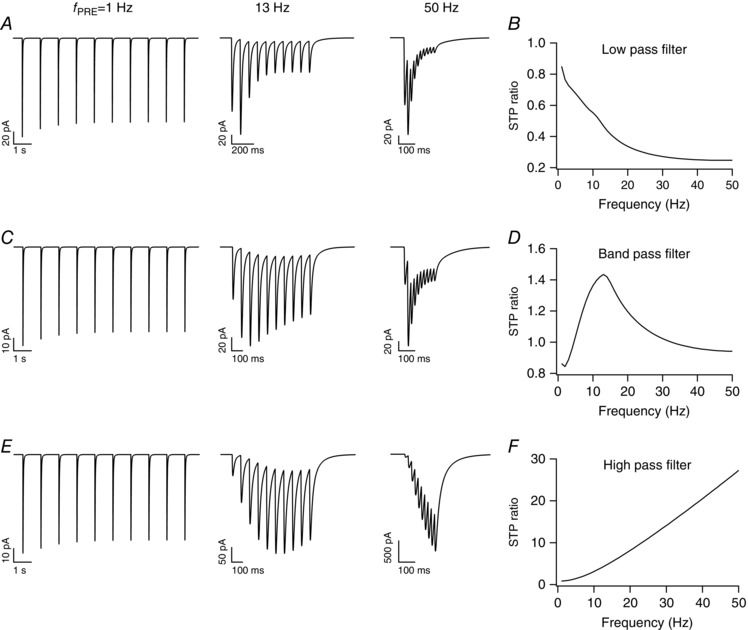
A, postsynaptic current traces for stimulus frequencies (f PRE) of 1 Hz (left), 13 Hz (middle) and 50 Hz (right). B, short‐term plasticity ratio (STPR) plotted as a function of stimulus frequency exhibits low‐pass filter characteristics. C–F, same as A and B, but with different parameters adjusted to achieve synaptic filters that exhibit band‐pass (C, D) and high‐pass (E, F) characteristics.
VGICs in the presynaptic terminal regulate synaptic filtering
The model described above provides a systematic framework to quantitatively assess the impact of individual voltage‐gated conductances and other presynaptic mechanisms in regulating synaptic filtering (Table 3). First, we assessed the impact of independently altering each of the six different VGICs expressed in the presynaptic terminal on synaptic filtering profiles, with all the other parameters retained to their respective base model values. We noted that increasing sodium channel conductance (Fig. 3 A) decreased the STP ratio in the model, along with a small reduction in f SR. Importantly, the selectivity strength Q SR (the ratio between STPR max and STPR 1Hz) of the synaptic filter reduced as a consequence of increasing sodium channel conductance (Fig. 3 A). In contrast, we found that an increase in the conductance of either delayed rectifier (Fig. 3 B) or A‐type (Fig. 3 E) potassium channels resulted in increases in the STP ratio and in Q SR, accompanied by a small increase in f SR. Increase in calcium channel conductances (Fig. 3 C for CaL and Fig. 3 D for CaN), however, decreased f SR, Q SR and STP ratio through increases in presynaptic calcium concentration (Table 3). Finally, increasing the HCN channel conductance decreased f SR, Q SR and STP ratio (Fig. 3 H) due to a depolarizing shift in the resting membrane potential (Fig. 3 F), which resulted in an increased calcium influx (Fig. 3 F) through CaL and CaN channels. We also noted that the impact of altering the HCN channel conductance on a train of EPSCs was dependent on the frequency of presynaptic stimulation (f PRE). Specifically, when f PRE was low (1 Hz; Fig. 3 G), the impact of altering HCN channels was reflected in all EPSC amplitudes. However, when f PRE increased (50 Hz; Fig. 3 G), the impact was confined to the first of the train of EPSCs, owing to the slow (de)activation time constants of HCN channels (Magee, 1998).
Table 3.
Impact of increasing individual channel conductances on different measurements
| Parameter | v PRE | [Ca]PRE | i EPSC | f SR | STPR max | STPR 50Hz | Q SR |
|---|---|---|---|---|---|---|---|
| g Na | Increases* | Increases | Increases | Decreases* | Decreases | Decreases | Decreases |
| g KDR | Decreases* | Decreases | Decreases | Increases* | Increases | Increases | Increases |
| g KA | Decreases | Decreases | Decreases | Increases* | Increases | Increases | Increases |
| g h | No change | Increases | Increases | Decreases* | Decreases | Decreases | Decreases |
| g CaN | No change | Increases | Increases | Decreases | Decreases | Decreases | Decreases |
| g CaL | No change | Increases | Increases | Decreases | Decreases | Decreases | Decreases |
*Small changes.
Figure 3. Short‐term plasticity profiles and synaptic filtering were critically dependent on voltage‐gated channel conductances expressed in the presynaptic terminal.
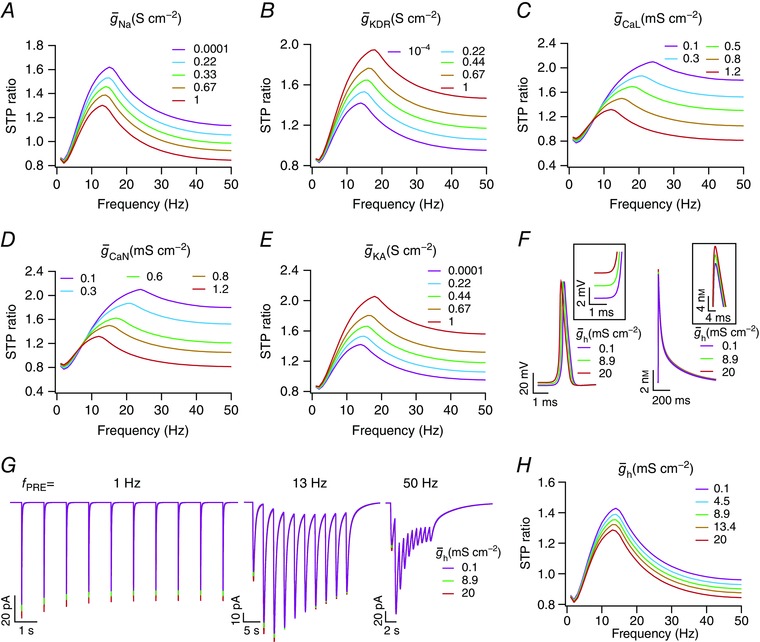
A–E, short‐term plasticity profiles ratio (STPR) plotted as functions of stimulus frequency (f PRE) for different maximal conductances of the fast sodium (A), delayed rectifier potassium (B), L‐type calcium (C), N‐type calcium (D) and A‐type potassium (E) channels expressed in the presynaptic terminal. F, left, representative AP traces, recorded at the presynaptic terminal, for three different values of HCN channel conductance in the terminal. Inset highlights the observation that higher HCN channel conductance results in depolarized resting membrane potential. Right, representative spike‐evoked calcium traces in the presynaptic terminal, recorded concurrent to the three AP traces on the left. Inset depicts the observation that higher HCN channel conductance results in higher calcium influx. G, excitatory postsynaptic current (EPSC) traces for 1, 13 and 50 Hz (f PRE) stimuli, for the same three values of HCN channel conductances in F, showing that EPSC amplitude slightly increases with increase in presynaptic HCN channel conductance. H, STPR plotted as functions of stimulus frequency (f PRE) for different maximal conductances of the HCN channel expressed in the presynaptic terminal. In these analyses, note that changes were limited to the maximal conductance of the specific channel subtype; all the other parameters were not altered from the base model values. [Color figure can be viewed at wileyonlinelibrary.com]
Mechanistically, conductance changes that caused calcium elevation, either through changes in the AP waveform or through modulation of calcium current triggered by the AP, resulted in elevated levels of neurotransmitter release for the first AP. Given that the time constant of neurotransmitter replenishment (τTT) remained the same, this resulted in lesser terminal neurotransmitter ([T]T) available for subsequent releases, thereby reducing the STP ratio especially for stimulus frequencies that are faster than the replenishment rate. Furthermore, such reduced availability of neurotransmitter also implies that the balance between short‐term depression and facilitation would now be tilted in favour of depression. This translates to a reduction in the frequency where the STP ratio attains its peak, which manifests as a reduction in f SR. Together, conductance changes that lead to an increase in the magnitude of AP‐induced calcium elevation (caused by changes in excitability and/or changes in calcium influx from the extracellular matrix through calcium channels) result in reductions of STP ratio, f SR and Q SR, with the quantitative details on the direction and strength of such changes being critically reliant on the kinetics and voltage‐dependence of individual channels.
Calcium‐ and release‐regulatory mechanisms in the presynaptic terminal regulate synaptic filtering
How do the different calcium‐ and release‐regulatory mechanisms present in the presynaptic terminal alter synaptic filtering? To address this, we independently altered each of the several calcium‐related parameters, with all the other parameters retained at their respective base model values, and assessed the STP profile with these altered parameters (Table 4). As expected from the model formulation, none of the calcium‐handling mechanisms altered the amplitude of the AP waveform in the terminal (Table 4). When we increased Ca th, the threshold on cytosolic calcium concentration for the activation of the plasma membrane calcium pump (eqn 7), we found that the amplitude of calcium elevation in response to the first AP was unchanged, given the relatively small amplitude of the first response. Additionally, for the same reason, the STP profile was unchanged for lower frequencies of presynaptic activation (f PRE). However, as the frequency of presynaptic stimulation increased, the temporally summated calcium crossed Ca th, resulting in a scenario where a reduction in Ca th led to a reduction in cytosolic calcium levels (because of pump activation), implying a reduction in the amount of neurotransmitter release. This resulted in a sharper fall in the STP ratio profile especially at higher values of f PRE, leading to a reduction in f SR, Q SR and STPR max with reduction in Ca th (Fig. 4 A, Table 4).
Table 4.
Impact of increasing individual calcium‐ and release‐related parameters on different measurements
| Parameter | v PRE | [Ca]PRE | i EPSC | f SR | STPR max | STPR 50Hz | Q SR |
|---|---|---|---|---|---|---|---|
| Ca th | No change | No change | No change | Increases | Increases | Increases | Increases |
| SERCA V max | No change | Decreases | Decreases | Increases | Decreases | Increases | Decreases |
| Buffer K D | No change | Increases | Increases | Decreases | Decreases | Decreases | Decreases |
| T buf | No change | Decreases | Decreases | Increases* | Increases | Increases | Increases |
| τTT | No change | No change | No change | Decreases* | Decreases | Decreases | Decreases |
| f T | No change | No change | Increases | Decreases* | Decreases | Decreases | Decreases |
*Small changes.
Figure 4. Short‐term plasticity profiles and synaptic filtering were critically dependent on parameters regulating the dynamics of presynaptic calcium and neurotransmitter release.
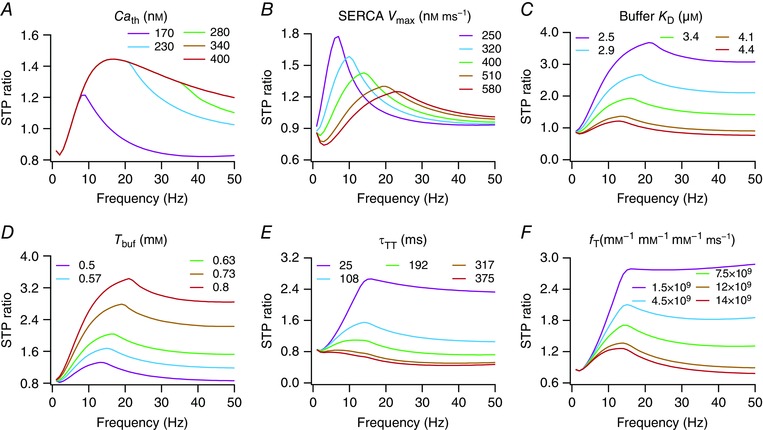
Short‐term plasticity profiles ratio (STPR) plotted as functions of stimulus frequency (f PRE) for different values of calcium threshold (Ca th) of plasma membrane calcium extrusion pumps (A), capacity (V max) of SERCA pump uptake (B), dissociation constant (K D) for the calcium buffer (C), total buffer (T buf) concentration (D), replenishment rate (τTT) of neurotransmitter at terminal (E) and intensity of neurotransmitter release (f T) into the cleft (F). [Color figure can be viewed at wileyonlinelibrary.com]
Next, we increased the V max of SERCA pumps (eqn 6) and found that it reduced the calcium response to the first AP and the first EPSC amplitude (Table 4). Given the Hill equation formulation in eqn (6), the effect of increasing V max would result in a reduction of in a manner that is also dependent on . Consequently, STPR max reduced with increase in SERCA V max, with a concurrent increase in f SR and a reduction in Q SR (Fig. 4 B, Table 4). Note that Ca th (within the tested range) had no significant impact on the calcium response to the first AP, but altered the temporal summation of the calcium response specifically for higher presynaptic frequencies. However, changing V max of the SERCA pump significantly altered both the first calcium response and the summation. This difference is merely a reflection of the difference in model formulation for the two pumps (a threshold based model for the plasma membrane pump, and a Hill equation‐based model for the SERCA pump), and results in their differential regulation of the STP ratio profile and synaptic filtering (Table 4).
Finally, whereas an increase in the dissociation constant K D of the calcium buffer (eqn 10) or a reduction in the total buffer concentration T buf increased and resulted in a reduction of STPR max, f SR and Q SR (Fig. 4 C, D, Table 4), an increase in either the transmitter replenishment time constant (τTT; eqn 11) or in the intensity of per‐AP transmitter release (f T; eqns 11 and 12) reduced STPR max, f SR and Q SR without altering (Fig. 4 E, F, Table 4). The impact of altering K D of the calcium buffer or T buf on the synaptic filters is simply explained by their ability to alter , and how this change in cytosolic calcium levels alters the release process (as in Figs. 3 and 4 A). An increase in τTT implies that the replenishment rate is slower, thereby limiting transmitter availability for subsequent releases. Therefore, for moderate increases in τTT the STPR reduced across a broad range of values for f PRE, also shifting the facilitation–depression balance in favour of depression. This shift in the balance was starkly observable when τTT was increased further, where the STPR profile showed depression across all values of f PRE (Fig. 4 E). A similar argument holds for increases in f T as well, where increasing f T would release a significant proportion of the available neurotransmitters in response to the first AP, thereby limiting transmitter availability for subsequent releases. This results in a shift in the facilitation–depression balance that would favour depression, a shift that manifested clearly for higher values of f PRE in cases when f T was increased to large values (Fig. 4 F). Together, these analyses clearly demonstrate that calcium‐ and release‐regulatory mechanisms expressed in the presynaptic terminal could critically regulate synaptic filtering and STP profiles, without changing the presynaptic voltage or the calcium influx from the extracellular matrix.
GSAs on the synaptic model revealed degeneracy in the manifestation of specific synaptic filters and STP profiles
The single‐parameter sensitivity analyses above (Figs. 3 and 4) provided us with insights on presynaptic mechanisms that could alter synaptic filtering with or without changes in presynaptic voltage or associated calcium influx. However, such single‐parameter sensitivity analyses, where all the other parameters are fixed at specific values, do not provide insights about the cross‐dependencies of parametric sensitivities. Specifically, it is well established, with several converging lines of evidence, that sensitivities of different measurements to specific parameters are critically dependent on other parametric combinations. In other words, whereas a specific measurement might be extremely sensitive to one parameter under one parametric regime, under another regime, that parameter might not have any impact on the measurement under consideration (Goldman et al. 2001; Narayanan & Johnston, 2010; Kispersky et al. 2012; Rathour & Narayanan, 2012 a; Anirudhan & Narayanan, 2015; Drion et al. 2015). In this context, and given the variability and plasticity in the expression profiles of different channels and receptors, it is critical that the dependence of physiological measurements on biophysical parameters accounts for interactions among the different constituent mechanisms that drive the phenomenon. Additionally, it is important to ask if there are specific constraints on parametric values and their cross‐dependencies in eliciting a valid combination of measurements that match with their respective physiological counterparts (Marder & Goaillard, 2006; Marder, 2011; Marder & Taylor, 2011; Rathour & Narayanan, 2012 a, 2014; Anirudhan & Narayanan, 2015).
An ideal means to address these questions and to assess the impact of complex interactions among constitutive components is the use of the GSA paradigm (Foster et al. 1993; Prinz et al. 2003, 2004; Taylor et al. 2009; Rathour & Narayanan, 2012 b, 2014; Anirudhan & Narayanan, 2015; Srikanth & Narayanan, 2015). In this procedure, instead of varying only a single parameter at a time, all parameters in the model are simultaneously varied through a random sampling procedure to find models that fit within physiologically relevant bounds on all measurements of interest. We performed a 15‐parameter (Table 1) GSA on our synaptic model to assess cross‐sensitivities among them in regulating synaptic filtering and STP profiles. Specifically, we first generated 7000 unique models, with each model generated by assigning random values to each of the 15 parameters. These random values were picked from respective uniform distributions that spanned a specific range around baseline values of the specific parameter (Table 1). As these were randomized models, it is expected that several of them would not match experimental ranges of physiological measurements associated with synaptic filtering and STP. Therefore, we subjected measurements computed from each of these 7000 models to a validation procedure, which required that each of the eight synaptic measurements fell within an experimentally determined measurement‐specific bound (Table 2). This validation procedure yielded 104 models (∼1.5%) that were within the specified measurement bounds, and these valid models were used for ensuing analysis.
All valid models, by definition, had their eight synaptic physiological measurements within experimental bounds. As an illustration, EPSC traces for different values of f PRE (Fig. 5) and associated synaptic filters (Fig. 6 A) of five valid models are shown to manifest very similar physiological characteristics. Despite these near‐identical synaptic filters and very similar measurement values (Figs. 5 and 6 A), the 15 parameters associated with these models did not cluster around specific values, but were spread across the entire span of the ranges (Fig. 6 B; Table 3) associated with each parameter. This was further confirmed by the histograms corresponding to each of these parameters from all 104 valid models, which showed that all parameters spanned the entire range of the assigned spread (Fig. 6 C, bottom panels). These observations offered clear evidence that several non‐unique combinations of the constituent parameters (each representing a structurally distinct synaptic component) could result in similar synaptic filters. Together, these results constitute a direct demonstration of degeneracy in the emergence of specific synaptic filters and associated STP profiles.
Figure 5. Traces of presynaptic AP and calcium concentration, together with postsynaptic current traces from five randomly selected valid models exhibit analogous characteristics.
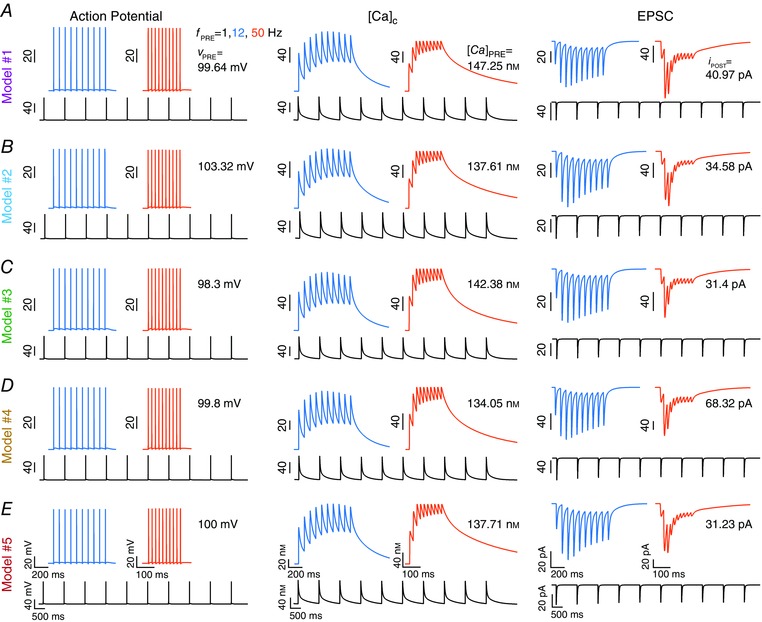
A–E, action potential (left) and calcium concentration (middle) in the presynaptic terminal, plotted with concurrently recorded postsynaptic currents (right) for three different stimulus frequencies (f PRE), 1, 12 and 50 Hz stimuli, plotted for five different models obtained after validation from a GSA procedure. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 6. Global sensitivity analysis reveals degeneracy and weak pairwise correlation between parameters in achieving analogous synaptic filtering and short‐term plasticity profiles.
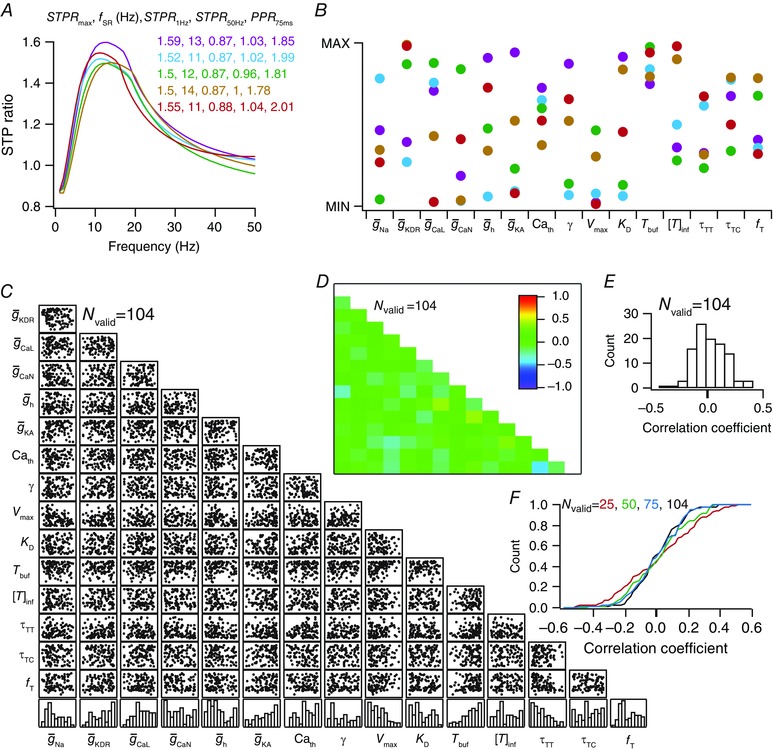
A, STP ratio profiles for models represented in Fig. 5. B, parameter values for the five selected valid models, plotted within minimum and maximum limits of the specific parameter, revealing degeneracy in arriving at analogous synaptic filtering and STP profiles. Parameters associated with each of the different models are depicted with identical markers. C, scatter‐plot matrix depicting pairwise correlation between the 15 parameters used in the GSA procedure. The bottom most row represents normalized histogram plots for each of the 15 parameters, derived from valid models. D, matrix depicting pairwise Pearson's correlation coefficients between the 15 different parameters. The coefficients are computed with reference to the scatter plot matrix shown in C. E, histogram of the 105 unique correlation coefficients in D, revealing weak pairwise correlations between parameters in models that resulted in analogous synaptic filtering and STP. All 104 valid models (N valid = 104) were used for the analyses presented in C–E. F, cumulative histogram of 105 unique pairwise correlation coefficients computed either with parameters from all valid models (N valid = 104) or from a subset of valid models (N valid = 25, 50, 75). Note that the cumulative histogram for the case where N valid = 104 corresponds to the histogram presented in E. [Color figure can be viewed at wileyonlinelibrary.com]
Weak pairwise correlations between valid model parameters reveal degeneracy in mechanisms compensating for changes in any specific model component
Whereas the analyses presented above demonstrated that non‐unique combinations of presynaptic components could result in near‐identical synaptic filtering, they do not provide insights into cross‐dependencies of these parameters in arriving at specific synaptic filters. For instance, these analyses lacked in their ability to address questions on the existence of correlated changes in sets of parameters in arriving at similar synaptic filtering profiles. Do changes in one parameter imply quantitatively equivalent changes in another parameter to maintain functional equivalence? Alternatively, are such changes in one parameter compensated for by changes in several other parameters towards robust functional homeostasis? To address these questions, we constructed pairwise scatter plots of the 15 parametric values in the 104 valid models (Fig. 6 C) and computed associated correlation coefficients for each of the 105 unique pairs (Foster et al. 1993; Taylor et al. 2009; Rathour & Narayanan, 2012 a, 2014; Srikanth & Narayanan, 2015). Of these, 103 pairs exhibited very weak correlations, with the correlation coefficients in the range –0.3 to 0.3, and the maximum (with reference to the absolute value) coefficient value was a weak –0.45 [R 2 = (–0.45)2 = 0.20] between f T and τTT (Fig. 6 D). This implies that the mechanistic basis to compensate for changes (in terms of achieving similar synaptic filters) in one parameter recruited several non‐unique combinations spanning all other parameters, rather than achieving such compensation through pairwise dependence on one other specific parameter.
An important question that emerged from the analyses above was whether 104 models sufficiently characterize the parameter space, and if stronger pairwise parameter correlations would have emerged if the parametric space had been sampled more densely. To address this question, we performed pairwise correlations on subsets of the valid models (Fig. 6 F), and investigated whether the pairwise correlations became weaker when the number of valid models was reduced. We found that the distribution of correlation coefficients became broader with a reduction in the number of valid models, indicating the emergence of stronger correlation coefficients when the number of valid models was reduced (Fig. 6 F). Therefore, with use of lower number of models, we are underestimating the weakness of the pairwise correlations, which is only expected to become weaker with an increase in the number of valid models. We noted this to be consistent with GSA models in the literature, where an increase in the number of valid models resulted in further weakening of pairwise correlation coefficients (Rathour & Narayanan, 2014). These observations further strengthen our conclusions about the adequacy of the 104 models for demonstrating weakness of pairwise correlations across valid model parameters. Together, these results demonstrating that parameters in the valid model population exhibited weak pairwise correlations add further evidence to degeneracy in presynaptic mechanisms that regulate synaptic filtering and STP.
Virtual knockout models
How do individual presynaptic voltage‐gated conductances contribute to different aspects of synaptic filters and STP within this framework of degeneracy? In other words, although it is clear that different channel combinations could yield analogous synaptic filters, do specific channels have a larger impact on specific measurements? To address this question within the GSA framework, we used the VKM approach (Rathour & Narayanan, 2014; Anirudhan & Narayanan, 2015). Here, we took each of the 104 valid models and virtually knocked out a specific channel from each of these models by setting the conductance associated with that channel to zero. We computed each of the eight measurements from these models where the channel was knocked out, and calculated the percentage difference between these measurements and those obtained from the corresponding valid model (where all channels were intact). We used these 104 measurement differences and their statistics, for each of the eight measurements, to quantify the impact of that specific channel individually on each measurement. We repeated this procedure for each of the six different channel conductances expressed in the presynaptic terminal (Na, KDR, CaL, CaN, h and KA), yielding a total of 104 (number of valid models) × 6 (number of channels) = 624 VKMs. Measurement differences, for each of the eight measurements, were computed from these VKMs (by comparing them with their respective base model measurements) and used as quantitative metrics of the impact of each channel on specific measurements (Figs. 7 and 8).
Figure 7. Virtual knockout of channels from valid models reveal differential dependence of synaptic filtering and short‐term plasticity on different presynaptic channels.
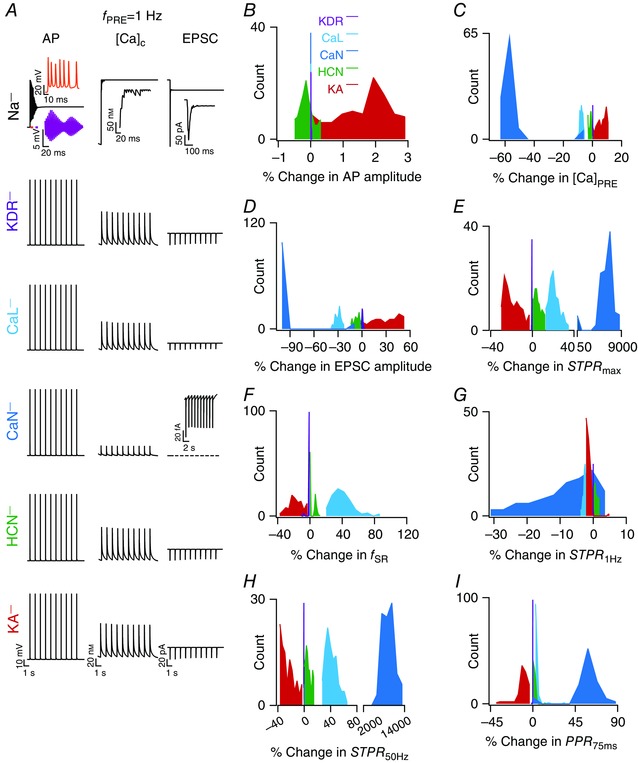
A, representative traces of AP (left), cytosolic calcium (middle) in the presynaptic terminal and postsynaptic current (right) traces, obtained after knockout of specific channels (label on the left extreme) from a specific valid model. For sodium (Na) channel knockout cases, insets show zoomed versions of the traces; the two insets in AP traces depict zoomed versions of the bars depicted in the main trace, whereas single insets in the calcium and current traces are for the initial 120 ms of the corresponding main traces. Inset in the current trace depicting the knockout of the N‐type calcium (CaN) channel represents a zoomed (on the current axis) version of the trace. B–I, distributions of percentage changes, computed after virtual knockout of individual channels, in AP amplitude at terminal (B), amplitude of terminal calcium response to the presynaptic spike (C), postsynaptic current response (D), maximum STP (STP) ratio STPR max (E), synaptic resonant frequency f SR (F), STP ratio for 1 Hz (f PRE) stimulus STPR 1Hz (G), STP ratio for f PRE = 50 Hz STPR 50Hz (H) and paired pulse ratio (PPR) for an inter‐pulse interval of 75 ms (I). [Color figure can be viewed at wileyonlinelibrary.com]
As expected, virtual knockout of terminal sodium channels resulted in ineffective AP propagation into the terminal, thereby making computation of the eight different measurements impossible (Fig. 7 A). Therefore, the quantification of measurements was performed only for VKMs associated with five channels: KDR, CaL, CaN, HCN and KA. First, we observed that knocking out any of KA, KDR, CaL, CaN or HCN channels resulted in small changes in AP amplitude (Fig. 7 B). Next, consistent with results in Fig. 3 and as expected from specific channel function in the context of calcium influx, knocking out KA channels resulted in an increase in [Ca]PRE, whereas deleting HCN, CaN or CaL channels decreased [Ca]PRE. We noted that there was significant variability in the amount of change in [Ca]PRE with each set of VKMs. Such differential dependence of measurements on virtual knockout of the channel was common across all channels and measurements (Fig. 7 C–I), which is to be expected as a direct consequence of variability in channel conductances across valid models (Fig 6 C). The impacts of these channels on all synaptic filter measurements, as observed from VKMs (Figs. 7 C–I and 8 A–E), were consistent with results from single sensitivity analyses, whereby conductance changes that led to an increase in the magnitude of AP‐induced calcium elevation resulted in reductions of STPR and f SR (Fig. 3, Table 3). In comparing results from VKMs (Figs. 7 C–I and 8 A–E) and those from single‐sensitivity analyses (Fig. 3, Table 3), note that VKM results are with reference to reducing the conductance value (setting it to zero), whereas those with single‐sensitivity analyses are presented with reference to an increase in the conductance value (Table 3).
An apparent exception to the consistency of VKM results (Figs. 7 and 8) with single‐sensitivity analyses (Fig. 3) was with reference to the CaN current, where knocking out CaN channels resulted in a significant reduction in the calcium influx (Fig. 7 A). This translated to a significant reduction in neurotransmitter release, thereby reducing the EPSC amplitude significantly (∼99% change in EPSC amplitude in most CaN VKMs; Fig. 7 D) and tilting the facilitation–depression balance in favour of facilitation. This switched the synaptic filters of these model neurons to high‐pass filters (within the 1–50 Hz range tested for f PRE), implying that we could not compute f SR (which is a measure of band‐pass structure in the STP profile) for VKMs corresponding to the CaN channels (Fig. 8 E). The significant reduction in calcium influx with VKMs was a direct consequence of setting CaN channel conductance to zero, which was not the case in the single sensitivity analyses (Fig. 3) where the conductance was never set to zero. Additionally, we also noted that the high‐pass nature of the synaptic filter was a direct outcome of low release that was consequent to low calcium influx when CaN channels were knocked out. Such low initial release implied that the availability of neurotransmitters for consequent releases was higher, and that neurotransmitter depletion never occurred within the 10 pulses, resulting in a scenario where neurons show only facilitation (residual calcium builds up to larger values for higher values of f PRE) and no depression within the 50 Hz limit on f PRE. This facilitation‐only STP profile, a logical extension to the increase in f SR with reduction in g CaN in Fig. 3, may also be gleaned from the dramatic increase in PPR 75ms, STPR max and STPR 50Hz, but not in STPR 1Hz (where the impact of residual calcium on consecutive releases was negligible), with CaN channel knockout (Figs. 7 and 8 E). Therefore, this apparent exception to the consistency of VKM results with single‐sensitivity analyses was just a reflection of quantitative rather than qualitative differences, and our conclusions on the significantly large contribution of the CaN current (in comparison to the CaL current; Figs. 7 and 8) to transmitter release is consistent with similar experimental observations in Schaffer collateral synapses (Ahmed & Siegelbaum, 2009).
Together, these results revealed the variable and differential impact of different presynaptic channels on synaptic filters and STP profiles, reflecting variability in expression of specific channels and their interaction with other presynaptic channels and mechanisms.
Discussion
The principal conclusion of this study is that the delicate balance between short‐term facilitation and depression required to attain specific synaptic filters and STP profiles can be achieved through a multitude of presynaptic mechanisms that are governed by non‐unique combinations of constituent parameters. In arriving at this conclusion, we first developed a model synapse that was endowed with presynaptic mechanisms, encompassing six different VGICs, calcium‐handling mechanisms and processes that regulated neurotransmitter availability in the terminal and the cleft. Different calcium‐handling mechanisms in the presynaptic terminal, encompassing pumps, buffering, diffusion and ER mechanisms that included calcium leak, ER calcium channels and SERCA pumps, were independently and specifically incorporated as dynamic systems. Whereas a dynamic system that specified a replenishment rate defined post‐release replenishment of terminal neurotransmitter, another dynamic system that specified a clearance rate governed neurotransmitter availability in the cleft. Next, we defined eight different physiological measurements that covered different aspects of synaptic filtering and STP, and measured them by stimulating the presynaptic terminal by trains of propagating APs of different stimulus frequencies. Together, this model and associated measurements provided us with an ideal setup to demonstrate the differential contributions of individual presynaptic mechanisms to different aspects of synaptic filtering and STP, thereby providing direct testable predictions on the role of each of these components and interactions among them in regulating synaptic filtering. Importantly, the model was amenable to design a random‐sampling global‐sensitivity analysis procedure that allowed us to demonstrate degeneracy in the manifestation of specific synaptic filters and STP profiles. The existence of such degeneracy was concluded from the ability of disparate parameters to elicit near‐identical STP profiles, and from the weak pairwise correlations that these disparate parametric values exhibited.
Interactions among constituent components govern synaptic filtering
It has been clear from a growing body of evidence, starting from the first quantitative description of APs (Hodgkin & Huxley, 1952) to more recent assessments involving several ion channels and/or calcium‐handling mechanisms (Goldman et al. 2001; Prinz et al. 2004; Narayanan & Johnston, 2010; Marder & Taylor, 2011; Kispersky et al. 2012; Rathour & Narayanan, 2012 a, b; Ashhad & Narayanan, 2013; Rathour & Narayanan, 2014; Anirudhan & Narayanan, 2015; Drion et al. 2015; Marder et al. 2015; Gjorgjieva et al. 2016), that neuronal physiology and plasticity emerge from spatiotemporal interactions among constituent components. Recent analyses have also demonstrated that the specific nature of these interactions and the qualitative/quantitative outcomes of these interactions are critically reliant not just on the dynamics of individual mechanisms but also on their relative abundance and their spatial localization profiles. Emergent phenomena that are outcomes of such interactions could yield very counterintuitive results, such as cases where an increase in sodium conductance results in a reduction in firing rate (Kispersky et al. 2012), or an increase in a potassium conductance increases firing rate (Drion et al. 2015) or shifts a long‐term plasticity profile towards the left (Narayanan & Johnston, 2010; Anirudhan & Narayanan, 2015).
In this context, results from our study demonstrate that the synaptic filters and STP profiles critically depend on the kinetics and abundance of specific voltage‐gated channels and calcium‐handling components in the presynaptic terminal. Whereas individual voltage‐gated channels and interactions among them altered synaptic filters through changes in excitability and consequent changes in the transmembrane calcium current, calcium‐ and release‐regulatory mechanisms altered these filters without changing the presynaptic voltage or the calcium influx from the extracellular matrix. In this context, it is important to distinguish between electrophysiological measurements (voltage and calcium current) and measures of calcium concentration, and the caution that needs to be exercised in employing one set of measures as a proxy for the other. Specifically, calcium concentration in a compartment is not a simple function of transmembrane voltage or calcium current, but is critically dependent on several non‐linear calcium‐handling mechanisms including pumps, buffers, ER mechanisms and diffusion. Calcium concentration and its kinetics could therefore be significantly altered without changes in the kinetics of transmembrane voltage or calcium current (e.g. Fig. 4, Table 4). This implies that extreme caution should be exercised in using calcium concentration and its kinetics as a quantitative proxy for electrical measurements such as voltage or calcium current, especially given the non‐linear nature of calcium‐handling and voltage‐dependent mechanisms expressed in these compartments (Sabatini & Regehr, 1998; Awatramani et al. 2005; Berger et al. 2007; Popovic et al. 2015).
The impact of interactions between channels and how they can drive physiological properties, in ways that can sometimes be contradictory, has been best elucidated with HCN channels as one among the interacting channels (Tsay et al. 2007; Dyhrfjeld‐Johnsen et al. 2009; Narayanan & Johnston, 2010; Pavlov et al. 2011; Migliore & Migliore, 2012; Rathour & Narayanan, 2012 a; Das & Narayanan, 2015; Mishra & Narayanan, 2015). With reference to presynaptic physiology, HCN channels have been shown to express in several presynaptic terminals (Southan et al. 2000; Cuttle et al. 2001; Lujan et al. 2005; Boyes et al. 2007; Rancz et al. 2007; Huang et al. 2011), and alter release properties through their interactions with other channels expressed in the terminal. For instance, in cortical excitatory synapses HCN channels inhibit synaptic release by suppressing the activity of T‐type calcium channels (Huang et al. 2011). However, our results suggest an increase in synaptic release with increase in HCN channel conductance (Fig. 3), consistent with a reduction in synaptic release with deletion of these channels (Figs. 7 and 8).
These differences are easily explained by noting differences in the specific channels that interacted with HCN channels. Whereas HCN channels interacted with a fast inactivating T‐type calcium channels in cortical synapses, in our model they interacted with non‐inactivating L‐type and slowly inactivating N‐type calcium channels (Ahmed & Siegelbaum, 2009). Specifically, the depolarization introduced by the presence of HCN channels resulted in reduced calcium influx through inactivation of T‐type calcium channels in cortical synapses (Huang et al. 2011). However, in our model this depolarization resulted in enhanced calcium influx by the activation of L/N‐type Ca2+ channels (Fig. 3 F, G), resulting in opposite directions of regulation. Together, this provides another stark example of how neuronal physiology is an emergent property that is critically reliant on interactions among channels and components, rather than a reflection of a single channel/component that expresses in the neuronal compartment. It is therefore essential that spatiotemporal interactions spanning all the different components be carefully assessed before assigning causal relationships between individual channels and specific physiological phenomena (Awatramani et al. 2005; Marder & Goaillard, 2006; Taylor et al. 2009; Marder & Taylor, 2011; Kispersky et al. 2012; Rathour & Narayanan, 2012 a, b , 2014; Drion et al. 2015; Mishra & Narayanan, 2015; Rathour et al. 2016).
Implications for degeneracy in synaptic filtering and STP
An important implication for the existence of degeneracy in synaptic filtering is that it is not essential for the protein‐targeting machinery in neurons to maintain each channel and each presynaptic component (pumps, buffers) at precise expression levels to maintain functional robustness (Marder & Goaillard, 2006; Hanus & Schuman, 2013; Rathour & Narayanan, 2014). The complexity associated with the number of presynaptic components and the variable expression profiles of each of them, instead of being an impediment in terms of combinatorial explosion of parametric combinations that contribute to the curse‐of‐dimensionality, turns out to be a critical advantage in terms of providing numerous routes to achieving functional robustness (Tononi et al. 1999; Edelman & Gally, 2001; Whitacre & Bender, 2010; Rathour & Narayanan, 2014; Anirudhan & Narayanan, 2015; Drion et al. 2015; Rathour et al. 2016). This constitutes an extremely critical advantage in adaptable systems in allowing for different possibilities towards achieving a goal, apart from providing a theoretically well‐grounded explanation for the variability in expression profiles of different components (Tononi et al. 1999; Edelman & Gally, 2001; Marder & Goaillard, 2006; Whitacre & Bender, 2010; Marder, 2011; O'Leary et al. 2014; Rathour & Narayanan, 2014; Anirudhan & Narayanan, 2015; Drion et al. 2015; Srikanth & Narayanan, 2015; Rathour et al. 2016). This advantage, conferred by the ability to achieve functional robustness through disparate routes, bestows synaptic structures with a broad set of options in maintaining plasticity profiles and filter structures, especially in cases where such robustness has been demonstrated to be critical in encoding, estimation, processing and decoding of afferent temporal information (Abbott et al. 1997; Tsodyks & Markram, 1997; Markram et al. 1998; Buonomano, 2000; Dittman et al. 2000; Fortune & Rose, 2001; Chung et al. 2002; Fuhrmann et al. 2002; Cook et al. 2003; Abbott & Regehr, 2004; Carlson, 2009; Pfister et al. 2010; Barak & Tsodyks, 2014).
A related implication, with reference to variability in expression profiles of individual components that is a necessary corollary in systems expressing degeneracy, is that the dependence of any functional measure on underlying components is significantly variable (Figs. 7 and 8). This implies that any perturbation that is specific to one component, or a perturbation that affects these components differentially, would result in differential changes in different measurements. The magnitude and direction of these changes critically depend on the expression profile of individual components in each of these different systems (O'Leary et al. 2013, 2014; Rathour et al. 2016), implying a significant dissociation between different forms of functional homeostasis (Anirudhan & Narayanan, 2015; Srikanth & Narayanan, 2015). As a specific example with reference to our study, this implies that the maintenance of homeostasis in synaptic filtering profiles (through certain changes in specific parameters) would not necessarily translate to presynaptic calcium homeostasis (or vice versa), given the differential dependence of these measurements on underlying components (Tables 3 and 4, Figs. 3, 4, 7 and 8). Therefore, an important question in systems that exhibit degeneracy is on the specific physiological measurement(s) that the system is required to maintain functional equivalence of (Nelson & Turrigiano, 2008; Turrigiano, 2011; Srikanth & Narayanan, 2015), a question that extends to our analyses as well. Specifically, from the perspective of synaptic information processing and homeostasis, which particular aspect of synaptic filters and STP does a synapse need to maintain functional equivalence of?
In addition to these, our results also suggest that these degenerate mechanisms involved in presynaptic release could critically contribute to degeneracy in long‐term synaptic plasticity profiles as well. Earlier studies have shown that disparate postsynaptic parametric combinations (voltage‐ and ligand‐gated ion channels) could result in analogous synaptic plasticity profiles, thereby providing a wide variety of mechanisms that could regulate plasticity profiles (Anirudhan & Narayanan, 2015). There are several lines of experimental evidence to support the idea that the expression profiles of different ion channels and receptors could significantly alter synaptic plasticity profiles (Watanabe et al. 2002; Nolan et al. 2004; Chen et al. 2006; Abraham, 2008; Lin et al. 2008; Chung et al. 2009; Lujan et al. 2009; Adelman et al. 2012; Cooper & Bear, 2012; Hulme et al. 2013; Sehgal et al. 2013; Anirudhan & Narayanan, 2015). Our results demonstrating significant degeneracy in the presynaptic mechanisms that regulate the strength of postsynaptic response (through modifications to release) add a significant complex dimension to degeneracy in achieving synaptic plasticity profiles. This implies that presynaptic intrinsic plasticity, involving changes in any or all of the channels, pumps, buffers or other intrinsically presynaptic components, could mediate long‐term synaptic plasticity (while also changing synaptic filters and STP profiles) through different combinations of constituent parameters.
In light of this, it would be of interest to ask if analogous long‐term synaptic plasticity profiles could be achieved through disparate combinations of parameters that span both pre‐ and postsynaptic mechanisms. The existence of such degeneracy spanning pre‐ and postsynaptic mechanisms, with the inclusion of other players such as astrocytes that contribute to the regulation of synaptic plasticity (Halassa & Haydon, 2010; Pannasch & Rouach, 2013; Araque et al. 2014), would significantly expand the power of degeneracy as a substrate for maintenance of robustness in plasticity profiles (Edelman & Gally, 2001; Whitacre & Bender, 2010; Anirudhan & Narayanan, 2015). Critically, with reference to dissociation between different forms of homeostasis and on the question of the specific physiological metric that a synapse needs to maintain functional equivalence of (Nelson & Turrigiano, 2008; Turrigiano, 2011; Srikanth & Narayanan, 2015), it is necessary to explore potential dissociations between homeostasis of synaptic strengths vs. homeostasis of short‐ or long‐term plasticity profiles. Specifically, is it necessary to maintain specific short‐ and long‐term plasticity profiles in addition to the maintenance of firing rate, calcium or synaptic homeostasis (Sippy et al. 2003; Carvalho & Buonomano, 2011; Jackman et al. 2016)? How do these different forms of homeostatic maintenance mechanisms interact with each other, and how do they ensure non‐interference with the encoding mechanisms that are essential in brain regions involved in learning and memory (that, by definition, require constitutive components to change)? Although there are lines of evidence for significant dissociations between these different forms of homeostasis and encoding (Sippy et al. 2003; Nelson & Turrigiano, 2008; Carvalho & Buonomano, 2011; Turrigiano, 2011; O'Leary et al. 2014; Anirudhan & Narayanan, 2015; Srikanth & Narayanan, 2015; Gjorgjieva et al. 2016; Hengen et al. 2016; Jackman et al. 2016), it is essential that future experiments assess these questions within the framework of degeneracy where non‐unique mechanistic combinations could synergistically achieve these functional goals.
From an experimental perspective, as most pharmacological treatments or genetic knockouts (that have been used in assessing their role in synaptic plasticity profiles) do not distinguish between the pre‐ or postsynaptic expression of ion channels, this would call for a more nuanced experimental approach to distinguish between the role of pre‐ and postsynaptic ion channels to changes in synaptic plasticity profiles. This also calls for a more holistic assessment of all synaptic mechanisms, spanning all aspects of synaptic transmission and pre‐ and postsynaptic filtering, independently in each experiment to tease apart the pre‐ and postsynaptic contributions to specific forms of synaptic plasticity. Finally, these observations also imply that mechanisms behind metaplasticity could be variable across different physiological and pathophysiological conditions, warranting systematic analyses on a case‐to‐case basis that avoids generalization of mechanisms just based on functional equivalence (Abraham, 2008; Narayanan & Johnston, 2010; Cooper & Bear, 2012; Ashhad & Narayanan, 2013; Hulme et al. 2013; Sehgal et al. 2013; Anirudhan & Narayanan, 2015).
Generalizability, limitations and future directions
Our analyses and conclusions in this study placed emphasis on the band‐pass structure of Schaffer collateral synapses, incorporating specific channels and mechanisms expressed in those synapses. However, it is clear that our conclusions on degeneracy in presynaptic mechanisms that regulate synaptic filters and STP are extendible to other synapses with different filter structures. Such extendibility is a direct outcome of the fact that the mechanistic details of how each of the individual channels and release mechanisms would alter release, either by altering excitability or the calcium dynamics, would remain the same. This scenario where multiple parameters regulate specific measurements directly points to degeneracy in synaptic physiology, where multiple components endowed with disparate parametric combinations could interact to elicit similar filters and STP profiles. Although such generalizations with reference to degeneracy might be straightforward, extreme care should be exercised in direct extensions of these conclusions with reference to specific interactions. As mentioned above, the specific nature of these interactions and how they alter synaptic physiology are functions of several parameters, including the expression and relative abundance of specific channels and/or mechanisms. In those scenarios, it is important that the model is modified to account for the specific channels and mechanisms expressed in the synaptic structure of interest. It may be noted that our model is generic in nature, with the ability to modify individual components and/or parametric values to achieve specific filter structures (Fig. 2).
With reference to limitations of our model, although our focus has been limited to presynaptic channels and mechanisms, it is clear that the presence of postsynaptic ion channels could also significantly alter temporal summation and frequency‐dependent filtering (Magee, 1998; Narayanan & Johnston, 2007, 2008, 2012; Johnston & Narayanan, 2008; Spruston, 2008; Hu et al. 2009; Vaidya & Johnston, 2012; Das & Narayanan, 2014; Stuart & Spruston, 2015; Rathour et al. 2016). A synaptic filter would therefore be defined by a combination of pre‐ and postsynaptic mechanisms. Future studies could explore the role of pre‐ and postsynaptic ion channels and calcium‐handling mechanisms that alter transmission‐triggered average (TTA), a measure that has been proposed as a metric to understand the combined role of pre‐ and postsynaptic mechanisms on neuronal response properties (Abbott & Regehr, 2004). Coupled with active dendrites and associated location dependence of the spike‐triggered average, STA (Das & Narayanan, 2014, 2015), a postsynaptic metric for neuronal filters (Rieke et al. 1999; Aguera y Arcas & Fairhall, 2003; Famulare & Fairhall, 2010; Ratte et al. 2013), the TTA offers a mechanism to understand the synaptic and extrasynaptic parametric space that goes into defining filtering of neuronal information. Future studies could assess this large parametric space with TTA as a metric, including presynaptic measures used here (Fig. 1) and postsynaptic measures of neuronal filtering and response dynamics derived from their impedance and STA (Narayanan & Johnston, 2007, 2008; Rathour & Narayanan, 2012 a, 2014; Das & Narayanan, 2014, 2015; Dhupia et al. 2014), and address questions on degeneracy and robustness in the combination of all these measurements that define neuronal filtering.
Finally, although our model was sufficiently detailed for addressing the specific questions in hand, there are several significant elements of synaptic transmission that have not been incorporated into the model. Specifically, as our focus was on VGICs, we did not include calcium‐activated potassium channels into our model. Further, although the expression of several G‐protein coupled receptors (GPCRs) on the membrane of the presynaptic terminal and their ability to activate several downstream signalling pathways are established (Schoepp, 2001; Schwartz et al. 2007; Regehr et al. 2009; Atwood et al. 2014), we did not incorporate GPCRs or associated signalling mechanisms in our model. Modelling neuromodulation of synaptic filters or assessing the role of retrograde messengers in altering synaptic filters would require the incorporation of these GPCRs along with associated signalling mechanisms. Furthermore, experimental observations have assigned a role for presynaptic store‐operated calcium channels in regulating release and STP (Emptage et al. 2001), which was not incorporated in our model. Apart from the absence of these presynaptic membrane components, our model also does not incorporate distinctions between reluctantly and willingly releasable vesicle pools to the framework. From existing theoretical and experimental evidence that link these pools to synaptic transmission and STP (Gingrich & Byrne, 1985; Zucker & Regehr, 2002; Mochida et al. 2008; Pan & Zucker, 2009; Sudhof, 2012, 2013, 2014; Mahfooz et al. 2016; Miki et al. 2016), it is reasonable to postulate that the differential recovery and release kinetics of these distinct pools would play a critical role in the specific characteristics of synaptic filters as well. Therefore, incorporation of these elements in addition to the stochastic nature of each constitutive element, the structural and location‐induced constraints on the priming, docking and release processes and the interaction of presynaptic terminals with astrocytic components (Nadkarni & Jung, 2007; Nadkarni et al. 2008, 2010, 2012; Pan & Zucker, 2009; De Pitta et al. 2011; Holderith et al. 2012; Bartol et al. 2015; Mahfooz et al. 2016; Miki et al. 2016) is critical in furthering the conclusions of our study. Future studies could incorporate each of these pre‐ and postsynaptic components to synaptic filters to assess their specific contributions to synaptic filters and neuronal plasticity, apart from assessing potential degeneracy in the maintenance of functional robustness of synaptic physiology in a manner that involves channels, receptors and mechanisms at both ends of the synapse. We postulate that the incorporation of these additional mechanisms would reinforce degeneracy in the emergence of synaptic filters and short‐ and long‐term plasticity profiles.
Additional information
Competing interests
The authors declare no competing interests.
Author contributions
CLM and RN conceived and designed the experiments; CLM performed the experiments; CLM analysed the data; CLM and RN co‐wrote the article.
Funding
This work was supported by the Department of Biotechnology‐Indian Institute of Science partnership programme (RN), the Department of Science and Technology (RN), and the Indian Institute of Science (RN).
Acknowledgements
We gratefully thank members of the cellular neurophysiology laboratory for helpful discussions and for critical comments on a draft of the manuscript.
Linked articles This article is highlighted by a Perspective by Prinz. To read this Perspective, visit https://doi.org/10.1113/JP273924.
References
- Abbott LF & Regehr WG (2004). Synaptic computation. Nature 431, 796–803. [DOI] [PubMed] [Google Scholar]
- Abbott LF, Varela JA, Sen K & Nelson SB (1997). Synaptic depression and cortical gain control. Science 275, 220–224. [DOI] [PubMed] [Google Scholar]
- Abraham WC (2008). Metaplasticity: tuning synapses and networks for plasticity. Nat Rev Neurosci 9, 387. [DOI] [PubMed] [Google Scholar]
- Adelman JP, Maylie J & Sah P (2012). Small‐conductance Ca2+‐activated K+ channels: form and function. Ann Rev Physiol 74, 245–269. [DOI] [PubMed] [Google Scholar]
- Aguera Y, Arcas B & Fairhall AL (2003). What causes a neuron to spike? Neural Comput 15, 1789–1807. [DOI] [PubMed] [Google Scholar]
- Ahmed MS & Siegelbaum SA (2009). Recruitment of N‐type Ca2+ channels during LTP enhances low release efficacy of hippocampal CA1 perforant path synapses. Neuron 63, 372–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allbritton NL, Meyer T & Stryer L (1992). Range of messenger action of calcium ion and inositol 1,4,5‐trisphosphate. Science 258, 1812–1815. [DOI] [PubMed] [Google Scholar]
- Andrasfalvy BK & Magee JC (2001). Distance‐dependent increase in AMPA receptor number in the dendrites of adult hippocampal CA1 pyramidal neurons. J Neurosci 21, 9151–9159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anirudhan A & Narayanan R (2015). Analogous synaptic plasticity profiles emerge from disparate channel combinations. J Neurosci 35, 4691–4705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Araque A, Carmignoto G, Haydon PG, Oliet SH, Robitaille R & Volterra A (2014). Gliotransmitters travel in time and space. Neuron 81, 728–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashhad S & Narayanan R (2013). Quantitative interactions between the A‐type K+ current and inositol trisphosphate receptors regulate intraneuronal Ca2+ waves and synaptic plasticity. J Physiol 591, 1645–1669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atwood BK, Lovinger DM & Mathur BN (2014). Presynaptic long‐term depression mediated by Gi/o‐coupled receptors. Trends Neurosci 37, 663–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Awatramani GB, Price GD & Trussell LO (2005). Modulation of transmitter release by presynaptic resting potential and background calcium levels. Neuron 48, 109–121. [DOI] [PubMed] [Google Scholar]
- Barak O & Tsodyks M (2014). Working models of working memory. Curr Opin Neurobiol 25, 20–24. [DOI] [PubMed] [Google Scholar]
- Bardo S, Cavazzini MG & Emptage N (2006). The role of the endoplasmic reticulum Ca2+ store in the plasticity of central neurons. Trends Pharmacol Sci 27, 78–84. [DOI] [PubMed] [Google Scholar]
- Bartol TM, Bromer C, Kinney J, Chirillo MA, Bourne JN, Harris KM & Sejnowski TJ (2015). Nanoconnectomic upper bound on the variability of synaptic plasticity. eLife 4, e10778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender RA, Kirschstein T, Kretz O, Brewster AL, Richichi C, Ruschenschmidt C, Shigemoto R, Beck H, Frotscher M & Baram TZ (2007). Localization of HCN1 channels to presynaptic compartments: novel plasticity that may contribute to hippocampal maturation. J Neurosci 27, 4697–4706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger T, Borgdorff A, Crochet S, Neubauer FB, Lefort S, Fauvet B, Ferezou I, Carleton A, Luscher HR & Petersen CC (2007). Combined voltage and calcium epifluorescence imaging in vitro and in vivo reveals subthreshold and suprathreshold dynamics of mouse barrel cortex. J Neurophysiol 97, 3751–3762. [DOI] [PubMed] [Google Scholar]
- Bouchard R, Pattarini R & Geiger JD (2003). Presence and functional significance of presynaptic ryanodine receptors. Progr Neurobiol 69, 391–418. [DOI] [PubMed] [Google Scholar]
- Boyes J, Bolam JP, Shigemoto R & Stanford IM (2007). Functional presynaptic HCN channels in the rat globus pallidus. Eur J Neurosci 25, 2081–2092. [DOI] [PubMed] [Google Scholar]
- Brain KL, Trout SJ, Jackson VM, Dass N & Cunnane TC (2001). Nicotine induces calcium spikes in single nerve terminal varicosities: a role for intracellular calcium stores. Neuroscience 106, 395–403. [DOI] [PubMed] [Google Scholar]
- Budde T, Meuth S & Pape HC (2002). Calcium‐dependent inactivation of neuronal calcium channels. Nat Rev Neurosci 3, 873–883. [DOI] [PubMed] [Google Scholar]
- Buonomano DV (2000). Decoding temporal information: a model based on short‐term synaptic plasticity. J Neurosci 20, 1129–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabezas C & Buno W (2006). Distinct transmitter release properties determine differences in short‐term plasticity at functional and silent synapses. J Neurophysiol 95, 3024–3034. [DOI] [PubMed] [Google Scholar]
- Carlson BA (2009). Temporal‐pattern recognition by single neurons in a sensory pathway devoted to social communication behavior. J Neurosci 29, 9417–9428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carnevale NT & Hines ML (2006). The NEURON Book. Cambridge University Press, Cambridge, UK. [Google Scholar]
- Carvalho TP & Buonomano DV (2011). A novel learning rule for long‐term plasticity of short‐term synaptic plasticity enhances temporal processing. Front Integr Neurosci 5, 20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Yuan LL, Zhao C, Birnbaum SG, Frick A, Jung WE, Schwarz TL, Sweatt JD & Johnston D (2006). Deletion of Kv4.2 gene eliminates dendritic A‐type K+ current and enhances induction of long‐term potentiation in hippocampal CA1 pyramidal neurons. J Neurosci 26, 12143–12151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung HJ, Ge WP, Qian X, Wiser O, Jan YN & Jan LY (2009). G protein‐activated inwardly rectifying potassium channels mediate depotentiation of long‐term potentiation. Proc Natl Acad Sci USA 106, 635–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung S, Li X & Nelson SB (2002). Short‐term depression at thalamocortical synapses contributes to rapid adaptation of cortical sensory responses in vivo. Neuron 34, 437–446. [DOI] [PubMed] [Google Scholar]
- Cook DL, Schwindt PC, Grande LA & Spain WJ (2003). Synaptic depression in the localization of sound. Nature 421, 66–70. [DOI] [PubMed] [Google Scholar]
- Cooper EC, Milroy A, Jan YN, Jan LY & Lowenstein DH (1998). Presynaptic localization of Kv1.4‐containing A‐type potassium channels near excitatory synapses in the hippocampus. J Neurosci 18, 965–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper LN & Bear MF (2012). The BCM theory of synapse modification at 30: interaction of theory with experiment. Nat Rev Neurosci 13, 798–810. [DOI] [PubMed] [Google Scholar]
- Cuttle MF, Rusznak Z, Wong AY, Owens S & Forsythe ID (2001). Modulation of a presynaptic hyperpolarization‐activated cationic current (I h) at an excitatory synaptic terminal in the rat auditory brainstem. J Physiol 534, 733–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A & Narayanan R (2014). Active dendrites regulate spectral selectivity in location‐dependent spike initiation dynamics of hippocampal model neurons. J Neurosci 34, 1195–1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A & Narayanan R (2015). Active dendrites mediate stratified gamma‐range coincidence detection in hippocampal model neurons. J Physiol 593, 3549–3576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Pitta M, Volman V, Berry H & Ben‐Jacob E (2011). A tale of two stories: astrocyte regulation of synaptic depression and facilitation. PLoS Comput Biol 7, e1002293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Mainen ZF & Sejnowski TJ (1998). Kinetic models of synaptic transmission In Methods in Neuronal Modeling, ed. Koch C. & Segev I. MIT Press, Cambridge: 1–25. [Google Scholar]
- Dhupia N, Rathour RK & Narayanan R (2014). Dendritic atrophy constricts functional maps in resonance and impedance properties of hippocampal model neurons. Front Cell Neurosci 8, 456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dingledine R, Borges K, Bowie D & Traynelis SF (1999). The glutamate receptor ion channels. Pharmacol Rev 51, 7–61. [PubMed] [Google Scholar]
- Dittman JS, Kreitzer AC & Regehr WG (2000). Interplay between facilitation, depression, and residual calcium at three presynaptic terminals. J Neurosci 20, 1374–1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrunz LE, Huang EP & Stevens CF (1997). Very short‐term plasticity in hippocampal synapses. Proc Natl Acad Sci USA 94, 14843–14847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodson PD & Forsythe ID (2004). Presynaptic K+ channels: electrifying regulators of synaptic terminal excitability. Trends Neurosci 27, 210–217. [DOI] [PubMed] [Google Scholar]
- Drion G, O'Leary T & Marder E (2015). Ion channel degeneracy enables robust and tunable neuronal firing rates. Proc Natl Acad Sci USA 112, E5361‐5370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyhrfjeld‐Johnsen J, Morgan RJ & Soltesz I (2009). Double trouble? Potential for hyperexcitability following both channelopathic up‐ and downregulation of I h in epilepsy. Front Neurosci 3, 25–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelman GM & Gally JA (2001). Degeneracy and complexity in biological systems. Proc Natl Acad Sci USA 98, 13763–13768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emptage NJ, Reid CA & Fine A (2001). Calcium stores in hippocampal synaptic boutons mediate short‐term plasticity, store‐operated Ca2+ entry, and spontaneous transmitter release. Neuron 29, 197–208. [DOI] [PubMed] [Google Scholar]
- Famulare M & Fairhall A (2010). Feature selection in simple neurons: how coding depends on spiking dynamics. Neural Comput 22, 581–598. [DOI] [PubMed] [Google Scholar]
- Fink CC, Slepchenko B, Moraru, II , Watras J, Schaff JC & Loew LM (2000). An image‐based model of calcium waves in differentiated neuroblastoma cells. Biophys J 79, 163–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fioravante D & Regehr WG (2011). Short‐term forms of presynaptic plasticity. Curr Opin Neurobiol 21, 269–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortune ES & Rose GJ (2001). Short‐term synaptic plasticity as a temporal filter. Trends Neurosci 24, 381–385. [DOI] [PubMed] [Google Scholar]
- Foster WR, Ungar LH & Schwaber JS (1993). Significance of conductances in Hodgkin‐Huxley models. J Neurophysiol 70, 2502–2518. [DOI] [PubMed] [Google Scholar]
- Fuhrmann G, Segev I, Markram H & Tsodyks M (2002). Coding of temporal information by activity‐dependent synapses. J Neurophysiol 87, 140–148. [DOI] [PubMed] [Google Scholar]
- Geiger JR & Jonas P (2000). Dynamic control of presynaptic Ca2+ inflow by fast‐inactivating K+ channels in hippocampal mossy fiber boutons. Neuron 28, 927–939. [DOI] [PubMed] [Google Scholar]
- Gingrich KJ & Byrne JH (1985). Simulation of synaptic depression, posttetanic potentiation, and presynaptic facilitation of synaptic potentials from sensory neurons mediating gill‐withdrawal reflex in aplysia. J Neurophysiol 53, 652–669. [DOI] [PubMed] [Google Scholar]
- Gjorgjieva J, Drion G & Marder E (2016). Computational implications of biophysical diversity and multiple timescales in neurons and synapses for circuit performance. Curr Opin Neurobiol 37, 44–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman DE (1943). Potential, impedance, and rectification in membranes. J Gen Physiol 27, 37–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman MS, Golowasch J, Marder E & Abbott LF (2001). Global structure, robustness, and modulation of neuronal models. J Neurosci 21, 5229–5238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halassa MM & Haydon PG (2010). Integrated brain circuits: astrocytic networks modulate neuronal activity and behavior. Ann Rev Physiol 72, 335–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han MH, Kawasaki A, Wei JY & Barnstable CJ (2001). Miniature postsynaptic currents depend on Ca2+ released from internal stores via PLC/IP3 pathway. Neuroreport 12, 2203–2207. [DOI] [PubMed] [Google Scholar]
- Hanus C & Schuman EM (2013). Proteostasis in complex dendrites. Nat Rev Neurosci 14, 638–648. [DOI] [PubMed] [Google Scholar]
- Hengen KB, Torrado Pacheco A, McGregor JN, Van Hooser SD & Turrigiano GG (2016). Neuronal firing rate homeostasis is inhibited by sleep and promoted by wake. Cell 165, 180–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL & Huxley AF (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117, 500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL & Katz B (1949). The effect of sodium ions on the electrical activity of giant axon of the squid. J Physiol 108, 37–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holderith N, Lorincz A, Katona G, Rozsa B, Kulik A, Watanabe M & Nusser Z (2012). Release probability of hippocampal glutamatergic terminals scales with the size of the active zone. Nat Neurosci 15, 988–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honnuraiah S & Narayanan R (2013). A calcium‐dependent plasticity rule for HCN channels maintains activity homeostasis and stable synaptic learning. PloS One 8, e55590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Graham LJ & Storm JF (2009). Complementary theta resonance filtering by two spatially segregated mechanisms in CA1 hippocampal pyramidal neurons. J Neurosci 29, 14472–14483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z, Lujan R, Kadurin I, Uebele VN, Renger JJ, Dolphin AC & Shah MM (2011). Presynaptic HCN1 channels regulate Cav3.2 activity and neurotransmission at select cortical synapses. Nat Neurosci 14, 478–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hulme SR, Jones OD & Abraham WC (2013). Emerging roles of metaplasticity in behaviour and disease. Trends Neurosci 36, 353–362. [DOI] [PubMed] [Google Scholar]
- Jackman SL, Turecek J, Belinsky JE & Regehr WG (2016). The calcium sensor synaptotagmin 7 is required for synaptic facilitation. Nature 529, 88–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston D, Magee JC, Colbert CM & Cristie BR (1996). Active properties of neuronal dendrites. Annu Rev Neurosci 19, 165–186. [DOI] [PubMed] [Google Scholar]
- Johnston D & Narayanan R (2008). Active dendrites: colorful wings of the mysterious butterflies. Trends Neurosci 31, 309–316. [DOI] [PubMed] [Google Scholar]
- Kirizs T, Kerti‐Szigeti K, Lorincz A & Nusser Z (2014). Distinct axo‐somato‐dendritic distributions of three potassium channels in CA1 hippocampal pyramidal cells. Eur J Neurosci 39, 1771–1783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kispersky TJ, Caplan JS & Marder E (2012). Increase in sodium conductance decreases firing rate and gain in model neurons. J Neurosci 32, 10995–11004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingauf J & Neher E (1997). Modeling buffered Ca2+ diffusion near the membrane: implications for secretion in neuroendocrine cells. Biophys J 72, 674–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li YX & Rinzel J (1994). Equations for InsP3 receptor‐mediated [Ca2+]i oscillations derived from a detailed kinetic model: a Hodgkin‐Huxley like formalism. J Theor Biol 166, 461–473. [DOI] [PubMed] [Google Scholar]
- Lin MT, Lujan R, Watanabe M, Adelman JP & Maylie J (2008). SK2 channel plasticity contributes to LTP at Schaffer collateral–CA1 synapses. Nat Neurosci 11, 170–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llano I, Gonzalez J, Caputo C, Lai FA, Blayney LM, Tan YP & Marty A (2000). Presynaptic calcium stores underlie large‐amplitude miniature IPSCs and spontaneous calcium transients. Nat Neurosci 3, 1256–1265. [DOI] [PubMed] [Google Scholar]
- Lujan R, Albasanz JL, Shigemoto R & Juiz JM (2005). Preferential localization of the hyperpolarization‐activated cyclic nucleotide‐gated cation channel subunit HCN1 in basket cell terminals of the rat cerebellum. Eur J Neurosci 21, 2073–2082. [DOI] [PubMed] [Google Scholar]
- Lujan R, Maylie J & Adelman JP (2009). New sites of action for GIRK and SK channels. Nat Rev Neurosci 10, 475–480. [DOI] [PubMed] [Google Scholar]
- Magee JC (1998). Dendritic hyperpolarization‐activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J Neurosci 18, 7613–7624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee JC (2000). Dendritic integration of excitatory synaptic input. Nat Rev Neurosci 1, 181–190. [DOI] [PubMed] [Google Scholar]
- Magee JC & Cook EP (2000). Somatic EPSP amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat Neurosci 3, 895–903. [DOI] [PubMed] [Google Scholar]
- Mahfooz K, Singh M, Renden R & Wesseling JF (2016). A well‐defined readily releasable pool with fixed capacity for storing vesicles at calyx of Held. PLoS Comput Biol 12, e1004855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E (2011). Variability, compensation, and modulation in neurons and circuits. Proc Natl Acad Sci USA 108 Suppl 3, 15542–15548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E & Goaillard JM (2006). Variability, compensation and homeostasis in neuron and network function. Nat Rev Neurosci 7, 563–574. [DOI] [PubMed] [Google Scholar]
- Marder E, Goeritz ML & Otopalik AG (2015). Robust circuit rhythms in small circuits arise from variable circuit components and mechanisms. Curr Opin Neurobiol 31, 156–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E & Taylor AL (2011). Multiple models to capture the variability in biological neurons and networks. Nat Neurosci 14, 133–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Gupta A, Uziel A, Wang Y & Tsodyks M (1998). Information processing with frequency‐dependent synaptic connections. Neurobiol Learn Mem 70, 101–112. [DOI] [PubMed] [Google Scholar]
- Meir A, Ginsburg S, Butkevich A, Kachalsky SG, Kaiserman I, Ahdut R, Demirgoren S & Rahamimoff R (1999). Ion channels in presynaptic nerve terminals and control of transmitter release. Physiol Rev 79, 1019–1088. [DOI] [PubMed] [Google Scholar]
- Migliore M, Cook EP, Jaffe DB, Turner DA & Johnston D (1995). Computer simulations of morphologically reconstructed CA3 hippocampal neurons. J Neurophysiol 73, 1157–1168. [DOI] [PubMed] [Google Scholar]
- Migliore M & Migliore R (2012). Know your current I h: interaction with a shunting current explains the puzzling effects of its pharmacological or pathological modulations. PloS One 7, e36867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miki T, Malagon G, Pulido C, Llano I, Neher E & Marty A (2016). Actin‐ and myosin‐dependent vesicle loading of presynaptic docking sites prior to exocytosis. Neuron 91, 808–823. [DOI] [PubMed] [Google Scholar]
- Mishra P & Narayanan R (2015). High‐conductance states and A‐type K+ channels are potential regulators of the conductance‐current balance triggered by HCN channels. J Neurophysiol 113, 23–43. [DOI] [PubMed] [Google Scholar]
- Mochida S, Few AP, Scheuer T & Catterall WA (2008). Regulation of presynaptic CaV2.1 channels by Ca2+ sensor proteins mediates short‐term synaptic plasticity. Neuron 57, 210–216. [DOI] [PubMed] [Google Scholar]
- Nadkarni S, Bartol TM, Sejnowski TJ & Levine H (2010). Modelling vesicular release at hippocampal synapses. PLoS Comput Biol 6, e1000983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadkarni S, Bartol TM, Stevens CF, Sejnowski TJ & Levine H (2012). Short‐term plasticity constrains spatial organization of a hippocampal presynaptic terminal. Proc Natl Acad Sci USA 109, 14657–14662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadkarni S & Jung P (2007). Modeling synaptic transmission of the tripartite synapse. Phys Biol 4, 1–9. [DOI] [PubMed] [Google Scholar]
- Nadkarni S, Jung P & Levine H (2008). Astrocytes optimize the synaptic transmission of information. PLoS Comput Biol 4, e1000088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R & Johnston D (2007). Long‐term potentiation in rat hippocampal neurons is accompanied by spatially widespread changes in intrinsic oscillatory dynamics and excitability. Neuron 56, 1061–1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R & Johnston D (2008). The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons. J Neurosci 28, 5846–5860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R & Johnston D (2010). The h current is a candidate mechanism for regulating the sliding modification threshold in a BCM‐like synaptic learning rule. J Neurophysiol 104, 1020–1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R & Johnston D (2012). Functional maps within a single neuron. J Neurophysiol 108, 2343–2351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson SB & Turrigiano GG (2008). Strength through diversity. Neuron 60, 477–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolan MF, Malleret G, Dudman JT, Buhl DL, Santoro B, Gibbs E, Vronskaya S, Buzsaki G, Siegelbaum SA, Kandel ER & Morozov A (2004). A behavioral role for dendritic integration: HCN1 channels constrain spatial memory and plasticity at inputs to distal dendrites of CA1 pyramidal neurons. Cell 119, 719–732. [DOI] [PubMed] [Google Scholar]
- Novak P, Gorelik J, Vivekananda U, Shevchuk AI, Ermolyuk YS, Bailey RJ, Bushby AJ, Moss GW, Rusakov DA, Klenerman D, Kullmann DM, Volynski KE & Korchev YE (2013). Nanoscale‐targeted patch‐clamp recordings of functional presynaptic ion channels. Neuron 79, 1067–1077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Leary T, Williams AH, Caplan JS & Marder E (2013). Correlations in ion channel expression emerge from homeostatic tuning rules. Proc Natl Acad Sci USA 110, E2645–2654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Leary T, Williams AH, Franci A & Marder E (2014). Cell types, network homeostasis, and pathological compensation from a biologically plausible ion channel expression model. Neuron 82, 809–821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan B & Zucker RS (2009). A general model of synaptic transmission and short‐term plasticity. Neuron 62, 539–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pannasch U & Rouach N (2013). Emerging role for astroglial networks in information processing: from synapse to behavior. Trends Neurosci 36, 405–417. [DOI] [PubMed] [Google Scholar]
- Pavlov I, Scimemi A, Savtchenko L, Kullmann DM & Walker MC (2011). I h‐mediated depolarization enhances the temporal precision of neuronal integration. Nat Commun 2, 199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfister JP, Dayan P & Lengyel M (2010). Synapses with short‐term plasticity are optimal estimators of presynaptic membrane potentials. Nat Neurosci 13, 1271–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poirazi P, Brannon T & Mel BW (2003). Pyramidal neuron as two‐layer neural network. Neuron 37, 989–999. [DOI] [PubMed] [Google Scholar]
- Popovic MA, Carnevale N, Rozsa B & Zecevic D (2015). Electrical behaviour of dendritic spines as revealed by voltage imaging. Nat Commun 6, 8436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Billimoria CP & Marder E (2003). Alternative to hand‐tuning conductance‐based models: construction and analysis of databases of model neurons. J Neurophysiol 90, 3998–4015. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D & Marder E (2004). Similar network activity from disparate circuit parameters. Nat Neurosci 7, 1345–1352. [DOI] [PubMed] [Google Scholar]
- Qian J & Saggau P (1999). Activity‐dependent modulation of K+ currents at presynaptic terminals of mammalian central synapses. J Physiol 519, 427–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rancz EA, Ishikawa T, Duguid I, Chadderton P, Mahon S & Hausser M (2007). High‐fidelity transmission of sensory information by single cerebellar mossy fibre boutons. Nature 450, 1245–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rathour RK, Malik R & Narayanan R (2016). Transient potassium channels augment degeneracy in hippocampal active dendritic spectral tuning. Sci Rep 6, 24678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rathour RK & Narayanan R (2012. a). Inactivating ion channels augment robustness of subthreshold intrinsic response dynamics to parametric variability in hippocampal model neurons. J Physiol 590, 5629–5652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rathour RK & Narayanan R (2012. b). Influence fields: a quantitative framework for representation and analysis of active dendrites. J Neurophysiol 107, 2313–2334. [DOI] [PubMed] [Google Scholar]
- Rathour RK & Narayanan R (2014). Homeostasis of functional maps in active dendrites emerges in the absence of individual channelostasis. Proc Natl Acad Sci USA 111, E1787–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratte S, Hong S, De Schutter E & Prescott SA (2013). Impact of neuronal properties on network coding: roles of spike initiation dynamics and robust synchrony transfer. Neuron 78, 758–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regehr WG (2012). Short‐term presynaptic plasticity. Cold Spring Harb Perspect Biol 4, a005702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regehr WG, Carey MR & Best AR (2009). Activity‐dependent regulation of synapses by retrograde messengers. Neuron 63, 154–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieke F, Warland D, van Steveninck RR & Bialek W (1999). Spikes: Exploring the Neural Code. MIT Press, Cambridge, MA, USA. [Google Scholar]
- Roberts WM, Jacobs RA & Hudspeth AJ (1990). Colocalization of ion channels involved in frequency selectivity and synaptic transmission at presynaptic active zones of hair cells. J Neurosci 10, 3664–3684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatini BL & Regehr WG (1998). Optical measurement of presynaptic calcium currents. Biophys J 74, 1549–1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoepp DD (2001). Unveiling the functions of presynaptic metabotropic glutamate receptors in the central nervous system. J Pharmacoly Exp Ther 299, 12–20. [PubMed] [Google Scholar]
- Schwartz EJ, Blackmer T, Gerachshenko T & Alford S (2007). Presynaptic G‐protein‐coupled receptors regulate synaptic cleft glutamate via transient vesicle fusion. J Neurosci 27, 5857–5868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sehgal M, Song C, Ehlers VL & Moyer JR Jr (2013). Learning to learn ‐ intrinsic plasticity as a metaplasticity mechanism for memory formation. Neurobiol Learn Mem 105, 186–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheng M, Liao YJ, Jan YN & Jan LY (1993). Presynaptic A‐current based on heteromultimeric K+ channels detected in vivo. Nature 365, 72–75. [DOI] [PubMed] [Google Scholar]
- Sippy T, Cruz‐Martin A, Jeromin A & Schweizer FE (2003). Acute changes in short‐term plasticity at synapses with elevated levels of neuronal calcium sensor‐1. Nat Neurosci 6, 1031–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjostrom PJ, Rancz EA, Roth A & Hausser M (2008). Dendritic excitability and synaptic plasticity. Physiol Rev 88, 769–840. [DOI] [PubMed] [Google Scholar]
- Sneyd J, Keizer J & Sanderson MJ (1995). Mechanisms of calcium oscillations and waves: a quantitative analysis. FASEB J 9, 1463–1472. [DOI] [PubMed] [Google Scholar]
- Southan AP, Morris NP, Stephens GJ & Robertson B (2000). Hyperpolarization‐activated currents in presynaptic terminals of mouse cerebellar basket cells. J Physiol 526, 91–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N (2008). Pyramidal neurons: dendritic structure and synaptic integration. Nat Rev Neurosci 9, 206–221. [DOI] [PubMed] [Google Scholar]
- Srikanth S & Narayanan R (2015). Variability in state‐dependent plasticity of intrinsic properties during cell‐autonomous self‐regulation of calcium homeostasis in hippocampal model neurons. eNeuro 2, 1–24, e0053‐0015.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelling J, Sauer U, Szallasi Z, Doyle FJ, 3rd & Doyle J (2004). Robustness of cellular functions. Cell 118, 675–685. [DOI] [PubMed] [Google Scholar]
- Stuart GJ & Spruston N (2015). Dendritic integration: 60 years of progress. Nat Neurosci 18, 1713–1721. [DOI] [PubMed] [Google Scholar]
- Sudhof TC (2012). Calcium control of neurotransmitter release. Cold Spring Harb Perspect Biol 4, a011353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudhof TC (2013). Neurotransmitter release: the last millisecond in the life of a synaptic vesicle. Neuron 80, 675–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudhof TC (2014). The molecular machinery of neurotransmitter release (Nobel lecture). Angew Chem Int Ed Engl 53, 12696–12717. [DOI] [PubMed] [Google Scholar]
- Taylor AL, Goaillard JM & Marder E (2009). How multiple conductances determine electrophysiological properties in a multicompartment model. J Neurosci 29, 5573–5586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi G, Sporns O & Edelman GM (1999). Measures of degeneracy and redundancy in biological networks. Proc Natl Acad Sci USA 96, 3257–3262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsay D, Dudman JT & Siegelbaum SA (2007). HCN1 channels constrain synaptically‐evoked Ca2+ spikes in distal dendrites of CA1 pyramidal neurons. Neuron 56, 1076–1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks MV & Markram H (1997). The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci USA 94, 719–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrigiano G (2011). Too many cooks? Intrinsic and synaptic homeostatic mechanisms in cortical circuit refinement. Annu Rev Neurosci 34, 89–103. [DOI] [PubMed] [Google Scholar]
- Vaidya S & Johnston D (2012). HCN channels contribute to the spatial synchrony of theta frequency synaptic inputs in CA1 pyramidal neurons In: Neuroscience Meeting Planner. Society for Neuroscience; New Orleans, LA. [Google Scholar]
- Veh RW, Lichtinghagen R, Sewing S, Wunder F, Grumbach IM & Pongs O (1995). Immunohistochemical localization of five members of the Kv1 channel subunits: contrasting subcellular locations and neuron‐specific co‐localizations in rat brain. Eur J Neurosci 7, 2189–2205. [DOI] [PubMed] [Google Scholar]
- Verkhratsky A (2002). The endoplasmic reticulum and neuronal calcium signalling. Cell Calcium 32, 393–404. [DOI] [PubMed] [Google Scholar]
- Watanabe S, Hoffman D, Migliore M & Johnston D (2002). Dendritic K+ channels contribute to spike‐timing dependent long‐term potentiation in hippocampal pyramidal neurons. Proc Natl Acad Sci USA 99, 8366–8371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitacre J & Bender A (2010). Degeneracy: a design principle for achieving robustness and evolvability. J Theor Biol 263, 143–153. [DOI] [PubMed] [Google Scholar]
- Zucker RS (1989). Short‐term synaptic plasticity. Annu Rev Neurosci 12, 13–31. [DOI] [PubMed] [Google Scholar]
- Zucker RS (1999). Calcium‐ and activity‐dependent synaptic plasticity. Curr Opin Neurobiol 9, 305–313. [DOI] [PubMed] [Google Scholar]
- Zucker RS & Regehr WG (2002). Short‐term synaptic plasticity. Ann Rev Physiol 64, 355–405. [DOI] [PubMed] [Google Scholar]


