Microfabricated tissues for investigating traction forces involved in cell migration and tissue morphogenesis

Abstract

Cell-generated forces drive an array of biological processes ranging from wound healing to tumor metastasis. Whereas experimental techniques such as traction force microscopy are capable of quantifying traction forces in multidimensional systems, the physical mechanisms by which these forces induce changes in tissue form remain to be elucidated. Understanding these mechanisms will ultimately require techniques that are capable of quantifying traction forces with high precision and accuracy in vivo or in systems that recapitulate in vivo conditions, such as microfabricated tissues and engineered substrata. To that end, here we review the fundamentals of traction forces, their quantification, and the use of microfabricated tissues designed to study these forces during cell migration and tissue morphogenesis. We emphasize the differences between traction forces in two- and three-dimensional systems, and highlight recently developed techniques for quantifying traction forces.

Introduction

Mechanical forces play an integral role in cellular behaviors as diverse as proliferation [1, 2], differentiation [3, 4], gene expression [5, 6], wound healing [7], tumor metastasis and invasion [8–10], collective migration [11, 12], and tissue morphogenesis [13]. In particular, traction stress, which refers to the force per unit area acting on the deformed cell–matrix interface, is a key mechanical cue in cellular systems. Traction forces originate from the contractile actomyosin network and can alter cellular behavior through a number of mechanisms collectively referred to as mechanotransduction [14]. However, the biophysical and biochemical mechanisms by which these forces induce changes in tissue form are not fully understood. The ability to accurately and precisely calculate traction forces is, therefore, important and will strengthen our quantitative understanding of their role in cell- and tissue-level processes.

The idea that the laws of mechanics can be applied to cells was first postulated in the late 1800s by Wilhelm His [15, 16]. Using the developing chicken embryo as a model, he proposed that differential growth rates in the germ layers gave rise to mechanical forces that are responsible for producing the final tissue form [15, 17]. Yet, despite this early insight, quantifying cell-generated mechanical forces such as traction forces—either in vivo or in culture—presents a tremendous challenge. The inherently small size of cells (~10 µm in diameter) means that traction forces act over a small area. When coupled with the fact that the magnitude of the corresponding forces is ~10 nN [18], it becomes clear that traction forces are inaccessible to macroscopic force measurements. Furthermore, mechanical forces act over both cell- and tissue-level length scales, which further complicates any attempts at measurement, since the scale at which forces should be measured is a non-trivial consideration [19]. Despite these challenges, a diverse group of experimental techniques enables the quantification of traction forces in two (2D) and three dimensions (3D) [20].

Several excellent reviews [20–23] have summarized the role of traction forces in various biological processes and the corresponding tools available to quantify them. Here, we focus specifically on the advancement of traction force microscopy (TFM) and microfabricated tissues for quantifying traction forces in the context of cell migration and tissue morphogenesis. Throughout the review, we discuss the differences between traction forces in 2D and 3D systems and highlight recent developments for traction force quantification. It should be noted that we use the term tractions in cases where traction stress and traction force can be used interchangeably or for consistency when referring to published work that used the term tractions. TFM has emerged as the most widely accepted approach for quantifying traction forces owing to a number of advantages [21]. Above all, TFM can be performed without specialized equipment, and tractions can be calculated using MATLAB code available online [21], which makes the technique readily accessible to most research labs. TFM is also remarkably versatile owing to the fact that force calculations are not inherently limited to any length scale [21].

We begin with a description of experimental progress in traction force quantification. Next, we discuss computational approaches to calculate traction forces, and provide specific examples for the application of TFM to cell migration and morphogenesis. Finally, we discuss the design and use of TFM in microfabricated tissues as well as strategies for overcoming limitations of conventional TFM. While both TFM [20–22] and micropatterning [24–26] have been previously reviewed separately, here we focus specifically on traction force quantification in the context of multidimensional cell migration and tissue morphogenesis.

Traction forces: multiple decades of experimental progress

The quantification of cell-generated traction forces was pioneered by Harris and co-workers in 1980 [27]. In this seminal study, traction forces were determined by measuring substratum deformations in the form of cell-induced wrinkles at the surface of a thin flexible silicone membrane with known elastic properties. This technique built off two similar approaches that had previously been used to study distortions and birefringence in gelatin [28] and thin plasma clots [29], but which were limited by substratum stability [27]. Quantifying traction forces from wrinkles in the substratum is inherently challenging, because the wrinkles are often larger than the cells and form gradually over time in a non-linear and chaotic manner [30]. Harris’s technique was subsequently improved by introducing a stretchable non-wrinkling silicone substratum that incorporated beads as fiducial markers [31, 32]. The 2D displacement of these beads was measured and used to calculate traction forces with higher accuracy than could be obtained by measuring wrinkles in the substratum [31, 32].

Modifications to the deformable substratum were also investigated to obtain additional improvements in traction force quantification. Burton and Taylor developed a new silicone polymer substratum with UV-tunable stiffness to control the size of wrinkles, such that the length could be measured and the movement of the substratum could be minimized [33]. An alternative approach quantified traction forces from the deformation of collagen gels, which were assumed to approximate an elastic material and were more representative of the ECM encountered by cells in an in vivo microenvironment [34]. After polyacrylamide (PA) gels were introduced as a cell culture platform [35, 36], these substrata were used to investigate the mechanical forces exerted by cells [37]. Compared to silicone substrata, PA gels exhibit a number of advantages: the stiffness can be tuned by changing the relative concentrations of acrylamide and bisacrylamide; substratum deformation is proportional to force applied over a range of forces; the optical properties of the material enable high-magnification imaging; substratum porosity allows media penetration, such that cells can be embedded within the gel; and PA is relatively inert [37, 38]. Thick PA gels have been used to produce spatial maps of traction forces exerted by fibroblasts during steady locomotion [30]. Recently, work using PA gels has improved computational and spatial resolution using fiducial markers that can be imaged in separate fluorescence channels [39]. Finally, tunable viscoelastic substrata have been used to study cell tractions in a micro environment that more closely represents human tissues [40].

The spatial resolution of traction force quantification was also improved with the creation of micropatterned substrata, such as arrays of microposts. Similar to PA gels, micropatterned substrata allow mechanical properties and surface chemistry to be tuned independently. These systems typically consist of elastic pillars that deform from cell-generated forces [41]. Alternative approaches have also used discrete arrays of cantilever sensors [42] to quantify traction forces at different positions under the cell. Provided that the density of pillars or cantilevers is high enough, the traction forces can be quantified at different focal adhesions within the same cell [43]. Arrays of microposts have also been used to measure the velocity and power of migrating cells [44]. In using these approaches, the density of pillars needs to be sufficiently high such that the surface can be approximated as a continuum [45]. In addition, any calculations performed must account for substratum warping that can occur if the pillars are made from the same elastic material as their underlying support [46].

Initially, 2D traction force calculations relied on an in-plane assumption that there was no stress normal to the substratum beneath the cells [47]. However, this assumption was found to be invalid under certain experimental conditions, because cellular contractility can induce traction forces normal to the underlying substratum [47, 48]. As a result, 2.5D TFM methods were developed to calculate both in-plane and normal traction forces [18, 47, 49]. Here, 2.5D refers to the ability of the TFM technique to quantify 3D traction forces—both in-plane and normal—for cells on a 2D planar surface. Both in-plane and normal traction forces were found to be of the same order of magnitude during the migration of many types of individual cells [47, 50]. The first quantification of traction forces in a purely 3D setting used the displacements of beads generated by cells embedded in gels of polyethylene glycol (PEG), from which the corresponding tractions were determined using linear elastic theory [51]. Additional studies have since quantified traction forces for individual cells embedded in highly non-linear biopolymer networks consisting of collagen, fibrin, and Matrigel [52]. Traction force calculations have also been performed for single cells [53] and tissues [54–56] embedded in 3D matrices of collagen and Matrigel. Taken together, these techniques are well suited to quantify cell-induced tractions in many different contexts and provide the user with the flexibility to choose the setup that best matches experimental requirements.

Quantifying traction forces

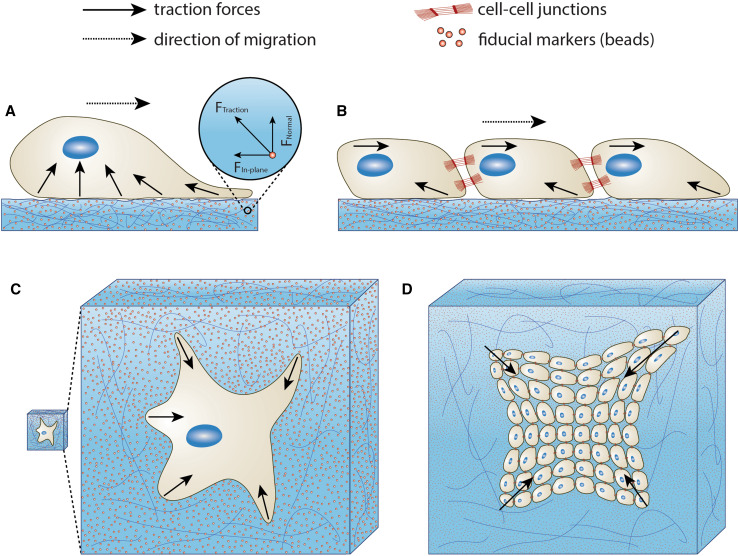
As described previously, traction forces are not measured explicitly. Rather, TFM relies on measuring the physical displacement of fiducial markers or the deformation of a substratum. For single isolated cells, local displacement data are combined with the appropriate constitutive equations to calculate local traction forces (Fig. 1a, c). For multicellular systems, global forces can be calculated from these local tractions using Newton’s laws of motion (Fig. 1b, d). In this section, we outline a previously described computational approach [21] for calculating local traction forces directly from experimentally measured displacement data. We further discuss the limitations associated with traction force calculations as well as some recent developments that aim to improve computational efficiency.

Fig. 1.

Single cell and multicellular traction forces in 2D and 3D systems. Traction forces exerted by a single cell migrating on a 2D substratum, b population of cells migrating collectively on a 2D substratum, c single cell migrating in a 3D matrix, and d population of cells migrating collectively in a 3D matrix. Cell-generated traction forces displace fiducial markers embedded in the substratum or matrix as cells migrate. Traction forces can be quantified by measuring the displacement of beads. Inspired by [20, 158]

For sufficiently small deformations of elastic substrata, discrete traction forces (F) can be calculated using Hooke’s law (Eq. 1):

$$F=kx,$$ 1

where k is the spring constant and x is the displacement [57]. The accuracy of the calculation is a function of the material properties of the substratum, the resolution of the displacement measurements, and the validity of the assumption that the deformations are sufficiently small [16]. Although Hooke’s law provides a simple approach to calculate traction forces at discrete locations, traction forces are actually distributed continuously throughout the substratum [21]. As a result, it is convenient to represent traction forces in terms of traction stress, which represents the traction force per unit contact area between the cell and the underlying substratum or the surrounding matrix [21]. Furthermore, if the substratum is assumed to be a linearly elastic solid, then the traction stress, $\mathit{\sigma }(\mathbf{x})$, is related to the displacement, $\mathit{u}(x)$, by Hooke’s law in tensor form [21, 58] (Eq. 2):

$$\mathit{\sigma }=\frac{E}{1-\mathit{\nu }}\left(\frac{1}{2}\left(\mathrm{\nabla }\mathit{u}+\mathrm{\nabla }{\mathit{u}}^T\right)+\frac{\mathit{\nu }\mathrm{\nabla }·\mathit{u}}{1-2\mathit{\nu }}\mathit{I}\right),$$ 2

where ν is Poisson’s ratio, E is the elastic modulus, and $\mathit{I}$ is the identity tensor. It is important to note that boundary conditions at the top and bottom surfaces of the substratum and the assumption of mechanical equilibrium ($\mathrm{\nabla }·\mathit{\sigma }=0$) are both required to solve Eq. 2 [58]. These assumptions give the following equation [21]:

$$(1-2\mathit{\nu }){\mathrm{\nabla }}^{\mathbf{2}}\mathit{u}+\mathrm{\nabla }(\mathrm{\nabla }·\mathit{u})=0,$$ 3

which can be solved using a variety of mathematical manipulations, including Fourier transforms [21, 59] and finite-element analysis [49, 60]. Using similar approaches, traction forces have been mapped for single cells and populations of cells cultured on a planar substratum (Fig. 2a, b) as well as embedded in a matrix (Fig. 2c, d).

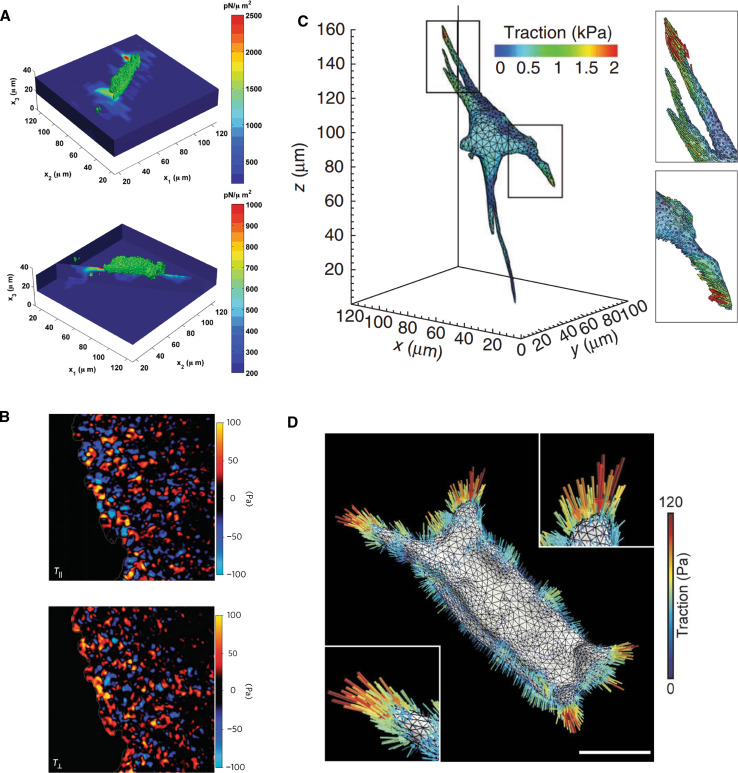
Fig. 2.

Visualizing traction force quantification. a In-plane (top) and normal (bottom) traction forces calculated for a single cell migrating on a 2D substratum. Figure from [159], licensed under creative commons. b In-plane (top) and normal (bottom) traction stresses for population of cells migrating collectively on a 2D substratum. Note that the image size is 750 μm by 750 μm. Reprinted by permission from Macmillan Publishers Ltd: Nature Physics [12], copyright (2009). c Traction stress map for single cell migrating in a 3D matrix. Reprinted by permission from Macmillan Publishers Ltd: Nature Methods [51], copyright (2010). d Traction stress map for population of cells migrating collectively in a 3D matrix. Figure from [54], licensed under creative commons. Scale bar is 50 μm

One drawback of the aforementioned approach is that calculating the traction stresses requires knowledge about the properties of the underlying matrix, such as the elastic modulus. This presents a challenge for in vivo systems where it may be difficult to characterize the mechanical properties of the ECM owing to its complex composition and because cells continuously remodel the ECM as they migrate. One potential solution was recently proposed whereby mean deformation metrics could be used to quantify cell–matrix interactions without the mechanical details of the matrix [61]. However, this method does not provide any information about cell tractions and cannot describe the effects of matrix stiffness without first knowing the mechanical properties of the matrix [61]. A second drawback is that the inverse calculations required to obtain traction stresses can be computationally expensive. One potential solution to this problem is digital volume correlation, which uses volume subsets to track 3D displacement fields. This method allows for the direct construction of traction stresses [62, 63] and, therefore, avoids the need for inverse calculations, allowing one to determine traction fields directly from volumetric confocal image stacks [18].

Computational advances in TFM calculations were realized with the understanding that explicitly quantifying traction stresses throughout the substratum requires displacement information to be processed using a statistical procedure [64]. Building on the work of Oliver [32] and Lee [31], Dembo used a Bayesian method to map traction forces from measurements of substratum displacement [64]. However, as pointed out by Schwarz [65], the solution obtained from the Bayesian method depends strongly on fluctuations in the experimental data. Alternative approaches, such as that of Tichonov [66] and one based on classical functional analysis [60], have also been proposed to circumvent the limitations of the Bayesian method. For more information, the interested reader is directed to recent reviews on the limitations associated with these approaches [67, 68].

Application 1: forces exerted during cell migration

The study of mechanical forces in cell migration was first performed qualitatively by examining changes in cell shape during the migration of isolated epithelial cells and cell sheets in 2D cell cultures [69]. While qualitative observations provide relative information about the magnitude of mechanical forces, these approaches are inherently limited by their inability to explicitly quantify forces in a reproducible manner. To that end, a variety of experimental tools have been developed to study the role of mechanical forces in migration [20] and the associated signaling pathways [70–72]. Studies using TFM-based analysis of 2D and 3D cell migration have generally reported traction stresses with orders of magnitude ranging from 10 to 10³ Pa [8, 48, 52]. Depending on the experimental conditions and cell type, the magnitude of traction stresses either remains constant or fluctuates during cell migration.

The role of traction forces in the migration of individual cells has been studied in fibroblasts [8], epithelial cells [45], Dictyostelium cells [50], cancer cells [9, 73], myoblasts [74], neutrophils [75], dendritic cells [76], keratinocytes [77], and bovine aortic endothelial cells [47], among others. Cells on 2D planar surfaces were found to exert both in-plane and normal tractions as they migrated (Fig. 1a). The relative magnitude of these tractions depends on a number of factors, including the cell type, the thickness and mechanical properties of the substratum [78], ligand density [79], chemotactic gradients [75], the cell disease state [8, 9], and the calculation approach. For example, a study of Dictyostelium cells on thick gel substrata [50] reported higher in-plane traction stress, while a similar study of Dictyostelium cells on thin gel substrata reported higher normal traction stress [48]. The contradictory results in these studies can likely be attributed to the fact that thick isotropic gels show a similar stiffness in response to in-plane and normal traction stresses, whereas thin gels do not. This discrepancy arises, because thin gels violate the macroscopic isotropy condition, meaning that properties such as gel stiffness vary in magnitude in the normal and in-plane directions within the gel [48, 80]. In general, in-plane traction forces are observed throughout the cell with the largest traction forces near the edge, while normal traction forces are concentrated near the center of the cell. The distribution of in-plane traction forces for individual cells is consistent with the idea that protrusions at the leading edge push forward while pulling the rest of the cell during migration. On the other hand, the distribution of normal traction forces is believed to arise from the compression of the nucleus, which is pushed down into the soft substratum by the cell cortex [50].

Far less is known about traction forces during the migration of cells in 3D microenvironments because of challenges associated with imaging and sample preparation. Specifically, measuring bead displacement in 3D gels can be problematic because of working distance limitations associated with high-magnification objectives [81]. Moreover, precisely controlling the 3D microenvironment surrounding migrating cells is difficult [82]. Nevertheless, a number of studies have investigated tractions for single isolated cells in 3D matrices [10, 51, 52]. Legant and co-workers reported that cells embedded in a 3D matrix mainly exerted shear tractions, but there were also small normal tractions close to the body of the cell [51]. Similar to single cells on planar surfaces, tractions were reported to increase with increasing distance from the cell’s center of mass [51]. Breast cancer cells were found to generate traction forces independent of collagen concentration and matrix stiffness in 3D, which is in contrast to the observations for cells on planar surfaces [52]. Moreover, 3D tractions were found to be considerably higher for invasive lung and breast cancer cells, and polarized traction fields were found to facilitate invasion [10].

In addition to studying individual cell migration, traction forces have been investigated during the collective migration of endothelial [83] and epithelial [11, 12, 45, 54, 83] cells. Reflecting the multicellular nature of collective migration, these migrating cellular cohorts exert larger tractions than cells migrating individually [45]. A study of the traction forces exerted by monolayers of Madin–Darby canine kidney (MDCK) epithelial cells found that in-plane traction stresses were smaller than normal traction stresses [83], though no clear trend between the magnitude of normal and in-plane stresses has been reported. For 2D systems consisting of sheets of cells on planar surfaces, the largest tractions were typically observed at the leading edge of the cell monolayer. This observation is consistent with the idea that leader cells—cells at the front of a migrating cell cohort—exert larger tractions than do follower cells [84]. For example, in sheets of MDCK epithelial cells, in-plane traction stress calculations revealed a decrease in average traction stress with increasing distance from the edge of the cell sheet [45]. In contrast, Trepat and co-workers found that collective migration of cell sheets on planar surfaces occurs through a global tug-of-war mechanism, and not as a result of cell pulling by leader cells or self-propelled cells [12]. A TFM technique known as monolayer stress microscopy [85] was recently created to generate stress maps throughout an entire cell sheet [83]. This approach revealed that local intercellular shear stress was minimized during collective migration [83]. During collective migration within 3D matrices, traction stresses were also found to be highest at the leading edge of the migrating cohort [54–56].

Taken together, the aforementioned studies demonstrate the remarkable utility of TFM for quantifying traction forces during the migration of individual cells and collectives in both 2D and 3D systems. That being said, the fact that TFM studies use different experimental conditions and analysis techniques makes it difficult to draw concrete comparisons and make conclusions about the role of traction forces during cell migration. Future work should continue to focus on the creation of generalized experimental protocols for investigating traction forces. This would allow researchers to determine the extent to which the magnitude and spatiotemporal distribution of traction forces present during migration are conserved across different cell types and experimental conditions.

Application 2: forces exerted during tissue morphogenesis

Given their role in cell migration, it is apparent that traction forces are also likely to be important in various morphogenetic processes [86–89]. Indeed, the role of mechanical forces in embryonic development has been recognized since the early twentieth century [90]. Moreover, the relationship between mechanical forces, cell growth and death [3, 91, 92], and tissue geometry is also well appreciated [93, 94]. Nonetheless, the physical mechanisms by which traction forces induce changes in tissue form during development remain largely unknown because it is difficult to explicitly quantify traction forces in vivo.

The primary challenge facing attempts to quantify traction forces in vivo arises from the complex heterogeneous microenvironment surrounding cells, which has poorly defined mechanical properties. To date, the only techniques available to determine forces or stresses in vivo are laser ablation [95] and the use of mechanically deformable injected microdroplets [96]. Laser ablation uses thermal energy to selectively destroy tissue at the cellular or sub-cellular levels [97] and induce relaxation of the ablated region, yielding values for the tensile forces present within the tissue. In contrast, the microdroplet technique is performed by injecting fluorescent oil microdroplets with defined mechanical properties near cell–cell or cell–ECM interfaces [96]. Deformation of the microdroplets, which are coated with ligands for a mechanical link to cell-surface adhesion receptors, can be used to determine anisotropic stresses in vivo. The forces that drive tissue morphogenesis have been investigated in various contexts, including epithelial spreading during zebrafish gastrulation [98], elongation of Drosophila melanogaster embryos [99], and differentiation of muscle cells before and after myotube formation [74].

Several excellent reviews discuss morphogenesis in a broader context [88, 89, 100], as well as the role of mechanical forces in morphogenesis [13, 87, 101–103]. Quantifying traction forces in vivo remains a key challenge that must be addressed to fully understand the role of these forces in morphogenesis. Future work should focus on the improvement of existing in vivo traction force techniques as well as the creation of more precise and accurate approaches. As these approaches proceed into and through their infancy, it is imperative to develop and use culture models that faithfully represent in vivo processes. Such models, discussed below, offer a unique avenue for precisely controlling the form of multicellular structures and the properties of the surrounding matrix. In particular, we highlight the ability of microfabrication-based methods to control 2D and 3D tissue form to more accurately represent in vivo conditions, standardize results to tissue shape, provide statistical analysis, and make heterogeneous environments by spatially controlling substratum properties.

Designing microfabricated tissues to study traction forces

Traditionally associated with materials science and microelectronics, microfabrication-based methods in biology rely on top-down schemes to dictate the placement and organization of ECM proteins [24–26]. For example, investigators in the 1990s used photolithography to define regions of protein adsorption on a silicon surface [104]. The advent of soft lithography in the same decade simplified the printing of proteins onto 2D surfaces [105, 106] and enabled the formation of micromolded 3D ECM structures [107]. Custom 3D ECM gels and scaffolds have also been generated using sacrificial molds [108], as well as inkjet and 3D printing [109, 110]. 2D or 3D microfabricated tissues can be formed when cells are added to the matrix framework fashioned by these methods and allowed to form multicellular structures.

Microfabricated tissues offer several advantages for investigating traction stresses. The engineering control provided by microfabrication enables investigators to parse the relationship between signaling, geometry, mechanics, and changes in tissue shape during culture processes that mimic in vivo behavior; one can control matrix cross-linking, stiffness, and ligand composition. Furthermore, fiducial markers can be incorporated into the 2D or 3D substratum. As described above, the displacement of these markers near the cell–matrix interface provides insight into the forces generated by cells and tissues. Microfabrication-based techniques can also be used to produce large arrays of identical 2D or 3D tissues with well-defined shapes and sizes. This feature of microfabrication-based systems ensures that experiments are particularly high-throughput, a valuable attribute for efficient statistical analyses and for investigating multiple conditions simultaneously.

Microfabricated tissues both recreate aspects of in vivo systems and also offer several advantages traditionally associated with cell culture. Tissues can be created from cells that have genetic modifications introduced via well-established transfection and transduction methods. Coculture is readily included within these systems, thereby enabling investigation of the physical and biochemical interplay between multiple cell types [111–113]. Finally, the motion of cells and matrix is easily imaged, providing investigators with a straightforward approach for quantifying live cell and tissue behavior. Taken together, microfabricated tissues have and will continue to provide valuable insight into multicellular processes. The following subsections detail some 2D- and 3D-microfabricated tissue systems that have been used, paying particular attention to those systems that quantify forces generated by individual cells and multicellular tissues.

Using 2D microfabricated tissues to investigate traction forces

2D tissues with tunable shapes and sizes are formed by exposing cells to surfaces that contain well-defined regions of matrix proteins surrounded by non-adhesive regions. The cells adhere to these regions and proliferate over time to fill the available matrix template. One common technique to produce a surface patterned with adhesive regions (the critical design requirement here) is to use stamps coated with ECM protein. This process, known as microcontact printing, transfers proteins [3, 114] or other ligands [91, 115] to a surface in a manner defined by the bas-relief of the stamp (Fig. 3a). The regions surrounding the deposited protein are then passivated, ensuring that cells adhere only in the desired pattern [116].

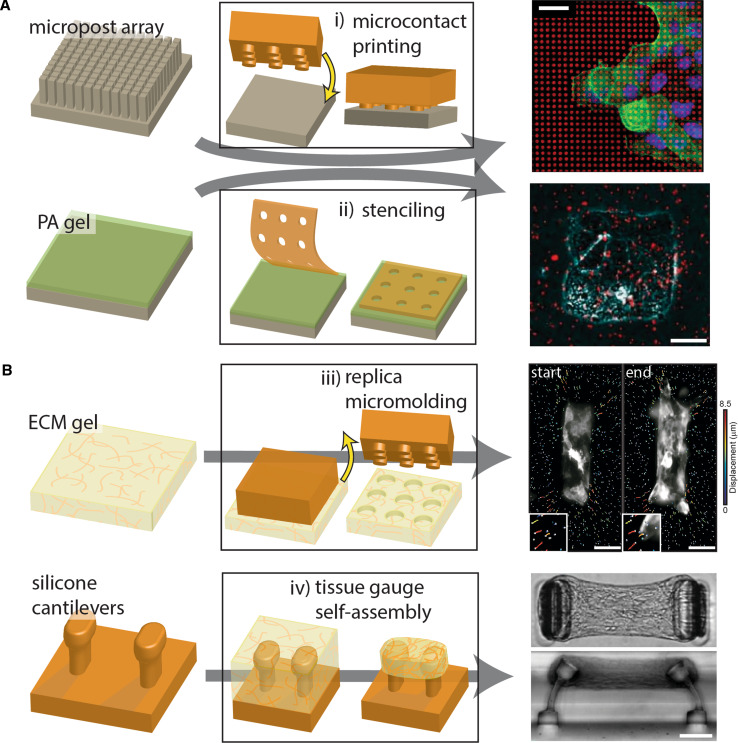
Fig. 3.

Summary of methods to produce 2D and 3D microfabricated tissues. a 2D microfabricated tissues can be produced by i) microcontact printing or ii) stenciling. When fabricated on micropost arrays or PA gels, these tissues can be used to quantify the traction forces involved in migratory and morphogenetic processes. The top-right image depicts microcontact-printed fibronectin on micropillars during a study of collective migration [120]; the bottom-right image depicts an engineered epithelial monolayer produced on a PA gel via stenciling [124]. Top-right image adapted with permission from Vedula et al. [120]. Copyright 2012, the National Academy of Sciences. Bottom-right image adapted from Gomez et al. [124] and reprinted with permission from Wiley-Liss Inc., copyright 2010. b Microfabricated tissues fully encapsulated within a 3D ECM microenvironment can be produced by iii) replica micromolding or iv) self-assembly into tissue gauges. Replica micromolding produces wells within an ECM gel, into which cells are added and allowed to form 3D tissues. Traction forces exerted by these tissues are calculated from the movement of fluorescent beads that have been incorporated into the surrounding gel (iii, right image). In addition, tissue gauges may be used to elucidate how levels of tension relate to tissue-level processes. These 3D microfabricated tissues self-assemble as a cell-laden ECM contracts against silicone micropillars. Top-right image adapted from Gjorevski et al. [54], licensed under creative commons. Bottom-right image adapted with permission from Legant et al. [136]. Copyright 2009, the National Academy of Sciences. Scale bars represent i) 20 μm, ii) 25 μm, iii) 50 μm, and iv) 100 μm

Microcontact printing can be used with either PA gels or flexible microposts to investigate traction forces generated by cells and tissues of specific geometry or configuration (Fig. 3a). PA gels directly stamped with inorganic oxidizing agents produce surface patterns presenting free aldehydes that can then bind to the desired matrix protein [117]. Alternatively, matrix micropatterns can be incorporated onto the gels during the PA polymerization step [118], which occurs between glass slides. One of the glass slides can be printed with the desired proteins and placed in contact with the polymerizing solution to transfer the protein from the slide to the gel. This technique provides a potential advantage when using very soft hydrogels, which are sensitive to unintentional mechanical agitation. Microcontact-printed PA gels have been used to quantify how the composition of ECM ligands influences the magnitude of traction forces [119]. These systems have revealed that traction forces also depend on cell shape and correlate with the differentiation of mesenchymal stem cells [117]. In micropatterned multicellular sheets, high levels of traction stress correlate with regions of elevated proliferation [93].

In a similar approach, distinct adhesive structures can be prepared by microcontact printing proteins directly onto elastic microposts [120–122]. The mechanical properties of the posts can be tuned by varying the ratio of silicone monomer to cross-linking agent or by adjusting the height of the pillars to provide a 1000-fold dynamic range of available post rigidities [121]. The protein of choice is stamped directly onto the surface of the microposts and the side regions are passivated. To date, experiments using microposts printed with distinct regions of protein have revealed that projected cell area, substratum stiffness, and post-density dictate the strengthening of focal adhesions in a manner that closely matches the trends observed for traction forces [122]. In the context of TFM, this system has been used to quantify traction forces within epithelial monolayers migrating along tracks of printed ECM ligands [120]. Microcontact printing offers well-established methods for investigating the traction forces generated by multicellular tissues.

In addition to microcontact printing, micropatterned PA gels can also be produced by stenciling islands of protein onto the surface by adsorbing solution through the holes in microfabricated membranes (Fig. 3a) [123]. In this way, the chemical conjugator (e.g. sulfo-SANPAH) binds only to regions defined by the holes in the membrane stencil, thereby enabling the production of well-defined islands of ECM protein on the PA surface. This technique has revealed that in epithelial tissues, epithelial-to-mesenchymal transition takes place in regions that experience high traction stress [124].

One drawback of the 2D microfabrication-based strategies described above is that they produce tissues with shapes defined in a photolithography step that occurs well in advance of the actual experiment. One strategy for overcoming this limitation and providing greater experimental flexibility may involve inkjet printing either the adhesive ligand or the cells themselves onto a surface [109]. More interestingly, switchable surface coatings [125–127] may be combined with the techniques described here to both define the initial adhesive regions and to provide temporal control of the shape of microfabricated tissues. In these studies, light-mediated cleavage or electrochemical desorption converts initially passivated regions into domains that support cell adhesion. Incorporating switchable surfaces with microposts or PA gels may enable quantification of the traction forces exerted in 2D as monolayers of cells migrate collectively from a confined region and along a dynamically defined path. 2D microfabricated tissues are currently well suited for investigating traction forces, migration, differentiation, and proliferation, though there will undoubtedly be many more advances in the coming years.

Using 3D microfabricated tissues to investigate traction forces

When deciding between 2D and 3D microfabricated tissues, the investigator is faced with trade-offs. On one hand, 2D microfabricated tissues are often simpler and easier to produce. On the other hand, 3D microfabricated tissues exist in a 3D ECM microenvironment that more accurately mimics in vivo conditions. 3D microfabricated tissues are generated by adding cells to 3D matrix scaffolds engineered into a desired shape and size. As described in the following section, these 3D scaffolds are often produced via micromolding of an ECM gel or through microfabrication of silicone elastomer support structures.

Replica micromolding can be used to produce 3D substrata within gels of ECM protein (Fig. 3b) [56, 107, 128, 129]. As with microcontact printing, this method uses silicone stamps with surface features defined via photolithography. In this case, a solution of ECM protein is allowed to gel around the stamp, and removing the stamp produces the inverse features in the gel. Cells can then be added to these scaffolds and a subsequent layer of solution can be allowed to gel on top of the cells, thereby producing 3D microfabricated tissues fully immersed within an ECM microenvironment.

3D microfabricated tissues produced via replica micromolding have been used to relate cell-generated traction forces to changes in gene expression, biochemical signaling, and 3D collective migration [55, 130–134]. These tissues often consist of tubular epithelial structures embedded within a gel of type I collagen. Recently, it was demonstrated that 3D tensile forces drive migration of invasive multicellular cohorts from these microfabricated tissues [54]. These tensile forces activate mechanically sensitive signaling pathways and facilitate matrix remodeling at the leading edge of the cohort. This was the first study to investigate the spatiotemporal nature of physical forces exerted by a migrating cohort fully embedded in 3D matrix.

Microfabricated tissue gauges provide another opportunity to quantify forces from 3D microscale constructs of cells (Fig. 3b) [135, 136]. Micrometer-scale cantilevers are constructed from silicone elastomer in a manner defined by a multilayer photolithographic process. A solution of collagen and cells can be added to the cantilevers and allowed to gel. The cells compact the collagen gel, forming 3D tissues suspended between multiple cantilevers. By monitoring changes in cantilever deflection, one can calculate the tension generated by the tissue during processes such as 3D wound healing [137]. These tissues have been especially useful for investigating relationships between physical forces generated by a tissue and ECM protein deposition and remodeling [135–137].

To date, most TFM-based studies involving microfabricated tissues have used replica micromolding or other similar techniques. Tissues may also be formed by polymerizing an ECM gel around a sacrificial mold, such as a glass micropipette [108]. Alternatively, 3D printing can be used to produce custom substrata via layer-by-layer additive manufacturing [110]. Given that this technology has been used to produce scaffolds for artificial organs, it seems plausible that 3D printing could generate TFM-accessible microenvironments that more accurately mimic in vivo conditions. Taken together, there are many exciting opportunities for using engineering-based approaches to study the traction forces associated with cell migration and tissue morphogenesis. A summary of microfabrication techniques that have been used to quantify traction forces is provided in Table 1.

Table 1.

Summary of microfabricated structures for quantifying traction forces

Microfabrication technique	Microstructure	Dimension	References
Microcontact printing	Islands of ECM	2D	–NIH 3T3 fibroblasts [119, 160, 161] –MDCK epithelial cells [120] –Mesenchymal stem cells [117]
Stenciling	Islands of ECM	2D	–Human airway smooth muscle cells [123] –SCp2 mouse mammary epithelial cells [124]
Replica micromolding	Multidimensional structures	3D	–EpH4 mouse mammary epithelial cells [54, 55, 134] –EpH4 mouse mammary epithelial cells and primary organoids [133]
Tissue gauges	Patterned surfaces and structures	3D	–NIH 3T3 fibroblasts and neonatal rat cardiomyocytes [136] –NIH 3T3 fibroblasts [135, 137]
3D printing	Patterned surfaces and structures	3D	–C2C12 skeletal muscle myoblasts [162]
Sacrificial molds	Multidimensional structures	3D	–Caco-2 colon carcinoma cells [163]

Additional biological insights enabled by microfabricated tissues

Beyond applications for TFM, microfabricated tissues can offer insight into an array of biological processes in development and disease. For example, microfabricated tissues have been used to elucidate the physical and chemical mechanisms involved in a developmental process called branching morphogenesis. Specifically, 3D microfabricated mammary epithelial tissues were used to reveal the interplay between tissue geometry and factors such as mechanical stress [55], autocrine inhibitory morphogen concentration [133], and epithelial-mesenchymal transition [124]. Microfabricated tissues have also been used as models to study diseases including cancer, where they revealed the relationship between mechanical stress and breast cancer cell invasiveness [113] as well as the interplay between interstitial fluid pressure, gene expression, and collective invasion of engineered breast tumors [108]. Additional biological processes, such as collective cell migration [54], wound healing [137], and cell sorting [138], have also been studied using microfabricated tissues. Interested readers can find a more comprehensive discussion of tissue micropatterning in literature [139].

Strategies for overcoming the limitations of conventional TFM

The spatiotemporal accuracy of quantified traction forces has been significantly improved since the original work of Harris and colleagues. Nevertheless, the accuracy of TFM is inherently limited because force is calculated implicitly from measured displacement data. Moreover, this calculation procedure can be computationally expensive, which limits the complexity of the biological systems that can be studied. Additional factors, including the resolution of the fiducial markers, substratum properties, and the validity of the underlying constitutive model used in force calculations, limit the accuracy of any traction forces that may be reported [16]. Limitations also arise from the difficulty associated with creating systems that recapitulate the in vivo microenvironment and that have well-defined mechanical properties. For example, a combination of spatial heterogeneities and large pore sizes in collagen gels can result in a breakdown of the continuous medium assumption [140]. Thus, the relevant mechanical properties of collagen are difficult to determine because of discrepancies between bulk rheology and micromechanics of the collagen network [140]. Furthermore, discrete fiducial markers cannot fully capture the deformation of a continuous substratum, and any deformations of the matrix in between markers remain uncertain [64, 65]. Finally, obtaining high-resolution images can be expensive and may limit the accessibility of the technology.

A recent alternative for measuring substratum deformation involves imaging deformations of fibrous matrix materials as opposed to embedded beads [141, 142]. These studies offer a new approach for calculating 3D displacement fields that may be advantageous in systems where bead displacement techniques are not feasible or have limited accuracy. For example, during remodeling of a fibrous matrix, reflection microscopy can be used to calculate matrix displacements and obtain qualitative information on cell tractions [141, 142]. Quantitative cell traction calculations rely on the assumption that the fibrous network is isotropic and can be approximated as linearly elastic [141]. In addition, molecular force sensors offer one strategy for improving the spatial resolution of quantified traction forces [143–147]. In contrast to TFM-based approaches that can only quantify traction forces exerted by the cell on its external microenvironment, molecular force sensors can be used to probe internal cellular forces [100]. One example is molecular tension-based fluorescence microscopy, which uses immobilized DNA hairpins that have a tunable force threshold to measure tension across integrins [148]. Another example uses a combination of super-resolution light microscopy and polypeptide fluorescence resonance energy transfer (FRET)-based tension sensors to visualize forces across individual molecules that are present within focal adhesions [149]. Myosin I has been used as a sensor for molecular force [150], and DNA hairpins have been used to probe traction forces with high spatial resolution [151]. A final example consists of a molecular tension sensor that uses a PEG polymer to create spatiotemporal maps of mechanical forces exerted by cell-surface receptors [152]. This tension sensor has well-characterized mechanical properties, is biocompatible, and shows minimal non-specific interactions [152]. That being said, a number of challenges must be addressed, including in vivo calibration [145], improved understanding of the relationship between measurements in culture and in vivo, and improved understanding of the appropriate simplifying assumptions [100].

Additional information about cell-generated mechanical forces can also be obtained by combining TFM with other experimental techniques. For example, AFM, which can be used to directly measure the mechanical properties of cells, has been combined with TFM to study how cells respond to applied forces [153, 154]. In a similar approach, incorporating magnetic particles within silicone micropillars enables one to study the response of cells to precisely applied forces [155]. Cellular traction forces have also been studied by combining TFM with optical tweezers. In particular, optical tweezers have been used to dictate the placement of beads, so that traction forces can be quantified locally [156, 157]. It has also been suggested that integrating TFM with molecular force sensors may provide a way to understand the interplay between extrinsic and intrinsic cellular forces [100]. While the aforementioned techniques have made improvements to conventional TFM, developing a complete understanding of traction forces in biological systems will require versatile techniques that can produce spatial maps of forces in vivo with high accuracy and precision.

Concluding remarks

Insight into the biophysical and biochemical mechanisms through which traction forces act is required for understanding a vast array of biological processes. Here, we describe experimental techniques and computational methods to quantify traction forces. Despite considerable progress and improvement in experimental and computational approaches, current TFM techniques cannot be used to quantify traction forces exerted within in vivo microenvironments, nor can they account for the complex heterogeneity present in native ECMs. As described here, microfabricated tissues provide an experimentally tractable means to quantify the traction forces exerted by and within multicellular cohorts. Coupled with improved computational approaches, microfabricated tissues will shed light on the tractions exerted by cells in heterogeneous non-linear microenvironments and provide valuable insight into processes that resemble in vivo migrational and morphogenetic movements.

Abbreviations

2D

Two-dimensional

3D

Three-dimensional

AFM

Atomic force microscopy

ECM

Extracellular matrix

FRET

Fluorescence resonance energy transfer

MDCK

Madin–Darby canine kidney

PA

Polyacrylamide

PEG

Polyethylene glycol

TFM

Traction force microscopy