Mis-estimation and Bias of Hyperpolarized ADC Measurements Due to Slice Profile Effects

Abstract

Purpose

To explore the impact of slice profile effects on ADC mapping of hyperpolarized substrates.

Methods

Slice profile effects were simulated using a Gaussian RF pulse with a variety of flip angle schedules and b-value ordering schemes. A long T₁ water phantom was used to validate the simulation results, and ADC mapping of hyperpolarized [¹³C,¹⁵N₂]urea was performed on the murine liver to assess these effects in vivo.

Results

Slice profile effects result in excess signal after repeated RF pulses, causing bias in HP measurements. The largest error occurs for metabolites with small ADCs, resulting in up to 10-fold overestimation for metabolites that are in more restricted environments. A mixed b-value scheme substantially reduces this bias, while scaling the slice-select gradient can mitigate it completely. In vivo, the liver ADC of hyperpolarized [¹³C,¹⁵N₂]urea is nearly 70% lower (0.99 ± 0.22 vs. 1.69 ± 0.21 × 10⁻³ mm²/s) when slice-select gradient scaling is employed.

Conclusion

Slice profile effects can lead to bias in hyperpolarized ADC measurements. A mixed b-value ordering scheme can reduce this bias compared to sequential b-value ordering. Slice-select gradient scaling can also correct for this deviation, minimizing bias and providing more precise ADC measurements of hyperpolarized substrates.

Introduction

Dissolution dynamic nuclear polarization (DNP) increases the spin-polarization of non spin-zero nuclei by four orders of magnitude, enabling near real-time MR imaging of carbon-13 nuclei (1). Coupled with the ability of magnetic resonance to spectroscopically resolve both substrate and downstream metabolites, hyperpolarized (HP) imaging of metabolically active substrates has enabled non-invasive imaging of cancer (2,3) and other metabolic diseases (4).

The majority of studies with hyperpolarized substrates attempt to estimate the metabolic conversion via metabolite ratios (5) or apparent reaction rates (6,7). In contrast, diffusion weighted MRI has the ability to probe the cellular-scale distribution of metabolites. Because of structural differences in the intra and extracellular microenvironments, diffusion weighted imaging (DWI) of HP substrates can potentially provide unique information about the cellular distribution (8-10) and transport (11,12) of these metabolites, offering insight into transporter expression, which has been shown to be significantly altered in malignant prostate cancer (13), metastatic renal cell carcinoma (14), and breast cancer (15).

Accurate quantification of diffusion coefficients and enzymatic activity are crucial for studying the cellular distribution and transport, as well as translating this technique to clinical studies. For dynamic imaging assessment of reaction rates, data must be acquired at multiple timeframes, so the polarization must be efficiently used over the entire imaging window. This requires either a constant low flip angle or a variable flip angle (VFA) scheme that typically ramp up to high flip angles for the final few RF pulses. In contrast, DWI is interested in the underlying distribution of HP substrates, so only one timeframe with multiple diffusion encodings (b-values) need to be acquired in order to estimate the apparent diffusion coefficient (ADC). Without the need to acquire data at multiple timeframes, high flip angles in rapid succession can be used to maximize SNR and use the hyperpolarization efficiently (10).

However, deviations from the expected signal evolution across the diffusion encodings will lead to modeling bias and parameter mis-estimation. Slice profile effects, which have previously been observed in thermal ¹H (16,17) and HP gas experiments (18), are caused by inherent imperfections in the excitation profile due to realistic (i.e. low time-bandwidth) RF pulses that results in through-slice flip angle variation. This yields excess signal from the edges of the slice after repeated RF pulses when the magnetization evolution is dominated by RF excitation, i.e. TR << T₁. In multi-shot acquisitions, this will result in a deviation from the predicted k-space filtering. However, the single-shot imaging techniques used in HP ¹³C imaging are more sensitive to this effect, as the excess signal will directly alter the signal intensity in each diffusion weighted image. Here, we will show that slice profile effects have the potential to significantly bias the ADC measurements of HP substrates, where only a few images (or spectra) are acquired with relatively high flip angles at different b-values in rapid succession. The goal of this study was to determine the impact of slice profile effects on ADC mapping of HP substrates, and to develop methods to negate bias and parameter mis-estimation.

Methods

Hyperpolarized spin simulations were performed using the Shinnar-Le Roux (SLR) algorithm (19) with the “rf_tools” RF pulse design library (http://rsl.stanford.edu/research/software.html) in MATLAB. The slice profile was simulated for a Gaussian pulse shape (256 point, 5-sigma), and the total signal after each RF pulse was determined by integration along the slice direction. In addition to a constant 30° flip angle, both an RF compensated flip schedule (20) and an RF and diffusion compensated flip schedule (10) were simulated. The RF and diffusion compensated flip schedule was initialized for an expected ADC of 0.8 × 10⁻³ mm²/s and the sequentially ordered b-values enumerated in Table 1. The RF compensated VFA schedule accounts for magnetization usage from prior RF pulses, which would maintain constant transverse magnetization throughout a non diffusion-weighted experiment. Similarly, the RF and diffusion compensated VFA schedule provides constant transverse magnetization by accounting for RF utilization as well as diffusion weighting. While both make more efficient use of the magnetization than a constant flip angle schedule, the RF and diffusion compensated VFA schedule was shown in (10) to provide the best ADC estimate in a hyperpolarized experiment. Designed this way, the final two images from the RF and diffusion compensated flip schedule can potentially be used to estimate the B₁ on a voxelwise basis.

Table 1.

Flip angle (in degrees) and b-value schemes used in this work. The RF variable flip angle (VFA) schedule accounts for magnetization usage from prior RF pulses and would provide constant signal at each TR if no diffusion weighting were employed (20). The RF and diffusion compensated VFA schedule is designed to provide constant signal for each diffusion weighted image by accounting for RF utilization as well as diffusion weighting (10), and was designed with the sequential b-value scheme. Simulations were performed with all three flip angle schedules using either the sequential or mixed b-value ordering schemes.

Acquisition Number	1	2	3	4	5	6	7	8
Constant flip angle	30.0	30.0	30.0	30.0	30.0	30.0	30.0	30.0
RF VFA	20.7	22.2	24.1	26.6	30.0	35.3	45.0	90.0
RF + diffusion VFA	30.8	31.5	32.6	34.2	36.6	40.7	45.0	90.0
Sequential b-value (s/mm2)	700	600	500	400	300	200	50	50
Mixed b-value (s/mm2)	700	400	50	200	600	300	500	50

To compensate for deviation due to slice profile effects, the slice-select gradient was scaled to yield the desired signal response (18). Briefly, the simulation calculated the fractional excess signal arising from slice profile effects. Gradient scaling coefficients were then calculated via fixed point iteration until the simulated signal response matched the desired response to within 1%. The slice select gradient is then scaled by this factor to correct for slice profile effects. For the slice profile simulations the TR was assumed to be much shorter than T₁, and the effects of diffusion on the transverse magnetization were neglected since slice profile effects are only dependent on the RF pulse shape and flip angle schedule. To assess the ADC bias induced by this effect, monoexponential decay curves were generated with ADC values ranging from 0.1 to 3.0 × 10⁻³ mm²/s. Simulations were performed for a sequential and mixed b-value ordering scheme (Table 1). Since slice profile effects result in excess signal after multiple RF pulses, a mixed b-value scheme can potentially minimize bias in ADC measurements arising from this effect. For each b-value, the diffusion-weighted signal was scaled by the simulated slice profile signal and then subsequently fit to a monoexponential decay to extract the ADC.

In vivo and phantom experiments were performed on a Varian 14T NMR imaging spectrometer (Palo Alto, CA, USA) with high-performance gradients (maximum gradient strength of 100 G/cm and a maximum slew-rate of 556 G/cm/ms) using a dual-tune ¹H/¹³C coil. All animal experiments followed a protocol approved by our local institutional animal research care and use committee. Data were acquired using a double spin-echo (DSE) sequence with a single shot, flyback EPI readout. A 1ms Gaussian RF pulse was used for slice-selective excitation, and a global adiabatic RF pulse (HS-AFP, 15ms duration) was used for refocusing. To validate the digital simulations, slice profile effects were assessed on the ¹H channel using a Millipore water phantom (T₁ = 3s at 14T) with the RF and diffusion compensated flip schedule. Data were acquired with a TR/TE of 80/66.3ms, a 32 × 32mm FOV, a 16 × 16 matrix, and a slice thickness of 5mm. Diffusion gradients were applied on all three axes using either the sequential or mixed b-value scheme (bipolar pulse width δ = 5.0ms, bipolar pulse separation Δ = 22.4ms) enumerated in Table 1. As long as TR<<T₁, this setup mimics the hyperpolarized scenario but provides a reproducible and high SNR phantom to rapidly evaluate different flip angle schedules and RF pulses.

To assess these effects in vivo, 90mg of [¹³C,¹⁵N₂]urea was polarized in a 3.35T HyperSense (Oxford Instruments, Abingdon, England) for 90 minutes and rapidly dissolved with 4.5g of 1mM phosphate-buffered saline (PBS) and 0.3mM EDTA. 350μL of 80 mM urea was injected via a tail-vein over 15s, with imaging starting 30s after the start of injection. Diffusion weighted imaging was performed with the aforementioned DSE, single shot flyback EPI pulse sequence, using the RF and diffusion compensated flip schedule in Table 1. Data were acquired with a TR/TE of 100/81.5ms, a 32 × 32mm FOV, a 16 × 16 matrix, and a slice thickness of 8mm. The sequential b-value scheme was used, and the slice-select gradient was either held constant or scaled to account for the expected signal deviation due to slice profile effects. To minimize signal loss from bulk motion, respiratory gating was used. Two b-values per respiratory trigger were acquired, yielding a total acquisition time of 2 - 3s dependent on the respiratory rate. For all n images, raw data were corrected for the flip angle θ_n as well as RF utilization from prior pulses to obtain data that are solely a function of diffusion weighting:

$$S_n=S_{n,raw}/\left(\sin \left({\theta }_n\right)\cdot \prod _{k=1}^{n-1}cos\left({\theta }_k\right)\right)$$ [1]

These RF corrected images are subsequently fit voxelwise to a monoexponential decay to calculate an apparent diffusion coefficient (ADC) map:

$$S(x,y,b)=S_0(x,y)e^{-b\cdot ADC}$$ [2]

Due to the short acquisition time, signal loss from T₁ decay was neglected. For analysis, an ROI was drawn over the liver from the high-resolution ¹H spin-echo images and applied to ¹³C data. Only voxels with a coefficient of determination (R²) of 0.8 or greater for the ADC fit were included in analysis.

Results

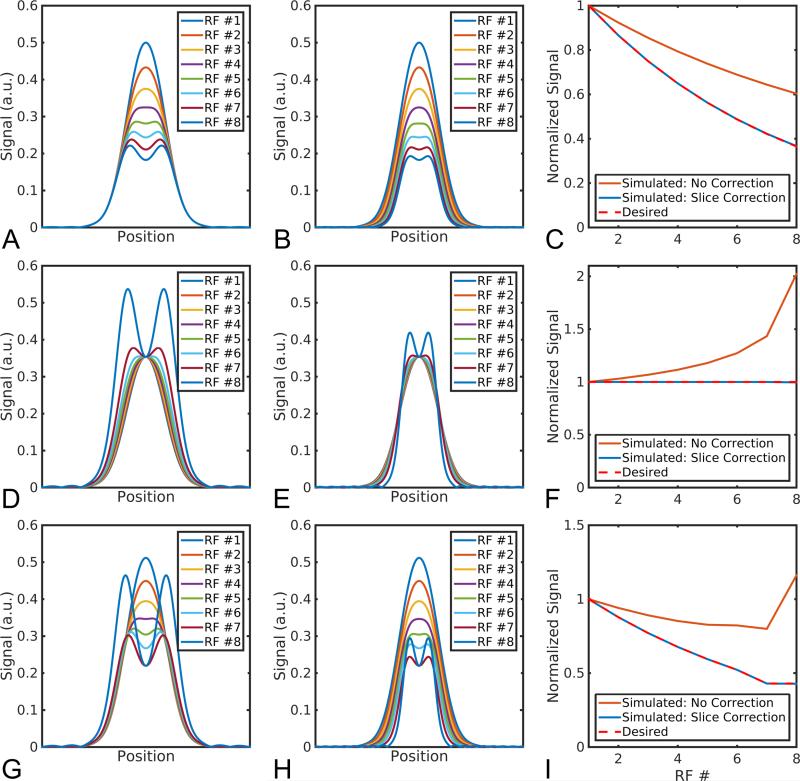
Simulations of the slice profile for HP spins for the three flip angle schedules can be seen in Figure 1. In a slice-selective MR experiment, the slice profile, or transverse magnetization in the slice direction, is a function of the longitudinal magnetization M_z prior to excitation and the excitation profile of the RF pulse. Because of the non-uniform flip angle in the through-slice direction, this results in a distorted slice profile at later RF pulses, giving rise to an effectively wider slice and excess signal arising from the transition bands, regardless of flip angle schedule (Figure 1A,D,G). In all flip angle schedules, excess signal arises immediately after the first RF pulse and increases to a maximum deviation of 1.65 for the constant 30° scheme (Figure 1C), 2.0 for the RF compensated VFA schedule (Figure 1F) and 2.7 for the RF and diffusion compensated VFA schedule (Figure 1I). This will lead to errors in ADC measurements and also precludes any meaningful B₁ estimate from the final two low b-value images from the RF and diffusion compensated flip schedule. This effect can be corrected for by scaling the slice-select gradient, which reduces excitation of the transition band while conforming to the desired overall signal response (Figure 1B,E,H).

Figure 1.

With a constant slice-select gradient, hyperpolarized signal is overestimated after the initial RF pulse because of excess signal in the transition band, regardless of the flip angle scheme (A,D,G). By scaling the slice-select gradient, the desired signal response can be achieved (B,E,H). The amount of excess signal is a function of the flip angle and RF excitation profile (C,F,I). RF flip angle used in each case: constant 30° (A-C); RF variable flip angle (D-F); RF and diffusion variable flip angle (G-I).

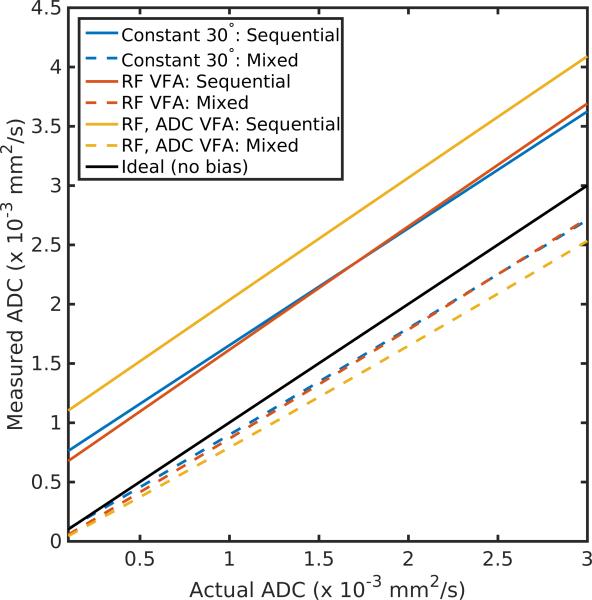
The outcome of simulations of slice profile effects on ADC estimates for the three flip angle schemes can be seen in Fig 2. For the sequential b-value scheme, slice profile effects lead to systematic overestimation of the ADC, regardless of the flip angle scheme employed. This is due to excess signal at later RF pulses, which correspond to lower b-values. The amount of bias is a function of the actual ADC, with the largest error occurring for metabolites with small ADCs, resulting in up to 10-fold overestimation for metabolites that are in more restricted environments. Although there is still some systematic underestimation, a mixed b-value scheme can greatly reduce the bias from slice profile effects, providing more precise ADC measurements without the need for gradient correction.

Figure 2.

Measured vs. actual ADC in the presence of slice profile effects for the three flip angle schedules explored in this work. For a sequential b-value scheme, where b-values are acquired in decreasing value, the ADC is systematically overestimated regardless of the flip angle scheme used. In contrast, a mixed b-value ordering greatly reduces the bias caused by slice profile effects.

Phantom results from a Millipore water phantom corroborate the digital simulations (Supporting Figure 1 & 2). Using the RF and diffusion compensated flip schedule, the measured signal evolution for both the constant and dynamic slice-select gradient agree well with the simulations (Supporting Figure 1), indicating the veracity of the simulations and the utility of using a long T₁ ¹H phantom as a stand-in for a hyperpolarized sample. Allowing sufficient time for T₁ recovery (TR = 15s), the ¹H ADC measured by the DSE sequence was 2.25 ± 0.05 × 10⁻³ mm²/s at room temperature, in good agreement with literature values (21). As in the digital simulations, the ADC measured using a short repetition time is strongly influenced by the order in which b-values are acquired. With a sequential b-value scheme, and a constant slice-select gradient, the ADC was measured to be 3.09 ± 0.12 × 10⁻³ mm²/s, overestimating the actual ADC by 37%. In contrast, a mixed b-value scheme minimizes this bias, underestimating the ADC but only by 8% (2.06 ± 0.06 × 10⁻³ mm²/s). Scaling the slice-select gradient to account for slice profile effects recovers the ADC to within 7% for the sequential b-value scheme (2.09 ± 0.05 × 10⁻³ mm²/s) or 3% for the mixed b-value acquisition (2.30 ± 0.06 × 10⁻³ mm²/s).

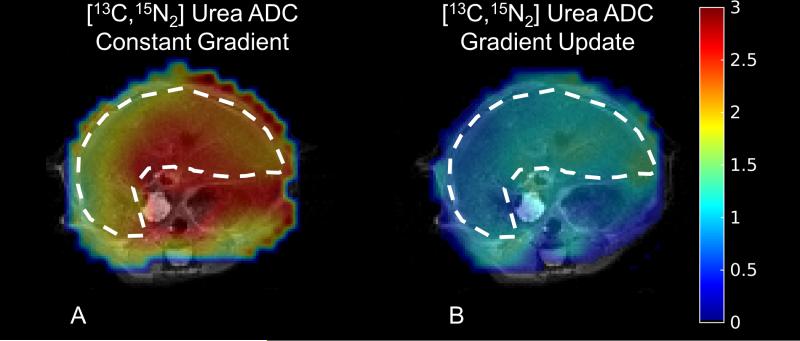
Finally, representative [¹³C,¹⁵N₂]urea ADC maps in the murine liver in vivo acquired using the sequential b-value scheme with and without gradient scaling to correct for slice profile effects can be seen in Figure 3 with the raw images in Supporting Figure 3. As with the digital simulations and phantom experiments, the liver ADC of ¹³C urea in the presence of gradient scaling is, on average, nearly 70% lower (0.99 ± 0.22 vs. 1.69 ± 0.21 × 10⁻³ mm²/s, Supporting Table 1). The ¹³C urea ADC measured when accounting for slice profile effects is in better agreement with the ADC of [1-¹³C]pyruvate measured with a slab excitation in vivo (10), which is also a predominantly extracellular metabolite.

Figure 3.

Representative ¹³C urea ADC maps measured in the murine liver neglecting slice profile effects (A) or accounting for them by scaling the slice select gradient (B). As evinced above, slice profile effects will lead to overestimation of the ADC with the sequential b-value scheme. The liver is highlighted with the dashed line, and the ADC is in units of 10⁻³ mm²/s.

Discussion

In this work, we show that slice profile effects can lead to bias in ADC measurements of hyperpolarized substrates. This effect can be corrected for by prospectively scaling the slice-select gradient to mitigate excess signal from the transition region of the slice, or by using a mixed b-value ordering scheme. While three different flip angle schedules were simulated, only the RF and diffusion compensated VFA schedule was assessed in vivo. The latter schedule was chosen because it makes the most efficient use of the hyperpolarization and produces the most precise estimate of ADC in the presence of noise (10).

Both the digital simulation and phantom/in vivo experiments used a sequential b-value ordering scheme, with b-values acquired in descending order. This was shown to overestimate the ADC, due to excess signal at low b-values. In contrast, a mixed ordering scheme, where high and low b-values are interleaved, was shown to improve accuracy in the presence of slice profile effects. This particular mixed b-value scheme was empirically chosen because it reduced bias in simulations of HP ADC experiments. While it did not completely mitigate mis-estimation over the entire ADC range, an exhaustive search jointly optimizing for both b-value ordering and b-values may be able to further reduce this bias. Prior work has largely avoided the bias introduced by slice profile effects by employing a mixed b-value ordering scheme (12), placing the transition regions where there is little to no hyperpolarized signal (10), or by acquiring multiple b = 0 images (8,9,22). While the multiple b = 0 approach implicitly accounts for slice profile effects, it increases the scan time and makes inefficient use of the hyperpolarization.

It is also important to note that the magnitude of ADC bias induced by slice profile effects is a function of not only the excitation profile (i.e. RF pulse shape), but also the flip angle and b-value schedule used in the acquisition. It is, however, largely independent of B₀ as long as T₁ can be neglected during the timeframe of the experiment. In order to facilitate the study of slice profile effects and the utility of hyperpolarized ADC mapping over a wide range of parameters, we have shared the slice profile code used in this work, which can be accessed at https://github.com/agentmess/hyperpolarized-mri-toolbox/.

RF pulses with a sharp excitation profile, such as a high time-bandwidth RF pulse, can be used to mitigate these aforementioned slice profile effects (18). While this approach is straightforward for ¹³C urea and other metabolically inert substrates, this poses a challenge for slice-selective metabolite specific imaging with EPI or spiral readouts (23), since a spectral-spatial RF pulse must be used to individually excite the multiple chemical species. Because of the inherent tradeoffs in spectral-spatial RF pulse design, a sharp excitation profile is not typically achievable with sufficient stopband suppression due to gradient limitations (24). For this reason we chose to evaluate the relatively low time-bandwidth Gaussian pulse shape.

The gradient correction utilized in this work is predicated on a homogenous spin density and uniform B₁ profile in the slice direction. This assumption will break down for thicker slices, where partial-volume effects will be more pronounced. Even if a small slice or frequency selective RF pulses are used, slice profile effects can also manifest due to the inherent B₁ profile of the coil. While this is less of a problem with volume coils, this can potentially be an issue when surface coils are used for RF transmission. In this instance the B₁ will vary radially, not just in the through-slice direction, and will lead to excess signal in an analogous manner.

Slice profile effects are less likely to manifest in dynamic imaging experiments, where the magnetization must be preserved over a longer imaging window (> 30s) in order to estimate the apparent reaction rate. T₁ decay and spins flowing into or out of the slice will further minimize this effect for dynamic imaging in vivo. However, this effect can manifest whenever high flip angles are used, such as the end of a VFA schedule or with approaches such as saturation recovery (25) that selectively excite the downstream metabolites with a 90° excitation.

To experimentally verify the slice profile effects, a ¹H water phantom at thermal equilibrium was used as a hyperpolarized phantom surrogate. As long as T₁ decay can be neglected during the experiment (i.e. TR << T₁), both thermal and hyperpolarized magnetization evolution will be dominated by RF excitation and the framework discussed here is valid. This provides a platform for rapid testing without the need to waste the enriched ¹³C substrate or the radical required for polarization (26). Moreover, the water ADC has been characterized over a wide range of temperatures (21), providing a gold-standard to assess the slice profile effects on ADC measurements. However, this approach may not be possible at all field strengths, since the ¹H T₁ will decrease at lower fields due to the weak dependence on B₀ (27).

Conclusion

Diffusion weighted imaging can be used to provide information on the distribution of hyperpolarized substrates. However, the imperfect excitation profile and the transient, non-recoverable hyperpolarization lead to excess signal at later flip-angles, and in conjunction with the b-value ordering can bias ADC estimation. A mixed b-value ordering scheme can reduce this bias compared to sequential b-value ordering. Slice-select gradient scaling can also correct for this deviation, minimizing bias and providing more precise ADC measurements of hyperpolarized substrates.