Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Feb 16.
Published in final edited form as: J Phys Chem Lett. 2017 Feb 1;8(4):779–784. doi: 10.1021/acs.jpclett.6b02759

All-Atom Molecular Dynamics Simulations of Entire Virus Capsid Reveal the Role of Ion Distribution in Capsid’s Stability

Elvira Tarasova †, Vladimir Farafonov ‡, Reza Khayat §, Noriaki Okimoto ||, Teruhisa S Komatsu ||, Makoto Taiji ||, Dmitry Nerukh ⊥,*
PMCID: PMC5391438  NIHMSID: NIHMS853607  PMID: 28129688

Abstract

Present experimental methods do not have sufficient resolution to investigate all processes in virus particles at atomistic details. We report the results of molecular dynamics simulations and analyze the connection between the number of ions inside an empty capsid of PCV2 virus and its stability. We compare the crystallographic structures of the capsids with unresolved N-termini and without them in realistic conditions (room temperature and aqueous solution) and show that the structure is preserved. We find that the chloride ions play a key role in the stability of the capsid. A low number of chloride ions results in loss of the native icosahedral symmetry, while an optimal number of chloride ions create a neutralizing layer next to the positively charged inner surface of the capsid. Understanding the dependence of the capsid stability on the distribution of the ions will help clarify the details of the viral life cycle that is ultimately connected to the role of packaged viral genome inside the capsid.

Graphical Abstract

graphic file with name nihms853607u1.jpg

Detailed knowledge of the structure and function of viruses at the molecular level is necessary for developing vaccines and drug treatments for diseases caused by these viruses. Recently such information became possible to obtain because experiments allow the measurement of structures of viral particles at atomistic resolution by X-ray crystallography and cryo-electron microscopy.1–5 However, since the measurements are performed at nonphysiological conditions (e.g., low temperature, crystal packing of the sample), the obtained structure may differ from the cellular environment. In addition, experiments do not resolve some parts of the viral particles (typically flexible or disordered) that can be important for the structure and the dynamics of the virus.1,2

Simulations of whole virus particles using molecular dynamics (MD) is an actively developing area of research.6–15 They (i) can provide detailed information about the structure and dynamics of the system in solution at atomistic and molecular levels and (ii) become feasible for relatively long simulated times by using high performance computation, including special-purpose computer systems, such as ANTON16 and MDGRAPE-4,17 and new algorithms.18–21

Here we report on the simulation study of Porcine Circovirus type 2 (PCV2). It refers to the family Circoviridae and has circular single-stranded DNA placed inside a nonenveloped icosahedral capsid. PCV2 is pathogenic and causes porcine circovirus-associated diseases.1,22–24 This virus represents a convenient object for MD simulations because it is one of the smallest viruses, with a diameter of about 20 nm, and its atomistic structure has been determined experimentally at 2.3 Å resolution by X-ray crystallography.1 The capsid consists of 60 copies of single gene product (elementary subunits), the structure of which is available in the Protein Data Bank (PDB ID 3R0R). Importantly, the flexible N-terminal ends of the proteins (33 residues) could not be resolved in the structure and, therefore, are absent in the PDB. Also, the crystallographic structure does not reflect the complete picture of interactions involving proteins constituting the capsid and the solvent at room temperature,12,25 where molecules of water and ions play a key role in the dynamical adjustment of the protein conformations. This is because, as commonly agreed, the hydration water is the main “driving force” of protein dynamics governing both local and large scale motions in proteins.26

The proteins of the PCV2 capsid are capable of spontaneously assembling into an empty capsid (also termed virus-like particle), which is stable in the absence of the DNA inside, as shown in experiments at physiological conditions (refs 27 and 28, and unpublished results) albeit at rather low resolution (only the overall shape of the empty capsid was visible). However, the reason for this stability of the empty capsid without the DNA inside is still unclear.

By performing the simulations under physiological conditions (e.g., pH, salinity, and temperature) using the crystallographic coordinates, we hypothesize that one of the possible reasons for the stability of the empty capsid is linked to the charges carried by the ions in solution, particularly chloride ions, that could mimic the genome in its absence and substitute its functions related to the maintenance of the capsid structure. The imitation of genome by negative charges has been already shown for satellite tobacco mosaic virus and satellite tobacco necrosis virus, where chloride ions are located at the same regions as the genome.9 Therefore, we consider cases with varying number of ions to check this hypothesis.

In this work, we report that while the crystallographic structure agrees reasonably well with the MD structures, a noticeable difference arises between the simulations of the capsids with low and high number of ions that confirms our hypothesis.

The PCV2 capsid consists of 60 copies of the structural subunits arranged in an icosahedral symmetric structure. The subunits are assembled without gaps with the exception of small pores at 5-fold axes, large enough for water and ion transport.

We perform MD simulations of the whole virus capsid at all-atom resolution in explicit water. The initial structure of the elementary subunit was taken from the X-ray measurements excluding the first 33 amino acids, the N-terminus (which we call “tail”), located inside the capsid.1 The sequence for the missing N-terminus is known from the sequence of the gene used to express the elementary subunit. In this work we used the structure of PCV2 consensus sequence virus-like particle, which was chosen for X-ray crystallography as the most convenient for expression. The structure of the N-termini was impossible to resolve most probably because of their disordered conformations.2 Note that the N-termini that we used are slightly negatively charged, which is in contrast to the real virus, where they possess significant positive charge. This facilitates their interaction with negatively charged DNA. In our case, however, the DNA is absent and, thus, the charge of the N-termini is not critical for the self-assembly of the capsid.

During the preparation of the initial capsids without the tails, the elementary subunit without the N-terminus was copied 60 times, taking into account the symmetry of the capsid, and assembled into a complete icosahedral capsid using VIPERdb Utilities.29 The same procedure was applied for the assembly of the capsid including tails, with the structure of the tails reconstructed based on the known sequence using the Homology Modeling method by Modeller30 and adding it to the elementary subunit from the PDB. Next, the structural refinements of the tails inside the whole capsid were performed using Molecular Operating Environment (MOE)31 program (Chemical Computing Group, Inc.)

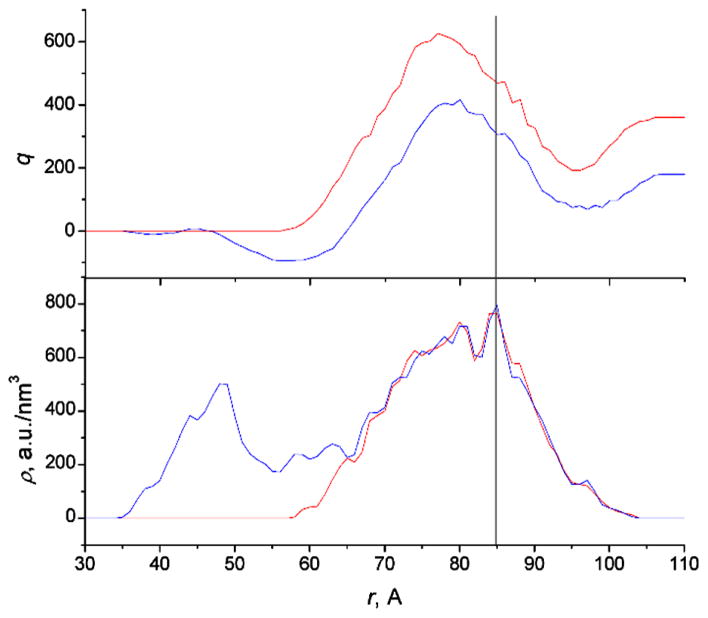
The capsid carries a large total positive charge of 360 |e| (without tails) or 180 |e| (with tails, which are negatively charged). The charge is distributed unevenly between the inner and the outer surfaces. In order to neutralize this excess charge correctly, we plotted the dependences of the integral charge of the capsid atoms on the distance from the capsid center of mass (COM), Figure 1. We used adjacent averaging to remove noise from the plots.

Figure 1.

Figure 1

Open in a new tab

Dependences of integral charge (top) and number density (bottom) of capsid atoms on the distance from the capsid center of mass. Red curves correspond to the capsid without tails, blue curves correspond to the capsid with tails. The vertical line corresponds to the middle of the capsid wall.

For comparison we also plotted the density of capsid atoms versus the distance from the capsid COM. The distinct well on the plot for the capsid with the tails corresponds to tails that are stretched toward the capsid center. The maxima on the density plots are located at ~8.5 nm and correspond to the middle of the capsid wall. The maxima of the charge plots, however, are located at a shorter distance of ~7.8 nm. This allowed us to conclude that the positive charge is concentrated at the inner surface of the capsid and has the magnitude equal to the value at the maximum of the charge plot (606 for the capsid without tails and 407 for the capsid with them). The outer surface carries the negative charge of smaller magnitude (246 for the capsid without the tails and 227 for the capsid with them). In total the capsid has positive charge. Because the capsid appeared to be highly polar, we decided to separately neutralize the charge of each surface.

The positive charge of the inner surface was neutralized with Cl− ions placed inside the capsid (606 ions for the capsid without the tails and 407 ions for the capsid with them). The negative charge of the outer surface was neutralized with Na+ ions placed in the bulk solution (246 for the capsid without the tails and 227 for the capsid with them). We will call the systems with these numbers of ions “neutralizing” further in the text. Finally, to simulate physiological conditions, we added 1720 Na+ and Cl− ions uniformly distributed in the system, which corresponds to 0.9 mass percent of NaCl buffer.

Also for both capsids we performed simulations with a reduced number of ions, where we placed half of the needed number of Cl− inside the capsids (300 in the capsid without tails and 200 in another one). To maintain the electroneutrality of the whole system, we also added ions outside the capsid (60 Cl− for the capsid without tails and 20 Na+ for the capsid with tails). The systems with these numbers of ions will be called “low” to distinguish them from the “neutralizing” systems. NaCl in physiological concentration (1720 Na+ and Cl−) was added as well. A detailed algorithm of adding ions is presented in the Supporting Information. We would like to stress that all simulated systems were electroneutral as a whole.

Two different force fields were used for each simulation: GROMOS53a632 and AMBER03,33 to investigate the dependence of the results on the force field details of interatomic interactions.

Different models of water were also chosen for the different force fields: SPC for GROMOS and TIP3P for AMBER. In total, eight systems were studied: four capsids with the neutralizing number of ions (two capsid without the tails and two capsids with the tails included), and four of the same systems with the deficit of ions inside. Table 1 summarizes the initial conditions of the systems in the AMBER force field.

Table 1.

Initial Composition of Modelled Systema

system capsid without tails
capsid with tails
NI LI NI LI
box size (nm) 26.68 26.68 26.65 26.65
inside outside inside outside inside outside inside outside
Ncompens 606 Cl− 246 Na+ 300 Cl− 60 Cl− 407 Cl− 227 Na+ 200 Cl− 20 Na+
NNa+ 1966 1720 1947 1740
NCl− 2326 2080 2127 1920
Nwater 568 707 569 199 559 368 559 782
Natoms 1 898 573 1 899 557 1 897 998 1 898 826
Open in a new tab
a

NI – System with the neutralizing number of ions; LI – System with the low number of ions; Ncompens – number of ions added to capsids for charge compensation. NNa+ – total number of sodium ions; NCl− – total number of chloride ions; Nwater – total number of water molecules; Natoms –total number of atoms in system.

The initial structures were equilibrated before the start of MD simulations via energy minimization and subsequent MD run with position restraints of the capsid, increasing the temperature from 200 to 300 K (see Supporting material for details). We used PME treatment of Coulomb interactions for the MD simulations. After the initial equilibration, we simulated each system for 10 ns and used these intervals for the analysis.

At the end of the 10 ns simulation, all capsids with the neutralizing number of ions preserved symmetry, whereas simulations with the low number of the ions lost the capsid symmetry during the simulation and showed clear signs of disintegration. The simulation of the system with the low number of ions and no tails in AMBER force field was then extended for additional 10 ns.

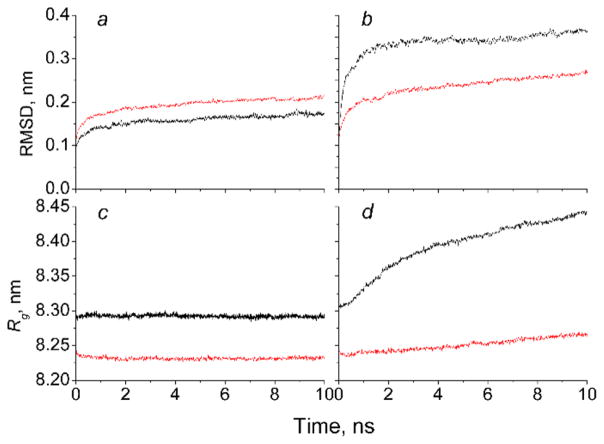
To quantitatively demonstrate the stability of the structure, we analyzed the change of root-mean-square deviation (RMSD) and the radius of gyration (Rg) for the backbone atoms of the whole capsids with time. Plots for AMBER force field are shown on Figure 2, plots for GROMOS force field are presented in the Supporting Information. The calculations of RMSD and Rg were performed for the same set of amino acids for all systems and did not include the tails.

Figure 2.

Figure 2

Open in a new tab

Time change of the root-mean-square deviation, RMSD, (top plots) and radius of gyration, Rg, (bottom plots) of backbone atoms from their initial structure as a reference structure in AMBER force field. The calculations of RMSD and Rg did not include the tail sequence for all structures and consisted of the same number of amino acids. Red is for the capsid with the tails, black is for the capsid without the tails. (a,c) Capsids with the neutralizing number of ions; (b,d) capsids with the low number of ions.

First consider the results obtained for the capsids with the neutralizing number of ions.

Figure 2a,c show RMSD and Rg values for the capsids with the neutralizing number of ions without tails (black curve) and with tails (red curve). A stable value of RMSD for the capsid without tails at 0.2 nm indicates a stable state of the viral particle and small deviation from the initial structure, which is a usual consensus in literature,8,34 together with constant values of Rg allow us to conclude that the capsid without tails is stable during 10 ns of simulation. Despite the presence of slow growth of RMSD for the capsid with the tails we can conclude that the capsid is in a stable state, because Rg remains constant. The growth of RMSD in the case with the tails could be explained by local rearrangements in the proteins or some movements of the parts of protein, which are connected with flexible tails that do not affect the overall shape of the capsid. This behavior coincides with experimental data.

Distinct results are obtained for the case where the low number of ions are placed inside the capsid (Figure 2b,d). Both structures demonstrate the continuous growth of RMSD. The value for the capsid without tails reaches almost ~0.4 nm, and the value for the structure with the tails is almost ~0.3 nm. Also, the continuous increase of Rg for both capsids suggests instability of the initial conformation of each capsid with the low number of ions.

It is noted that for all cases with low number of ions (Figure 2b,d), the capsids demonstrate drastical change and they lose their symmetry, which suggests that the initial structure is not stable for the conditions. The loss of symmetry for the capsid without tails and with the tails happens at different rates. We conclude that the capsid with tails has additional interactions between the tails and the inner surface of the capsid that play the role of anchors, which prevent rapid destruction of the structure; however, it is not enough for maintaining the symmetrical structure.

Plots for the same systems in GROMOS force field show similar behavior (Supporting Information).

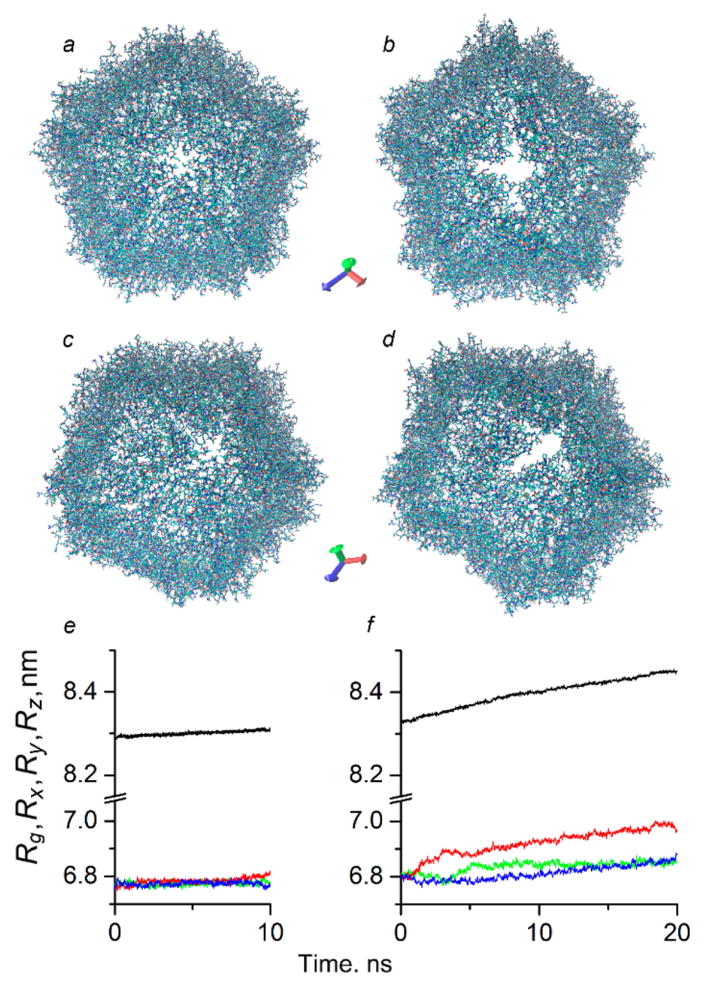
Figure 3 shows the results of the simulations for the capsids without tails in the GROMOS force field with the neutralizing number of ions (a,c) and with the low number of ions (b,d). The systems with low number of ions develop cracks in the capsid shell in the region of 5-fold axis (Figure 3b,d), which is the reason for the loss of the symmetry and growing values of RMSD and Rg.

Figure 3.

Figure 3

Open in a new tab

Atomistic structures of PCV2 capsid without tails after simulations: (a,c) the atomistic structures of PCV2 capsid with the neutralizing number of ions, (e) radius of gyration for different axis (green is X-axis, red is Y-axis, blue is Z-axis); (b,d) the capsid structures with the low number of ions and (f) radius of gyration for different axis.

Coinciding values of Rg with respect to x-, y-, and z-axes unchanged with time (Figure 3e,f) demonstrate the preservation of the symmetry for the system with the neutralizing number of ions (Figure 3e), while increasing in different way values of Rg indicate the loss of the symmetry for the system with the low number of ions (Figure 3f) that shows that the capsid expands unevenly, developing large cracks in the shell. This behavior does not have a tendency to change with time, even after additional 10 ns of simulation, Figure 3f.

Summarizing, the results obtained for eight systems after 10 ns of MD simulation show that the number of ions inside plays the key role in the stability of the capsid and in maintaining its symmetry.

We additionally plotted the dependences of the integral charge of the capsid atoms on the distance from the capsid’s center of mass for the final structures in order to assess the change in comparison to the initial structure. The plots are shown in the Supporting Information. The plots are very similar to the initial ones, and the heights of the maxima remained unchanged.

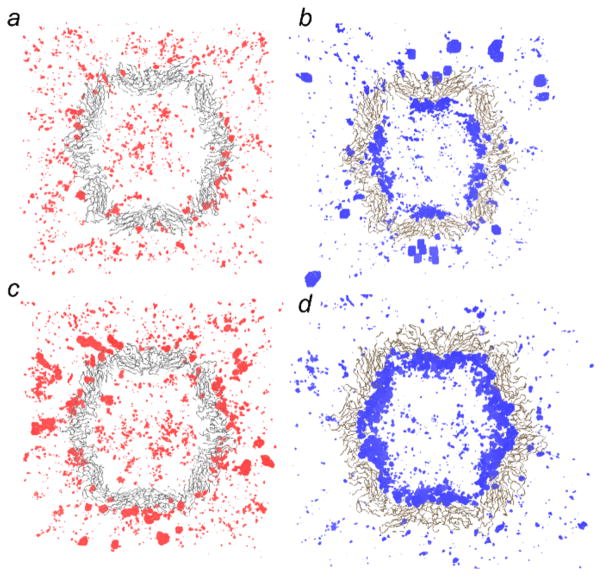
The loss of the capsid symmetry and the formation of the cracks at certain regions, that we observed, suggests the hypothesis that there is a qualitative difference in the distribution of the ions inside the capsids. Figure 4d shows that next to the positive inner wall of the capsid, a tight layer of chloride ions is formed when the number of ions is correct. However, in the case of the low number of ions (Figure 4b), the chloride ions are accumulated unevenly on the inner capsid surface, forming distinct voids near the pores. We illustrate the case of ion distribution in the capsid without tails because the presence of the tails complicates the picture.

Figure 4.

Figure 4

Open in a new tab

Distribution of ions after the first nanosecond of MD simulation for the low number of ions (top) and for the neutralizing number of ions (bottom). Red density (a,c) represents the density of sodium ions, and blue density (b,d) is the density of chloride ions averaged over one nanosecond of simulation. The pictures of the capsids with ions are sliced along the middle of the capsid.

We suggest two possible mechanisms that explain the loss of the capsid symmetry.

  1. When the capsid has insufficient number of chloride ions inside, its positive inner wall is covered by negative ions unevenly, and some areas of the wall have a deficit of the negative ion charges (these areas are mostly in the vicinity of the capsid’s pores; Figure 4b). Because of this unbalanced charge distribution, the unneutralized positive parts of the inner wall are attracted toward the negative cloud of the chloride ions inside the capsid, causing this part of the wall to collapse inside and flattening the roughly spherical shape of the capsid at this location. This correlates with the conclusions of ref 9, where the authors observed accumulation of chloride ions inside the 5-fold symmetry pores.

  2. As we observed during the simulation, the lack of chloride ions in and around the pores allows sodium ions to pass through the pore, increasing the already excessive unneutralized positive charge of the inner wall in the vicinity of the pore, which leads to weakening of the interactions between the subunits and eventual appearance of wide cracks in the capsid at these locations. In the case of the neutralizing number of chloride ions inside the capsid, the chloride ions form a tight layer of negative charge evenly distributed on the inside surface. This layer is matched by a similar positive layer of sodium ions on the outside surface of the capside (Figure 4c,d). These two layers of large opposite charges are strongly attracted to each other, stabilizing the whole structure of the capsid.

In conclusion, our simulations demonstrate that the neutralizing number of ions (especially chloride ions) is necessary for the stability of the capsid, and the chloride ions cover the positive inner wall of the capsid, creating the tight layer of negative charge.

Lastly, comparing the two used force fields, we conclude that AMBER produces the structure of the stable capsid that more closely matches the crystallographic structure. Whether this signifies the better suitability of AMBER force field for PCV2 simulations or GROMOS will also present the stable result is unclear; more simulation time is needed for conclusive results.

Also, our results show that the RMSD between the structure with the neutralizing number of ions with and without the N-termini in solution at 300 K and X-ray structure at 100 K crystal packing environment is not high. This demonstrates that the crystallographic structure reflects the structure in vivo.

Supplementary Material

Supplemental

Acknowledgments

E.T. acknowledges support from the Royal Society of Chemistry (Researcher Mobility Fellowship, 550074), the Great Britain Sasakawa Foundation (grant 4679), and the 5 top 100 Russian Academic Excellence Project at the Immanuel Kant Baltic Federal University; R.K. was funded by NIH National Institute of General Medical Sciences and National Institute of Allergy and Infectious Diseases (5SC1AI114843) and by Grant Number 5G12MD007603-30 from the National Institute on Minority Health and Health Disparities. This work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) funded by the UK High-End Computing Consortium for Biomolecular Simulation (grant number EP/L000253/1). The supporting data of this study are stored at the University of Aston. Details of how to request access to these data are provided in the documentation available from the University of Aston research data repository at http://dx.doi.org/10.17036/6e8e1a26-aa8d-4cfc-aed1-551b081cd391

Footnotes

Author Contributions

The manuscript was written through contributions of all authors.

The authors declare no competing financial interest.

Supporting Information

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.6b02759.

Detailed description of the preparation of the structures for the simulations, the simulation process, RMSD(t) and Rg(t) plots for GROMOS force field, and the charge distribution in final configurations (PDF)

References

  • 1.Khayat R, Brunn N, Speir JA, Hardham JM, Ankenbauer RG, Schneemann A, Johnson JE. The 2.3-angstrom structure of porcine circovirus 2. J Virology. 2011;85:7856–7862. doi: 10.1128/JVI.00737-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Perilla JR, Hadden JA, Goh BC, Mayne CG, Schulten K. All-atom molecular dynamics of virus capsids as drug targets. J Phys Chem Lett. 2016;7:1836–1844. doi: 10.1021/acs.jpclett.6b00517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Lane SW, Dennis CA, Lane CL, Trinh CH, Rizkallah PJ, Stockley PG, Phillips SE. Construction and crystal structure of recombinant STNV capsids. J Mol Biol. 2011;413:41–50. doi: 10.1016/j.jmb.2011.07.062. [DOI] [PubMed] [Google Scholar]
  • 4.Wang X, Ren J, Gao Q, Hu Z, Sun Y, Li X, Rowlands DJ, Yin W, Wang J, Stuart DI, et al. Hepatitis A virus and the origins of picornaviruses. Nature. 2015;517:85–88. doi: 10.1038/nature13806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Duquerroy S, Da Costa B, Henry C, Vigouroux A, Libersou S, Lepault J, Navaza J, Delmas B, Rey FA. The picobirnavirus crystal structure provides functional insights into virion assembly and cell entry. EMBO J. 2009;28:1655–1665. doi: 10.1038/emboj.2009.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Goh BC, Perilla JR, England MR, Heyrana KJ, Craven RC, Schulten K. Atomic modeling of an immature retroviral lattice using molecular dynamics and mutagenesis. Structure. 2015;23:1414–1425. doi: 10.1016/j.str.2015.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Miao Y, Johnson JE, Ortoleva PJ. All-atom multiscale simulation of cowpea chlorotic mottle virus capsid swelling. J Phys Chem B. 2010;114:11181–11195. doi: 10.1021/jp102314e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Freddolino PL, Arkhipov AS, Larson SB, McPherson A, Schulten K. Molecular dynamics simulations of the complete satellite tobacco mosaic virus. Structure. 2006;14:437–449. doi: 10.1016/j.str.2005.11.014. [DOI] [PubMed] [Google Scholar]
  • 9.Larsson DS, van der Spoel D. Screening for the location of RNA using the chloride ion distribution in simulations of virus capsids. J Chem Theory Comput. 2012;8:2474–2483. doi: 10.1021/ct3002128. [DOI] [PubMed] [Google Scholar]
  • 10.Andoh Y, Yoshii N, Yamada A, Fujimoto K, Kojima H, Mizutani K, Nakagawa A, Nomoto A, Okazaki S. All-atom molecular dynamics calculation study of entire poliovirus empty capsids in solution. J Chem Phys. 2014;141:165101. doi: 10.1063/1.4897557. [DOI] [PubMed] [Google Scholar]
  • 11.Zink M, Grubmüller H. Primary changes of the mechanical properties of southern bean mosaic virus upon calcium removal. Biophys J. 2010;98:687–695. doi: 10.1016/j.bpj.2009.10.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Wieder M, Perricone U, Seidel T, Boresch S, Langer T. Comparing pharmacophore models derived from crystal structures and from molecular dynamics simulations. Monatsh Chem. 2016;147:553–563. doi: 10.1007/s00706-016-1674-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Zhao G, Perilla JR, Yufenyuy EL, Meng X, Chen B, Ning J, Ahn J, Gronenborn AM, Schulten K, Aiken C, et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics. Nature. 2013;497:643–646. doi: 10.1038/nature12162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Perilla JR, Goh BC, Cassidy CK, Liu B, Bernardi RC, Rudack T, Yu H, Wu Z, Schulten K. Molecular dynamics simulations of large macromolecular complexes. Curr Opin Struct Biol. 2015;31:64–74. doi: 10.1016/j.sbi.2015.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Larsson DS, Liljas L, van der Spoel D. Virus capsid dissolution studied by microsecond MD simulation. PLoS Comput Biol. 2012;8:e1002502. doi: 10.1371/journal.pcbi.1002502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Shaw DE, Grossman JP, Bank JA, Batson B, Butts JA, Chao JC, Deneroff MM, Dror RO, Even A, Fenton CH, et al. SC14: International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE Computer Society; New York: 2014. Anton 2: Raising the Bar for Performance and Programmability in a Special-Purpose Molecular Dynamics Supercomputer; pp. 41–53. [Google Scholar]
  • 17.Ohmura I, Morimoto G, Ohno Y, Hasegawa A, Taiji M. MDGRAPE-4: a special-purpose computer system for molecular dynamics simulations. Philos Trans R Soc, A. 2014;372:20130387. doi: 10.1098/rsta.2013.0387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.De Vivo M, Masetti M, Bottegoni G, Cavalli A. Role of molecular dynamics and related methods in drug discovery. J Med Chem. 2016;59:4035–4061. doi: 10.1021/acs.jmedchem.5b01684. [DOI] [PubMed] [Google Scholar]
  • 19.Korotkin I, Nerukh D, Tarasova E, Farafonov V, Karabasov S. Two-phase flow analogy as an effective boundary condition for modelling liquids at atomistic resolution. Journal of Computational Science. 2016;17(2):446–456. [Google Scholar]
  • 20.Korotkin I, Karabasov S, Nerukh D, Markesteijn A, Scukins A, Farafonov V, Pavlov E. A hybrid molecular dynamics/fluctuating hydrodynamics method for modelling liquids at multiple scales in space and time. J Chem Phys. 2015;143:014110. doi: 10.1063/1.4923011. [DOI] [PubMed] [Google Scholar]
  • 21.Markesteijn A, Karabasov S, Scukins A, Nerukh D, Glotov V, Goloviznin V. Concurrent multiscale modelling of atomistic and hydrodynamic processes in liquids. Philos Trans R Soc, A. 2014;372:20130379. doi: 10.1098/rsta.2013.0379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Meng X-J. Fields Virology. Lippincott Williams & Wilkins; Philadelphia, PA: 2013. [Google Scholar]
  • 23.Rose N, Opriessnig T, Grasland B, Jestin A. Epidemiology and transmission of porcine circovirus type 2 (PCV2) Virus Res. 2012;164:78–89. doi: 10.1016/j.virusres.2011.12.002. [DOI] [PubMed] [Google Scholar]
  • 24.Segalés J. Porcine circovirus type 2 (PCV2) infections: clinical signs, pathology and laboratory diagnosis. Virus Res. 2012;164:10–19. doi: 10.1016/j.virusres.2011.10.007. [DOI] [PubMed] [Google Scholar]
  • 25.Terada T, Kidera A. Comparative molecular dynamics simulation study of crystal environment effect on protein structure. J Phys Chem B. 2012;116:6810–6818. doi: 10.1021/jp2125558. [DOI] [PubMed] [Google Scholar]
  • 26.Nerukh D, Karabasov S. Water–peptide dynamics during conformational transitions. J Phys Chem Lett. 2013;4:815–819. doi: 10.1021/jz400051p. [DOI] [PubMed] [Google Scholar]
  • 27.Fan H, Ju C, Tong T, Huang H, Lv J, Chen H. Immunogenicity of empty capsids of porcine circovius type 2 produced in insect cells. Vet Res Commun. 2007;31:487–496. doi: 10.1007/s11259-007-3469-7. [DOI] [PubMed] [Google Scholar]
  • 28.Nawagitgul P, Morozov I, Bolin SR, Harms PA, Sorden SD, Paul PS. Open reading frame 2 of porcine circovirus type 2 encodes a major capsid protein. J Gen Virol. 2000;81:2281–2287. doi: 10.1099/0022-1317-81-9-2281. [DOI] [PubMed] [Google Scholar]
  • 29.Carrillo-Tripp M, Shepherd CM, Borelli IA, Venkataraman S, Lander G, Natarajan P, Johnson JE, Brooks CL, Reddy VS. VIPERdb2: an enhanced and Web API enabled relational database for structural virology. Nucleic Acids Res. 2009;37:D436–D442. doi: 10.1093/nar/gkn840. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
  • 31.Molecular Operating Environment (MOE), 2013.08. Chemical Computing Group Inc; Montreal, QC, Canada: 2016. [Google Scholar]
  • 32.Oostenbrink C, Villa A, Mark AE, Van Gunsteren WF. A biomolecular forcefield based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. J Comput Chem. 2004;25:1656–1676. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
  • 33.Duan Y, Wu C, Chowdhury S, Lee MC, Xiong G, Zhang W, Yang R, Cieplak P, Luo R, Lee T, et al. A point-charge forcefield for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J Comput Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
  • 34.Roberts JA, Kuiper MJ, Thorley BR, Smooker PM, Hung A. Investigation of a predicted N-terminal amphipathic α-helix using atomistic molecular dynamics simulation of a complete prototype poliovirus virion. J Mol Graphics Modell. 2012;38:165–173. doi: 10.1016/j.jmgm.2012.06.009. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental
NIHMS853607-supplement-Supplemental.pdf (605.4KB, pdf)

RESOURCES