Using recurrent neural network models for early detection of heart failure onset

Abstract

Objective: We explored whether use of deep learning to model temporal relations among events in electronic health records (EHRs) would improve model performance in predicting initial diagnosis of heart failure (HF) compared to conventional methods that ignore temporality.

Materials and Methods: Data were from a health system’s EHR on 3884 incident HF cases and 28 903 controls, identified as primary care patients, between May 16, 2000, and May 23, 2013. Recurrent neural network (RNN) models using gated recurrent units (GRUs) were adapted to detect relations among time-stamped events (eg, disease diagnosis, medication orders, procedure orders, etc.) with a 12- to 18-month observation window of cases and controls. Model performance metrics were compared to regularized logistic regression, neural network, support vector machine, and K-nearest neighbor classifier approaches.

Results: Using a 12-month observation window, the area under the curve (AUC) for the RNN model was 0.777, compared to AUCs for logistic regression (0.747), multilayer perceptron (MLP) with 1 hidden layer (0.765), support vector machine (SVM) (0.743), and K-nearest neighbor (KNN) (0.730). When using an 18-month observation window, the AUC for the RNN model increased to 0.883 and was significantly higher than the 0.834 AUC for the best of the baseline methods (MLP).

Conclusion: Deep learning models adapted to leverage temporal relations appear to improve performance of models for detection of incident heart failure with a short observation window of 12–18 months.

OBJECTIVE

Before diagnosis of a disease, an individual’s progression mediated by pathophysiologic changes distinguishes those who will eventually get the disease from those who will not. Detection of temporal event sequences that reliably distinguish disease cases from controls may be particularly useful in improving predictive model performance. We investigated whether recurrent neural network (RNN) models could be adapted for this purpose, converting clinical event sequences and related time-stamped data into pathways relevant to early detection of disease.

Electronic health record (EHR) data capture rich clinical and related temporal information. Patient health care encounters are well documented (eg, diagnoses, medications, and procedures) and time-stamped. However, EHR data are highly complex, given the structure and breadth of information captured (spanning provider behavior, care utilization, treatment pathways, and patient disease state) and irregular sampling frequency. To date, most predictive modeling work using EHR data rely on aggregate features (eg, event count and event average). Temporal relations among disaggregated features (eg, medication ordered at one time and procedure performed at another) are not captured using these methods.

We applied RNN models to heart failure (HF) cases and controls using longitudinal EHR data, and compared the model performance to traditional machine learning approaches. HF is one of the leading causes of morbidity and mortality among elderly individuals in developed economies and accounts for significant and growing health care expenditures.^1,2 Improved early detection could open new opportunities for delaying or preventing progression to diagnosis of HF and reduce cost.

BACKGROUND AND SIGNIFICANCE

Early detection of heart failure

Onset of HF is associated with a high level of disability, health care costs, and mortality (roughly 50% risk of mortality within 5 years of diagnosis).^1,2 There has been relatively little progress in slowing the progression of this disease, largely because it is difficult to detect before actual diagnosis. As a consequence, intervention has primarily been confined to the time period after diagnosis, with little or no impact on disease progression. Earlier detection of HF could lead to improved outcomes through patient engagement and more assertive treatment with angiotensin-converting enzyme inhibitors or angiotensin II receptor blockers, mild exercise, reduced salt intake, and possibly other options.^3–6

Previous work on early detection of HF has relied on conventional modeling techniques, such as logistic regression or support vector machine (SVM), that use features representing the aggregation of events in an observation window and exclude temporal relations among events in the observation window.^7–9 In contrast, recurrent neural network (RNN) methods capture temporal patterns present in longitudinal data. RNN models have proven effective in many difficult machine learning tasks, such as image captioning¹⁰ and language translation.¹¹ Extending these methods to health data is sensible.

Applications of deep learning

Deep learning methods have recently led to a renaissance of neural network–based models. Pioneering studies introduced stacked restricted Boltzmann machines¹² and stacked autoencoders,¹³ which showed impressive performance in image processing, employing the layer-wise pretraining technique. Since then, variations of neural network application have explored deep architectures in computer vision,^14–16 audio processing,^17,18 and natural language processing (NLP),^11,19–21 among other fields.

RNN models are naturally suited to temporal sequenced data, and several variants have been developed for sequenced features. Hochreiter and Schmidhuber²² proposed long short-term memory (LSTM), exhibiting impressive performance in numerous sequence-based tasks such as handwriting recognition,²³ acoustic modeling of speech,²⁴ language modeling,²⁵ and language translation.²⁶ Cho et al.¹¹ proposed the gated recurrent unit (GRU) model, structurally similar to but simpler than LSTM, and showed comparable, if not better, performance.²⁷ In the RNN work described herein, we used the GRU structure to model the temporal relations among health data from patient EHRs to predict the future diagnosis of HF.

Health care applications of deep learning

Researchers have recently started to apply deep learning methods to clinical applications. Lasko et al.²⁸ used autoencoders to learn phenotypic patterns from serum uric acid measurements. Che et al.²⁹ used deep neural networks with incremental learning on clinical time series data to discover physiologic patterns associated with known clinical phenotypes. Both works,^28,29 however, focused on learning patterns from clinical records rather than predicting a clinical event. Hammerla et al.³⁰ applied restricted Boltzmann machines on time series data collected from wearable sensors to predict the disease state of Parkinson’s disease patients. Lipton et al.³¹ used LSTM for multilabel diagnosis prediction using pediatric ICU time series data (eg, heart rate, blood pressure, glucose level, etc.). Both of these studies^30,31 used multivariate time series data from patients, which focused on very different clinical conditions, with continuous time series data. Our study focuses on early detection of HF for the general patient population based on widely available EHR data such as time-stamped codes (diagnosis, medication, procedure).

Deep learning techniques have been recently applied to clinical text data (eg, PubMed abstracts, progress notes) using Skip-gram^20,32,33 to learn relationships among clinical processes or unified medical language system (UMLS) concepts. Choi et al.³⁴ applied Skip-gram to longitudinal EHR data to learn low-dimensional representations for medical concepts such as diagnosis codes, medication codes, and procedure codes,³⁵ and to learn representations of medical concepts. We borrowed from this prior work to leverage similar representation of medical concepts through Skip-gram but focus on temporal modeling using RNN for predicting HF.

Time series analysis of EHRs

Traditional time series methods using linear models for low-dimensional data have been widely applied to EHRs: modeling the progression of chronic kidney disease to kidney failure using the Cox proportional hazard model,³⁶ the progression of Alzheimer’s disease using the hidden Markov model³⁷ and fused group Lasso,³⁸ the progression of glaucoma using using a 2-dimensional continuous-time hidden Markov model,³⁹ the progression of lung disease using graphical models with the Gaussian process,⁴⁰ the progression of chronic obstructive pulmonary disease using the Markov jump process,⁴¹ and the progression of multiple diseases using the Hawkes process.⁴² These previous works were not able to model high dimensional non-linear relations as well as RNN. We focused on predicting the onset of HF using longitudinal structured patient data such as diagnosis, medication, and procedure codes. We used RNN, which provides a nonlinear improvement in model generalization and more scalability than many of the traditional methods, thanks to a more optimized software package and parallel architecture such as a graphics processing unit.

MATERIALS AND METHODS

GRU model for HF prediction

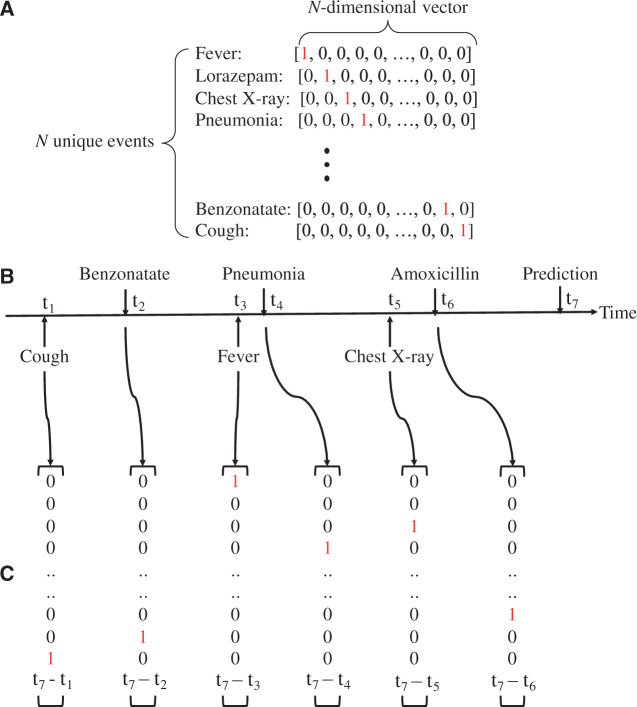
To represent clinical events in EHR data as computable event sequences, we adopted the one-hot vector format, often used for NLP tasks.⁴³Figure 1A provides an example of how EHR events are represented as a set of one-hot vectors. Each of the N unique clinical events was represented as an N-dimensional vector, where one dimension is set to 1 and the rest are 0. Using these one-hot vectors, a sequence of clinical events (Figure 1B) can be converted to a sequence of one-hot vectors (Figure 1C). Such sequences were used to train the models, as described in the next section.

Figure 1.

(A) One-hot vector encoding of clinical events. t in (B) indicates the time at which the event occurs, assuming we make the prediction at time t₇. We appended the time duration feature at the end of the one-hot vector, as shown in (C).

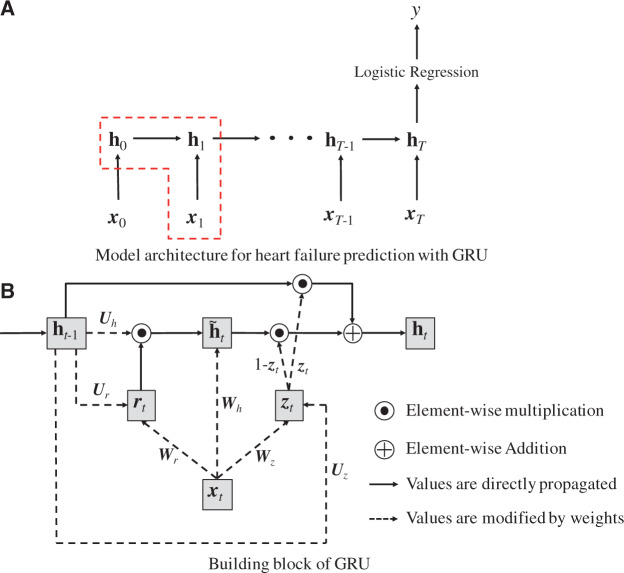
The proposed GRU model for HF prediction is an extension of the RNN framework, schematically depicted in Figure 2.

Figure 2.

The GRU model architecture (A), and building blocks (B). Note that vectors are denoted in bold lowercase, matrices in bold uppercase, and scalars in plain lowercase letters.

Given a sequence of clinical visits of length T (Figure 2A), the GRU accepts an input vector ${\mathit{x}}_t$ (in our base case, one-hot vectors representing clinical codes) at each timestep t, while storing information in a single hidden layer $\mathit{h}$ whose state changes over time $({\mathit{h}}_{t-1},{\mathit{h}}_t,{\mathit{h}}_{t+1})$. After seeing the entirety of clinical events, we applied logistic regression to the final hidden state vector ${\mathit{h}}_T$ and produced the scalar value y, which estimates the patient-specific risk score for future diagnosis of HF.

The dashed box of Figure 2A corresponds to the GRU model we used for HF prediction. GRU has 4 components (Figure 2B): ${\mathit{z}}_t$, the update gate at timestep t; ${\mathit{r}}_t$, the reset gate at timestep t; ${\tilde{\mathit{h}}}_t$, the intermediate memory unit at timestep t; and ${\mathit{h}}_t$, the hidden layer at timestep t. The mathematical formulation of Figure 2B is as follows:

$${\mathit{z}}_t=\sigma \left({\mathit{W}}_z{\mathit{x}}_t+{\mathit{U}}_z{\mathit{h}}_{t-1}+{\mathit{b}}_z\right)$$

$${\mathit{r}}_t=\sigma \left({\mathit{W}}_r{\mathit{x}}_t+{\mathit{U}}_r{\mathit{h}}_{t-1}+{\mathit{b}}_r\right)$$

$${\tilde{\mathit{h}}}_t=\text{tanh}\left({\mathit{W}}_h{\mathit{x}}_t+{\mathit{r}}_t\odot {\mathit{U}}_h{\mathit{h}}_{t-1}+{\mathit{b}}_h\right)$$

$${\mathit{h}}_t={\mathit{z}}_t\odot {\mathit{h}}_{t-1}+\left(1-{\mathit{z}}_t\right)\odot {\tilde{\mathit{h}}}_t$$

where $\sigma$() is the sigmoid function, and Ws, Us, and bs are the weight matrices and bias terms for calculating both gates ${\mathit{z}}_t$ and ${\mathit{r}}_t$ and the intermediate memory unit ${\tilde{\mathit{h}}}_t$, respectively. Note that in GRU, the previous hidden layer ${\mathit{h}}_{t-1}$ and the current input ${\mathit{x}}_t$ do not directly change the value of the current hidden layer ${\mathit{h}}_t$. Instead, they change the values of both gates ${\mathit{z}}_t$, ${\mathit{r}}_t$ and the intermediate memory unit ${\tilde{\mathit{h}}}_t$. Then the current hidden layer ${\mathit{h}}_t$ is determined by ${\tilde{\mathit{h}}}_t$ and ${\mathit{z}}_t$, where $\odot$ denotes element-wise multiplication (ie, Hadamard product) and both gates have values between 0 and 1. Therefore, if ${\mathit{r}}_t$ is close to 0, ${\tilde{\mathit{h}}}_t$ will disregard ${\mathit{h}}_{t-1}$. If ${\mathit{z}}_t$ is close to 1, ${\mathit{h}}_t$ will disregard ${\mathit{x}}_t$ and retain the same value as ${\mathit{h}}_{t-1}$. Simply put, the reset gate allows the hidden layer to drop any information that is not found to be useful in predicting the future, and the updated gate controls how much information from the previous hidden layer should be retained in the current hidden layer. This characteristic of GRU is especially useful as it is not easy to identify information essential to predicting HF diagnosis, given the enormous volume of EHR data. GRU model training learns to keep or ignore particular inputs (eg, diagnoses, medications, procedures) at each timestep as it sees fit.

We also tested a GRU model to determine if feature representation of the time between an event and the index date in combination with the one-hot input vectors improved model performance. Specifically, the model was trained by appending to the input vector ${\mathit{x}}_t$an extra dimension that represents the time as a logarithm of the number of days between the event time t and the index date T. We applied logarithm transformation to minimize the skewed distribution of the durations. We also explored the time between consecutive visits or without logarithm transformation, but the above method provided the best result.

The logistic regression model applied to the final state of the hidden layer ${\mathit{h}}_t$ is formulated as

$$y=\sigma \left({\mathit{w}}^{\text{T}}{\mathit{h}}_T+b\right)$$

where $\mathit{w}$ and $b$ are the weight vector and bias for logistic regression. To learn the parameters of the proposed model, we set the cross-entropy of the scalar outcome y as the loss function and tried to minimize it in terms of W_{z,r,h}, U_{z,r,h}, b_{z,r,h}, w, and b. The loss function is as follows:

$$\text{Loss}=-{\displaystyle \sum }_{i=1}^P\left(c^{(i)}\log y^{(i)}+\left(1-c^{(i)}\right)\text{log}\left(1-y^{(i)}\right)\right)$$

where P is the total number of patients, $c^{(i)}$ is the HF case indicator for the i-th patient where 1 indicates HF case and 0 control, and $y^{(i)}$ is the risk score of the i-th patient calculated by the model. Minimization can be performed through the back-propagation and mini-batch stochastic gradient descent.⁴⁴ The gradients are automatically calculated by Theano,⁴⁵ a deep learning software for Python.

Medical concept vectors

We constructed medical concept vectors that improve the one-hot vectors as the input ${\mathit{x}}_t$. We leveraged an NLP embedding technique, Skip-gram,²⁰ to train vector representations of diagnosis codes, medication codes, and procedure codes. The resulting vector representation, denoted as a medical concept vector, is intended to capture the hidden relations among various codes.

We trained medical concept vectors by sliding a fixed-size window on a sequence of codes, maximizing the log probability at each step as follows:

$$\text{Maximize} \frac{1}{T}{\displaystyle \sum }_{t=1}^T{\displaystyle \sum }_{-w\le j\le w,j\ne 0}\log p\left(c_{t+j}|c_t\right),$$

$$\text{where} p\left(c_{t+j}|c_t\right)=\frac{\text{exp}\left(v{\left(c_{t+j}\right)}^{\text{T}}v\left(c_t\right)\right)}{{{\displaystyle \sum }}_{c=1}^N\text{exp}\left(v{\left(c\right)}^{\text{T}}v\left(c_t\right)\right)}$$

where T is the number of codes in all of a patient’s visits, w is the size of the window, c_t is the code at position t, and v(c_t) is the vector representation of the code c_t. Simply put, Skip-gram tries to maximize the inner product of the vector representations of temporally proximal concepts. The size of the window and the dimensionality of the vector representation are hyperparameters generally set to 5 and 50–1000, respectively.²⁰ We trained the medical concept vectors using the encounter, medication order, procedure order, and problem list, with window size 5 and resulting dimensionality 100. Our other work presented the Skip-gram application for health care with a focus on interpretation of the resulting medical concept vectors.³⁵ This study, on the other hand, focuses on the sequential nature of the longitudinal EHR by using RNN for early detection of HF.

Data description

Data were from Sutter Palo Alto Medical Foundation (Sutter-PAMF) primary care patients. Sutter-PAMF is a large primary care and multispecialty group practice that has used an Epic Systems Corporation EHR for more than a decade. EHR data on primary care patients were extracted from encounters occurring between May 16, 2000, and May 23, 2013. The EHR dataset documented care delivered in the outpatient setting and included demographics, tobacco and alcohol consumption, clinical and laboratory values, International Classification of Disease version 9 (ICD-9) codes associated with encounters, orders, and referrals, procedure information in Current Procedural Terminology (CPT) codes, and medication prescription information in medical names. The dataset contained approximately 58 652 000 medical codes assigned to patients. Provider notes were not used in the present work, but could be included in a future effort.

Definitions of cases and controls

A density sampling design was used for the longitudinal records of the Sutter-PAMF patient population.⁴⁶ Cases met the criteria for incident onset of HF, described in Vijayakrishnan et al.⁴⁷ and adapted from Gurwitz et al.⁴⁸ Incident cases were of patients 40–85 years of age at the time of HF diagnosis. HF diagnosis (HFDx) was operationally defined as follows: (1) Qualifying ICD-9 codes for HF appeared as an encounter diagnosis or as the indication for a medication order. (Qualifying ICD-9 codes are listed in the supplementary material.) Qualifying ICD-9 codes with image and other related orders were excluded, because these orders often represented a suspicion of HF, where the results are often negative. (2) A minimum of 3 clinical encounters with qualifying ICD-9 codes had to occur within 12 months of each other, where the date of diagnosis was assigned to the earliest of the 3 dates. If the time span between the first and second appearance of the HF diagnostic code was >12 months, the date of the second encounter was used as the first qualifying encounter. The point upon each patient’s timeline at which incident HF was established was denoted as HFDx.

Up to 10 eligible primary care clinic-, sex-, and age-matched (in 5-year intervals) controls were selected for each incident HF case, yielding an overall ratio of 9 controls per case. Each control was also assigned an index date, which was the HFDx timepoint of the matched case. Primary care patients were eligible to be controls if they did not meet the operational criteria for HF diagnosis prior to the HFDx timepoint plus 182 days of their corresponding case. Other details on matching are described in the supplementary section.

We extracted all records from the 18-month period before the HFDx, constituting an interval that could be partitioned into an observation window and a prediction window. The medical records within the observation window were used as the dataset for training models. Diagnosis, medication, and procedure codes assigned to each patient were temporally ordered. Multiple diagnoses/medications/procedures at a single visit were represented as multiple one-hot vectors with a random order.

Model evaluation

Baseline models for performance comparison

We trained 4 classification models—regularized logistic regression, multilayer perceptron (MLP), support vector machine (SVM), and K-nearest neighbor (KNN)—in addition to our proposed gated recurrent unit (GRU) model.

Training strategy

All models were trained using the dataset created from the 18-month period before the HFDx. We iteratively divide the data into train, validation, and test with a ratio of 5:1:1, and report the model performance on the test set as the area under the ROC curve (AUC). Since probability is not explicitly estimated using the baseline SVM, we used the confidence score of SVM to calculate the AUC. Detailed training strategy is given in the supplementary material.

Input features and algorithms

We noticed that the sparseness and high-dimensionality of one-hot coded input vectors could be mitigated via 2 alternative approaches:

The traditional approach is to use standard medical concept groupers. ICD-9 diagnosis codes can be grouped by the Clinical Classification Software (CCS) diagnosis grouper⁴⁹ into 283 groups, medication codes can be grouped by the Generic Product Identifier⁵⁰ into 96 groups, and CPT procedure codes can be grouped by the CCS procedure grouper⁵¹ into 244 groups. Alternatively, medical concept vectors based on Skip-gram can be used to capture relations among diagnoses, medications, and procedures.

Training data for the 2 GRU models (with and without time duration information) were constructed in the same fashion for all 3 types of input (one-hot encoding, grouped codes, and medical concept vectors based on Skip-gram).

Logistic regression, MLP, SVM, and KNN were also trained with these 3 types of aggregated feature vectors. In the aggregated one-hot vector, each dimension represents the total number of occurrences of a specific code in the observation window. Aggregated grouped code vectors and aggregated medical concept vectors are generated in the same fashion, except the one-hot vectors are replaced by grouped code vectors or pretrained medical concept vectors. All aggregated input vectors were normalized to zero mean and unit variance.

Evaluation strategy

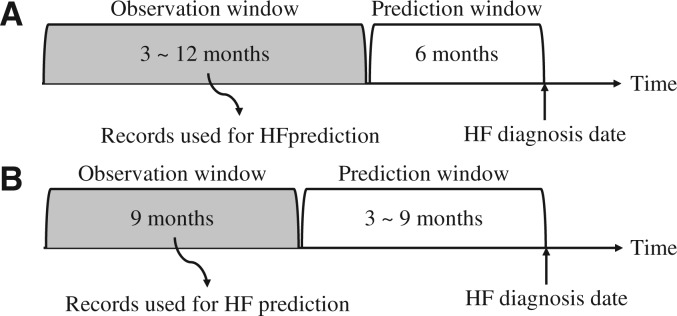
The utility of a model is related, in part, to how much data are required for application and how far into the future an accurate prediction can be made. We conducted experiments to examine model performance for varying lengths of the prediction window (ie, time before HFDx) and the observation window (ie, length of time before the beginning of the prediction window), where features were only extracted from the defined observation window (Figures 3A and B). Note that we trained separate models for each observation window size so that models could learn optimal features from patient records of different lengths.

Figure 3.

Two experimental settings where we alternately changed the length of the prediction window and the observation window. In (A), the prediction window was fixed at 6 months, while we varied the length of the observation window. In (B), the observation length was fixed at 9 months, while we varied the length of the prediction window.

Implementation details

The GRU models, logistic regression, and MLP were implemented with Theano 0.7.⁴⁵ Adadelta⁵² was used for model training because it does not depend strongly on the learning rate setting. SVM and KNN were implemented with Python Scikit-Learn 0.16.1. An Ubuntu machine with Xeon E5-2697, 128 GB memory, and Nvidia Tesla K80 was used to train all models. Hyperparameters used for training each model are described in the supplementary section. We have made our codes and synthetic data available on a public repository (https://github.com/mp2893/rnn_predict).

EXPERIMENT RESULTS

Data processing

From random samples of 265 336 Sutter-PAMF patients, 4178 incident HF cases and 29 139 control patients were identified. The average number of clinical codes assigned to each patient was approximately 72, and there were 18 181 unique clinical codes (6910 diagnosis codes, 6897 medication codes, and 4374 procedure codes) in total. The full sample of 265 336 was used for training the medical concept vectors, and the incident HF cases and controls were used for all other model training and evaluation tasks.

Performance of HF diagnosis prediction models

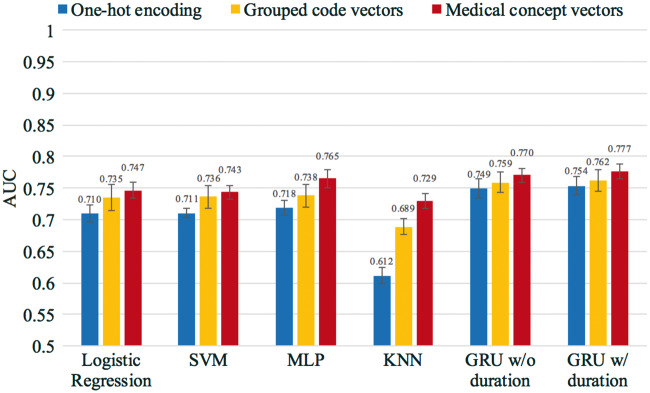
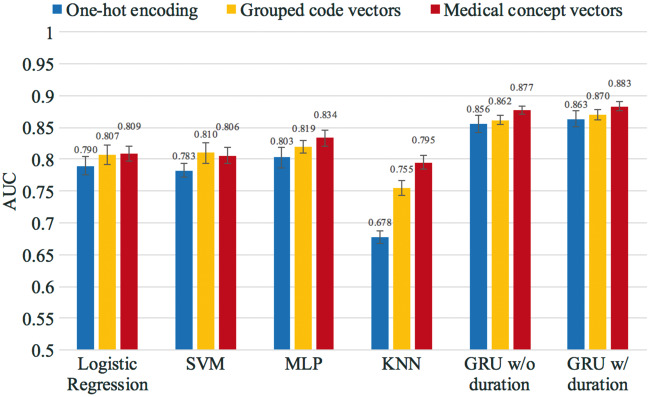
The average AUC of cross-validation for all models is shown in Figure 4, where all models were trained and tested using the dataset created with the 12-month observation window and the 6-month prediction window. The colors in Figure 4 represent different training input vectors, and the error bars indicate the standard deviation derived from the cross-validation. GRU models outperformed other models, as shown in Figure 4.

Figure 4.

Heart failure prediction performance of the GRU and baseline models. All models were trained and tested using the dataset created from the 12-month observation window and the 6-month prediction window. The values of the AUC and the standard error are provided in the supplementary section.

We increased the observation window to the full 18 months of patient history and zero prediction window, as shown in Figure 5. All models were again trained and tested for this experiment. The GRU model consistently outperformed all the other methods, with 0.883 AUC. Models trained using the medical concept vectors significantly outperformed models trained by one-hot vectors, and also outperformed models trained by grouped code vectors.

Figure 5.

Heart failure prediction performance of the GRU and baseline models. All models were trained and tested using the dataset created from the 18-month observation window and 0-month prediction window. The values of the AUC and the standard error are provided in the supplementary section.

Prediction/observation length and prediction power

Tables 1 and 2 show the cross-validation AUCs resulting from experiments described in Figures 3A and B. These tables show that GRU outperformed all other models in all observation and prediction window sizes.

Table 1.

AUCs of models while varying the observation window length

Observation window (months)	Logistic regression	SVM	MLP	KNN	GRU w/duration
3	0.7210	0.7192	0.7312	0.7038	0.7395
4	0.7272	0.7256	0.7427	0.7084	0.7463
5	0.7314	0.7297	0.7455	0.7154	0.7516
6	0.7344	0.7327	0.7486	0.7165	0.7529
7	0.7388	0.7353	0.7530	0.7175	0.7606
8	0.7422	0.7398	0.7587	0.7253	0.7641
9	0.7441	0.7420	0.7603	0.7274	0.7680
10	0.7461	0.7434	0.7621	0.7311	0.7713
11	0.7462	0.7432	0.7639	0.7272	0.7746
12	0.7467	0.7435	0.7649	0.7293	0.7768

The length of the prediction window was fixed at 6 months. The highest AUCs among all models are shown in bold.

Table 2.

AUCs of models that varied by length of prediction window between 3 and 9 months

Prediction window (months)	Logistic regression	SVM	MLP	KNN	GRU w/ duration
3	0.7511	0.7479	0.7650	0.7373	0.7711
4	0.7473	0.7439	0.7632	0.7303	0.7678
5	0.7458	0.7414	0.7620	0.7302	0.7687
6	0.7441	0.7420	0.7603	0.7274	0.7680
7	0.7426	0.7405	0.7617	0.7239	0.7658
8	0.7396	0.7366	0.7569	0.7197	0.7651
9	0.7341	0.7334	0.7558	0.7206	0.7610

The length of the observation window was fixed at 9 months. The highest AUCs are in bold.

Prediction time

Table 3 shows the time required to make a prediction for a single patient for each model. We used models that were trained by medical concept vectors. The time was calculated by averaging the times the models took to make predictions on the test sets from the 6-folds using only the CPU.

Table 3.

Prediction times of various models for a single patient

Performance metric	Logistic regression	SVM	MLP	KNN	GRU
Prediction time (seconds)	0.000002	0.000034	0.000259	36.66	0.020408

Scalability of our approach

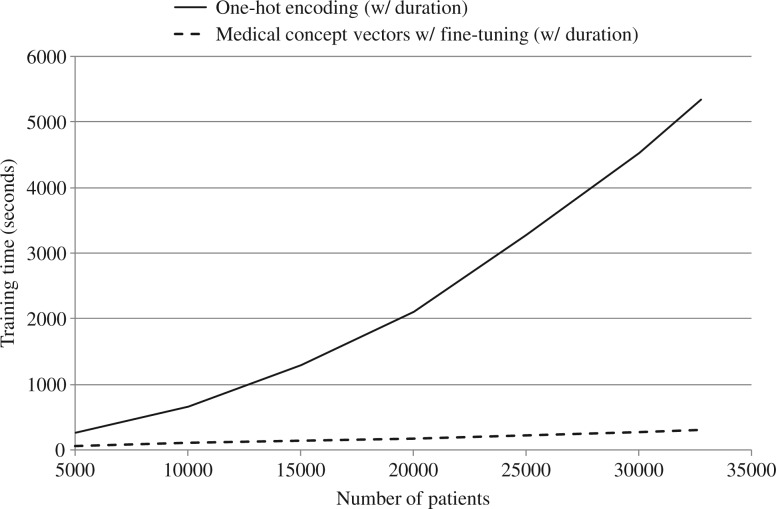
Figure 6 depicts the training time of 2 different GRU models for varying numbers of patients, with maximum gradient decent epoch set to 10.

Figure 6.

Training time vs number of patients.

Error analysis

We analyzed the incorrect predictions made by the GRU model using temporal data and trained on the 12-month observation window and the 6-month prediction window. We sampled 100 patients each from false negatives (FNs), false positives (FPs), true positives (TPs), and true negatives (TNs). This procedure was performed for all 6-folds, which gave us 600 FN/TN/TP/FP samples. The characteristics of the samples are shown in Table 4.

Table 4.

Characteristics of TN, FN, TP, and FP samples

Metric	Avg. no. of visits	Avg. visit frequency	Avg. no. of codes per visit	Top 10 most frequent codes
True negative	12.10	Every 20.6 days	3.08	1. Allergic rhinitis 2. Multiple immunotherapy 3. Hyperlipidemia 4. Routine medical examination 5. Screening mammogram 6. Psoriasis 7. Vaccine administration 8. Screening for cancer 9. Need for prophylactic influenza vaccination 10. Hypothyroidism
False negative	13.43	Every 19.0 days	2.94	1. Hypertension 2. Hyperlipidemia 3. Diabetes 4. Hypothyroidism 5. Keratosis 6. Need for prophylactic influenza vaccination 7. Routine medical examination 8. Esophageal reflux 9. Senile cataract 10. Screening mammogram
True positive	31.72	Every 9.7 days	3.05	1. Atrial fibrillation 2. Hypertension 3. Diabetes 4. Long-term use of anticoagulants 5. Hyperlipidemia 6. Chronic kidney disease 7. Anemia, unspecified 8. Coronary atherosclerosis 9. Edema 10. Chronic airway obstruction
False positive	29.95	Every 10.5 days	3.09	1. Atrial fibrillation 2. Hypertension 3. Long-term use of anticoagulants 5. Diabetes 4. Hyperlipidemia 6. Chronic kidney disease 7. Anemia 8. Coronary atherosclerosis 9. Edema 10. Therapeutic drug monitoring

Many of the incorrect predictions made by the GRU model can be attributed to visit frequency (Table 4). The second and third columns of Table 4 suggest that the GRU tends to give high prediction scores to patients who frequently visit the hospital. The fourth column, however, suggests that the number of codes assigned at each visit does not generally affect HF prediction.

The second aspect is the type of code. The last column shows that the GRU tends to give high prediction scores to patients with heart-related diseases such as atrial fibrillation and coronary atherosclerosis. Use of anticoagulants also seems to play an important role. Hypertension, an important factor for cardiovascular disease,⁵³ is also frequent in patients with high prediction scores. However, hypertension, being a very common disease among adults,⁵³ does not seem to qualify as an important feature in predicting HF, since it is also frequent among patients with low prediction scores. Overall, we can see that frequent codes are similar between FN samples and TN samples, and also between FP samples and TP samples.

The two most likely explanations for FN samples showing a similar pattern to TN samples are: (1) FN samples are related to acute HF (e.g., due to myocardial infarction) that shows little symptomatology before manifestation, and (2) there could be missing data of FN samples due to either lack of hospital visits or visits to hospitals that are not associated with Sutter. FP samples seem to be from patients who did not have HF even though their symptoms were very similar to those of patients with TP samples. Diseases that are highly related to HF, such as atrial fibrillation and coronary atherosclerosis,⁵⁴ do not always lead to HF. Overall, although the GRU shows impressive predictive performance, it seems to be confused by some cases and controls with similar patterns. We predict that using even richer information such as lab results or medical notes will help overcome this challenge and yield an even higher AUC.

Discussion

The GRU model results in Figure 4 represent state-of-the-art prediction performance achieved by applying deep learning to discover complex relationships within EHR data. Of the models evaluated, the best performance was achieved with GRU that used temporal data and was trained with medical concept vectors. GRU models also significantly outperformed traditional machine learning models that rely on aggregate features (Figure 4) and trained with one-hot vectors or grouped code vectors. However, the baseline models trained with medical concept vectors showed comparable performance to the GRU models trained with one-hot vectors. This result suggests a potential benefit of medical concept vectors, which is especially useful when a good domain ontology is absent. Interestingly, the performance gain for GRU models achieved by using duration information was modest. We suspect this is due to the irregular pattern of patients’ hospital visits. Although applying logarithm transformation improved the performance sightly, the innate irregularity of the visit pattern seems to make it difficult for the GRU to learn predictive duration features.

From Table 1, we see that GRU outperforms all the baseline models regardless of the observation window size. It seems that the longer the observation window, the more effectively all models performed. The GRU model produced the highest AUC when the prediction window was reduced to zero, and all data were used for the observation window. While this result is interesting from a methodological standpoint, such a model has limited clinical utility because it does not predict HF well in advance of a physician. We can see from Table 2 that all models performed better when predicting near-future HF cases. However, the prediction window size does not seem to affect the predictive performance as much as the observation window size. This suggests that access to duration of patient history is crucial for accurate HF prediction, perhaps because signs of incident disease manifest over a period of time.

Apart from KNN, which requires distance calculation between all data points at prediction time, GRU, being a sequential model, requires the longest time to make a prediction for a patient, as can be seen in Table 3. However, it is still able to compute HF risk for 1 million patients in 200 seconds using 100 central processing units, so cost will not pose a problem in real-world clinical application.

The GRU model using one-hot vectors displayed a super-linear relationship between training time and number of patients, as shown in Figure 6. On the other hand, the GRU model using medical concept vectors showed a linear increase. We attribute this to 2 causes. First, compared to medical concept vectors, whose dimensions are fixed, one-hot vectors increase their dimensionality as new patients are added to the training data, since new patients have new medical codes (diagnoses, medications, procedures). Second, one-hot vectors are very high-dimensional, and therefore use large amounts of VRAM, which leads to frequent garbage collection. Although the training time of the one-hot GRU models behaves near-linearly after 20 000 patients, it is still unfavorable to the medical concept vector case. Thus, we recommend using medical concept vectors to train GRU, as they both improve model performance and significantly reduce training time.

The GRU model that included temporal relations trained on medical concept vectors provided the best performance of all methods evaluated. So far our work has only taken a data-driven approach. We expect that model performance would benefit from using longer observation periods and incorporating well-established expert medical knowledge, such as higher-level features and medical ontologies. Still, using only the raw medical order records, we were able to produce innovative, state-of-the-art results for HF diagnosis prediction. Note that in a real-world setting, however, the performance of the GRU model could be different depending on the nature of the actual cohort.

Although this work focused on HF, our approach is general and may be applied to a wide array of health care–related prediction problems. Further, the medical concept vectors we used to encode medical data were shown to generally improve the performance of both deep learning and conventional models, and thus may have utility in numerous health care applications where rich information needs to be succinctly represented.

Future work will focus on evaluating model performance for prediction windows beyond nine months, which may yield models with even greater clinical implication, and adding higher-level features and medical ontologies. Another possible enhancement is to consider using separate HF prediction models for different disease groups, such as hypertension and diabetes, which can potentially be more discriminative as the cohort is more homogeneous. However, we have to make sure a sufficient sample size is available for each disease group before developing separate RNN models. Visualizing the temporal dynamics of RNN models is another research direction, where currently only limited work with narrow application focus has been attempted.⁵⁵

CONCLUSION

We proposed a novel predictive model framework for HF diagnosis using GRU deep learning methods. Compared to popular methods such as logistic regression, MLP, SVM, and KNN, GRU models exhibited superior performance in predicting HF diagnosis. By analyzing the results, we described the importance of respecting the sequential nature of clinical records. Future work will include incorporating expert knowledge into our framework and expanding our approach to additional health care applications.

Contributors

Edward Choi implemented the method and conducted all the experiments. All authors were involved in developing the ideas and writing the paper.

Funding

This work was supported by National Science Foundation grants IIS-1418511 and CCF-1533768 and National Heart, Lung, and Blood Institute grant 1R01H116832-01.

Competing interests

The authors have no competing interests to declare.

SUPPLEMENTARY MATERIAL

Supplementary material are available at Journal of the American Medical Informatics Association online.