Multicolour localization microscopy by point-spread-function engineering

Abstract

Super-resolution microscopy has revolutionized cellular imaging in recent years^1–4. Methods relying on sequential localization of single point emitters enable spatial tracking at ~10–40 nm resolution. Moreover, tracking and imaging in three dimensions is made possible by various techniques, including point-spread-function (PSF) engineering^5–9 –namely, encoding the axial (z) position of a point source in the shape that it creates in the image plane. However, a remaining challenge for localization-microscopy is efficient multicolour imaging - a task of the utmost importance for contextualizing biological data. Normally, multicolour imaging requires sequential imaging^{10, 11}, multiple cameras¹², or segmented dedicated fields of view^{13, 14}. Here, we demonstrate an alternate strategy, the encoding of spectral information (colour), in addition to 3D position, directly in the image. By exploiting chromatic dispersion, we design a new class of optical phase masks that simultaneously yield controllably different PSFs for different wavelengths, enabling simultaneous multicolour tracking or super-resolution imaging in a single optical path.

The ability to detect and localize a point source (fluorescent molecule, quantum dot, scattering nanoparticle) with nanometric precision using a standard visible-light microscope has transformed the field of biological imaging, enhancing applications such as single-particle tracking (SPT^15–17 and yielding powerful new sub-wavelength imaging modalities (e.g. (F-) PALM, STORM, and their relatives ^{2–4, 18}).

In biological samples, contextual information is of paramount importance. The trajectory of a protein, or a structure within a cell is much more informative when it is related to other proteins, organelles, or the cell membrane^{13, 19, 20}. A standard way of creating such context is labelling different targets using different-colour emitters. However, imaging different emission colours normally requires either splitting the field of view of the camera between the different colours¹³, adding another camera ¹² (and possibly another objective¹⁴), imaging sequentially^{10, 11}, or using diffractive gratings^{21, 22}. Complications arising from such solutions can include the addition of optical components (and therefore possibly aberrations), the need for multicolour image registration, inability to measure different colours simultaneously, and restriction to thin samples.

Here, we add the spectral degree of freedom to localization microscopy by using PSF engineering²³, referring to the modification of the microscope’s PSF, namely, the image detected when observing a point source. This is achieved by placing an optical phase shaping element, e.g. a dielectric phase mask¹³ or a liquid crystal spatial light modulator (LC-SLM)²⁴ in the Fourier plane of a 4f system, in the detection path of a standard fluorescence microscope (See Supplementary Information for more details).

PSF engineering has already been used to encode emitter properties in the shape of the PSF: e.g. the axial (z) position^5–9 or the orientation of an emitter^{25, 26}. This work extends the capabilities of PSF engineering to the spectral regime. By exploiting the spectral dependence of the optical element in the pupil plane, we design masks that produce different, controllable, phase delay patterns for different colours (wavelengths). A similar concept has been previously used to demonstrate simultaneous trapping and imaging of micro-particles^{27, 28}. Here, the spectral dependence provides different PSFs for different colours, to implement multicolour super-resolution imaging and 3D tracking. We mainly use a LC-SLM for phase modulation; however, the method applies for dielectric phase masks as well (see demonstration in Supplementary Information). The approach has the benefit of avoiding extra optical elements (that cause aberrations), while enabling simultaneous imaging of multiple, distinguishable emitters of different colours. In addition, multicolour image registration, while still necessary, is simplified, as all colours go through exactly the same optical elements (see Supplementary Information).

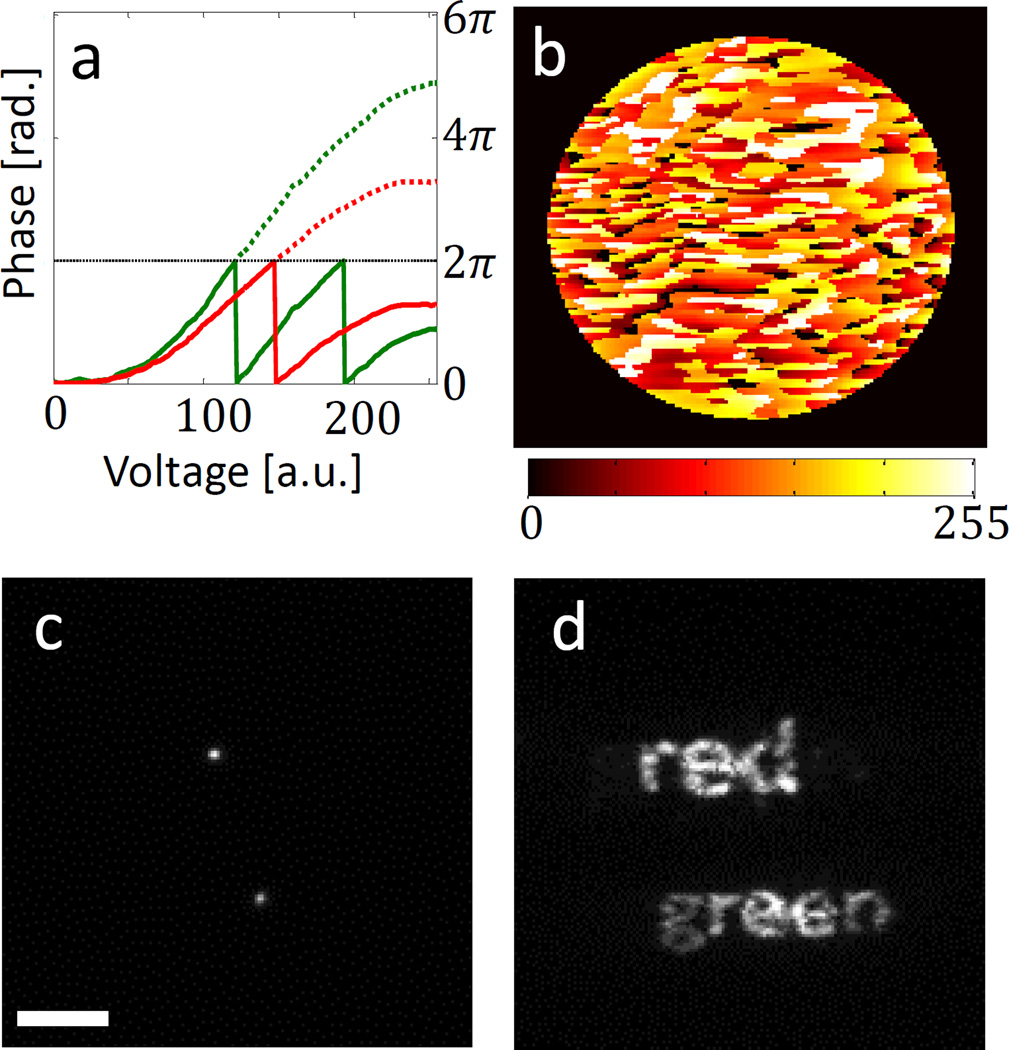
The generality of the method is demonstrated experimentally in Fig. 1. Figure 1a shows the phase delay vs. voltage relation at two different wavelengths – 559 nm (green) and 699 nm (red) – arising from the spectral dependence of the liquid crystal device (see Supplementary Information for the calibration procedure). Using these relations, we design input voltage patterns to apply to the SLM (Fig. 1b), such that the two wavelengths experience two different desired phase delay patterns, and consequently exhibit different PSFs. For example, Fig. 1c shows an image of two in-focus subwavelength fluorescent microspheres with peak emission wavelengths of 559 nm and 699 nm (green and red), when the SLM is turned off. This corresponds to the standard PSF of the microscope. By loading the voltage pattern shown in Fig. 1b, the wavelength dependence of the PSF becomes clear, where the PSFs from the two microspheres actually spell out the words “green” and “red”, respectively (Fig. 1d).

Figure 1. Dual-colour mask SLM implementation.

a, A LC-SLM pixel’s phase response as a function of input voltage for two wavelengths: 559 nm (green) and 699 nm (red). The dotted lines show unwrapped phases. b, Input “red-green” LC-SLM voltage pattern (8-bit grey scale). c, Two fluorescent microspheres (red and green) imaged with the LC-SLM off. d, The same two microspheres imaged with the pattern on. Scale bar = 5 µm.

Of course, for multicolour imaging applications, there are much more practical PSFs than the ones shown in Fig. 1d, e.g. ones that also encode 3D position efficiently (featuring high Fisher information)^{6–9, 29}. One can think of various ways to distinguish between colours, since phase delay patterns experienced by different wavelengths can be drastically different (as is apparent in Fig. 1); therefore, there is an enormous amount of design freedom. We demonstrate the applicability of our method in two example applications: Dual-colour particle tracking, and super-resolution imaging, each using a different PSF design, matching different application requirements.

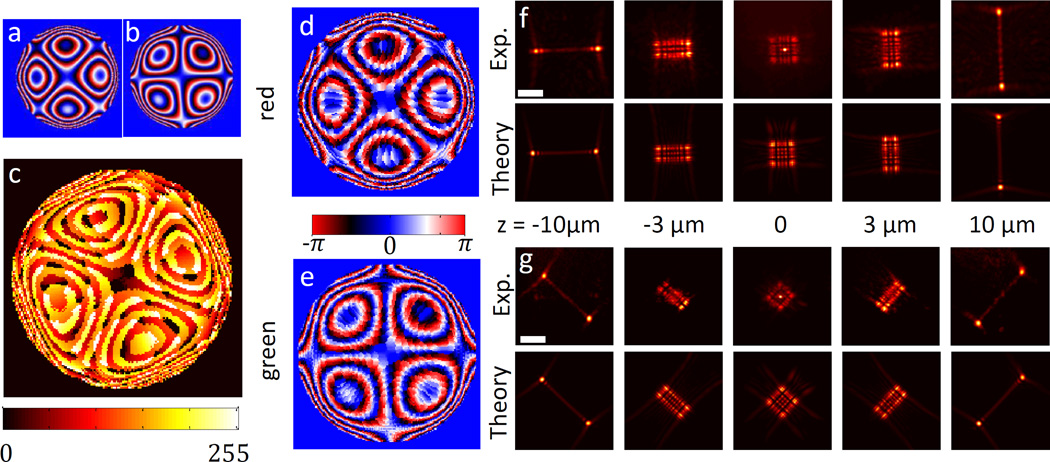
As a first demonstration of our approach, we design a mask for dual-colour 3D localization over a large depth range. The design is based on a recently published PSF for large z-range localization, termed the Tetrapod mask⁸. The most prominent feature of this PSF is two lobes that vary in separation distance as a function of emitter depth. The axis along which the two lobes are separated rotates 90°, depending upon whether the emitter is above or below the focal plane. The applicable z-range of this PSF is ~20 µm. In order to distinguish between two colours (engineered for green and red microspheres), we rotate the second PSF by 45°. The resulting design is shown in Fig. 2. Figure 2a and 2b show the two different desired phase masks used for red and green, respectively, serving as input to our optimization algorithm, which solves a pixel-wise weighted least squares problem to determine the optimal voltage pattern (see Supplementary Information for details). Figure 2c shows our algorithm’s output: a single voltage pattern that (to a good approximation) produces the desired patterns for the two different wavelengths. In practice, the phase patterns experienced by the different wavelengths are not identical to the desired patterns, since a compromise needs to be found for both colours. However, the resulting phase patterns and PSFs are very similar to the desired ones, as seen in Fig. 2d-g.

Figure 2. Dual-colour 20µm Tetrapod mask.

a, Desired phase pattern for red (699 nm). b, Desired phase pattern for green (559 nm) c, Resulting SLM voltage pattern from design algorithm. d, Calculated phase delay experienced by red wavelength and e, by green wavelength. f, Experimentally measured PSF for a 40 nm red microsphere, in a 20 µm z-range (top), and theoretically calculated desired PSF, corresponding to a (bottom). g, Experimentally measured PSF for a 100 nm green microsphere, in a 20 µm z-range (top), and theoretically calculated desired PSF, corresponding to b (bottom). Scale bar is 5 µm.

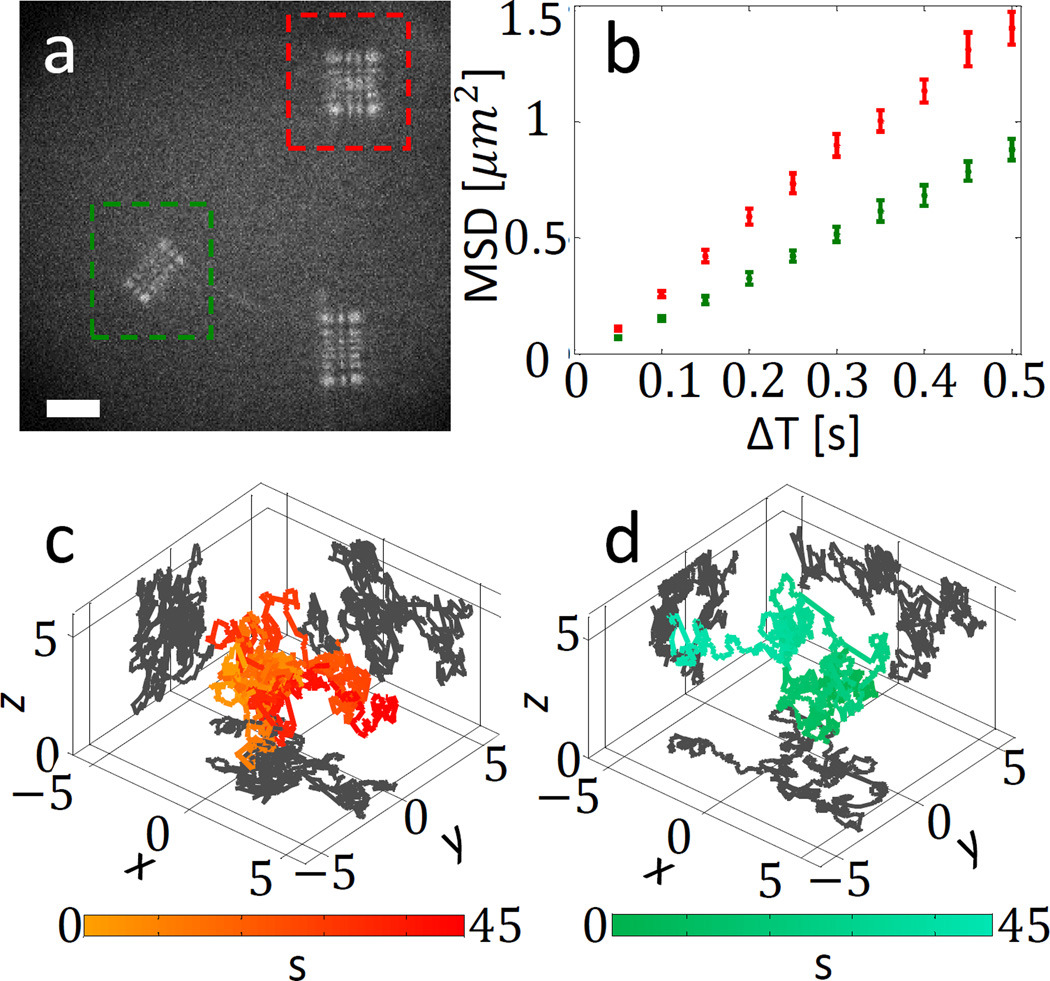
Next, we use the designed voltage pattern to simultaneously track different coloured microspheres in 3D, as they randomly diffuse in solution (water with ~55% sucrose). Figure 3a shows an example 50 ms movie frame, with a red microsphere (48±0.6 nm diameter, obtained from manufacturer specs) and a green microsphere (100±0.6 nm) marked by a red and a green box. As the microspheres diffuse freely, they are tracked for 45 seconds. In each frame, each microsphere is localized using maximum likelihood estimation (MLE) fitting to a numerical PSF model (See Supplementary Information), and the two trajectories are obtained. The mean-squared-displacement curves of the two marked spheres are shown in Fig. 3b, and the individual trajectories are shown in Fig. 3c and 3d.

Figure 3. Simultaneous 3D multicolour microsphere diffusion.

a, One frame from recorded diffusion movie (Supplementary video 1), following diffusion of a red microsphere (marked in red) and a green microsphere (marked in green). The PSF is a multicolour 20 µm Tetrapod with a 45 degree rotation between the colours as in Fig. 2. Scale bar = 5 µm. b, Mean squared displacement (MSD) curves for the two microspheres. c and d, red microsphere and green microsphere 3D trajectories. Axes units are in µm. Colour scale encodes time in seconds.

From the MSD curves, the diffusion coefficient of each microsphere can be obtained. The ratio between the measured diffusion coefficients (D_red = 0.52±0.045 µm²/s, D_green = 0.27±0.023 µm²/s) corresponds to theory, as D should scale like the inverse of the radius³⁰: experimental D_green/D_red = 0.52±0.09 µm²/s and theoretical D_green/D_red = 0.48±0.009 µm²/s. The average localization precision per frame, obtained by localizing immobilized microspheres under similar imaging conditions (See Supplementary Information) is (20, 23, 45) nm for the green microsphere (~18k average detected signal photons per frame) and (12,13,39) nm for the (somewhat brighter) red microsphere (~34k average detected signal photons per frame).

The great freedom in designing a multicolour mask enables creative solutions. For example, consider the problem of 3D two-particle tracking (e.g. differently-colour-labelled biomolecules) that are interacting and are known to be in proximity. In such a case, their (different) PSFs would overlap in image space, making fitting more challenging. To overcome this problem, one can simply add a linear phase ramp to one of the colours, resulting in a lateral shift of the PSF of one colour (see Supplementary Information for a demonstration, figure S9, as well as for a more general discussion of the overlap problem).

Next, we demonstrate how using a multicolour PSF can facilitate a simple method for simultaneous multicolour super-resolution imaging of biological specimens. We image fixed BSC-1 cells, with microtubules marked by anti-alpha-tubulin antibodies labelled with Alexa647 (a red fluorescent dye), and mitochondria marked via anti-ATPB primary and Alexa532-labeled secondary antibodies (a green fluorescent dye). We perform dual-colour super-resolution imaging by acquiring a sequence of images of blinking single molecules. In contrast to conventional PALM/STORM experiments, both colour labels are excited simultaneously, and recorded on the same region of the camera. Using our technique, the colour of each emitter is encoded in its PSF.

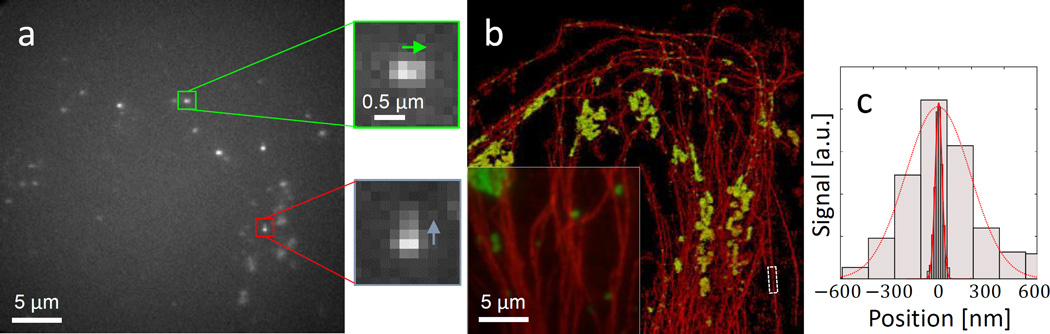
A key parameter determining the precision to which one can determine the position of a fluorescent point source is the number of detected photons. The phase-only LC-SLM we use (Boulder Nonlinear Systems) is designed to modulate only one polarization of the light. In all measurements described earlier in this work, light polarized in the unmodulated direction was filtered out by a polarizer upstream of the SLM. In this experiment, in order to take advantage of a maximal number of signal photons, we employ an approach that uses both polarizations of light impinging on the SLM. The light polarization that is not modulated by the LC-SLM produces a ‘standard’ PSF in the image plane. In order to encode colour, we modulate the other polarization by a dual-colour mask that laterally shifts the standard PSF in the y direction for red, and in the x direction for green. The combined result of both polarizations in the image plane is therefore a PSF that is elongated vertically for red and horizontally for green emitters (see Fig. 4a insets).

Figure 4. Multicolour super resolution cell imaging.

a, Raw data from recorded super-resolution imaging movie. Two example PSFs of a green label (horizontally elongated) and a red label (vertically elongated) are enlarged in the green and red insets, showing arrows in the elongation direction. b, Super-resolution image obtained by localizing each emitter in the movie and assigning its colour (red = microtubules, green = mitochondria). Inset shows diffraction limited data. c, histogram of all localizations within dotted white box surrounding a ~2 µm long microtubule section in b (dark grey, FWHM = 53 nm), and diffraction limited intensity cross-section from the same region (light grey, FWHM =329 nm).

The super-resolution imaging results are shown in Fig 4. Approximately 430k emitters were localized in 61k movie frames. Each identified PSF was localized using a 2D Gaussian fit, and colour discrimination was performed according to the direction of elongation (horizontal = green, vertical = red). The attainable resolution is demonstrated by the microtubule FWHM of 53 nm obtained from a histogram of localizations in a microtubule section (Fig. 4b and Fig. 4c). Considering a known ~25 nm microtubule diameter, this corresponds to a localization precision (standard deviation) of ~21 nm. Repeated localizations of single molecules that are on for multiple frames in the movie yield a comparable precision.

In conclusion, we have demonstrated a new method to encode spectral information in the PSF of a microscope. In general, PSF engineering for 3D imaging exploits optical aberrations for encoding depth; here we have used chromatic aberrations for encoding colour. The novel approach triggers many possible questions and research directions about its capabilities and limitations. For example: What is the cost of compromising between different wavelengths in a single mask? What is the minimal spectral separation for different emitters? How many different colours can be modulated using such a multicolour phase mask?

Using numerical simulations and measurements we may begin to answer these questions. In terms of signal compromise, the elongated PSF used in the cell measurement (Fig. 4) is ~13% dimmer than the standard PSF. In terms of spectral separation, we find that using our design method on a LC-SLM one can reliably generate a dual-colour 20 µm Tetrapod mask for two emitters that have spectral means separated by 60 nm or more (See Supplementary Information for these results). Note that a major limitation of implementing a multicolour mask using a LC-SLM is the limited modulation range of the device (~4π at 633 nm), and specifically, its spectral dependence. This is because, ultimately, the approach relies on finding voltage values that generate sufficiently different phase delays for different wavelengths.

A second limitation of the LC-SLM is that it modulates only one polarization, which limits the detectable signal and degrades emitter detectability, localization precision and consequently spatial resolution. Techniques do exist to modulate both polarizations³¹; in this work we overcome this limitation to some extent by utilizing the unmodulated part of the emitted light; however, this solution is limited to 2D imaging.

Indeed, a dielectric mask seems to hold high potential for multicolour PSF implementation. Note that designing a multicolour mask becomes increasingly difficult as one increases the number of phase-masks that need to be satisfied simultaneously (one per wavelength). Yet, using a dielectric phase mask approach, we calculate that it is possible to generate a multicolour mask for even 5 different colours, in a 300 nm spectral range. For the above results and further characterization see Supplementary Information.

We note that there are key parameters in this novel design process that are not yet optimal. For example, the Tetrapod PSF is designed to be optimally informative for 3D localization^{7, 8}. However, a rotated Tetrapod PSF is not necessarily an optimal multicolour PSF. An interesting and useful challenge would be to employ an information maximization approach⁷ to design an optimal mask for spectral discrimination as well as 3D imaging.

Previous work has shown that large range 3D PSFs are specifically suitable for low-density tracking of individual emitters⁸. On the other hand, super-resolution microscopy ((F)PALM/STORM) over a large axial range with a 3D PSF introduces additional challenges, e.g. high and spatially non-uniform background, and multiple-emitter overlap due to the large emitter density (See Supplementary Information for overlap discussion and simulation). These challenges can be addressed by improved algorithms and experimental background reduction strategies.

The presented method will enable simple and scalable simultaneous multicolour localization microscopy. While its applicability is demonstrated here for particle tracking and super-resolution imaging, the range of possible uses encompasses a multitude of microscopy and imaging applications that can benefit from multicolour PSFs – from chromatic aberration correction to high throughput spectroscopy.

Methods

Optical Setup

All imaging experiments were performed on the experimental system shown schematically in supplementary Fig. S1. A 4f optical processing system was built alongside the side-port of an Olympus IX71 microscope frame, with a 100x/1.4 NA oil-immersion objective lens (UPlanSApo 100x/1.4 NA, Olympus). The 4f system consisted of two 150 mm achromat lenses (Edmund Optics), a polarizing beamsplitter (B. Halle) to reject light polarized perpendicular to the axis along which the SLM is capable of modulating phase, a 512x512 pixel SLM (XY Phase Series, Boulder Nonlinear Systems), and assorted mirrors for beam-steering. An EMCCD camera (iXon897, Andor) was used to record data. Imaging experiments were performed using simultaneous illumination by a 641 nm diode laser (CUBE, Coherent), and the 514 nm line of an Ar-ion laser (Innova 90, Coherent). Excitation light was reflected off of a multi-bandpass dichroic (FF425/532/656-Di01-25x36, Semrock), and fluorescence was transmitted through the same dichroic, and passed through an additional multi-bandpass emission filter (Em01-R442/514/647-25, Yokogawa), a notch filter (ZET635NF, Chroma), and 514 long pass filter (Semrock).

LC-SLM multicolour mask design

Given a set of N wavelengths λ_i, i = 1 … N and N corresponding desired phase patterns D(x, y)_i, i = 1 … N, an SLM voltage pattern V(x, y) is sought that minimizes a weighted least squared phase distance between the all N desired phase patterns and the actual corresponding phase masks. The following pixel-wise optimization is therefore performed: $v_{xy}=\text{argmin}{\sum }_{i=1}^N{w}_i·{\mathit{\text{Dist}}}_{2\pi }{(P_i(v_{xy}),D_{xy,i})}^2$, where P_i(v) is the phase delay that wavelength λ_i experiences when voltage v is set on the SLM pixel, and the phase distance function is defined as: ${\mathit{\text{Dist}}}_{2\pi }(a,b)=2\pi ·|\frac{a-b}{2\pi }-[\frac{a-b}{2\pi }\left]\right|$. In addition, since the addition of any constant phase to any desired pattern is allowed, this degree of freedom is also optimized. The optimization is performed numerically using Matlab (The MathWorks, Inc., Natick, Massachusetts, United States). See Supplementary Information for more details.

Diffusion experiment

Diffusion experiments were carried out in a 55% (w/v) sucrose aqueous solution. Two coverglass slides (Fisher Premium Cover Glass, no. 1) were adhered with double-sided tape (3M) forming a diffusion chamber approximately 50µm in height. A dilute concentration of fluorescent microspheres (F8803 & F8789, Invitrogen) were added to the solution and allowed to diffuse at room temperature.

Cell Labelling and Imaging

For cell imaging experiments, cultured BS-C-1 (Cercopithecus aethiops epithelial kidney, ATCC CCL-26) cells were plated onto cleaned glass coverslips (Fisher Premium Cover Glass, no. 1.5 and cultured for 48 hours in high glucose, DMEM media containing 10% (v/v) fetal bovine serum (both Gibco). Cells were then fixed in chilled 4% (w/v) paraformaldehyde (Electron Microscopy Sciences) for 20 minutes and then incubated with 10mM NH₄Cl (Sigma) for 10 minutes. Next, cells were permeabilized with 3x washing steps containing 0.2% (v/v) Triton-X 100 in pH 7.4 PBS (both Sigma) with a 5 minute incubation between each wash and placed in blocking solution (3% w/v BSA in PBS, both Sigma) for 1 hour before labeling for 2 hours with Alexa-647-labeled monoclonal rabbit anti-alpha-tubulin primary antibodies (ab190573, Abcam) and mouse mitochondrial-marking anti-ATPB primary antibodies (ab14730, Abcam) using a 1:200 dilution in 3% w/v BSA. Cells were then washed 3x with 0.2% Triton-X 100 with a 3 minute waiting step between each wash. Goat anti-mouse Alexa 532-conjugated secondary antibody (A11002, Thermofisher) labelling was then performed with 1:500 dilution for one hour followed by 5X washing steps of 0.2% Triton-X 100. Samples were then shielded from light and kept at 4° C until imaged.

Super-resolution imaging was performed 2–3 days after fixing cells. Samples were placed in a custom coverglass slide holder (Tokai Hit Co. Ltd., Japan) and warmed to room temperature and then placed in blinking media³² (700µg/mL Glucose Oxidase, 50µg/mL Catalase, 0.55M Glucose, 140mM 2-Mercaptoethanol, all Sigma in 0.1M pH 8.0 Tris·HCl buffer, Invitrogen). The sample was scanned at low-intensity laser illumination for suitable regions and then imaged with high intensity (10kW/cm²) 641 nm light and (5kW/cm²) 514 nm light, with a rising intensity of the 405 nm activation laser (0-500W/cm²)³².

Fitting algorithm

In brief, emitter localizations of Tetrapod PSF data were performed using maximum likelihood estimation with a numerical scalar imaging model, taking into account refractive index mismatch, using a custom Matlab code. The elongated PSF in the cell experiment was fit using a custom Matlab code that performs 2D Gaussian fitting, and colour discrimination was decided by ratio of Gaussian standard deviations along both axes. For more fitting details see Supplementary Information.