Abstract
X-ray luminescence computed tomography (XLCT), which aims to achieve molecular and functional imaging by X-rays, has recently been proposed as a new imaging modality. Combining the principles of X-ray excitation of luminescence-based probes and optical signal detection, XLCT naturally fuses functional and anatomical images and provides complementary information for a wide range of applications in biomedical research. In order to improve the data acquisition efficiency of previously developed narrow-beam XLCT, a cone beam XLCT (CB-XLCT) mode is adopted here to take advantage of the useful geometric features of cone beam excitation. Practically, a major hurdle in using cone beam X-ray for XLCT is that the inverse problem here is seriously ill-conditioned, hindering us to achieve good image quality. In this paper, we propose a novel Bayesian method to tackle the bottleneck in CB-XLCT reconstruction. The method utilizes a local regularization strategy based on Gaussian Markov random field to mitigate the ill-conditioness of CB-XLCT. An alternating optimization scheme is then used to automatically calculate all the unknown hyperparameters while an iterative coordinate descent algorithm is adopted to reconstruct the image with a voxel-based closed-form solution. Results of numerical simulations and mouse experiments show that the self-adaptive Bayesian method significantly improves the CB-XLCT image quality as compared with conventional methods.
Keywords: Optical molecular imaging, X-ray luminescence computed tomography, image reconstruction, X-ray imaging
I. Introduction
Transmission X-ray computed tomography (XCT) imaging is indispensable in pre-clinical and clinical studies. The modality, however, falls short in providing sufficient contrast for probing the molecular bases of diseases. X-ray luminescence computed tomography (XLCT) has recently been proposed as a new molecular imaging modality for various biomedical applications [1]–[3]. This modality utilizes X-ray-excitable nanophosphors that produce visible or near-infrared (NIR) luminescence upon X-ray excitation [4]–[6]. The strategy empowers X-ray imaging with the ability of extracting physiological or biological signatures through simultaneous measurements of X-ray luminescence and transmission signals. In this approach, the two modalities work synergistically to produce dual modality images that are inherently registered in three-dimensional (3-D) space [4]. With the combination of high sensitivity of optical detection and high spatial resolution of X-ray imaging, XLCT shows important advantages when compared with traditional optical imaging techniques, such as fluorescence molecular tomography (FMT) [7]–[9] or bioluminescence tomography (BLT) [10]–[12]. Thanks to the principles of X-ray excitation and optical emission, the optical background in XLCT is essentially zero, thus effectively removing a significant factor limiting the sensitivity in optical imaging such as FMT [9]. Furthermore, owing to the high penetrating power and limited scattering of X-rays in biological tissues, XLCT has much higher spatial resolution and improved imaging depth. The emergence of XLCT opens new possibilities to achieve 3-D imaging of different molecular targets by X-rays, such as epidermal growth factor receptor [13] or folate receptor-α expression [14].
Continuous efforts have been devoted to XLCT imaging studies [15]–[24] since the first demonstration of the feasibility of XLCT [1]. Cong et al. used a scattering-compensated forward model to mitigate the X-ray scattering problem and showed image quality improvement with simulation study [17]. Li et al. utilized X-ray beam locations as excitation priors in their reconstruction algorithm and achieved good spatial resolution in the case of deep-located target [18], [19]. In practice, the imaging time of narrow beam-based XLCT is long due to its small excitation area, hindering the practical applications of XLCT. A cone beam XLCT (CB-XLCT) imaging system was investigated recently by Chen et al. [20]–[22], and applied to small animal imaging by Liu et al. [23]. For whole-body mouse imaging [24], CB-XLCT has the obvious advantage of time efficiency as compared with narrow beam XLCT. However, the image reconstruction of CB-XLCT is a severely ill-conditioned inverse problem because of diffusive transport of optical photons in biological tissues, leading to inferior image quality. This is akin to the problem existing in FMT and BLT.
To take advantage of the useful features of cone beam geometry with minimal compromise in image quality, it is necessary to explore effective reconstruction methods for CB-XLCT imaging. Bayesian methods have recently been successfully used to reconstruct positron emission tomography (PET) [25], BLT [26], FMT [27] and dynamic FMT [28] images. The technique provides a natural framework to utilize various kinds of prior information for improved image reconstruction. In this work, we develop, for the first time, a Bayesian theory-based method to solve the severely ill-conditioned CB-XLCT inverse problem. In our method, a Gaussian Markov random field (GMRF) model is used to construct the prior model, which utilizes the spatial correlations between neighboring voxels to constrain the solution. Different from the conventional Tikhonov regularization that applies overall regularization on the solution, the GMRF model regularizes the solution locally. An alternating optimization scheme is presented to automatically calculate the unknown hyperparameters used in the prior model, and an iterative coordinate descent (ICD) algorithm is adopted to optimize the objective function to reconstruct the image with a voxel-based closed-form solution. Numerical simulations and in vivo mouse experiments are performed to test the performance of the proposed approach. Our results show that the proposed method improves traditional reconstruction methods and provides a robust technique for CB-XLCT image reconstruction.
II. Theory
A. Forward Problem
In XLCT imaging, X-rays emitted by the X-ray source travel through the biological tissues and provide an excitation field in the imaging object. According to the Lambert-Beer law, the X-ray intensity distribution X(r) can be given by
| (1) |
where X(r0) is the intensity of X-ray at the initial position r0, r is a point on the path of X-ray propagation, and μt(τ) is the X-ray attenuation coefficient that can be computed from the transmission XCT data.
As a consequence of interaction with the X-ray excitation field, the nanophosphors distributed in the imaging object emits visible or NIR light, as sketched in Fig. 1(a). The emission light can be expressed with a linear relationship adopted in the previous works [17]–[24]
| (2) |
where S(r) is the light source energy density, n(r) is the nanophosphor concentration, and ε is the light yield which can be defined as the quantum yield per unit nanophosphor concentration [17].
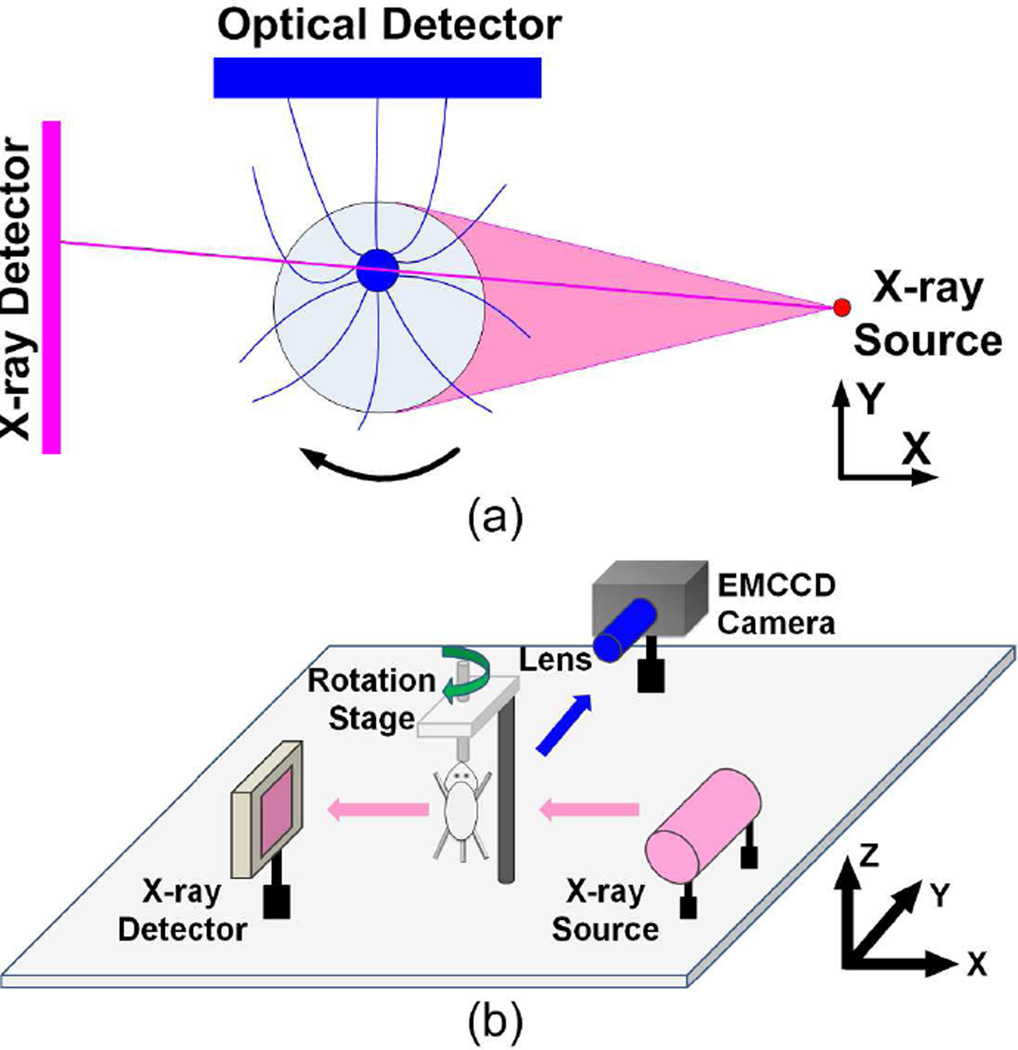
Fig. 1.
(a) Principle of CB-XLCT imaging. A cone beam X-ray source is used to excite the target filled with nanophosphors, while an optical detector is used to measure the visible or NIR luminescence emitted by the target. (b) Schematic diagram of the hybrid CB-XLCT/XCT imaging system. A rotation stage is positioned in the center of the hybrid imaging system. The imaging object is fixed in the rotation stage and rotated continuously.
Since biological tissues have highly scattering and weakly absorbing properties in the visible or NIR spectral window, the transport of the emitted light can be modeled by the diffusion equation (DE) [28]
| (3) |
where Ω is the image domain, Φ(r) is the photon fluence generated by the light source S(r), μa(r) is the absorption coefficient, D(r) is the diffusion coefficient given by , with representing the reduced scattering coefficient. The DE is constrained by the Robin boundary condition [27].
| (4) |
where ∂Ω denotes the boundary of Ω, v is the outward unit normal vector on ∂Ω, and ρ is the boundary mismatch parameter and accounts for the light reflection on the boundary surface.
Using the finite element method (FEM), we can discretize Eqs. (2) and (3) into a matrix form and relate nanophosphor concentration with the photon fluence according to
| (5) |
where Φ = [Φ(r1), ⋯, Φ(rN)]T is the photon fluence vector, n = [n(r1), ⋯, n(rN)]T is the nanophosphor concentration vector, N is the number of voxels in the discrete domain, A and F are matrices of size N × N and their elements are given by
| (6) |
| (7) |
where ψi(r) and ψj(r) are the corresponding elements of the test function of the FEM. Because the matrix A is positive definite, Eq. (5) can be recast into
| (8) |
where M = εA−1F.
For tomography, the imaging object is rotated from 0° to 360° to obtain luminescence signals at different angles, as sketched in Fig. 1(a). At each angle, the cone beam X-ray source irradiates the imaging object, and the luminescence signals are acquired by the optical detector. In projection s(s = 1, ⋯, S), suppose that Ms measurement points are acquired, then measurement points are collected for the whole circle. For projection s, by only retaining the measurable values of Φ on the surface, Eq. (8) becomes
| (9) |
where , and Ws includes the corresponding rows of matrix Ms = εA−1Fs.
Assembling measurements from all projections and considering the noise of the measurement system, we get
| (10) |
where ζ = [ζ1, ⋯, ζM]T is the additive noise vector, y = [y1, ⋯, yM]T is the photon fluence vector measured by the optical detector, is the measurable photon fluence vector predicted by the DE, is the weight matrix of size M × N, and x = [x1, ⋯, xN]T = [n(r1), ⋯, n(rN)]T is the unknown nanophosphor concentration vector to be reconstructed.
B. Inverse Problem
The XLCT image reconstruction is an ill-conditioned problem in which the solution is usually underdetermined and noise sensitive. A Bayesian method, with which all available information about the inverse problem can be easily incorporated, is employed to solve the CB-XLCT inverse problem. In this approach, the maximum a posteriori (MAP) estimation of the unknown concentration distribution x from the measurement vector y based on Bayesian theorem can be written as [27]
| (11) |
where p(x|y) is the posterior probability of x given y, p(y|x) is the conditional probability of y given x (the measurement model), and p(x) is the prior probability of x (the prior model). The measurement model p(y|x) models the physical properties of the system, while the prior model p(x) models the image characteristics such as smoothness that one would expect in the solution.
The measurement model in the Bayesian framework is constructed based on a shot-noise model, which assumes independent measurement noise described by a Gaussian distribution with the variance proportional to the signal amplitude [29]. Specially, the model is written as
| (12) |
where M is the number of measurements, κ is an unknown hyperparameter related to the noise variance, and Λy is the covariance matrix for measurement vector y. For XLCT problem, the boundary measurements are assumed to be statistically independent. Thus Λy becomes a diagonal matrix and is given by
| (13) |
The prior model in the Bayesian framework is the most important unique part that enables the prior information to be used to constrain the inverse problem for improved reconstruction quality. Since the neighboring voxels tend to have the same or similar concentration distribution, this feature is used to construct the prior model. In many image reconstruction problems, the Markov random field (MRF) model has proved effective in describing the spatial correlations between neighboring voxels [30]
| (14) |
where ∂j denotes the neighboring voxels of voxel j. In MRF, the conditional distribution of a voxel is only a function of this voxel’s neighbors. According to the Hammersley–Clifford theorem, if the density function is constrained to be strictly positive, then a random field is a Markov random field if and only if its density function has the form of a Gibbs distribution. Since the concentration distribution is nonnegative, a Gibbs distribution is adopted here to model the density function mathematically. Gibbs distribution represents any distribution with a density function that can be put into the form [31]
| (15) |
where Z is a normalization constant for the distribution, β is the Gibbs prior parameter, and V is the potential function. In this work, the GMRF model with a Gibbs distribution is used to construct the prior model
| (16) |
where N is the number of voxels, σ is a normalization hyper-parameter, and bj−k is the weighting coefficient corresponding to the j th and kth voxels. The coefficients bj−k are assigned to be inversely proportional to the distance, under the requirement of ∑k∈∂j bj−k = 1. The choice of a quadratic form of GMRF model enables us to solve the inverse problem self-adaptively with high efficiency, as will be discussed in the subsequent section.
With the measurement and prior models constructed, by substituting Eqs. (12) and (16) into Eq. (11), and removing the constant terms, the objective function for image reconstruction can be written as
| (17) |
C. Hyperparameter Estimation and Image Reconstruction
The image reconstruction process can be described by a joint estimation given by
| (18) |
An alternating optimization scheme is employed to solve the above joint estimation problem [28]. In this scheme, the unknown hyperparameters are alternately estimated in each iteration, and the image is updated each time after the estimated hyperparameters are obtained. In updating the image, a voxel-wise iterative coordinate descent (ICD) algorithm is adopted to minimize the objective function [32]. More specifically, in each iteration of the alternating optimization scheme, κ, σ and x are updated sequentially abiding by the following relations:
| (19) |
| (20) |
| (21) |
where the ICD_update operation denotes one iteration of the ICD algorithm.
Given an image x̂ at the beginning of an iteration, the MAP estimates of κ and σ are given in a closed form by using maximum likelihood estimation, as follows
| (22) |
| (23) |
This closed-form solution reduces the computation complexity of hyperparameter estimation.
With the hyperparameters κ and σ estimated in each iteration, the objective function defined in Eq. (17) can be simplified as
| (24) |
In our calculation, the updated image is then obtained by applying the ICD_update operation to Eq. (24). The ICD algorithm is implemented by sequentially updating each voxel of the image. After all voxels are updated, the above procedure is repeated. A complete update of all voxels in the image is called as a scan [30]. Thus, the ICD algorithm proceeds scan after scan until a stop criterion is satisfied, e.g., the value of objective function is less than a threshold, or a preset scan number is achieved. To be efficient, each voxel in a scan is updated with random order, and the updated voxel is used in the subsequent calculation of the scan. In each scan, voxel j is updated by optimizing the following objective function with a nonnegative constraint
| (25) |
where
| (26) |
where W*j denotes the j th column of the weight matrix W.
Minimization of Eq. (25) is equivalent to solving a one-dimensional function. This can be achieved by finding the root of the derivative of the objective function defined in Eq. (25), i.e.,
| (27) |
where e = y − Wx̂. The solution of the above equation is given by
| (28) |
where
| (29) |
| (30) |
| (31) |
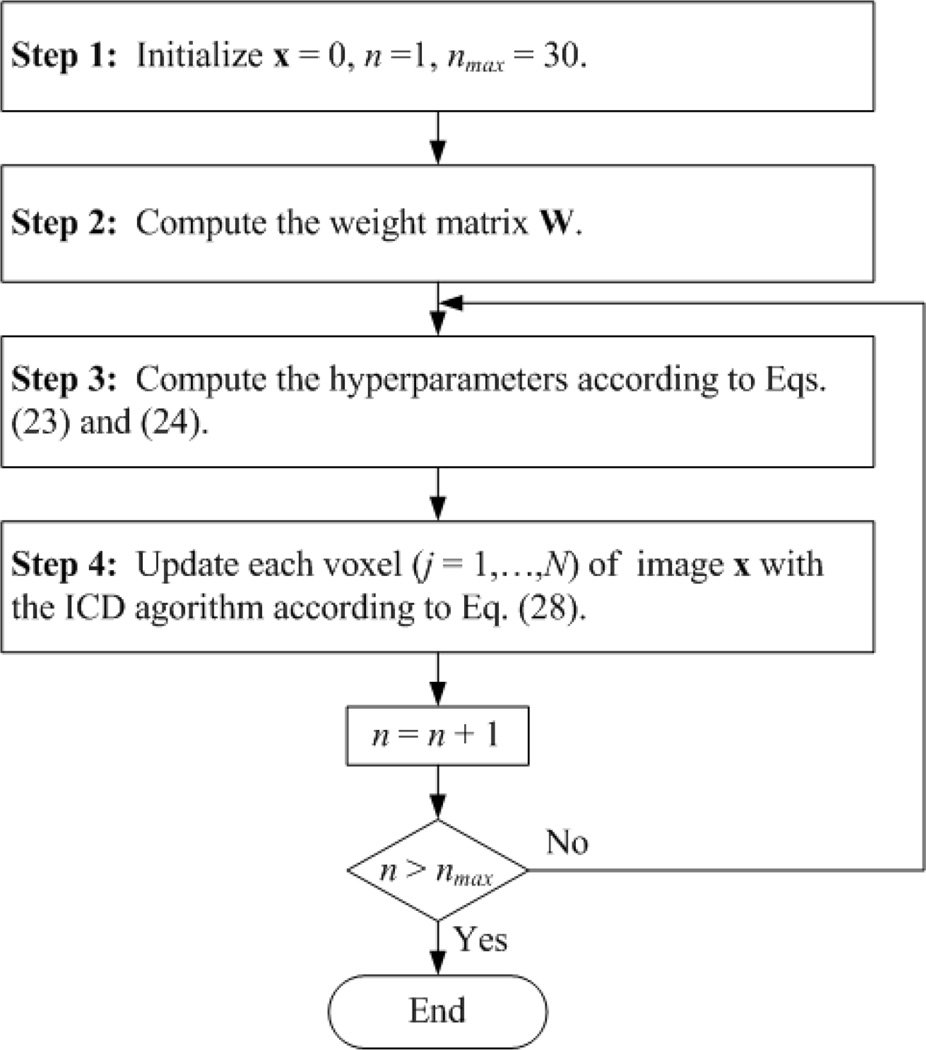
For convenience, the flow chart of the proposed method is recapitulated in Fig. 2. Note that, with all the unknown hyperparameters calculated automatically by using the alternating optimization scheme, the XLCT reconstruction process 5 is made self-adaptive; with the image updated via a voxel-based closed-form solution by using the ICD algorithm, the XLCT reconstruction process is made computationally more efficient.
Fig. 2.
Flow chart of the proposed Bayesian method.
III. Methods
Phantom experiments were first carried out to evaluate the accuracy of the forward model. Then, numerical simulations and in vivo mouse experiments were carried out to evaluate the performance of the proposed method (MAP-GMRF). For comparison, three traditional methods, algebraic reconstruction technique (ART), Tikhonov regularization [33], and stagewise orthogonal matching pursuit (StOMP) based on L0 regularization [34], were also implemented to reconstruct the image.
A. Hybrid CB-XLCT/XCT System
Fig. 1(b) shows the hybrid CB-XLCT/XCT system used in the phantom and in vivo mouse experiments. The system included a cone beam X-ray source, an X-ray detector, an electron-multiplying charge-coupled device (EMCCD) camera and a rotation stage. The X-ray source used in the system was a microfocus X-ray source (XTF5011, Oxford Instrument, UK) with the maximal power of 50 W, and could irradiate 47 µm cone beam X-rays. The transmitted X-rays were detected by a CMOS X-ray flat panel detector (C7921-02, Hamamatsu, Japan) with a pixel size of 50 µm covering a 1032 × 1012 digital image matrix. A −70°C cooled EMCCD camera (Andor, Belfast, Northern Ireland, UK) coupled with a Nikkor 60-mm f/2.8D lens (Nikon, Melville, NY) was positioned at 90° towards the X-ray source, and was used to collect the luminescence signals emitted from the imaging object. The X-ray source, X-ray detector and EMCCD camera were placed 31.5 cm, 7.0 cm and 31.2 cm away from the rotational center of the rotation stage, respectively.
B. Accuracy of Forward Model
Phantom experiments were first carried out in order to test the accuracy of the forward model. Specifically, a glass cylinder (3.0 cm in diameter) containing a mixture of water and intralipid was employed as the phantom, with the optical properties of μa = 0.02 cm−1 and . A transparent glass tube (4 mm in diameter) filled with Eu3+-doped gadolinium oxysulfide (Gd2O2S:Eu3+, with a density of 7.4 g/mL) nanophosphors was placed in the phantom to simulate the target [23]. The emitted luminescence signals of the nanophosphors are primarily between 600 and 750 nm [18]. The phantom was placed on the rotation stage of the imaging system and rotated for 360°. During this process, 24 projections were acquired by the EMCCD camera with an angular increment of 15°. The voltage and current of the X-ray source were set to 48 kV and 0.8 mA, respectively. The X-ray beam was filtered with 0.4 mm Al. The exposure time, EM gain and binning of EMCCD were set to 5 s, 5, and 1 × 1, respectively.
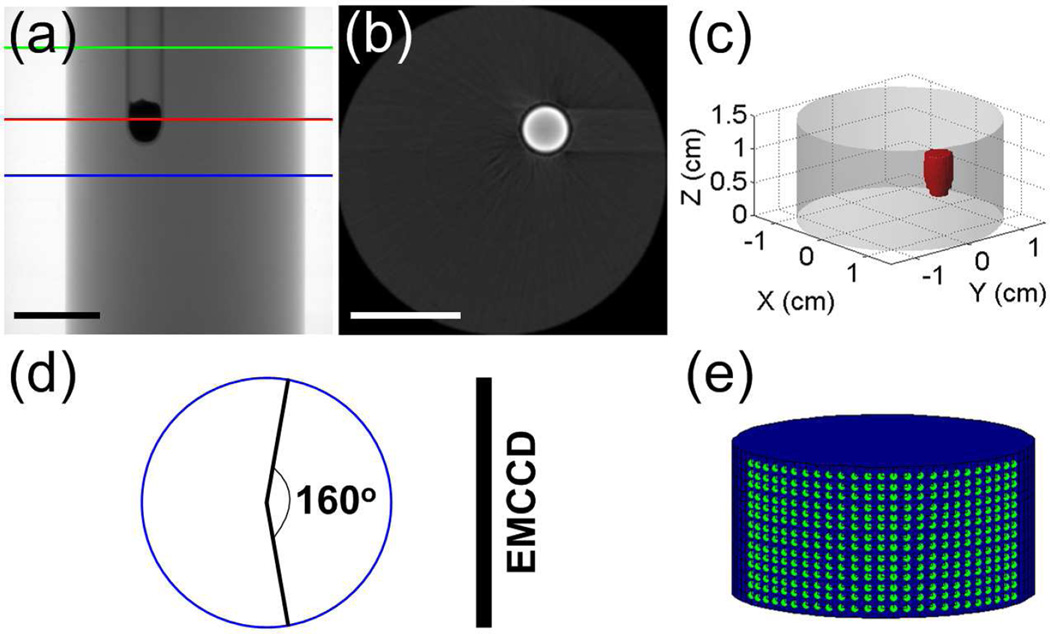
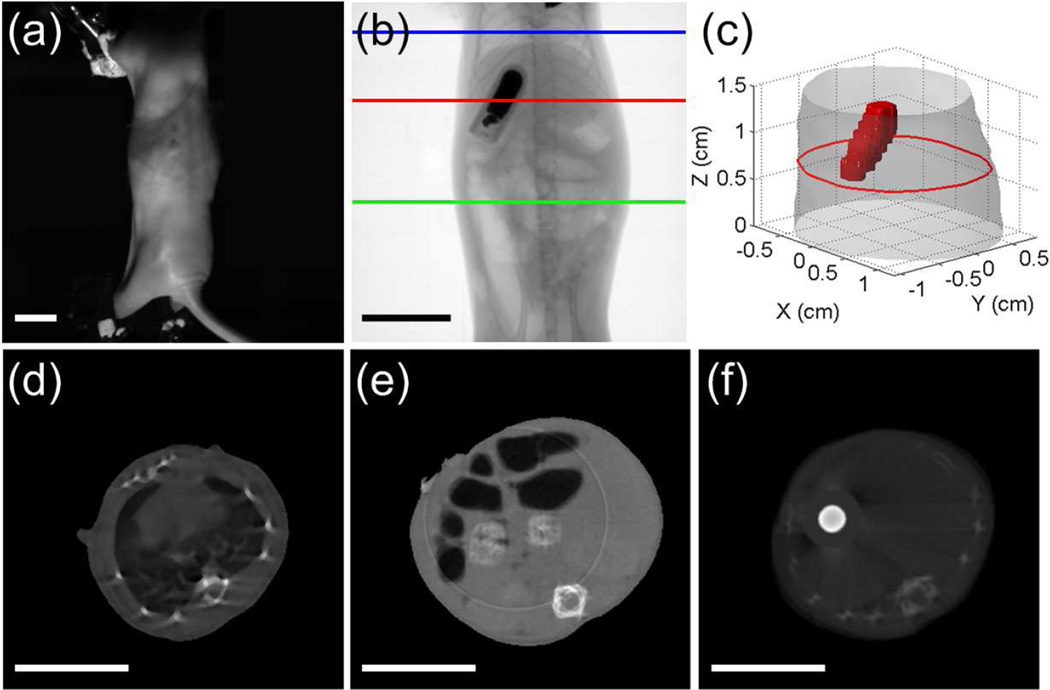
Fig. 3 provides some details of the phantom experiments. Fig. 3(a) shows a representative X-ray projection image of the phantom. The region between the blue and green lines was selected for the study. Fig. 3(b) shows the XCT slice for an axial cut indicated by the red line in Fig. 3(a). The target can be seen clearly in the image. The target region in all XCT slices was segmented. Fig. 3(c) is the 3-D rendering of the phantom, in which the red object denotes the target. For each excitation angle, the luminescence signals at an array of measurement points within a field-of-view (FOV) of 160° were acquired using the EMCCD camera, as shown in Fig. 3(d). Fig. 3(e) shows the distribution of the measurement points at an excitation angle, with 1 mm distance along the Z axis and 5° distance along the circular arc.
Fig. 3.
Illustration of the phantom experiments. (a) Representative X-ray projection of the phantom. The region between the blue and green lines is used for the study. (b) Representative XCT slice of the phantom, corresponding to the slice indicated by the red line in (a). (c) 3-D display of the phantom and target. (d) FOV used for boundary measurements. (e) Distribution of the measurement points. Scale bars in (a) and (b): 1 cm.
In order to test how well the XLCT forward model fits the corresponding physical reality, we utilized the 3-D phantom shown in Fig. 3(c) to simulate the forward process and calculate the boundary luminescence signals according to Eqs. (1)–(9). Specifically, the X-ray intensity distribution inside the phantom was generated based on Eq. (1). Upon X-ray excitation, the target emitted X-ray luminescence as described by Eq. (2). The luminescence propagated in the phantom to the boundary according to Eqs. (3) and (4). The boundary luminescence signals at different angles were then computed based on Eq. (9). The theoretical values predicted by the forward model were compared directly with that measured by the EMCCD camera.
C. Numerical Simulations
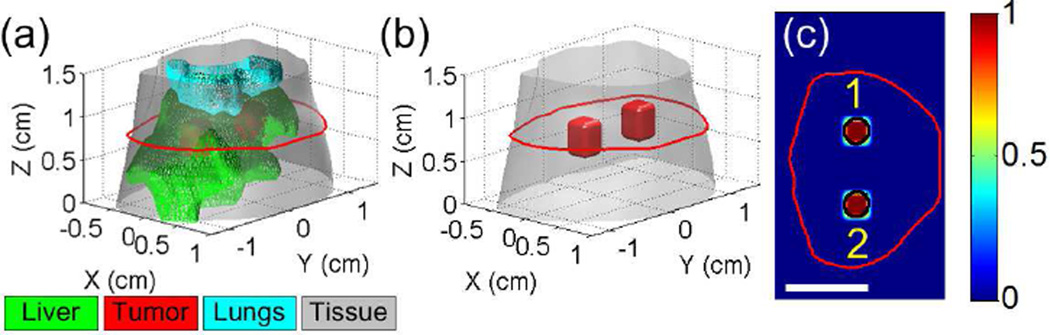
Numerical simulations were first implemented to test the performance of the proposed method. As shown in Fig. 4(a), a Digimouse atlas [35] containing the liver and lungs was employed to construct a 3-D simulation model. Two hypothetical cylindrical tumors of 3 mm in diameter and 4 mm in height were placed in the liver. For clarity, Fig. 4(b) displays the 3-D locations of the two tumors only, and Fig. 4(c) shows the central slice across the tumors.
Fig. 4.
(a) The 3-D Digimouse model used for simulation studies. The mouse torso from the neck to the bottom of liver (totally 1.5 cm in height) is selected for the study. The maximal radius of the 3-D model is about 1.6 cm. The liver and lungs are included in the model. Two hypothetical tumors are placed in the liver. (b) 3-D display of the tumor locations. (c) A representative slice of the simulation model, as indicated by the red line in (a). The black circles indicate the locations of the two tumors. Scale bar in (c): 1 cm.
The simulation was done based on the forward model described in Eqs. (1)–(9). The cone beam X-ray source was assumed to be monochromatic with an energy of 20 keV, corresponding to the average effect of polychromatic X-ray source of around 50 kV. The light yield ε was set to be 0.15 cm3/mg[17], and the X-ray attenuation coefficient was set to be μt = 0.5 cm−1 according to the XCT reconstruction results of the in vivo mouse experiments. The scattering of X-rays was neglected. A heterogeneous forward model was constructed by assigning adequate optical properties to the segmented organs [35]. The simulation model was rotated for 360°, with 24 projections (S = 24) acquired from the surface with an angular increment of 15°. Then, zero-mean white Gaussian noise was added to generate noisy boundary measurements with signal-to-noise ratio (SNR) set as 35 dB. The ART, Tikhonov, StOMP and MAP-GMRF methods were implemented to process the noisy boundary measurements and reconstruct the concentration distributions. The Tikhonov method used analytical solution with the regularization parameter determined by the L-curve method [36]. The numbers of iteration of the ART, StOMP and MAP-GMRF methods were empirically chosen to be 3000, 100 and 30, respectively, to ensure convergence of the calculation.
D. Mouse Experiments
Mouse experiments were conducted under the protocol approved by the Institutional Animal Care and Use Committee of Tsinghua University. In this study, a female BALB/c nude mouse (about 22 g) was anesthetized during the experiments, and a transparent glass tube (3 mm in diameter) filled with Gd2O2S:Eu3+ nanophosphors was implanted into the abdominal cavity to simulate a tumor targeted by nanophosphor probes. The mouse was fixed on the rotation stage of the system and rotated for 360°. The voltage and current of the X-ray source with a tungsten target were set to 48 kV and 0.8 mA, respectively, and the beam was filtered with 0.4 mm Al. During the rotational process, 24 projections (S =24) were acquired by the EMCCD camera with an angular increment of 15°. The exposure time, EM gain and binning of EMCCD were set to 2 s, 20, and 1 × 1, respectively. The rotational speed of the mouse was 6°/s, and the total time of full rotation was 60 s. As a result, the XLCT imaging time was about 108 s.
After collecting the luminescence data, the transmission projections were acquired to get the anatomical information of the mouse. The X-ray attenuation coefficients were reconstructed by using the Feldkamp–Davis–Kress (FDK) algorithm [37]–[39] and used to calculate the X-ray excitation field of XLCT. In this data collection process, X-ray projections were obtianed with an angular increment of 1°, and the imaging time of each projection was 1.25 s.
E. Evaluation
Several indexes were used to quantitatively evaluate the proposed reconstruction method and the forward model. Given a region of interest (ROI), the contrast-to-noise ratio (CNR) [40] is used to evaluate the image contrast of the ROI
| (32) |
where the subscript ROI and BCK denote the target and background in the 3-D imaging model, respectively, μ and σ2 are the mean value and variance, respectively, wROI and wBCK are weighting factors determined by the relative volumes of the ROI and background, respectively.
The location error (LE) is used to evaluate the localization accuracy of the reconstruction. It is given by calculating the Euclidean distance between the actual and reconstructed target positions
| (33) |
where p = [x, y, z] denotes the 3-D coordinate vector, and p0 and pr denote the centers of the actual and reconstructed targets, respectively.
The Dice coefficient [41] is used to evaluate the similarity of the actual and reconstructed target regions
| (34) |
where x and x̂ denote the actual and reconstructed target regions, respectively, and |x| denotes the number of voxels in the region x.
The normalized mean square error (NMSE) is used to evaluate the relative error between the actual and reconstructed results
| (35) |
where x and x̂ are the actual and reconstructed images, respectively. The NMSE is also used to evaluate the accuracy of the forward model, in which case x and x̂ denote the measured and predicted boundary vectors, respectively.
Additionally, the cosine similarity [42] is also used to evaluate the accuracy of the forward model
| (36) |
where y0 and y1 denote the measured and predicted boundary vectors, respectively.
IV. Results
A. Accuracy of Forward Model
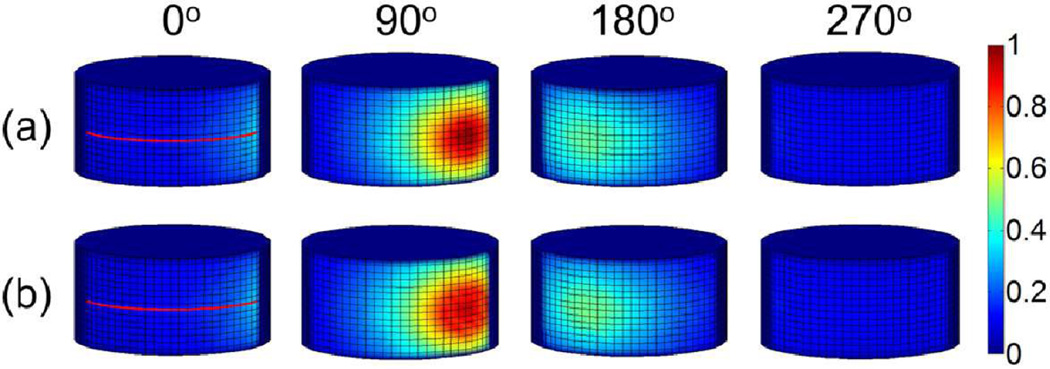
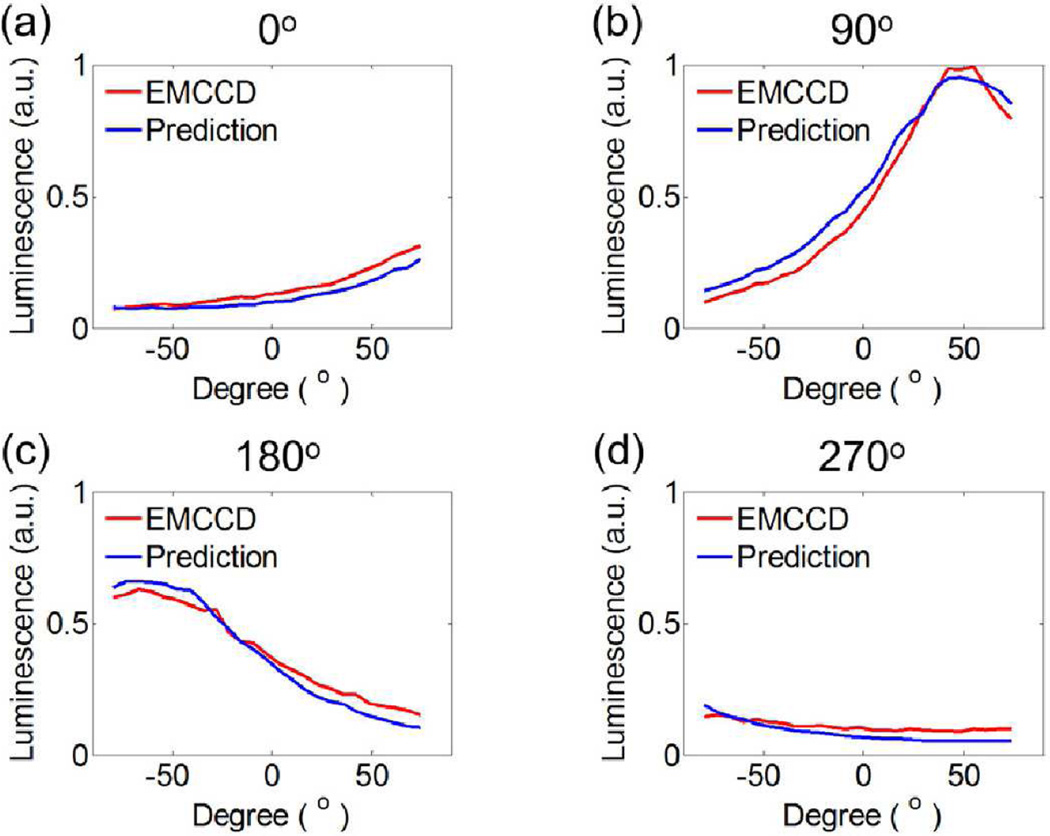
Four representative images of luminescence signals on the 3-D phantom surface, acquired by the EMCCD camera and predicted by the forward model, are displayed in Fig 5(a) and 5(b), respectively. The corresponding luminescence profiles along the red lines shown in Fig. 5 are displayed in Fig. 6. It is seen from Figs. 5 and 6 that the model calculations agree with the actual measurements very well.
Fig. 5.
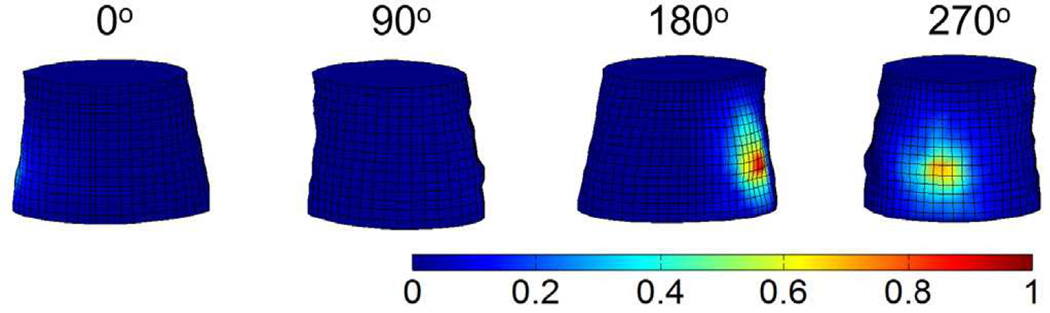
Phantom results of XLCT forward model. (a) Four representative luminescence projections measured by the EMCCD camera at different excitation angles (0°, 90°, 180° and 270°). (b) The corresponding luminescence projections predicted by the forward model. The measurements on the boundary surface of the cylindrical phantom are normalized to the maximal value.
Fig. 6.
Luminescence profiles along the red lines shown in Fig. 5 for the four representative excitation angles (0°, 90°, 180° and 270°). a.u., arbitrary unit.
Table I summarizes the cosine similarity R and the NMSE between the measurement data and the model prediction. It is interesting to point out that the highest R and the least NMSE occur at 90°, whereas the lowest R and the largest NMSE occur at 270°. That is, the best and worst predictions are achieved at 90° and 270°, respectively, primarily because the luminescence signal level changes from angle to angle. When the signal is weaker, the measurement noise is relatively larger, leading to less desirable agreement.
TABLE I.
Quantitative Evaluation of the Forward Model
| Indexes | 0° | 90° | 180° | 270° | All angles |
|---|---|---|---|---|---|
| R | 0.98 | 0.99 | 0.96 | 0.94 | 0.97 |
| NMSE | 0.05 | 0.02 | 0.06 | 0.09 | 0.05 |
The quantitative indexes calculated from the whole set of measurement points (i.e., the measured photon fluence vector described in Eq. (10)) assembled from all of the 24 luminescence projections are also shown in Table I. Once again, the accuracy of the forward model is demonstrated.
B. Numerical Simulations
Fig. 7 shows four representative projections of the X-ray luminescence at the Digimouse surface, corresponding to the excitation angles of 0°, 90°, 180° and 270°, respectively. The ART, Tikhonov, StOMP and MAP-GMRF methods were implemented to process the noisy boundary measurements (SNR = 35 dB) and reconstruct the nanophosphor concentration distributions.
Fig. 7.
Representative projections of the X-ray luminescence at the Digimouse surface. The four projections were acquired at different excitation angles (0°, 90°, 180° and 270°).
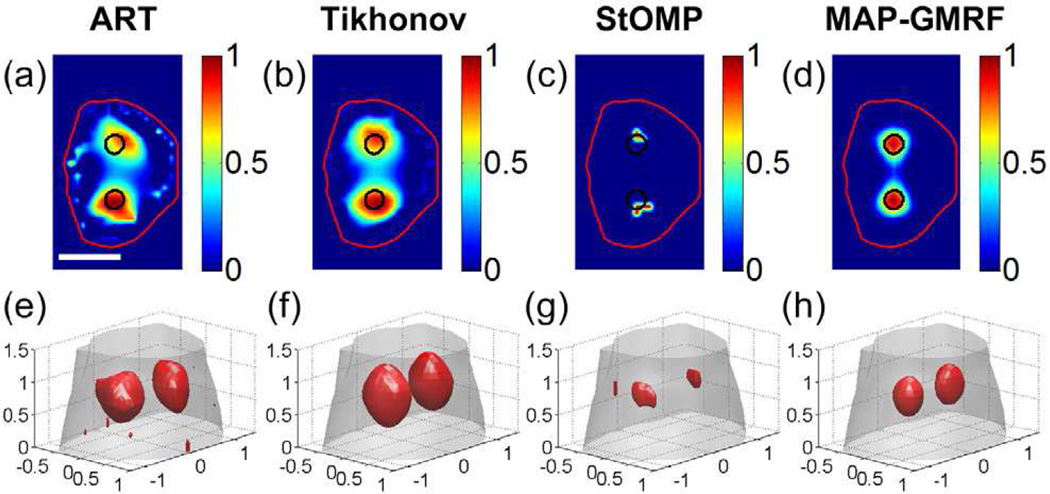
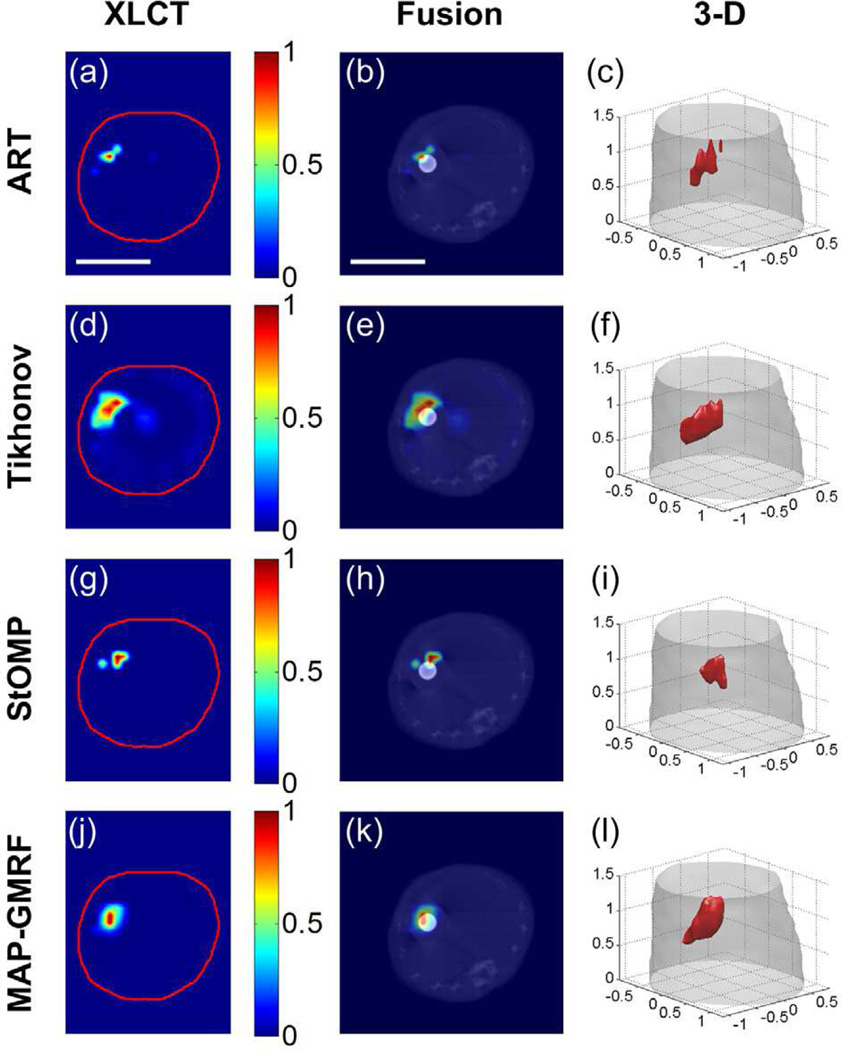
The reconstruction results of the numerical simulations are shown in Fig. 8. Specifically, Figs. 8(a)–(d) display the reconstruction results for the slice shown in Fig. 4(c), and Figs. 8(e)–(h) show the 3-D rendering of the reconstructed images. All images are normalized to the maximal intensive value. The actual locations of the two targets are indicated by the black circles. It is seen from Figs. 8(a) and 8(e) that the ART method yields noisy result and distorted target shapes, because the method is known to be very sensitive to measurement noise. Although the Tikhonov method improves the reconstructions with the help of regularization, the technique also suffers from noisy data and results in over-smoothed target shapes (see Figs. 8(b) and 8(f)), primarily because the regularization is applied to the entire image domain. With sparse regularization, the StOMP method yields smaller but distorted targets accompanied with large localization errors (see Figs. 8(c) and 8(g)). This is attributed to that the L0 methods may easily converge to a biased solution in the presence of remarkable measurement noise [43]. In contrast, the MAP-GMRF method yields the least noisy solution with the best target locations among the four methods (see Figs. 8(d) and 8(h)), as a benefit of the local regularization strategy adopted by the prior model of the Bayesian method.
Fig. 8.
XLCT reconstruction results using the ART, Tikhonov, StOMP and MAP-GMRF methods in the Digimouse study. (a)–(d) show the representative results on an axial slice indicated in Fig. 4(c). The black circles are the actual locations of the two targets. (e)–(h) are the 3-D rendering of the reconstruction results. The red objects represent the recovered targets. Scale bar in (a): 1 cm.
Table II summarizes the quantitative analysis results of the four different reconstruction methods. The MAP-GMRF method yields the highest CNR and Dice coefficient, indicating that the targets are best recovered. Additionally, the proposed method yields the lowest NMSE, indicating that the reconstruction has the least relative error. Furthermore, the proposed method leads to the least LE1 and LE2 for the two targets shown in Fig. 4(c), indicating that the positions of the two targets determined by the MAP-GMRF method are the closest to their actual positions. These data quantitatively confirm the observations made in Fig. 8.
TABLE II.
Quantitative Analysis of the Numerical Simulations
| Indexes | ART | Tikhonov | StOMP | MAP-GMRF |
|---|---|---|---|---|
| CNR | 2.72 | 3.65 | 2.80 | 9.34 |
| Dice | 0.45 | 0.40 | 0.36 | 0.90 |
| NMSE | 0.91 | 0.82 | 0.90 | 0.36 |
| LE1 (cm) | 0.55 | 0.18 | 0.21 | 0.05 |
| LE2 (cm) | 0.72 | 0.20 | 0.52 | 0.05 |
C. Mouse Experiments
Fig. 9 summaries the XCT results of the mouse experiments. Fig. 9(a) shows a white light image of the mouse taken by the EMCCD camera. Fig. 9(b) shows a representative X-ray projection image of the mouse. The region between the blue and green lines was selected for the 3-D reconstruction. The implanted cylindrical target indicated by the red line can be seen in the projection image. Fig. 9(c) is the 3-D rendering of the target and the mouse contour which is generated from the XCT slices. Figs. 9(d)–(f) are the XCT slices indicated by the blue, green and red lines shown in Fig. 9(b), respectively. The target can be clearly seen in Fig. 9(f). All XCT slices of the investigated region were manually segmented to separate the liver, lungs and other tissues. A heterogeneous forward model was constructed by assigning the corresponding optical properties to the segmented organs [35].
Fig. 9.
XCT results of the mouse experiments. (a) White light image of the mouse. (b) Representative X-ray projection image of the mouse. The mouse torso between the blue and green lines (totally 1.5 cm in height) is selected for the study. The red line passes across the glass tube filled with nanophosphors and served as the target. (c) 3-D rendering of the XCT results. The maximal radius of the 3-D model is about 1.3 cm. The red object is the target, and the red circle corresponds to the outline of the mouse at the height indicated by the red line shown in (b). (d)–(f) The corresponding XCT slices indicated by the blue, green and red lines in (b), respectively. The target could be seen clearly in (f). Scale bars: 1 cm.
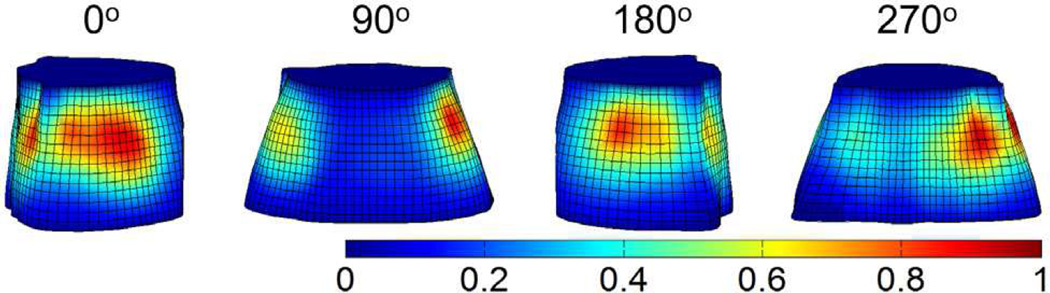
Fig. 10 shows four representative projections of the X-ray luminescence emitted from the mouse surface. They were selected from the 24 projections acquired by the EMCCD camera, corresponding to the excitation angles of 0°, 90°, 180° and 270°, respectively. The ART, Tikhonov, StOMP and MAP-GMRF methods were implemented to process the boundary measurements and reconstruct the nanophosphor concentration distributions.
Fig. 10.
Four representative luminescence projections of the mouse surface, measured by the EMCCD camera at different excitation angles (0°, 90°, 180° and 270°).
Fig. 11 shows the XLCT reconstruction results of the mouse experiments. Figs. 11(a), 11(d) 11(g) and 11(j) show the red-line slice in Fig. 9 reconstructed with the ART, Tikhonov, StOMP and MAP-GMRF methods, respectively. All the images are normalized to the maximal intensive value. Figs. 11(b), 11(e) 11(h) and 11(k) show the fusion images of the XLCT and XCT reconstructions, and Figs. 11(c), 11(f), 11(i) and 11(l) show the 3-D rendering of the XLCT results. It can be seen from Figs. 11(a)–(c) that the ART method yields distorted target shape with a relatively large location error. Thanks to the regularization strategy, the Tikhonov method obtains better target shape compared to the ART method. However, it is also observed from Figs. 11(d)–(f) that the Tikhonov method suffers from noisy results, over-smoothed target shape and low localization accuracy. Although the StOMP calculation converges, it suffers from large localization error and target shape distortion (see Figs. 11(g)–(i)). In contrast, the MAP-GMRF method yields the best image quality in terms of target shape and localization accuracy among the four methods (see Figs. 11(j)–(l)).
Fig. 11.
XLCT reconstruction results of the mouse experiments. (a), (d), (g) and (j) show the reconstruction results of ART, Tikhonov, StOMP and MAP-GMRF, respectively, for the slice shown in Fig. 9(f). The red circle indicates the outline of the mouse. (b), (e), (h) and (k) present the fusion of XLCT and XCT images. 3-D rendering of the XLCT reconstruction results are displayed in (c), (f), (i) and (l). The red objects represent the recovered targets. Scale bars in (a) and (b): 1 cm.
Table III shows the quantitative analysis results of the reconstructions obtained with the four methods. Similar to the numerical simulations, the MAP-GMRF method yields the highest CNR, Dice coefficient as well as the smallest LE, indicating that the target has been recovered with the best image contrast and localization accuracy. Additionally, the proposed method yields the smallest NMSE, indicating that the least relative error is achieved.
TABLE III.
Quantitative Analysis of the Mouse Experiments
| Indexes | ART | Tikhonov | StOMP | MAP-GMRF |
|---|---|---|---|---|
| CNR | 2.01 | 2.11 | 1.17 | 5.06 |
| Dice | 0.11 | 0.20 | 0.10 | 0.60 |
| NMSE | 1.01 | 1.54 | 1.06 | 0.79 |
| LE (cm) | 0.40 | 0.47 | 0.23 | 0.09 |
V. Discussion and Conclusion
In this work, we have established a Bayesian theory-based reconstruction method for CB-XLCT. The underlying strategy here is to construct a local regularization pattern via the prior model of the Bayesian theory to effectively mitigate the ill-conditioness of the inverse problem. A unique advantage of the proposed algorithm is that it is capable of automatically estimating the optimal values of the regularization parameters, thus avoiding the common problem of manual and inaccurate determination of the regularization parameters.
In our previous work on FMT [27] and dynamic FMT [28], it has been shown that Bayesian theory provides an effective mathematical framework through which various reconstruction methods can be flexibly deduced to improve the image quality. This work represents the first application of Bayesian theory in CB-XLCT. Through numerical simulations and in vivo mouse experiments, we have demonstrated that the proposed method outperforms other reconstruction methods, and demonstrated its efficacy in improving the image quality of CB-XLCT. Among the four different approaches, the proposed MAP-GMRF method yields the best image quality in terms of target contrast and localization accuracy (see Figs. 8 and 11, Tables II and III).
Compared with conventional narrow beam XLCT, a primary advantage of CB-XLCT is the significantly reduced imaging time. For 3-D imaging of the mouse experiments described in this work, it would take hours for the narrow beam XLCT [2], whereas it only takes a few minutes for the cone beam scanner. The X-ray dose deposited to the imaging objects in CB-XLCT would be similar to that of narrow beam scanning, when the X-ray source energy and imaging region are identical in the two imaging modes. However, the spatial resolution of CB-XLCT tends to be lower because of the ill-conditioness of the inverse problem here. Of course, the spatial resolution improvement of narrow beam excitation is accompanied with the cost of increased imaging time [22].
Although the proposed MAP-GMRF method is focused on a CB-XLCT imaging geometry, it can be extended to the narrow beam XLCT system [1] or fan beam XLCT system [44]. With some adequate modifications, the proposed method can also be used to improve the XLCT image quality in the case of limited angles [15]. Finally, we point out that the formulation and algorithm described in this work can be extended to tackle many other inverse problems, such as PET, FMT and BLT, by replacing the XCLT forward model with appropriate forward models.
There are a few issues that are worth of further discussion. Firstly, both Gaussian noise model [20], [28], [44] and Poisson noise model [1], [17] have been used to model the EMCCD camera noise. It is known that the Poisson distribution approaches to the Gaussian distribution as the sample size increases. Since the number of the photons acquired by the EMCCD camera is usually large in XLCT imaging, it is reasonable to use any of these two noise models. Although the Gaussian noise model was used to simulate the noise from the EMCCD camera in this work, one may also elect to proceed with an alternative approach using the Poisson noise model. Secondly, during the animal experiment, the mouse was kept in deep anesthesia. With slow rotation of 6°/s, the adverse effects of internal organ motion was minimized. We monitored the mouse throughout the scanning process to ensure that its position was not changed. Thus no motion correction was applied in the image reconstruction. Thirdly, accurate segmentation of the imaging subject is an important step toward high quality XLCT imaging. The segmentation should be done under the guidance of knowledge of mouse anatomy and with extra caution. Fourthly, the X-ray beam-hardening effect, which would increase the average energy of the beam when traveling through the imaging object, was not considered in the forward model. Practically, considering the small size of a mouse, the influence of beam hardening should be negligible for the system studied here. The effect would become more pronounced as the size of imaging object increases. In general, inclusion of beam-hardening effect should further improve the accuracy of XLCT imaging. Under the assumption that the beam hardening effect is negligible, the forward model used in this work is applicable to XLCT systems with either monochromatic or polychromatic X-ray source. In the latter case, the light yield ε defined in Eq. (2) represents a spectral average effect of the excitation X-ray beam. Finally, the X-ray transmission and luminescence data were collected separately in this work. Simultaneous acquisition of the two sets of data would speed up the scanning and mitigate any adverse effect of anatomical change occurred between the two scans. Improved data acquisition and integration of the two modalities will be investigated in next generation of system design to maximally utilize the technical capacity of the XLCT imaging strategy.
In conclusion, we have presented a novel Bayesian method for CB-XLCT reconstruction. The work lays foundation for future CB-XLCT development. To the best of our knowledge, this is the first time that the Bayesian theory is used to solve the XLCT inverse problem. By taking advantage of the prior model provided by the Bayesian framework, the proposed method is capable of modeling the spatial correlations of neighboring voxels with the GMRF model, and leads to significant improvements in image quality compared with conventional methods. Future work will focus on incorporating more prior information into the prior model to make full use of the advantages of Bayesian method.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grant No. 61601019, 81571836, 61322101; the Beijing Natural Science Foundation under Grant No. 7164270; the Fundamental Research Funds for the Central Universities under Grant No. 2015JBM026; the China Postdoctoral Science Foundation under Grant No. 2015M570032; the China Scholarship Council under Grant No. 201507095005; Guangdong Innovation Team of Image-Guided Therapy under Grant No. 2011S013, and the National Institutes of Health under Grant No. 1R01 EB016777.
Contributor Information
Guanglei Zhang, Department of Biomedical Engineering, School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China; Department of Radiation Oncology, School of Medicine, Stanford University, Stanford, CA 94305, USA.
Fei Liu, Department of Biomedical Engineering, School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China.
Jie Liu, Department of Biomedical Engineering, School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China.
Jianwen Luo, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing 100084, China.
Yaoqin Xie, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China.
Jing Bai, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing 100084, China.
Lei Xing, Department of Radiation Oncology, School of Medicine, Stanford University, Stanford, CA 94305, USA.
References
- 1.Pratx G, Carpenter CM, Sun C, Xing L. X-ray luminescence computed tomography via selective excitation: A feasibility study. IEEE Trans. Med. Imag. 2010;29(12):1992–1999. doi: 10.1109/TMI.2010.2055883. [DOI] [PubMed] [Google Scholar]
- 2.Pratx G, Carpenter CM, Sun C, Rao RP, Xing L. Tomographic molecular imaging of X-ray-excitable nanoparticles. Opt. Lett. 2010;35(20):3345–3347. doi: 10.1364/OL.35.003345. [DOI] [PubMed] [Google Scholar]
- 3.Carpenter CM, Pratx G, Sun C, Xing L. Hybrid X-ray/optical luminescence imaging: Characterization of experimental conditions. Med. Phys. 2010;37(8):4011–4018. doi: 10.1118/1.3457332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ahmad M, Pratx G, Bazalova M, Xing L. X-ray luminescence and x-ray fluorescence computed tomography: New molecular imaging modalities. IEEE Access. 2014;2:1051–1061. [Google Scholar]
- 5.Sun C, Carpenter CM, Pratx G, Xing L. Facile synthesis of amine-functionalized Eu3+-Doped La(OH)3 nanophosphors for bioimaging. Nanoscale Res. Lett. 2011;6(24):1–7. doi: 10.1007/s11671-010-9768-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen H, Moore T, Qi B, Colvin DC, Jelen EK, Hitchcock DA, He J, Mefford OT, Gore JC, Alexis F, Anker JN. Monitoring pH-triggered drug release from radioluminescent nanocapsules with X-ray excited optical luminescence. ACS Nano. 2013;7(2):1178–1187. doi: 10.1021/nn304369m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Soubret A, Ntziachristos V. Fluorescence molecular tomography in the presence of background fluorescence. Phys. Med. Biol. 2006;51(16):3983–4001. doi: 10.1088/0031-9155/51/16/007. [DOI] [PubMed] [Google Scholar]
- 8.Ale A, Ermolayev V, Herzog E, Cohrs C, de Angelis MH, Ntziachristos V. FMT-XCT: in vivo animal studies with hybrid fluorescence molecular tomography-X-ray computed tomography. Nat. Methods. 2012;9:615–620. doi: 10.1038/nmeth.2014. [DOI] [PubMed] [Google Scholar]
- 9.Zhang G, Liu F, Zhang B, He Y, Luo J, Bai J. Imaging of pharmacokinetic rates of indocyanine green in mouse liver with a hybrid fluorescence molecular tomography/x-ray computed tomography system. J. Biomed. Opt. 2013;18(4):040505-1–040505-3. doi: 10.1117/1.JBO.18.4.040505. [DOI] [PubMed] [Google Scholar]
- 10.Wang G, Cong W, Durairaj K, Qian X, Shen H, Sinn P, Hoffman E, McLennan G, Henry M. In vivo mouse studies with bioluminescence tomography. Opt. Express. 2006;14(17):7801–7809. doi: 10.1364/oe.14.007801. [DOI] [PubMed] [Google Scholar]
- 11.Lv Y, Tian J, Cong W, Wang G, Luo J, Yang W, Li H. A multilevel adaptive finite element algorithm for bioluminescence tomography. Opt. Express. 2006;14(18):8211–8223. doi: 10.1364/oe.14.008211. [DOI] [PubMed] [Google Scholar]
- 12.Feng J, Qin C, Jia K, Zhu S, Yang X, Tian J. Bioluminescence tomography imaging in vivo: Recent advances. IEEE J. Sel. Top. Quant. 2012;18(4):1394–1402. [Google Scholar]
- 13.Sokolov K, Follen M, Aaron J, Pavlova I, Malpica A, Lotan R, Richards-Kortum R. Real-time vital optical imaging of precancer using anti-epidermal growth factor receptor antibodies conjugated to gold nanoparticles. Cancer Res. 2003;63:1999–2004. [PubMed] [Google Scholar]
- 14.Dam G, Themelis G, Crane L, et al. Intraoperative tumor-specific fluorescence imaging in ovarian cancer by folate receptor-α targeting: first in-human results. Nat. Med. 2011;17(10):1315–1319. doi: 10.1038/nm.2472. [DOI] [PubMed] [Google Scholar]
- 15.Carpenter CM, Pratx G, Sun C, Xing L. Limited-angle X-ray luminescence tomography: Methodology and feasibility study. Phys. Med. Biol. 2011;56(12):3487–3502. doi: 10.1088/0031-9155/56/12/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Carpenter CM, Sun C, Pratx G, Liu H, Chen Z, Xing L. Radioluminescent nanophosphors enable multiplexed small-animal imaging. Opt. Express. 2012;20(11):11598–11604. doi: 10.1364/OE.20.011598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cong W, Shen H, Wang G. Spectrally resolving and scattering compensated X-ray luminescence/fluorescence computed tomography. J. Biomed. Opt. 2011;16(6):066014-1–066014-7. doi: 10.1117/1.3592499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li C, Di K, Bec J, Cherry SR. X-ray luminescence optical tomography imaging: Experimental studies. Opt. Lett. 2013;38(13):2339–2341. doi: 10.1364/OL.38.002339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li C, Martinez-Davalos A, Cherry SR. Numerical simulation of x-ray luminescence optical tomography for small-animal imaging. J. Biomed. Opt. 2014;19(4):046002-1–046002-3. doi: 10.1117/1.JBO.19.4.046002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen D, Zhu S, Yi H, Zhang X, Chen D, Liang J, Tian J. Cone beam X-ray luminescence computed tomography: A feasibility study. Med. Phys. 2013;40(3):031111-1–031111-14. doi: 10.1118/1.4790694. [DOI] [PubMed] [Google Scholar]
- 21.Chen D, Zhu S, Chen X, Chao T, Cao X, Zhao F, Huang L, Liang J. Quantitative cone beam X-ray luminescence tomography-X-ray computed tomography imaging. Appl. Phys. Lett. 2014;105(19):191104-1–191104-4. [Google Scholar]
- 22.Chen D, Zhu S, Cao X, Zhao F, Liang J. X-ray luminescence computed tomography imaging based on X-ray distribution model and adaptively split Bregman method. Biomed. Opt. Express. 2015;6(7):2649–2663. doi: 10.1364/BOE.6.002649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu X, Liao Q, Wang H. In vivo x-ray luminescence tomographic imaging with single-view data. Opt. Lett. 2013;38(22):4530–4533. doi: 10.1364/OL.38.004530. [DOI] [PubMed] [Google Scholar]
- 24.Liu X, Liao Q, Wang H. Fast x-ray luminescence computed tomography imaging. IEEE Trans. Biomed. Eng. 2014;61(6):1621–1627. doi: 10.1109/TBME.2013.2294633. [DOI] [PubMed] [Google Scholar]
- 25.Kamasak M, Bouman CA, Morris ED, Sauer K. Direct reconstruction of kinetic parameter images from dynamic PET data. IEEE Trans. Med. Imag. 2005;24(5):636–650. doi: 10.1109/TMI.2005.845317. [DOI] [PubMed] [Google Scholar]
- 26.Feng J, Jia K, Qin C, Yan G, Zhu S, Zhang X, Liu J, Tian J. Three-dimensional bioluminescence tomography based on Bayesian approach. Opt. Express. 2009;17(19):16834–16848. doi: 10.1364/OE.17.016834. [DOI] [PubMed] [Google Scholar]
- 27.Zhang G, Cao X, Zhang B, Liu F, Luo J, Bai J. MAP estimation with structural priors for fluorescence molecular tomography. Phys. Med. Biol. 2013;58(2):351–372. doi: 10.1088/0031-9155/58/2/351. [DOI] [PubMed] [Google Scholar]
- 28.Zhang G, Pu H, He W, Liu F, Luo J, Bai J. Bayesian framework based direct reconstruction of fluorescence parametric images. IEEE Trans. Med. Imag. 2015;34(6):1378–1391. doi: 10.1109/TMI.2015.2394476. [DOI] [PubMed] [Google Scholar]
- 29.Ye JC, Webb KJ, Bouman CA, Millane RP. Optical diffusion tomography using iterative coordinate descent optimization in a Bayesian framework. J. Opt. Soc. Am. A. 1999;16(10):2400–2412. [Google Scholar]
- 30.Bouman CA, Sauer K. A generalized Gaussian image model for edge-preserving map estimation. IEEE Trans. Image Process. 1993;2(3):296–310. doi: 10.1109/83.236536. [DOI] [PubMed] [Google Scholar]
- 31.Hebert TJ, Leahy R. Statistic-based MAP image reconstruction from poisson data using Gibbs priors. IEEE Trans. Signal Process. 1992;40(9):2290–2303. [Google Scholar]
- 32.Zhang G, Liu F, Pu H, He W, Luo J, Bai J. A direct method with structural priors for imaging pharmacokinetic parameters in dynamic fluorescence molecular tomography. IEEE Trans. Biomed. Eng. 2014;61(3):986–990. doi: 10.1109/TBME.2013.2292714. [DOI] [PubMed] [Google Scholar]
- 33.Guo X, Liu X, Wang X, Tian F, Liu F, Zhang B, Hu G, Bai J. A combined fluorescence and micro-computed tomography system for small animal imaging. IEEE Trans. Biomed. Eng. 2010;57(12):2876–2883. doi: 10.1109/TBME.2010.2073468. [DOI] [PubMed] [Google Scholar]
- 34.Donoho DL, Tsaig Y, Drori I, Starck JL. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory. 2012;58(2):1094–1121. [Google Scholar]
- 35.Zhang G, He W, Pu H, Liu F, Chen M, Bai J, Luo J. Acceleration of dynamic fluorescence molecular tomography with principal component analysis. Biomed. Opt. Express. 2015;6(6):2036–2055. doi: 10.1364/BOE.6.002036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hansen PC. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992;34:561–580. [Google Scholar]
- 37.Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm. J. Opt. Soc. Am. A. 1984;1(6):612–619. [Google Scholar]
- 38.Dong D, Zhu S, Qin C, Kumar V, Stein JV, Oehler S, Savakis C, Tian J, Ripoll J. Automated recovery of the center of rotation in optical projection tomography in the presence of scattering. IEEE J. Biomed. Health Inform. 2012;17(1):198–204. doi: 10.1109/TITB.2012.2219588. [DOI] [PubMed] [Google Scholar]
- 39.Zhu S, Tian J, Yan G, Qin C, Feng J. Cone beam micro-CT system for small animal imaging and performance evaluation. Int. J. Biomed. Imaging. 2009;2009:960573. doi: 10.1155/2009/960573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang G, Pu H, He W, Liu F, Luo J, Bai J. Full-direct method for imaging pharmacokinetic parameters in dynamic fluorescence molecular tomography. Appl. Phys. Lett. 2015;106(8):081110. doi: 10.1109/TBME.2013.2292714. [DOI] [PubMed] [Google Scholar]
- 41.An Y, Liu J, Zhang G, Ye J, Du Y, Mao Y, Chi C, Tian J. A novel region reconstruction method for fluorescence molecular tomography. IEEE Trans. Biomed. Eng. 2015;62(7):1818–1826. doi: 10.1109/TBME.2015.2404915. [DOI] [PubMed] [Google Scholar]
- 42.Nguyen DV, Bai L. Cosine similarity metric learning for face verification; Proc. 10th Asian Conf. Computer Vision; 2010. [Google Scholar]
- 43.Dutta J, Ahn S, Li C, Cherry SR, Leahy RM. Joint L1 and total variation regularization for fluorescence molecular tomography. Phys. Med. Biol. 2012;57:1459–1476. doi: 10.1088/0031-9155/57/6/1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cong W, Wang G. X-ray fan-beam luminescence tomography. Austin J Biomed Eng. 2014;1(5):id1024-1–id1024-4. [Google Scholar]