CH₃NH₃PbI₃ perovskites: Ferroelasticity revealed

Evidence and control of ferroelastic (but not ferroelectric) domains in CH₃NH₃PbI₃ perovskite are provided.

Abstract

Ferroelectricity has been proposed as a plausible mechanism to explain the high photovoltaic conversion efficiency in organic-inorganic perovskites; however, convincing experimental evidence in support of this hypothesis is still missing. Identifying and distinguishing ferroelectricity from other properties, such as piezoelectricity, ferroelasticity, etc., is typically nontrivial because these phenomena can coexist in many materials. In this work, a combination of microscopic and nanoscale techniques provides solid evidence for the existence of ferroelastic domains in both CH₃NH₃PbI₃ polycrystalline films and single crystals in the pristine state and under applied stress. Experiments show that the configuration of CH₃NH₃PbI₃ ferroelastic domains in single crystals and polycrystalline films can be controlled with applied stress, suggesting that strain engineering may be used to tune the properties of this material. No evidence of concomitant ferroelectricity was observed. Because grain boundaries have an impact on the long-term stability of organic-inorganic perovskite devices, and because the ferroelastic domain boundaries may differ from regular grain boundaries, the discovery of ferroelasticity provides a new variable to consider in the quest for improving their stability and enabling their widespread adoption.

INTRODUCTION

In the past few years, organic-inorganic perovskite (OIP) materials have drawn significant attention due to their potential for realizing the next generation of low-cost and high-efficiency solar cells (1–4). The power conversion efficiency (PCE) of small-size (typically <16 mm²) perovskite solar cells improved considerably, from 3.9% in 2009 to 22.1% in 2016 (5, 6). Perhaps even more remarkably, the PCE of large devices (>1 cm²) has rapidly approached 20% (7). This extraordinary performance benefits from OIPs’ unusual combination of properties, including a strong optical absorption, small exciton binding energy, high carrier mobility, long charge carrier lifetime, long charge diffusion length, and small density of deep traps despite the large point defect densities typical of solution-processed films (8, 9). However, the pace of knowledge gathering on OIPs fundamental properties has generally lagged far behind the pace of efficiency improvement. For example, the widespread observation of current hysteresis in OIP devices and the recent observation of the switchable diode and photovoltaic effects initially spurred the speculation that OIPs could be ferroelectric at room temperature (10–15). This hypothesis prompted the fascinating idea that the internal field, due to spontaneous polarization, might be at the origin of the high PCE in OIP solar cells by aiding the separation of photoexcited electron-hole pairs and thus reducing charge recombination (16). However, solid experimental evidence of ferroelectricity of OIP materials is still lacking, and recent publications (17, 18) even question the very polarity of the CH₃NH₃PbI₃ (MAPbI₃) structure, a necessary requirement for ferroelectricity. In addition, several recent studies conclusively showed that ion migration and the associated charge doping are responsible for the observed hysteretic effects and excluded ferroelectricity as a possible origin (19). Domain-like structures have been recently observed by piezoresponse force microscopy (PFM) imaging (20), but no reproducible evidence for polarization–electric field hysteresis loops (the “smoking gun” for ferroelectricity) has been provided for either thin-film or single-crystal MAPbI₃ devices. Hermes et al. (20) have proposed that the domain-like structures consist of twin domains that form in CH₃NH₃PbI₃ during the cubic-tetragonal phase transition because of strain, thus indicating a ferroelastic rather than a ferroelectric behavior. However, these claims still lack the conclusive support of macroscopic and strain-related evidence.

Here, a combination of microscopic (polarized light optical microscopy) and nanoscopic [PFM and photothermal induced resonance (PTIR)] characterization techniques provides solid evidence for the ferroelastic behavior of CH₃NH₃PbI₃. This conclusion is supported by measurements of CH₃NH₃PbI₃ in the pristine state and under applied stress and electrical bias. Ferroelastic behavior of microscopic and nanoscopic domains was observed in both CH₃NH₃PbI₃ polycrystalline samples and single crystals as a function of the applied stress. Because grain size and grain boundaries are important factors that influence the long-term stability of OIP devices (one of the most important issues hindering their widespread adoption), the results presented here could have important implications for their practical application.

RESULTS

Akin to ferroelectricity and ferromagnetism, for which multiple orientation states can coexist in a crystal at zero electric and magnetic field, respectively, ferroelasticity occurs when spontaneous strain enables the coexistence of different orientation states in a crystal, which can be switched from one state to another by external stress (21, 22). The ferroelastic orientation state in a material is determined by its unique spontaneous strain tensor, similar to how spontaneous polarization leads to ferroelectricity. According to the available data (17), MAPbI₃ exists in three crystallographic phases: cubic ($\mathit{P}\mathit{m}\overline{3}\mathit{m}$), above 327 K; tetragonal (I4/mcm), between 327 and 162 K; and orthorhombic (Pnma), below 162 K. The cubic-tetragonal transition, which lowers the symmetry from the m3m to the 4/mmm centrosymmetric point group, is a purely ferroelastic transition according to Aizu’s classification (that is, the resulting tetragonal phase can be ferroelastic but not ferroelectric) (23, 24).

Three different types of samples were fabricated using three different established methods: two-step spin-coating with thermal annealing (samples A1 and A2) (25), and doctor blading with in situ annealing (samples B1 and B2) (26), and inverse temperature crystallization single crystal growth (sample C) (27). Spin-coating and doctor blading yielded polycrystalline films with grain sizes (areas) ranging from 0.25 to 4 μm². Sample A1 was deposited on poly[bis(4-phenyl)(2,4,6-trimethylphenyl)amine]–coated indium tin oxide (ITO) substrates, and sample A2 was spin-coated on a zinc sulfide optical prism to enable characterization with the PTIR technique. Sample B1 has a thickness of ≈600 nm and was deposited on a flexible polyethylene terephthalate substrate to study stress-induced changes of OIP ferroelastic domains. Sample B2 was deposited on a rigid ITO substrate to study the effect of the electrical bias on the domain structures. The recently developed single crystal growth method yielded a very thin single crystal with lateral dimensions of 2 mm × 5 mm and a thickness of 20 μm (sample C). Sample fabrication details can be found in Materials and Methods.

To investigate the ferroelastic properties and to demonstrate control of the ferroelastic state in MAPbI₃, we synthesized a large and thin (20 μm) single crystal (sample C) with ferroelastic domains wide enough to (i) be measured in situ with optical microscopy and (ii) enable the application of stress macroscopically. The coexistence of multiple orientation states within a crystal requires the formation of domain boundaries, for which the energetics in relation to external fields is well described by the Ginzburg-Landau formalism (28, 29). Symmetry determines which domain boundaries are permissible. The MAPbI₃ cubic-to-tetragonal transition divides a crystal into a system of tetragonal twins (ferroelastic domains) whose orientation, on average, must retain the higher symmetry of the prototypical cubic phase. The transition from the cubic $\mathit{P}\mathit{m}\overline{3}\mathit{m}$ phase to the I4/mcm tetragonal phase (m3mF4/mmm transition according to Aizu) (23) can produce six types of domain orientations (22), hereafter referred to as ZY, Z−Y, ZX, Z−X, XY, and −XY (see Fig. 1D). These domain orientations are characterized by domain walls intersecting at 0°, 90°, or 45° in the principal planes of the crystal [that is, (001), (100), and (010) families], but they may also intersect at about 70° and 110° in other planes [for example, the (110) plane].

Fig. 1. Polarized light optical images and domain configurations in a MAPbI₃ single crystal (sample C).

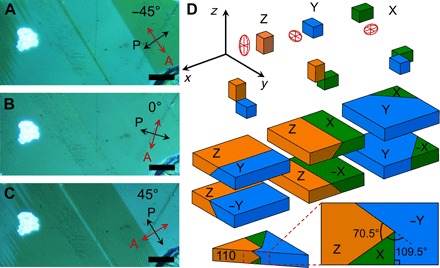
(A to C) Reflection-mode polarized optical micrographs (crossed Nicols) showing contrast reversal of domain groups as a function of sample rotation relative to the polarizer-analyzer (P-A) pair. At 0° relative angle, the domain groups are indistinguishable, and, at 45° and −45°, the domain contrast is maximum; that is, θ_e = 90°. The red and black arrows indicate the analyzer orientation and polarizer orientation, respectively. The light intensity of a bright dust particle is insensitive to the sample rotation. Scale bars, 5 μm. (D) Permissible domains of the MAPbI₃ tetrahedral phase. At the cubic-to-tetrahedral transition, the tetrahedral unit cell can form with the c axis aligned along any of the three axes (x, y, and z) of the parental cubic phase, leading to three possible configurations (X, Y, and Z). To preserve crystal integrity, the a axes of different domains must coincide (32), leading to six possible domain orientations that are characterized by domain walls intercepting at 0°, 90°, or 45° in the principal planes of the parental phase and at ≈70° and ≈110° in the (110) plane.

Polarized light optical microscopy is a simple yet effective method to study the ferroelastic materials (30). Because the refractive index is a directional property in anisotropic crystals, the intensity of light transmitted through or reflected by these crystals depends on the relative orientation of the principal optical axes with respect to the direction of the linear polarization of the incident light. Interaction with the crystal rotates the light polarization direction, which is typically detected by passing the light through an analyzer with polarization perpendicular to the polarization of the incident light. Polarized light microscopy images (Fig. 1, A to C) show domains within the large MAPbI₃ crystal. The bright domains correspond to the reflected light with the polarization plane parallel to the analyzer. Sample rotation relative to the polarizer-analyzer pair identifies the extinction angle (θ_e, the angle at which a group of domains becomes extinct). An additional sample rotation through θ_e/2° makes the domain groups indistinguishable, leaving only domain walls faintly visible (Fig. 1B). On the basis of Fig. 1, θ_e was 90°, as expected for the tetragonal phase.

Sample C was glued to a flexible substrate, which was bent upward or downward to create tensile or compressive strain in the crystal, respectively. The evolution of the domain structure in the MAPbI₃ crystal under stress, an inherent feature of ferroelastic materials, is reported in Fig. 2. We have chosen the domain group area fraction (F) with respect to the whole field of view to be a relevant descriptor of the sample behavior: $\mathit{F}=\frac{{\text{Area}}_{\text{bright}}-{\text{Area}}_{\text{dark}}}{{\text{Area}}_{\text{bright}}+{\text{Area}}_{\text{dark}}}$. Thus, F = 1 (−1) implies that the entire field of view is filled with a bright (dark) single domain, and F = 0 implies equal areas for dark and bright domains. Figure 2 shows the domain area fraction–versus–stress plot together with optical images at selected points of the stress cycle (points A to H). Although the F-versus-stress plot has a complex shape and differs from the classic strain-stress hysteresis curve [note that its relationship with strain is nontrivial (31)] (21), it represents and consolidates the rich data displayed by multiple images well (Fig. 2). Starting with an approximately equal domain population (Fig. 2A; F ≈ 0), the system evolved into a state with predominantly bright domains under tensile stress (F increases). The most important observation is that a new family of bright domains with walls tilted 70° and 109° with respect to the old domains appears in response to the application of a large tensile stress (Fig. 2B). The formation of these domains is associated with a minimum in the domain area fraction (at stress ≈ 0.5 a.u.). Consequently, the preceding F maximum (at stress = 0.3 a.u.) must arise because of minimization of the system’s energy in the wake of transition that yields the 70° domains. Releasing the stress gradually reduces the density of the new domains (reflecting a decrease in the elastic energy stored in the material) until their disappearance (Fig. 2, B to E) and yields a negative F (Fig. 2, C to F). Upon further increase in compressive stress, the system undergoes a sharp transition characterized by the complete disappearance of bright domains (Fig. 2, F and G). Beyond this point, the crystal yielded, cracking and relieving some of the strain. The nearly zero stress domain pattern reappeared (Fig. 2H), and the system became only weakly responsive to the applied stress afterward. The plot is clearly hysteretic and nonlinear, which is typical for ferroelastic materials, and indicates that the domains in sample C (i) are affected by external stress, (ii) exist at nominally zero stress, and (iii) do not return to the same state upon stress cycling, that is, revealing the hysteretic nature of material’s response to the applied stress.

Fig. 2. Evolution of the domain structure in sample C under external stress.

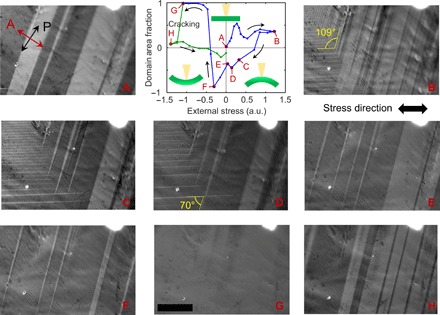
Domain area fraction (F) versus applied uniaxial stress graph and polarized light micrograph images corresponding to letter labels. Arrows indicate the sequence of the applied stress throughout the experiment. (A) to (H) Correspond to selected points on the graph. Application of tensile stress (positive) leads to shifts of domain boundaries and formation of new types of domains (tilted 70° and 109° to the old domains). A prominent nonlinearity is observed. Compressive stress eventually erases all domains and, after point G (where only one bright domain exists in the field of view), leads to fracturing (cracking) of the crystal and to a drastic change in the domain structure. Data points following cracking are marked in green. Uncertainty in the F values was estimated to be ≈0.03, taken as the largest of the uncertainties calculated from selected points in the graph (see Materials and Methods for details). Scale bars, 10 μm. The domain area fraction was calculated for a field of view larger than shown (530 μm × 710 μm). Micrographs were grayscaled. The graph insets show schematics of sample bending relative to the incident light (yellow cone). Stress in the graph is shown in arbitrary units (a.u.).

The appearance of the 70° domain walls is unusual for a tetragonal crystal. Twins in SrTiO₃ (32) and KMnF₃ (33) (I4/mcm group), for example, show only 0°, 45°, and 90° domain walls. This apparent discrepancy allows one to estimate the crystal orientation, which could not be measured directly by electron backscattered diffraction because of electron irradiation damage to the material. Although 70° domain walls are not permitted for the principal planes, they are possible for the (110) plane (see Fig. 2D). By comparing the domain schematic in Fig. 1D with Fig. 2 (B to D), we conclude that the wide bright and dark domains in Fig. 2 could be identified as Z and −Y, whereas the needle-like bright domains that grow from the left under tensile stress could be identified as X domains according to the classification introduced earlier, suggesting that the top plane of our sample should be (110). Hermes et al. (20) observed only 0° and 90° domain walls in the (110) MAPbI₃ plane, presumably because they did not strain their sample enough to induce the formation of X domains. X-ray microdiffraction measurements would be necessary to unambiguously identify the crystallographic orientation of the sample and the nature of its domains.

Next, we provide evidence of ferroelasticity and intragrain strain in perovskite thin films (with small grains) using PFM (34, 35). PFM enables detection of the electrically induced mechanical response of a sample. To avoid sample degradation, we performed the PFM measurements in a nitrogen environment. Although stripe domains were observed in both samples, sample B1 always shows higher stripe density than sample A1. Stripe domains are not observed in all grains of sample A1, and the stripe orientation differs among adjacent grains (fig. S1D). The doctor blading process was conducted at a significantly higher temperature (145°C) than spin-coating (105°C). Consequently, it is reasonable to expect that sample A1 may have smaller internal stress than sample B1, driven by the difference of the thermal expansion coefficients between the perovskite and the substrate and by the temperature difference with respect to ambient conditions. Other factors, such as film crystallization temperature and the substrate material, may also be important. Sample B1 (Fig. 3B) also shows that the orientation of two groups of stripes within a grain intersects at ≈70°, which is consistent with the domain configuration described in Fig. 1D.

Fig. 3. Observation of ferroelastic domain pattern by PFM.

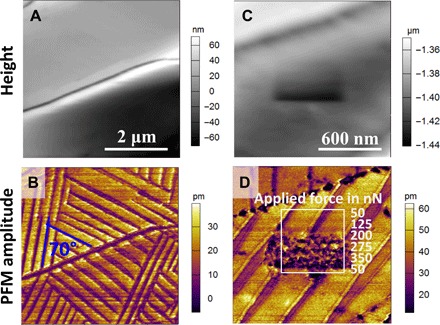
(A and B) Topography and PFM amplitude images of sample B1 (fabricated by doctor blade–coating) showing different oriented ferroelastic domains. (C and D) High-resolution topography and PFM amplitude images of sample B1 showing that the application of a localized load by the AFM tip does not change the long-range characteristics of stripes.

To examine whether the ferroelastic twin domains can be switched by external stress applied locally, we gradually increased the force exerted by the PFM tip while scanning the area enclosed by the white square in Fig. 3D. The loading force is controlled and maintained by a typical feedback loop of contact-mode atomic force microscopy (AFM). We observed that a 200-nN loading force was sufficient to damage the surface of the perovskite film, making the direct observation of ferroelastic domain switching with the force supplied locally by the PFM tip challenging. Hence, to demonstrate the stress tunability of the ferroelastic domains, we performed PFM imaging using a low loading force (<40 nN) before, during, and after application of a macroscopic stress to the OIP film by bending the film (bending radius, 2 cm). Figure 4 (A and B) shows the morphology and corresponding ferroelastic domains in the pristine state (no external stress). Under tensile stress (Fig. 4, C and D), the narrow stripes coalesced, forming wider stripes, and the dark purple domains disappeared. After relieving the stress, the domain pattern did not return to the original state and the ratio between light and dark domains changed (Fig. 4, E and F). The height images obtained before and after stressing the sample appear unaltered, except for the sharp ridges that are smoothed in the latter. In contrast to the PFM amplitude images, the PFM phase images show only very weak contrast at the ferroelastic domain boundaries (see representative phase image in fig. S2C). Strong and weak contrast in the amplitude and phase PFM images, respectively, can be considered a strong indicator that the sample may not be ferroelectric (10).

Fig. 4. PFM observation of ferroelastic domain pattern modulated by external stress.

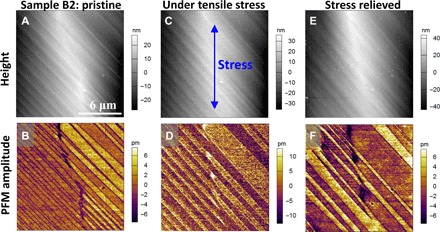
Topography and PFM amplitude images of sample B2 (fabricated by doctor blade–coating) in pristine state (A and B), under tensile stress (C and D), and after relieving the stress (E and F). The blue arrow in (C) indicates the direction of the applied stress.

To further test whether the ferroelastic domains could also display ferroelectricity, we investigated sample B2 with PFM by sweeping the applied bias with the tip at specific locations and on a larger scale by measuring PFM images under applied bias (fig. S1). However, no change of the phase signal (fig. S1A) was observed following the local sweep of the dc bias (±2.5 V). It is likely that the applied dc bias may not be sufficient to switch the polarization of the film that is hundreds of nanometers thick. Application of dc bias (±2 V) to sample A1 also did not induce any significant contrast changes in the PFM phase image (fig. S1, F to H). The local ion concentration may also be altered by the dc bias and affect the strength of the piezoresponse. Thus, no conclusion regarding the ferroelectric properties of the sample can be made on the basis of the obtained data.

To further characterize the domains at the nanoscale and investigate in situ whether they are susceptible to electrical bias, we used the PTIR technique (36, 37). PTIR is a novel method that combines the lateral resolution of AFM with the specificity of absorption spectroscopy. PTIR was initially developed in the mid-infrared (IR) (36) and has attracted much interest for enabling label-free composition mapping (38–41), material identification (42), and conformational analysis (43, 44) at the nanoscale. For example, PTIR data yielded direct evidence of MA⁺ electromigration in OIP lateral structure solar cells (39). Very recently, we extended PTIR to the visible and near-IR spectral ranges (45), an advance that has enabled the determination of the local bandgap in CH₃NH₃PbI_3−xCl_x films and estimating the local Cl⁻ content as a function of the annealing process (46). In our PTIR setup, a pulsed wavelength-tunable laser (spot size ≈30 μm) is used to illuminate the sample via total internal reflection (Fig. 5A). An AFM tip contacting the sample locally transduces the thermal expansion of the sample due to light absorption into cantilever oscillations that are monitored by the AFM four-quadrant detector. The amplitude of the cantilever oscillation (PTIR signal) is proportional to the absorbed energy (47, 48) and yields nanoscale absorption spectra (vibrational or electronic) when sweeping the laser wavelength while holding the tip at a given location. Alternatively, PTIR absorption maps are obtained by illuminating the sample at a given wavelength at a time and by plotting the PTIR signal as a function of the tip position. To enable PTIR characterization at both mid-IR and visible ranges, we fabricated a polycrystalline OIP lateral device on the surface of a zinc sulfide prism by spin-coating (sample A2; see Materials and Methods for details). Here, we show that the PTIR transduction scheme enables the visualization of ferroelastic domains, thanks to their orientation-dependent anisotropic thermal expansion coefficient.

Fig. 5. Observation of ferroelastic domains by PTIR and their insensitivity to the applied electric field.

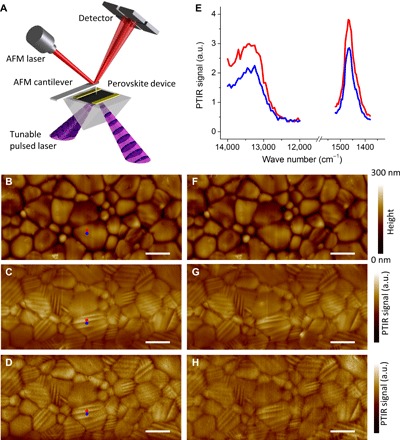
(A) Schematic illustration of the PTIR measurement. An AFM cantilever measures the thermal expansion resulting from light absorption. (B) AFM topography image of the sample A2 area between electrodes and corresponding PTIR images of (C) CH₃ asymmetric deformation of the methylammonium ion (1468 cm⁻¹) and (D) electronic transition above the bandgap (13,250 cm⁻¹ and 1.64 eV) of the as-prepared sample. (E) Representative electronic (left) and vibrational (right) absorption spectra obtained from contiguous bright (red dot) and dark (blue dot) striations visible in PTIR images. (F) Sample A2 AFM topography image and corresponding PTIR images at 1468 cm⁻¹ (G) and 13,250 cm⁻¹ (H) obtained after applying a bias of 0.86 V·μm⁻¹ for 1 min (in plane electric field). Scale bars, 2 μm.

Figure 5B shows the topography of the OIP layer in the area between the device electrodes (see fig. S3 for a larger field of view). The PTIR maps obtained by illuminating the sample at 1468 cm⁻¹ (6.81 μm), corresponding to the CH₃ asymmetric deformation of the methylammonium ion (Fig. 5C), and at 13,250 cm⁻¹ (1.64 eV, ≈755 nm; Fig. 5D), corresponding to electronic excitation just above the bandgap, show stripe domains on most grains. The width of the domains ranges from 100 to 225 nm. In previous work (49), we indentified one grain in a MAPbI₃ film showing similar striations, which were tentatively related to the beginning of the perovskite decomposition process during high-temperature annealing. Here, we argue that these striations should be ascribed to the presence of ferroelastic domains instead. Figure 5E shows representative PTIR spectra measured from two adjacent striations. Previously, Chae et al. (46) showed that local bandgap value in CH₃NH₃PbI_3−xCl_x correlates with the Cl⁻ content (x) and decreases upon annealing. By linearly fitting the electronic spectra absorption profile, we derive an optical bandgap of 1.57 ± 0.10 eV, suggesting a negligible Cl⁻ content (that is, x ≈ 0). Throughout the manuscript, the uncertainty of the bandgap represents a single SD in the linear fitting of the PTIR absorption spectra. The PTIR spectra of contiguous domains share the same spectral characteristics; that is, the spectra differ only in intensity (not in peak position or optical bandgap), suggesting that the spectral differences arise from structural factors, such as crystal orientation or crystal anisotropy, rather than from composition variations. Typically, the intensity of vibrational excitations in crystals depends on the relative orientation between linearly polarized incident light and the crystal dipole moment. However, polarization-dependent PTIR maps (fig. S4) show that the striation patterns and their relative intensities for all crystals are the same with both s-polarization (in the sample plane) and p-polarization (polarization components in and out of the sample plane) excitation. This is not surprising because the MA⁺ exhibits fast rotational dynamics within the perovskite inorganic framework (50). Because the sample thermal expansion coefficient in the vertical direction modulates the PTIR signal amplitude (38, 48), the differences in the PTIR intensity are attributed to the differences in the local thermal expansion coefficient (α), which, in MAPbI₃, is larger along the a axis (α_a = 1.32 × 10⁻⁴ m/(m·K)) than along the c axis (α_c = −1.06 × 10⁻⁴ m/(m·K)) (51). The observation of the same striation patterns in the PTIR images corresponding to both vibrational absorption (Fig. 5C) and electronic absorption (Fig. 5D) further supports this interpretation. In other words, the striations result from differences in thermomechanical transduction rather than from optical absorption (that is, composition variations). Because the ferroelastic twinning that takes place during the cubic-tetragonal phase transition occurs independently in each grain, the ferroelsatic domain patterns (striations) are unique to each grain.

Hermes et al. (20) provided evidence of ferroelastic domains in MAPbI₃ but did not show concomitant ferroelectricity. However, the authors argued that the absence of polarization switching under a tip-applied bias in their samples was not sufficient to definitely exclude ferroelectricity because the vertically applied field may not be effective in switching domains with in-plane polarization components (20). To test that possibility, the lateral device structure in sample A2 was leveraged to apply an electric field (up to 1 V·μm⁻¹) in the sample plane. The AFM topography images (Fig. 5F) and the PTIR maps (Fig. 5, G and H) obtained after applying a lateral electric field of 0.86 V·μm⁻¹ for 1 min do not show any differences with respect to the topographic and PTIR images of the same area obtained before electrical poling (Fig. 5, B to D). In summary, we do not observe evidence of electrical polarization switching of the domain structure in all our tests. No change in topography and in the PTIR maps was observed with an applied electric field of up to 1 V·μm⁻¹.

DISCUSSION

In conclusion, different nanoscale and microscopic techniques provide solid evidence of ferroelasticity in both MAPbI₃ polycrystalline films and single crystals that were obtained using different fabrication methods. No evidence of concomitant ferroelectricity was observed for the experimental conditions and materials studied here. We show that the configuration of MAPbI₃ ferroelastic domains in OIPs can be controlled with applied stress, and we propose strain engineering as a new lever to control the optoelectronic properties of OIP devices. Because poor long-term stability is an obstacle for the deployment of OIP devices on a large scale and because grain boundaries are an important factor in determining the stability of these devices, our results could have considerable implications for their practical application. OIP grain sizes are typically determined on the basis of scanning electron microscopy or AFM topographic images, which may or may not reflect the internal grain structure appropriately. In addition, an increasing number of observations suggest that OIP with nominally identical composition may display significantly different thermal or chemical stability; thus, it will be important to understand whether differences in the grain structure are related to grain stability. It is possible that the single crystals and polycrystalline films reported in the literature may consist of ferroelastic twin domains. We believe that our observations will foster studies aimed at determining the role of ferroelastic domains and strain engineering to improve the OIP chemical and thermal stability and photovoltaic performance.

MATERIALS AND METHODS

Sample preparation

Two-step spin-coating of perovskite polycrystalline films

Sample A1 was fabricated using the procedure described in our previous work (25). Sample A2 was prepared by a multicycle spin-coating process described in our previous work (52).

Doctor blade–coating of perovskite polycrystalline films

Films were fabricated using a modification of the procedure used in our previous work (26). The perovskite precursor solution (MAPbI₃/dimethyl sulfoxide; 1 M) was doctor blade–coated on an ultraviolet ozone–treated ITO substrate at room temperature and heated at 145°C in a semienclosed chamber for 5 min, yielding a crystalline perovskite film. Subsequently, the film was annealed in situ at 100°C for 30 min to remove the solvent. The single crystal was grown by using inverse temperature crystallization (27).

Polarized-light optical microscopy

These measurements were performed in reflection mode in the crossed Nicols configuration on a commercially available microscope. For the stress measurements, a MAPbI₃ crystal (about 2 mm × 5 mm × 20 μm in size) was attached to a stainless steel plate (17.2 mm × 12.5 mm × 0.22 mm) using polyimide adhesive tape. The plate was placed between the jaws of a miniature vice in a glove bag under the microscope. The generated stress was proportional to the plate buckling. The domain fraction F was calculated as $\mathit{F}=\frac{{\text{Area}}_{\text{bright}}-{\text{Area}}_{\text{dark}}}{{\text{Area}}_{\text{bright}}+{\text{Area}}_{\text{dark}}}$. Uncertainty in F was calculated as the ratio of the sum of uncertainties of each domain boundary (domain boundary area) to the total area of the image for a few representative points (A, 0.016; E, 0.020; F, 0.018) and the last two points on the graph close to zero stress (0.030 and 0.029).

PFM measurements

A commercial AFM was used to perform the PFM measurements. The MAPbI₃ films were characterized in a small closed cell with continuous dry nitrogen flow to prevent film degradation. The films were grounded through the ITO layer. An ac bias with an amplitude of 1 V was applied to the film via a Pt/Ir-coated Si tip. A resonance enhancement mode (dual ac resonance tracking) was used to amplify the piezoresponse signal (53). The typical drive frequency was in the range of 320 to 360 kHz, depending on the contact resonant frequency. The typical loading force for PFM scan was in the range of 20 to 40 nN, which did not damage the film surface during the PFM imaging.

To measure the piezoresponse on the MAPbI₃ film that was macroscopically deformed, we fixed the film along with the flexible substrate on a customized rigid plastic bridge with a radius of curvature of 20 mm using double-sided tape. The central region of the MAPbI₃ film where the maximum tensile stress occurs was studied using PFM. The same location was traced and scanned before, during, and after the stress application.

The switching spectroscopy PFM technique was used to acquire the hysteresis loops from the MAPbI₃ film. A typical triangle-square dc wave with ac bias was applied (54). The off-state data (that is, when dc bias = 0) were used to plot the hysteresis loops. The amplitude loop reveals the strain hysteresis, whereas the phase loop demonstrates the polarization switching process if it exits.

PTIR characterization

PTIR experiments were carried out in nitrogen atmosphere using a modified commercial PTIR setup that consists of an AFM microscope operating in contact mode and three tunable pulsed laser sources (lasers A, B, and C), which have been described previously (40, 45). Two of the three laser sources (lasers A and C) were used in this work. Laser A consists of a Q-switched diode-pumped Nd:YAG (yttrium-aluminum-garnet) laser (1064 nm), one optical parametric oscillator (OPO) based on a periodically poled lithium niobate crystal, and a second OPO based on a noncritically phase-matched ZnGeP₂ (ZGP) crystal. Laser A emits 10-ns pulses that are tunable from 4000 to ≈1025 cm⁻¹ (from 2.5 to 9.76 μm) at a repetition rate of 1 kHz and with linewidths between 5 and 16 cm⁻¹, depending on the wavelength. Laser C consists of a nanosecond Q-switched diode-pumped Nd:YAG pump laser and an OPO based on a beta barium borate nonlinear crystal integrated into a single enclosure. Laser C emits 10-ns pulses with <1-nm linewidth at a repetition rate of 1 kHz in the range from 400 to 2300 nm. The low repetition rate of the laser ensured that a new pulse would excite a sample and cantilever after they had returned to equilibrium. The typical laser spot size was ≈30 μm at the sample. PTIR experiments were obtained by flowing nitrogen gas (0.12 dm³·s⁻¹) in custom enclosure built around the sample.

MAPbI₃ samples for PTIR analysis were fabricated according to the procedure described above directly on a zinc sulfide right-angle prism with Au electrodes fabricated by photolithography and lift-off technique using a custom spinner adaptor. A voltage source unit was used for electrical poling sample A2 by applying a maximum of 7 V between two Au electrodes (spaced by 7 μm).

PTIR spectra were obtained by averaging the cantilever deflection amplitude from 256 individual laser pulses at each wavelength and tuning the laser at intervals of 4 and 50 cm⁻¹ for lasers A and C, respectively. PTIR images were recorded by illuminating the sample with a constant wavelength while scanning the AFM tip. The AFM height and the PTIR signal acquisition were synchronized so that, for each AFM pixel, the PTIR signal was an average over 32 laser pulses. The pixel sizes were 20 nm × 20 nm for Fig. 5 and 50 nm × 50 nm for all images in the Supplementary Materials. Commercially available 450-μm-long silicon contact-mode AFM probes with a nominal spring constant between 0.07 and 0.4 N/m were used.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/4/e1602165/DC1

fig. S1. PFM measurements on sample A1 do not show evidence of ferroelectric behavior.

fig. S2. Representative PFM images showing strong amplitude contrast and very weak phase contrast.

fig. S3. Observation of ferroelastic domains by PTIR.

fig. S4. Observation of ferroelastic domains by PTIR with s- and p-polarization.