We report a current-induced, persistent, long-lived, and rewritable electron spin polarization in a 3D topological insulator.
Keywords: Topological insulators, topological surface states, spintronics, spin polarization, spin life time, nuclear spin
Abstract
Topological insulators (TIs), with their helically spin-momentum–locked topological surface states (TSSs), are considered promising for spintronics applications. Several recent experiments in TIs have demonstrated a current-induced electronic spin polarization that may be used for all-electrical spin generation and injection. We report spin potentiometric measurements in TIs that have revealed a long-lived persistent electron spin polarization even at zero current. Unaffected by a small bias current and persisting for several days at low temperature, the spin polarization can be induced and reversed by a large “writing” current applied for an extended time. Although the exact mechanism responsible for the observed long-lived persistent spin polarization remains to be better understood, we speculate on possible roles played by nuclear spins hyperfine-coupled to TSS electrons and dynamically polarized by the spin-helical writing current. Such an electrically controlled persistent spin polarization with unprecedented long lifetime could enable a rechargeable spin battery and rewritable spin memory for potential applications in spintronics and quantum information.
INTRODUCTION
With an increased interest in spin logic devices compatible with the existing semiconductor technology, manipulating electron spins in nonmagnetic semiconductors has been one of the most active research directions in spintronics (1), promising smaller, faster, less power-consuming information-processing and communication devices. However, several technical challenges have to be overcome in semiconductor spintronics, such as efficient spin injection, long spin lifetime, and efficient spin transport, manipulation, and detection (2, 3). A particularly important goal is to generate a controllable electronic spin polarization that can have a long lifetime, using all-electric approaches that are free from magnetic materials (1–3).
Three-dimensional (3D) topological insulators (TIs) represent a new class of electronic quantum phases with strong spin-orbit coupling, hosting spin-helical topological surface states (TSSs) protected by time-reversal symmetry (4–6). One of the most fundamental and marked properties of TSS is spin-momentum locking (SML), where the electron spin is “locked” in plane and perpendicular to its momentum, making 3D TIs highly promising for applications in nanoelectronics and spintronics (4, 6). Several recent experiments in 3D TIs have demonstrated current-induced helical spin polarization attributed to the SML (7–14). The observed spin polarization reverses upon reversing the current, requires a DC current to maintain it, and vanishes as soon as the current is removed. However, for many applications, a persistent and long-lived spin polarization (sometimes referred to as a spin “battery” or memory) may be desired.
Here, we report spin potentiometric measurements in Bi2Te2Se (BTS221) TI thin flakes that have revealed a new phenomenon not observed previously in TIs: a current-induced persistent electron spin polarization (ESP). A voltage between a ferromagnetic (FM) and one of the nonmagnetic contacts is monitored as a function of an in-plane magnetic (B) field (Fig. 1A) applied to magnetize the FM contact (fig. S1). We observe a hysteretic step-like voltage change when the B field is swept between the opposite directions, resulting in a clear difference in the voltage detected between the opposite FM magnetizations. Such a voltage difference (δV) measured by spin potentiometry is a measure of spin chemical potential (μ↑ − μ↓ = −eδV, where −e is the electron charge), representing an out-of-equilibrium ESP. However, in stark contrast to previous experiments, such a spin signal (δV)—both its sign and amplitude—shows little dependence on the sign and magnitude of a relatively small DC detection current (Id). The Id-independent spin signal is observed to persist for many hours even without any bias current. A marked “writing” effect on the spin signal is also realized by applying a large DC “writing current” (Iw) for an extended time at zero magnetic field that can reverse the persistent spin signal depending on the direction of Iw (analogous to “charging” a battery and setting its polarity). Although exact mechanisms giving rise to the observed long-lived persistent ESP are not yet clear at this point, we speculate on a possible scenario where nuclear spins—coupled with spin-momentum–locked TSS electrons via hyperfine interaction—can be dynamically polarized by a (sufficiently large) helical spin-polarized current carried by TSS electrons and, in turn, act back on the TSS electron spins to give the observed persistent, out-of-equilibrium ESP.
Fig. 1. Detection of current (Id)–independent spin signal in a Bi2Te2Se (BTS221) thin flake by spin potentiometry.
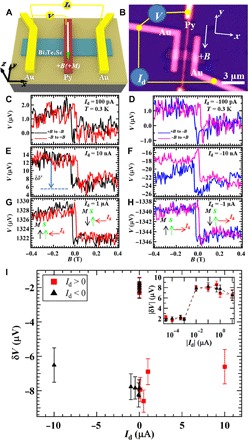
(A) Schematic 3D device structure used in the potentiometric measurement, showing a three-terminal electrical connection. The TI surface defines the x-y plane, and the surface normal defines the z direction. The two outside nonmagnetic (for example, Au) contacts (the left is grounded) are used to inject a DC bias current, and the middle FM (for example, Py) contact is magnetized by an in-plane magnetic B field (labeled) along its easy axis (y direction, with −y defining the positive B and M direction). The middle FM contact is a tunneling probe (with a thin Al2O3 tunnel barrier underneath in our devices). (B) Optical image of device A used in the potentiometric measurement. (C to H) Voltage measured by the FM spin detector (Py) on device A as a function of in-plane magnetic field for representative bias currents (Id) of 100 pA (C), −100 pA (D), 10 nA (E), −10 nA (F), 1 μA (G), and −1 μA (H). The directions of Id (red arrow), the inferred channel (top surface) spin polarization S (dashed green arrow), and Py magnetization M (black arrow) are labeled in (G) and (H). (I) The voltage change δV = V+M − V−M [marked by the arrow in (E) and defined as the spin signal indicating the presence of channel spin polarization] as a function of the applied DC bias current. Here, δV is extracted from forward sweep traces (backward sweeps yield similar results). All the measurements were performed at the temperature T = 0.3 K.
RESULTS
We performed the spin potentiometric measurements (schematically illustrated in Fig. 1A) on exfoliated BTS221 thin flakes placed on top of SiO2/Si substrates (Fig. 1B). We usually apply a small (detection) current (Id) between the two “outside” Au contacts and monitor the voltage (V) between an Au contact and a middle FM [permalloy (Py)] contact, as an in-plane B field is applied to magnetize the Py contact (Fig. 1A and fig. S1). The representative results (Fig. 1, C to H, and fig. S2) of a three-terminal spin device [Fig. 1, A and B; a similar setup to what we previously used on other samples to demonstrate a current-induced spin polarization (14)] are measured on a 10-nm-thick flake (device A; Fig. 1B) at T = 0.3 K, with moderate bias current (Id) ranging from 100 pA to 1 μA [positive current (left) and negative current (right)]. As we sweep an in-plane magnetic B field between the ±y directions (orthogonal to the current direction; note that we define positive B field to be along the −y direction) to switch the magnetization (M) of the Py detector, the voltage (V) it measures shows a clear hysteretic step-like switching behavior, exhibiting a low (high) voltage state when the Py detector is magnetized to the −y (y) direction. It is interesting to note that the same trend of the step-like voltage change is observed regardless of the polarity of Id. This is qualitatively different from previous spin potentiometry measurements where the trend of the step-like change reverses upon reversing Id that indicates a current (Id)–induced spin polarization due to SML (7, 14). We quantitatively define the spin signal as follows: δV = V+M − V−M (labeled in Fig. 1E), reflecting the step-like voltage change near the coercive field. The δV versus Id is plotted in Fig. 1I, showing a very weak Id dependence where δV stays around a few negative microvolts even when Id is varied over four orders of magnitude [inset of Fig. 1I, and figs. S2 and S3; the notable increase of |δV| between |Id| = 10 and 100 nA in Fig. 1I is more specific to this device and not commonly observed in other devices (for example, fig. S3)]. The above Id-independent spin signal is again in contrast to previous measurements (7, 11, 14), where the spin signal (δV) is found to be approximately proportional to Id. The direction of the channel (top surface of our sample) spin polarization S can be determined from the sign of δV in our spin potentiometric measurements, based on the fact that an FM contact with magnetization M primarily probes the channel spins oriented along the same direction as the FM majority spins (oriented antiparallel to M) and thus will measure a lower voltage (higher electron chemical potential) if S is antiparallel to M (14–16). The determined directions of S (labeled in the insets of Fig. 1, G and H) are the same for both the positive and negative Id. Our observations suggest that the electronic spin polarization revealed by spin potentiometry in this sample is not induced or controlled by the current (Id) we applied in these measurements but rather arise from a different origin that is intrinsic to the sample or setup before these measurements.
We further found that the sign of δV in our device can be (re)set by applying a relatively large DC bias current for an extended time (referred to as a writing current, Iw, to distinguish from the relatively small Id in Fig. 1 that does not affect δV). In this experiment, we usually apply a large Iw between the two outside Au contacts in a four-terminal device (Fig. 2A) for an extended time at zero B field, and then the spin signal is measured by spin potentiometry (Fig. 2B; the four-terminal configuration is found to give a similar spin potentiometry signal as measured in three-terminal configurations) with a small Id. Figure 2 (C to H) shows the results measured on a 25-nm-thick BTS221 flake (device B) at T = 1.6 K. After applying a Iw = −40 μA for 2 hours, spin potentiometric measurements (Fig. 2B) were performed with Id = ±0.5 μA (shown in Fig. 2, C and D). We observe a similar step-like voltage change as that in Fig. 1, with a negative δV, for both the positive and negative Id, indicating the presence of a channel spin polarization whose direction is independent of Id. We then apply a large positive Iw = 50 μA for 0.5 hours. Afterward, spin potentiometry was performed (Fig. 2, E and F) with Id = ±0.5 μA, and the sign of the spin signal (δV) is reversed to positive, which is opposite to that in Fig. 2 (C and D) (after Iw = −40 μA), indicating that the direction of the spin polarization S has now been reversed after the application of a reversed Iw (but still independent of Id). Remarkably, the sign of δV can be reversed again and back to the case in Fig. 2 (C and D) after applying a negative Iw = −40 μA for 3 hours, as shown in Fig. 2 (G and H). Similar effects are also observed when Iw is applied during sample cooling (fig. S4) or at a higher temperature (~26 K; fig. S5). We clearly see that the sign of the spin signal and the direction of the channel spin polarization S are determined by Iw (reversing Iw reverses S) but are independent of Id (as long as Id is small enough). We find that the spin signal δV also increases with the increasing writing current Iw (fig. S6) and writing time (fig. S7). Such a current (Iw)–induced writing effect (where the induced spin polarization persists even after Iw is turned off) of spin polarization has not been previously observed in 3D TIs. We further note that the direction of S is consistent with that of the TSS spin polarization induced by Iw (see arrows indicating the directions of S and Iw in Fig. 2, C to H) according to the helicity of SML of the TSS (7, 11, 14).
Fig. 2. Writing current effect on the spin signal.
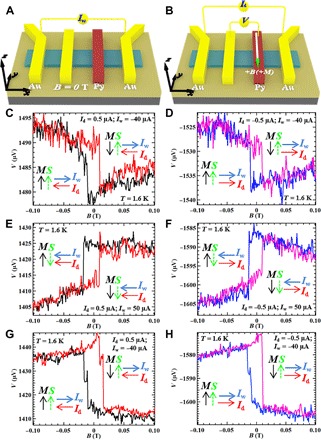
(A and B) Schematic four-terminal device structures and measurement setups for writing current and spin potentiometry. (C to H) Voltage detected by the FM contact as a function of in-plane magnetic field measured on device B at the relatively small Id of 0.5 μA (C, E, and G) and −0.5 μA (D, F, and H) after applying a large Iw of −40 μA for 2 hours (C and D), 50 μA for 0.5 hours (E and F), and −40 μA for 3 hours (G and H). The trend of the B field–induced voltage change, which measures the direction of the channel spin polarization, is independent of the relatively small Id but is set by the direction of the large Iw (applied at B = 0 T and before the spin potentiometric measurement). The directions of Id, Iw, channel spin polarization S as determined by the spin signal, and Py magnetization M are labeled by the corresponding arrows. All the measurements are performed at T = 1.6 K.
Figure 3 shows spin potentiometric measurements at T = 1.6 K in another device (“C”; a 30-nm-thick BTS221 flake, with a four-terminal configuration shown in Fig. 2, A and B) at a series of DC bias currents Id increasing from relatively small to very large values (±80 μA), where we found the spin signal transitions from being largely Id-independent to linearly dependent on Id. At a small Id = ±0.01 μA, the spin signal δV is about −0.5 μV for both the positive and negative currents (Fig. 3, A and B), and the trend of the signal is qualitatively similar to those presented in Fig. 1, suggesting a channel spin polarization S along the +y direction and independent of Id. In contrast, at a large Id such as ±80 μA (Fig. 3, I and J), a qualitatively different behavior is observed. Upon reversing Id, the step-like change in the measured spin potential now reverses its trend, and spin signal δV reverses its sign (δV ~1.8 μV for Id = 80 μA and δV ~−2 μV for Id = −80 μA). Such a behavior that δV reverses upon reversing Id is more similar to that studied in previous spin potentiometric measurements on TIs, indicating an Id-induced and reversible helical spin polarization (7, 11, 14). As labeled by the arrows in Fig. 3 (I and J), the direction of S is locked to such a large Id in a way that is consistent with the spin helicity of TSS. At intermediate positive currents (Fig. 3, C and E), the voltage signal exhibits a “transitional” behavior, where the trend of the step-like change undergoes reversals (sometimes even during measurements taken at the same Id; see some examples marked by the brown arrows in Fig. 3, C and E). The dependence of the spin signal δV on Id is summarized in Fig. 3K, where two distinct behaviors are observed: (i) at |Id| < 5 μA, δV is always negative and relatively constant, about −0.5 μV, independent of both the polarity and amplitude of Id; (ii) at |Id| > 10 μA, δV reverses its sign with reversing Id and is largely linearly dependent on Id.
Fig. 3. Spin signal transitioning from being largely independent on the bias current (Id) to linearly dependent on Id when Id increases.
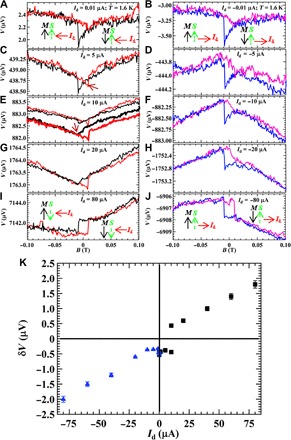
(A to J) The voltage detected by the FM contact as a function of in-plane magnetic field measured on device C for representative bias currents (Id) of 0.01 μA (A), −0.01 μA (B), 5 μA (C), −5 μA (D), 10 μA (E), −10 μA (F), 20 μA (G), −20 μA (H), 80 μA (I), and −80 μA (J). The upper and lower sets of traces in (E) show two repeated sets of measurements. The directions of the bias current Id, channel spin polarization S as determined by the spin signal, and Py magnetization M are labeled by the corresponding arrows in (A), (B), (I), and (J). (K) The spin signal δV as a function of the bias current Id. All measurements were performed with a four-terminal configuration at T = 1.6 K.
Figure 4 shows various studies of the dependences of the Id-independent spin signal (in the small Id region) on the out-of-plane component of the B field, gate voltage, and temperature. Figure 4A shows the voltage V measured on device A as a function of B field titled away from the surface at various different angles θ (depicted in the inset of Fig. 4A). We see that the coercive field (BC; labeled in Fig. 4A) increases as θ increases, whereas the in-plane component of the coercive field (BC·cosθ) and the measured spin signal δV are independent of θ, as summarized in Fig. 4B. Our results demonstrate that the spin signal δV is independent on the out-of-plane component of the magnetic field and also suggest the absence of the Hanle effect in our TI system. It is known that the Fermi level of a bulk-insulating TI sample can be tuned by gating. Figure 4C shows the spin potentiometric measurements at Id = ±1 μA on device D (a 17-nm-thick flake) at different back-gate voltages. The extracted spin signals δV and the corresponding voltage V0 (measured separately at B = 0 T) as functions of the back-gate voltage Vg are presented in Fig. 4D. When Vg is tuned from 50 to −170 V, V0 measured at Id = 1 μA exhibits an on-off ratio of ~2, and the spin signal δV is significantly enhanced as the Fermi level is tuned closer to the charge neutrality point of TSS at a negative Vg (Fig. 4, C and D). We further found that the detected Id-independent spin signal δV measured on device E (a ~20-nm-thick flake) decreases with increasing temperature T and is observable up to ~76 K (Fig. 4E and fig. S8).
Fig. 4. Dependences of the spin signal on out-of-plane B field component, gate voltage, and temperature.
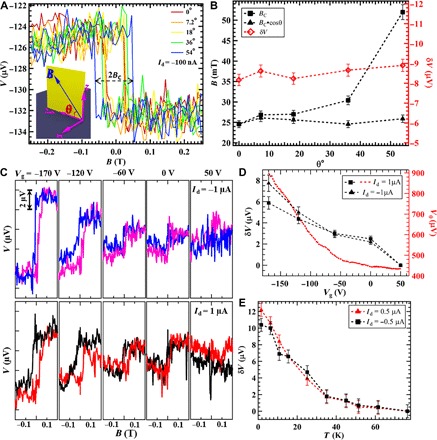
(A and B) Effect of perpendicular (out-of-plane) magnetic field on spin signals. In this experiment, the magnetic B field was tilted away from the sample (device A) surface plane (x-y) by an angle θ [depicted in the inset in (A)]. Data are measured at Id = −100 nA and T = 0.3 K. (A) Magnetic field dependence of the voltage at different angles. (B) The coercive field Bc [marked in (A) for the θ = 54° (trace)], Bc·cosθ (in-plane component of Bc), and spin signal δV as functions of θ. (C and D) Gate dependence of the spin signal measured on device D. (C) The measured voltage V as a function of the in-plane magnetic field measured at T = 1.6 K and Id = −1 μA (top) and 1 μA (bottom) at various back-gate voltages Vg. (D) The extracted spin signal δV (left axis; black symbols) and the voltage V0 (right axis; red dashed line; measured at B = 0 T before performing the spin potentiometry) as a function of Vg. The measurements were performed at T = 1.6 K. (E) Temperature T dependence of the measured spin signal from device E up to 76 K. Devices D and E have a four-terminal configuration (Fig. 2B)
The largely Id-independent spin signal at small Id suggests that it can be observed even with no Id applied. Figure 5A shows the open-circuit voltage measured at T = 1.6 K in device F [a 15-nm-thick flake, with a four-terminal configuration, but only the inner two contacts connected to the voltmeter (inset of Fig. 5C) and the two outer current leads disconnected after measuring an Id-independent spin voltage signal similar to Fig. 1]. The open-circuit voltage exhibits a hysteretic step-like change between the opposite directions of M with δV ~1.3 μV, indicating the presence of a channel spin polarization S even in the absence of any detection current Id. Remarkably, we found that the spin signal is still observable after waiting for t = 45 hours but with a reduced δV (~0.6 μV), as shown in Fig. 5B. The dependence of the spin signal δV on the elapsed time (t) is shown in Fig. 5C, where δV decreases from 1.3 to ~0.5 μV in the first 2 to 3 hours and then stabilizes at ~0.6 μV in the remaining time, suggesting that the channel spin polarization persists for more than 45 hours. We also measured the open-circuit spin signal at an elevated T = 45 K, as shown in Fig. 5 (D to F). At t = 0 hour, a spin signal δV ~0.11 μV can still be observed (Fig. 5D). However, it is no longer detectable after 10 hours (Fig. 5E), indicating that the channel spin polarization has disappeared. The time dependence of the δV shown in Fig. 5F also indicates that δV decays more rapidly with time at T = 45 K compared to that at T = 1.6 K (Fig. 5C).
Fig. 5. Persistent spin signal and its time dependence.
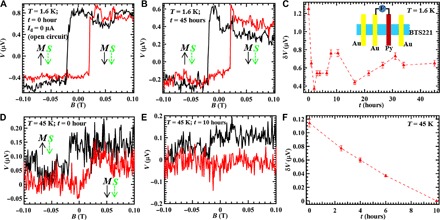
(A) Open-circuit voltage detected by the FM contact as a function of the in-plane magnetic B field measured on device F with the source-drain electrical connection open, showing a spin signal δV ~1.3 μV. (B) Open-circuit voltage versus B measured after t = 45 hours. (C) Spin signal δV versus elapsed time t, where δV gradually decreases to ~0.5 μV in the first 3 hours and stays around ~0.6 μV in the next 42 hours. The measurements in (A) to (C) were performed at T = 1.6 K. Inset shows the schematic of the open-circuit measurement in device F. (D) Open-circuit voltage versus B measured at T = 45 K. (E) Open-circuit voltage versus B measured at T = 45 K after t = 10 hours. (F) δV versus t measured at T = 45 K. The directions of Py magnetization M (black arrow) and the inferred channel (top surface) spin polarization S (dashed green arrow) are labeled in (A), (B), and (D).
DISCUSSION
In our study, we have observed a long-lived persistent out-of-equilibrium spin polarization in the TSS conduction electrons even without any bias current. At low temperature, such an electronic spin polarization can persist for at least ~2 days, which is several orders of magnitude higher than the typical lifetime of electron spins [typically shorter than 1 μs (1–3, 17), in rare cases reaching ~1 ms (17)] when directly injected optically (18) or electrically (19) into semiconductors (17). Thus far, nuclear spins are the only known entities that can give an extraordinary long lifetime (capable of reaching many hours or longer, which is close to what we observed) of injected spin polarizations, reflecting the fact that nuclear spins are usually better isolated with much longer relaxation time (in some cases reaching >1 day; Fig. 6 and table S1). Previous studies have also shown that it is possible to extend the electron spin lifetime (reaching thousands of seconds) by coupling to nuclear spins through the hyperfine interaction (20–23). We have compared our measured spin polarization lifetime with previously reported spin relaxation time (T1) of nuclear spin polarizations (NSPs) in a variety of systems (24–41), as shown in Fig. 6 (the same data are also shown in table S1). It is notable that our achieved spin lifetime (>45 hours, even at zero magnetic field) exceeds (by 50% or more) the longest lifetime (~30 hours in B = 5 T) in these previous measurements and is orders of magnitude longer than those lifetimes (where the longest was <1 min) previously measured at zero B field.
Fig. 6. Comparison of the spin polarization lifetime that we measured with the lifetime of the NSP reported in different systems from previous literature.
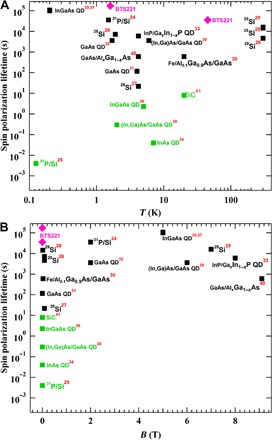
(A) Spin polarization lifetime as a function of temperature and (B) spin polarization lifetime as a function of magnetic B field. The red superscripts refer to the corresponding references. Previous data measured at B = 0 T are highlighted in green. QD, quantum dot.
It is known that the nuclear spins can be dynamically polarized by spin-polarized electrons through hyperfine interaction (42, 43). Although we do not have direct measurements or evidence of NSP in our experiment, we speculate that nuclear spins (near the surface) hyperfine-coupled to TSS electrons and dynamically polarized by the spin-helical writing current (Fig. 7) may have played important roles and may be part of a possible explanation to our observation (see more detailed discussions in the Supplementary Materials). In our experiment, a large Iw can create an out-of-equilibrium spin polarization in the TSS conduction electrons due to the SML, resulting in a large chemical potential difference (44) between the spin-up and spin-down electrons (for example, Fig. 7, A and B). An electron from the more occupied “majority” spin state that flips its spin and transfers to the less occupied “minority” spin state will induce an opposite nuclear spin flop (Fig. 7A) owing to the hyperfine interaction (without which a full spin reversal of a TSS electron would not be allowed by time-reversal symmetry) (45). Such a hyperfine interaction–enabled electron-nucleus spin flip-flop process results in a dynamic NSP by a current-induced ESP (Fig. 7A). Reversing Iw reverses not only the direction of the TSS ESP via SML but also the induced NSP, as shown in Fig. 7B. We further speculate that the polarized nuclear spins could act back again on the TSS electron spins through the hyperfine interaction and polarize the electron spins, giving rise to a spin potential difference (δV) in electrons (shown in Fig. 7, C and D) measured by spin potentiometry (44).
Fig. 7. Schematics depicting a proposed mechanism of spin polarization transfer between the electrons and nuclei via the spin flip-flop process due to the hyperfine interaction.
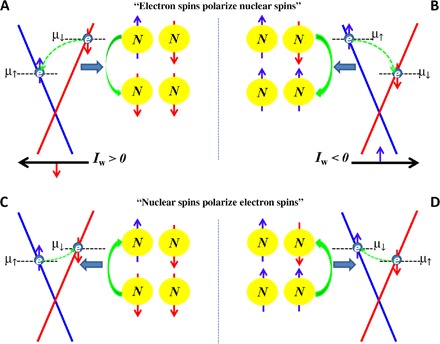
(A and B) Current-induced NSP: A large writing current Iw (A) induces (via SML of TSS) an ESP, which dynamically polarizes nuclear spins by the hyperfine interaction–enabled electron-nuclear spin flip-flop process. Reversing Iw (B) can reverse the NSP due to the reversed TSS ESP. (C and D) An existing NSP induces an ESP through hyperfine interaction–enabled spin flip-flop process, depicted as spin-down (C) and spin-up (D) polarized cases. Because of the long lifetime of nuclear spins, the induced ESP (and the measured spin signal) can persist for a long time (even in the absence of any driving current) but can be reversed by a large Iw (A and B) that reverses the nuclear spins.
If the nonequilibrium persistent ESP in our 3D TI samples is indeed maintained by a background NSP as we hypothesized, our observations suggest that both the ESP and NSP in our system are highly persistent and robust (with long lifetime, lack of Hanle effect, among others), possibly coupled (or even effectively locked) to each other in a way that helps stabilize each other (significantly reducing the relaxation rate to give long lifetime) and providing each other with an internal field that far exceeds the external magnetic field. An interesting question calling for further studies would be to investigate whether the spin-helical nature of the TI surface state electrons (with only one spin state at each momentum and thus only half the Fermi surface of the conventional 2D electrons) may bring novel physics and behavior in the coupling with nuclear spins and relaxation of NSP/ESP differently from what are known in conventional metals (46) and semiconductors. In addition, compared with previously studied coupled nuclear-electron spin systems, we speculate that several possible factors in our TI samples might contribute to a highly suppressed nuclear spin relaxation: (i) The 3D TI samples are bulk insulating with few bulk charge carriers at low temperatures, thus largely avoiding what would be an important channel of NSP relaxation (via bulk carriers) in conventional metals and doped semiconductors. (ii) The TSS ESP is concentrated at the surface; this gives rise to a gradient in an effective magnetic field (Knight field due to the ESP) from the surface to the bulk. It has been shown that the spin diffusion could be suppressed in a magnetic field gradient (47). The decrease of the persistent spin signal with increasing temperature in our experiments could arise from a combination of several materials and technical issues: (i) Our BTS221 sample is bulk insulating only at relatively low temperatures. As temperature rises, there will be an increasing amount of thermally activated conducting carriers in the bulk (no longer insulating) that can provide an extra channel to relax nuclear spins. (ii) The spin potentiometric measurement itself can also become less efficient at higher T because of the increased bulk conduction (loading the surface state spin signal) as well as possible degradation of the Al2O3 tunneling barrier at higher T.
Several recent experiments [including our previous study (14)] performing spin potentiometric measurements (7, 9, 14) in TIs have observed a linearly Id-dependent spin potential signal indicating current-induced (electron) spin polarization, but have not observed an Id-independent (or open-circuit, persistent) spin signal and a writing current (Iw) effect, as reported in this work. It is possible that the NSP in the samples studied in those previous experiments (7, 9–14) may not have been sufficiently developed to have notable effects on the ESP. We note that differences in the measurement procedure and history (such as the magnitude and duration of the applied current) can have strong influences on the results (for example, figs. S5 to S7). For example, in cases such as Fig. 1 (where we did not intentionally apply a large writing current), the persistent spin signal is found to develop after performing many measurements (before those in Fig. 1) with a relatively small current but over an extended time (which may have slowly polarized the nuclear spins). Although all the details and factors affecting the NSP remain to be better understood, we note that the samples used in this work, where we have observed Id-independent persistent spin signal (and at larger current a transition to Id-dependent spin signal), are also much smaller (less than a few micrometers in size) than those used in previous studies (7, 11, 14) [tens or hundreds of micrometers in size, even though our previous measurement (14) used BTS221 flakes exfoliated from the same bulk crystal as in our current work]. We speculate that in smaller-sized samples, it may be easier for the current to drive the TSS electrons into a stronger out-of-equilibrium state (with a larger spin-potential difference), enhancing the electron-nuclear spin flip-flop process. We also speculate that other factors such as disorder and the fabrication process may affect the environment of nuclear spins and effective coupling between the electrons and nuclei, and thus the ability for current to polarize nuclear spins.
In summary, we report the observation of a persistent ESP in a 3D TI with a long time scale. Such a persistent source of ESP and spin potential (even after the injection current is removed) may be used as a spin battery (40) or spin capacitor in spintronics (3, 48). The possibility of electrically controlled and rewritable electronic and nuclear spin memory or storage may also open potential applications in solid-state spin-based quantum computing and information processing (24, 48).
MATERIALS AND METHODS
Device fabrication
The high-quality bulk 3D TI crystals of BTS221 were grown by the Bridgman method (49–51). Thin TI flakes (typical thickness of ~10 to 40 nm and lateral size of up to ~5 μm) were exfoliated from the bulk crystals using the “scotch tape method” (52) and placed on top of standard doped Si substrates with a 285-nm-thick SiO2. To fabricate a thin Al2O3 tunneling barrier (used for spin detection) and protect the sample surface from oxidation, we immediately transferred the exfoliated flakes into a high-vacuum e-beam evaporator and coated them with a 0.7-nm-thick Al film under a pressure of 2.0 × 10−8 torr. After reexposing the sample in air, the Al film was fully oxidized into Al2O3. The FM [50-nm-thick Py (Ni0.80Fe0.20)] and nonmagnetic (70-nm-thick Au) electrodes were fabricated by two rounds of e-beam lithography and e-beam evaporation. Before depositing the Au contacts, the samples were dipped in a BOE (buffered oxide etch) (HF/H2O, 1:6) solution to remove the thin layer of Al2O3 so that Ohmic contacts can be achieved.
Characterization of our magnetic (Py) electrodes
Our magnetic (Py) electrodes were characterized by magnetic force microscopy at room temperature.
Spin potentiometric measurements
The spin potentiometric measurement was performed in a three- or four-terminal configuration involving one FM inner contact (Py) and two or three nonmagnetic outer contacts (Au), as schematically shown in Figs. 1A and 2B, respectively. A DC source-drain bias current can be applied between the two outmost Au electrodes. A voltage (potential difference) was measured between the Py and the adjacent Au contact (to its left) using a high-impedance voltmeter. We define a positive current as flowing from right to left along the −x direction, and a positive in-plane magnetic B field as applied in the −y direction along the easy axis (Figs. 1A and 2B) of the FM electrode. All measurements were performed in a He-3 cryostat with the base temperature Tbase = 300 mK or a variable temperature cryostat with Tbase = 1.6 K.
Supplementary Material
Acknowledgments
We thank L. Bouchard, B. Piot, and P. Crowell for the informative discussions. Funding: We acknowledge support by the DARPA (Defense Advanced Research Projects Agency) MESO (Mesodynamic Architectures) program (grant N66001-11-1-4107). S.D. acknowledges support from Purdue University. Y.P.C. and J.T. also acknowledge later support from NSF (grant 1641101). The early stage of this work has also benefited from a joint seed grant from the Birck Nanotechnology Center at Purdue and the Midwestern Institute for Nanoelectronics Discovery (MIND) of Nanoelectronics Research Initiative (NRI). Author contributions: I.M. synthesized the TI bulk crystal. J.T. fabricated the devices, performed transport measurements, and analyzed the data with advice from Y.P.C. S.H. and S.D. helped with the theoretical understanding. J.T. and Y.P.C. wrote the paper, with discussions and comments from all other coauthors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/4/e1602531/DC1
note S1. More discussions on the possible mechanisms for the persistent spin polarization, dynamical spin polarization between TSS electrons and nuclear spins, and the interplay of the SML of TSS electrons and hyperfine interaction between the TSS electron spins and nuclear spins.
fig. S1. Characterization of the magnetic (Py) electrodes.
fig. S2. Complete data set on the current dependence of the measured spin signal in device A.
fig. S3. Spin signal largely independent on Id measured in additional devices.
fig. S4. The writing current effect on the spin signal during cooling.
fig. S5. The writing current effect on the spin signal measured at 26 K.
fig. S6. Effect of the magnitude of writing current Iw on the spin signal.
fig. S7. Effect of current writing time on the spin signal.
fig. S8. Temperature dependence of the measured spin signal.
table S1. Lifetime of the NSP reported in different systems from previous literature.
REFERENCES AND NOTES
- 1.Žutić I., Fabian J., Das Sarma S., Spintronics: Fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004). [Google Scholar]
- 2.Awschalom D. D., Flatte M. E., Challenges for semiconductor spintronics. Nat. Phys. 3, 153–159 (2007). [Google Scholar]
- 3.Wolf S. A., Awschalom D. D., Buhrman R. A., Daughton J. M., von Molnár S., Roukes M. L., Chtchelkanova A. Y., Treger D. M., Spintronics: A spin-based electronics vision for the future. Science 294, 1488–1495 (2001). [DOI] [PubMed] [Google Scholar]
- 4.Qi X.-L., Zhang S.-C., The quantum spin Hall effect and topological insulators. Phys. Today 63, 33–38 (2010). [Google Scholar]
- 5.Hasan M. Z., Kane C. L., Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
- 6.Qi X.-L., Zhang S.-C., Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
- 7.Li C. H., van’t Erve O. M., Robinson J. T., Liu Y., Li L., Jonker B. T., Electrical detection of charge-current-induced spin polarization due to spin-momentum locking in Bi2Se3. Nat. Nanotechnol. 9, 218–224 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Tian J. F., Childres I., Cao H. L., Shen T., Miotkowski I., Chen Y. P., Topological insulator based spin valve devices: Evidence for spin polarized transport of spin-momentum-locked topological surface states. Solid State Commun. 191, 1–5 (2014). [Google Scholar]
- 9.Dankert A., Geurs J., Kamalakar M. V., Charpentier S., Dash S. P., Room temperature electrical detection of spin polarized currents in topological insulators. Nano Lett. 15, 7976–7981 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Liu L., Richardella A., Garate I., Zhu Y., Samarth N., Chen C.-T., Spin-polarized tunneling study of spin-momentum locking in topological insulators. Phys. Rev. B 91, 235437 (2015). [Google Scholar]
- 11.Lee J. S., Richardella A., Hickey D. R., Mkhoyan K. A., Samarth N., Mapping the chemical potential dependence of current-induced spin polarization in a topological insulator. Phys. Rev. B 92, 155312 (2015). [Google Scholar]
- 12.Tang J., Chang L.-T., Kou X., Murata K., Choi E. S., Lang M., Fan Y., Jiang Y., Montazeri M., Jiang W., Wang Y., He L., Wang K. L., Electrical detection of spin-polarized surface states conduction in (Bi0.53Sb0.47)2Te3 topological insulator. Nano Lett. 14, 5423–5429 (2014). [DOI] [PubMed] [Google Scholar]
- 13.Ando Y., Hamasaki T., Kurokawa T., Ichiba K., Yang F., Novak M., Sasaki S., Segawa K., Ando Y., Shiraishi M., Electrical detection of the spin polarization due to charge flow in the surface state of the topological insulator Bi1.5Sb0.5Te1.7Se1.3. Nano Lett. 14, 6226–6230 (2014). [DOI] [PubMed] [Google Scholar]
- 14.Tian J. F., Miotkowski I., Hong S., Chen Y. P., Electrical injection and detection of spin-polarized currents in topological insulator Bi2Te2Se. Sci. Rep. 5, 14293 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hammar P. R., Johnson M., Potentiometric measurements of the spin-split subbands in a two-dimensional electron gas. Phys. Rev. B 61, 7207–7210 (2000). [Google Scholar]
- 16.Park Y. H., Cheol Jang H., Koo H. C., Kim H.-j., Chang J., Han S. H., Choi H.-J., Observation of gate-controlled spin—Orbit interaction using a ferromagnetic detector. J. Appl. Phys. 111, 07C317 (2012). [Google Scholar]
- 17.E. Y. Tsymbal, I. Žutić, Eds., Handbook of Spin Transport and Magnetism (Chapman and Hall/CRC, 2011). [Google Scholar]
- 18.Oestreich M., Hübner J., Hägele D., Klar P. J., Heimbrodt W., Rühle W. W., Ashenford D. E., Lunn B., Spin injection into semiconductors. Appl. Phys. Lett. 74, 1251–1253 (1999). [Google Scholar]
- 19.Lou X., Adelmann C., Crooker S. A., Garlid E. S., Zhang J., Reddy K. S. M., Flexner S. D., Palmstrøm C. J., Crowell P. A., Electrical detection of spin transport in lateral ferromagnet-semiconductor devices. Nat. Phys. 3, 197–202 (2007). [Google Scholar]
- 20.Vink I. T., Nowack K. C., Koppens F. H. L., Danon J., Nazarov Y. V., Vandersypen L. M. K., Locking electron spins into magnetic resonance by electron–nuclear feedback. Nat. Phys. 5, 764–768 (2009). [Google Scholar]
- 21.Maurer P. C., Kucsko G., Latta C., Jiang L., Yao N. Y., Bennett S. D., Pastawski F., Hunger D., Chisholm N., Markham M., Twitchen D. J., Cirac J. I., Lukin M. D., Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012). [DOI] [PubMed] [Google Scholar]
- 22.G. Slavcheva, P. Roussignol, in Optical Generation and Control of Quantum Coherence in Semiconductor Nanostructures, G. Slavcheva, P. Roussignol, Eds. (Springer Berlin Heidelberg, 2010). [Google Scholar]
- 23.Feher G., Electron spin resonance experiments on donors in silicon. I. Electronic structure of donors by the electron nuclear double resonance technique. Phys. Rev. 114, 1219–1244 (1959). [Google Scholar]
- 24.Kane B. E., A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998). [Google Scholar]
- 25.Dehollain J. P., Muhonen J. T., Tan K. Y., Saraiva A., Jamieson D. N., Dzurak A. S., Morello A., Single-shot readout and relaxation of singlet and triplet states in exchange-coupled 31P electron spins in silicon. Phys. Rev. Lett. 112, 236801 (2014). [DOI] [PubMed] [Google Scholar]
- 26.Saeedi K., Simmons S., Salvail J. Z., Dluhy P., Riemann H., Abrosimov N. V., Becker P., Pohl H.-J., Morton J. J. L., Thewalt M. L. W., Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830–833 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Steger M., Saeedi K., Thewalt M. L. W., Morton J. J. L., Riemann H., Abrosimov N. V., Becker P., Pohl H.-J., Quantum information storage for over 180 s using donor spins in a 28Si “semiconductor vacuum”. Science 336, 1280–1283 (2012). [DOI] [PubMed] [Google Scholar]
- 28.Sapoval B., Lepine D., Desaimantation d’un systeme de spins nucleaires dilues relaxation spin-reseau dans le silicium tres pur. J. Phys. Chem. Solids 27, 115–124 (1966). [Google Scholar]
- 29.Ladd T. D., Maryenko D., Yamamoto Y., Abe E., Itoh K. M., Coherence time of decoupled nuclear spins in silicon. Phys. Rev. B 71, 014401 (2005). [Google Scholar]
- 30.Strand J., Lou X., Adelmann C., Schultz B. D., Isakovic A. F., Palmstrøm C. J., Crowell P. A., Electron spin dynamics and hyperfine interactions in Fe/Al0.1Ga0.9As/GaAs spin injection heterostructures. Phys. Rev. B 72, 155308 (2005). [Google Scholar]
- 31.Shiogai J., Ciorga M., Utz M., Schuh D., Arakawa T., Kohda M., Kobayashi K., Ono T., Wegscheider W., Weiss D., Nitta J., Dynamic nuclear spin polarization in an all-semiconductor spin injection device with (Ga,Mn)As/n-GaAs spin Esaki diode. Appl. Phys. Lett. 101, 212402 (2012). [Google Scholar]
- 32.Maletinsky P., Kroner M., Imamoglu A., Breakdown of the nuclear-spin-temperature approach in quantum-dot demagnetization experiments. Nat. Phys. 5, 407–411 (2009). [Google Scholar]
- 33.Chekhovich E. A., Makhonin M. N., Skiba-Szymanska J., Krysa A. B., Kulakovskii V. D., Skolnick M. S., Tartakovskii A. I., Dynamics of optically induced nuclear spin polarization in individual InP/GaxIn1−xP quantum dots. Phys. Rev. B 81, 245308 (2010). [Google Scholar]
- 34.Fong C. F., Ota Y., Harbord E., Iwamoto S., Arakawa Y., p-shell carrier assisted dynamic nuclear spin polarization in single quantum dots at zero external magnetic field. Phys. Rev. B 93, 125306 (2016). [Google Scholar]
- 35.Latta C., Srivastava A., Imamoğlu A., Hyperfine interaction-dominated dynamics of nuclear spins in self-assembled ingaas quantum dots. Phys. Rev. Lett. 107, 167401 (2011). [DOI] [PubMed] [Google Scholar]
- 36.Maletinsky P., Badolato A., Imamoglu A., Dynamics of quantum dot nuclear spin polarization controlled by a single electron. Phys. Rev. Lett. 99, 056804 (2007). [DOI] [PubMed] [Google Scholar]
- 37.Chekhovich E. A., Makhonin M. N., Tartakovskii A. I., Yacoby A., Bluhm H., Nowack K. C., Vandersypen L. M. K., Nuclear spin effects in semiconductor quantum dots. Nat. Mater. 12, 494–504 (2013). [DOI] [PubMed] [Google Scholar]
- 38.Oulton R., Greilich A., Verbin S. Y., Cherbunin R. V., Auer T., Yakovlev D. R., Bayer M., Merkulov I. A., Stavarache V., Reuter D., Wieck A. D., Subsecond spin relaxation times in quantum dots at zero applied magnetic field due to a strong electron-nuclear interaction. Phys. Rev. Lett. 98, 107401 (2007). [DOI] [PubMed] [Google Scholar]
- 39.Greilich A., Shabaev A., Yakovlev D. R., Efros A. L., Yugova I. A., Reuter D., Wieck A. D., Bayer M., Nuclei-induced frequency focusing of electron spin coherence. Science 317, 1896–1899 (2007). [DOI] [PubMed] [Google Scholar]
- 40.Würtz A., Müller T., Lorke A., Reuter D., Wieck A. D., Electrical readout of the local nuclear polarization in the quantum hall effect: A hyperfine battery. Phys. Rev. Lett. 95, 056802 (2005). [DOI] [PubMed] [Google Scholar]
- 41.Simin D., Kraus H., Sperlich A., Ohshima T., Astakhov G. V., Dyakonov V., Locking of electron spin coherence over fifty milliseconds in natural silicon carbide arXiv:1602.05775v2 (2016). [Google Scholar]
- 42.Smet J. H., Deutschmann R. A., Ertl F., Wegscheider W., Abstreiter G., von Klitzing K., Gate-voltage control of spin interactions between electrons and nuclei in a semiconductor. Nature 415, 281–286 (2002). [DOI] [PubMed] [Google Scholar]
- 43.Kikkawa J. M., Awschalom D. D., All-optical magnetic resonance in semiconductors. Science 287, 473–476 (2000). [DOI] [PubMed] [Google Scholar]
- 44.Hong S., Diep V., Datta S., Chen Y. P., Modeling potentiometric measurements in topological insulators including parallel channels. Phys. Rev. B 86, 085131 (2012). [Google Scholar]
- 45.Lunde A. M., Platero G., Hyperfine interactions in two-dimensional HgTe topological insulators. Phys. Rev. B 88, 115411 (2013). [Google Scholar]
- 46.A. Abragam, The Principles of Nuclear Magnetism (Clarendon Press, Oxford, 1961). [Google Scholar]
- 47.Berman G. P., Chernobrod B. M., Gorshkov V. N., Tsifrinovich V. I., Spin diffusion and relaxation in a nonuniform magnetic field. Phys. Rev. B 71, 184409 (2005). [Google Scholar]
- 48.McCamey D. R., Van Tol J., Morley G. W., Boehme C., Electronic spin storage in an electrically readable nuclear spin memory with a lifetime >100 seconds. Science 330, 1652–1656 (2010). [DOI] [PubMed] [Google Scholar]
- 49.Ren Z., Taskin A. A., Sasaki S., Segawa K., Ando Y., Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306 (2010). [Google Scholar]
- 50.Jia S., Ji H., Climent-Pascual E., Fuccillo M. K., Charles M. E., Xiong J., Ong N. P., Cava R. J., Low-carrier-concentration crystals of the topological insulator Bi2Te2Se. Phys. Rev. B 84, 235206 (2011). [Google Scholar]
- 51.Cao H., Liu C., Tian J., Xu Y., Miotkowski I., Hasan M. Z., Chen Y. P., Controlling and distinguishing electronic transport of topological and trivial surface states in a topological insulator arXiv:1409.3217 (2014). [Google Scholar]
- 52.Novoselov K. S., Jiang D., Schedin F., Booth T. J., Khotkevich V. V., Morozov S. V., Geim A. K., Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. U.S.A. 102, 10451–10453 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Feher G., Nuclear polarization via “hot” conduction electrons. Phys. Rev. Lett. 3, 135–137 (1959). [Google Scholar]
- 54.Wald K. R., Kouwenhoven L. P., McEuen P. L., van der Vaart N. C., Foxon C. T., Local dynamic nuclear polarization using quantum point contacts. Phys. Rev. Lett. 73, 1011–1014 (1994). [DOI] [PubMed] [Google Scholar]
- 55.Sarma S. D., Fabian J., Xuedong H., Zutic I., Theoretical perspectives on spintronics and spin-polarized transport. IEEE Trans. Magn. 36, 2821–2826 (2000). [Google Scholar]
- 56.Lo C. C., Weis C. D., van Tol J., Bokor J., Schenkel T., All-electrical nuclear spin polarization of donors in silicon. Phys. Rev. Lett. 110, 057601 (2013). [DOI] [PubMed] [Google Scholar]
- 57.M. I. Dyakonov, Ed., Spin Physics in Semiconductors (Springer, 2008). [Google Scholar]
- 58.Trowbridge C. J., Norman B. M., Kato Y. K., Awschalom D. D., Sih V., Dynamic nuclear polarization from current-induced electron spin polarization. Phys. Rev. B 90, 085122 (2014). [DOI] [PubMed] [Google Scholar]
- 59.Strand J., Schultz B. D., Isakovic A. F., Palmstrøm C. J., Crowell P. A., Dynamic nuclear polarization by electrical spin injection in ferromagnet-semiconductor heterostructures. Phys. Rev. Lett. 91, 036602 (2003). [DOI] [PubMed] [Google Scholar]
- 60.Chan M. K., Hu Q. O., Zhang J., Kondo T., Palmstrøm C. J., Crowell P. A., Hyperfine interactions and spin transport in ferromagnet-semiconductor heterostructures. Phys. Rev. B 80, 161206 (2009). [Google Scholar]
- 61.Koumoulis D., Chasapis T. C., Taylor R. E., Lake M. P., King D., Jarenwattananon N. N., Fiete G. A., Kanatzidis M. G., Bouchard L.-S., NMR probe of metallic states in nanoscale topological insulators. Phys. Rev. Lett. 110, 026602 (2013). [DOI] [PubMed] [Google Scholar]
- 62.Nisson D. M., Dioguardi A. P., Peng X., Yu D., Curro N. J., Anomalous nuclear magnetic resonance spectra in Bi2Se3 nanowires. Phys. Rev. B 90, 125121 (2014). [Google Scholar]
- 63.Mukhopadhyay S., Krämer S., Mayaffre H., Legg H. F., Orlita M., Berthier C., Horvatić M., Martinez G., Potemski M., Piot B. A., Materna A., Strzelecka G., Hruban A., Hyperfine coupling and spin polarization in the bulk of the topological insulator Bi2Se3. Phys. Rev. B 91, 081105 (2015). [Google Scholar]
- 64.Koumoulis D., Morris G. D., He L., Kou X., King D., Wang D., Hossain M. D., Wang K. L., Fiete G. A., Kanatzidis M. G., Bouchard L.-S., Nanoscale β-nuclear magnetic resonance depth imaging of topological insulators. Proc. Natl. Acad. Sci. U.S.A. 112, E3645–E3650 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Taylor R. E., Leung B., Lake M. P., Bouchard L.-S., Spin–lattice relaxation in bismuth chalcogenides. J. Phys. Chem. C 116, 17300–17305 (2012). [Google Scholar]
- 66.Koumoulis D., Leung B., Chasapis T. C., Taylor R., King D. Jr, Kanatzidis M. G., Bouchard L.-S., Understanding bulk defects in topological insulators from nuclear-spin interactions. Adv. Funct. Mater. 24, 1519–1528 (2014). [Google Scholar]
- 67.Young B.-L., Lai Z.-Y., Xu Z., Yang A., Gu G. D., Pan Z.-H., Valla T., Shu G. J., Sankar R., Chou F. C., Probing the bulk electronic states of Bi2Se3 using nuclear magnetic resonance. Phys. Rev. B 86, 075137 (2012). [Google Scholar]
- 68.Nisson D. M., Dioguardi A. P., Klavins P., Lin C. H., Shirer K., Shockley A. C., Crocker J., Curro N. J., Nuclear magnetic resonance as a probe of electronic states of Bi2Se3. Phys. Rev. B 87, 195205 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/4/e1602531/DC1
note S1. More discussions on the possible mechanisms for the persistent spin polarization, dynamical spin polarization between TSS electrons and nuclear spins, and the interplay of the SML of TSS electrons and hyperfine interaction between the TSS electron spins and nuclear spins.
fig. S1. Characterization of the magnetic (Py) electrodes.
fig. S2. Complete data set on the current dependence of the measured spin signal in device A.
fig. S3. Spin signal largely independent on Id measured in additional devices.
fig. S4. The writing current effect on the spin signal during cooling.
fig. S5. The writing current effect on the spin signal measured at 26 K.
fig. S6. Effect of the magnitude of writing current Iw on the spin signal.
fig. S7. Effect of current writing time on the spin signal.
fig. S8. Temperature dependence of the measured spin signal.
table S1. Lifetime of the NSP reported in different systems from previous literature.


