Synthetic apertures for visible imaging are a promising approach to achieving subdiffraction resolution in long-distance imaging.
Keywords: Computational Imaging, Fourier Ptychography, Phase Retrieval, Synthetic Aperture Imaging
Abstract
Synthetic aperture radar is a well-known technique for improving resolution in radio imaging. Extending these synthetic aperture techniques to the visible light domain is not straightforward because optical receivers cannot measure phase information. We propose to use macroscopic Fourier ptychography (FP) as a practical means of creating a synthetic aperture for visible imaging to achieve subdiffraction-limited resolution. We demonstrate the first working prototype for macroscopic FP in a reflection imaging geometry that is capable of imaging optically rough objects. In addition, a novel image space denoising regularization is introduced during phase retrieval to reduce the effects of speckle and improve perceptual quality of the recovered high-resolution image. Our approach is validated experimentally where the resolution of various diffuse objects is improved sixfold.
INTRODUCTION
Imaging objects from large standoff distances is a requirement in many computer vision and imaging applications such as surveillance and remote sensing. In these scenarios, the imaging device is sufficiently far away from the object that imaging resolution is fundamentally limited not by magnification but rather by the diffraction of light at the limiting aperture of the imaging system—using a lens with a larger aperture will lead to increased spatial resolution. Physically increasing the aperture of the lens, by building a larger lens, results in expensive, heavy, and bulky optics and mechanics. Details on the rapid increase in cost and weight as the focal length increases can be found in part A of the Supplementary Materials. A number of techniques have been proposed to improve spatial resolution for various imaging systems, including refractive telescopes (1–6), holography (7–11), and incoherent superresolution (12–16).
The resolution of an imaging system is proportional to both the lens aperture size and the wavelength of the electromagnetic spectrum used. In long-wavelength regimes (such as radar), the direct coupling between image resolution and aperture size can be mitigated using synthetic aperture radar (SAR) techniques. SAR improves radio imaging resolution by capturing multiple measurements of a static object using a mobile recording platform, such as an airplane or satellite (Fig. 1A). For SAR, the resolution is determined by the synthetic aperture size, which can be many orders of magnitude larger than the physical aperture size. Stitching together multiple radar returns is possible because the full complex field (amplitude and phase) is directly measured by the antenna with picosecond timing resolution. However, to make a comparable measurement using visible light, a detector would have to continuously record information with a time resolution greater than 1 fs, a requirement well beyond the capabilities of modern devices. As such, current camera sensors record only the intensity of the incoming optical field, and all phase information is lost. Here, we seek to extend the concept of synthetic apertures for visible imaging (SAVI), paving the way toward long-distance, subdiffraction-limited imaging (Fig. 1B).
Fig. 1. Creating synthetic apertures to improve image resolution.
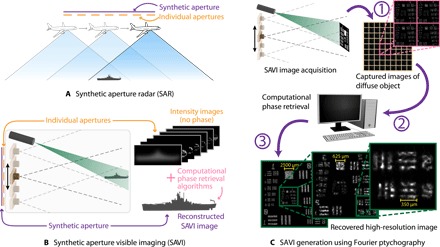
Objects illuminated with a coherent wave reflect a signal back toward the detector that diffracts to an area larger than the aperture of the receiver. (A) SAR is a technique to increase the resolution of mobile radar imaging systems by scanning the antennae over the synthetic aperture. (B) We extend the principles of SAR to create SAVI. A coherent source (for example, a laser) illuminates a distant target, and the reflected signal is captured by a camera. The camera system is translated to capture all of the light that would enter the desired synthetic aperture. Unlike SAR, phase information cannot be recorded for visible light. Therefore, high-resolution image reconstruction necessitates postcapture computational phase recovery. (C) Experimental implementation of SAVI in three steps. (1) A diffuse object is illuminated with a coherent source, and overlapping images are captured. Each image has low resolution and suffers from speckle. (2) Missing phase information is recovered computationally, which requires redundancy between captured intensity images. (3) A high-resolution image is reconstructed using the recovered phase. Additional examples of captured data and reconstructions are shown in Figs. 3 and 4.
Fourier ptychography (FP) has emerged as a powerful tool to improve spatial resolution in microscopy. In FP, multiple low-resolution images with different illumination angles are captured and stitched together (17–27). Redundancy between measurements permits computational recovery of the missing phase information (18, 25, 28–31). See part B of the Supplementary Materials for a detailed discussion on previous work in FP microscopy and related phase retrieval techniques, as well as comparison with other methods for high-resolution imaging.
Adapting the technique to long-distance imaging requires two important modifications of previous FP microscopy implementations. First, the separation distance between the object and the camera increases by orders of magnitude. Second, a reflection imaging geometry must be used so that the illumination source and the camera are placed on the same side of the object. Dong et al. (20) and Holloway et al. (32) succeeded in the first task, scaling up the working distance to 0.7 and 1.5 m, respectively. Reflective FP microscopy setups have been proposed to fulfill the second task (33–35). However, these systems either require small working distances (34, 35) or exhibit limited reconstruction performance (33). Here, we present a highly flexible implementation based on separate illumination and imaging optical paths.
The results presented in this paper also differ from previous works in one key regard. We demonstrate FP for optically rough surfaces, that is, surfaces that produce speckle. This is more conducive to imaging everyday objects that scatter incident light in random directions. In Fig. 2, a comparison with existing FP implementations is shown. Previous works have relied on smooth objects and are loosely represented by the transmissive data set adapted from Holloway et al. (32) shown on the left side of Fig. 2. A sample data set of a diffuse object collected in a reflection mode geometry is shown on the right. The immediate difference between the two data sets is that the random phase associated with diffuse objects effectively spreads out information across the entire Fourier domain. As a consequence of the random phase, the spatial information is obfuscated by the resultant speckle.
Fig. 2. Differences when recovering optically rough objects.

Previous FP methods, particularly transmissive geometries, have assumed that the scene consists of smooth objects with a flat phase. Left: Simulation of recovering a smooth resolution target in a transmissive geometry, adapted from Holloway et al. (32). The recovered Fourier magnitude (shown on a log scale) follows a nicely structured pattern with a peak at the dc component and decaying magnitudes for high spatial frequencies. Right: Simulation of recovering a rough resolution target in a reflective geometry. Diffuse objects spread Fourier information more uniformly, and the Fourier magnitude does not exhibit any meaningful structure. The difference in Fourier patterns is evident in the captured images taken from the same locations in both modalities. The diffuse reflectance results in captured and reconstructed images that contain speckle.
The works most closely related to this paper are the synthetic aperture holographic setup proposed by Tippie et al. (11) and the optical synthetic aperture approach of Beck et al. (36). Tippie et al. (11) experimentally demonstrated synthetic aperture off-axis holographic capture of diffuse objects at a large standoff distance. Our approach can be interpreted as a reference-free extension of synthetic aperture holography in which computational reconstruction algorithms are used in place of interferometric capture, resulting in more stable implementations and widening the variety of application scenarios that could benefit from the approach. Beck et al. (36) seek to extend SAR techniques into optical wavelengths in the near-infrared regime of the electromagnetic spectrum. To record phase measurements, the object is raster-scanned by moving an aperture. The return signal is then demodulated using a reference signal to reduce the frequency to approximately 100 kHz, which can be sampled with commercially available analog-to-digital converters (ADCs). In contrast to the study of Beck et al. (36), our approach is reference-less, which improves signal strength and reduces hardware complexity, and markedly improves data acquisition rates by not having to raster-scan the illumination over the scene.
Here, we show, for the first time, long-range, high-resolution imaging of diffuse targets—well beyond the diffraction limit imposed by the imaging optics—using synthetic aperture FP-based techniques. An overview of the proposed SAVI creation technique is illustrated in Fig. 1C. We demonstrate, using our experimental test-bed, a sixfold improvement in image resolution. In addition, we introduce an image space regularization technique that reduces the speckle visible in the reconstructed images, which results in improved perceptual image quality.
RESULTS
To validate the proposed method of creating SAVI, we constructed a table top device to capture images of objects under coherent illumination. Image recovery is performed in MATLAB.
Experimental setup
A simplified rendering of the experimental setup is shown in Fig. 3A, and the physical setup is shown in Fig. 3B. A laser diode (Edmund Optics #64-825) operating at 532 nm is passed through a spatial filter and a 2-inch-diameter focusing lens to illuminate an object 1 m away. For clarity, the spatial filter has been represented as a pinhole, and the camera body has been removed in Fig. 3A. Additional optical elements, such as neutral density filters and polarizers, have also been omitted from the diagram.
Fig. 3. Experimental setup for reflection mode FP and results of common objects.
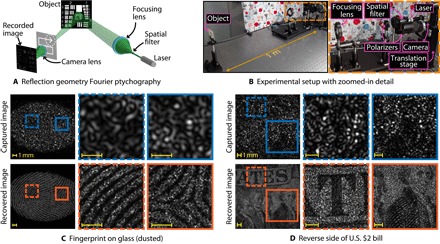
(A) A simplified rendering of the experiment and (B) the experimental setup for reflection mode FP. An object is placed 1 m away from the illumination source and camera. To satisfy the Fraunhofer approximation for a short optical path, a lens is used to focus coherent light onto the aperture of the camera lens. Multiple images are acquired to create a large synthetic aperture by translating the camera and lens using a translation stage. In the bottom row, examples are shown using SAVI to improve spatial resolution in long-range imaging for everyday diffuse objects. Images captured with a small aperture are unrecognizable because of diffraction blur and speckle. Following reconstruction, fine details are visible, permitting scene identification. (C) Fingerprint deposited on glass. The fingerprint is coated in diffuse powder to provide contrast against the glass. (D) Reverse side of a U.S. $2 bill. Scale bars, 1 mm.
Light scattered off of the object is collected by a camera positioned near the focusing lens. To satisfy the Fraunhofer diffraction approximation for a short optical path, we used a lens to focus the coherent illumination at the aperture plane of the camera lens. Whereas the model in Materials and Methods assumes free space propagation, we show in part C of the Supplementary Materials that the analysis holds for converging spherical waves. Imaging over larger distances would not require a lens to satisfy the far-field conditions, and the focusing lens would be repurposed as a collimating lens instead. Low-resolution images are captured by moving the camera (both the lens and the sensor) on an XY translation stage to sample a larger region of Fourier space.
All of the results presented in this paper use the same experimental setup described above with the following parameters and components. The camera used is a Point Grey machine vision camera (BFLY-PGE-50A2M-CS) equipped with an Aptina MT9P031 complementary metal-oxide-semiconductor (CMOS) image sensor with a pixel pitch of 2.2 μm. In front of the sensor is a lens with a focal length of 75 mm and an aperture diameter of 2.5 mm (f/30), which produces a diffraction spot size of ~39 μm on the sensor. For the U.S. Air Force (USAF) target and fingerprint data sets, adjacent positions of the camera are 0.7 mm apart to ensure sufficient overlap between samples in the Fourier domain. A grid of 19 × 19 images is captured to produce a synthetic aperture of 15.1 mm, six times larger than the lens’ aperture. The parameters used to capture the reverse side of a U.S. $2 bill in Fig. 3D are slightly modified. A 21 × 21 grid of images is collected with adjacent positions separated by 0.6 mm, yielding a synthetic aperture of 14.5 mm.
Exposure bracketing and image averaging are used to increase the dynamic range and reduce read noise, respectively. At each position, the camera records images with three different shutter times (doubling the exposure between each). For each exposure time, between 5 and 10 images are averaged to reduce read noise. The exposures are then joined together to yield a high–dynamic range image. An image sensor with a larger ADC and larger pixels could be substituted to decrease acquisition time instead of using averaging and exposure bracketing.
Accurate alignment of the low-resolution images is crucial to accurately reconstruct a high-resolution image. Checkerboard fiducial markers are placed at the periphery of the object, outside of the region illuminated by coherent light, to allow for the ease of alignment postcapture using standard tools (37). If fiducial markers are not present, diffuse images can be aligned by correlating speckle patterns in adjacent images (11). In long-distance imaging, it is likely that only a portion of the scene will be illuminated and key features in the rest of the scene may be used for image alignment, which matches the operating parameters of our experimental setup.
SAVI for diffuse objects
In the bottom row of Fig. 3, two common objects are illuminated with coherent light: In Fig. 3C, a fingerprint deposited on glass is presented, and Fig. 3D shows the reverse side of a U.S. $2 bill. A single captured image for either object is unrecognizable because of the extreme degradation from speckle and diffraction blur. After reconstruction using FP, which amounts to a sixfold improvement in resolution, both images are recognizable and fine details can be clearly observed.
The ability to resolve biometric markers from large standoff distances has many applications in surveillance and authentication. Current methods of data collection are often intrusive, for example, using a fingerprint scanner. In Fig. 3C, we show how a fingerprint can be recovered from a piece of glass by means of SAVI. The fingerprint is coated with powder to provide relief against the transparent glass. Fine features necessary to identify the print are recovered, as shown in the zoomed-in regions. Because of the limitations in the current prototype, only stationary objects can be recovered; however, a real-time acquisition system would enable contactless on-the-fly authentication of users simply holding a finger aloft.
Capturing legible text and images is also of interest in surveillance scenarios, such as verifying payment amounts at retail outlets. However, recovering the high-resolution image for the U.S. $2 bill (Fig. 3D) introduced an unanticipated problem during reconstruction. Unlike the fingerprint, the intensities on the cloth are not binary, which results in reduced contrast between the foreground and background. To combat the added difficulty of recovering such a varied object, the overlap between adjacent measurements was increased to 76%, and a 21 × 21 grid was sampled. An analysis of recovering scenes with low contrast is examined in Discussion.
During phase retrieval, a high-resolution estimate of the phase emanating from the scene is recovered. As expected for a diffusely scattering object, the phase exhibits a random profile in the range [−π, π]. Here, we are primarily interested in recovering a high-resolution intensity image of the scene; thus, the randomness in the recovered phase has no impact. The recovered phase estimate for the U.S. $2 bill is discussed and shown in part F of the Supplementary Materials.
USAF resolution target
To quantitatively investigate the performance of SAVI, we image a negative USAF chrome-on-glass target with flat white paint applied to the chrome surface of the target, as suggested in the work of Tippie et al. (11). The target is imaged through the back of the glass plate to retain the high-resolution features characteristic of the resolution chart. An example of a captured image is shown in the first row of Fig. 4A.
Fig. 4. FP for improving spatial resolution in diffuse objects.
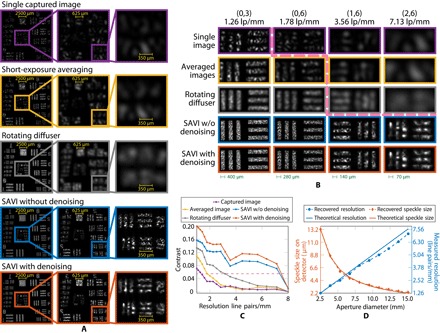
A USAF resolution target is used to characterize the performance of the proposed method to create SAVI. (A) Resolution of a USAF target under coherent light under various imaging modalities. First row: Captured images exhibit large diffraction blur and speckle. Second row: Averaging short-exposure frames of a vibrating target reduces speckle. Third row: A rotating diffuser removes temporal coherence to approximate an incoherent source at the expense of light efficiency. Fourth row: SAVI without the denoising step described in the “Suppressing speckle” section in Materials and Methods. Fifth row: SAVI using denoising improves the contrast of the fourth row. (B) Magnified regions of various bar groups recovered by the five techniques. The pink line demarcates resolvable features. Scale bars at the bottom of each column show the size of a single bar in that column. (C) Contrast of the bars as a function of feature size. Features above the pink dashed line are resolvable. Resolution in the captured image deteriorates rapidly (purple). Mimicking an incoherent source via averaging (yellow) or rotating diffuser (gray) increases spatial resolution. SAVI without (blue) and with (orange) a regularizer markedly increases resolution. Use of the regularizer improves image contrast. See the main text for a complete explanation of the contrast metric. (D) Speckle size and resolution loss are inversely proportional to the size of the imaging aperture. By increasing the synthetic aperture to just over six times the size of the camera’s aperture, we observe a sixfold increase in resolution (blue lines and circles) accompanied by a corresponding decrease in speckle size (orange lines and diamonds). The measured and predicted values are shown in dashed and solid lines, respectively. Speckle size computed without the use of the denoising regularizer. Note that the slight deviation of measured improvement is a consequence of discretization of the resolution chart. See fig. S4 discussed in part D of the Supplementary Materials for further details.
The specular reflections off of the glass and chrome surfaces of the target are orders of magnitude stronger than the diffuse light scattered by the painted surface. To mitigate the effects of specular reflection, we adjusted the angle between the illumination, object, and camera so that the direct reflection does not enter the synthetic aperture of the camera system. In addition, crossed polarizers are used to attenuate the contributions of diffracted direct illumination (at the boundaries of the bars).
Directly imaging the target results in a characteristic speckle pattern (first row of Fig. 4A). For the given imaging geometry, resolution is limited to 1.26 line pairs per millimeter or a bar width of 397 μm. A common method to reduce speckle noise, and increase resolution, is to average multiple short-exposure images of a varying speckle field to extract spatial frequencies beyond the capability of any single measurement (1, 3). To induce a change in speckle pattern, we vibrated the target and acquired a sequence of 361 short-exposure images, equal to the number of images used to create the synthetic aperture. The exposure duration is set to be 1/5 of the middle exposure time used during FP data collection. The average of the short-exposure images is shown in the second row of Fig. 4A. As expected, the resolution of the averaged image surpasses that of the captured image, and 280-μm features are now resolvable.
Speckle can also be suppressed by inserting a rotating diffuser in the optical path before the object (38) to destroy the temporal coherence of the illumination source. As shown in the third row of Fig. 4A, imaging with a rotating diffuser improves resolution so that features as small as 157 μm are resolvable. A consequence of using a rotating diffuser is that light intensity falls off as 1/d2, which greatly affects the intensity measured by the camera and limits the effective working distance of the system.
Whereas individual images exhibit significant blur and diffraction, which can be partially mitigated by averaging, the resulting image from FP has a sixfold improvement in resolution with resolvable features as small as 70 μm (fourth row of Fig. 4A). The increased resolution is also accompanied by a corresponding sixfold decrease in speckle size; however, the speckle is still present in the final reconstruction. By introducing a denoising prior into the reconstruction algorithm, the effect of the speckle can be further mitigated to improve contrast while retaining the same resolution improvements as traditional FP algorithms. The full reconstruction with regularization is shown in the fifth row of Fig. 4A.
Zoomed-in details of the five imaging scenarios are shown in Fig. 4B. Images above the dashed pink line are not resolvable. Notice that the resolution and contrast quickly deteriorate for individual captured images and the averaged image while using the rotating diffuser increases resolution marginally better. The images obtained using FP exhibit higher resolution than those obtained by directly measuring the scene; furthermore, the addition of the denoiser reduces variation within the speckle regions to improve contrast.
The USAF resolution chart can be used to quantify the resolving power of an optical system. Many metrics to compute contrast rely on the ratio of the maximum value to the minimum value along a cross section perpendicular to the bar orientation. This is a serviceable definition in most cases; however, when speckle is present, the random distribution of intensities can skew contrast measurements. We add a slight modification to the standard contrast metric to account for the variable intensity due to speckle. Bar positions are known a priori, and the average intensities of the white () and black () bars are used to compute contrast. The contrast C is further scaled by the average intensity in the bright and dark regions to account for speckle migration during reconstruction
| (1) |
Bar locations are manually located using a high-resolution image of the USAF target and are scaled to the correct size for each test image. The threshold for resolvability must be adjusted to compensate for the additional scaling in Eq. 1. We define a contrast value of 0.05 to be the resolution limit.
Contrast plots for the USAF target are presented in Fig. 4C. Contrast for the observation image and the averaged short-exposure image rapidly deteriorates in agreement with observations made in Fig. 4 (A and B). Reconstruction of the synthetic aperture image using the full complement of measurements significantly improves resolution. Including the image space denoising during reconstruction increases the contrast in the bars, which aids in discrimination of fine spatial features.
Resolution gains and speckle reduction
Because the goal of the proposed method is to emulate a larger synthetic aperture, and diffraction blur and speckle size are inversely proportional to the size of the imaging aperture, it is expected that the improvement in resolution should increase linearly with the increase in aperture diameter. To illustrate this effect, the USAF target was reconstructed with varying synthetic aperture sizes by only using subsets of the full 19 × 19 data set. In this manner, the size of the synthetic aperture was increased from 2.5 to 15.1 mm in steps of 0.7 mm. Figure 4D shows that the resolution improves and speckle size decreases according to theory. Recovery was performed without the use of the denoising regularizer so that an accurate measurement of the speckle size was obtained. Speckle size is measured as the full width at half maximum of the autocorrelation function of the intensity pattern (39). A region of the registration square at the top of the target (the square between group 1, element 1 and group 0, element 2) is chosen to measure the speckle size, and the reported value is the average of both the vertical and horizontal profiles. It should also be noted that the discrete nature of the USAF target causes the measured resolution to deviate from the predicted values; further details are provided in part D of the Supplementary Materials. The measured speckle size decreases according to theoretical predictions and demonstrates a sixfold improvement in spatial resolution.
DISCUSSION
Experimental results introduced in Results suggest that FP is a promising technique to achieve subdiffraction imaging at large standoff distances. However, there is still a long way to go before a full-scale implementation is realized.
One important area of further study is modeling and accounting for objects with low contrast. Although it is known that the difference in intensity between the background and foreground affects perceptual resolution in the presence of speckle (40), it is unclear how this affects the reconstruction performance of FP algorithms. We have observed that, for objects with a range of intensities (low contrast), such as the U.S. $2 bill shown in Fig. 3D, a greater amount of overlap may be required to obtain a satisfactory reconstruction.
Even with a good reconstruction, features may still be hard to make out if the contrast is low. In Fig. 5, we simulate super-resolving a complex object whose amplitude has varying brightness ratios. The owl is the brightest element (amplitude of 1), the background is the darkest element, and the brightness of the text and camera is the average of the owl and the background. The minimum amplitude varies from 0.1 to 0.5, and a simulated FP data capture is generated, matching the experimental parameters used for the USAF and fingerprint data sets (focal length, 75 mm; aperture diameter, 2.5 mm; overlap, 72%; synthetic aperture size, 15.1 mm). As the contrast decreases in the amplitude of the high-resolution object, a larger area of the captured images (left column of Fig. 5) exhibits speckle. The reconstruction quality decreases as the contrast increases (right column of Fig. 5). Speckle appears in the background, and fine features that can be seen with a relatively high contrast (first row) are no longer resolvable (third row).
Fig. 5. Simulated reconstructions for varying background/foreground contrast ratios.

Objects with strong contrast between the foreground and background amplitude values have a higher fidelity reconstruction than those where the background and foreground amplitudes are similar. The high-resolution complex object used for testing is shown in the top row. Simulation parameters are chosen to match the experimental parameters used in Fig. 4. The bottom three rows represent reconstructions where the amplitude in the high-resolution object is varied to different intensity ranges. Reconstruction quality falls as the contrast in the amplitude decreases. This suggests that a more robust signal model is necessary to suppress speckle for objects with low contrast.
Naturally, when the amplitude of the background is nonzero, speckles will form. Removing the speckle from the background will require stronger regularization than the method presented in this paper and is a promising avenue of research. Alternative strategies, such as destroying temporal coherence to reduce speckle contrast, have been used in FP microscopy (35) and may be of some benefit in near- to mid-range macroscopic imaging.
CONCLUSION
We have presented the first implementation of a macroscopic, reflective FP imaging system that is capable of reconstructing diffuse objects. Sixfold resolution improvements are validated experimentally, and reconstructions of other common objects demonstrate the versatility of FP to recover diffuse objects. These findings suggest that creating a SAVI is feasible and that the prospects are good for building a full-scale imaging platform in the near future.
As promising as these results are, there are still additional factors that will need to be overcome in a full-scale SAVI implementation. Here, we have only considered diffraction to be the limiting factor in spatial resolution loss. Atmospheric turbulence, long the bane of astronomers, will also affect image measurements made over large distances. There is some hope that the redundancy in the measurements for FP can help mitigate the effects of turbulence, just as aberrations and imperfections in the pupil function can be modeled and corrected, but significant research will be needed before dynamic effects can be incorporated into the model. Although this study has not solved every challenge that SAVI will face, we believe that our results lay important groundwork toward achieving its practical implementation.
MATERIALS AND METHODS
FP relies on the use of monochromatic illumination sources to provide coherent illumination. An overview of the forward model of FP is provided here.
Image formation model
In this experiment, we assumed a standard imaging geometry; that is, a source illuminates an object that reflects light back toward a camera. The source emits a field that is monochromatic with wavelength λ and is spatially coherent across the surface of the object of interest. The illumination field interacts with the object, and a portion of the field will be reflected back toward the imaging system. The field emanating from the object is a constant two-dimensional complex wave, ψ(x, y).
ψ(x, y) propagates over a sufficiently large distance z toward the imaging system to satisfy the far-field Fraunhofer approximation. The field at the aperture plane of the camera is related to the field at the object through a Fourier transform (41)
| (2) |
where k = 2π/λ is the wave number, and is the two-dimensional Fourier transform scaled by 1/λz. For simplicity, we dropped the multiplicative phase factors and the coordinate scaling from the analysis, although these could be accounted for after phase retrieval if desired. To further reduce clutter, spatial coordinates (x, y) were represented by the vector x, and frequency coordinates (u, v) were represented as u.
The field that intercepts the pupil of the imaging system, Ψ(u), is effectively the Fourier transform of the field at the object plane. Because of the finite diameter of the lens, only a portion of the Fourier transform was imaged onto the camera sensor. Let the transmittance of the pupil be given by P(u). For an ideal circular lens, P(u) is defined as
| (3) |
where d is the diameter of the lens.
The camera lens was focused on the image sensor and therefore also fulfilled the Fraunhofer approximation (41), such that the field at the sensor plane (again ignoring phase offsets and scaling) was the Fourier transform of the field immediately after the lens. Because the image sensor only recorded optical intensity, the final image is given as
| (4) |
where c is the center of the pupil. In Eq. 4, the shift of the camera aperture to capture different regions of the Fourier domain is represented by the equivalent shift of the Fourier pattern relative to the camera. Because of the finite extent of the lens aperture, the recorded image will not contain all of the frequency content of the propagated field Ψ(u). For a lens with diameter d and focal length f, the smallest resolvable feature within one image will be approximately 1.22λf/d.
Recovering high-resolution magnitude and phase
To facilitate the creation of a synthetic aperture, the camera was recentered in the Fourier plane at N different locations ci, i = 1, …, N. One consequence of sampling in the Fourier domain is that the images must be stitched together in the Fourier domain. From Eq. 4, the image sensor only recorded the intensity of the complex field and contained no information about the phase. It is therefore necessary to computationally recover the phase of the N intensity measurements. To ensure that sufficient information is available for postcapture phase retrieval, care must be taken to provide sufficient overlap between adjacent camera positions. From previous works, it is known that ≥65% overlap is typically required for phase retrieval to converge to an adequate solution (18, 25, 32).
Here, we expanded on the image recovery algorithm proposed by Ou et al. (18) and extended by Tian et al. (25), in which both an estimate of the high-resolution field Ψ(u) and an estimate of the pupil function P(u) were recovered. From Eq. 2, recovering Ψ(u) effectively recovered ψ(x) because the fields were related through a Fourier transform. We sought to solve the following optimization problem
| (5) |
where Φ(u, ci) is the optical field immediately following the aperture at the ith position, Φ(u, ci) = Ψ(u − ci)P(u).
Defining the data fidelity term of the reconstruction to be the L2 error between measured and estimated intensities in Eq. 5 resulted in a nonconvex optimization problem. Phase retrieval is typically solved using an iterative update scheme similar to that popularized by Gerchberg (42) and Fienup (43). In the mth iteration, the estimate of Φ(u) is propagated to the image plane for each camera position ci, whereupon the measured image intensities are enforced
| (6) |
| (7) |
| (8) |
| (9) |
Differences between successive estimates of the field Φ(u, ci) were used to update the estimates of Ψ(u) and P(u) in the Fourier domain. Following the formulation in the study of Tian et al. (25), the estimate of Ψ(u) is given by
| (10) |
The adaptive update step size |Pm(u + ci)|/|Pm(u)|max was used by Tian et al. (25) and was based on the work of Rodenburg and Faulkner (44). The contribution of the pupil function was first divided out of the difference, and the remainder was used to update the estimate of Ψ(u). A similar update step was used to update the estimate of the pupil function but with the roles of Ψ(u) and P(u) reversed
| (11) |
In the update steps shown in Eqs. 10 and 11, a small value (τ1 and τ2, respectively) was added to prevent division by zero. In the study of Ou et al. (18), the updated pupil function was constrained to lie within the support of the initial guess, which corresponded to the numerical aperture of the lens. A similar strategy was used in this work, with the support being twice as large as the initial guess to accommodate differences between the experimental setup and the forward model (such as the aperture not being a perfect circle).
Initial estimates of Ψ(u) and P(u) must be provided. The initial estimate of the pupil function is defined to be an ideal circular aperture from Eq. 3 with a diameter determined by the aperture. A common initialization of Ψ(u) for weakly scattering objects is to upsample any ofthe recorded images (often an image near the dc component) and take its Fourier transform (17, 18, 25). Here, we opted to take the Fourier transform of the average of all N captured intensity images. Averaging independent measurements of the field suppresses speckle in the initial estimate (1, 3).
Optically rough objects
Typical applications of FP in microscopy have dealt with objects that have gradual changes in refractive index. This, in turn, leads to transfer functions with relatively smooth phase components. However, the surfaces of most real-world objects are “optically rough” and exhibit random phase.
When coherent light reflects off of an object, each point along the surface acts as a secondary source of spherical illumination. The constituent components of the reflected optical field will be composed of a summation of each of the secondary sources. If the variation in path length exceeds the wavelength of the incident light (λ ~ 550 nm), the secondary sources will be out of phase with one another. Summation of the dephased point sources leads to destructive interference that manifests as speckle (45, 46).
Suppose that the variation of surface height is at least equal to λ and is uniformly distributed. For any point in the optical field, the probability of measuring an intensity I (squared amplitude) follows a negative exponential distribution (39)
| (12) |
where μ is the mean intensity. It should be noted that Eq. 12 holds for fully developed speckle, whereby polarized light maintains its polarization state after reflection. Most real-world objects exhibit subsurface scattering that destroys the polarization state of the incident light. In such a case, the intensity distribution is given as (47)
| (13) |
For the purposes of this paper, it is sufficient to say that speckle intensity follows a negative exponential distribution.
In an imaging geometry, the apparent speckle size is compounded by diffraction blur induced by the aperture of the lens. Hence, the speckle size at the sensor plane is approximately twice that of the smallest resolvable image features (2.44λf/d) (39). FP is used to reduce diffraction blur by synthetically increasing the aperture diameter. In the presence of speckle, FP also reduces speckle size.
The formation of speckle is compatible with the analysis of the formation model given here and used in other previous work and, in fact, is a natural consequence of the object having a randomly distributed phase. Previous FP implementations have generally avoided dealing with speckle by imaging thin biological samples, which naturally have a smooth phase, by using partially coherent light (48), or by a combination of the two. Here, we presented results for what we believe to be the first macroscopic FP imaging system that recovers optically rough objects.
Suppressing speckle
FP reduces speckle size by reducing diffraction blur; however, the variation in the remaining speckle remains large. We introduced an additional step to the recovery algorithm described in Materials and Methods (see “Recovering high-resolution magnitude and phase”) to help suppress speckle in the estimate of Ψ(u). In this section, we describe the speckle suppression method used during reconstruction; we compare it with an alternate speckle suppression technique of averaging independent measurements (1, 3) in Results (see “SAVI for diffuse objects”).
From Eqs. 12 and 13, speckle intensity follows a negative exponential distribution, which is consistent with a multiplicative noise model. It is important to note that speckle is not noise in the conventional sense. The underlying random phase of the object distorted the intensity field recorded by the sensor. Because our goal was to recover a high-resolution intensity image, it is desirable to mitigate any distortion that manifests as speckle. In this sense, we refer to speckle as “noise.” Recovering a high-resolution estimate of the magnitude and phase may be useful to determine material properties and may be accomplished by running a second reconstruction that omits the speckle suppression step.
Much of the research related to image denoising techniques, including the state-of-the-art BM3D algorithm (49), assume an additive noise model. Because the goal was to eventually recover a high-quality intensity image, the intensity of was denoised during image recovery. To overcome the multiplicative distortions caused by speckle, we first took the natural logarithm of the intensity at iteration m to convert the noise into a more convenient additive model
| (14) |
where the new variable ξm(x) was modeled as the true (noise-free) signal ξ′(x) corrupted by additive noise η(x)
| (15) |
Extracting an updated estimate, ξm+1(x), that better approximates ξ′(x) can be achieved using any of the standard image denoising techniques. Here, a straightforward image noise suppression method was used: wavelet decomposition followed by soft-thresholding wavelet components whose magnitudes exceed ρ (50). Denoising was accomplished by decomposing ξ using an orthogonal wavelet basis W and denoising operator D(α, ρ)
| (16) |
| (17) |
We used symlet wavelets of order eight as the basis for wavelet decomposition and decomposed these wavelets to the second level. The value of ρ may be set a priori or may be updated automatically, for example, using Stein’s unbiased risk estimator (51). The latter method was adopted in this work. Finally, the amplitude of ψm+1(x) was updated in a manner similar to Eq. 9
| (18) |
which was then transformed back into the Fourier domain as Ψm+1(u), and the recovery algorithm proceeded as previously described. In the proposed speckle suppression, large coefficients in the wavelet domain were removed, which was similar to imposing a histogram constraint commonly used in phase retrieval (52) in the wavelet domain.
Denoising was applied every s iterations of the recovery algorithm. Spacing out denoising allows adequate time for information transfer and reinforcement between the spatial and Fourier domains during phase retrieval. The recovery algorithm effectively has an outer loop to perform the denoising and an inner loop for phase retrieval. A visual representation of the complete recovery algorithm is shown on the left side of Fig. 6.
Fig. 6. Recovering high-resolution images with FP and phase retrieval.
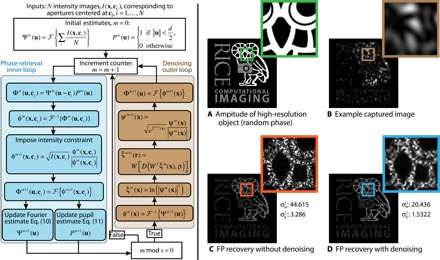
The complete recovery algorithm for SAVI is presented on the left side of the figure. A high-resolution estimate of Ψ(u) is recovered by iteratively enforcing intensity measurement constraints in the spatial domain and updating estimates of the spectrum in the Fourier domain. Image denoising is applied every s iterations to suppress the influence of speckle noise in the final reconstruction. Left branch (blue): Traditional FP recovery algorithm used by Ou et al. (18) and Tian et al. (25). Right branch (brown): Image denoising to reduce speckle noise in the estimate of Ψ(u). To illustrate how image recovery improves resolution, a simulation is shown on the right. (A and B) A complex object with an amplitude shown in (A) and having uniformly distributed phase in the range [−π, π] is recorded by a diffraction-limited imaging system (B). (C) FP reduces diffraction blur and speckle size, leading to increased resolution, but still suffers from the presence of speckle and reconstruction artifacts. (D) Incorporating a denoising regularizer in the FP recovery algorithm reduces variation in speckle intensity and reduces the effect of reconstruction artifacts. Brightness in the outsets has been increased to highlight the artifacts. View digitally to see the fine details.
The right side of Fig. 6 demonstrates the benefit of incorporating the denoising step into the recovery algorithm in the presence of subjective speckle. A simulated high-resolution complex object was imaged by a diffraction-limited system. The amplitude is shown in Fig. 6A, and the phase is randomly distributed in the range [−π, π]. Direct observation of the object resulted in an image degraded by diffraction blur and speckle; one such example is shown in Fig. 6B. Using FP without the denoising regularization resulted in artifacts in the reconstruction, as shown in Fig. 6C. Incorporating the denoising step during reconstruction, as in Fig. 6D, reduced some of the artifacts present in Fig. 6C and improved overall contrast by reducing the intensity variation in the speckle regions. The brightness of the outsets in Fig. 6 (B to D) was increased to highlight the presence of reconstruction artifacts.
To compare the performance between Fig. 6C and Fig. 6D, the variance of the white owl, , and the gray text and camera, , was computed. Without denoising, the variance of the white and gray regions was 44.6 and 3.2 pixels, respectively (with a maximum intensity of 255). Using the proposed denoising method reduced the variance by 55% to 20.4 and 1.5 pixels in the white and gray regions, respectively.
Supplementary Material
Acknowledgments
Funding: This work was supported in part by NSF grants IIS-1116718, CCF-1117939, and CCF-1527501; NSF CAREER grant IIS-1453192; ONR grants 1(GG010550)//N00014-14-1-0741 and N00014-15-1-2735; DARPA REVEAL grant HR0011-16-C-0028; and a Northwestern University McCormick Catalyst grant. Computational support was provided, in part, by the Big-Data Private-Cloud Research Cyberinfrastructure MRI award funded by the NSF under grant CNS-1338099 and by Rice University. Author contributions: O.C. and A.V. conceived the idea, contributed to the design of the theory and the algorithms, and oversaw the experiments. J.H., Y.W., and M.K.S. designed and performed the experiments and contributed to the development of the theory and the algorithms. All authors participated in the writing and the revisions of the manuscript. Competing interests: A.V. is a consultant with Light.co. All other authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/4/e1602564/DC1
Supplementary Materials
fig. S1. Cost and weight increase rapidly when improving lens resolution.
fig. S2. Comparison with incoherent superresolution methods for diffuse surfaces.
fig. S3. A simplified depiction of the imaging geometry.
fig. S4. Discretization in the USAF resolution chart.
fig. S5. Convergence of proposed phase retrieval algorithm.
fig. S6. Example of recovered phase map.
REFERENCES AND NOTES
- 1.Fried D. L., Optical resolution through a randomly inhomogeneous medium for very long and very short exposures. J. Opt. Soc. Am. 56, 1372–1379 (1966). [Google Scholar]
- 2.Korff D., Analysis of a method for obtaining near-diffraction-limited information in the presence of atmospheric turbulence. J. Opt. Soc. Am. 63, 971–980 (1973). [Google Scholar]
- 3.Miller M. G., Schneiderman A. M., Kellen P. F., Comparison of methods for processing short-exposure data from large telescopes. Astrophys. J. 186, L91–L93 (1973). [Google Scholar]
- 4.Knox K. T., Thompson B. J., Recovery of images from atmospherically degraded short-exposure photographs. Astrophys. J. 193, L45–L48 (1974). [Google Scholar]
- 5.Hardy J. W., Active optics: A new technology for the control of light. Proc. IEEE 66, 651–697 (1978). [Google Scholar]
- 6.Wang J. Y., Markey J. K., Modal compensation of atmospheric turbulence phase distortion. J. Opt. Soc. Am. 68, 78–87 (1978). [Google Scholar]
- 7.Hillman T. R., Gutzler T., Alexandrov S. A., Sampson D. D., High-resolution, wide-field object reconstruction with synthetic aperture Fourier holographic optical microscopy. Opt. Express 17, 7873–7892 (2009). [DOI] [PubMed] [Google Scholar]
- 8.Martínez-León L., Javidi B., Synthetic aperture single-exposure on-axis digital holography. Opt. Express 16, 161–169 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Massig J. H., Digital off-axis holography with a synthetic aperture. Opt. Lett. 27, 2179–2181 (2002). [DOI] [PubMed] [Google Scholar]
- 10.Mico V., Zalevsky Z., García-Martínez P., García J., Synthetic aperture superresolution with multiple off-axis holograms. J. Opt. Soc. Am. A 23, 3162–3170 (2006). [DOI] [PubMed] [Google Scholar]
- 11.Tippie A. E., Kumar A., Fienup J. R., High-resolution synthetic-aperture digital holography with digital phase and pupil correction. Opt. Express 19, 12027–12038 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Baker S., Kanade T., Limits on super-resolution and how to break them. IEEE Trans. Pattern Anal. Mach. Intell. 24, 1167–1183 (2002). [Google Scholar]
- 13.Lin Z., Shum H.-Y., Fundamental limits of reconstruction-based superresolution algorithms under local translation. IEEE Trans. Pattern Anal. Mach. Intell. 26, 83–97 (2004). [DOI] [PubMed] [Google Scholar]
- 14.P. Milanfar, Super-Resolution Imaging (CRC Press, 2010). [Google Scholar]
- 15.Freeman W. T., Jones T. R., Pasztor E. C., Example-based super-resolution. IEEE Comput. Graph. Appl. 22, 56–65 (2002). [Google Scholar]
- 16.D. Glasner, S. Bagon, M. Irani, in IEEE 12th International Conference on Computer Vision, Kyoto, 29 September to 2 October 2009. [Google Scholar]
- 17.Zheng G., Horstmeyer R., Yang C., Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 7, 739–745 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ou X., Zheng G., Yang C., Embedded pupil function recovery for Fourier ptychographic microscopy. Opt. Express 22, 4960–4972 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Horstmeyer R., Ou X., Chung J., Zheng G., Yang C., Overlapped Fourier coding for optical aberration removal. Opt. Express 22, 24062–24080 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dong S., Horstmeyer R., Shiradkar R., Guo K., Ou X., Bian Z., Xin H., Zheng G., Aperture-scanning Fourier ptychography for 3D refocusing and super-resolution macroscopic imaging. Opt. Express 22, 13586–13599 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Li P., Batey D. J., Edo T. B., Rodenburg J. M., Separation of three-dimensional scattering effects in tilt-series Fourier ptychography. Ultramicroscopy 158, 1–7 (2015). [DOI] [PubMed] [Google Scholar]
- 22.Tian L., Waller L., 3D intensity and phase imaging from light field measurements in an LED array microscope. Optica 2, 104–111 (2015). [Google Scholar]
- 23.Horstmeyer R., Chung J., Ou X., Zheng G., Yang C., Diffraction tomography with Fourier ptychography. Optica 3, 827–835 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dong S., Shiradkar R., Nanda P., Zheng G., Spectral multiplexing and coherent-state decomposition in Fourier ptychographic imaging. Biomed. Opt. Express 5, 1757–1767 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tian L., Li X., Ramchandran K., Waller L., Multiplexed coded illumination for Fourier ptychography with an LED array microscope. Biomed. Opt. Express 5, 2376–2389 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dong S., Bian Z., Shiradkar R., Zheng G., Sparsely sampled Fourier ptychography. Opt. Express 22, 5455–5464 (2014). [DOI] [PubMed] [Google Scholar]
- 27.Guo K., Dong S., Nanda P., Zheng G., Optimization of sampling pattern and the design of Fourier ptychographic illuminator. Opt. Express 23, 6171–6180 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Gerchberg R. W., Saxton W. O., A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35, 237–246 (1972). [Google Scholar]
- 29.Fienup J. R., Phase retrieval algorithms: A comparison. Appl. Opt. 21, 2758–2769 (1982). [DOI] [PubMed] [Google Scholar]
- 30.Maiden A. M., Rodenburg J. M., An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 109, 1256–1262 (2009). [DOI] [PubMed] [Google Scholar]
- 31.Yeh L.-H., Dong J., Zhong J., Tian L., Chen M., Tang G., Soltanolkotabi M., Waller L., Experimental robustness of Fourier ptychography phase retrieval algorithms. Opt. Express 23, 33214–33240 (2015). [DOI] [PubMed] [Google Scholar]
- 32.Holloway J., Asif M. S., Sharma M. K., Matsuda N., Horstmeyer R., Cossairt O., Veeraraghavan A., Toward long-distance subdiffraction imaging using coherent camera arrays. IEEE Trans. Comput. Imaging 2, 251–265 (2016). [Google Scholar]
- 33.B. Salahieh, thesis, University of Arizona, Tucson, AZ (2015). [Google Scholar]
- 34.Pacheco S., Zheng G., Liang R., Reflective Fourier ptychography. J. Biomed. Opt. 21, 026010 (2016). [DOI] [PubMed] [Google Scholar]
- 35.Ou X., Chung J., Horstmeyer R., Yang C., Aperture scanning Fourier ptychographic microscopy. Biomed. Opt. Express 7, 3140–3150 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Beck S. M., Buck J. R., Buell W. F., Dickinson R. P., Kozlowski D. A., Marechal N. J., Wright T. J., Synthetic-aperture imaging laser radar: Laboratory demonstration and signal processing. Appl. Opt. 44, 7621–7629 (2005). [DOI] [PubMed] [Google Scholar]
- 37.Itseez, Open Source Computer Vision Library (2015); http://opencv.org/.
- 38.Kubota S., Goodman J. W., Very efficient speckle contrast reduction realized by moving diffuser device. Appl. Opt. 49, 4385–4391 (2010). [DOI] [PubMed] [Google Scholar]
- 39.J. C. Dainty, Laser Speckle and Related Phenomena (Springer-Verlag, 1975), vol. 9, 298 pp. [Google Scholar]
- 40.Artigas J. M., Buades M. J., Felipe A., Contrast sensitivity of the visual system in speckle imagery. J. Opt. Soc. Am. A 11, 2345–2349 (1994). [DOI] [PubMed] [Google Scholar]
- 41.J. W. Goodman, Introduction to Fourier Optics (Roberts and Company Publishers, 2005). [Google Scholar]
- 42.Gerchberg R. W., Super-resolution through error energy reduction. J. Mod. Opt. 21, 709–720 (1974). [Google Scholar]
- 43.Fienup J. R., Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 3, 27–29 (1978). [DOI] [PubMed] [Google Scholar]
- 44.Rodenburg J. M., Faulkner H. M. L., A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 85, 4795–4797 (2004). [Google Scholar]
- 45.Oliver B. M., Sparkling spots and random diffraction. Proc. IEEE 51, 220–221 (1963). [Google Scholar]
- 46.Rigden J. D., Gordon E. I., The granularity of scattered optical maser light. Proc. IRE 50, 2367–2368 (1962). [Google Scholar]
- 47.A. E. Ennos, Speckle interferometry, in Laser Speckle and Related Phenomena (Springer-Verlag, 1975), vol. 9, pp. 203–253. [Google Scholar]
- 48.McKechnie T. S., Image-plane speckle in partially coherent illumination. Opt. Quantum Electron. 8, 61–67 (1976). [Google Scholar]
- 49.Dabov K., Foi A., Katkovnik V., Egiazarian K., Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 16, 2080–2095 (2007). [DOI] [PubMed] [Google Scholar]
- 50.Donoho D. L., Johnstone J. M., Ideal spatial adaptation by wavelet shrinkage. Biometrika 81, 425–455 (1994). [Google Scholar]
- 51.Donoho D. L., Johnstone I. M., Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 90, 1200–1224 (1995). [Google Scholar]
- 52.Elser V., Phase retrieval by iterated projections. J. Opt. Soc. Am. A 20, 40–55 (2003). [DOI] [PubMed] [Google Scholar]
- 53.Gabor D., A new microscopic principle. Nature 161, 777–778 (1948). [DOI] [PubMed] [Google Scholar]
- 54.Kim M. K., Principles and techniques of digital holographic microscopy. SPIE Rev. 1, 18005 (2010). [Google Scholar]
- 55.Papoulis A., A new algorithm in spectral analysis and band-limited extrapolation. IEEE Trans. Circuits Syst. 22, 735–742 (1975). [Google Scholar]
- 56.A. Zomet, A. Rav-Acha, S. Peleg, Robust super-resolution, in Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, 8 to 14 December 2001. [Google Scholar]
- 57.Pham T. Q., Van Vliet L. J., Schutte K., Robust fusion of irregularly sampled data using adaptive normalized convolution. EURASIP J. Adv. Signal Process. 2006, 083268 (2006). [Google Scholar]
- 58.Vandewalle P., Süsstrunk S., Vetterli M., A frequency domain approach to registration of aliased images with application to super-resolution. EURASIP J. Adv. Signal Process. 2006, 071459 (2006). [Google Scholar]
- 59.Kirkland A. I., Saxton W. O., Chand G., Multiple beam tilt microscopy for super resolved imaging. J. Electron Microsc. (Tokyo). 46, 11–22 (1997). [Google Scholar]
- 60.Kirkland A. I., Saxton W. O., Chau K.-L., Tsuno K., Kawasaki M., Super-resolution by aperture synthesis: Tilt series reconstruction in CTEM. Ultramicroscopy 57, 355–374 (1995). [Google Scholar]
- 61.Li P., Edo T. B., Rodenburg J. M., Ptychographic inversion via Wigner distribution deconvolution: Noise suppression and probe design. Ultramicroscopy 147, 106–113 (2014). [DOI] [PubMed] [Google Scholar]
- 62.Rodenburg J. M., Bates R. H. T., The theory of super-resolution electron microscopy via Wigner-distribution deconvolution. Philos. Trans. R. Soc. London A 339, 521–553 (1992). [Google Scholar]
- 63.Horstmeyer R., Yang C., A phase space model of Fourier ptychographic microscopy. Opt. Express 22, 338–358 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Horstmeyer R., Heintzmann R., Popescu G., Waller L., Yang C., Standardizing the resolution claims for coherent microscopy. Nat. Photonics 10, 68–71 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/4/e1602564/DC1
Supplementary Materials
fig. S1. Cost and weight increase rapidly when improving lens resolution.
fig. S2. Comparison with incoherent superresolution methods for diffuse surfaces.
fig. S3. A simplified depiction of the imaging geometry.
fig. S4. Discretization in the USAF resolution chart.
fig. S5. Convergence of proposed phase retrieval algorithm.
fig. S6. Example of recovered phase map.


