Abstract
This study proposes an approach to improve the perceptual quality of speech separated by binary masking through the use of reconstruction in the time-frequency domain. Non-negative matrix factorization and sparse reconstruction approaches are investigated, both using a linear combination of basis vectors to represent a signal. In this approach, the short-time Fourier transform (STFT) of separated speech is represented as a linear combination of STFTs from a clean speech dictionary. Binary masking for separation is performed using deep neural networks or Bayesian classifiers. The perceptual evaluation of speech quality, which is a standard objective speech quality measure, is used to evaluate the performance of the proposed approach. The results show that the proposed techniques improve the perceptual quality of binary masked speech, and outperform traditional time-frequency reconstruction approaches.
I. INTRODUCTION
In real-life scenarios, a speech signal is usually corrupted by noise. Many speech processing applications desire to separate the speech signal from the noisy background. This is often termed the cocktail-party problem. Humans have the remarkable ability of perceiving speech in the presence of noise. Computational approaches have been proposed to separate the target speech signal from a noisy recording. Despite extensive research over decades speech separation systems struggle to produce a level of performance close to human listeners.
One approach known as computational auditory scene analysis (CASA) often attempts to separate speech from noise by means of binary masking (Wang and Brown, 2006): which is related to the masking phenomenon of audition whereby a sound within a critical band is rendered inaudible when another louder sound is present in the same band (Moore, 2003). A binary mask identifies speech dominant and noise dominant units in a time-frequency (T-F) representation. A speech estimate is then produced by applying the binary mask directly to the T-F representation of the mixture. Binary masks have been shown to substantially improve the intelligibility of speech signals corrupted by noise (Brungart et al., 2006; Kim et al., 2009; Li and Loizou, 2008; Wang et al., 2009). However, one perceived weakness of binary masking is the resulting quality of the separated speech. This occurs because mask estimation is error prone, resulting in portions of the speech erroneously removed and portions of the noise erroneously retained. This degrades speech quality, which is typically evaluated by comparing the estimated speech against the clean speech (Araki et al., 2005; Mowlaee et al., 2012; Wang, 2008). Estimated binary masks may also cause musical noise or cross-talk problems (Madhu et al., 2008), which also lead to poorer perceptual quality.
Methods have been proposed to address the speech quality problems associated with binary masking. For example, cepstral domain smoothing on a binary mask has been shown to reduce musical noise (Madhu et al., 2008). In Araki et al. (2005), musical noise is reduced by employing finer frame shifts when generating T-F representations, i.e., the overlap amount between successive time frames in a T-F representation is increased beyond the commonly used 50%. These methods reduce the effects of musical noise, however, they do not address the errors in mask estimation.
Speech separation has also been investigated using model-based approaches. Non-negative matrix factorization (NMF) (Lee and Seung, 1999; Seung and Lee, 2001) is a popular model-based approach that has been extensively used for source separation (Smaragdis, 2007; Virtanen, 2007; Wilson et al., 2008). With NMF, a signal is decomposed into two matrices, a basis matrix and an activation matrix. It is assumed that the signal and the two matrices are non-negative. The main concept behind NMF is that the product of the basis and activation matrix provides an accurate estimation of the signal. When used for speech signals, the basis matrix represents the spectral structure, while the activation matrix linearly combines the elements in the basis matrix to form an estimate of the speech signal. When separating speech from noise, supervised NMF uses trained speech and noise models to compute an activation matrix that together approximates noisy speech. The speech model and activations are either used directly as a signal estimate or to produce a Wiener mask that is applied to a T-F representation of noisy speech. Supervised NMF has been shown to be beneficial for source separation (Smaragdis, 2007; Virtanen, 2007; Wilson et al., 2008) and robust automatic speech recognition (Raj et al., 2010), however, it requires a separate model for each of the sources present in a mixture.
Sparse representation approaches also represent a signal as a linear combination of exemplars from a dictionary. Unlike NMF, the dimensionality of each exemplar is much smaller than the number of exemplars in the dictionary (i.e., the dictionary is overcomplete). The goal is to find the smallest set of exemplars that, when linearly combined, best represent a target signal. When overcomplete dictionaries are used, it has been shown that a unique set of exemplars can represent a signal if the number of these exemplars is sufficiently small (Candes et al., 2006; Donoho, 2006). There are many approaches for determining how the exemplars are linearly combined and these approaches have been used for automatic speech recognition (ASR) (Sainath et al., 2011), robust ASR (Gemmeke and Cranen, 2008; Gemmeke et al., 2010; Gemmeke et al., 2011; Gemmeke, 2011) and source separation (Blumensath and Davis, 2007; Schmidt and Olsson, 2007; Shashanka et al., 2007). These approaches require separate dictionaries for different sound sources (speaker and noise) present in a signal. The methods in Gemmeke and Cranen (2008) and Gemmeke et al. (2010) are missing feature reconstruction approaches that use a binary mask and a dictionary for improved performance. These methods use the speech dominant T-F units and the dictionary to generate estimated values for the noise dominant T-F units. The reconstruction is, however, problematic at low signal-to-noise ratios (SNRs) because few T-F units are identified as speech dominant at low SNRs, making it difficult to generate a reasonable estimate.
Our goal in this paper is to improve the perceptual quality of noisy speech on the basis of a binary mask and speech dictionary. Initially a binary mask is estimated from a noisy mixture and it is then used to separate the speech and noise signals. We choose to use binary masks because this approach has been shown to produce intelligible speech from very noisy mixtures (Brungart et al., 2006; Li and Loizou, 2008; Kim et al., 2009; Healy et al., 2013). The separated speech and noise estimates from a binary mask are then used to generate a ratio mask (Srinivasan et al., 2006), which will be shown to improve speech quality. We view masking as the first stage, although the focus of this study is on the second stage where reconstruction is applied to the estimated speech signal for improved speech quality. In the reconstruction stage, each time frame of the separated speech is replaced by a linear combination of clean speech basis vectors. Both NMF and sparse reconstruction techniques will be studied. Unlike related approaches (Smaragdis, 2007; Virtanen, 2007; Wilson et al., 2008; Gemmeke and Cranen, 2008; Gemmeke, 2011), we do not use NMF or sparse representations for separating speech from noise, but rather we use them for reconstruction to improve the perceptual quality of separated speech by binary masking. Our approach also does not require separate source and noise models. Compared to Gemmeke and Cranen (2008) and Gemmeke et al. (2010), we use different masking techniques and entire time frames to reconstruct speech. A number of experiments are performed to assess the overall quality of separated speech at different SNRs and with different noises. The results show that the proposed techniques produce higher speech quality compared to related methods.
The rest of the paper is organized as follows. An overview of the proposed approach is presented in Sec. II. Section III describes ideal binary masks and the approach for estimating ratio masks for separating speech. The reconstruction techniques are presented in Sec. IV. Section V evaluates and compares the proposed system with other approaches. Finally, concluding remarks are given in Sec. VI.
II. SYSTEM OVERVIEW
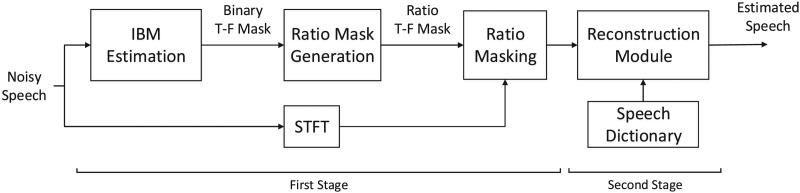
A diagram of the proposed approach for improving speech separated by binary masking is given in Fig. 1. A binary mask, which is estimated from the noisy speech mixture, is applied to the short-time Fourier transform (STFT) of the mixture to produce estimated STFTs for the speech and the noise, respectively. Speech and noise time-domain estimates are generated from these STFTs and a ratio mask is computed. The ratio mask is then applied to the original noisy mixture, resulting in an STFT for the estimated speech.
FIG. 1.
Block diagram of the proposed approach.
The resulting STFT is augmented to incorporate temporal continuity between successive STFT time frames. Reconstruction (NMF or sparse) is then used to improve the quality of the separated speech. With NMF reconstruction, the STFT magnitude of the speech signal separated by the ratio mask is represented as a linear combination of basis vectors from a pre-trained speech basis matrix. With sparse reconstruction, the STFT magnitude of the speech signal separated by the ratio mask is represented as a sparse linear combination of STFT magnitudes from a clean speech dictionary. Finally, the reconstructed STFT magnitude is combined with the STFT phase of noisy speech, and overlap-and-add synthesis is used to produce the final estimate of the speech signal. The following sections describe these steps in more detail.
III. MASK ESTIMATION
The first stage of our approach is presented in this section, i.e., the generation of a binary mask from a noisy mixture and a ratio mask from the speech and noise that are separated by a binary mask.
A. Binary mask estimation
One of the main goals of CASA is to estimate the ideal binary mask (IBM), which is a two-dimensional binary matrix used to label T-F units of a mixture signal as noise or speech dominant (Wang, 2005). Given the T-F representations of the speech, S(t, f), and noise, N(t, f), the IBM is defined as follows:
| (1) |
where t and f index the time and frequency dimensions, respectively. An estimate of the speech signal is generated by applying the IBM to the T-F representation of the mixture. Likewise, a noise estimate is generated by applying the complement (i.e., replacing 1's in the IBM with 0's and 0's with 1's) of the IBM to the mixture.
In real situations, a system does not have access to the pre-mixed speech and noise components of a mixture, so the IBM must be estimated. Since our goal is to improve the perceptual quality of speech separated by binary masking we evaluate two different IBM estimation approaches, namely the approaches of Kim et al. (2009) and Wang and Wang (2013).
IBM estimation is treated as a binary classification problem in Kim et al. (2009). In particular, amplitude modulation spectrogram (AMS) features along with delta features computed across time and frequency are used to train a 256-component Gaussian mixture model (GMM) for each binary label: speech dominant and masker dominant. Separate GMMs are trained for each frequency channel, where 25 channels are used. In the testing stage, the AMS and delta features are computed from the noisy speech signal. Then a Bayesian classifier based on the GMMs is used to estimate the binary label for each T-F unit. This IBM estimation approach will be denoted as GMM.
In Wang and Wang (2013) deep neural networks (DNNs) are trained to generate a binary mask by classifying whether a T-F unit is speech or noise dominant. A separate DNN is trained for each channel of a 64-channel gammatone filterbank. The following features are extracted from gammatone filter responses: AMS, relative spectral transform and perceptual linear prediction (RASTA-PLP), and mel-frequency cepstral coefficients (MFCC), as well as their deltas (Wang and Wang, 2013). The same features are also extracted from test utterances, and used along with the trained DNN classifiers to generate a binary mask. This approach will be denoted as DNN.
B. Ratio mask generation
Estimated IBMs are error prone, and these errors remove portions of the speech and retain portions of the noise. Such errors negatively impact perceptual quality so we propose to produce a more continuous mask to mitigate some of these problems. We compute a ratio mask from the noise and speech estimates that are obtained by applying an estimated IBM to the mixture. Other techniques for producing more continuous masks were investigated, such as setting the noise dominant units to a small nonzero value (Anzalone et al., 2006) or adding back some amount of noise (Cao et al., 2011), but we find that these methods do not improve perceptual quality. A ratio mask, RM(t, f), is generated from the STFT magnitudes of the speech and noise ( and ) estimates (Srinivasan et al., 2006),
| (2) |
is computed by first applying the binary mask to the mixture STFT, and then performing overlap and add synthesis to produce a time-domain speech estimate. is the STFT of the time-domain speech estimate. is computed similarly, however, the complement of the binary mask is applied to the mixture STFT. Speech is then separated by applying the ratio mask to the STFT magnitude of the original mixture.
IV. RECONSTRUCTION
This section describes the second stage of our approach. We first explain how the STFT magnitudes of speech separated by ratio masking are augmented to incorporate temporal continuity between adjacent frames. The process of cleaning the augmented STFT magnitudes using reconstruction is then described.
The STFT is computed by first dividing the input signal into a sequence of 20 ms frames, with a 10 ms overlap between successive frames. A Hamming window is then applied to each frame. The 320-point discrete Fourier transform is then computed within each frame, resulting in a N × T T-F representation, where N = 320 and T defines the number of time frames for the STFT. The magnitude and phase responses of the STFT are extracted, where the magnitude response will be further processed, while the phase response will be used later to synthesize a speech estimate in the time domain.
The human speech production system produces an acoustic signal that varies slowly with time. Continuity between neighboring frames in a T-F representation result from this slow varying nature. In order to leverage temporal continuity between nearby frames from the STFT of the separated speech, we concatenate several consecutive STFT time frames into a single frame as in Gemmeke et al. (2009); Gemmeke et al. (2011). Specifically, M (an odd integer) frames from the original STFT are concatenated to a single augmented frame. This is accomplished by using a sliding window that is centered at the current frame. The STFT magnitudes for frames before and after the current frame are combined into a single frame along with the STFT magnitude of the current time frame. If the current frame is preceded by fewer than frames, the first frame of the STFT is repeatedly counted toward . Likewise, if the current frame is not followed by frames, the last frame of the STFT is repeated. This results in an augmented MN × T STFT magnitude response.
The augmented STFT magnitudes inevitably contain noise components that negatively affect the perceptual quality of the separated speech. To combat this effect, reconstruction techniques are used to clean the magnitude response of the augmented STFT. More specifically, we propose sparse and NMF-based reconstruction in the second stage.
A. Sparse reconstruction of ratio masked speech
Sparse reconstruction uses a linear combination of basis vectors to represent a signal (Elad and Aharon, 2006b). The signal in our approach is the augmented STFT magnitude S, as defined above. The basis vectors collectively form a dictionary, D, which in our case is the concatenation of augmented STFT magnitude responses computed from clean speech utterances. Each basis vector is normalized by its L2-norm. Note that the clean speech utterances used for the dictionary differ from the utterances used for testing. Defining S as , each frame of the augmented STFT magnitude st is approximated as follows:
| (3) |
where is an activation vector that selects the dictionary entries used for linear combination. Each st is M · N dimensional, whereas is K dimensional.
Defining A as [], the augmented STFT magnitude is approximated as the product of the dictionary D and the activation matrix A
| (4) |
where , and . Typically, the dictionary D is overcomplete in the sense of M · N K.
The goal of sparse reconstruction is to determine the activation matrix A so that when it is combined with the dictionary D, the resulting representation effectively approximates the speech separated by ratio masking. Many approaches exist to find the activation matrix. The approach by Carmi et al. (2009) and used in Sainath et al. (2011) is termed approximate Bayesian compressive sensing (ABCS), which is an iterative approach that uses the maximum a posteriori (MAP) estimate. Gemmeke et al. (2011) use an iterative approach computationally equivalent to NMF to minimize the generalized Kullback-Leibler (KL) divergence between the true data and the approximation, while enforcing sparsity with the Lp norm of the activation matrix. We solve A using orthogonal matching pursuit (OMP), which is beneficial for sparse approaches for image denoising in computer vision (Elad and Aharon, 2006a; Mairal et al., 2008). Given D and S, OMP determines A by solving the following equation:
| (5) |
The first term is the cost function between S and DA that measures the distance between the augmented STFT magnitude and the approximation based on the linear combination of dictionary entries. The constraint ensures that only a small number of dictionary entries are used to approximate each time frame of the estimated speech, where L restricts the maximum number of dictionary entries to use. OMP solves Eq. (5) using a greedy approach. It is an iterative algorithm that at each iteration selects the dictionary entry that maximizes its inner product with the residual, which is the difference between the signal, st, and the current approximation . The activation weight for this dictionary entry is set to the computed inner product. The residual is then updated after determining the new activation weights and these steps are repeated (Pati et al., 1993). We use the fast implementation of the orthogonal matching pursuit algorithm in Mairal et al. (2009, 2010) to solve for the activation matrix.
With the activation matrix solved, the augmented STFT magnitude of the separated speech signal is approximated using Eq. (4). The augmented STFT MN × T matrix is then converted back to a N × T matrix. For each frame of the augmented STFT matrix the frames before and after the current frame are unwrapped and appropriately placed at the correct time frame. Sliding this window across frames results in multiple STFT magnitude responses for each time frame. These responses are then averaged resulting in the STFT magnitude response for the speech estimate. The estimated STFT magnitude response is then combined with the noisy phase response from the mixture to produce a sparsely reconstructed STFT. An estimate of the speech signal is finally produced by performing overlap-and-add synthesis on the sparsely reconstructed STFT. This approach is denoted as estimated ratio mask (ERM)/Sparse reconstruction.
B. NMF reconstruction of ratio masked speech
The goal of NMF is to approximate a given non-negative matrix as the product of two non-negative matrices, which are iteratively learned by minimizing a cost function of the given matrix and the approximation. In our case, NMF is used to approximate the augmented STFT magnitude S of speech separated by a ratio mask. The two matrices used for approximation are the trained basis matrix that defines the spectral features and the activation matrix that linearly combines the spectral features from the trained basis matrix. In our NMF reconstruction, the basis matrix is trained from the clean speech dictionary D, which is described in Sec. IV A, using the approach described in Gemmeke et al. (2011). The training process is described next.
Given a dictionary D, one learns a trained basis matrix Wtr and a trained activation matrix Htr. The dictionary is approximated as the product of these two matrices (i.e., ), where , and . K is the number of entries in the dictionary and B is the number of basis vectors. M and N are as defined in Sec. IV A.
The trained basis and activation matrices are found by minimizing a cost function between the dictionary and its approximation, where additional constraints may be imposed. There are a multitude of NMF methods, and here we use the approach defined by Eggert and Korner (2004) and Schmidt (2007) where generalized KL divergence between D and WtrHtr is used as the cost function along with a constraint to enforce sparsity:
| (6) |
The KL divergence between D and WtrHtr is denoted as and λ is a sparsity parameter. According to Seung and Lee (2001), the cost function is convex in Wtr only or Htr only, but not in both. Thus one cannot find a global minimum. However techniques can be used to find local minima. Specifically, Seung and Lee (2001) show that a multiplicative update rule for determining Wtr and Htr finds a local minimum for the cost function. We use the NMF implementation in Grindlay (2010) to solve for the matrices, where Wtr and Htr are randomly initialized. The update rules are shown below
| (7) |
where “.*” denotes element-wise multiplication, 1H is an all-one matrix with the same dimensions as D, and 1W is an all-one square matrix with dimensions MN × MN. All divisions in Eq. (7) represent element-wise division.
Once Wtr is found, the augmented STFT magnitude of speech separated by a ratio mask, S, is approximated as the product of the trained basis matrix and a new activation matrix H (i.e., S ≈ WtrH). H is computed using Eq. (7), however the basis matrix Wtr is held constant for each iteration and S is used in place of D.
The augmented STFT magnitude of a speech signal separated by a ratio mask is reconstructed as WtrH. The augmented STFT MN × T matrix is then converted back to a N × T matrix as described in Sec. IV A. The estimated STFT magnitude response is then combined with the noisy phase response from the mixture to produce an NMF-reconstructed STFT. An estimate of the speech signal is finally produced by performing overlap-and-add synthesis on the NMF-reconstructed STFT. This approach is denoted as ERM/NMF reconstruction.
V. EVALUATION AND COMPARISON
In this section, the proposed system is evaluated to determine its ability to produce high quality separated speech. Our reconstruction approach will also be compared against other reconstruction approaches, namely missing feature reconstruction, sparse reconstruction and vector quantization. Our approach will also be compared with supervised NMF and supervised sparse speech separation.
A. Experiment setup
Our reconstruction approach using GMM based (Kim et al., 2009) and DNN based (Wang and Wang, 2013) binary mask estimators are evaluated with 60 clean male speech signals from the IEEE corpus (Rothauser et al., 1969). Each signal is down sampled to 12 kHz and is mixed with three non-speech noises at SNRs of −5 and 0 dB, resulting in a testing set of 360 noisy speech mixtures. The noises used match those in Kim et al. (2009) and they are babble, factory, and speech-shaped noise. Random cuts from each noise are used to generate the mixtures. A different set of 390 clean IEEE male speech utterances are mixed with random cuts of the above noises at −5 and 0 dB SNRs for training the channel-specific DNN classifiers, and mixed at −5, 0, and 5 dB SNRs for training a Bayesian classifier for the GMM masks. The Bayesian classifier is trained for each noise type, as defined in Kim et al. (2009). Sixty-four DNN classifiers are trained using the features extracted from 64-channel gammatone filterbank responses as defined in Sec. III A. The parameter values for feature extraction are given in Wang et al. (2013).
The sparse reconstruction dictionary consists of the augmented STFT magnitudes of 270 clean speech signals selected from the IEEE corpus that differ from the testing and training signals. The STFTs are augmented using M = 5 frames, i.e., two before and two after the current frame. For ERM/Sparse reconstruction, the value of L is set to 5. For ERM/NMF reconstruction, a basis matrix is trained from the dictionary described above, where the trained basis matrix consists of 80 basis vectors. For training and testing, 200 iterations are used to generate the basis and activation matrices. The sparsity parameter λ is set to 0.1. See Sec. V E for how these parameter values are chosen.
B. Comparison reconstruction systems
We compare our reconstruction against three commonly used STFT magnitude reconstruction approaches, namely missing feature reconstruction (Raj et al., 2004; Zhao et al., 2012), sparse reconstruction (Gemmeke et al., 2010), and vector quantization (VQ) that is based on the version in Radfar et al. (2007). For comparisons, the VQ approach replaces the reconstruction module in our proposed system, while the missing feature reconstruction and sparse reconstruction approaches perform reconstruction using the STFT-domain binary mask. In all cases, temporal continuity is incorporated by using augmented STFTs, where the number of stacked frames is identical to our proposed method (i.e., M = 5). Unless stated otherwise, the parameters for each approach are empirically determined to maximize performance.
As presented in Raj et al. (2004) and Zhao et al. (2012), missing feature reconstruction uses speech-dominant T-F units and Gaussian mixture models coupled with a universal background model (GMM-UBM) to replace the values in noise dominant T-F units, where the speech and noise dominant T-F units are determined by the estimated binary mask. The GMM-UBM is trained from the corresponding utterances that are used to train the sparse reconstruction dictionary. We empirically determine that 1024 Gaussians are used, along with diagonal covariance matrices for the GMM-UBM. This form of reconstruction will be denoted as GMM-UBM reconstruction.
Sparse reconstruction is similar to missing feature reconstruction, where the speech-dominant T-F units are used to estimate new values for the noise dominant T-F units. However, a dictionary is used in place of the GMM-UBM. For each time frame, the speech dominant T-F units along with the corresponding entries in the dictionary are used to determine an activation matrix. An augmented magnitude estimate is generated by multiplying the activation matrix with the complete dictionary, where the values for the speech-dominant T-F units are replaced by the corresponding values in the noisy speech mixture. The values for the noise-dominant T-F units are bounded by the corresponding values of the noisy speech (i.e., a noise dominant T-F unit takes the minimum of the noisy speech and estimated value). Sparse reconstruction differs from our proposed ERM/Sparse reconstruction approach in that we use a ratio mask rather than just a binary mask for separation, and we use the entire time frame rather than just the speech-dominant T-F units in a time frame to determine an activation matrix. We also use an orthogonal matching pursuit (OMP) algorithm to determine the activation matrix, rather than an iterative approach based on NMF as in Gemmeke et al. (2010).
The VQ approach used simply amounts to K-means clustering, where each time frame of the augmented STFT magnitude of speech separated by ratio masking is replaced with the closest codeword from a pre-trained VQ codebook. The codebook for the VQ approach is also trained with utterances in the sparse reconstruction dictionary, and 2048 code words are used in the codebook. A splitting technique is used to train the codebook, where the initial set of training data is iteratively split into clusters (Linde et al., 1980), where the average value of all the augmented STFT time frames within each cluster corresponds to a codeword. For reconstruction, the time frame of the augmented STFT of ratio masked speech is replaced by the closest codeword from the codebook, where closeness is measured in terms of mean square error.
C. Comparison separation approaches
Our employment of NMF is for reconstruction of already-separated speech, whereas NMF is typically used as a separation approach. We also compare our approach against such an supervised NMF speech separation approach based on Raj et al. (2010). In addition, we compare our system to a supervised sparse separation approach described in Gemmeke et al. (2011). Both approaches use trained speech and noise models to separate speech from the background noise. For supervised NMF, the speech model is identical to the speech basis matrix used for ERM/NMF reconstruction, while the noise basis matrix (i.e., noise model) is trained from the augmented STFTs of the noise utterances mentioned in Sec. V A. We modify the approach described in Raj et al. (2010) by incorporating a sparsity parameter as described in Sec. IV B, which is set to 0.1 (as in our proposed ERM/NMF approach). For supervised sparse separation, the speech model is identical to the dictionary from ERM/Sparse reconstruction, while the concatenation of the augmented (i.e., M = 5) STFT magnitudes of the noise data is used as the noise model. In both cases, all other parameter values match those used for our proposed methods. These systems were tested with the same 60 test utterances, and each utterance was mixed with the three noises at −5 and 0 dB.
D. Experimental results
The speech quality from the proposed method and the comparison methods is evaluated with PESQ, which is a standard objective perceptual speech quality measure (ITU-T, 2001). PESQ scores are between −0.5 and 4.5, where higher scores correspond to higher perceptual speech quality. A PESQ score is computed by comparing the clean speech signal in the mixture against the estimated speech signal. This is possible because we have access to the pre-mixed clean signal for each test mixture.
The average PESQ scores for unprocessed mixtures, the signals separated by estimated binary masks (EBMs), the signals separated by estimated ratio masks, and the signals separated by the ideal binary mask are shown in Table I for each IBM estimation approach. For the GMM masks, applying the EBM to the mixture results in an improvement of PESQ score compared to the unprocessed mixture. PESQ scores also improve with the DNN masks at 0 dB, but at −5 dB applying the EBM to a mixture results in a lower PESQ score compared to the unprocessed mixture. Speech quality is improved when ERMs are used instead of EBMs in both cases, but these results are still not as good as the IBM results, indicating that there is still room for improvement.
TABLE I.
Average PESQ and STOI scores for noisy speech, speech separated by the IBM, speech separated by EBMs, and speech separated by ERMs for GMM and DNN masks.
| PESQ Score | STOI Score | ||||
|---|---|---|---|---|---|
| −5 dB | 0 dB | −5 dB | 0 dB | ||
| Mixture | 1.34 | 1.62 | 0.54 | 0.66 | |
| IBM | 2.37 | 2.73 | 0.83 | 0.89 | |
| GMM | EBM | 1.45 | 1.81 | 0.71 | 0.77 |
| ERM | 1.48 | 1.85 | 0.72 | 0.78 | |
| DNN | EBM | 1.18 | 1.69 | 0.60 | 0.72 |
| ERM | 1.35 | 1.80 | 0.60 | 0.74 | |
The average short-time objective intelligibility (STOI) scores for the signals are also shown in Table I. STOI is a recently established objective measure that quantifies the intelligibility of an altered speech signal (Taal et al., 2011). STOI scores range between 0 and 1, where higher scores indicate higher intelligibility. As shown in Table I, the STOI scores, in both IBM estimation approaches, for the EBM-masked speech are greater than the STOI scores of unprocessed mixtures, while the IBM-masked speech yields the highest STOI scores. STOI scores for ratio masked speech are approximately equal to those for binary masked speech.
Table II shows the average PESQ scores for our systems (ERM/NMF and ERM/Sparse) and the other reconstruction approaches when estimated or ideal masks are used. In this and subsequent tables, boldface indicates best result. For the GMM masks, the performance with GMM-UBM reconstruction is worse than that of the EBM and it is approximately equivalent to the unprocessed mixtures at −5 dB (see Table I). For the DNN masks, GMM-UBM reconstruction improves performance compared to EBM and ERM. For both masks, sparse reconstruction, ERM/VQ, ERM/NMF, and ERM/Sparse reconstruction offer noticeable improvements over the unprocessed mixtures, estimated binary and ratio masks at each SNR. Like ERM/NMF, ERM/Sparse reconstruction considerably outperforms GMM-UBM reconstruction, sparse reconstruction and ERM/VQ reconstruction approaches. ERM/Sparse reconstruction also produces slight improvements over ERM/NMF reconstruction at both SNRs. The results of NMF and sparse reconstruction when applied to binary masked speech (i.e., EBM/NMF and EBM/sparse) are also shown. When the estimated masks are used, EBM/Sparse reconstruction performs about the same as ERM/Sparse reconstruction for the GMM masks, but noticeably worse for the DNN masks. The performance for the proposed ERM/Sparse approach is comparable to the EBM/Sparse approach for the GMM masks, because the performance for the binary and ratio masks is comparable. When the ideal masks are used, EBM/Sparse reconstruction produces the highest speech quality compared against all the other approaches. However, even this sparse reconstruction approach is a little worse than the IBM alone, suggesting that no reconstruction is needed when IBM estimation is accurate.
TABLE II.
Average PESQ scores for different STFT magnitude reconstruction approaches using estimated or ideal masks. “[First Stage]/[Second Stage]” refers to the first and second stage methods, and EBM means that a binary mask is used in the first stage and ERM means that a ratio mask is used.
| GMM | DNN | Ideal | ||||
|---|---|---|---|---|---|---|
| −5 dB | 0 dB | −5 dB | 0 dB | −5 dB | 0 dB | |
| GMM-UBM reconstruction | 1.36 | 1.75 | 1.48 | 1.85 | 1.95 | 2.21 |
| Sparse reconstruction | 1.74 | 2.04 | 1.51 | 2.03 | 2.23 | 2.54 |
| EBM/NMF | 1.72 | 2.02 | 1.49 | 1.92 | 2.10 | 2.41 |
| EBM/Sparse | 1.83 | 2.14 | 1.52 | 2.00 | 2.35 | 2.66 |
| ERM/VQ | 1.77 | 1.97 | 1.63 | 1.89 | 1.76 | 2.04 |
| ERM/NMF | 1.85 | 2.14 | 1.73 | 2.15 | 2.30 | 2.66 |
| ERM/Sparse | 1.86 | 2.17 | 1.74 | 2.16 | 2.25 | 2.58 |
We conducted experiments where a proportion (i.e., 1% to 7%) of the noise was added back to the speech separated by ratio masks. Adding this noise resulted in roughly an 8% improvement in PESQ scores for the approaches listed in Table II using estimated masks. Although the PESQ scores were improved by adding noise, we noticed that adding noise seemed to degrade the perceptual quality during informal listening, which may indicate a potential limitation with PESQ. Hence we have decided not to add noise in our proposed methods.
The STOI results are provided in Table III. Both ERM/Sparse and ERM/NMF reconstruction produce noticeable improvements in STOI scores compared to the other reconstruction approaches when the GMM masks are used. Only sparse reconstruction and our ERM/NMF and ERM/Sparse approaches improve performance over the unprocessed mixtures, estimated binary and ratio masks at each SNR. When the DNN masks are used sparse reconstruction produces the best STOI scores. The larger point is that incorporating our reconstruction stage generates significant speech quality improvements over binary masking using estimated masks, and does so without degrading speech intelligibility as measured by STOI.
TABLE III.
Average STOI scores for different STFT magnitude reconstruction approaches using GMM, DNN, or ideal masks. Boldface indicates the approach that produced the best result for a condition.
| GMM | DNN | Ideal | ||||
|---|---|---|---|---|---|---|
| −5 dB | 0 dB | −5 dB | 0 dB | −5 dB | 0 dB | |
| GMM-UBM Reconstruction | 0.61 | 0.72 | 0.64 | 0.73 | 0.79 | 0.85 |
| Sparse Reconstruction | 0.74 | 0.80 | 0.70 | 0.81 | 0.85 | 0.90 |
| ERM/VQ | 0.71 | 0.73 | 0.68 | 0.75 | 0.74 | 0.80 |
| ERM/NMF | 0.78 | 0.82 | 0.68 | 0.79 | 0.82 | 0.88 |
| ERM/Sparse | 0.77 | 0.82 | 0.67 | 0.78 | 0.79 | 0.86 |
A PESQ analysis of the voiced and unvoiced components of the reconstructed speech from the different approaches is shown in Table IV, where the performance is averaged over both masking approaches. The PESQ score for the voiced signal is determined from the voiced clean speech signal and the voiced estimated speech signal. The PESQ score for the unvoiced signal is computed similarly using the unvoiced clean and estimated speech signals. The voiced and unvoiced signals for each mixture result from synthesizing the predetermined voiced frames and unvoiced frames of the mixture, respectively. The voiced and unvoiced frames of a mixture are determined from clean speech using Praat (Boersma and Weeknink, 2012). Clearly both ERM/NMF and ERM/Sparse reconstruction approaches offer significant improvements over the comparison approaches for voiced frames at both SNRs, while ERM/VQ reconstruction performs the best for unvoiced frames. As expected PESQ scores are generally higher at voiced frames indicating better separation.
TABLE IV.
Voiced and unvoiced PESQ analysis of the different reconstruction approaches.
| −5 dB | 0 dB | |||
|---|---|---|---|---|
| Voiced | Unvoiced | Voiced | Unvoiced | |
| GMM-UBM reconstruction | 1.38 | 1.16 | 1.77 | 1.38 |
| Sparse reconstruction | 1.63 | 1.07 | 2.06 | 1.39 |
| ERM/VQ | 1.69 | 1.25 | 1.92 | 1.46 |
| ERM/NMF | 1.79 | 1.17 | 2.19 | 1.39 |
| ERM/Sparse | 1.79 | 1.21 | 2.20 | 1.45 |
Table V shows the average PESQ scores evaluated for each interference, where the performance is averaged over both masking approaches. This table shows that the ERM/Sparse approach performs best for babble and factory noise at each SNR, while ERM/NMF performs best for speech shaped noise at each SNR. Each of our proposed approaches is noticeably better than the other reconstruction approaches at each noise type.
TABLE V.
Average PESQ scores for reconstruction approaches by noise.
| −5 dB | 0 dB | |||||
|---|---|---|---|---|---|---|
| Babble | Factory | Speech shaped | Babble | Factory | Speech shaped | |
| GMM-UBM Reconstruction | 1.52 | 1.38 | 1.36 | 1.88 | 1.74 | 1.79 |
| Sparse Reconstruction | 1.75 | 1.63 | 1.51 | 2.11 | 2.03 | 1.96 |
| ERM/VQ | 1.77 | 1.76 | 1.58 | 1.99 | 1.96 | 1.84 |
| ERM/NMF | 1.81 | 1.85 | 1.71 | 2.14 | 2.21 | 2.08 |
| ERM/Sparse | 1.82 | 1.88 | 1.69 | 2.19 | 2.24 | 2.07 |
One issue that has not been addressed thus far regards the use of estimated binary masks, since it lowers the perceptual quality of the separated speech as shown in Table I for the DNN masks at −5 dB. To determine whether binary masking is useful, the reconstruction approaches are applied directly to the mixture by omitting masking-based separation. Note that GMM-UBM reconstruction and sparse reconstruction require a binary mask, so their performance without masking is not computed. The other reconstruction models were trained with the same 270 training utterances. The same 60 test utterances were mixed with the 3 noises at −5 and 0 dB, and the average speech quality results are shown in Table VI. Comparing this table and Table II, it is clear that the average PESQ score at each SNR with no masking is lower than the average PESQ score with masking. Also, the average performance for each reconstruction approach without masking is lower than or only slightly greater than the average performance of the unprocessed mixtures at each SNR. Thus, although binary masking alone may lower speech quality it provides a useful intermediate result that can be utilized in subsequent reconstruction. In other words, the proposed two-stage model is better than a one-stage model.
TABLE VI.
Average PESQ and STOI scores for different reconstruction approaches when applied directly to the mixture.
| PESQ | STOI | |||
|---|---|---|---|---|
| −5 dB | 0 dB | −5 dB | 0 dB | |
| MIX/VQ | 1.38 | 1.58 | 0.47 | 0.53 |
| MIX/NMF | 1.37 | 1.62 | 0.56 | 0.67 |
| MIX/Sparse | 1.37 | 1.66 | 0.56 | 0.67 |
We also compare our proposed approach to supervised NMF (Raj et al., 2010) and supervised sparse (Gemmeke et al., 2011) separation approaches. The PESQ and STOI results for these supervised separation approaches are listed in Table VII along with our ERM/NMF reconstruction and ERM/Sparse reconstruction results (copied from Tables II and III). Our model with either ERM/NMF or ERM/Sparse reconstruction clearly outperforms both supervised separation approaches in terms of PESQ and STOI, suggesting that reconstructing speech separated by binary masking outperforms traditional supervised speech separation approaches.
TABLE VII.
Average PESQ and STOI scores for supervised NMF and Sparse separation, along with the proposed ERM/NMF and ERM/Sparse reconstruction approaches.
| PESQ | STOI | |||
|---|---|---|---|---|
| −5 dB | 0 dB | −5 dB | 0 dB | |
| Supervised NMF | 1.51 | 1.82 | 0.58 | 0.70 |
| Supervised Sparse | 1.47 | 1.72 | 0.61 | 0.71 |
| GMM ERM/NMF | 1.85 | 2.14 | 0.78 | 0.82 |
| GMM ERM/Sparse | 1.86 | 2.17 | 0.77 | 0.82 |
| DNN ERM/NMF | 1.73 | 2.15 | 0.68 | 0.79 |
| DNN ERM/Sparse | 1.74 | 2.16 | 0.67 | 0.78 |
E. Parameter selection
Many parameters affect the performance of the above mentioned approaches. In this section, we address how the different parameter values effect each approach using the experimental setup described above.
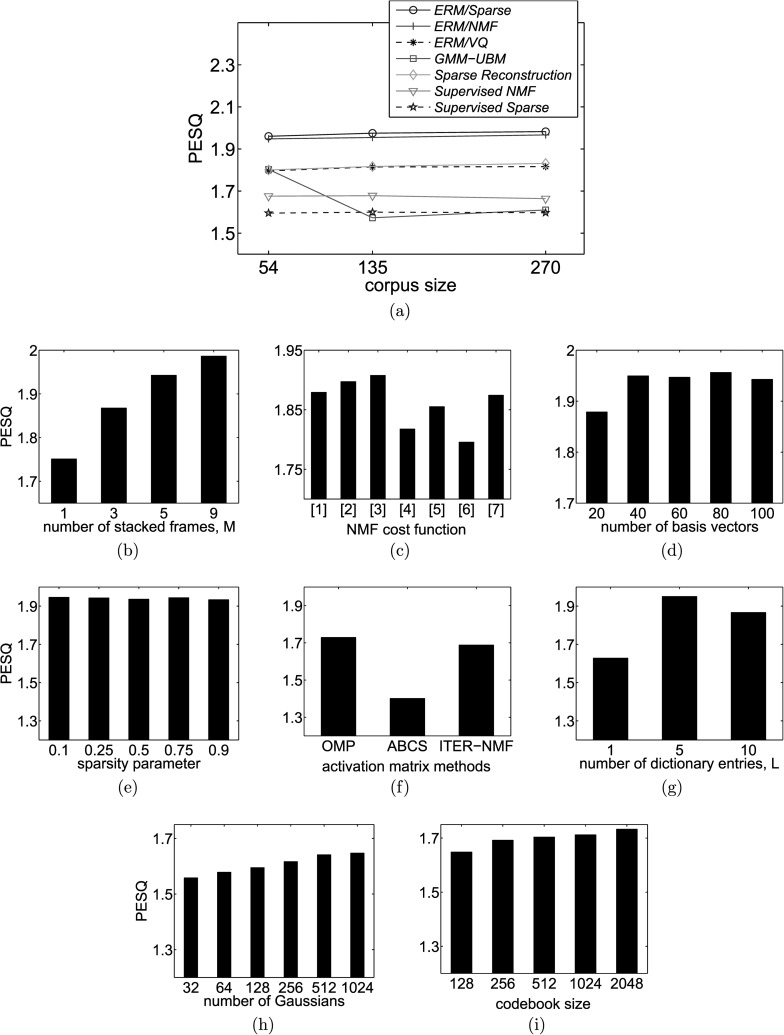
One important parameter for all reconstruction approaches is the size of the data used for training the different models (i.e., speech dictionary, basis matrix, codebook, and GMM). Using 270 utterances for ERM/Sparse reconstruction may be computationally expensive, so we assess the performance of all approaches using smaller training sizes of 135 and 54 utterances, while the remaining parameters are unchanged. In other words, the GMM used for GMM-UBM reconstruction, the codebook for ERM/VQ, the speech basis matrix for ERM/NMF and supervised NMF, as well as the speech dictionary used for ERM/Sparse, sparse and supervised sparse reconstruction, are trained using 135 speech utterances or 54 speech utterances in each case. The average PESQ score at each training size is shown in Fig. 2(a). Note that ERM/Sparse reconstruction outperforms all other approaches at each size, indicating that a smaller training size may be used for ERM/Sparse reconstruction without much loss of speech quality. The performance changes little as the model size increases for all approaches except for GMM-UBM reconstruction where performance degrades as the model training size increases from 54 to 135 utterances. In this case, with larger training sizes we find that more noise dominant T-F units are being replaced by the noisy speech values rather than estimated values, since GMM-UBM reconstruction is a bounded approach. The estimated value is dependent on the Gaussian means, and at larger training sizes we find that the mean values are larger, resulting in larger estimated values than the noisy speech values.
FIG. 2.
Parameter evaluations for the different reconstruction approaches. (a) Comparisons of the average PESQ score for the different reconstruction approaches with different numbers of utterances used to train the models. (b) Comparison of the number of frames used to augment the STFT. (c) Comparison between the different NMF variants. [1] KL diverengence (Seung and Lee, 2001); [2] Euclidean norm (Seung and Lee, 2001); [3] generalized KL divergence (Eggert and Korner, 2004; Schmidt, 2007); [4] Smaragdis (2004); [5] Cichocki et al. (2006); [6] Choi (2008); [7] Wilson et al. (2008). (d) Comparison of the number of basis vectors used for ERM/NMF. (e) Comparison of λ for ERM/NMF. (f) Comparison of different approaches for generating the activation matrix. (g) Comparison of the number of dictionary entries used for ERM/Sparse. (h) Comparison of the number of Gaussians used in the GMM-UBM. (i) Comparison of the codebook sizes to used for ERM/VQ.
All reconstruction approaches are affected by the number of frames that are used to augment the STFT. In Fig. 2(b) we show how the PESQ scores of our ERM/NMF reconstruction approach change with the number of stacked frames, M. The figure shows that the performance increases as the number of stacked frames increases, which is expected since this allows more information to be used in the reconstruction. We elect to use five frames since the further increase in performance does not seem to justify the increase in computational time.
We considered many NMF variants in terms of the cost function, when developing our ERM/NMF approach. We evaluated the different NMF variants on our test data and the results for seven different cost functions are shown in Fig. 2(c). The approach by Eggert and Korner (2004) and Schmidt (2007) uses generalized KL divergence as its cost function along with a sparsity constraint and performs slightly better than the other approaches, and hence it is used in our system. This NMF approach is also affected by the number of vectors in the basis matrix and the sparsity constraint. Figures 2(d) and 2(e) evaluate ERM/NMF reconstruction using different values for the mentioned parameters. Notice that the values used in our approach, i.e., 80 basis vectors and λ equal to 0.1, produce the best results in each case. ERM/Sparse reconstruction is dependent on the cost function used to approximate the activation matrix. The variants considered are ABCS (Carmi et al., 2009), an NMF approach (Gemmeke et al., 2011), and OMP (Mairal et al., 2009, 2010). The comparison of these three approaches is shown in Fig. 2(f), where OMP performs the best. Figure 2(g) shows how OMP varies with the number of dictionary entries, L, and 5 entries give the best scores.
The number of Gaussians and the codebook size used for the GMM-UBM reconstruction and ERM/VQ reconstruction approaches, respectively, were also empirically determined. Figures 2(h) and 2(i) show the results of the two approaches when different parameter values are used. We use the parameters that produce the best results.
VI. CONCLUDING REMARKS
We have proposed a novel approach to speech quality enhancement. Given a binary mask and the STFT of a mixture we produce a ratio mask for higher quality. We then incorporate a second stage using sparse and NMF reconstruction to further clean the speech separated by masking. Our reconstruction stage to enhance separated speech improves perceptual quality over binary masked speech, ratio masked speech, and supervised speech separation. It is also worth noting that speech quality gains of the proposed approach do not come at the expense of speech intelligibility.
The evaluations show that ERM/Sparse reconstruction produces better speech quality and outperforms GMM-UBM reconstruction, sparse reconstruction, and ERM/VQ reconstruction approaches. Although ERM/NMF reconstruction performance is slightly worse than ERM/Sparse reconstruction, the computational efficiency of ERM/NMF reconstruction is superior, particularly when larger model sizes are used. Therefore, in situations where computational efficiency is most important, ERM/NMF reconstruction is preferred.
ACKNOWLEDGMENTS
The authors would like to thank Xiaojia Zhao and Yang Shao for providing their implementation of missing feature reconstruction. We also thank Jort Gemmeke for providing his sparse reconstruction implementation. This research was supported by an AFOSR grant (FA9550-12-1-0130), an NIDCD grant (R01 DC012048), and the Ohio Supercomputer Center.
REFERENCES
- 1. Anzalone, M. C. , Calandruccio, L., Doherty, K. A. , and Carney, L. H. (2006). “ Determination of the potential benefit of time-frequency gain manipulation,” Ear Hear. 27, 480–492. 10.1097/01.aud.0000233891.86809.df [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Araki, S., Makino, S., Sawada, H., and Mukai, R. (2005). “ Reducing musical noise by a fine-shift overlap-add method applied to source separation using a time-frequency mask,” in Proceedings of ICASSP, Vol. 3, pp. 81–84. [Google Scholar]
- 3. Blumensath, T., and Davis, M. E. (2007). “ Compressed sensing and source separation,” in Independent Component Analysis and Blind Source Separation, edited by Davies M. E., James C. J., Abdallah S., and Plumbley M. D. (Springer Verlag, New York: ), pp. 341–348. [Google Scholar]
- 4. Boersma, P., and Weeknink, D. (2012). “ Praat: Doing phonetics by computer (Version 5.3.32),” Available: http://www.praat.org/ (Last viewed 5/30/13).
- 5. Brungart, D., Chang, P., Simpson, B., and Wang, D. (2006). “ Isolating the energetic component of speech-on-speech masking with ideal time-frequency segregation,” J. Acoust. Soc. Am. 120, 4007–4018. 10.1121/1.2363929 [DOI] [PubMed] [Google Scholar]
- 6. Candes, E. J. , Romberg, J., and Tao, T. (2006). “ Stable signal recovery from incomplete and inaccurate measurements,” Commun. Pure Appl. Math. 59, 1207–1223. 10.1002/cpa.20124 [DOI] [Google Scholar]
- 7. Cao, S., Li, L., and Wu, X. (2011). “ Improvement of intelligibility of ideal binary-masked noisy speech by adding background noise,” J. Acoust. Soc. Am. 129, 2227–2236. 10.1121/1.3559707 [DOI] [PubMed] [Google Scholar]
- 8. Carmi, A., Gurfil, P., Kanevsky, D., and Ramabhadran, B. (2009). “ ABCS: Approximate Bayesian compressed sensing,” Tech. Rep., Human Language Technologies, IBM, pp. 1–18. [Google Scholar]
- 9. Choi, S. (2008). “ Algorithms for orthogonal nonnegative matrix factorization,” in Proceedings IJCNN, pp. 1828–1832. [Google Scholar]
- 10. Cichocki, A., Amari, S. I. , Zdunek, R., Kompass, R., Hori, G., and He, Z. (2006). “ Extended SMART algorithms for non-negative matrix factorization,” in Proceedings of ICAISC, pp. 548–562. [Google Scholar]
- 11. Donoho, D. L. (2006). “ Compressed sensing,” IEEE Trans. Inf. Theory 52, 1289–1306. 10.1109/TIT.2006.871582 [DOI] [Google Scholar]
- 12. Eggert, J., and Korner, E. (2004). “ Sparse coding and NMF,” in IEEE Int. Conf. Neural Networks 4, 2529–2533. [Google Scholar]
- 13. Elad, M., and Aharon, M. (2006a). “ Image denoising via learned dictionaries and sparse representation,” in IEEE Comput. Soc. Conf. Comput. Vision Pattern Recognit. 1, 895–900. [Google Scholar]
- 14. Elad, M., and Aharon, M. (2006b). “ Image denoising via sparse and redundant representations over learned dictionaries,” IEEE Trans. Image Proc. 15, 3736–3745. 10.1109/TIP.2006.881969 [DOI] [PubMed] [Google Scholar]
- 15. Gemmeke, J., and Cranen, B. (2008). “ Using sparse representations for missing data imputation in noise robust speech recognition,” in Proceedings of EUSIPCO, pp. 1–5. [Google Scholar]
- 16. Gemmeke, J., Van Hamme, H., Cranen, B., and Boves, L. (2010). “ Compressive sensing for missing data imputation in noise robust speech recognition,” IEEE J. Sel. Top. Signal Process. 4, 272–287. 10.1109/JSTSP.2009.2039171 [DOI] [Google Scholar]
- 17. Gemmeke, J. F. (2011). “ Noise robust ASR: missing data techniques and beyond,” Ph.D. thesis, Radboud University Nijmegen, The Netherlands, pp. 1–169. [Google Scholar]
- 18. Gemmeke, J. F. , ten Bosch, L., Boves, L., and Cranen, B. (2009). “ Using sparse representations for exemplar based continuous digit recognition,” in Proceedings of EUSIPCO, pp. 1755–1759. [Google Scholar]
- 19. Gemmeke, J. F. , Virtanen, T., and Hurmalainen, A. (2011). “ Exemplar-based sparse representations for noise robust automatic speech recognition,” IEEE Trans. Audio, Speech, Lang. Process. 19, 2067–2080. 10.1109/TASL.2011.2112350 [DOI] [Google Scholar]
- 20. Grindlay, G. (2010). “ NMFLib,” Available: http://code.google.com/p/nmflib/ (Last viewed 5/30/13).
- 21. Healy, E. W. , Yoho, S. E. , Wang, Y., and Wang, D. L. (2013). “ An algorithm to improve speech recognition in noise for hearing-impaired listeners,” J. Acoust. Soc. Am. 134, 3029–3038. 10.1121/1.4820893 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. ITU-T. (2001). “ Perceptual evaluation of speech quality (PESQ), an objective method for end-to-end speech quality assessment of narrowband telephone networks and speech codecs,” p. 862.
- 23. Kim, G., Lu, Y., Hu, Y., and Loizou, P. (2009). “ An algorithm that improves speech intelligibility in noise for normal-hearing listeners,” J. Acoust. Soc. Am. 126, 1486–1494. 10.1121/1.3184603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Lee, D., and Seung, H. S. (1999). “ Learning the parts of objects by non-negative matrix factorization,” Nature 401, 788–791. 10.1038/44565 [DOI] [PubMed] [Google Scholar]
- 25. Li, N., and Loizou, P. (2008). “ Factors influencing intelligibility of ideal binary-masked speech: Implications for noise reduction,” J. Acoust. Soc. Am. 123, 1673–1682. 10.1121/1.2832617 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Linde, Y., Buzo, A., and Gray, R. M. (1980). “ An algorithm for vector quantizer design,” IEEE Trans. Commun. 28, 84–95. 10.1109/TCOM.1980.1094577 [DOI] [Google Scholar]
- 27. Madhu, N., Breithaupt, C., and Martin, R. (2008). “ Temporal smoothing of spectral masks in the cepstral domain for speech separation,” in Proceedings of ICASSP, pp. 45–48. [Google Scholar]
- 28. Mairal, J., Bach, F., Ponce, J., and Sapiro, G. (2009). “ Online dictionary learning for sparse coding,” International Conference on Machine Learning, pp. 689–696. [Google Scholar]
- 29. Mairal, J., Bach, F., Ponce, J., and Sapiro, G. (2010). “ Online learning for matrix factorization and sparse coding,” J. Mach. Learn. Res. 11, 19–60. [Google Scholar]
- 30. Mairal, J., Elad, M., and Sapiro, G. (2008). “ Sparse representation for color image restoration,” IEEE Trans. Image Process. 17, 53–69. 10.1109/TIP.2007.911828 [DOI] [PubMed] [Google Scholar]
- 31. Moore, B. C. J. (2003). An Introduction to the Psychology of Hearing, 5th ed. (Academic, San Diego, CA: ), Chap. 3, pp. 89–147. [Google Scholar]
- 32. Mowlaee, P., Saeidi, R., Christensen, M. G. , Tan, Z., Kinnunen, T., Franti, P., and Jensen, S. H. (2012). “ A joint approach for single-channel speaker identification and speech separation,” IEEE Trans. Audio, Speech, Lang. Process. 20, 2586–2601. 10.1109/TASL.2012.2208627 [DOI] [Google Scholar]
- 33. Pati, Y. C. , Rezaiifar, R., and Krishnaprasad, P. S. (1993). “ Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition,” in Proceedings of the 27th Annual Asilomar Conference on Signals, Systems and Computers, Vol. 1, 40–44. [Google Scholar]
- 34. Radfar, M. H. , Dansereau, R. M. , and Sayadiyan, A. (2007). “ Monaural speech segregation based on fusion of source-driven with model-driven techniques,” Speech Commun. 49, 464–476. 10.1016/j.specom.2007.04.007 [DOI] [Google Scholar]
- 35. Raj, B., Seltzer, M. L. , and Stern, R. M. (2004). “ Reconstruction of missing features for robust speech recognition,” Speech Commun. 43, 275–296. 10.1016/j.specom.2004.03.007 [DOI] [Google Scholar]
- 36. Raj, B., Virtanen, T., Chaudhuri, S., and Singh, R. (2010). “ Non-negative matrix factorization based compensation of music for automatic speech recognition,” in Proceedings of Interspeech, pp. 717–720. [Google Scholar]
- 37. Rothauser, E. H. , Chapman, W. D. , Guttman, N., Hecker, M. H. L. , Nordby, K. S. , Silbiger, H. R. , Urbanek, G. E. , and Weinstock, M. (1969). “ IEEE recommended practice for speech quality measurements,” IEEE Trans. Audio Electroacoust. 17, 225–246. 10.1109/TAU.1969.1162058 [DOI] [Google Scholar]
- 38. Sainath, T. N. , Ramabhadran, B., Picheny, M., Nahamoo, D., and Kanevsky, D. (2011). “ Exemplar-based sparse representation features: from TIMIT to LVCSR,” IEEE Trans Audio, Speech, Lang. Process. 19, 2598–2613. 10.1109/TASL.2011.2155060 [DOI] [Google Scholar]
- 39. Schmidt, M. (2007). “ Speech separation using non-negative feature and sparse non-negative matrix factorization,” Tech. Report, pp. 1–15.
- 40. Schmidt, M. N. , and Olsson, R. K. (2007). “ Linear regression on sparse features for single-channel speech separation,” IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, pp. 26–29. [Google Scholar]
- 41. Seung, H. S. , and Lee, D. (2001). “ Algorithms for non-negative matrix factorization,” Adv. Neural Inf. Process. Syst. 13, 556–562. [Google Scholar]
- 42. Shashanka, M. V. S. , Raj, B., and Smaragdis, P. (2007). “ Sparse overcomplete decomposition for single channel speaker separation,” in Proceedings of ICASSP, pp. 641–644. [Google Scholar]
- 43. Smaragdis, P. (2004). “ Non negative matrix factor deconvolution: extraction of multiple sound sources from monophonic inputs,” Independent Component Analysis and Blind Signal Separation, pp. 494–499. [Google Scholar]
- 44. Smaragdis, P. (2007). “ Convolutive speech bases and their application to supervised speech separation,” IEEE Trans. Audio, Speech, Lang. Process. 15, 1–12. 10.1109/TASL.2006.876726 [DOI] [Google Scholar]
- 45. Srinivasan, S., Roman, N., and Wang, D. L. (2006). “ Binary and ratio time-frequency masks for robust speech recognition,” Speech Commun. 48, 1486–1501. 10.1016/j.specom.2006.09.003 [DOI] [Google Scholar]
- 46. Taal, C. H. , Hendriks, R. C. , Heusdens, R., and Jensen, J. (2011). “ An algorithm for intelligibility prediction of time frequency weighted noisy speech,” IEEE Trans. Audio, Speech, Lang. Process. 19, 2125–2136. 10.1109/TASL.2011.2114881 [DOI] [Google Scholar]
- 47. Virtanen, T. (2007). “ Monaural sound source separation by nonnegative matrix factorization with temporal continuity and spareness criteria,” IEEE Trans. Audio, Speech, Lang. Process. 15, 1066–1074. 10.1109/TASL.2006.885253 [DOI] [Google Scholar]
- 48. Wang, D. L. (2005). “ On ideal binary mask as the computational goal of auditory scene analysis,” in Speech Separation by Humans and Machines, edited by Divenyi P. (Kluwer Academic, Norwell, MA: ), pp. 181–197. [Google Scholar]
- 49. Wang, D. L. (2008). “ Time–frequency masking for speech separation and its potential for hearing aid design,” Trends Amplif. 12, 332–353. 10.1177/1084713808326455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Wang, D. L. , and Brown, G., Eds. (2006). “ Fundamentals of computational auditory scene analysis,” in Computational Auditory Scene Analysis: Principles, Algorithms, and Applications (Wiley-IEEE Press, Hoboken, NJ: ), Chap. 1, pp. 1–37. [Google Scholar]
- 51. Wang, D. L. , Kjems, U., Pedersen, M. S. , Boldt, J. B. , and Lunner, T. (2009). “ Speech intelligibility in background noise with ideal binary time-frequency masking,” J. Acoust. Soc. Am. 125, 2336–2347. 10.1121/1.3083233 [DOI] [PubMed] [Google Scholar]
- 52. Wang, Y., Han, K., and Wang, D. L. (2013). “ Exploring monaural features for classification-based speech segregation,” IEEE Trans. Audio, Speech, Lang. Process. 21, 270–279. 10.1109/TASL.2012.2221459 [DOI] [Google Scholar]
- 53. Wang, Y., and Wang, D. L. (2013). “ Towards scaling up classification-based speech separation,” IEEE Trans. Audio, Speech, Lang. Process. 21, 1381–1390. 10.1109/TASL.2013.2250961 [DOI] [Google Scholar]
- 54. Wilson, K., Raj, B., Smaragdis, P., and Divakaran, A. (2008). “ Speech denoising using nonnegative matrix factorization with priors,” in Proceedings of ICASSP, pp. 4029–4032. [Google Scholar]
- 55. Zhao, X., Shao, Y., and Wang, D. L. (2012). “ CASA-based robust speaker identification,” IEEE Trans. Audio, Speech, Lang. Process. 20, 1608–1616. 10.1109/TASL.2012.2186803 [DOI] [Google Scholar]