Abstract
Formant bandwidth estimation is often observed to be more challenging than the estimation of formant center frequencies due to the presence of multiple glottal pulses within a period and short closed-phase durations. This study explores inherently different statistical properties between linear prediction (LP)–based estimates of formant frequencies and their corresponding bandwidths that may be explained in part by the statistical bounds on the variances of estimated LP coefficients. A theoretical analysis of the Cramér-Rao bounds on LP estimator variance indicates that the accuracy of bandwidth estimation is approximately twice as low as that of center frequency estimation. Monte Carlo simulations of all-pole vowels with stochastic and mixed-source excitation demonstrate that the distributions of estimated LP coefficients exhibit expectedly different variances for each coefficient. Transforming the LP coefficients to formant parameters results in variances of bandwidth estimates being typically larger than the variances of respective center frequency estimates, depending on vowel type and fundamental frequency. These results provide additional evidence underlying the challenge of formant bandwidth estimation due to inherent statistical properties of LP-based speech analysis.
I. INTRODUCTION
Formant bandwidth estimation is generally considered to be challenging due to several factors related to speech production and voice production characteristics. For example, formant bandwidth estimation has been reported to be particularly sensitive to multiple pulses within one glottal cycle and short closed-phase durations of sustained vowels (Hanson and Chuang, 1999). In addition, bandwidth estimation difficulties have also been ascribed to “irregularities in the glottal source spectrum” that may interact with vocal tract acoustics (Klatt, 1980). In continuous speech waveforms, formant tracking is particularly challenging due to the time-varying nature of the glottal source and vocal tract resonators, and algorithms often do not take into account closed-glottis versus open-glottis conditions (Sjölander and Beskow, 2005; Boersma and Weenink, 2009).
Accurate estimation of formant characteristics necessitates the use of external source excitation, such as a neck-mounted vibration source with known sinusoidal inputs swept across a range of fundamental frequencies (Fant, 1962; Fujimura and Lindqvist, 1971). In the more natural and unconstrained speech setting, two approaches are commonly used to estimate formant parameters from the radiated acoustic signal. The first popular approach involves the application of parametric models, such as linear prediction (LP) analysis, to derive speech parameters that compactly describe the resonance properties of a series of acoustic tubes (Atal and Hanauer, 1971). Alternatively, model-free estimation of formant parameters can be performed directly on the time-domain waveform (House and Stevens, 1958) or speech spectrum (Bogert, 1953; Dunn, 1961). Bandwidth estimation has proven difficult using these approaches, and thus investigators have resorted to applying empirically derived relationships between formant frequency and bandwidth (Fant, 1972; Hawks and Miller, 1995; Tappert et al., 1963) or to simply fixing the formant bandwidths to standard values (Olive, 1971; Iseli et al., 2007; Deng et al., 2006).
In the LP-based characterization of an all-pole system, formant candidates are computed by solving the Yule−Walker set of equations to derive weights on past samples to predict a future sample (Atal and Hanauer, 1971). Roots of the resulting prediction polynomial yield complex-conjugate pole pairs whose locations dictate the center frequency and bandwidth of corresponding digital resonators. Statistical analysis of the Yule−Walker equations yields confidence intervals for each weighting coefficient (Jirak, 2012). In fact, the lower bound on variances—the Cramér-Rao bound (CRB)—of the LP coefficient estimates are known to differ depending on the coefficient index in the asymptotic case (Friedlander, 1984) and in short-duration sequences that are more applicable to speech analysis with high fundamental frequencies and short glottal closed phases (Friedlander and Porat, 1989).
Real speech signals are often produced with both voiced and unvoiced characteristics that introduce added complexities, such as the determination of the closed phase of quasi-periodic source excitation (Alku et al., 2009) and the presence of both poles and zeros in the filter transfer function. Such challenges are well known for the various methods of LP analysis, especially for speakers with high fundamental frequencies and/or who are affected by voice disorders (Alku, 2011). Previous theoretical work confirmed the significant increase in the Cramér-Rao lower bound of source parameters when harmonics approach formant frequencies (Mehta et al., 2011). The Monte Carlo approach lends itself to the analysis of vowels synthesized with mixed-source (stochastic plus deterministic) excitation signals to gain additional insight into the inherent properties of LP algorithms that are hypothesized to generalize to multiple types of all-pole signals.
The purpose of the current study is to highlight and understand differences between the accuracies of estimating formant frequencies versus formant bandwidths by exploring the statistical properties inherent in the transformation of LP coefficients to formant parameters using both theoretical and empirical treatments. The theoretical approach derives formant frequencies and bandwidths from multiple sets of LP coefficients that are randomly generated by perturbing baseline sets with additive noise with a covariance structure equal to the Cramér-Rao lower bound. In the empirical approach, formant parameters are estimated from Monte Carlo simulations of synthesized all-pole waveforms using the autocovariance method of LP and LP polynomial factorization.
II. METHODS
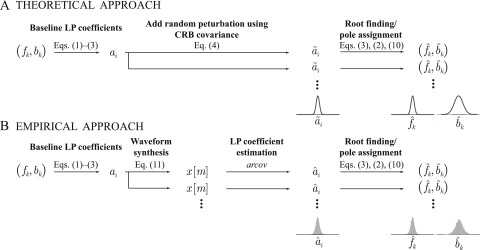
Figure 1 outlines the two approaches taken in this study. The main difference between the two methodological approaches is that the theoretical treatment sets the variances on the LP coefficient distributions ai a priori instead of empirically deriving this variance of LP coefficients from synthesized waveforms. Both theoretical and empirical treatments seek to reveal any systematic differences between the estimation of formant frequencies fk and their associated bandwidths bk when the LP coefficient histograms are propagated through the nonlinear algorithms of root finding and pole assignment.
FIG. 1.
(Color online) Outline of approaches taken to investigate the estimation of given sets of formant frequency and bandwidth (fk, bk). (A) The theoretical approach bypasses waveform synthesis and generates multiple LP coefficient sets by adding variances equal to the CRB of the corresponding baseline coefficient set ai. (B) The empirical approach synthesizes multiple autoregressive processes x[m] and estimates LP coefficients that are transformed to estimated formant frequency-bandwidth pairs . Of interest is the comparison of and dispersions between the empirical (gray histograms) and theoretical (solid lines) approaches.
A. Theoretical lower bounds of frequency and bandwidth estimators
Figure 1(A) illustrates the theoretical approach that investigated the effects of the nonlinear transformation from LP coefficients to formant parameters. Vowel-like parameters were generated by setting fk according to average formant frequencies obtained from adult male speakers producing the following 10 vowels: /i/, /ı/, /ɛ/, /æ/, /ɑ/, /ɔ/, /℧/, /u/, /ʌ/, and /ɝ/ (Peterson and Barney, 1952). Formant bandwidths followed the relation bk = 80 + 120fk/5000 (Mannell, 1998). In contrast to the empirical treatment in Sec. II B, here the statistical properties of formant frequency and bandwidth estimators were determined without the need for waveform generation.
Baseline LP coefficients ai were generated given a set of formant center frequencies fk and associated two-sided, 3-dB bandwidths bk for k ∈ {1, 2, 3}. We parameterized the kth digital resonator to form the following complex-conjugate pole pair (Gold and Rabiner, 1968):
| (1) |
where fs = 10 kHz is the sampling rate, and all parameters are in units of hertz.
Using the speech production model of Schafer and Rabiner (1970), a cascade of K second-order digital resonators modeled the all-pole transfer function T(z):
| (2) |
which can be written in terms of the LP coefficients ai,
| (3) |
where the p coefficients in the denominator can be derived by matching each ai of the prediction polynomial to the coefficients of the multiplied-out polynomial in the denominator of Eq. (2). Thus the baseline fk and bk values were transformed to a baseline set of LP coefficients ai for each vowel type by applying Eqs. (1)−(3) in succession.
The baseline set ai was perturbed with additive noise to yield multiple instantiations of the LP coefficients using the following equation:
| (4) |
where wi is a multivariate Gaussian distribution with covariance structure given by the CRB, a lower bound on the mean-square error of unbiased estimators and thus a lower bound on the variance of the unbiased LP coefficient estimators.
The CRB is known to be different for each LP coefficient estimator (Friedlander, 1984; Friedlander and Porat, 1989), and these differences are potentially further amplified by the nonlinear transformation between LP coefficients and formant frequency and bandwidth parameters. The effects of the transformation in this best-case estimation scenario are investigated in the current theoretical treatment.
The CRB is the inverse of the Fisher information matrix J∞ consisting of the stochastic excitation power σ2 and the p LP coefficients. In the asymptotic condition when sample size M is large, an approximation of J∞ is known to be (Friedlander and Porat, 1989)
| (5) |
where Rp is the p-by-p covariance matrix derived from the LP coefficients as
| (6) |
where the elements of the p-by-p Toeplitz matrices A1 and A2 are specified by the following formulas:
| (7a) |
| (7b) |
For the short durations (M < 100) of windows typically encountered in speech analysis, the asymptotic Fisher information J∞ must be modified to yield accurate CRB values for LP coefficients. Exact computations of the CRB can be derived from the exact Fisher information matrix JM according to the following equation (Friedlander and Porat, 1989):
| (8) |
where the elements of the (p + 1)-by-(p + 1) matrix are given by
| (9a) |
| (9b) |
| (9c) |
where 1 ≤ {i, j} ≤ p and tr{·} denotes the trace operator.
A Monte Carlo analysis was performed for each vowel type by generating 10 000 sets of the perturbed LP coefficients using Eq. (4), where the covariance structure of wi was given by JM−1 after removing the first row and column associated with the CRB of σ2 in Eq. (5). Each set of 's was propagated through the processes of LP polynomial factorization [parameters in Eq. (2) derived from Eq. (3)] and the following pole-to-formant parameter relations to obtain estimates of and (Gold and Rabiner, 1968):
where k ∈ {1, 2, 3} and each pair was ordered such that < . Figure 1(A) schematizes distributions (solid lines) that will be parameterized in terms of bias and variance in this theoretical treatment.
B. Empirical estimation of LP coefficients
Figure 1(B) illustrates the generation of an autoregressive (AR) process that is synthesized given a set of formant center frequencies fk and associated two-sided, 3-dB bandwidths bk. As in the theoretical approach of Sec. II A, we set baseline center frequencies fk to values obtained by Peterson and Barney (1952) for the 10 vowels /i/, /ɪ/, /ɛ/, /æ/, /ɑ/, /ɔ/, /℧/, /u/, /ʌ/, and /ɝ/. Baseline synthesized bandwidths followed the same relation bk = 80 + 120fk/5000 (Mannell, 1998). In contrast to the theoretical treatment, here the statistical properties of formant frequency and bandwidth estimators were determined by analyzing a waveform synthesized using both stochastic-only and mixed-excitation sources at multiple fundamental frequencies.
The baseline fk and bk values were transformed to a baseline set of LP coefficients ai for each vowel type by applying Eqs. (1)−(3) in succession. The resulting LP coefficients were then used to generate the discrete-time stochastic AR(p) process x[m],
| (11) |
where m is the sample index, and u[m] was white Gaussian noise with variance σ2 in the stochastic-only case. In the mixed-excitation cases, u[m] was a periodic source signal-derivative of the Rosenberg type B pulse (Rosenberg, 1971)—with additive white Gaussian noise at a signal-to-noise ratio of 20 dB.
A Monte Carlo analysis of 10 000 instantiations of the AR(6) time series u[m] was performed to explore the statistical properties of LP-based estimates of resonator frequency and bandwidth. The waveform sampling rate was set to fs = 10 kHz, and waveforms of sample length M = 100 (10 ms) were generated with σ2 = 1 (results are independent of σ2). LP analysis of the mixed-excitation source was performed with a priori knowledge of the closed phase from the known periodic source signal.
The covariance method of LP (Matlab's arcov function) with order p = 6 yielded LP coefficient estimates that were transformed to associated center frequency and bandwidth estimates for k ∈ {1, 2, 3} using two steps. First, polynomial factorization of the prediction polynomial in the denominator of Eq. (3) obtained estimates of the complex-conjugate pole pairs in Eq. (2). Second, the pole pairs yielded and using the pole-to-formant parameter transformation in Eq. (10).
C. Statistical evaluation of Monte Carlo simulations
Both theoretical and empirical methods described in Secs. II A and II B, respectively, yielded distributions for and (1 ≤ k ≤ p/2) over the 10 000 simulations for each vowel type. In addition, the empirical approach yields distributions of the estimated LP coefficients (1 ≤ i ≤ p). The resulting distributions are each parameterized by bias and standard deviation values with respect to the known synthesis parameters fk, bk, and ai, respectively. Of particular interest are any systematic disparities between formant frequency and bandwidth estimates among the different vowel types and fundamental frequencies. For example, finding a larger standard deviation for a given parameter's distribution would indicate greater uncertainty (lower accuracy) in the estimation of that parameter.
III. RESULTS
A. Theoretical variance of center frequency and bandwidth estimators
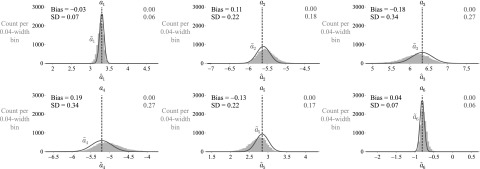
Figure 2 displays illustrative results of the theoretical approach in which CRB-based variability was added to each LP coefficient using Eq. (4) for coefficients pertaining to the adult male vowel /ɑ/, where fk = (730, 1090, 2440) Hz and bk = (98, 106, 134) Hz. The dispersion dictated by the CRB of each coefficient was very similar to the empirical dispersion of estimated LP coefficients derived from the synthesized AR processes. Coefficient pairs , , and exhibited similar biases and variances—LP coefficient estimates are known to correlate with each other (Friedlander and Porat, 1989)—revealing a pattern of statistical symmetry that might play a role in influencing the accuracy of formant frequency and bandwidth estimators. Although CRB analysis assumed unbiased estimators, the bias observed for the LP coefficients was approximately half the value of the standard deviation (SD).
FIG. 2.
(Color online) Distribution of each LP coefficient. In the theoretical approach (solid lines), the CRB dictates the dispersion of each LP coefficient, yielding distributions of . In the empirical approach (gray histograms), LP coefficients are estimated from the stochastic AR(6) process x[m] for each of 10 000 instantiations of u[m]. Baseline LP coefficients represent the three formants of the adult male vowel /ɑ/. Vertical dashed lines indicate true LP coefficients. Bias and SD are given for each empirically derived histogram (left values) and each induced distribution (right values).
Table I reports the SD of histograms for each formant parameter within each of the 10 vowel configurations. Similar to the results observed in Fig. 2, the standard deviation of the center frequency distributions were almost twice that of the bandwidth estimates in all cases. These results indicate that, even in the best-case scenario where LP coefficient estimators exhibit their smallest variances (the CRB), the LP-based computation of formant bandwidths is less accurate than the computation of their respective center frequencies. According to Bartlett's test, the distributions of LP coefficient estimates did not exhibit the same variance within each vowel type.
TABLE I.
Standard deviations (in Hz) of formant frequency and bandwidth estimates obtained in the CRB analysis for 10 vowel configurations (Peterson and Barney, 1952).
| Vowel | ||||||
|---|---|---|---|---|---|---|
| /i/ | 28.5 | 48.7 | 34.9 | 65.9 | 36.9 | 72.1 |
| /ɪ/ | 28.1 | 50.2 | 34.3 | 65.4 | 35.8 | 68.1 |
| /ɛ/ | 28.5 | 51.1 | 33.2 | 63.1 | 35.7 | 67.3 |
| /æ/ | 29.0 | 52.8 | 33.1 | 61.5 | 34.6 | 66.0 |
| /ɑ/ | 30.1 | 56.9 | 32.6 | 56.6 | 34.8 | 65.0 |
| /ɔ/ | 30.5 | 59.7 | 32.0 | 57.4 | 34.2 | 66.0 |
| /℧/ | 28.7 | 52.4 | 31.0 | 55.4 | 33.9 | 63.0 |
| /u/ | 27.9 | 51.5 | 30.5 | 53.6 | 33.8 | 64.5 |
| /ʌ/ | 29.4 | 54.0 | 31.1 | 57.2 | 34.4 | 65.3 |
| /ɝ/ | 28.6 | 52.0 | 33.2 | 63.7 | 34.7 | 63.1 |
B. Empirical dispersion of center frequency and bandwidth estimates
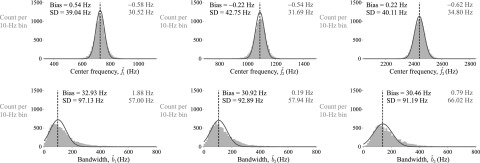
Figure 3 displays illustrative distributions of the derived and parameters for each perturbed set of LP coefficients for the adult male vowel /ɑ/. Recall that the formant center frequencies and bandwidths were estimated from each of 10 000 randomly generated sets of LP coefficients using the covariance method of LP, prediction polynomial factorization, and Eq. (10). The differences between the SD of the center frequency estimators and the SD of the bandwidth estimators are greater than a factor of 2. The discrepancies of the estimator biases demonstrate that the accuracy of estimating the center frequency parameter is higher than that of estimating the bandwidth parameter. In addition, the distributions of the bandwidth estimators skewed to the left and did not follow a Gaussian shape.
FIG. 3.
(Color online) Distributions of estimated center frequencies (top row) and bandwidths (bottom row). In the theoretical treatment (solid lines), center frequency and bandwidth estimates are derived from the LP coefficients perturbed according to the CRB of the corresponding coefficient index. In the empirical treatment (gray histograms), estimates for each of three formant parameters are derived from the LP coefficient sets generated in the waveform-based approach (stochastic excitation). Vertical dashed lines denote baseline values of the adult male vowel /ɑ/. Also reported for each distribution are bias relative to the baseline value and SD.
Table II reports dispersion in terms of SD associated with the distributions of formant frequency and bandwidth estimates for the 10 vowel configurations with stochastic-only excitation. The SD of bandwidth estimates were significantly different from the SD of the associated center frequency estimates across all vowels via a two-sample F-test for equal variances. The average ratio of the SD of bandwidth estimates to the SD of center frequency estimates over all vowels and formant numbers was 2.3, providing empirical evidence that the relatively higher variance of bandwidth estimators potentially contribute to difficulties in computing these values, even in the synthesized settings. In addition, a significant discrepancy was observed between the average absolute bias of the bandwidth distribution (31.4 Hz) and the average absolute bias of the center frequency distribution (0.4 Hz).
TABLE II.
Standard deviations (in Hz) of formant and bandwidth estimates across 10 000 simulations of the 10 synthesized all-pole waveforms with stochastic-only excitation. Average ratio of over all vowels and formants is 2.3.
| Vowel | ||||||
|---|---|---|---|---|---|---|
| /i/ | 38.9 | 79.2 | 41.5 | 93.0 | 43.2 | 99.2 |
| /ɪ/ | 37.3 | 81.2 | 42.1 | 97.7 | 43.6 | 98.4 |
| /ɛ/ | 34.9 | 83.6 | 40.7 | 91.7 | 42.6 | 94.9 |
| /æ/ | 36.2 | 83.9 | 39.7 | 92.8 | 42.4 | 96.2 |
| /ɑ/ | 39.0 | 97.8 | 42.8 | 92.7 | 41.0 | 92.8 |
| /ɔ/ | 40.9 | 109.2 | 44.3 | 91.7 | 40.5 | 91.9 |
| /℧/ | 37.6 | 88.2 | 39.9 | 87.3 | 40.6 | 92.3 |
| /u/ | 38.5 | 85.7 | 39.1 | 82.2 | 39.8 | 89.8 |
| /ʌ/ | 36.8 | 89.5 | 39.5 | 85.4 | 40.7 | 91.1 |
| /ɝ/ | 36.5 | 85.9 | 43.3 | 102.2 | 45.1 | 97.2 |
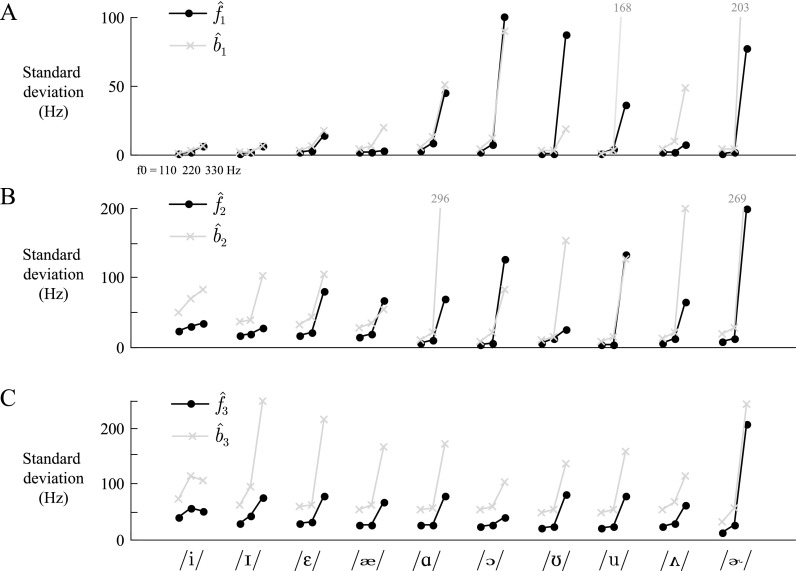
Figure 4 shows the SD of the formant frequency and bandwidth estimates from the Monte Carlo analysis of synthesized vowels with mixed-source excitation at fundamental frequencies of 110, 220, and 330 Hz. As in the stochastic-only synthesis, the standard deviation of the formant bandwidth estimates was typically over two times as high as the standard deviation of the formant frequency estimates on average, with this uncertainty becoming more apparent at higher formants and fundamental frequencies. Of note, the estimation of both frequency and bandwidth was accurate to within 6 Hz for the first formant and 13 Hz for the second formant across all vowels, except for signals at the highest fundamental frequency. Bandwidth estimates became significantly more challenging when estimating parameters of the third formant, and estimation of both center frequency and bandwidth suffered at f0 of 330 Hz.
FIG. 4.
LP analysis of mixed-excitation waveform synthesis with source signal-to-noise ratio of 20 dB. Standard deviations are reported for estimates of center frequency (dark circles) and bandwidth (gray ×'s) of the (A) first, (B) second, and (C) third formant across 10 000 simulations for each of 10 all-pole vowel configurations at fundamental frequency (f0) values of 110, 220, and 330 Hz. Vertical axis ranges were set for optimal visualization, with specific values indicated for out-of-range points.
IV. DISCUSSION
This study focused on the statistical assumptions underlying LP analysis, informing the measurement and analysis of real speech waveforms where the estimation of formant bandwidths has proven challenging for decades. As with any analysis technique, speech scientists must temper their desire for perfect accuracy by recognizing resolution tradeoffs and absolute bounds inherent in certain estimation algorithms. Alternative domains for estimating formant bandwidths may prove to increase accuracy, such as the real cepstrum or regularized LP cepstrum (Deng et al., 2007; Mehta et al., 2012). Large-scale error analysis of vocal tract formants and bandwidths would benefit from the availability of reference databases such as the vocal tract resonance (VTR) database of Deng et al. (2006). Whereas the VTR database contains formant frequency trajectories corrected for plausibility, the bandwidth information is untouched after an automated pass and thus requires validation prior to being useful as an acoustically relevant ground truth (Deng et al., 2006).
The statistical properties of LP coefficient estimators given here assumed unbiased distributions. Nonzero biases in the empirical analysis of Fig. 2 indicate that biases are evident in these estimators that serve to increase the total variance of each estimate. Thus the CRB equations could be further refined in the instance of biased estimators, such as through the derivations in Eldar (2004).
The empirical analysis of mixed-excitation waveforms that include a periodic source and white Gaussian noise input yielded better resolution at a low fundamental frequency for first-formant parameters than that in the stochastic-only case. The second and third formants proved more challenging to estimate with the presence of harmonic components. When dealing with higher fundamental frequencies, even some center frequency variances were observed to surpass corresponding bandwidth variances; in particular, see the standard deviation of center frequencies versus bandwidths for vowel /ɔ/ in Fig. 4(B) and 4(C).
Reasons for the higher uncertainty include the limited number of samples (shorter closed phase) from which to estimate frequency parameters and the sparser harmonic sampling of the underlying formant envelope in the frequency spectrum. The theoretical CRB results of this study suggest an additional limitation on the resolution of formant parameter estimation due to the underlying statistical properties of LP analysis. Future work warrants the investigation of vowel dependence on the statistical properties of LP coefficients and source−filter interactions between harmonic and resonance components.
V. CONCLUSION
This study addressed the difficulty of estimating formant bandwidths relative to their associated center frequencies. Monte Carlo simulations of all-pole vowels demonstrated that the distributions of estimated LP coefficients yield inherent statistical differences between LP-based estimates of formant frequency and bandwidth. The variances of bandwidth estimates are typically larger than the variances of their respective center frequency estimates. A theoretical analysis of the CRBs of LP estimator variance also indicated that the accuracy of bandwidth estimates is also lower (approximately twice as low) as that of center frequency estimates.
ACKNOWLEDGMENTS
Work supported in part by the U.S. Army Research Office under PECASE Award W911NF-09-1-0555; by the U.S. Office of Naval Research under Award N00014-14-1-0819; by the UK EPSRC under Mathematical Sciences Established Career Fellowship EP/K005413/1; by the UK Royal Society under a Wolfson Research Merit Award; and by Marie Curie FP7 Integration Grant PCIG12-GA-2012-334622 within the 7th European Union Framework Program. Support also received from a grant from the NIH National Institute on Deafness and Other Communication Disorders (R33 DC011588) and the Voice Health Institute. Manuscript contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH. The authors thank D. Rudoy (Rudoy, 2010), whose work inspired the current study.
References
- 1. Alku, P. (2011). “ Glottal inverse filtering analysis of human voice production—A review of estimation and parameterization methods of the glottal excitation and their applications,” Sadhana: Indian Acad. Sci. Proc. Eng. 36, 623–650. 10.1007/s12046-011-0041-5 [DOI] [Google Scholar]
- 2. Alku, P., Magi, C., Yrttiaho, S., Backstrom, T., and Story, B. (2009). “ Closed phase covariance analysis based on constrained linear prediction for glottal inverse filtering,” J. Acoust. Soc. Am. 125, 3289–3305. 10.1121/1.3095801 [DOI] [PubMed] [Google Scholar]
- 3. Atal, B. S., and Hanauer, S. L. (1971). “ Speech analysis and synthesis by linear prediction of the speech wave,” J. Acoust. Soc. Am. 50, 637–655. 10.1121/1.1912679 [DOI] [PubMed] [Google Scholar]
- 4. Boersma, P., and Weenink, D. (2009). “ Praat: Doing phonetics by computer,” version 5.1.40, University of Amsterdam, The Netherlands, http://www.fon.hum.uva.nl/praat/ (Last viewed 13 July 2009).
- 5. Bogert, B. P. (1953). “ On the band width of vowel formants,” J. Acoust. Soc. Am. 25, 791–792. 10.1121/1.1907176 [DOI] [Google Scholar]
- 6. Deng, L., Acero, A., and Bazzi, I. (2006). “ Tracking vocal tract resonances using a quantized nonlinear function embedded in a temporal constraint,” IEEE Trans. Audio Speech Lang. Process. 14, 425–434. 10.1109/TSA.2005.855841 [DOI] [Google Scholar]
- 7. Deng, L., Lee, L. J., Attias, H., and Acero, A. (2007). “ Adaptive Kalman filtering and smoothing for tracking vocal tract resonances using a continuous-valued hidden dynamic model,” IEEE Trans. Audio Speech Lang. Process. 15, 13–23. 10.1109/TASL.2006.876724 [DOI] [Google Scholar]
- 8. Dunn, H. K. (1961). “ Methods of measuring vowel formant bandwidths,” J. Acoust. Soc. Am. 33, 1737–1746. 10.1121/1.1908558 [DOI] [Google Scholar]
- 9. Eldar, Y. (2004). “ Minimum variance in biased estimation: Bounds and asymptotically optimal estimators,” IEEE Trans. Signal Process. 52, 1915–1930. 10.1109/TSP.2004.828929 [DOI] [Google Scholar]
- 10. Fant, G. (1962). “ Formant bandwidth data,” Speech Transm. Lab. Q. Progr. Status Rep. 3, 1–2. [Google Scholar]
- 11. Fant, G. (1972). “ Vocal tract wall effects, losses, and resonance bandwidths,” Speech Transm. Lab. Q. Progr. Status Rep. 13, 28–52. [Google Scholar]
- 12. Friedlander, B. (1984). “ On the computation of the Cramer-Rao bound for ARMA parameter estimation,” IEEE Trans. Acoust. 32, 721–727. 10.1109/TASSP.1984.1164391 [DOI] [Google Scholar]
- 13. Friedlander, B., and Porat, B. (1989). “ The exact Cramer-Rao bound for Gaussian autoregressive processes,” IEEE Trans. Aerosp. Electron. Syst. 25, 3–7. 10.1109/7.18656 [DOI] [Google Scholar]
- 14. Fujimura, O., and Lindqvist, J. (1971). “ Sweep-tone measurements of vocal-tract characteristics,” J. Acoust. Soc. Am. 49, 541–558. 10.1121/1.1912385 [DOI] [PubMed] [Google Scholar]
- 15. Gold, B., and Rabiner, L. (1968). “ Analysis of digital and analog formant synthesizers,” IEEE Trans. Audio Electroacoust. 16, 81–94. 10.1109/TAU.1968.1161954 [DOI] [Google Scholar]
- 16. Hanson, H. M., and Chuang, E. S. (1999). “ Glottal characteristics of male speakers: Acoustic correlates and comparison with female data,” J. Acoust. Soc. Am. 106, 1064–1077. 10.1121/1.427116 [DOI] [PubMed] [Google Scholar]
- 17. Hawks, J. W., and Miller, J. D. (1995). “ A formant bandwidth estimation procedure for vowel synthesis,” J. Acoust. Soc. Am. 97, 1343–1344. 10.1121/1.412986 [DOI] [PubMed] [Google Scholar]
- 18. House, A., and Stevens, K. (1958). “ Estimation of formant band widths from measurements of transient response of the vocal tract,” J. Speech Hear. Res. 1, 309–315. 10.1044/jshr.0104.309 [DOI] [PubMed] [Google Scholar]
- 19. Iseli, M., Shue, Y.-L., and Alwan, A. (2007). “ Age, sex, and vowel dependencies of acoustic measures related to the voice source,” J. Acoust. Soc. Am. 121, 2283–2295. 10.1121/1.2697522 [DOI] [PubMed] [Google Scholar]
- 20. Jirak, M. (2012). “ Simultaneous confidence bands for Yule−Walker estimators and order selection,” Ann. Stat. 40, 494–528. 10.1214/11-AOS963 [DOI] [Google Scholar]
- 21. Klatt, D. H. (1980). “ Software for a cascade/parallel formant synthesizer,” J. Acoust. Soc. Am. 67, 971–995. 10.1121/1.383940 [DOI] [Google Scholar]
- 22. Mannell, R. H. (1998). “ Formant diphone parameter extraction utilising a labelled single speaker database,” in Proceedings of the Fifth International Conference on Spoken Language Processing, 30 November−1 December, Sydney, Australia, Vol. 5, pp. 2003–2006. [Google Scholar]
- 23. Mehta, D. D., Rudoy, D., and Wolfe, P. J. (2011). “ Joint source-filter modeling using flexible basis functions,” in Proceedings of the IEEE International Conference Acoustics, Speech and Signal Processing, 22–27 May, Prague, pp. 5888–5891. [Google Scholar]
- 24. Mehta, D. D., Rudoy, D., and Wolfe, P. J. (2012). “ Kalman-based autoregressive moving average modeling and inference for formant and antiformant tracking,” J. Acoust. Soc. Am. 132, 1732–1746. 10.1121/1.4739462 [DOI] [PubMed] [Google Scholar]
- 25. Olive, J. P. (1971). “ Automatic formant tracking by a Newton−Raphson technique,” J. Acoust. Soc. Am. 50, 661–670. 10.1121/1.1912681 [DOI] [PubMed] [Google Scholar]
- 26. Peterson, G. E., and Barney, H. L. (1952). “ Control methods used in a study of the vowels,” J. Acoust. Soc. Am. 24, 175–184. 10.1121/1.1906875 [DOI] [Google Scholar]
- 27. Rosenberg, A. E. (1971). “ Effect of glottal pulse shape on the quality of natural vowels,” J. Acoust. Soc. Am. 49, 583–590. 10.1121/1.1912389 [DOI] [PubMed] [Google Scholar]
- 28. Rudoy, D. (2010). “ Nonstationary time series modeling with application to speech signal processing,” Doctoral dissertation, Harvard University, Cambridge, MA. [Google Scholar]
- 29. Schafer, R. W., and Rabiner, L. R. (1970). “ System for automatic formant analysis of voiced speech,” J. Acoust. Soc. Am. 47, 634–648. 10.1121/1.1911939 [DOI] [PubMed] [Google Scholar]
- 30. Sjölander, K., and Beskow, J. (2005). “ WaveSurfer for Windows,” version 1.8.5, KTH Royal Institute of Technology, Stockholm, Sweden, http://www.speech.kth.se/wavesurfer/ (Last viewed 19 November 2011).
- 31. Tappert, C. C., Martony, J., and Fant, G. (1963). “ Spectrum envelopes for synthetic vowels,” Speech Transm. Lab. Q. Progr. Status Rep. 4, 2–6. [Google Scholar]