Comparing otoacoustic emissions evoked by chirp transients with constant absorbed sound power and constant incident pressure magnitude

Abstract

Human ear-canal properties of transient acoustic stimuli are contrasted that utilize measured ear-canal pressures in conjunction with measured acoustic pressure reflectance and admittance. These data are referenced to the tip of a probe snugly inserted into the ear canal. Promising procedures to calibrate across frequency include stimuli with controlled levels of incident pressure magnitude, absorbed sound power, and forward pressure magnitude. An equivalent pressure at the eardrum is calculated from these measured data using a transmission-line model of ear-canal acoustics parameterized by acoustically estimated ear-canal area at the probe tip and length between the probe tip and eardrum. Chirp stimuli with constant incident pressure magnitude and constant absorbed sound power across frequency were generated to elicit transient-evoked otoacoustic emissions (TEOAEs), which were measured in normal-hearing adult ears from 0.7 to 8 kHz. TEOAE stimuli had similar peak-to-peak equivalent sound pressure levels across calibration conditions. Frequency-domain TEOAEs were compared using signal level, signal-to-noise ratio (SNR), coherence synchrony modulus (CSM), group delay, and group spread. Time-domain TEOAEs were compared using SNR, CSM, instantaneous frequency and instantaneous bandwidth. Stimuli with constant incident pressure magnitude or constant absorbed sound power across frequency produce generally similar TEOAEs up to 8 kHz.

NOMENCLATURE

ADC

analog-to-digital converter

CSM

coherence synchrony modulus

DAC

digital-to-analog converter

DFT

discrete Fourier transform

DPOAE

distortion product otoacoustic emission

GD

group delay

GS

group spread

IB

instantaneous bandwidth

IF

instantaneous frequency

peSPL

peak-to-peak equivalent sound pressure level

rms

root-mean-square

SD

standard deviation

SE

standard error of the mean

SEL

sound exposure level

SFOAE

stimulus frequency otoacoustic emission

SNR

signal-to-noise ratio

SPL

sound pressure level

Stm

stimulus

TEOAE

transient-evoked otoacoustic emission

TM

tympanic membrane

G

acoustic conductance

G₀

reference acoustic conductance, ${10}^{-8}$ m⁴ s/kg (SI)

W

absorbed sound power

W₀

reference absorbed sound power, $4\times {10}^{-18}$ Watt

L_F

sound spectrum level of forward pressure at the probe tip

L_G

conductance level at the probe tip

L_P

sound spectrum level of pressure at the probe tip

L_Q

sound spectrum level of incident pressure at the probe tip in calibration tube

L_Qe

sound spectrum level of incident pressure at the probe tip in ear

L_TM

sound spectrum level of equivalent pressure at the TM in ear of same area as calibration tube

L_TMe

sound spectrum level of equivalent pressure at the TM in ear

L_W

absorbed sound power level

I. INTRODUCTION

In response to transient sound presented in the ear canal, a transient-evoked otoacoustic emission (TEOAE) (Kemp, 1978) is generated within the cochlea through a distribution of reflections arising from the structural irregularities in outer hair cells and related structures along the organ of Corti (Zweig and Shera, 1995). On the basis of the compressive nonlinearity of the function of outer hair cells in response to sound stimuli presented at low to moderate levels (Zwicker, 1979), differential procedures have been developed to analyze the TEOAE by separating out the approximately linear growth of the sound stimulus from the compressively nonlinear growth of the TEOAE. Earlier procedures (Kemp et al., 1986) were refined to provide TEOAE data to frequencies as high as 4–5 kHz, and later procedures provide TEOAE data out to as high as 15 kHz (Goodman et al., 2009). As the bandwidth of the sound stimuli that generate TEOAEs has increased, the need to control for the frequency variations of ear-canal acoustics at high frequencies has become ever more important to interpret and clinically utilize TEOAEs.

The first goal of the present study is to compare different approaches to control for standing-wave effects in the ear canal in the design of the sound stimuli used to measure TEOAEs. The second goal is to compare TEOAEs measured using two types of sound stimuli with differing frequency variations over the TEOAE measurement bandwidth, one based on incident sound pressure and the other based on absorbed sound power. The study analyzes data obtained from adult human ears with normal function. The main hypothesis is that TEOAEs recorded using transient sound stimuli with fixed peak-to-peak levels are nearly equivalent across different calibration techniques, one using constant incident sound pressure across frequency and the other using constant absorbed sound power across frequency.¹ While the emphasis in this report is on TEOAEs, the issues related to stimulus calibration across frequency are shared in part in measuring other responses to sound, including distortion product (DP) OAEs and stimulus-frequency (SF) OAEs, whether measured using fixed stimulus frequencies or a swept-tone or chirp paradigm.

A. Stimulus control for standing wave effects

A constant-voltage method is a simple approach to calibrate the sound stimulus level, for which a constant voltage level is applied at all test frequencies to the receiver(s) in the TEOAE probe inserted into the ear canal. Other calibration methods have been devised: the sound pressure spectrum level L_P may be calibrated in a coupler (or artificial ear simulator) or using a real-ear measurement. The stimulus spectrum is then adjusted so as to equalize the total L_P measured by a microphone at a particular location in the coupler or ear canal. Siegel (2007) describes these methods and contrasts their properties in terms of OAE measurements.

Rather than calibrating based on the total pressure, Goodman et al. (2009) constructed a procedure to maintain a constant level L_Q of incident pressure across frequency, and used it to measure click-evoked OAEs (termed click TEOAEs) and behavioral hearing thresholds to 15 kHz. L_Q is measured as the sound pressure spectrum level in a transient stimulus (or temporally gated tone for the case of calibrating a stimulus for DPOAE or SFOAE measurements) for the probe inserted into a long tube closed at its far end. The round-trip acoustic delay time within the tube is sufficiently long to measure a steady-state response to the transient sound at sufficiently short times that the acoustic response ends before the first sound reflection returns from the opposite end of the tube. Because of the absence of standing waves within the long tube, the resulting total pressure is equal to the incident pressure (Keefe, 1997; Keefe and Schairer, 2011).

Another approach to calibrating the sound stimulus evoking the OAE relies on the measurement of an acoustic reflectance or admittance response in the ear canal. Some basic definitions are needed. It is sufficiently accurate for present purposes to assume that the sound field in the ear canal is described by frequency (or time) at each location along the central axis of the ear canal. While present at high frequencies, contributions from the three-dimensional nature of the sound field are small and are not considered in this report. The total pressure at any location in the ear canal may be represented in terms of a forward pressure wave directed toward the tympanic membrane (TM) and a reverse pressure wave directed away from the TM. The (acoustic) pressure reflectance at a particular location and sound frequency is the ratio of the reverse pressure to the forward pressure. The (acoustic) admittance at the probe tip is the ratio of the volume velocity directed into the ear canal to the total pressure at the probe tip. The pressure reflectance and admittance are transfer functions that may also be defined at the TM or any other location within the interior of the ear canal.

With the additional information provided by a reflectance/admittance measurement, it is possible to calibrate a sound stimulus in terms of other variables besides total pressure, for example, in terms of constant absorbed sound power (W) spectrum level L_W (Keefe and Levi, 1996; Keefe and Schairer, 2011) or constant forward pressure spectrum level L_F (Scheperle et al., 2008). Calibrating the ear-canal sound in terms of absorbed sound power helped interpret a tip-to-tail level difference of the suppression tuning curve of SFOAEs at high frequencies (Keefe and Schairer, 2011).

Scheperle et al. (2011) described benefits of quantifying ear-canal sound level in terms of forward pressure rather than total pressure for clinical DPOAE measurements, and described technical improvements to measure L_F up to 10 kHz. They raised the issue of whether middle-ear status should be taken into account when calibrating the ear-canal stimulus level, as the cochlea may not act as an ideal power detector. The question of whether the cochlea is a detector of pressure, power or some other variable appears largely unrelated to the choice of using a pressure variable or absorbed power in the ear canal that is coupled to the TM in the context of measuring an OAE or other physiological or behavioral response. Neglecting small contributions from OAEs, the power absorbed by the middle ear is dissipated by the power absorbed within the middle ear and the power delivered to the inner ear. Neglecting third-window effects within the inner ear and assuming that power transmission within the cochlea takes the form of a one-dimensional traveling wave on the basilar membrane with fluid coupling, the power delivered to the basal end of the cochlea is proportional to the squared magnitude of the forward pressure of the cochlear transmission line times the input conductance of that line. The sound power absorbed by the middle ear is an upper limit to the power injected into the cochlea. Thus, a measurement of absorbed sound power level by the middle ear may be related to either transmitted power into the cochlea or forward pressure level in the cochlear traveling wave. This summary omits other relevant properties of cochlear mechanics, such as the presence of a reflected traveling wave from the helicotrema (at low frequencies).

Souza et al. (2014) described nine alternative procedures to estimate ear-canal stimulus level up to 20 kHz, including three procedures for $L_P,$ L_F, and $L_W.$ Two procedures were based on calibrated measurements in an ear-canal simulator designed to mimic the characteristics of an average adult ear. These two shared with L_Q the reliance on measurements in some type of coupler rather than an ear. Advantages of L_Q are that it can be used at all audible frequencies whereas the accuracy of the artificial ear simulators does not extend beyond 8 kHz (Souza et al., 2014), and the coupler sound field is influenced by standing waves that do not affect $L_Q.$ Although L_Q was not investigated in Souza et al. (2014), they studied an incident pressure spectrum level $L_{\mathit{Q}\mathit{e}},$ which may be expressed in terms of L_Q and the estimated ear-canal area in each test ear. For example, a larger or smaller ear-canal area by 50% would lead, respectively, to a order-of-magnitude decrease in L_Q in the ear canal by about 3.5 dB or increase by 6.0 dB, respectively (as described below). This range is similar to the ∼10 dB spread in L_Qe reported by Souza et al.

Souza et al. (2014) estimated the total pressure spectrum level at the TM using an interpolation between pressure levels measured in the ear-canal at the probe tip and $L_Q.$ They observed that the level of the eardrum pressure magnitude $\left|P_m\right|$ exceeded L_Q at the half-wavelength frequency of the ear-canal standing wave. Their interpolation was based on the assumption that the pressure magnitude $\left|P_m\right|$ at the frequency of the first quarter-wavelength pressure null closely approximated the incident pressure magnitude $\left|Q\right|,$ whose level is $L_Q.$ They confirmed this assumption in measurements performed with an ear simulator, but the assumption has not been tested in real-ear measurements, for which L_Qe in each ear differs from L_Q in an ear simulator due to the difference in areas between the ear canal and the entryway tube of the ear simulator. In addition, L_Q may differ in the ear simulator relative to the area of the tubes used to calibrate the reflectance measurement. This assumption in human ears is expected to be valid to within the variability of $\left|L_{\mathit{Q}\mathit{e}}-L_Q\right|.$

Finally, Souza et al. (2014) considered two alternative variables with which to estimate ear-canal stimulus level based on the magnitudes of the transmitted forward pressure and the integrated pressure. Each variable has problems of interpretation. For the forward pressure P_Fm at the TM boundary of the middle ear, Withnell et al. (2009) defined a transmitted forward pressure into the middle ear as $P_{\mathit{F}\mathit{m}}(1-R_m).$ If the TM were at some interior location within a one-dimensional acoustical transmission line at which a reflected pressure was $P_{\mathit{F}\mathit{m}}\hspace{0.17em}{R}_m,$ the term $P_{\mathit{F}\mathit{m}}(1-R_m)$ would be the transmitted forward pressure wave past that location. However, the TM forms a boundary of the ear canal modeled as an acoustic transmission line of finite length, and no forward sound pressure wave is directly transmitted through the TM. The difference in the total pressure P_m acting over the TM relative to the pressure in the middle-ear cavity generates a mechanical motion of the TM and the structures into which it is coupled (assuming these pressures are uniform) (Zwislocki, 1962). Thus, the transmitted forward pressure level in duct acoustics is not closely related to the problem of estimating the ear-canal sound level.

Lewis et al. (2009) defined an integrated pressure as the sum of the magnitudes of the forward and reverse pressures at the probe tip, but inaccurately described its associated integrated pressure level as the sound level entering the middle ear. Consider a probe inserted in a leak-free manner into a cylindrical ear canal terminated at its end by the TM, such that ear-canal losses are sufficiently small to neglect. The sum of the magnitudes of the forward and reverse pressures at the probe tip equals the sum of the magnitudes of the forward and reverse pressures at the TM, but this latter sum is not equal to the magnitude of the pressure at the TM. This is because the pressure reflectance R_m of the middle ear at the TM has a non-zero phase, or equivalently, a non-zero group delay (Keefe et al., 2015; Feeney et al., 2016).

Souza et al. (2014) concluded that forward pressure was advantageous because it quantified stimulus phase and had a smaller dependence on insertion depth in the canal compared to absorbed sound power and incident sound pressure. The present report did not consider any insertion-depth dependence of the estimates of these quantities, but calculated all acoustical variables at the probe tip. In a calibration using constant level of incident sound pressure or of absorbed sound power, the stimulus phase is completely specified in terms of the magnitude and phase of the incident sound pressure, total ear-canal sound pressure and the source reflectance. An attractive property of absorbed sound power at the probe tip is that its calculation does not require the estimation of ear-canal area from measured acoustic data. In contrast, a calibration using forward sound pressure at the probe tip relies on estimating, or directly measuring, the area at the probe tip. A second attractive property is that conservation of energy in a one-dimensional description of the ear-canal sound field requires that the absorbed sound power at the probe tip over a given measurement duration is equal to the absorbed sound power at the eardrum plus the absorbed sound power at any interior location between the probe tip and eardrum. The latter interior losses are mainly due to power loss at the ear-canal walls. Thus, the absorbed sound power at the probe tip is an upper bound to that at the eardrum. To the extent that the wall losses in the short section of ear canal between the probe tip and eardrum are small, then the absorbed power at the probe tip is approximately equal to that at the eardrum. The latter is the power absorbed by the middle ear.

B. Chirp TEOAEs

As the bandwidth of click TEOAEs has increased in past years, the technical requirements for the probe have become more strict because of the need to generate short-duration stimuli with more high-frequency content without creating excessive distortion. Such system distortion would interfere with a TEOAE measurement. While TEOAEs have been most commonly measured using click stimuli, they can also be measured with other stimuli including chirps. One important property of a chirp is that its crest factor, which is defined as the ratio of its peak amplitude to its root-mean-square (rms) amplitude, is smaller than for the click, because the energy in the chirp is more spread out over time than in the click. Thus, chirps have attractive properties for TEOAE measurements in that they limit the onset amplitude of system distortion.

Each of the two chirp stimuli used in a recent TEOAE study (Keefe et al., 2016) was constructed by filtering a click stimulus by an allpass filter. The click stimulus was designed to have an approximately constant incident pressure spectrum at all frequencies in the analysis bandwidth (0.7–8 kHz). Because the gain of any allpass filter is unity at all frequencies, the magnitude spectra of the click and chirp stimuli were the same. One allpass filter resulted in a positive chirp with a linear group delay whose local frequency in the stimulus waveform increased with increasing time. The other allpass filter resulted in a negative chirp with a linear group delay whose local frequency in the stimulus waveform decreased with increasing time. The negative chirp was a time-reversed positive chirp.

The use of the click, positive chirp and negative chirp stimuli afforded the opportunity to test whether the resulting TEOAEs differed in their properties across the three stimulus-phase conditions. TEOAEs had substantially the same, but not identical, properties across stimulus conditions once the effects of stimulus-phase differences were removed from the TEOAE responses. The stimulus-phase difference of either chirp TEOAE relative to the click TEOAE was removed by applying the inverse of the allpass filter to the TEOAE waveform. The resulting inverse-filtered TEOAE waveform was termed the equivalent-click TEOAE. The click TEOAE and equivalent-click TEOAEs were parameterized in terms of four signal-processing moments: group delay (GD), group spread (GS), instantaneous frequency (IF) and instantaneous bandwidth (IB) that are further described below. Small TEOAE differences that were observed across the three conditions of stimulus phase included mean differences in their signal-processing moments (GD, GS, IF, and IB), and in particular, between TEOAEs recorded with positive- and negative-chirp stimuli. These differences were concluded to be related to spatial-temporal differences in the nonlinear mechanics on the basilar membrane.

As described above, a prior measurement of wideband reflectance in the test ear provides additional information with which to adjust the calibration of the sound stimulus in the ear canal that is used in subsequent TEOAE testing. The present study preferentially weighted the positive and negative chirp stimulus spectra so as to generate a constant level of absorbed sound power in the test ear across the frequency range. The null hypothesis is that the resulting TEOAE responses are identical across the constant L_Q and constant L_W stimulus conditions when the peak-to-peak equivalent (pe) sound pressure level (SPL) is held approximately fixed in each condition.

This is a comparison of two stimulus conditions that should each ameliorate the effects of standing waves in the ear canal. What is being examined is whether there is any practical difference in calibrating in terms of the incident pressure magnitude versus absorbed sound power, for which the first does not require a reflectance measurement and the second does require one. In the event that the null hypothesis is rejected, the resulting data would provide useful information on effects of spatial-temporal differences in the nonlinear mechanics on the basilar membrane that are involved in the generation of the observed TEOAEs.

II. THEORY: CALIBRATING THE SOUND STIMULUS

This section expands on the literature review of stimulus calibration in Sec. I by describing the quantitative theory underlying the calibration of the sound stimulus. This theory is relevant for evoked OAE measurements and other measurements involving sound delivery in the ear canal. All acoustical variables are measured as discrete-time waveforms in terms of a sample period T and duration of N samples. The discrete Fourier transform (DFT) of the waveform is calculated and analyzed at discrete frequencies for integers k between 0 and $N-1.$ Because real signals are analyzed, it is sufficient to consider k between 0 and $N/2.$

A. Power, pressure, forward pressure, and incident pressure

The (acoustic) conductance $G[k]$ at f_k is the real part of the measured acoustic admittance $Y[k]$ at the probe tip. A reference conductance G₀ is defined equal to 1 mmho or 0.001 mho (CGS), which is ${10}^{-8}$ m⁴ s/kg (SI). The mmho unit is a standard unit in audiological testing. The conductance level is defined as

$$L_G[k]=10\hspace{0.17em}\text{log}\hspace{0.17em}G\left[k\right]/G_0.$$ (1)

The absorbed sound power $W[k]$ is

$$W\left[k\right]=\frac{1}{2}G\left[k\right]\hspace{0.17em}\left|P\right[k]{|}^2,$$ (2)

and expressed as an absorbed sound power spectrum level L_W relative to W₀ by

$$L_W[k]=10\hspace{0.17em}\text{log}\hspace{0.17em}(W\left[k\right]/W_0).$$ (3)

The common logarithm is used throughout this report. The reference value used for absorbed power is $W_0=4\times {10}^{-18}$ Watt. This value was selected so that L_W = 0 dB for a sinusoidal tone at 0 dB SPL delivering power into a conductance of 1 mmho. With these definitions, the normalized levels satisfy

$$L_W=L_P+L_G.$$ (4)

Assume for the moment that the ear canal has the same area as the calibration tube used to measure the incident pressure $Q[k].$ Then, the total pressure spectrum in the ear canal $P[k]$ at the probe tip is related to the incident pressure spectrum $Q[k],$ the source pressure reflectance $R_0[k]$ of the probe, and the pressure reflectance $R[k]$ of the ear by (Keefe, 1997)

$$P\left[k\right]=Q\left[k\right]\left(\frac{1+R\left[k\right]}{1-R_0\left[k\right]\hspace{0.17em}R\left[k\right]}\right).$$ (5)

The corresponding incident sound pressure spectrum level $L_Q[k]$ is calculated in the same manner as L_P for total ear-canal pressure. When $R[k]$ is zero (e.g., in the long tube), then $P[k]$ is equal to $Q[k]$ in Eq. (5).

The $P[k]$ may be decomposed as the sum of a forward pressure $P_F[k]$ traveling toward the TM and a reverse pressure $P_R[k]$ traveling back toward the probe microphone, i.e.,

$$P\left[k\right]=P_F\left[k\right]+P_R\left[k\right],$$ (6)

with

$$P_R\left[k\right]=R\left[k\right]\hspace{0.17em}{P}_F\left[k\right].$$ (7)

Using Eqs. (5)–(7), the forward pressure satisfies (Keefe, 1997)

$$P_F\left[k\right]=\frac{Q\left[k\right]}{1-R_0\left[k\right]\hspace{0.17em}R\left[k\right]}.$$ (8)

This relation describes how forward pressure is a superposition of the incident pressure and all the multiple internal reflections in the ear canal between the probe and TM. The case of different areas is considered below, in which in the tube is replaced in Eqs. (5) and (8) by a different $Q_e[k]$ in the ear.

Souza et al. (2014) reported a greater sensitivity for L_W than for L_F in measuring behavioral hearing thresholds above 5 kHz when results from two probe insertion depths were compared in the same test session.

B. Estimating an equivalent pressure at the TM

Swept-tone stimulus-frequency (SF) OAEs have been measured using a procedure with constant equivalent pressure level at the TM under the assumptions that the ear canal has a cylindrical geometry and an immobile TM (Chen et al., 2014). The latter assumption allows estimation of the ear-canal length from a “quarter-length frequency” in the measured sound pressure level. Chen et al. used measurements in 30 different tube lengths to calculate the ear pressure level at the TM from pressure recordings at the probe tip.

This section describes the calculation of an equivalent pressure at the TM from measured data, in which the term equivalent refers to the use of a model with which to calculate the response at the TM. In contrast to Chen et al. (2014), this technique allows for the presence of TM mobility. A cylindrical model of ear-canal acoustics is used for a loss-free acoustic wave number $k_0=2\pi f/\lambda$ for sound of frequency f and wavelength λ traveling in a canal of length x, in which a time dependence $e^{j2\pi ft}$ is assumed. The forward and reverse pressures at the probe are P_F and $P_R,$ respectively, and the forward and reverse pressures at the TM are P_Fm and $P_{\mathit{R}\mathit{m}},$ respectively. The pairs of forward and reverse pressures are related according to wave motion between the probe and TM, i.e.,²

$$\begin{array}{c}{P}_{\mathit{F}\mathit{m}}=e^{-j{k}_{0}x}\hspace{0.17em}{P}_F,\\ P_{\mathit{R}\mathit{m}}=e^{j{k}_{0}x}\hspace{0.17em}{P}_R.\end{array}$$ (9)

For the forward-directed wave impinging on the TM, the pressure reflectance R_m at the TM is

$$R_m=P_{\mathit{R}\mathit{m}}/P_{\mathit{F}\mathit{m}}.$$ (10)

The ear reflectance R just beyond the probe tip in Eqs. (5) and (7) is related to the ear reflectance R_m at the TM by the round-trip path-length distance 2x between the probe and TM:

$$R=R_m\hspace{0.17em}{e}^{-2j{k}_{0}x}.$$ (11)

It follows from Eqs. (5)–(11) that the total pressure $P_m=P_{\mathit{F}\mathit{m}}+P_{\mathit{R}\mathit{m}}$ and forward pressure at the TM are

$$\begin{array}{c}{P}_m\left(f\right)=\frac{Q\hspace{0.17em}\left(1+R_m\right)e^{-j{k}_{0}x}}{1-R_0\hspace{0.17em}{R}_m\hspace{0.17em}{e}^{-2j{k}_{0}x}},\\ P_{\mathit{F}\mathit{m}}\left(f\right)=\frac{Q\hspace{0.17em}{e}^{-j{k}_{0}x}}{1-R_0\hspace{0.17em}{R}_m\hspace{0.17em}{e}^{-2j{k}_{0}x}}.\end{array}$$ (12)

Equations (11) and (12) for pressure at the TM converge to Eqs. (5)–(8) for pressure at the probe tip as x approaches zero. The sound pressure spectrum level using $\left|P_m\right|$ is termed $L_{\mathit{T}\mathit{M}}.$

The quarter-wavelength condition at frequency $f_{\lambda /4}$ occurs at $k_{0}x=\pi /2,$ at which the total pressure at the TM is

$$P_m\left(f_{\lambda /4}\right)=\frac{-jQ\hspace{0.17em}\left(1+R_m\right)}{1+R_0\hspace{0.17em}{R}_m}.$$ (13)

The magnitude $\left|P_m(f_{\lambda /4})\right|$ differs from $\left|Q\right|$ by the factor $\left|(1+R_m)/(1+R_0\hspace{0.17em}{R}_m)\right|,$ with each reflectance evaluated at frequency $f_{\lambda /4}.$ This differs from the assumption in Souza et al. (2014) that $\left|P_m\right|$ in the ear and $\left|Q\right|$ are equal at frequency $f_{\lambda /4}$ using $\left|Q\right|$ measured in the long tube. Another difference is that $\left|Q\right|$ measured in the ear and in the long tube are unequal if their areas differ.

If the length between the probe and TM is known and if the ear-canal area is equal to that of the anechoic tube in which L_Q was measured, then it is possible to estimate the total and forward pressure at the TM using this model by replacing R_m on the right hand side of Eq. (12) by R measured at the probe tip based on Eq. (11). The resulting expression for P_m is

$$P_m\left(f\right)=\frac{Q\hspace{0.17em}\left(e^{-j{k}_{0}x}+R{e}^{j{k}_{0}x}\right)}{1-R_0\hspace{0.17em}R}.$$ (14)

Here written in a reflectance representation, Eq. (14) is equivalent to an expression relating TM pressure to the probe-tip pressure in an admittance representation (Rabinowitz, 1981).

The incident pressure in the anechoic tube $Q[k]$ is scaled by the characteristic impedance Z_c that varies inversely with the tube area S. When the probe is inserted into an ear canal of area S_e at the probe tip, the resulting incident pressure in the ear $Q_e[k]$ is scaled by its characteristic impedance that varies inversely with its area $S_e.$ Thus, $Q_e[k]$ is estimated by³

$$Q_e\left[k\right]=Q\left[k\right]\hspace{0.17em}(S/S_e).$$ (15)

A final real-ear estimate of the pressure P_me at the TM is obtained by substituting $Q_e[k]$ for $Q[k]$ in Eq. (14) as follows:

$$P_{\mathit{m}\mathit{e}}\left(f\right)=\frac{Q(S/S_e)\hspace{0.17em}\left(e^{-j{k}_{0}x}+R{e}^{j{k}_{0}x}\right)}{1-R_0\hspace{0.17em}R}.$$ (16)

Its resulting sound pressure spectrum level is termed $L_{\mathit{T}\mathit{M}\mathit{e}}.$ After the calibration to measure $Q[k]$ and $R_0[k]$ and the ear measurement of $R[k],$ Eqs. (14) and (16) may be used to calculate $L_{\mathit{T}\mathit{M}}[k]$ and $L_{\mathit{T}\mathit{M}\mathit{e}}[k],$ respectively, once the distance x between the probe and TM is measured, e.g., using procedures in Keefe et al. (2015).

III. METHODS

A. Subjects and clinical tests

1. Subjects

Procedures for adult participants were approved by the Institutional Review Board at Boys Town National Research Hospital. The numbers of subjects and test ears and related data are summarized in Table I, such that data were analyzed from one ear per subject. The clinical tests included immittance at 226 Hz with a tympanometer (Tympstar, Grason-Stadler, Inc., Eden Prairie), air-conduction audiograms at octave frequencies between 0.25 and 8 kHz with additional tests at 3 and 6 kHz (model 61, Grason-Stadler, Inc., Eden Prairie) and bone-conduction audiograms (RadioEar, Eden Prairie) at octave frequencies from 0.25 to 4 kHz. Data were analyzed from those adult subjects whose clinical tests satisfied the following clinical inclusion criteria: (1) normal 226-Hz tympanometry (peak-compensated static admittance magnitude between 0.3 and 1.7 mmho, and middle-ear pressure within ±100 daPa), (2) normal pure-tone air-conduction thresholds of 25 dB hearing level or better at all frequencies from 0.25 to 8 kHz, and (3) air-bone gaps of 10 dB or less at octave frequencies between 0.25 and 4 kHz.

TABLE I.

Subject Inclusion.

Number of Subjects			Number of Ears			Age (years)
Female	Male	Total	Left	Right	Total	Range	Mean
23	7	30	22	36	58	19–51	29

B. General measurement procedures

All data were acquired at a sample rate of 22.05 kHz using custom software on a computer with a two-channel, 24 bit sound card (CardDeluxe, Chanhassen) and bi-directional serial port (RS-232). The same ear probe (Titan, Interacoustics, Middelfart) was used in all tests. It had two receiver ports driven by digital-to-analog converter channel one (DAC1) and DAC2 to deliver sound stimuli and a microphone port recorded by the analog-to-digital converter (ADC) to measure acoustic pressure. An additional port exiting the probe tip communicated air-pressure changes generated by the pump in the tympanometer (AT235, Interacoustics, Middelfart, Denmark, with modified firmware).

C. Reflectance and admittance methods

Ambient-pressure and tympanometric reflectance/admittance tests were first performed in the test ear using procedures described in Keefe et al. (2015) prior to TEOAE testing. Whenever possible, all tests used the same probe insertion. The ear reflectance R and admittance Y at the probe tip were measured in response to an acoustic click over a frequency range 0.2 to 8 kHz at ambient pressure in the ear canal, and at varying air pressure between 200 daPa and –300 daPa using down- and up-swept tympanograms. The peSPL of the incident pressure waveform of the click was approximately 92 dB for adult ears.

As described in Keefe et al. (2015), the area S_e of the ear-canal at the probe tip was acoustically estimated from Y, and the length x between the probe and a mid-TM region was acoustically estimated from R. With the assumption that the ear canal had a constant cross-sectional area along its length, the real-ear incident pressure Q_e was estimated using Eq. (15) in terms of S_e and the real-ear pressure P_me at the TM was estimated using Eq. (16) in terms of S_e and x.

The initial test order was a downswept reflectance tympanogram from an initial air pressure in the ear canal of 200 daPa down to –300 daPa, the ambient reflectance, and an upswept reflectance tympanogram from –300 to 200 daPa. The reflectance tympanometry tests provided a strong test of a leak-free probe insertion, inasmuch as it was impossible to pressurize to 200 daPa in the ear canal in the presence of any leak between the probe and ear-canal wall. In most ear tests in the present study, the probe remained in place between reflectance and TEOAE tests, so that the adequate seal of the probe in the ear canal was confirmed for both tests.

D. TEOAE methods

TEOAEs evoked using transient stimuli with an approximately constant incident pressure magnitude were measured using a double-evoked procedure as described in Keefe et al. (2016). These methods are summarized herein. If the probe placement is adjusted prior to the TEOAE tests, the operator assesses the real-time recording of the TEOAE stimuli, such that a substantially reduced amplitude is evidence of a possible leak. After inserting the probe in a leak-free manner into the ear canal, the electrical input signal to DAC1 produces the transient stimulus at a reference level. On the basis of measurements of the incident pressure with the probe inserted into a long, reflection-less tube, the DAC2 produces essentially the same acoustic transient signal as does DAC1, except that its signal level is set 12 dB larger than the reference level for DAC1.

The (approximately) constant L_Q chirp stimuli used in the present study are identical to those used in Keefe et al. (2016), which were each generated in terms of a click stimulus with electrical input spectrum $V_{\mathit{c}\mathit{k}}[k].$ Starting with a click stimulus, a reference voltage spectrum $V_{\mathit{c}\mathit{k}}[k]$ in the DFT of the electrical input signal applied to DAC1 generates a reference stimulus pressure spectrum $P_{\mathit{c}\mathit{k}}[k]$ in the measured data. For the allpass filter spectrum $H[k]$ used to produce either the positive or negative chirp, the electrical signal generating that chirp is calculated from the inverse DFT of $V_{\mathit{c}\mathit{h}}[k]=H[k]\hspace{0.17em}{V}_{\mathit{c}\mathit{k}}[k],$ and has a duration of N = 1536 samples. The allpass filter has a fixed sweep rate across frequency of 174.6 Hz/ms. A chirped pressure waveform $p_{\mathit{c}\mathit{h}}[n]$ with samples n = 1 to N – 1 is measured with this electrical signal in the long tube or test ear, and its pressure spectrum $P_{\mathit{c}\mathit{h}}[k]$ is calculated using the DFT. After the chirp data are obtained, an equivalent-click pressure spectrum $P_{\mathit{c}\mathit{k}}[k]$ is calculated using the inverse allpass filter by $P_{\mathit{c}\mathit{k}}[k]=H^{-1}[k]\hspace{0.17em}{P}_{\mathit{c}\mathit{h}}[k],$ and an equivalent-click pressure waveform $p_{\mathit{c}\mathit{k}}[n]$ is calculated as the inverse DFT of $P_{\mathit{c}\mathit{k}}[k].$ The electrical input signal to DAC2 produces a similar transient stimulus at a level 12 dB above this reference level.

Sound is recorded from ADC measurements of $p_1[n]$ in response to the electrical input signal to DAC1 alone, $p_2[n]$ in response to the electrical input signal to DAC2 alone, and $p_{12}[n]$ in response to the simultaneous presentation of the electrical input signals to DAC1 and DAC2. A TEOAE residual pressure $p_d[n]$ is calculated as

$$p_d\left[n\right]=p_1\left[n\right]+p_2\left[n\right]-p_{12}\left[n\right].$$ (17)

Data are highpass filtered in real time to exclude low-frequency noise, and buffers of outlier data are excluded from the analysis to control for any intermittent transient noise. Acoustic data are stored in 228 buffers over a measurement duration of about 1 min (after excluding outliers). These buffers are time-averaged into $L=16$ averaging blocks, with each block containing an average of 18 buffers of data. Data are analyzed in each block in the frequency domain in each $\frac{1}{6}$ octave from 0.71 to 8 kHz and in the time domain in each $\frac{1}{6}$ doubling in center times from 0.63 to 18 ms. Signal averaging across the L blocks is performed by coherent and incoherent averaging in order to calculate mean signal and noise components.

The stimulus-phase difference of either chirp TEOAE relative to the click TEOAE is removed by applying the inverse allpass filter to the TEOAE waveform $p_d[n]$. The output is the equivalent-click representation of $p_d[n]$. Much of the subsequent TEOAE processing uses an analytic signal representation of the TEOAE waveform $p_d[n]$ from which its corresponding spectrum $P[k]$ is calculated using the DFT.

Multi-window averaging is performed in the time and frequency domains on the L blocks of $p_d[n]$ to improve the overall signal-to-noise ratio (SNR) on the order of 5–6 dB (Keefe et al., 2016). The SNR (in dB) is calculated over the L blocks in the time and frequency domains, as is the coherence synchrony modulus (CSM), which varies from 0 for a random noise signal to 1 for a deterministic signal (Keefe, 2012, 2014; Keefe et al., 2016). The SNR is a measure of the ratio of TEOAE signal to noise energy, while CSM is a measure of the phase synchrony of the TEOAE. A TEOAE is classified as present based on SNR if SNR exceeds its minimum criterion value SNR_crit at a p = 0.05 level. A TEOAE is classified as present based on CSM if CSM exceeds its minimum criterion value CSM_crit at a p = 0.05 level.

In the analytic-signal representation of $p_d.$ IF is proportional to the temporal phase gradient of the TEOAE waveform, and IB is proportional to the temporal gradient of the sound pressure spectrum level of the TEOAE envelope. Both IF and IB are normalized to have units of frequency. Using an analytic-signal representation of the TEOAE spectrum GD is proportional to the spectral phase gradient of the TEOAE spectrum, and GS is proportional to the spectral gradient of the sound pressure spectrum level of the TEOAE spectral level. Both GD and GS are normalized to have units of time.

GD and GS are each averaged with a weighting of squared spectral amplitude over each $\frac{1}{6}$ octave bandwidth of frequency. This smoothed GD is calculated at center frequencies for which CSM exceeds ${\text{CSM}}_{\text{crit}},$ and the smoothed GS is calculated at center frequencies for which SNR exceeds ${\text{SNR}}_{\text{crit}}$. IF and IB are averaged with a weighting of squared temporal envelope amplitude over each interval of $\frac{1}{6}$ doubling of time. This smoothed IF is calculated at times for which CSM exceeds ${\text{CSM}}_{\text{crit}},$ and the smoothed IB is calculated at times at which SNR exceeds ${\text{SNR}}_{\text{crit}}$.

IV. RESULTS

A. Stimulus calibration comparisons

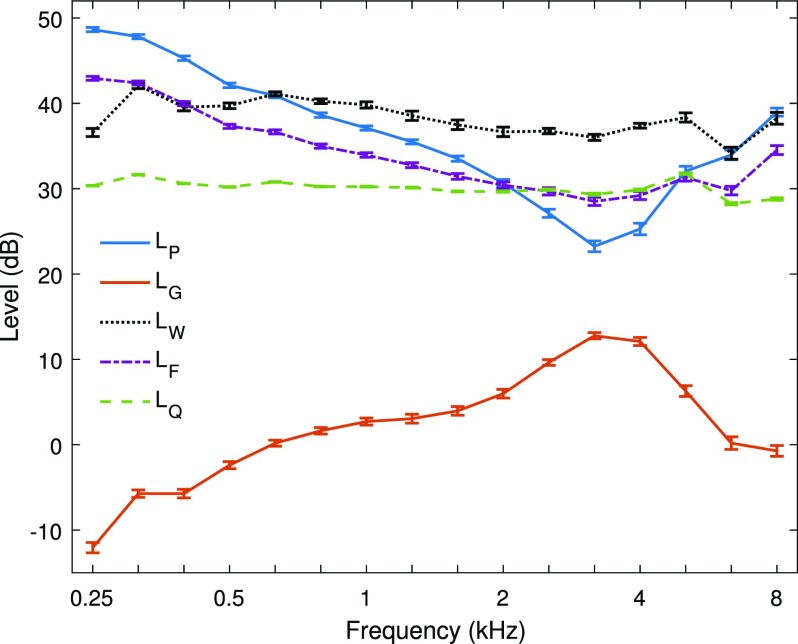
From the measured reflectance/admittance data in the adult participants in this study, the mean ±1 standard error (SE) of the mean of $L_P,$ $L_G,$ L_W, and L_F are shown in Fig. 1 at third-octave frequencies between 0.25 and 8 kHz. The corresponding mean ±1 SE of the incident pressure spectrum level L_Q is shown from the measurement in the long tube. The sound stimulus for the reflectance/admittance measurements had an L_Q that was approximately constant across frequency to within a range of 5.0 dB (see Table II). The mean L_P in the ear canal at the probe tip in Fig. 1 was maximal at low frequencies and much larger than L_Q due to the multiple internal reflections within the ear canal [see Eq. (5)]. The mean L_P had a relative minimum near 3.2 kHz close to the nominal quarter-wavelength frequency associated with ear-canal acoustics between the probe and TM (mainly due to the phase of $R[k]$). Consistent with Chan and Geisler (1990), this quarter-wavelength frequency increased with decreased insertion depth of the probe (not shown).

FIG. 1.

(Color online) The adult-ear mean ±1 SE of the sound pressure spectrum level $L_P,$ conductance level $L_G,$ absorbed sound power spectrum level $L_W,$ incident sound pressure spectrum level L_Q and forward sound pressure spectrum level L_F are plotted as a function of 1/3 octave frequency.

TABLE II.

The range of each of the total, forward and incident-pressure level is specified over all third-octave frequencies from 0.25 to 8 kHz. Each SD is calculated for the frequency average of the mean $L_P-L_W,$ $L_F-L_W$, and $L_Q-L_W$ over all third-octave frequencies and over a nominal OAE bandwidth from 0.63 to 8 kHz.

Response	Range (dB)	SD (dB) over 0.25–8 kHz	SD (dB) over 0.63–8 kHz
Lp	25.4	6.7	4.6
LF	14.4	3.8	1.3
LQ	5.0	3.1	3.2
LW	7.9	—	—
LG	24.8	—	—

The mean conductance level L_G in Fig. 1 was minimal at low frequencies with a relative maximum near 3.2 kHz. The mean absorbed sound power spectrum level $L_W,$ which from Eq. (4) was numerically equal to the sum of L_P and $L_G,$ was relatively constant across frequency. The range of L_W was only 7.9 dB (see Table II) compared to the ranges of about 25 dB for L_P and $L_G.$ The mean L_G data in normal adult ears in the present study were similar to previous mean L_G data (Keefe et al., 1993).

The mean forward pressure level L_F showed a relative maximum at low frequencies with smaller levels than L_P at low frequencies and larger levels at frequencies near 3.2 kHz (i.e., the quarter-wavelength resonance). The elevated levels of L_F compared to L_Q at low frequencies arose from the multiple internal reflections within the ear canal described by Eq. (8). The mean L_F was intermediate between the means of L_Q and L_P at all frequencies. The variations in the mean levels of L_P and L_F were large compared to their respective SEs except at 2 and 5 kHz, at which the means were similar.

The level difference $L_F-L_P$ evident in the responses in Fig. 1 was similar to previous studies on DPOAE and SFOAE suppression measurements. Keefe and Abdala (2007) reported mean measurements of $L_F-L_P$ in ears of adults, full-term newborns, and infants of age 1.5–6 months, that showed mean values as large as +6 dB near 3 kHz in adults with smaller maximum mean values in infants. The mean $L_F-L_P$ was close to –5 dB at frequencies below 0.7 kHz at all ages. The average spectral shape of $L_F-L_P$ in adult ears has been replicated (Keefe and Schairer, 2011; Richmond et al., 2011), with median values close to –5 dB at low frequencies and a smaller peak of about 2 dB just above 4 kHz.

The variation in the mean pressure levels $L_P,$ L_F, and L_Q across frequency were compared relative to L_W by calculating the standard deviation (SD) of each of them across frequency, i.e., these SDs were for $L_P-L_W,$ $L_F-L_W$, and $L_Q-L_W.$ It is the variation of these level differences across frequency that is important in the present context, inasmuch as the absolute value of the 0 dB reference of L_W would vary with the particular normalization constant W₀ in Eq. (3) used to calculate $L_W.$

The SD was calculated across the total third-octave frequency range from 0.25 to 8 kHz and also across the range from 0.63 to 8 kHz. The latter band approximated the bandwidth of the TEOAE data. These SDs for $L_P-L_W$ were 6.7 dB over the total bandwidth and 4.6 dB over the TEOAE bandwidth (see Table II). The mean $L_F-L_W$ difference in adult ears had less variation across frequency than the mean $L_P-L_W,$ with differences exceeding 5 dB at frequencies below 0.5 kHz. The SDs of $L_F-L_W$ were 3.8 dB over the total bandwidth and 1.3 dB over the TEOAE bandwidth, which were smaller for each bandwidth compared to the SDs of $L_P-L_W$ (see Table II).

For the selected value of $W_0,$ the mean $L_Q-L_W$ difference in adult ears had less variation than $L_P-L_W,$ and was within ±5 dB at all frequencies except for a 7 dB difference at 6.3 kHz. The variations across frequency in $L_Q-L_W$ and $L_F-L_W$ were small compared to the variation in $L_P-L_W,$ because $L_Q,$ L_F and L_W each controlled for standing waves in the ear canal. The SD of $L_Q-L_W$ was 3.1 dB over the total bandwidth, and 3.2 dB over the TEOAE bandwidth (see Table II). The SD was smaller for $L_Q-L_W$ than for $L_F-L_W$ over the total bandwidth, but larger over the TEOAE bandwidth. A constant L_F calibration of an evoked OAE stimulus would differ from a constant L_W calibration by a SD of about 1.3 dB across an OAE frequency range up to 8 kHz.

The estimated ear-canal length x in 58 test ears had a mean of 1.85 cm and area S_e of 0.459 cm². Table III compares these mean length and area estimates to those obtained in a separate study (Feeney et al., 2016) using the same measurement procedures. The mean length and area estimates agree to within their measurement SEs.

TABLE III.

The mean and SE of the ear-canal area at the probe tip and length between probe and eardrum were acoustically estimated in the present study and in Feeney et al. (2016) in groups of adult ears with normal hearing.

		Area (cm2)		Length (cm)
Study	Number of Ears	Mean	SE	Mean	SE
Present study	58	0.459	0.038	1.85	0.08
Feeney et al. (2016)	57	0.444	0.032	1.83	0.09

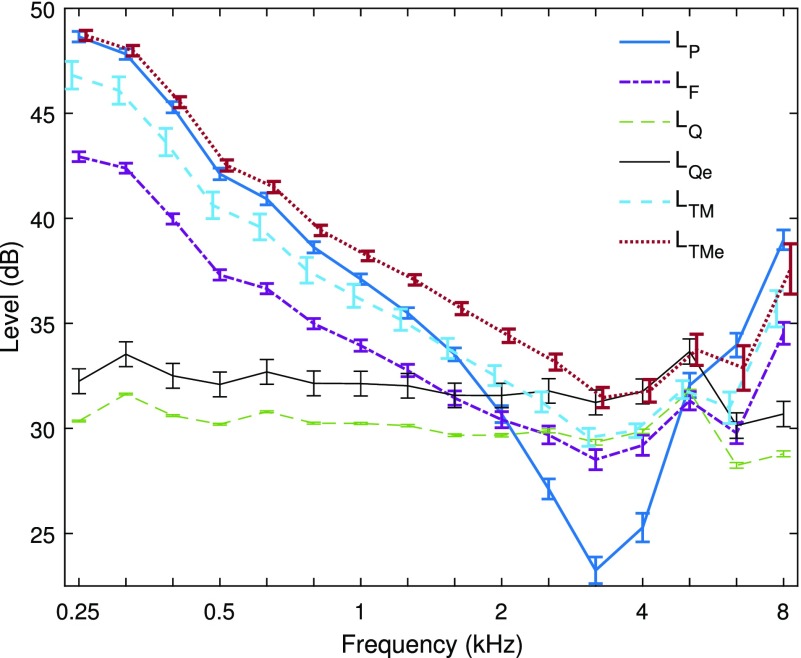
The mean length and area from the present study were used to calculate a mean $Q_e[k]$ [see Eq. (15)] and $L_{\mathit{Q}\mathit{e}},$ and to calculate a mean $P_{\mathit{m}\mathit{e}}[k]$ [see Eq. (16)] and $L_{\mathit{T}\mathit{M}\mathit{e}}.$ The tube area S = 0.495 cm² was slightly larger than the mean $S_e.$ Figure 2 shows that this area difference increased the mean L_Qe by 1.9 dB (SE of 0.59 dB) relative to $L_Q,$ and thereby increased L_TMe relative to $L_{\mathit{T}\mathit{M}}$. L_TMe and L_TM are plotted in Fig. 2 with $L_P,$ $L_Q,$ L_Qe, and $L_F.$ The ear-canal pressure was uniform in the limit of low frequencies so that the pressure levels at the probe and TM should converge in this limit, as pointed out by Souza et al. (2014). This convergence occurred for L_P and L_TMe at 0.25 kHz, while L_TM was 1.9 dB lower at this frequency. For this reason, it is more accurate to use Q_e rather than Q to estimate the real-ear pressure level at the TM. The mean L_TMe exceeded the mean $L_F,$ L_Qe, L_Q, and L_TM at all frequencies, and exceeded the mean L_P at frequencies up to 5.7 kHz.

FIG. 2.

(Color online) $L_P,$ $L_F,$ and L_Q data are redrawn from Fig. 1 along with the adult-ear mean ±1 SE of $L_{\mathit{T}\mathit{M}},$ L_Qe, and $L_{\mathit{T}\mathit{M}\mathit{e}}.$ Some curves are displaced laterally to remove overlap of their SEs.

Above about 5 kHz, the SE of L_TMe was slightly larger than the SE of L_TM because of additional variability in the ear-canal area estimates, and it was larger than the SE of $L_F.$ At frequencies below 2 kHz, the SE of L_TMe was smaller than that of $L_{\mathit{T}\mathit{M}}.$ The SE of L_TMe was larger than that of L_P at frequencies above 5 kHz, but slightly smaller at frequencies (3.2 and 4 kHz) that were close to the minimum in the mean $L_P.$ The SE of the mean L_Q was much smaller than the SEs for all other ear-canal measurements in the figure, as it was based on the group of calibration-tube measurements rather than real-ear measurements. This illustrates the repeatability of the L_Q calibration.

B. Constant L_W stimulus calibration

The power-weighted calibration of the TEOAE stimulus relies on an initial measurement of the admittance at the probe tip, from which the conductance G is obtained, and an initial measurement of the TEOAE chirp stimulus using the reference chirp stimulus with approximately constant $L_Q.$ This initial constant L_Q TEOAE measurement has a relatively short measurement duration of 10 s, as the interest is on the stimulus response rather than the TEOAE. The TEOAE measurements with the reference stimulus are those described in Keefe et al. (2016). The constant L_W (or power-weighted) stimulus design is described below for the chirp created by DAC1 applied to receiver 1. The power-weighted stimulus design is the same for the chirp created by DAC2 applied to receiver 2, so that it is sufficient to consider the pressure spectrum $P[k]$ measured in response to the DAC1/receiver 1 chirp.

A reference voltage spectrum $V[k]$ in the DFT of the electrical input signal applied to DAC1 generates a reference stimulus pressure spectrum $P[k]$ in the measured data. The constant-voltage calibration described in Sec. III D has a constant $|V[k]|$ for all k in the analysis passband. The power spectrum from Eq. (2) is $W[k]=G[k]{\left|P[k]\right|}^2/2.$ Aside from an overall normalization constant C that is determined below, a power-weighted reference voltage is defined by rescaling the voltage spectral component magnitude from $|V[k]|$ to $|CV[k]{(G[k])}^{-1/2}|.$ This creates a similar rescaling of the acoustic response variable $|Q[k]|$ to $|CQ[k]{(G[k])}^{-1/2}|.$

The in-the-ear method to generate a power-weighted chirp stimulus is based on the fact that the electrical input waveform for the positive chirp has a constant sweep rate (Keefe et al., 2016) so that its local frequency increases linearly with increasing time. Any particular sample number n in the chirp stimulus is thereby associated with a local frequency that does not vary across test ears. The time-to-frequency mapping of the chirp is used to define a mapping of each sample n to its local frequency in each DFT bin k, at which the conductance $G[k]$ is obtained from the reflectance/admittance measurement.

Inasmuch as the reflectance/admittance at ambient pressure is measured prior to any TEOAE measurement, $G[k]$ is known over the set of DFT frequencies used in that test. The sixth-octave average measurement of the conductance is calculated for each individual ear in a manner similar to that shown for the group mean conductance in Fig. 1, and extrapolated across the full range of frequencies up to the Nyquist rate (11.025 kHz). The conductance for any frequency below 0.25 kHz is set equal to the conductance at 0.25 kHz. The conductance for any frequency above 8 kHz is set equal to the conductance at 8 kHz.

Each sample number n in the electrical input waveform of the chirp is associated with a local frequency, with N = 1536 frequencies defined over the N-sample chirp. The third-octave values of the inverse square root of the conductance ($1/\sqrt{G}$) are resampled to this grid of local frequencies to provide a waveform $g_{\mathit{i}\mathit{n}\mathit{v}}[n],$ in which the value is the linearly interpolated value of $1/\sqrt{G}$ at the local frequency associated with each sample. The electrical input waveform $v[n]$ of the reference chirp is multiplied on a sample-by-sample basis by $g_{\mathit{i}\mathit{n}\mathit{v}}[n]$ to obtain a power-weighted electrical input waveform, and re-scaled by a constant to match the full dynamic range of the DACs. Such a multiplication does not require an additional forward or inverse DFT. The resulting power-weighted chirp stimulus is presented at a moderate level for 7.5 s in the test ear. The digital attenuation of DAC1 is adjusted so that the resulting peSPL of the constant L_W chirp waveform approximately matches the peSPL of the constant L_Q chirp waveform. This determines the constant C in the above.

The rationale for this normalization is that the onset of probe distortion is largely controlled by peak levels related to a criterion peSPL. In practice, the criterion peSPL usually occurred at a similar sample number, and hence a similar local frequency, in both stimulus conditions. In terms of frequency variation, the power-weighted stimulus level was increased at frequencies at which the conductance was small. Extrapolating from the plot of the mean L_G in Fig. 1, the power-weighted stimulus increased signal energy at frequencies below about 2 kHz and above 5 kHz.

The conductance at the probe tip is positive in a test ear because sound energy is dissipated within the ear, so that the inverse square root of conductance is well defined at all frequencies. A potential pitfall in this approach would occur if the conductance were unusually small at a particular frequency in the TEOAE bandwidth. This would result in an increased value of $1/\sqrt{G}$ at such a local frequency. A significantly increased variation in the electrical input waveform of the power-weighted stimulus might introduce an amplitude modulation effect into the bandwidth of the local frequency. To reduce the risk of such effects, the conductance smoothed over each $\frac{1}{6}$ octave frequency band is used in the power weighting procedure rather than the conductance at each DFT bin frequency. To further control for this risk, any value of conductance lower than 0.5 mmho is set equal to 0.5 mmho. The linear chirp introduces a frequency modulation of the local frequency over the TEOAE frequency band in which the chirp waveform has only a slowly varying amplitude so as to avoid any additional frequency modulation effects due to amplitude modulation.

C. Comparison of TEOAEs across stimulus conditions

This section describes the effect on ambient TEOAEs of using a sound stimulus with equal absorbed sound power by the ear across frequency (i.e., constant L_W) versus a sound stimulus with approximately equal incident pressure level across frequency (i.e., termed constant L_Q). The procedures to measure TEOAEs with (approximately) constant L_Q stimulus are those described in Keefe et al. (2016). Measurements were obtained in 58 adult ears with normal hearing.

1. TEOAE example in an adult ear

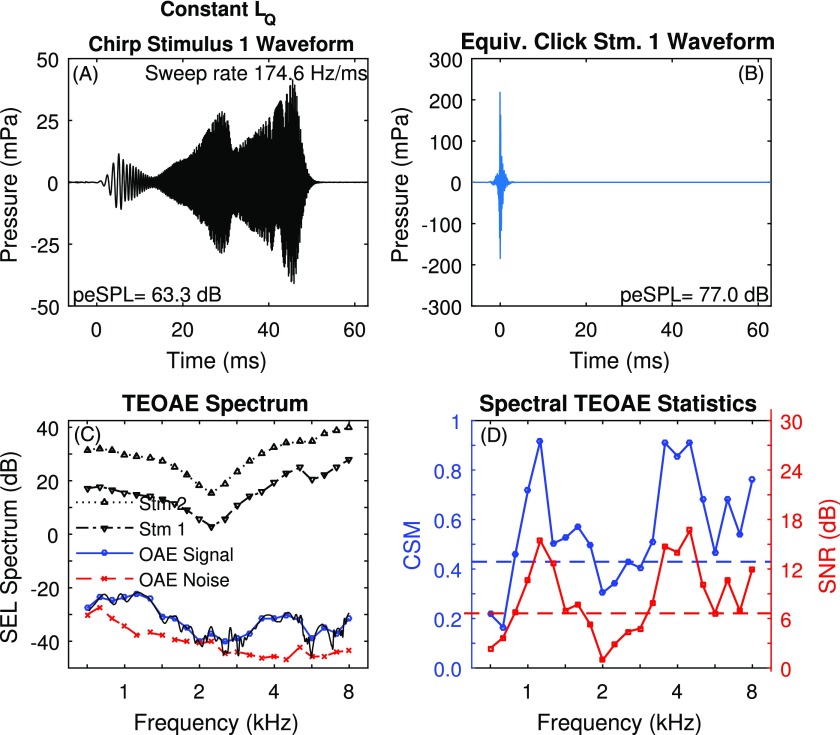
An example of a typical TEOAE measurement using the constant L_Q stimulus in an adult ear is shown in Fig. 3. From the foregoing discussion, the reference stimulus (Stm 1) had an approximately constant incident-pressure spectrum level across frequency despite the maxima and minima evident in the ear recording. The time-averaged positive chirp waveform of Stm 1, which is shown in Fig. 3(A), had a sweep rate of 174.6 Hz/ms from low to high frequencies, and a peSPL of 63.3 dB. This chirp waveform was transformed into an equivalent click waveform using an allpass filter that was the inverse of that used to generate the chirp stimulus, with the result shown in Fig. 3(B). The peSPL of the equivalent click was 77.0 dB, or 13.7 dB higher than that of the chirp. In contrast, the total sound exposure level (SEL) (see Keefe et al., 2016) was the same for the chirp and equivalent click responses.

FIG. 3.

(Color online) Subject A results for unweighted TEOAE with $\frac{1}{6}$ octave frequency averaging. (A) Chirp stimulus waveform (Stm 1) with its peSPL. (B) Equivalent click stimulus waveform with its peSPL. C. SEL spectrum levels for Stm 1 and Stm 2, and TEOAE signal and noise. The unsmoothed TEOAE signal is also plotted as a function of DFT frequency. D. CSM (left axis) and SNR (right axis) are plotted (solid lines) along with their respective criterion values CSM_crit and SNR_crit (dashed lines).

For an individual ear, it is convenient to show the SEL spectrum levels of the stimuli and TEOAE response using a finer frequency resolution ($\frac{1}{6}$ octave frequencies between 0.7 and 8 kHz) so as to observe the individual properties, whereas a coarser frequency resolution was adopted in group analyses. These frequency-averaged SEL spectrum levels are plotted in Fig. 3(C) for the Stm 1 and Stm 2 responses, for which the Stm 2 stimulus was presented 12 dB higher than for Stm 1. The SEL spectrum levels were approximately 12 dB apart, except for small differences (e.g., near 5.7 kHz) created from the individual differences in the different types of receivers used to generate Stm 1 and Stm 2 (each receiver had its own variability across different probes as further described in Keefe et al., 2016). The TEOAE residual pressure calculated in Eq. (17) from the Stm 1 and Stm 2 waveforms ($p_1[n]$ and $p_2[n],$ respectively) does not require that the waveforms be similar (Keefe, 1998; Keefe and Ling, 1998). The frequency-averaged SEL spectrum levels are shown in Fig. 3(C) for the TEOAE signal and TEOAE noise, which were obtained from coherent and incoherent averaging, respectively, over all L blocks. The SEL spectrum level shown in the same panel for the TEOAE signal at each DFT bin frequency illustrates the TEOAE fine structure.

The $\frac{1}{6}$ octave averages of SNR and CSM for the TEOAE residual signal in this ear are shown in Fig. 3(D), in which the corresponding values of SNR_crit and CSM_crit are plotted as horizontal dashed lines. The SNR values in Fig. 3(D) are the difference in the SEL spectrum levels for TEOAE signal and noise in Fig. 3(C). On the basis of CSM, the TEOAE was classified as present at center frequencies from 0.89–1.78, 2.52, and 3.2–8 kHz, and absent at center frequencies from 0.71–0.79, 2.0–2.25, and 2.83 kHz. On the basis of SNR, the classification results for the TEOAE were the same as for CSM, except that the TEOAE was classified as absent at 2.52 kHz. This single disagreement between CSM and SNR in this example may be considered a TEOAE of borderline status at 2.52 kHz. The lower SNRs between 2 and 2.83 kHz are also evident in the signal and noise levels in Fig. 3(C).

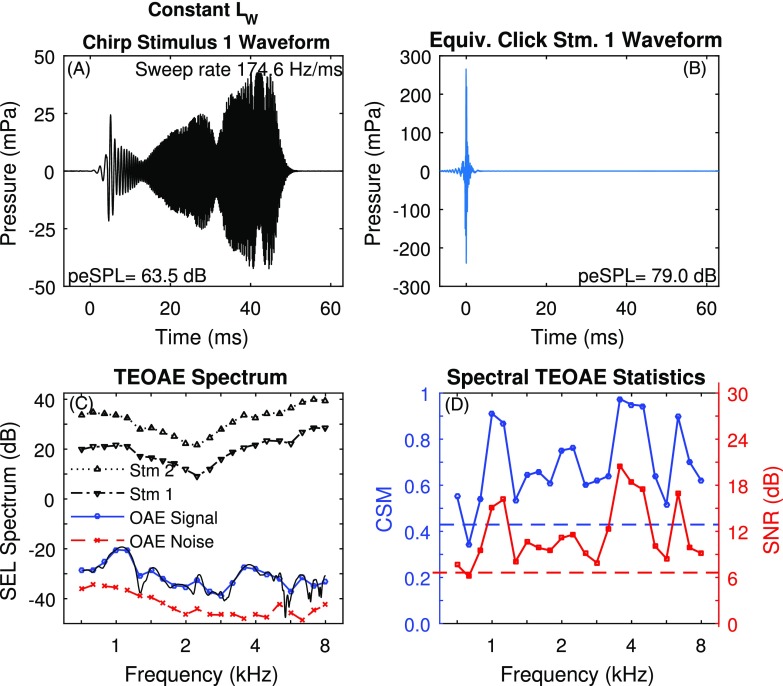
The TEOAE results measured in the same ear using the constant L_W stimulus are shown in Fig. 4, which has the same format as the results in Fig. 3 for TEOAEs using the constant L_Q stimulus. Comparing panel A in the two figures, the chirp waveform had a slightly different temporal envelope for this power-weighted stimulus, which was due to the weighting according to the interpolated inverse square root of the conductance. Although not shown, the conductance level L_G for this ear was similar to the mean L_G in Fig. 1. The peSPL was 63.5 dB for the constant L_W chirp compared to 63.3 dB for the constant L_Q chirp. This relative agreement was a result of normalizing the constant L_W stimulus amplitude after the initial 7.5 s of data collection to approximate the peSPL of the constant L_Q stimulus. In Fig. 4(B), the peSPL of 79.0 dB for the equivalent click response was 15.5 dB larger than for the chirp response in Fig. 4(A).

FIG. 4.

(Color online) Subject A results for power-weighted TEOAE with $\frac{1}{6}$ octave frequency averaging. (A) Chirp stimulus waveform (Stm 1) with its peSPL. (B) Equivalent click stimulus waveform with its peSPL. (C) SEL spectrum levels for Stm 1 and Stm 2, and TEOAE signal and noise. The unsmoothed TEOAE signal is also plotted as a function of DFT frequency. (D) CSM (left axis) and SNR (right axis) are plotted (solid lines) along with their respective criterion values (dashed lines).

Comparing panel C in Figs. 3 and 4, the SEL spectrum levels of Stm 1 and Stm 2 were slightly different for the constant L_W stimuli relative to the constant L_Q stimuli, with a relative increase in level in the constant L_W condition around 2 to 2.5 kHz. The TEOAE for the constant L_W condition had improved CSM and SNR overall in Fig. 4(D) compared to the constant L_Q condition. The TEOAE in the constant L_W condition was classified as present at all frequencies except 0.79 kHz by both CSM and SNR. Some of the benefit in the TEOAE at low frequencies was associated with a lower TEOAE noise level compared to that of the TEOAE in the constant L_Q condition. Notwithstanding that fact, the constant L_W stimulus revealed a TEOAE signal in the 2.0–2.83 kHz band that had been largely absent in the other stimulus condition.

The relative difference in TEOAE levels resulted, in part, from a difference in using a stimulus with an incident pressure spectrum level L_Q that was approximately constant compared to a stimulus with an absorbed sound power spectrum level L_W that was constant. Aside from the overall gain factor to match peSPLs, the mean $L_Q-L_W$ level difference inferred from data in Fig. 1 was indicative of the calibration level differences across frequency. These were relatively small because each of the constant L_Q and constant L_W types of OAE tests controlled for standing waves in the ear canal. Much larger differences would be evident in a TEOAE measured using a constant L_W stimulus compared to a TEOAE recorded with equal total pressure level L_P across frequency, because the total pressure would be strongly influenced by standing waves in the ear canal.

2. TEOAE group analyses

Group analyses of TEOAEs were calculated based on third-octave averages of CSM and SNR, inasmuch as the larger bandwidth provided more averaging across frequency. The mean ±1 SE of the SEL spectrum of the reference chirp (Stm 1) is shown in Fig. 5(A) for each of the constant L_W and L_Q stimulus conditions. The corresponding mean total SEL and peSPL are shown in Table IV. The mean SEL was 0.9 dB larger in the constant L_W test than the constant L_Q test. While the power-weighting procedure used only 7.5 s of data to adjust the weighted stimulus in each test ear to the peSPL from the weighted test, these results indicate a mean change of 0.6 dB in peSPL occurred after 1 min of data collection. The peSPL of the equivalent click representation of the stimulus was also slightly larger in the constant L_W condition by 0.8 dB.

FIG. 5.

The adult-ear mean ±1 SE of the SEL spectra of is plotted for the L_W and L_Q conditions for (A) stimuli and (B) TEOAE signals. Data are offset horizontally to aid in visualizing the SEs.

TABLE IV.

The mean and SE of the sound levels of the stimuli evoking the TEOAE are listed below for the total SEL and peSPL of the reference chirp stimuli in the constant L_W and constant L_Q conditions, and the peSPL of the equivalent click response of each reference chirp stimulus.

	Constant $L_W$ Chirp		Constant $L_Q$ Chirp
Sound level	Mean (dB)	SE (dB)	Mean (dB)	SE (dB)
SEL	39.2	0.47	38.3	0.36
peSPL (Chirp)	59.2	0.34	58.6	0.34
peSPL (Equivalent Click)	72.4	0.54	71.6	0.42

In Fig. 5(A), the mean SEL spectrum level of the constant L_W chirp stimulus differed from that of the constant L_Q chirp stimulus at 7 of 11 third-octave frequencies by more than the square root of the sum of squares of the SEs over the two stimulus conditions. The third-octave frequencies with larger mean differences ranging from 1 to 3 dB occurred at 1–2.5 kHz, and again at 5 and 6.3 kHz. These differences in stimulus level are in accord with the discussion above based on the frequency dependence of the conductance.

The mean ±1 SE of the SEL spectrum of the residual TEOAE response is shown in Fig. 5(B) for each stimulus condition. The mean difference in TEOAE spectrum level between the stimulus conditions exceeded the square root of the sum of squares of the SEs at only 4 third-octave frequencies (1.6, 2.5, 3.2, and 6.3 kHz). At each of these frequencies, the spectrum level was also higher for the constant L_W condition for the reference stimulus. The mean difference in TEOAE level ranged from only 1.0 to 1.2 dB. For a cochlear compression ratio of 40% between output TEOAE signal amplitude and the reference stimulus amplitude, a difference in TEOAE level of 1 dB would predict a difference in reference stimulus level of 2.5 dB, which is in the range of the observed differences. No statistical analyses of the TEOAE levels were performed based on this similarity in mean responses relative to their SEs, inasmuch as the “constant L_Q” stimulus across frequency was only approximately constant to within ±4 dB in level (Keefe et al., 2016). The trends in mean differences are consistent with cochlear compression of slightly higher stimulus levels in the L_W compared to the L_Q stimulus condition.

For the residual TEOAE for each stimulus condition versus frequency, Fig. 6(A) shows the mean ±1 SE of CSM and Fig. 6(B) shows the mean ±1 SE of SNR. The mean CSM was slightly larger relative to the separation in the SEs for the constant L_W condition at 1.6 and 3.2 to 4 kHz, and the mean SNR was slightly larger at 0.8, 1.6, and perhaps 3.2 kHz. The frequency dependencies of GD and GS [see Figs. 6(C) and 6(D), respectively] for the constant L_Q condition were similar to the positive-chirp TEOAE in Keefe et al. (2016). With reference to the dashed line in Fig. 6(C) that is proportional to $1/f$ and intersects 11 kHz at 1 ms, the mean GD decreased with increasing frequency with a slope that fluctuated around this value. Cochlear mechanics have an approximate scaling symmetry (Siebert, 1968; Rhode, 1971; Zweig, 1976) that predicts this $1/f$ slope. Greater separation of mean GD occurred relative to their SEs, with smaller mean GD in the constant L_W condition at 1–4 kHz (except at 3.2 kHz) and 5.0 kHz. The general tendency was for smaller GD in the constant L_W condition at frequencies with larger stimulus SEL spectra in Fig. 5(A). This is the expected effect, namely, that GD is reduced at larger stimulus levels for chirp TEOAEs (Keefe et al., 2016). The mean GS responses were separated by more than their SEs at 1 and 4 kHz, with smaller GS in the constant L_W condition.

FIG. 6.

Plots versus frequency are shown for the L_W and L_Q conditions for (A) CSM, (B) SNR, (C) GD with $1/f$, and (D) GS. The critical CSM and SNR values are shown in horizontal dotted lines in A and B. The straight dotted line $11/f$ (with f in kHz) in (C) represents the predicted GD for a human ear with a cochlear scale symmetry. Data are offset horizontally to aid in visualizing the SEs.

For the residual TEOAE spectrum for each stimulus condition versus time, Fig. 7(A) shows the mean ±1 SE of CSM and Fig. 7(B) shows the mean ±1 SE of SNR. The mean CSM was slightly larger relative to the separation in the SEs for the constant L_W condition only at 5 and 6.3 ms, and the mean SNR was slightly larger at those times and perhaps also at 12.7 ms. In Fig. 7(C), the mean IF was smaller in the constant L_W condition at the shortest times (0.63 and 0.79 ms), and at times between 3.2 and 5.0 ms. The mean IF was larger in the constant L_W condition at 16 ms. A slope of IF proportional to $1/t$ is predicted for such a scaling symmetry (Keefe, 2012), and is shown in the dotted line. The mean IF fluctuated around this trend line for both stimulus conditions at times longer than 1.6 ms. The mean IB was similar in the two stimulus conditions [Fig. 7(D)], except for smaller values in the constant L_W condition at 5.0 and 8 ms.

FIG. 7.

Plots versus time are shown for the L_W and L_Q conditions for (A) CSM, (B) SNR, (C) IF, and (D) IB. The critical CSM and SNR values are shown in horizontal dotted lines in A and B. The straight dotted line $11/t$ (with t in ms) in (C) represents the predicted IF for a human ear with a cochlear scale symmetry. Data are offset horizontally to aid in visualizing the SEs.

V. DISCUSSION

The experimental results in Fig. 2 and Table II revealed that $L_{\mathit{Q}\mathit{e}},$ $L_{\mathit{T}\mathit{M}},$ $L_{\mathit{T}\mathit{M}\mathit{e}},$ L_F, and L_W have potential benefits in stimulus calibration compared to one based on $L_P.$ The constant L_Q stimulus calibration used for CEOAEs by Goodman et al. (2009) had less variation with respect to L_W than did L_P with respect to $L_W.$ The constant L_Q stimulus calibration does not require a separate reflectance/admittance measurement in the test ear to generate the constant L_Q stimulus for subsequent CEOAE or chirp TEOAE testing. The other stimulus calibrations based on $L_{\mathit{Q}\mathit{e}},$ $L_{\mathit{T}\mathit{M}},$ $L_{\mathit{T}\mathit{M}\mathit{e}},$ L_F, and L_W require either a reflectance/admittance measurement or some other means to completely specify the stimulus properties. The present study has the limitation that TEOAE were only measured using the constant L_Q and constant L_W stimuli, so that the properties of TEOAEs measured using other stimulus calibrations were unexamined. Notwithstanding that limitation, this study provides novel findings on the extent to which TEOAEs differ using two types of stimuli, each of which was calibrated to a quantity (L_Q or L_W) that was much less affected by standing waves than would be the case for stimuli calibrated with constant $L_P.$

The TEOAE results in the adult group with normal hearing (see right panel, Fig. 5) showed no differences of practical interest for TEOAE levels measured using a constant L_W method and an approximately constant L_Q method, under the constraint that the peSPL in the ear canal was nearly the same. Compared to OAE measurements using stimuli calibrated with constant $L_P,$ OAE measurements with stimuli calibrated to relatively constant $L_Q,$ $L_{\mathit{Q}\mathit{e}},$ L_W, or L_F across frequency would all substantially eliminate standing-wave effects in the ear canal up to 8 kHz.

Because the mean L_F was intermediate between the mean L_Q and L_W at all frequencies in Fig. 2, it is predicted that the TEOAE stimuli with constant L_F would lie between the unweighted stimuli with constant L_Q and power-weighted stimuli with constant L_W in Fig. 5 (left) after normalizing for constant peSPL.

Although of considerable interest in terms of basic theory, a model-based estimate of sound pressure spectrum level at the TM is not an attractive candidate to calibrate ear-canal sound level because of the need to acoustically estimate the ear-canal area and length, and the need to specify or acoustically estimate the variation in the cross-sectional area of the ear canal between the probe and TM. Moreover, the sound field that acts over the spatially extended TM is inhomogeneous (Tonndorf and Khanna, 1972), and the TM has its own micromechanics (de La Rouchefoucauld et al., 2010; Cheng et al., 2010). Keefe et al. (2015) reviews these issues in a description of the procedures used to define and calculate the ear-canal length and area. That article reports measurements of an equivalent admittance at the TM using the same model used to estimate the equivalent pressure at the TM in the present study. Combining results from this earlier study and the present study, model-based estimates can be calculated and interpreted from reflectance/admittance measurements for the equivalent pressure at the TM as well as the equivalent admittance of the TM.

The general similarity in mean TEOAE signal levels (to within about 1 dB) using the constant L_W and constant L_Q stimulus conditions were consistent with the slight relative mean level differences in the stimuli under the two conditions (to within 3 dB). The mean GDs were slightly reduced in the constant L_W stimulus condition at frequencies for which the stimulus spectrum levels exceeded those in the constant L_Q condition. Other mean differences in IF, GS, and IB appeared at frequencies with differing spectral levels, and were similar to the level dependence in these moments observed in click TEOAE recordings (Keefe, 2012). After normalizing all stimuli for peSPL, the facts that the stimulus spectrum levels for the constant L_F condition were intermediate across frequency between the stimulus spectrum levels for the constant L_W and L_Q conditions, and that the TEOAE properties were generally similar between these stimulus conditions, lead to a prediction that the TEOAE properties of a constant L_F stimulus are generally similar to those for the constant L_Q and L_W conditions.

An exception to this prediction may occur in the vicinity of the half-wavelength frequency, and at approximately harmonic multiples thereof, i.e., an ear-canal length between the probe and TM equal an integral number of half-wavelengths of sound. For a constant L_Q stimulus, the frequency of the half-wavelength resonance would occur near a local maximum of $L_P,$ which was likely just above 8 kHz in the measured data (see Fig. 3). Just below the half-wavelength condition, a constant L_Q stimulus (see Fig. 2) or constant L_W stimulus (see Fig. 1) produced an increased level in eardrum pressure level L_TMe near 8 kHz relative to a constant L_F stimulus (see Fig. 2). Using a constant L_F stimulus would decrease TEOAE levels near the half-wavelength resonance frequency compared to the constant L_Q and constant L_W conditions. Higher-frequency TEOAE measurements would be helpful in examining these half-wavelength effects.

A relevant property of this group of normal ears is that the SE of their mean conductance was small (see Fig. 1). It would be of interest to compare TEOAEs in a group of test ears with both normal and conductive-impaired middle-ear function. These ears would have a much larger variation in conductance, which might therefore result in a larger distribution of constant L_W stimulus levels across frequency compared to normal-hearing ears. More research is needed in other adult groups with middle-ear dysfunction and with sensorineural hearing loss to assess the relative benefits of measuring TEOAEs with these alternative methods of stimulus calibration in the ear canal.

VI. CONCLUDING REMARKS

Mean TEOAE levels measured using chirp stimuli in adult ears were similar for procedures with an approximately constant incident sound pressure spectrum level and with a constant absorbed sound power level, under the constraint that the peSPL in the two procedures was approximately the same. On the basis of adult-ear measurements of reflectance and admittance, the frequency variations with respect to the incident sound pressure level in an average adult ear were compared for the mean and SE of the sound pressure levels in individual ears for total pressure (at the probe tip), incident pressure, forward pressure, absorbed sound power, and an equivalent pressure at the TM. The latter was calculated based on a transmission-line model in an ear canal assumed to have a cylindrical geometry between the probe and the TM.