Comparisons of transient evoked otoacoustic emissions using chirp and click stimuli

Abstract

Transient-evoked otoacoustic emission (TEOAE) responses (0.7–8 kHz) were measured in normal-hearing adult ears using click stimuli and chirps whose local frequency increased or decreased linearly with time over the stimulus duration. Chirp stimuli were created by allpass filtering a click with relatively constant incident pressure level over frequency. Chirp TEOAEs were analyzed as a nonlinear residual signal by inverse allpass filtering each chirp response into an equivalent click response. Multi-window spectral and temporal averaging reduced noise levels compared to a single-window average. Mean TEOAE levels using click and chirp stimuli were similar with respect to their standard errors in adult ears. TEOAE group delay, group spread, instantaneous frequency, and instantaneous bandwidth were similar overall for chirp and click conditions, except for small differences showing nonlinear interactions differing across stimulus conditions. These results support the theory of a similar generation mechanism on the basilar membrane for both click and chirp conditions based on coherent reflection within the tonotopic region. TEOAE temporal fine structure was invariant across changes in stimulus level, which is analogous to the intensity invariance of click-evoked basilar-membrane displacement data.

LIST OF ABBREVIATIONS

ADC

analog-to-digital converter

BM

basilar membrane

CEOAE

click-evoked otoacoustic emission

CSM

coherence synchrony modulus

DAC

digital-to-analog converter

DFT

discrete Fourier transform

DPOAE

distortion product otoacoustic emission

ERB

equivalent rectangular band

GD

group delay

GS

group spread

IB

instantaneous bandwidth

IF

instantaneous frequency

IQR

inter-quartile range

LSF

least squares fit

peSPL

peak-to-peak equivalent sound pressure level

SE

standard error of the mean

SEL

sound exposure level

SNR

signal-to-noise ratio

SFOAE

stimulus frequency otoacoustic emission

SOAE

spontaneous otoacoustic emission

SPL

sound pressure level

TEOAE

transient-evoked otoacoustic emission

I. INTRODUCTION

Transient-evoked otoacoustic emission (TEOAE) responses provide information related to cochlear nonlinearity and outer hair cell function. Such data have translational clinical importance in evaluating peripheral auditory function in adult and infant ears. In the context of a multi-year study of wideband clinical diagnosis and monitoring of middle-ear and cochlear function, acoustic data were acquired in a battery including TEOAE, reflectance, and wideband acoustic stapedial muscle reflex tests. This report describes TEOAE test procedures and compares TEOAE recordings using chirp and click stimuli in adult ears with normal hearing.¹

The use of chirps in signal processing was introduced for use in radar (Klauder et al., 1960) and subsequently applied in communications science (Schroeder, 1970). TEOAEs were first measured using chirp stimuli by Neumann et al. (1994). Keefe (1998) described the calculation of a chirp stimulus for one receiver by applying an allpass filter to a click stimulus. A double-evoked procedure was used to measure a chirp-evoked stimulus-frequency otoacoustic emission (SFOAE) by applying the same allpass filter to create chirps for both receivers, or a distortion-product otoacoustic emission (DPOAE) by using different allpass filters to generate the two stimuli evoking the DPOAE (Keefe and Ling, 1998). The chirp-evoked otoacoustic emission (OAE) (or chirp TEOAE) was analyzed as an equivalent click-evoked otoacoustic emission (or equivalent-click TEOAE) by applying the inverse allpass filter to the chirp TEOAE. The naming convention in this report is that a click-evoked otoacoustic emission described in any previously published article is termed a CEOAE, and a CEOAE measured in the present study is termed a click TEOAE.

A chirp may be alternatively described as a swept sinusoidal tone, in which the phase function selected for the frequency-domain allpass filter of the chirp determines the filter group delay (GD), which in turn controls the local (or instantaneous) frequency of the time-domain chirp or swept-tone stimulus. Some articles on OAEs have used a term like swept-tone for sweep rates that are much slower than those used for chirps. For example, swept-tone SFOAEs have been measured for frequencies from 0.55–1.45 kHz using a digital heterodyne procedure (Choi et al., 2008), and for frequencies up to 4 kHz using a log chirp and dechirping approach (Bennett and Özdamar, 2010b). The latter approach for swept-tone SFOAEs was extended to 7 kHz in Bennett and Özdamar (2010a) using a wavelet analysis. At low to moderate stimulus energies for frequencies in the range of 1–2.5 kHz in human ears, CEOAEs and discrete-tone SFOAEs were nearly equivalent in terms of their generation mechanism on the basilar membrane (BM) (Kalluri and Shera, 2007). Using a double-evoked procedure for swept-tone SFOAE measurements, Kalluri and Shera (2013) reported close agreement between discrete-tone and swept tone SFOAEs in four adult ears up to 8.5 kHz.

The present study analyzes TEOAEs in normal adult ears recorded using click and chirp stimuli with the same magnitude spectrum, but varying phase. The term “chirp TEOAE” is used inasmuch as the sweep rate is much faster than in other studies reporting “swept-tone SFOAE” measurements. If the generation region of the TEOAE would functionally depend on the relative times at which the input stimulus energy to the cochlea is presented across frequency, then the resulting TEOAE properties might differ between the chirp- and click-evoked OAEs. Otherwise, the TEOAE properties would be identical between the click and chirp stimulus conditions, which extends the hypothesis tested by Kalluri and Shera (2007) to new stimulus conditions of bandwidth and sweep rate.

Click and chirp TEOAEs are analyzed in the present study in terms of their first- and second-order signal-processing moments (Keefe, 2012). These moments as functions of frequency include GD and group spread (GS), respectively. These moments as functions of time include instantaneous frequency (IF) and instantaneous bandwidth (IB), respectively. For TEOAEs generated in the tonotopic region of the cochlear traveling wave, the GD is relatively large for lower frequencies and the IF is relatively large for short times.

CEOAE and SFOAE levels have a compressive response growth at moderate stimulus levels, i.e., the evoked OAE amplitude grows more slowly than the stimulus amplitude. CEOAE growth rates are compressive in the long-latency component generated in the tonotopic region of the cochlear traveling wave, but nearly linear for multiple components generated at shorter times (Goodman et al., 2009; Lewis and Goodman, 2015). Click and chirp TEOAEs are compared in the present study at two stimulus levels differing by 6 dB in order to evaluate whether a compressive growth is observed.

The main hypothesis in this study is that TEOAEs have nearly identical properties across stimulus conditions (click versus chirp) under the constraints that the stimuli have the same energy spectrum and that the effects of any stimulus phase differences are removed from the TEOAE responses that are compared. The TEOAE properties that are examined include signal level, a coherence synchrony measure (CSM), the signal-to-noise ratio (SNR), and the TEOAE moments. Notwithstanding these comparisons on theoretical grounds, it may be beneficial to use chirp rather than click stimuli in clinical translational measurements. For a fixed energy spectrum, the chirp spreads the stimulus energy out over longer times compared to the click, and this may result in reduced system distortion for chirp compared to click TEOAEs.

II. TEOAE MEASUREMENT THEORY

A. TEOAE click stimulus design

Receiver 1 generated wideband stimuli from a digital-to-analog converter (DAC) channel 1. Receiver 2 was selected to produce high-level activators from a DAC2. Such high levels were appropriate for tests of the acoustic stapedius muscle reflex (although no such reflex data are reported herein). Both DACs and receivers were used to deliver TEOAE test stimuli. While receiver 2 had a more limited high-frequency response than receiver 1, the electrical input waveforms to DAC1 and DAC2 were separately calibrated to produce approximately the same acoustic click waveforms and spectra in both receivers.

The buffer length of the DAC click waveform was N = 800 samples (duration 36.3 ms). The electrical waveform output by each DAC was calculated such that the resulting acoustic stimulus output by the DAC measured in a long anechoic tube approximated the finite impulse response of a Kaiser window filter (passband from 0.7 to 8 kHz). The long tube had a circular cross-sectional area of 0.495 cm², which is in the range of area measurements in adult human ear canals. The coiled polyethylene tube was closed at its far end with a length of 30.5 m. The nominal round-trip time for sound propagation within the tube was about 177 ms. Due to viscothermal losses at the tube walls over its entire length and back, the reflected sound pressure amplitude was negligible upon its return to the probe. As a result, the measured waveform at the probe corresponded to the incident pressure waveform in the absence of any reflections. This calibration approach reduces standing-wave effects, and was previously used in studies of reflectance (Liu et al., 2008), wideband acoustic stapedius reflex (Keefe et al., 2010), and CEOAEs (Goodman et al., 2009).

The measured peak pressure amplitude of the click recorded in this long tube occurred at sample number 236, which was identified as the zero of the time axis. This buffer length and relative placement of the click stimulus enabled analyses of TEOAE responses out to 25.6 ms after the click peak.

The discrete Fourier transform (DFT) of the electrical signal for the click stimulus was the complex voltage spectrum $V_{\mathit{c}\mathit{k}}[k]$ of the click in the kth frequency band. This signal was band limited to the passband of the Kaiser window filter. The click voltage spectrum $V_{\mathit{c}\mathit{k}}[k]$ in the present study was applied to the receiver to generate in the long tube an approximately constant incident pressure magnitude across frequency to within ±4 dB in level.

The click stimulus waveform, e.g., $p_1[n]$, is parameterized by twice the standard deviation (SD) σ_t of the waveform about its maximum amplitude as described in the Appendix. The measured incident pressure waveform in the long tube had a temporal width of 2σ_t = 0.442 ms. This may usefully be compared with the period of 0.125 ms at the maximum frequency of 8 kHz in the click bandwidth.

B. TEOAE chirp stimulus design

Chirps have the advantage over clicks in spreading the energy out in time, and thereby reducing the peak amplitudes relative to those of the click for the same total signal energy. Suzuki et al. (1995) introduced an allpass filter $H[k]$ with unit magnitude response to generate a chirp filter of the form

$$H[k]=\{\begin{array}{cc}{e}^{j\rho k^2},\hfill & 0\le k\le N/2,\hfill \\ H^{*}[N-k],\hfill & N/2<k<N.\hfill \end{array}$$ (1)

The unit imaginary number is j, and $H^{*}[k]$ is the complex conjugate of $H[k]$. The present study used this chirp filter.

To prevent time-domain aliasing of the output chirp waveform, Suzuki et al. (1995) restricted the real coefficient ρ to the following discrete set of allowed values:

$$\rho =M\pi /{(N/2)}^2,$$ (2)

for integer M. This restriction ensured that $H[N/2]=e^{jM\pi }$, which equaled +1 for even M and −1 for odd M, so that a discontinuity in phase at the end of the chirp ($k=N/2$) was avoided. The present study used an even value of M. The inverse allpass filter spectrum $H^{-1}[k]$ was constructed by changing ρ to −ρ in Eq. (1).

A band limited voltage spectrum $V_{\mathit{c}\mathit{h}}[k]$ of the electrical signal generating the chirp was created by convolving this allpass filter with the complex voltage spectrum $V_{\mathit{c}\mathit{k}}[k]$ of the electrical signal generating the click. The electrical signal generating the chirp was calculated from the inverse DFT of $V_{\mathit{c}\mathit{h}}[k]=H[k]\hspace{0.17em}{V}_{\mathit{c}\mathit{k}}[k]$. With the probe inserted into the ear canal or calibration tube, a chirped pressure waveform $p_{\mathit{c}\mathit{h}}[n]$ was measured with this electrical signal, and its pressure spectrum $P_{\mathit{c}\mathit{h}}[k]$ was calculated using the DFT. After the chirp data were obtained, an equivalent-click pressure spectrum $P_{\mathit{c}\mathit{k}}[k]$ was calculated using the inverse allpass filter by $P_{\mathit{c}\mathit{k}}[k]=H^{-1}[k]\hspace{0.17em}{P}_{\mathit{c}\mathit{h}}[k]$, and an equivalent-click pressure waveform $p_{\mathit{c}\mathit{k}}[n]$ was calculated as the inverse DFT of $P_{\mathit{c}\mathit{k}}[k]$.²

The GD ${\tau }_g[k]$ of the allpass filter was calculated as the negative gradient of the phase of $H[k]$ in Eq. (1) with respect to 2π times the frequency with the result

$${\tau }_g[k]=-(4MT/N)k.$$ (3)

The linear chirp had a GD that varied linearly with k. The magnitude change in ${\tau }_g[k]$ between k = 0 and $k=N/2$ (i.e., k at the Nyquist frequency) was 2MT. To prevent time-domain aliasing, the GD should not exceed the buffer duration NT of the transient. The maximum chirp duration would be achieved by choosing M_max so that the magnitude change in GD would equal the buffer duration, i.e., with $\left|M_{\text{max}}\right|=N/2$.

The chirp swept through frequencies from zero to the Nyquist frequency ${(2T)}^{-1}$ as the GD changed by 2MT. Thus, the sweep rate β (in Hz/s) was

$$\beta =\left|{(4M{T}^2)}^{-1}\right|.$$ (4)

The choice of positive M in Eq. (2) generated a positive chirp with local frequency increasing linearly with increasing time. The choice of negative M generated a negative chirp with local frequency decreasing linearly with time.

The chirp buffer length was N = 1536 samples (69.6 ms), which was almost twice the duration of the click buffer. In order to measure a substantively complete TEOAE response generated by a chirp stimulus, a value of M = 696 samples was used to calculate ρ in Eq. (2) for the phase function of the positive chirp, and M = −696 samples for the negative chirp. The negative chirp was a time-reversed positive chirp. This value of $\left|M\right|$ was slightly less than $\left|M_{\text{max}}\right|=768$ samples to provide additional time in the buffer for the delayed TEOAE response. Moreover, the effective chirp duration in the chirp buffer was reduced by a factor of about 0.7, inasmuch as the chirp envelope was negligible at times at which the local frequency varied from zero to 0.5 kHz or exceeded 8 kHz. This provided sufficient time to capture all of the TEOAE response within the buffer except for any synchronous spontaneous otoacoustic emission (SOAE) components.

The choice of sweep rate was motivated by a heuristic rationale derived from the operation of an analog heterodyne narrowband analyzer. For a given bandwidth, the dwell time of a sweep is the time interval in which the local frequencies lie within the bandwidth. A typical constraint on the maximum sweep rate is that the dwell time be on the order of a couple of periods of the center frequency of the analyzer bandwidth. This allows sufficient settling time during the sweep to estimate the average signal magnitude at that center frequency. The chirp sweep rate was chosen with respect to a half-octave analysis bandwidth for frequencies between 1 and 8 kHz, for which the most narrow half-octave bandwidth of about 348 Hz occurred at 1 kHz. The dwell time at 1 kHz is at least two periods or 2 ms, so that the criterion sweep rate would be 348/2 = 174 Hz/ms. For $\left|M\right|=696$ samples, the corresponding chirp sweep rate from Eq. (4) was 174.6 Hz/ms, which is in substantial agreement. The rationale is merely a heuristic in the sense that an inverse filter was used instead of a swept spectrum analysis method. With the inverse filter technique, the chirp sweep rate may be chosen arbitrarily as long as the chirp and its TEOAE response fit within a single buffer.

While the allpass filter $H[k]$ in Eq. (1) used a quadratic phase function of ρk², a linear “rotation” number k₀ was added to the phase function so that the equivalent-click impulse response of the filter was approximately centered within the same N-sample buffer. That is, each transient in its buffer was preceded by silence and followed by at least 25 ms of silence to provide a time interval to measure the TEOAE response. To that end, the quadratic phase function ρk² used in the filter $H[k]$ was replaced by ρk(k − k₀), in which k₀ was empirically adjusted to a fixed value for all subsequent measurements.

C. Nonlinear TEOAE residual and buffers for data averaging

After inserting the probe into the ear canal (or calibration coupler), the electrical input signal to DAC1 produced the transient stimulus (click, positive or negative chirp) at a desired level. The electrical input signal to DAC2 produced the substantively identical transient stimulus at a level 12 dB above this desired level. A double-evoked procedure (Keefe, 1998; Keefe and Ling, 1998) was used to extract a nonlinear TEOAE waveform from analog-to-digital converter (ADC) measurements of p₁[n] at the nth time sample in response to the electrical input signal to DAC1 alone, $p_2[n]$ in response to the electrical input signal to DAC2 alone, and $p_{12}[n]$ in response to the simultaneous presentation of the electrical input signals to DAC1 and DAC2. The TEOAE residual pressure $p_d[n]$ was calculated as

$$p_d[n]=p_1[n]+p_2[n]-p_{12}[n].$$ (5)

Aside from system noise, the $p_d[n]$ is zero for measurements in a linear system, whereas it quantifies a TEOAE residual in the ear due to the compressive nonlinearity of the outer hair cell function. Because each DAC outputs its electrical signal at the same voltage level and polarity in $p_1[n]$ and $p_{12}[n]$ for DAC1, and $p_2[n]$ and $p_{12}[n]$ for DAC2, any harmonic distortion from the probe or measurement system cancels out for each channel in Eq. (5). Contributions to $p_d[n]$ from the measurement system in the form of intermodulation distortion and system noise were estimated by recordings in the long tube. Any intermodulation distortion would be confined to times at which the transient stimulus had significant signal energy. These were times close to t = 0 for the click.

The trio of electrical input signals to generate $p_1[n],\hspace{0.17em}{p}_2[n]$, and $p_{12}[n]$ was synchronously output over a nominal measurement duration of 1 min, and responses were stored in multiple response buffers. The number of response buffers was K = 552 for the click stimulus of duration 800 samples, and K = 288 for the chirp stimuli of duration 1536 samples. Data were highpass filtered in real time to exclude low-frequency noise (the highpass filter used a Kaiser window design with attenuations of 3 dB at 0.66 kHz and 40 dB at 0.4 kHz). This filter also included the effect of the frequency variations in microphone sensitivity based on manufacturer data. A median absolute deviation test was used with the cumulative dataset to identify and exclude outliers in the response buffers relative to the medians of the peak-to-peak amplitude, crest factor, and noise energy.

The K buffers of data were analyzed using a combination of time and frequency averaging as in previous studies of SFOAEs (Schairer et al., 2003) and CEOAEs (Goodman et al., 2009) to calculate signal and noise spectral levels of each stimulus and TEOAE response. In those CEOAE tests, each of the K = 552 buffers was assigned to one of a set of L = 24 averaging blocks, such that each successive response buffer was placed in a different block than the preceding response buffer. Once all buffers were assigned to a block, the time average of the responses in each block was calculated. The value of K was an integer multiple of L = 24, so that each block included a time average of $B=K/L$ response waveforms, with B = 23 for click responses. In TEOAE tests using chirp stimuli, the corresponding sizes were K = 288 buffers, L = 16 blocks, and B = 18 time averages.

Many evoked OAE studies using a combination of time averaging into two blocks, from which a mean and standard error (SE) of the mean may be calculated. The use of only two blocks leads to increased variability in estimating OAE noise levels relative to using a greater number of blocks. The present work uses L = 16 or 24 blocks of sub-averages, which provide smoother estimates of the noise levels across time or frequency (Schairer et al., 2003).

D. TEOAE detection using SNR and CSM, and the analytic TEOAE signal

The strength of the TEOAE amplitude in this sum of spectra was quantified using the SNR (as a level in dB), and the phase synchrony of the TEOAE was quantified using the CSM. The procedures used to calculate the SNR and CSM follow those for CEOAEs in Keefe (2012), which also reviews previous work on which these procedures were based. A TEOAE magnitude was detected if its SNR averaged over the K blocks was greater than or equal to a criterion SNR. This SNR_crit was the minimum needed to achieve correct detection of signal in noise with an error rate p in a two-alternative forced-choice paradigm and was given by

$${\text{SNR}}_{\text{crit}}=10\hspace{0.17em}{\text{log}}_{10}(-2\hspace{0.17em}\ln (2p)),$$ (6)

which equals 6.6 dB for p = 0.05.

To define CSM, a continuous-time, continuous-frequency representation of the TEOAE residual waveform $p_d(t)$ and spectrum $P_d(f)$ are adopted. The analytic signal s(t) (Cohen, 1995) is defined in terms of the measured TEOAE residual waveform and the unit imaginary number j by

$$s(t)=p_d(t)+j{p}_{\mathit{d}\mathit{H}}(t),$$ (7)

in which the real $p_{\mathit{d}\mathit{H}}(t)$ is the Hilbert transform of p_d. The analytic signal is parameterized in terms of real functions called the instantaneous amplitude A(t) and phase $\Phi (t)$ by

$$s(t)=A(t)\hspace{0.17em}{e}^{j\Phi (t)}.$$ (8)

The spectrum S(f) of the analytic signal for f > 0 is expressed in terms of the TEOAE residual spectrum $P_d(f)$ for f > 0 by

$$S(f)=2\hspace{0.17em}{P}_d(f),$$ (9)

and S(f) is zero for negative frequencies. It is parameterized in terms of real functions called the spectral amplitude B(f) and spectral phase $\Psi (f)$ by

$$S(f)=B(f)\hspace{0.17em}{e}^{j\Psi (f)}.$$ (10)

CSM was calculated in the time domain using the phasor $e^{j\Phi (t)}$ and in the frequency domain using the phasor $e^{j\Psi (f)}$. CSM was defined as the length of the sum of the phasors in the L blocks divided by L. CSM in the frequency domain was averaged over all DFT bins within each fractional octave bandwidth. CSM in the time domain was averaged over all samples in each fractional doubling in time. A criterion CSM_crit was defined such that any smaller CSM than CSM_crit signified that a synchronous TEOAE was absent, and any larger CSM signified that a synchronous TEOAE was present. CSM_crit for a given p value is approximated by

$${\text{CSM}}_{\text{crit}}={[{(1+2L)}^2-{(\ln \hspace{0.17em}p+(1+2L))}^2]}^{1/2}/(2L).$$ (11)

For p = 0.05, CSM_crit was 0.3515 for CEOAEs with L = 24 blocks, and 0.4293 for chirp TEOAEs with L = 16.

E. Signal-processing moments of TEOAEs

CEOAE moments were defined and measured in Keefe (2012) based on an analytic signal formulation based on p_d and signal-processing moments described in time-frequency analysis (Cohen, 1995). The reduction of the chirp TEOAE residual to an equivalent-click TEOAE residual p_d is the initial step that enables TEOAE moments to be calculated based on either a click or equivalent-click signal. After that step, the procedure to calculate the TEOAE moments is the same for either the click or equivalent-click waveform. Within each ear test, the moments were calculated in each time or frequency bin for each of the L buffers to estimate the mean and SE of the mean.

The spectral moments of the analytic signal in Eq. (8) are the IF and IB defined as

$$\begin{array}{c}\text{IF}\left(t\right)=\frac{1}{2\pi }\frac{d\Phi \left(t\right)}{\mathit{d}\mathit{t}},\\ \text{IB}\left(t\right)=\frac{1}{2\pi }\left|\frac{d\hspace{0.17em}\ln \hspace{0.17em}A\left(t\right)}{\mathit{d}\mathit{t}}\right|.\end{array}$$ (12)

The IF is the temporal phase gradient, IB is the magnitude of the temporal gradient of the log-amplitude, and IF and IB have units of frequency. IB is proportional to the temporal gradient of the sound pressure level (SPL) of the TEOAE, i.e., its decay rate. A steep decay rate over a brief time interval is associated with a large IB over that time interval.

The temporal moments of the spectrum of an analytic signal in Eq. (10) are the GD and GS defined as

$$\begin{array}{c}\text{GD}\left(f\right)=-\frac{1}{2\pi }\frac{d\Psi \left(f\right)}{\mathit{d}\mathit{f}},\\ \text{GS}\left(f\right)=\frac{1}{2\pi }\left|\frac{d\hspace{0.17em}\ln \hspace{0.17em}B\left(f\right)}{\mathit{d}\mathit{f}}\right|.\end{array}$$ (13)

The GS is the magnitude of the spectral gradient of the log-amplitude, and is an effective duration, or local temporal spread, of the GD of the TEOAE. Both GD and GS have units of time. GS is proportional to the slope (i.e., level per unit frequency) of the TEOAE SPL spectrum. A peakier spectrum around a particular frequency f is associated with increased GS(f).

III. METHODS

A. Subjects and clinical tests

Procedures for adult participants in Exp. 1 were approved by the Institutional Review Boards at Boys Town National Research Hospital and the University of Washington. The numbers of subjects and test ears and related data are summarized in Table I. The clinical tests included immittance at 226 Hz with a tympanometer (Grason-Stadler, Inc., Eden Prairie, MN), air-conduction audiograms at octave frequencies between 0.25 and 8 kHz with additional tests at 3 and 6 kHz (audiometer, model 61, Grason-Stadler, Inc., Eden Prairie, MN), and bone-conduction audiograms (RadioEar, Eden Prairie, MN) at octave frequencies from 0.25 to 4 kHz. Data were analyzed from those subjects whose clinical tests satisfied the following inclusion criteria for normal hearing: (1) normal 226-Hz tympanometry (peak-compensated static admittance magnitude between 0.3 and 1.7 mmho, and middle-ear pressure within ±100 daPa), (2) air-conduction thresholds of 25 dB hearing level or better at all frequencies from 0.25 to 8 kHz, and (3) air-bone gaps of 10 dB or less at octave frequencies between 0.25 and 4 kHz.

TABLE I.

Subject inclusion.

# Subjects			# Ears			Age (years)
Female	Male	Total	Left	Right	Total	Range	Mean
20	12	32	32	32	64	19–46	26

B. General measurement procedures

All research data were acquired at a sample rate of 22.05 kHz using custom software running on a Windows computer with a two-channel, 24 bit sound card (CardDeluxe, Chanhassen, MN) and a bi-directional serial port (RS-232). The ear probe (Titan, Interacoustics, Middelfart) used in all measurements had two receiver ports driven by DAC1 and DAC2 to deliver sound stimuli and one microphone port recorded by the ADC to measure acoustic pressure. An additional port exiting the probe tip transmitted air-pressure changes generated by the pump in the tympanometer (AT235, Interacoustics, with modified firmware).

Wideband ambient-pressure and tympanometric reflectance tests were first performed in each ear using procedures described in Keefe et al. (2015) prior to TEOAE testing. All tests used the same probe insertion whenever possible. The initial test order was a downswept reflectance tympanogram from an initial air pressure in the ear canal of 200 daPa down to −300 daPa, the ambient reflectance, and an upswept reflectance tympanogram from −300 to 200 daPa. While reflectance results are not analyzed herein, the reflectance tympanometry tests provided a strong test (and would be a strong test even in the absence of any sound) that the probe insertion for TEOAE testing was leak free, inasmuch as it was not possible to pressurize to 200 daPa in the ear canal if any leak were present between the probe and ear-canal wall. In most ear tests in the present study, the probe remained in place between reflectance and TEOAE tests, so that there was high confidence of an adequate probe insertion for TEOAE measurements. When the probe placement was adjusted prior to the TEOAE tests, the operator assessed the real-time recording of the TEOAE stimuli, such that a reduced amplitude was evidence of a possible leak.

C. TEOAE methods

Whereas SPL quantifies the sound level of a repeated transient sound, sound exposure level (SEL) quantifies the sound level of a single transient sound. A single double-evoked transient sound stimulus was a sequence of three separate, more elementary, transient sounds, each at its own sound level as described below. The double-evoked transient sound was repeated in time to enable signal averaging. The sound level of each of the elementary transients was quantified using SEL and related measures that are described in the Appendix.

1. Setting the stimulus level and time origin

The incident pressure was measured in the long tube across a range of DAC1 gains, with the relative gain of DAC2 fixed so that the level of the $P_2[k]$ pressure in the DAC2 signal response was always 12 dB larger than the level of the $P_1[k]$ pressure in the DAC1 signal response. Thus, the onset of distortion was mainly controlled by the output sound level from receiver 2. The residual pressure waveform $p_d[n]$ in the tube was calculated using Eq. (5). The DFT was used to calculate the residual pressure spectrum $P_d[k]$, and thence the so-called residual SEL spectrum in the tube using Eq. (A3). The residual SEL spectrum in the tube was dominated by a broadband noise in the absence of any intermodulation distortion components generated by the probe or any other components of the measurement system. The maximum DAC1 gain and maximum DAC2 gain values were identified at which no distortion was present, as assessed by the absence of any elevation in the residual SEL spectrum in the long-tube recording between 0.7 and 8 kHz.

The DAC1 gain factor used in ear tests was at least 9 dB below the maximum DAC1 gain factor, and the DAC2 gain factor was at least 9 dB below the maximum DAC2 gain factor. This provided a range of 6 dB in which ear-canal standing wave effects might elevate the microphone pressure through pressure doubling, and thereby lead to intermodulation distortion in the ear recording, and an additional 3 dB of attenuation to account for individual variability in the ear-canal area. The absence of measurable distortion was further confirmed through recordings in an artificial ear simulator (Bruel & Kjaer, IEC 711, Skodsborgvej).³

Click TEOAE data were acquired at two stimulus levels with ΔL = −6 and 0 dB. Chirp TEOAE data were acquired with ΔL = 0 and 6 dB. Click and chirp TEOAEs were compared at ΔL = 0 dB, and the response growth of the TEOAE was assessed using recordings at the pair of stimulus levels for each stimulus condition. Click TEOAE data were not recorded at ΔL = 6 dB because the criterion for absence of distortion was not satisfied at this level.

When using chirp stimuli, the TEOAE residual was defined for both the chirp pressure waveforms and the corresponding equivalent-click pressure waveforms after applying the inverse allpass filter. Whether for click or chirp stimuli, the measured TEOAE was analyzed in terms of the click or equivalent-click response in Eq. (5) based on CEOAE methods described in Keefe (2012). The 2012 study used a measurement duration of 5 min (with 32 blocks for averaging), whereas the present study used a measurement duration of 1 min. The total measurement time was shorter in the present study to enhance the translational relevance of the approach for clinical utilization. The time origin was first assigned to align with the time of the peak amplitude of p₁ recorded in the long tube using the click stimulus. After that assignment, the equivalent-click waveforms calculated from each chirp were constrained in the long tube to have their peak amplitudes at t = 0 in the incident pressure response. This was the same time origin in all ear recordings.

2. Multi-window analyses of TEOAEs

A multi-window spectrum analysis was performed using the analytic signal representation to improve the frequency-domain SNR for click TEOAEs and for chirp TEOAEs after transformation to an equivalent-click TEOAE. Whitehead et al. (1995) showed that shorter time windows improved the SNR of high-frequency CEOAEs. Keefe et al. (2011) analyzed double-evoked CEOAEs using a multi-window technique and showed intermediate results of the effect of three windows on the CEOAE residual p_d and the SNR levels in early-, middle-, and late-windowed CEOAE frequency spectra. This multi-window technique was further refined (Keefe, 2012) to calculate CEOAE moments, and is similar to the technique used in the present study.

An initial onset window for all click and equivalent-click TEOAE residual waveforms was applied that was zero for t < 0.625 ms and one for t ≥ 0.9 ms. It had a sine-squared shape between 0.625 and 0.9 ms. Because the maximum frequency of the stimuli was 8 kHz, any TEOAE generated in the initial 0.625 ms was small. This contrasts with click TEOAE waveforms recorded up to 16 kHz, which show a high-frequency TEOAE residual at times earlier than 0.625 ms (Goodman et al., 2009). Early, middle, and late temporal windows were defined that overlapped with onset and offset ramps at 3 and 8 ms with a ramp duration of 2.5 periods of the local tonotopic frequency of a corresponding CEOAE. This local tonotopic frequency was estimated to be 4 kHz (with corresponding period 0.25 ms) for an average CEOAE latency in an adult human ear of 3 ms, and 1.5 kHz (with corresponding period 0.67 ms) for an average CEOAE latency of 8 ms. These temporal windows differed slightly from those in Keefe (2012), which overlapped at 4 and 8 ms with similarly defined ramps.

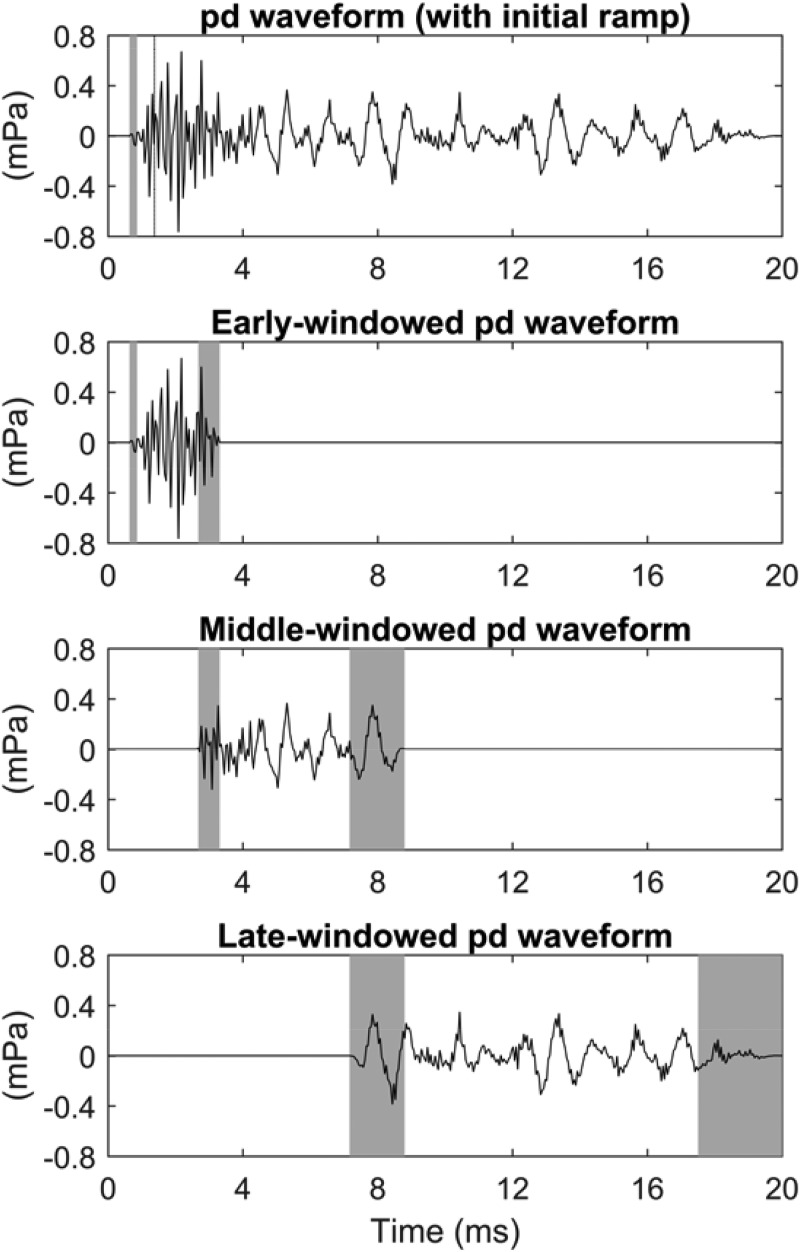
The results of this windowing for the mean equivalent-click TEOAE residual waveform p_d data are shown in Fig. 1. The top panel shows p_d after zeroing out the signal at short times up to 0.625 ms and multiplication by the onset ramp between 0.625 and 0.9 ms. The lower three panels in Fig. 1 show the effect of multiplying this p_d waveform by the early, middle, and late windows with boundaries at 3 and 8 ms.

FIG. 1.

Effect of windowing on p_d in test ear A for positive chirp stimulus. Row 1: single-windowed TEOAE (row 1). Row 2: early-windowed TEOAE. Row 3: middle-windowed TEOAE. Row 4: late-windowed TEOAE. The shaded regions in each row show times at which the waveform was windowed using cosine-squared onset and/or offset ramps.

This multi-window procedure is used to calculate p_d in each of the L blocks, and these data are used to calculate TEOAE responses described in the results. The integer subscript l for block number varies in the range from 1 to the number of blocks L, so that the lth block residual pressure waveform is $p_{d,l}[n]$. It is windowed at short, intermediate, and long-time intervals to give $p_{d,lq}[n]$ for block l as modified by the windows q = 1, 2, and 3 (see Fig. 1). The analytic waveform is calculated for each $p_{d,lq}[n]$, and the DFT gives the spectrum $S_{\mathit{l}\mathit{q}}[k]$ of each analytic signal, which is averaged over the L blocks to give $S_q[k]$. The (non-normalized) coherent “signal energy” is $E_{\mathit{S}\mathit{q}}={\left|S_q[k]\right|}^2$. The incoherent energy ${\left|S_q[k]\right|}^2$ is the mean of ${\left|S_{\mathit{l}\mathit{q}}[k]\right|}^2$ over the L blocks, and the “noise energy” is defined as $E_{\mathit{N}\mathit{q}}=({\left|S_q[k]\right|}^2-E_{\mathit{S}\mathit{q}})/(L-1)$. These relations for the spectrum of the analytic signal are formally the same as those in Schairer et al. (2003) for real signals. A spectral weighting coefficient $W_q[k]$ is calculated for each q as the ratio of the noise energy to the signal energy $W_q[k]=E_{\mathit{N}\mathit{q}}[k]/E_{\mathit{S}\mathit{q}}[k]$, i.e., it is a SNR based on the spectrum of the analytic signal of the TEOAE residual. SNR-weighted signal energy ${\tilde{E}}_{\mathit{S}\mathit{q}}$ and noise energy ${\tilde{E}}_{\mathit{N}\mathit{q}}$ are calculated by

$$\begin{array}{c}{\tilde{E}}_{\mathit{S}\mathit{q}}\left[k\right]=\frac{\sum _{q=1}^3{W}_q\left[k\right]\hspace{0.17em}{E}_{\mathit{S}\mathit{q}}\left[k\right]}{\sum _{q=1}^3{W}_q\left[k\right]},\\ {\tilde{E}}_{\mathit{N}\mathit{q}}\left[k\right]=\frac{\sum _{q=1}^3{W}_q\left[k\right]\hspace{0.17em}{E}_{\mathit{N}\mathit{q}}\left[k\right]}{\sum _{q=1}^3{W}_q\left[k\right]},\end{array}$$ (14)

and converted to SNR-weighted SEL signal and noise spectra, respectively. These are smoothed over the frequency range centered at each 1/6 octave frequency, and used to plot results.⁴

For each block response l, a SNR-weighted spectrum of the analytic signal ${\tilde{S}}_l[k]$ is calculated by

$${\tilde{S}}_l\left[k\right]=\frac{\sum _{q=1}^3{W}_q\left[k\right]\hspace{0.17em}{S}_{\mathit{l}\mathit{q}}\left[k\right]}{\sum _{q=1}^3{W}_q\left[k\right]}.$$ (15)

The weighting increases the contribution of temporally windowed components with large spectral SNR. The spectrum ${\tilde{S}}_l[k]$ of the analytic signal is expressed in terms of its magnitude ${\tilde{B}}_l[k]$ and phase ${\tilde{\Psi }}_l[k]$ using Eq. (10). The ${\tilde{\Psi }}_l[k]$ is averaged over all L blocks at each k and used to calculate a SNR-weighted CSM as explained in the sentence after Eq. (10). GD and GS are calculated at each block l and frequency bin k using a discrete-frequency form of Eq. (13). Following Keefe (2012), GD and GS are smoothed over the frequency range centered at each 1/6 octave frequency and all L blocks using the squared magnitude ${\tilde{B}}_l^2[k]$ as a weighting coefficient for each term.

A multi-window temporal analysis is performed using the analytic signal representation to improve the time-domain SNR for click TEOAEs and for chirp TEOAEs after transformation to an equivalent-click TEOAE. Three real window functions ($G_q[k]$ with q of 1, 2, and 3) are designed in the frequency domain with equal bands of logarithmic frequency over the TEOAE analysis range (0.7–8 kHz). Each function equals 2 at all frequencies in the passband except for squared cosine tapers in the frequency domain at the band edge frequencies (1.60 and 3.58 kHz). Otherwise the function has the value zero. Overlapping pairs of functions sum to 2 in their shared transition band. Each transition band extends over 0.2 times the transition band edge frequencies. An analytic signal $s_{\mathit{l}\mathit{q}}[n]$ waveform in filter q of the residual pressure $p_{d,l}[n]$ in block l is calculated as the inverse DFT of each of the products of $P_{d,l}[k]$ and $G_q[k]$. The factor of 2 in the passband of $G_q[k]$ is the same factor of 2 in Eq. (9). Using Eq. (7), the real part of $s_{\mathit{l}\mathit{q}}[n]$ is the residual pressure waveform $p_{d,lq}[n]$ filtered by the window function q in block l.

The temporal envelope of $s_{\mathit{l}\mathit{q}}[n]$ is $\left|s_{\mathit{l}\mathit{q}}[n]\right|>0$, from which its mean ${\mu }_{s,q}[n]$ and SD ${\sigma }_q[n]$ are calculated over the L blocks for each window function q and sample n. A temporal weighting coefficient is calculated as $w_q[n]={({\mu }_q[n]/{\sigma }_q[n])}^2$, which is a SNR of the envelope of the qth filtered analytic function. For each block response l, a SNR-weighted pressure waveform ${\tilde{p}}_l[n]$ is calculated by

$${\tilde{p}}_{d,l}\left[n\right]=\frac{\sum _{q=1}^3{w}_q\left[n\right]\hspace{0.17em}{p}_{d,lq}\left[n\right]}{\sum _{q=1}^3{w}_q\left[n\right]}.$$ (16)

The weighting increases the contribution of spectrally filtered components with large temporal SNR. The analytic signal ${\widehat{s}}_l[n]$ of $p_{d,l}[n]$ is calculated, and parameterized in terms of its magnitude ${\widehat{A}}_l[n]$ and phase ${\widehat{\Phi }}_l[n]$ using Eq. (8).

The calculation of the time-domain moments IF and IB using ${\widehat{s}}_l[n]$ generally parallel that of the frequency-domain moments GD and GS using ${\tilde{S}}_l[k]$ described above and in Keefe (2012). Using a weighting proportional to amplitude squared, the time-domain forms of CSM and SNR are smoothed across 1/6 doublings of time, and IF and IB are smoothed over the L blocks and across 1/6 doublings of time.

Based on the tonotopic tuning of high frequencies at the basal end of the BM and low frequencies at the apical end, IF would have larger values at short times diminishing to smaller values at long times. However, the calculated and smoothed IF had larger values at longer times due to sensitivity to high-frequency measurement noise in the waveform in the absence of a high-frequency TEOAE at longer times. To correct for this noise effect, the bandwidth of the TEOAE residual waveform p_d used to calculate IF (and also IB) was decimated twice by factors of 2 and 4 so as to lowpass filter the waveform by filter cutoff frequencies that were reduced by a factor of 2 for each decimation stage.⁵ The waveform duration was split into three time bins in which the shortest time bin extended over approximately one-half the duration of logarithmic time, and the other two blocks extended over approximately one-quarter of this duration. With the choice of 1/6 doublings in time, the time bins included these center times (in ms): 0.63–3.56, 4–8, and 8.98–18.0. The corresponding sample rate in the shortest-time bins was 22.05 kHz, with successive sample rates downsampled by factors of 2 and 4, respectively. Thus, the maximum (or Nyquist) signal frequency represented in the p_d waveform in these three time bins was 11.025, 5.513, or 2.756 kHz, respectively. The additional smoothing controlled for non-band limited artifacts that might otherwise arise with the use of the phase gradient to calculate IF. This bias in IF at longer times was not controlled by the use of CSM_crit, because a TEOAE with a low-frequency component at longer times was classified as present due to its phase coherence at lower frequencies. However, its calculated IF was biased toward the higher local frequencies that contained noise. No decimation of p_d was needed to calculate GD and GS.

TEOAE moments were calculated only at those times and frequencies at which the TEOAE residual in the analytic representation was classified as present. Namely, GD was calculated at frequencies with CSM ≥ CSM_crit and GS at frequencies with SNR ≥ SNR_crit. IF was calculated at times with CSM ≥ CSM_crit and IB at times with SNR ≥ SNR_crit. These constraints reduced the variability in estimating each moment.

IV. RESULTS

A. TEOAEs in an individual ear

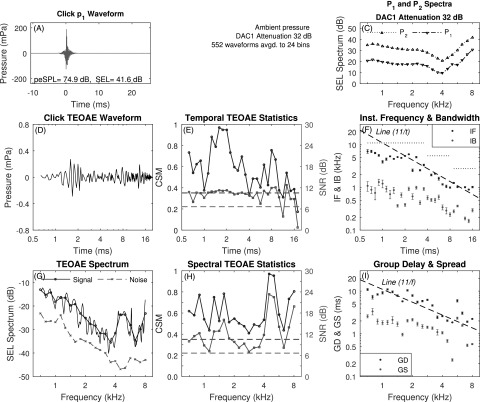
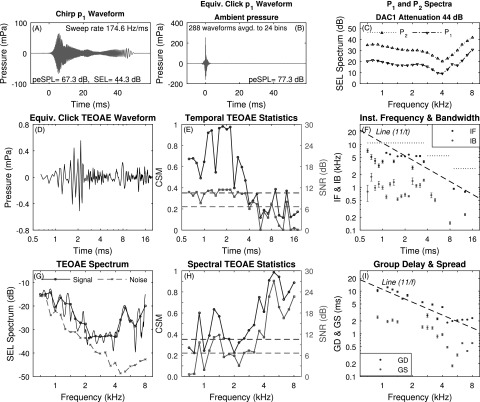
A case study is presented for measurements in test ear A of TEOAEs elicited using the click, positive chirp, and negative chirp stimuli. The mean p₁ waveform of the click stimulus is displayed in Fig. 2(A) with the SEL spectra for P₁ and P₂ in Fig. 2(C). The p₁ stimulus had a peak-to-peak equivalent sound pressure level (peSPL) of 74.9 dB with a total SEL of 41.6 dB. The frequency variations in the spectra of P₁ and P₂ in Fig. 2(C) were due to acoustic standing waves in the ear canal.

FIG. 2.

(Color online) Click TEOAE with three-window averaging (test ear A). A: mean p₁ waveform. Panel B intentionally absent to facilitate comparisons with Figs. 3 and 5. C: mean P₁ and P₂ spectra. D: mean p_d waveform. E: CSM and SNR vs time. F: IF and IB vs time (reference dashed line proportional to 1/t with IF of 11 kHz at 1 ms). Horizontal dotted lines show Nyquist frequency over three sets of time bins. G: TEOAE signal and noise spectra (fine structure, thin solid line). H: CSM and SNR vs frequency. I: GD and GS vs frequency (reference dashed line proportional to 1/f with GD of 11 ms at 1 kHz). Horizontal dashed lines in E and H show CSM_crit and SNR_crit.

Figure 2(D) shows the mean TEOAE residual waveform p_d after the three-window noise reduction technique on a logarithmic time axis. Such an axis reveals the short-time response with a peak amplitude near 1.7 ms. Figure 2(E) shows the corresponding CSM and SNR measures that assess the ability to detect phase and magnitude information, respectively, in the TEOAE waveform, and also shows CSM_crit and SNR_crit. CSM and SNR classified the TEOAE waveform as present at most time samples, with isolated dropouts at 11.3 ms, and at and above 16 ms.

The mean ±1 SE of smoothed IF and IB are shown in Fig. 2(F) at all times at which CSM and SNR, respectively, exceeded the criterion value.⁶ With reference to the dashed line in this panel that is proportional to 1/t and intersects 11 kHz at 1 ms, the mean IF decreased with increasing time with a similar slope. Cochlear mechanics have an approximate scaling symmetry (Siebert, 1968; Rhode, 1971; Zweig, 1976). A slope of IF proportional to 1/t is predicted for such a scaling symmetry (Keefe, 2012). The three horizontal dotted lines show the Nyquist frequency that is the upper bound of IF at each of three sets of time bins. These resulted from the use of decimating the sample rate as described in Sec. III. The mean IB decreased with a slope less than that of 1/t. This decimation in sample rate procedure was used in all subsequent analyses of IF and IB data.

Figure 2(G) shows the mean signal and noise SEL spectra of the TEOAE residual spectrum P_d at 1/6 octave frequency bins, and the SEL spectrum of the fine structure of P_d at the 265 DFT bins between 0.7 to 8 kHz. TEOAE fine structure was present at all frequencies. The TEOAE was classified as present based on both CSM and SNR at every frequency [see Fig. 2(H)]. For this reason, the mean ±1 SE of the smoothed GD and GS are plotted in Fig. 2(I) at all frequencies. The mean GD decreased approximately as 1/f, which is consistent with the presence of a cochlear scale symmetry (Sisto et al., 2007), although there were fluctuations about this 1/f line. For comparison purposes, a trend line (dashed line) is shown in the panel with a slope of 1/f that has the value 11 ms at 1 kHz. The presence of multiple internal reflections would tend to increase the mean GD. The mean GS decreased with increasing frequency with a slightly reduced slope.

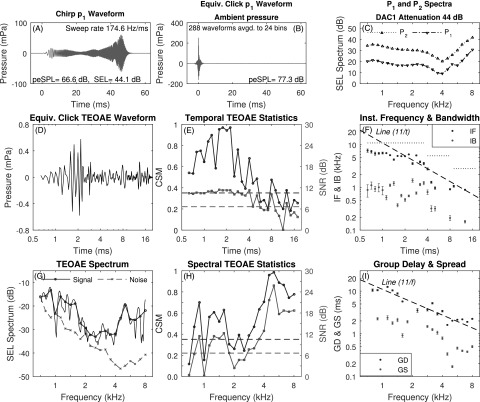
For data recorded in test ear A using the positive chirp stimuli and analyzed using the three-window procedure, the mean p₁ waveform of the chirp response is displayed in Fig. 3(A) with the corresponding mean equivalent-click p₁ waveform displayed in Fig. 3(B). The SEL spectra for P₁ and P₂ are plotted in Fig. 3(C). Comparing text in Fig. 3(A) with Fig. 2(A), the total SEL of 44.1 dB for the positive chirp was 2.5 dB larger than the total SEL of 41.6 dB for the click. This mean increase of 2.5 dB in the stimulus level of the positive (and negative) chirp compared to the click occurred across all test ears. The peSPL was 77.3 dB for the equivalent-click pressure associated with p₁ measured using the positive chirp [see Fig. 3(B)], which was 2.4 dB larger than the peSPL of the click. Leaving aside this level difference, which was inadvertently introduced in stimulus calibration, the peSPL was 66.6 dB for the positive chirp compared to 74.9 dB for the click. This demonstrates the reduction in peak levels using chirps compared to clicks. For the positive chirp SEL spectra in Fig. 3(C), P₁ and P₂ had a similar relative level dependence on frequency as did the click SEL spectra in Fig. 2, except for a slight offset in overall level.

FIG. 3.

(Color online) Equivalent-click TEOAE for positive chirp stimulus with three-window averaging (test ear A). A: mean p₁ chirp waveform. B: equivalent-click response of mean p₁ chirp waveform. C: mean P₁ and P₂ spectra. D: mean p_d waveform. E: CSM and SNR vs time. F: IF and IB vs time. Horizontal dotted lines show Nyquist frequency over three sets of time bins. G: TEOAE signal and noise spectra (fine structure, thin solid line). H: CSM and SNR vs frequency. I: GD and GS vs frequency.

The time-domain equivalent-click TEOAE data in Figs. 3(D)–3(F) were analyzed from the positive chirp data, and may be compared with the corresponding time-domain click TEOAE data in Figs. 2(D)–2(F). For the positive chirp condition, the TEOAE waveform had a larger amplitude at short times near 2 ms in this ear (panel D), which is the expected effect of a 2.5 dB larger stimulus level. However, the temporal CSM and SNR values were generally lower for the positive chirp condition than the click condition at times later than 5 ms. The IF and IB values were similar for positive chirp and click conditions at short times up to about 4 ms, but were defined in fewer time bins for the positive chirp condition at later times at which CSM and SNR, respectively, did not exceed their critical values.

The frequency-domain equivalent-click TEOAE data in Figs. 3(G)–3(I) for test ear A were analyzed from the positive chirp data, and may be compared with the corresponding time-domain click TEOAE data in Figs. 2(G)–2(I). The noise SEL spectrum was larger at low frequencies in the positive chirp condition than the click condition. For this reason, the CSM and SNR were lower for the positive chirp condition [Fig. 3(H)] than the click condition [Fig. 2(H)], so that the TEOAE was classified as present, and thus GD and GS were calculated in fewer frequency bins in Fig. 3(I) than for the click condition in Fig. 2(I). Except for this difference, the mean GD and GS were similar at most frequencies for the positive chirp and click conditions, which supports the theory of a similar generation mechanism.

An important contributor to the difference in noise level between the positive chirp and click conditions was that the chirp stimulus buffers were longer than the click stimulus buffers, so that a 1 min recording averaged 552 click responses but only 288 chirp responses. Balancing this practical advantage for the click TEOAEs, it is possible to use larger SELs for the chirp stimuli than for the click stimuli for a given maximum peSPL. This would result in larger SEL spectrum levels for chirp compared to click stimuli. That is, an increased signal level is possible for chirps in a measurement system limited by peak levels.

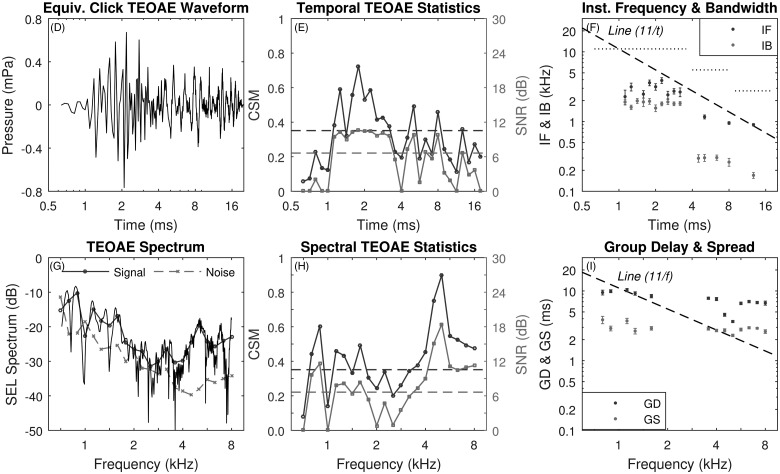
Based on the same positive chirp data as plotted in Figs. 3(A)–3(C), the effects of single-window averaging on the positive chirp TEOAE results are shown in Figs. 4(D)–4(I). These TEOAE results may be compared with those based on the three-noise reduction technique in Figs. 3(D)–3(I). The mean TEOAE residual waveform [panel (D)] and spectra [panel (G)] from the single-window averaging were noisier than results obtained using the three-window averaging. In each panel [(D)–(I)] of these two figures for the positive chirp condition, the TEOAE response was always much noisier using the single-window technique than the three-window technique. CSM and SNR were reduced in the single-window results both as a function of time [panel (E)] and frequency [panel (H)] compared to CSM and SNR in the three-window results. Averaging across frequencies, the mean SEL spectrum of the positive chirp TEOAE noise was −35.7 dB for the three-window average and −30.0 dB for the single-window average. This resulted in a noise reduction of 5.7 dB using the multi-window averaging. The frequency-averaged mean SEL spectrum of the positive chirp TEOAE signal was −24.3 dB for the three-window average and −22.8 dB for the single-window average, a signal reduction of 1.5 dB using the multi-window averaging. This 1.5 dB difference was in part due to the fact that increased noise level in the single-window average also tended to increase the estimated signal level in the single-window average when the SNR was relatively low. The single-window GD was much larger at and above 4 kHz than the three-window GD, which was much closer to the GD predicted based on the presence of a cochlear scale symmetry. This illustrates the noise sensitivity of estimating GD.

FIG. 4.

(Color online) Equivalent-click TEOAE for positive chirp stimulus with single-window averaging (test ear A). D: mean p_d waveform. E: CSM and SNR vs time. F: IF and IB vs time. Horizontal dotted lines show Nyquist frequency over three sets of time bins. G: TEOAE signal and noise spectra (fine structure, thin solid line). H: CSM and SNR vs frequency. I: GD and GS vs frequency.

Based on the same click data as were plotted in Figs. 2(A)–2(C), the effects of single-window averaging on click TEOAEs were also assessed (not shown) in relation to the three-window averaging in Figs. 2(D)–2(I). Averaging across frequencies, the frequency-averaged noise level in the single-window TEOAE spectrum was 5.6 dB larger than the noise level in the three-window TEOAE spectrum.

These single-ear comparisons show that the multi-window technique reduced the TEOAE noise level by about 5–6 dB compared to the single-window technique for TEOAEs generated by both click and positive chirp stimuli. A similar reduction in noise level was observed for all TEOAE types and for all test ears that were analyzed. For this reason, all subsequent TEOAE analyses and plots used the multi-window noise-reduction technique.

For data recorded using the negative chirp stimuli in test ear A, the mean p₁ waveform of the negative chirp response is displayed in Fig. 5(A), and its corresponding mean equivalent-click pressure waveform is displayed in Fig. 5(B). The SEL spectra for P₁ and P₂ are plotted in Fig. 5(C). Comparing the text in Fig. 5(A) with Fig. 3(A), the total SEL was 44.3 dB for the negative chirp versus 44.1 dB for the positive chirp, and the peSPL was 67.3 dB for the negative chirp versus 66.6 dB for the positive chirp. For their respective equivalent-click waveforms shown in Figs. 5(B) and 3(B), the peSPL was 77.3 dB for both positive and negative chirp conditions. As expected, the mean levels of the positive- and negative-chirp stimulus responses were similar. Comparing the TEOAEs analyzed in terms of the equivalent-click pressure residual for the negative and positive chirp stimulus conditions in Figs. 5(D)–5(I) and Figs. 3(D)–3(I), respectively, the responses were similar to one another. This supports the theory of a similar generation mechanism for positive and negative chirps, for which their stimuli had the same overall magnitude but were very different in terms of their phase.

FIG. 5.

(Color online) Equivalent-click TEOAE for negative chirp stimulus with three-window averaging (test ear A). A: mean p₁ chirp waveform. B: Equivalent-click response of mean p₁ chirp waveform. C: mean P₁ and P₂ spectra. D: mean p_d waveform. E: CSM and SNR vs time. F: IF and IB vs time. Horizontal dotted lines show Nyquist frequency over three sets of time bins. G: TEOAE signal and noise spectra (fine structure, thin solid line). H: CSM and SNR vs frequency. I: GD and GS vs frequency.

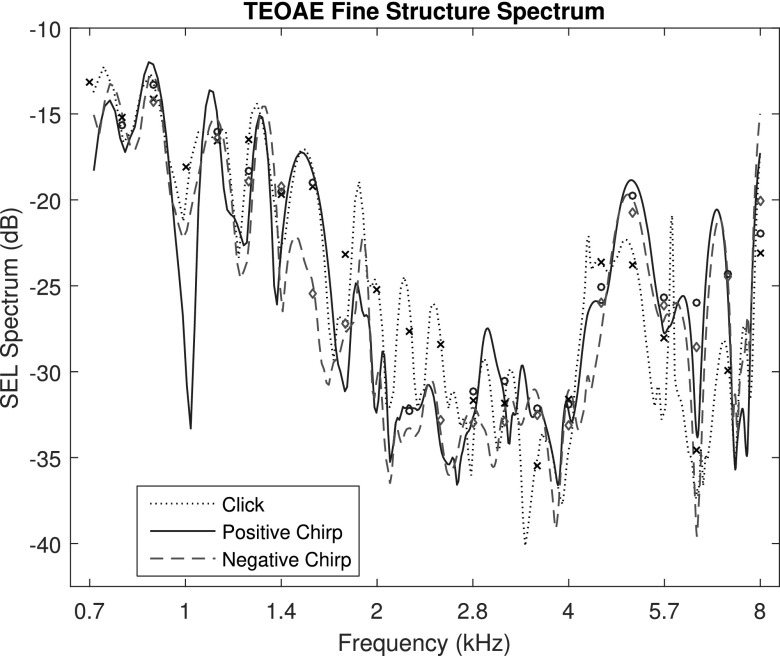
The SEL spectral fine structure of the TEOAE residual signals for test ear A are compared in Fig. 6 for the click condition across its 265 linearly-spaced DFT frequencies between 0.7 and 8 kHz, and for the positive and negative chirp conditions across their 508 DFT frequencies between 0.7 and 8 kHz. The frequencies at which maxima and minima occurred were similar across conditions. The levels of the maxima were somewhat more than 5 dB larger for the click condition at frequencies between 1.8 and 4.4 kHz, and more than 5 dB smaller at 3.4 kHz. To enable viewing of the signal fine structure, the noise levels are not plotted here [although they are individually plotted in Figs. 2(G), 3(G), and 5(G)]. At some frequencies for some conditions, the minima of the fine structure was below the noise level, e.g., for the positive chirp response near 1 kHz. This is a case for which the deep notch in fine structure was a noise effect. The calculated correlation coefficient between the fine structure levels of the positive and negative chirp TEOAEs was 0.905 over the 508 frequencies. This is a measure of the high similarity of these two chirp responses in Fig. 6. No correlations were calculated between the TEOAE fine structures of either of the chirps with the click, as the spectra had different numbers of frequency bins.

FIG. 6.

(Color online) For test ear A, the fine structure of the TEOAE signal is plotted for the click, and positive and negative chirp conditions. Markers plotted at mean signal levels at 1/6 octave frequencies with SNR ≥ SNR_crit.

To control for noise effects and to compare click and chirp levels, the 1/6 octave SEL spectra of the TEOAE residual are also plotted in Fig. 6 for the click (marker ×), positive chirp (marker ○), and negative chirp (marker diamond) conditions, but only at frequencies at which SNR ≥ SNR_crit. Of the 22 center frequencies over the entire bandwidth, the TEOAE was classified as present for all 3 stimulus conditions at 14 of these frequencies. The correlations between levels across these 14 frequencies were 0.987 between positive and negative chirps, 0.885 between positive chirp and click, and 0.881 between negative chirp and click. Thus, the positive and negative chirp TEOAEs were more similar to one another, although there was substantial similarity between the levels of the click TEOAE and either of the chirp TEOAEs, despite the 2.5 dB difference in stimulus level between clicks and chirps. The 1/6 octave interval corresponded to a 12% spacing of frequency bins, which attenuated much of the fine structure in the spectral response.

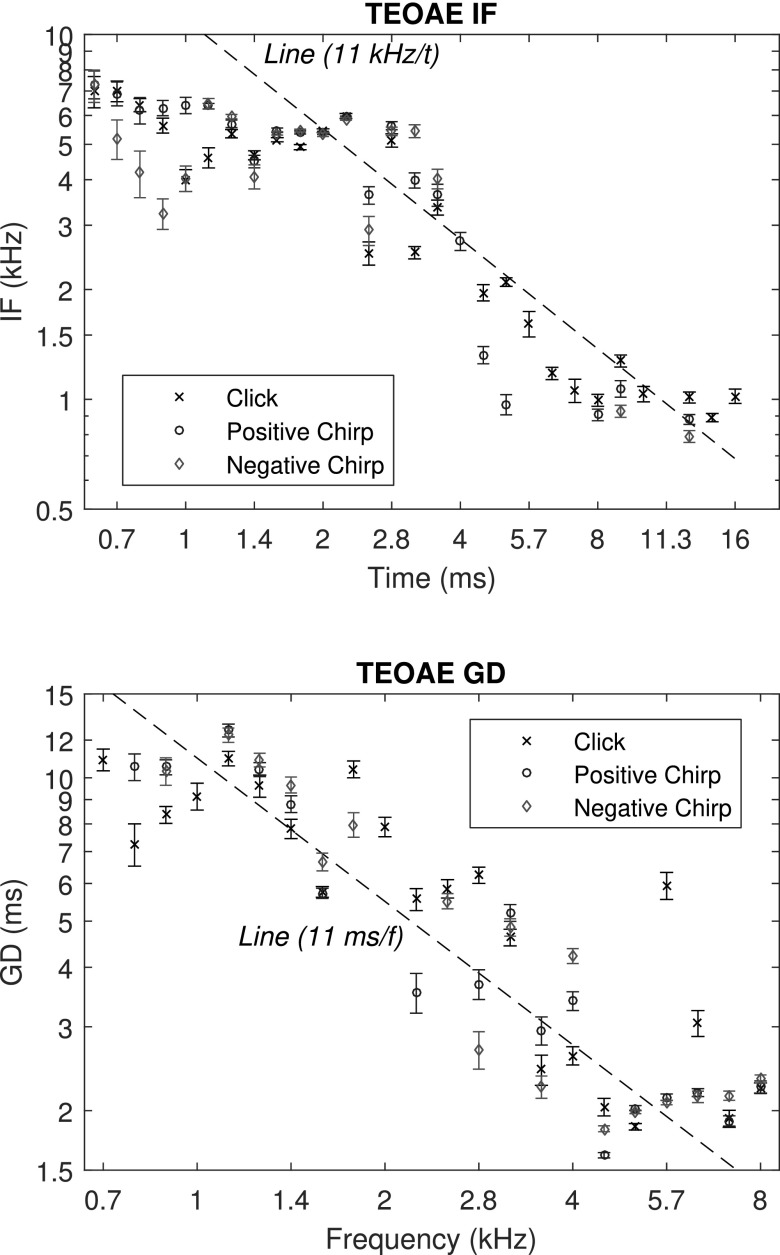
For test ear A, the top panel of Fig. 7 shows the mean IF vs time for the three stimulus conditions. IF was relatively constant in the range of 5–7 kHz for times between 0.6 and 2.2 ms for the click and positive chirp conditions. The maximum IF was slightly below the maximum frequency (8 kHz) in the stimulus. IF was smaller for the negative chirp TEOAE at short times up to 1.4 ms. IF decreased approximately overall as 1/t at later times up to 11 ms, and had values at longer times in the range of 0.8 to 1 kHz, which was approximately equal to the lowest frequency of 0.7 kHz in the stimulus. The click and positive chirp IF were defined at most times as long as 16 ms, whereas the negative chirp IF was not calculated between 4 and 8 ms due to a lack of phase synchrony.

FIG. 7.

(Color online) IF and GD for test ear A. Top: mean ±1 SE of the 1/6 doubling, time-averaged IF of the TEOAE signal is plotted for the click, and positive and negative chirp conditions at times for which CSM ≥ CSM_crit. Bottom: the mean ±1 SE of the 1/6 octave frequency-averaged GD of the TEOAE signal is plotted for the click, positive chirp, and negative chirp conditions, at frequencies for which CSM ≥ CSM_crit.

The mean ±1 SE of GD is shown in the bottom panel of Fig. 7. The mean GD fluctuated between 8 and 13 ms for frequencies between 0.7 and about 1.4 kHz, and decreased as 1/f (with considerable variability about that slope line) at higher frequencies up to 5 kHz. Between about 4.5 and 8 kHz, GD typically had values of about 2 ms, with a value as large as 5.8 ms at 5.7 kHz in the click condition. These responses provide additional evidence to that in Keefe (2012) of the ability to estimate IF and GD from TEOAEs recorded in individual ears with relatively small SEs.

TEOAE data were acquired in each ear at two stimulus levels differing by 6 dB for each stimulus condition. Even though the chirp stimulus levels were 2.5 dB larger than the click stimulus level, these levels are collectively referred to as a relative comparison level (ΔL) of 0 dB (to within ±3 dB). This terminology is adopted because TEOAE data were also acquired at a relative click stimulus level that was 6 dB lower (ΔL = −6 dB), and at a relative chirp level that was 6 dB higher (ΔL = 6 dB).

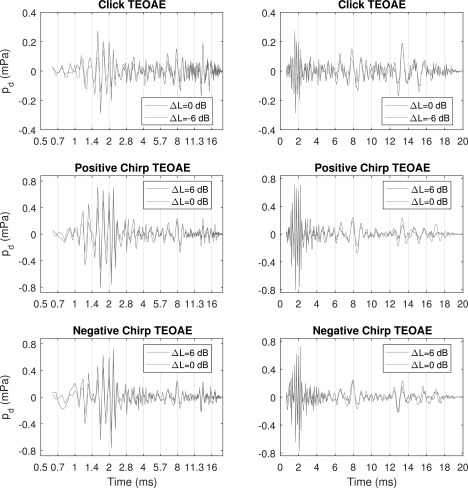
For test ear A, Fig. 8 shows the mean TEOAE waveforms for each stimulus condition and each stimulus level as a function of logarithmic time (left) to show p_d at times shorter than about 8 ms, and as a function of linear time (right) to show p_d at times longer than about 4 ms. The p_d for the click condition shows that the temporal fine structure was aligned across stimulus levels differing by 6 dB. The equivalent-click p_d for each of the positive and negative chirp conditions shows that the temporal fine structure was also aligned across stimulus levels differing by 6 dB. This alignment was quantified by the correlation of p_d at the two test levels for each stimulus condition, with results of 0.82 for the click, 0.82 for the positive chirp, and 0.83 for the negative chirp. Correlations were slightly reduced at times in which noise effects played a role.

FIG. 8.

(Color online) TEOAE p_d waveforms versus logarithmic time (left) and linear time (right). Top: click condition at ΔL = −6 and 0 dB. Middle: positive chirp condition at ΔL = 0 and 6 dB showing the equivalent-click p_d waveform. Bottom: negative chirp condition at ΔL = 0 and 6 dB showing the equivalent-click p_d waveform.

Based on comparisons between different rows of Fig. 8, TEOAE temporal fine structures were also similar across stimulus conditions. The correlations of the p_d waveforms between the click and positive chirp, click and negative chirp, and positive and negative chirps were 0.77, 0.73, and 0.86, respectively, at ΔL = 0 dB. The correlation of the p_d waveforms between the positive and negative chirps at ΔL = 6 dB was 0.88. There were times at which the temporal envelope of the click waveform differed from the envelopes of the chirps in Fig. 8, e.g., between 1 and 2 ms and at later times at which the peaks in the click condition were larger, e.g., near 6, 8, and 14 ms. These larger peaks in the click condition occurred for a SEL that was 2.5 dB larger for the chirps than the click. To summarize for test ear A, the pattern of peaks, dips, and zero crossings of the TEOAE residual waveforms in Fig. 8 were approximately invariant in their timing as a function of stimulus level and stimulus condition. The temporal alignment of zero crossings largely accounted for the high correlations.

B. Group comparisons of TEOAEs for click and chirp stimuli

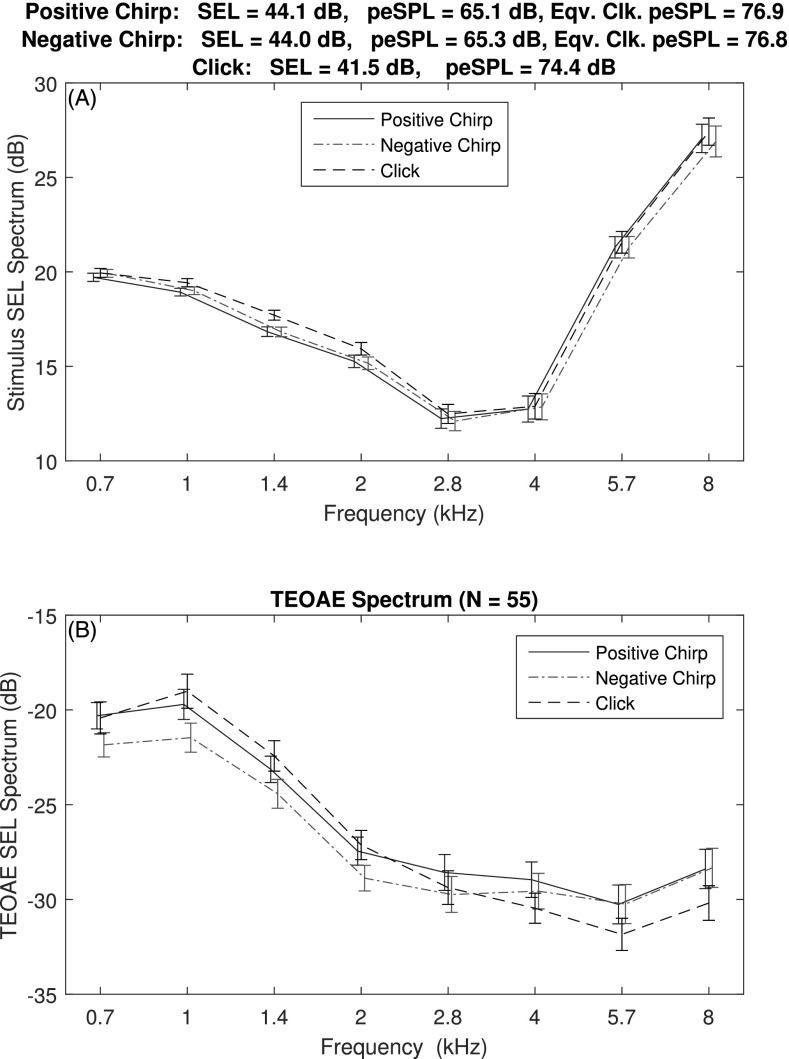
TEOAEs were recorded in a group of 55 normal-hearing adults. The corresponding mean ±1 SE of the half-octave averaged SEL spectra of the P₁ stimulus generated by DAC1 are shown in the top panel of Fig. 9. These are the data collectively referred to as at the relative level ΔL = 0 dB. The mean total SEL was about 2.5 dB smaller for the click (41.5 dB) than for the positive chirp (44.1 dB) or negative chirp (44.0 dB), whereas the total SELs of the positive and negative chirps were equal to within 0.1 dB. The mean SEL spectra plotted for the clicks and chirps were similar with respect to their SEs, except that the mean click SEL spectrum may have been slightly larger at 1.4 kHz.

FIG. 9.

(Color online) Top: Mean ±1 SE of the SEL spectrum for the reference stimulus pressure in a group of adult ears with normal hearing for each stimulus type (positive and negative chirps, click). Bottom: mean ±1 SE of the measured SEL spectrum of the corresponding TEOAE. The title lists the total SEL and the peSPL for each stimulus type. The equivalent-click peSPL is also listed for each chirp.

The mean ±1 SE of the half-octave averaged SEL spectra of the TEOAE residuals are shown in the bottom panel of Fig. 9 for the click and chirp stimulus conditions. The mean spectral levels were similar across stimulus types, although the TEOAE SEL spectrum of the negative chirp was about 2 dB less at 0.7 and 1 kHz than for TEOAEs generated by the other stimulus types. The mean TEOAE SEL spectrum of the click was about 2 dB less at 5.7 and 8 kHz. Inasmuch as the ±1 SE range of the TEOAE SEL was also about 2 dB, it appears that the strength of the TEOAE level was nearly the same for a click or chirp stimulus with the same total SEL. No statistical analyses were performed because of the 2.5 dB offset in click and chirp stimulus levels, and the overall absence of any clinically meaningful differences in the TEOAE spectra for the three stimulus types.

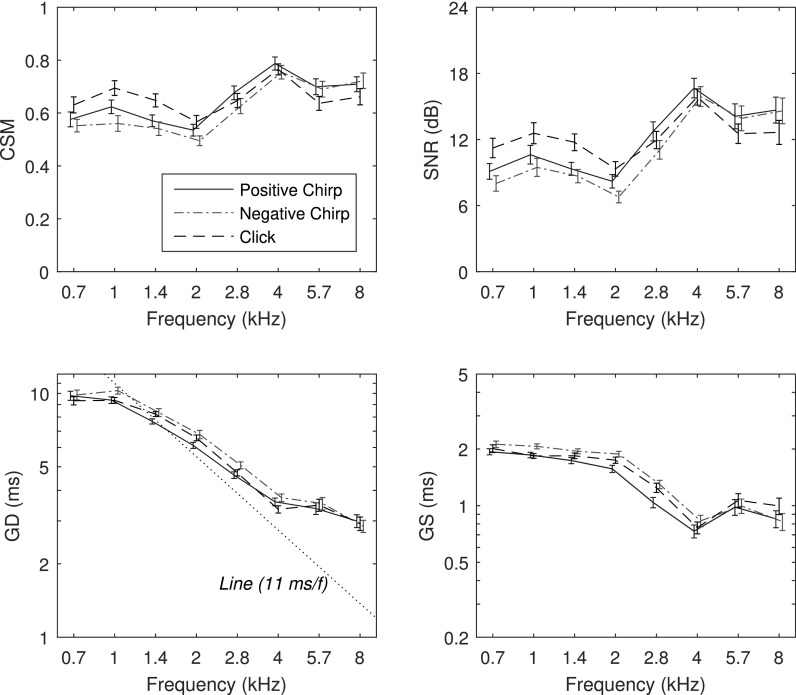
The mean ±1 SE of CSM and SNR are shown in the top row of Fig. 10 as functions of frequency. CSM was in the range of 0.6 to 0.8 with larger values for click TEOAEs at 1 and 1.4 kHz. CSM for positive and negative chirp conditions were in the range of their SEs at all frequencies. The mean SNR varied from 7 to 17 dB across frequency and stimulus condition with slightly larger values for clicks than chirps at 0.7 and 1.4 kHz. The patterns of CSM and SNR were similar to one another across frequency and stimulus condition.

FIG. 10.

(Color online) Adult group data in the frequency domain (mean ±1 SE): CSM (top left), SNR (top right), GD (bottom left), and GS (bottom right). CSM and SNR statistics were calculated over all test ears. GD and GS statistics were calculated at each frequency for those ears with TEOAEs present based on CSM and SNR, respectively.

Percentiles of ears with TEOAEs classified as present based on CSM and SNR were calculated at each frequency for each stimulus type at both stimulus levels. Percentiles were further averaged over all 8 half-octave frequencies (0.7–8 kHz) to calculate a single percentile of ears with TEOAEs present, as shown in the top half of Table II. Percentiles were larger for SNR than for CSM, which means that significant TEOAE amplitude was detected more easily than was a significant TEOAE phase. This means that even though a TEOAE spectral component is present based on amplitude, a spectral phase responses such as GD may have insufficient phase synchrony to provide an interpretative response, thus increasing the variability in estimates of GD. TEOAEs were classified as present in most ears based on SNR, with mean percentiles ranging from 95%–98%. Except for the constant 98% for SNR at both stimulus levels, the percentiles of ears with TEOAEs increased with increasing stimulus level. For CSM, chirp TEOAEs were classified as present in more ears at ΔL = 6 dB than at ΔL = 0 dB.

TABLE II.

Percent of adult ears with TEOAEs based on CSM and SNR. The relative stimulus level ΔL is normalized as zero for the comparison condition between click and chirp TEOAEs (see Figs. 10–12). Data are percentiles averaged over all eight frequencies or all nine times.

		ΔL	% of ears with TEOAEs
Variable	Classifier	(dB)	Click	Positive Chirp	Negative Chirp
Frequency	CSM	−6	66
	CSM	0	82	77	72
	CSM	6		89	85
	SNR	−6	98
	SNR	0	98	96	95
	SNR	6		98	98
Time	CSM	−6	65
	CSM	0	82	71	71
	CSM	6		82	82
	SNR	−6	94
	SNR	0	97	94	95
	SNR	6		96	96

GD and GS data for individual ears were included in the group average at each frequency for which CSM and SNR, respectively, were larger than their criterion values. Thus, the number of data used in the averaging differed at each frequency, such that the mean percentiles of ears used across frequency are the data in Table II. The resulting mean ±1 SE of GD and GS are shown in the bottom row of Fig. 10 for TEOAEs recorded using the click and chirp stimuli at ΔL = 0 dB. For all stimulus conditions, the mean GD was relatively constant near 9–11 ms between 0.7 and 1 kHz, decreased with increasing frequency with a slope slightly less negative than −1 ms/kHz between 1 and 4 kHz, and decreased at higher frequencies from about 3.5 to 3 ms at 8 kHz. The mean GD for the click condition was usually within the SEs of the mean GD for the positive chirp condition. Such similarity of GD is evidence of a similar generation mechanism. The mean GD was slightly larger for the negative chirp than the positive chirp, and this difference exceeded their respective SEs between 1 and 2 kHz. The mean GD for the click was intermediate between these two chirp GDs between 1 and 2.8 kHz. Thus, the evidence suggests a small mean difference in the GDs in this mid-frequency region that is deserving of further investigation as regards possible differences in generation mechanisms across stimulus conditions. For all stimulus conditions, GS was close to 2 ms between 0.7 and 2 kHz and decreased to values in the range of 0.7 to 1 ms between 4 and 8 kHz. The trends in the mean differences in GS between stimulus conditions paralleled the trends in the mean differences in GD, especially at frequencies between 0.7 and 4 kHz.

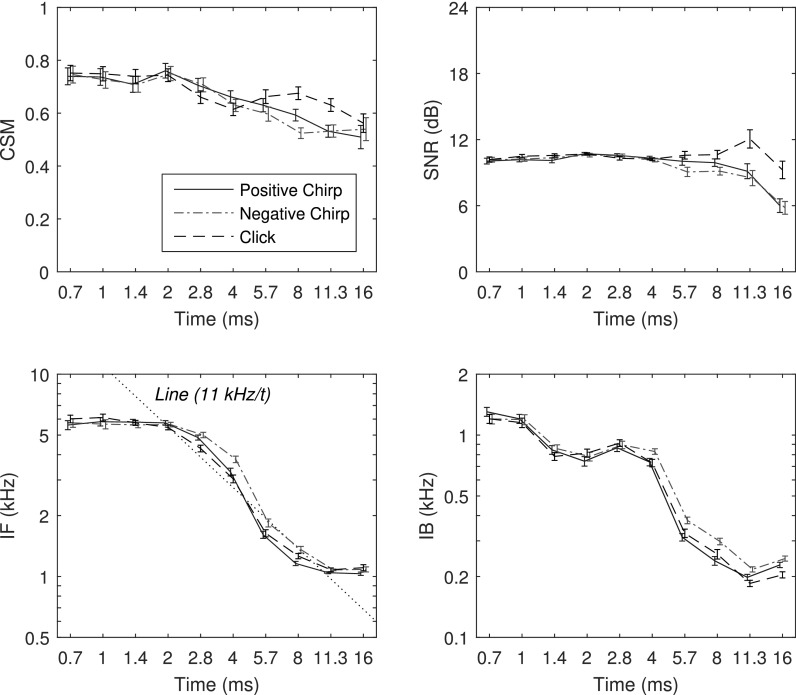
The mean ±1 SE of CSM and SNR as functions of time are shown in the top row of Fig. 11 for TEOAEs recorded using click and chirp stimuli at relative levels of ΔL = 0 dB. The mean CSM in Fig. 11 ranged from 0.8 to 0.5 with larger values at shorter times. The mean differences in CSM for positive and negative chirps were in the range of their SEs at all times except for a larger CSM for the positive chirp at 8 ms. The mean CSM for the click TEOAE was similar to that for the chirps except that the click CSM was larger than either of the chirp CSMs at 8 and 11.3 ms. The mean SNR as a function of time was relatively constant near 10 dB for all stimulus conditions at short times up to 4 ms, with larger values for the click condition at 11.3 and 16 ms. The mean SNR was similar for the positive and negative chirps except for a slightly larger value for the positive chirp at 5.7 ms.

FIG. 11.

(Color online) Adult group data in the time domain (mean ±1 SE): CSM (top left), SNR (top right), IF (bottom left), and IB (bottom right). The CSM and SNR statistics were calculated over all test ears. The IF and IB statistics were calculated at each time for those ears with TEOAEs present based on CSM and SNR, respectively.

The percentiles of ears with TEOAEs classified as present based on CSM and SNR were calculated at each time for each stimulus type at each of two stimulus levels. These percentiles were further averaged over all 10 half-doublings in time (between 0.7 and 16 ms) to calculate a single percentile of ears with TEOAEs present. These values are listed in the bottom half of Table II. TEOAEs were classified as present in most ears based on SNR, with mean percentiles ranging from 94%–97%. TEOAEs were also classified as present in most ears based on CSM, with mean percentiles ranging from 65%–82%. As for the frequency data in this table, the percentiles were larger for SNR than for CSM, which means that significant TEOAE amplitude in time was detected more easily than was a significant TEOAE phase. The percentiles of ears with TEOAE waveforms present increased with increasing stimulus level in all comparison pairs, and especially so for CSM.

IF and IB data for individual ears were included in the group average at each time for which CSM and SNR, respectively, were larger than their criterion values. The number of data used in the averaging differed at each time, although the mean percentiles of ears used across time are the data in Table II. The resulting mean ±1 SE of IF and IB are shown in the bottom row of Fig. 11 for TEOAEs recorded using the click and chirp stimuli at ΔL = 0 dB. For all stimulus conditions, IF was relatively constant near 6 kHz between 0.7 and 2 ms, decreased with increasing time (with a slope close to −1 kHz/ms) between 2 and 8 ms, and was relatively constant near 1 kHz between 11.3 and 16 ms. Mean IF for the click condition was almost always within the SEs of the mean IF for the positive chirp condition. The largest differences occurred between 4 and 5.7 ms with a slightly larger mean IF for the negative chirp than the other conditions (relative to their SEs). The mean IB decreased non-monotonically from 1.2 kHz down to 0.2 kHz with increasing time between 0.7 and 11.3 ms. The mean IB was slightly larger for the negative chirp conditions compared to the other conditions at times between 4 and 8 ms.

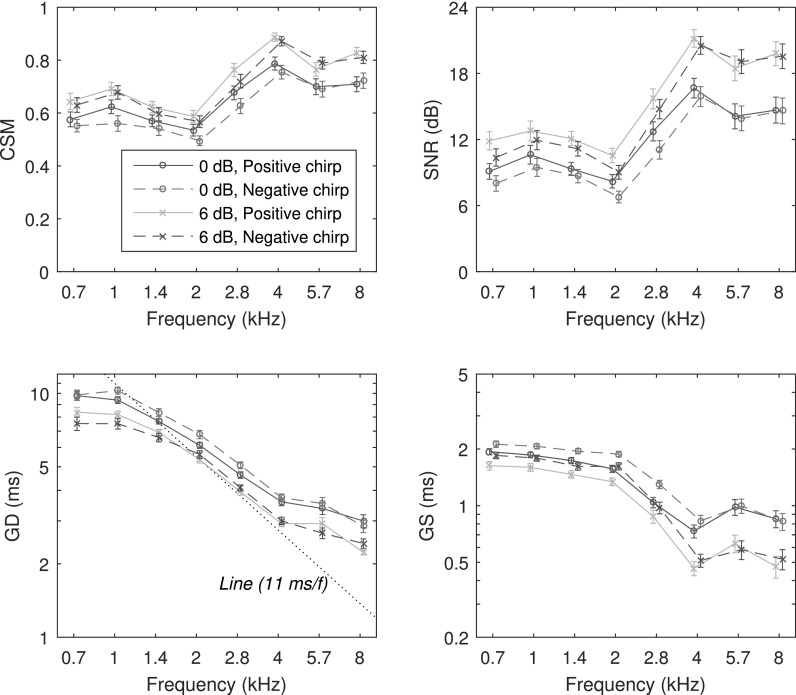
Chirp TEOAE measures at stimulus levels ΔL of 0 and 6 dB are shown as functions of frequency in Fig. 12 for CSM, SNR, GD, and GS (data for ΔL = 0 dB are repeated from Fig. 10). The CSM and SNR increased with increasing stimulus level for both chirp conditions, with the largest increases at higher frequencies. Consistent with previous CEOAE results (Keefe, 2012), GD decreased at the higher stimulus level at all frequencies for chirp TEOAEs. A similar level dependence was observed for click TEOAEs, but is not plotted. GS also decreased with increasing stimulus level for both chirp conditions. The largest decreases in GS with increasing stimulus level occurred at higher frequencies (4–8 kHz).

FIG. 12.

(Color online) Level dependence of adult group chirp TEOAE data in the time domain (mean ±1 SE): CSM (top left), SNR (top right), GD (bottom left), and GS (bottom right). The 0 dB data in the legend are the same chirp data shown in Fig. 10. The 6 dB data are chirp TEOAEs recorded at a 6 dB higher stimulus level. CSM and SNR statistics were calculated over all test ears. GD and GS statistics were calculated at each frequency for those ears with TEOAEs present based on CSM and SNR, respectively.

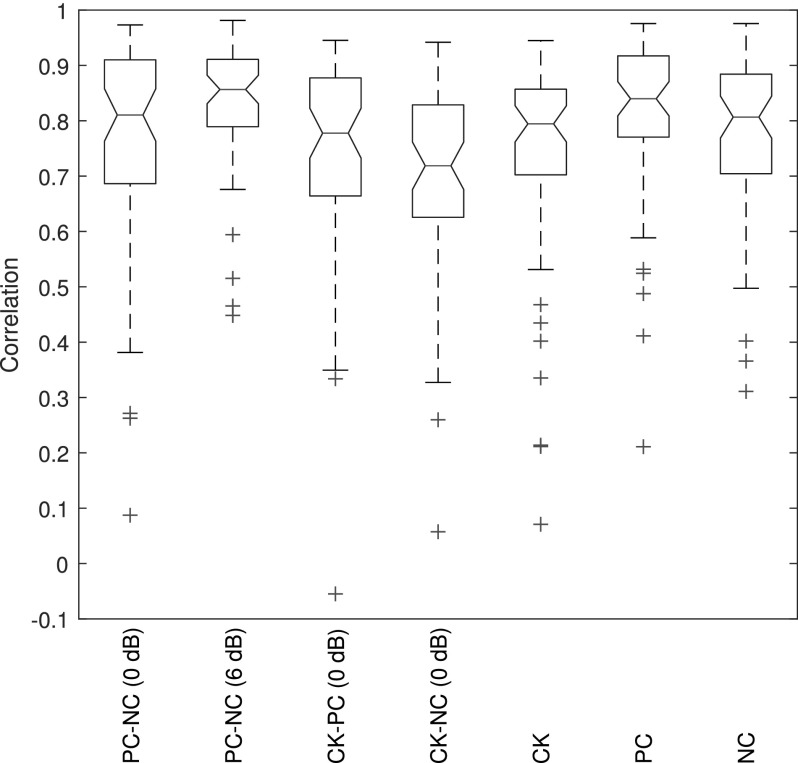
Correlations between the TEOAE spectral fine structure for positive and negative chirp conditions were evaluated in each ear over the 508 DFT bins between 0.7 and 8 kHz. Correlations were calculated at all frequencies whether the TEOAE was classified as present or not. For the relative level ΔL = 0 dB, the median (mean) correlation across all test ears was 0.87 (0.83) with an interquartile range (IQR) from 0.80 to 0.92. For the relative level ΔL = 6 dB, the median (mean) correlation was 0.90 (0.85) with an IQR from 0.82 to 0.93. This correlation exceeded 0.58 in 95% of ears at ΔL = 0 dB, and exceeded 0.53 in 95% of ears at ΔL = 6 dB.

V. DISCUSSION

Chirp stimuli might be preferable to click stimuli in TEOAE measurements in terms of the onset of system distortion, to the extent that this onset is controlled by peak amplitude. No system distortion in the residual SEL was observed for the click and chirp recordings in the long tube or artificial ear simulator at stimulus levels 9 dB higher than those used in ear measurements. When system distortion first occurred at higher levels in long-tube recordings, it occurred at frequencies near 5 kHz. These probe characteristics led to artifacts that emerged in preliminary recordings of multiple sets of TEOAE tests over tens of minutes. The recording duration was restricted to avoid such artifacts in the present study, and to increase the translational applicability.

Multiple temporal and spectral windows were used to analyze the click TEOAE and the equivalent-click TEOAE derived from a chirp TEOAE. These windows were effective at increasing the SNR and CSM relative to a single window analysis. This extended previous results with clinical CEOAEs (Whitehead et al., 1995) and double-evoked CEOAEs (Keefe et al., 2011; Keefe, 2012). Such waveforms had higher-frequency TEOAE components at shorter times and lower-frequency TEOAE components at longer times, as contrasted with some equal distribution of the signal component at a given frequency throughout the waveform. By separating a single analysis window into three windows, it was possible to improve the SNR and CSM of the TEOAE inasmuch as the signal tended to be localized within one or two of the windows at any particular analysis frequency. Thus, a SNR-weighted average over the three windowed buffers preferentially selected out the buffer with the largest SNR.

Long and Talmadge (1997) described a least squares fit (LSF) method to extract one or more SOAEs from a background of noise, in which the amplitude and frequency of a sinusoidal tone representing a SOAE component were model parameters that were adjusted to best fit the data. Their data were analyzed using the LSF model using a single sinusoidal tone in noise. A LSF approach was used to estimate the emission amplitude and phase in a set of windowed buffers from swept-tone DPOAE (Long et al., 2008) and SFOAE (Kalluri and Shera, 2013) recordings. The method used in the present study to extract a chirp TEOAE by transforming it into an equivalent-click TEOAE differs from the LSF method, but both share the goal of extracting a single OAE component. For chirp TEOAEs and swept-tone SFOAEs, this single component is the dominant component that is generated in the tonotopic region of the stimulus. A challenge in using the LSF method with the present dataset is that a typical buffer duration might be 20 ms in a LSF analysis, in which the stimulus frequency would sweep over a range of 3.49 kHz at the sweep rate of 174.6 Hz/ms. Thus, the TEOAE fine structure might be difficult to extract in a LSF analysis. Comparisons of TEOAEs analyzed using the LSF method and the present allpass-filter method are a topic of future research.

Click and chirp TEOAE responses were compared in the frequency domain in terms of signal level, SNR, CSM, GD, and GS. The TEOAEs were compared in the time domain in terms of signal level, SNR, CSM, IF, and IB. A general conclusion is that click and chirp TEOAEs were overall similar to one another after the chirp TEOAE was transformed to an equivalent-click TEOAE response. This similarity supports a theory that TEOAEs are generated by the compressive nonlinearity of outer hair cell function in the tonotopic region of the BM. However, there were several conditions in which mean differences were observed in TEOAEs for the different stimulus conditions, and a near invariance in TEOAE fine structure was observed across stimulus level. These are further considered below in terms of the underlying cochlear mechanisms.

The mean TEOAE spectrum level was 2–3 dB lower at 1 and 1.4 kHz for the negative-chirp condition than for the click condition (bottom panel, Fig. 9), although the corresponding stimulus level was less than 1 dB lower at 1 kHz and less than 2 dB lower at 1.4 kHz (top panel, Fig. 9). This is a borderline change, even though the mean differences were larger than the SEs. It should be noted that the total SEL of the chirps were 2.5 dB larger than that of the click, but these were calculated in the time domain using Eq. (A2) (see the Appendix), and the chirps had a larger noise contribution because of the longer time duration. A 2.5 dB difference in stimulus level might be associated with a 1 dB change in TEOAE level if the cochlear compression ratio were 40%. Thus, the interpretation of such small mean differences in these data was ambiguous. The mean click TEOAE spectrum levels were lower than the mean chirp TEOAE spectrum levels at 5.7 and 8 kHz, although the mean difference was on the order of the SEs. The stimulus spectrum levels were similar for clicks and chirps at 5.7 and 8 kHz.

There was no such ambiguity in comparing positive- and negative-chirp TEOAEs, because their durations, number of averages, and total SEL were the same. The mean TEOAE SEL spectrum was slightly lower for the negative chirp condition at 0.7 and 1 kHz (see Fig. 9, bottom), although this level difference was on the order of the SEs. The mean GD was larger for negative-chirp TEOAEs than for positive-chirp TEOAEs at frequencies from 1 to 2.8 kHz, although this mean difference was large compared to the SEs only at 1 kHz (see Fig. 10). The mean GS in the same figure was larger for negative-chirp than positive-chirp TEOAEs at frequencies from 0.7 to 2.8 kHz, with the mean difference large compared to the SEs between 1 and 2.8 kHz. There was substantial overlap in the IF and IB responses between the positive and negative chirp conditions at most times (see Fig. 11), except for slightly larger mean IF between 4 and 8 ms, and slightly larger mean IB between 8 and 16 ms, in the negative chirp condition.

TEOAE residual levels were substantially similar in normal ears under two conditions, one measurement using click stimuli and other measurements using positive and negative chirp stimuli. Substantial similarity means that the differences across stimulus condition in mean TEOAEs as functions of frequency and time were small relative to their SEs or of approximately the same order (see Figs. 9–12). Notwithstanding that overall result, there were a few small differences in TEOAEs according to stimulus type that may be due to nonlinear interactions.

A. Theoretical perspectives

Experimental measurements of BM displacement in mammalian ears generated by clicks show invariance in the temporal fine structure of the displacement waveform as a function of click intensity (Robles et al., 1976; Recio and Rhode, 2000). This finding constrains the form of admissible theories of cochlear mechanics (de Boer and Nuttall, 2000) and suggests that the local resonance frequencies of the cochlear partition are intensity invariant (Shera, 2001b). Neglecting middle-ear effects, the click sound stimulus in the ear canal also acts as a click input to the BM. One might therefore expect that CEOAE waveforms have a similar intensity invariance in their temporal fine structure at varying click levels.

The coherent reflection emission theory predicts that SFOAEs are generated within the tonotopic region of the traveling wave as a result of coherent scattering from spatially distributed irregularities along the BM (Zweig and Shera, 1995). SFOAE GDs are generally similar to measured CEOAE GDs (Keefe, 2012), which supports the theory of a similar generation mechanism for CEOAEs.

The fact that click and chirp stimuli differ in phase means that the stimulus energy is present at different times in a chirp relative to a click. If the generation region of the TEOAE depends on the relative times at which the input stimulus energy to the cochlea is presented across frequency, then the resulting TEOAE level might be predicted to differ between the click- and chirp-evoked OAEs. With chirp stimuli using a fast sweep rate, there is the possibility of a larger contribution from nonlinear temporal interactions on the BM (Kemp and Chum, 1980; Kapadia and Lutman, 2000a,b; Verhulst et al., 2011) that may differ across the stimulus types. These studies analyzed CEOAEs recorded from pairs of clicks of similar or alternating polarity, in which CEOAE suppression was observed (with enhancement in a few conditions) with inter-click delays of about 1–6 ms (and to a lesser extent out to 12 ms). An analogous nonlinear temporal interaction may vary in TEOAEs due to the variation in stimulus phase in clicks and chirps, even when the stimulus amplitude spectrum is fixed.

For a given frequency at low sound levels, the BM velocity has a maximum amplitude at a tonotopic location x_c along the longitudinal x axis of the BM (x = 0 at the stapes footplate), and its amplitude is rapidly quenched at more apical BM locations. The local wavelength is long at basal locations x $\ll$ x_c on the BM and much shorter in the region close to x_c (Zweig, 1976). A consequence of this wave motion is that the phase velocity of the traveling wave is fast in the basal regions, and slows in the region close to the tonotopic peak. This is observed in mammalian ears (Recio and Rhode, 2000). A click or impulse signal at the stapes footplate contains all signal frequencies. The frequency-specific traveling waves separate as the lower frequency components travel away from the basal end with a faster initial phase velocity than that of the higher frequency components. One-way travel times are on the order of half the measured GD for the click TEOAE (Shera et al., 2005), assuming that click TEOAEs are generated as coherent reflection emissions. From the GD data for the click TEOAE in Fig. 10, these travel times ranged from about 5 ms at 1 kHz down to 1.5 ms at 8 kHz.

When the stimulus at a given cochlear place includes two (or more) different frequency components, two-tone suppression may be observed in the mechanical responses of the BM (Ruggero et al., 1992). Such effects are observed across the frequency range 0.5 to 8 kHz in SFOAE suppression (Keefe et al., 2005) and are related to nonlinear temporal interactions with CEOAEs generated by pairs of clicks with inter-click delays on the order of 1–6 ms (Kemp and Chum, 1980; Kapadia and Lutman, 2000a,b; Verhulst et al., 2011). These delays are on the order of the cochlear travel times. Different frequency components present at the same time with significant amplitudes at the same or nearby locations on the BM can suppress the amplitude of motion of the other components. This interaction depends on the relative amplitudes of the components.

The present study used a chirp stimulus with an effective duration of 42 ms, which was much longer than the 5 ms scale of cochlear travel times. This means that frequency components in the chirps that were much more widely separated in time than 5 ms were effectively non-interacting on the BM. This is in contrast to the click stimulus, for which frequency components of the traveling wave overlap in time and space at the basal end. At more apical locations, nonlinear interactions including suppression were possible within this chirp duration in which lower-frequency stimulus components occurred at earlier times in the positive chirp and at later times in the negative chirp compared to relatively higher-frequency stimulus components. For example, each 4 ms interval of the chirp contained a 702 Hz range of stimulus frequencies [based on the sweep rate in Eq. (4)] around the nominal center frequency at the midpoint of the time interval. Two-tone suppression is asymmetrical with respect to whether the suppressor frequency is lower or higher than the probe frequency at which suppression is measured. In general, so-called low-side suppression is stronger for suppressor frequencies less than the probe frequency, while high-side suppression is present as well but over a much more restricted range of suppressor frequencies. This suggests that positive- and negative-chirp TEOAEs might differ if suppression differed as a function of sweep polarity.

The equivalent rectangular bandwidth (ERB) estimated from SFOAEs (Shera et al., 2002) and CEOAEs (Keefe, 2012) in human ears predict ERBs of approximately 79 Hz at 1 kHz, and 338 Hz at 8 kHz. The chirps in the present study would include a 702 Hz band of frequencies in 4 ms that would span multiple ERBs, especially at low frequencies, and the traveling waves generated by these chirps might interact over such times along an extended length along the BM. This condition was not satisfied in other studies measuring swept-tone SFOAEs. For example, the sweep rates used in Kalluri and Shera (2013) varied in the range from 2–16 Hz/ms, so that a 4 ms interval within the swept tone would include a maximum frequency range of 64 Hz, which is less than 1 ERB. To the extent that any chirp and click TEOAE differences are apparent in the experimental results, the use of fast chirp sweep rates may serve as a probe of the underlying cochlear mechanics. On the other hand, a finding of no difference between TEOAEs generated by either of the chirps with the click, or between the positive and negative chirps, would suggest a common generation mechanism on the BM of the various TEOAE types with respect to nonlinear temporal processes or two-tone suppression.

It is relevant to consider chirp measurements of BM displacement in chinchilla at a location x that varied from 1 to 4 mm from the basal end of the cochlea (Recio and Rhode, 2000). These data showed BM displacements over a much longer duration using a positive chirp than a negative chirp at the same stimulus level,⁷ especially at lower stimulus levels. This asymmetry may be due to the fact that the low frequencies have a shorter travel time to a basal location than the high frequencies, so the response duration is stretched out in time for the positive chirp (low frequencies precede high frequencies), and compressed in time for the negative chirp (high frequencies precede low frequencies). This explanation was described and experimentally confirmed in guinea pig ears by Summers et al. (2003). The underlying phenomenon is similar to the frequency glide effect for click data in Recio and Rhode (2000), which was explained in terms of traveling-wave dispersion across frequency in Shera (2001a). In a non-invasive chirp TEOAE measurement, the round-trip traveling-wave dispersion occurs in a similar manner for positive and negative chirps as it is referenced to the TEOAE signal after exiting the cochlea and arriving at the ear canal. A similar asymmetry in TEOAEs for positive and negative chirp conditions does not arise after removing the stimulus phase differences through the inverse filter to calculate the equivalent-click p_d. Suppose that point BM displacement measurements similar to those of Recio and Rhode and Summers et al. were analyzed with TEOAE measurements using click, positive chirp, and negative chirp stimuli in the same mammalian ear. It is predicted that the equivalent-click TEOAE transformed from the chirp TEOAE to remove stimulus phase effects would show a similar near invariance between click TEOAEs and equivalent-click TEOAEs as was observed in the present study.

A particular example illustrates theoretical issues. Consider two frequency components f₁ and $f_2>f_1$ elicited by a transient click that are close in frequency [i.e., $(f_2-f_1)\ll f_2],$ such that each propagates as a cochlear traveling wave. Each component may be viewed as a frequency-centered pulse of effective duration according to the selected bandwidth of the narrowband filter extracting the component. Their corresponding tonotopic locations on the BM are at $x_{c1}$ and $x_{c2}<x_{c1}$. For present purposes, a cochlear scale symmetry is assumed with a forward transmission delay of 5.5 periods to the tonotopic place at 1 kHz, although the coefficient of 5.5 increases with increasing frequency in human ears due to the fact that the scale symmetry is only approximate (Shera and Guinan, 2003). The corresponding travel time is about $t_{c1}=5.5/f_1$ for the f₁ component and $t_{c2}=5.5/f_2$ for the f₂ component, so that $t_{c2}<t_{c1}$. Factoring in the spatial dependence of the phase velocity, the location of the f₁ component peak at any time t varies as $x_1(t)$, with $x_{c1}=x_1(t_{c1})$. For a click stimulus, the onset is t = 0 for both components and the f₂ component reaches its tonotopic peak first at $t=t_{c2}$. The location of the peak of the f₁ component at time $t=t_{c2}$ is $x_1(t_{c2})<x_{c1}$. This f₁ component at time t_c2 produces large amounts of two-tone suppression of the f₂ component.

A positive chirp delays high frequencies relative to low, so that the onset time of the f₂ component is delayed by a time τ > 0 relative to the onset of the f₁ component. The onset time of the f₁ component of the positive chirp is fixed at t = 0. The f₁ component arrives at its tonotopic place at t = t_c1, and is rapidly quenched at later times. The f₂ component arrives at its tonotopic place at the time $t=t_{c2}+\tau$, which is less than t_c1 for small τ, but larger than t_c1 for larger τ. Depending on the choices of f₂ − f₁ and τ, there is scope for nonlinear interactions at the f₂ place.

A negative chirp corresponds to the case τ < 0. In this case, the f₂ component has an onset time of $t=-|\tau |$, and arrives at its tonotopic place at $t=t_{c2}-|\tau |$. The f₁ component arrives at its tonotopic place at t = t_c1. Since t_c2 < t_c1, then $t=t_{c2}-|\tau |$ is even earlier in time. Thus, the nonlinear interactions at the f₂ place would be more temporally isolated in the negative chirp. The positive chirp can counteract effects of cochlear dispersion by increasing spatial-temporal overlap in BM displacement while the negative chirp cannot because it decreases the spatial-temporal overlap. The larger GD and GS at intermediate frequencies (see Fig. 10) and larger IF and IB at intermediate times (see Fig. 11) for the negative-chirp condition relative to the positive-chirp condition may be explained by such interactions. Future research might analyze the different stimulus conditions using a nonlinear time-domain cochlear model.

CEOAE latency is often defined as the time of a localized maximum in the envelope of the CEOAE. A near level invariance has been reported for CEOAE latencies (Goodman et al., 2009, 2011; Moleti et al., 2012). This means that the time at which an individual maximum occurs has only a small variation with stimulus level. The present study showed a near intensity invariance in the temporal fine structure of a click TEOAE residual waveform in test ear A (see Fig. 8, top row), which was paralleled by a high correlation in the spectral fine structure of a click TEOAE residual level across stimulus level. In group analyses, the degree to which the temporal fine structure of p_d was invariant with the 6 dB change in stimulus level was evaluated by the correlation between p_d at the two levels. The median correlation was 0.80 for the click condition (CK boxplot in Fig. 13), compared to which the analogous correlation in test ear A was 0.82.

FIG. 13.

(Color online) Box and whiskers plot for pair-wise correlations of TEOAE residual waveforms in all adult ears. The pairs are positive and negative chirps at ΔL = 0 dB [PC-NC (0 dB)], positive and negative chirps at ΔL = 6 dB [PC-NC (6 dB)], click and positive chirp at ΔL = 0 dB [CK-PC (0 dB)], click and negative chirp at ΔL = 0 dB [CK-NC (0 dB)], click at ΔL of 0 and 6 dB [CK], positive chirp at ΔL of 0 and 6 dB [PC], negative chirp at ΔL of 0 and 6 dB [NC]. The box is the IQR with horizontal line as median, and outliers shown with + markers.

A corresponding near intensity invariance in temporal fine structure was also observed for the equivalent-click p_d for the positive and negative chirp conditions (see the PC and NC boxplots in Fig. 13), with median correlations of 0.84 and 0.81, respectively, at ΔL = 0 dB. In addition, the median correlation in p_d between the click and the positive or negative chirp condition was 0.78 and 0.72, respectively. The median correlation between positive and negative chirps was 0.81 and 0.86 at ΔL of 0 and 6 dB, respectively. Across all 7 correlation boxplots in Fig. 13, the 25th percentiles ranged from 0.63 to 0.79, and the 75th percentiles ranged from 0.83 to 0.92. These provide further evidence of the strong similarity of the TEOAE generation mechanism in the click and chirp conditions, once the effect of the chirp stimulus phase was removed by transforming p_d to an equivalent-click waveform.

Bennett and Özdamar (2010b) reported a mean correlation of 0.38 between CEOAE and click-equivalent TEOAE waveforms in 26 ears, in which the click-equivalent TEOAE was transformed from a swept-tone TEOAE. This correlation was calculated for a smaller range of post-stimulus times between 2.5 and 12.5 ms. These correlations were smaller than those found in the present study, which may reflect methodological differences.

Based on a comparison of CEOAE and equivalent-click TEOAE waveforms from six subjects over this range of post-stimulus times, Bennett and Özdamar (2010b) observed that the two OAE types “were generally phase and time aligned.” This was consistent with Wilson (1980), who first reported a similarity in CEOAE waveforms at varying click levels despite a strong effect of compressive nonlinearity on amplitude.

In particular, the near intensity invariance in the temporal fine structure of the click TEOAE suggests that it is closely related to the near intensity invariance in temporal fine structure of click-evoked BM displacement data described above. This close relationship is evidence that the click TEOAE is mainly generated within the region basal to the tonotopic place. This conclusion is also supported by the group data on GD and IF (see Figs. 10 and 11), and applies as well to chirp TEOAEs given their similarities in the data described above. A limitation of the present study is that the stimulus level range was only 6 dB. It is important to evaluate whether TEOAEs show a near intensity invariance of temporal fine structure over a broader range of stimulus levels.

CEOAE moments were measured in Keefe (2012) at peSPLs of 38 to 73 dB for p₁, whereas the peSPL for p₁ for the click TEOAE in the present study was 74.4 dB at ΔL = 0 dB and 68.4 dB at ΔL = −6 dB. The peSPLs in separate studies are not easily compared as the stimulus bandwidth was 16 kHz in the 2012 study compared to 8 kHz in the present study. With that caveat, the moments are compared with those measured in the 2012 study at 73 dB peSPL. The mean GD was similar except that at 8 kHz (and to a lesser extent at 5.7 kHz), such that the GD of 3 ms (see Fig. 10) was slightly larger than the GD of 2.2 ms in the 2012 study. The mean GS was similar in the two studies, such that both showed a decrease between 2 and 4 kHz (see Fig. 10). The mean IF and IB were similar in the two studies for short times up to 5.7 ms, whereas IF and IB were lower in the present study at times from 11.3 to 16 ms. This difference at long times may be due to differences in the decimation procedures used to band limit IF and IB in the two studies, and differences in noise levels due to shorter averaging times in the present study.

Multiple component OAEs may be extracted by identifying multiple peaks at different latencies from time-frequency or wavelet analyses of OAE recordings. Evidence exists for the presence in human ears of TEOAEs at shorter latencies (Withnell et al., 2008) and faster growth rates with increasing stimulus level (Goodman et al., 2009). Short-latency TEOAEs do not appear to be produced by intermodulation distortion at the basal end of the cochlea (Lewis and Goodman, 2014). Some components may be generated in more basal parts within the tonotopic region of the BM (Sisto et al., 2013; Lewis and Goodman, 2015). In addition, tone-burst SFOAEs do not generally show evidence of intermodulation distortion components except at higher test levels (60 dB SPL) (Konrad-Martin and Keefe, 2003), in which such distortion was absent at lower levels (40–50 dB SPL). Multiple component OAEs may also arise from multiple internal reflections within the cochlea.

Multiple distinct regions of the BM contribute to a single TEOAE response at a particular frequency. Experimental evidence shows the presence of multiple maxima of different latencies but similar frequency content in the temporal envelope of the emission (Goodman et al., 2009, 2011; Moleti et al., 2012), and Sisto et al. (2015) explain these multiple contributions to the OAE as arising from a basal distribution of reflection sources. GS is an effective duration, or local temporal spread, of the TEOAE that is characterized as having a single GD. GS might be expected to increase in the presence of multiple components, each having its own GD. The mean GS decreased with increasing stimulus level in all stimulus conditions (see lower right panel, Fig. 12). A similar finding was reported for GS in Keefe (2012) for click stimuli over a 30 dB range of stimulus levels. For a single-component TEOAE that is generated at its tonotopic place, a reduction of GS at higher stimulus levels is interpreted as a smaller temporal spread of GD.

The standard interpretation of the moments (GD, GS, IF, and IB) is based on a single-component signal in the underlying time-frequency representation, whereas the moments are not as easily interpreted for a signal with multiple components (Cohen, 1995). One possibility is that the amplitude dependence of GS in the present study and Keefe (2012) is associated with the temporal spread of the dominant component of the TEOAE generated from the region just basal to the tonotopic place. This is consistent with the level dependence in GS in Fig. 12 and Keefe (2012). This is an area for further research. Overall, the experimental evidence in human ears is that the single largest TEOAE component is generated near the tonotopic place and has a compressive response growth, for which Fig. 8 shows compressive growth in the time-domain waveforms (i.e., less than a two-fold increase in amplitude for a 6 dB increase in stimulus level).

The presence of SOAEs might lead to variations in TEOAEs with stimulus phase. This is because SOAEs behave as independent oscillators interacting in a nonlinear manner with an external signal, whether a click or a chirp. No SOAE data were acquired in this study to investigate this possible relationship.

B. Clinical translation

While the cochlear mechanics in an ear with normal function may be better studied at relatively lower stimulus levels at which the mechanics are less compressively nonlinear, the translational use of TEOAEs in clinical studies may benefit from relatively higher stimulus levels. These may more easily allow the test to identify a change in the TEOAE response over time in a longitudinal screening study or a weaker TEOAE response in an ear with peripheral auditory dysfunction. For example, SFOAEs were more accurate in classifying adult ears with sensorineural hearing loss or normal hearing at 50 dB SPL than at lower levels (Ellison and Keefe, 2005). This optimum level was larger than the 40 dB SPL used in many SFOAE studies of basic generation mechanisms in normal-hearing ears. For measuring TEOAEs, the chirp stimuli are advantageous in this respect as they can generate larger overall SELs than click stimuli.

The main advantage of using fast sweep rates, as in the present study, was the ability to exclude intermittently noisy responses. The presence of intermittent noise in a more slowly swept sine wave response might require an analysis that identifies times within each sweep at which the noise level is excessively high.

VI. CONCLUDING REMARKS

The use of a multi-window noise-reduction procedure was effective in reducing TEOAE noise levels relative to a single-window procedure. The main hypothesis was that TEOAEs have nearly identical properties across stimulus conditions (click, positive chirp, negative chirp) under the constraints that the stimuli have the same energy spectrum and that the effects of any stimulus phase differences are removed from the TEOAE responses. This hypothesis was confirmed by our results: to first order across the three conditions of stimulus phase, the TEOAEs had properties consistent with a compressively nonlinear generation site basal to the tonotopic region. The measured TEOAEs had relatively long GDs in substantial agreement with previous measurements of CEOAEs that were consistent with the coherent reflection theory of OAE generation. To second order, the TEOAEs showed systematic small mean differences in their signal-processing moments (GD, GS, IF, and IB) that varied across the three conditions of stimulus phase, and in particular, between TEOAEs recorded with positive- and negative-chirp stimuli. These differences appear to be related to spatial-temporal differences in the nonlinear mechanics on the BM in response to differences in stimulus phase.

An analysis in a single ear with normal hearing showed that the fine structures of the residual TEOAE level were highly correlated across frequency and across time between the positive and negative chirps, and between the chirps and the click conditions. The temporal fine structure of the TEOAE waveform had stimulus-phase invariance, once the effect of stimulus phase was removed from the TEOAE waveform, and a near-intensity invariance. These findings were based on high correlations between TEOAE waveforms across stimulus level and stimulus conditions (click, positive chirp, negative chirp), and an overall high similarity in TEOAE moments.

APPENDIX

1. Relations for SEL and parameterizing a transient sound

The sound exposure (or “signal-processing energy”) E of a discrete-time pressure waveform $p[n]$ at sample n with sample period T and sample duration N is defined by

$$E=T\sum _{n=0}^{N-1}p{[n]}^2.$$ (A1)

The total SEL of this waveform is defined in terms of a reference time T_ref and the reference root mean squared pressure p_ref = 20 μPa by

$$\begin{array}{c}\text{SEL}=10\hspace{0.17em}\hspace{0.17em}{\text{log}}_{10}\left(\frac{E}{T_{\text{ref}}\hspace{0.17em}{p}_{\text{ref}}^2}\right)\\ =10\hspace{0.17em}\hspace{0.17em}{\text{log}}_{10}(\frac{T}{N{T}_{\text{ref}}\hspace{0.17em}{p}_{\text{ref}}^2}(\sum _{k=1}^{N/2-1}2{\left|P\left[k\right]\right|}^2+{\left|P\left[0\right]\right|}^2+{\left|P[N/2]\right|}^2)).\end{array}$$ (A2)

The bottom relation is expressed in terms of a sum of the squared magnitude of the complex pressure spectrum $P[k]$. The $P[k]$ is calculated from the N-sample DFT of $p[n]$, and is the component at the kth frequency $f_k=k/(NT)$, with k ranging from 0 to N/2 for even N. From the lower relation in Eq. (A2), a frequency-averaged integrated band sound-pressure level $⟨L_{\mathit{E}\mathit{b}}⟩$ is defined as an average level over a frequency band between k₁ > 0 and k₂ ≥ k₁ (and $k_2<N/2$) by

$$⟨L_{\mathit{E}\mathit{b}}(k_1,k_2)⟩=10\hspace{0.17em}\hspace{0.17em}{\text{log}}_{10}(\frac{T}{N{T}_{\text{ref}}\hspace{0.17em}{p}_{\text{ref}}^2}\frac{1}{\left(k_2-k_1+1\right)}\sum _{k=k_1}^{k_2}2{\left|P\left[k\right]\right|}^2).$$ (A3)

The special case k₂ = k₁ is the integrated band sound-pressure level over the bandwidth $({(\mathit{N}\mathit{T})}^{-1})$ of the DFT bin, which is the discrete-time, discrete-frequency version of that defined for this bandwidth by Young (1970). Otherwise, the frequency bands from k₁ to k₂ were selected in the current study to match a given fractional octave average, e.g., a one-half octave spacing. The $⟨L_{\mathit{E}\mathit{b}}⟩$ in Eq. (A3) is more concisely termed the SEL spectrum in this report. Similar quantities were defined in Goodman et al. (2009). However, they used the reference time T_ref equal to the duration (NT) of the buffer containing the transient, whereas the present work adopted the standard value of T_ref = 1 s (ANSI, 2005). The definition T_ref = 1 s makes the SEL and the SEL spectrum independent of the stimulus buffer length in the computer implementation, which used longer buffer durations NT for chirps than for clicks. The definition of $⟨L_{\mathit{E}\mathit{b}}(k_1,k_2)⟩$ in Eq. (A3) was selected to provide frequency averaging of the fine structure of the TEOAE.

A transient sound may be parameterized in the following manner. The SD σ_t of the transient is defined in terms of its average time $⟨t⟩$ (or first moment) and Eq. (A1) by

$$\begin{array}{c}⟨t⟩=(T/E)\hspace{0.17em}\sum _{n=0}^{N-1}Tn\hspace{0.17em}p{[n]}^2,\\ {\sigma }_t=\sqrt{T^2/12+(T/E)\hspace{0.17em}\left(\sum _{n=0}^{N-1}{(T\hspace{0.17em}n)}^2\hspace{0.17em}p{[n]}^2\right)-{⟨t⟩}^2}.\end{array}$$ (A4)

The first term under the square root derives from the single-sample variance in a discrete-time click that is zero for all n except n = 0, and for which the other terms under the square root are zero. For measured $p[n]$ waveforms, the second and third terms are the conventional SD in terms of the second and first moments in time. The mean latency is defined as $⟨t⟩$ and its temporal width is defined as 2σ_t for a general transient, although its interpretation is most direct for a transient with a central maximum in its temporal envelope. This width comprises ±1 SD about its mean latency.