Drude Polarizable Force Field for Aliphatic Ketones and Aldehydes, and their Associated Acyclic Carbohydrates

Abstract

The majority of computer simulations exploring biomolecular function employ Class I additive force fields (FF), which do not treat polarization explicitly. Accordingly, much effort has been made into developing models that go beyond the additive approximation. Development and optimization of the Drude polarizable FF has yielded parameters for selected lipids, proteins, DNA and a limited number of carbohydrates. The work presented here details parametrization of aliphatic aldehydes and ketones (viz. acetaldehyde, propionaldehyde, butaryaldehyde, isobutaryaldehyde, acetone, and butanone) as well as their associated acyclic sugars (D-allose and D-psicose). LJ parameters are optimized targeting experimental heats of vaporization and molecular volumes, while the electrostatic parameters are optimized targeting QM water interactions, dipole moments, and molecular polarizabilities. Bonded parameters are targeted to both QM and crystal survey values, with the models for ketones and aldehydes shown to be in good agreement with QM and experimental target data. The reported heats of vaporization and molecular volumes represent a compromise between the studied model compounds. Simulations of the model compounds show an increase in the magnitude and the fluctuations of the dipole moments in moving from gas phase to condensed phases, which is a phenomenon that the additive FF is intrinsically unable to reproduce. The result is a polarizable model for aliphatic ketones and aldehydes including the acyclic sugars D-allose and D-psicose, thereby extending the available biomolecules in the Drude polarizable FF.

Introduction

Molecular mechanics force fields (FFs) have been used extensively in computer simulations for exploring complex biological phenomena. The majority of these simulations employ Class I additive force fields.[1–4] While the use of Class I additive FFs have yielded excellent agreement with experimental properties for a variety of systems, they treat electrostatic interactions using a fixed-charge, or additive model. This is a major drawback because the electron distribution of a molecule is influenced by the surrounding environment. Thus, models that go beyond the additive approximation by including the explicit treatment of polarization have been the subject of ongoing work for over 30 years.[5]

To account for the fixed-charge approximation in additive force fields polarization is treated in a mean-field way by adjusting the partial atomic charges to overestimate the gas phase molecular dipoles. Hence, the electrostatic interactions of the molecule in aqueous systems are more accurately treated. While including polarizability implicitly has in many cases yielded good agreement with experimental molar volumes and heats of vaporization[6–10] as well as free energies of hydration,[11–14] there is room for improvement in these properties as well as for the application of force fields in the context of biomolecules.[15] Indeed, recent advances in polarizable force fields are now yielding improvements in a range of systems.[16–24]

Explicit treatment of polarizability introduces a new term into the potential energy function, U_polar.[25,26] Current polarizable FFs differ in the method used to treat U_polar including the use of induced dipoles,[27–31] fluctuating charges,[32–38] or the classical Drude oscillator.[25,39,40] Briefly, in the induced dipole model, the functional form of U_polar is based on introducing an induced dipole onto atoms in addition to the partial atomic charge. This is performed, as an example, in the AMOEBA polarizable FF, in addition to treatment of the static contribution to the electrostatics with a multipole expansion out to quadrapoles.[21,41,42] The fluctuating charge model, also known as the charge equilibration model, is based on allowing the partial atomic charges to fluctuate in response to the electric field. The polarization energy is related to the absolute (Mulliken) electronegativity[43,44] and the hardness of the atom,[45] which themselves are dependent on the electron affinity and ionization potential of an atom and are measures of the ability of the electronic distribution to distort in response to the electric field. The CHARMM CHEQ polarizable force field[35,46,47] is based on the fluctuating charge model and Berne, Friesner and coworkers have presented models that use both fluctuating charge and induced dipole treatments of electronic polarization.[48–50] Other efforts include the POSSIM model that is based on induced dipoles[51] and a variation of the fluctuating charge model applied to water that allows for changes in the molecular polarizability as a function of environment has been presented.[52]

Models based on the classical Drude oscillator[53–55] (also known as the Shell or charge-on-spring (COS) model) account for polarization by introducing a charged particle, referred to as the Drude oscillator, that is harmonically attached to the nucleus of the parent atom. The atomic polarizability in the Drude FF is simply the Drude charge squared divided by the force constant on the harmonic term between the Drude particle and the atomic core. In practice, the sum of the charge on the nucleus and Drude particle are adjusted to yield the partial atomic charge on the atom. Thus, for a fixed set of atomic positions, the Drude particles can relax in the surrounding electric field yielding the polarization response. This relaxation can be performed via energy minimization, which is equivalent to a self-consistent field (SCF) calculation. However, due to the computational demand of treating the Drude particles via a SCF calculation, the Drude particles are instead treated as classical dynamic variables in the context of an extended Lagrangian formalism.[56] This is achieved by assigning a small mass (0.4 AMU) to the Drude particle from the parent atom and applying specific thermostats to the real particles and the center of mass of the nucleus-Drude particle pair.[56] Additionally, for computational expediency, Drude particles are not attached to hydrogen atoms in the Drude force field developed in this study. More detailed descriptions of polarizable force fields have been published elsewhere.[25,26]

Development and optimization of the CHARMM Drude polarizable FF has been the subject of ongoing work in our laboratory in collaboration with Roux and coworkers since 2000.[54] To date, protein,[20] DNA,[22], ions,[57] and limited carbohydrate[17,58,59] and lipid[16] parameters are available. The CHARMM Drude Polarizable FF has been successfully implemented in CHARMM,[60,61] NAMD,[62,63] GROMACS,[64,65] and recently OpenMM[66] (Huang and MacKerell, Work in progress). In NAMD the computational demand was shown to be 2.4 to 3.6 more than the additive force field when taking into account both the overhead for the treatment of polarization and the need to use a 1 fs integration time steps vs. 2 fs typically used for additive force fields.[63] Benchmarking of ubiquitin in aqueous solution on 64 cores showed a 2 to 5 time improvement in speed in GROMACS over NAMD or CHARMM, respectively.[65] Recently, a polarizable energy function based on thermal Drude oscillators was introduced in LAMMPS.[67,68] The work presented here details parametrization of aliphatic aldehydes and ketones (viz. acetaldehyde, propionaldehyde, acetone, and butanone) as shown in Figure 1 as well as their associated acyclic sugars (D-allose and D-psicose) as part of the development of a comprehensive polarizable force field for biomolecules. Given that Drude FF parameters are optimized with transferability in mind, the acyclic sugars can be considered as an extension of the polyols previously parametrized in this laboratory[17] with the addition of a ketone or aldehyde functionality. Accordingly, the developed aldehyde and ketone parameters are used in combination with the existing polyol parameters in the optimization of a Drude model for D-allose and D-psicose.

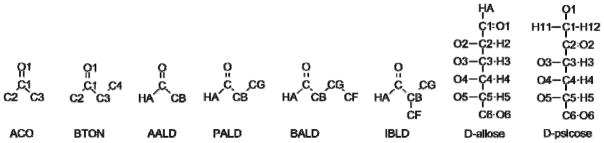
Figure 1.

Model compound ketones and aldehydes: acetone (ACO), butanone (BTON), acetaldehyde (AALD), propionaldehyde (PALD), butyraldehyde (BALD) and isobutyraldehyde (IBLD) with corresponding linear sugars D-allose and D-psicose. Methyl, methylene and linear sugar hydroxyl hydrogens are omitted for clarity.

Computational Methods

Calculations were performed with the program CHARMM, version c38a1,[69] and the Drude force field.[16,17,20,22,58,59] All Drude and additive MD simulations employed a 1 fs time step and were performed at 298 K unless otherwise noted. Periodic boundary conditions and the Drude velocity Verlet integrator were used in all condensed phase MD simulations.[56] Quantum mechanical (QM) calculations were performed using Gaussian03[70] and QCHEM.[71]

Internal parameters (bonds and valence angles, equilibrium values and force constants, and the dihedral force constant, phase and multiplicities) were optimized targeting QM geometries and vibrational data performed at the MP2/6-31G(d) model chemistry. Bond and angle parameters were verified against crystal survey data[72] as performed previously for the additive CHARMM model for acetone and acetaldehyde.[73] Force constants for the bonds and angles were adjusted to fit QM vibrational target data. Vibrational frequencies were analyzed using the MOLVIB[74] utility in CHARMM from which the normal mode potential energy distributions were determined. QM frequencies were scaled by 0.9434.[75] Dihedral parameters were fit to QM potential energy scans (PES) obtained at the MP2/6-31G*//RIMP2-ccPVQZ model chemistry using a least squares fitting algorithm developed specifically for parameter optimization.[76]

For transferability, optimization of the electrostatic parameters (i.e. charges, polarizabilities (alpha) and Thole scale factors[77]) was first performed for acetone and acetaldehyde, with the final parameters transferred to butanone and propionaldehyde, respectively, by adding a methyl group whose electrostatic parameters were derived from ethane and adjusted to reproduce the QM dipole moments. Initial parameters for acetone and acetaldehyde were obtained using GAAMP.[78] Default values for the 1–4 interaction scaling factors, weights for water interactions, and weights for Thole and polarizability constraints were employed, while the MP2/6-31G(d) model chemistry was used to generate PES used as target data to fit the torsion parameters. For acetone, the methyl carbons and methyl hydrogens were considered equivalent, while methyl hydrogens were considered equivalent for acetaldehyde. The partial atomic charge of oxygen was restrained at 0 using a charge restraint of 10 such that the oxygen charge is located on the virtual particles representing the lone pairs.

Additional optimization of the partial atomic charges, alpha and Thole values were performed targeting dipole moments and molecular polarizabilities obtained at the MP2/6-31+G(d)//MP2/cc-pVQZ model chemistry. The position of the lone pairs (LP) of the oxygen atom was directly taken from the Drude model of N-methyl acetamide (NMA).[79] Anisotropic polarizabilities[80] on the oxygen atoms were used as obtained from GAAMP. Partial atomic charges were fit to reproduce QM dipole moments using an Monte Carlo simulated annealing procedure[81] and refined targeting molecular polarizabilities such that the MM molecular polarizability was roughly 70–85% of the QM molecular polarizability.[25,54,82–84] Validation of the scaling of the molecular polarizabilities was based on the reproduction of experimental dielectric constants of pure solvents. Partial charges were verified for acetone and acetaldehyde using water interactions obtained at the MP2/6-31G(d)//MP2/cc-pVQZ model chemistry with counterpoise correction for basis set superposition error (BSSE).[85,86] Acetone and acetaldehyde electrostatic parameters were then transferred to butanone and propionaldehyde, respectively, as described above, with manual adjustments made to the partial atomic charge, alpha and Thole values to better reproduce the dipole moments of multiple conformations of these molecules.

Lennard-Jones (LJ) parameters were optimized targeting experimental data for the small model compounds acetone, butanone, acetaldehyde, and propionaldehyde, including neat liquid heats of vaporization (ΔH_vap) and molecular volumes (V_m) using molecular dynamics (MD) simulations as in previously published parametrization studies.[17,87–93] Condensed phase MD simulations used the particle mesh Ewald (PME) approach for electrostatic interactions employing a real space cutoff of 12 Å and sixth order spline. LJ interactions were treated using a switching function from 10 to 12 Å, with long range contributions treated using an isotropic long range correction (LRC).[94] Neat liquid simulations were performed using a box of 125 pre-equilibrated solute molecules. Aqueous solution simulations were performed using a solute molecule immersed in a box of 250 SWM4-NDP water molecules.[95] All properties were calculated based on the average of 4 independent simulations that differed based on the random seed used to assign the velocities. Heats of vaporization and molecular volumes were calculated from the last 600 ps of 1 ns MD simulations performed at the following temperatures (acetone=298 K, butanone=314 K, acetaldehyde=283 K, propionaldehyde=298 K). The free energies of solvation and dielectric constants were used to verify the external parameters and, when necessary, fine tune the LJ parameters. Dielectric constants were calculated using 20 ns simulations at temperatures at which the experimental dielectric constants were obtained (acetone=293.2 K, butanone=293.2 K, acetaldehyde=291.2 K, propionaldehyde=290.2 K). Averages were obtained from the last 19 ns with the dielectric calculated as previously described.[96] Free energies of solvation were obtained from free energy perturbation (FEP)[97] simulations as previously described,[87,98] by performing 50 ps equilibration and 200 ps production simulations for each lambda window. Averages were obtained from the production phase.

Crystal simulations were performed to validate the quality of the final parameters for the model compound acetone. Structures were obtained from the Cambridge Structural Database[72] for three different temperatures and used as starting structures for MD simulations, with periodic boundary conditions corresponding to the unit cell length and angle parameters of the respective crystals. The Langevin thermostat was employed, with the reference temperature set to the temperature at which the crystals were obtained. A pressure of 1 atm was used with full relaxation of crystal cell lengths allowed. Hydrogen bond lengths were constrained using SHAKE[99] and the Drude hard wall distance was set at 0.2 Å. Each acetone crystal system was minimized first with 200 steps of steepest descent (SD) using harmonic restraints of 10⁶ kcal/(mol·Å²) on all atoms, followed by 200 steps of SD and 200 steps of adapted basis Newton-Rhapson[100] using a harmonic restraint of 5 kcal/(mol·Å²) on non-hydrogen atoms. Crystals were then equilibrated for 200 ps using harmonic restraints of 1.0 kcal/(mol·Å²) on the non-hydrogen atoms. After equilibration, the restraints were removed and the simulations run for 13 ns. Values reported were calculated based on the last 12 ns of each simulation.

Internal parameters for the acyclic sugars D-psicose and D-allose were optimized by combining parameters from the polyols previously parametrized in this laboratory[17] with those from ketone or acetaldehyde, respectively. Only bond and angle parameters containing the linkage between the two molecules were optimized using QM target data obtained at the MP2/6-31G* model chemistry. Dihedrals were optimized using QM target data obtained at the MP2/6-31G*//RIMP2/cc-pVQZ model chemistry. Dihedral PES were fit using a least-squares fitting procedure[76] developed in this laboratory.

Results and Discussion

The results presented here represent those based on the final set of optimized parameters after self-consistent optimization of both the nonbonded and bonded terms. The final topology and parameter information is included in Table S5 of the supporting information.

Nonbonded parameters

Table 1 shows the QM and MM dipole moments for acetone (ACO), butanone (BTON), acetaldehyde (AALD), and propionaldehyde (PALD). For AALD, the individual contributions to the MM dipole are in excellent agreement with QM, while for ACO the contribution to the dipole arises from the C=O group due to the symmetry of the molecule and this is slightly underestimated in the Drude model. Compared to the C36 additive FF,[73] the Drude model is better able to reproduce the QM dipole moments demonstrating the importance of incorporating polarizability as well as the C36 additive FF charges being developed primarily targeting HF/6-31G(d) interactions with water. As mentioned, for transferability the charges, alphas and Thole factors from ACO and AALD were transferred to BTON and PALD, respectively. The additional methyl group’s charge and alpha parameters were obtained from ethane and the Thole factors were manually adjusted to fit the QM dipole moments of the gauche and cis (defined using O-C-CB-CG dihedral angle) conformations of BTON and PALD. While the difference between the MM and QM dipole moments is small for each conformation, the relative differences between the gauche and cis conformations is not maintained in the MM dipoles. In both BTON and PALD, the gauche MM dipole moment is lower than the cis when it should be greater based on the QM dipole moments. However, given that the difference in the QM dipoles between the two states was less than 0.3 D, this level of disagreement was considered acceptable.

Table 1.

Dipole moments and molecular polarizabilities of acetone (ACO), acetaldehyde (AALD), butanone (BTON) and propionaldehyde (PALD). Results for both the gauche and cis conformations are presented for BTON and PALD. QM values were obtained at the MP2/6-31+G(d)//MP2/cc-PVQZ levels of theory. C36 values were as reported previously for the CHARMM36 additive force field.[73]

		Dipole Moments (Debye)					Molecular Polarizability (Å3)
		x	y	z	Total	MM-QM	xx	yy	zz	Total	MM – QM
ACO
	Drude	0.00	−2.82	0.00	2.82	−0.13	5.15	5.03	3.02	13.20	−4.78
	C36	0.00	−3.57	0.00	3.57	0.62
	QM	0.00	−2.95	0.00	2.95		6.49	6.66	4.83	17.98
BTON
gauche	Drude	−1.29	1.80	0.90	2.39	−0.62	7.56	6.01	4.86	18.43	−4.67
	QM	−2.04	2.08	0.76	3.01		8.55	8.00	6.56	23.10
cis	Drude	0.92	−2.72	0.00	2.87	0.06	8.34	5.98	4.14	18.45	−4.73
	QM	0.21	−2.80	0.00	2.81		8.82	8.06	6.30	23.18
AALD
	Drude	2.69	0.93	0.00	2.85	0.06	4.56	2.71	2.39	9.66	−3.10
	C36	3.28	0.64	0.00	3.35	0.56
	QM	2.54	1.15	0.00	2.79		5.07	4.36	3.32	12.76
PALD
gauche	Drude	2.48	0.18	1.06	2.70	−0.20	5.82	4.83	3.06	13.71	−4.30
	QM	2.66	0.08	1.15	2.90		7.04	5.44	5.53	18.01
cis	Drude	−1.57	2.10	0.00	2.62	−0.06	6.95	3.74	3.39	14.08	−3.82
	QM	−1.55	2.18	0.00	2.68		6.54	6.52	4.84	17.90

The molecular polarizability values are also shown in Table 1. In a previous study by Lamoreaux and coworkers,[56] it was found that the molecular polarizability needed to be scaled down to prevent overestimation of the dielectric constant. While the reason for the scaling is still a point of discussion (see [25] and discussion therein), for consistency and transferability of the parameters it was maintained for the carbonyls. Accordingly, for all of the compounds in the present work, the MM molecular polarizability is roughly 70 to 90% that of the QM values. Validation of the scaling was based primarily on reproduction of the pure liquid dielectric constants, which are presented below.

The water interactions for ACO and AALD are presented in Table 2 and Figure 2 for Drude, C36, and QM. The relative differences between the QM and MM interaction energies are all less than 0.95 kcal/mol, while the differences in the interaction distances are 0.02 Å or less. The root mean square deviations (RMSD) for the interaction energies and distances between ACO and water are 0.69 kcal/mol and 0.02 Å, respectively. Those for AALD and water are 0.26 kcal/mol and 0.01 Å, respectively. The Drude interaction energies and distances are in better agreement with the QM than the C36 results, which in part arises from the introduction of lone pairs on the carbonyl oxygen in the Drude FF. Also, the interaction of water with the aldehydic hydrogen in Drude is in satisfactory agreement with the QM data, while the additive C36 FF interaction is too favorable. Finally, it should be noted that optimization of the additive C36 charges targeted QM HF/6-31G(d) data, which would lead to differences versus the QM data being targeted for the polarizable force field.

Table 2.

Water minimum interaction energies (E, kcal/mol) and distances (R, Å) for acetone (ACO), acetaldehyde (AALD), cis butanone (BTON), and cis propionaldehyde (PALD). QM values were obtained at the MP2/6-31G(d)//MP2/cc-PVQZ levels of theory with counterpoise correction for basis set superposition error (BSSE). [85,86] C36 values are reported for acetone and acetaldehyde and were obtained from [73]. Water interaction pairs are shown in Figure 2 and 3. Root mean square differences (RMSD) are shown. Hydrogen water interactions are not included for the methyl groups.

Pair	EQM	EDrude	EC36	EDrude - EQM	EC36 - EQM	RQM	RDrude	RC36	RDrude - RQM	RC36 - RQM
ACO
Pair 1	−5.52	−4.57	−7.19	0.95	−1.67	2.06	2.08	1.71	0.02	−0.35
Pair 2	−4.03	−3.85	−6.49	0.18	−2.46	2.1	2.12	1.69	0.02	−0.41
RMSD				0.68	2.1				0.02	0.38
BTON
Pair 1	−5.55	−4.68		0.87		2.06	2.07		0.01
Pair 2	−4.12	−3.94		0.18		2.12	2.11		−0.01
RMSD				0.63					0.01
AALD
Pair 1	−5.05	−4.62	−6.07	0.43	−1.02	2.08	1.96	1.81	−0.12	−0.27
Pair 2	−4.66	−4.58		0.08		2.09	1.95		−0.14
Pair 3	−3.58	−3.86	−4.96	−0.28	−1.38	2.15	2	1.83	−0.15	−0.32
Pair 4	−1.41	−1.39	−2.48	0.02	−1.07	2.56	2.46	2.18	−0.1	−0.38
RMSD				0.26	1.17				0.13	0.33
PALD
Pair 1	−2.63	−1.99		0.64		2.83	2.82		−0.01
Pair 2	−4.71	−4.65		0.06		2.09	1.94		−0.15
Pair 3	−3.7	−3.98		−0.28		2.15	1.99		−0.16
Pair 4	−1.36	−1.5		−0.14		2.56	2.45		−0.11
RMSD				0.36					0.12

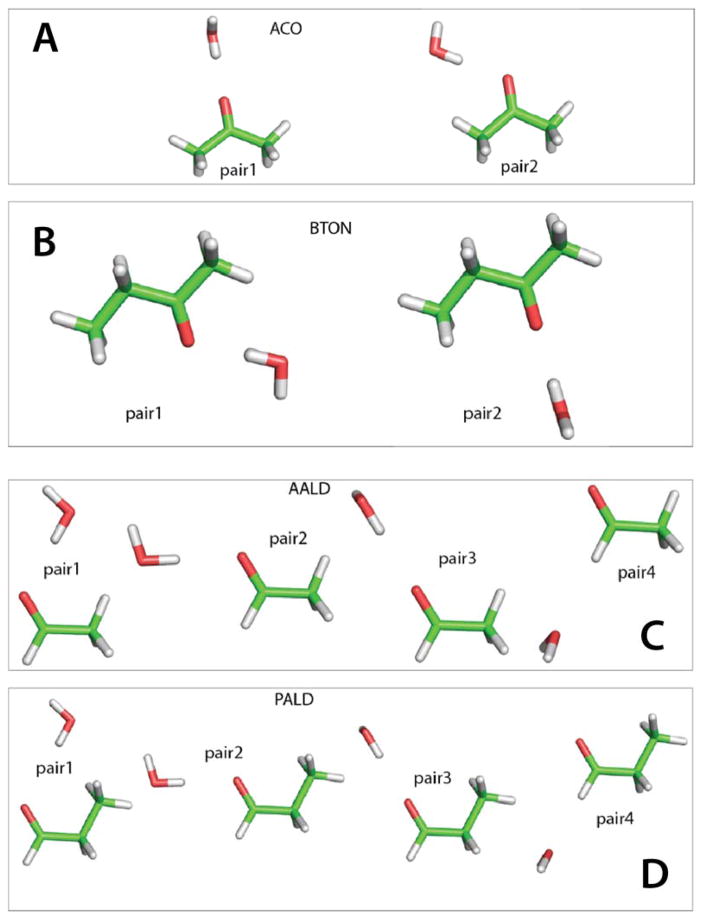
Figure 2.

Water interaction pairs for A) acetone (ACO), B) acetaldehyde (AALD), C) butanone (BTON) and D) propionaldehyde (PALD) corresponding to the interacting pairs in Table 2.

Water interactions for BTON and PALD are shown in Table 2 and Figure 2. The cis conformations were selected for water interaction calculations because these conformations have lower relative energies compared to the gauche conformations (see below). The RMSD values for the interaction energies in BTON and PALD are 0.63 and 0.36 kcal/mol, respectively, and the interaction distances have an RMSD of 0.01 and 0.12 Å, respectively. Though the interaction energy of Pair 1 could be improved in the ketones, modification of the charges would impact the dipole moments and polarizabilities and further refinement of the charges was not undertaken. However, since the water interactions impact the hydration free energies of each compound, an NBFIX term, which was used for the results presented in Table 2, was required as discussed below.

Table 3 shows the heats of vaporization and molecular volumes for ACO, BTON, AALD, and PALD. The MM heats of vaporization are overestimated in all of the small model compounds, though the Drude heats of vaporization are within 3% of the experimental values and were thus deemed acceptable. The molecular volumes represent a compromise between ACO and BTON and between AALD and PALD, being underestimated in ACO and AALD yet overestimated in BTON and PALD. The LJ parameters were specifically optimized to achieve this balance. Notably, specific carbonyl carbon and oxygen atom types were used for the ketones and aldehydes to obtain reasonable agreement with the experimental data (Table S5). The heats of vaporization and molar volumes for acetone in the C36 additive FF[73] are 7.37 kcal/mol and 124.47 ų, respectively. For acetaldehyde, they are 6.21 kcal/mol and 94.84 ų, respectively. Thus, the Drude model generally represents an improvement over the additive C36 force field for these properties.

Table 3.

Heats of vaporization, (ΔH_vap, kcal/mol), molecular volumes (V_m, ų), hydration free energies (ΔG_solvation, kcal/mol) and dielectric constants (ε) for model compounds from the Drude force field and from experimental data (Exp). Properties were obtained at the same temperature as the experimental conditions: ACO 298 K, BTON 314 K, AALD 283 K, and PALD 298 K for heats of vaporization and molar volumes; ACO and BTON 293.2 K, AALD 291.2 K, PALD 290.2 K for dielectric constants. Standard deviations were calculated based on the average of 4 simulations. Butryaldehyde (BALD) and isobutryaldehyde (IBLD) ΔG_solvation calculations performed at 298 K.

	ΔHvap	% error (Drude - Exp)	Vm	% error (Drude - Exp)	ΔGsolvation	% error (Drude - Exp)	ε
ACO
Drude	7.58 ± 0.07	1.32	121.60 ± 0.09	−0.88	−3.77 ± 0.13	−2.12	17.12 ± 0.06
Exp	7.48		122.67		−3.85		21.00
BTON
Drude	7.99 ± 0.14	−1.13	156.10± 0.24	1.94	−3.34 ± 0.10	−8.98	15.00 ± 0.33
Exp	8.08		153.07		−3.64		18.60
AALD
Drude	6.78 ± 0.04	2.65	89.58 ± 0.21	−2.86	−4.10 ± 0.19	15.46	22.32 ± 0.26
Exp	6.60		92.14		−3.50		21.00
PALD
Drude	6.89± 0.04	−3.63	124.29 ± 0.47	2.53	−3.43 ± 0.13	−0.29	14.55 ± 0.21
Exp	7.14		121.14		−3.44		18.50
BALD
Drude					−3.07 ± 0.25	−3.58
Exp					−3.18
IBLD
Drude					−2.61 ± 0.34	−8.55
Exp					−2.86

The optimized LJ and electrostatic parameters were further optimized and validated against experimental hydration free energies as shown in Table 3. To achieve reasonable agreement between the experimental and Drude free energies of solvation, the introduction of NBFIX terms, as previously performed,[88] was required between the carbonyl carbon and oxygen for both the aldehydes and ketones with the water oxygen (ODW). For the ketones the minimum distance (R_min) was unchanged for both the oxygen and carbon with the well depths adjusted to improve the free energies of aqueous solvation. Both R_min and the well depths were adjusted for the aldehydes (Table S5). The optimization of the NBFIX terms targeted AALD, PALD, ACO and BTON. Hydration free energies for butyraldehyde (BALD) and isobutyraldehyde (IBLD) were calculated to further optimize and validate of the aldehyde parameters. With the aldehydes the quality of the agreement of AALD was sacrificed to yield improved agreement with the larger aldehyde model compounds while the hydration free energies for the two ketones are in satisfactory agreement with experiment. The final NBFIX values also gave good agreement with the QM interaction energies with water, as discussed above.

A final validation of the nonbond parameters involved the dielectric constants of the pure solvents. As shown in Table 3, the MM dielectric constants are all in acceptable agreement with the experimental values. While the level of agreement could potentially be improved, especially with the ketones, the overall level of agreement with all the QM and experimental data indicated that the final scaling of the molecular polarizabilities was acceptable.

Bonded parameters

Tables 4 and 5 show the bond and valence angle values for ACO, BTON, AALD, PALD obtained from the Drude FF and QM optimized structures, and from a survey of crystallographic data (CSD)[72] for ACO and AALD, as previously reported.[73] For the ketones, only bonds and valence angles involving non-hydrogen atoms are shown, while those containing the aldehydic hydrogen are included for the aldehydes. All bonds and angles are in excellent agreement with the QM values, as indicated by small relative differences. Bonds are within 0.02 Å, while angles are within 3°. For ACO and AALD, the MM bond length and valance angles are also in good agreement with the CSD values with the largest deviation coming from the HA-C=O in acetaldehyde at 3.8°, though the standard deviation of this angle from the crystallographic survey is over 3° and, in general, hydrogens are poorly resolved in X-ray crystallographic studies.

Table 4.

Bond lengths in Å and angles in degrees for acetone (ACO) and acetaldehyde (AALD) from QM optimizations at the MP2/6-31G(d) level of theory, crystallographic surveys as reported in [73] and Drude calculations. Crystal survey error is shown in parenthesis.

Atoms	QM	Crystal	MM	MM-QM	MM-Crystal
ACO
C1-O1	1.23	1.21 (0.04)	1.22	−0.01	0.01
C1-C2/C1-C3	1.51	1.47 (0.05)	1.50	−0.01	0.03
C2/C3-C1-O1	121.75	121.04 (3.96)	121.82	0.07	0.78
C2-C1-C3	116.50	117.46 (3.67)	116.35	−0.15	−1.11
AALD
C-O	1.22	1.22 (0.05)	1.22	0	0
C-CB	1.50	1.48 (0.05)	1.50	0	0.02
C-HA	1.11	0.97 (0.06)	1.10	−0.01	0.13
CB-C-O	124.30	124.93 (3.71)	124.77	0.47	−0.16
HA-C-O	120.33	117.15 (3.76)	118.52	−1.81	1.37
HA-C-CB	115.37	117.53 (3.22)	116.71	1.34	−0.82

Table 5.

Bond lengths in Å and angles in degrees for the butanone (BTON) and propionaldehyde (PALD) gauche and cis conformations from QM optimizations at the MP2/6-31G(d) level of theory and Drude calculations.

	Atoms	QM	MM	MM-QM
BTON gauche	C1-O1	1.23	1.22	−0.01
	C2-C1	1.52	1.50	−0.02
	C1-C3	1.52	1.50	−0.02
	C3-C4	1.53	1.54	0.01
	C2-C1-O	121.21	121.55	0.34
	O-C1-C3	121.47	121.33	−0.14
	C2-C1-C3	117.32	117.11	−0.21
	C1-C3-C4	113.13	112.56	−0.57
BTON cis	C1-O1	1.23	1.22	−0.01
	C2-C1	1.51	1.50	−0.01
	C1-C3	1.52	1.50	−0.02
	C3-C4	1.52	1.54	0.02
	C2-C1-O	121.64	121.36	−0.28
	O-C1-C3	121.69	122.30	0.61
	C2-C1-C3	116.67	116.34	−0.33
	C1-C3-C4	113.08	114.90	1.82
PALD gauche	C-O	1.22	1.22	0.00
	C-CB	1.51	1.50	−0.01
	CB-CG	1.53	1.53	0.000
	C-HA	1.11	1.10	−0.01
	HA-C-O	120.35	119.23	−1.12
	HA-C-CB	114.94	117.45	2.51
	CB-C-O	124.70	123.33	−1.37
	C-CB-CG	111.06	111.28	0.22
PALD cis	C-O	1.22	1.22	0.00
	C-CB	1.51	1.50	−0.01
	CB-CG	1.52	1.54	0.02
	C-HA	1.11	1.10	−0.01
	HA-C-O	120.28	118.96	−1.32
	HA-C-CB	115.51	116.98	1.47
	CB-C-O	124.22	124.06	−0.16
	C-CB-CG	113.10	114.30	1.2

The MM and QM molecular vibrations for ACO and AALD are shown in Tables 6 and 7 using the internal coordinate system of Pulay.[101] For simplicity only the most dominant normal mode contributing to each frequency is presented. MM frequencies were obtained by optimizing the MM force constants to reproduce the scaled QM frequencies. Most notable are the low frequency vibrations that describe larger conformational deformations in the molecules as these dominate during MD simulations. While the MM frequency for the O=C-CB-HB1 torsion in AALD is larger than ideal, the remaining MM frequencies are in excellent agreement with the QM scaled frequencies. Moreover, the MM frequencies for ACO are all within 5% of their QM target values.

Table 6.

Vibrational analysis of acetone (ACO) using the internal coordinate system of Pulay [101]. QM frequencies were obtained at the MP2/6-31G(d) level of theory. Frequencies in cm⁻¹.

Mode	MM	QM
CHtors	98.2	85.8
dCCC	396.2	471.6
wCO	540.3	627.8
rCO	520.3	661.4
sCC	713.7	813.2
rCH3	887.5	990.0
rCH3′	912.4	940.7
sCCas	1167.9	1044.9
dCH3	1385.4	1342.6
dCH3a	1410.3	1422.0
dCH3a′	1419.6	1426.7
sCO	1733.6	1588.5
sCH3	2849.5	2934.1
sCH3a	2912.0	3048.3
sCH3a′	2914.0	3006.2

Table 7.

Vibrational analysis of acetaldehyde (AALD) using the internal coordinate system of Pulay [101]. QM frequencies were obtained at the MP2/6-31G(d) level of theory. Frequencies in cm⁻¹.

Mode	MM	QM
tCH3	139.2	195.3
dCCC	514.5	632.1
sCC	811.4	974.6
rCH3′	828.8	916.2
rCH3	981.3	974.8
wCHO	1039.5	955.4
rCHa	1268.8	1372.6
dCH3	1386.9	1339.2
dCH3a	1410.2	1391.5
dCH3a′	1419.1	1407.0
sCO	1722.6	1622.0
sCHa	2817.0	2823.1
sCH3	2848.5	2933.5
sCH3a′	2912.0	3005.6
sCH3a	2914.6	3048.8

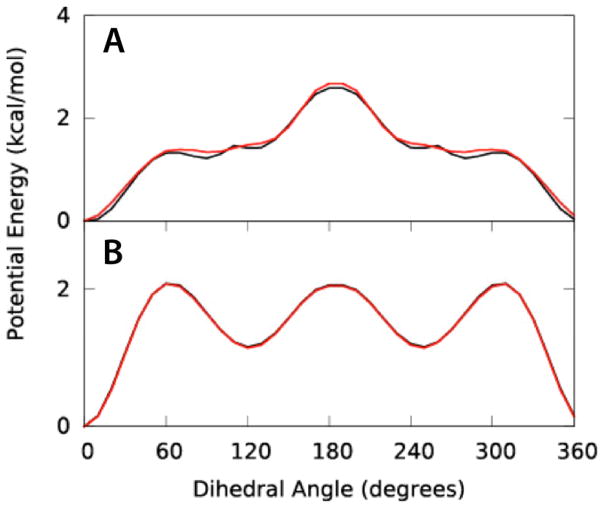
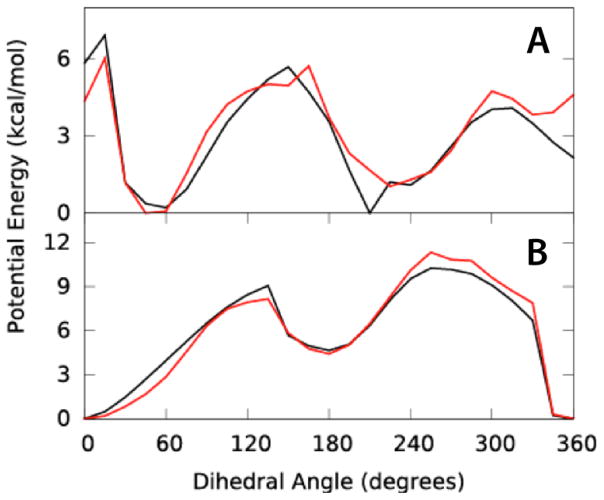
Dihedral parameters for BTON and PALD were optimized using potential energy scans for all torsions containing the C1-C3 and C-CB bonds, respectively. QM and MM PES are shown in Figure 3. MM PES were targeted to QM scans obtained at the MP2/6-31G*//RIMP2-ccPVQZ model chemistry using 1-, 2-, 3- and 6-fold terms and phase angles of 0° or 180°. In general, excellent agreement is achieved between MM and QM PES with an RMSD of 0.05 for BTON and 0.007 for PALD, with RMSDs prior to fitting of 0.47 and 0.65, respectively.

Figure 3.

Dihedral potential energy scans for A) BTON and B) PALD. QM (black) and MM (red) PES are shown for dihedrals C2-C1-C3-C4 bond for BTON and O-C-CB-CG for PALD.

Parameters for butryaldehyde and isobutryaldehyde were transferred from propionaldehyde and any missing dihedral parameters were optimized to reproduce QM target data obtained at the MP2/6-31G*//RIMP2-ccPVQZ model chemistry as performed above (data not shown).

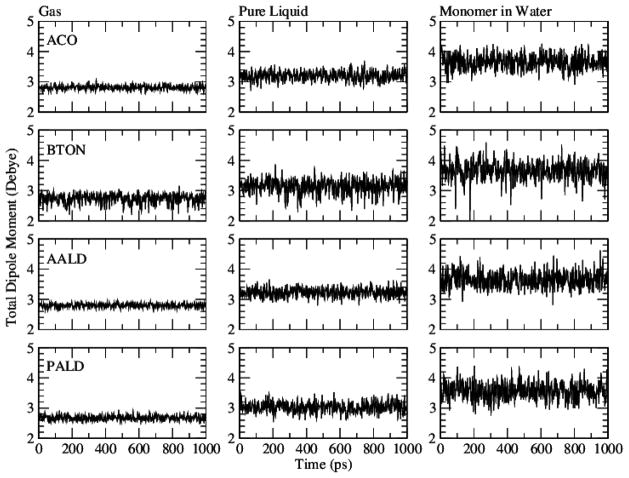
Dipole moments as a function of environment

Figure 4 shows the dipole moments as a function of time for MD simulations of ACO, AALD, BTON, and PALD in the gas phase, as pure liquids, and in aqueous solution. The strength of polarizable force fields rests in the ability of the dipole to vary in response to the environment. This is clearly illustrated by the increase in the magnitude and the variations of the dipole moment in moving from gas phase to condensed phase. The averages and RMS fluctuations of the dipole moments are shown in Table 8. In ACO and AALD the gas phase averages are both 2.8 D, while in the condensed phase simulations, the averages increase to 3.2–3.7 D for both ACO and AALD. Moreover, the RMS fluctuations increase from less than 0.06 in the gas phase to 0.1 to 0.2 D in the condensed phases, indicating that the dipole moments of the individual monomers in the condensed phase respond to the molecules in the local environment, whether those molecules are other monomers (pure liquid) or water molecules (aqueous solution). Similar results are obtained with BTON and PALD. The average dipoles increase from 2.6 to 2.7 in the gas phase to 3.0 to 3.7 D in the condensed phases with the RMS fluctuations increasing from approximately 0.05 to 0.3 D. Unlike ACO and AALD, BTON and PALD can assume a cis or gauche conformation during MD and therefore two populations of dipole moments are represented in the dipole moment time series (Figure S1) leading the slightly higher RMS fluctuations. In going from gas to condensed phase the average dipole moment increases as expected due to the presence of surrounding molecules. Within the condensed phase simulations, the monomer in aqueous solution has a larger dipole moment because water is a more polar solvent as opposed to the pure liquids and thus the polarization response to water is larger. Notably, this is a phenomenon that the additive FF is intrinsically unable to reproduce, which highlights the importance of including polarizability.

Figure 4.

Dipole moments as a function of time for acetone (ACO), butanone (BTON), acetaldehyde (AALD), and propionaldehyde (PALD) in the gas phase (left column), pure liquid (middle column), and aqueous solution (right column).

Table 8.

The average dipole moments (Debye) and average RMS fluctuations (RMSF) of the dipole moments for acetone (ACO), butanone (BTON), acetaldehyde (AALD), and propionaldehyde (PALD) from gas and condensed phase simulations (pure liquid and aqueous solution). Averages and standard error of the mean (SEM) are calculated over 4 simulations.

		Gas	Pure Liquid	Water
ACO	Avg ± SEM	2.814 ± 0.003	3.189 ± 0.005	3.665 ± 0.009
	RMSF ± SEM	0.056 ± 0.002	0.130 ± 0.003	0.216 ± 0.007
BTON	Avg ± SEM	2.733 ± 0.003	3.145 ± 0.007	3.668 ± 0.006
	RMSF ± SEM	0.135 ± 0.004	0.199 ± 0.002	0.25 ± 0.01
AALD	Avg ± SEM	2.794 ± 0.002	3.217 ± 0.006	3.670 ± 0.020
	RMSF ± SEM	0.053 ± 0.002	0.124 ± 0.005	0.213 ± 0.006
PALD	Avg ± SEM	2.672 ± 0.002	3.029 ± 0.002	3.573 ± 0.008
	RMSF ± SEM	0.066 ± 0.002	0.141 ± 0.004	0.237 ± 0.003

Crystal simulations

Crystal simulations were performed to validate the nonbond parameters for acetone. A total of 3 different crystals were studied, with the initial crystal structures based on coordinates obtained from the CSD.[72] The 3 crystals are at different temperatures, with the simulations performed at the respective temperatures. Unit cell lengths and volumes are shown in Table 9 for the Drude and additive force fields. The agreement between the Drude cell lengths and experiment is slightly worse than the additive FF relative to experiment. Percent differences for the average A, B, and C cell lengths over all 3 crystal conformations using the Drude FF are −1.57, 4.76, and −5.23%, and those for the additive FF are −1.56, 3.23, and −2.58%, respectively, indicating that both are unable to accurately reproduce experimental crystal phase conditions. Compared to experiment, the Drude average unit cell volumes are all systematically too small relative to both experiment and the additive FF. Percent differences in the unit cell volumes for the Drude FF compared to experiment are −2.99, −1.97, and −2.25% compared to percent differences below 2% for the additive FF. A similar trend was observed in parametrization studies of the polyols and hexapyranose saccharides where smaller unit cell volumes were obtained with the Drude force field, though the final volumes were still slightly larger than the experimental values. Though not optimal, the present results were considered acceptable given the low temperatures of the crystals (110 to 150 K).

Table 9.

Crystal lattice parameters (Å) and volumes (ų) for acetone (ACO) from crystal simulations using the Drude and CHARMM36 additive (C36) FFs. Simulations were performed at the same temperature at which experimental crystals were measured: hixhif03 at 110K, hixhif05 at 113K, and hixhif02 at 150K. Standard deviations were calculated based on the average of 3 simulations. Percent differences (% Diff) are calculated for Drude – experiment.

CSID	Force field	R factor %	A	% Diff	B	% Diff	C	% Diff	Volumer	% Diff
hixhif03	Drude	5.85	8.61± 0.00	−6.50	8.37± 0.00	7.29	20.78± 0.00	−4.23	1496.24± 0.14	−3.08
	C36	5.85	8.72 ± 0.00	−5.16	8.12 ± 0.00	4.43	21.40 ± 0.00	−1.21	1514.00 ± 0.09	−1.87
	Exp.		9.17		7.76		21.66		1542.28
hixhif05	Drude	4.91	6.60± 0.00	3.18	5.42± 0.00	1.48	10.03± 0.00	−6.98	359.32± 0.04	−2.01
	C36	4.91	6.50 ± 0.00	1.69	5.46 ± 0.00	2.20	10.29 ± 0.00	−4.28	364.69 ± 0.02	−0.51
	Exp.		6.39		5.34		10.73		366.56
hixhif02	Drude	5.28	8.71± 0.00	−1.84	8.40± 0.00	4.76	20.90± 0.00	−5.41	1528.31± 0.07	−2.31
	C36	5.28	8.75 ± 0.01	−1.37	8.24 ± 0.02	2.91	21.50 ± 0.02	−2.47	1548.62 ± 3.05	−0.96
	Exp.		8.87		8.00		22.03		1563.56
Average	Drude			−1.72		4.51		−5.54		−2.47
	C36			−1.61		3.18		−2.65		−1.12

As a final check of the crystal simulations, selected distances and angles were measured from the Drude simulations and compared to experimental bond length and valence angles. These results are reported in the Supplementary Information (Tables S1–S3) and show an acceptable agreement between the Drude lengths relative to those from the crystal lattice, which is expected given that the bond and angle lengths for ACO were targeted to both QM and crystal survey data.

D-allose and D-psicose

Initial parameters for D-allose and D-psicose were obtained by combining optimized parameters from the previously published polyols[17] with the ketone and aldehyde parameters developed here. Bond and angle lengths were optimized using QM target data obtained at the MP2/6-31G* level of theory, in which only terms containing the covalent linkage between functional groups were considered. As shown in Table S4, bond and angle lengths were within 0.3 Å and 4°, respectively, and deemed acceptable without further refinement.

Dihedral terms were parametrized using potential energy scans for all torsions containing the C1-C2 and C2-O2 bonds for D-allose and C1-C2 and C2-C3 bonds for D-psicose. QM and MM PES are shown in Figures 5 and 6 for D-allose and D-psicose, respectively. Fitting was performed using 1-, 2-, 3- and 6-fold terms and phase angles of 0° or 180°.

Figure 5.

Dihedral potential energy scans for D-allose. QM (black) and MM (red) PES are shown for dihedrals containing the O1-C1 bond (top) and C2-O2 bond (bottom).

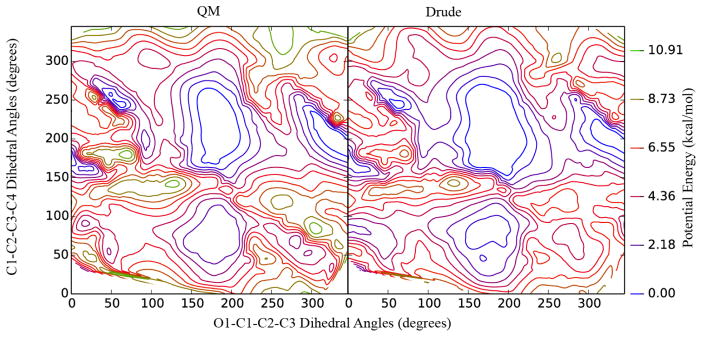
Figure 6.

2-dimensional dihedral potential energy scans for D-psicose. QM (left) and Drude surfaces (right) are shown for dihedrals containing the C1-C2 and C2-C3 bonds.

In general, there is excellent agreement between the QM and MM PES. For D-allose, the C1-C2 bond represents the linkage between acetaldehyde parametrized here and the previously published polyols.[17] After fitting, the root mean-squared error (RMSE) in the potential energy for torsions containing this linkage was 0.74 kcal/mol. It was also necessary to optimize torsions containing the C2-O2 linkage due to the effect of the aldehyde on the rotation of the C2 hydroxyl group. For these torsions, the RMSE after optimization was 0.56 kcal/mol. The C1-C2 and C2-C3 bonds in D-psicose represent the linkages between the ketones and linear polyols with RMSEs of 0.92 kcal/mol.

Conclusion

The work presented here details parametrization of aliphatic aldehydes and ketones, including acyclic sugars such as D-allose and D-psicose, as part of the development of a comprehensive Drude polarizable FF for biomolecules. LJ parameters for the model compounds are optimized targeting experimental heats of vaporization and molecular volumes, while the electrostatic parameters are optimized to reproduce QM water interactions, dipole moments, and molecular polarizabilities. Bonded parameters are targeted to both QM and crystal survey values, with the models for ketones and aldehydes shown to yield properties in good agreement with QM and experimental target data. Compared to the C36 additive FF,[73] the Drude model is better able to reproduce the QM dipole moments demonstrating the importance of incorporating polarizability as well as the C36 additive FF charges being developed primarily targeting HF/6-31G(d) interactions with water. Of note in the water interactions is that the Drude interaction energies and distances are also in better agreement with the QM than the C36 results, which in part arises from the introduction of lone pairs on the carbonyl oxygen in the Drude FF and the aforementioned C36 FF targeting HF/6-31G(d) interactions versus MP2/6-31G(d)//MP2/cc-pVQZ interactions in the Drude FF.

The strength of a polarizable FF is in the ability of the dipole to vary in response to the environment. This is clearly illustrated in the simulations of the model compound ketones and aldehydes by the increase in the magnitude and the fluctuations of the dipole moment in moving from gas phase to condensed phase. Specifically, in the condensed phase simulations, the monomers in aqueous solution have a larger dipole moment because water is a protic polar solvent capable of forming hydrogen bonds with the monomers, which induces a larger polarization response arising from fluctuation of the partial atomic charges of the monomer; as opposed to the pure liquids that are aprotic and cannot form hydrogen bonds. Importantly, this is a phenomenon that the additive FF is intrinsically unable to reproduce, which highlights the necessity of including polarizability. Accordingly, utilization of a polarizable force field is important for scenarios in which molecular species encounter environments of varying polarity or ionic or hydrogen bond interactions during the simulation, as discussed in more detail in a recent review.[102]

Parameters from the small model ketones and aldehydes were used in combination with the recently parametrized polyols[17] for the optimization of D-allose and D-psicose, with bonded parameters corresponding to the linkage between the two compounds optimized to target QM values. In general, the bonds and angles required little optimization, indicating that the initial parameters for the linear polyols and small model ketones and aldehydes are transferable to the larger acyclic sugars. The result is a model for acyclic sugars D-allose and D-psicose, thereby extending the available biomolecules in the CHARMM Drude polarizable FF.