Across space and time: Infants learn from backward and forward visual statistics

Abstract

This study investigates whether infants are sensitive to backward and forward transitional probabilities within temporal and spatial visual streams. Two groups of 8-month-old infants were familiarized with an artificial grammar of shapes, comprised of backward and forward base pairs (i.e., two shapes linked by strong backward or forward transitional probability) and part-pairs (i.e., two shapes with weak transitional probabilities in both directions). One group viewed the continuous visual stream as a temporal sequence, while the other group viewed the same stream as a spatial array. Following familiarization, infants looked longer at test trials containing part-pairs than base pairs, though they had appeared with equal frequency during familiarization. This pattern of looking time was evident for both forward and backward pairs, in both the temporal and spatial conditions. Further, differences in looking time to part-pairs that were consistent or inconsistent with the predictive direction of the base pairs (forward or backward) indicated that infants were indeed sensitive to direction when presented with temporal sequences, but not when presented with spatial arrays. These results suggest that visual statistical learning is flexible in infancy and depends on the nature of visual input.

To accurately represent the structure of their visual environment, infants must detect and extract meaningful signals from the massive amounts of noisy input encountered in the first few years of life. A growing number of studies suggest that infants are sensitive to statistical regularities in the visual domain, which enables them to extract patterns for further processing (Fiser & Aslin, 2002; Kirkham, Slemmer & Johnson, 2002; Kirkham, Slemmer, Richardson, & Johnson, 2007; Tummeltshammer & Kirkham, 2013; Wu, Gopnik, Richardson, & Kirkham, 2011). This visual statistical sensitivity is thought to facilitate many perceptual and cognitive processes such as action prediction, spatial cueing, causation, object recognition, and category learning (Baldwin, Andersson, Saffran, & Meyer, 2008; Sobel & Kirkham, 2006; Tummeltshammer & Kirkham, 2013; Wu, et al., 2011; Younger & Cohen, 1986).

This research begs the question of whether infants’ early emerging statistical sensitivities may be input general or input specific. There has been limited inquiry into the bounds of visual statistical learning in infancy and the extent to which the mechanism may be dependent on stimulus characteristics, context, or manner of presentation. The current study investigates the flexibility of infants’ sensitivity to visual statistical regularities by manipulating two critical features of the input stream: visual context (i.e., temporal sequence or spatial array) and statistical properties (i.e., backward or forward transitional probability).

I. Temporal and spatial statistics

Much of the research on infant statistical learning has been undertaken in relation to early language comprehension, considering which statistical signals are utilized by infants to discover word boundaries, phonetic contrasts, and grammar structure in a speech stream (Gomez & Gerken, 1999; Maye, Werker, & Gerken, 2002; Pelucchi, Hay, & Saffran, 2009b; Saffran, Aslin, & Newport, 1996). Paradigms using artificial language sequences have been adapted to pure auditory, visual, and motor domains to investigate the possibility of similar processes or even a domain-general statistical learning mechanism (Baldwin et al., 2008; Kirkham et al., 2002; Saffran, et al., 1999; Thiessen, 2011). For example, Kirkham and colleagues (2002) familiarized infants with a temporal stream of six colored shapes that loomed onscreen. The continuous sequence could be segmented into three pairs using transitional probability: The first shape in a pair always predicted the second (within-pair TP=1.0) while the second shape did not predict the next pair (between-pair TP=0.33). After familiarization, infants as young as 2 months looked longer at sequences that violated this statistical pattern, providing the first evidence that infants make use of transitional probability to parse a visual sequence. Fiser and Aslin (2002) conducted a visual statistical learning investigation using spatial arrays, in which they familiarized infants with two items that reliably co-occurred beside a third item that occurred randomly. They found that infants looked longer at arrays containing co-occurring shapes than at arrays made up of items that did not reliably co-occur, indicating that conditional statistics may also play a role in infants’ parsing of the spatial world.

An accepted interpretation of these findings is that infants isolate visual regularities by comparing statistical distributions, such as item frequency and conditional probability, via a ‘statistical learning’ mechanism (e.g., Aslin & Newport, 2012). This view suggests that infants perform statistical computations over a set of input, making rapid and automatic predictions about individual items within the set. For example, when watching others’ actions, they may compute the transitional probability of subsequent movements, in order to anticipate which movement is likely to occur next and identify the action’s endpoints (e.g., Baldwin et al., 2008). Indeed infants’ statistical learning capabilities have been demonstrated experimentally with a multiple statistics across a variety of inputs (e.g., Marcovitch & Lewkowicz, 2009, Thiessen & Erickson, 2013).

Another possible interpretation is that infants’ sensitivity to statistical distributions may be the by-product of an ‘associative learning’ strategy (or ‘chunking’, e.g., Miller, 1956). According to this view, individual elements that frequently co-occur are extracted and stored as a structured chunk (Perruchet & Peereman, 2004). Infants’ responses, then, reflect a memory-based recognition of regularities encountered in the environment without ascribing sophisticated computational abilities to infants (see models, PARSER [Perruchet & Vintner, 1998] and TRACX [French, Addyman, & Mareschal, 2011]). As noted by Perruchet and colleagues, statistical learning and chunking explanations converge at many points, as both are considered automatic, incidental, pre-attentive, domain-general processes that largely lead to the same behavioral responses (Perruchet & Peereman, 2004; Perruchet and Pacton, 2006). Further, these processes may not be mutually exclusive (e.g., chunk-based representations may arise from a sensitivity to statistical regularities) and may even be selectively recruited when relevant.

Although the Kirkham, et al. (2002) and Fiser & Aslin (2002) studies provide some converging evidence for extending infants’ use of conditional probabilities to the visual domain, it is unclear whether the same learning mechanism can be implicated across all types of input. For example, while auditory input is temporal in nature and relies on temporal cues to highlight meaningful features (e.g., pitch, prosody, semantics), visual input is spatial in nature and emphasizes spatial relations at many levels of processing (e.g., retinotopic mapping, object tracking, navigation)¹. With different features and neural architectures implicated in their processing, it is not obvious that auditory and visual information would elicit the same sensitivities from infant learners. Even within a single domain, it remains inconclusive whether the same mechanism can be implicated for learning both temporal and spatial inputs.

II. Backward and forward probabilities

Visual streams containing both backward and forward conditional probabilities provide an interesting opportunity to evaluate the input-specificity of infant statistical learning. While some statistics, such as pair frequency, do not contain any information about order or direction, conditional probabilities can differ when computed with respect to the forward direction (i.e., X followed by Y) or backward direction (i.e., Y preceded by X). Consider the following example, illustrated by Perruchet and Desaulty (2008): In English the letter q is always followed by u, but u can be preceded by many letters other than q. Therefore, the forward probability q→u is 1.0, while the backward probability q←u is actually much lower. Recent research in the domain of language comprehension has demonstrated that infants and adults are sensitive to statistical regularities defined in the backward as well as the forward direction (Jones & Pashler, 2007; Pelucchi, Hay, & Saffran, 2009a; Perruchet & Desaulty, 2008). However, language is inherently a temporal input, which suggests a need to be receptive to temporal order. Thus sensitivity to backward and forward statistics could be input-specific, not domain-general.

It is currently unknown whether infants are able to detect backward probabilities in a continuous visual stream, and further, it is unclear whether infants can learn from both backward and forward statistics within the same set of input. Is a visual event represented with respect to what came before it, as much as it may strongly predict the next event? Since backward and forward probabilities within a single pair of events can differ, sensitivity to this difference would lend support to the idea that infants encode events with respect to their conditional statistical relationships. However, failing to discriminate between backward and forward probabilities would rather suggest that infants bind co-occurring events into associative chunks independent of their predictive direction.

The goals of the present study are: 1) to determine whether infants are sensitive to both backward and forward transitional probabilities in a visual stream, and 2) to test whether infants extract the same statistical regularities from temporal and spatial presentations. Two groups of 8-month-old infants were familiarized to an artificial grammar of shapes, comprised of backward and forward base pairs (i.e, two shapes linked by strong backward or forward transitional probability) and part-pairs (i.e., two shapes with weak transitional probabilities in both directions). One group viewed a temporal sequence, with shapes looming one at a time in the center of the screen, while the other group viewed a spatial array, with shapes moving across the screen in horizontal rows. Following familiarization, all infants saw test trials of base pairs and part-pairs, which had appeared with equal frequency in the familiarized pattern. Consistent with previous findings using natural speech, we predicted that infants would discriminate both backward and forward base pairs from part-pairs, demonstrated by differences in looking time (Pelucchi, Hay, & Saffran, 2009a). Further, we hypothesized that infants would show evidence of encoding the backward or forward direction of the base pairs, looking longer at part-pairs that were inconsistent with the predictive direction of the base pair (e.g., longer looking to XA than to DZ if A→D were a forward pair, since A should predict D). While differences in looking times in either direction would indicate that infants indeed discriminated between base pairs and part-pairs on the basis of their transitional probability, we expected a novelty preference (i.e., longer looking at the part-pairs) due to previous findings using similar visual stimuli with familiarization/test procedures in our laboratory (e.g., Kirkham, et al., 2002; Kirkham, et al., 2007; Wu & Kirkham, 2011)².

Method

Participants

Forty-four full-term 8-month-old infants participated in this between-subjects experiment: 22 infants in the Temporal condition (10 females, M=7 months 29.8 days, Range = 7m 7d – 9m 1d), with three additional infants excluded due to fussiness, and 22 infants in the Spatial condition (11 females, M=7 months 28.5 days, Range=7m 9d – 8m 28d), with three additional infants excluded due to fussiness. Infants were recruited on a voluntary basis via local advertisements. Informed consent was received from all caregivers, and all babies received a small gift.

Apparatus & Stimuli

Visual stimuli were displayed on a 23” screen and sounds were played through stereo external speakers on either side of the display. Infants and their eye movements were monitored using a Tobii TX300 eye-tracker with a video camera built-in below the display. Infants viewed streams of 11 unique colorful shapes (see a sample in Figure 1). The shapes were animated to loom in the center or to stream across the screen using Adobe Director software. The video clips were shown via Tobii’s Studio presentation software.

Figure 1.

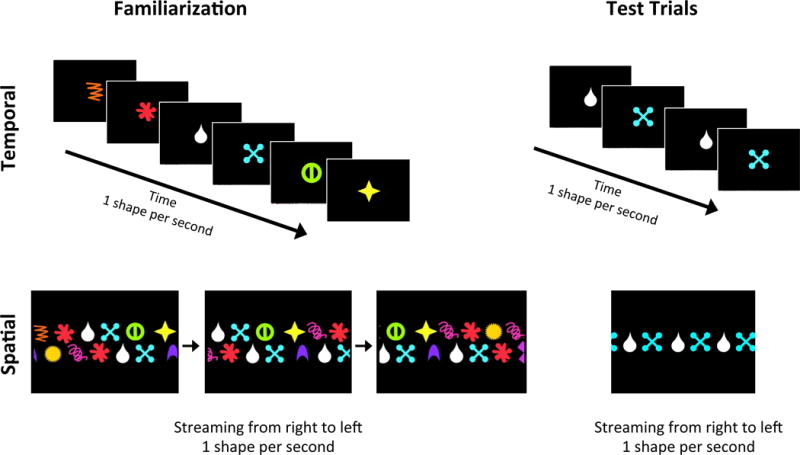
Sample visual streams presented to infants in the Temporal (top) and Spatial (bottom) conditions. During familiarization, the stream comprised of base pairs and part-pairs was presented continuously (left), and during test trials, a single base pair or part-pair was presented multiple times (right). It is worth noting that although shapes were displayed at the same rates, in comparison to the temporal condition, the spatial condition presented more shapes onscreen at the same time and each shape was visible for a longer duration.

Design & Procedure

Infants were tested individually in a quiet room, seated on their caregiver’s lap approximately 60 cm away from the screen. All infants viewed a continuous stream of colorful shapes, presented as either a temporal sequence (Temporal condition) or a spatial array (Spatial condition). A familiarization/test procedure was used: Infants saw the probabilistic pattern repeated several times, and their looking time was subsequently measured as they viewed specific test items taken from the familiarized pattern.

The continuous stream of shapes was comprised of three forward base pairs (AD, BD, and CD), three backward base pairs (EF, EG, and EH) and three single shapes (X, Y, and Z). The forward base pairs were linked by strong forward probabilities, as the first shape always predicted the second shape (e.g., C→D = 1.0). The backward base pairs were linked by strong backward probabilities, as the first shape always preceded the second shape (e.g., E←F = 1.0). Forward base pairs had weak backward probabilities, as three different shapes could precede the second shape (i.e., A, B, C←D). Backward base pairs had weak forward probabilities, as three different shapes could follow the first shape (i.e., E→F, G, H). Finally, the single shapes (X, Y, and Z) had weak transitional probabilities in both directions and could precede or follow any base pairs (e.g., Z→A, B, C, E and D, F, G, H←Z). These unpaired shapes formed weak “part-pairs” with the shapes adjacent to them. Following familiarization, looking times to base pairs and part-pairs were compared to determine whether infants were sensitive to the transitional probabilities in the stream. Shapes were randomly assigned to the pairings for each infant, so that looking time measures would not be biased by any arbitrary shape or shape pair preferences. Two pairs (AD and EH) and one single shape (X) appeared twice as often as the others, in order to balance the frequencies of base pairs and part-pairs compared at test. If infants parsed the stream using pair-frequency, then base pairs would be indistinguishable from part-pairs. Thus any differences in looking time to base pairs and part-pairs at test could be taken as evidence of infants’ sensitivity to the transitional probabilities.

Temporal condition

Infants in the Temporal condition viewed this stream as a temporal sequence, with forward and backward transitional probabilities indicating which shapes appeared before and after a given shape in time. The shapes loomed one at a time in the center of the screen for one second, resulting in a 48-second block of 48 shapes (see Figure 1, as well as Supporting Information, clip 1). Infants viewed three blocks of temporal sequences, as determined by an independent pilot test using infant-controlled habituation. This length of familiarization was sufficient for infants to become familiar with the shape transitions, but not to become fussy or inattentive. Thus across the entire Temporal familiarization, infants viewed the more frequent base and part-pairs 24 times each and the less frequent base and part-pairs 12 times each. A short attention-grabbing video clip (Elmo from Sesame Street) was inserted between each familiarization block and abstract sounds (e.g. bring, ding-dong, honk) were inserted randomly to attract less attentive infants back to the screen, but offer no additional cues for segmenting the stream.

Spatial condition

Infants in the Spatial condition viewed this stream as a spatial array that moved across the screen from left-to-right or right-to-left (between subjects) for 48 seconds (see Figure 1, as well as Supporting Information, clip 2). The same base pairs and part-pairs were contained in the stream (see Table 1); but in this case, the forward and backward transitional probabilities indicated which shapes appeared on the left or right of a given shape in space. Infants viewed four blocks of the spatial arrays, as an independent pilot test using infant-controlled habituation determined that infants took longer to habituate to the stream when presented as a spatial array than when presented as a temporal sequence. Thus across the entire spatial familiarization, infants viewed the more frequent base and part-pairs 32 times each and the less frequent base and part-pairs 16 times each. The same attention-grabbing video clip and abstract sounds were used to maintain infants’ attention to the screen.

Table 1.

Elements comprising the probabilistic visual stream with their transitional probabilities and pair frequencies. In order to balance the pair frequencies of the base pairs and part-pairs presented at test, some shapes differed in their individual frequencies (i.e., one forward base pair, one backward base pair, and one single shape appeared twice as often as the others).

	Base Pairs	Single Shapes	Transitional Probability		Test Pair Frequency
			Pairs	Part-Pairs	Pairs	Part-Pairs
Forward	A D A D B D C D	X X Y Z	TPfor = 1.0 C→D TPback = 0.25 C←D	TPfor = 0.25 D→Z TPback = 0.5 D←Z	BD = 1/24 CD = 1/24	DZ = 1/24 XA = 1/24
Backward	E F E G E H E H	X X Y Z	TPfor = 0.25 E→F TPback = 1.0 E←F	TPfor = 0.5 Y→E TPback = 0.25 Y←E	EF = 1/24 EG = 1/24	YE = 1/24 HX = 1/24
Sample sequence of 48 shapes: ADXEGYADZEHXEFZCDXADYEFXBDZADXEHYBDXEHXCDYEHZEGX
Parsed using within-pair probabilities: AD-X-EG-Y-AD-Z-EH-X-EF-Z-CD-X-AD-Y-EF-X-BD-Z-AD-X-EH-Y-BD-X-EH-X-CD-Y-EH-Z-EG-X

Following Temporal or Spatial familiarization, all infants viewed test trials of base pairs and part-pairs taken from the familiarized pattern. Each test pair was repeated six times in a single trial that lasted 12 seconds. There were 8 test trials, the order of which was counter-balanced across participants: 4 base pairs, 2 forward (i.e., BD and CD) and 2 backward (i.e., EF and EG); and 4 part-pairs, 2 forward (i.e., DZ and XA) and 2 backward (YE and HX). Since base pairs and part-pairs presented at test had appeared with equal frequency during familiarization (e.g., CD appeared as often as DZ), any differences in infants’ mean looking times could be attributed to their sensitivity to the transitional probabilities in the stream. Importantly, two part-pairs were inconsistent with the predictive direction of a forward or backward base pair (i.e., XA was inconsistent with forward base pair A→D as A should always predict D; and HX was inconsistent with backward base pair E←H as H should always be preceded by E). The other two part-pairs were consistent with the base pair statistics (i.e., DZ and YE, since D and E could be preceded or followed by multiple shapes). Thus, if infants were sensitive to whether base pairs were forward or backward, then they should look longer at the inconsistent part-pairs than the consistent part-pairs.

Data Analysis

Infants’ looking times to base pairs and part-pairs at test were compared between the Temporal and Spatial conditions. Following from previous visual statistical learning studies, we hypothesized that infants would demonstrate longer mean looking times for part-pairs than base pairs (e.g., Kirkham, et al., 2002; Kirkham, et al., 2007; Marcovitch & Lewkowicz, 2009; Wu, et al., 2011). Further, we hypothesized that if they were sensitive to both forward and backward transitional probabilities, then infants would look longer at part-pairs than both backward and forward base pairs (i.e., no interaction with direction). Finally, we hypothesized that infants would look longer at part-pairs that were inconsistent, rather than consistent, with the predictive direction of the forward and backward base pair probabilities, indicating that they had encoded the base pairs’ directions (e.g., if A→D is encoded as a forward pair, then XA should be more surprising than DZ, since A should predict D but D must not be preceded by A).

Results

During test trials, infants looked longer at part-pairs than base pairs. This was apparent for infants in the Temporal condition (part-pairs M=7.90 s, SD=1.99 s; base pairs M=6.64 s, SD=2.60 s) as well as for infants in the Spatial condition (part-pairs M=7.44 s, SD=1.95 s; base pairs M=6.83 s, SD=2.19 s). Eighteen out of 22 infants showed a preference for part-pairs in the Temporal condition (Wilcoxin Signed Ranks test, z=3.49, p<0.001), and 16 out of 22 infants in the Spatial condition (z=2.18, p=0.03). As looking times were not normally distributed, parametric tests using log-transformed looking time data were conducted to confirm this result: Temporal t(21)=3.98, p=0.001; Spatial t(21)=2.41, p=0.02.

Log-transformed looking times were further examined in a 2(Condition: Temporal, Spatial) × 2(Direction: backward, forward) × 2(Type: base pairs, part-pairs) mixed ANOVA, which showed a main effect of Type, F(1,42)=17.27, p<0.001, η_p²=0.29, confirming that infants indeed looked longer at part-pairs than base pairs. A marginal effect of Direction was also apparent, F(1,42)=3.80, p=0.06, η_p²=0.08, as infants looked slightly longer at forward direction test trials compared to backward direction test trials. There were no other effects or interactions, all p>0.11, indicating that longer looking at part-pairs than base pairs was evident for both backward and forward probabilities and persisted in both the Spatial and Temporal conditions. Planned separate post-hoc comparisons confirmed that the preference for part-pairs was significant in both the forward direction, t(43)=3.67, p=0.001, and the backward direction, t(43)=2.82, p=0.007. Raw looking times for these variables are shown in Figure 2.

Figure 2.

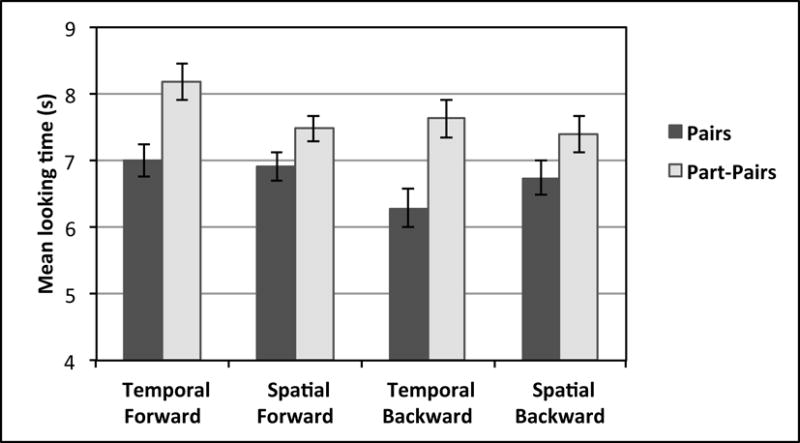
Mean looking times (in seconds) at test for base pairs and part-pairs; separated by Temporal and Spatial conditions.

Finally, the four part-pair test trials were divided according to whether the part-pairs were consistent or inconsistent with the predictive direction of the base pair from which the part-pair item was taken (i.e., whether the part-pair item should have predicted another item with a backward or forward probability of 1.0). Mean looking times were compared in separate 2 2(Direction: backward, forward) × 3(Type: base pairs, consistent part-pairs, inconsistent part-pairs) repeated measures ANOVAs. In the Temporal condition, there was a main effect of Type, F(2,42)=9.12, p<0.001, and no effect of Direction or interaction (p>0.490). A post-hoc Friedman Ranks test showed that infants looked longest at inconsistent part-pairs, less at consistent part-pairs, and least at base pairs, χ²=12.09, p=0.002. However, in the Spatial condition, no main effect of Type emerged, F(2,42)=0.144, p=0.866, nor any effect of Direction or interaction, indicating that infants did not discriminate between the consistent and inconsistent part-pairs. This result suggests that infants who saw the temporal presentation were sensitive to the predictive directions of the base pairs, while infants who saw the spatial presentation were not. Raw looking times for these comparisons are shown in Figure 3.

Figure 3.

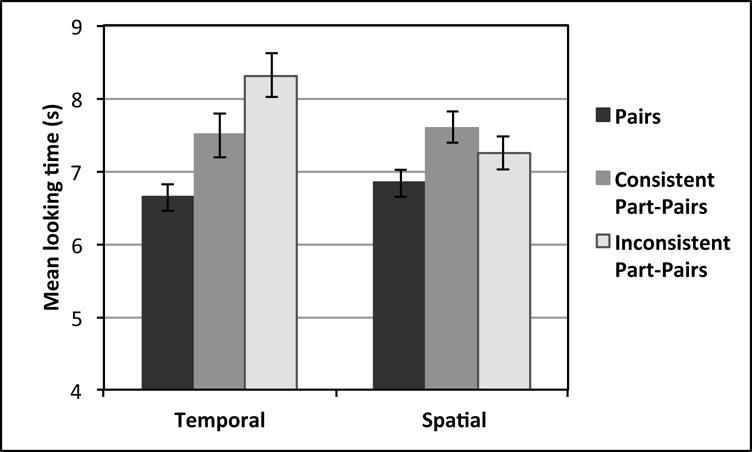
Mean looking times (in seconds) at test for base pairs, consistent part-pairs (i.e., DZ and YE), and inconsistent part-pairs (i.e., XA and HX); separated by Temporal and Spatial conditions.

Discussion

The results of the present study provide the first evidence that infants are sensitive to both backward and forward transitional probabilities in a continuous stream of visual input. Following familiarization with sequences containing both backward and forward transitional probabilities, infants looked longer at part-pairs than base pairs, though base and part-pairs were equally familiar and frequent. This result is consistent with previous studies of visual statistical learning, in which infants also showed preferences for unrelated items (Marcovitch & Lewkowicz, 2009; Wu, et al., 2011). Infants’ looking preferences were apparent for both forward and backward directions, indicating that they were sensitive to both forward and backward transitional probabilities when parsing the visual stream. This result suggests that both directions are of critical importance to the infant visual learner. Indeed, forward and backward statistical relations may serve different, but equally important, functions: Forward relations facilitate prediction and planning, while backward relations support explanation and causal attribution. Future studies may investigate whether infants use both forward and backward statistics to modify their visual behavior. A few studies have shown that infants make use of forward statistical regularities in planning saccades, showing faster latencies to statistically predictable locations (Amso & Davidow, 2012; Kirkham, et al., 2007; Tummeltshammer & Kirkham, 2013).

Further, differences in sensitivity to violations of the forward or backward transitional probabilities indicate that infants may not encode temporal and spatial visual regularities in the same way. When presented with temporal sequences, infants looked longer at inconsistent, compared to consistent, part-pairs, indicating that they had encoded the predictive direction of the base pairs (e.g., represented A→D as a forward pair and looked longer when A appeared without D). This result was apparent for both backward and forward pairs (i.e., no Type × Direction interactions), such that infants showed no advantage in sensitivity to one direction of transitional probability over the other. This finding is consistent with a study by Turk-Browne and Scholl (2009), who showed that adults encode visual triplets with their temporal order, though they can also recognize the triplets independent of order. However, when presented with spatial arrays, infants showed no differences in looking time to consistent and inconsistent part-pairs, suggesting that they had not encoded the base pairs as forward or backward (e.g., looked equally long when A appeared without D or D appeared without A). Rather, infants who saw the spatial presentations may have bound the paired shapes into associative chunks without preserving information about their direction (e.g., representing A→D as single unit AD).

It has been suggested that infants’ responses on statistical learning tasks may emerge from an ‘associative learning’ or ‘chunking’ strategy, reflecting memory-based recognition of regularities in the environment without demanding statistical computations (French, Addyman, & Mareschal, 2011; Perruchet & Peereman, 2004; Perruchet & Pacton, 2006). Though many statistical learning tasks can indeed be accomplished using associative learning, sensitivity to more subtle statistical features (such as whether pairs are linked by backward or forward conditional probabilities) supports the engagement of a more computational strategy. Further work is needed to disentangle the roles of memory-based chunking and statistical learning accounts in infants’ deconstruction and representation of their visual experience. The present results indicate that infants’ sensitivity to visual regularities depends on the nature of the input stream, suggesting that statistical learning mechanisms may be selectively recruited when relevant.

There are a number of fundamental distinctions between temporal and spatial presentations that may account for the observed differences in infants’ sensitivities across the two conditions. First, temporal and spatial presentations place different demands on the cognitive resources necessary to accomplish statistical learning, namely attention and working memory. In temporal sequences, items are presented one-by-one such that the order of information is fixed and the targets of attention are pre-selected for the learner. Spatial arrangements, on the other hand, present multiple relations at the same time and attention can be freely allocated, such that items may be fixated in many different orders. Equivalent learning, then, would depend on infants’ ability to distribute attention evenly across all items in the spatial display. Studies with adults have suggested that success in statistical learning may indeed depend on the efficient deployment of attention (Baker, Olson, & Behrmann, 2004; Fiser & Aslin, 2001; Turk-Browne, Junge, & Scholl, 2005). Further, temporal information is transient and can only be reviewed in memory, whereas spatial information is readily available for visual inspection. This difference in perceptual access may affect the depth and detail of encoding, with temporal relations encoded more robustly than spatial relations. Pilot work using infant-controlled habituation indicated that infants required more trials to habituate to the spatially presented stream than the temporally presented stream, justifying the difference in length of familiarization used in the current experiment. This pilot result is consistent with the idea that spatial and temporal relations may have different processing and encoding demands, as the speed of habituation is thought to reflect information processing time (e.g., Dember & Earl, 1957; Fantz, 1964; Hunter & Ames, 1988; Sokolov, 1963). The difference in familiarization length is unlikely to have produced the present results, as one would expect longer familiarization in the spatial condition to yield greater sensitivity, which is the opposite of what we observed.

Second, statistical direction may not be equally salient or relevant in temporal and spatial relations, as these dimensions emphasize different features of a visual event. Fiser and Aslin (2001) suggest that higher-order statistical information may only be represented when it is necessary to solve a particular task; otherwise visual feature processing would be computationally intractable. Accordingly, infants may only show sensitivity to the direction of statistical relations when it signals a meaningful distinction. While one could argue that directionality is inherent to temporal positions (i.e., before and after) and critically informative to temporally defined events (e.g., identifying cause and effect), it is unclear whether the same is true of spatial positions (i.e., above, below, beside). It may be informative to represent two items as adjacent in space, but their absolute position is likely to be flexible or to depend on vantage point. For the developing child, it may be particularly adaptive to employ flexible, context-relevant learning mechanisms that are sensitive to the nature of visual input, as these mechanisms will operate more efficiently over the young learner’s rapidly changing representations. For example, the physical layout of a room, inherently spatial in nature, may take on a highly relevant temporal quality when the infant begins to self-locomote and needs to plan her path and navigate obstacles. Conversely, language, which is primarily temporal when spoken to the infant, may become spatially represented once the child learns to read and becomes highly familiar with the left-to-right (or some other coherent) structure of written words³. In this way, such developmental milestones can profoundly alter the child’s environmental input, with a likely consequence of tuning their sensitivities to the consistent and relevant features of that input.

In conclusion, the present study has demonstrated that infants are sensitive to both forward and backward transitional probabilities within continuous visual streams. Importantly, infants’ sensitivity to conditional statistics depends on the nature of visual input. That is, infants may encode and represent statistical information differently across domains, depending on its salience or relevancy, providing evidence for a flexible statistical learning strategy with a variety of applications in infant cognitive development.

Research Highlights.

• Eight-month-old infants demonstrate sensitivity to both backward and forward conditional probabilities, looking longer at unrelated part-pairs than at statistically related base pairs taken from a familiarized visual stream.

• Infants demonstrate this sensitivity whether familiarized with the conditional probabilities in a temporal sequence of looming shapes or in a spatial array of streaming shapes.

• Infants are sensitive to the direction of the conditional relationship between paired items (i.e., whether one item should be preceded or followed by another) when presented in a temporal sequence, but not when presented in a spatial array.