Unraveling Mg²⁺–RNA binding with atomistic molecular dynamics

Abstract

Interaction with divalent cations is of paramount importance for RNA structural stability and function. We report here a detailed molecular dynamics study of all the possible binding sites for Mg²⁺ on an RNA duplex, including both direct (inner sphere) and indirect (outer sphere) binding. In order to tackle sampling issues, we develop a modified version of bias-exchange metadynamics, which allows us to simultaneously compute affinities with previously unreported statistical accuracy. Results correctly reproduce trends observed in crystallographic databases. Based on this, we simulate a carefully chosen set of models that allows us to quantify the effects of competition with monovalent cations, RNA flexibility, and RNA hybridization. Our simulations reproduce the decrease and increase of Mg²⁺ affinity due to ion competition and hybridization, respectively, and predict that RNA flexibility has a site-dependent effect. This suggests a nontrivial interplay between RNA conformational entropy and divalent cation binding.

INTRODUCTION

The relevance of ribonucleic acid (RNA) in molecular biology has systematically grown since the discovery that it can catalyze chemical reactions (Doudna and Cech 2002), and RNA is now considered a key player in many of the regulatory networks of the cell (Morris and Mattick 2014). Functions such as catalysis and regulation of gene expression rely on the peculiar structure and dynamics of RNA molecules. The folding of RNA three-dimensional structure stands in a delicate balance between canonical interactions and strong electrostatics mediated by the presence of cations. Cations, together with water, are indeed crucial to compensate for the large repulsion between the charged phosphate groups present in the RNA backbone. They allow for the formation of tertiary contacts (Tinoco and Bustamante 1999; Lipfert et al. 2014), and can also provide entropic stabilization to RNA motifs (Fiore et al. 2012). Among cations, Mg²⁺ is particularly relevant because of its double charge and small radius (Oliva and Cavallo 2009). Mg²⁺ can be both directly and indirectly bound to RNA, that is RNA atoms can be part of the Mg²⁺ inner coordination sphere or interact through hydrogen bonds with its hydration sphere (Bowman et al. 2012). The inner sphere ions mainly contribute to the formation of specific structural motifs (Petrov et al. 2011). The outer sphere ones might also bind to specific motifs and additionally take part in the ion atmosphere and stabilize RNA structures by screening electrostatic repulsion (Draper 2004). Several experimental works have provided valuable insights on the thermodynamics of RNA–Mg²⁺ interactions in solution (Draper 2008; Erat and Sigel 2011; Bizarro et al. 2012; Kirmizialtin et al. 2012a). Titration experiments have been used to characterize the overall affinity of RNA for Mg²⁺ (Sigel and Sigel 2010). Affinities for individual Mg²⁺ binding sites on RNA nucleosides and small RNA motifs have also been reported (Freisinger and Sigel 2007). The role of functional metal ions on small RNAs has also been investigated through nuclear magnetic resonance spectroscopy (Hoffmann et al. 2003; Campbell et al. 2006; Bartova et al. 2016). However, the precise characterization of typical Mg²⁺ binding sites in large RNA molecules has largely been obtained by analyzing crystal structures (Banatao et al. 2003; Auffinger et al. 2011). A recent database survey allowed for a classification of all the binding modes observed in crystallographic structures (Zheng et al. 2015). Molecular modeling could in principle provide a powerful tool to bridge the gap between detailed crystallographic structures and solution experiments (Schlick 2010). In this respect, several works at different levels of resolution have been reported, ranging from quantum-chemistry calculations (Tongraar and Rode 2001; Petrov et al. 2011; Kolev et al. 2013; Mlýnský et al. 2015; Casalino and Magistrato 2016), to explicit solvent molecular dynamics (MD) (Allnér et al. 2012; Kirmizialtin et al. 2012b; Pan et al. 2014), implicit solvent methods (Hayes et al. 2015; Henke and Mak 2016), and coarse-grained models (Hyeon and Thirumalai 2011). Among the computational methods, MD presents an excellent compromise between accuracy and computational cost, though the development of an appropriate parametrization for Mg²⁺–RNA interactions is still a debated topic (Panteva et al. 2015a; Bergonzo et al. 2016). Moreover, due to the high energetic barriers involved in Mg²⁺–RNA and Mg²⁺–water interaction (Bleuzen et al. 1997), which brings the lifetime of these complexes to the ms timescale, coupling of MD with enhanced sampling methods is required.

In this article, we use a unique combination of enhanced sampling techniques together with a recently published parametrization (Allnér et al. 2012) for Mg²⁺ to compute its affinity on a flexible RNA duplex. RNA duplexes are the most recurring motifs observed in ribosomal RNA (Gutell et al. 1994). The computed affinities for all the relevant binding sites are compared with previously reported thermodynamic data and with an analysis of the protein databank (PDB). Furthermore, by performing simulations on an appropriately chosen set of model systems, we are able to investigate the interplay between Mg²⁺–RNA binding affinity and competition with monovalent ions, RNA flexibility, and RNA hybridization.

RESULTS

The main output of our simulations is the binding affinity of Mg²⁺ on all the possible binding sites in an RNA duplex. We first report a detailed analysis of the obtained affinities and the correspondence with frequencies from the PDB. A comparison with the thermodynamic data available for nucleosides and a dinucleoside monophosphate is reported in Supplemental Information 4. Then, we show a set of simulations performed in different conditions to dissect the important contributions to Mg²⁺–RNA binding. The reported affinities were calculated by averaging over atoms of the same type in the central bases of the duplex, so as to mitigate terminal effects. For all the reported quantities we also computed statistical errors. For a quantity whose best estimate is X and the confidence interval is [X − Δ₁,X + Δ₂], the value is reported as $X_{-{\mathrm{\Delta }}_1}^{+{\mathrm{\Delta }}_2}$. Errors are computed by block averaging over four blocks without discarding any part of the simulation. When relevant we also discuss the results obtained by applying a correction that enforces the experimental affinity on all the binding sites of a nucleoside (MaxEnt correction, see Materials and Methods).

Mg²⁺ binding on a flexible duplex

Table 1 reports the binding affinity for Mg²⁺ of a flexible RNA duplex in the presence of explicit K⁺ and Cl⁻. Reported results are obtained with the large simulation box (≈11,000 water molecules). With our approach, one can obtain affinities for both inner and outer sphere binding on all the possible binding sites. For the sake of clarity, we define as outer sphere binding any state in which an explicit water molecule is between Mg²⁺ and an electronegative donor.

TABLE 1.

Calculated Mg²⁺ affinities on a duplex and PDB frequencies from Zheng et al. (2015)

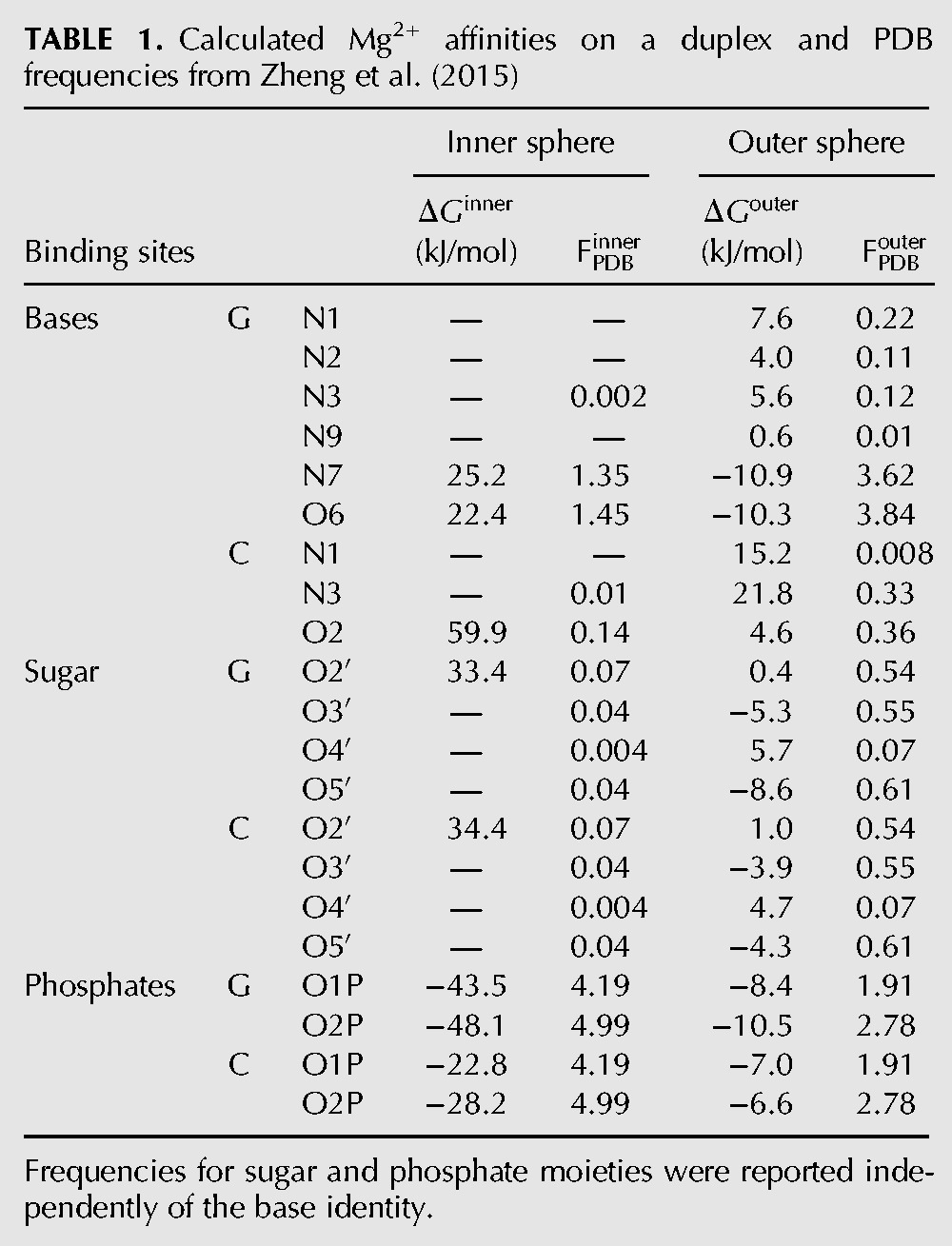
Affinity for inner sphere binding is dominated by the phosphates, with a preference for the strand composed of guanines. We observed a significant preference for direct binding on G–O2P with respect to the G–O1P. Nitrogens that are involved in base-pairing never formed direct contacts with Mg²⁺. Affinity of C-O2 was extremely low, being surpassed by the O2′ in the sugar moiety. The only atoms in the nucleobase displaying significant affinities were G–O6 and G–N7. All these observations are in striking agreement with interaction frequencies observed in the PDB taken from Zheng et al. (2015) that are also reported in Table 1. The only exception is the inversion in the binding free energies of C–O2 and O2′. Our underestimation of the affinity of C–O2 might be biased by our choice to simulate an RNA duplex. Indeed, affinity of C–O2 is expected to be increased when cytosine is not involved in a canonical base pair. Interestingly, in a simulation performed on an isolated nucleoside (see Supplemental Information 4) the affinity of C–O2 was significantly larger.

When looking at outer sphere binding, both nucleobase and phosphate backbone contribute to the overall affinity (see Table 1). Also in this case, there is a preference for the strand composed of guanines, and binding on G–O2P is more favorable with respect to binding on G–O1P. The affinity of G–O6 and G–N7 is comparable to the affinity of phosphates. Also the sugar oxygens have a relatively large affinity. These observations agree with the interaction frequencies observed in the PDB. The only two exceptions are related to O5′ and O3′, for which the reported frequency is low, and to the G–O6 and G–N7 affinities, which are in the inverse order but within error of each other. The former discrepancy could be related to the fact that, at variance with our approach, in the reported experimental frequency the outer sphere binding with phosphates was excluded from the count on the O5′ and O3′ interaction frequencies. The latter discrepancy could be related to the sequence we choose to sample. It must be also noticed that binding of Mg²⁺ on G–N7 can happen in a large variety of equivalent and consequently noncomparable structural contexts. Moreover, the difference in the reported experimental frequencies is very small.

One might be tempted to convert the observed frequencies into binding free energies that can be quantitatively compared with our results. Even though the correlation is good (R² = 0.61 for inner sphere and R² = 0.67 for outer sphere binding), indicating that the ranking is consistent, the slope of the fitting line is very far from unity (see Supplemental Information 5). This might be due to imbalance in the force field (Panteva et al. 2015a) as well as to the fact that PDB distributions are not necessarily representative of the canonical ensemble. Additionally, it is not clear how much these frequencies could be used to anticipate the location of Mg²⁺ ions in solution.

Remarkably, our calculation can recapitulate the most important trends observed in experimental frequencies, namely: preference for G with respect to C; preference for major groove with respect to minor groove; relative preference between all the relevant binding sites.

Dissecting contributions to affinity

We then repeated the calculations in several different conditions with the aim of dissecting all the contributions to RNA–Mg²⁺ binding affinity. Simulations with explicit K⁺ ions were compared with equivalent simulations using a uniform positive background (UB+) in order to account for ion competition effects. In the same spirit, simulations with flexible RNA were compared against equivalent ones with rigid RNA, in order to account for flexibility and conformational entropy effects. These simulations are performed with a box containing approximately 2100 water molecules, which is large enough to observe a clearly flat free-energy profile as a function of the distance of the Mg²⁺ from the CoM_RNA. Profiles obtained with control simulations are shown in Supplemental Information 3. The hybridization effects on Mg²⁺ affinity can be clarified by comparing simulations done on single-stranded (ssRNA) and double-stranded RNA (dsRNA). The conditions for each set of simulations are discussed in detail in Materials and Methods.

Ion competition

We first use our simulations to quantify how much the competition with K⁺ influences the RNA affinity for Mg²⁺. To this aim we compared the affinities on individual binding sites using either a uniform positive background (UB+) or explicit K⁺ ions. To avoid complications related to the interaction of counterions and coions, we only added four monovalent cations so as to neutralize the system. Inner sphere binding free energies reported in Figure 1A shows the effect of explicit K⁺ ions on Mg²⁺–RNA affinity. Here it is possible to appreciate that competition of K⁺ ions decreases the overall Mg²⁺ affinity, both when RNA is kept rigid and when it is modeled as flexible. The change in the total binding free energy is quantified as ${10.5}_{-0.7}^{+1.0}$ kJ/mol for flexible RNA and as ${9.5}_{-0.6}^{+0.7}$ kJ/mol for rigid RNA. The effect of the presence of K⁺ ions on the affinity can also be rationalized by measuring the Mg²⁺ affinity on individual sites when there is a K⁺ ion in proximity of the same site. Results are reported in Figure 2 and are consistent with the fact that the decreased affinity is an effect of the competition between the two species for the same binding site. We notice that the effect of competition is local and propagates in a few cases to the nearest-neighbor binding sites, suggesting that also a short model duplex can be used to quantify ion competition.

FIGURE 1.

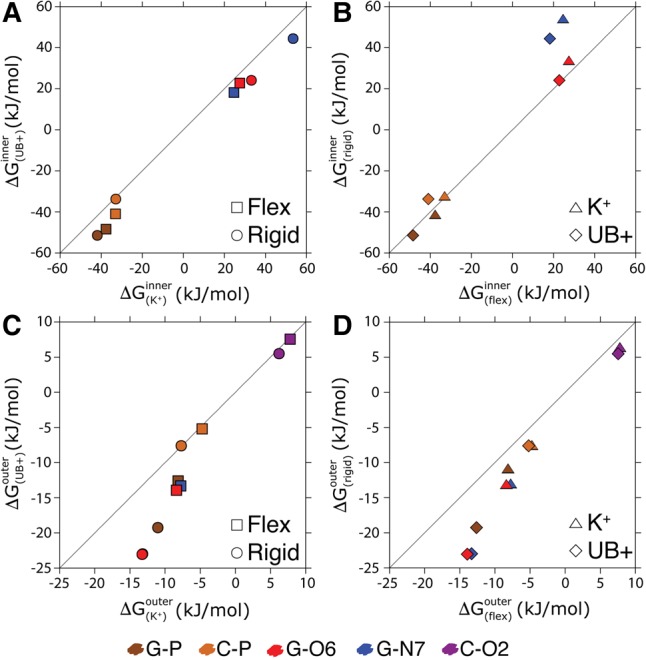
Specific Mg²⁺ binding affinities on a $\begin{array}{r}\mathrm{GGGG}\\ \mathrm{CCCC}\end{array}$ duplex under different simulation conditions. The affinities were obtained in a flexible and rigid duplex both with explicit K⁺ ions and without, thus with a uniform positive background (UB+). Plots A and C show the effect of ion competition (K⁺ versus UB+) for inner and outer sphere Mg²⁺ binding, respectively. Plots B and D show the effect of flexibility (flex versus rigid) for inner and outer sphere Mg²⁺ binding, respectively.

FIGURE 2.

Conditional Mg²⁺ affinity for phosphate oxygens upon K⁺ binding. Each square represents in a color scale the affinity of Mg²⁺ on a specific binding site (vertical axis) when a K⁺ is close to another binding site (horizontal axis). Since K⁺ rarely occupies some of the binding sites, statistical errors for those sites are large. An equivalent matrix including all the Mg²⁺ binding sites is reported in Supplemental Information 6.

The binding free energies for the indirectly bound ions are also reported (Fig. 1C) and follow a similar trend being reduced by ${4.9}_{-0.03}^{+0.03}$ kJ/mol for flexible RNA and ${9.3}_{-0.06}^{+0.06}$ kJ/mol for rigid RNA. Errors are much smaller here since the number of binding and unbinding events is significantly larger in the case of outer sphere binding.

The affinities for the specific binding sites of the set of systems used to dissect the contributions to Mg²⁺ affinity are reported in Supplemental Information 7. Equivalent data obtained including MaxEnt corrections are shown in Supplemental Information 8. The changes in binding free energies due to ion competition are not affected by the corrections on the Mg²⁺ parametrization, indicating that these results are robust with respect to the imbalance between binding on nucleobases and phosphates observed in the original force field.

RNA flexibility

We then compared the results obtained with a rigid RNA molecule with those obtained with a flexible one. The flexible RNA molecule had minor restraints so as to conserve its secondary structure, but still could undergo significant local deformations. Flexibility effects on the affinity of the inner sphere bound ions are reported in Figure 1B. The effect of flexibility is not trivial. In the system where cations are explicitly included, the affinity of Mg²⁺ on flexible RNA is decreased by ${3.9}_{-0.7}^{+0.9}$ kJ/mol with respect to rigid RNA. In the system where cations are replaced with a UB+, the affinity of Mg²⁺ on flexible RNA with respect to rigid is decreased by ${2.9}_{-0.6}^{+0.8}$ kJ/mol.

The values of affinity for the indirectly bound ions (Fig. 1D) follow the same direction, decreasing by ${4.3}_{-0.05}^{+0.05}$ kJ/mol in the simulation with explicit K⁺ ions and ${8.7}_{-0.04}^{+0.04}$ kJ/mol to the one with a UB+.

Also, these values are barely affected by the corrections on the Mg²⁺ parametrization, indicating that these results are robust with respect to the imbalance between the binding affinity of nucleobases and phosphates observed in the original force field. Equivalent data obtained including MaxEnt corrections are shown in Supplemental Information 8.

By dissecting the contribution of the individual binding sites to the overall affinity, it can be seen that the central phosphate of the guanine (G-P), which contributes most to the overall affinity, has a greater affinity for Mg²⁺ when RNA is kept frozen. This is true for all the three G-Ps.

Interestingly, the affinity on the nucleobase binding sites located in the major groove (G–O6 and G–N7) is affected by flexibility with an opposite trend. The lower affinity in the ideal rigid structure indicates that the duplex should undergo slight rearrangements so as to bind Mg²⁺ on the major groove. Figures in Supplemental Information 9 and Supplemental Information 10 show the conditional probability distributions of all RNA backbone dihedrals consequent to Mg²⁺ direct binding for all phosphates. No significant rearrangement can be appreciated on the backbone dihedrals. We notice, however, that a very small repositioning of the phosphates could lead to a significant change in the electrostatic interaction with Mg²⁺ that would explain the observed differences. Therefore, the structural integrity of the duplex was maintained even when Mg²⁺ was directly bound to RNA. It is also relevant to say that for ≈1% of the simulation time, flexible RNA underwent reversible transitions to ladder-like structures (Banáš et al. 2010). This is consistent with what has been observed in recent simulations of restrained RNA duplexes (Bergonzo et al. 2015). Reversibility was checked by monitoring the continuous trajectories so as to avoid false transitions to be observed just due to replica exchanges. To assess the impact of these structures on Mg²⁺ binding, we recomputed all the affinities by excluding all the snapshots where at least one of the glycosidic torsions was in the range (−90°,0°), which corresponds to the high anti conformation observed in ladder-like structures. Only the affinities for O5′ at the 5′ termini were affected. All the other affinities were within the statistical error from the calculation including all the data, indicating that transition to ladder-like structures is not correlated with Mg²⁺ binding. Since only the affinities for nonterminal nucleotides are discussed in this work, the presence of ladder-like structures does not affect the reported results.

Duplex hybridization

Finally, we compare the affinity of Mg²⁺ with a double-stranded RNA (dsRNA) against the one with a pair of single-stranded RNAs with the same sequence. The calculations were performed for both systems in a box that was large enough to contain the two separated strands and in identical ionic conditions. Also, these simulations were performed using neutralizing cations only, so that the affinities reported for the duplex presented in this section corresponded to a lower ionic strength in comparison with those presented above. In all these simulations, RNA was kept rigid. Indeed, sampling all the conformations available for an ssRNA is a formidable task (Bergonzo et al. 2014; Gil-Ley and Bussi 2015) and would have made it virtually impossible to obtain converged values for the binding affinities. Moreover, the capability of current force fields to correctly reproduce the conformational ensembles of ssRNA has been questioned (Bergonzo et al. 2015; Condon et al. 2015; Bottaro et al. 2016; Gil-Ley et al. 2016). To allow for the affinities to be comparable, it was necessary to also treat the dsRNA as rigid. Affinities for inner sphere binding are reported in Figure 3A. Overall, the affinity in the dsRNA was larger, indicating that hybridization and Mg²⁺ binding act cooperatively. In other words, when a Mg²⁺ ion is interacting with RNA, the hybridization free energy is expected to be decreased by $9_{-0.9}^{+1.4}$ kJ/mol, further stabilizing the duplex. We also notice that the overall affinity on the dsRNA is dominated by direct interactions with the phosphate. However, it is interesting to see this effect on individual binding sites. In Figure 3, it can be seen that the affinity with the G–O6 is affected by hybridization in the opposite manner, so that affinity in the ssRNA is enhanced. This is consistent with the fact that electronegative atoms in the base are more accessible to divalent ions. However, since the contribution of bases to the overall affinity on the dsRNA is negligible with respect the contribution of phosphates, this effect is not visible in the overall affinity.

FIGURE 3.

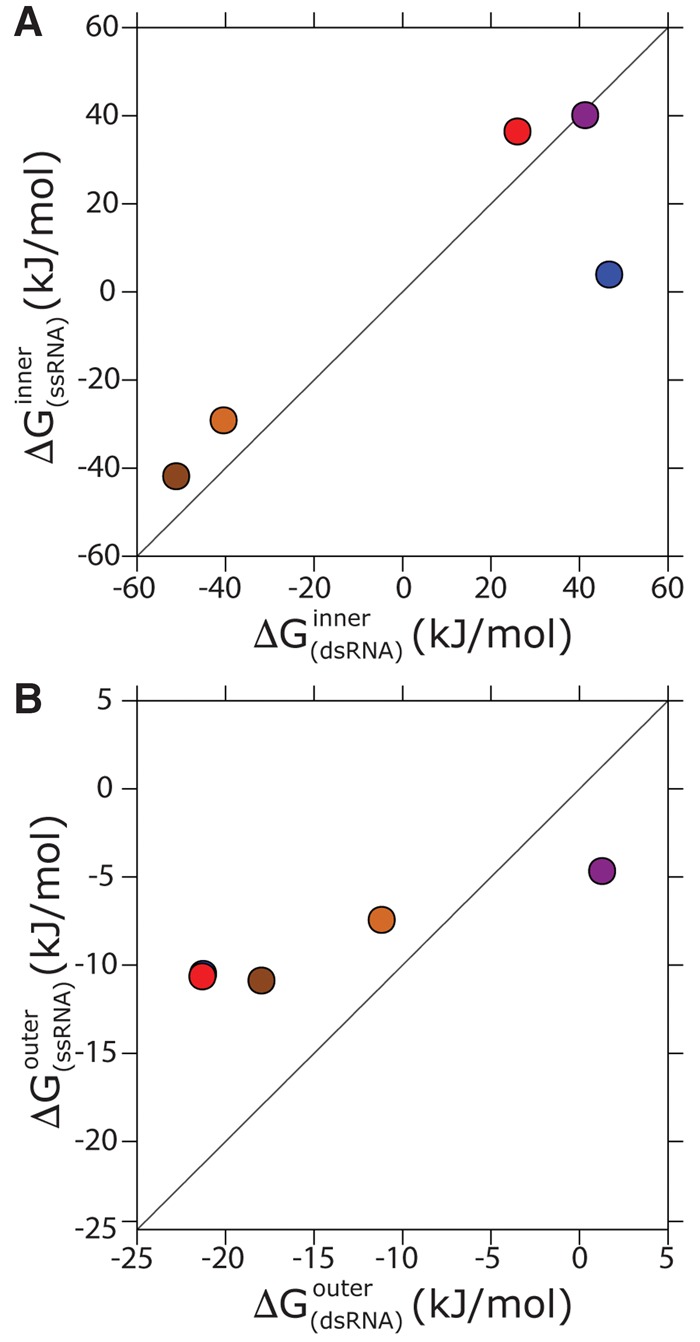
Mg²⁺ binding affinities on a dsRNA versus ssRNA. Plot A shows inner sphere binding and plot B outer sphere. The points are color coded according to Figure 1.

It is also possible to compare the affinity of Mg²⁺ ions that are directly bound with that of ions that are indirectly bound. As can be seen in Figure 3B, hybridization increases the stability of indirect binding sites as well, by ${9.7}_{-0.1}^{+{0.1}_{}}$ kJ/mol.

DISCUSSION

In this article, we present extensive molecular dynamics simulations investigating the binding affinity of Mg²⁺ on all the possible binding sites in an RNA duplex. Calculations are performed using state-of-the-art force fields and a modified version of bias-exchange metadynamics.

The enhanced sampling method we used is an improved version of the bias-exchange metadynamics (BE-MetaD) procedure designed for this application. At variance with the original approach, we here added different penalizing potentials in each replica to avoid binding events that would trap Mg²⁺ in undesired positions. This procedure was necessary here to achieve converged affinities. The idea of forbidding different events in different replicas can be straightforwardly generalized to cases where one wants to study competing rare events under the same conditions, and could provide a significant improvement in the applicability of BE-MetaD to the description of complex free-energy landscapes. To help reproducibility of our results and application of the procedure to different systems, we included sample input files in Supplemental Information 2.

Overall, our procedure provides statistically converged affinities for the modeled systems. To further check convergence, we applied the same protocol on a symmetric duplex (see Supplemental Information 11). This check would show if the reported statistical error were underestimated, since a difference in the affinity between the sides of a perfectly symmetric duplex could only arise from statistical uncertainty. Our results rely on a few methodological choices and approximations that we here discuss in detail. It is known that the current RNA force fields may not properly describe unstructured single-stranded oligonucleotides (Bergonzo et al. 2015; Condon et al. 2015; Bottaro et al. 2016). In this work, we focused the investigation on dsRNAs and on rigid ssRNA. With respect to the Mg²⁺ ion itself we assessed the chosen force field by testing the effect of an a posteriori adjustment of its interactions with RNA so as to enforce binding affinities to be in agreement with potentiometric titration experiments on nucleosides. Similarly to a recently published parametrization (Panteva et al. 2015b), this procedure did not affect the ion–water and ion–ion interactions. However, the qualitative consistency between the results with and without the corrections indicates robustness with respect to the Mg²⁺ force field choice. Another point to consider is that in our simulations we assumed a single Mg²⁺ ion binding to RNA at any time, implying an infinite Mg²⁺ dilution. To verify the effect of the neglecting extra Mg²⁺ in the buffer we performed an extra control simulation including an appropriate MgCl₂ buffer. Our results on the competition between K⁺ and Mg²⁺ suggest that it would be very difficult for multiple Mg²⁺ to bind on the same site. However, the double charge of Mg²⁺ could allow for longer range interactions, affecting the affinity of the neighboring binding sites. One in principle should thus simulate a replica corresponding to each pair of potentially cooperative binding sites. Ideally, this could be done after an initial screening where the most important binding sites have been identified. Additionally, since our simulation box only had enough ions to counterbalance the negative charge of RNA backbone, our results did not include the effect of anions. To verify the effect of the neglecting Cl⁻ in the buffer, we performed an extra control simulation including an appropriate KCl buffer. We notice that in all these simulations the number of ions rather than their chemical potential is kept constant. This limitation could be overcome using a very large simulation box and an extra potential to control ionic strength in the spirit of Perego et al. (2015). Additionally, the reported control simulations performed with a large box allow the possible artifacts related to box size to be assessed. Here the Mg²⁺ binding affinity might be affected by a larger effective cation concentration in the vicinity of the RNA (see Supplemental Information 3). However, our results show that relative binding affinities are virtually independent on this effect. Finally the reported results were obtained using a single RNA sequence in an A-form helix. Sequence and structure dependent effects will be the subjects of a further investigation.

Our results show that the overall affinity of the inner sphere (direct) bound Mg²⁺ cations on an RNA duplex is largely dominated by the interaction with phosphates. On the contrary, outer sphere (indirect) bound Mg²⁺ cations interact more strongly with the nucleobases. We observe that there is a significant preference for inner Mg²⁺ binding on the guanines with respect to cytosines. Interestingly, this is consistent in all our simulations including the ones performed with two separated single strands in the A-helix. This suggests that indirect contacts with guanine N7 might provide extra stabilization. Additionally, we see an overall preference between the three moieties of a nucleotide in the following order: phosphate > bases > sugar. The affinities on specific binding atoms follows the trend O2P > O1P > G–O6 > G–N7 > sugar hydroxyls > C–O2. This trend is not the same when considering the outer sphere contacts, where it is changed to G–N7 ≈ G–O6 ≈ O2P > O1P > sugar hydroxyls. Our procedure captures the experimental trends observed in the PDB binding frequencies both for inner and outer sphere binding. It must be noticed that the PDB survey reported in Zheng et al. (2015) considers binding with a variety of RNA motifs. However, the most common RNA motif present in the PDB is the A-helix, which is the same motif addressed by our study. Although Mg²⁺ is expected to mostly bind on specific structures and to stabilize tertiary contacts, the comparison of our study with the discussed PDB analysis indirectly confirms that the patterns of the electrostatic field in the neighborhood of a helix are representative for the general trend observed in structured RNAs. It must be also observed that the interpretation of primary X-ray data is not trivial and the assignment of many of the reported density peaks to Mg²⁺ ions have been recently challenged (Leonarski et al. 2016). However, whereas these errors could affect the interpretation of specific important structures, we expect the overall statistics to be reliable. Moreover, we notice that, although the ranking are correctly reproduced by our calculations, the reported frequencies are not proportional to $e^{\frac{-\mathrm{\Delta }{G}^i{\mathrm{Mg}}^2+}{k_{B}T}}$. It is not clear whether the frequencies from the PDB can be assumed as representative of a Boltzmann ensemble. This discrepancy could also be related to an imbalance inherent to the force field in the description of interactions of Mg²⁺ with phosphates and bases, which has also been reported in Panteva et al. (2015a,b). Ions in MD simulations are usually described by charged van der Waals spheres. Although this model has proven to be very useful, its accuracy is still debated. The main source of doubt comes from the fact that usual MD does not explicitly include polarizations effects.

Our procedure also allowed for the dissection of the effect of ion competition, RNA flexibility, and RNA hybridization to Mg²⁺ affinity. We found that, for both inner and outer sphere binding, ion competition and RNA flexibility reduce Mg²⁺ overall binding affinity while hybridization increases it.

The effect of ion competition on the inner sphere binding was independent of solute flexibility and amounted to ≈10 kJ/mol. The same was true for outer sphere binding on a rigid RNA. However, the effect for outer sphere binding on flexible RNA was significantly smaller (≈4 kJ/mol). This indicates that local rearrangements that are possible in the flexible RNA could compensate for the repulsion between the cations.

Interestingly, RNA flexibility decreased its affinity for Mg²⁺. We recall that the total affinity is dominated by the phosphates. Affinity on the nucleobases was on the other hand increased by flexibility. We argue that the flexibility of RNA might affect binding affinity in two opposite ways. First, the enthalpic contribution to the affinity could be increased by RNA flexibility when local rearrangements lead to more favorable RNA–Mg²⁺ interactions. On the other hand, binding of RNA with Mg²⁺ constrains RNA leading to a loss in its conformational entropy (Bergonzo et al. 2016). Interestingly, it has been recently suggested that multivalent cations make RNA helices more rigid (Drozdetski et al. 2016). The simulation of rigid RNA allowed us to explicitly ignore changes in the RNA conformational entropy. We observe that nucleobases are significantly constrained by Watson–Crick pairing and require a local rearrangement so as to bind Mg²⁺. Conversely, phosphates are accessible for Mg²⁺ binding even in a rigid RNA model. We hypothesize that in the case of Mg²⁺ binding on phosphates, the second effect dominates over the first effect, leading to a decreased affinity in the flexible model.

During the revision process of this article, an alternative approach was proposed to find Mg²⁺ binding sites with large affinity using a grand-canonical Monte Carlo scheme (Lemkul et al. 2016). Since the approach presented here addresses the same problem in an orthogonal direction, the two schemes might be combined so as to allow for an even more efficient simulation protocol.

We here presented a computational approach to the detailed characterization of Mg²⁺–RNA binding. To this aim, we introduced a modified version of bias-exchange metadynamics. Our results reproduce statistics observed in structural databases and allow for a dissection of the most important contribution to Mg²⁺–RNA interactions, shading a new light on the interplay between RNA flexibility and binding with divalent cations. We foresee the application of our computational approach to the characterization of Mg²⁺ binding sites on a repertoire of RNA motifs and sequences. Although there is still controversy regarding Mg²⁺ ion parameters and the accuracy of the simple models used, the trends in the binding affinities would likely be consistent. Additionally, the introduced procedure could be used as a benchmark to compare several models. More generally, our procedure could be used to trustfully quantify affinities of ions or small ligands when multiple competing binding sites have to be simultaneously assessed.

MATERIALS AND METHODS

The initial RNA structure was generated using the make-na webserver (Macke and Case 1997) as an ideal A-form helix with sequence $\begin{array}{r}\mathrm{GGGG}\\ \mathrm{CCCC}\end{array}$ (see Fig. 4). Molecular dynamics (MD) simulations of the duplex were performed using GROMACS 4.6.7. (Pronk et al. 2013) RNA was described using the AMBER-ff99 force field with parmbsc0 and χOL corrections (Cornell et al. 1995; Pérez et al. 2007; Zgarbová et al. 2011). These parameters are available at http://github.com/srnas/ff. The modeling of the monovalent ions (K⁺ and Cl⁻), was done using the parameters proposed by Cheatham and coworkers (Joung and Cheatham III 2008). For Mg²⁺ we used a parametrization developed in Allnér et al. (2012), which is also discussed further below. The duplex was solvated in a truncated dodecahedral box filled with explicit TIP3P water molecules (Jorgensen et al. 1983). Ions were added by substituting randomly selected water molecules. Bonds were constrained using the LINCS algorithm, and the integration of the equations of motion was performed with a 2-fs time step. The temperature was set to 300 K, and it was kept constant by a stochastic velocity rescale thermostat (Bussi et al. 2007). Nonbonded interactions were calculated using the Verlet cutoff scheme, and electrostatics using particle-mesh Ewald (Darden et al. 1993). The cutoff was initially set to 1 nm and is adjusted adaptively so as to balance the load of real-space and reciprocal-space contributions. Pressure was kept constant at 1 bar using the Berendsen barostat for the equilibration phase (Berendsen et al. 1984) and the Parrinello–Rahman scheme during the production runs (Parrinello and Rahman 1981). Simulations with a rigid duplex had the RNA atomic positions kept fixed, and were performed at constant volume.

FIGURE 4.

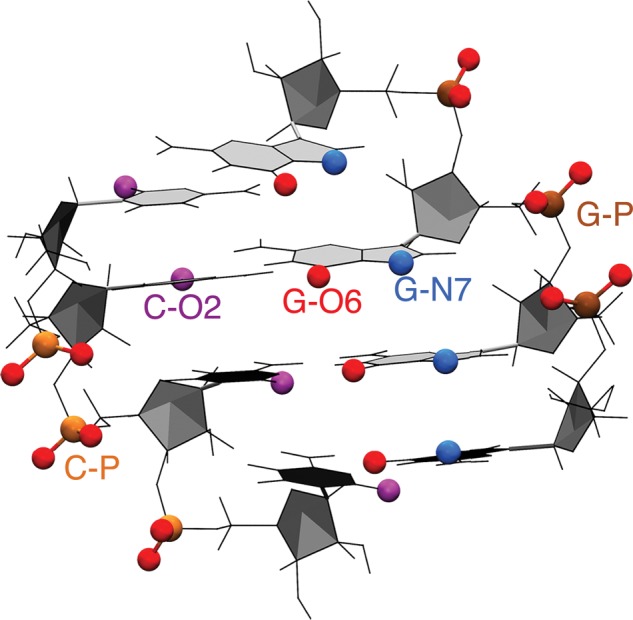
A-form RNA duplex with sequence $\begin{array}{r}\mathrm{GGGG}\\ \mathrm{CCCC}\end{array}$. Target Mg²⁺ binding sites are highlighted.

Enhanced sampling simulations were then performed combining GROMACS with PLUMED 2.2 (Tribello et al. 2014). A modified version of bias-exchange metadynamics (BE-MetaD) (Piana and Laio 2007) was used to sample all the possible sites for inner sphere Mg²⁺ binding. In each replica we applied a bias potential according to MetaD in its well-tempered formulation (Laio and Parrinello 2002; Barducci et al. 2008), acting simultaneously on two collective variables, namely coordination number with water (CN_W) and distance d_i between Mg²⁺ and i-th target binding sites, resulting in as many replicas as potential binding sites. A sample bidimensional free-energy surface profile is shown on Supplemental Information 1. In this work we identify the possible binding sites for both inner and outer sphere binding using the name of the corresponding ligand (as highlighted in Fig. 4). To this aim, we only considered binding sites with an expected affinity large enough to require enhanced sampling (phosphates, O6 and N7 in guanine, O2 in cytosine, see Fig. 4). We chose these sites based on preliminary simulations that we performed for all four RNA nucleosides and a guanine dinucleoside monophosphate and also on available experimental information (Sigel and Sigel 2010; Zheng et al. 2015). This procedure resulted in 18 replicas and a total simulation time of 9 µs (18 replicas × 0.5 µs). With the exception of a control simulation, all the MD runs contained only one Mg²⁺ ion, which is the one being biased by the MetaD. In the control simulation including multiple Mg²⁺ ions only one of them was biased. The coordination number of the remaining Mg²⁺ with water was restrained so as to avoid them directly binding to RNA. In simulations performed with a larger box to study RNA hybridization the total time was 3.6 µs (18 replicas × 0.2 µs). The number of atoms, number of water molecules, number of ions, and length for each simulation are summarized in Table 2. Additionally, penalty bias potentials were added to avoid the competition of different binding sites in the same replica. This is not usually done in BE-MetaD but was required here to avoid Mg²⁺ to be trapped in unbiased binding sites. We also tried using the conventional BE-MetaD approach, but the sampling was undermined due to the Mg²⁺ being stuck in other positions. To ensure that the RNA helical structure was maintained through the enhanced sampling simulations, restraints were added to the distance and angles of all the hydrogen bonds corresponding to the four Watson–Crick base pairs. All the replicas were run simultaneously, and the acceptance rate was calculated taking into account the bias potentials introduced by the MetaD and penalty potentials on the unbiased binding sites. All the replicas have the same temperature, and the difference between the ensembles comes from the bias introduced by the MetaD and from the penalty potentials, which are unique for each replica. The acceptance for an exchange between replica i and replica j is thus evaluated as

$$\alpha =min\left(1,e^{{\displaystyle -\frac{V_i(q_j)+V_j(q_i)-V_i(q_i)-V_j(q_j)}{k_{B}T}}}\right).$$

Here, V_i is the bias potential acting on replica i, including both the MetaD potential and the penalty bias potential, and q_i are the coordinates for the replica i. Ergodicity was thus ensured by accelerating the binding and unbinding events on all the possible binding sites with significant free-energy barriers. A sample input file for one of the model systems is provided in Supplemental Information 2.

TABLE 2.

Table containing the list of the studied systems, its components, and the total simulation time

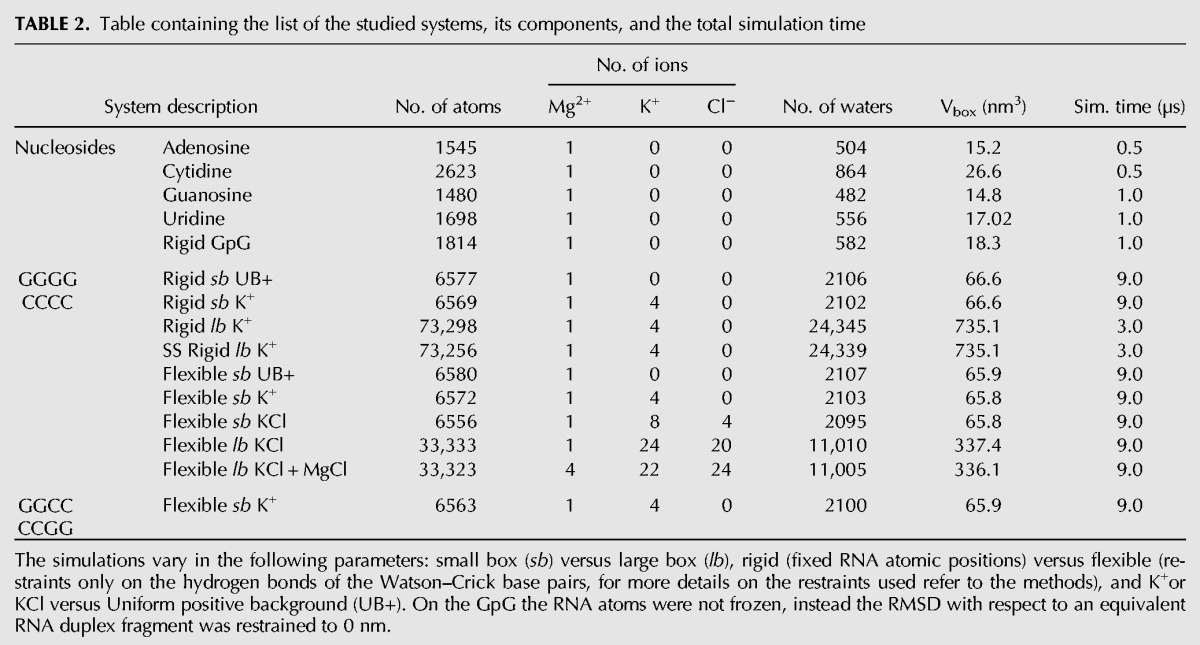
The K_a related to individual binding sites were calculated using the equilibrium distributions recovered from the BE-MetaD simulations. The simulations were reweighted using the umbrella sampling relationship (Torrie and Valleau 1977), combining the last bias from MetaD (Branduardi et al. 2012) and the penalty bias potentials added on the different replicas. Data from different replicas were combined with the weighted histogram analysis method (WHAM) (Kumar et al. 1992). This procedure is closely related to the standard way used to analyze BE-MetaD simulations (Marinelli et al. 2009) but was here performed in a binless fashion that allows a large number of restraints to be simultaneously reweighted. The binding free energy at the standard 1 M Mg²⁺ concentration was calculated accounting for the probability of the cation to be found in the bulk region (Gilson et al. 1997). The bulk region was defined as a spherical shell around the center of mass of the RNA duplex (CoM_RNA) in which the free-energy profile as a function of the Mg²⁺–CoM_RNA distance was flat (see Supplemental Information 3). The total weight w_i corresponding to the i-th binding site was obtained by accumulating the corresponding WHAM weights, and the affinities were computed as

$$K_a^i=\frac{w_i}{w_{\mathrm{shell}}}{V}_{\mathrm{shell}}.$$

Here, w_shell is the total weight accumulated in the bulk (shell) region and V_shell is its volume. Mg²⁺ binding free energies were then defined as $\mathrm{\Delta }{G}_i=-k_{B}T\log K_a^i$. Since K_a is expressed in molar units, a positive ΔG indicates that at a nominal Mg²⁺ concentration of 1 M one would expect the probability of finding a Mg²⁺ bound to be smaller than the probability of finding no Mg²⁺ bound.

The following set of simulations were designed and performed in order to evaluate the effect of the box size and of the ionic composition of the buffer: (I) a flexible duplex in a large box (≈11000 explicit water molecules) and a buffer of KCl at 0.1 M concentration; (II) a flexible duplex with the same box and a buffer with KCl and MgCl₂ at 0.1 M and 0.02 M concentration, respectively; (III) a flexible duplex with a smaller box (≈2100 explicit water molecules) and a buffer of KCl at 0.1 M concentration. In this way, by comparing the affinities and the free energy of the biased Mg²⁺ against the center of mass of the RNA duplex (see Supplemental Information 3) we could single out the effect of having extra Mg²⁺ in the bulk [(I) versus (II)] and the effects of the box size in the Mg²⁺ affinity [(I) versus (III)].

To dissect the contributions to Mg²⁺–RNA binding we performed calculations on the following systems using a box with ≈2100 explicit water molecules: (a) a flexible duplex with and without explicit K⁺; (b) a rigid duplex with and without explicit K⁺; (c) a rigid duplex and two rigid separated strands with sequences GGGG and CCCC in a larger simulation box (≈24000 explicit water molecules). In this latter case the K⁺ concentration was ≈0.01 M. When not using explicit monovalent ions, K⁺ was replaced by a uniform positive background (UB+). This combination of setups allowed for the following factors to be considered: ion competition, RNA flexibility, and RNA hybridization. All the simulations followed the same protocols described above.

It is important to consider that a proper description of the kinetic and thermodynamic behavior of Mg²⁺ cations is very difficult to achieve without explicitly taking polarization and charge transfer effects into account (Spångberg and Hermansson 2004; Petrov et al. 2011). Several models have been introduced to effectively include polarization either using standard force field terms (Allnér et al. 2012; Li et al. 2013), by means of ad hoc modified Lennard–Jones potentials (Panteva et al. 2015b), or within a Drude model (Yu et al. 2010). We here decided to opt for the parameters developed in Allnér et al. (2012) which were optimized to improve Mg²⁺ kinetic behavior in water and interaction with phosphate. We already used these parameters in previous applications to model ATP-bound Mg²⁺ and to describe the effect of Mg²⁺ on tertiary contacts in a riboswitch (Di Palma et al. 2015; Pérez-Villa et al. 2015). We notice that a proper balance in Mg²⁺–RNA interaction is not granted by available force fields (Panteva et al. 2015a). For this reason, we checked the robustness of the reported results by using a reweighting procedure. We applied a pragmatic correction, adding a posteriori a contribution to the interaction between Mg²⁺ and individual binding sites on RNA proportional to a switching function $V_{\mathrm{correction}}=\sum _i{{\lambda }_i(1+{(d_i/R_0)}^6)}^{-1}$. Here, d_i is the distance between Mg²⁺ and the i-th target binding site. R₀ is a cutoff radius that defines the directly bound state and is chosen to correspond to the barrier separating inner and outer sphere binding. λ_i are Lagrangian multipliers found with an iterative procedure so as to enforce the experimental value of the affinity on individual binding sites. Affinities calculated on nucleosides as well as λ_i and R₀ values are reported in Supplemental Information 4. The weight used to compute the affinities are then corrected by a factor

$$e{}^{-{\displaystyle \frac{V_{\mathrm{correction}}}{k_{B}T}}}.$$

This procedure follows the MaxEnt prescription (Pitera and Chodera 2012) stating that the minimal correction to a force field so as to enforce the average value of an observable should be proportional to the same observable. This procedure is expected to provide results comparable to those reported in Panteva et al. (2015b). The difference between the results with or without these corrections is discussed when appropriate.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.