Practical data handling pipeline improves performance of qPCR-based circulating miRNA measurements

Abstract

Since numerous miRNAs have been shown to be present in circulation, these so-called circulating miRNAs have emerged as potential biomarkers for disease. However, results of qPCR studies on circulating miRNA biomarkers vary greatly and many experiments cannot be reproduced. Missing data in qPCR experiments often occur due to off-target amplification, nonanalyzable qPCR curves and discordance between replicates. The low concentration of most miRNAs leads to most, but not all missing data. Therefore, failure to distinguish between missing data due to a low concentration and missing data due to randomly occurring technical errors partly explains the variation within and between otherwise similar studies. Based on qPCR kinetics, an analysis pipeline was developed to distinguish missing data due to technical errors from missing data due to a low concentration of the miRNA-equivalent cDNA in the PCR reaction. Furthermore, this pipeline incorporates a method to statistically decide whether concentrations from replicates are sufficiently concordant, which improves stability of results and avoids unnecessary data loss. By going through the pipeline's steps, the result of each measurement is categorized as “valid, invalid, or undetectable.” Together with a set of imputation rules, the pipeline leads to more robust and reproducible data as was confirmed experimentally. Using two validation approaches, in two cohorts totaling 2214 heart failure patients, we showed that this pipeline increases both the accuracy and precision of qPCR measurements. In conclusion, this statistical data handling pipeline improves the performance of qPCR studies on low-expressed targets such as circulating miRNAs.

INTRODUCTION

MiRNAs are small noncoding RNA molecules that bind to target mRNAs and thereby inhibit their translation into a protein (Bartel 2004). The presence of miRNAs in circulation makes them easily accessible and consequently they have emerged as a novel class of biomarkers for a wide range of diseases, including cardiovascular diseases (Gilad et al. 2008; Tijsen et al. 2012; Romaine et al. 2015). However, studies on circulating miRNAs show very low reproducibility. A recent review of 11 similar studies, together identifying 31 heart failure-related miRNAs, showed that only five of these miRNAs could be reproduced in more than one study and that none could be reproduced in more than two studies (Romaine et al. 2015).

MiRNA biomarker identification often starts with a high-throughput screen (e.g., microarray), after which the most promising candidates are validated by quantitative polymerase chain reaction (qPCR) measurements. Despite the fact that qPCR is a sensitive method, challenges arise when working with target quantities near the detection limit of qPCR, as is the case for many circulating miRNAs. This leads to missing data, which is handled and interpreted differently between studies, leading to differences in outcome.

To date, there is no consensus on how to handle missing data in qPCR studies in a statistically valid manner. Therefore, we propose an analysis pipeline to standardize the handling of results in low-target quantity qPCR experiments, such as in the case of circulating miRNAs, to assure statistical validity and improve reproducibility.

Occurrence of missing data in qPCR results

Quantitative PCR is a sensitive method to quantitatively assess miRNA levels (Zampetaki and Mayr 2012). The real-time monitoring of the fluorescence associated with the amplification of cDNA derived from specific miRNA species (Gibson et al. 1996) results in an amplification curve. There are various software packages to analyze the qPCR curve, resulting in a quantification cycle (C_q) or, using an estimate of the amplification efficiency value to perform the calculation, in a starting concentration (N₀) (Ruijter et al. 2013).

Before the C_q or N₀ values can be used in the statistical analysis of the experiment, their validity has to be ascertained. Firstly, a check that the correct product is amplified has to be carried out. Some monitoring chemistries allow a melting curve analysis for this purpose; otherwise gel electrophoresis is an option. When an off-target product is amplified, C_q or N₀ values have to be set to missing. Next, the quality of the amplification curves should be sufficient to allow analysis. Several methods are available to perform such a quality control (Bar et al. 2003; Ruijter et al. 2009; Sisti et al. 2010; Tichopad et al. 2010). In general, to allow analysis of amplification curves, these curves should at least consist of an exponential phase and a plateau phase. If not, the curve analysis software rules out these reactions and marks the results as missing. The absence of amplification or the absence of a plateau phase most often indicates that the template concentration was under the detection limit of the qPCR assay. However, deviating amplification curves do not just occur at low concentrations and, therefore, some require a different missing data handling. Finally, results are often set to missing when there is a large difference in C_q values between replicate reactions. Although such discordant replicates are mostly considered to be due to technical variation or pipetting errors, the Poisson effect that occurs by chance when pipetting from the cDNA stock to the reaction plate cannot be ignored.

RESULTS

Both imputation and exclusion of all missing data leads to analysis bias

Since it is known that circulating miRNAs can occur in low concentrations or might even be totally absent from circulation, a large number of missing values can be expected. Furthermore, it is known that with decreasing concentration of the target, the chance of finding a so-called nondetect increases (McCall et al. 2014). This is confirmed in our own qPCR experiments, which show that among a total of 10,008 qPCR results on 12 different miRNAs from cohort I, low concentrations (high C_q) of the measured miRNAs result in more measurements with missing values (Fig. 1).

FIGURE 1.

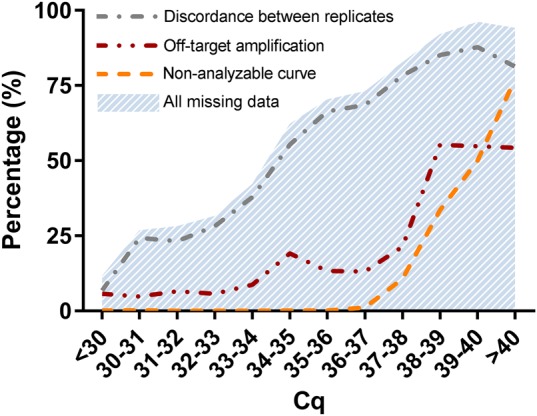
Fraction of measurements that resulted in missing data from a total of 10,008 qPCR results to measure the expression of 12 different miRNAs (from cohort I). Data are considered missing when one of the replicate reactions (i) has off-target amplification, (ii) has an amplification curve that did not pass the qPCR curve quality control (nonanalyzable curve), or (iii) when the two replicates are more than 0.5 cycles apart, which is more than can be expected from pipetting error (discordance between replicates). All categories and thus the total number of missing data increases with increasing C_q value and thus lower input concentration.

Missing data can be handled in different ways. Total exclusion of missing data leads to loss of data points and thus to loss of statistical power. The common practice is therefore to substitute a missing value with a C_q value equal to the maximum number of cycles run on the PCR machine. However, this method sets the N₀ to an impossibly low value (McCall et al. 2014). Moreover, generally, only the curves that cannot be analyzed are substituted with this low value, while also the number of reactions with off-target amplification and the number of discordant replicates increase with a decreasing input concentration (Fig. 1). As described in detail in Materials and Methods, multiple imputation can be applied to replace the missing values with estimates based on patient characteristics. These imputed values are thus estimated from the distribution of values that were high enough to be measured. However, such an imputation ignores the fact that some missing data are truly zero. Therefore, multiple imputations of all missing values will wrongly increase the average outcome. To handle missing data correctly, it should be distinguished and divided into two categories: (i) missing data that represent an “undetectable” value because the concentration of the target in the sample is either a true zero or too low to be measured quantitatively, and (ii) “invalid” values that are missing due to a technical failure and thus represent true missing values (missing at random).

Minimizing loss of data due to imprecision in replicates

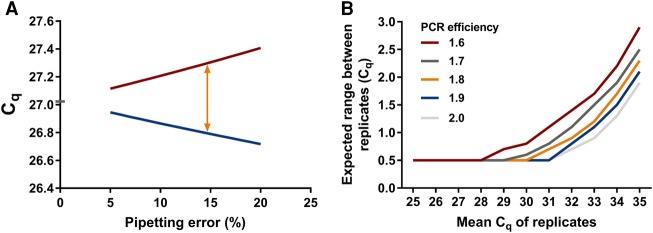
qPCR data are commonly analyzed by calculating the mean of the results of replicate reactions to reduce the effects of technical variation. Unfortunately, missing data and discordance can occur among replicates. During the experiment, only a small amount of cDNA (usually 1 µL) is pipetted from the stock to the qPCR plate. Therefore, variation can occur due to pipetting error. A rule of thumb is that when the variation between replicate C_q values is more than 0.5 cycles, the data cannot be trusted, and both replicates should be discarded (Nolan et al. 2006). As shown in Figure 2A, this 0.5 cycles difference is to be expected when there is ∼15% pipetting error and the template is present at a high concentration. However, pipetting is a random sampling action and its result will, therefore, always follow a Poisson distribution (Altman 1990). This means that at low target concentrations, the variation due to the Poisson effect becomes larger than the pipetting error and unavoidably a relatively large range of C_q values will be found, even with highly skilled operators (Fig. 2B). Consequently, when working at low concentrations, many measurements will be discarded unnecessarily, causing loss of statistical power, when the 0.5 cycles rule is strictly adhered to.

FIGURE 2.

Sources of variation in observed C_q values between replicates. (A) Relation between pipetting error and C_q range between replicate measurements. A pipetting error of 15% leads to a range of 0.5 between replicates. Red line represents the C_q of the pipetting error down and blue line represents the C_q of the pipetting error up. Orange arrow indicates where the 0.5 cycles between replicates is expected, which is at 15% pipetting error. For the calculations behind this figure, see calculation 1 in Materials and Methods. (B) The maximum acceptable C_q difference between replicates increases with increasing mean C_q of the replicates (lower copy number input in the reaction) and is dependent on the PCR efficiency. Note that in the graph, 0.5 cycles is considered to be the maximum allowable C_q range for C_q values where pipetting error is the prevalent cause of variation. For the calculations behind this figure, see calculation 2 in Materials and Methods.

Handling missing data

In conclusion, missing data can occur from off-target amplification, nonanalyzable amplification curves, and discordance between replicates. Because the majority, but not all missing data arise as a result from a low concentration of the target (Fig. 1), missing data due to low concentration must be distinguished from data missing at random. Here we propose a practical analysis pipeline to classify missing data from qPCR experiments into two categories: invalid and undetectable measurements, and to handle them accordingly to improve qPCR accuracy and precision.

Data handling pipeline

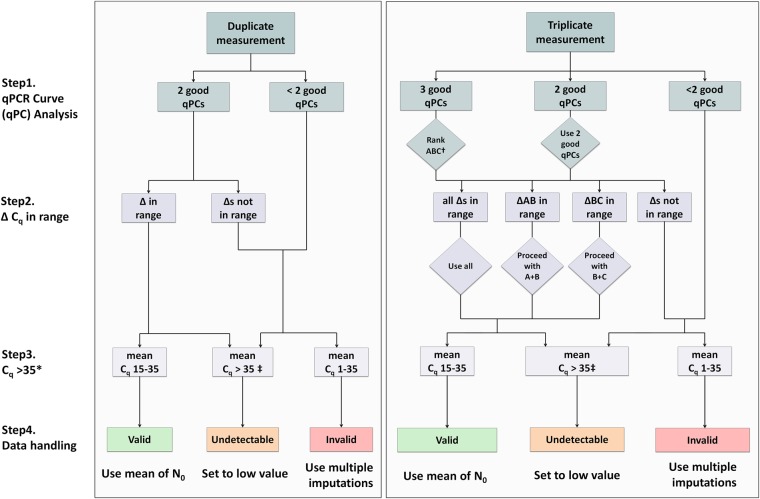
We propose a data handling pipeline that deals with the above described issues (Fig. 3). This pipeline consists of four steps to categorize the results of the qPCR analysis in valid, invalid, and undetectable and handles those categories accordingly. A documented SPSS and R syntax, for practical use of the data handling pipeline and an example of the required data format, are available for download at http://www.hfrc.nl.

FIGURE 3.

Flow diagram of the data handling pipeline for duplicate and triplicate measurements. An extensive description of the pipeline is given in the Results. Briefly, in step 1, melting and amplification curve analysis is performed by the user. In step 2, the ΔC_q of the replicates must be evaluated to check if they are in the allowed range of each other (for the maximal acceptable range between replicates, see Table 1). Then, based on a critical C_q value, in step 3, each measurement is categorized as valid, invalid, or undetectable and is handled accordingly. (*) For most PCR machines and experiments, a critical value of 35 will be optimal; however, this critical C_q may be changed by the user if inappropriate for the experiment. (†) When using triplicates and all reactions are OK, replicates A, B, and C must be ranked based from lowest to highest C_q. This step avoids discarding all replicates when two out of three are in range of each other and can therefore still be used in the analysis. (‡) A C_q of zero (no amplification) must be considered the same as having a C_q > 35. qPC = qPCR curve.

Step 1: Curve analysis

The first step in the pipeline is analysis of the reaction, consisting of confirmation of the correct product and evaluation of the amplification curve quality. Confirmation of the correct product is done by a manual melting curve analysis. Note that when hydrolysis probe assays (e.g., Taqman) are used, melting curve analysis is not required; a validated probe assay implies that only the correct amplification product results in fluorescence. In this case, one can start at step 2 (or at “rank ABC” in the case of triplicates). Amplification curve quality control can be done by hand or can be performed by a qPCR curve analysis program such as LinRegPCR (Ruijter et al. 2009). When off-target amplification occurs or when the amplification curve cannot be analyzed, the observed C_q value can never be converted into a reliable, valid N₀. However, off-target amplification can occur due to a low target concentration. Therefore, when a deviating melting peak is observed, the categorization into invalid or undetectable of the result depends on the C_q value of the associated amplification curve, and one must proceed to step 3 to handle the reaction based on the mean C_q of the replicates. When triplicate reactions are run and only one out of three shows off-target amplification, this one replicate must be discarded and one can proceed through the steps using the other two replicates.

Step 2: Handling replicate measurements

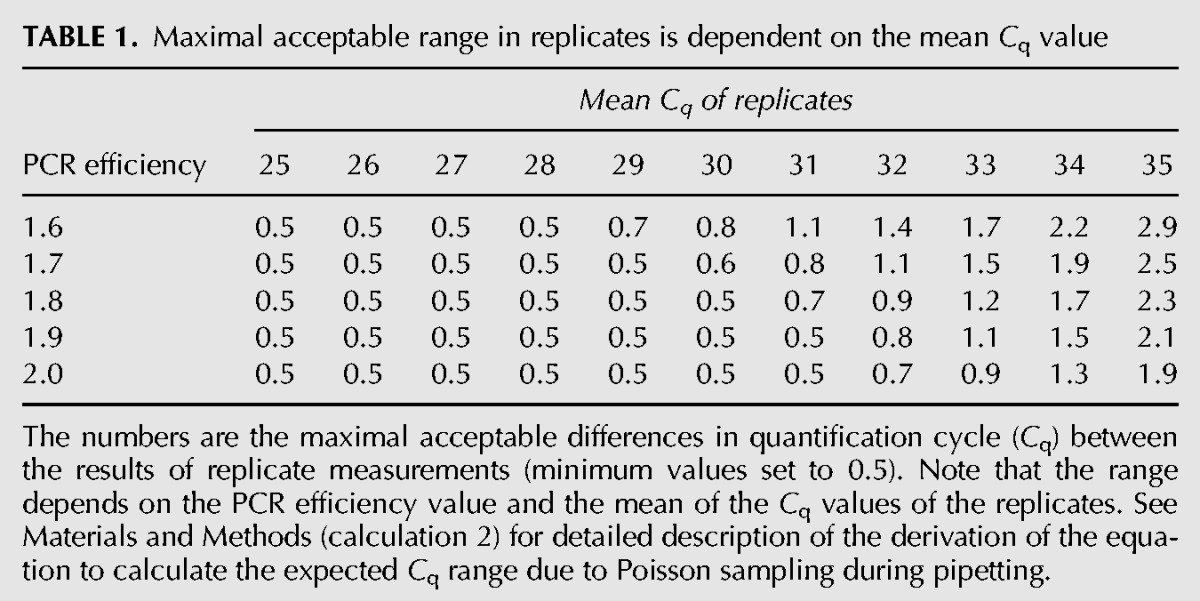
Most qPCR reactions are conducted as replicates. To avoid unnecessary loss of data points (discarding all replicates with >0.5 cycles difference), as discussed above, we used the Poisson distribution to calculate the acceptable C_q range between replicate measurements for different template numbers in the reaction. The acceptable C_q range is defined as the interval in which 95% of the C_q values are expected to be found, given a certain C_q value (Table 1; Fig. 2B; details on the calculations are described in calculation 2 in Materials and Methods). We propose that whenever the replicates are within this acceptable range, the mean of the C_q or therefrom calculated N₀ values can be used in the analysis. If the replicates are not in range, it is not possible to determine accurately which of the replicate measurements is correct and therefore there is no reliable result. In the case of triplicates, it can happen that two replicates are in range of each other and the third replicate is an outlier. Then, the former replicates are most likely the accurate ones and one can proceed using only these two replicates. Therefore, with triplicates, replicates A, B, and C must be ranked from lowest to highest C_q.

TABLE 1.

Maximal acceptable range in replicates is dependent on the mean C_q value

Step 3: Reactions with a C_q value above 35 are considered too low to be quantitatively measured (undetectable)

When the concentration of a miRNA is very low, there are two possible options, either the concentration is too low to result in detectable amplification, resulting in a missing C_q value set by the analysis program, or the concentration is just high enough to give amplification, resulting in amplification with a high C_q value. However, such high C_q values often result from amplification curves that do not reach the plateau phase, because the number of cycles is limited by the user. Therefore, above a critical C_q value, reactions should be considered to have an input that is too low to be reliably quantitatively measured. Note, however, that in a qualitative diagnostic assay, such reactions should be reported as positive because the correct product was amplified.

We propose to set the critical C_q value at 35 cycles. This is the C_q value resulting from an input of approximately 10 copies of template in the reaction (Shipley 2013). This observation comes from general experience and is supported by an easy calculation (see calculation 3 in Materials and Methods), which shows that an optimal qPCR with a primer concentration of 1 µmol/L and 10 template molecules in a reaction, reaches the end of the exponential phase after approximately 35 cycles where amplicon and primer concentrations become similar (Gevertz et al. 2005). Moreover, the Poisson effect that occurs when an average of 10 copies of template are pipetted from stock to the reaction plate leads to a coefficient of variation of ∼30%. This means that above a C_q of 35 there is too much random variation for reliable quantification. Therefore, all reactions that have a C_q value of more than 35, and those marked as “no amplification” (C_q of 0), are considered to contain an undetectable amount of template. Note that for this pipeline to work, the number of cycles that are run on the PCR machine should be high enough to reach a C_q of 35. Therefore, we propose to set the number of PCR cycles on the machine to at least 45 cycles. Although for most PCR machines and experiments a critical value of 35 will be optimal, the number of cycles that is needed to reach the quantification threshold when starting with 10 copies in the reaction can differ between experiments. There are various factors of data processing known that can influence the observed C_q value and can affect the assumed relation between an input of 10 copies and a C_q of 35. These factors are (i) preprocessing of the fluorescence data, such as curve smoothing (Spiess et al. 2015); (ii) the applied monitoring chemistries, probe types, and platforms (Ruijter et al. 2014); (iii) the method of determining the C_q value (Ruijter et al. 2013). The critical C_q of 35 may therefore have to be changed by the user.

Step 4: Handling missing data and normalization

After following the above protocol, the resulting data set consists of valid expression values, invalid values, which are missing values at random due to technical error, and undetectable values, which are missing due to low target input.

Handling invalid values: Because invalid measurements occur at low C_q values, the technical or biological replicates of these measurements are valid values in the data set. Consequently, invalid values can easily be imputed. The applied imputation method should be multiple imputation, since most of the variation in a qPCR experiment is caused by differences at the interindividuals level (Kitchen et al. 2010). The multiple imputation method renders the best estimate of that specific miRNA concentration based on all variables that underlie the observed differences in the data set (Sinharay et al. 2001). It was shown that with multiple imputation, in some cases up to 80% of the missing data can be reliably imputed (Souverein et al. 2006). This means that even when there is a large number of invalid data, their imputation will generally not alter the medical or biological conclusions of the experiment.

Handling undetectable values: Debate exists on what is the best method for substitution of undetectable values. Since the qPCR detection limit is variable between experiments and targets, we propose to look up the highest C_q for every measured miRNA. That value represents the lowest observed miRNA input that produces an analyzable result. Then, to substitute the undetectable value, the N₀ can be calculated from this C_q +1. This leaves all undetectable results for every measured miRNA with low value, adjusted for target and experiment properties.

After the imputation and substitution steps for invalid and undetectable values, respectively, the data are log-transformed, to account for the non-normal distribution, and normalized, to correct for differences in RNA extraction, RT reaction yield, and sample composition. Normalization is a prerequisite for accurate qPCR expression profiling and lack of valid normalization can have a large effect on the results (Vandesompele et al. 2002). Presently, there is no consensus on the method of normalization of miRNA qPCR results and several methods have been proposed, among which are exogenous and endogenous reference targets. Reference genes can be selected by following a workflow such as that proposed in the review of Schwarzenbach et al. (2015) or Marabita et al. (2016). Using a similar workflow, we recently identified and validated blood product specific normalization panels consisting of the most stable endogenous miRNAs and showed that these panels are preferred over other normalization methods (Kok et al. 2015). We recommend using these panels for normalization.

Validation of the proposed pipeline

Improving biomarker precision

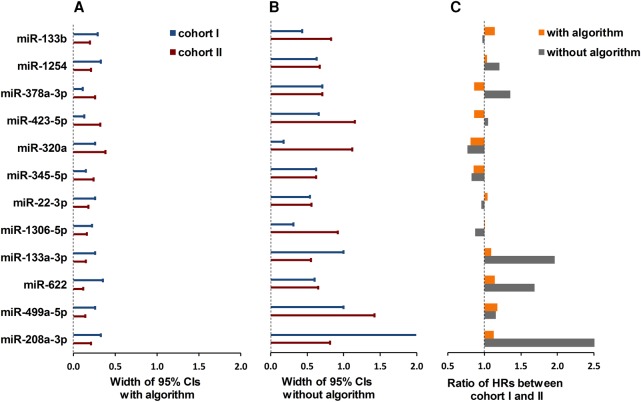
When performing two separate qPCR experiments that measure the same predictor and outcome, results are expected to be similar. However, similar results can only be obtained when the qPCR results are precise enough. To determine the effect of the proposed data handling pipeline on precision, we validated the data handling pipeline in two large cohorts (n = 834 and n = 1380, respectively) of heart failure patients. MiRNAs were measured by qPCR and analyzed with and without the proposed pipeline. In the analysis without the pipeline, all data that showed off-target amplification, nonanalyzable curves and discordance between replicates were excluded. Cox regression was used to assess the prognostic value of 12 heart failure-related miRNAs on mortality and morbidity. When using the analysis pipeline, the 95% confidence intervals around the HRs were much tighter (Fig. 4A) than without the analysis pipeline (Fig. 4B), indicating that the HRs were more reliably determined. More importantly, the ratios of the HRs between cohort I and cohort II were lower and closer to 1 when the pipeline was applied, indicating more reproducible results between cohorts (Fig. 4C). This was especially true for low-expression miRNAs such as miR-208a-3p and miR133a-3p. As mentioned in the Introduction, results from many similar studies on circulating miRNAs are reported to be highly divergent (Romaine et al. 2015). The more consistent results between two cohorts for almost all candidate miRNAs, therefore, indicate that precision is increased when using the data handling pipeline.

FIGURE 4.

Analysis of data with and without the pipeline. The graph shows the 95% confidence intervals (CIs) around the hazard ratios (HRs) of 12 miRNAs for the prediction of cardiovascular events when the data are (A) handled with and (B) without the proposed data handling pipeline in both cohort I (blue whiskers) and cohort II (red whiskers). The bars in panel C show the ratios between the HRs of both cohorts for each miRNA. Because the cohorts measure the same outcome, a ratio close to 1 is expected. Panel C shows that this is true for most miRNAs when data are analyzed with the pipeline (orange bars); analysis without the pipeline (gray bars) results in large differences between cohorts.

Improving biomarker accuracy

We conducted a second validation experiment to investigate the accuracy of the results after application of the proposed pipeline. Previous studies showed that miR-499a-5p is upregulated in plasma when the myocardium is damaged (Corsten et al. 2010). Therefore, we analyzed the relation between miR-499a-5p expression and the expression of hs-troponin T (another accepted marker of myocardial damage) in a large cohort of 834 cases of heart failure. We hypothesized that the two markers are correlated and thus we investigated the differences in miR-499a-5p expression among quartiles of hs-troponin T expression. Heart failure patients do not have acute and extensive myocardial damage and therefore their miR-499a-5p expression is low and differences in miRNA expression are subtle. These properties are both needed for an optimal test performance of the pipeline.

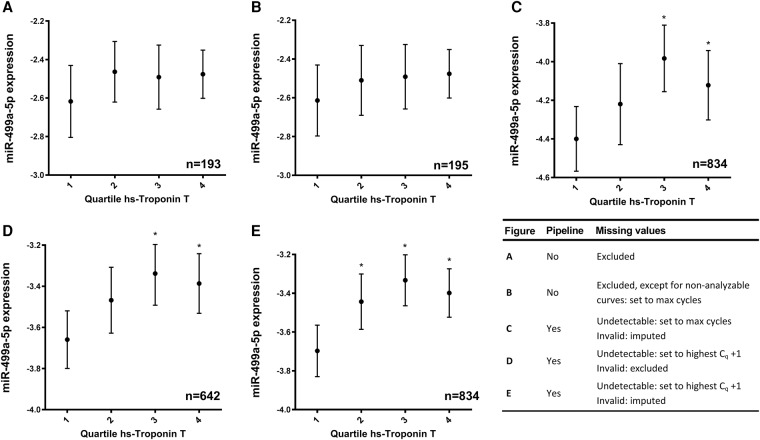
We compared five different scenarios of qPCR data handling. In analysis A (Fig. 5A), all measurements that resulted in missing values were excluded. In analysis B (Fig. 5B), missing values due to nonanalyzable curves were set to the number of cycles in the qPCR run, which may lead to unrealistically low N₀s. In analysis C (Fig. 5C), data were handled with the pipeline for categorization of missing data, and then invalid data were replaced by multiple imputation, but the undetectable values were set to the number of cycles in the run. Further effects of multiple imputation were tested in analysis D (Fig. 5D), in which invalid results were excluded from the analysis and undetectable results were set to one cycle above the maximum reliable C_q found for the miRNA. In analysis E (Fig. 5E), the complete missing data handling pipeline was implemented.

FIGURE 5.

Relation between miR-499a-5p expression and quartiles of hs-troponin T expression. MiR-499a-5p expression is given as normalized and log-transformed arbitrary fluorescence units. Results are given as mean (dots) with 95% CI around the mean (whiskers). Panels A and B show the use of a standard method for data analysis in which all missing values are excluded (A) or discordant duplicates and bad melting curves are excluded but nonanalyzable curves are set to the number of cycles in the qPCR run (B). Consequently, only a small fraction of the data can be used for analysis (n = 193 and n = 195 in analyses A and B, respectively). Panels C, D, and E show the analysis using the data handling pipeline described in this article. In panel C the undetectable category is set to the number of cycles in the qPCR run and the invalid category is imputed using multiple imputation (n = 834); in panel D the undetectable category is set to the highest reliable C_q +1 and the invalid category is excluded (n = 642); and in panel E the undetectable category is set to the highest reliable C_q +1 and the invalid category is imputed using multiple imputation (completely according to the proposed pipeline; n = 834). (*) P < 0.05 compared with the first quartile.

We found higher levels of miR-499a-5p with increasing hs-troponin T in all the analyses; however, both analyses without the pipeline (Fig. 5A,B) resulted in considerable loss of data and, therefore, no significant differences between miRNA-499a-5p levels between hs-troponin T quartiles were observed. Analysis of variance and F-tests (Supplemental Table 1), however, showed smaller variances in analyses A and B compared with the analysis with the pipeline. This is due to the selective exclusion of all reactions that resulted in low values; although seemingly more precise, these results are highly inaccurate.

Using the pipeline, 77% (n = 641) of the data discarded in analyses A and B could be “saved” and included in the analysis that resulted in more narrow 95% confidence intervals. However, setting undetectable results to the number of cycles in the run (Fig. 5C) showed significantly higher variances in all quartiles (Supplemental Table 1). Thus, substitution of undetectable values with impossibly low N₀’s leads to imprecise results. Both analysis D and the complete pipeline, analysis E, resulted in similar variances (Supplemental Table 1). However, due to the exclusion of invalid values, instead of imputation, analysis D (Fig. 5D) lacked statistical power, which increased the 95% confidence intervals and, therefore, the significant difference between the first and the second quartile was lost. Only the complete pipeline (Fig. 5E) showed a significant difference in miR-499a-5p expression between the first and all other quartiles, hereby showing the best accuracy in detecting myocardial damage.

DISCUSSION

We propose a pipeline to handle missing values resulting from qPCR-based measurements of circulating miRNAs, based on data that can be obtained by all available qPCR platforms and technologies. Missing values can be the result of technical errors, but are most often due to template levels that are too low to measure reliably with qPCR. Exclusion as well as wrong imputation methods of these missing values can lead to false analysis results. We show that missing values due to low concentrations can be distinguished from missing data due to technical errors by setting a critical value at a C_q of 35 and considering higher C_q values as true undetectable values. Furthermore, we show that with lower template concentrations, large differences between replicate measurements can be expected to occur. Therefore, these larger differences between replicates should be accepted in the analysis. Using these statistical rules, we propose a protocol on how qPCR data should be handled and we demonstrate that this pipeline indeed increases precision as well as accuracy in qPCR measurements of circulating miRNAs.

This data handling pipeline is important for reliable measurements on miRNAs by qPCR. Firstly, the pipeline prevents misclassification of undetectable values and values missing at random, thus avoiding the introduction of bias due to inappropriate substitution or imputation. Subsequently, since many circulating miRNAs have a very low concentration, the large measurement error due to random sampling is taken into account to avoid unnecessary discarding of data. At the same time the pipeline makes sure that only accurate data are used. Furthermore, our proposed method to handle the difference between the replicates based on their mean C_q and the associated expected C_q range, retains the maximum number of valid data while preserving quantitative accuracy. Thereby, we managed to save 77% of the data that would have been excluded without the analysis pipeline.

Although a multitude of publications describe how to perform qPCR experiments (Zhao and Fernald 2005; Nolan et al. 2006; VanGuilder et al. 2008; Zampetaki and Mayr 2012), this is the first article that proposes a standardized protocol on how to handle so-called missing data in the analysis of qPCR measurements. This is of importance, since the way these data are handled is diverse between researchers and largely determines the data used in, and therefore the outcome of, the statistical analysis of experiments. Nonetheless, the data processing is rarely described in articles, and this omission may explain part of the irreproducibility of results in miRNA and other qPCR studies. Our results show that the proposed pipeline can contribute to more reliable and more reproducible results.

In this study, we only addressed miRNA data. However, since this protocol is based on the qPCR kinetics that apply to DNA as well as cDNA, reverse transcribed from mRNA, it is highly likely that this protocol will benefit all types of qPCR measurements, especially those with low expression levels.

Conclusions

We show that a pipeline for handling missing data in qPCR experiments contributes to more reliable and reproducible qPCR results when measuring circulating miRNAs. We propose to use this data handling protocol as a standard for qPCR experiments in general.

MATERIALS AND METHODS

Definitions

Off-target amplification is defined as amplification that, in the melting curve analysis, shows a melting peak at a different melting temperature than the positive control or a melting curve that shows multiple melting peaks. A nonanalyzable amplification curve is defined as an amplification curve that does not meet the quality criteria of the qPCR curve software. In this study, the curve analysis program LinRegPCR was used (Ruijter et al. 2009). The target is defined as the specific product to be measured, in this article the cDNA copy of the miRNAs including the ligated primer.

In this article, a measurement is defined as the act of measuring the concentration of the miRNA in a sample using qPCR. This measurement results in a C_q value. When the melting curve and amplification curve are correct, the C_q value determined from the amplification curve can be used to calculate the starting concentration (N₀), which is thus defined as the result of the qPCR measurement.

A sample is defined as the total of RNA extracted from the blood that was drawn from the patient or control subject and reverse transcribed into cDNA. From this cDNA, a small amount (usually 1 µL) is transferred to the qPCR plate to be amplified. In this manuscript, the cDNA equivalent to the initial amount of (mi)RNA in one well of one plate is referred to as a “reaction.”

Cohorts for validation of the proposed pipeline

In this article, we used two large independent cohorts on circulating miRNAs to illustrate common pitfalls during qPCR data handling and to validate the proposed pipeline. In brief, cohort I consecutively included 834 ambulatory patients treated for heart failure (HF) in an outpatient setting between August 2006 and June 2011. Cohort II prospectively enrolled 1750 HF patients between 2007 and 2015. From the latter cohort, the first 1380 patients were used for miRNA measurement and analysis.

In the first validation, the data from both cohorts were used with and without application of the proposed pipeline to illustrate the effect of this pipeline on the precision of the hazard ratios determined for a set of candidate miRNA markers. To this end, we assessed the prognostic value of 12 miRNAs on heart failure related mortality and morbidity. In the second validation, data of cohort I were used to determine the effect of data handling on the relation between quartiles of hs-troponin T and miR-499a-5p expression.

qPCR measurements

Blood collection and processing

In both cohort I and II, whole-blood samples were collected by venipuncture in EDTA tubes and were centrifuged. Plasma was separated, then aliquoted and frozen within 1 h of collection. Samples were stored at −70°C. Samples were stored between 2006 and 2011 (cohort I) and between 2007 and 2015 (cohort II) and were thawed for further analysis in 2014–2015.

RNA isolation

In cohort I, RNA was isolated from 500 µL plasma using the mirVana kit (Thermofisher Scientific) according to the manufacturer's instructions. The RNA pellet was collected in 100 µL RNAse free water. In cohort II, RNA was extracted from 200 µL plasma using 750 µL TRIzol LS reagent (Invitrogen Corp.) and was incubated for 10 min at room temperature followed by 200 µL chloroform. The mixture was centrifuged at 12,000g for 10 min, and the aqueous layer was transferred to a new tube. RNA was precipitated by isopropanol and washed with 75% ETOH subsequently. The RNA pellet was collected in 50 µL RNAse free water. Nucleic acid quantification could not be performed due to the low concentration of RNA in plasma. DNAse and RNAse treatment was omitted since previous experiments showed no difference of miRNA expression in plasma with and without these treatments.

Reverse transcriptase of miRNAs

In both cohorts, complementary DNA was obtained from high abundant miRNAs (miR-1254, -378a-3p, -423-5p, -320a, -345-5p, -22-3p, -486-5p) using the miScript reverse transcription kit (Qiagen) according to the manufacturer's instruction. More specifically, the RT reaction consisting of 7.5 μL RNA from the isolation, 0.5 µL miscript RT, and 2 µL of 5× RT Buffer was incubated at 37°C for 60 min and at 95°C for 5 min and held at 4°C for 5 min. cDNA was diluted in a 1:8 (cohort I) or 1:5 (cohort II) ratio using nuclease free water.

For less abundant miRNAs (miR-133a-3p, -133b, -208a-3p, -499a-5p, -622, -1306-5p), qScript microRNA cDNA Synthesis Kit (Quanta BioSciences) was used, according to the manufacturer's protocol. Specifically, first, a poly(A) tailing reaction was performed using 3 µL of RNA, 2 µL of poly(A) tailing Buffer (5×), 4 µL of nuclease-free water, and 1 µL Poly(A) polymerase. This was incubated for 60 min at 37°C followed by 5 min on 70°C. Subsequently, 10 µL of this poly(A) tailing reaction, 9 µL of miRNA cDNA reaction mix and 1 µL of qscript RT were incubated for 20 min at 42°C followed by 5 min at 85°C. cDNA was diluted in a 1:8 (cohort I) or 1:5 (cohort II) ratio using nuclease free water. Both a nontemplate control and a no-RT control were included in the measurement to assure that products were not the result of genomic DNA or RNA.

Quantification and analysis of miRNA expression by RT-qPCR

Expression levels of each miRNA were quantified by RT-qPCR using Sybr Green (Roche) and miRNA primers (Eurofins; primer sequences are shown in Supplemental Table 2) in a total volume of 10 µL according to the manufacturer's instruction. This mix contained 5 µL of SybrGreen dye, both 0.5 µL of forward primer and 0.5 µL of reverse primer from a 10 pmol/µL stock, 2 µL of RNase-free water, and 2 µL of template cDNA. RT-qPCR reactions were run in duplicates on the Light cycler 480 (Roche). The reaction mixture was preincubated at 5°C for 10 sec, followed by 45 cycles of 95°C for 10 sec, 58°C or 55°C for 20 sec (dependent on the primer character) and 72°C for 30 sec. Melting curve analysis was done by hand and melting curves were marked as bad when the melting curve deviated from the positive control or showed multiple peaks. Raw fluorescence data were analyzed using LinRegPCR quantitative qPCR data analysis software version 2014.6 (Ruijter et al. 2009). PCR efficiencies were between 1.67 and 2.09 for all miRNAs. Data were normalized to miR-486-5p and log10-transformed before statistical analysis.

Hs-troponin T measurement

Hs-troponin T levels were measured (via electrochemiluminescence immunoassay using an hs-cTnT assay and the Modular Analytics E 170 system [Roche]). The hs-cTnT assay had an analytic range of 3–10,000 ng/L. At the 99th percentile value of 13 ng/L, the coefficient of variation was 9%. The analytic performance of this assay has been validated and complies with the recommendations of the ESC-ACCFAHA-WHF Global Task Force for use in the diagnosis of myocardial necrosis (Bassand et al. 2007). Assays were run with reagents from lot 157123, which was unaffected by the analytical issues that emerged with Roche hs-cTnT assays.

Multiple imputation

Invalid data were imputed using multiple imputation. Multiple imputation is a frequently used technique in clinical research to estimate the missing values based on all available patient characteristics. This method consists of three steps: (i) imputation, (ii) analysis, and (iii) pooling. In the imputation step, values of the missing data are estimated by random sampling from the distribution of the nonmissing, observed data and adjusted to the characteristics of the sample (e.g., when imputing a missing value of the weight of a patient, taking in account the gender and length of the patient will produce a more accurate estimate). To correct for uncertainty about the imputed value, the imputation step is repeated to create five or more different imputed data sets. In the next step, the statistical analysis is performed on each imputed data set separately, and in the final step, all analysis results are pooled to create a final result. Multiple imputation is incorporated in the most widely used statistical analysis software programs such as SPSS for Windows. The exact formulas describing this method can be found in the original work of Rubin (1987).

Statistical analysis

ANOVA with post hoc Student's t-tests were used to calculate differences in miR-499a-5p expression in quartiles of hs-troponin T. F-tests were used to test differences in variance between the different ways of data handling in the validation experiment. Variables with a skewed distribution, e.g., the miRNA expression levels, were log-transformed before they were analyzed. Statistical analyses were performed using SPSS for Windows Version 23. A P-value <0.05 was considered statistically significant.

Calculations

Calculation 1. A difference of 0.5 cycles between replicates is expected with 15% pipetting error

The basic equation for PCR kinetics (Ruijter et al. 2009) can be rewritten to calculate the C_q, the number of cycles needed to reach the threshold,

$$C_{\mathrm{q}}=\frac{\log N_{\mathrm{q}}-\log N_0}{\log E},$$ (1)

from the starting concentration (N₀), the quantification threshold (N_q), and the PCR efficiency (E), defined as the fold increase per cycle. Assuming that N₀ follows a normal distribution, the effect of a pipetting error (P), randomly up or down, on the starting concentration N_0(P) is

$$N_{0(P)}=(1\pm P)\times N_0.$$ (2)

When combining Equation 1 and Equation 2, the C_q that corresponds to a certain pipetting error can be calculated as

$$\begin{array}{rl}{C}_{\mathrm{q}(\mathrm{up},\mathrm{down})}& =\frac{\log N_q-\log \{(1\pm P)\times N_0\}}{\log E}\\ & =\frac{log{N}_q-\log (1\pm P)+log{N}_0}{\log E}.\end{array}$$ (3)

The C_q range for a certain pipetting error P is then given by

$$C_{\mathrm{q}}\text{range}=\frac{\log (1+P)}{\log E}-\frac{\log (1-P)}{\log E}.$$ (4)

Note that this range is dependent on the PCR efficiency but independent of N_q and N₀. Using Equation 4, with mean PCR efficiency of 1.9, a C_q range of 0.5 is reached with 15% pipetting error (Fig. 2A).

Calculation 2: Expected C_q range between replicates

It is commonly accepted that with an input of 10 template copies in the reaction and a PCR efficiency between 1.8 and 2, a C_q value of approximately 35 will be observed (Shipley 2013, see also calculations 3).

By definition, the relation between the number of template copies in a reaction and the observed C_q value is given by the basic equation for PCR kinetics:

$$N_q=N\times E^{C_q},$$ (5)

with the quantification threshold (N_q) and a given PCR efficiency (E). However, according to the above rule of thumb, for 10 copies of template Equation 5 can be written as

$$N_q=10\times E^{(35)}.$$ (6)

Combining those equations shows that for an observed C_q value the number of template copies (N) pipetted into the PCR reaction can be approximated with

$$N=10\times E^{(35-C_q)}.$$ (7)

At low concentrations (N), the actual input in the PCR reaction is strongly subject to a Poisson sampling error during pipetting. Using the relationship between Poisson and χ² distributions (Johnson et al. 1993), the 95% confidence interval of N is given by

$$\frac{1}{2}{\chi }_{(0.025;2N)}^2\le N\le \frac{1}{2}{\chi }_{(0.975;2N+2)}^2.$$ (8)

The upper and lower limits of this interval in actual number of copies in the reaction will be observed as the lower and upper limits of the range of C_q values. As shown in calculation 1, the basic equation for PCR kinetics can be converted into an equation to calculate the C_q value from N_q, E, and N₀ (calculations 1, Equation 1). This equation can be extended into an equation for the difference in C_q values (delta C_q) for 2 inputs (N_up and N_low).

$$\mathrm{delta}{C}_q=\frac{\log (N_{\mathrm{up}})-\log (N_{\mathrm{low}})}{\log E}.$$ (9)

With N_up and N_low as the upper and lower limit from Equation 8, the delta C_q in Equation 9 then gives the width of the 95% range of the expected C_q values for a combination of average input copy number and PCR efficiency. Given the effect of Poisson error on sampling, this range of C_q values should be considered as unavoidable and thus acceptable. Table 1 and Figure 2B show this expected range of C_q values for PCR efficiency values from 1.6 to 2.

Calculation 3. Amplification of 10 copies results in a C_q of 35

When 1 µL of a primer solution with a concentration of 1 µM is pipetted into the reaction this is equivalent to an amount of 1 pmol primers in the reaction. Based on the Avogadro constant, this equals a number of 6.022E+11 copies of primers in the reaction. Using the basic equation for PCR kinetics (calculations 1, Equation 1), we can calculate the number of amplicon copies in the sample after a given number of cycles. When the reaction starts with 10 copies and the PCR efficiency (E) is 1.9, the number of amplicon copies and the number of remaining primer molecules become similar after 38 cycles. When this happens, the competition between amplicon and primers during the annealing step of the PCR will decrease the PCR efficiency and the reaction will enter the plateau phase. Competition will already start when the amplicon number reaches one-tenth of the primer concentration, about three cycles earlier (Gevertz et al. 2005). Therefore, this calculation also shows that for a reaction that starts with 10 copies of template, the exponential phase of the PCR will end at approximately 35 cycles. For other primer concentrations and PCR efficiency values, this calculation gives different but similar results.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.