Statistical significance of seasonal warming/cooling trends

Significance

The question whether a seasonal climatic trend (e.g., the increase of spring temperatures in Antarctica in the last decades) is of anthropogenic or natural origin is of great importance because seasonal climatic trends may considerably affect ecological systems, agricultural yields, and human societies. Previous studies assumed that the seasonal records can be treated as independent and are characterized by short-term memory only. Here we show that both assumptions, which may lead to a considerable overestimation of the trend significance, do not apply to temperature data. Combining Monte Carlo simulations with the Holm–Bonferroni method, we demonstrate how to obtain reliable estimates of the statistical significance of seasonal climatic trends and apply our method to representative atmospheric temperature records of Antarctica.

Abstract

The question whether a seasonal climate trend (e.g., the increase of summer temperatures in Antarctica in the last decades) is of anthropogenic or natural origin is of great importance for mitigation and adaption measures alike. The conventional significance analysis assumes that (i) the seasonal climate trends can be quantified by linear regression, (ii) the different seasonal records can be treated as independent records, and (iii) the persistence in each of these seasonal records can be characterized by short-term memory described by an autoregressive process of first order. Here we show that assumption ii is not valid, due to strong intraannual correlations by which different seasons are correlated. We also show that, even in the absence of correlations, for Gaussian white noise, the conventional analysis leads to a strong overestimation of the significance of the seasonal trends, because multiple testing has not been taken into account. In addition, when the data exhibit long-term memory (which is the case in most climate records), assumption iii leads to a further overestimation of the trend significance. Combining Monte Carlo simulations with the Holm–Bonferroni method, we demonstrate how to obtain reliable estimates of the significance of the seasonal climate trends in long-term correlated records. For an illustration, we apply our method to representative temperature records from West Antarctica, which is one of the fastest-warming places on Earth and belongs to the crucial tipping elements in the Earth system.

In the last decades, estimations of the magnitude of deterministic trends in natural records have become an important issue, due to anthropogenic global warming (1). Although the estimation of a trend by linear regression is an easy task, the estimation of its statistical significance and its error bar is complicated, because the natural persistence of the records also becomes an issue.

In the absence of persistence (white noise) as well as in short-term persistent records, the distribution of the trend follows a Student’s t distribution from which the significance $S$, its $p$ value $p=1-S$, and the error bars of the trend can be determined (see, e.g., refs. 2–4 and Methods). In many natural records like temperature data, river flows, sea level heights, wind fields, midlatitude cyclones, or Antarctic sea ice extent, the assumption of white noise or short-term memory is not valid, due to strong long-term memory in the data (5–27) (Methods).

Here we consider seasonal temperature records. A “season” can be a calendar day (without leap day), a week, a month, or combinations of months like meteorological winter, spring, summer, and autumn. Let us consider a daily mean temperature record with a length of $L$ years. When a season is defined as a certain calendar day, the corresponding seasonal record consists of the $L$ temperature data at that calendar day (e.g., January 10), in chronological order. By definition, there are 365 of these seasonal records. When a season is a certain month (e.g., March), the corresponding seasonal record consists of the $L$ March mean temperatures. Finally, when a season consists of three consecutive months (e.g., spring), the corresponding seasonal record comprises the $L$ spring mean temperatures. We are interested in the estimation of the statistical significance of seasonal climatic trends, e.g., of increasing spring temperatures at a certain location in Antarctica.

Seasonal climate trends are of great importance, because they may considerably affect ecological systems, agricultural yields, and human societies, thus creating major challenges for crop rotation management (28), river-borne transportation (29), and power generation (30), as well as for the control of pests and vector-borne diseases (31).

Results and Discussion

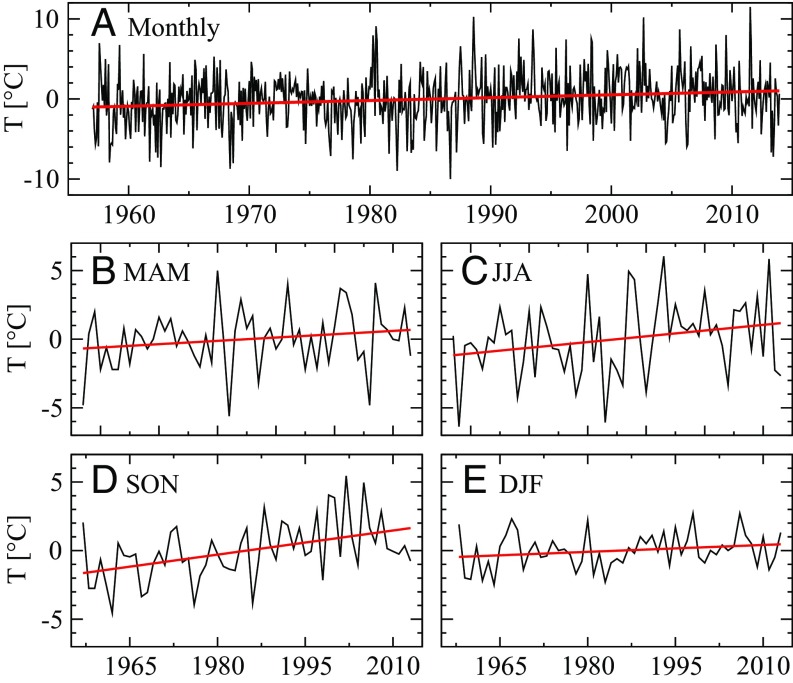
Fig. 1 shows, for illustration, the four seasonal temperature trends at Byrd station between 1957 and 2013 (32), in austral autumn, winter, spring, and summer. The data were obtained from the Byrd Polar and Climate Research Center at The Ohio State University (33). The Byrd station is located inside West Antarctica, which is one of the fastest-warming regions on Earth and belongs to the crucial tipping elements in the Earth system (34, 35). The red line in each panel of Fig. 1 shows the warming trend obtained from linear regression. For the significance analysis, the relative trend $x$ (ratio between trend magnitude and standard deviation (SD) around the trend line) is relevant. The Byrd record is known to be long-term persistent with the Hurst exponent $h=\mathrm{\hspace{0.17em}0.65}$ (23, 26) (Methods).

Fig. 1.

Temperature data at Byrd station. (A) The monthly record between 1957 and 2013. (B–E) show the mean seasonal temperatures, for austral (B) autumn (March–April–May, MAM), (C) winter (June–July–August, JJA), (D) spring (September–October–November, SON), and (E) summer (December–January–February, DJF). The straight red lines are the regression lines. The magnitudes $\mathrm{\Delta }$ of the trends and the standard deviations $\sigma$ around the trend line for MAM, JJA, SON, and DJF are (in degrees Celsius) $(1.35,2.08)$, $(2.34,2.63)$, $(3.27,1.89)$, and $(1.10,1.24)$, respectively. The corresponding relative trends $x=\mathrm{\Delta }/\sigma$ are 0.650, 0.889, 1.729, and 0.891, respectively.

The conventional procedure for evaluating the statistical significance of seasonal climate trends is based on three assumptions (see, e.g., refs. 32 and 36–40): (i) The magnitudes of the seasonal trends can be obtained by linear regression as in Fig. 1, (ii) the seasonal records are independent of each other, and (iii) the persistence in each seasonal record can be characterized by an autoregressive process of first order (AR1) between the same seasons over a year’s distance. Under these assumptions, the significance of seasonal climate trends has been obtained by applying Eqs. 4 and 5 to the underlying seasonal record.

It is obvious that assumption ii is not valid in monthly records where subsequent months are coupled such that the lag-1 autocorrelation function is different from zero; this happens, for example, when the record of interest can be described by an AR1 process or is long-term persistent. Assumption iii is not valid in long-term persistent records where events separated by large time spans are also correlated. However, as we show next, the conventional treatment cannot be applied even to white noise records where assumptions ii and iii are trivially satisfied.

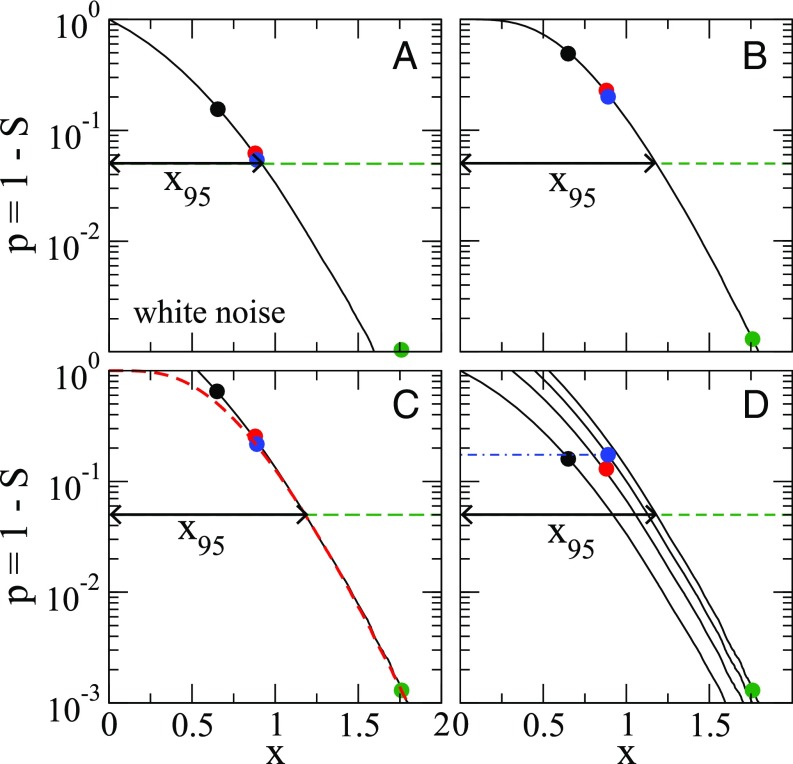
To see this point, let us assume that the Byrd record can be modeled by white noise. Under this assumption, following the conventional treatment, the dependence of the significance $S$ on the relative trend $x$ can be obtained from Eq. 4, for the same length $L=\mathrm{\hspace{0.17em}57}$ as our standard example. The result for $p=\mathrm{\hspace{0.17em}1}-S$ is shown in Fig. 2A. From the figure, one can read off the $p$ values of the four relative trends at Byrd station shown as full circles. If a $p$ value is below its significance level $\alpha =\mathrm{\hspace{0.17em}0.05}$ (shown as dashed horizontal line in the figure), we consider a trend as significant. The intersection of $p(x)$ with the dashed horizontal line yields the error bar $x_{95}$ (Methods). One can see that, under the white noise assumption, spring has a highly significant trend, with a $p$ value well below ${10}^{-3}$, whereas fall has a $p$ value of 0.16 and is clearly not significant.

Fig. 2.

The significance ($p$ value) of the relative seasonal warming trends $x$ at Byrd station. The black, red, blue, and green circles refer to austral fall (MAM), summer (DJF), winter (JJA), and spring (SON), respectively. It is assumed that the natural variability of the record can be described, to a first-order approximation, by white noise. (A) The result of the conventional approach is compared with (B) the result of Monte Carlo simulations where, for white noise records with the same length as the Byrd record, the significance of the largest seasonal relative trend (absolute value) has been determined. Also shown are the $p$ values for (C) the Bonferroni approach and (D) the Holm–Bonferroni approach. The dash-dotted horizontal line in D is the $p$ value of the warming trends in JJA, MAM, and DJF. The Bonferroni approach yields, for $p$ values below 0.3, the same result as obtained in B for the largest seasonal relative trend, shown in C as the dashed red curve. In all panels, $x_{95}$ refers to the relative trend at $S=\mathrm{\hspace{0.17em}0.95}$ ($p=\mathrm{\hspace{0.17em}0.05}$) and can be regarded as an error bar for the relative trend.

To test if the $p$ value for the largest seasonal trend has been obtained correctly, we performed Monte Carlo simulations. We generated a large number of Gaussian white noise records $\{y_i\},i=\mathrm{\hspace{0.17em}1},\mathrm{\dots },4L$, again for $L=\mathrm{\hspace{0.17em}57}$. The four seasonal subrecords are $\{y_1,y_5,\mathrm{\dots }{y}_{4L-3}\},\{y_2,y_6,\mathrm{\dots }{y}_{4L-2}\},\{y_3,y_7,\mathrm{\dots }{y}_{4L-1}\}$, and $\{y_4,y_8,\mathrm{\dots }{y}_{4L}\}$. In each record, we calculate the maximum of the absolute values of the four relative trends in the four subrecords. Then we determine the probability density function of the maximum relative trend $x$, from which we derive the $p$ value of the maximum trend by simple integration. By construction, $p(x)$ is exact for the maximum trend and provides upper bounds for the lower-ranked trends. The result is shown in Fig. 2B. One can see that the proper $p$ value of the maximum trend is exactly a factor of 4 larger than the value obtained by the conventional treatment. Again, the intersection of $p$ with $\alpha =\mathrm{\hspace{0.17em}0.05}$ yields the error bar $x_{95}$.

The reason for the considerable underestimation of the $p$ value of the maximum trend by the conventional treatment is that several significance tests (here four for the four seasons) are performed on the same record (Multiple Testing Problem). To demonstrate this, we test, in a gedankenexperiment, the statistical significance of the relative trends of the 365 calendar day subrecords, in a purely white noise surrogate temperature record, with a significance level $\alpha =\mathrm{\hspace{0.17em}0.05}$. By definition, 5% of the 365 records, i.e., 18 records, will have a $p$ value below 0.05, suggesting that there is a significant trend in these subrecords. Accordingly, the null hypothesis that there is no external trend involved in any of the 365 subrecords will be rejected for 18 calendar days.

The necessity of taking into account multiple testing in sequential datasets is well known in genetics, particularly in genome-wide association studies, where associations between genetic variants like single-nucleotide polymorphisms and traits like diseases are investigated (for details, see ref. 41). Before multiple testing correction became the standard practice, most of the early results of these association studies could not be replicated. Multiplicity is also an issue in climate science when estimating the significance of trends in a large number of stations or grid points (see, e.g., refs. 42 and 43); a challenge is the proper handling of the spatial correlations between the records (44).

There are several procedures that take multiple testings into account (Methods). Within the Bonferroni approach (45), one of $m$ seasons has a significant trend if its $p$ value is below $\alpha /m$, for any chosen threshold value $\alpha$. This rule is the equivalent of multiplying each individual $p$ value by $m$ and comparing the result with $\alpha$. This way, the $p$ values from Fig. 2A are multiplied by a factor of 4. The result is shown in Fig. 2C. The figure shows that the Bonferroni curve is nearly identical with $p(x)$ from Fig. 2B, showing that the Bonferroni method yields an accurate description of the significance of the maximum seasonal trend in the white noise case where the data exhibit no memory.

A less conservative method is the Holm–Bonferroni method (46), which yields better upper bounds for the $p$ values of the lower trends than the Bonferroni method. Within this method, first, the relative seasonal trends are ranked. By definition, rank-1 season has the largest and rank-m season has the lowest relative trend, in absolute values. Next, one compares the $p$ value $p_{[k]}$ of the rank-$k$ season with $\alpha /(m+1-k)$, which is the equivalent of multiplying $p_{[k]}$ by $m+1-k$ and comparing the result with $\alpha$. If the trend in the rank-$k^{\ast }$ season is not significant, then the trends in all higher-ranked seasons must be considered as not significant. The error bar is the same as for the Bonferroni method.

The result of this analysis is shown in Fig. 2D. By definition, the $p$ value of the strongest warming trend remains the same as in Fig. 2C, whereas the $p$ values of the other three warming trends are now comparable and slightly above ${10}^{-1}$. According to Holm (46), $p_{[3]}$ and $p_{[4]}$ cannot fall below $p_{[2]}$, so they are set equal to $p_{[2]}$.

Because our Monte Carlo method also yields upper bounds for the lower-ranked trends, the minimum value of both methods gives the better estimate. One can see that, for the second-largest trend, Holm–Bonferroni yields a smaller $p$ value ($p_{[2]}=\mathrm{\hspace{0.17em}0.17}$) than our Monte Carlo simulations ($p_{[2]}=\mathrm{\hspace{0.17em}0.21}$). Accordingly, the Holm–Bonferroni method yields the better estimate for $p_{[2]}$.

Next we study how the situation changes when the data exhibit long-term memory characterized by a Hurst exponent $h$ above 1/2 (Methods). As for the white noise case, we basically assume that a monthly temperature record characterized by a certain Hurst exponent can be modeled by long-term correlated surrogate data with the same Hurst exponent. In long-term correlated surrogate data, by construction, the Hurst exponents of the 12 monthly subrecords only vary statistically around their mean. To test, if this assumption holds also for temperature records, we have considered the historical millennium run of the Hamburg Atmosphere–Ocean Coupled Circulation Model ECHO-G (see, e.g., ref. 19). We found that, for all grid points considered, the Hurst exponents of the 12 monthly subrecords varied in the same statistical way as for the surrogate data, thus supporting our hypothesis.

For determining the statistical significance of the seasonal climate trends, we follow closely the prescription detailed above for the white noise case. First, we generate a large number of long-term correlated records with the same length $L$ and the same detrended fluctuation analysis 2 (DFA2) exponent $h$ as the record of interest, for Byrd $L=\mathrm{\hspace{0.17em}57}$ and $h=\mathrm{\hspace{0.17em}0.65}$ (23, 26, 47). For details, see refs. 48 and 49. Then we consider, in each record, the four seasons and determine (i) the absolute values of their relative trends $x_1,\mathrm{\dots }{x}_4$ as well as (ii) their maximum relative trend. From i, we obtain the probability density function of all seasonal relative trends, and, from ii, we obtain the probability density function of the maximum seasonal relative trend, as discussed above. From both functions, we derive the corresponding trend significances.

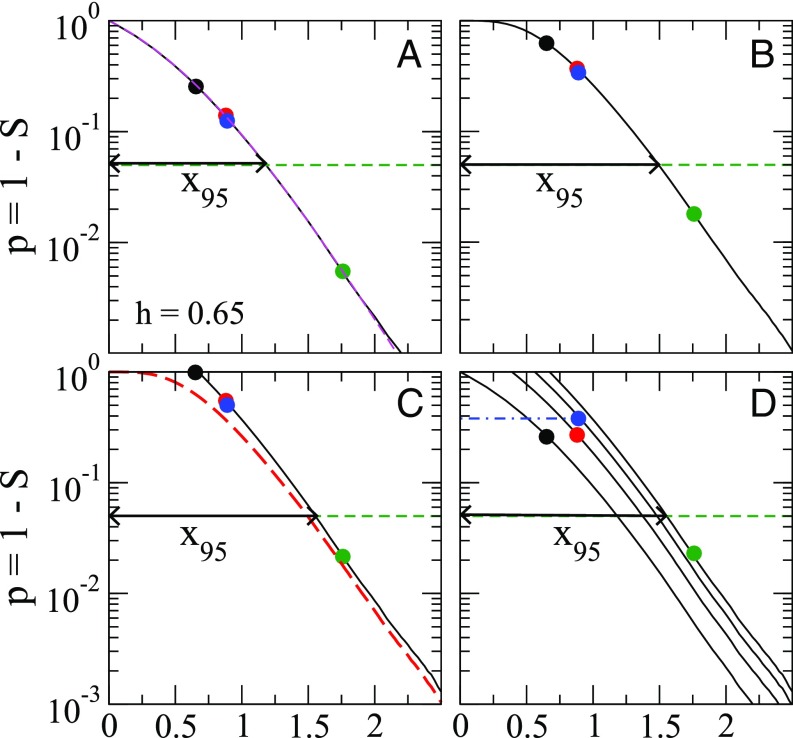
Fig. 3A shows the resulting $p$ value for case a, when multiple testing has not been taken into account. Fig. 3A is the analog of Fig. 2A for long-term persistent records. The figure shows the expected result that, due to the long-term persistence, the $p$ value is strongly enhanced compared with the white noise case, i.e., the significance of all trends is reduced. Fig. 3 B–D is fully equivalent to Fig. 2 B–D. Fig. 3B shows that the $p$ value of the maximum trend is further increased by a factor of 3.4. Fig. 3 C and D describes the application of the Bonferroni method and the Holm–Bonferroni method to the long-term persistent data. Fig. 3C shows that, due to the long-term memory, the Bonferroni method slightly exaggerates the $p$ value of the relative trends. Except for the lowest-ranked seasonal trend, the $p$ values in Fig. 3B are lower than those in Fig. 3D and thus give the better estimate.

Fig. 3.

Same as Fig. 2, but for long-term correlated records with the same length and Hurst exponent $h=\mathrm{\hspace{0.17em}0.65}$ as the Byrd record (23, 26, 47). Due to the long-term correlations, the curve in B does not agree with the Bonferroni result obtained in C.

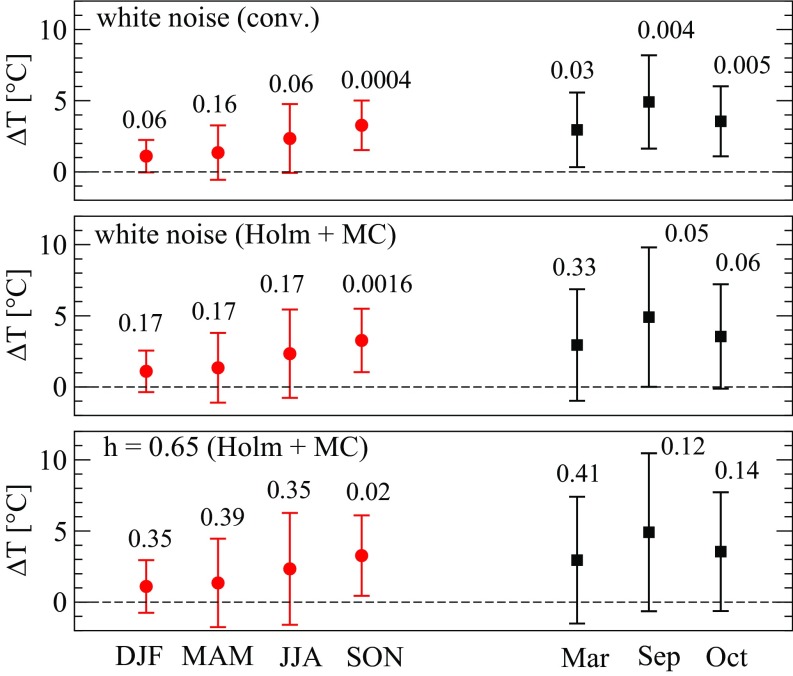
We also performed a similar analysis for the monthly warming trends at Byrd station. Fig. 4 summarizes our results for the warming trends of (i) the four seasons at Byrd station and (ii) the three months (March, September, and October) with the largest relative trend. Our final result (Fig. 4, Bottom) shows that only spring (SON) has a significant warming trend ($\mathrm{\Delta }={\mathrm{\hspace{0.17em}3.3}}^{\circ }$C) at the 98% significance level ($p=\mathrm{\hspace{0.17em}0.02}$). The other seasons have $p$ values above 0.35. Accordingly, their warming trends are far from being significant. None of the months has a significant warming trend.

Fig. 4.

Seasonal warming trends with error bars and $p$ values (on top of the error bars) for the Byrd record, for the four seasons and the 3 mo with the largest relative trends. (Top) The result of the conventional analysis under the assumption that the natural variability of the record can be considered as Gaussian white noise (Fig. 2A). (Middle) The result of our combined Monte Carlo–Holm method, again under the assumption of white noise (Fig. 2 B and D). (Bottom) The result of our combined Monte Carlo–Holm method for long-term correlated records with Hurst exponent $h=0.65$ (Fig. 3 B and D). The differences between the three treatments are most pronounced for the monthly data. In the conventional treatment under the white noise assumption, all three months have a highly significant trend, whereas, in the Monte Carlo–Holm treatment, all monthly trends are far from being significant.

In contrast, when applying the conventional procedure (where the persistence in each seasonal record has been assumed to follow an AR1 process) to the seasonal records, one finds (32) that spring warming is highly significant at the 99.9% significance level ($p=\mathrm{\hspace{0.17em}0.001}$, i.e., 50 times lower than our value), and winter warming is significant at the 95% significance level ($p=\mathrm{\hspace{0.17em}0.05}$, i.e., 7 times lower than our value). The other seasons were not significant. In addition, both September and October warming are highly significant, at the 99% and 95.2% significance level.

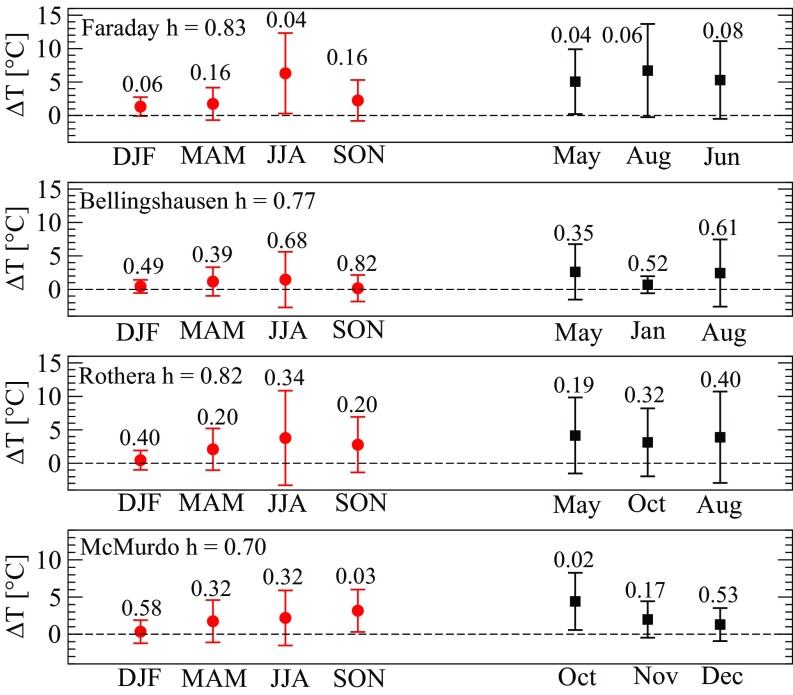
In addition to the Byrd reconstruction, we have studied the four longest observational temperature records in West Antarctica (McMurdo, Rothera, Faraday-Vernadsky, and Bellingshausen). Fig. 5 summarizes our results for the warming trends of the four seasons and the 3 mo with the largest relative trends at the four West Antarctic stations. The figure shows that, for Rothera (1978–2013) and Bellingshausen (1968–2013), the monthly and seasonal warming trends are not significant. For Faraday-Vernadsky (1951–2013), May warming ($\mathrm{\Delta }={\mathrm{\hspace{0.17em}5.1}}^{\circ }$C) and winter warming ($\mathrm{\Delta }={\mathrm{\hspace{0.17em}6.31}}^{\circ }$C) are significant, with $p=\mathrm{\hspace{0.17em}0.04}$. At McMurdo (1957–2013), where the warming trend of the whole record is not significant, with $p=\mathrm{\hspace{0.17em}0.09}$ (24), October warming ($\mathrm{\Delta }={\mathrm{\hspace{0.17em}4.4}}^{\circ }$C) and spring warming ($\mathrm{\Delta }={\mathrm{\hspace{0.17em}3.2}}^{\circ }$C) are significant, with $p=\mathrm{\hspace{0.17em}0.02}$ and 0.03, respectively.

Fig. 5.

Seasonal warming trends with error bars and $p$ values (on top of the error bars) for the West Antarctic stations Rothera (36 y), Faraday/Vernadsky (62 y), Bellingshausen (44 y) (all on the Peninsula), and McMurdo (56 y). The temperature records of Faraday/Vernadsky, Bellingshausen, Rothera, and McMurdo are long-term persistent with Hurst exponents $h=0.83,0.77,0.82$, and 0.70, respectively (24). The figure shows the result of our Monte Carlo–Holm treatment.

Finally, we also inspected the nine longest observational temperature records in East Antarctica (Halley, Syowa, Mawson, Davis, Mirny, Casey, Dumont d′Urville, Vostok, and Amundsen-Scott). It is remarkable that all monthly and seasonal warming trends were nonsignificant, with $p$ values well above 0.1. The only significant seasonal trend in East Antarctica is the cooling trend of austral fall ($\mathrm{\Delta }=-{\mathrm{\hspace{0.17em}1.61}}^{\circ }$C at Dumont d′Urville (1957–2013), where $p=\mathrm{\hspace{0.17em}0.04}$.

In conclusion, we have shown that previous estimations of seasonal temperature trends strongly overestimated the statistical significance of the trend, because two effects, (i) multiple testing and (ii) long-term persistence, have been neglected. By using Monte Carlo simulations, we have shown explicitly how both effects must be taken into account. When one aims to study the significance of a seasonal trend in a multirecord case, e.g., temperature data on many grid points, one has to consider two kinds of multiplicity, (i) the known spatial multiplicity (42–44) and (ii) the seasonal multiplicity considered here.

Our method is valid for all climate records that are characterized by linear long-term memory. As examples, we considered Antarctic temperature records. Our approach can be easily generalized to records characterized by autoregressive processes. For climate records with nonlinear correlations like precipitation and river flows, our approach can be considered as only a first-order approximation. For achieving more reliable results for these cases, one needs an accurate statistical model encompassing the proper linear and nonlinear correlations. At present, such a model is not available.

Methods

Significance of Trends: Conventional Method.

We consider the annual record $\{y_i\}$ with length $L$. From the regression line $r_i=ai+b$, we obtain the magnitude of the trend $\mathrm{\Delta }=a(L-1)$ and the fluctuations around the trend, characterized by the SD $\sigma ={[(1/L){\sum }_{i=1}^L{(y_i-r_i)}^2]}^{1/2}$. The relevant quantity we are interested in is the relative trend,

$$x=\mathrm{\Delta }/\sigma .$$ [1]

For assessing if an observed trend in a data set may be due to its natural variability or not, one needs to know the probability $S(x,L)$ that, in statistical model records with the same persistence properties as the considered data set, a relative trend between $-x$ and $+x$ occurs. $S(x)$ is called the “statistical significance of the trend $x$,” and its deviation from 1 is called $p$ value.

If $p(x)$ is below a certain significance level $\alpha$ (usually $\alpha$ is 0.05 or 0.01), one usually assumes that the considered trend cannot be fully explained by the natural variability of the record. The relation $p(x_{\alpha }\mathit{\text{;}}L)=\mathrm{\hspace{0.17em}1}-S(x_{\alpha }\mathit{\text{;}}L)=\alpha$ defines the upper and lower limits $\pm x_{\alpha }$ of the considered significance interval (also called confidence interval). By the above assumption, relative trends $x$ between $-x_{\alpha }(L)$ and $x_{\alpha }(L)$ can be regarded as natural. If $x$ is above $x_{\alpha }$, the part $x-x_{\alpha }$ cannot be explained by the natural variability of the record and thus can be regarded as minimum external relative trend,

$$x_{\mathrm{ext}}^{\min }=x-x_{\alpha }.$$ [2]

Similarly, the external relative trend cannot exceed

$$x_{\mathrm{ext}}^{\max }=x+x_{\alpha },$$ [3]

which thus represents the maximum external relative trend. According to 2 and 3, $\pm x_{\alpha }(L)$ can be regarded as error bars for an external relative trend in a record of length $L$.

For uncorrelated Gaussian data (white noise), the distribution $Q(x\mathit{\text{;}}L)$ of the relative trends $x$ follows the Student’s t distribution,

$$Q(x;L)=\frac{\mathrm{\Gamma }(\frac{l(L)+1}{2})}{\mathrm{\Gamma }(\frac{l(L)}{2})\sqrt{\pi l(L)}a}{\left(1+\frac{{(x/a)}^2}{l(L)}\right)}^{-\frac{l(L)+1}{2}},$$

with $l(L)=L-2$ and $a=(\sqrt{12}(L-1)/\sqrt{L^2+2})/\sqrt{l(L)}\cong \sqrt{12/l(L)}$ (see, e.g., ref. 2). $\mathrm{\Gamma }$ denotes the $\mathrm{\Gamma }$-function. Integration of $Q$ between $-x$ and $+x$ yields the significance $S$,

$$S(x\mathit{\text{;}}L)=2\frac{x}{a}\frac{\mathrm{\Gamma }\left(\frac{1}{2}[l(L)+1]\right)}{\sqrt{\pi l}\mathrm{\Gamma }(\frac{l(L)}{2})}\times {}_{2}F_1\left(\frac{1}{2},\frac{1}{2}[l(L)+1]\mathit{\text{;}}\frac{3}{2}\mathit{\text{;}}-\frac{{(x/a)}^2}{l(L)}\right).$$ [4]

Here ${}_{2}F_1$ is the hypergeometric function.

For short-term persistent records described by AR1, Eq. 4 remains the same, only $l(L)$ has to be substituted by

$$I(L)=L[1-C(1)]/[1+C(1)],$$ [5]

where $C(1)$ is the lag-1 autocorrelation function (see, e.g., ref. 4). In practice, one determines $C(1)$ from the detrended anomalies, after the regression line has been substracted from the annual data. We note, however, that Eq. 5 is only valid for large records where the fluctuations of $C(1)$ can be neglected. For short records, these fluctuations must be taken into account for obtaining a correct estimate of the significance (see also ref. 3). In the conventional estimations of the statistical significance of seasonal trends (see, e.g., refs. and 32, 36–40), it has been tacitly assumed that Eqs. 4 and 5 can be applied to the seasonal records.

Apart from the purely statistical approach described above, physics-based (”deterministic”) models of the coupled atmosphere–ocean dynamics (AOGCMs) have been used for the detection and quantification of ”total” natural climate variability. The simulations have been used in the sense of sanity checks for data analysis, because the amplitude of variability needs to be consistent in observations and (ensemble) model runs (50, 51). Note, however, that AOGCM calculations are cumbersome and costly, so the accomplishment of (computed) statistical significance is quite a challenge.

The Multiple Testing Problem.

Often, when analyzing a data set, several null hypotheses $H_1,H_2,\mathrm{\dots },H_m$ with the corresponding $p$ values $p_1,\mathrm{\dots },p_m$ are tested. In this multiple testing problem, the likelihood that at least one of these tests will incorrectly reject it’s null hypothesis and therefore falsely conclude the presence of a statistically significant effect is higher than the chosen significance level $\alpha$. For instance, when the significance of temperature trends in $m$ grid points (see, e.g., refs. 42 and 43) is tested, $H_n$ is the hypothesis that the trend at grid point $n$ is within natural variability, $n=\mathrm{\hspace{0.17em}1},2\mathrm{\dots },m$. When considering climatic trends in $m$ seasons as in this article, $H_n$ is the hypothesis that the trend in season $n$ is within natural variability, $n=1,2\mathrm{\dots },m$.

There are several procedures to take multiple testings into account. In the Bonferroni approach (45), the significance level $\alpha$ is divided by the number $m$ of null hypotheses that are tested. If a $p$ value is below $\alpha /m$, then the null hypothesis is rejected at level $\alpha$.

A less conservative method is the Holm–Bonferroni method (46): First, the $p$ values are ranked from lowest to highest, $p_{[1]}$, $\mathrm{\dots }$, $p_{[m]}$. The associated null hypotheses are $H_{[1]}$, $\mathrm{\dots }$, $H_{[m]}$. If a $p_{[k]}$ value is below $\alpha /(m+1-k)$, the associated null hypothesis $H_{[k]}$ is rejected at level $\alpha$. If $H_{[k^{\ast }])}$ is not rejected, then all $H_{[k]}$ with rank $k>k^{\ast }$ are also not rejected.

Long-Term Memory.

In records with long-term memory, the autocorrelation function $C(s)\cong (1-\gamma )s^{-\gamma }$ of the (detrended) anomalies decays by a power law. Because $C(s)$ shows strong finite size effects (52) (the results are only valid for $s<N/50$ where $N$ is the record length), one usually considers the DFA2 fluctuation function $F(s)$ (53) to detect the long-term memory. To obtain $F(s)$, one divides the seasonally detrended monthly record $\{y_i^{\ast }\},i=\mathrm{\hspace{0.17em}1},\mathrm{\dots },N$ into nonoverlapping windows $\mu$ of lengths $s$. Then one focuses, in each segment $\mu$, on the cumulated sum $Y_i$ of the $\{y_i^{\ast }\}$, and determines the variance $F_{\mu }^2(s)$ of the $Y_i$ around the best polynomial fit of order 2. After averaging $F_{\mu }^2(s)$ over all segments $\mu$ and taking the square root, one arrives at the desired fluctuation function $F(s)$. One can show that, in long-term persistent records,

$$F(s)\approx s^h,$$ [6]

where the exponent $h$ can be associated with the Hurst exponent and is related to the correlation exponent $\gamma$ by $h=\mathrm{\hspace{0.17em}1}-\gamma /2$. By definition, in DFA2, the influence of external linear trends on $F(s)$ is eliminated. It has also been shown that weak nonlinearities of the external trend do not influence the Hurst exponent (53). It is important to note that the finite-size effects in the DFA2 fluctuation function (the results are valid for $s<N/4$) are considerably smaller than in $C(s)$. Accordingly, DFA2 also is suited to detect long-term memory in short records (as long as $N$ is above 400).

In refs. 23, 24, 26, 47, and 54, DFA2 has been applied to the monthly Antarctic records considered here. It has been shown explicitly (23, 24) that, for each record, the fluctuation function $F(s)$ agreed with the fluctuation function of long-term correlated surrogate data with the same length and Hurst exponent $h$.

When a record is fully characterized by a certain Hurst exponent $h$, the significance $S$ of a relative trend $x$ depends only on $h$ and the record length $N$. It has been shown recently by Tamazian et al. (54) that $S(x,N)$ also follows Eq. 4, but with different parameters $a$ and $l$. These parameters depend on $h$ and $N$ and have been tabulated (for $0.5\le h\le \mathrm{\hspace{0.17em}1.5}$ and $N\ge \mathrm{\hspace{0.17em}400}$) in ref. 54. Accordingly, for given $h$ and $N$, the trend significance can be obtained straightforwardly from ref. 54, making the trend estimation as easy as for short-term persistent processes.