Frequency and potential dependence of reversible electrocatalytic hydrogen interconversion by [FeFe]-hydrogenases

Significance

Hydrogenases are among the most active of enzymes, with active sites that compare with platinum metals in regard to rates of hydrogen production and oxidation. Attached to an electrode, [FeFe]-hydrogenases behave as reversible electrocatalysts close to the equilibrium potential, with only a minimal overpotential being required to oxidize H₂ or reduce protons. Electrochemical impedance spectroscopy, which uses a small amplitude potential modulation over a wide frequency range, has been used to measure the “electrocatalytic exchange rate”—the “idle speed” at which the cycle runs back and forth at the formal potential. The results also quantify the efficacy of Fe–S clusters, at the active site or in the relay, in controlling the rates of catalytic electron flow.

Abstract

The kinetics of hydrogen oxidation and evolution by [FeFe]-hydrogenases have been investigated by electrochemical impedance spectroscopy—resolving factors that determine the exceptional activity of these enzymes, and introducing an unusual and powerful way of analyzing their catalytic electron transport properties. Attached to an electrode, hydrogenases display reversible electrocatalytic behavior close to the 2H⁺/H₂ potential, making them paradigms for efficiency: the electrocatalytic “exchange” rate (measured around zero driving force) is therefore an unusual parameter with theoretical and practical significance. Experiments were carried out on two [FeFe]-hydrogenases, CrHydA1 from the green alga Chlamydomonas reinhardtii, which contains only the active-site “H cluster,” and CpI from the fermentative anaerobe Clostridium pasteurianum, which contains four low-potential FeS clusters that serve as an electron relay in addition to the H cluster. Data analysis yields catalytic exchange rates (at the formal 2H⁺/H₂ potential, at 0 °C) of 157 electrons (78 molecules H₂) per second for CpI and 25 electrons (12 molecules H₂) per second for CrHydA1. The experiments show how the potential dependence of catalytic electron flow comprises frequency-dependent and frequency-independent terms that reflect the proficiencies of the catalytic site and the electron transfer pathway in each enzyme. The results highlight the “wire-like” behavior of the Fe–S electron relay in CpI and a low reorganization energy for electron transfer on/off the H cluster.

Despite their giant size, many redox enzymes are now established as reversible electrocatalysts through investigations by protein film electrochemistry (PFE) (1). Attached to an electrode, these enzymes catalyze rapid oxidation and reduction, with only a minimum overpotential being required to swap the current direction either side of the equilibrium potential (2–5). Of particular interest are hydrogenases, which catalyze the oxidation and production of H₂ with activities that may rival platinum (6–11) and are inspirational in the quest for future electrocatalysts as well as in artificial photosynthesis (12, 13).

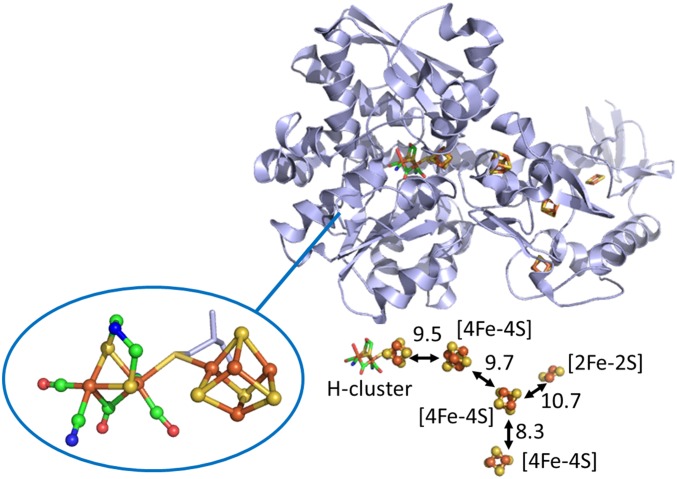
The enzymes known as [FeFe]-hydrogenases contain a unique bimetallic active site known as the H cluster (Fig. 1), which contains six Fe atoms in two domains: a 2Fe domain that is the site for H₂ activation and a [4Fe–4S] cluster domain that presumably acts as the immediate electron donor/acceptor and internal electron buffer within the H cluster (14–16). Key representatives are hydrogenase 1 from a fermentative anaerobe Clostridium pasteuranium (CpI) and hydrogenase A1 from a photosynthetic alga Chlamydomonas reinhardtii (CrHydA1). Fig. 1 shows that CpI contains an electron transfer relay consisting of three [4Fe–4S] clusters and one [2Fe–2S] cluster (17). The assumed natural redox partner of CpI is a 2[4Fe–4S] ferredoxin (18). The internal relay allows long-range electron transport (ET) between the H cluster and the protein surface, and it may be significant that it branches into two pathways that could provide improved coupling to an electrode surface. In contrast, CrHydA1 contains only the H cluster: in the living cell, it receives electrons from photosystem I via a small [2Fe–2S] ferredoxin known as PetF (19). No accessory internal Fe–S clusters are present to mediate or store electrons.

Fig. 1.

Structure of the [FeFe]-hydrogenase I (CpI) from Clostridium pasteurianum, Protein Data Bank (PDB) ID code 3C8Y. A close-up view of the active site H cluster is also shown (Lower Left) along with the [FeS]-cluster relay and intersite distances (Lower Right) measured in angstrom units.

For enzymes, PFE has focused entirely on net catalytic electron flow that is observed as direct current (DC) in voltammograms (2, 3, 10). Use of DC cyclic voltammetry as opposed to single potential sweeps alone helps to distinguish rapid, steady-state catalytic activity at different potentials from relatively slow, potential-dependent changes in activity that are revealed as hysteresis (10). However, only net electron flow is observed and little information is obtained on certain inherent factors that underline the reversible nature of the catalysis. For example, it would be significant to know how rapidly the catalytic cycle can turn back and forth at the equilibrium potential: this unusual quantity is related to the familiar exchange current for an electrode reaction that is obtained by extrapolating the exponential current–overpotential relationship (a Tafel plot) and is the catalytic resemblant of the Marcus electron self-exchange rate (at zero driving force) (20). In reality, the electrocatalytic exchange constant encompasses a combination of long-range electron transfer efficiency and inherent catalytic proficiency of the active site, and cannot be extracted directly by voltammetric methods. Additionally, to understand the “design principles” of an electron transport enzyme, it is highly relevant to measure and resolve the responses to a bias, analogous to electronic circuitry: we might thus distinguish between limitations due to time-dependent chemical steps occurring at the active site from those due to the properties of relay sites that mediate long-range ET in what is often casually referred to as “wire-like” conductivity. Such information can be obtained by electrochemical impedance spectroscopy (EIS), which uses a small-amplitude sinusoidal AC voltage to measure the impedance components at given values of the electrode potential (20–23). Impedance is generalized resistance and the opposite of conductance—the electronic term expressing the ease of electron flow. We have now used EIS to study CrHydA1 and CpI: our goals have been to determine, quantitatively, the catalytic proficiency of the H cluster in terms of electrocatalytic exchange rate, and to examine the influence of the electron relay in mediating long-range electron transfer.

Results and Discussion

Cyclic Voltammetry.

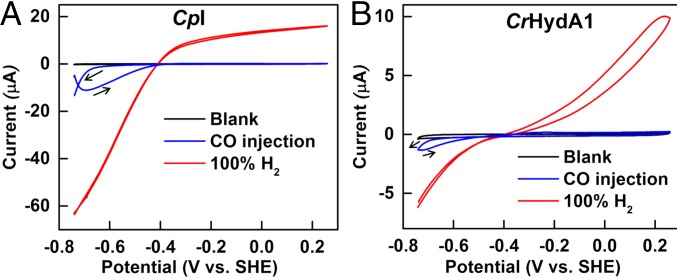
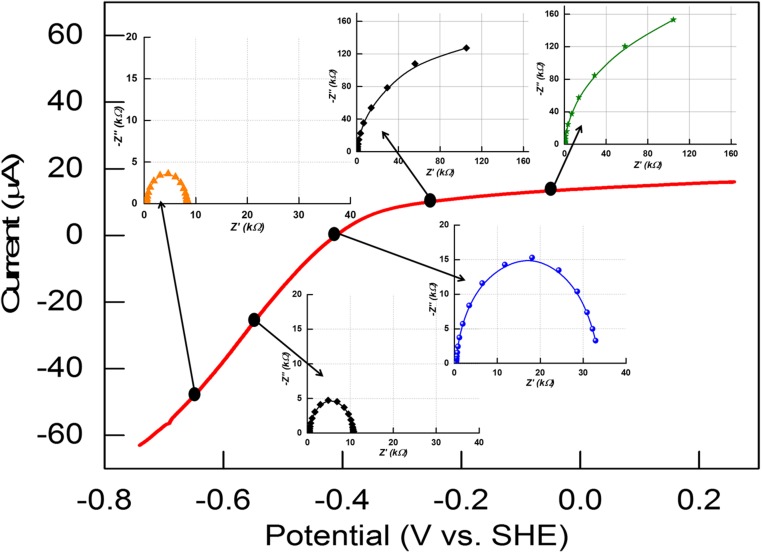
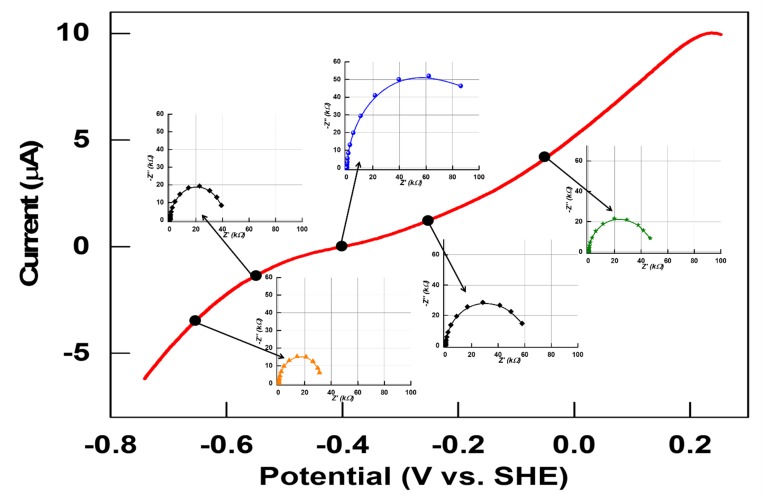
All experiments were carried out at 0 °C, with 0.10 M sodium phosphate buffer at pH 7.0, under strictly anaerobic conditions, using a rotating disk pyrolytic graphite edge (PGE) electrode at which CpI and CrHydA1 adsorb tightly on the rough surface in a highly electroactive state (2). Under 100% H₂, catalytic activity is close to optimal for each enzyme and electrode rotation at 1,000 rpm ensured that H₂ mass transport is not limiting (24). The catalytic electrochemistry of CpI and CrHydA1 is highly reproducible (Fig. 2) (24). In either case, the steady-state catalytic current (red traces) changes direction sharply either side of the equilibrium 2H⁺/H₂ potential, justifying the description of [FeFe]-hydrogenases as reversible electrocatalysts with Pt-like activity. There are notable differences: CpI appears particularly efficient at catalyzing H₂ evolution, whereas the H₂ oxidation current levels off within 0.2 V of the reversible value. Although not cutting the x axis as sharply as CpI, CrHydA1 catalyzes both H₂ production and H₂ oxidation reactions at similar rates for a given overpotential. At more positive potentials, both hydrogenases undergo conversion to an inactive oxidized form, the conversion being more rapid for CrHydA1 and evident from the hysteresis observed during H₂ oxidation; hence, we restricted EIS measurements to an upper potential limit of 0 V vs. SHE. Both hydrogenases are inhibited by carbon monoxide, which binds tightly at a potential more positive than −0.5 V but is released at a potential below −0.6 V(24, 25). This inhibition provides a benign and reversible “on/off switch” by which to identify the impedance components that are unique to electrocatalysis.

Fig. 2.

Cyclic voltammetry profiles of [FeFe]-hydrogenases, CpI (A) and CrHydA1 (B), on PGE electrodes and equilibrated with 100% H₂ flowing in the headspace (red trace): the trace shows that, depending upon the potential applied, both H₂ oxidation and H⁺ reduction are carried out by the enzyme. When CO is injected, the enzymes are unable to carry out H₂ oxidation, and H⁺ reduction begins at a more negative potential (below −0.6 V vs. SHE) where CO is released (blue trace). Conditions: pH 7.0 (0.10 M phosphate buffer); temperature, 0 °C; scan rate, 20 mV⋅s⁻¹.

Electrochemical Impedance Spectroscopy.

Nyquist spectra at equilibrium potential.

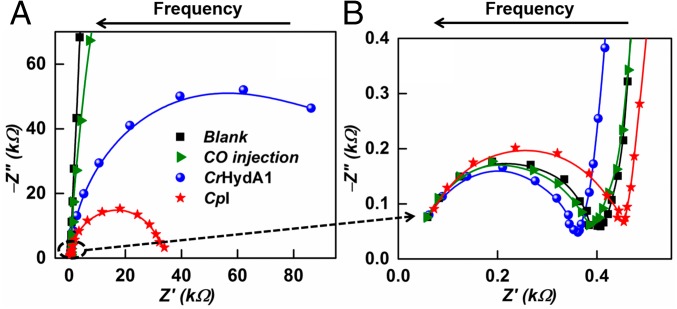
Detailed insight into the processes taking place at the enzyme-modified electrodes was provided by EIS, where the system responds to the application of a small perturbation [10 mV root-mean-square (rms)] modulation over a range of frequencies at different potentials under steady-state conditions. The modulation amplitude was chosen as the best compromise to obtain conditions closest to the equilibrium potential without adverse noise. Fig. 3A shows EIS spectra for CpI and CrHydA1 adsorbed at a PGE electrode under 1-bar H₂, recorded at the equilibrium cell potential [the potential of zero net current, which we also define as the formal potential of the reversible hydrogen electrode (RHE)] in the frequency range of 0.1 Hz to 100 kHz. At high frequency (see expanded plot in Fig. 3B), the results obtained for CpI and CrHydA1 are similar and resemble the results obtained for a blank PGE electrode and that observed when CO is introduced to inhibit electrocatalysis (shown for CpI). The Nyquist spectra for both CpI and CrHydA1 with CO inhibition almost overlay each other, and hence only data for CpI are shown. The EIS spectra show similar high-frequency arcs (Fig. 3B) that deviate in behavior at lower frequencies to give almost straight lines in the case of blank and CO-inhibited enzymes, and semicircular arcs of different radii for the two enzymes catalyzing 2H⁺/H₂ interconversion.

Fig. 3.

(A) Impedance spectra of the [FeFe]-hydrogenase systems at the equilibrium potential. (B) Enlargement focusing on the high-frequency details. Conditions: pH 7.0 (0.10 M phosphate buffer); temperature, 0 °C. The symbols are experimental data points, and the lines represent the fits obtained.

Modeling catalytic electron transport by equivalent circuit analysis.

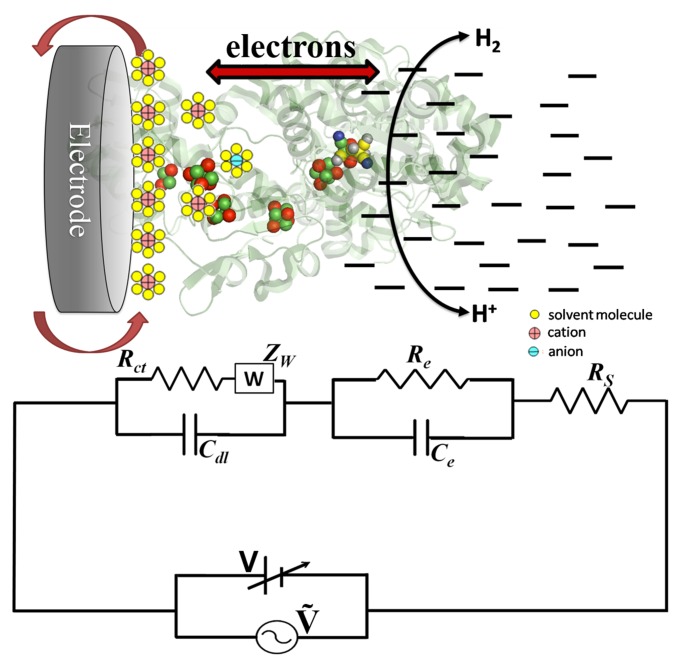
The results and discussion are based upon the scheme shown in Fig. 4, which represents the entire catalytic charge transport process at the electrode–enzyme solution region in terms of an equivalent circuit diagram. The circuit consists of three components in series; the cell resistance, the impedance due to the electrical double layer, and the impedance that describes catalytic electron flow through the enzyme, each of which is revealed in turn as the frequency is lowered. By considering all of the circuit elements, the net impedance at any point on the spectra is given as follows: Z = Z′ + jZ″, where Z′ and Z″ are the real and imaginary components of EIS (26, 27). Algebraic manipulation of Z′ + jZ″ leads to values for resistance R and capacitance C at each given frequency. Further details are given in ESI.

Fig. 4.

Equivalent circuit used to fit the Nyquist spectra obtained for hydrogenases attached to an electrode, with a schematic showing the dominance of circuit elements in the different regions of charge transfer.

The cell resistance.

The cell resistance R_s was revealed from the extrapolated intercept of the high-frequency semicircle with the Z′ axis and was the same for all experiments, which were conducted under the same conditions with the same electrochemical cell. The value is 57.5 Ω.

The electrical double layer.

The high-frequency arc and midfrequency portions of the EIS spectra are modeled by the cell elements R_ct, C_dl, and W. The R_ct and C_dl elements describe the ion transport inside the double layer formed at the electrode, whereas W corresponds to the semiinfinite diffusion of the charged particles and has the form Z_W = α /(jω)^1/2 (22, 27). The arc intercepts the Z′ axis at R_ct + R_s, and it is likely that the slightly differing values of R_ct reflect differences in the surface characteristics of the two enzymes. The fact that R_ct values vary so little provides confidence to interpret the remaining data, which relate to the specific electrocatalytic activities of each enzyme.

Catalytic electron transport through the enzyme.

The low-frequency arc that appears when catalytic activity is not inhibited by CO shows that each enzyme molecule attached to the electrode behaves as a resistor and capacitor connected in parallel (20). To understand how this relates to electron flow back and forth through an enzyme attached to the electrode, we consider what is happening at the limits of the arc. At the high-frequency limit, the impedance response is simply R_ct and is similar for both enzymes with and without CO: even with uninhibited enzyme, the frequency is sufficiently high that the enzyme is unable to contribute through catalytic turnover. The response in the low-frequency region represents the resistance R_e to electron flow. The responses at intermediate frequencies across the arc reflect the increasing and decreasing contributions from the frequency-dependent catalytic activity as electrons are now able to flow back and forth between the electrode and H₂ or H⁺_aq in solution. The frequency-independent resistance R_e quantifies the difficulty of moving electrons from the electrode to the active site and reflects such factors as distance, medium, and the influence of an FeS relay (28, 29). The frequency-dependent resistance arises from the capacitance C_e (as 1/ωC): it reflects engagement of the cyclic contribution from reversible chemical steps ranging from binding/release of H₂ to atom/ion transfer, as well as electron transfers that are tightly coupled to these steps (30, 31). Expressed another way, R_e represents the DC resistance always offered by the combined electron relay and active site, whereas C_e is analogous to a time-dependent charging and discharging of the active site (this is a Faradaic process because catalytic cycling allows electrons to flow). The variation of R_e and C_e with potential allows more in-depth interpretation of the electrocatalytic activity than is possible from voltammograms.

Quantitative values from EIS spectra at the equilibrium potential (E = 0 V vs. RHE) were extracted by fitting the experimental data (23) and are summarized in Table 1. Agreement between the theoretical fits and the experimental Nyquist spectra is within 1.3%, and R_S has been independently fitted for each set of data. Most notably, the much lower R_e value for CpI compared with that for CrHydA1 shows that electron flow through CpI is particularly facile. This result is as expected because CpI has an extensive relay system of low-potential FeS clusters to connect the H cluster with the distal [4Fe–4S] and [2Fe–2S] clusters that each lie within 8 Å of the accessible protein surface, whereas the H cluster of CrHydA1 has no internal relay. In biology, the buried H cluster in CrHydA1 must exchange electrons directly with a small protein—a ferredoxin known as PetF—in encounters that are necessarily transient but likely to be more efficient in regard to electronic coupling than achieved with an electrode. A calculated protein–protein structure suggests a distance of 11 Å between the H cluster of CrHydA1 and the [2Fe–2S] cluster of PetF (32). Negligible differences between the blank and CO-inhibited enzymes, in the values of all of the elements, reflect the fact that the inhibitor CO acts as an excellent “off” switch in both cases (24): notably, noncatalytic electron transfers to and within the enzyme barely register in the EIS experiments.

Table 1.

Parameters obtained by fitting the experimental Nyquist spectra for the enzymes on PGE electrode (at equilibrium potentials) to yield equivalent circuits by MATLAB software

Condition	RS, Ω	Rct, Ω	Cdl, μF	Re, kΩ	Ce, μF
Blank	57.5	350.2	0.031	—	—
CO inhibition	57.5	350.1	0.031	—	—
CpI (H2)	57.5	410.7	0.022	28.6	14.8
CrHydA1 (H2)	57.5	338.3	0.038	119.8	10.8

Determination of exchange current density.

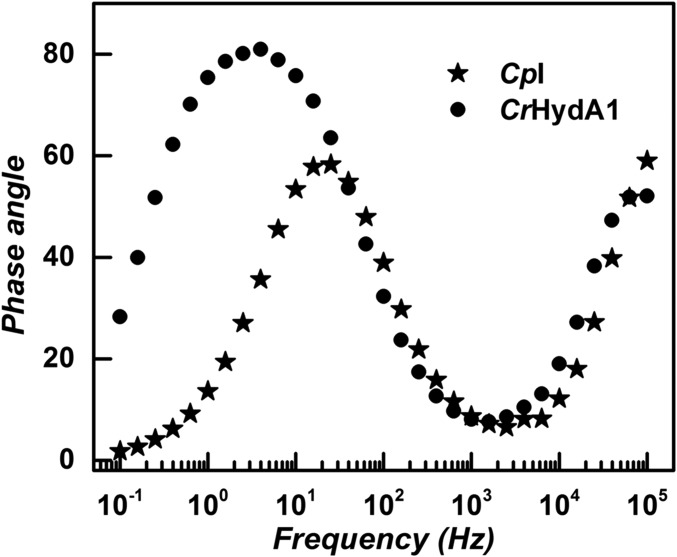
The exchange current density i₀ at the equilibrium cell potential was determined from the expression, i₀ = RT/nFR_e, where R, T, n, and F are the universal gas constant, temperature in Kelvin, overall number (=2) of electrons taking part in the reaction, and Faraday’s constant, respectively (33). In a typical experiment as just described, an exchange current density of 27.7 μA⋅cm⁻² was obtained for CpI, whereas that of CrHydA1 was nearly fivefold lower at 6.07 μA⋅cm⁻². To draw molecular-level conclusions from these data requires knowing the electroactive coverage Γ for each case (current density = nk_exFΓ) as this allows the exchange turnover frequency k_ex to be determined. However, neither CpI nor CrHydA1 are present at high enough coverage to exhibit nonturnover signals that are due to simple, noncatalytic oxidation and reduction of internal electron transfer components. However, an independent value of k_ex could be determined from a Bode plot, an alternate means of presenting the data in which phase angle is plotted against frequency.

Determination of catalytic exchange frequency: Analysis of Bode plots at the equilibrium potential.

Fig. 5 shows Bode plots for CpI and CrHydA1 at the equilibrium potential. The time constant at the peak maxima is related to the electrocatalytic exchange rate constant k_ex. For CpI, the peak in the phase angle corresponds to a higher frequency (f) than for CrHydA1, signifying a smaller time constant. Quantitatively, using k_ex = 2πf, the k_ex values for CpI and CrHydA1 are 157 and 25 s⁻¹, corresponding to 78 and 12 molecules H₂ per second, respectively. These are useful but approximate values erring on the high side, as the modulation amplitude (10 mV rms equates to E_eq ± 5 mV) can never be zero.

Fig. 5.

Bode representations for the [FeFe]-hydrogenases poised at the equilibrium potential. Conditions: pH 7.0 (0.10 M phosphate buffer); temperature, 0 °C. The symbols are experimental data points, and the lines are included to guide the eye.

By backcalculation, the k_ex values allow estimation of the electroactive coverage in the experiment conducted. We obtained 0.91 × 10⁻¹² mol⋅cm⁻² for CpI, and 1.26 × 10⁻¹² mol⋅cm⁻² for CrHydA1. The low values are consistent with the inability to observe any signals due to Fe–S clusters under noncatalytic (CO-inhibited) conditions.

Analysis of Nyquist spectra to resolve the dependences of catalytic turnover rate on potential.

Impedance measurements (Fig. 6) were carried out at various potentials from −1.0 to −0.250 V vs. saturated calomel electrode (SCE), the blue symbols corresponding to the equilibrium potential. Figs. S1 and S2 show how impedance spectroscopy measurements relate to the cyclic voltammograms at different potentials. For both CpI and CrHydA1, applying an increasing overpotential in the proton-reducing direction causes the low-frequency semicircles to contract in size and cut the x axis at increasingly lower Z′ values on the right. However, CpI and CrHydA1 show completely different behavior upon increasing the overpotential in the H₂ oxidation direction: whereas CrHydA1 displays the expected semicircle contraction, CpI shows a strong expansion.

Fig. 6.

Impedance measurements at various potentials vs. SHE: (A) at electrode potentials where CpI catalyzes net H⁺ reduction [black arrow signifies decreasing (more negative) electrode potential]; (B) at electrode potentials where CpI catalyzes the net oxidation of H₂ [black arrow signifies increasing (more positive) electrode potential]; (C) at electrode potentials where CrHydA1 catalyzes net H⁺ reduction [black arrow signifies decreasing (more negative) electrode potential]; (D) at electrode potentials where CrHydA1 catalyzes the net oxidation of H₂ [black arrow signifies increasing (more positive) electrode potential]. Conditions: pH 7.0 (0.10 M phosphate buffer), temperature, 0 °C. The symbols are experimental data points, and the lines are the theoretical fit.

Fig. S1.

A series of EIS spectra measured at different potentials of cyclic voltammograms for CpI.

Fig. S2.

A series of EIS spectra measured at different potentials of cyclic voltammograms for CrHydA1.

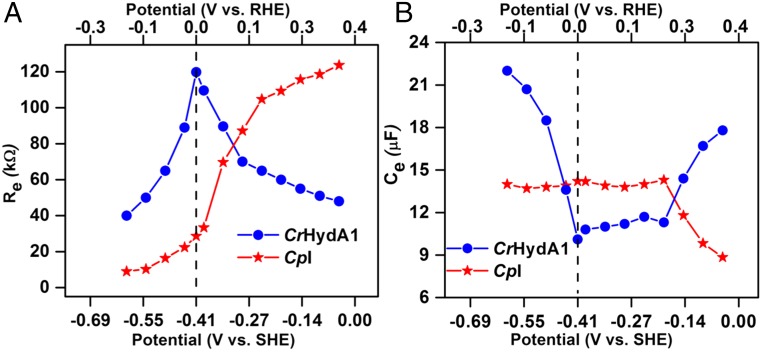
Fig. 7A shows how R_e values vary within a narrow potential range (±0.4 V) on either side of the equilibrium value. The results were obtained by fitting the Nyquist spectra to the standard model for the circuit shown in Fig. 4. The two enzymes are distinguished by their contrasting behavior either side of the equilibrium potential (0 V vs. RHE): notably, the potential dependences of R_e closely mirror the DC voltammograms shown in Fig. 2. For CpI, R_e is low and fairly constant at potentials less than −0.15 V vs. RHE but increases steeply after the potential is raised through E_RHE = 0 before starting to level off above 0.2 V vs. RHE. In contrast, for CrHydA1, R_e is maximal around E_RHE = 0 and falls away either side, coincident with catalytic rates increasing fairly symmetrically. Fig. 7B shows how C_e values vary with potential. First, for CpI, C_e remains constant and large up to an overpotential η = 0.2, thereby showing that the active site operates proficiently over an equally large overpotential each side of E_RHE = 0. Only above 0.2 V vs. E_RHE does the decrease in C_e suggest that the H₂ oxidation rate is becoming limited by a decrease in the catalytic efficacy of the H cluster. In contrast, the equivalent C_e data for CrHydA1 show a broad and constant minimum extending between 0 and +0.2 V vs. E_RHE, then increasing either side, the latter correlating broadly with decreasing R_e and lowering of ET limitation.

Fig. 7.

Potential-dependent variation of (A) R_e, and (B) C_e, extracted from the low-frequency arcs of Nyquist spectra at various potentials for the [FeFe]-hydrogenases adsorbed on a PGE electrode. The symbols are experimental data points, and the lines are included to guide the eye. The vertical broken line marks the formal reversible hydrogen potential (RHE) derived from the measured zero-current potential and used to correlate the upper RHE scale with the lower SHE scale.

Although both hydrogenases contain the H cluster, with the basic arrangement of atoms expected to be conserved, the environments and routes for H₂ and H⁺ transport may differ (16). Without ruling these factors out in terms of influence, by far the most obvious difference between CpI and CrHydA1 is the presence of an extended FeS relay in the former case. For CpI, the fact that the internal Fe–S relay offers little resistance at potentials close to and more negative than E_RHE = 0 must be an important factor in determining the catalytic bias that lies well in favor of H₂ evolution vs. H₂ oxidation at neutral pH values. According to a recent model (3), which assumes that the H₂ concentration is high enough that its binding or dissociation are removed from consideration, a key factor in determining the catalytic bias of an enzyme is the difference between the reduction potential of the site(s) at which electrons enter or leave the enzyme and the reduction potential of the reaction being catalyzed: even a small difference (<50 mV) can result in a large difference between oxidation and reduction rate. The FeS centers of CpI that are detectable by EPR have an average reduction potential of approximately −420 mV vs. SHE (18, 34), although specific values for the two distal FeS centers are currently unknown and may be more negative. Lacking a long-range FeS relay, CrHydA1 displays no such catalytic bias; instead, as confirmed by the R_e values, the catalytic rate is limited by electron transfer in each direction.

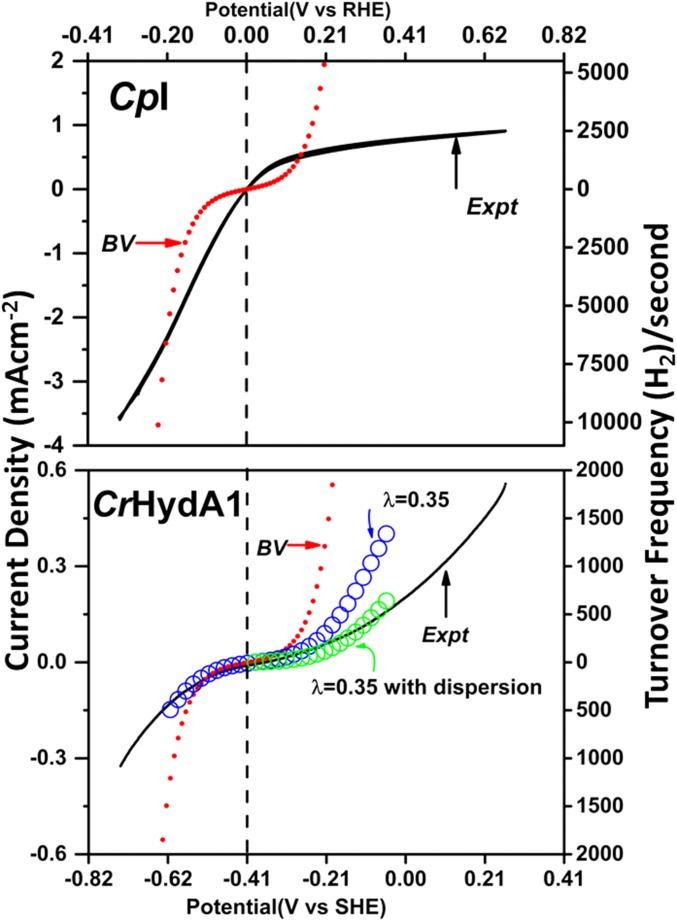
The Butler–Volmer equation, i_E = i₀{exp(−αηF/RT) − exp((1 − α)ηF/RT)}, where η is the overpotential, was used as a first approximation to calculate how the electrocatalytic current should vary with electrode potential if it is limited by interfacial one-electron transfers (3). Fig. 8 shows the results obtained by inputting either exchange current density i₀ (left-hand ordinate) or electrocatalytic exchange rate expressed as H₂ molecules per second (right-hand ordinate). For CpI, the catalytic current close to E_RHE = 0 greatly exceeds the BV model in each direction, a consequence of ET being mediated through the low-potential electron relay. For CrHydA1, the BV model gives good agreement between observed and calculated curves over the range E ± 0.1 V vs. E_RHE, but at higher overpotentials, the observed values drop away. Use of a Marcus–Hush–Chidsey (MHC) model with reorganization energy λ = 0.35 eV gave a better fit (35), and a further improvement was obtained by introducing some dispersion (optimized at βd₀ = 11; Fig. S3) that is expected in view of the complexity of protein interactions with the rough electrode surface (36). Although the MHC approach is approximate, and λ is likely to vary across the wide potential range where different intermediate states dominate, there is no doubt that it is more applicable than the BV model. A simulation and list of variables giving the best fit for CpI are given in Fig. S4 and Table S1. The electrocatalytic exchange rate for CrHydA1 is thus controlled by long-range ET and the value of 12 molecules H₂ per second must understate the inherent activity of the H cluster. Even at 0 °C, CpI attains a turnover frequency exceeding 5,000 s⁻¹ for H₂ evolution (molecules H₂ produced per molecule of enzyme) at η = 0.2 V, whereas H₂ oxidation is limited to below 2,000 s⁻¹. The values may be compared with the broad result of 21,000 ± 12,000 s⁻¹ for H⁺ reduction at 25 °C, pH 7.0 with η ∼ 0.1 V, reported for a similar enzyme (HydA from Clostridium acetobutylicum) (11). It is probable that similar rates would be observed for CrHydA1 were long-range electron transfer to be more efficient, no doubt a result of the PGE electrode being a poor substitute for the natural ET partner PetF (19). As long realized, the H cluster is a superb catalyst of H₂ activation; the low value for λ suggests that it is also optimized for electron transfer.

Fig. 8.

Analysis of voltammograms for CpI and CrHydA1 scaled with respect to current densities and turnover frequencies determined from the experiments described in this paper. Comparisons are made in each case with current–potential dependencies calculated using a simple Butler–Volmer model. The vertical broken line marks the equilibrium potential at E_RHE = 0. For CrHydA1, comparisons are also shown with current–potential dependencies determined using MHC theory (open circles) with λ = 0.35 eV, with and without inclusion of some dispersion (see text). The vertical broken line marks the formal reversible hydrogen potential (RHE) derived from the measured zero-current potential and used to correlate the upper RHE scale with the lower SHE scale.

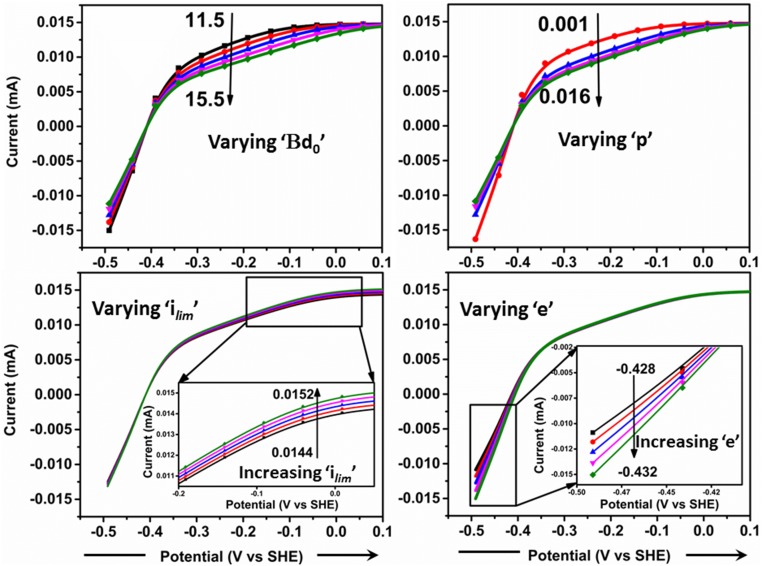
Fig. S3.

Schemes showing effects of varying factors βd₀, the quantity p, i_lim, and e on the value of j. The values of the parameters, unless being explicitly varied, are βd₀ = 13.5, p = 0.006, i_lim = 0.0148, and e = −0.430.

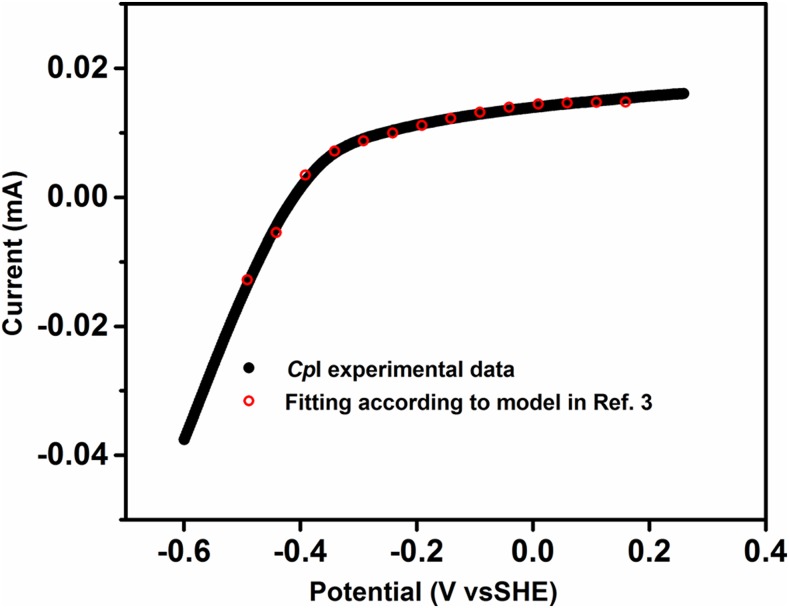
Fig. S4.

The best fit of the experimental data to the model in ref. 3, obtained using the variables i_lim = 0.0148, βd₀ = 13.5, p = 0.006, and e = −0.430 V.

Table S1.

Values of the variables producing the best fit and corresponding information about the catalytic bias in CpI

Variable	Information about the enzyme
βd0 = 13.5	A larger value of βd0 results in a more shallow increase in current with increasing overpotential. For a β value in the range 10–12 nm−1, the point of entry d0 is calculated to be 1.125−1.35 nm.
The value of e = −0.430 leads to e2 = 2.008	A value of e2 > 1 (EOx/R < Eeqm) indicates a catalytic entity that is more proficient at catalyzing the cathodic (reduction) reaction relative to the anodic (oxidation) reaction.
p = 0.006	When p < < 1, the inherent rate constants for the catalytic reaction are small compared with k0.

Materials and Methods

CpI and CrHydA1 were prepared as described previously, using the semisynthetic procedure (37). All electrochemical experiments were carried out using a Ivium CompactStat E800 workstation equipped with a frequency response analyzer. A PGE electrode was used as working electrode in the main thermostated (0 °C) compartment of a three-electrode cell, in which a Pt wire was used as the counterelectrode and a SCE contained in a Luggin capillary side arm maintained at room temperature was used as a nonisothermal reference (24). To form each film of enzyme, 1 μL of 50 μM enzyme solution was pipetted onto the freshly polished PGE electrode, and excess solution was removed after 1 min. The electrochemical cell was housed in a glove box (Vacuum Atmospheres, O₂ < 5 ppm). The main compartment contained 0.10 M phosphate buffer at pH 7.0, and H₂ gas (100%) was flowed through the cell headspace. The electrode was rotated at 1,000 rpm. Potentials were converted to the standard hydrogen scale using E_SHE = E_SCE + 241 mV to relate to most literature available (20). A formal RHE scale was generated using the potential of zero net current. To switch off hydrogenase electrocatalysis, the flow of H₂ was stopped, 5 mL of CO-saturated buffer was injected into the cell to give an initial concentration of 77 μM CO, and a potential of −250 mV (vs. SCE) was applied for 5 min before recording impedance measurements (24). Due care was taken, for example, by conducting experiments at 0 °C, to maximize enzyme film stability, which was checked by recording a cyclic voltammogram after each set of impedance measurements.

Experimental Conditions for EIS Measurements

Resistance is normally defined as the ratio between voltage V and current I through Ohm’s law $\left(R=V/I\right)$. However, this relationship is limited to an ideal resistor, and it is therefore necessary to introduce a circuit element “impedance” that accounts for more complex behavior. Electrochemical impedance is measured by applying a small potential modulation: the current response to a sinusoidal potential is a sinusoidal wave at the same frequency but shifted in phase. The excitation signal as a function of time has the following form:

$$V\left(t\right)=V_0\cos \left(\omega t\right),$$

where $V\left(t\right)$ is the potential at time t, $V_0$ is the amplitude of the signal, and $\omega =2\pi f$ is the angular frequency. The response current $I\left(t\right)$ is shifted in phase ($\varnothing$) and has a different amplitude, $I_0$:

$$I\left(t\right)=I_0\cos \left(\omega t-\varnothing \right).$$

The impedance is therefore expressed in terms of a magnitude,$Z_0$, and a phase shift,

$$Z\left(t\right)=\frac{V\left(t\right)}{I\left(t\right)}=\frac{V_0\cos \left(\omega t\right)}{I_0\cos \left(\omega t-\varnothing \right)}=Z_0\frac{\cos \left(\omega t\right)}{\cos \left(\omega t-\varnothing \right)}.$$

An AC response model for the enzyme-modified electrodes is summarized in Fig. 4 of the main article. In an EIS experiment, a constant potential $V$ is combined with a frequency-dependent sinusoidal modulation voltage $\stackrel{\sim }{V}$ through the equation $\stackrel{\sim }{V}=V_{\mathrm{m}}\hspace{0.17em}\exp \left[j\left(\omega t\right)\right]$, where $\omega$ is the perturbation frequency, $V_{\mathrm{m}}$ is the amplitude of the AC signal, and $j=\sqrt{-1}$. Generally, a sufficiently small voltage modulation is used, that is, k_BT/|e| ∼ 25 mV (rms) to avoid a nonlinear response. In the experiments described, AC modulation voltages of 5 and 10 mV (rms) were tested; they gave similar results at each frequency, but better resolution was obtained with 10-mV modulation. Data obtained using an AC modulation voltage of 20 mV were distorted by a nonlinear response. Hence, an AC modulation amplitude of 10 mV was used for all EIS measurements. Measurements were carried out at different potentials in the frequency range of 0.1 Hz to 100 kHz.

The frequency-dependent Nyquist plot is represented by complex impedance ($Z$), which has real ($Z\prime$) and imaginary ($Z^{″}$) components. The net impedance ($Z$) is a series combination of impedances due to the cell resistance, electrical double layer, and catalytic electron transport through the enzyme. Considering the individual impedance elements, the net impedance (Z) is given by the following:

$$Z=R_s+\frac{1}{Z_{C_{dl}}+\frac{1}{R_{ct}+Z_w}}+\frac{1}{Z_{C_e}+\frac{1}{R_e}},$$

where $Z\prime =Re\left\{Z\right\}$ and $Z^{″}=-Im\left\{Z\right\}$ are the real and imaginary parts of the complex impedance.

To obtain the exchange rate constant, the frequency (f) response was analyzed using a Bode plot in which net impedance $Z_0$ and/or phase angle ($\varnothing$) are plotted against log f. The net impedance for a Bode plot is given by the following:

$$Z\left(\omega \right)=Z_0\left(\cos \varnothing +j\sin \varnothing \right).$$

Selected EIS spectra around cyclic voltammograms for CpI and CrHydA1 are shown below to help clarify the measurements of impedance data.

Computational Modeling Using Marcus–Hush–Chidsey Theory

The following equations used to model the electrocatalytic voltammetry of CrHydA1 are based on equations 7 and 8 in ref. 35. Rate constants were also converted into current density (in milliamperes per square centimeter) using i = kFAΓ (F is Faraday constant, A is geometric electrode area, and Γ is surface coverage). The equations were written as a program in Wolfram Mathematica 10.4 to obtain the theoretical current density curve shown in Fig. 8 of the main article:

$$f\left[y{\_}_{,}\lambda \_\right]≔25\ast \mathrm{1,000}\ast \mathrm{96,485}\ast 1.26e-12\ast \hspace{0.17em}\mathrm{Exp}\left[-0.5\ast 42.51\hspace{0.17em}y\right]\ast \frac{\mathrm{NIntegrate}\left[\frac{\mathrm{Exp}\left[-\frac{{\left(x-42.51y\right)}^2}{170.04\ast \lambda }\right]}{2\mathrm{Cosh}\left[\frac{x}{2}\right]},\left\{x,-\mathrm{10,000},\hspace{0.17em}\mathrm{10,000}\right\}\right]}{\mathrm{NIntegrate}\left[\frac{\mathrm{Exp}\left[--\frac{{\left(x\right)}^2}{170.04\lambda }\right]}{2\mathrm{Cosh}\left[\frac{x}{2}\right]},\left\{x,-\mathrm{10,000},\hspace{0.17em}\mathrm{10,000}\right\}\right]},$$

$$g\left[y{\_}_{,}\lambda \_\right]≔25\ast \mathrm{1,000}\ast \mathrm{96,485}\ast 1.26e-12\ast \hspace{0.17em}\mathrm{Exp}\left[0.5\ast 42.51\hspace{0.17em}y\right]\ast \frac{\mathrm{NIntegrate}\left[\frac{\mathrm{Exp}\left[-\frac{{\left(x-42.51y\right)}^2}{170.04\ast \lambda }\right]}{2\mathrm{Cosh}\left[\frac{x}{2}\right]},\left\{x,-\mathrm{10,000},\hspace{0.17em}\mathrm{10,000}\right\}\right]}{\mathrm{NIntegrate}\left[\frac{\mathrm{Exp}\left[--\frac{{\left(x\right)}^2}{170.04\lambda }\right]}{2\mathrm{Cosh}\left[\frac{x}{2}\right]},\left\{x,-\mathrm{10,000},\hspace{0.17em}\mathrm{10,000}\right\}\right]}.$$

The equations correspond to reduction (f) and oxidation (g). The two variables are y and λ: y is the overpotential term and equivalent to (E − E_f⁰), where E is the applied potential and E_f⁰ is the formal potential of the 2H⁺/H₂ couple; λ is the reorganization energy term, measured in electronvolts. For the modeling, the k₀ value was 25 s⁻¹ and α was 0.5.

Computational Modeling for CrHydA1 Including Effect of Dispersion

The effect of inhomogeneity (dispersion) of interfacial electron transfer rate constants was introduced as described in ref. 36 (equation 6a in that article). The assumption was made that the exchange rate constant value of 25 s⁻¹ corresponds to k_min: hence k₀^min =k₀^maxexp(−βd₀), where βd₀ is the decay constant × distance of closest approach (equation 3 of ref. 36). This results in the following equation, where k_cat is the turnover frequency:

$$h\left(k\mathrm{cat},\beta d0,y,\lambda \right)=\frac{\left(\frac{\log \left(\frac{\left(0.04\ast k\mathrm{cat}/\mathrm{Exp}\left[-\beta d0\right]\right)\ast \mathrm{Exp}\left[-0.5\ast 42.51y\right]+\left(\mathrm{Exp}\left[-42.51y\right]+1\right)}{\left(0.04\ast k\mathrm{cat}/\mathrm{Exp}\left[-\beta d0\right]\right)\ast \mathrm{Exp}\left[\beta d0\right]\ast \mathrm{Exp}\left[-0.5\ast 42.51y\right]+\left(\mathrm{Exp}\left[-42.51y\right]+1\right)}\right)}{\beta d0}+1\right)25\hspace{0.17em}\ast \mathrm{1,000}\ast \mathrm{96,485}\ast 1.26e-12\ast \mathrm{Exp}\left[0.5\ast 42.51\hspace{0.17em}y\right]\ast \mathrm{NIntegrate}\left[\frac{E^{-\left(\frac{{\left(x-42.51y\right)}^2}{170.04\lambda }\right)}}{2\cosh \left(\frac{x}{2}\right)},\left\{x,-\mathrm{10,000},\mathrm{10,000}\right\}\right]}{\left(\mathrm{Exp}\left[-42.51\ast y\right]+1\right)\ast \mathrm{NIntegrate}\left[\frac{E^{-\left(\frac{x^2}{170.04\lambda }\right)}}{2\cosh \left(\frac{x}{2}\right)},\left\{x,-\mathrm{10,000},\hspace{0.17em}\mathrm{10,000}\right\}\right]}.$$

Computational Modeling for CpI with Incorporation of a Catalytic Bias

The model described in ref. 3 was adopted to model the electrocatalytic voltammetry of CpI. The input function, j, depends on i_lim, βd₀, and the quantity p (the ratio of the rate constants for the catalytic reaction compared with exchange rate constant, k₀):

$$j[i\hspace{0.17em}\lim ,\beta d0,p,E,e]:\left(i\hspace{0.17em}\lim \left(\left(\exp \left(42.51\left(E-e\right)\right)-2.008\right)/\left(\beta d0\left(\mathrm{Exp}\left(42.51\left(E-e\right)\right)+1\right)\right)\right)\log \left(\frac{p\mathrm{Exp}\left(0.5\ast 42.51\left(E-e\right)\right)+\left(\mathrm{Exp}\left(42.51\left(E-e\right)\right)+1\right)}{\left(\mathrm{Exp}\left(-\beta d0\right)\left(\mathrm{Exp}\left(42.51\left(E-e\right)\right)+1\right)\right)+p\mathrm{Exp}\left(0.5\ast 42.51\left(E-e\right)\right)}\right)\right).$$

Additionally, j depends on the applied potential E and the effective potential (e) of the relay center that serves as the electron entry/exit point (the best fit was obtained with e = −0.43 V vs. SHE). The variation of j with i_lim, βd₀, and the quantity p are plotted in Fig. S3. The best fit is shown in Fig. S4 and was obtained with i_lim = 0.0148, βd₀ = 13.5, p = 0.006, and e = −0.430 V.