Automatic image quality assessment and measurement of fetal head in two-dimensional ultrasound image

Abstract.

Owing to the inconsistent image quality existing in routine obstetric ultrasound (US) scans that leads to a large intraobserver and interobserver variability, the aim of this study is to develop a quality-assured, fully automated US fetal head measurement system. A texton-based fetal head segmentation is used as a prerequisite step to obtain the head region. Textons are calculated using a filter bank designed specific for US fetal head structure. Both shape- and anatomic-based features calculated from the segmented head region are then fed into a random forest classifier to determine the quality of the image (e.g., whether the image is acquired from a correct imaging plane), from which fetal head measurements [biparietal diameter (BPD), occipital–frontal diameter (OFD), and head circumference (HC)] are derived. The experimental results show a good performance of our method for US quality assessment and fetal head measurements. The overall precision for automatic image quality assessment is 95.24% with 87.5% sensitivity and 100% specificity, while segmentation performance shows 99.27% ($\pm 0.26$) of accuracy, 97.07% ($\pm 2.3$) of sensitivity, 2.23 mm ($\pm 0.74$) of the maximum symmetric contour distance, and 0.84 mm ($\pm 0.28$) of the average symmetric contour distance. The statistical analysis results using paired $t$-test and Bland–Altman plots analysis indicate that the 95% limits of agreement for inter observer variability between the automated measurements and the senior expert measurements are 2.7 mm of BPD, 5.8 mm of OFD, and 10.4 mm of HC, whereas the mean differences are $-0.038\pm 1.38\mathrm{mm}$, $-0.20\pm 2.98\mathrm{mm}$, and $-0.72\pm 5.36\mathrm{mm}$, respectively. These narrow 95% limits of agreements indicate a good level of consistency between the automated and the senior expert’s measurements.

1. Introduction

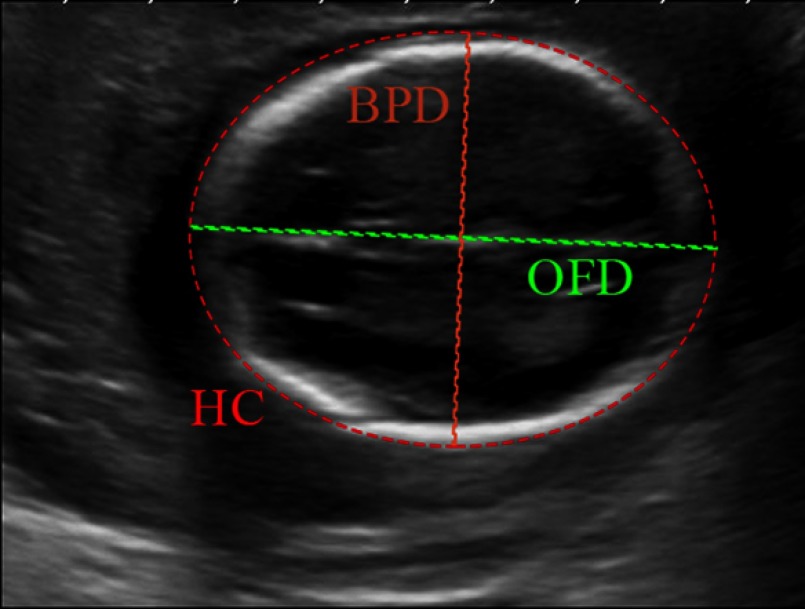
Obstetric ultrasound (US) imaging is commonly used in daily clinical practice due to its noninvasive nature, low–cost, and real-time acquisition.¹ The main goals of the fetal US scan are to estimate the gestational age (GA) and weight, confirm growth patterns, and show the presence of possible abnormalities. A set of standard fetal US biometrics is used in routine practice, which includes: crown-rump length, biparietal diameter (BPD), occipital–frontal diameter (OFD), head circumference (HC), femur length (FL), and abdominal circumference.^2,3 Among these biometrics, fetal head-related measurements, such as BPD and HC (Fig. 1), are recommended for the GA estimation during the GA ranging from 13 to 25 completed weeks,^2,4 and also for estimating fetal weight.^5,6 The current obstetric US examinations require sonographers to perform measurements manually. The accuracy of the measurements is highly dependent on operator training, skill, and experience.

Fig. 1.

The biometric measurements of the fetal head. The BPD measurement is taken on the outer border of the parietal bones (outer to outer) at the widest part of skull. The OFD is measured between the outer border of the occipital and frontal edges of the skull at the point of the midline (outer to outer) across the longest part of skull. The HC is the HC calculated from the formula $\mathrm{HC}=\pi (\mathrm{BPD}+\mathrm{OFD})/2$.²

Recent studies^7,8 reported that intraobserver and interobserver variability exist in routine practice. Inconsistent US image quality⁹ is one of the main reasons that leads to the intraobserver and interobserver variability. In this study, inconsistent image quality means the scan itself presents variances in specific anatomic structures (e.g., head) captured by different operators. A good quality fetal head US image is recommended to be captured in a correct imaging plane as required by the guidelines.¹⁰ To this end, automatic approaches for fetal US image quality assessment and biometric measurements are needed to ensure the image captured at a correct imaging plane during the obstetric US examination and to provide accurate and reproducible fetal biometric measurements.¹¹ It is noted that a good quality image means that the image is acquired at a correct imaging plane.

Fetal head boundary detection is performed as a prerequisite step for image quality assessment (i.e., whether the scan is captured at the correct imaging plane) and accurate biometric measurements. According to the obstetric US guidelines,^5,10 the assessment of fetal head US image is based on the appearance of anatomic structures in the image, including skull shape, skull orientation, and the midline. These features are calculated from the segmented head structure and then fed into a random forest (RF) classifier to automatically assess the image quality.

Over the past few years, a number of fetal head segmentation (detection) methods have been investigated, including Hough transform-based methods,^12,13 parametric deformable models,¹⁴ active contour models,¹⁵ texton-based methods,¹⁶ and machine learning^17–19 with varying degrees of success. For example, Anto et al.²⁰ proposed fetal skull segmentation in two-dimensional (2-D) US images using pixel intensities and an RF classifier. Namburete and Nobel¹⁷ considered local statistics and shape features, which are fed into a RF classifier to obtain the probability maps of the pixels belonging to the fetal skull in 2-D US images. However, only a few attempts^21,22 have been made at automating quality assessment in fetal 2-D US images. A few studies have considered automatic detection of the fetal standardized plane from three-dimensional (3-D) US volumes. Cuingnet et al.²³ proposed a fast fetal head detection and alignment method in 3-D US volumes. The fetal skull is segmented using a shape model followed by a template deformation algorithm. The standardized plane is detected using weighted Hough transform and an RF classifier. Sofka et al.²⁴ proposed a system for automatic fetal head and brain measurements from 3-D US volumes. Several fetal head and brain anatomical structures are detected and measured while corresponding standardized planes are determined.

To address current clinical challenges in 2-D obstetric US imaging, we aim to develop a good quality-assured, fully automated 2-D US fetal head measurement system. Such a system can remove or reduce elements of human inconsistency, and provides more accurate and reproducible image quality assessment and measurements. Figure 2 shows the main framework of our method. A texton-based US fetal head segmentation is first adopted¹⁶ in which a filter bank is designed to extract texton features specific to US fetal anatomic structures; multiscale local brightness and texture cues are taken into account for an initial skull boundary detection, which is then followed by the identification of the fetal skull using a supervised learning-based method. The image quality assessment step includes skull midline detection and feature calculation from the segmented head region, and classification of US image quality using an RF classifier.

Fig. 2.

Flow diagram of the proposed algorithm for fetal head segmentation and image quality assessment.

The remainder of the paper is organized as follows: Sec. 2 introduces our method in detail; Sec. 3 presents the experimental results and further discussions; the conclusion is given in the final section.

2. Materials and Methods

2.1. Fetal Head Ultrasound Images

Two datasets with a total of 41 fetal head US images collected from the United Lincolnshire Hospitals NHS Trust are used in this experiment. The US images are obtained in clinical practice by trained sonographers using Toshiba Aplio 780, Toshiba Aplio 790, Toshiba Aplio 500 (Toshiba Medical Systems, Tokyo, Japan), and GE Voluson 730 (GE Healthcare, Pollards Wood, UK) US machines. The sonographers use an obstetric setting on the scanners and appropriately optimize images during scanning. The image datasets collected from 41 patients cover different GAs (from 20 to 35 weeks) and different image qualities (poor and good). Each image is stored as a DICOM format with a size of $717\times 538\text{pixels}$. Two experts (one senior denoted as expert 1 and the other junior as expert 2) provided ground truths by manually delineating the fetal head twice for each image in the datasets, and then the BPD, OFD, and HC were obtained from the delineated skulls. Each US image is graded as either “poor” or “good” quality by expert 1. In the datasets, there are 22 images of good quality and 19 images of poor quality. Images with mixed qualities (e.g., good or poor) with approximately even distribution are obtained from each US machine. To train and validate our method, we randomly selected 10 images from the good quality dataset and 10 images from the poor image set, so in total, 20 images are used as training samples and the remaining 21 images are used as testing images.

2.2. Texton-Based Fetal Head Segmentation

Nonlinear diffusion filtering^25–27 is used as a preprocessing step to remove speckle noise in US images. Multiscale and multiorientational local intensity and texture cues extracted from a texton map specific to the US anatomic structures are then combined for the initial skull boundary detection. Different from our previous work,¹⁶ where a support vector machine (SVM) was used to identify skull segments from the initial boundary candidates, an RF algorithm²⁸ is used for skull boundary identification. In the following subsections, each step is summarized. More details could be found in Ref. 16.

2.2.1. Initial fetal head boundary detection using textons and brightness

A fetal skull maximum response 7 (FSMR7) filter bank is employed to extract the texton features from a US fetal image, which includes a set of Gaussian derivatives. More specifically, two types of filters are used: a second-order derivative of Gaussian filter and a matched filter.²⁹ This is based on an assumption that the cross-sectional intensity profile of the bone (skull) structure can be approximated as Gaussian-like curves,³⁰ whereas the intensities of those structures are on average higher than those of the surrounding tissues. These spatial filters used for skull features extraction are also consistent in their assumption of the skull cross-sectional profile “analyzed” in spatial domain.

The fetal skull in US image may rotate to any orientation and varies in thickness over the different fetal US images. Both sets of anisotropic filter kernels (second-order derivative of Gaussian and the matched filter) are applied at three scales to extract skull orientation variant features and cover various thicknesses. At each scale ($\sigma =1$, 3, and 5 pixels, where $\sigma$ represents the scale of the filter), both second-order derivative of Gaussian and matched filter kernels are rotated in 12 orientations (0-, 15-, 30-, 45-, 60-, 75-, 90-, 105-, 120-, 135-, 150-, and 165-deg). The standard isotropic Gaussian filter is also employed to extract general image features from the background. Therefore, there are a total of 73 filter kernels in the filter bank.

For the anisotropic filters, at each scale, the maximal response across all 12 orientations is considered. Therefore, among 73 filter kernels in the filter bank, only seven filter responses (among which three are from second-order derivative of Gaussian from three scales and another three are from the matched filter, with one from the isotropic Gaussian filter) are considered at three scales. We named it as the FSMR7 filter bank. Figure 3 shows the maximal response of fetal head across 12 orientations at scale$\sigma =5$ for both the second-order derivate of (a) Gaussian, (b) the matched filter, and (c) the response to the standard Gaussian at scale $\sigma =1$. These features are further used to generate textons.

Fig. 3.

Examples of maximal responses to the designed filter bank. (a) Fetal head response to the second derivative of Gaussian at scale $\sigma =5$, (b) response to the matched filter at scale $\sigma =5$, and (c) response to the standard Gaussian filter at scale $\sigma =1$.

Given an image $I(x,y)$, textons are calculated by employing a seven-dimensional (7-D) $k$-means clustering algorithm on the filter responses (i.e., seven maximal responses from FSMR7 to construct a 7-D feature space), which are then aggregated based on the distances calculated from membership to clustering centers. The number of clusters (textons, $k$) is chosen empirically according to the number of tissues that may be present in the US images. Our experiments show $k=32$ are sufficient to generate good primitives (clusters/textons). In the next stage, the texton map is generated by assigning each pixel in the image to the nearest texton. Each texton is assigned a texton $id$ using one of gray levels (from 1 to $k=32$). Therefore, the texton map is a grayscale image with values between 1 and 32. The generated texton map ($Tmap$) is used to calculate the texture-oriented gradient that provides significant local information for the initial skull boundary detection.¹⁶ The oriented gradient magnitude at each pixel $(x,y)$ is calculated by employing the ${\chi }^2$ distance of histograms between two-half discs defined as

$${\chi }^2(g,h)=\frac{1}{2}\sum _i\frac{{(g_i{h}_i)}^2}{g_i+h_i},$$ (1)

where the two-half discs are generated by splitting a circular disc of radius $r$ drawn at a location $(x,y)$ of the image along the diameter at an orientation of $\theta$, and $g_i$ and $h_i$ are the histograms calculated from the two-half discs, respectively.

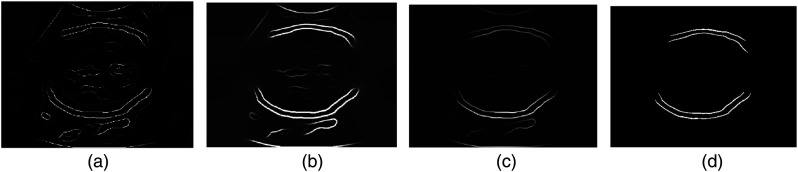
Equation (1) forms an oriented gradient magnitude. Both image intensity and texture ($Tmap$) channels ($i=2$) are taken into account for the histogram calculation. The general local cue (denoted by $mPb$) is then obtained by calculating the maximum response of the oriented gradient magnitudes across all predefined orientations ($\theta$). The spectral (global) signals ($sPb$) are incorporated by employing spectral clustering³¹ according to the maximal $mPb$. The final global probability of boundary ($gPb$) is formed as a weighted sum of $mPb$ and $sPb$.^16,31 This process allows weak boundaries to be determined and excluded from strong boundaries while preserving contour quality. Example results with respect to the $mPb$, $sPb$, and $gPb$ are shown in Figs. 4(a)–4(c), respectively. As we can see from Fig. 4, those weak boundaries presented in (a) and (b) that are related to the fetal brain are reduced in (c) while the skull contours are preserved with a high-probability level. The final skull boundaries shown in Fig. 4(d) are identified using an RF classifier, which is discussed in the following section.

Fig. 4.

Examples of $mPb$, $sPb$, and $gPb$ extracted from a fetal head US image and the final identified fetal head contours. (a) Local boundaries $mPb$, (b) spectral boundaries $sPb$, (c) globalized probability of boundary $gPb$, and (d) final identified fetal head boundaries.

2.2.2. Fetal head boundary identification, segmentation, and measurement

It is common that nonskull bright structures are presented adjacent to the skull in US fetal images [shown in Fig. 4(c)]. To further identify the true skull segments (i.e., remove the false segments) two steps are used. First, the global boundary probability map ($gPb$) obtained in Sec. 2.2.1 is binarized by an optimal threshold. The gray-level co-occurrence matrix³² is used to calculate the optimum threshold by finding the gray level corresponding to the maximum of the total second-order local entropy of the object and the background. Second, the objects in the binary image are further classified into skull and nonskull boundaries. Different from our previous work in Ref. 16 where an SVM is used to identify skull segments from the initial boundary candidates, an RF classifier is used for skull boundary identification. RF is an ensemble technique that uses multiple decision trees. Each node in the trees includes a set of training examples and the predictor. Splitting starts from the root node and then continues at every node. The procedure is performed based on the feature representation and allocating the partitions to the right and left nodes. The tree grows until a specified tree depth is reached. During the bagging process and at each attribute split, a random subset of features is used. In RF, by generating a large number of trees, the most popular class is voted.²⁸

A set of features based on the prior knowledge of the fetal skull is constructed for training the RF. These features include shape, location, and orientation of the structure. To obtain the shape features, each initial skull boundary segment is fitted by an ellipse that best represents the boundary. The length of major- and minor-axes and an eccentricity derived from the fitted ellipse are considered as shape features. The eccentricity of the ellipse is the ratio of the distance between the foci of the ellipse and its major axis. It is used to represent the curvature of the boundary. For example, if the eccentricity of a structure is 1, it denotes a line segment; while 0 indicates a circle. The position and orientation of the boundary are also taken into account based on the guidelines considered in the clinical work flow² on the appearance of the skull’s position and orientation within the 2-D US images. An RF classifier containing 500 decision trees was trained using 10 fold cross validation to identify the true skull boundaries. Figure 4(d) shows an example of the boundary identification using the trained RF model, where some nonhead boundaries have been removed.

The final head segmentation is obtained by fitting an ellipse on the identified skull boundaries, in which the direct least square ellipse fitting method³³ is used to construct a closed head contour. Both BPD and OFD are obtained by calculating the minor axis length and the major axis length of the fitted ellipse, respectively. The formula $\mathrm{HC}=\pi (\mathrm{BPD}+\mathrm{OFD})/2$ is used to calculate the HC.

2.3. Fetal Head Ultrasound Image Quality Assessment

The studies published in Refs. 9 and 34 have indicated that the poor quality of US fetal images (e.g., incorrect imaging plane) is one of the important sources leading to inaccurate measurements. Although a set of quality criteria^2,9,10,34 has been defined to guide the routine fetal biometric measurements, the large intraobserver and interobserver variability of fetal image acquisition in clinical practice (e.g., reported in Refs. 7 and 8) significantly affects the accuracy of fetal biometric measurements. We proposed an automated fetal US image quality assessment method (with a focus on the fetal head). Our automatic method is based on the clinical criteria, in which the appearances of the head shape profile, appropriate angle, and midline in fetal head US image are used as the main features to assess US image quality.

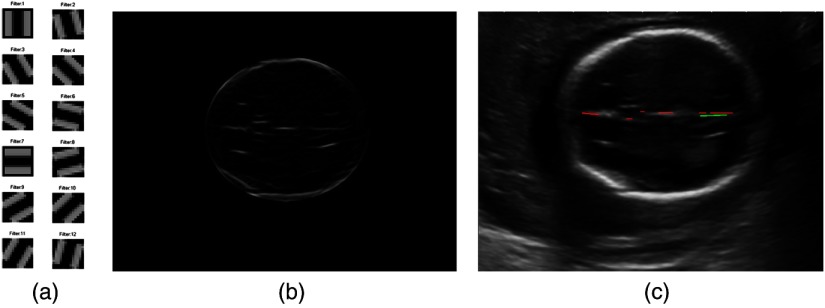
In this study, the skull region [region of interest (ROI)] is determined using the segmented fetal head region described in Sec. 2.2. The matched filter²⁹ is then designed to detect the skull midline within the ROI, where the scale parameter sigma $\sigma =1$ of size $13\times 13\text{pixel}$ filter kernel was empirically chosen. The filter kernel is rotated in 12 orientations. This filter bank is shown in Fig. 5(a). An example of the maximal response to the filter bank across all orientations is shown in Fig. 5(b), where we can see that most of the bar structures are enhanced in the image. It is noted that, in general, the midline can be approximated to be a line or bar structure. However, in most cases, the midline may not be presented as a continuous line (i.e., may appear as a number of small line segments) in a US image due to the artifacts, signal drop, and the natural properties of the midline in the US images. To fully detect the midline, the following two steps are used. First, the initial response to the matched filter is further binarized using the Sobel edge detection. The binarized image contains edges (contours) of the bar structures in the ROI (head region). Second, the standard Hough transform (SHT)³⁵ is adopted to “analyze” the linear components of these contours, from which a set of feature vector related to the midline is then extracted. This assumes a line can be given in the following parametric representation:

$$D=x*\cos \theta +y*\sin \theta ,$$ (2)

where $D$ is the distance from the origin to the line along the direction, which is perpendicular to the line, and $\theta$ denotes the angle between the $x$ axis and this vector. The rows and columns in a 2-D matrix $H$ correspond to the $D$ and $\theta$ values. The peaks of the Hough transform matrix (denoted by $H$) are located with a default threshold $[0.5*\max (H)]$. The line segments can be detected according to the calculated $H$ and peaks.

Fig. 5.

The matched filter used to extract midline feature (a) is the filter bank, (b) is an example of the maximal response to the filter bank, and (c) is the detected lines using Hough transform analysis, where the green line is the longest line segment and the other detected line segments are shown in red lines.

Based on the clinical guideline,² two main features: skull midline features and skull shape and orientation features are considered to assess the image quality. For example, in clinical practice, the fetal head is required to be captured within a certain range of orientations (e.g., acquisition angle between biparietal diameter and US beam $<30\mathrm{deg}$).⁹ The skull midline echo should also appear as close as possible to the OFD. In our study, the orientation feature is learned from good quality training data. The detected lines using the SHT [Eq. (2)] from the whole head region are further analyzed according to the Euclidean distance between the OFD and these lines, where only the lines with distances $\le 2\mathrm{mm}$ are considered for midline-related feature calculation.

Given a midline in a fetal US image, the midline feature vector is then defined by $F_{\text{midline}}=[f^{\mathrm{ml}},f^{\mathrm{o}},f^{\text{sum}\mathrm{l}},f^{\mathrm{l}\text{count}}]$, where the $f^{\mathrm{ml}}$ denotes the longest line segment detected by the Hough transform. The $f^{\mathrm{o}}$ is the orientation of the longest line [green line in Fig. 5(c)], while other line structures shown in the red lines in Fig. 5(c) are used to generate the features $f^{\text{sum}\mathrm{l}}$ and $f^{\mathrm{l}\text{count}}$, which denote the sum of the length of all other lines [red line in Fig. 5(c)] and the total number of the line objects, respectively.

In addition to the midline features discussed earlier, the skull shape and orientation features are also considered for the image quality assessment. This is because the fetal head in a good quality US image should be presented as an oval or rugby football shape.^2,9 The skull features are derived from the identified fetal skull boundaries [Fig. 4(d)]. The skull feature vector $F_{\text{skull}}=(f^{\text{convex}},f^{\text{solidity}},f^{\text{orentation}})$ includes a convex area, solidity of structure, and orientation of the structure, in which the convex area is the number of the pixels in the smallest convex polygon that can contain the structure (boundary). The solidity feature is calculated by area/convex area, where the term “area” is the actual number of pixels in the structure. The solidity feature provides the curvature profile of the structure. For a straight structure, the value of the solidity is 1; while for an arc structure, the solidity should be a fractional number between 0 and 1. The orientation of the structure indicates whether the head is captured within a certain range of angles. The skull feature vector ($F_{\text{skull}}$) together with the midline feature vector ($F_{\text{midline}}$) are fed into an RF classifier to grade the fetal US images into good or poor image quality. Specifically, in our experiment, the number of trees is 500, which is determined by observing the out-of-bag error among different numbers of trees. We set the default number of features as three in the feature bagging process and the default cutoff value of 0.5. The ground truths (grading labels) are provided by expert 1. Finally, the trained model (classifier) is further used in the testing phase to assess the quality of the fetal head US images.

2.4. Evaluation Methods

Our automated segmentation algorithm is validated using two evaluation methods: region-based measures³⁶ and contour distance-based measures.³⁷ The region-based measurement is used to compare the regions produced by our automatic and manual segmentation. Four region-based measure parameters (precision, accuracy, sensitivity, and specificity) are used in our experiment. The distance-based measure is the calculation of the difference in millimeters between manually and automatically segmented contours of structures. The maximum symmetric contour distance (MSD), the average symmetric contour distance (ASD), and the root mean square symmetric contour distance (RMSD) are used to assess the performance. The MSD is the maximum distance between two contours. A higher MSD value indicates a larger difference between the two contours. The parameter ASD is the average distance between the two contours. The ASD equals zero if the two contours are identical. The RMSD is the variant of the ASD, the larger difference compared to the ground truth can be emphasized by a larger value of RMSD. The results per image are averaged to obtain the overall automatic segmentation performance compared with manual segmentation.

The Bland–Altman plots³⁸ are employed to compare the biometry measurements between our method and the experts and to assess the interobserver and intraobserver variability. This evaluation method provides statistical significance to validate the clinical value of our method in routine obstetric examinations.

3. Experimental Results and Discussion

Two experiments were carried out to validate our fetal head segmentation and the US image quality assessment method. The fetal biometric measurements are directly derived from the segmented region. In our experiment, the primary aim of evaluation of the automated measurement is to validate the robustness of the automatic segmentation method especially for those challenging (i.e., poor quality) images. Therefore, the biometric measurements obtained from both good and poor images are considered. The proposed fetal head segmentation and measurement method are evaluated on the dataset described in Sec. 2.1. Table 1 shows the average interobserver and intraobserver variability over all images. The intraobserver variability for experts 1 and 2 shown in Table 1 is obtained by comparing two manual segmentation results that were delineated twice by each expert. We can observe that although the intraobserver variability is close for the two experts, the interobserver variability reflects the different levels of two experts’ experiences. For the intraobserver variability, the overall precision of the two experts is approximate to 97% with similar standard deviations. The MSD, ASD, and RMSD of two experts’ intraobserver variabilities have on average minor differences, while expert 1 has less disagreement (0.44 of ASD) between the two independent manual segmentations compared to that of expert 2 (0.49 of ASD). For the interobserver variability, the 93.90% of precision together with relatively larger distances of MSD, ASD, and RMSD comparing to the corresponding intraobserver variability (2.4 of MSD, 0.98 of ASD, and 1.18 of RMSD) show that there are some degrees of disagreements of head delineation between the two experts. These results reflect the reproducibility of manual segmentations using the experimental dataset, and can be used as a reference to comparatively assess the performance of our automated-segmentation method.

Table 1.

Intraobserver and interobserver variability of manual segmentation and automatic segmentation evaluation results.

Parameters (head)	Intraobserver variability-E1a	Intraobserver variability-E2a	Interobserver variability-E1 versus E2	Our method ($\mathrm{GT}=\mathrm{E}1$)
Pre. (%)	97.17% (1.58)b	96.91% (1.28)	93.90% (2.41)	94.63% (1.71)
Acc. (%)	99.61% (0.23)	99.56% (0.18)	99.14% (0.36)	99.27% (0.26)
Sen. (%)	98.10% (1.52)	98.63% (1.01)	94.76% (2.61)	97.07% (2.30)
Spe. (%)	99.85% (0.13)	99.72% (0.26)	99.86% (0.17)	99.60% (0.25)
MSD (mm)	1.32 (0.70)	1.33 (0.53)	2.40 (0.92)	2.23 (0.74)
ASD (mm)	0.44 (0.25)	0.49 (0.20)	0.98 (0.40)	0.84 (0.28)
RMSD (mm)	0.57 (0.30)	0.60 (0.25)	1.18 (0.47)	1.05 (0.34)

^aE1 = Expert 1; E2 =Expert 2.

^bResults are given as an average value (standard deviation) for each measure.

In our experiment, the segmentations produced by our method are compared to manual segmentations produced by expert 1. The corresponding evaluation results are shown in the last column of Table 1. The results show that on average, the fetal head segmentation performance of our method outperforms the interobserver variability between two experts. The evaluation parameters derived from our method (precision, accuracy, sensitivity, MSD, ASD, and RMSD) are better than the values of the interobserver variability. The lower standard deviation of each parameter presented in parentheses in Table 1 also reflects the robustness of the method. This shows a good performance of our method for fetal head segmentation.

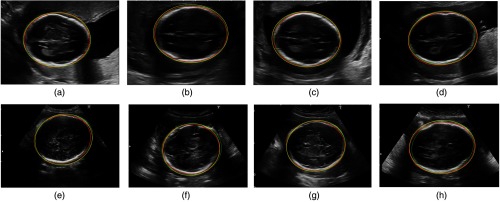
Figure 6 shows examples of automatic segmentation compared to the experts’ segmentations, where the test images include good- and poor-quality images graded by expert 1. As we can observe from the good-quality images (a) to (d), the results obtained from automatic segmentation and expert segmentation are almost identical. This is because there are fewer uncertainties on the fetal skull in the good images compared to that of the poor images (e) to (h). We conjectured that one important factor that influences the segmentation is that the fetal skull appearing as fuzzy boundaries in the image. This may result in difficulties of accurate delineation of the skull boundary.

Fig. 6.

Examples of our automatic segmentations comparing to two experts segmentations on the good quality and poor quality cases. The contours of structures produced by the automatic method are shown in green (dot lines), contours delineated by experts 1 and 2 are shown in red and yellow (solid line), respectively. (a)–(d) are fetal head segmentations in the good-quality images and (e)–(h) are the segmentations in the poor-quality images.

Moreover, for many poor-quality images, the missing boundaries (on the OFD direction) also cause the large uncertainty for the delineation. Normally, the skull presented in such US images is an incomplete structure in the areas around the horizontal left and right points, while the ellipse is fitted (automatically or manually) based on the visible structures in US images. This may lead to the disagreements in the ellipse estimations among different experts, and thus may lead to the disagreements of segmentations. For example, comparing automatic segmentation (green dotted line) with expert 1’s segmentation (red solid line), we can see from Figs. 6(e) and 6(f), although the contours on the superior and inferior side of the skull (BPD direction) are almost identical, the main disagreement occurs on the right side of the image, due to the missing skull boundaries in that area. The disagreements of skull delineation from the two experts are also derived from the disagreements of identifying bone structures in the areas where the skulls have fuzzy boundaries [i.e., red and yellow lines on the inferior side of the skull in Fig. 6(e)]. Commonly, these phenomena are characterized as flocculent structures surrounding the highlighted bone structures in which the discriminations between bone and nonbone structures cannot be preattentively perceived.

Bland–Altman plots and paired $t$-test are used to assess the measurement consistency between the automated and the manual methods. The intraobserver and interobserver variability of the manual fetal head biometric measurements are reported in Table 2. The comparative measurement results between our method and the expert 1 are shown in the last column of Table 2. It can be observed that the intraobserver variability of BPD and OFD for each expert is very small, at $<1\mathrm{mm}$ level, whereas the interobserver variability between the two experts shows a significant difference, the average difference of BPD is 1.23 mm with a standard deviation of 1.53 mm, the average difference of OFD is 2.76 mm with a standard deviation of 2.58 mm, and the 6.37 mm of HC with a 5.04 mm of standard deviation. The differences of all the measurements between two experts are significant at the $p<0.01$ confidence level (the corresponding $p$ values of BPD, OFD, and HC are $p=0.0015$, $p=8.42\times {10}^{-5}$, and $p=1.15\times {10}^{-5}$, respectively).

Table 2.

Intraobserver and interobserver variability of manual and automatic biometric measurements for fetal head.

Parameters (head)	Intraobserver variability-E1a	Intraobserver variability-E2	Interobserver variability-E1 versus E2	Our method (GT = E1)
BPD (mm)	0.18 (0.52)b	$-0.16(1.23)$	1.23 (1.53)	$-0.038$ (1.38)
OFD (mm)	0.78 (1.66)	$-0.41(2.02)$	2.76 (2.58)	$-0.20$ (2.98)
HC (mm)	1.55 (2.86)	$-0.91(3.79)$	6.37 (5.04)	$-0.72$ (5.36)

^aE1 = Expert 1, E2 =Expert 2.

^bResults are given as an average value (standard deviation) for each measure.

It can also be observed in the last column of Table 2 that the mean difference of BPD between our method and expert 1 reaches $-0.038\mathrm{mm}$ with a 1.38 mm standard deviation, and the mean difference of OFD and HC are $-0.20\pm 2.98$ and $-0.72\pm 5.36\mathrm{mm}$, respectively. The paired $t$-test results showed that there is no significant difference between our method and expert 1 for all biometric measurements at $p=0.90$ of BPD, $p=0.76$ of OFD, and $p=0.54$ of HC.

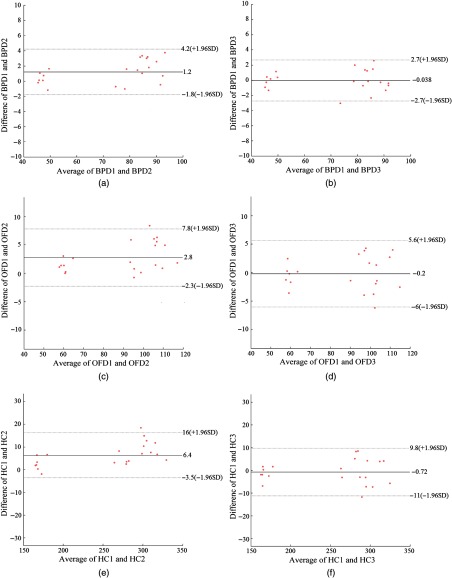
Figure 7 shows the Bland–Altman plots for a set of biometrical measurements (BPD, OFD, and HC) obtained by the automated and manual methods. Compared with the two experts, the mean difference of BPD is 1.2 mm with a 95% confidence interval $-1.8$ to 4.2 mm. The mean difference of OFD is 2.8 mm with a 95% confidence interval $-2.3$ to 7.8 mm, and the mean difference of HC is 6.4 mm with a 95% confidence interval $-3.5$ to 16 mm.

Fig. 7.

Interobserver variability in fetal biometric measurements (BPD, OFD, and HC). (a)–(c) are the interobserver variability between two experts; and (d)–(f) are the differences between automatic and manual measurements, where BPD 1 denotes the expert 1, BPD 2 is expert 2, and BPD 3 denotes automatic measurements, same for OFD and HC.

The relatively large mean differences for all biometric measurements shown in Table 2 (interobserver variability-E1 versus E2) indicate that there are significant inconsistencies between the two experts. The appearances of blurred fetal skull in the poor-quality images are more likely to cause high disagreements for the fetal head delineation. From Fig. 7, we summarize that the 95% limits of agreements for interobserver variability between the automated method and expert 1 measurements are 2.7 mm of BPD, 5.8 mm of OFD, and 10.4 mm of HC. The small inter-observer variability and relatively narrow limits shown in Fig. 7 indicate a good level of agreement between the automatic and the manual measurements. The 95% limits of agreement for HC between the automatic and the manual measurements are also narrower than the recently reported interobserver variabilities exiting in the clinical practice, 11.0 mm of HC⁸ and 12.1 mm of HC.⁷

It is noted that it would be nice to also consider GA comparisons derived from manual measurements and our automated measurements. However, the main reason that the GA evaluation is not included in our current study is because the GA regression equation recommended by Loughna et al.² is suggested to be used to estimate GA ranging from 13 to 25 weeks. In the clinics, the best practice is to establish GA in the first trimester. While for our image dataset, the GA ranges from 20 to 35 weeks (e.g., second and third trimesters). At these stages of pregnancy (second and third trimesters) the scans are generally for growth and not to establish GA, so that comparison of GA may not be very helpful. In the case of growth assessment, our current absolute measurements and their reproducibility are important.

The performance of the automatic fetal US images quality assessment method is validated using the classification parameters of accuracy, specificity, and sensitivity. The classification results are summarized in Table 3. The overall accuracy for automatic image quality classification (good or poor) is 95.24% with 87.5% of sensitivity and 100% specificity. The results demonstrated the good performance of our quality-assessment method. The 100% specificity also indicates that there are no poor images that were misclassified as good images, namely all images that are not captured at the correct imaging plane can be detected.

Table 3.

Evaluation results of automatic fetal US image quality assessment.

Parameters (%)	Our method (%)
Accuracy	95.24
Sensitivitya	87.5
Specificitya	100

^aThe term sensitivity also equals to truth positive ratio and the specificity also equals to 1-false positive ratio.

Our automatic fetal segmentation and image quality assessment algorithm were implemented on a workstation with Interl(R) Core (TM) i7-4770 CPU; 16 GB RAM, using mixed programming languages of MATLAB™ and C++. The portability of our algorithm was also considered. It is a cross-platform application, which was originally developed in Mac OS and Linux and currently we have imported it into Window OS. The portability of our method allows us to easily deploy the algorithm as an embedded system application in different clinical machines. Moreover, on the average, the computation time is 166.53 s per image. We are working on code optimization to further improve the algorithm’s efficiency.

Owing to the long process of the ethical approval and patient recruitment, only 41 patients were involved in the current study. To further validate our method, currently, we are working on collecting more clinical data. In the meantime, we will also consider investigating the method using fetal US videos as recently proposed by Maraci et al.³⁹ The temporal features derived from the neighboring frames in fetal US video data can provide additional information to improve the accuracy of image quality assessment and fetal biometric measurements. Moreover, adapting our current method from 2-D US images to videos that enable the possibility of real-time selection of the correct imaging plane (i.e., image quality assessment) during US image acquisition will be further investigated in the near future.

4. Conclusion

We present an automated method for US fetal head image quality assessment and fetal biometric measurements in 2-D US images. A texton-based fetal head segmentation method is used as a first step to obtain the head region. Both shape- and anatomic-based features (e.g., midline and skull orientation) calculated from the segmented head region using the matched filter designed specific to the US fetal head structure are then fed into an RF classifier to determine whether the image is acquired from a correct imaging plane (e.g., good- or poor-quality image). Fetal head measurements (BPD, OFD, and HC) are then derived from a direct ellipse fitted to the identified skull boundary.

The evaluation results show that our segmentation method outperforms the intervariability between two experts. On average, our method reaches 94.63% precision, 99.27% accuracy, and 0.84 mm ASD. The paired $t$-test and Bland–Altman plots analysis on the automatic biometric measurements show that the 95% limits of agreements for interobserver variability between automatic measurements and expert 1 measurements are 2.7 mm of BPD, 5.8 mm of OFD, and 10.4 mm of HC. These narrow limits indicate a good level of consistency between the automatic and the manual measurements. The overall accuracy for automatic image quality classification (good or poor) is 95.24% with 87.5% sensitivity and 100% specificity. The good performance of our automated-image quality assessment ensures the US image is captured at a correct imaging plane during the obstetric US examination, leading to accurate and reproducible fetal biometric measurements.

Biographies

Lei Zhang is a postdoctoral researcher at the University of Lincoln working in the Laboratory of Vision Engineering (LoVE). His research interests are in computer vision, biomedical image processing, and machine learning, in general, and medical image processing, image segmentation, object detection, and deep learning in particular. His current research aims at learning better primitives of structures to make multimodalities and large-scale vision feasible and affordable.

Nicholas J. Dudley is a principal physicist at Lincoln County Hospital, UK. He graduated from the University of Leicester with his BSc degree in physics with astrophysics, and later received his MSc degree in medical physics from the University of Leeds and his PhD from the University of Derby. He has almost 40 years of experience in medical imaging in the healthcare sector, with over 40 publications, and has interests in ultrasound physics and fetal measurement.

Tryphon Lambrou is an senior lecturer at the Lincoln School of Computer Science, UK, and is also an honorary lecturer with the Department of Medical Physics and Bioengineering, University College London, UK. Previously, he held several postdoctoral positions with the University College London and King’s College London. His research interests include signal/image processing, medical image analysis and segmentation, statistical shape modeling, image registration, and pattern recognition.

Nigel Allinson holds the distinguished chair of image engineering at the University of Lincoln. He has over 30 years of experience in many aspects of capturing, processing, and understanding images. He has cofounded five spinout companies based on the research in his research group. He was awarded the MBE for services to engineering in 2012.

Xujiong Ye is a reader in the School of Computer Science, University of Lincoln, UK. She received her PhD, MSc, and BSc degrees from Zhejiang University, China. She has over 15 years of research and development experience in medical imaging and processing from both academia and industry. She has over 50 publications and has been granted one patent in the fields of medical image processing, computer vision, and machine learning.

Disclosures

The authors declare they have no conflict of interest with regard to the work presented.