Kinetics of Nucleotide Entry into RNA Polymerase Active Site Provides Mechanism for Efficiency and Fidelity

Abstract

During transcription, RNA polymerase II elongates RNA by adding nucleotide triphosphates (NTPs) complementary to a DNA template. Structural studies have suggested that NTPs enter and exit the active site via the narrow secondary pore but details have remained unclear. A kinetic model is presented that integrates molecular dynamics simulations with experimental data. Previous simulations of trigger loop dynamics and the dynamics of matched and mismatched NTPs in and near the active site were combined with new simulations describing NTP exit from the active site via the secondary pore. Markov state analysis was applied to identify major states and estimate kinetic rates for transitions between those states. The kinetic model predicts elongation and misincorporation rates in close agreement with experiment and provides mechanistic hypotheses for how NTP entry and exit via the secondary pore is feasible and a key feature for achieving high elongation and low misincorporation rates during RNA elongation.

Graphical abstract

1. Introduction

The universally conserved process of transcription connects gene storage in DNA to expression of the encoded proteins. The key step in this process is the copy of DNA to RNA to be used as the template for protein synthesis. RNA polymerase (Pol II) is the central enzyme in eukaryotes, synthesizing complementary RNA based on DNA. To carry out this task efficiently and reliably, Pol II must simultaneously achieve low error rates and high RNA synthesis rates. The intrinsic rate of nucleotide misincorporation during processive forward elongation is less than 1 in 1,000, while proofreading by backtracking and with the assistance of TFIIS remove misincorporated nucleotides to further reduce error rates 10- to 100-fold [1–4].

High-resolution atomistic structures of RNA polymerases [5] have motivated detailed mechanistic analyses [6] including elaborate computational studies [7–10]. Nevertheless, it has not been fully resolved how exactly RNA polymerase is able to reliably discriminate between cognate and mismatched nucleotides during RNA elongation. Certainly, base pair formation of canonical vs. mismatched base pairs plays a role, but the effective discrimination against mismatch incorporation greatly exceeds what would be expected from differences in base pair free energies [3]. The trigger loop (TL) in Pol II has been implicated for having a key role in achieving a high degree of fidelity as mutations of the TL and nearby residues are correlated with poor discrimination against non-complementary NTPs [11–14]. It is believed that an open TL is required for NTPs to bind to the active site and that TL closing promotes the advancement towards a catalytically competent state [11, 15–17]. Moreover, experimental and computational studies suggest that closing of the TL is hindered by a mismatched NTP in the active site [15, 18], thereby slowing down elongation rates. On the other hand, structural data and simulations also suggest that mismatched NTPs are unstable in the active site and that they have a tendency to transition to the template-independent entry (E) site located in the secondary pore [18, 19]. This has led to a mechanistic hypothesis where a cognate NTP entering the active site would bind stably, followed quickly by TL closing, and progression to catalysis, whereas mismatched NTPs entering the active site would oppose TL closing and leave through the secondary pore without incorporation [18].

The mechanism described above implies the secondary pore as an exit pathway for mismatched NTPs, the secondary pore is also commonly considered as the main NTP entry path from bulk solvent to the deeply buried Pol II active site [20]. A previous theoretical study of NTP entry via the secondary pore found a significant barrier for entry based on electrostatic analysis [21], but introduction of a kinetic E site allowed entry to the A site on time scales consistent with NTP incorporation rates [21]. Nevertheless, significant narrowing of the secondary pore towards the active site raises doubts to what extent simultaneous entry and exit is possible. As a consequence, the main channel, located between the two largest subunits (β and β′ in bacteria and Rpb1 and Rpb2 in eukaryotes), has been proposed as an alternative entry route based on kinetic experiments [22]. More specifically, transient state kinetics and millisecond phase kinetics results indicate that an NTP complementary to the i+2 template position may affect RNA elongation. This finding would be consistent with NTPs initially binding in the main channel templated to the i+2 DNA base before shuttling to the active site [23]. However, there is no structural evidence of NTP binding in the main channel and the main channel is almost entirely occupied with DNA in the latest crystal structures and models of Pol II with complete transcription bubbles [24, 25]. Simulations have also found that, due to space constraints, NTP entry via the main channel is unlikely [24].

In support of NTP entry via the secondary pore, NTPs have been seen in crystal structures to bind not just to the active site but also to the E site located in the secondary pore [26] and previously suggested to lie on the path towards active site binding [27]. Furthermore, when viewed from the bulk environment, the secondary pore has a strong positive electrostatic potential against a negative background (Fig. 1) that appears to be ideally suited for attracting negatively charged NTPs to the secondary pore. Finally, there is strong inhibition of transcription in the presence of microcin J25 [28], which binds to the secondary pore of bacterial RNA polymerase [29] although contacts with the E. coli RNAP trigger loop could also allow for other possible modes of inhibition.

Figure 1. RNA polymerase II structure, electrostatics, and secondary pore.

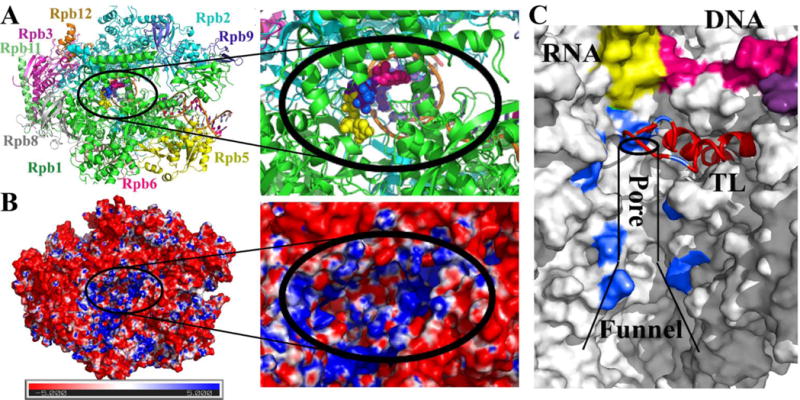
10-subunit S. cerevisiae Pol II complex with open trigger loop and the three initial UTP sites (shown as spheres colored yellow, blue, and pink) that were used as the starting models in this study. Colors distinguish different subunits (Rpb1–4, 5–6, 8–12) and nucleic acid components (A). Electrostatic potential in the secondary pore projected onto the molecular surface according to the Poisson-Boltzmann equation calculated via APBS [30] with red and blue colors indicating negative and positive potentials respectively (B). Secondary pore with the nascent RNA shown in yellow, residues lining the pore used to define the NTP position within the pore (cf. Section 2.1) in blue, and the trigger loop in red (C).

Taken all of the evidence together, it appears that NTPs should both enter and exit the active site via the secondary pore, although it is not entirely clear how this may be possible. Additional questions revolve around whether NTPs simply bind at the A (or E site) or whether there are additional non-specific binding sites, and if so, whether there are mechanistic advantages to secondary pore entry and/or one or more non-specific binding sites. These issues are addressed here via molecular dynamics (MD) simulations. The MD results showed multiple distinct binding states in the pore and provided estimates of relative free energies and kinetic transition rates from Markov state analysis. The simulation data were combined with previous results for mismatch-dependent TL dynamics and A-to-E site transitions as well as experimental data to build a complete kinetic model for NTP entry, discrimination, and RNA incorporation. Simulation of the kinetic model produced elongation and misincorporation rates in agreement with experiment. The results show that simultaneous NTP entry and exit via the secondary pore is indeed possible. Furthermore, alternative hypothetical variations of the model where NTPs did not enter via the secondary pore, bypassed secondary pore binding sites, or were not discriminated between mismatched and cognate bases during active site entry resulted in increased error rates or slowed elongation rates. Taken together, the secondary pore appears to be critical for allowing Pol II to maintain both high elongation and low misincorporation rates.

2. Methods

2.1 Molecular Dynamics Simulations

In a previous study we simulated the 10-subunit S. cerevisiae Pol II complex consisting of Rpb1–3, Rpb5–6, and Rpb8–12 with open (PDB ID: 2E2J) and closed TL (PDB ID: 2E2H) conformations based on crystal structures with cognate and mismatched NTPs placed in the active site [11, 18]. In those simulations, we observed spontaneous transitions from the A to the E site for mismatched CTP and UTP which served as the starting point for the present work. As in our previous work, we considered Pol II in atomistic detail embedded in explicit solvent with counterions [18]. Here, MD simulations of the 10-subunit Pol II complex were carried out to sample UTP dynamics in the secondary pore. As in previous simulations, UTP was modeled in complex with Mg²⁺ and coordination with the Mg²⁺ ion was largely retained throughout the majority of the simulations (see Section 3.1). Since direct simulation of diffusion of a substrate from the bulk to a buried active site is difficult, we searched for an exit channel starting with the UTP bound inside Pol II. Random acceleration molecular dynamics (RAMD) were used to drive the UTP to the bulk solvent in order to explore possible exit pathways. In RAMD simulations [31], random forces are added to a group of atoms (usually a ligand) to reduce the distance between the ligand and the protein surface in otherwise conventional MD simulations. More specifically, a random force F = m kr₀ with a force constant k=0.25 kcal/mol/Å/amu was applied to UTP atoms with mass m with the direction vector r₀ changing randomly every 50 steps (0.1 ps). RAMD simulations were started from three initial UTP conformations near the A and E sites from previous simulations [18]. Simulation snapshots instead of crystal structures were used to avoid the need for extensive additional equilibration and to allow the combination of results with our previous simulations. 100 separate RAMD simulations were carried out until a maximum distance of 80 Å between the centers of mass of the protein and the UTP were reached. This led to an ensemble of exit path trajectories ranging in length between 500 ps and 40 ns. From the initial RAMD simulations snapshots were projected onto the second pore normal and 20 representative snapshots were selected with an interval of 4 Å along the pore normal to cover the entire secondary pore (Fig. S1). Each snapshot from the RAMD simulations then served simply as a starting structure for additional unbiased MD simulations. For each snapshot, four replicates of 50 ns unbiased MD simulations were carried out with different initial velocities resulting in a total amount of sampling of 4 μs. All of the simulations were carried out with NAMD, version 2.9, using the CHARMM27/36 parameter set [32, 33] for the protein and nucleic acids and the TIP3P model [34] for water. Modifications of parameters for deprotonated cysteines and the 3′-OH group of the terminal RNA base are described in our previous paper [16]. The parameters for UTP were built by combining the existing parameters for ATP and nucleic acids. The electrostatic interactions were calculated via the particle-mesh Ewald method [35]. Van der Waals interactions and the direct electrostatic sum were truncated at 10 Å with a switching function effective at 8.5 Å. All of the heavy atom-hydrogen bonds were constrained by the SETTLE algorithm [36] to allow a time step of 2 fs. A Langevin thermostat and barostat were used to maintain an NPT ensemble at 298 K and 1 bar. The Multiscale Modeling Tools for Structural Biology (MMTSB) Tool Set [37] was used for analysis. Structural figures were generated using VMD [38].

From the unbiased trajectories, 10,000 snapshots were extracted at 5 ps intervals from each of the 80 simulations, skipping the first 5 snapshots (25 ps) of each trajectory. In one simulation, the UTP left the simulation box and entered on the other side of the enzyme and therefore only part of that trajectory was utilized. The total of nearly 800,000 snapshots was used to generate a two-dimensional potential of mean force (PMF) as a function of two pore distance coordinates (Fig. S1). The snapshots were also submitted to MSMBuilder [39], version 3.3, to construct an MSM and extract relative populations and kinetic rates between different states. Pairwise distances between the UTP (atoms C1′, PG, and C2) and selected residues lining the secondary pore and near the active site (Rpb1 N479, D485, E593, K620, R720, K752, F755, L824, T827, N953, L1081, H1085, S1091, G1360) were used as the feature for clustering conformations into microstates. K-centers clustering was used to generate 100 microstates. Using a lag time of 25 ns, the microstates were combined into 41 macrostates by MSMBuilder. Further projection onto the two-dimensional PMF and visual inspection of the resulting macrostates led to grouping into six major states based on spatial proximity of the UTP locations in the secondary pore (cf. Section 3.1).

2.2 Kinetic network model

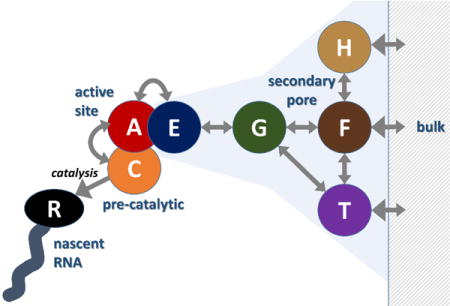
A kinetic network model for NTP entry/exit and RNA elongation was constructed using results from the MSM and previous MD simulations and experimental data (Fig. 3A, Table 1). The NTP-centric model consisted of nodes for the A, E, G, F, T, and H secondary pore binding sites and a catalytically competent C state that is reached after the TL closes with an NTP in the A site. Each of these nodes can be empty or occupied by either a cognate or mismatch NTP. The F state is broad enough to allow occupancy by up to four NTPs but we limited simultaneous occupancy to two copies assuming that electrostatic repulsion would be too large with more copies. NTP occupancy for E, G, F, T and H sites was considered to be independent of each other. The occupancy of A, E, and C sites is mutually exclusive because multiple NTPs would spatially overlap if simultaneously present. NTPs can enter the model from bulk solvent by binding to F, H, or T sites. The catalysis step removes an NTP from the C site to elongate RNA. Based on the MSM, the H site only connects to the F site. From the F and T sites the G site can be reached, and only the G site connects to the E site.

Figure 3. Kinetic network model and predicted elongation and misincorporation rates.

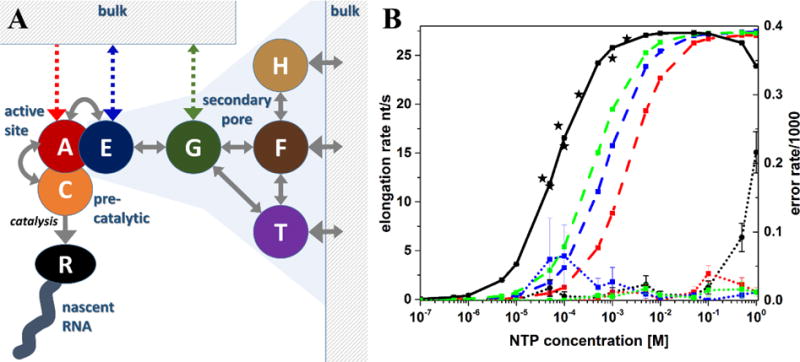
Kinetic network model capturing NTP entry and RNA elongation with the main model represented by solid gray lines and alternate, hypothetical NTP entry pathways indicated as dashed lines (A). Elongation (black solid line and colored dashed lines; left scale) and misincorporation (dotted lines; right scale) rates as a function of bulk NTP concentration predicted from kinetic model. Black lines show results for full kinetic network model. Red, blue, and green lines correspond to alternative models where NTPs directly enter A, E, or G sites, respectively. Experimental pause-free elongation rates from single-molecule study of Pol II [40] are shown as black stars (B).

Table 1.

Kinetic network parameters.

Transition	States	Forward rate		Backward rate		Source
		Cognate	Mismatch	Cognate	Mismatch
Bulk entry to secondary pore	bulk – H	0.75 μs−1 M−1		3.8 μs−1		MSM/Exp.[40]
	bulk – F	1.35 μs−1 M−1		0.55 μs−1		MSM/Exp.[40]
	bulk – T	1.42 μs−1 M−1		0.18 μs−1		MSM/Exp.[40]
Secondary pore dynamics	H – F	6.8 μs−1		1.2 μs−1		MSM
	F – T	5.2 μs−1		1.5 μs−1		MSM
	T – G	0.76 μs−1		0.28 μs−1		MSM
	F – G	2.8 μs−1		0.58 μs−1		MSM
E site binding	G – E	3.4 μs−1		1.8 μs−1		MSM
Active site binding	E – A	13.1 μs−1		0.08 μs−1	25.8 μs−1	MD[18]
Trigger loop closing	A – C	150 s−1	15–150 sc−1	5 s−1	5–4,450 s−1	MD[41]/Exp.[17]
NTP incorporation	C – R	35 s−1	0.7 s−1	0	0	Exp.[15, 40]

Transitions and associated kinetic rates used in kinetic network model. If no rate is given for mismatch bases, the rates for cognate bases were applied. Rates estimated directly from MD have a lower limit of about 0.25 μs⁻¹ based on the total aggregate simulation time used for constructing the MSM model.

Bidirectional kinetic rates between the E, G, T, F, and H states were obtained from the MSM output. More specifically, since we combined several macrostates into superstates (see Table 2 and Section 3.2), we estimated rates between superstates based on the average rate for all macrostate pairs that connect those two superstates. The rates for binding to T, F, and H states were estimated based on rates from bulk solvent macrostates but scaled to match RNA elongation rates as a function of NTP concentration obtained from experimental data [40]. The fit to the experimental data was necessary because we did not explore the full ligand binding landscape in the simulations. The resulting binding rates were on the order of 1 μs⁻¹M⁻¹ consistent with NTP binding rates (k_on) in other enzymes of 0.5–1 μs⁻¹M⁻¹ [42, 43]. Since the simulations underlying the MSM only considered UTP, a central assumption is that binding sites and transition rates are not strongly dependent on the nucleotide type.

Table 2.

Secondary pore binding states.

Superstate	MSM Macrostates	ΔG [kcal/mol]	Interacting residues	Mutants
E	2, 13, 29	−3.87	R766B*, R1020B*, K752*	R1020A
G	8, 26, 33	−3.10	K752*, R619*, K518
T	6, 19, 24, 32	−2.44	R726*, H1085*	R726H/P, H10851
F	0, 3, 10–12, 16, 18, 20, 22, 27, 31, 36, 40	−3.65	K1290, K1300, R731, R720, K1286, R590, K620
H	5, 14, 21, 28, 30, 39	−2.84	R19B, K601
Bulk	1, 4, 7, 9, 15, 17, 23, 25, 34, 35, 37, 38	0.0	N/A

Superstates of UTP in the secondary pore with free energies relative to bulk solvent, contributing MSM macrostates, and key interacting secondary pore residues. Mutants with known effects on RNA elongation or misincorporation rates are listed as well.

Superscripts indicate Pol II subunits

^Bfor Rpb2;

^Hfor Rpb8

^*: fully conserved.

¹many mutations are lethal, some have altered elongation rates and/or altered phenotypes in the context of double mutants [46, 47].

The kinetics for the A-E transition was estimated from previous MD simulations where spontaneous transitions from the A to the E site were observed for mismatched NTPs during 100-ns simulations and PMFs for the A-E transition were calculated for cognate and mismatched base pairs [18]. We assumed Arrhenius behavior and estimated A to E rates according to barrier heights in the PMFs to be proportional to e^{−4.2 kcal}/^mol/kT and e^{−0.8 kcal/mol/kT} at 298K for cognate and mismatch nucleotides, respectively using a pre-factor of 100 μs⁻¹ to obtain rates in the tens of nanoseconds range for mismatches to be consistent with the time scale of spontaneous A to E transitions. We also explored pre-factors of 1 and 10 μs⁻¹ but found little difference in the results (Table 3). The reverse (E to A) rates were then obtained simply based on the free energy differences between the A and E sites in the PMFs. We obtained identical rates for the E to A transition for either cognate or mismatch NTPs (Table 2), without imposing such a requirement, but consistent with the expectation that mismatch NTPs would not be distinguished until the A site is reached.

Table 3.

Elongation and error rates at [NTP] = 5 mM from kinetic network simulations.

Mism. catalyt. rate [s−1]	TL closing1 [ms−1]	AG (TL mism.)2 [kcal/mol]	E➔A rate [μs−1]	E/G/H/T/F rate scaling	Elongation rate [nt/s]	Error rate [1/1000]	Mismatch elongation rate3 [nt/s]
35	0.15	1	13.1	1	27.2 (0.07)	0.484 (0.068)	0.691 (0.014)
17.5	0.15	1	13.1	1	27.2 (0.05)	0.291 (0.067)	0.341 (0.010)
3.5	0.15	1	13.1	1	26.9 (0.10)	0.058 (0.021)	0.078 (0.003)
0.7	0.15	1	13.1	1	27.1 (0.04)	0.023 (0.013)	0.017 (0.001)
0.35	0.15	1	13.1	1	27.1 (0.06)	0.030 (0.015)	0.025 (0.014)
0.7	0.08	1	13.1	1	22.5 (0.04)	0.049 (0.030)	0.023 (0.005)
0.7	0.08/0.008	1	13.1	1	22.6 (0.06)	0.010 (0.010)	0.021 (0.002)
0.7	0.15/0.015	1	13.1	1	27.1 (0.08)	0.035 (0.019)	0.030 (0.007)
0.7	0.30	1	13.1	1	30.0 (0.09)	0.000 (0.000)	0.018 (0.005)
0.7	0.30/0.030	1	13.1	1	29.9 (0.08)	0.007 (0.007)	0.022 (0.005)
0.7	0.15	1	1.31	1	27.0 (0.06)	0.011 (0.008)	0.017 (0.003)
0.7	0.15	1	0.13	1	27.1 (0.08)	0.017 (0.009)	0.020 (0.001)
0.7	0.15	1	13.1	0.1	26.9 (0.04)	0.012 (0.006)	0.029 (0.009)
0.7	0.15	1	13.1	0.01	25.0 (0.06)	0.055 (0.015)	0.019 (0.002)
0.7	0.15	2	13.1	1	27.1 (0.06)	0.000 (0.000)	0.033 (0.031)
0.7	0.15	0	13.1	1	27.0 (0.06)	0.037 (0.014)	0.076 (0.007)
0.7	0.15/0.015	0	13.1	1	27.1 (0.17)	0.062 (0.033)	0.065 (0.005)
0.7	0.15	−2	13.1	1	25.6 (0.08)	1.622 (0.091)	0.568 (0.017)
0.7	0.15/0.015	−2	13.1	1	26.4 (0.09)	0.733 (0.067)	0.200 (0.000)
0.7	0.15	1	13.14	1	14.7 (0.03)	3.543 (0.316)	0.117 (0.004)
0.7	0.15	1	A5: kon=1 μs−1M−1		19.3 (0.02)	0.011 (0.011)	0.001 (0.000)
0.7	0.15	1	13.1	E6: kon=1 μs−1M−1	23.9 (0.05)	0.009 (0.006)	0.002 (0.000)
0.7	0.15	1	13.1	G7: kon=1 μs−1M−1	25.3 (0.03)	0.017 (0.008)	0.009 (0.004)

¹:two values indicate different TL closing rates for cognate/mismatch bases;

²:difference in free energy between open and closed trigger loop in the presence of a mismatched NTP in the active site (positive values indicate that TL closing is unfavorable in the presence of a mismatched NTP);

³: in the absence of cognate bases;

⁴: A-E rates were the same for mismatches and cognate bases;

⁵: NTPs enter A site directly (k_off=0 and exit via secondary pore is possible);

⁶: NTPs enter and exit E site directly bypassing G/H/T/F states (k_off=0.55 μs⁻¹, same as F-bulk rates);

⁷: NTPs enter and exit G site directly bypassing H/T/F states (k_off=0.55 μs⁻¹, same as F-bulk rates). Parameters that, consistent with experiment, result in overall elongation rates around 26–27 nt/s [40] and mismatch elongation rates that are reduced by about three orders of magnitude [44, 45] are shown in bold. Statistical errors estimated from block averaging by comparing results for 1,000 s segments from the kinetic simulations are given in parentheses.

The A-C transition depends primarily on TL closing, which we also studied previously via MD simulation [41]. A PMF obtained previously suggests that the open TL state is about 2 kcal/mol less favorable than the closed TL state when a cognate NTP is present in the active site [41] corresponding to a ratio between forward and backward rates of 30. The highest transition state barrier for TL closing was estimated to be about 5 kcal/mol, but this value likely underestimates the real transition state barrier and additional smaller barriers exist. Therefore, TL transition rates are at the minimum on the microsecond scale, but they could be much longer. A recent kinetic analysis of E. coli RNA polymerase found an optimal fit of pause-free velocities as a function of NTP concentration with a TL closing rate of 150 s⁻¹ at near-saturating NTP concentration of 1 mM [17]. Despite differences between prokaryotic and eukaryotic RNA polymerases, we found that using this value resulted in good agreement of the elongation rate at saturating conditions with experimental data for the eukaryotic RNA polymerase [40]. When using faster or slower TL closing rates, maximal elongation rates become significantly over- or underestimated (Table 3). Depending on when the major kinetic barrier is encountered during TL closing, the A-C rate may or may not differ between cognate and mismatch bases and we tested a range of values from 15 s⁻¹ to 150 s⁻¹ for the A-C rate in the presence of a mismatch base. The relative free energy of the closed TL with a mismatch was assumed to be higher than with a cognate base consistent with the spontaneous TL opening in the presence of a mismatch seen in previous simulations. A difference of 1 kcal/mol already gives error rates well below 1/1,000 (Table 3) but we also tested the effect of larger and smaller free energy differences (2 and 0 kcal/mol). We note that TL closing is only accounted for in the A-C rate, or in other words, closing of the TL without an NTP in the A site is not considered here. E-A transition and A-C transitions were modeled as independent kinetic processes. It is possible that these processes are dynamically coupled, which would accelerate the A-C transition in our model, or that TL closing in the absence of an A site nucleotide may hinder NTP entry, which would slow down the E-A transition in our model. However, we are using effective TL closing rates from experiments to describe the A-C kinetics without any assumptions about the exact mechanism. Furthermore, we found that slower E-A rates do not have a strong effect in our model.

The catalytic rate was set to 35 s⁻¹ based on previous kinetic analyses [15, 40]. This rate covers not just the actual bond formation step but also the following pyrophosphate release, nucleic acid translocation and TL opening steps that are necessary to complete the cycle and allow the next NTP to bind to the active site [16]. Catalytic rates for mismatches are expected to be slower. We tested values from 0.35 s⁻¹ to 35 s⁻¹ and analyzed mismatch incorporation rates in the absence of cognate bases. A mismatch catalytic rate of 0.7 s⁻¹ (1/50th of the cognate base catalytic rate) resulted in an approximately 2,000-fold reduction for mismatch incorporation rates vs. cognate base incorporation (see Table 3), consistent with experimentally observed rate reductions by three orders of magnitude for different types of mismatches [44, 45]. We subsequently used this value in our kinetic model.

The kinetic model was simulated using an in-house program where each state could be either empty or occupied by a cognate or mismatch NTP. Transitions would change the occupancy of states by either binding NTPs to binding sites, moving NTPs between connected states, or accumulating NTPs that are incorporated into elongated RNA. Transitions were allowed to occur stochastically according to probabilities p = τ * r from the kinetic rate r and a fixed simulation time step τ. More specifically, at each time step, the simulation algorithm loops through all of the transitions, draws a random number between 0 and 1 and if the random is lower than the transition probability and the transition is possible, it is executed. For example, a transition from A to E could only occur if A is occupied and E is empty. The simulation time is then advanced by the time step and the algorithm is repeated. Using a time step of 10 ns, simulations were carried out until 10,000 s were reached, during which incorporated cognate and mismatched NTPs were accumulated. Simulations were repeated as a function of NTP concentrations and model parameters.

Simulations were also carried out for alternate models, where NTPs enter directly to the A, E, or G sites to explore the importance of the E, G, F, T, and H sites (see Table 3). In these models, binding to the T, F, H sites was disabled. When entering via the A site, NTPs could exit but not enter via the secondary pore via E, G, T, F, and H sites to model a scenario where NTPs enter via the main channel and exit via the secondary pore. When entering via the E site, G, H, T, and F states were ignored and, when entering via the G site, H, T, and F states were ignored to model hypothetical scenarios without those additional binding sites in the secondary pore.

3. Results

3.1 NTP sampling in the secondary pore

MD simulations of the 10-subunit Pol II complex were carried out to sample UTP dynamics in the secondary pore. In all cases, the UTP exited through the secondary pore via a broad ensemble of pathways (Fig. 2A). Separate exit pathways were identified from visual inspection based on how NTPs exited relative to the TL. The main path (86%; black pathway in Fig. 2A) goes besides the TL. Two additional paths go through (6%; red pathway in Fig. 2A) and above the TL (8%; blue pathway in Fig. 2A). The TL adopts somewhat different conformations as the NTPs exit via the different pathways, but, in all cases, the TL remained in the open form (see Fig. S4). The initial paths were further refined by unbiased MD simulations with a fully flexible Pol II complex for a total of 4 μs simulation. Individual unbiased simulations were too short to observe UTPs spontaneously diffusing through the entire pore in a single trajectory, but there was extensive overlap between different simulations (Fig. S1) and individual trajectories showed partial transitions between different states (Fig. S1). A comprehensive thermodynamic and kinetic picture of NTP-secondary pore interactions could thus be constructed (Fig. S1).

Figure 2. NTP exit pathways via secondary pore from molecular dynamics simulations.

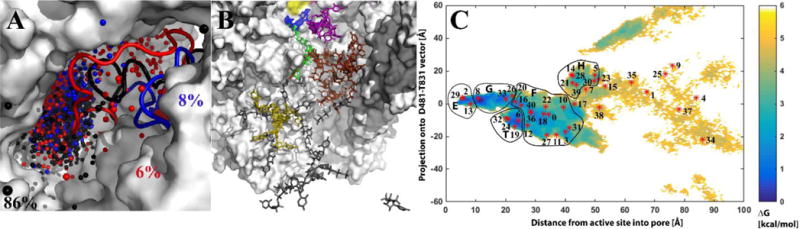
Secondary pore exit pathways based on NTP center of mass positions (shown as black, red, and blue spheres) from 100 RAMD simulations projected onto the initial structure of Pol II. The trigger loop is shown in cartoon representation and colored corresponding to each pathway. Percentages indicate the relative occurrence of each pathway (A). Macrostates from MSM shown as UTP orientations within the secondary pore of the initial structure of Pol II. Conformations grouped into superstates are colored as follows: E, blue; G, green; T, purple; F, brown; H, tan; and bulk, grey (B). PMF for NTP positions in the secondary pore from snapshots of unbiased simulations as a function of the distance from the active site and projection onto the Cα D481→Cα T831 vector. Binding states used in the kinetic model (Fig. 3) are indicated as letters (C).

UTP sampling was projected onto two orthogonal reaction coordinates (Fig. S1) and a PMF was calculated (Fig. 2C). The sampling at the active and E sites is constrained but as the pore widens into the funnel, multiple minima appear. The minima correspond to kinetically and structurally distinct states as described in detail below and were named G (gate), F (funnel), T (trigger loop), and H (hind funnel) (Fig. 2C). The T state was observed only in the two minor paths.

The simulations indicate that the NTPs are attracted to the secondary pore relative to bulk solvent. The most favorable binding is at the E site with about 4 kcal/mol stabilization relative to bulk solvent, but binding at the other states is also favorable (Table 1). Our results agree partially with a previous continuum electrostatic analysis of secondary pore energetics [21] that reported an attractive outer funnel region, although we do not find as significant of a barrier for entry into the E site. The difference in observations may be due to the more detailed atomistic model with full dynamics of both the enzyme and UTP.

At all binding sites, the UTP triphosphate tail is restrained by electrostatic interactions, while the pyrimidine group is flexible and formed various hydrogen bond interactions within the pore. Key amino acid residues for binding to the E site are R766^B, R1020^B and K752. The G site is formed by R619, K752, and in part by K518, and the T site involved R731 and the protonated H1085 (Table 2 and Fig. S2). All these residues are fully conserved except for K518. The F state consisted of four main binding sites interacting with a variety of non-conserved residues. The H site locates between the funnel and the bulk, formed by R19^B and K601. The UTP retained a coordinated Mg²⁺ ion at the E, G and F sites, but only sodium ions were associated with the UTP when bound to the T and H states and in bulk (Fig. S3). We note that additional free Mg²⁺ ions were not present in the solvent. Concentrations of free Mg²⁺ are less than 1 mM under biological conditions [48] which would translate to at most one free Mg²⁺ ion for the entire simulation system, which, if included, would require substantially longer simulation times to obtain adequate sampling convergence. An additional Mg²⁺ could facilitate the rebinding of Mg²⁺ to the NTPs instead of the sodium in the T, H and bulk states, which may in turn affect the binding and kinetic data extracted from the simulations. More specifically, if the UTP was associated with only one Na⁺ ion instead of Mg²⁺, the remaining larger unscreened charge could lead to stronger binding and slower kinetics with respect to T and H states. However, since UTP-Mg²⁺ binding to F sites resulted in similar energies and kinetics as for T and H states, we expect this effect to be only moderate at worst.

A Markov state model (MSM) was built from the combined set of trajectories (cf. Section 2.1) to obtain kinetic information. When using lag times of tens of nanoseconds, the number of macrostates and implied timescales stabilized (see Figs. S5 and S6). With a lag time of 25 ns we obtained 41 macrostates (Fig. 2B), 12 of which were considered bulk solvent based on the average UTP location (Table 2). The remaining 29 states were grouped by visual inspection into five superstates: E, G, F, T, and H (Table 2). The grouping was determined based on conformational overlap to obtain UTP-pore interaction sites that are both kinetically and structurally distinct. Mapping of several macrostates onto each of the superstates (Table 2 and Fig. 2C) suggests that conformations more readily transition to other sites within the secondary pore than interconvert within the same site.

3.2 Kinetic network model simulation

An NTP-centric kinetic network model was constructed for NTP entry/exit via the secondary pore, binding to the active site, closing of the TL, and RNA elongation (cf. Section 2.2). The kinetic model was simulated using a stochastic algorithm. Fig. 3 shows the resulting elongation and misincorporation rates as a function of NTP concentration averaged from simulations over 10,000 s. The reported concentration refers to the cognate NTP while the concentration of mismatch NTPs was assumed to be three times greater (to account for the three other NTPs). Deoxy-NTPs were not considered here since dNTP concentrations are significantly lower than NTP concentrations [49]. The simulation results compare favorably with experimental elongation rates from a previous single molecule analysis [40]. Saturation was reached at an NTP concentration of about 5 mM after which the elongation rate remained constant until about 100 mM. At even higher, physiologically not relevant concentrations, elongation rates decrease slightly. Predicted misincorporation rates are less than 0.5 in 10,000 base incorporations for concentrations up to 100 mM but increase sharply beyond 100 mM, presumably due to congestion in the secondary pore that prevents the exit of mismatched NTPs.

Various aspects of the model were subsequently varied. Reduced forward and backward rates for the A-E transition and transition rates between E, G, T, F, and H states by factors of 10 and 100 had little impact on the results (Table 3). The largest effect was a slight reduction in elongation rates when E/G/H/T/F rates were reduced 100-fold. This would be expected since these rates are fast compared to the TL closing and catalytic rates but it also means that uncertainties in the estimation of these rates within 1–2 orders of magnitude are not critical. We note, that a reduction in E/G/H/T/F rates by one order of magnitude has a negligible to small effect across a wide range of NTP concentrations, a 100-fold E/G/H/T/F rate decrease does lead to reduced elongation rates at very low (0.05 mM) and high (500 mM) NTP concentrations as well as significantly increased error rates at 500 mM NTP (see Table S1).

TL closing rates in the presence of a cognate base strongly effect elongation rates and the rate used here was chosen to reproduce experimental data. The presence of a mismatch is known to hinder TL closing, but it is unclear whether the selection against mismatches by the TL is mostly kinetic, mostly thermodynamic, or both. Thermodynamic selection is based on the relative free energy of a mismatched NTP with a closed TL. From previous simulations we found that the closed TL is more stable than the open TL by 2 kcal/mol in the presence of a cognate base. Assuming the same relative free energy (−2 kcal/mol) for a mismatch base results in large error rates (Table 3) while ten-fold slower TL closing rates led to two-fold lower but still high error rates. On the other hand, if the mismatch is less stable with a closed TL error rates are reduced dramatically whereas reduced TL closing rates in the presence of a mismatch had little further effect (Table 3). This seems to suggest that selection against mismatches by the TL is largely controlled by thermodynamics rather than altered TL closure kinetics in the presence of a mismatch.

Mismatch binding to the A site is assumed to be less favorable than for cognate bases resulting in faster A-E transition rates for mismatches. Consequently, setting A-E rates for mismatches to the same value as for cognate bases while maintaining selectivity against mismatches during TL closing resulted in large error rates as well as significantly reduced elongation rates. In this case, mismatched NTPs would become competitive inhibitors to the polymerization reaction when they cannot quickly leave the A site. This is not supported by the experimental data since elongation rates are only slightly affected even at very high NTP concentrations [40] and illustrates the importance of one or more pre-insertion sites to allow the rapid selection of cognate NTPs. Consistent with these findings, S476I/N479Y and E529Q mutations, which interact with intermediate states of the A-E transition have been reported to lead to slow and error-prone Pol II while substitutions of E529 to shorter sidechains (E529A/D) lead to faster elongation [50, 51].

So far, we assumed NTP entry and exit via the T/F/H secondary pore binding sites. In alternative scenarios, NTPs may directly enter the A site via the main channel while exiting only via the secondary pore, enter and exit the E site directly without visiting G/T/F/H states, or enter and exit the G site directly bypassing the T/F/H states at the outer regions of the pore. We explored these scenarios and found in all cases low error rates similar to the full kinetic model (Table 3) suggesting that secondary pore entry is not essential for fidelity. However, assuming k_on rates for A site, E site, or G site binding of 1 μs⁻¹ M⁻¹, a typical value for NTP binding to enzymes [42, 43], led to underestimated elongation rates at low concentrations (Table 3 and Fig. 3). In order to match the concentration-dependent elongation rates from experiment [40], it would be necessary to set k_on=33 μs⁻¹ M⁻¹ for direct A site binding, k_on=11 μs⁻¹ M⁻¹ for direct E-site binding, and k_on=6 μs⁻¹ M⁻¹ for direct G-site binding, all of which are larger than the optimized k_on rates for H/F/T state binding of 0.750–1.4 μs⁻¹ M⁻¹ in the full kinetic model (Table 1). Essentially, this analysis reproduces the thermodynamic gradient in the secondary pore, but it illustrates that such a gradient is necessary to achieve the experimental elongation rates given physiological NTP concentrations and typical k_on rates for the initial NTP binding sites when NTP enter Pol II from the bulk.

4. Discussion

We present extensive simulations of NTP dynamics in the secondary pore from which a kinetic network model was constructed for NTP entry and exit via the secondary pore. The model was coupled with previous results for the mismatch-dependent A-E transition and TL dynamics to arrive at a complete NTP-centric kinetic model for NTP entry and RNA incorporation. One key insight of this work is that Pol II function can be achieved with NTPs entering and exiting primarily via the secondary pore, a view that so far has not been universally accepted. The kinetic network model built based primarily on MD results generates high elongation rates close to experimental values and very low misincorporation rates, well below 1 in 1,000. Our analysis emphasizes the central role of the A site in selecting mismatches based on differential thermodynamic stability and supports that both the mismatch-sensitive A to E transition and TL closure are key determinants of fidelity.

A second insight is that multiple binding site in the secondary pore appear to be the key for simultaneously achieving high elongation and low error rates. According to our analysis, there are multiple distinct NTP binding sites in the secondary pore with favorable binding free energies relative to bulk solvent. NTPs are thermodynamically attracted to reach the E site, but we identified an additional kinetically-distinct intermediate site, termed the G site, between the initial NTP binding sites and the E site, so that binding of NTPs to the A site (or even the E site) from bulk solvent does not occur directly but via several kinetic intermediate steps. The kinetics for transitions between secondary pore binding sites estimated here are fast relative to TL closing rates so that NTP transitions in the secondary pore are not overall rate-limiting and do not appear to contribute directly to fidelity. Nevertheless, the presence of multiple binding sites in the secondary pore with transitions on microsecond time scales provides a mechanism for allowing the simultaneous exit and entry of NTPs as mismatches leave and cognate bases enter the active site. When alternate scenarios were considered where entering NTPs bypass the initial T/H/F binding sites, the intermediate G site, or the secondary pore altogether led to lower elongation rates, especially at low NTP concentrations when typical kon rates for NTP binding were assumed. This implies that the multiple secondary pore NTP binding sites, in particular the T, H, and double-occupancy F sites, may serve as a staging platform that can accommodate all four types of NTPs simultaneously and from where NTPs would transition one by one to the A site (via the G and E sites) until the cognate base is added to the RNA. Our emphasis on multiple non-specific NTP binding sites is consistent with earlier kinetic modeling of the NTP addition cycle by Larson et al. [15], but differs from the assumption of just a single NTP binding in the kinetic analysis by Dangkulwanich et al. [40]. In the latter case, model fitting to experimental elongation rate measurements resulted in an NTP binding equilibrium constant K = k_off/k_on of about 9.2 μM. In our model, the overall binding equilibrium from bulk to the A site obtained by multiplying equilibrium constants for binding via multiple sites (e.g. bulk➔T➔G➔E➔A) using the rate constants given in Table 1, is about 150 μM, an order of magnitude larger, but this may be considered comparable within the uncertainties of the different kinetic models. However, if there was just a single NTP binding site and one assumes that k_off is at least 1 ms⁻¹ consistent with previous assumptions [40], K = 9.2 μM implies k_on>100 μs⁻¹ M⁻¹ which is two orders of magnitude larger than typical NTP binding site k_on rates. So, again, we would make the argument that a single NTP binding site without any intermediate non-specific binding sites is not sufficient to explain the observed concentration-dependent elongation rates.

Our model describes cognate and mismatch bases in a generic manner without considering DNA sequence effects. A more detailed model would consider different concentrations for different NTPs under physiological conditions and differences in kinetic rates and secondary pore interactions as a function of NTP type and require additional simulation data for parametrization. Moreover, we do not consider backtracking and pausing that is believed to occur in a mismatch-dependent manner [10, 45, 52]. The coupling of pyrophosphate release to Pol II dynamics and a possible interference with NTP entry or exit via the secondary pore was also ignored.

The results presented here rely to a large extent on results from MD simulations that may be unreliable in accurately estimating kinetic rates. However, the rates estimated from MD apply to the fastest rates where variations by two orders of magnitude can be tolerated without affecting the overall results significantly. To further validate our model, we suggest new Pol II mutants that would be expected to exhibit altered kinetic properties. More specifically, we speculate that mutations of residues involved in coordinating an NTP in the G and E site would affect overall elongation rates, especially at low NTP concentrations. Residues involved in binding NTPs at the T, F, H sites are expected to be less sensitive because of redundancy.

Although we studied the eukaryotic Pol II enzyme here, the general findings should be equally relevant for bacterial and archaeal RNA polymerase because of structural and functional similarities and similar kinetic behavior. Therefore, the detailed picture of NTP binding sites in the secondary pore of Pol II could serve as a basis for developing new small molecule inhibitors of bacterial RNA polymerase in potential antibacterial applications. We propose inhibitors that target the G and E sites specific to the bacterial environment.

Our model focuses on NTPs but it could be combined with the Pol II-centric kinetic models developed by the Huang group that consider translocation, backtracking and pausing, bridge helix dynamics, and pyrophosphate release [8, 10]. Explicit consideration of translocation, bridge helix dynamics, and pyrophosphate release by itself and possibly coupled with NTP entry would provide a better basis for estimating the A➔C transition rate in contrast to our current model where all of these processes are lumped together with the chemical catalysis step into a single rate that was fit to experimental data. Furthermore, the consideration of backtracking and pausing, also likely coupled to NTP entry and in particular the presence of mismatches, would result in a more complete kinetic model for the entire functional cycle of Pol II rather than current model that can only estimate pause-free elongation and error rates.

5. Conclusions

A comprehensive kinetic model for NTP entry and RNA incorporation within Pol II is presented based on previous simulations, new simulations of an NTP in the secondary pore, and experimental data. The main conclusion from this work is that simultaneous entry and exit of NTPs via the secondary pore is possible and a key feature of achieving both high elongation rates and low error rates in Pol II. Our model predicts that efficient mismatch discrimination requires not just mismatch-dependent TL closing but also a mismatch-sensitive A-E transition that allows mismatched NTPs to quickly shuttle in and out of the active site while cognate NTPs remain stably bound. The detailed view of NTP binding in the secondary pore suggests residue mutations to be tested in biochemical studies but also provides a basis for the development of RNA polymerase inhibitors that bind in the secondary pore. Future work aims at expanding our current NTP-centric model to provide a comprehensive view of all kinetic steps involved in RNA elongation by Pol II.

Highlights.

• NTP entry pathways during transcription from simulations and network modeling

• Multiple kinetic checkpoints enable high fidelity and elongation rates

• Secondary pore entry and exit is possible and a key feature of efficient elongation

Abbreviations

CHARMM

Chemistry at Harvard molecular mechanics

DNA

deoxyribonucleic acid

MD

molecular dynamics

NMR

nuclear magnetic resonance

MMTSB

multi-scale modeling tools in structural biology

MSM

Markov state model

NAMD

nanoscale molecular dynamics

NPT

constant number of particles, pressure, and temperature ensemble

NTP

nucleotide triphosphate

PDB

protein data bank

Pol II

RNA polymerase II

PME

particle-mesh Ewald

RAMD

random acceleration molecular dynamics

RNA

ribonucleic acid

RpbX

RNA polymerase bX domain, TFIIS, transcription factor II-S

TIP3P

transferable interaction potential-3 point

TL

trigger loop

UTP

uridine triphosphate

VMD

visual molecular dynamics