Perceptual Category Learning and Visual Processing: An Exercise in Computational Cognitive Neuroscience

Abstract

The field of computational cognitive neuroscience (CCN) builds and tests neurobiologically detailed computational models that account for both behavioral and neuroscience data. This article leverages a key advantage of CCN – namely, that it should be possible to interface different CCN models in a plug-and-play fashion – to produce a new and biologically detailed model of perceptual category learning. The new model was created from two existing CCN models: the HMAX model of visual object processing and the COVIS model of category learning. Using bitmap images as inputs and by adjusting only a couple of learning-rate parameters, the new HMAX/COVIS model provides impressively good fits to human category-learning data from two qualitatively different experiments that used different types of category structures and different types of visual stimuli. Overall, the model provides a comprehensive neural and behavioral account of basal ganglia-mediated learning.

1. Introduction

The goal of computational cognitive neuroscience (CCN) is to build and test neurobiologically detailed computational models that can account for behavioral and neuroscience data [Ashby and Helie (2011); O’Reilly et al. (2012)]. Even so, researchers who build and test CCN models are typically interested in one subprocess more than others. For example, researchers interested in visual perception might couple a detailed model of some regions in visual cortex with an oversimplified model of response selection that produces a stylized output, whereas researchers interested in motor performance might couple a detailed model of primary motor cortex with an oversimplified model of visual perception that produces a stylized input to the motor module.

If two different CCN models are both faithful to the available neuroscience data and if they each model brain regions that are connected, then it should be possible to create a new model by linking the two together, and this new model should be consistent with all the behavioral and neuroscience data that are consistent with either model alone. This article leverages this property of CCN modeling by combining two well-established CCN models – the model of processing in visual cortex called HMAX [Riesenhuber and Poggio (1999)] and the model of procedural learning in the striatum that is included in the COVIS model of category learning [Ashby et al. (1998); Ashby and Waldron (1999)]. We believe that the combined model provides the best available and most comprehensive account of learning in several qualitatively different kinds of categorization tasks.

2. Category Learning

Categorization is the act of responding the same to all members of one stimulus class and differently to members of other classes. It is a key skill required of every organism because, for example, it allows prey and nutrients to be approached and predators and toxins to be avoided. There is now abundant evidence that multiple memory systems contribute to perceptual category learning, and that different systems dominate under different conditions depending on the structure of the contrasting categories and the training conditions [e.g., Ashby and Maddox (2005, 2010); Eichenbaum and Cohen (2001); Poldrack et al. (2001); Poldrack and Packard (2003); Squire (2004)]. For example, evidence suggests that declarative memory systems dominate when optimal performance is possible with an explicit rule that is easy to describe verbally.

The focus of this article is on learning that is mediated by the (nondeclarative) procedural memory system [e.g., Squire (2004); Willingham (1998); Willingham et al. (1989)]. Procedural memories are the memories of skills that are learned through practice. Traditionally these have been motor skills, but recent evidence suggests that procedural learning is also critical for the acquisition of many cognitive skills [e.g., Ashby and Ennis (2006); Seger (2008); Seger and Miller (2010)]. In contrast to learning that is mediated by declarative memory systems, procedural learning is slow and incremental and it requires immediate and consistent feedback. Much evidence suggests that procedural learning is mediated largely within the basal ganglia [e.g., Mishkin et al. (1984); Willingham (1998)].

Evidence suggests that procedural learning dominates in two different types of categorization tasks – information-integration (II) and unstructured category-learning tasks. II tasks are those in which accuracy is maximized only if information from two or more incommensurable stimulus dimensions (or components) is integrated at some pre-decisional stage [Ashby and Gott (1988)]. An example is shown in Figure 2. II categories are similarity-based in the sense that perceptually similar stimuli tend to belong to the same category, but the optimal strategy in II tasks is difficult or impossible to describe verbally [Ashby et al. (1998)]. Explicit-rule verbal strategies, such as “respond A if the stimulus has bars with steep orientation,” lead to sub-optimal levels of accuracy. Combining multiple such verbal rules sometimes helps – for example combining a rule about orientation with one about thickness might improve accuracy. However, this compound rule will still lead to suboptimal performance unless information on multiple dimensions is integrated – that is, unless the values on multiple dimensions are directly compared. Although category membership in an II task is easily defined mathematically, a verbal description of that mathematical rule is not natural. For example, in Figure 2, a verbal description of the mathematical rule that defines category membership is: “respond A if the width of the stimulus bars is greater than their orientation.” But since width and orientation are incommensurable, this is comparing apples and oranges. Such incommensurability is a hallmark of II tasks, which is why the optimal strategy in II tasks is difficult to describe verbally.

Figure 2.

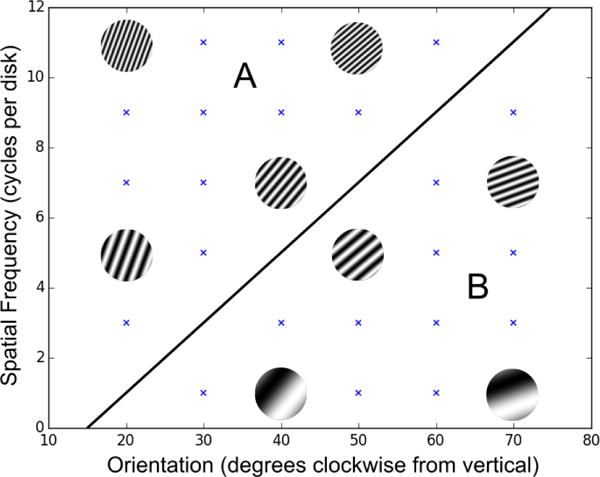
Example of II categories. Each point represents a stimulus with the specified spatial frequency and orientation. Example stimuli are shown. The category decision boundary is denoted by the diagonal line.

In unstructured category-learning tasks, the stimuli are assigned to each contrasting category randomly, and thus there is no rule- or similarity-based strategy for determining category membership. Because similarity can not be used to learn the categories, the stimuli are typically visually distinct (i.e., non-confusable) and low in number. For example, each category generally includes 8 or fewer exemplars (and 4 is common). Figure 4 shows some examples. Unstructured category-learning tasks are similar to high-level categorization tasks that have been studied for decades in the cognitive psychology literature. For example, Lakoff (1987) famously motivated a whole book on a category in the Australian aboriginal language Dyirbal that includes women, fire, dangerous things, some birds that are not dangerous, and the platypus. Similarly, Barsalou (1983) reported evidence that ad hoc categories such as things to sell at a garage sale and things to take on a camping trip have similar structure and are learned in similar ways to other common categories.

Figure 4.

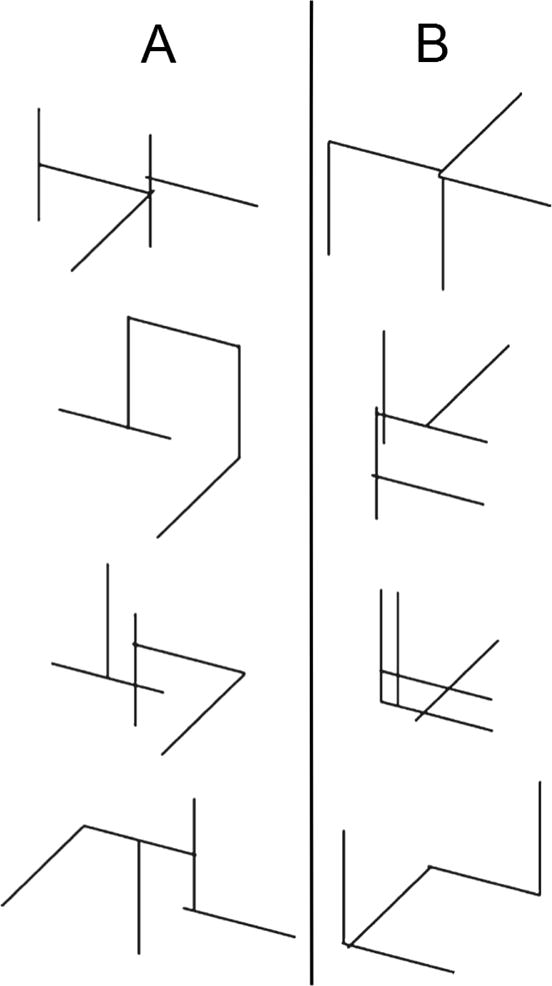
Examples of stimuli assigned to the two contrasting categories (i.e., A and B) in the unstructured category learning experiment reported by Crossley, Madsen, and Ashby (2012).

The evidence is good that success in II and unstructured categorization tasks depends on striatal-mediated procedural learning [Ashby and Ennis (2006); Seger (2008); Seger and Miller (2010)]. A complete review is beyond the scope of this article, but briefly, patients with striatal dysfunction are highly impaired in these tasks [e.g., Ashby et al. (2003b); Filoteo et al. (2001, 2005); Knowlton et al. (1996); Sage et al. (2003); Shohamy et al. (2004); Witt et al. (2002)], and almost all fMRI studies of II and unstructured category learning have reported significant task-related activity in the striatum, rather than say in the medial temporal lobes [e.g., Lopez-Paniagua and Seger (2011); Nomura et al. (2007); Poldrack et al. (2001); Seger and Cincotta (2002, 2005); Seger et al. (2010); Waldschmidt and Ashby (2011)]. Behaviorally, one feature of traditional procedural-learning tasks is that switching the locations of the response keys interferes with performance [Willingham et al. (2000)], presumably because procedural learning includes a motor component. In agreement with this result, switching the locations of the response keys interferes with II and unstructured categorization performance but not with performance in control tasks where optimal accuracy is possible with an explicit rule [Ashby et al. (2003a); Crossley et al. (2012); Maddox et al. (2004); Spiering and Ashby (2008)].

3. HMAX, COVIS, and HMAX/COVIS

3.1. HMAX

HMAX is a computational implementation of the simple-to-complex “Standard Model” of visual processing [Hubel and Wiesel (1962)]. It simulates processing in the cortical ventral visual stream thought to mediate object recognition in humans and other primates [Ungerleider and Haxby (1994)]. This stream extends from primary visual cortex, V1, to inferotemporal cortex, IT, forming a processing hierarchy in which the complexity of neurons’ preferred stimuli and receptive field sizes progressively increase.

The HMAX model is described in detail elsewhere [Riesenhuber and Poggio (1999); Jiang et al. (2006); Serre et al. (2007b); Cox and Riesenhuber (2015)]. Briefly, input images are densely sampled by arrays of two-dimensional Gabor filters, the so-called S1 units, each responding preferentially to a bar of a certain orientation, spatial frequency and spatial location, thus roughly resembling properties of simple cells in striate cortex. In the next step, C1 cells, which roughly resemble complex cells [Serre and Riesenhuber (2004)], pool the output of sets of S1 cells with the same preferred orientation (using a maximum, MAX-pooling function) and with similar preferred spatial frequencies and receptive field locations, to increase receptive field size and broaden spatial frequency tuning. Thus, a C1 unit responds best to a bar of the same orientation as the S1 units that feed into it, but over a range of positions and scales. To increase feature complexity, neighboring C1 units of similar spatial frequency tuning are then grouped to provide input to an S2 unit, roughly corresponding to neurons tuned to more complex features, as found in V2 or V4. Intermediate S2 features can either be hard-wired [Riesenhuber and Poggio (1999)] or learned directly from image sets by choosing S2 units to be tuned to randomly selected patches of the C1 activations that result from presentations of images from a training set [Serre et al. (2007a,b)]. This latter procedure results in S2 feature dictionaries better matched to the complexity of natural images [Serre et al. (2007b)], and a similar set of 4,075 features extracted from natural images was used in the present simulations (using the hmin package, see below).

To achieve size invariance over all filter sizes and position invariance over the modeled visual field while preserving feature selectivity, all S2 units selective for a particular feature are again pooled by a MAX operation to yield C2 units. Consequently, a C2 unit will respond at the same level as the most active S2 unit with the same preferred feature, but regardless of its scale or position. C2 units are comparable to V4 neurons in the primate visual system [Cadieu et al. (2007)]. Finally, these C2 units can then be combined to serve as inputs to “view-tuned” units selective for particular views of a complex object (e.g., a face or a car) as might be found for example, in ventral temporal cortex at the top of the ventral visual stream.

3.2. The COVIS Procedural-Learning Model

The COVIS procedural-learning model is based on open loops from visual cortical areas through the direct pathway of the basal ganglia to premotor areas of cortex [for details, see Ashby et al. (1998); Ashby and Crossley (2011); Ashby et al. (2007); Cantwell et al. (2015)]. The major structures and projections in the model are shown in Fig. 1. Synpatic plasticity occurs at three different types of synapses: 1) synapses between cortical pyramidal neurons and medium spiny neurons (MSNs) in the striatum, 2) synapses between neurons in the centremedian and parafasicular nuclei in the thalamus and the striatal cholinergic interneurons known as the TANs, and 3) synapses between neurons in visual cortical neurons and neurons in premotor cortex (SMA and/or dorsal premotor cortex). Briefly, with visual categories, synapses between visual cortical neurons and MSNs in the body and tail of the caudate learn which stimuli cluster together, whereas synapses between neurons in preSMA and MSNs in the putamen learn what motor response is appropriate for each cluster. The thalamus/TAN synapses mediate learning of environmental contexts associated with reward, and the long-range cortical-cortical connections mediate the transition to automatic responding. The model successfully accounts for an enormous amount and diversity of data – including single-unit recordings of several neuron types within the striatum [Ashby and Crossley (2011)], neuroimaging results [Waldschmidt and Ashby (2011); Soto et al. (2013, 2016)], learning deficits of Parkinson’s disease patients [Hélie et al. (2012a,b)], and a wide variety of behavioral data [Ashby et al. (1998); Ashby and Crossley (2011); Ashby et al. (2007); Cantwell et al. (2015); Crossley et al. (2013); Valentin et al. (2014, 2016)].

Figure 1.

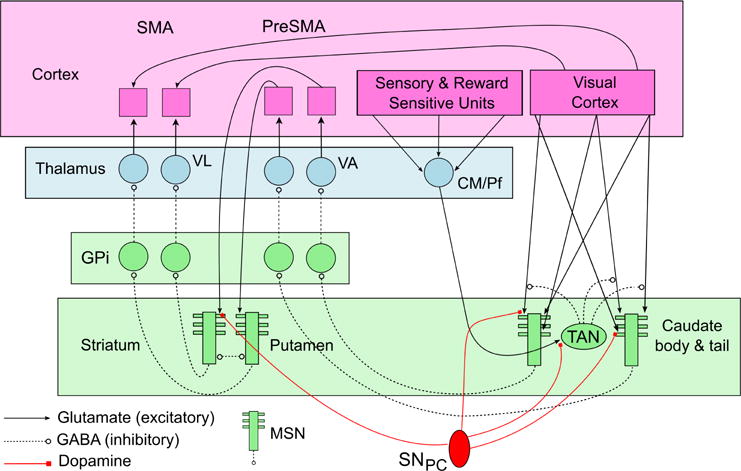
Schematic showing some of the structure of the COVIS procedural-learning model. (MSN = medium spiny neuron, SN_PC = substantia nigra pars compacta, TAN = tonically active neuron, GP_texti = internal segment of the globus pallidus, VL = ventral lateral nucleus, VA = ventral anterior nucleus, CM/Pf = centremedian and parafasicular nuclei, SMA = supplementary motor area)

Despite the model’s many successes, previous applications have grossly oversimplified activation in visual cortex – essentially assuming that each stimulus has a (unique) corresponding visual unit tuned to it. Activation in all other units is modeled as a spiking neuron. Firing in striatal MSNs and TANs as well as in neurons in premotor cortex is modeled with a modification of the Izhikevich (2003) spiking-neuron model, and firing in all other units is typically modeled with the quadratic integrate-and-fire model [Ermentrout and Kopell (1986)].

Learning at cortical-striatal and thalamic-TAN synapses follows reinforcement learning rules (also known as three-factor learning) [Calabresi et al. (1992); Suri and Schultz (1998); Wickens et al. (1996)] in which synaptic strengthening requires strong presynaptic activity, postsynaptic activity strong enough to activate NMDA receptors, and DA above baseline (which requires positive feedback). If the first two conditions hold but DA is below baseline, then the synapse is weakened. The three-factor learning rule requires specifying exactly how much DA is released on each trial. The COVIS procedural-learning model assumes that the amount of DA release is proportional to the reward prediction error (RPE), defined as the value of the obtained reward minus the value of the predicted reward. Thus, in this model DA release increases above baseline following unexpected reward, and the more unexpected the reward, the greater the release, and DA levels decrease below baseline following the unexpected absence of reward, and the more unexpected the absence, the greater the decrease [as is consistent e.g., with Schultz et al. (1997); Tobler et al. (2003)].

3.3. Combining HMAX and COVIS

As mentioned earlier, previous implementations of the COVIS procedural-learning model have assumed a highly stylized sensory input. The model has been applied to many different experiments, but all of these used one of two qualitatively different kinds of stimulus sets. A number of applications have been to II categorization experiments that include many perceptually similar stimuli that vary across trials on two continuous stimulus dimensions. An example is shown in Figure 2. A common approach to modeling data from experiments of this type is to assume a large ordered array of units in sensory cortex (e.g., 10,000 units), each tuned to a different stimulus. Each unit responds maximally when its preferred stimulus is presented and its response decreases as a Gaussian function of the distance in stimulus space between the stimulus preferred by that unit and the presented stimulus (the Gaussian function models a tuning curve). Activation in each unit equals the height of this Gaussian function during the duration of stimulus presentation, and zero at all other times.

The second type of application has been to experiments that include only a few perceptually distinct stimuli (typically 12 or fewer). Included in this list are unstructured categorization experiments and instrumental (or operant) conditioning studies. In this case, each stimulus is assumed to activate a unique unit in sensory cortex. The idea is that the units in sensory cortex maximally tuned to each stimulus are far enough apart in sensory space that the tuning curve of each sensory unit does not overlap the units tuned to any other stimuli. In these applications, during stimulus presentation, activation in the unit associated with the presented stimulus equals some positive constant and activation in all other units equals zero.

Although both of these approaches have been quite successful, they clearly make no serious attempt to model visual processing. In fact, it is not immediately obvious that the model would even be able to learn if given inputs that are more biologically realistic.

Since both HMAX and the COVIS procedural-learning model aim to be biologically grounded models, and since it is known that all of extrastriate visual cortex projects directly to the striatum, it should be possible to combine these models without substantive modification. We call this combination HMAX/COVIS. As a model of perceptual category learning, HMAX/COVIS has some major advantages over previous models. HMAX models the visual processing and takes bitmap images as its inputs. Therefore, the combined HMAX/COVIS model also takes bitmaps as input. To our knowledge, no other model of human category learning possesses this feature. Furthermore, the same HMAX/COVIS architecture can theoretically be used for virtually any visual inputs, whereas COVIS alone requires remodeling of the visual input for different tasks.

A minimal implementation of HMAX (dubbed HMIN) was retrieved from the internet (http://cbcl.mit.edu/jmutch/hmin/). The input to HMIN is an unmodified 128 pixel × 128 pixel bitmap image. We took the activations in the C2 layer of HMIN as the relevant output that then serves as visual input to COVIS. A minimal implementation of the COVIS procedural-learning model was also taken from previous work [Cantwell et al. (2015)]. This minimal version lacked striatal TANs and the long-range cortical-cortical projections, and it included only one loop through the striatum. No other modifications were made except to remove the primitive “visual system” it already had. Thus, the only substantive modeling problem was how to translate each C2 activation into something appropriate for COVIS.

Units in the striatal layer of COVIS are activated in proportion to the weighted sum of the inputs from the visual system. For this reason, it is advantageous for there to be a reasonable amount of variation in the input vector as the stimuli change over the course of the experiment. To achieve this from the C2 activations, a linear scaling was used and extreme values were discarded.

Specifically, the i^th C2 activation, denoted X_i, was transformed to:

$$Y_i=\left(\frac{X_i-\overline{X}}{s_X}\right)+0.5,$$ (1)

where $\overline{X}$ and s_X were the approximate mean and standard deviation of all X_i across all stimuli used in our two applications. Note that this linear transformation¹ resets the mean to 0.5 and the standard deviation to approximately 1.0. Next, any Y_i values that fell outside of the 0 to 1 interval were then reset to 0. It was observed that the extreme values tended to be constant across stimuli, and that almost all of the C2 variation that occurred as the stimuli in our applications varied were in values close to the C2 mean $\overline{X}$. Thus, this transformation was chosen to emphasize the intermediate values (values close to $\overline{X}$), and to spread these out across the 0 to 1 interval.

Values above 1 were reset to 0 because they carried no diagnostic information (since they had roughly the same value for all stimuli) and the COVIS procedural model selects a response based on a weighted sum of all inputs. Therefore, if all weights are equal (as they are in the beginning of learning) then the largest inputs dominate this weighted sum, and if the largest inputs have no diagnostic value, then learning will be compromised. In principle, the model should still be able to learn under these conditions – by driving the weights on the large and useless inputs to 0 – but we did not explore this option. Instead, we reasoned that the resetting to 0 was akin to directing perceptual attention away from irrelevant visual features. Such attentional phenomena are inherent to any object-based task. One example occurs during figure-ground segregation. As another, note that the stimuli in Figure 2 are all circular disks of the same diameter. Instructions to participants in this task stress that stimulus size and shape are irrelevant to the categorization decision, which encourages subjects to direct attention at the spatial frequency and orientation of the grating².

Some assumption had to be made about how to interpret C2 output, and this is a fairly conservative, mostly linear transformation. This process is similar to normalization, which has been argued to be a canonical neural computation [Carandini and Heeger (2012)]. Beyond this exceedingly simple interface, no additional structure was added to create the combined model. All parameter values in both models were set to values from previous applications, with the exception of two learning rates in COVIS.

4. Testing HMAX/COVIS

The most rigorous test of HMAX/COVIS would be against data from experiments that used the two qualitatively different types of visual stimuli discussed earlier. If the same HMAX/COVIS model could account for data from experiments that used such different types of stimuli then that model would represent a significant advance over any current categorization models. For this reason, we tested the model against learning data from two different categorization experiments – an II category-learning task and an unstructured category-learning task.

4.1. II Category Learning

Figure 2 describes the stimuli and categories in the II task used in the current experiment. Note that the two categories are composed of circular sine-wave gratings that vary in the spatial frequency (i.e., thickness) and orientation of the dark and light bars. The solid line denotes the category boundary. Note that no verbal rule correctly separates the two categories. Many articles have reported the results of II tasks that used similar stimuli and category structures [e.g., Ashby and Maddox (2005, 2010)]. Even so, for a fair comparison, it is critical that the model and human participants learn to classify exactly the same visual images. For this reason, we collected data from a new II task that used the stimuli shown in Figure 2. Each of the 30 stimuli shown there were rendered as a 128 × 128 bitmap image, and both the model and every participant were shown these same bitmaps. Stimuli were shown one at a time, and corrective feedback was provided following each response.

4.1.1. Methods

Participants

Seventeen participants completed the study and received course credit for their participation. All participants had normal or corrected to normal vision. Each participant learned the category structures shown in Figure 2.

Stimuli and Category Structure

Stimuli were 30 Gabor patches (i.e., sine-wave gratings with Gaussian masks, rather than the circular uniform masks used to create Figure 2) – 15 in each category. The stimuli differed across trials only in the orientation and spatial frequency of the dark and light bars. Values for orientation and frequency were assigned to uniformly cover the spatial frequency/bar width space (i.e., as in Figure 2). The optimal decision bound for these categories is the line y = x, which would achieve 100% accuracy.

To convert the sampled values into orientations and spatial frequencies the following transformations were chosen:

$$\begin{array}{c}\text{Spatial}\text{Frequency}=(x+7.5)/60(\text{cycles}\text{per}\text{degree})\\ \text{Orientation}=0.9y+20(\text{degrees})\end{array}$$

These values were selected so as to give roughly equal salience to both dimensions.

Procedure

The experiment was run on computers using PsychoPy [Peirce (2007)]. Before the experiment, participants were told that they would learn to categorize novel stimuli. An initial set of on-screen instructions told participants that two buttons would be used (the ‘f’ and ‘j’ keys), and that initially they would have to guess, having not seen such stimuli before. The experimental session consisted of 12 blocks of 50 trials each. Between each block there was a participant-terminated rest period. The stimuli were shuffled and presented in a random order for each participant.

At the start of each trial a fixation crosshair was presented for 600ms. Following this, a response-terminated stimulus was presented for a maximum of 3000ms. Auditory feedback was given immediately after each response. A happy sound was played after each correct response – the notes E, G#, and B were played in quick succession with an organ sound. Incorrect responses were followed with a negative sound: G then E with a klaxon sound.

4.1.2. Results

Figure 3 shows the block-by-block accuracies (mean across participants). Ignore the red and blue curves for now. Note that accuracy increased with training from about 63% correct in block 1 to about 82% correct in block 12.

Figure 3.

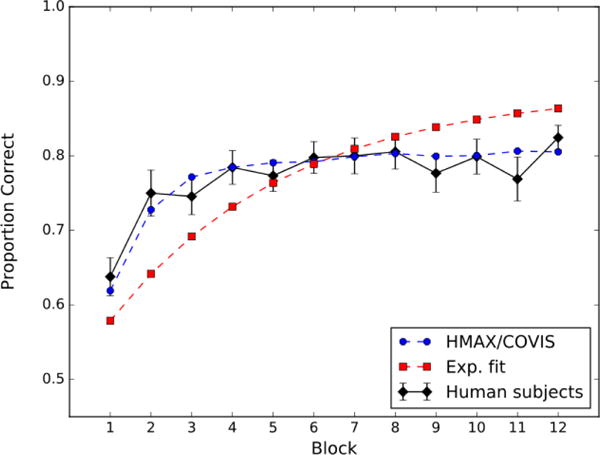
Accuracy by block (50 trials) for the II task. The black curve denotes the data from the human participants, the broken blue curve denotes fits by HMAX/COVIS, and the broken red curve denotes fits by an exponential function (i.e., Equation 5).

4.2. Unstructured Category Learning

We chose to test the model against the unstructured category-learning data reported by Crossley et al. (2012). In this experiment, participants learned to categorize 16 stimuli that were each randomly assigned to one of two categories of 8 stimuli each. Some examples of the stimuli that were used are shown in Figure 4. The block-by-block accuracies (mean across participants) are shown in Figure 5. Ignore the red and blue curves for now. Note that accuracy increased with training from about 63% correct in block 1 to about 82% correct in block 12.

Figure 5.

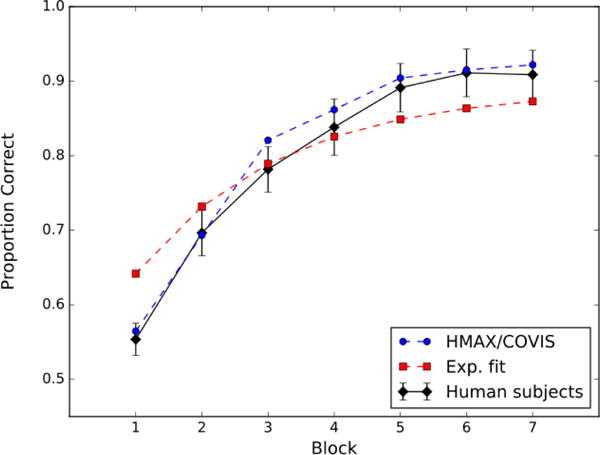
Accuracy by block (100 trials) for the unstructured category-learning task reported by Crossley, Madsen, and Ashby (2012). The black curve denotes the data from the human participants, the broken blue curve denotes fits by HMAX/COVIS, and the broken red curve denotes fits by an exponential function (i.e., Equation 5).

4.3. Model Fitting

We fit HMAX/COVIS to the learning curves shown in Figures 3 and 5, and as a comparison we also fit an exponential function that had the same number of free parameters. First we describe the fitting process for both models and then we compare the results.

4.3.1. HMAX/COVIS

Fitting HMAX/COVIS to the data required adjusting only two learning rates in the COVIS striatum – namely, the constant of proportionality on trials when synaptic strengthening occurs and the constant of proportionality on trials when synaptic weakening occurs. To begin, we set the initial synaptic strengths between HMAX output j and COVIS striatal unit k, denoted by w_jk, to a random value that was sampled from a uniform [0.1, 0.2) distribution. During training, each synaptic strength was updated after each trial via a biologically plausible reinforcement learning algorithm [Ashby and Helie (2011)]. Specifically, after feedback on trial n, the strength of the synapse between HMAX output unit j and COVIS striatal unit k was adjusted as follows:

$$\begin{array}{l}{w}_{jk}(n+1)=w_{jk}(n)\\ +\alpha Y_j(n){[V_k(n)-{\theta }_{\text{NMDA}}]}^{+}{[D(n)-D_{\mathit{base}}]}^{+}[w_{\mathit{max}}-w_{jk}(n)]\\ +\beta Y_j(n){[V_k(n)-{\theta }_{\text{NMDA}}]}^{+}{[D_{\mathit{base}}-D(n)]}^{+}{w}_{jk}(n)\end{array}$$ (2)

where Y_j(n) is the j^th HMAX output on trial n (transformed according to Eq. 1), V_k(n) is the total activation in the k^th COVIS striatal unit on trial n [see, e.g., Cantwell et al. (2015)], [g(t)]⁺ is equal to g(t) when g(t) > 0 and 0 otherwise, θ_NMDA represents the activation threshold for post-synaptic NMDA receptors, D(n) represents the amount of dopamine released on trial n, D_base is the baseline dopamine level, w_max is the maximum synaptic strength, and α and β are the learning rates. Equation 2 specifies that three factors are required to strengthen or weaken a synapse. In either case there must be presynaptic activation (i.e., Y_j(n) > 0) and postsynaptic activation must be above the threshold for NMDA receptor activation (i.e., V_k(n) > θ_NMDA). If these two conditions are met then the synapse is strengthened if dopamine is above baseline (i.e., D(n) > D_base) and the synapse is weakened if dopamine is below baseline (i.e., D(n) < D_base).

To complete the model, we must specify how much dopamine is released on each trial. Following the standard approach and as in previous applications [e.g., Ashby and Crossley (2011); Cantwell et al. (2015)], we assumed that dopamine release is a piecewise linear function of the reward prediction error on trial n, which is defined as RPE(n) = R_n − P_n, where R_n is the value of the obtained reward and P_n is the value of the predicted reward. We assumed that R_n = 1 on trials when reward feedback is given, R_n = 0 in the absence of feedback, and R_n = −1 when error feedback is given. The predicted reward, P_n is assumed to equal a simple temporally discounted average of past rewards:

$$P_{n+1}=P_n+0.075(R_n-P_n),$$ (3)

where the constant 0.075 reflects the amount of temporal discounting [and is the same value used by Ashby and Crossley (2011)]. Finally, we assumed that the amount of dopamine release is related to the RPE in the manner consistent with the dopamine firing data reported by Bayer and Glimcher (2005). Specifically, we assumed that

$$D(n)=\{\begin{array}{ll}1\hfill & \text{if}\text{RPE}>1\hfill \\ .8\text{RPE}+.2\hfill & \text{if}-.25\le \text{RPE}\le 1\hfill \\ 0\hfill & \text{if}\text{RPE}<-.25\hfill \end{array}$$ (4)

Thus, note that in this model synaptic strengthening can only occur following positive feedback and weakening can only occur following negative feedback. Furthermore, the amount of synaptic strengthening increases with the unexpectedness of the reward.

In the present applications, the values of all constants in this model were set to the same numerical values that were used by Cantwell et al. (2015). The only exceptions were the two learning rates, α and β in Equation 2, which were treated as free parameters.

4.3.2. Exponential Learning Curve

As a comparison, we also fit an exponential function to the learning curve from each experiment. The exponential function, which has a long history as a model of learning curves [Estes (1950); Hull (1943); Thurstone (1919)], is still widely used today [e.g., Leibowitz et al. (2010)]. Specifically, the exponential model that we fit assumes that

$$P(n)=a-(a-0.5){\mathrm{e}}^{-bn},$$ (5)

where P(n) is proportion correct on trial n, and a and b are free parameters. Note that this function equals 0.5 on “trial 0” and asymptotes at a after many trials of training. The parameter b characterizes the learning rate.

4.3.3. Results

HMAX/COVIS and the exponential learning curve were both fit simultaneously to the learning curves from the II and unstructured category-learning experiments (i.e., the curves shown in Figures 3 and 5). To fit HMAX/COVIS, we first re-rendered the image of each stimulus as a 128 × 128 bitmap, which then served as input to the model. Next, the model was run through exactly the same sequence of trials as the human participants.

For both models, two free parameters were estimated: α and β from Equation 2 in the case of HMAX/COVIS, and a and b from Equation 5 in the case of the exponential function. In both cases the parameters were estimated using the method of least squares. Note that the exponential model must necessarily predict identical learning curves in the two experiments since the same values of a and b were used to fit both curves (although the two experiments included different numbers of trials). In contrast, HMAX/COVIS predicts that the two learning curves will be different – even though α and β did not vary across conditions – because the predicted accuracy of the model depends on the trial-by-trial feedback it receives, which will differ across experiments.

The results are shown in Figures 3 and 5. The broken blue curves show the fits of HMAX/COVIS and the broken red curves show the fits of the exponential model. The overall mean-square error (MSE) is 0.000713 for HMAX/COVIS and 0.00518 for the exponential model, indicating that HMAX/COVIS fits substantially better than the exponential model (by about an order of magnitude). Furthermore, the better fit of HMAX/COVIS is seen in both experiments. In the II experiment, the MSE is 0.000346 for HMAX/COVIS and 0.00309 for the exponential model. In the unstructured category-learning experiment, the MSE is 0.000367 for HMAX/COVIS and 0.00208 for the exponential model.

If the exponential model is fit separately to the data from each experiment, so that the number of free parameters in the model doubles from 2 to 4, then the two-parameter version of HMAX/COVIS still provides the better absolute fit, although its advantage is sharply reduced. In this case, the overall MSE is 0.000953 for the exponential model, compared to 0.000713 for HMAX/COVIS. So HMAX/COVIS fits slightly better than an atheoretical curve-fitting approach that has twice as many free parameters, and the neurobiological detail of HMAX/COVIS gives it the extra advantage of making many other predictions that are outside the scope of the exponential model.

5. Discussion

This article leverages one of the core advantages of CCN; namely, that it should be possible to interface different CCN models in a plug-and-play fashion. As a strong demonstration of this property, we constructed a new and biologically detailed model of visual category learning from two existing CCN models: the HMAX model of visual object processing and the COVIS model of procedural category learning. The models were combined in a simple two-step procedure. First, the primitive visual module in COVIS was replaced by an unmodified version of HMAX, and second, the HMAX outputs were rescaled in a piecewise linear way to facilitate communication between HMAX and the striatal learning component of COVIS.

In line with the expectations of CCN modeling, the new HMAX/COVIS model provided impressively good fits to human category-learning data from two experiments that used qualitatively different types of category structures (II versus unstructured) and different types of visual stimuli. It is also noteworthy that the human learning curves for the two tasks are somewhat different: the II curve plateaus earlier and stays lower than the learning curve for the unstructured categories. Impressively, the model accounts for this difference.

The new HMAX/COVIS model is a significant improvement over either model alone, and to our knowledge is unique in the literature³. Using bitmap images as inputs and by adjusting only a couple of learning-rate parameters, HMAX/COVIS can account for

• II category learning (as demonstrated in Figure 3).

• unstructured category learning (as demonstrated in Figure 5).

• single-unit recordings from MSNs and TANs during instrumental conditioning [based on Ashby and Crossley (2011), who modeled data from experiments that all included only a single stimulus].

• many behavioral phenomena from instrumental conditioning experiments, including fast reacquisition after extinction, the partial reinforcement extinction effect, spontaneous recovery, and renewal [based on Crossley et al. (2016), who modeled data from experiments that all included only a single stimulus].

• the effects of feedback delays on II category learning [based on Valentin et al. (2014), who used essentially the same II categories as in Figure 2].

• the result that recovery from a full reversal is quicker than learning new categories constructed from the same stimuli [based on Cantwell et al. (2015), who used II categories that were essentially the same as in Figure 2].

• deficits by patients with Parkinson’s disease in II and unstructured category learning [based on Hélie et al. (2012a)].

• unlearning and failures of unlearning (e.g., renewal) during II categorization [based on Crossley et al. (2013, 2014)].

The fact that HMAX/COVIS takes bitmap images as inputs is a significant advance. First, it eliminates the arbitrariness that previously existed in the modeling of stimulus sets. In particular, HMAX/COVIS eliminates the need for the experimenter to make ad hoc decisions regarding the choice of stimulus representation (e.g., whether to use a feature-based or Gestalt representation of the stimuli), thus avoiding potential concerns as to whether observed simulation results might have depended on the choice of a particular hand-crafted “high-level” stimulus representation. Second, it removes free parameters from COVIS (e.g., the width parameter on the radial basis functions), which makes applications of the model less a matter of curve fitting and more a matter of testing a priori predictions. This elimination of parameters in turn should make it easier to identify components of the model that most oversimplify the underlying structure and function, and therefore that are in the most need of revision.

In addition, the model also has the potential to account for a variety of phenomena associated with the transition to automatic responding that occurs after extended practice. In the Figure 1 model, this transition is mediated by Hebbian learning at synapses between visual cortex and SMA [Ashby et al. (2007)]. The idea is that reinforcement learning at cortical-striatal synapses quickly begins to activate the correct postsynaptic targets in SMA more strongly than incorrect targets. This allows cortical-cortical Hebbian learning to gradually learn the correct stimulus-response associations. Eventually these associations become strong enough that the subcortical path through the striatum is no longer needed to initiate the correct motor response, at which point the behavior could be said to have become automatized. It seems highly likely that HMAX/COVIS would display similar properties if the HMAX outputs were connected to the two motor output units (fully interconnected at first) and the strength of these synapses were modified with a biologically detailed version of Hebbian learning. A test of this prediction should be the goal of future research.