Abstract
The objective of this study was to investigate the efficacy of modulated ultrasound signals in the measurement of bone properties as an early indicator of osteoporosis. Twenty-one trabecular bone cubes were harvested from sheep femoral condyles and the cube axes corresponded to the anatomic superior-inferior (SI), antero-posterior (AP), and medio-lateral (ML) orientations. Micro-CT measurements were made on those samples to obtain bone volume fraction (BV/TV), trabecular thickness (Tb.Th), and trabecular separation (Tb.Sp). Ultrasound tests were performed in the three orthogonal orientations using pulse and frequency modulated ultrasound. The comparison of the frequency modulated attenuation (FMA) with the broadband ultrasound attenuation (BUA) was made within the frequency band between 300 and . Results showed that FMA demonstrated higher correlations to the trabecular structure properties in the SI orientation ( for BV/TV, for Tb.Th, for Tb.Sp) than BUA ( for BV/TV, for Tb.Th, for Tb.Sp). In the AP orientation, FMA had higher correlation to Tr.Sp than BUA , and relatively lower correlation to BV/TV and Tb.Th than BUA ( for BV/TV and for Tb.Th). The results suggested that FMA could be a new ultrasound index for bone properties assessment.
I. INTRODUCTION
Osteoporosis is characterized as the loss of bone mass and weaken trabecular structures that consequently causes non-traumatic fractures in bones.1 It is a major health threat to the elderly population. Currently, dual energy x-ray absorptiometry (DXA) is the most commonly used diagnostic tool for osteoporosis, which measures the bone mineral content or bone mineral density (BMD). However, the DXA derived BMD is based on the attenuation of X-ray through bone tissue. It is not the true volume density but a plane density in the unit of , and is the projection of the two-dimensional (3D) volume onto a two-dimensional (2D) plane. Since 1980s, ultrasound has become an alternative, non-radioactive physical modality in the assessment of bone properties because it has the potential to measure not only the bone quantity but also the bone quality.2–7 Currently, commercialized quantitative ultrasound (QUS) devices have been used as a preliminary diagnostic tool for osteoporosis in clinic, for example, the Achilles Express from GE healthcare and UBIS 5000 Ultrasound Bone Sonometer from by Diagnostic Medical Systems in France.
The QUS measurements are based on two fundamental ultrasonic parameters, the ultrasound velocity (UV) and the broadband ultrasound attenuation (BUA). UV is determined by Young’s modulus and density of the ultrasound medium. A simple equation exists to denote the relationship if the medium is a long uniform bar,
| (1) |
where is the ultrasound wave velocity, and and are Young’s modulus and density of the long bar, respectively. Although ultrasound propagation in bone is much more complicated than in a uniform bar, experimental data have shown that UV has high linear correlation to BMD and modulus.8–12 Ultrasound attenuation is the energy loss during its propagation through the medium. It is mainly caused by the acoustic scattering from the porous trabecular structure and the heat dissipation due to the viscosity of the bone. The attenuation is frequency dependent on bone and, in particular, linearly proportional to the frequency from .13 The slope of this linear segment of the attenuation is defined as BUA. nBUA is the BUA normalized to the width of the bone sample to minimize the width effect. BUA has been reported to be a good indicator of mechanical and structural properties of bone.14–17
Ultrasound attenuation is, in fact, the frequency response of bone to the transmission ultrasound. Since the past decade, the ultrasound backscatter has become the focus as an alternative tool to assess bone properties, especially the structural properties of trabecular bone such as porosity and trabecular thickness.18–22 It is also the frequency response of reflected ultrasound from the bone sample normalized to the frequency spectrum of ultrasound reflected from the reference phantom surface.19,23,24 The ultrasound backscatter measurement uses the pulse-echo mode and has the advantage over the transmission mode in the attenuation measurement because it enables ultrasound to access critical anatomic locations such as femoral neck and spine where transmission attenuation measurement is difficult to perform. Theoretic and experimental studies also showed that the ultrasound backscatter was promising in identifying the trabecular structure such as trabecular thickness and porosity.25,26
Both ultrasound attenuation and backscatter demonstrated that the ultrasonic frequency response from bone was the good indicator of the trabecular bone structure. In those studies, ultrasound pulse was generated by applying an electric pulse with high amplitude and short duration to the ultrasound transducer. This electric pulse has a broad uniform power spectrum much wider than the frequency response of the transducer. Thus the waveform and frequency spectrum of the ultrasound pulse were mainly determined by the transducer and may not be optimal to measure the frequency response of bone. This paper presents an alternative approach to improve the efficacy of the ultrasound measurement of bone properties with the emphasis on the modulated ultrasound signal as the primary measurement signal. The electric signal driving the ultrasound transducer can be predefined to obtain the desired ultrasound waveform and frequency spectrum within the frequency response of the transducer. Modulated ultrasound has been successfully used in medical ultrasound, mostly in medical imaging as a technique to enhance signal to noise ratio.27–30 However, it is still a new signal modality in bone measurement. Literatures search showed that only a few studies used ultrasound signals other than broadband pulse in the bone measurement. Nowicki et al.31 explored the feasibility of using modulated ultrasound excitation in the estimation of ultrasound attenuation in bone. They found that the modulated ultrasound signal had improved signal to noise ratio, deep penetration into bone tissue, and highly reduced peak pressure amplitudes of the transmitted ultrasound. The work reported in this paper employed frequency modulated ultrasound signal to interrogate the structure of trabecular bone from sheep femoral condyle. The structure parameters such as BV/TV, trabecular thickness, and trabecular space were measured using micro-CT measurement. The correlation analysis was performed to study relationship between the ultrasound attenuation from the modulated ultrasound signal and the structural parameters. The results were compared to the correlation of BUA to the trabecular structure to demonstrate the efficacy of the new ultrasound parameter.
II. MATERIALS AND METHOD
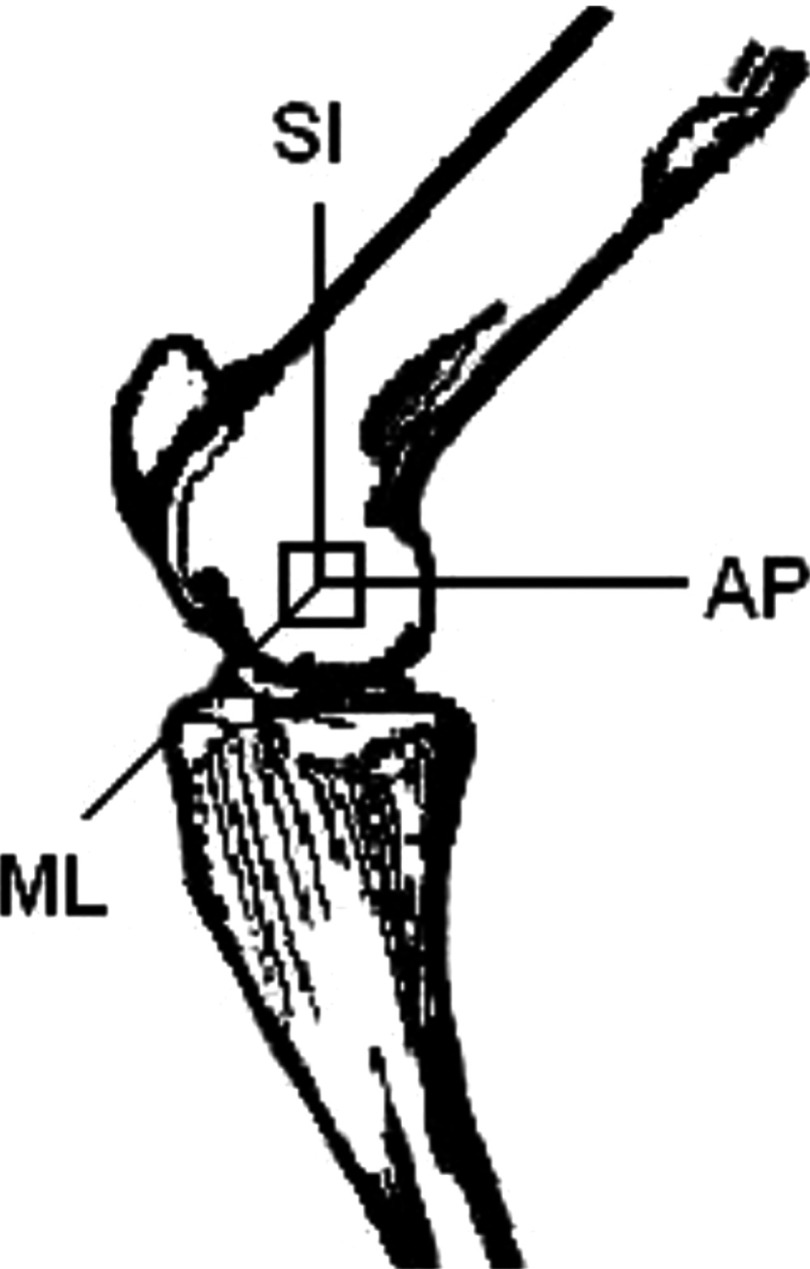
Twenty-one trabecular bone samples of were harvested from sheep femoral condyles using a low-speed diamond blade saw (Microslice, Metals Research Limited, Cambridge, England) with continuous water irrigation. Prior to cutting, the femoral shaft was placed at a 45° angle to the blade such that the axes of the cube corresponded to the physiologic superior-inferior (SI), antero-posterior (AP), and medio-lateral (ML) directions. Figure 1 is the illustration of the location of the bone sample in femoral condyle. The SI orientation was considered as major trabecular orientation because it was weight bearing. The choice of sample from sheep femoral condyle instead of human calcaneus was due to the tissue availability.
FIG. 1.
The anatomic position of the cubic trabecular bone from sheep femoral condyle and the three orthogonal orientations of the cubed sample.
The trabecular structure parameters were measured using 32 (SCANCO , SCANCO, Bassersdorf, Switzerland). For each sample, a series of cross-sectional 2D gray-scale images were obtained and visualized at the resolution of . The gray-scale images were then processed using a local thresholding method into binary images. Pixels with intensity equal or larger than the threshold were considered to be bone pixels of value 1, while those with intensities lower than the threshold were considered to be background with value 0. The threshold was determined as the binary image after thresholding best matched trabecular bone pattern from the original gray-scale image where the area for bone tissue was preserved. This process was performed on at least four samples and the average of the threshold values from those samples was set as the standard threshold for the entire sample set. An , region of interest was then selected for each image to calculate the trabecular structural parameter.
Structural indices were assessed from the 3D images rendered from the 2D cross-sectional images. The volume of the trabeculae (BV) was calculated using tetrahedrons representing the enclosed volume of the triangulated surface used for the surface area calculation. BV was also normalized to the total volume of the sample (TV) to obtain the relative bone volume (BV/TV). Mean trabecular thickness (Tb.Th) was determined from the local thickness at each voxel representing bone. With this technique, thickness can be estimated without a model assumption. Trabecular separation (Tb.Sp) was calculated applying the same technique as used for the direct thickness calculation to the non-bone sections of the 3D image.
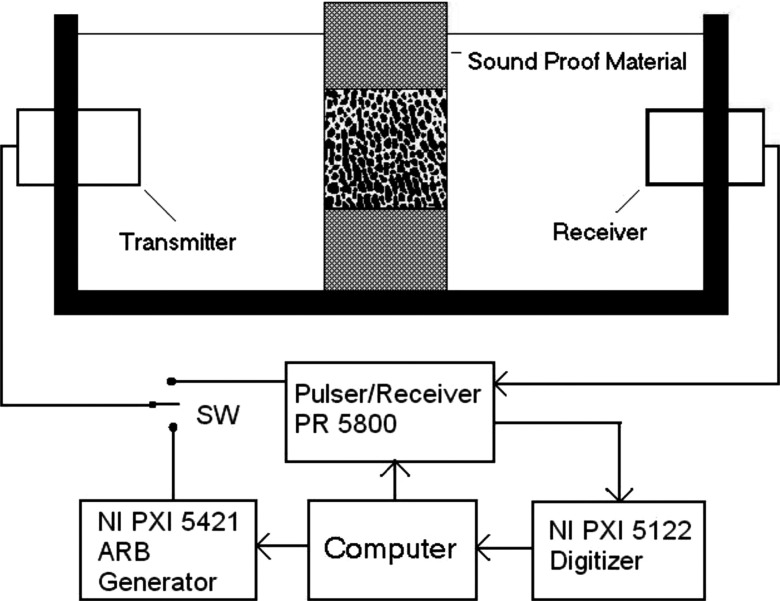
Ultrasound attenuation measurement was performed using insertion method.6 As a comparison, both BUA and the frequency modulated attenuation (FMA) were measured on each sample. Two identical broadband unfocused ultrasound transducers of in diameter with a center frequency at (Olympus NDT, MA) were mounted on opposite sides of a water tank (Fig. 2). The separation of the transducers was approximately . The bone sample was positioned in the ultrasound path using a sample holder. There are two signal sources for the ultrasound transmitter, a high voltage pulse from the pulser/receiver (PR 5800, Olympus NDT, MA) for BUA measurement and frequency modulated signal from arbitrary waveform generator (PX 5421, National Instruments, TX) for FMA measurement. The modulated ultrasound signal in this study was linear frequency sweep signal between 300 and to match the same frequency band where BUA was calculated. A switch was used to select the signal according to the type of attenuation measurements. The ultrasound signal from the receiver was amplified by the pulser/receiver and sent to the high speed digitizer (PXI 5122, National Instruments) to be digitized for further analysis. The entire device was automated by a personal computer (Dimension 8100, Dell, TX) using LABVIEW (National Instruments, TX) as the software platform for the control and measurement. Both the arbitrary waveform generator and the high speed digitizer were connected to the computer through PXI bus, an industrial version of the PCI bus in personal computers. The computer also adjusted the pulse energy and the amplifier gain of the pulser/receiver (Olympus 5800PR, MA) via GPIB bus. In BUA measurement, the ultrasound transmitter was driven by the pulser/receiver at the energy level of . Based on the equipment specification, the peak to peak amplitude of the driving signal was at this energy level. In FMA measurement, the modulated signal waveform was first created by the computer and downloaded to the arbitrary waveform generator to drive the ultrasound transmitter. The amplitude of the modulated signal to drive the ultrasound transducer was peak to peak and the duration of the signal was . The sampling frequency of the high speed digitizer was set at and 5000 data point or of signal was recorded for each signal.
FIG. 2.
The ultrasound device setup for bone structural properties measurement using broadband pulse and frequency modulated signals. The pulser/receiver generated broadband pulse and served as the ultrasound receiver for both pulse and frequency modulated signals. The arbitrary waveform generator (NI PXI 5421) generated the frequency modulated signals. The received ultrasound signals were digitized by high speed digitizer (NI PXI 5122). The entire setup was controlled by a desktop computer through LABVIEW.
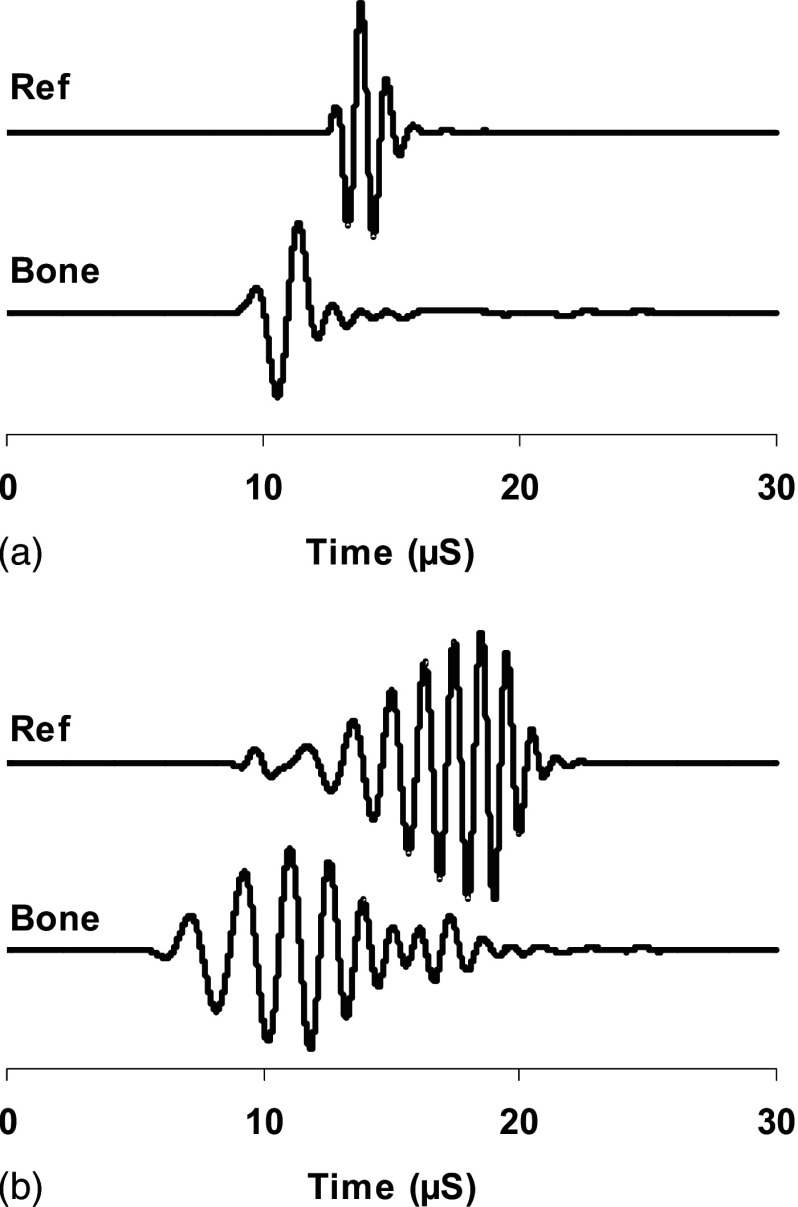
The insertion method requires measuring two ultrasound signals. One is the reference signal where the bone sample is not in the ultrasound path. The other signal is the bone signal where the bone sample is inserted in the ultrasound path. Figure 3 shows the reference signals and bone signals in pulse [Fig. 3(a)] and frequency modulation [Fig. 3(b)]. The ultrasound energy is proportional to the square of the acoustic pressure and consequently the voltage of the electric signal from the ultrasound receiver. Therefore, we used the square of voltage to represent the ultrasound energy and the coefficient that converts the voltage back to acoustic pressure was canceled out during the attenuation calculation because it was the ratio of reference signal energy to the bone signal energy. During the measurement of FMA, the frequency modulated signal envelope was first extracted using Hilbert transformation. The signal energy was then calculated from the envelope using the following equation:
| (2) |
where was the acoustic energy and was the signal envelope. The integration represented the time average of the acoustic energy and was independent to the transfer function of the transducers. The FMA was then calculated as shown in
| (3) |
where is the ultrasound energy of the reference signal and is the ultrasound energy of the bone signal.
FIG. 3.
These were the examples of ultrasound broadband pulses (a) and frequency modulated signals (b). The reference signals (Ref) were directly from the transmitter to the receiver and the bone signals (Bone) were the signals from the transducer, through the bone sample to the receiver.
The BUA measurement was performed using the ultrasound pulse. Fast Fourier transform was applied to both reference and bone signals to calculate the frequency spectra. The attenuation function as frequency was obtained by dividing the frequency spectrum of the reference signal to the frequency spectrum of the bone signal between 300 and . The linearity was further verified by checking the attenuation vs frequency curve. The slope of the attenuation function was calculated as the BUA. To minimize the effect of sample thickness, both FMA and BUA were normalized to the sample thickness in the orientation of ultrasound measurement. Due to the anisotropy of the ultrasound response to the trabecular bone, ultrasound measurement was done in all three orthogonal orientations, i.e., SI, ML, and AP shown in Fig. 1.
III. RESULTS
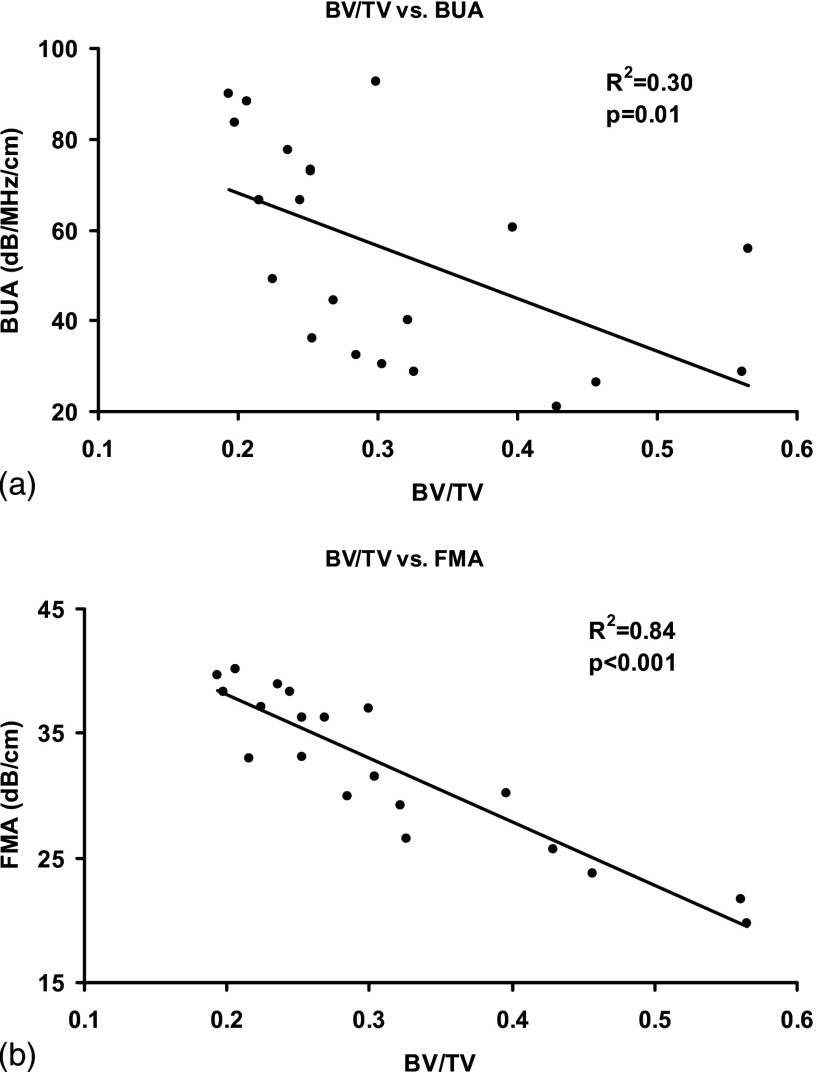
Correlation analysis was performed between ultrasound parameters and the structure properties of the trabecular samples. FMA and BUA were the ultrasound parameters and BV/TV, trabecular thickness (Tb.Th), and trabecular separation (Tb.Sp) were the trabecular structure properties. Results showed that both FMA and BUA were sensitive to the anisotropy of the trabecular structure and thus, their values were dependent on the orientation of the ultrasound measurement. For each bone structural parameter, Pearson correlation was done with respect to FMA and BUA in the predetermined SL, AP, and ML orientations using SPSS software (Chicago, IL). Figure 4 illustrates the linear correlation of BUA in SI orientation to BV/TV [Fig. 4(a)] and FMA in SI orientation to BV/TV [Fig. 4(b)], respectively. It showed that BUA and FMA behaved differently in the prediction of BV/TV through linear regression. Table I is the summary of the value and the corresponding values from all the correlations of BUA in three orthogonal orientations and their average value to BV/TV, trabecular thickness (Tb.Th), and trabecular separation (Tb.Sp). Table II is the summary of the value and the corresponding values from all correlations of FMA in three orthogonal directions and their average value to BV/TV, trabecular thickness, and trabecular separation. BUA and FMA have demonstrated modest to excellent correlations to the structure properties if they were measured in either SI or AP direction. In SI orientation, FMA had higher correlations to BV/TV, trabecular thickness, and trabecular space than BUA with the values more than doubled. In AP orientation, BUA had higher correlation to BV/TV than FMA and higher correlation to trabecular thickness than FMA . However, the differences of those values were much smaller than those in the SI orientation. Also in the AP orientation, FMA was superior in the correlation to the trabecular space to BUA with value of 0.64 vs 0.33. In the ML orientation, Both FMA and BUA failed to correlate to the structure properties of the trabecular bone. The average BUA and FMA values from the three directions were also calculated and correlation analysis was performed. The average process may reduce the sensitivity of the FMA and BUA to the structural anisotropy of the trabecular bone. The results showed that the average FMA has higher correlation to BV/TV and trabecular space than the averaged BUA and similar correlations to the trabecular thickness as the average BUA.
FIG. 4.
Correlation between BV/TV to BUA (a) and FMA measured in SI orientation. The correlation was higher between BV/TV and FMA than between BV/TV and BUA .
TABLE I.
The value of the correlation of BUA in three orientations and their average to BV/TV, Th, and Tb.Sp. The -values were also listed.
| US direction | BV/TV | Tb.Th | Tb.Sp |
|---|---|---|---|
| SI | 0.30 | 0.27 | 0.33 |
| AP | 0.64 | 0.58 | 0.48 |
| ML | 0.01 | 0.04 | 0.00 |
| AVG | 0.58 | 0.47 | 0.58 |
TABLE II.
The value of the correlation of FMA in three orientations and their average to BV/TV, Tb.Th, and Tb.Sp. The -values were also listed.
| US direction | BV/TV | Tb.Th | Tb.Sp |
|---|---|---|---|
| SI | 0.84 | 0.77 | 0.70 |
| AP | 0.48 | 0.31 | 0.64 |
| ML | 0.00 | 0.02 | 0.06 |
| AVG | 0.63 | 0.44 | 0.74 |
Further analysis was done to identify if the correlations of FMA to the bone structural properties was significantly different from those of BUA to the same bone properties. In the previous analysis, it has been demonstrated that both FMA and BUA were linearly correlated to the bone structural properties and those ultrasound parameters are dependent on BV/TV, trabecular thickness, and trabecular space. Analysis of covariance (ANCOVA) was the statistical tool to examine the statistical difference between FMA and BUA when their dependence on the bone properties was considered. For each ANCOVA test, only one bone property was considered as the covariate to the FMA and BUA. Table III shows the -value of the ANCOVA test. The values were all less than 0.001, which indicated that the linear correlations of FMA to BV/TV, trabecular thickness, and trabecular space are significantly different from those of BUA to the respective bone properties.
TABLE III.
The -values of the ANCOVA analysis of the correlation of FMA and BUA to one of bone structure properties, BV/TV, Tb.Th, and Tb.Sp. The three parameters were chosen as the covariates, respectively.
| AP | ML | SI | AVG | |
|---|---|---|---|---|
| BV/TV | ||||
| Tb.Th | ||||
| Tb.Sp | 0.001 |
IV. DISCUSSION
FMA and BUA are the indices derived from ultrasound attenuation. It was expected that both indices had the similar performance in the assessment of bone properties. The results clearly demonstrated that FMA was a potential ultrasound index for the assessment of bone quantity and trabecular structure. Both FMA and BUA measured in SI and AP orientations were the good indicators of the bone properties if linear regression was employed. The correlations of FMA to the trabecular structural properties such as BV/TV, trabecular thickness, and trabecular space were similar or even better than those of BUA. They also showed little correlation to the same bone properties if measured in ML orientation.
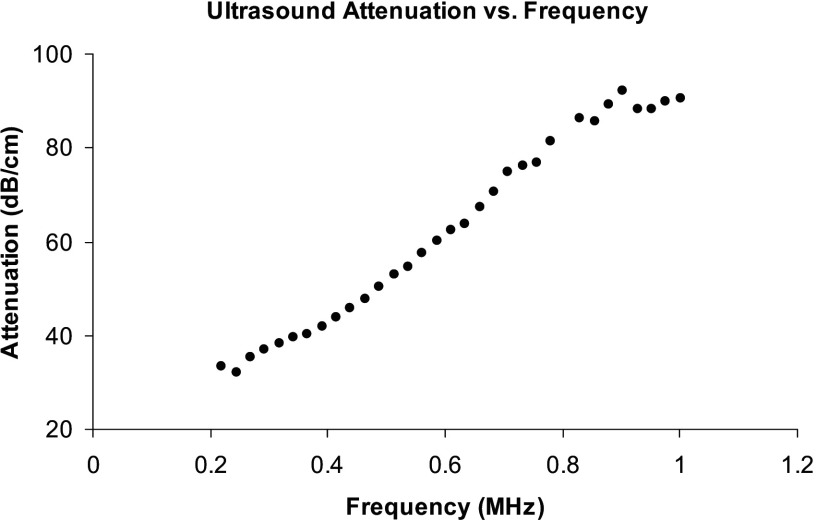
Even though FMA and BUA were derived from the ultrasound attenuation, they have fundamental difference in how the attenuation data were analyzed. BUA is defined as the slope of the linear section of the attenuation vs frequency curve and often normalized to the sample width to minimize its effect on attenuation. Human calcaneus has been reported to have a good linear dependence of ultrasound attenuation on frequency.33 Chaffai et al.34 further showed that a nonlinear power fit would be a good representation of the relationship. The mean value of was close to 1 (1.09) but had a substantial variation (0.4-2.2). Thus, BUA was dependent on the frequency range if was away from 1 and the attenuation lost the linear frequency dependency. When the linear dependency disappeared, the value BUA was meaningless. Figure 5 shows a typical relationship between the ultrasound attenuation and the frequency of the tested samples. Linear correlation was observed to be between 250 and . However, the slope between 250 and was 12% different from the slope between 300 and . BUA was equivalent to the derivative of ultrasound attenuation to frequency and thus was very sensitive to the variations of the attenuation. Therefore, the slight deviation from linearity of the ultrasound attenuation can easily be amplified in BUA. On the contrary, FMA took a different approach to analyze the ultrasound attenuation. It was derived from the time average of the ultrasound energy. It was the integration process that was suppressive to the variations such as noise from the measurement. Therefore, FMA should be more stable than BUA.
FIG. 5.
The dependence of ultrasound attenuation on frequency of the bone samples. Linearity was observed between 250 and .
When ultrasound waves travel through bone, the bone can be considered as a filter to the ultrasound signal. Ultrasound attenuation is the direct measurement of such frequency response determined by the trabecular architecture. It is still promising that the frequency response to ultrasound can be used to derive the bone properties even though the true mechanism of how such response is determined by the trabecular architecture is still not clear. BUA is the slope of the linear relationship of ultrasound attenuation to frequency within a certain frequency band. It is one of the prominent features of the ultrasound response but not a conclusive index that can represent all types of bone responses to ultrasound. It is not sufficient to use BUA as the only ultrasound attenuation index to characterize bone properties. FMA employs frequency modulated ultrasound signal to measure the ultrasound attenuation within an interested frequency band. In this study, the ultrasound signals, also called frequency sweep signals, were linearly modulated between 300 and within the period of . The choice of this particular frequency band was for the comparison between BUA and FMA in their capacity of bone properties assessment. Frequency sweep signal has been widely used in the measurement of the frequency response of electronic systems. It is a sinusoid function by nature with its frequency increasing linearly with time. It was equivalent to multiple sinusoidal signals in time sequence within one signal. The envelope of the frequency sweep signal represents the amplitudes of those sinusoidal signals and can be considered as the frequency spectrum of the frequency sweep signal, i.e., at a specific time instant, the envelope is the amplitude of the sinusoidal signal at that instant frequency. By changing the lower and upper bounds of the swept frequency, the frequency sweep signal can examine the details of the ultrasonic attenuation at any specified frequency band. Thus, FMA is considered as the ultrasound attenuation within a specified frequency band. When the lower and upper bounds approach to one frequency, FMA will be the ultrasound attenuation at that frequency. Compared to BUA, FMA is more flexible and can reveal the attenuation details that are most sensitive to bone properties.
One of the prominent features of the trabecular structure is quasi-periodic. When ultrasound wave interacts with this type of structure, the scattered ultrasound wave also becomes quasi-periodic and its quasi-frequency is related to the mean scatterer spacing (MSS). Pereira et al.26 employed the singular spectrum analysis to estimate the MSS from backscattered ultrasound signals from human trabecular bone. They compared MSS with the trabecular separation of the same bone sample and found good agreement between the two parameters. The frequency related to MSS was around . FMA can be a good candidate for searching such frequency. Although FMA was derived from the transmitted ultrasound, the same principle can be readily used in the analysis of backscattered ultrasound signals. Therefore, FMA is promising in bone properties assessment when it is tuned to a specific frequency band that is the most sensitive to the bone properties of interest. This unique advantage over BUA can make FMA a more favorable ultrasound parameter for the assessment of bone properties.
Another advantage of FMA over BUA is energy efficiency. The broadband ultrasound pulse in BUA measurement has a wide frequency range only limited by the frequency response of the transducer. However, if the interested band was narrower than its frequency response, it is surely not energy efficient because some of the energy outside the interested frequency band is wasted. In addition, the excitation voltage to the transducer has to be very high, usually hundreds of volts, in order to deliver enough energy to penetrate bone samples in a very short period of the pulse. Further, the maximum ultrasound energy allowed for clinic diagnosis is low and it is important to focus the limited energy within the targeted frequency band. The frequency modulated ultrasound has a unique property that its energy is always contained within the predetermined frequency band. Its longer duration than the broadband pulse allows the same amount of ultrasound energy to be delivered at low power and reduces the driving voltage to the transducer. It was showed that peak was sufficient in this study for bone measurement. FMA uses the energy efficient frequency modulated ultrasound for the bone property measurement.
The poor correlation of FMA and BUA in the ML orientation to the trabecular bone properties was contradictory to the findings in two other orientations. Ultrasound attenuation in this orientation was also linearly dependent on frequency. This confirmed that the BUA values were valid. Since both FMA and BUA measurements had the same conclusion, it was unlikely that this phenomenon was due to the experimental error. Current data did not support the assumption that the lack of correlation was solely due to the anisotropic structure of the samples. Although the real mechanism of this phenomenon is not known, it can be suggested that the trabecular architecture of the tested samples viewed from the ML orientation interacted with the incoming ultrasound wave in a complete different way that invalidated the assumption of linear correlation of ultrasound attenuation to bone structural properties.
Future work is required to improve the performance of the FMA. First, it is crucial to identify the optimal frequency bands that are most sensitive to the bone properties of interest. Narrow frequency bands will be more efficient because it can minimize the average effect of FMA over the frequency band. This requires a screening of a series of narrow frequency bands that cover a broader frequency spectrum. It is expected that those optimal frequency bands are specific to the anatomic locations of the bone. Second, the adjustment of the ultrasound signal is preferred before driving the transducer to compensate the frequency response of the transducer for the best performance of the FMA. In this study, the electric signal that drove the transducer had uniform amplitude. However, the amplitude of the generated ultrasound also had an amplitude modulation due to the frequency response of the transducer. This effect was minimized by the normalization of the energy of reference signal to bone signal because both signals included the same frequency response of the transducers. However, it is optimal to generate frequency sweep ultrasound signal with uniform amplitude. This requires the addition of amplitude modulation prior to driving the transducer to compensate its frequency response. Lastly, FMA is one of many parameters that can be derived from the new signal modality. Other parameters such as the frequency at the peak of the waveform envelope are also potential candidates for bone property measurements. The frequency modulated signal can also be modified for the measurement of ultrasound backscatters from bone to improve its performance.
ACKNOWLEDGMENTS
This work is kindly supported by the National Osteoporosis Foundation, the National Space Biomedical Research Institute (Grant Nos. TD00207 and TD00405, Y.-X.Q.) through NASA Cooperative Agreement No. NCC 9-58 and New York Advanced Center for Biotechnology.
REFERENCES
- 1.Marcus R., Feldman D., and Kelsey J., Osteoporosis (Academic, San Diego, 2001), p. 32. [Google Scholar]
- 2.Behari J. and Singh S., “Ultrasound propagation in ‘in vivo’ bone,” Ultrasonics 19, 87–90 (1981). 10.1016/0041-624X(81)90114-1 [DOI] [PubMed] [Google Scholar]
- 3.Firoozbakhsh K. and Cowin S. C., “An analytical model of Pauwels’ functional adaptation mechanism in bone,” J. Biomech. Eng. 103, 246–252 (1981). [DOI] [PubMed] [Google Scholar]
- 4.Bonfield W. and Tully A. E., “Ultrasonic analysis of the Young's modulus of cortical bone,” J. Biomed. Eng. 4, 23–27 (1982). 10.1016/0141-5425(82)90022-X [DOI] [PubMed] [Google Scholar]
- 5.Ashman R. B., Cowin S. C., Van Buskirk W. C., and Rice J. C., “A continuous wave technique for the measurement of the elastic properties of cortical bone,” J. Biomech. 17, 349–361 (1984). 10.1016/0021-9290(84)90029-0 [DOI] [PubMed] [Google Scholar]
- 6.Langton C. M., Palmer S. B., and Porter R. W., “The measurement of broadband ultrasonic attenuation in cancellous bone,” Eng. Med. 13, 89–91 (1984). 10.1243/EMED_JOUR_1984_013_022_02 [DOI] [PubMed] [Google Scholar]
- 7.Ashman R. B., Corin J. D., and Turner C. H., “Elastic properties of cancellous bone: Measurement by an ultrasonic technique,” J. Biomech. 20, 979–986 (1987). 10.1016/0021-9290(87)90327-7 [DOI] [PubMed] [Google Scholar]
- 8.Evans J. A. and Tavakoli M. B., “Ultrasonic attenuation and velocity in bone,” Phys. Med. Biol. 35, 1387–1396 (1990). 10.1088/0031-9155/35/10/004 [DOI] [PubMed] [Google Scholar]
- 9.Turner C. H. and Eich M., “Ultrasonic velocity as a predictor of strength in bovine cancellous bone 85,” Calcif. Tissue Int. 49, 116–119 (1991). 10.1007/BF02565132 [DOI] [PubMed] [Google Scholar]
- 10.Han S., Rho J., Medige J., and Ziv I., “Ultrasound velocity and broadband attenuation over a wide range of bone mineral density,” Osteoporosis Int. 6, 291–296 (1996). 10.1007/BF01623387 [DOI] [PubMed] [Google Scholar]
- 11.Hodgskinson R., Njeh C. F., Currey J. D., and Langton C. M., “The ability of ultrasound velocity to predict the stiffness of cancellous bone in vitro,” Bone (Osaka) 21, 183–190. 1997 10.1016/S8756-3282(97)00098-7 [DOI] [PubMed] [Google Scholar]
- 12.Lin W., Mittra E., and Qin Y. X., “Determination of ultrasound phase velocity in trabecular bone using time dependent phase tracking technique,” ASME J. Biomech. Eng. 128, 24–29 (2006). 10.1115/1.2132369 [DOI] [PubMed] [Google Scholar]
- 13.Wear K. A., “The effect of phase cancellation on estimates of calcaneal broadband ultrasound attenuation in vivo,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 54, 1352–1359 (2007). 10.1109/TUFFC.2007.395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bauer D. C., Gluer C. C., Cauley J. A., Vogt T. M., Ensrud K. E., Genant H. K., and Black D. M., “Broadband ultrasound attenuation predicts fractures strongly and independently of densitometry in older women. A prospective study,” Arch. Intern Med. 157, 629–634 (1997). 10.1001/archinte.157.6.629 [DOI] [PubMed] [Google Scholar]
- 15.Bouxsein M. L., Coan B. S., and Lee S. C., “Prediction of the strength of the elderly proximal femur by bone mineral density and quantitative ultrasound measurements of the heel and tibia,” Bone (Osaka) 25, 49–54 (1999). 10.1016/S8756-3282(99)00093-9 [DOI] [PubMed] [Google Scholar]
- 16.Gluer C. C., Wu C. Y., and Genant H. K., “Broadband ultrasound attenuation signals depend on trabecular orientation: An in vitro study,” Osteoporosis Int. 3, 185–191 (1993). 10.1007/BF01623674 [DOI] [PubMed] [Google Scholar]
- 17.Langton C. M., Njeh C. F., Hodgskinson R., and Currey J. D., “Prediction of mechanical properties of the human calcaneus by broadband ultrasonic attenuation,” Bone (Osaka) 18, 495–503 (1996). 10.1016/8756-3282(96)00086-5 [DOI] [PubMed] [Google Scholar]
- 18.Chaffai S., Peyrin F., Berger G., and Laugier P., “Relationships between ultrasonic attenuation, velocity and backscatter and cancellous bone micro-architecture,” J. Bone Miner. Res. 14, S376 (1999). [Google Scholar]
- 19.Hakulinen M. A., Toyras J., Saarakkala S., Hirvonen J., Kroger H., and Jurvelin J. S., “Ability of ultrasound backscattering to predict mechanical properties of bovine trabecular bone,” Ultrasound Med. Biol. 30, 919–927 (2004). 10.1016/j.ultrasmedbio.2004.04.006 [DOI] [PubMed] [Google Scholar]
- 20.Wear K. A. and Armstrong D. W., “The relationship between ultrasonic backscatter and bone mineral density in human calcaneus,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 47, 777–780 (2000). 10.1109/58.852057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wear K. A. and Laib A., “Relationship between ultrasonic backscatter and trabecular thickness in human calcaneus: Theory and experiment,” J. Bone Miner. Res. 17, S419 (2002). [Google Scholar]
- 22.Wear K. A., “The effect of trabecular material properties on the frequency dependence of backscatter from cancellous bone,” J. Acoust. Soc. Am. 114, 62–65 (2003). 10.1121/1.1554692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Roux C., Roberjot V., Porcher R., Kolta S., Dougados M., and Laugier P., “Ultrasonic backscatter and transmission parameters at the os calcis in postmenopausal osteoporosis,” J. Bone Miner. Res. 16, 1353–1362 (2001). 10.1359/jbmr.2001.16.7.1353 [DOI] [PubMed] [Google Scholar]
- 24.Wear K. A. and Laib A., “The dependence of ultrasonic backscatter on trabecular thickness in human calcaneus: Theoretical and experimental results,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 50, 979–986 (2003). 10.1109/TUFFC.2003.1226542 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nicholson P. H., Strelitzki R., Cleveland R. O., and Bouxsein M. L., “Scattering of ultrasound in cancellous bone: Predictions from a theoretical model,” J. Biomech. 33, 503–506 (2000). 10.1016/S0021-9290(99)00208-0 [DOI] [PubMed] [Google Scholar]
- 26.Pereira W. C. A., Bridal S. L., Coron A., and Laugier P., “Singular spectrum analysis applied to backscattered ultrasound signals from in vitro human cancellous bone specimens,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 51, 302–312 (2004). 10.1109/TUFFC.2004.1320786 [DOI] [PubMed] [Google Scholar]
- 27.Misaridis T. and Jensen J. A., “Use of modulated excitation signals in medical ultrasound. Part I: Basic concepts and expected benefits,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 177–191 (2005). 10.1109/TUFFC.2005.1406545 [DOI] [PubMed] [Google Scholar]
- 28.Misaridis T. and Jensen J. A., “Use of modulated excitation signals in medical ultrasound. Part II: Design and performance for medical imaging applications,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 192–207 (2005). 10.1109/TUFFC.2005.1406546 [DOI] [PubMed] [Google Scholar]
- 29.Misaridis T. and Jensen J. A., “Use of modulated excitation signals in medical ultrasound. Part III: High frame rate imaging,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 208–219 (2005). 10.1109/TUFFC.2005.1406547 [DOI] [PubMed] [Google Scholar]
- 30.Pedersen M. H., Misaridis T. X., and Jensen J. A., “Clinical evaluation of chirp-coded excitation in medical ultrasound,” Ultrasound Med. Biol. 29, 895–905 (2003). 10.1016/S0301-5629(02)00784-6 [DOI] [PubMed] [Google Scholar]
- 31.Nowicki A., Litniewski J., Secomski W., Lewin P. A., and Trots I., “Estimation of ultrasonic attenuation in a bone using coded excitation,” Ultrasonics 41, 615–621 (2003). 10.1016/S0041-624X(03)00181-1 [DOI] [PubMed] [Google Scholar]
- 32.Nazarian A., Snyder B. D., Zurakowski D., and Muller R., “Quantitative micro-computed tomography: A non-invasive method to assess equivalent bone mineral density,” Bone (Osaka) 43, 302–311 (2008). 10.1016/j.bone.2008.04.009 [DOI] [PubMed] [Google Scholar]
- 33.Wear K. A., “Ultrasonic attenuation in human calcaneus from ,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 48, 602–608 (2001). 10.1109/58.911743 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chaffai S., Padilla F., Berger G., and Laugier P., “In vitro measurement of the frequency-dependent attenuation in cancellous bone between 0.2 and ,” J. Acoust. Soc. Am. 108, 1281–1289 (2000). 10.1121/1.1288934 [DOI] [PubMed] [Google Scholar]