Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Mar 16;29(7):3181–3188. doi: 10.1021/acs.chemmater.7b00260

Influence of Rb/Cs Cation-Exchange on Inorganic Sn Halide Perovskites: From Chemical Structure to Physical Properties

Young-Kwang Jung †, Ji-Hwan Lee †, Aron Walsh †,‡,*, Aloysius Soon †,*
PMCID: PMC5393911  PMID: 28435185

Abstract

graphic file with name cm-2017-00260c_0006.jpg

CsSnI3 is a potential lead-free inorganic perovskite for solar energy applications due to its nontoxicity and attractive optoelectronic properties. Despite these advantages, photovoltaic cells using CsSnI3 have not been successful to date, in part due to low stability. We demonstrate how gradual substitution of Rb for Cs influences the structural, thermodynamic, and electronic properties on the basis of first-principles density functional theory calculations. By examining the effect of the Rb:Cs ratio, we reveal a correlation between octahedral distortion and band gap, including spin–orbit coupling. We further highlight the cation-induced variation of the ionization potential (work function) and the importance of surface termination for tin-based halide perovskites for engineering high-performance solar cells.

Introduction

Organic–inorganic hybrid halide perovskite materials have been intensively investigated in recent years.1−11 The efficiency of solar cells made up of these materials has shown a drastic increase from 3.8% in 2009 to 22.1% in 2016.1,2 Despite the high efficiency of perovskite solar cells, two concerns hinder these materials from being an ideal solar cell technology. One issue is the presence of an organic cation (e.g., CH3NH3+), which is regarded as a principal cause of low thermal compositional stability. Recently, replacing the organic by inorganic cations has been suggested as a way to improve thermal stability.12 The other concern is the presence of lead (Pb), which is well-known for its toxicity. Replacing Pb by tin (Sn) or germanium (Ge) has been suggested as a way to overcome this issue.7−9,13,14

CsSnI3, a tin-based lead-free inorganic halide perovskite, is a p-type semiconductor with a high hole mobility. It has a band gap of 1.3 eV, low exciton binding energy of 18 meV, and high optical absorption coefficient of 104 cm–1, which are favorable properties for a light-absorbing material in solar cells.15−17 There have been a few attempts to fabricate solar cells using CsSnI3 as an active layer, but their maximum efficiency was only near 2%.18−20 This low efficiency of CsSnI3-based solar cells can be explained mainly by two view points, namely, band energy level alignment in devices and thermodynamic phase stability resulting in mixed-phase thin films.

Appropriate band alignment, in particular, between the absorber and charge extraction layers, is essential for efficient photovoltaic devices. However, the exact band energy levels of CsSnI3 are still controversial,21,22 and a way to modulate their electron addition and removal energies has not been well studied. According to Chung et al., the energy of the valence band maximum (VBM) and conduction band minimum (CBM) are −4.92 and −3.62 eV, respectively.21 Here, the VBM level is too high to transfer holes from CsSnI3 to standard hole transfer materials (HTM) such as Spiro-OMeTAD.23 On the other hand, according to Zhang et al., the levels of VBM and CBM are measured to be −5.74 and −4.47 eV, respectively.22 In contrast, the CBM level is now too low to transfer electrons from CsSnI3 to standard electron transfer materials (ETM) such as TiO2.23 Hence, understanding of the absolute band energies of CsSnI3 and finding ways to modulate them are important for using CsSnI3 as a light-absorbing layer in solar cells.

At room temperature, CsSnI3 has two coexisting polymorphs (γ and Y phases) that belong to the Pnma space group. Transition from the black γ phase to yellow Y phase has been observed in ambient conditions, though both phases have stable phonon modes and similar free energies.17,24,25 Because of the different crystal/atomic structure and electronic properties of the Y phase (i.e., with nonperovskite structure and an indirect band gap of 2.6 eV), this unwanted phase transition can significantly decrease the solar cell efficiency as found in other hybrid perovskite-based solar cells.17,26,27

Recently, it has been suggested that mixing the A-site cations (e.g., combining Cs and Rb) could stabilize the preferred perovskite phase, which has been attributed to an increase in configurational entropy and a corresponding decrease in the free energy of this phase.26−28 Additionally, a cation-induced band gap tuning effect has also been reported.29,30 Thus, it seems very viable that both phase stability improvement and electronic properties modulation can be achieved simultaneously by the mixing of A-site cations in CsSnI3.

In this paper, we explain the impact of the smaller Rb+ cation substitution for the larger Cs+ cation based on crystal structure, thermodynamic stability, and band gap, including a partially substituted cation solid solution system (RbxCs1–xSnI3). Insights into the atomic-scale processes are gained by using a first-principles density functional theory (DFT) approach, including the calculation of the electronic band structures of CsSnI3 and RbSnI3 with spin–orbit coupling (SOC) effects to identify cation-induced changes. We further investigate the surface chemistry within an ab initio atomistic thermodynamic framework. Finally, we predict absolute energy levels depending on their surface and highlight the importance of controlling surface termination for determining band energy levels of the material as well as the influence of cation exchange on these inorganic Sn halide perovskites.

Methods

First-Principles Calculations

All calculations are performed using Kohn–Sham DFT as implemented in the Vienna Ab initio Simulation Package (VASP).31,32 Projector augmented-wave (PAW)33,34 pseudopotentials are used to treat core atomic states, and the valence electron configurations of Rb, Cs, Sn, and I are explicitly taken as 4s24p65s1, 5s25p66s1, 4d105s25p5, and 5s25p5, respectively. The convergence of the total energy and forces are considered within 10–5 eV and 10–4 eV/Å, respectively. To address the effect of SOC on our system, we have included this perturbatively only for our electronic band structure calculations.

For the exchange-correlation (xc) functional, the generalized gradient approximation (GGA) due to Perdew, Burke, and Ernzerhof (PBE) is employed for all geometry/structural optimizations.35 A plane-wave kinetic cutoff energy of 600 eV is used for all PBE calculations. The Brillouin-zone integrations are performed using a Γ-centered k-point grid of 6 × 6 × 5 for all bulk calculations, whereas a 6 × 6 × 1 k-point grid is used for all surface calculations. The symmetric (001) surface slab model used in this work consist of 11 atomic layers (AL) and a vacuum region of 15 Å. The atomic positions are fully relaxed while keeping the innermost three center ALs fixed to bulk values.

To obtain more accurate absolute band energy levels with respect to the vacuum level, we have also performed additional nonlocal hybrid DFT calculations within the HSE06 xc approximation36,37 because PBE is known to severely underestimate the band gap. Although the band gap of CsSnI3 from our HSE06+SOC calculation (0.86 eV) is underestimated with respect to the experimental value (∼1.3 eV), this difference agrees well with that from previous studies.38−40 For the HSE06 and HSE06+SOC calculations, we have adopted a lower plane-wave kinetic cutoff energy of 300 eV with a Γ-centered k-point grid of 3 × 3 × 3 and 3 × 3 × 1 for the bulk and surface systems, respectively. For these HSE06 calculations, we have carefully tested for convergence with respect to the band gap, and further details can be found in Table S2.

Mixing Thermodynamics

To examine the cation exchange effects, we use the orthorhombic γ-phase CsSnI3 unit cell, which is the reported stable perovskite phase for CsSnI3 at room temperature.15,41,42 On the basis of the unit cell of γ-CsSnI3, which has four different A-cation sites, five different compositions of Rb and Cs (RbxCs1–xSnI3, x = 0.00, 0.25, 0.50, 0.75, and 1.00) are considered.

To assess the thermodynamic stability of RbxCs1–xSnI3 cation solid solution, we calculate the Helmholtz free energy of mixing for each composition according to

graphic file with name cm-2017-00260c_m001.jpg 1

where ΔU and ΔS are the internal energy and entropy of mixing and T is the absolute temperature. The internal energy of mixing is then calculated using

graphic file with name cm-2017-00260c_m002.jpg 2

where ERbxCs1–xSnI3, ERbSnI3, and ECsSnI3 are the total energies of RbxCs1–xSnI3, RbSnI3, and CsSnI3, respectively. The entropy of mixing is calculated in the homogeneous limit according to

graphic file with name cm-2017-00260c_m003.jpg 3

where kB is the Boltzmann constant.

Recently, the thermodynamic stability of the CsxFA1–xPbI3 cation solid solution (where FA stands for formamidinium, CH(NH2)2) and MAPb(I1–xBrx)3 anion solid solution (where MA represents methylammonium, CH3NH3) have been successfully studied with similar approaches.26,43

Surface Chemistry

Because of the presence of three elements in the ABX3 system, the surfaces of perovskite crystals can be terminated in a number of ways. To compare the relative energetic stability of two different surface terminations (AX or BX2 terminations) of the ABX3 (001) surface, which are not stoichiometric, we employ the ab initio atomistic thermodynamics (aiAT) approach.44 This allows us to calculate the surface energies and compare their relative thermodynamic stabilities under different growth conditions.44−46

In the aiAT approach, the surface energy (γ) is defined as a function of chemical potential per surface area (A) following

graphic file with name cm-2017-00260c_m004.jpg 4

where Gsurf is the Gibbs free energy of the surface, μi is the chemical potential of the various species i present in the system, and Ni is the number of the species i. For this work, to reflect the general synthesis reaction of halide perovskites (i.e., AX + BX2 → ABX3),17,21,22 here we simply use i as the bulk components CsI, RbI, and SnI2, respectively, rather than atomic species Cs, Rb, Sn, and I.

For sufficiently large particles of these inorganic Sn halide perovskites at ambient temperatures, bulk ABX3 could be considered as a thermodynamic reservoir where the surface is equilibrated. This assumption constrains the chemical potentials of AX and BX2 (i.e., μAX and μBX2 accordingly) to the specific Gibbs free energy of ABX3 (GABX3bulk) as defined by

graphic file with name cm-2017-00260c_m005.jpg 5

Consequently, eq 5 can reformulate eq 4 to express the surface free energy only as a function of μBX2,

graphic file with name cm-2017-00260c_m006.jpg 6

Here, the use of symmetric surface slab models necessitates a factor of 1/2. This definition now allows us to compare two different terminations of the ABX3 (001) surface whose thermodynamic stability is then governed by the change in the BX2 chemical potential. Likewise, it is trivial to express the dependence of the surface energy on the change in the chemical potential of SnI2 (ΔμSnI2) by referencing the total energy of the bulk tin iodide per formula unit (ESnI2bulk), where ΔμSnI2 = μSnI2 – ESnI2. Environment-independent surface energy calculations, which have been used in oxide perovskites, are also performed and compared with the aiAT approach in Figures S3 and S4.63,64

Results and Discussion

Stability of the Rb/Cs Solid Solution

Among the various known CsSnI3 bulk phases, i.e., the α (Pm3m), β (P4/mbm), γ (Pnma), and Y (Pnma) (see Figure S1), the most stable and application-relevant orthorhombic perovskite phase (γ) is chosen for the solid-solution modeling.17,24 Our calculated lattice parameters of CsSnI3 (a0 = 8.94, b0 = 8.69, and c0 = 12.52) agree well with both experimental measurements (a0 = 8.67, b0 = 8.64, and c0 = 12.38) and theoretical calculations (a0 = 8.94, b0 = 8.71, and c0 = 12.50).17,47

On the other hand, RbSnI3 has been reported to exist in a nonperovskite structure (i.e., the Y-phase) due to the small cationic size of Rb+.17 A comparison of our calculated bulk properties of the various polymorphs of both CsSnI3 and RbSnI3 can be found in Table S1 and are in good agreement with those in the reported literature.17,25,47

To assess the possibility of perovskites with different size cations (Cs larger than Rb), the Goldschmidt tolerance factor (t) is calculated using48,49

graphic file with name cm-2017-00260c_m007.jpg 7

where ri is taken as the ionic radius of element i (i.e., rRb = 1.52 Å, rCs = 1.67 Å, rSn = 1.10 Å, and rI = 2.20 Å).8,50

The t for the Rb cation in a SnI6 octahedral cage is calculated as 0.80, which is rather comparable to that for the Cs cation (0.83). This lends support to the possibility of forming a perovskite-structured RbxCs1–xSnI3 solid solution. t values of ∼0.80 further suggest that the A-site cation might be too small to sustain a perfect cubic perovskite structure and will consequently be distorted to favor the orthorhombic perovskite structure.8,29 To confirm the relative stability of mixed Rb/Cs perovskite in the orthorhombic phase as compared to other perovskite-structured phases (such as tetragonal phase), we find that, for example, orthorhombic γ-Rb0.5Cs0.5SnI3 is energetically more favorable than tetragonal β-Rb0.5Cs0.5SnI3 by ∼0.04 eV/formula unit in its formation energy.

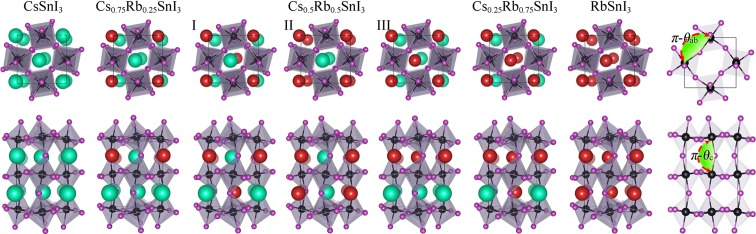
Optimized bulk atomic structures of RbxCs1–xSnI3 solid solution models (with varying x values) are depicted in Figure 1. All considered, RbxCs1–xSnI3 are represented by one unique structure with the exception of when x = 0.5, where three distinct structures can be formed by a combinatorial occupation of Rb and Cs atoms at the A-cation site: I (with the same elements located in the diagonal direction, ⟨111⟩), II (with the same elements located in the vertical direction, ⟨001⟩), and III (with the same elements located in the horizontal direction, ⟨110⟩).

Figure 1.

Figure 1

Open in a new tab

Atomic structure of RbxCs1–xSnI3 for x = 0.00, 0.25, 0.50 (I, II, and III), 0.75, and 1.00 and a scheme for defining distortion angles (θab and θc) with only SnI6 octahedral frameworks (shaded in pale purple). Cs, Rb, Sn, and I are represented by green, red, black, and purple spheres, respectively.

To systemically analyze this effect of cation exchange on the bulk characteristics of these solid solutions, we plot their bulk properties in Figure 2 as a function of the ratio Rb/Cs, i.e., x in RbxCs1–xSnI3. Here, all markers represent calculated values, and dashed lines are drawn according to Vegard’s law, where CsSnI3 and RbSnI3 are set as two end constituents. The calculated values are tabulated in Table S3.

Figure 2.

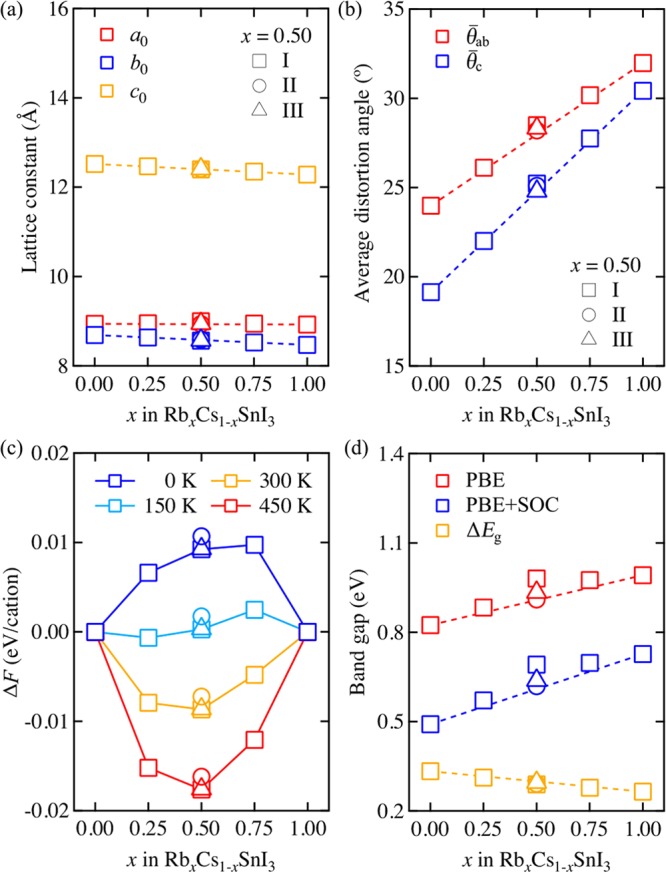
Figure 2

Open in a new tab

(a) Lattice constants (a0, b0, and c0), (b) average distortion angles (θ̅ab and θ̅c), (c) Helmholtz energy of mixing (ΔF for various temperatures), and (d) electronic band gap for RbxCs1–xSnI3 as a function of x. Dashed lines are drawn according to Vegard’s linear relation using the two end-member constituents where x is 0.00 (CsSnI3) and 1.00 (RbSnI3). ΔEg in (d) is derived from the calculated difference between the electronic band gaps with and without the SOC effect.

In Figure 2a, our calculated lattice constants show small changes as the Rb fraction increases, following a linear trend as predicted from Vegard’s law. Specifically, a decreasing tendency is found for both b0 and c0, but a0 is hardly changed with x. To quantify the degree of octahedral distortion in these solid solutions, we define θab and θc (which are labeled and shown in Figure 1) by measuring the Sn–I–Sn bonding angles in the SnI6 octahedral frameworks for each unit cell within the ab-plane and along the c-axis and then subtracting them from 180°. The θab and θc are thus, by definition, 0° when the SnI6 octahedral frameworks are in perfect cubic phase (i.e., not distorted).

The average value of distortion angles, θ̅ab and θ̅c in Figure 2b, show an increasing linear trend ensuing Vegard’s linear law. The calculated θab and θc values are detailed in Figure S2 and further listed in Table S3. In terms of crystal structure, this clearly supports the fact that the size of A cations in tin-based halide perovskites hardly affects their lattice constants (consequentially, volume), whereas it significantly alters the internal distortion of the structure (i.e., the SnI6 octahedral framework). It is due to the open structure and flexibility of perovskite, where SnI6 octahedrons form a corner-sharing framework. We also find that there are no large differences in the bond lengths of the SnI6 octahedrons, ranging from 3.17 to 3.19 Å in CsSnI3 and 3.18 to 3.20 Å in RbSnI3.

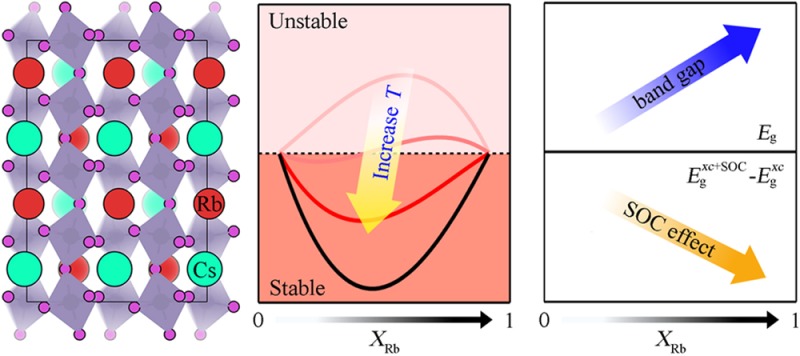
The Helmholtz free energy of mixing is calculated and plotted as a function of x in RbxCs1–xSnI3 in Figure 2c. At 0 K, where the entropy of mixing does not affect the free energy, all values for the considered solid-solution models of RbxCs1–xSnI3 are thus positive, indicating that the solid solutions prefer to phase separate into the constituents CsSnI3 and RbSnI3. However, as temperature increases, which strengthens the contribution of entropy following eq 1, the solid solutions gradually stabilize with a negative free energy of mixing. At room temperature of 300 K, all solid solutions of RbxCs1–xSnI3 are calculated to be more stable than the constituent phases. Although vibrational contributions are not considered here, they are not expected to alter this conclusion.

The RbxCs1–xSnI3 solid solution has a good thermodynamic stability at room temperature, which is well above the calculated critical temperature of 140 K within the generalized quasi-chemical approximation (GQCA).43,51 In contrast, anion mixing in the CH3NH3Pb(I1–xBrx)3 solid solution shows a miscibility gap around room temperature and having a critical temperature of 343 K.43,51

Relativistic Band Gap Bowing

In Figure 2d, the calculated band gaps of RbxCs1–xSnI3 without the SOC effect (EgPBE) are represented with higher values than those calculated with the SOC effect (Eg). To quantify the influence of SOC on our calculated band gaps, we simply take the numerical difference (ΔEg) between EgPBE and Eg. Contrary to the increasing linear (Vegard’s relation) trend of the band gap, the influence of SOC on the band gap decreases linearly as x in RbxCs1–xSnI3 increases. This result agrees with the distortion effect on the band gap and SOC for lead-based perovskite, which was reported by Amat et al.29

By combining our results in Figure 2b and d, we argue that in terms of the structure–property relationship in these all-inorganic Sn halide perovskites, the small cationic size of Rb is responsible for the increasing distortion of the SnI6 octahedral frameworks and consequent widening of the band gaps while reducing the SOC effects in these RbxCs1–xSnI3 solid solutions. As is clearly depicted in Figure 2, all bulk characteristics of these all-inorganic Sn halide perovskites nicely obey the Vegard’s linear relation and thus allow one to easily estimate various characteristics of a regular solid solution based on the properties of its end-member constituents CsSnI3 and RbSnI3.

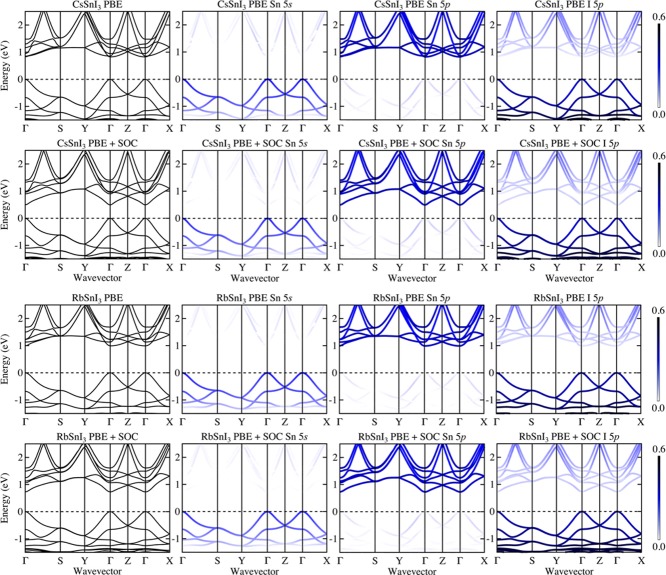
To further explore the correlation between the A-cation exchange and SOC effects, we calculate the electronic band structures for both CsSnI3 and RbSnI3 with PBE and PBE+SOC. Following previous studies,17,39,52 the orbitals of A-site cations (Rb and Cs), the d orbital of Sn, and the s and d orbitals of I hardly contribute to the band edges. Thus, in Figure 3, we plot the total band structure and the orbital-projected band structures due to the s, p orbital of Sn and p orbital of I (which are mainly responsible for the orbital character of the band edges). It clearly shows that valence bands are mainly comprised of Sn 5s and I 5p, whereas the conduction bands have a dominant Sn 5p character and some weak contribution from I 5p.

Figure 3.

Figure 3

Open in a new tab

PBE(+SOC) calculated electronic band structures and their orbital contributions for CsSnI3 and RbSnI3. The total band structure is shown in the first column, and the orbital-projected contributions due to Sn 5s, Sn 5p, and I 5p are depicted from the second to fourth columns. Specifically, the PBE+SOC plots for CsSnI3 and RbSnI3 are displayed in the second and fourth row, respectively. The occupation of the states are colored according to the legends on the far right, ranging from 0 to 0.6 per state.

Referring to the third column of Figure 3, following the Y-Γ-Z and the Γ-S paths, significant band splitting in the conduction bands due to the influence of SOC is observed. In an atomic picture, the three empty 5p orbitals of Sn are degenerate (with T symmetry), but in a crystal these are split (i.e., T → A + E) by the crystal field. Finally, the symmetry of the doubly degenerate (E) band is removed by spin–orbit coupling.53 In contrast, the SOC effects in the valence band are found to be negligible.

Connecting with the distortion trends in Figure 2b, the relevant electronic band properties of these perovskites are primarily determined by the SnI6 octahedral frameworks, and the A-site cations play a role in modulating the structure of these octahedral frameworks and other structure-related properties, such as the distortion angle of the octahedron and band gap. It is similar to the role of organic molecules in hybrid perovskites, but organic molecules can further distort the octahedra due to their anisotropic shape and charge distribution.54 We note that band engineering by controlling the bond angle distributions has been explored in detail by Filip et al. for a range of halide perovskites.55

Surface Thermodynamics

To gain insight into A-cation exchange and surface termination effects on the absolute energy of the valence and conduction bands (EVBM and ECBM), we investigate the surfaces of each end-member constituent, CsSnI3 and RbSnI3, and assume Vegard’s linear relation. We choose the (001) surface of orthorhombic CsSnI3 and RbSnI3, which are expected to be the most stable surface energies following other perovskite studies.56,57 We consider two terminations: CsI and SnI2 termination for the CsSnI3(001) surface (CsSnI3(001):CsI and CsSnI3(001):SnI2) and RbI and SnI2 termination for the RbSnI3(001) surface (RbSnI3(001):RbI and RbSnI3(001):SnI2). After relaxing the slab geometries, we examine the relative thermodynamic stabilities of these surfaces with different terminations. Finally, the electrostatic potential of the crystal is aligned with the vacuum level to access the ionization potential and electron affinity.

The atomic geometries of the relaxed surface slab models are depicted in Figure 4. CsSnI3(001):CsI and RbSnI3(001):RbI maintain the bulk-like tilted SnI6 octahedrons at the surface, whereas CsSnI3(001):SnI2 and RbSnI3(001):SnI2 have exposed truncated octahedrons (also see Figure S5). Here, we focus on the influence of the surface termination rather than the surface orientation of the slab given that the surface motifs here are also commonly found on other nonpolar surfaces.

Figure 4.

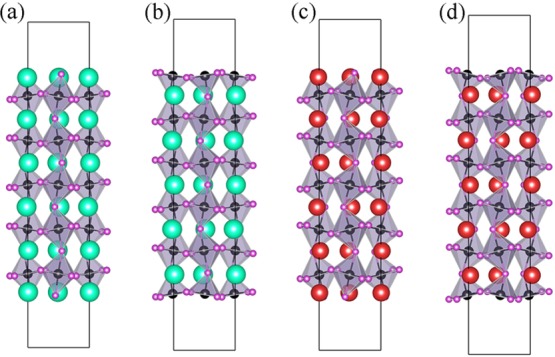
Figure 4

Open in a new tab

Side view of the atomic structures of CsSnI3(001) with (a) CsI and (b) SnI2 terminations and RbSnI3(001) with (c) RbI and (d) SnI2 terminations. The representation of the colored atoms here follows that of Figure 1.

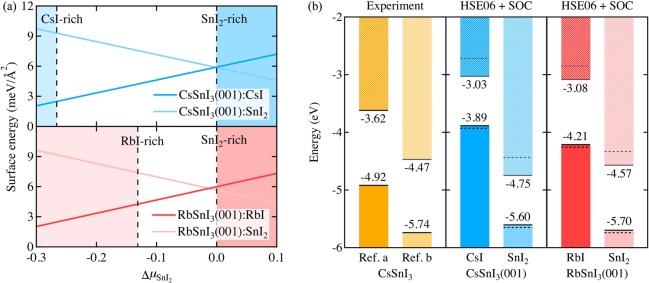
According to the calculated surface energy as a function of the change in the SnI2 chemical potential (ΔμSnI2) in Figure 5a, both CsSnI3(001):CsI and RbSnI3(001):RbI have lower surface energies under CsI- and RbI-rich conditions, whereas CsSnI3(001):SnI2 and RbSnI3(001):SnI2 exhibit lower surface energies only under SnI2-rich conditions. However, the surface energy difference between CsSnI3(001):CsI (or RbSnI3(001):RbI) and CsSnI3(001):SnI2 (or RbSnI3(001):SnI2) is considerable (>3 meV/Å2) under CsI (or RbI)-rich conditions, whereas the difference is more subtle (<0.5 meV/Å2) under SnI2-rich conditions.

Figure 5.

Figure 5

Open in a new tab

(a) Calculated surface energy as a function of the change in the SnI2 chemical potential (ΔμSnI2) for all surface terminations of CsSnI3(001) and RbSnI3(001). ΔμSnI2 for CsI-, RbI-, and SnI2-rich conditions are determined as −0.27, −0.13, and 0 eV, respectively. (b) Band energy level alignment diagrams: EVBM and ECBM levels from experiments (for CsSnI3)21,22 and HSE06+SOC calculated values for CsSnI3(001) and RbSnI3(001). All energy levels are aligned with respect to the absolute vacuum level (set to 0 eV). The energy levels in horizontal solid and dashed lines refer to the HSE06-calculated EVBM and ECBM levels with and without consideration of the SOC effect, respectively.

To relate the changes in the chemical potentials to the changes in mole fraction or species concentration during synthesis, we employ an ideal solution model to aid discussion.58 Therefore, our results indicate that CsSnI3(001):CsI (or RbSnI3(001):RbI) will be dominant under excess CsI (or RbI) during synthesis, whereas CsSnI3(001):CsI (or RbSnI3(001):RbI) and CsSnI3(001):SnI2 (or RbSnI3(001):SnI2) will be competitive depending on the immediate environment under excess SnI2 conditions.

Absolute Electron Energies

Given the periodic boundary constrains of a bulk unit cell, the absolute electronic energy level with respect to an external vacuum level cannot be obtained. To overcome this limitation, we use the core energy level and vacuum level as proper reference states.46,59 Because both terminations, CsI (or RbI) and SnI2, have the possibility to appear at the surface, we decided to consider both terminations for aligning the absolute energy levels. First, we set an external vacuum level, which is obtained by an electrostatic potential calculation of (001) relaxed surface slab models, as a reference level. We then perform core level calculations with both bulk and slab unit cells. The Sn 1s level is chosen as the representative core level in this study. Finally, the absolute energy levels of the VBM and CBM of the bulk phases (with respect to external vacuum level) are then calculated by

graphic file with name cm-2017-00260c_m008.jpg 8
graphic file with name cm-2017-00260c_m009.jpg 9

where ϵVBMKS and ϵCBM are the bulk Kohn–Sham eigenvalues, ESn1sbulk is the average Sn 1s levels of the Sn atoms in the bulk phase, ESn1s is that of the Sn atoms within the innermost three layers of the surface slab model, and Vvac is the vacuum level derived from the planar average electrostatic potential of the surface slab models.

Following this band alignment procedure (Figure 5b), we find that both the ionization potential and electron affinity of Sn-based perovskites are highly dependent on their surface termination. For CsSnI3, the band energy level difference between the CsI and SnI2 terminations is around 1.6 eV and covers the range previously reported by experimental measurements.21,22 Here, we note that underestimation of the band gap in our calculation when compared to experimental results agrees with previous studies.38−40 This would be corrected by using more sophisticated theories of electronic excitations, such as GW+SOC, or considering anharmonicity of these perovskites.40,60,61 However, in this study, we focus on the terminations of surface models within the HSE06+SOC scheme due to computational limitations.

Here, we reason that the conflicting experimental reports of band energy levels may have been a case of comparing the band energy levels of different surface terminations present in the prepared samples. Moreover, by comparing the band energy levels between CsSnI3 and RbSnI3, we find that the A-cation-induced band energy level changes are much weaker than that due to a difference in surface terminations in Sn-based perovskites.

Interestingly, the effect of A-cation exchange on band energy levels differs depending on the actual surface termination, i.e., by applying Vegard’s relation, both EVBM and ECBM levels of the RbI (CsI)-terminated surface are predicted to be lowered in a linear fashion with increasing value of x in RbxCs1–xSnI3 (with EVBM showing a larger decrease). On the other hand, for the SnI2-terminated surface of the RbxCs1–xSnI3 solid solution, we find that the EVBM is predicted to decrease marginally, whereas the ECBM will shift to higher energies with an increasing value of x. Furthermore, by comparing band energy levels with and without SOC (see Table S5), it is clear that SOC lowers the ECBM level due to the splitting of the conduction band edge. Here, we note that there are no surface states within band gaps in our slab models in Figure 4 (see Figure S6) and both the PBE- and HSE06-derived band energy level alignments support this argument (see Figure S7).

In addition to resolving the experimental controversy, our results suggest that the optimal electron and hole extraction layers for CsSnI3 and the Cs/Rb mixture will depend on how the sample is grown. For instance, samples with SnI2-rich surfaces will require much deeper electron and hole extraction layers to achieve high photovoltaic performance. This could be a general issue for inorganic halide perovskites, which will require a combination of crystal engineering of morphology and electronic engineering of contacts to realize high-efficiency solar cells. Future work should consider how morphology and defects could further affect absolute band edge positions and surface states.

Conclusions

In summary, the effect of cation mixing has been investigated in tin halide perovskites. Although the description of partial site occupancy from first-principles atomistic theories is challenging, we have followed a practical computational procedure, which both agrees well with existing experimental observations and provides new fundamental insights into the behavior of the solid solutions. We demonstrated that the RbxCs1–xSnI3 alloy becomes stable by configurational entropy and follows Vegard’s law well in terms of lattice constants, distortion angles, and band gap. Because of the increase of octahedron distortion, the effect of spin–orbit coupling on the band gap is decreased. We also showed how the ionization potentials and electron affinities vary strongly with surface termination, which can be tuned with synthesis conditions. This resolves an existing controversy and provides a guideline to develop more efficient photovoltaic architectures. Although our study focused on the inorganic Cs/Rb mixture, the structural properties of the organic CH3NH3/CH(NH2)2 mixture have recently been shown to follow Vegard’s law, so a similar computational procedure could be followed to investigate their properties.62

Acknowledgments

This work was supported by a Samsung Research Funding Center of Samsung Electronics (Grant No. SRFC-MA1501-03). The work at ICL was supported by the EPSRC (Grant Nos. EP/K016288/1 and EP/M009580/1) and the ERC (Grant No. 277757). Computational resources have been provided by the KISTI Supercomputing Center (Grant No. KSC-2016-C3-0009).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.chemmater.7b00260.

  • Detailed bulk and surface properties of the polymorphs (CsSnI3 and RbSnI3) and their solid solutions and their thermodynamic stabilities, surface band structures, and band level alignment under the influence of SOC effect and various xc functionals (PDF)

Author Contributions

Y.-K.J. and J.-H.L. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

cm7b00260_si_001.pdf (10.3MB, pdf)

References

  1. NREL, Best Research-Cell Efficiencies. http://www.nrel.gov/ncpv/images/efficiency_chart.jpg (accessed March 16, 2017).
  2. Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
  3. Frost J. M.; Butler K. T.; Brivio F.; Hendon C. H.; van Schilfgaarde M.; Walsh A. Atomistic Origins of High-Performance in Hybrid Halide Perovskite Solar Cells. Nano Lett. 2014, 14, 2584–2590. 10.1021/nl500390f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Jeong B.; Hwang I.; Cho S. H.; Kim E. H.; Cha S.; Lee J.; Kang H. S.; Cho S. M.; Choi H.; Park C. Solvent-Assisted Gel Printing for Micropatterning Thin Organic–Inorganic Hybrid Perovskite Films. ACS Nano 2016, 10, 9026–9035. 10.1021/acsnano.6b05478. [DOI] [PubMed] [Google Scholar]
  5. Jeong B.; Cho S. M.; Cho S. H.; Lee J. H.; Hwang I.; Hwang S. K.; Cho J.; Lee T.-W.; Park C. Humidity Controlled Crystallization of Thin CH3NH3PbI3 Films for High Performance Perovskite Solar Cell. Phys. Status Solidi RRL 2016, 10, 381–387. 10.1002/pssr.201600004. [DOI] [Google Scholar]
  6. Sun Y.-Y.; Agiorgousis M. L.; Zhang P.; Zhang S. Chalcogenide Perovskites for Photovoltaics. Nano Lett. 2015, 15, 581–585. 10.1021/nl504046x. [DOI] [PubMed] [Google Scholar]
  7. Kadro J. M.; Pellet N.; Giordano F.; Ulianov A.; Muntener O.; Maier J.; Gratzel M.; Hagfeldt A. Proof-of-Concept for Facile Perovskite Solar Cell Recycling. Energy Environ. Sci. 2016, 9, 3172–3179. 10.1039/C6EE02013E. [DOI] [Google Scholar]
  8. Green M. A.; Ho-Baillie A.; Snaith H. J. The Emergence of Perovskite Solar Cells. Nat. Photonics 2014, 8, 506–514. 10.1038/nphoton.2014.134. [DOI] [Google Scholar]
  9. Sun Y.-Y.; Shi J.; Lian J.; Gao W.; Agiorgousis M. L.; Zhang P.; Zhang S. Discovering Lead-Free Perovskite Solar Materials with a Split-Anion Approach. Nanoscale 2016, 8, 6284–6289. 10.1039/C5NR04310G. [DOI] [PubMed] [Google Scholar]
  10. Kim J.; Lee S.-H.; Lee J. H.; Hong K.-H. The Role of Intrinsic Defects in Methylammonium Lead Iodide Perovskite. J. Phys. Chem. Lett. 2014, 5, 1312–1317. 10.1021/jz500370k. [DOI] [PubMed] [Google Scholar]
  11. Kim J.; Lee S.-H.; Chung C.-H.; Hong K.-H. Systematic Analysis of the Unique Band Gap Modulation of Mixed Halide Perovskites. Phys. Chem. Chem. Phys. 2016, 18, 4423–4428. 10.1039/C5CP05982H. [DOI] [PubMed] [Google Scholar]
  12. Sutton R. J.; Eperon G. E.; Miranda L.; Parrott E. S.; Kamino B. A.; Patel J. B.; Hörantner M. T.; Johnston M. B.; Haghighirad A. A.; Moore D. T.; Snaith H. J. Bandgap-Tunable Cesium Lead Halide Perovskites with High Thermal Stability for Efficient Solar Cells. Adv. Energy Mater. 2016, 6, 1502458. 10.1002/aenm.201502458. [DOI] [Google Scholar]
  13. Noel N. K.; Stranks S. D.; Abate A.; Wehrenfennig C.; Guarnera S.; Haghighirad A. A.; Sadhanala A.; Eperon G. E.; Pathak S. K.; Johnston M. B.; Petrozza A.; Herz L. M.; Snaith H. J. Lead-Free Organic–Inorganic Tin Halide Perovskites for Photovoltaic Applications. Energy Environ. Sci. 2014, 7, 3061–3068. 10.1039/C4EE01076K. [DOI] [Google Scholar]
  14. Krishnamoorthy T.; Ding H.; Yan C.; Leong W. L.; Baikie T.; Zhang Z.; Sherburne M.; Li S.; Asta M.; Mathews N.; Mhaisalkar S. G. Lead-Free Germanium Iodide Perovskite Materials for Photovoltaic Applications. J. Mater. Chem. A 2015, 3, 23829–23832. 10.1039/C5TA05741H. [DOI] [Google Scholar]
  15. Shum K.; Chen Z.; Qureshi J.; Yu C.; Wang J. J.; Pfenninger W.; Vockic N.; Midgley J.; Kenney J. T. Synthesis and Characterization of CsSnI3 Thin Films. Appl. Phys. Lett. 2010, 96, 221903. 10.1063/1.3442511. [DOI] [Google Scholar]
  16. Chen Z.; Yu C.; Shum K.; Wang J. J.; Pfenninger W.; Vockic N.; Midgley J.; Kenney J. T. Photoluminescence Study of Polycrystalline CsSnI3 Thin Films: Determination of Exciton Binding Energy. J. Lumin. 2012, 132, 345–349. 10.1016/j.jlumin.2011.09.006. [DOI] [Google Scholar]
  17. Chung I.; Song J.-H.; Im J.; Androulakis J.; Malliakas C. D.; Li H.; Freeman A. J.; Kenney J. T.; Kanatzidis M. G. CsSnI3: Semiconductor or Metal? High Electrical Conductivity and Strong Near-Infrared Photoluminescence from a Single Material. High Hole Mobility and Phase-Transitions. J. Am. Chem. Soc. 2012, 134, 8579–8587. 10.1021/ja301539s. [DOI] [PubMed] [Google Scholar]
  18. Chen Z.; Wang J. J.; Ren Y.; Yu C.; Shum K. Schottky Solar Cells Based on CsSnI3 Thin-Films. Appl. Phys. Lett. 2012, 101, 093901. 10.1063/1.4748888. [DOI] [Google Scholar]
  19. Kumar M. H.; Dharani S.; Leong W. L.; Boix P. P.; Prabhakar R. R.; Baikie T.; Shi C.; Ding H.; Ramesh R.; Asta M.; Graetzel M.; Mhaisalkar S. G.; Mathews N. Lead-Free Halide Perovskite Solar Cells with High Photocurrents Realized Through Vacancy Modulation. Adv. Mater. 2014, 26, 7122–7127. 10.1002/adma.201401991. [DOI] [PubMed] [Google Scholar]
  20. Sabba D.; Mulmudi H. K.; Prabhakar R. R.; Krishnamoorthy T.; Baikie T.; Boix P. P.; Mhaisalkar S.; Mathews N. Impact of Anionic Br– Substitution on Open Circuit Voltage in Lead Free Perovskite (CsSnI3–xBrx) Solar Cells. J. Phys. Chem. C 2015, 119, 1763–1767. 10.1021/jp5126624. [DOI] [Google Scholar]
  21. Chung I.; Lee B.; He J.; Chang R. P. H.; Kanatzidis M. G. All-Solid-State Dye-Sensitized Solar Cells with High Efficiency. Nature 2012, 485, 486–489. 10.1038/nature11067. [DOI] [PubMed] [Google Scholar]
  22. Zhang J.; Yu C.; Wang L.; Li Y.; Ren Y.; Shum K. Energy Barrier at the N719-dye/CsSnI3 Interface for Photogenerated Holes in Dye-Sensitized Solar Cells. Sci. Rep. 2014, 4, 6954. 10.1038/srep06954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Gao P.; Grätzel M.; Nazeeruddin M. K. Organohalide Lead Perovskites for Photovoltaic Applications. Energy Environ. Sci. 2014, 7, 2448–2463. 10.1039/C4EE00942H. [DOI] [Google Scholar]
  24. Huang L.-y.; Lambrecht W. R. L. Lattice Dynamics in Perovskite Halides CsSnX3 with X = I, Br, Cl. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 195201. 10.1103/PhysRevB.90.195201. [DOI] [Google Scholar]
  25. da Silva E. L.; Skelton J. M.; Parker S. C.; Walsh A. Phase Stability and Transformations in the Halide Perovskite CsSnI3. Phys. Rev. B 2015, 91, 144107. 10.1103/PhysRevB.91.144107. [DOI] [Google Scholar]
  26. Yi C.; Luo J.; Meloni S.; Boziki A.; Ashari-Astani N.; Grätzel C.; Zakeeruddin S. M.; Röthlisberger U.; Grätzel M. Entropic Stabilization of Mixed A-Cation ABX3 Metal Halide Perovskites for High Performance Perovskite Solar Cells. Energy Environ. Sci. 2016, 9, 656–662. 10.1039/C5EE03255E. [DOI] [Google Scholar]
  27. Saliba M.; Matsui T.; Seo J.-Y.; Domanski K.; Correa-Baena J.-P.; Nazeeruddin M. K.; Zakeeruddin S. M.; Tress W.; Abate A.; Hagfeldt A.; Grätzel M. Cesium-Containing Triple Cation Perovskite Solar Cells: Improved Stability, Reproducibility and High Efficiency. Energy Environ. Sci. 2016, 9, 1989–1997. 10.1039/C5EE03874J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Syzgantseva O. A.; Saliba M.; Grätzel M.; Rothlisberger U. Stabilization of the Perovskite Phase of Formamidinium Lead Triiodide by Methylammonium, Cs, and/or Rb Doping. J. Phys. Chem. Lett. 2017, 8, 1191–1196. 10.1021/acs.jpclett.6b03014. [DOI] [PubMed] [Google Scholar]
  29. Amat A.; Mosconi E.; Ronca E.; Quarti C.; Umari P.; Nazeeruddin M. K.; Grätzel M.; De Angelis F. Cation-Induced Band-Gap Tuning in Organohalide Perovskites: Interplay of Spin-Orbit Coupling and Octahedra Tilting. Nano Lett. 2014, 14, 3608–3616. 10.1021/nl5012992. [DOI] [PubMed] [Google Scholar]
  30. Gou G.; Young J.; Liu X.; Rondinelli J. M. Interplay of Cation Ordering and Ferroelectricity in Perovskite Tin Iodides: Designing a Polar Halide Perovskite for Photovoltaic Applications. Inorg. Chem. 2017, 56, 26–32. 10.1021/acs.inorgchem.6b01701. [DOI] [PubMed] [Google Scholar]
  31. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  32. Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  33. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  34. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  35. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  36. Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 2003, 118, 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
  37. Heyd J.; Scuseria G. E.; Ernzerhof M. Erratum: “Hybrid Functionals Based on a Screened Coulomb Potential” [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 2006, 124, 219906. 10.1063/1.2204597. [DOI] [Google Scholar]
  38. Lang L.; Yang J.-H.; Liu H.-R.; Xiang H.; Gong X. First-Principles Study on the Electronic and Optical Properties of Cubic ABX3 Halide Perovskites. Phys. Lett. A 2014, 378, 290–293. 10.1016/j.physleta.2013.11.018. [DOI] [Google Scholar]
  39. Huang L.-y.; Lambrecht W. R. L. Electronic Band Structure, Phonons, and Exciton Binding Energies of Halide Perovskites CsSnCl3, CsSnBr3, and CsSnI3. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 165203. 10.1103/PhysRevB.88.165203. [DOI] [Google Scholar]
  40. Lang L.; Zhang Y.-Y.; Xu P.; Chen S.; Xiang H. J.; Gong X. G. Three-Step Approach for Computing Band Offsets and Its Application to Inorganic ABX3 Halide Perovskites. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 075102. 10.1103/PhysRevB.92.075102. [DOI] [Google Scholar]
  41. Scaife D. E.; Weller P. F.; Fisher W. G. Crystal Preparation and Properties of Cesium Tin (II) Trihalides. J. Solid State Chem. 1974, 9, 308–314. 10.1016/0022-4596(74)90088-7. [DOI] [Google Scholar]
  42. Yamada K.; Funabiki S.; Horimoto H.; Matsui T.; Okuda T.; Ichiba S. Structural Phase Transitions of the Polymorphs of CsSnI3 by Means of Rietveld Analysis of the X-Ray Diffraction. Chem. Lett. 1991, 20, 801–804. 10.1246/cl.1991.801. [DOI] [Google Scholar]
  43. Brivio F.; Caetano C.; Walsh A. Thermodynamic Origin of Photoinstability in the CH3NH3Pb(I1–xBrx)3 Hybrid Halide Perovskite Alloy. J. Phys. Chem. Lett. 2016, 7, 1083–1087. 10.1021/acs.jpclett.6b00226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Stampfl C. Surface Processes and Phase Transitions from Ab Initio Atomistic Thermodynamics and Statistical Mechanics. Catal. Today 2005, 105, 17–35. 10.1016/j.cattod.2005.04.015. [DOI] [Google Scholar]
  45. Soon A.; Todorova M.; Delley B.; Stampfl C. Thermodynamic Stability and Structure of Copper Oxide Surfaces: A First-Principles Investigation. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 125420. 10.1103/PhysRevB.75.125420. [DOI] [Google Scholar]
  46. Lee T.; Lee Y.; Jang W.; Soon A. Understanding the Advantage of Hexagonal WO3 as an Efficient Photoanode for Solar Water Splitting: A First-Principles Perspective. J. Mater. Chem. A 2016, 4, 11498–11506. 10.1039/C6TA03659G. [DOI] [Google Scholar]
  47. Heifets E.; Eglitis R. I.; Kotomin E. A.; Maier J.; Borstel G. Ab Initio Modeling of Surface Structure for SrTiO3 Perovskite Crystals. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 64, 235417. 10.1103/PhysRevB.64.235417. [DOI] [Google Scholar]
  48. Eglitis R. I. Ab Initio Hybrid DFT Calculations of BaTiO3, PbTiO3, SrZrO3 and PbZrO3 (111) Surfaces. Appl. Surf. Sci. 2015, 358, 556–562. 10.1016/j.apsusc.2015.08.010. [DOI] [Google Scholar]
  49. Grote C.; Berger R. F. Strain Tuning of Tin–Halide and Lead–Halide Perovskites: A First-Principles Atomic and Electronic Structure Study. J. Phys. Chem. C 2015, 119, 22832–22837. 10.1021/acs.jpcc.5b07446. [DOI] [Google Scholar]
  50. Goldschmidt V. M. Die Gesetze der Krystallochemie. Naturwissenschaften 1926, 14, 477–485. 10.1007/BF01507527. [DOI] [Google Scholar]
  51. Liu X.; Hong R.; Tian C. Tolerance Factor and the Stability Discussion of ABO3-Type Ilmenite. J. Mater. Sci.: Mater. Electron. 2009, 20, 323–327. 10.1007/s10854-008-9728-8. [DOI] [Google Scholar]
  52. Shannon R. D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1976, 32, 751–767. 10.1107/S0567739476001551. [DOI] [Google Scholar]
  53. Sher A.; van Schilfgaarde M.; Chen A.-B.; Chen W. Quasichemical Approximation in Binary Alloys. Phys. Rev. B: Condens. Matter Mater. Phys. 1987, 36, 4279–4295. 10.1103/PhysRevB.36.4279. [DOI] [PubMed] [Google Scholar]
  54. Xiao Z.; Lei H.; Zhang X.; Zhou Y.; Hosono H.; Kamiya T. Ligand-Hole in [SnI6] Unit and Origin of Band Gap in Photovoltaic Perovskite Variant Cs2SnI6. Bull. Chem. Soc. Jpn. 2015, 88, 1250–1255. 10.1246/bcsj.20150110. [DOI] [Google Scholar]
  55. Even J.; Pedesseau L.; Katan C.; Kepenekian M.; Lauret J.-S.; Sapori D.; Deleporte E. Solid-State Physics Perspective on Hybrid Perovskite Semiconductors. J. Phys. Chem. C 2015, 119, 10161–10177. 10.1021/acs.jpcc.5b00695. [DOI] [Google Scholar]
  56. Walsh A. Principles of Chemical Bonding and Band Gap Engineering in Hybrid Organic-Inorganic Halide Perovskites. J. Phys. Chem. C 2015, 119, 5755–5760. 10.1021/jp512420b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Filip M. R.; Eperon G. E.; Snaith H. J.; Giustino F. Steric Engineering of Metal-Halide Perovskites with Tunable Optical Band Gaps. Nat. Commun. 2014, 5, 5757. 10.1038/ncomms6757. [DOI] [PubMed] [Google Scholar]
  58. Haruyama J.; Sodeyama K.; Han L.; Tateyama Y. Termination Dependence of Tetragonal CH3NH3PbI3 Surfaces for Perovskite Solar Cells. J. Phys. Chem. Lett. 2014, 5, 2903–2909. 10.1021/jz501510v. [DOI] [PubMed] [Google Scholar]
  59. Haruyama J.; Sodeyama K.; Han L.; Tateyama Y. Surface Properties of CH3NH3PbI3 for Perovskite Solar Cells. Acc. Chem. Res. 2016, 49, 554–561. 10.1021/acs.accounts.5b00452. [DOI] [PubMed] [Google Scholar]
  60. Kwak J.; Kim C.-E.; Min Y.; Lee J.-H.; Soon A.; Jeong U. The Effect of Se Doping on the Growth of Te Nanorods. CrystEngComm 2015, 17, 5734–5734. 10.1039/C4CE02431A. [DOI] [Google Scholar]
  61. Yang R. X.; Butler K. T.; Walsh A. Assessment of Hybrid Organic–Inorganic Antimony Sulfides for Earth-Abundant Photovoltaic Applications. J. Phys. Chem. Lett. 2015, 6, 5009–5014. 10.1021/acs.jpclett.5b02555. [DOI] [PubMed] [Google Scholar]
  62. Xu P.; Chen S.; Xiang H.-J.; Wei S.-H.; Gong X.-G. Influence ofDefects and Synthesis Conditions on the Photovoltaic Performance of Perovskite Semiconductor CsSnI3. Chem. Mater. 2014, 26, 6068–6072. 10.1021/cm503122j. [DOI] [Google Scholar]
  63. Patrick C. E.; Jacobsen K. W.; Thygesen K. S. Anharmonic Stabilization and Band Gap Renormalization in the Perovskite CsSnI3. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 201205. 10.1103/PhysRevB.92.201205. [DOI] [Google Scholar]
  64. Weber O.; Charles B.; Weller M. Phase Behaviour and Composition in the Formamidinium-Methylammonium Hybrid Lead Iodide Perovskite Solid Solution. J. Mater. Chem. A 2016, 4, 15375–15382. 10.1039/C6TA06607K. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cm7b00260_si_001.pdf (10.3MB, pdf)

Articles from Chemistry of Materials are provided here courtesy of American Chemical Society

RESOURCES