Events per variable (EPV) and the relative performance of different strategies for estimating the out-of-sample validity of logistic regression models

Abstract

We conducted an extensive set of empirical analyses to examine the effect of the number of events per variable (EPV) on the relative performance of three different methods for assessing the predictive accuracy of a logistic regression model: apparent performance in the analysis sample, split-sample validation, and optimism correction using bootstrap methods. Using a single dataset of patients hospitalized with heart failure, we compared the estimates of discriminatory performance from these methods to those for a very large independent validation sample arising from the same population. As anticipated, the apparent performance was optimistically biased, with the degree of optimism diminishing as the number of events per variable increased. Differences between the bootstrap-corrected approach and the use of an independent validation sample were minimal once the number of events per variable was at least 20. Split-sample assessment resulted in too pessimistic and highly uncertain estimates of model performance. Apparent performance estimates had lower mean squared error compared to split-sample estimates, but the lowest mean squared error was obtained by bootstrap-corrected optimism estimates. For bias, variance, and mean squared error of the performance estimates, the penalty incurred by using split-sample validation was equivalent to reducing the sample size by a proportion equivalent to the proportion of the sample that was withheld for model validation. In conclusion, split-sample validation is inefficient and apparent performance is too optimistic for internal validation of regression-based prediction models. Modern validation methods, such as bootstrap-based optimism correction, are preferable. While these findings may be unsurprising to many statisticians, the results of the current study reinforce what should be considered good statistical practice in the development and validation of clinical prediction models.

1 Introduction

Predicting the occurrence of an adverse event or outcome is important in clinical, population health, and health services research. Clinical prediction models allow clinicians to assess patient prognosis quantitatively and permit effective risk stratification of patients.

An important issue in developing a clinical prediction model is assessing how well it performs in subjects who are similar to those used for model development.¹ Throughout this paper, we use the term ‘out-of-sample’ performance to denote the performance of the model in subjects who were not used in model development, but who are similar to those used for developing the model. A simple approach to validation is to assess the model’s apparent performance in the sample in which it was derived. However, this usually results in optimistic estimates of performance, since the model is optimized for performance in the sample in which it was derived. A commonly used approach is to split randomly the sample into derivation and validation samples.^2–4 The model is developed on the derivation sample and its performance is subsequently evaluated on the validation sample. An alternative approach that has been advocated by different authors is to use bootstrap-based methods for assessing model performance.^5,6 While bootstrap-based methods for validating the performance of prediction models have been shown to have desirable properties,⁷ many clinical investigators may favour split-sample approaches, arguing that this approach has greater transparency and face validity.

A key concept in the development of prediction models for binary outcomes is the number of events per variable (EPV).⁸ When outcomes are binary, the number of events is the smaller of the number of subjects who experienced the outcome and the number of subjects who did not experience the outcome. The number of EPV is the number of events divided by the number of predictor variables considered in developing the prediction model; strictly speaking, it is the number of events divided by the number of degrees of freedom required to represent all of the variables in the model. Thus, a three-level categorical variable would require two degrees of freedom. Similarly, if a continuous variable was modelled using linear and quadratic terms then two degrees of freedom would be required. Peduzzi et al. demonstrated that roughly 10 EPVs were required for accurate estimation of regression coefficients in a logistic regression model.⁸ In the related field of discriminant analysis, Lachenbruch and Goldstein suggest that it is sufficient to have three subjects in each group for each parameter that is being estimated⁹ (p. 70). However, this required number of subjects may increase or decrease depending on how separated the two groups are.

The objective of the study was to compare the effect of the number of EPV when developing a clinical prediction model on the relative performance of three methods for assessing the out-of-sample accuracy of a prediction model: (i) the apparent performance in the sample in which it was derived, (ii) split-sample derivation and validation, and (iii) bootstrap-based methods to correct the optimism of the apparent performance of the model in the sample in which it was derived. Obviously, differences between the methods would diminish as the number of EPV in the analytic sample increased and stability would improve when the test sample was fairly large. We were specifically interested in determining the value of the number of EPV at which differences between the methods were negligible and in examining the relative efficiency of split-sample methods compared to competing approaches such as bootstrap-based methods for optimism correction.

The paper is structured as follows. In Section 2, we describe different methods for assessing the predictive accuracy of a clinical prediction model. In Section 3, we conduct an extensive series of analyses to examine the effect of the number of EPV on the relative performance of these different methods. Our analyses are based on examining a logistic regression model for predicting mortality within 1 year of hospitalization for heart failure using a single clinical dataset. The performance of each method was compared with that of the out-of-sample prediction of the model, when a very large independent test sample other than the analytic sample was used for model validation. In Section 4, we report the results of our analyses. In Section 5, we summarize our findings and place them in the context of the existing literature.

2 Measuring the predictive accuracy of a logistic regression model

2.1 The c-statistic

When outcomes are binary, the c-statistic is the probability that a randomly selected subject who experienced the outcome has a higher predicted probability of experiencing the outcome than a randomly selected subject who did not experience the outcome. It can be calculated by taking all possible pairs of subjects consisting of one subject who experienced the outcome of interest and one subject who did not experience the outcome. The c-statistic is the proportion of such pairs in which the subject who experienced the outcome had a higher predicted probability of experiencing the event than the subject who did not experience the outcome (i.e. out of all possible pairs in which one subject experiences the outcome and one subject does not experience the outcome, it is the proportion of pairs that are concordant).^5,6 The c-statistic is equivalent to the area under the receiver operating characteristic curve and is a central measure of performance in many studies on predicting binary outcomes.

2.2 Methods for estimating out-of-sample performance

We considered three different methods for assessing the out-of-sample performance of a prediction model. These methods each provide estimates of how well the model would predict outcomes in an independent sample that originates from the same underlying population.

2.2.1 Apparent performance

A simple approach is to assess model performance directly in the sample in which it was developed. Using the fitted regression model, the predicted probability of the outcome is determined for each subject in the analytic sample. A summary measure of model performance, such as the c-statistic, is then reported. A limitation of this approach is that the model is optimized for performance in the sample in which it was developed. Subsequent predictions in subjects who were not used in model development are likely to have poorer accuracy than that which was reported in the analytic sample. Apparent performance estimates are hence optimistic. The magnitude of optimism is expected to decrease as the effective sample size of the model derivation sample increases.

2.2.2 Split-sample assessment of performance

Using the split-sample approach, the sample is divided into two parts: a derivation sample and a validation sample. Frequently, these two sub-samples are of the same size² (p. 420), although using two-thirds of the data for model derivation and one-third for model validation has also been used. The prediction model is estimated in the derivation sample. The estimated model is then applied to make predictions for subjects in the validation sample. The predictive accuracy of the model is estimated based on these predictions for the subjects in the validation sample. This estimate of predictive accuracy in the validation sample is used as an estimate of out-of-sample performance.

2.2.3 Bootstrap methods for optimism-corrected performance

A criticism of split-sample methods for estimating out-of-sample performance is that it is relatively inefficient due to its reduction of the size of both the sample used for model development and for model validation.⁷ Furthermore, variability in the estimated performance can be induced through the reliance on a single split of the sample in derivation and validation components. A popular method for correcting the inherent optimism in estimates of model performance obtained on the same sample used to develop the model is based on the bootstrap.^1,5,6,10 To do so, one develops a prediction model in the analytic sample (the original sample). One then assesses the apparent performance of the estimated model in the analysis sample in which it was derived. As above, this is denoted as the apparent performance. One then draws a bootstrap sample with replacement from the original analysis sample and develops a prediction model in this bootstrap sample. Care should be given to perform all the steps that were taken to develop the original prediction model, such as selection of predictors and estimation of regression coefficients. We record the performance of this model (the bootstrap model) on the bootstrap sample in which it was developed (i.e. the apparent performance of the bootstrap model in the bootstrap sample). We then apply the bootstrap model to the analytic sample to obtain an estimate of its out-of-sample performance. The optimism is defined as the difference between the bootstrap performance (apparent performance of the bootstrap model) and its out-of-sample performance. This bootstrap process is then repeated at least 100 times. Model optimism is then averaged across all the bootstrap iterations. As a final step, one then subtracts the optimism estimate from the apparent performance to obtain the optimism-corrected performance estimate.

3 Methods

We used a series of empirical analyses to examine the effect of the number of EPV on the relative performance of different methods for assessing the out-of-sample predictive accuracy of a logistic regression model. In this section, we describe the data that were used for these analyses, the clinical prediction model, and the statistical analyses.

3.1 Data source

The Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study was a study designed to improve the quality of care provided to patients with cardiovascular disease in Ontario, Canada.¹¹ During the study, detailed clinical data on patients hospitalized with congestive heart failure between 1 April 1999 and 31 March 2001 (Phase 1) and between 1 April 2004 and 31 March 2005 (Phase 2) at 103 hospitals in Ontario, Canada were obtained by retrospective chart review. Data on patient demographics, vital signs and physical examination at presentation, medical history, and results of laboratory tests were collected. The EFFECT-HF sample consisted of 18,284 patients. Of these, 255 patients on dialysis were excluded, since the clinical prediction model under consideration was not intended for use on these patients. Of the remaining 18,029 patients, an additional 1792 patients with missing data on baseline covariates that were necessary to estimate the clinical prediction model were excluded. This left a total of 16,237 patients for analysis (8521 patients in Phase 1 and 7716 patients in Phase 2). Within 1 year of hospital admission, 5181 (31.9%) patients died. The exclusion of patients with missing data was done for pragmatic reasons. This exclusion was unlikely to have an impact on our conclusions as we used random samples from the overall analytic sample to estimate and validate prediction models. In applied clinical research studies, investigators may want to consider more sophisticated statistical approaches, such as multiple imputation, when addressing the issue of missing data. In applying an existing clinical prediction model to patients who are missing data on some of the necessary predictor variables, the user should consider using available methods for imputing these missing predictor variables.

3.2 Clinical prediction model

We examined the performance of the EFFECT-HF mortality prediction model, which uses 11 variables to predict the probability of 1-year mortality.¹² The prediction model includes four continuous variables: age, respiratory rate, systolic blood pressure, and urea nitrogen and seven dichotomous variables: sodium concentration <136 mEq/l, haemoglobin <10.0 g/dl, cerebrovascular disease, dementia, chronic obstructive pulmonary disease, hepatic cirrhosis, and cancer. The four continuous covariates were all modelled as linear, continuous covariates. Prior studies that found that the use of flexible methods to model non-linear relationships between continuous covariates and the log-odds of the outcome resulted in very minor improvements in model accuracy for predicting mortality in cardiovascular patients.^13,14 In the data used for the current analyses, only 120 (0.74%) patients had hepatic cirrhosis. In some of the analyses, this resulted in analytic samples in which no patients had hepatic cirrhosis. For this reason, we excluded hepatic cirrhosis as a covariate from the prediction model (the exclusion of such a variable with a very low prevalence is discussed in Section 5). Thus, the prediction model had 10 predictor variables. The distribution of each of the 10 predictor variables is summarized in Table 1, along with the adjusted odds ratio for death within 1 year of hospitalization.

Table 1.

Distribution of risk factors in the clinical prediction model and odds ratios for 1-year mortality.

Variable	Distribution (median/ (1st, 25th, 75th, and 99th percentiles) or %)a	Odds ratio for 1-year mortality (95% confidence interval)
Age	78 (44, 70, 84, 97)	1.041 (1.037–1.045)
Respiratory rate (breaths per minute)	24 (20, 20, 28, 45)	1.025 (1.019–1.031)
Systolic blood pressure (beats per minute)	145 (90, 124, 169, 200)	0.987 (0.985–0.988)
Urea nitrogen	8.4 (2.9, 6.1, 12.2, 20.0)	1.104 (1.096–1.113)
Sodium concentration <136 mEq/l	21.3%	1.365 (1.253–1.487)
Haemoglobin <10.0 g/dl	12.7%	1.196 (1.076–1.329)
Cerebrovascular disease	17.4%	1.323 (1.207–1.450)
Dementia	9.0%	2.132 (1.892–2.402)
Chronic obstructive pulmonary disease	25.0%	1.297 (1.194–1.408)
Cancer	11.6%	1.663 (1.495–1.849)

^aContinuous variables are reported as medians (1st, 25th, 75th, and 99th percentiles). Dichotomous variables are reported as the percentage of subjects with the condition.

3.3 Statistical analyses

We conducted a series of analyses to compare the effect of the number of EPV in the study sample on the agreement between the true out-of-sample performance of the model with estimates obtained using different methods to estimate out-of-sample performance.

We allowed the empirical or observed number of EPV in the analysis sample to range from 5 to 100 in increments of 5. In the EFFECT-HF sample described earlier, there were 16,237 subjects and the 1-year mortality rate was 31.9%. The EFFECT-HF mortality prediction model contains 10 variables. For a given number of EPV, we would require 10 × EPV events in the analysis sample. Given the observed 1-year event rate of 0.319, an analysis sample of size 10 × EPV/0.319 would be expected to have the required number of EPV. We then drew a random sample of size 10 × EPV/0.319 from the EFFECT-HF sample. We refer to this random sample as the analysis sample. We calculated the observed number of EPV in the randomly selected sample. If, when rounded to the nearest integer, it was equal to the desired number of EPV, the random selected sample was retained, otherwise it was discarded and random samples were drawn until one with the desired observed number of EPV was drawn. The remainder of the EFFECT-HF (those subjects not included in the analysis sample) was used for model validation. Performance in the validation sample of a model estimated in the analysis sample was used as the estimate of the true out-of-sample performance of the regression model. Since the number of EPV ranged from 5 to 100, the size of the analysis samples ranged from 157 to 3135, while the size of the independent validation sample ranged from 16,080 to 13,101. The decision to use the remainder of the EFFECT-HF sample as the validation sample (regardless of its sample size in a given EPV scenario) was made for reasons of accuracy and precision. This allowed for the estimation of the out-of-sample performance with the greatest accuracy and precision.

Once a given analysis sample and validation sample were selected, the following statistical analyses were conducted:

1. The EFFECT-HF mortality prediction model was estimated in the entire analysis sample. The c-statistic of the model was estimated. This is the apparent performance of the model in the sample in which it was derived.

2. Split-sample validation was used to assess model performance. The analysis sample was randomly split into two equally sized components: a derivation sample and a validation sample. The coefficients for the EFFECT-HF model were estimated in the derivation sample. These coefficients were then applied to the validation sample and predicted probabilities of the occurrence of the outcome were determined for each subject. The c-statistic of the estimated model was computed using the estimated probabilities in the validation sample.

3. The coefficients of the EFFECT-HF model were estimated in the entire analysis sample and the apparent performance of the model was estimated using the c-statistic (as in the first analysis described earlier). Bootstrap methods were then used to derive an optimism-corrected measure of model performance. One hundred bootstrap iterations were used to compute the optimism-corrected measure of performance. As a sensitivity analysis, we performed analyses with 500 bootstrap iterations for EPV 5, 10, 15, and 20.

4. The predicted probability of 1-year mortality was estimated for each subject in the independent validation data using the regression model estimated in the entire analysis sample (the model estimated in the first analysis described earlier). This estimate served as the true out-of-sample performance estimate.

For a given value of the number of EPV (5–100 in increments of 5), the above analyses were repeated 1000 times (i.e. for each number of EPV, we drew sequential random samples until 1000 were obtained with the desired number of EPV). For each value of the observed number of EPV, we summarized the analyses as follows. First, we computed the mean c-statistic obtained using each of the four analyses described earlier across all iterations with the observed number of EPV, with the standard deviation used to describe variability. Second, we computed the mean squared error (MSE) of the c-statistic estimated using each of the three methods described earlier. For a given value of the number of EPV, we used the estimate of the c-statistic determined in (4) earlier (when averaged across the 1000 iterations of the analysis) as the true value of the c-statistic when applied to an independent validation sample. The MSE of the estimated c-statistics was then determined as $\frac{1}{1,000}\sum _{i=1}^{1,000}(c_i-c_{\mathrm{true}})2$, where c_i denotes the estimated c-statistic in the ith iteration of the analysis.

4 Results

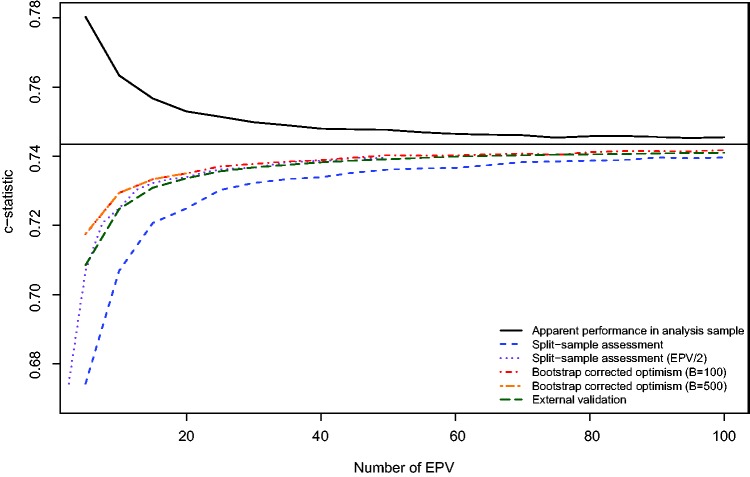
The relation between the number of EPV and the mean estimated c-statistic for each of the three analytic methods is described in Figure 1. We superimposed an additional line representing the mean c-statistic of the model estimated in the full analytic sample when applied to the independent validation sample as a reference to which each of the other methods can be compared. Furthermore, the horizontal line denotes the apparent performance of the prediction model when estimated in the entire EFFECT-HF sample. In examining this figure, several observations warrant comment. The use of the apparent performance of the prediction model in the analysis sample resulted in an overly optimistic estimate of the predictive accuracy of the estimated model, as was theoretically expected. Even when the number of EPV was very large, this method resulted in estimates of performance that were modestly optimistic compared to estimates derived from the other approaches. For instance, when the number of EPV was 100, the mean c-statistic from the apparent performance of the model in the analysis sample was 0.746, whereas the mean out-of-sample estimate of the c-statistic was 0.741. When the number of EPV was 10, the mean apparent performance was 0.763, while the mean out-of-sample estimate of performance was 0.725. In contrast, split-sample assessment of performance resulted in estimates of performance that were overly pessimistic. The magnitude of pessimism was substantial when the number of EPV was less than or equal to 20 (compared with external validation, the pessimism ranged from 0.034 for EVP = 5 to 0.009 for EPV = 20). Furthermore, the use of bootstrap-corrected estimates of performance and an external validation sample tended to result in essentially indistinguishable estimates of performance when the number of EPV was equal to or greater than 20. When the number of EPV was less than 20, then the use of bootstrap correction resulted in estimates of performance that were modestly greater than those obtained using an independent validation sample. Since the horizontal line denotes the apparent performance of the prediction model in the full EFFECT-HF sample (N = 16,237 and 5181 deaths) (c-statistic = 0.743), it is also the asymptote to which all methods appear to be converging as the number of EPV increases. Because of the large sample size and favourable EPV value, it is reasonable to take this number as the true performance of the model. Under this assumption, it appears that when the number of EPV is less than 20, then bootstrap-corrected measures of performance are closest to those obtained using an independent validation sample. When the number of EPV was less than or equal to 20, the use of 500 bootstrap samples yielded essentially identical results to when 100 bootstrap samples were used.

Figure 1.

Mean estimated c−statistic for different validation methods.

In order to examine further the penalty incurred by using split-sample validation, we superimposed a line on Figure 1 of the estimated c-statistic obtained using split-sample validation against the number of EPV divided by two (i.e. by using the expected number of EPV in the derivation sample). This shifts the original curve for the results from split-sample validation to the left. Thus, the range of this curve is from 2.5 to 50 EPV. This line is very similar to the two curves obtained using bootstrap correction and the independent validation sample. Thus, the bias in estimating the c-statistic using split-sample methods with an analysis sample of a given size is approximately equal to the observed bias when using bootstrap correction with a sample of half that size. In other words, the penalty incurred by using split-sample validation is that one halves the sample size in the analysis sample.

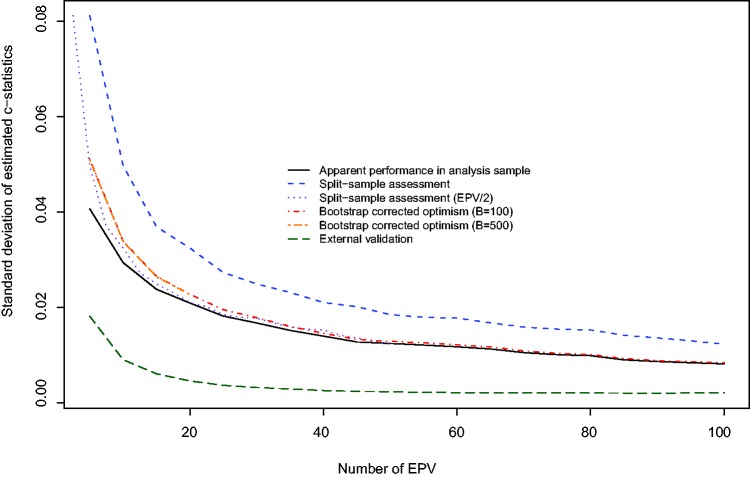
From Figure 2 we note that the use of an external validation sample resulted in the lowest variability in the estimated c-statistic across the 1000 iterations of the analyses. This assessment merely reflects uncertainty of the developed models, rather than uncertainty in the validation data sets, which were of large size. Conversely, split-sample assessment resulted in the greatest variability in estimating performance. When the number of EPV was less than 40, then the use of the apparent performance in the analysis sample displayed modestly less variability than displayed by the estimates produced using bootstrap correction. As above, we superimposed on Figure 2 a plot of the standard deviation of the estimated c-statistic obtained using split-sample validation against the number of EPV divided by two. Again, we note that the lines for split-sample methods agree with the line for bootstrap correction with a sample of half that size.

Figure 2.

Standard deviation of estimated c−statistic for different validation methods.

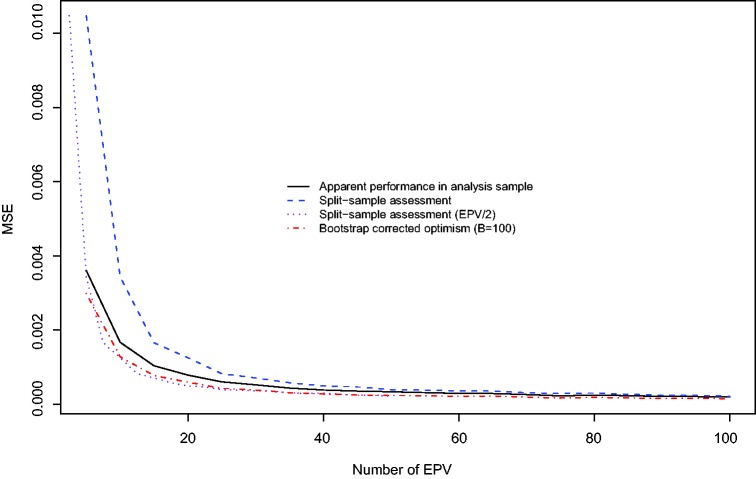
The relation between the number of EPV and the MSE of the three different methods for estimating the performance of the prediction model is described in Figure 3. Split-sample assessment resulted in estimates of performance with the highest MSE, while bootstrap-corrected optimism resulted in estimates with the lowest MSE. Interestingly, the use of the apparent performance in the analysis sample resulted in estimates with lower MSE than did the use of split-sample assessment.

Figure 3.

Mean squared error (MSE) of different estimation methods.

5 Discussion

We conducted an extensive set of empirical analyses to examine the effect of the number of EPV on the relative performance of three different methods for assessing the predictive accuracy of a logistic regression model. We confirmed that the use of apparent performance resulted in an optimistic assessment of model performance, with a bias over 0.005 in c statistic until EPV = 100. A bootstrap-corrected approach had the lowest MSE. The use of split-sample assessment resulted in too pessimistic an assessment of model performance. Furthermore, the use of split-sample assessment resulted in the greatest variability in assessing the performance of the prediction model. Remarkably, the use of the apparent performance resulted in estimates with lower MSE compared to the use of split-sample estimation. For bias, variance and MSE of the estimated c-statistic, the penalty incurred by using split-sample validation in the analysis sample was approximately equal to reducing the observed number of EPV by a proportion equivalent to the proportion of the sample that was withheld for model validation.

There are important implications of our results for clinical investigators developing and validating clinical prediction models. First, our perception is that many clinical investigators prefer to use a split-sample method to assess the performance of the derived model. While clinical investigators may favour split-sample assessment on clinical grounds, our results suggest that the use of split-sample assessment should be discouraged on statistical grounds. The split-sample approach results in far too pessimistic and unstable estimates of performance, while we can readily use modern methods such as the bootstrap to correct for the optimism in apparent performance estimates. The penalty of substantially reducing the effective sample size likely outweighs arguments such as greater transparency and face validity. Second, clinical investigators frequently do not have the luxury of having a second, independent, sample arising from the same population for use as an external validation sample. Our results, based on empirical analyses conducted in a single dataset, demonstrate that once the number of EPV is at least 20 in the analytic sample, then bootstrap-corrected assessment of performance will likely coincide with the assessment of performance if an independent sample from the same population were available. Even when the number of EPV is less than this number, the differences between the two approaches tended to be minimal (e.g. difference in mean c-statistic was approximately 0.004 when the number of EPV was equal to 10). The primary advantage to the use of an independent validation sample from the same population is the decreased variability in the estimated performance of the derived model.

The findings of the current study are in line with those from an earlier study comparing different methods of assessing model performance.⁷ However, there are several important reasons for retaining a focus on the same issue: first, in the 13 years since the publication of the earlier study, split-sample validation continues to be a popular and frequently implemented approach. Thus, it is important to explore further and highlight its limitations. Second, one of our secondary objectives was to examine the number of EPV at which the use of the bootstrap for optimism correction had a similar performance to true out-of-sample validation. Third, in the current study, we determined the approximate penalty in the number of EPV that was incurred by using split-sample validation compared to using bootstrap-corrected optimism.

Berk suggested that the best way to validate the predictive accuracy of a model is to apply it to new data.¹⁵ Snee agreed that application of the derived model to new data is the preferred approach to model validation.² However, he suggests that this is often impractical or is not feasible. As an alternative, he suggested that a reasonable approach would be to use split-sample validation. Furthermore, Snee suggests that using half the data for model development and half the data for model validation appears to be the most popular method (p. 420). In the context of ordinary least squares regression, Picard and Berk provide guidelines for the proportion of the available data that should be used for model development, with the remainder being reserved for model validation.⁴ They suggested that the neglect of the use split-sample validation was due to a ‘wide-spread (and often mistaken) notion that data splitting is grossly inefficient for both prediction and validation’ (p. 140). Our findings show that split-sample validation is quite inefficient compared to bootstrap-corrected assessment of performance. Furthermore, split-sample validation even had greater MSE compared to the MSE of the naïve apparent performance of the model in the sample in which it was developed. Picard and Berk do characterize an important limitation of bootstrap-based methods for assessing performance (p. 143). They suggest that it may be difficult to automate specific steps in model development that involved subjective human judgment or decisions (e.g. decisions about applying range constraints to certain variables based on graphical displays or about whether to employ a non-linear or linear relationship between a given continuous covariate and the outcome). Indeed, we considered a pre-specified 10 predictor model, while models may be often selected based on findings in the analytical sample. Various methods may be used. Some, such as stepwise selection, can readily be included in bootstrap procedures, while others may be more difficult to repeat systematically, such as graphical inspections of data for outliers or non-linearities.

There are certain other limitations to the current study. First, in our simulations, we did not consider all possible methods for estimating the out-of-sample performance of a prediction model. Our focus was on comparing the performance of split-sample validation with that of methods based on bootstrap correction. Our comparisons were motivated by the observation that split-sample validation is frequently used in the biomedical literature and that bootstrap correction has been proposed as a promising alternative.¹ Two recently discussed methods are the ‘leave-one-out’ and ‘leave-pair-out’ methods described by Airola et al.¹⁶ (the leave-one-out approach dates back to at least 1968, when it was examined by Lachenbruch and Mickey in the context of discriminant analysis¹⁷). Given the number of sub-samples in which the candidate model must be fit, it was not feasible to examine the performance of these two approaches using the sample sizes that were used in the current study. In a recent study, Smith et al. used a set of empirical analyses in two datasets to compare the performance of different methods for optimism correction when the number of EPV was equal to 5 (i.e. when the number of EPV was very low).¹⁸ They found that the ‘leave-one-out’ approach resulted in estimates of the c-statistics that were systematically lower than the true c-statistic. Both bootstrap correction, ‘leave-pair-out’, and 10-fold cross-validation (both with and without replication) resulted in estimated c-statistics that did not differ significantly from the true value. A second limitation was our exclusion of the variable denoting hepatic cirrhosis from the clinical prediction model. This was done due to the low prevalence of patients with this condition, which resulted in some of the derivation samples having no patients with this condition. An alternative approach would be to use stratified sampling for model development and a stratified bootstrap for validation, with strata formed by the infrequent covariate. However, the behaviour of such a procedure requires further study prior to its widespread implementation. A different approach would be to use methods from the data mining and machine learning literature, such as regression trees, random forests, or boosted regression trees,^19–22 which do not require that the variable display variability in all samples. Regardless of the method used, we would note that, in general, rare characteristics are of interest only if they have a strong effect.^23,24 A third limitation was our focus on the c-statistic for assessing model performance. Other measures of model performance such as the generalized $R_N^2$ index and the Brier Score have been proposed for evaluating the performance of logistic regression models.⁵ In the current study, we have focused on the c-statistic due to its popularity for quantifying the performance of clinical prediction models. A fourth limitation was that our study was based on empirical analyses conducted in a single dataset. As such, our methods warrant replication in different settings to confirm the generalizability of our findings.

Validation of the performance of clinical prediction models is an important component to assess alongside their development. Validation of such models allows investigators and clinicians to understand the accuracy of these models in patients who were not used in model development. Patients may be rather similar to those in whom the model was developed (internal validation), or differ in aspects such as time and place of treatment, allowing us to study generalizability (external validation).¹ Split-sample validation is a popular method in the clinical literature for model validation, but does not deserve such popularity. The penalty incurred by split-sample validation is approximately equal to a reduction of the sample size by a proportion equivalent to the proportion of the sample that was withheld for model validation. We encourage the use of modern validation procedures, such as bootstrap optimism correction in studies of model development.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) received no financial support for the research, authorship, and/or publication of this article.